Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Dec 22;6(1):448–455. doi: 10.1021/acsomega.0c04881

Key Factor Analysis and Model Establishment of Blasting Dust Diffusion in a Deep, Sunken Open-Pit Mine

Yuan Wang †,‡, Cuifeng Du †,‡,*, Haiyue Xu †,‡
PMCID: PMC7807780  PMID: 33458496

Abstract

graphic file with name ao0c04881_0008.jpg

Blasting dust is the main source of atmospheric pollution in deep, sunken open-pit mines (DSOMs), which affects seriously the normal work and production in the mines. Here, the influencing factors and a diffusion model with regard to blasting dust diffusion were investigated and proposed in a representative mine. Dimensional analysis and multiple nonlinear regression analysis were applied to establish a mathematical model of the blasting dust diffusion. A high multiple correlation coefficient of 91.4% was obtained, indicating a highly reliable model. This study provides a theoretical basis for rationally arranging production and avoiding air pollution in the DSOMs.

1. Introduction

Dust pollution in deep, sunken open-pit mines (DSOMs) is one of the main factors affecting the normal work and production in the mines.1−3 Blasting, which generally requires a large amount of explosives, is the main source of atmospheric pollution in DSOMs, which results in vast and also tremendous dust dispersion degrees.4−6 The dust together with other toxic and harmful gases generated at the moment of blasting is easily stagnated at the bottom of the mines due to the complex circulation structure, affecting seriously the working environment and normal production. If these pollutants flow with the wind, they will further aggravate the regional environment nearby, destroy the ecology, and endanger the health of residents.7−9 Therefore, it is urgent to carry out relevant research on the basic diffusion law of blasting dust in DSOMs.

The diffusion law of blasting dust in DSOMs was studied qualitatively. For example, Zhao studied the movement of dust and established partial conditions of dust particles moving with the wind current.10 Hodkinson conducted a study on the movement and diffusion law of dust particles of different sizes in the wind flow and obtained dust concentrations decreasing with the increase of wind speed.11 Zhang inversely calculated the emission load of blasting dust by measuring the dust concentration in the air and the amount of dust deposition on the ground.12 Yang concluded that the bottom of the DSOM was a weak-wind area and the dust was not easily dissipated unless artificial assistance was applied.13 Zhang et al. used the box model cloud diffusion theory to discuss the applicability of the blasting cloud model.14 Ge et al. found that the settlement of dust particles of different sizes depended closely on gravity.15 The existence of complex circulation in DSOMs was also discovered to affect the diffusion of blasting dust.16−21 The methods of field measurement, numerical simulation, and theoretical analysis were used in our previous work to study the complex circulation structure and its influencing factors in the DSOM. With the increase of incoming wind speed, the center position of the complex circulation in the open-pit mine was found to be raised, and the center width and thickness were also increased. The complex circulation structure was discovered to be present in both vertical and horizontal directions, whose central axis revealed an inverted U-shaped structure.

Most of the above studies on the diffusion of blasting dust in DSOMs were qualitative analysis, while related quantitative analysis is still lacking. In this paper, a field experiment and numerical simulation were used to study the blasting dust diffusion of the DSOM under the influence of different factors through orthogonal experiments. Dimensional analysis and multiple nonlinear regression analysis were used to establish the DSOM blasting dust. The mathematical model of diffusion provides a theoretical basis for improving the economic efficiency of mines to ensuring the health of employees, establishing corresponding methods of avoiding air pollution in the mines.

2. Results and Discussion

The overview of the experimental mine and four measuring points are shown in Figure 1a. The wind speed and direction of different height layers in the stope were measured by a method of bundling the anemometer with a sounding balloon, as shown in Figure 1b.

Figure 1.

Figure 1

Open in a new tab

(a) Vertical overhead view denoting the measuring point distribution. (b) Photograph showing the test system for wind speed and direction at different heights.

2.1. Numerical Simulation and Its Reliability Analysis

2.1.1. Numerical Simulation Results

The factor level table is shown in Table 1. The mining depth of the open-pit mine is an important factor affecting the ventilation of the DSOM. A relative depth ρ can be used to determine the degree of difficulty of natural ventilation,22 which is expressed as

2.1.1.

where H is the actual mining depth, L is the average plane size of the closed circle, L1 is the length of the closed circle, L2 is the width of the closed circle. It is generally believed that ρ < 0.1, ρ = 0.1–0.2, and ρ > 0.2 indicate that the natural ventilation conditions are good, mildly difficult, and difficult, respectively, and the relative depth of each model pit in the orthogonal experiment and the degree of difficulty of natural ventilation were calculated, as shown in Table 2.

Table 1. Factor Level Table.
  factor
level wind speed (m/s) wind direction (°) depth of the pit (m) length of the long axis (m) slope angle of the long axis (°)
1 2 0 300 1400 40
2 3 30 400 2000 44
3 4 60 500 2600 47
4 5 90 600 3200 50
Open in a new tab
Table 2. Relative Depth and Degree of Difficulty of Natural Ventilation of Each Model Pit in the Orthogonal Experiment.
model number depth of the pit H characteristic length of pit entrance 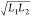Inline graphic relative depth ρ degree of difficulty of natural ventilation
11,111 300 1400 0.21 difficult
12,222 400 1673 0.24 difficult
13,333 500 1908 0.26 difficult
14,444 600 2117 0.28 difficult
21,234 400 1908 0.21 difficult
22,143 300 2117 0.14 mildly difficult
23,412 600 1400 0.43 difficult
24,321 500 1673 0.30 difficult
31,342 500 2117 0.24 difficult
32,431 600 1908 0.31 difficult
33,124 300 1673 0.18 mildly difficult
34,213 400 1400 0.29 difficult
41,423 600 1673 0.36 difficult
42,314 500 1400 0.36 difficult
43,241 400 2117 0.19 mildly difficult
44,132 300 1908 0.16 mildly difficult
Open in a new tab

As the degree of natural ventilation in this mine is difficult, the mine meets the requirements of research on the diffusion of blasting dust under different ventilation conditions. According to part 1 of “Occupational Exposure Limits of Hazardous Factors in Workplaces”, i.e., Chemical Hazardous Factors Regulations,23 the average exposure limit of the time-weighted average allowable concentration of mine dust is 8 mg/m3. As the dust in the stope shows a trend of continuous diffusion and then a gradual decrease, it can be considered that the dust time-weighted concentration is unlikely to exceed the standard after the dust concentration is below the exposure limit. Therefore, the time taken from the maximum dust concentration after blasting to a decreased concentration lower than 8 mg/m3 was selected as the evaluation index of the degree of difficulty of dust diffusion in the DSOM.

2.1.2. Reliability Verification of the Simulation of the Wind Flow Field and Dust Concentration

In order to verify the reliability of the numerical simulation, a geometric model with the same size as the experimental mine was established and meshed, and the steady-state and transient simulations were performed. The measured point no. 2 was selected for the verification. The numerical simulation results of the wind direction at different heights were the same as those measured on-site (Figure 2a,b). The direction of wind flow at the upper part of the pit was almost consistent with the direction of ambient wind, while the direction of wind flow at the bottom of the pit presented a large drift angle with that of ambient wind, showing a possible existence of a complex circulation structure. The simulation was consistent with the field measurement, and the ideal model could better reflect the distribution trend of the wind flow field.

Figure 2.

Figure 2

Open in a new tab

(a, b) Numerical simulations (a) and measured results (b) of wind directions at different heights of measuring point no. 2. (c) Comparison of the simulated and measured wind speeds at different heights of measuring point no. 2. (d) Curve comparison between the simulated and the measured blasting dust concentration.

The actual measurement and simulation results of the wind flow direction and wind speed at different vertical heights of this point were compared. As shown in Figure 2c, both the simulation and the field test values of the wind speeds show generally the same trend, i.e., first decreasing and then increasing with an increase in altitude, and both of them have a minimum value at an altitude of −140 m. The wind speeds increase slowly when the altitude is above 80 m. The volatility presented by the simulation results is not as severe as the actual measured case, which is probably due to the local disturbance caused by the existence of the temperature inversion layer that was not considered in the simulation. However, the overall changing trend is the same and the extreme points are close, indicating better reliability of the simulation.

Based on the wind flow simulation, the blasting dust was included into the model to simulate its diffusion in the corresponding wind flow field. CFD-POST software was used to observe the dust diffusion and the change of dust concentration at 50 m downwind from the blasting position. The comparison of the simulation and corresponding field test of the dust concentration at different moments after the blasting is shown in Figure 2d. The changing trend, peak concentration, and peak-appearing time of the dust concentration curve obtained by numerical simulations are consistent with the actual measurement, and a peak appears at 100 s after reaching the first peak at 60 s. The peak at 100 s is due to the compression of dust caused by aerodynamic action, which further boosts the formation of a local concentration of dust. Thus, the reliability of this dust diffusion simulation is also relatively high.

2.1.3. Analysis of Numerical Simulation Results

The results of the orthogonal experiment were analyzed by using the diffusion time as the index. The order of the influencing factors on the dust concentration from high to low in turn was the length of the long axis, wind direction, depth of the pit, slope angle of long axis, and wind speed. At the same time, the level with the longest dust diffusion time of each influencing factor was selected and combined. The combination of the most difficult meteorological conditions and pit size for mine-blasting dust diffusion was a wind speed of 2 m/s, an angle between the wind direction and long axis of 90°, a squared pit closed circle with a side length of 1400 m, a pit depth of 400 m, and a pit slope angle of 44° (i.e., model M). After simulating the flow field and dust diffusion of the model M, it took 13,850 s for the concentration to reach 8 mg/m3 and it was kept for 60 s. According to the results of orthogonal experiments, it was found that model M had the longest dust diffusion time and the most difficult dust diffusion. On the basis of this model, one of the variables was deliberately changed to quantitatively analyze the influence of different factors on the wind flow and the dust diffusion time.

2.1.3.1. Effect of Wind Speed on Dust Diffusion

Model M was used to simulate the dust diffusion under different wind speeds, and the results are shown in Figure 3a. The main reason for the long diffusion time at 2 m/s is the slow wind speed and insufficient power for dust diffusion. As the wind speed increases, the power of dust diffusion increases, and hence the diffusion time decreases (when the wind speed is 2–3 m/s). However, with a further increase of wind speed, the high-speed wind also increases the intensity of the compound circulation and expands its influence range so that a large amount of dust enters the influence range of the compound circulation once it is ejected, increasing the degree of difficulty of dust diffusion (wind speed of 3–4 m/s). The decrease in diffusion time when the wind speed is 4–5 m/s can be derived from the increased wind speed at the bottom of the pit. As a result, the dust diffusion power increases, and the diffusion difficulty decreases.

Figure 3.

Figure 3

Open in a new tab

(a) Dust diffusion time under different wind speeds. (b) Dust diffusion time under different wind directions.

2.1.3.2. Influence of Wind Direction on Dust Diffusion

By changing the wind direction of model M, the time taken for the downward blasting dust diffusion under different winds was obtained, as shown in Figure 3b. When the wind direction is 0–30°, the blasting dust diffusion time increases slightly, but when the wind direction is 60° shifted with the long axis, the diffusion time will be significantly reduced. The dust diffusion time rises rapidly and reaches the maximum value of 13,850 s with the angle further increased to 90°. According to the simulation results (see Figure 4), the influence of the wind direction on dust diffusion time is reflected in its influence on the shape of wind flow. When the direction of the wind flow is parallel to the direction of the long axis (Figure 4a), the wind flow will present a different structure with the length of the long axis, which will affect the dust diffusion. When the wind direction is 30° (Figure 4b), the complex circulation pattern can still be maintained, and the equivalent long axis length along the wind flow direction is the longest, so the difficulty of its diffusion increases and the dust diffusion time also increases. When the wind direction is further increased to 60° (Figure 4c), the complex circulation structure is destroyed, and the rotation direction of the wind flow in the pit is consistent with the direction of the ambient wind flow. At this time, the rotation of the wind flow will not hinder the spread of dust but wrap the dust particles in the rotating wind flow for transportation. Out of the mine pit, the downward dust diffusion speed of the wind is significantly accelerated, and the diffusion time is the shortest among all angles. However, when the wind flow direction is parallel to the short axis with a constant length and slope angle (Figure 4d), the short axis length and slope angle will cause greater difficulty in dust spreading. Therefore, when the angle between the wind flow and the long axis is 90°, the difficulty of dust diffusion is greater than that at 0°. Therefore, in order to reduce the influence of the wind flow direction on the equivalent length of the long axis, the use of characteristic length Inline graphic will be relatively better.

Figure 4.

Figure 4

Open in a new tab

Air flow in the mine under different wind directions of (a) 0°, (b) 30°, (c) 60°, and (d) 90°, respectively.

2.1.3.3. Impact of Pit Depth on Dust Diffusion

By changing the wind directions of model M, the initial blasting dust concentration under different pit depths was obtained (Figure 5a). The dust concentration in the initial stage of blasting gradually decreases with time when the depth is increased. At the same time, the dust concentration also increases with the increase of depth. It is indeed relatively difficult for dust to diffuse in a deeper mine.

Figure 5.

Figure 5

Open in a new tab

(a) Initial blasting dust concentration under different pit depths. (b) Dust diffusion time under different lengths of the long axis;. (c, d) Streamline diagrams of complex circulation structure in mines with long axis lengths of (c) 1400 m and (d) 3200 m, respectively.

2.1.3.4. Effect of Long Axis Length on Dust Diffusion

By increasing the length of the long axis of model M by a gradient of 600 m, we simulated the diffusion of blasting dust and obtained four levels of dust diffusion time (Figure 5b). The dust diffusion is much more difficult when the length of the long axis is 1400 m. As the length of the long axis increases, the dust diffusion time fluctuates slightly but the overall trend is downward, which is basically the same as the result of the range analysis. Since the wind direction of this model is perpendicular to the length of long axis, the influence of the long axis length on the coverage region of the complex circulation is not significant. The effect of the length of the long axis is mainly reflected in the expansion of the horizontal structure of the complex circulation (Figure 5c,d). With the increase of the long axis length, the complex circulation structure is extended in the horizontal direction, and the horizontal structure of the complex circulation becomes greater, which can produce better separation and diffusion effects on the dust. As a result, the dust concentration can be dispersed rapidly.

2.1.3.5. Effect of the Long-Axis Slope Angle on Dust Diffusion

By changing the slope angle of the long axis of model M, we simulated the diffusion of blasting dust to obtain four levels of diffusion time (Figure 6a). The relationship between the time of blasting dust diffusion and the slope angle of the long axis is not significant. It is believed that the role of the slope angle in dust diffusion is mainly reflected in the suction of dust in the negative pressure area of the leeward slope. In terms of suction (as shown in Figure 6b–d, when the dust moves upward along the leeward slope from the bottom of the pit to the top of the leeward slope with the help of complex circulation wind flow, the greater negative pressure will speed up the dust diffusion, and then the dust will leave the complex circulation structure and enter the outside atmosphere. In this model, the change of the long axis slope angle will affect the side slope rather than the leeward or windward slope; hence, it cannot affect the suction effect for the dust, which can only have a weak influence on the structure of the complex circulation.

Figure 6.

Figure 6

Open in a new tab

(a) Dust diffusion time under different slope angles of the long axis. (b, c) Schematic diagrams of the suction effect of the negative pressure area on the dust mass corresponding to (b) 800 s, (c) 900 s, and (d) 1000 s after blasting where the blue ball denotes the boundary of the concentration of 0.01 mg/m3.

2.2. Model Establishment of the Blasting Dust Diffusion in the DSOM

The dimensional analysis methods are usually applied to classify the physical quantities involved in a problem and then draw the causal relationships among them. The theoretical core of the dimensional analysis method is the π theorem, whose core content is that, if there are i variables in a problem and the number of basic quantities is j, the problem can be expressed by i – j independent dimensionless relations. According to the results of field experiments and numerical simulations, the diffusion of blasting dust in the DSOM is affected by the distribution area of the complex circulation structure and the intensity of turbulence. Therefore, the main parameters that affect the blasting dust diffusion time T are considered as the surface wind speeds v, the angle α between the wind direction and the long axis, the depth H of the pit, the leeward slope angle β, the length L1 of the long axis of the closed circle, the length L2 of the short axis of the closed circle, the length l1 of the long axis of the pit bottom, and the length l2 of the short axis of the pit bottom. At the same time, the diffusion and settlement of dust will be affected by the gravity acceleration g. In addition, the structure of the complex circulation is difficult to measure directly and quantitatively and whether the presence of the complex circulation will significantly affect the surface wind speed of the pit. Therefore, the pit bottom wind speed vB is introduced as a physical quantity to characterize the coverage and strength of the complex circulation. In order to avoid the influence of ground fluctuation and boundary layer effects on the wind speed measurement, according to the requirements of GB/T 35227-2017 Ground Meteorological Observation Specification for wind direction and wind speed,24 the pit bottom speed vB corresponding to 10 m above the ground surface was selected to represent the wind speed of the bottom pit. Since there is already parameter α to characterize the wind direction, the closed circle size and the pit bottom size can be simplified into the pit depth characteristic length 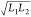Inline graphic and the pit bottom characteristic length 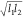Inline graphic. The dust diffusion time can be expressed as

2.2. 2

or directly written as

2.2. 3

The basic dimensions involved in these physical quantities only include time T and length L, which are expressed accordingly in Table 3.

Table 3. Physical Quantity and its Dimension Expression Affecting the Diffusion of Blasting Dust.

physical quantity symbol dimension expression
dust diffusion time Tdiffusion T
surface wind speeds v L·T–1
pit bottom wind speed vB L·T–1
gravity acceleration g L·T–2
angle between the wind direction and the long axis α no dimension
leeward slope angle β no dimension
depth of the pit H L
length of the long axis of the closed circle L1 L
closed circle pit depth characteristic length 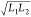Inline graphic L
pit bottom characteristic length 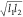Inline graphic L
Open in a new tab

According to the π theorem, the number of dimensionless power groups is equal to the difference between the number of variables and the number of basic dimensions. The number of dimensionless groups in this dimensional analysis is 8. Since the angle between the wind flow and the long axis of the open-pit mine and the leeward slope angle are dimensionless quantities, π1–π6 can be used to represent 6 dimensionless groups, which can be expressed as

2.2. 4

The number of core physical quantities is the same as the number of basic dimensions (i.e., two), and at the same time, the physical quantities should include all dimensions. Hence, physical quantities v and L1 are selected as the core physical quantities. Using the exponential function, the dimensionless parameters dimensionless parametric equations π1–π6 are listed as follows in eq 5 by the physical quantities 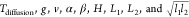Inline graphic and the core physical quantities v and L1.

2.2. 5

Substituting the dimensions of each physical quantity, eq 5 can be further expressed as

2.2. 6

According to the π theorem, one can obtain

2.2. 7
2.2. 8

According to the dimensional analysis theory, one can get

2.2. 9

Equation 10 can be obtained by taking the logarithms on both sides of eq 9.

2.2. 10

Through multiple nonlinear regression analysis, the regression coefficient of physical quantities is obtained by using software of Statistical Package for the Social Sciences (SPSS). The blasting dust diffusion model of the DSOM can be established as follows by bringing the regression coefficient into eq 10

2.2. 11

As can be seen, the depth of the open pit H, the angle α between the wind direction and the long axis, and the angle β of the long axis slope have strong impacts on the dust diffusion, while the length of the long axis of the closed circle L1, the acceleration of gravity g, the surface wind speed at the bottom of the pit vB, and the surface wind speed v have weak impacts on the dust diffusion, where L1, g, and v are negatively related to the dust diffusion time. The longer the length of the long axis, the greater the gravitational acceleration, and the stronger the surface wind, the faster the dust diffusion speed will be, which are consistent with the real situation. According to eq 11, a multiple correlation coefficient of 91.4% is obtained, which is greater than 90%, indicating a good correlation of variables with the dissipation time and a highly reliable analysis. The mathematical model can truly reflect the diffusion law of the blasting dust in the DSOM under different weather conditions.

3. Conclusions

Based on the field test, the numerical simulation, and the theoretical analysis of DSOM, the diffusion time taken from the maximum of dust concentration after blasting to a decreased concentration of less than 8 mg/m3 was selected as an indicator of the degree of difficulty of dust diffusion in a DSOM. Based on orthogonal experiments and controlled variable experiments, it has been determined that the long-axis slope angle, the length of the long-axis of the closed circle, the depth of the pit, the wind speed, and the wind direction are the main factors influencing the dust diffusion in the DSOM. Then, based on dimensional analysis and multiple non-linear regression, a mathematical model regarding the blasting dust diffusion in the DSOM is proposed with a high multiple correlation coefficient of 91.4%, which possesses high reliability and can better reflect the relationship between the blasting dust diffusion time and various parameters. From the proposed model, the depth of the open pit, the angle between the wind direction and the long axis, and the angle of the long axis slope are shown to impact the dust diffusion severely, while the length of the long axis, the acceleration of gravity, the surface wind speed at the bottom of the pit, and the surface wind speed have weak impacts on the diffusion where the length of the long axis, the acceleration of gravity, and the surface wind speed have negative correlations. The establishment of this efficient and reliable theoretical model for the diffusion of blasting dust is of great significance to avoiding possible damages of equipment and personnel health in DSOMs.

4. Experimental Section

4.1. Overview of the Experimental Mine

The experimental mine is located at 118°32′-118°36′ east longitude and 40°06′-40°09′ north latitude. The geological structure belongs to the subsidence zone of Yanshan mountain, and the lithology is dominated by gneiss. It has a warm temperate semi-humid monsoon climate, and the dominant wind direction is northwest wind throughout the year. The closed zone of the open-pit iron mine is located at an altitude of +83 m. The mining area is trending from southwest to northeast, which is defined as the long axis direction and is 3395 m long. The longest longitudinal working face is 1318 m in the southeast-northwest trend. The deepest point is −210 m above sea level and the total depth is close to 300 m, which is a typical DSOM. Field experiments were carried out to test the continuous changes of wind speed at different vertical heights in four typical locations and the changes in the dust concentration during blasting.

4.2. Distribution and Test Methods of Field Test Points

On the premise of ensuring the safety of mine production and testers, four measuring points were selected, i.e., no. 1, no. 2, no. 3, and no. 4, which are indicated in Figure 1a. It is preliminarily determined that the main height of the test was between −210 and +80 m. The wind speed and direction of different height layers in the stope were measured by the method of bundling the anemometer with the sounding balloon (Figure 1b). The experimental team measured the changes of the dust concentration during one blasting in the −130 m platform. As the blasting safety zone was delimited within 50 m and unrelated persons were not allowed to enter, three measuring points of 50, 60, and 70 m in the northeast of the blasting area were taken, and a dust meter was used to test the change of the dust concentration at different heights after blasting.

4.3. Numerical Simulation

Due to the different existing forms of mines and the diverse wind flow structures, both meteorological conditions and stope sizes will have great impacts on the complex circulation structure and dust diffusion. Therefore, regardless of the interaction among various factors, the L16 (45) orthogonal table was selected to process the experiment to investigate the influence of different factors on the dust diffusion of DSOMs.

Acknowledgments

This work was financially supported by the National Key R&D Program of China and the Fundamental Research Fund for the Central Universities [grant nos. 2018YFC0604605 and FRF-TP-19-039A1].

The authors declare no competing financial interest.

References

  1. Li X. Dust pollution and prevention strategies in open-pit mining process. World Nonferr. Metal 2019, 17, 41–42. [Google Scholar]
  2. Ma Y.; Cui Z.; Hou Y. Pollution and prevention measures of dust in open-pit mining process. Recyclable Resour. Circ. Econ. 2018, 8, 25–27. [Google Scholar]
  3. Dong J. Dust pollution in open pit mining and its prevention. Inner Mongolia Coal Econ. 2017, 24, 8–9. [Google Scholar]
  4. Alvarado M.; Gonzalez F.; Fletcher A.; Doshi A. Towards the development of a low cost airborne sensing system to monitor dust particles after blasting at open-pit mine sites. Sensors 2015, 15, 19667–19687. 10.3390/s150819667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jiang Z.; Jiang L.; Chen J. Numerical simulation of dust concentration distribution regularities of down-the-hole drilling in open-pit mine. J. Shenzhen Univ., Sci. Eng. 2013, 30, 313–318. 10.3724/SP.J.1249.2013.03313. [DOI] [Google Scholar]
  6. Liu J.; Li Z.; Bai H.; Zhang Z.; Cao T.; Chen Z. Research on influence factors of blasting dust emission of open-pit mine. Blasting 2017, 34, 169–174. [Google Scholar]
  7. Jin L.-h.; Han L.; Zheng X.-z.; Chen S.; Qiaoxiu L. Fractal expression of dust volume dispersion in bench blasting in open air. China Saf. Sci.J. 2016, 26, 139–144. [Google Scholar]
  8. Han B.; Yan B.; Zhao N.; Zhang J.; Sun J.; Lei X.; Li C.; Liu H.; Chen J. The influence of the functional capacity on subjective well-being and quality of life of patients with silicosis. Aging Ment. Health 2013, 17, 707–713. 10.1080/13607863.2013.788996. [DOI] [PubMed] [Google Scholar]
  9. Chen X.-h. On surface mining process dust pollution and measures. Build Technol. Dev. 2016, 43, 158–159. [Google Scholar]
  10. Zhao Y.The theory and technology of mine dust prevention; Coal Industry Press: Beijing, 1995. [Google Scholar]
  11. Hodkinson R. J. Studies by a radio-active tracer method of the turbulent diffusion of gas and fine dust in mine ventilation currents. Saf. Mines Res. Establ. 1956, 133, 32. [Google Scholar]
  12. Zhang X.; Li H. The calculation and analysis of the dust discharge amount of open-pit blasting. Met. Mine 1996, 3, 41–44. [Google Scholar]
  13. Yang Y.-x. Regularity of pollution caused by dust diffusion in stope of deep-digging open pit mine. Min. Eng. 2003, 5, 48–51. [Google Scholar]
  14. Zhang X.; Wang L.; Gao Y. Research on numerical simulation of blasting cloud diffusion. J. Saf. Sci. Technol. 2014, 9, 83–88. [Google Scholar]
  15. Ge S.; Huang Z.; Jing D.; Chen X.; Han F. Blasting-dust diffusion rule and water stemming ratio optimization for open-pit mine. J. Liaoning Technol. Univ. 2017, 36, 225–231. [Google Scholar]
  16. Nikitin B. C.; Bitecorov H. B.. The ventilation of open pit; Metallurgical Industry Press: Beijing, 1981; pp. 47–60. [Google Scholar]
  17. Du C. F.; Bai X. Q. Numerical simulation of effect factors of recirculation in deep open pit. Min. Res. Dev. 2013, 33, 84–87. [Google Scholar]
  18. Du C.; Zhao Y.; Li Y. Numerical simulation and experimental study on distributions of flow field in stope of deep sunken open-pit mines. J. Northeast Univ., Nat. Sci. 2014, 6, 875–879. [Google Scholar]
  19. Du C.; Jin W.; Wang Y. Experimental study on influential factors of spatial morphology of compound circulation in deep-open surface mines. Rev. Fac. Ing. 2017, 16, 999–1008. [Google Scholar]
  20. Du C.; Jin W.; Wang P. Experimental study on evaluation indexes of central point and region of complex circulation. Technol. Bull. 2017, 20, 257–266. [Google Scholar]
  21. Wang Y.; Du C.; Jin W.; Wang P. Establishment of criterion equation for decision parameter of recombination circulation in deep sunken open-pit mine. J. China Coal Soc. 2018, 43, 1365–1372. [Google Scholar]
  22. Ding Y.; Wu Q.; Huang H. Two suggestions for strengthening natural ventilation measures in deep concave open-pit mines. Met. Mine 1992, 5, 34–37. [Google Scholar]
  23. The National Health Commission of the People’s Republic of China . GBZ2.1–2019 Occupational exposure limits for hazardous factors in the workplace part 1: chemical hazardous factors; China Standard Press: Beijing, 2019; pp. 9.
  24. The General Administration of Quality Supervision . Inspection and Quarantine of the People’s Republic of China. GB/T 35227–2017 Specification for ground meteorological observation wind direction and wind speed; China Standard Press: Beijing, 2017; pp. 4.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES