Evaluation of an a priori scatter correction algorithm for cone-beam computed tomography based range and dose calculations in proton therapy

Abstract

Background and purpose

Scatter correction of cone-beam computed tomography (CBCT) projections may enable accurate online dose-delivery estimations in photon and proton-based radiotherapy. This study aimed to evaluate the impact of scatter correction in CBCT-based proton range/dose calculations, in scans acquired in both proton and photon gantries.

Material and methods

CBCT projections of a Catphan and an Alderson phantom were acquired on both a proton and a photon gantry. The scatter corrected CBCTs (corrCBCTs) and the clinical reconstructions (stdCBCTs) were compared against CTs rigidly registered to the CBCTs (rigidCTs). The CBCTs of the Catphan phantom were segmented by materials for CT number analysis. Water equivalent path length (WEPL) maps were calculated through the Alderson phantom while proton plans optimized on the rigidCT and recalculated on all CBCTs were compared in a gamma analysis.

Results

In medium and high-density materials, the corrCBCT CT numbers were much closer to those of the rigidCT than the stdCBCTs. E.g. in the 50% bone segmentations the differences were reduced from above 300 HU (with stdCBCT) to around 60–70 HU (with corrCBCT). Differences in WEPL from the rigidCT were typically well below 5 mm for the corrCBCTs, compared to well above 10 mm for the stdCBCTs with the largest deviations in the head and thorax regions. Gamma pass rates (2%/2mm) when comparing CBCT-based dose re-calculations to rigidCT calculations were improved from around 80% (with stdCBCT) to mostly above 90% (with corrCBCT).

Conclusion

Scatter correction leads to substantial artefact reductions, improving accuracy of CBCT-based proton range/dose calculations.

1. Introduction

The potential of proton therapy is currently being explored, also for tumour sites influenced by daily variations in anatomy caused e.g. by organ motion or patient positioning and posture changes. However, the proton range is highly sensitive to density changes [1], potentially degrading the delivered dose distribution [2], [3]. To calculate the impact of such factors, and potentially adapting for their influence, on-line high-quality volumetric imaging is required to reliably calculate the delivered dose.

Different technologies for volumetric in-room imaging in radiotherapy have been developed, including X-ray-based technologies such as computed tomography (CT) on rails as well as both C-arm and gantry mounted cone-beam (CB) CT [4]. Magnetic resonance imaging incorporated into the gantry could also be used [5] but has so far only been implemented for photon gantries [6]. CBCT systems are available from most proton therapy vendors, but CBCTs acquired on these systems can not immediately be used for dose calculations since their CT numbers do not represent the true density due to the nature of the image acquisition. Unlike the practically 1D detector in a CT, the 2D detector of a CBCT will receive more scatter due to the cone-shaped beam, creating scatter from the entire field of view (FOV) at every projection. Back-projection of these CB projections therefore creates artefacts, i.e. wrong CT numbers, caused by this scatter [7]. Two different approaches for CBCT-based dose estimation has been explored: Either to obtain the anatomy of the patient, for deformable registration of a planning CT (pCT) on which the dose calculation is performed [8], or by using software-level improvement of the image quality, to allow direct calculations of the dose on the improved CBCT reconstruction [8], [9], [10].

Niu et al. developed a scatter correction algorithm which used the a priori information of the pCT to estimate scatter and subtract it from the CB projections before reconstruction [7], [8]. The algorithm was subsequently implemented and has shown great potential for reducing artefacts of CBCT scans, as shown in a study investigating inter-fractional range differences and dosimetric changes of proton plans for head and neck patients [11], [12]. However, this implementation was only tested against one CBCT scanner type, specifically on photon (c-arm) gantries. Previous studies have compared this scatter correction method against a raw reconstruction, the Boellaard uniform scatter correction method [13], [14], and the Adaptive Scatter Kernel Superposition (ASKS) method [7], [15]. However, contemporary proton therapy CBCT solutions have a different geometry and a higher pulse current than what these previous studies have investigated. The aim of this study was therefore to investigate the improvement in CBCT quality achieved with scatter correction with respect to proton range and dose estimations, on image sets acquired in both proton and photon gantries.

2. Material and methods

2.1. Image reconstruction and the a priori scatter correction

The scatter correction method was implemented with a user interface using the Qt framework and efficient C++ libraries [16]. The algorithm takes both a pCT and the CB projections as input, where we introduced an image reader for the Varian file-formats. Initial processing of the CB projections included subtraction of the calibration image, i.e., a projection with no object between the source and the detector, with (photon gantry) and without (proton gantry) the bow-tie filter. Due to the long source-imager distance (SID), a bow-tie filter was considered unnecessary for the large proton gantry (Table 1). The projections were initially reconstructed with RTK [17] using a regular Feldkamp-Davis-Kress (FDK) algorithm [18] (rawCBCT). The rawCBCT had an image size of 512x512x200 and a pixel size in the x- and y-direction determined by the 512 pixels divided by the FOV diameter from the projection geometry, and a slice thickness of 1 mm. The pCT was then registered to the rawCBCT, first rigidly (rigidCT), where the CT was also interpolated to the same voxel-size as the rawCBCT, and then by deformable registration (deformCT) using Plastimatch [19]. The mutual information (MI) registration method was used for Thorax and Pelvis, while the mean squared error (MSE) method was used for Head and Catphan as MSE showed better results for head and neck patients in a study by Kim et al. [11]. While the deformable registration should not be necessary for phantoms like these, it was performed to simulate the workflow for real patients. The deformCT was then forward projected onto the same angles as the CB projections. The raw CB projections were multiplied by a factor determined from the mean intensity of the two projection sets, before the two projection sets were subtracted. These residual projections were then smoothed with both a Gaussian and a median filter to yield a simulation of the scatter and beam hardening [20]. The scatter maps were finally subtracted from the original CB projections before again reconstructing to a scatter corrected CBCT (corrCBCT) (source code available at: gitlab.com/agravgaard/cbctrecon).

Table 1.

CB configuration and settings. The Catphan phantom was imaged with the same setting as for the head. A half-fan scan is a full rotation, 2 π angle space, with the detector displaced to increase the radial FOV, while the full-fan has an angle-space of about 1 π, with no displacement of the detector.

CB	Photon gantry			Proton gantry
Source-Detector Distance [cm]	150			370
Source-Isocenter Distance [cm]	100			270
Scan-type	Full-fan	Half-fan		Full-fan	Half-fan
Region	Head	Thorax	Pelvis	Head	Thorax	Pelvis
Voltage [kV]	100	125	125	100	125	125
Current [mA]	15	15	60	154	154	176
Pulse length [ms]	20	20	20	15	15	40

All CB projections were also reconstructed with a regular FDK algorithm (rawCBCT), and with the standard proprietary built-in Varian reconstruction algorithm for the given gantry type (stdCBCT), for comparison with the corrCBCT. Additionally, the photon gantry system had an iterative reconstruction (iterCBCT) option that was used with its default settings for comparison.

2.2. Image materials

Image data sets of two different phantoms were used: The Catphan 604 phantom and the Alderson phantom (Head, Thorax, and Pelvis sections). CBCT scans were acquired on both a proton therapy gantry (Varian ProBeam Dynamic Peak Imaging OBI; Danish Centre for Particle Therapy, DCPT, Aarhus, Denmark) and on a photon therapy gantry (TrueBeam OBI; Aarhus University Hospital, Aarhus, Denmark). The voltage, current and pulse length settings of the different gantries are detailed in Table 1. The main differences between the two CBCT systems were the extended SID and the higher pulse current of the image system in the proton gantry. For each projection data set, a CT was acquired on a clinical dual-energy CT scanner (Siemens Somatom Definition Edge, DCPT, Denmark) with “Monoenergetic Plus” 90 keV, split filter (120 kV TwinBeam), with 64x0.6 mm collimation, reconstructed using the “Q34s” kernel for less beam hardening with the “Admire” iterative reconstruction set to level 3 [21]. The CT scans had a 1.5 mm / 2 mm slice thickness (for Catphan and Head / Thorax and Pelvis) and an image size of 512x512 pixels with a reconstruction diameter of 300 mm / 500 mm (Catphan and Head / Thorax and Pelvis). The CT scans extended beyond the limits of the CBCT scans in the superior-inferior directions.

2.3. CT number accuracy analysis

The Catphan phantom was segmented into the different regions corresponding to different materials. For each material the median Hounsfield Unit (HU) and its standard deviation (SD) were calculated. The segmentation was done with the “Grow from seeds” method (Supplementary material Figure S1) and the statistics were computed using Slicer3D [22], [23]. The calculated values for each of the reconstructions were compared against those of the rigidCT.

2.4. Water equivalent path length calculations

For all reconstructions and CT scans, proton ranges were calculated as water equivalent path length (WEPL) maps from a point far anterior to every point posterior of the couch in a grid of 1-by-1 mm spacing. The WEPL calculation was done by first translating the CT numbers of the (CB)CT scans into stopping power ratios, using the clinical conversion (look-up table) from CT number in HU to stopping-power ratio for the CT scan protocol (Supplementary Material Table S1), and then accumulating interpolated stopping power values along a given path and multiplying by the step-size. The WEPL difference maps were calculated by subtracting the WEPL map of the rigidCT from that of the given CBCT, from which median differences and standard deviations were derived. The rigidCT was used as the ground truth, as the phantoms should not have internal movement. The WEPL maps were calculated for the three sections of the Alderson phantom, and these maps were further divided into three subregions for the analysis, to isolate artefacts that may only have appeared in part of the image.

2.5. Dose comparisons and data analysis

Single beam spot scanning proton plans for three gantry angles (0, 90 and 180 degrees) at couch angle 0 degrees, were optimized using Varian Eclipse 13.7[21], [22] to a spherical target of 2.5 cm radius at the centre of the rigidCT. The fluence maps were then applied onto all CBCT reconstructions, for each beam angle.

The dose distributions of all treatment plans calculated on all reconstructions and registrations of the CT scans were compared using a gamma analysis [24] implemented in Plastimatch. A threshold dose value was set to 10% of the prescription dose and a dose difference tolerance of 1%, 2% or 3% of the prescription dose was used together with a spatial tolerance of 1, 2 and 3 mm, respectively. The analysis resulted in a pass rate for each plan, i.e. percentages of voxels passing the gamma evaluation. The gamma pass rates of the stdCBCT were compared against those of the corrCBCT, iterCBCT and deformCT, using the “Data Analysis using Bootstrap-Coupled ESTimation” (DABEST) framework [25] to compute the mean paired difference with 95% confidence intervals as well as the raw data with mean and SD.

For the Catphan segmentation and the WEPL differences, the median was used instead of mean and similar measures to limit the impact of outliers (caused by errors in segmentation and edge alignment errors e.g. at the air gap between the Alderson slices).

All data analysis was carried out in in-house scripts made in R (www.r-project.org) [26] (source code and data is available at [27], [28], [29]).

3. Results

3.1. CT number segmentation analysis

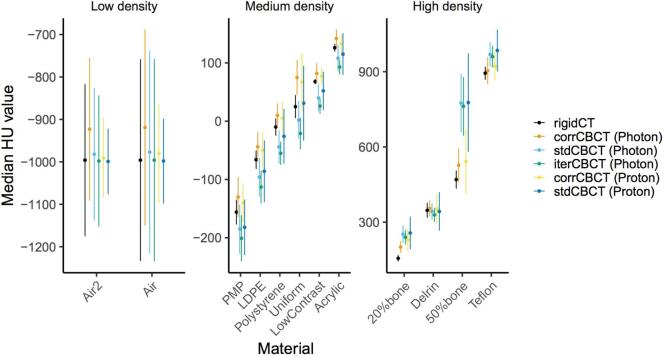
For medium and high-density regions in the Catphan phantom the corrCBCT CT numbers were overall closer to those of the rigidCT, though generally slightly higher. On the contrary the stdCBCT and iterCBCT had generally lower CT numbers than the rigidCT. For the low-density segmentations, the corrCBCT for the photon gantry had higher CT numbers than the rigidCT, while all other CBCT scans had values similar to those of the rigidCT (Fig. 1).

Fig. 1.

Median of CT numbers in HU of the catphan segmentations with SD as error bars. Seperated into groups of low, medium and high density to enhance the visibility of differences. The Materials on the x-axis reflect the naming in the Catphan 604 manual, with Uniform being “Uniform Housing” and Air and Air2 are just the upper and lower otherwise equivalent air segmentations.

The 50% bone segmentations showed the largest differences in CT numbers between the CBCT scans, with the corrCBCTs performing the best: The stdCBCT and iterCBCT were about 300 HU higher than the rigid CT (stdCBCT: 305 and 307, iterCBCT: 292), with SDs of more than 100 HU, while the corrCBCT had a median of 72 and 57 HU higher than the rigidCT median value, for the proton and photon gantry respectively.

For low density materials the corrCBCT showed the largest deviations from the rigidCT, in particular on the photon gantry, e.g. a CT number 77 HU too bright for air (compared to a difference of 16 HU for air on the proton gantry).

3.2. Residual water equivalent path length projection

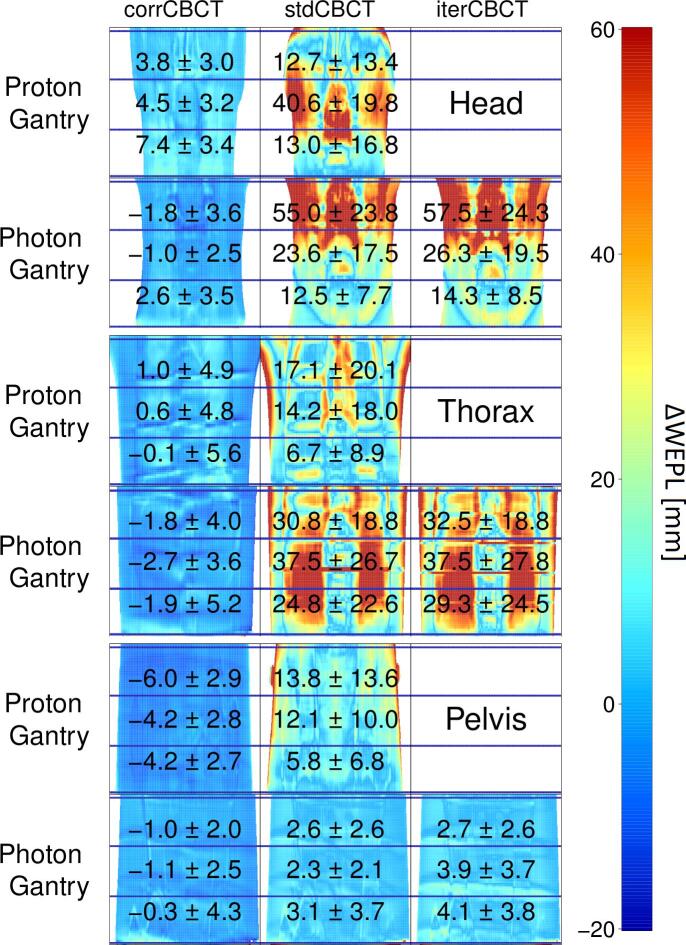
For the Alderson phantom, the WEPL calculated on the corrCBCT were in better agreement with the rigidCT than the stdCBCT and iterCBCT, both with a smaller median difference and SD (standard deviation) from the rigidCT over the residual WEPL maps for both the proton and photon gantry reconstructions (Fig. 2).

Fig. 2.

Posterior to anterior WEPL differences between rigidCT and the given CBCT with median ± SD for each sub-region, indicated by the horizontal blue lines, displayed on top. The color scale is cut off at 60 mm, and points above that value have the same red color. The Photon and Proton rows represent the given gantry, and the columns the CBCT scans.

The median WEPL differences of the corrCBCT from the rigidCT through the Alderson phantom ranged from −6.0 mm in the upper pelvis to 7.4 mm in the lower head, while for the stdCBCT it ranged from 2.3 mm in the middle of the pelvis to 55.0 mm in the upper head, and similarly for the iterCBCT from 3.9 mm in middle pelvis to 57.5 mm in the upper head. The SD values for the corrCBCT were between 2.0 and 5.6 mm, while the stdCBCT and iterCBCT had a similar SD range between 2.1 and 23.8 mm and 2.6 and 27.8 mm respectively.

3.3. Treatment plan analysis

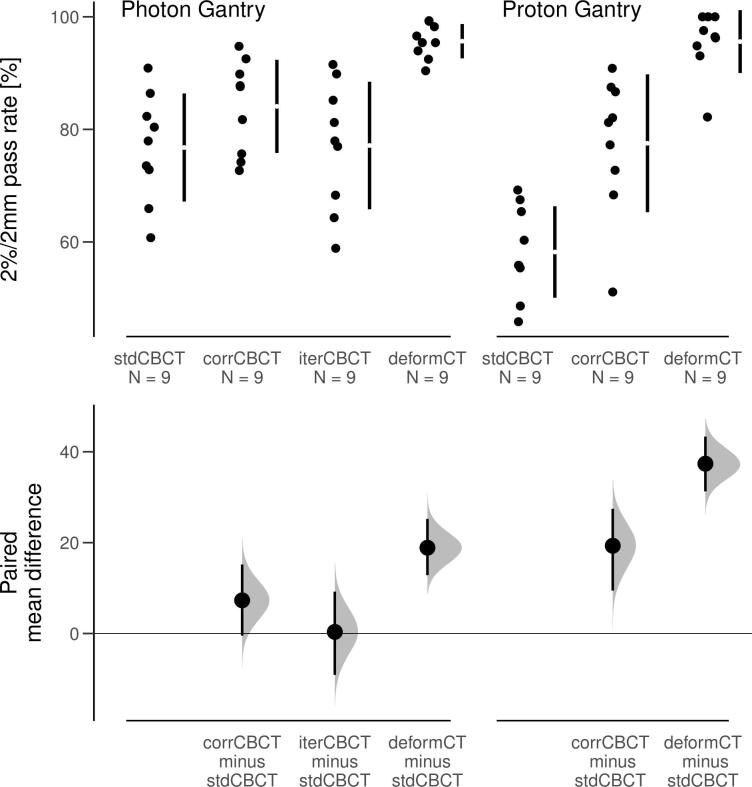
The corrCBCT had higher gamma pass rates for all except one dose plan (Supplementary Material, Figure S2). The iterCBCT performed almost equivalent to the stdCBCT with respect to gamma pass rates (Fig. 3). The 2%/2mm gamma pass rate mean paired difference of the corrCBCT from the stdCBCT was 19 and 7 percent points for the proton and photon gantry respectively. The 1%/1mm and 3%/3mm results showed a similar pattern (Supplementary Material, Figure S3-S4).

Fig. 3.

Upper: Gamma pass rates for a 2% over 2 mm tolerance from comparison of recalculated dose on the given CT with the original dose distribution on the rigidCT, for different tolerance criteria. Lower: The paired mean difference from the stdCBCT with 95% CI, as computed by the DABEST framework.

The only treatment plan that did not show a higher gamma pass rate for the corrCBCT was the 180 degree gantry angle plan calculated on the head of the Alderson phantom (see Supplementary material, Figure S5).

4. Discussion

The a priori scatter correction method we applied improved the CBCT image quality substantially from the clinical standard in our data, and a larger improvement was observed in regions of high density and steep density gradients, such as air to bone.

Several studies have developed methods for adapting the CBCT of the day to the pCT for re-evaluation of the plan on-line and adapt if necessary [10], [13], [30], [31], [32]. In this study, we have adapted a method implemented by Park et al. [13], to be usable across platforms and in particular for the proton gantry CB [33], for potential implementation in a clinical workflow. The method introduced initially by Niu et al. [7] compared the results to those of the ASKS method [15] currently used in Varian photon gantry systems. Niu et al. found that compared to the ASKS their scatter correction method reduced image distortions near the object centre and resulted in greater overall uniformity [7]. However, if there were errors in the deformed pCT these might create blooming artefacts in the corrected CBCT, but as the ASKS method does not use prior information it will not create these artefacts. Park et al. compared their method to the uniform scatter correction method which only showed small improvements over the rawCBCT compared to those of the a priori scatter correction.

Kim et al. [11], [12] used the same implementation of the a priori scatter correction as in the present study to improve the quality of weekly CBCT scans for 13 head and neck patients. This allowed them to compare the WEPL differences to the distal surface of delineated tumours throughout treatment as a measure of the proton dose deterioration with a range calculation uncertainty of 2%. Additionally, they found that the MI registration method would sometimes have problems distinguishing the immobilization mask from the skin, while the MSE method performed better in this regard and might therefore be preferable.

The spherical targets we used for the treatment plan analysis were placed in the centre of the CT. For the Alderson phantom this means the target was in the heart for the lung section and behind the nasal cavity for the head region. The large differences in densities from bone to air can create significant streak artefacts, thereby making these challenging areas.

Despite the Catphan segmentations of air in the stdCBCT and iterCBCT had values closer to those of the rigidCT than the corrCBCT, the WEPL results showed the opposite. The largest deviations in WEPL were observed in the stdCBCT and iterCBCT when going through the lungs and nasal cavities of the Alderson phantom for the photon gantry. Meanwhile the WEPL results for proton gantry were more consistent with the Catphan segmentation results, in which the bony structures gave the largest deviations for the stdCBCT. This suggests that the correction will be most beneficial in the regions where protons are more sensitive to changes [30]. The proton gantry CB had a longer SID and no bow-tie filter, which could be part of the reason for the differences. However, the proton gantry CB used a different pulse current than the photon gantry CB, so we avoid a direct comparison, although both reflect the clinical standard for the given gantry.

When using the algorithm on patient data errors in the deformation of the CT can create excessive or negative scatter, i.e. the blooming artefacts mentioned by Niu et al. [7]. However, we have already implemented tools like those used in other clinical studies [31] to take care of potential issues such as movement of air or large tumour growth/shrinkage. We observed this effect in the scatter correction of the head scan of the Alderson phantom, where a headrest was present in the CT scan but absent in the CB scan. This becomes particularly visible in the gamma pass rate results for 180 degree gantry angle. Furthermore, the same method has been applied on patient data from Elekta systems in other studies [11], [12], [34], [35] and has shown very good results.

An alternative approach was presented in a study by Veiga et al., showing clinical results of an on-line adaptive workflow for proton therapy of lung cancer patients involving deformable registration of the pCT to the CBCT [31]. The dose deterioration of the proton plan was measured by changes in WEPL. They concluded that the method could provide “clinical indicators” like those of a repeat CT scan. Although the workflow could be automated further [31], and the dose re-calculation speed and accuracy could be improved [36]. Promising results are also being obtained using deep learning based correction methods (e.g. convolutional neural networks or cycle generative adversarial networks) [9], [44], [45].

A complete scatter correction can in our implementation be performed in less than 70 s on a desktop computer (Intel i7-5960X) with Nvidia graphics (GTX TITAN X). By storing the scatter maps and raw projections a neural net can be trained to further reduce the time required for scatter correction [9]. Using the deformation of the pCT to the rawCBCT on the contours of the pCT [37], [38], [39], as well as a fast and reliable proton dose calculation engine [36], [40], [41], it would be possible to recalculate the plan in minutes, opening the potential for adaptive strategies. We are currently working on automating and simplifying the process [42], [43], so it can be used easily, for on-line range verification with WEPL, or with the embedded support for the goPMC proton dose calculation engine [36], [41].

In conclusion, we have reproduced previously published results for other platforms and gantry systems and found that the image quality, and specifically the dose and WEPL calculation accuracy of scatter corrected reconstructions was substantially improved compared to both the standard clinical and the iterative reconstruction, in particular in regions with bone or steep density gradients.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Figure S1.

Left: Axial view of the Catphan phantom (rigidCT). Right: 3D volume rendering of the segmentations.

Figure S2

Gamma pass rates by region in the Alderson phantom and gantry type, with shapes indicating the beam angle, and colors for gamma pass rate tolerances.

Figure S3

DABEST for 1%/1mm gamma pass rate tolerance.

Figure S4

DABEST for 3%/3mm gamma pass rate tolerance.

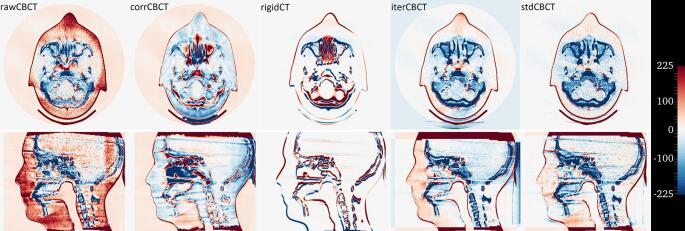
Figure S5.

Heatmap of HU value differences from the deformCT, with axial and sagittal view of the center slices of the Alderson head (Photon Gantry), for the given (CB)CT. From left to right: rawCBCT, corrCBCT, rigidCT, stdCBCT and iterCBCT. A negative value indicates the given (CB)CT is too bright (dense) and vice versa.

Table S1

Empirical clinical HU look up table for stopping power ratios. The minimum and maximum value of short integers should be respectively -32768 and 32767 on LP64 and LLP64 systems.