Evaluating the impact of cone-beam computed tomography scatter mitigation strategies on radiotherapy dose calculation accuracy

Abstract

Background and purpose

The scatter induced image quality degradation of cone-beam computed tomography (CBCT) prevents more advanced applications in radiotherapy. We evaluated the dose calculation accuracy on CBCT of various disease sites using different scatter mitigation strategies.

Materials and methods

CBCT scans of two patient cohorts (C1, C2) were reconstructed using a uniform (USC) and an iterative scatter correction (ISC) method, combined with an anti-scatter grid (ASG). Head and neck (H&N), lung, pelvic region, and prostate patients were included. To achieve a high accuracy Hounsfield unit and physical density calibrations were performed. The dose distributions of the original treatment plans were analyzed with the γ evaluation method using criteria of 1%/2 mm using the planning CT as the reference. The investigated parameters were the mean γ (γ_mean), the points in agreement (P_γ≤1) and the 99th percentile (γ_1%).

Results

Significant differences between USC and ISC in C1 were found for the lung and prostate, where the latter using the ISC produced the best results with medians of 0.38, 98%, and 1.1 for γ_mean, P_γ≤1 and γ_1%, respectively. For C2 the ISC with ASG showed an improvement for all imaging sites. The lung demonstrated the largest relative increase in accuracy with improvements between 48% and 54% for the medians of γ_mean, P_γ≤1 and γ_1%.

Conclusions

The introduced method demonstrated high dosimetric accuracy for H&N, prostate and pelvic region if an ASG is applied. A significantly lower accuracy was seen for lung. The ISC yielded a higher robustness against scatter variations than the USC.

1. Introduction

Cone-beam computed tomography (CBCT) scanners are widely used for image-guided radiotherapy, mainly for patient positioning [1], [2], [3]. Over the course of treatment, changes in anatomy (e.g. due to weight loss, tumor shrinkage) can also be detected. Dose calculation and adaptive radiotherapy with the use of CBCT could avoid the acquisition of additional planning CTs (pCT), which involves increased patient dose and work-load. However, compared to conventional CT, the image quality of CBCT is lower mostly due to increased detected scatter-to-primary ratio (SPR) caused by the cone shaped beam covering the large area flat panel imager. As a consequence, the Hounsfield unit integrity is compromised and dose calculation accuracy is negatively affected [4]. Efforts are made to reduce the effect of the scattered radiation and therefore also improve the dosimetric accuracy of CBCT scans. A number of hardware and software solutions (e.g. anti-scatter grid (ASG), collimation, beam blocker, adaptive scatter kernel superposition) have been proposed [5], [6], [7]. But even with those methods there are some residual CT number differences requiring additional post-processing. Furthermore, Hounsfield unit (HU) to physical or electron density (PD/ED) calibration is required for dose calculation. Numerous post-processing and HU-ED/PD calibration methods have been evaluated in the literature including stoichiometric, phantom- and population-based calibration, density override techniques, and region of interest (ROI) mapping [8], [9], [10], [11]. Previous studies focused on the calibration [12], [13] or specific imaging sites e.g. lung [14] or head and neck (H&N) [15]. Others consisted of only a small patient cohort [16], [17].

In this study we evaluated the dosimetric accuracy of CBCT scans acquired with and without an ASG and reconstructed using either the clinical uniform correction or the newly implemented iterative correction. This was performed for several imaging sites on a phantom and a large number of patients to determine if and for which combination of scatter correction and disease site a phantom-based calibration can be used as a universal and accurate method for dose calculation.

2. Materials and methods

2.1. CBCT

CBCTs were acquired on linac CBCT integrated scanners (Synergy, XVI 5.0, Elekta Ltd, Crawley, UK) augmented with in-house developed software. Scans were acquired with the bow-tie filter in place and in small (25 cm) or medium (40 cm) field of view (S-/M-FOV) with variable cranial-caudal collimation ranging from 25 cm (no collimation) to 12.5 cm. The reconstructed voxel size was 1 × 1 × 1 mm³. The scanners had an optional fiber interspaced ASG with a 15:1 grid ratio and a 44 cm⁻¹ line frequency (Philips Medical Systems, Best, The Netherlands). Additional software based scatter corrections were performed using either a uniform (USC) [18] or iterative scatter correction (ISC) algorithm [19]. Details of the correction algorithms can be found in the Supplementary Material (A).

2.2. Phantoms and patients

For the phantom study, pCTs and CBCTs (MFOV) with and without ASG of a male Alderson Radiation Therapy Phantom (Radiology Support Devices, CA, USA) were acquired and radiation therapy technologists generated typical treatment plans assuming tumor and organ position. A H&N plan (oropharynx) of 70 Gy planned prescribed dose, a lung plan (tumor location in central right lung) of 66 Gy, and a prostate plan of 77 Gy were created. The latter was calculated on a 12.5 cm collimated CBCT scan, which represented a typical prostate plan, and on an uncollimated scan, which represented other tumor locations in the pelvic region including prostate with sacral lymph nodes.

Two different patient cohorts with their corresponding patient specific plans were evaluated (Table 1) including palliative treatments and hypofractionation. The difference between USC and ISC both with an ASG was compared with the first cohort (C1) consisting of patients treated at the beginning of this study on the same CBCT scanner since mounting the ASG. Here the same CBCT scan was used for both reconstructions. With the second cohort (C2), the Elekta standard setting (USC without ASG) was compared to the advanced configuration including the ASG and ISC. Here the two CBCT scans were acquired on different days because the ASG had to be installed in between. Therefore the number of patients was limited. Details of the acquisition parameters can be found in the Supplementary Material (Table A.1).

Table 1.

Patient cohort with the range of the planned dose for the two studies.

Site	Number of Patients		Planned dose [Gy]
	Cohort 1	Cohort 2	Cohort 1	Cohort 2
Head & neck	18	14	30 – 70	46 – 70
Lung	16	8	20 – 66	46 – 66
Pelvic region	17	11	25 – 77	25 – 75
Prostate	21	5	65–77	77

2.3. Hounsfield unit and physical density calibration

We used the CIRS CBCT Electron Density and Image Quality phantom (CIRS Inc., Norfolk, Virginia, USA) for the two consecutive calibrations. As the HU accuracy depends on the imaged volume and detected residual scatter [13], different phantom configurations were utilized (Fig. 1). The importance of a site specific calibration is demonstrated in the Supplementary Material (B). For the H&N and pelvic region, the HU calibration was performed using the available CT Number Linearity inserts (ranging from air to Teflon) in a linear regression of the measured CBCT grey-value of the inserts to their known ideal HU (Fig. B.2). The linear relations were used to convert the CBCT grey-values to the HU. For the lung calibration, the same procedure was applied but the physical density inserts were used because the phantom part with the HU calibration inserts was removed for this configuration (see Fig. 1B). The nominal HU of the density inserts were taken from a pCT.

Fig. 1.

A is the pelvic configuration of the CIRS phantom, B the lung configuration and C the head and neck configuration. D-F are the corresponding axial slices containing the density inserts. The CT Number Linearity inserts are located in the red layer shown in A and C. For the lung configuration, the inner sections of the phantom (062MA-01, 062MQA-50) were removed while for the H&N configuration the outer parts (062MA-02, 062MA-36) were removed. The phantom includes eight or 16 tissue equivalent inserts with known physical density. The parts on the left side in A and B are put aside for visualization purposes and are put back in place for image acquisition. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The HU-PD calibration was performed similar to Saw et al. [20] using PD instead of ED because the employed treatment planning system (TPS) utilizes PD. Eight different tissue equivalent inserts ranging from lung (inhale) to solid dense bone were used. Each insert was present in the inner and the outer part of the phantom (see Fig. 1). For the pelvis, where outer and inner inserts were present, the values of the two corresponding inserts were averaged. Having established this HU-PD relation for the three imaging sites for both USC and ISC (Fig. B.3), we adapted the voxel values of the CBCT scans according to the difference between CBCT and pCT HU-PD curve because the use of only one HU-PD table in the TPS makes a potential implementation in the clinic easier. The adaptation was done with a 7-piecewise linear interpolation between known points of the pCT and the CBCT plus extrapolation(s). An extrapolation to HU = −1000 was necessary when the insert of air (PD = 0) showed HU greater than −1000.

2.4. Truncation correction and image registration

Lung cancer patients were scanned with a SFOV resulting in truncated reconstructions. To allow dose calculation, the missing data was patched from the pCT. After the two calibrations and a rigid registration of the pCT to the CBCT, we applied a transition zone. Outside and at the edge of the FOV, the pCT was weighted 100%. Towards the CBCT rotation axis, the weighting of the pCT decreased and the weighting of the CBCT increased piecewise linearly in 20 steps until 2 cm (voxel size 1 × 1 × 1 mm³) towards the axis the CBCT was weighted 100%.

The calibrated CBCT was first rigidly registered to the pCT using the bony anatomy to correct for setup errors. The residual anatomical differences were corrected with an in-house developed B-spline deformable image registration (DIR) algorithm [21], [22], deforming the pCT to the CBCT obtaining the modified CT (mCT), which was considered the ground truth. The result was four scans for every patient, the two original CBCTs with USC and ISC, and their respective mCTs. For the phantom scans only the rigid registration was necessary, resulting in only two CBCTs and the unchanged pCT.

2.5. Dose calculation and gamma analysis

Doses were calculated in Pinnacle 9.10 (Philips Radiation Oncology Systems, Fitchburg, WI, USA). The original treatment plans including the coordinates of the iso-center were applied to the CBCTs and the mCTs. These were IMRT (Intensity Modulated Radiation Therapy) plans for lung patients and VMAT (Volumetric Modulated Arc Therapy) plans otherwise. As in the clinic, a 4 mm dose grid was used. The calculated dose distributions were evaluated with the γ analysis method [23], [24]. In this study a distance criterion of 2 mm and a local dose difference of 1% were used. The dose calculated on the CBCTs was compared to the reference dose obtained from the mCTs. We analyzed the doses with in-house developed software for the volumes enclosed by the 20% and 50% maximum dose of the mCT/pCT isodose surface allowing a differentiation between low and high dose area. The mean value (γ_mean), the points in agreement (P_γ≤1) and the 99th percentile (γ_1%) were used as evaluation metrics and the results were interpreted based on commonly used γ passing rates [25]. The quartile coefficients of dispersion (QCD) of these metrics were also inspected.

We tested significance with the Wilcoxon signed-rank test (paired samples) with an α of 0.05. For the phantom we assumed no anatomical differences and therefore used the mean relative dose difference instead of the γ analysis.

3. Results

3.1. Phantom study

The results of the dosimetric analysis for the 20% isodose surface are shown in Table 2. In the case of USC and ISC both with ASG only the prostate with USC demonstrated noticeably higher dose differences. When the ASG use was compared to the USC without ASG, the values indicated a better dose agreement between pCT and CBCT for the scans with ASG. The results for the 50% isodose evaluation are presented in the Supplementary Material (C).

Table 2.

Mean (±SD) relative dose difference for the phantom plans of the three imaging sites for uniform and iterative scatter correction for the volume enclosed by the 20% isodose surface.

Site	USC w/ASG [%]	ISC w/ASG [%]	USC w/o ASG [%]
Head & neck	1.0 ± 3.5	1.1 ± 3.6	2.6 ± 10.1
Lung	1.2 ± 1.6	1.2 ± 1.4	1.4 ± 2.8
Pelvic region	1.1 ± 1.0	1.2 ± 1.1	3.4 ± 2.1
Prostate	2.0 ± 1.4	1.2 ± 1.1	2.4 ± 1.8

3.2. Patient study

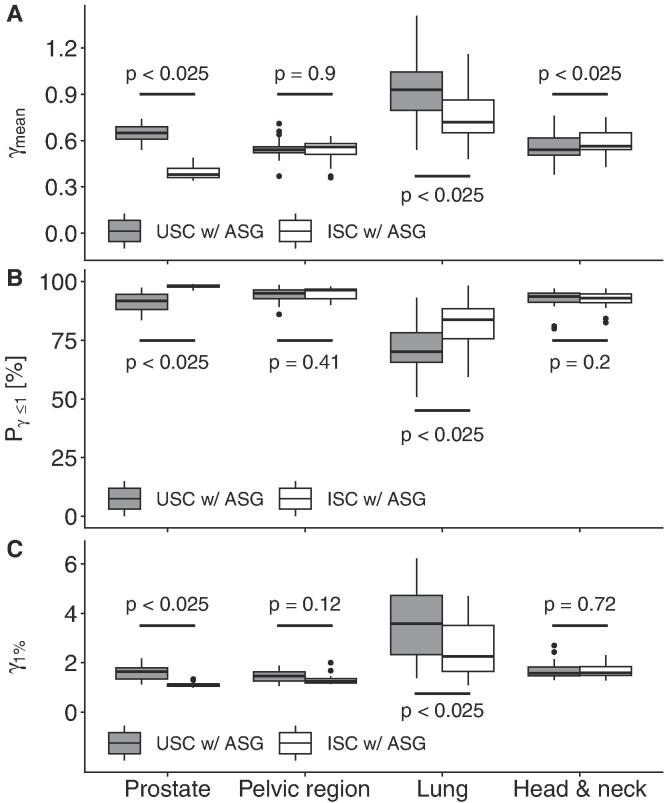
The results of the evaluation for the volume enclosed by the 20% isodose surface for C1 are shown in Fig. 2. Here, only for prostate and lung significant improvements from USC to ISC were observed and the γ_mean of H&N demonstrated significant worsening. The prostate group produced the largest improvement for γ_mean (0.27) and the lung group for P_γ≤1 (14 percent points) and γ_1% (1.3) (medians).

Fig. 2.

Boxplots of the mean γ values (γ_mean) (A), Points in agreement (P_γ≤1) (B), and 99th percentile (γ_1%) (C) for the four imaging sites for C1, comparing uniform and iterative scatter correction both with anti-scatter grid for the volume enclosed by the 20% isodose surface. The significance (p-value) between uniform and iterative SC are also shown.

The lung site exhibited highly significant (i.e. for all three metrics p < 0.025) worse results than the other three sites for USC and ISC. The ISC exhibited better results for prostate than for the other sites while the USC had a strong tendency (i.e. significant for γ_mean and P_γ≤1, and p < 0.1 for γ_1%) towards worse results compared to the pelvic region.

It is notable that the QCD and the distances between minimum and maximum of the three parameters γ_mean, P_γ≤1, and γ_1% were most of the times larger for the USC than for the ISC, especially visible for γ_1% (Fig. 2C). The largest spread of all sites presented the lung with ranges of 0.5–1.4, 51–98%, and 1.1–6.2 for γ_mean, P_γ≤1, and γ_1%, respectively.

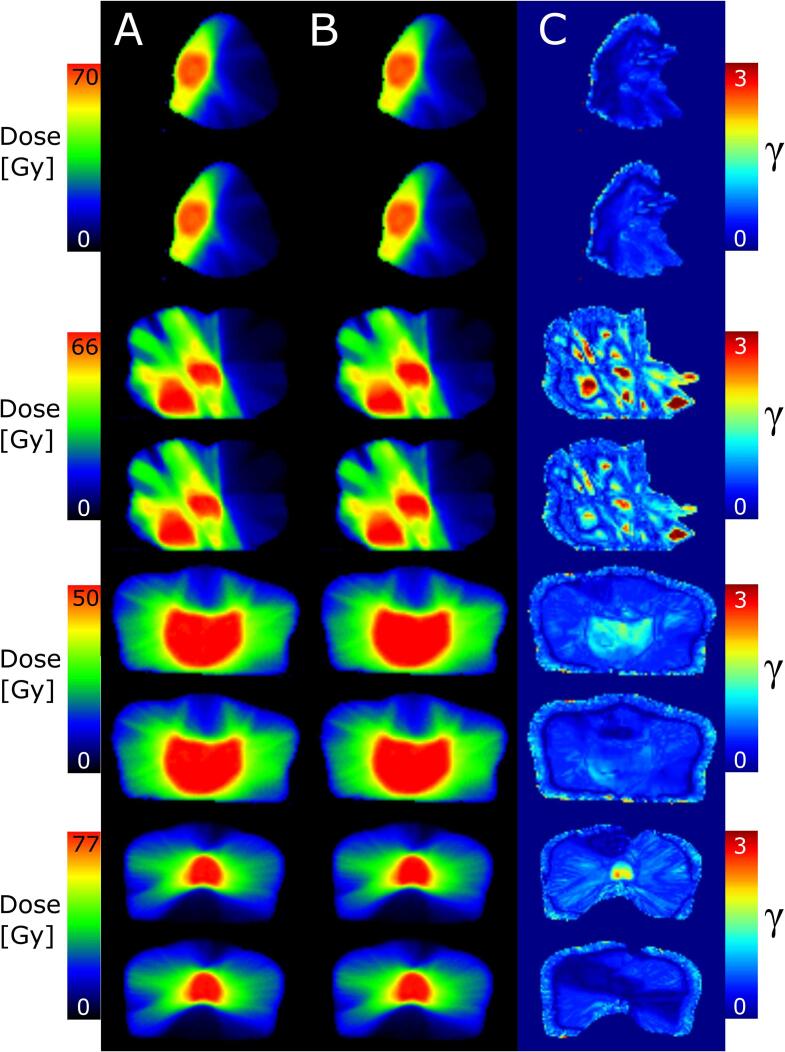
Significant differences in C1 between the 20% and 50% isodose surfaces for all metrics were observed for the prostate. The results for the 50% isodose were worse for the USC and better for the ISC. The lung with USC also demonstrated significant worse results. The examples of γ maps and their corresponding dose distributions (mCT and CBCT) for each disease site (Fig. 3) supported these findings. Prostate with ISC yielded the lowest and prostate and lung with USC the highest γ values in the high dose region. The corresponding dose-volume histograms to Fig. 3 are shown in Fig. D.1.

Fig. 3.

Dose distributions based on the mCT (column A) and CBCT (column B) and the corresponding γ-map (column C) for one patient of each disease site (C1). For each patient USC (upper row) and ISC (lower row) are presented. From top to bottom the disease sites are head and neck, lung, pelvic region, and prostate. The colorbars for A and B are scaled to the planned dose. Discontinuities on the right side of H&N and lung are because the minimum dose for A and B is set to 10% of the maximum mCT dose to avoid problems for the gamma calculation at low doses. This does not influence the γ analysis because the evaluation is up to the 20% isodose.

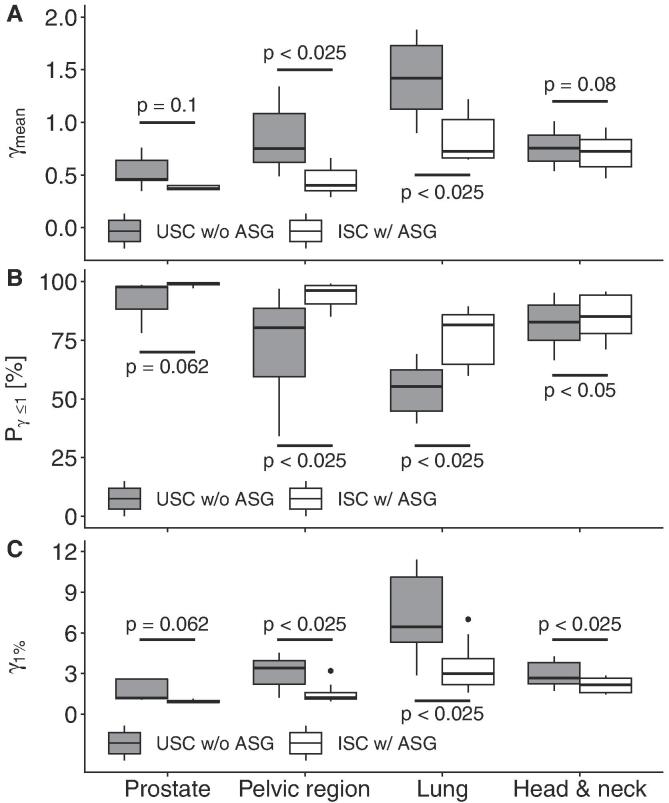
The results for C2 are displayed in Fig. 4. We found improved dosimetric accuracy for the ISC with ASG for all sites, with all but prostate being statistically significant. The improvements of the medians of the γ_mean ranged from 0.03 (H&N) to 0.70 (lung), of the P_γ≤1 from 2 (prostate) to 26 percent points (lung) and of the γ_1% from 0.3 (prostate) to 3.5 (lung).

Fig. 4.

Boxplots of the mean γ values (γ_mean) (A), Points in agreement (P_γ≤1) (B), and 99th percentile (γ_1%) (C) for the four imaging sites for C2, comparing the uniform scatter correction (SC) without anti-scatter grid (ASG) and iterative SC with ASG for the volume enclosed by the 20% isodose surface. The significance (p-value) between uniform and iterative SC are also shown.

4. Discussion

In this study we analyzed the dose calculation accuracy on CBCT scans of different disease sites with varying image quality depending on the applied scatter mitigation strategy. In consideration of Crowe et al. [25], good dosimetric accuracy was obtained with the use of an ASG for all disease sites tested except lung. The chosen γ criteria were stricter than the usual 3 mm and 3%, global dose normalization, which gave us a higher certainty in the results, leaving room for other uncertainties during treatment. We found that the USC without fiber interspaced ASG was dosimetrically inferior to the configurations utilizing an ASG.

When comparing the USC and ISC both with ASG, the phantom results demonstrated negligible differences between scatter correction algorithms and imaging sites with the exception of the USC for prostate, where the mean relative dose difference was larger (2% compared to 1–1.2%). The phantom study indicates that the USC as well as the ISC with ASG are superior to the USC without ASG. We can assume no anatomical differences and that, besides minor registration errors, the dose discrepancy came from the CBCT inaccuracy.

The patient studies confirmed these findings. The first patient cohort (C1), where USC and ISC both with ASG were compared, displayed negligible differences in H&N and pelvic region, similar to the phantom study. Worse results for the USC for prostate were also seen. The reason for the latter might be the collimation. The prostate scans were collimated while the calibration was done with the uncollimated CIRS phantom scan and therefore corresponded better to the pelvic region. An additional calibration with collimation could improve the results. However, the ISC for prostate demonstrated improved results. This suggests that the ISC performs better when less scatter is present (collimation) but is more robust to scatter variations than the USC and therefore more robust to an inaccurate calibration, which is supported by the smaller QCD and minimum-maximum ranges of the ISC. In our second comparison (C2) we found significant improvements from USC without ASG to ISC with ASG for the H&N, lung and the pelvic region. The lack of significance for the prostate is probably due to the low number of patients. These improvements demonstrate that not only the ISC but also the ASG leads to improvements in dosimetric accuracy. For imaging sites, where the USC and ISC were not significantly different in C1 (pelvic region and H&N), the improvements in C2 were due to the ASG, otherwise due to a combination of ASG and ISC. Since the ISC did not always lead to a higher accuracy but the ASG did, in patient and phantom study, applying an ASG is more important than the ISC.

The only imaging site that displayed unsatisfying results is lung. The C1 value range illustrates that in some cases the dose accuracy was high but in general too unreliable. The significant improvement from USC to ISC proved that the scatter correction had a substantial influence. Considering the similar accuracy for all sites in the phantom and that the phantom was scanned with a MFOV, the large dose differences in the patient study might be due to SFOV truncation and the deriving inaccuracy of the CBCT [26]. The influence of the pCT data on the dose calculations was limited because most of the treatment beams entered where CBCT data was present (unpatched sites), so most padding was done in the low dose region. Furthermore, we can assume that dose differences between mCT and CBCT occurred due to anatomical differences and motion (DIR inaccuracy). The highest γ-values were seen directly in the lung, where most motion is present, and in the transition zone of the patching. The unpatched sides of the lung in lateral, posterior and anterior direction, showed lower values (see Fig. 3). Better results could be obtained by increasing the FOV. This would reduce CBCT inaccuracies and eliminate the need for patching, which decreases uncertainties in the anatomical agreement of pCT and CBCT. The downside would be an increase in scanning time and therefore in patient dose. Another possibility might be a better patching algorithm, which includes pCT data during reconstruction [27], [28].

The sufficient accuracy for most imaging sites is in agreement with former research [10], [14], [17]. The worse outcome for lung was seen in other studies as well, even if the extent was smaller for some methods and lung was considered accurate enough [10], [17]. One possible reason for this discrepancy is the use of different metrics. While we used γ evaluation, most studies employed DVH metrics leading to differing acceptance criteria. Fotina et al. [11] utilized DVH and γ metrics (3%/3 mm) (γ_mean, P_γ≥1), and presented results similar to ours for prostate and H&N. Only for lung our results seem considerably worse. This can be easily explained by the strict γ criteria of 1%/2mm. With their criteria our results would be similar to Fotina et al. for lung and better for prostate and H&N. Thus comparable or superior results would be reached with our simple phantom-based calibration instead of density override or ROI mapping by Fotina et al. That also contradicts other studies that demonstrated unsatisfactory dosimetric accuracy for phantom-based calibration methods and required more complicated techniques, e.g. patient (group)-based calibration [10], [17]. Poludniowski et al. proposed a phantom-based calibration method with good dosimetric accuracy but a more advanced scatter correction strategy including Monte-Carlo simulations was applied [29]. Thing et al. compared the dosimetric accuracy of two image processing strategies for lung cancer patients [30]. Even if their simple strategy was not accurate enough they obtained better results than us. This might be explained by different CBCT acquisition (fast 4D instead of 3D) and treatment plans (VMAT instead of IMRT). The second strategy led to excellent accuracy but included, amongst others, scatter and beam hardening corrections based on patient specific Monte-Carlo simulations. This indicates that for lung more advanced image processing techniques need to be applied to achieve a satisfying accuracy.

One limitation of this study was the generation of mCTs using DIR. Due to the reduced image quality of the USC without ASG, especially for pelvic scans (high SPR), the DIR accuracy was also reduced. Consequently, part of the dose difference between the CBCT without ASG and its corresponding mCT was induced by these DIR inaccuracies and associated anatomical discrepancies in the mCT. How much of the inaccuracies were due to the DIR have to be investigated in another study. Fortunately, DIR was only necessary for the accuracy evaluation of this method but is not needed when the method is applied. Another limitation was that not all possible disease sites were included (e.g. breast, upper-abdomen, extremities). Therefore, a generalization to the whole body is not possible.

A potential translation into the clinic requires the generation of the calibration curves prior to imaging. After acquisition, the calibrated CBCT image can be used to calculate the dose of the day and therefore dose accumulation over treatment instead of using DIR to adapt the pCT to the daily CBCT anatomy. Furthermore, it would be possible to validate after every fraction if the dose distribution still fits the requirements. If that is not the case, a new treatment plan could be generated. Here, a DIR of the delineations for ROIs might be necessary if the image quality of the CBCT does not allow ROI delineation.

In conclusion, this study has demonstrated that applying an ASG led to accurate dose calculation with CBCT for the prostate, pelvis, and H&N region based on phantom-based calibrations. This allows more extensive adaptive radiotherapy (e.g. replanning on CBCT) and to calculate the dose of the day. Although the USC already displayed satisfying results in combination with an ASG, the ISC was superior because of its higher accuracy for prostate and lung, especially in the high dose region, and its overall stability for all imaging sites. The accuracy of dose calculation for lung was not acceptable and further investigation is needed.

Supplementary data

The following are the Supplementary data to this article: