Hypothesis tests

Key points.

• •Hypothesis tests are used to assess whether a difference between two samples represents a real difference between the populations from which the samples were taken.
• •A null hypothesis of ‘no difference’ is taken as a starting point, and we calculate the probability that both sets of data came from the same population. This probability is expressed as a p-value.
• •When the null hypothesis is false, p-values tend to be small. When the null hypothesis is true, any p-value is equally likely.

Learning objectives.

By reading this article, you should be able to:

• •Explain why hypothesis testing is used.
• •Use a table to determine which hypothesis test should be used for a particular situation.
• •Interpret a p-value.

A hypothesis test is a procedure used in statistics to assess whether a particular viewpoint is likely to be true. They follow a strict protocol, and they generate a ‘p-value’, on the basis of which a decision is made about the truth of the hypothesis under investigation. All of the routine statistical ‘tests’ used in research—t-tests, χ² tests, Mann–Whitney tests, etc.—are all hypothesis tests, and in spite of their differences they are all used in essentially the same way. But why do we use them at all?

Comparing the heights of two individuals is easy: we can measure their height in a standardised way and compare them. When we want to compare the heights of two small well-defined groups (for example two groups of children), we need to use a summary statistic that we can calculate for each group. Such summaries (means, medians, etc.) form the basis of descriptive statistics, and are well described elsewhere.¹ However, a problem arises when we try to compare very large groups or populations: it may be impractical or even impossible to take a measurement from everyone in the population, and by the time you do so, the population itself will have changed. A similar problem arises when we try to describe the effects of drugs—for example by how much on average does a particular vasopressor increase MAP?

To solve this problem, we use random samples to estimate values for populations. By convention, the values we calculate from samples are referred to as statistics and denoted by Latin letters ($\overline{x}$ for sample mean; SD for sample standard deviation) while the unknown population values are called parameters, and denoted by Greek letters (μ for population mean, σ for population standard deviation).

Inferential statistics describes the methods we use to estimate population parameters from random samples; how we can quantify the level of inaccuracy in a sample statistic; and how we can go on to use these estimates to compare populations.

Sampling error

There are many reasons why a sample may give an inaccurate picture of the population it represents: it may be biased, it may not be big enough, and it may not be truly random. However, even if we have been careful to avoid these pitfalls, there is an inherent difference between the sample and the population at large. To illustrate this, let us imagine that the actual average height of males in London is 174 cm. If I were to sample 100 male Londoners and take a mean of their heights, I would be very unlikely to get exactly 174 cm. Furthermore, if somebody else were to perform the same exercise, it would be unlikely that they would get the same answer as I did. The sample mean is different each time it is taken, and the way it differs from the actual mean of the population is described by the standard error of the mean (standard error, or SEM). The standard error is larger if there is a lot of variation in the population, and becomes smaller as the sample size increases. It is calculated thus:

$$\text{SEM}=\frac{\text{SD}}{\sqrt{n}}$$

where SD is the sample standard deviation, and n is the sample size.

As errors are normally distributed, we can use this to estimate a 95% confidence interval on our sample mean as follows:

$$95\%\text{CI}=\overline{x}\pm (1.96\times \text{SEM})$$

We can interpret this as meaning ‘We are 95% confident that the actual mean is within this range.’

Some confusion arises at this point between the SD and the standard error. The SD is a measure of variation in the sample. The range $\overline{x}\pm (1.96\times \text{SD})$ will normally contain 95% of all your data. It can be used to illustrate the spread of the data and shows what values are likely. In contrast, standard error tells you about the precision of the mean and is used to calculate confidence intervals.

One straightforward way to compare two samples is to use confidence intervals. If we calculate the mean height of two groups and find that the 95% confidence intervals do not overlap, this can be taken as evidence of a difference between the two means. This method of statistical inference is reasonably intuitive and can be used in many situations.² Many journals, however, prefer to report inferential statistics using p-values.

Inference testing using a null hypothesis

In 1925, the British statistician R.A. Fisher described a technique for comparing groups using a null hypothesis, a method which has dominated statistical comparison ever since. The technique itself is rather straightforward, but often gets lost in the mechanics of how it is done. To illustrate, imagine we want to compare the HR of two different groups of people. We take a random sample from each group, which we call our data. Then:

• (i)Assume that both samples came from the same group. This is our ‘null hypothesis’.
• (ii)Calculate the probability that an experiment would give us these data, assuming that the null hypothesis is true. We express this probability as a p-value, a number between 0 and 1, where 0 is ‘impossible’ and 1 is ‘certain’.
• (iii)If the probability of the data is low, we reject the null hypothesis and conclude that there must be a difference between the two groups.

Formally, we can define a p-value as ‘the probability of finding the observed result or a more extreme result, if the null hypothesis were true.’ Standard practice is to set a cut-off at p <0.05 (this cut-off is termed the alpha value). If the null hypothesis were true, a result such as this would only occur 5% of the time or less; this in turn would indicate that the null hypothesis itself is unlikely. Fisher described the process as follows: ‘Set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.’³ This probably remains the most succinct description of the procedure.

A question which often arises at this point is ‘Why do we use a null hypothesis?’ The simple answer is that it is easy: we can readily describe what we would expect of our data under a null hypothesis, we know how data would behave, and we can readily work out the probability of getting the result that we did. It therefore makes a very simple starting point for our probability assessment. All probabilities require a set of starting conditions, in much the same way that measuring the distance to London needs a starting point. The null hypothesis can be thought of as an easy place to put the start of your ruler.

If a null hypothesis is rejected, an alternate hypothesis must be adopted in its place. The null and alternate hypotheses must be mutually exclusive, but must also between them describe all situations. If a null hypothesis is ‘no difference exists’ then the alternate should be simply ‘a difference exists’.

Hypothesis testing in practice

The components of a hypothesis test can be readily described using the acronym GOST: identify the Groups you wish to compare; define the Outcome to be measured; collect and Summarise the data; then evaluate the likelihood of the null hypothesis, using a Test statistic.

When considering groups, think first about how many. Is there just one group being compared against an audit standard, or are you comparing one group with another? Some studies may wish to compare more than two groups. Another situation may involve a single group measured at different points in time, for example before or after a particular treatment. In this situation each participant is compared with themselves, and this is often referred to as a ‘paired’ or a ‘repeated measures’ design. It is possible to combine these types of groups—for example a researcher may measure arterial BP on a number of different occasions in five different groups of patients. Such studies can be difficult, both to analyse and interpret.

In other studies we may want to see how a continuous variable (such as age or height) affects the outcomes. These techniques involve regression analysis, and are beyond the scope of this article.

The outcome measures are the data being collected. This may be a continuous measure, such as temperature or BMI, or it may be a categorical measure, such as ASA status or surgical specialty. Often, inexperienced researchers will strive to collect lots of outcome measures in an attempt to find something that differs between the groups of interest; if this is done, a ‘primary outcome measure’ should be identified before the research begins. In addition, the results of any hypothesis tests will need to be corrected for multiple measures.

The summary and the test statistic will be defined by the type of data that have been collected. The test statistic is calculated then transformed into a p-value using tables or software. It is worth looking at two common tests in a little more detail: the χ² test, and the t-test.

Categorical data: the χ² test

The χ² test of independence is a test for comparing categorical outcomes in two or more groups. For example, a number of trials have compared surgical site infections in patients who have been given different concentrations of oxygen perioperatively. In the PROXI trial,⁴ 685 patients received oxygen 80%, and 701 patients received oxygen 30%. In the 80% group there were 131 infections, while in the 30% group there were 141 infections. In this study, the groups were oxygen 80% and oxygen 30%, and the outcome measure was the presence of a surgical site infection.

The summary is a table (Table 1), and the hypothesis test compares this table (the ‘observed’ table) with the table that would be expected if the proportion of infections in each group was the same (the ‘expected’ table). The test statistic is χ², from which a p-value is calculated. In this instance the p-value is 0.64, which means that results like this would occur 64% of the time if the null hypothesis were true. We thus have no evidence to reject the null hypothesis; the observed difference probably results from sampling variation rather than from an inherent difference between the two groups.

Table 1.

Summary of the results of the PROXI trial. Figures are numbers of patients.

		Group
		Oxygen 80%	Oxygen 30%
Outcome	Infection	131	141
	No infection	554	560
Total		685	701

Continuous data: the t-test

The t-test is a statistical method for comparing means, and is one of the most widely used hypothesis tests. Imagine a study where we try to see if there is a difference in the onset time of a new neuromuscular blocking agent compared with suxamethonium. We could enlist 100 volunteers, give them a general anaesthetic, and randomise 50 of them to receive the new drug and 50 of them to receive suxamethonium. We then time how long it takes (in seconds) to have ideal intubation conditions, as measured by a quantitative nerve stimulator. Our data are therefore a list of times. In this case, the groups are ‘new drug’ and suxamethonium, and the outcome is time, measured in seconds. This can be summarised by using means; the hypothesis test will compare the means of the two groups, using a p-value calculated from a ‘t statistic’. Hopefully it is becoming obvious at this point that the test statistic is usually identified by a letter, and this letter is often cited in the name of the test.

The t-test comes in a number of guises, depending on the comparison being made. A single sample can be compared with a standard (Is the BMI of school leavers in this town different from the national average?); two samples can be compared with each other, as in the example above; or the same study subjects can be measured at two different times. The latter case is referred to as a paired t-test, because each participant provides a pair of measurements—such as in a pre- or postintervention study.

A large number of methods for testing hypotheses exist; the commonest ones and their uses are described in Table 2. In each case, the test can be described by detailing the groups being compared (Table 2, columns) the outcome measures (rows), the summary, and the test statistic. The decision to use a particular test or method should be made during the planning stages of a trial or experiment. At this stage, an estimate needs to be made of how many test subjects will be needed. Such calculations are described in detail elsewhere.⁵

Table 2.

The principle types of hypothesis test. Tests comparing more than two samples can indicate that one group differs from the others, but will not identify which. Subsequent ‘post hoc’ testing is required if a difference is found.

Type of data	Number of groups
	1 (comparison with a standard)	1 (before and after)	2	More than 2	Measured over a continuous range
Categorical	Binomial test	McNemar's test	χ2 test, or Fisher's exact (2×2 tables), or comparison of proportions	χ2 test	Logistic regression
Continuous (normal)	One-sample t-test	Paired t-test	Independent samples t-test	Analysis of variance (ANOVA)	Regression analysis, correlation
Continuous (non-parametric)	Sign test (for median)	Sign test, or Wilcoxon matched-pairs test	Mann–Whitney U test	Kruskal–Wallis test	Spearman's rank correlation

Controversies surrounding hypothesis testing

Although hypothesis tests have been the basis of modern science since the middle of the 20th century, they have been plagued by misconceptions from the outset; this has led to what has been described as a crisis in science in the last few years: some journals have gone so far as to ban p-values outright.⁶ This is not because of any flaw in the concept of a p-value, but because of a lack of understanding of what they mean.

Possibly the most pervasive misunderstanding is the belief that the p-value is the chance that the null hypothesis is true, or that the p-value represents the frequency with which you will be wrong if you reject the null hypothesis (i.e. claim to have found a difference). This interpretation has frequently made it into the literature, and is a very easy trap to fall into when discussing hypothesis tests. To avoid this, it is important to remember that the p-value is telling us something about our sample, not about the null hypothesis. Put in simple terms, we would like to know the probability that the null hypothesis is true, given our data. The p-value tells us the probability of getting these data if the null hypothesis were true, which is not the same thing. This fallacy is referred to as ‘flipping the conditional’; the probability of an outcome under certain conditions is not the same as the probability of those conditions given that the outcome has happened.

A useful example is to imagine a magic trick in which you select a card from a normal deck of 52 cards, and the performer reveals your chosen card in a surprising manner. If the performer were relying purely on chance, this would only happen on average once in every 52 attempts. On the basis of this, we conclude that it is unlikely that the magician is simply relying on chance. Although simple, we have just performed an entire hypothesis test. We have declared a null hypothesis (the performer was relying on chance); we have even calculated a p-value (1 in 52, ≈0.02); and on the basis of this low p-value we have rejected our null hypothesis. We would, however, be wrong to suggest that there is a probability of 0.02 that the performer is relying on chance—that is not what our figure of 0.02 is telling us.

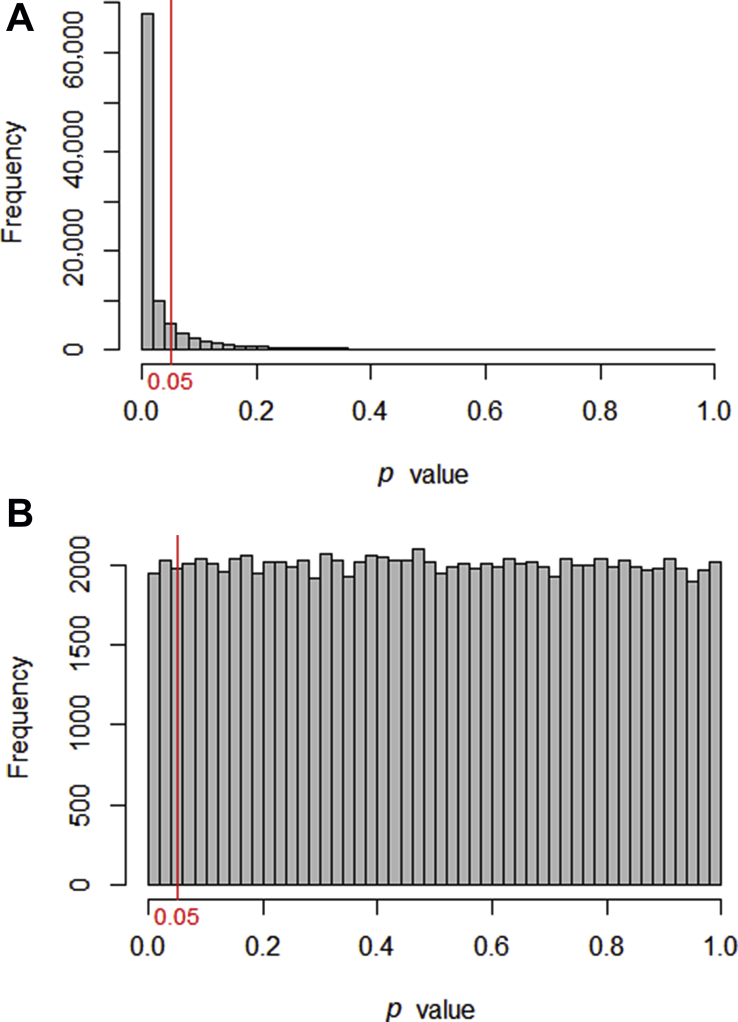
To explore this further we can create two populations, and watch what happens when we use simulation to take repeated samples to compare these populations. Computers allow us to do this repeatedly, and to see what p-values are generated (see Supplementary online material).⁷ Fig 1 illustrates the results of 100,000 simulated t-tests, generated in two set of circumstances. In Fig 1a, we have a situation in which there is a difference between the two populations. The p-values cluster below the 0.05 cut-off, although there is a small proportion with p >0.05. Interestingly, the proportion of comparisons where p <0.05 is 0.8 or 80%, which is the power of the study (the sample size was specifically calculated to give a power of 80%).

Figure 1.

The p-values generated when 100,000 t-tests are used to compare two samples taken from defined populations. (a) The populations have a difference and the p-values are mostly significant. (b) The samples were taken from the same population (i.e. the null hypothesis is true) and the p-values are distributed uniformly.

Figure 1b depicts the situation where repeated samples are taken from the same parent population (i.e. the null hypothesis is true). Somewhat surprisingly, all p-values occur with equal frequency, with p<0.05 occurring exactly 5% of the time. Thus, when the null hypothesis is true, a type I error will occur with a frequency equal to the alpha significance cut-off.

Figure 1 highlights the underlying problem: when presented with a p-value <0.05, is it possible with no further information, to determine whether you are looking at something from Fig 1a or Fig 1b?

Finally, it cannot be stressed enough that although hypothesis testing identifies whether or not a difference is likely, it is up to us as clinicians to decide whether or not a statistically significant difference is also significant clinically.

Hypothesis testing: what next?

As mentioned above, some have suggested moving away from p-values, but it is not entirely clear what we should use instead. Some sources have advocated focussing more on effect size; however, without a measure of significance we have merely returned to our original problem: how do we know that our difference is not just a result of sampling variation?

One solution is to use Bayesian statistics. Up until very recently, these techniques have been considered both too difficult and not sufficiently rigorous. However, recent advances in computing have led to the development of Bayesian equivalents of a number of standard hypothesis tests.⁸ These generate a ‘Bayes Factor’ (BF), which tells us how more (or less) likely the alternative hypothesis is after our experiment. A BF of 1.0 indicates that the likelihood of the alternate hypothesis has not changed. A BF of 10 indicates that the alternate hypothesis is 10 times more likely than we originally thought. A number of classifications for BF exist; greater than 10 can be considered ‘strong evidence’, while BF greater than 100 can be classed as ‘decisive’.

Figures such as the BF can be quoted in conjunction with the traditional p-value, but it remains to be seen whether they will become mainstream.

Declaration of interest

The author declares that they have no conflict of interest.

MCQs

The associated MCQs (to support CME/CPD activity) will be accessible atwww.bjaed.org/cme/home by subscribers to BJA Education.

Biography

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, Wales, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee, and an examiner for the Primary FRCA.

Matrix codes: 1A03, 2A04, 3J03

Supplementary material

The following is the Supplementary data to this article: