Non-inferiority statistics and equivalence studies

Key points.

• •Traditional statistical methods were designed to demonstrate differences and cannot easily show that a new treatment is similar to an older one.
• •Non-inferiority can be shown if the difference between two treatments does not cross a predefined inferiority margin.
• •Non-inferiority studies need to be carefully planned; failings in the design of the study may make accepting an inferior treatment more likely.

Learning objectives.

By reading this article, you should be able to:

• •Describe why traditional superiority trials cannot demonstrate equivalence.
• •Describe how a non-inferiority trial works.
• •Calculate the number of participants required for a simple non-inferiority trial, and analyse the trial result.
• •Understand and critically appraise a non-inferiority trial.

Traditionally, much of medical research has involved finding differences between newer treatments and the previous standard of care, with the hope of showing that the newer treatment is better. Medical statistics has reflected this, with a focus on demonstrating a difference by rejecting the ‘null hypothesis’ that both treatments are similar (so-called ‘superiority studies’). Increasingly, however, new treatments are being developed that may not be better in clinical practice, but which offer advantages in terms of cost, ease of use, or adverse effects. In such a situation it would not be ethical to perform a trial comparing the new treatment to a placebo; instead, the newer drug is usually compared with the working treatment, which is referred to as an ‘active control’. This has led to a new type of statistical test that can demonstrate that two treatments are ‘similar’ to each other in terms of their clinical effectiveness. Although the statistics are straightforward and use familiar concepts, there are important differences in the way that these tests are designed and reported. Such tests can be divided into non-inferiority tests, which try to demonstrate that the new treatment is not worse than the old treatment, and equivalence tests, which attempt to demonstrate that the new treatment is neither better nor worse. As the usual objective is to identify that the new treatment is no worse than the current treatment (and investigators are usually very happy if it should turn out to be better than current treatment), equivalence studies are rare; however, for completeness, they are discussed at the end of this article.

Why traditional statistical tests cannot demonstrate similarity

When a ‘traditional’ test does not demonstrate a difference between treatments, this is often presented (erroneously) as evidence of similarity, in spite of the fact that we have all been taught that ‘absence of evidence is not evidence of absence’. It may be that no difference exists, or it may be that the study was not of sufficient power to detect the difference between groups.

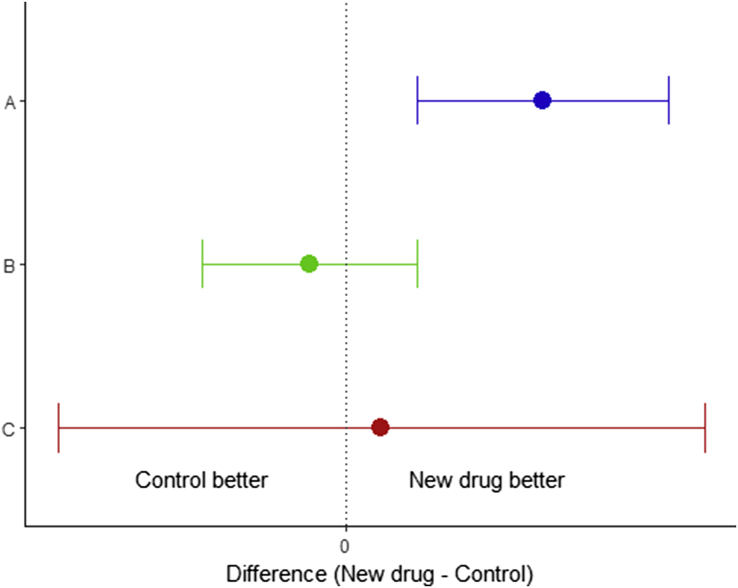
This can be understood more readily by referring to Fig 1, in which a new treatment is compared with an older treatment (often referred to as an ‘active control’). Here we have represented three clinical trials as confidence intervals (CI), bearing in mind that mathematically, testing with CIs is the same as using P-values. In situation A (blue), the 95% CI does not cross the line of no difference and hence we can reject the null hypothesis. In situation B (green) there is no statistically significant difference: the 95% CI includes ‘no difference’, so we cannot reject the null hypothesis. However, this does not mean that we can assume that the two treatments are the same; the null hypothesis is merely one of the range of values that the difference could take. This is further compounded in situation C (red), where an underpowered study has led to a very wide CI, and hence a very large range of possible values for the difference.

Fig. 1.

Traditional statistical tests, represented as 95% confidence intervals. The vertical line at 0 represents no difference, which is the null hypothesis. In situation A (blue), there is a statistically significant difference between the two treatments. In B (green) and C (red), there is no significant difference. However this cannot be taken as evidence of similarity, as ‘no difference’ is only one of a range of values the result can take.

Ultimately, random samples cannot be used to show that two populations are identical; there will always be a CI representing a range of values, of which ‘identical’ is merely one possibility.

Statistical techniques for undertaking a non-inferiority trial

The solution is to construct an ‘inferiority margin’ (often represented by the symbol d or d_NI, although some authors use Δ). This margin represents the maximum reduction in effectiveness that you would be willing to accept while still considering the treatments to be equal. To illustrate this, imagine that you are considering changing your motor car, and you are worried about fuel efficiency. The newer model has many attractive ‘extras’ that are very tempting, and the salesman assures you that it has the same fuel consumption as your current model. If your current model achieves 40 miles per gallon (mpg), and the new model achieves 39.4 mpg, you may consider this to be close enough to make no difference. However, if the newer model only had a fuel consumption of 30 mpg, you would feel that the salesman had misled you. You might decide to place an inferiority margin at 38.5 mpg; any value less than 38.5 mpg will be considered inferior.

With our defined inferiority margin in place we can go on to test for non-inferiority, using a similar process to a traditional superiority trial, but with the inferiority margin taking the place of ‘no difference’ as the null hypothesis. A P-value approach is possible; however, most trials choose to report CIs on the grounds that they are easier to interpret and do not risk confusion with a superiority trial.

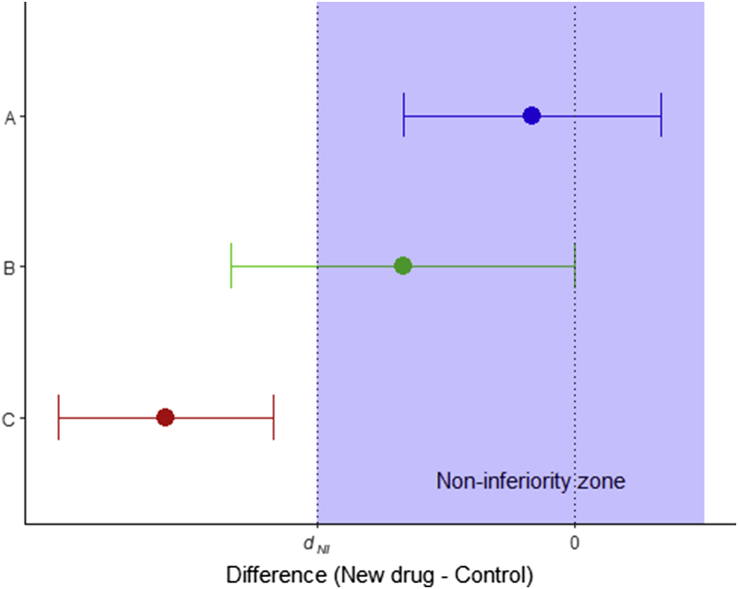
Possible outcomes are demonstrated in Fig 2. In situation A (blue) the 95% CI is entirely within the zone of non-inferiority, and we can therefore conclude that the new treatment is not inferior; in situation B (green) the 95% CI crosses the inferiority margin, and hence we cannot conclude that it is non-inferior. In case C (red) the entire CI is outside the non-inferiority zone, and in this case we can conclude that the new treatment is inferior. As the 95% CI also excludes the ‘no difference’ line, this trial would also demonstrate a statistically significant difference on traditional superiority testing (with the old treatment demonstrating superiority).

Fig. 2.

Possible outcomes in a non-inferiority trial. In A (blue), non-inferiority is demonstrated. In B (green), non-inferiority is not demonstrated, and the trial is inconclusive. In C (red), the new treatment is inferior.

As our inferiority margin has replaced ‘no difference’ as the null hypothesis, there are important differences in the error types and error rates when compared with a traditional superiority test. In a superiority test, a type 1 error means finding a significant difference, when no difference exists. In a non-inferiority trial a type 1 error means concluding non-inferiority when the new treatment is in fact inferior. A type 2 error (traditionally, failing to find a difference when a difference exists) now means that inferiority has been concluded in a treatment which is non-inferior. However, in both cases the error rates remain as in superiority studies: type 1 error rate is α (the significance level); type 2 error rate is β (1–power) (see Table 1).

Table 1.

Status of the null hypothesis, error types, and error rates in superiority and non-inferiority studies

	Superiority study	Non-inferiority study
Null hypothesis (H0)	Treatment = control	Treatment ≤ inferiority margin
Alternate hypothesis (H1)	Treatment ≠ control	Treatment > inferiority margin
Type 1 error	Deciding treatment ≠ control when no difference exists	Deciding treatment non-inferior when it is inferior
Type 2 error	Deciding treatment = control when a difference exists	Deciding treatment inferior when it is non-inferior
Type 1 error rate	α (significance cut-off)	α (significance cut-off)
Type 2 error rate	β (1–power)	β (1–power)

Choosing the inferiority margin

A variety of methods exist to help choose the inferiority margin.¹ However, the figure chosen should be appropriate to clinical practice, and must be set and documented before the trial begins—both to ensure that the trial is fair, but also because the margin is required to calculate the sample size. It is important to ensure that the inferiority margin is set high enough to be better than placebo. For example, if we have an anti-emetic (‘drug A’) that we know works in 50% of patients, a manufacturer might suggest that when testing a new agent (‘drug B’) we would want it to work in at least 30% of patients to be considered non-inferior. This might not seem unreasonable until we discover that in the original trials of drug A, nausea was successfully treated by placebo in 34% of cases. Thus in allowing an inferiority margin of 30%, we would be willing to accept a new drug which may work less well than a placebo.

In determining the margin, it may be necessary to perform a meta-analysis of the previous placebo trials. The full details are beyond the scope of this article, and the interested reader is directed to the article by Schumi and Wittes.¹

Calculating sample size

The process of calculating a sample size it not dissimilar to the methods used for a superiority study.² The researcher selects the significance (α) and power levels (1–β), and these need to be converted into their relevant z-values using a table (Table 2); we also require the standard deviation (σ), and the inferiority margin d_NI. For normally distributed data, the number needed per arm will be:

$$\text{Number}\text{per}\text{arm}=\frac{{2(Z_{1-\beta }+Z_{1-\alpha })}^2{\sigma }^2}{{(\left({\mu }_{\text{new}}-{\mu }_{\text{control}}\right)-d_{\text{NI}})}^2}$$ (1)

Table 2.

z-Values for commonly used percentiles

x	z1–x
0.200	0.842
0.100	1.282
0.050	1.645
0.025	1.960
0.010	2.326
0.001	3.090

The expression (μ_new–μ_control) represents the expected difference between the two treatments. For a type 1 error rate of 2.5% and a power of 0.9, and where we have no evidence of a difference between treatments, this formula reduces to:

$$\text{Number}\text{per}\text{arm}=21\times {\left(\frac{\sigma }{d_{\text{NI}}}\right)}^2,$$ (2)

which can easily be calculated by hand. As the test will be one-sided, the type 1 error rate is set at half what of is normally used for a two-sided test.³

Data analysis

As mentioned above, it is possible to use a P-value approach to analyse the data, but CIs are far more intuitive. The CI we require is the interval around the mean difference between the outcome measures in the treatments, usually at the 95% (1–2α) confidence level (the lower level of which is the one-sided 97.5% CI). The formula is:

$$\left({\mu }_{\text{new}}-{\mu }_{\text{control}}\right)\pm 1.96\sqrt{\frac{{\sigma }_{\text{new}}^2}{n_{\text{new}}}+\frac{{\sigma }_{\text{control}}^2}{n_{\text{control}}}},$$ (3)

where 1.96 is the appropriate z-value from Table 2. This can now be compared with our inferiority limit. If the interval remains above the inferiority limit, then non-inferiority has been demonstrated according to the standards we have set. Box 1 contains a worked example.

Box 1. Worked example.

A manufacturer develops a new, short-acting neuromuscular blocking agent which we will call ‘drug X’. The manufacturer believes that its profile makes it a suitable alternative to suxamethonium for rapid-sequence induction of anaesthesia. The researcher undertakes a meta-analysis of the literature and concludes that the mean onset time for suxamethonium is 52 (standard deviation, 8) s, and the manufacturer sets the inferiority margin at 5 s—indicating that we would accept the drug X taking 5 s longer without considering this to be a major disadvantage. They decide that a two-sided 95% confidence limit will be appropriate to compare the outcomes, and wish to have a power of 0.9. Using the briefer Formula (2), and taking d_NI=5 and σ=8, the formula becomes

$$\text{Number}\text{needed}\text{per}\text{arm}=21\times {\left(\frac{8}{5}\right)}^2=53.76$$

Thus, a suitable number per arm is 54 participants (not including dropouts). If the researcher had evidence to suggest that drug X was better, then Formula (1) could be used; depending on the difference in means this may well lead to a smaller required sample size, essentially because of the greater difference between drug X and the inferiority margin.

The researcher decides to proceed, and obtains the following results: mean time to acceptable conditions for tracheal intubation is 56.7 (6.3) s for suxamethonium, and 58.8 (7.3) s for drug X, with 55 patients per arm. Putting these values into Formula (3) gives

$$\left(58.8-56.7\right)\pm 1.96\sqrt{\frac{{7.3}^2}{55}+\frac{{6.3}^2}{55}}=-0.448\text{to}2.648\text{s}$$

As this is well below the inferiority margin of 5 s, we can conclude that drug X is not inferior to succinylcholine with respect to time to tracheal intubation.

Alt-text: Box 1

Other considerations when designing or interpreting non-inferiority trials

Because of the way these trials are set up, a trial that is poorly designed or performed will be more likely to find non-inferiority and thus be ‘successful’. In this way, these trials reward poor research practice, and so it is important that the researcher demonstrates that all steps have been taken to ensure a fair trial—even more so than would be expected for a superiority trial. It is particularly important to be aware of a number of factors that have been referred to as the ‘ABC’ of non-inferiority trials: Assay sensitivity, Bias, and the assumption of Constancy.⁴

Assay sensitivity is the ability of the trial to detect a difference if it exists. As a trivial example, a broken blood pressure machine that always reads the same value would find no difference between patients taking an antihypertensive or a placebo; it is therefore not surprising that this equipment would find any new drug to be non-inferior to the antihypertensive. Many trials rely on surrogate outcome measures, which may appear reasonable but would not be able to detect a difference in any trial. Researchers often try to ensure assay sensitivity by using the same methodology which demonstrated a drug–placebo difference in earlier studies. However, this does rely on the constancy assumption (see below).

Bias can be defined as a systematic tendency in a trial that will adversely influence the result. In most clinical trials we can avoid it by randomising and blinding, but in non-inferiority trials we need to be aware that bias can exist between the current trial and any previous placebo-controlled studies. If drug A is better than placebo, and we show that drug B is non-inferior to drug A, we are in effect comparing drug B with the placebo. Is that a fair comparison? We need to be satisfied that the non-inferiority trial has used a similar group of patients and drug dose to the original trials. Underdosing the older, established drug or running the trial in a group of patients where the condition might be easier to treat will give an unfair advantage to the new treatment.

The constancy assumption is the requirement that the active control has the same effect now as it always had, and the methods of measuring the outcomes still work. Although this is usually the case, it is worth questioning whether situations have changed. Medicine is complex, and many conditions are now treated with lifestyle advice and medication, meaning that the effect that a particular drug may have had over placebo 40 yrs ago may not be the same as it does now. Of particular importance is the avoidance of ‘biocreep’.⁵ This occurs when non-inferiority comparisons are made on successive drugs, potentially leading to the acceptance of a drug which has no superiority over placebo. For example, if drug A is better than placebo, drug B is non-inferior to drug A by a small margin so drug B becomes standard treatment. Drug C is now compared with drug B, and this process continues, with the inferiority margin ‘creeping’ closer and closer to the placebo effect each time. The fear is that we eventually end up accepting a drug which does not work.

Trial analysis

RCTs are often analysed using ‘intention to treat’ (ITT) analysis, in which participants are counted in the group they were originally allocated to, even if they discontinued the treatment. There are multiple reasons for this, but one of the main ones is that it gives you a practical ‘real world’ view of a treatment. If a cholesterol-lowering medication treatment works in 95% of cases, but if its adverse-effect profile were so unacceptable that the majority of patients stop taking it, then the actual effect that this drug would have if prescribed would be minimal. The alternative to ITT is per protocol analysis, in which participants are compared on the basis of the treatment they actually received. A useful way to summarise the difference would be to say that ITT shows what happens when a treatment is prescribed, whereas per protocol shows what the treatment actually does when taken. The effect of ITT on superiority studies is to bring the two study arms closer together; hence, we can be more confident in any difference found—in effect, saying ‘we found a difference in spite of the participants who switched groups’. However, in a non-inferiority trial we wish to minimise factors that would make the two study arms seem artificially similar; hence, per protocol analysis is a more correct way to proceed.⁶ The most convincing results are those in which non-inferiority is found using both ITT and per protocol analyses.⁷

Combining study methodology: as good as or better

As discussed at the beginning of this article, a superiority trial that fails to find a difference should not be used as evidence of equivalence. However, when a non-inferiority trial finds two treatments to be similar, it may be because they are the same, or it may be because the newer treatment is better. Indeed, once non-inferiority has been shown it is possible to perform a superiority study on the same data without the need for any statistical penalty to preserve the type 1 error rate. This is referred to as an ‘As good as, or better than’ trial. As with all statistical analyses, the statistical procedures and significance levels should be clearly decided and documented before the trial begins. Also the analysis should be per protocol for the non-inferiority analysis, but ITT for the subsequent superiority analysis.

Equivalence trials

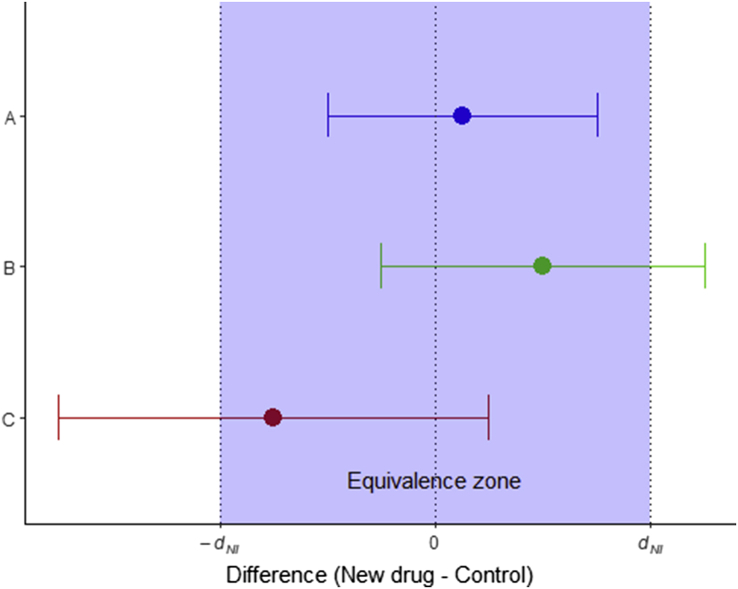
It is unusual to use equivalence trials in medicine—normally a treatment which has more than its required effect is considered a useful property. Equivalence can be shown using a ‘two one-sided test’ (TOST) procedure. This is a simple extension of the non-inferiority test described above, with a ‘superiority’ margin (+d_NI) and the inferiority margin (–d_NI). To conclude equivalence, the appropriate CI must lie completely within the range (–d_NI, +d_NI) (see Fig. 3).

Fig. 3.

Possible outcomes during an equivalence trial. Drug A would be considered equivalent to the active control; in drugs B and C equivalence has not been shown.

Declaration of interest

The author declares that they have no conflict of interest.

MCQs

The associated MCQs (to support CME/CPD activity) will be accessible at www.bjaed.org/cme/home by subscribers to BJA Education.

Biography

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee and an examiner for the Primary FRCA examination.

Matrix codes: 1A03, 2A04, 3J03