FRET-Based Determination of the Exchange Dynamics of Complex Coacervate Core Micelles

Abstract

Complex coacervate core micelles (C3Ms) are nanoscopic structures formed by charge interactions between oppositely charged macroions and used to encapsulate a wide variety of charged (bio)molecules. In most cases, C3Ms are in a dynamic equilibrium with their surroundings. Understanding the dynamics of molecular exchange reactions is essential as this determines the rate at which their cargo is exposed to the environment. Here, we study the molecular exchange in C3Ms by making use of Förster resonance energy transfer (FRET) and derive an analytical model to relate the experimentally observed increase in FRET efficiency to the underlying macromolecular exchange rates. We show that equilibrated C3Ms have a broad distribution of exchange rates. The overall exchange rate can be strongly increased by increasing the salt concentration. In contrast, changing the unlabeled homopolymer length does not affect the exchange of the labeled homopolymers and an increase in the micelle concentration only affects the FRET increase rate at low micelle concentrations. Together, these results suggest that the exchange of these equilibrated C3Ms occurs mainly by expulsion and insertion, where the rate-limiting step is the breaking of ionic bonds to expel the chains from the core. These are important insights to further improve the encapsulation efficiency of C3Ms.

Introduction

Complex coacervate core micelles (C3Ms) are used as encapsulators for a wide variety of (bio)molecules.^1,2 The formation of these C3Ms is based on associative liquid–liquid phase separation of oppositely charged polyelectrolytes from the water phase. Macroscopic phase separation is prevented by a neutral, hydrophilic block that is attached to at least one of the two polyelectrolytes. These neutral blocks form the corona of the micelle, while the polyelectrolytes form the micelle core. The hydrophilic environment of the core allows for the incorporation of charged or hydrophilic compounds, which can be subsequently protected against external compounds by the micelle corona. Since the core formation relies on electrostatic attraction, the C3Ms can respond to changes in salt concentration and, in some cases, also to changes in the pH. Their protecting corona and ability to respond to external triggers make the C3Ms promising drug and gene delivery tools.^3,4

Up to now, studies on C3Ms have mainly focused on their average static properties at varying environmental conditions like different ionic strengths and different pH-values. However, these average static properties do not reveal the underlying molecular exchange of the C3Ms. Even when the C3Ms are completely equilibrated and the average static properties do not change in time, the C3Ms are still a dynamic system where molecular exchange can occur continuously. Only a few studies have focused on this C3M exchange dynamics⁵⁻⁹ and provided some indications for the C3M exchange mechanisms and the corresponding governing parameters. Yet, to date, the exact C3M exchange mechanisms are still unresolved, while their exchange dynamics can largely determine their encapsulation efficiency. After all, the exchange dynamics determines the rate at which the cargo is exposed to the surroundings and thus the level of protection that the C3M gives. Furthermore, in some cases, the final structure of the C3Ms is governed by their preparation pathways.¹⁰⁻¹⁴ This demonstrates that kinetic effects can determine the C3M properties and thus their encapsulation efficiency.

To interpret C3M exchange experiments, the exchange mechanisms are usually divided into two main groups. The first one is the expulsion of one polymer or a small cluster of polymers followed by insertion into another micelle. In the second case, the micelle splits into two parts of both substantial sizes, which can subsequently merge again with other micelles. This type of exchange is called fission and fusion and differs from the expulsion and insertion exchange in that all formed clusters still have a substantial micelle corona. Therefore, for fission and fusion, the merging of the micelles is considered to be the rate-limiting step as this requires substantial restructuring of the micelle corona polymers, while for the expulsion and insertion case, the expulsion from the core is considered to be rate limiting.

During the initial micellization of C3Ms, both exchange mechanisms might occur, as we have recently shown using Langevin dynamics simulations.⁸ We observed that for oppositely charged polyelectrolytes with matched lengths and weak nonelectrostatic attraction, the expulsion/insertion exchange is strongly favored, while for unmatched chain lengths and stronger nonelectrostatic interactions, the fission/fusion mechanism might become more important. A recent small-angle X-ray scattering (SAXS) study showed that after the very fast initial micellization, a slower rearrangement of the micelles can occur.⁷ This rearrangement was concentration independent, suggesting that the exchange during these rearrangements occurs mainly by expulsion/insertion.

The exchange mechanisms during initial C3M formation and rearrangement might deviate from the exchange of equilibrated C3Ms due to the differences in micelle size during the different stages.¹⁵ Therefore, it is important to determine the exchange dynamics of equilibrated micelles as well. Both SAXS and dynamics simulations cannot be used to study the exchange in this equilibrated state due to the absence of structural rearrangements and the relatively long equilibration times, respectively. For amphiphilic diblock copolymer micelles, time-resolved small-angle neutron scattering (TR-SANS) measurements have been used to follow the exchange of equilibrated micelles.¹⁶⁻²² However, this requires the synthesis of deuterated polymers and the use of advanced and not broadly available equipment. A more accessible way to follow the exchange dynamics of equilibrated micelles is to make use of Förster resonance energy transfer (FRET), which is a nonradiative energy transfer from an excited donor fluorophore to a nearby acceptor fluorophore. In these experiments (Figure 1a), micelles with donor fluorophores in their core are mixed with micelles with acceptor fluorophores in their core. When the micelles exchange, the donor and acceptor can become part of the same micelle core, which means that they are close enough to each other for FRET to occur. The increase in FRET efficiency over time is thus a measure for the micelle exchange rate.

Figure 1.

Overview of the C3M exchange experiments. (a) Schematic representation of the FRET-based micelle exchange experiment. (b) Chemical structures of the fluorescently labeled donor polymer (poly(3-sulfopropyl methacrylate)-sulfo-cyanine3 amine (PSPMA-sCy3)) and acceptor polymer (PSPMA-sCy5).

This FRET approach has already been used to follow the exchange dynamics of C3Ms at different charge stoichiometry ratios⁵ and to follow the formation and exchange dynamics of protein-containing C3Ms.⁶ Both studies took the increase in FRET efficiency normalized to the final FRET efficiency as a direct measure for the micelle exchange rate and neglected any other factors that affected the normalized FRET increase. This approach suffices to give a general idea of the exchange time scales and showed that the protein-containing C3Ms exchanged much faster than the C3Ms composed of only polymers. However, to further elucidate the exchange mechanisms, more quantitative comparisons of the exchange rates are essential, and in that case these other factors cannot be neglected. In fact, the FRET efficiency does not increase linearly with increasing exchanged chain fraction and also depends on parameters like the micelle core size and the acceptor and donor fluorophore properties. A more advanced description is thus needed to relate the observed normalized FRET increase to the underlying micelle exchange rates.

In this paper, we aim to use FRET for a quantitative measure of the molecular exchange dynamics of C3Ms. We first derive an analytical model that describes the FRET increase for a given exchange rate taking into account the dependence of FRET on the micelle core size, the nonlinear increase in FRET efficiency with increasing acceptor number, and the variations in the number of fluorophores per micelle. In this way, we show that fitting the normalized FRET increases with a simple exponential function results in an overestimation of the micelle exchange rate. In addition, we show that in some cases, the observed increase in normalized FRET efficiency does not only depend on the exchange rate but also on the initial number of fluorophores per micelle, micelle core, fluorophore size, Förster radius, and micelle mixing ratio. Therefore, in the subsequent experiments, we pay special attention to characterizing the fluorescence properties of the equilibrated micelles. We show that the C3M exchange can take place over a broad range of time scales. The overall exchange rate can be strongly increased by increasing the ionic strength while changing the length of the unlabeled homopolymer has little effect on the exchange of the labeled homopolymer. These observations suggest that the splitting off of one or a few polymers is the rate-limiting step for the exchange of these C3Ms. Together, these results help to better understand the C3M exchange both by identifying additional important exchange parameters and by facilitating a better comparison of future FRET-based C3M exchange studies.

Materials and Methods

Materials

The reversible addition–fragmentation chain transfer (RAFT) agent 4-cyano-4-(phenylcarbonothioylthio)pentanoic acid (CTA), the coupling agents N-ethyl-N′-(3-dimethylaminopropyl)carbodiimide hydrochloride (EDC·HCl) and 1-hydroxybenzotriazole hydrate (HOBt), the macroRAFT chain transfer agent poly(ethylene glycol) 4-cyano-4-(phenylcarbonothioylthio)pentanoate M_n = 10 000 g mol^–1 (PEG-CTA), the negative monomer 3-sulfoproyl methacrylate potassium salt (KSPMA), and the positive monomer 2-trimethylammonioethyl methacrylate chloride (TMAEMA) in 80 wt % aqueous solution and the radical initiator 4,4′-azobis(4-cyanovaleric acid) (ACVA) were all purchased from Sigma-Aldrich. The radical initiator 2,2′-azobis[2-(2-imidazolin-2-yl)propane]dihydrochloride (VA-044) was purchased from WAKO chemicals. The donor and acceptor dyes with the amine linker, sulfo-cyanine3 amine, and sulfo-cyanine5 amine were purchased from Lumiprobe. The aprotic base N,N-diisopropylethylamine (DIPEA) was purchased from TCI and potassium chloride (KCl) was purchased from VWR. Dimethylformamide (DMF), acetone, and methanol were purchased from Biosolve. The TMAEMA monomer was run over an alumina column to remove the inhibitor. All other materials were used as received.

Fluorescently Labeled RAFT Agent Synthesis

The sulfo-cyanine3 amine dye was coupled to the carboxyl group of the RAFT chain transfer agent using EDC/HOBt coupling: sulfo-cyanine3 amine (25 mg, 35 μmol) was dissolved in 3.2 mL of DMF and the CTA (15 mg, 54 μmol), EDC·HCl (13 mg, 68 μmol), HOBt (9 mg, 68 μmol), and DIPEA (12 mL, 68 μmol) were added. After 16 h of stirring at room temperature, the crude product was concentrated by rotary evaporation and purified by column chromatography on a silica gel with a mobile phase of acetone/methanol (3/1, v/v). The purified product sulfoCy3-CTA was concentrated by rotary evaporation and dried under vacuum at 40 °C (yield: 24 mg, 73%). Functionalization of the RAFT agent was checked by ¹H NMR (Figure S1). The same protocol was used to synthesize sulfoCy5-CTA, and only the sulfo-cyanine3 amine was replaced by sulfo-cyanine5 amine (yield: 20 mg, 63%).

Synthesis of the PSPMA Homopolymers

For the synthesis of the negatively charged poly(3-sulfopropyl methacrylate) (PSPMA) homopolymer with the sulfo-cyanine3 dye attached to its end (Figure 1b), the sulfoCy3-CTA (24 mg, 25 μmol) was dissolved in 16 mL of Milli-Q. Subsequently, KSPMA (0.73 g, 3.0 mmol) and ACVA (1.3 mg, 5 μmol) were added. The reaction mixture was degassed with N₂ for 30 min and then reacted at 70 °C for 16 h. Subsequently, the reaction mixture was dialyzed against Milli-Q and freeze-dried to yield the fluorescent PSPMA-sCy3 polymer (0.51 g, 50%).

For the synthesis of the PSPMA-sCy5 polymer, the sulfoCy5-CTA (20 mg, 20 μmol) was dissolved in 16 mL of a Milli-Q/DMF (3/1, v/v) mixture. Subsequently, KSPMA (0.59 g, 2.4 mmol) and ACVA (1.1 mg, 4 μmol) were added. The reaction mixture was degassed with N₂ for 30 min and then reacted at 70 °C for 16 h. Subsequently, the reaction mixture was dialyzed against Milli-Q and freeze-dried to yield the fluorescent PSPMA-sCy5 polymer (0.44 g, 72%).

The synthesis of the unlabeled PSPMA homopolymers is described elsewhere.¹⁴

The number average molecular weights (M_n) and weight average molecular weights (M_w) of the PSPMA polymers were determined using an Agilent aqueous gel permeation chromatography (GPC) equipped with a refractive index detector and using PL aquagel Mixed-M as the column. NaNO₃ (0.2 M)–NaH₂PO₄ (0.01 M) buffer solution (pH = 7.0) with NaN₃ (0.2 wt %) was used as the eluent at a flow rate of 0.6 mL min^–1 at 30 °C. The column was calibrated using poly(methacrylic acid) standards. The number average molecular weights are 2.7 × 10⁴, 1.7 × 10⁴, 1.3 × 10⁴ g mol^–1, and 2.8 × 10⁴ g mol^–1 for PSPMA-sCy3, PSPMA-sCy5, unlabeled PSPMA₅₁, and unlabeled PSPMA₁₃₂, respectively. The corresponding weight average molecular weights are 4.6 × 10⁴, 2.8 × 10⁴, 1.6 × 10⁴, and 5.1 × 10⁴ g mol^–1.

Synthesis of the PEG-b-PTMAEMA Diblock

To synthesize the PEG-b-PTMAEMA diblock, the PEG-CTA (0.3 g, 30 μmol), the TMAMEA monomer (0.50 g, 2.4 mmol), and the VA-044 radical initiator (1.9 mg, 6 μmol) were dissolved in Milli-Q to give a final volume of 10 mL. The reaction mixture was degassed with N₂ for 30 min and then reacted at 44 °C for 16 h. Subsequently, the reaction mixture was dialyzed against Milli-Q and freeze-dried to yield the PEG-b-PTMAEMA diblock (0.65 g, 81%). Based on the ¹H NMR spectrum, the average degree of polymerization of the PTMAEMA block was estimated to be 75 (Figure S2).

Micelle Preparation

To prepare the micelles, stock solutions of 10 mM KCl and 2 M KCl, stock solutions of the negatively charged homopolymers PSPMA-sCy3, PSPMA-sCy5, PSPMA₅₁, and/or PSPMA₁₃₂ and a stock solution of the positively charged diblock copolymer PEG-b-PTMAEMA were mixed in this order to give the micelle sample with the desired monomer and KCl concentrations. In all cases, the micelles were prepared at equal charge stoichiometry (3-sulfopropyl methacrylate (SPMA)/TMAEMA = 1:1). Unless otherwise indicated, the final KCl concentration was 100 mM and the final SPMA monomer concentration was 1 mM, with 20% of these SPMA monomers being part of fluorescently labeled PSPMA (PSPMA-sCY3 and/or PSPMA-sCy5) and the remaining 80% being part of the unlabeled PSPMA₁₃₂. The micelles were allowed to equilibrate for at least 24 h before they were used for fluorescence or light scattering measurements.

Light Scattering Measurements

Static light scattering measurements were performed on an ALV instrument equipped with a 660 nm laser over a detection angle range from 30 to 120° in intervals of 2°. At every detection angle, five runs of 30 s were performed. The Rayleigh ratio R at each detection angle θ was calculated using

1

Here I_sample(θ), I₀(θ), and I_ref(θ) are the sample, solvent, and reference scattering intensities, respectively, n₀ and n_ref are the refractive index of the solvent and reference, respectively, and R_ref is the Rayleigh ratio of the reference. The refractive index of the solvent is n₀ = 1.3332. We have used toluene as a reference with n_ref = 1.496 and R_ref = 8.56 × 10^–4 m^–1.²³ To estimate the micelle molar mass from the measured Rayleigh ratio, we have used Zimm analysis and Guinier analysis. According to the Zimm approximation, the Rayleigh ratio is given by

2

where C is the mass concentration, M_w is the molar mass of the scattering particle, R_g is its radius of gyration, q = (4πn₀/λ) sin(θ/2) is the scattering vector with λ the laser wavelength, and K is an optical constant given by

3

where N_av is Avogadro’s number and dn/dC is the specific increase in the refractive index of the micelles, for which we have used a weighted average of the increase in the refractive index of PEG, PSPMA, and PTMAEMA, which are 0.135, 0.125, and 0.158 mL g^–1, respectively.²⁴⁻²⁶ In the Guinier approximation, the Rayleigh ratio is given by

4

For the Zimm approximation, the micelle molar mass M_w thus follows from the intercept when extrapolating to a zero detection angle, and for the Guinier approximation, the micelle molar mass follows from the intercept when extrapolating to a zero detection angle. Data points measured at angles smaller than 70° were excluded from the analysis because they showed an upturn in scattering intensity. This is presumably due to the presence of a small fraction of aggregates and was observed earlier in light scattering measurements of C3Ms.²⁷ Also, data points measured at a detection angle above 118° were excluded from the analysis because these data points showed a lot of scattering. The micelle molar masses that were obtained in this way and an example of a Zimm plot and a Guinier plot are given in the Supporting Information (Table S1 and Figure S3). Based on the molar mass of the micelles and the molar mass of the homopolymer and diblock, the number of homopolymers in the micelles can be estimated. We have performed the light scattering measurements at different KCl concentrations to obtain the molar mass of donor micelles at a SPMA monomer concentration of 1 mM, with all SPMA monomers being part of a PSPMA-sCy3 homopolymer (100% label percentage). Subsequently, we have used the donor micelle molar masses to estimate both the number of donors in donor micelles and the number of acceptors in acceptor micelles. This is because the acceptor micelles absorbed part of the laser light and, therefore, their molar mass could not be determined by light scattering measurements.

Fluorescence Spectroscopy Measurements

Fluorescence spectroscopy measurements were performed using an Agilent Cary Eclipse fluorescence spectrophotometer connected to a PCB-150 circulating water bath. All measurements were performed at 25 °C. An excitation wavelength of 530 nm was used, except for the self-quenching measurements of the acceptor micelles, for which an excitation wavelength of 620 nm was used. For the measurements of the equilibrated micelles, a single emission spectrum of the equilibrated sample was recorded. For the micelle exchange measurements, the equilibrated donor and acceptor micelles solutions were added to the cuvette in the desired ratio, mixed, and placed in the spectrophotometer. An emission spectrum was recorded every minute. For measurements that took longer than 16 h, the measurement interval was increased to 5 min after the first few hours.

To determine the FRET efficiency, the recorded spectra were first corrected for direct acceptor excitation by subtracting the spectrum of the acceptor micelles excited at 530 nm. Subsequently, the spectrum was fit with a linear combination of fixed log-normal functions to determine the relative contribution of the donor and acceptor emission to the overall emission spectrum (Section S3, Supporting Information). Finally, the FRET efficiency E was calculated by

5

where the donor intensity I_D and acceptor intensity I_A follow from the integration of the donor and acceptor part of the emission spectrum, respectively.

Analytical Model

To extract the micelle exchange dynamics from the observed FRET increase, we need a description of how this FRET increase depends on both the micelle exchange rate and on other micelle and fluorophore properties. In this section, we derive an analytical model that provides this description. We will first derive how the FRET efficiency depends on the Förster radius, micelle core size, donor size, and the number of fluorophores in the micelle. Subsequently, we will derive how the distribution of fluorophore numbers changes in time for a given micelle exchange rate. Finally, by combining these results, we obtain an analytical description of the FRET increase in time as a function of the micelle exchange rate(s) and the micelle and fluorophore properties.

The energy transfer efficiency E between a single donor and acceptor is given by

6

where k_D is the rate of photon emission from the donor and k_A is the rate of energy transfer to the acceptor. In the case of FRET, k_D/k_A = (r/R_F)⁶, where r is the donor–acceptor separation distance and R_F their Förster radius. In the core of each micelle, a given donor may be surrounded by i acceptors to which the donor can transfer its excited state energy. In this case, the energy transfer efficiency per donor becomes

7

where n_A,j is the number of acceptors that have a distance r_j to the donor. Here, we assumed that the energy transfer efficiency per donor does not depend on the number of donors in the micelle core; in other words, the energy transfer of a donor to a certain acceptor does not hinder the energy transfer of another donor to this same acceptor.

When the acceptor fluorophores distribute themselves homogeneously over the micelle core, the number of acceptors n_A at a distance r from the donor is given by n_A = ρ_A4πr² dr, where ρ_A is the number density of the acceptors in the micelle core. This gives for the energy transfer efficiency per donor

8

where R₀ is the size of the donor fluorophore. The acceptor number density is given by ρ_A = n_A/(4/3πR_m³), where R_m is the micelle core radius. The energy transfer efficiency per donor can thus also be written as

9

where we grouped different geometrical constants in a single constant ν = R_F⁶/(R_mR₀³).

During the micelle exchange experiments, we measure the FRET efficiency averaged over all of the donors in the sample. Not all of the donors will have the same FRET efficiency since not every micelle will contain exactly the same number of acceptors. Initially, the micelles that started with only acceptors (the acceptor micelles) will contain much more acceptors than the micelles that started with only donors (the donor micelles). In addition, also within the donor and acceptor micelle populations, the number of acceptors per micelle will vary because exchange events do not take place at exactly the same time for every micelle. The average FRET efficiency per donor in a donor micelle ⟨E_D⟩ is given by

10

where n_A is the number of acceptors in a donor micelle and P(n_A) denotes the probability to find a donor micelle with n_A acceptors. Similarly, the average FRET efficiency per donor in an acceptor micelle ⟨E_A⟩ is given by

11

where we used m_A to indicate the number of acceptors in an acceptor micelle. When donor micelles contain on average ⟨n_D⟩ donors, the total number of donors in donor micelles is given by n_D,tot = ⟨n_D⟩f_Dq, where f_D is the fraction of donor micelles and q is the total number of micelles. For the acceptor micelles with on average m_D donors per micelle, the total number of donors in acceptor micelles is given by m_D,tot = ⟨m_D⟩f_Aq, where f_A = 1 – f_D is the fraction of acceptor micelles. When the donor micelles contain on average N_D donors at the start of the mixing experiment, the total number of donors in the sample is f_DN_Dq. The FRET efficiency averaged over all donors in the sample at a certain time t is thus given by

12

To calculate the average FRET efficiency of the sample as a function of time, we thus need to know the probability distributions of the number of donors and acceptors per micelle for the donor and acceptor micelles and how these distributions change in time. These changes in time are related to the exchange of the donor and acceptor fluorophores. When one fluorophore splits off from a micelle with n fluorophores, the number of micelles with n fluorophores decreases by 1 and the number of micelles with n – 1 fluorophores increases by 1. When one fluorophore merges with a micelle with n fluorophores, the number of micelles with n fluorophores decreases by 1, and this time the number of micelles with n + 1 fluorophores increases by 1.

The dissociation of fluorescently labeled chains from the micelles is a stochastic process for which we can define the average rate at which a chain splits off as k. A micelle with n fluorescently labeled chains has an n times larger chance that one fluorescently labeled chain splits off than a micelle with only one fluorescently labeled chain. The rate at which a micelle with n fluorophores goes to n – 1 fluorophores is thus given by nk.

The total number of splitting events of donors in a time period dt is the sum of all splitting events of the donor and acceptor micelles: k(∑_nDP(n_D)n_D + ∑_mDP(m_D)m_D) dt = kN_D dt. In the same way, we can describe the total number of splitting events of the acceptors in a time period dt with k(∑_nAP(n_A)n_A + ∑_mAP(m_A)m_A) dt = kM_Adt, where M_A is the average number of acceptors in acceptor micelles at the start of the mixing experiment.

The average micelle size does not change in time. Therefore, the total number of merge events should be equal to the total number of splitting events and is thus given by kN dt. Here, we have used the general notation N to indicate the initial number of donors in donor micelles or the initial number of acceptors in acceptor micelles. The insertion can take place in any micelle and does not depend on the number of fluorophores in the micelle. The probability that a fluorophore is inserted in a donor micelle of n fluorophores is thus just given by the probability to find a donor micelle with n fluorophores, which is given by f_DP(n). In the same way, the probability that a fluorophore is inserted in an acceptor micelle with n fluorophores is given by f_AP(n). The general notation of the merge rate thus becomes fNk, where f can denote both the fraction of donor micelles and the fraction of acceptor micelles.

The expulsion rates and insertion rates together give the change in time of the probability P(n) to find a micelle type with n fluorophores

13

This system of differential equations can be solved analytically (Section S7, Supporting Information) to give

14

with

15

for the probability distribution of the number of acceptors in donor micelles and for the probability distribution of the number of donors in acceptor micelles and

16

with

17

for the probability distribution of the number of donors in donor micelles and for the probability distribution of the number of acceptors in acceptor micelles. Equations 14 and 16 are both Poisson distributions with an average λ(t) and μ(t), respectively. The average number of donors in acceptor micelles is thus given by ⟨n_D(t)⟩ = λ(t) = f_DN_D(1 – e^–kt) and the average number of donors in donor micelles by ⟨m_D(t)⟩ = μ(t) = N_D(f_D + (1 – f_D) e^–kt).

To derive eqs 13–17, we have assumed that the fluorophores exchange independently from each other. This is true when micelle exchange takes place by expulsion and insertion, and every chain contains maximal one fluorescent label. However, when the micelles exchange mainly by fusion and fission, the chains will exchange in clusters and thus do not exchange independently. For small clusters, we expect that the results will not deviate that much from independent fluorophore exchange, especially when the label fraction is low and, therefore, the number of fluorophores per cluster is low. For the exchange of large clusters with large fluorophore numbers, eqs 14–17 cannot be used to describe the fluorophore exchange. Therefore, our analytical model for FRET micelle exchange experiments is limited to micelle exchange that takes place by expulsion and insertion or by fission and fusion of small clusters.

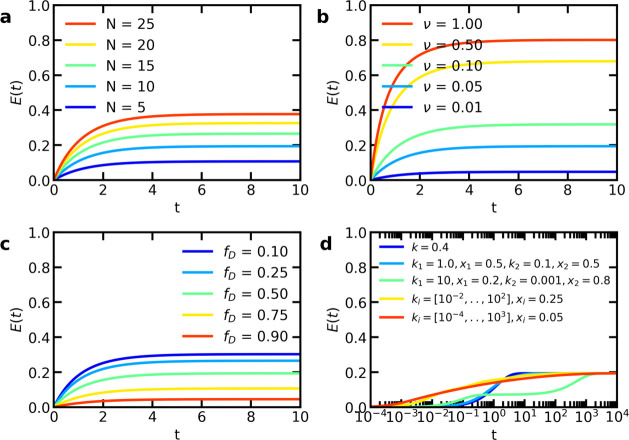
Once we know the experimental parameter ν and how the distributions of fluorophores per micelle change in time (eqs 14 and 16), we can predict how the FRET efficiency will change in time (eq 12). A change in the initial number of fluorophores, the experimental constant ν, the fraction of donor micelles f_D, and the exchange rate k can all affect the time evolution of the FRET efficiency (Figure 2). In earlier FRET exchange experiments of C3Ms,^5,6 the increase in FRET efficiency has been fitted with an exponential function E(t) = E(∞)[1 – e^–kt], where it was assumed that the rate constant k is a direct measure for the micelle exchange rate. This exponential function gives a slower increase in FRET efficiency compared to our analytical model (Figure 3). This suggests that fitting the FRET efficiency increase with a simple exponential function results in an overestimation of the micelle exchange rate. In addition, for the exponential function, the increase in normalized FRET efficiency E(t)/E(∞) only depends on the exchange rate k, while according to our analytical model, this increase can be affected by changes in the initial average fluorophore number (Figure 3a), the experimental constant ν (Figure 3b), and the fraction of donor micelles f_D (Figure 3c). These effects of N, ν, and f_D occur especially for larger N and ν values (Figure 4). A faster increase in normalized FRET efficiency thus does not necessarily mean that the micelle exchange is faster but might also be caused by differences in other parameters, which the simple exponential fit does not take into account.

Figure 2.

Model predictions of the FRET efficiency E as a function of time after mixing t for (a) different fluorophore numbers N_D = N_A = N; (b) different experimental constants ν; (c) different donor micelle fractions f_D; and (d) different fluorophore types with the exchange rate k_i and fraction x_i. Unless otherwise indicated, N = 10, ν = 0.05, f_D = 0.5, and k =0.4.

Figure 3.

Model predictions of the normalized FRET efficiency E(t)/E(∞) as a function of time after mixing t for (a) different fluorophore numbers N_D = N_A = N; (b) different experimental constants ν; (c) different donor micelle fractions f_D; and (d) different fluorophore types with the exchange rate k_i and fraction x_i. Unless otherwise indicated, N = 10, ν = 0.05, f_D = 0.5, and k = 0.4. Dashed lines indicate the exponential function E(t) = E(∞)[1 – e^–kt] with k = 0.4.

Figure 4.

Effect of larger N or ν-values on the model predictions of the normalized FRET efficiency E(t)/E(∞) as a function of time after mixing t for (a, d) different fluorophore numbers N; (b, e) different experimental constants ν; and (c, f) different donor micelle fractions f_D. For the top row (a–c), N is increased (unless otherwise indicated N_D = N_A = N = 100 and ν = 0.05), while for the bottom row (d–f) ν is increased (unless otherwise indicated N_D = N_A = N = 10 and ν = 2.0). The exchange rate k is 0.4. Unless otherwise indicated, f_D = 0.5.

Up to now, we have considered the case of a single fluorophore type, where all fluorophores have the same exchange rate k. In reality, the polydispersity of the chains and/or micelles or other sources of heterogeneity will lead to a distribution of exchange rates and we thus need to consider different fluorophore types, each with their own exchange rate k_i.

To find the distribution of the total number of donor or acceptor fluorophores in a donor or acceptor micelle, we make use of the fact that for random variables n₁ and n₂ with Poisson distributions with averages λ₁ and λ₂, the sum of these random variables n = n₁ + n₂ is also a Poisson distribution with a mean λ = λ₁ + λ₂. After summation of all fluorophore types, each with their own exchange rate k_i, we thus get for the number of donors in acceptor micelles and vice versa again a Poisson distribution . At this time, the average of the Poisson distribution is given by

18

Here, N_i is the initial average number of fluorophores per micelle of fluorophore type i and is given by N_i = x_iN, where x_i is the fraction of this fluorophore type. For the number of donors in donor micelles and the number of acceptors in acceptor micelles, we also get a Poisson distribution with as average

19

Equations 18 and 19 imply that for a given average fluorophore number to initial fluorophore number ratio ⟨n⟩/N, the Poisson distribution will always be the same irrespective of the rates at which the fluorophores exchange. We will use this later on to estimate the fraction of chains that has exchanged at a certain time.

The occurrence of multiple exchange rates can broaden the time scales over which the increase in FRET efficiency takes place (Figures 2d and 3d). For similar exchange rates, this broadening effect is relatively small as shown by the relatively small change for the exchange with k₁ = 1.0 and k₂ = 0.1 as compared to the exchange with k = 0.4. For large differences in exchange rates, a substantial broadening of time scales occurs.

Results and Discussion

To perform the FRET-based C3M exchange experiments, we have synthesized a negatively charged homopolymer with the donor or acceptor fluorophore attached to its end (Figure 1b). Specifically, we have coupled a sulfo-cyanine3 dye (donor) or a sulfo-cyanine5 dye (acceptor) to a RAFT agent and subsequently used these fluorescently labeled RAFT agents to perform the polymerization of 3-sulfopropyl methacrylate (SPMA) to give PSPMA-sCy3 and PSPMA-sCy5, respectively. Using this labeling protocol, we expect that the fluorophores will interfere less with the electrostatic attraction between the polyelectrolytes because we have not replaced any charged group to functionalize the polymers. Nevertheless, the introduction of these fluorophores can still affect the micelle properties by introducing additional stabilizing or destabilizing interactions between the fluorophores themselves or between the fluorophores and polyelectrolytes. Another advantage of our labeling protocol is that we have limited the number of fluorophores per chain to one, which increases the chance that the fluorophores exchange independently. This independent exchange is one of the assumptions that we have used to derive the analytical model. Although the number of fluorophores per chain is fixed, we can still vary the number of fluorophores per micelle by varying the ratio of the labeled and unlabeled PSPMA homopolymer. We define the label fraction α as the number of SPMA monomers that are part of a fluorescently labeled homopolymer divided by the total number of SPMA monomers. We make the micelles by mixing the PSPMA homopolymers at a 1:1 charge ratio with the diblock copolymer PEG-b-PTMAEMA, where PTMAEMA is the positively charged block.

Fluorescence of Equilibrated Micelles

According to the model, the micelle core size, donor size, and Förster radius can have substantial effects on the increase in FRET efficiency, even when the FRET efficiency is corrected for the final FRET efficiency E(∞) of the completely mixed micelles (Figure 4). Therefore, before starting the exchange experiments, we first determine the fluorescence properties of the equilibrated donor micelles, acceptor micelles, and mixed micelles.

Inside the micelle, the local fluorophore concentration can be high. Hence, we first check whether self-quenching occurs. Indeed, for label fractions larger than 0.2, the fluorescence intensity does no longer increase proportionally with the increasing fluorophore fraction (Figure 5a,b), indicating that self-quenching takes place. The self-quenching effects are stronger for the acceptors than for the donors. The main explanation for this difference is probably the shorter length of the acceptor polymers and, therefore, a higher number of acceptors per micelle at equal label fractions. This difference in self-quenching will affect the measured apparent FRET efficiency. Therefore, in the micelle exchange experiments, we will use a label fraction of α = 0.2. An additional advantage of this low label fraction is that we further increase the chance that the fluorophores exchange independently.

Figure 5.

Fluorescence of the equilibrated micelles at different label fractions. Fluorescence intensity of the donor micelles (a) and acceptor micelles (b) at different label fractions α normalized to the intensity at a label fraction α = 0.1. The dashed lines indicate the theoretical intensity without self-quenching. (c) Normalized fluorescence spectra of the mixed micelles at different label fractions after correction for direct acceptor excitation. (d) FRET efficiency as a function of label fraction α. E_measured is the experimentally measured FRET efficiency and E_corrected is the FRET efficiency after correction for differences in self-quenching of the donor and acceptor. The solid red line indicates the model prediction for N_D = 33, N_A = 55, and ν = 0.03.

The final FRET efficiency of the completely mixed micelles can be found by first mixing the donor and acceptor polymers and subsequently adding the oppositely charged diblock copolymer to form the micelles. Increasing the number of donors and acceptors per micelle should decrease the average distance between the fluorophores and, therefore, the FRET efficiency should increase. Indeed, at larger label fractions, the contribution of the donor fluorescence becomes smaller and the contribution of the acceptor fluorescence becomes larger (Figure 5c).

To compare the FRET efficiencies at different label fractions with each other, the measured FRET efficiencies have to be corrected for the differences in donor and acceptor self-quenching. As a first approximation, we use the ratio between the measured intensity of the donor micelles compared to the theoretical intensity, when no self-quenching would have occurred, as a correction factor for the donor intensity and do the same for the acceptor intensity. At the same label fraction, the donor micelles contain two times more donors than the end FRET micelles. The same applies to the acceptor micelles. Therefore, we have used, for example, the donor micelles at α = 0.5 to calculate the correction factor for the mixed micelles at α = 1.0. After these corrections, we can construct a plot of the FRET efficiency of the mixed micelles E(∞) as a function of label fraction (Figure 5d). This end FRET efficiency depends on the number of donors and acceptors per micelle and the experimental constant ν. The number of donors and acceptors per micelle at a label fraction of α = 1.0 can be roughly estimated using light scattering experiments (Table 1). By multiplying this fluorophore number by the label fraction, we can also get the fluorophore numbers for other label fractions. Subsequently, we can compare our data to the model predictions to roughly estimate ν (Figure 5d). This gives ν = 0.03.

Table 1. Micelle Characteristics at Different Salt Concentrations^a.

[KCl] (mM)	ND	NA	ν
10	46	76	0.03
100	33	55	0.03
200	25	41	0.03
300	27	44	0.03
400	24	39	0.02

^aN_D and N_A are estimated from light scattering experiments of the donor micelles with α = 1.0. ν is estimated by comparing the experimentally measured FRET efficiency at different label fractions with the model predictions. For these model predictions, the N_D and N_A values obtained by the light scattering experiments are used.

The obtained value for ν is quite low. For example, if we take a Förster radius of 5.2 nm, which is the Förster radius of the cyanine3 and cyanine5 pair in water,²⁸ and take a micelle core size of ∼10 nm^9,29 and a donor size of ∼2 nm, we would get ν ≈ 2.5. A possible explanation for the lower ν value is that the attachment to the polymer restricts the movement of the fluorophores, resulting in a lower Förster radius and a larger effective donor size. In addition, the Förster radius within a complex coacervate environment might differ from the Förster radius in water. Because of the third power or even sixth power dependence, small changes in R_F, R₀, and R_M can have large effects on ν.

The low ν in combination with relatively low N values would mean that the normalized FRET efficiency E(t)/E(∞) is little affected by variations around N or ν. This would make the data comparison of different experiments easier because, in that case, changes in E(t)/E(∞) will be mainly caused by changes in exchange rates and not by differences in N or ν. We note that although this might apply to this C3M system, this does not necessarily have to be the case for all C3Ms. For example, for protein-containing C3Ms, higher FRET efficiencies were found,⁶ indicating larger N or ν values. Indeed, the number of fluorescent proteins per micelle³⁰ is larger than the number of fluorescently labeled chains per micelle (Table 1). For these larger fluorophore numbers, variations in N and ν affect the normalized FRET increase more (Figure 4a–c).

Micelle Exchange at 100 mM KCl

Now we have characterized the fluorescence of the equilibrated C3Ms and can start to focus on their exchange. First, we consider micelles at a 100 mM KCl concentration. At this salt concentration, the micelles show a broad exchange time range (Figure 6). The first exchange takes place within 1 min, while even after 16 h, the micelles would not have reached their completely mixed state yet. This largely differs from the measured exchange of protein-containing C3Ms, where the final FRET efficiency seems to be reached within 5 min.⁶ On the other hand, Holappa et al. have also observed a broad time range for C3Ms consisting of polymers only.⁵ They explained the large differences in time scales by two different processes, with the expulsion and insertion being the fast process and fission and fusion being the slow process. However, this cannot be the full explanation. First, if all fluorescently labeled chains are equivalent, they can all exchange by expulsion and insertion and all chains would have already been exchanged by this mechanism before fission and fusion starts to play a role. Therefore, to observe largely different time scales, different populations of fluorescently labeled chains should be present, where each population has its own exchange rate k_i. It might be that the slower exchanging chains indeed have a larger tendency to exchange by fission and fusion, but this is not necessarily the case. In addition, if the micelle exchange takes place by only two distinct processes as was suggested by Holappa et al., the FRET efficiency would show a stepwise increase in a logarithmic time scale (Figure 3d), while here the FRET efficiency seems to increase continuously. This indicates a broad distribution of different exchange rates.

Figure 6.

Micelle exchange experiments at 100 mM KCl: normalized FRET efficiency E(t)/E(∞) as a function of time after mixing t for (a) different monomer concentrations; (b) different unlabeled homopolymer lengths, and (c) different fractions of donor micelles.

A logarithmic relaxation has also been observed for amphiphilic diblock copolymer micelles.^16−18,20 Often, this logarithmic relaxation is explained by some polydispersity of the polymers in combination with a strong dependence of the exchange rate on the polymer core block length,¹⁸⁻²⁰ although computer simulations have suggested that in some cases even for monodisperse chains, logarithmic relaxation might occur.³¹ Also, in our case, polydispersity probably has played a role, as the donor and acceptor polymer have a dispersity of 1.7 and 1.6, respectively. This is high for polymers synthesized by RAFT polymerization and is probably caused by the fact that the polymerization of SPMA can be prone to termination reactions as we have observed earlier by following the reaction with ¹H NMR spectroscopy.¹⁴ To further discuss the effect that this large polydispersity might have on the exchange, we first need to know more about the exchange mechanisms. Therefore, we will first focus on these mechanisms and come back to the polydispersity effect later in this paper.

The first step in elucidating the exchange mechanisms of micelles is to check their concentration dependence. For fission and fusion, the merging is considered to be rate limiting, which is a second-order process and, therefore, should be concentration dependent, while for expulsion and insertion, the splitting is considered to be rate limiting, which is a first-order process and, therefore, concentration independent. In our case, only at lower concentrations an increase in the concentration results in a faster increase of the FRET efficiency (Figure 6a). Increasing the monomer concentration above 1 mM does not increase the exchange rate any further. This indicates that at least for higher concentrations no second-order process is rate limiting and, therefore, splitting is probably the rate-limiting step. The concentration dependence at lower concentrations might mean that here the merging step is rate limiting. Alternatively, the FRET increase might be slower because at these lower concentrations the probability of merging with the original micelle might become higher.

The rate-limiting splitting step at higher concentrations can be an expulsion process or a fission process. To determine which of these two split mechanisms prevails, we have measured the exchange for two different unlabeled homopolymer lengths (Figure 6b). For fission, multiple chains split off simultaneously and we therefore expect a stronger effect of changing the unlabeled homopolymer than for expulsion. In the Langevin dynamics simulations of the initial C3M exchange, we saw that decreasing the polyelectrolyte length can increase the fission rate.⁸ Here, we decrease the polyelectrolyte length of the majority (80%) of the homopolymers and, therefore, expect an increase in the exchange rate if fission is rate-limiting. This is not the case: the effect of changing the homopolymer length on the exchange rate seems negligible. This suggests that the splitting occurs mainly by expulsion, where in every split step only one or two homopolymers split off.

We note that this expulsion-dominated exchange differs from the recently observed fission-dominated dissociation of micelles upon an increase in the salt concentration.⁹ This can be explained by the fact that we measure the exchange of equilibrated micelles, while the dissociating micelles are not in equilibrium and can gain free energy by decreasing their aggregation number with the largest gain when the micelle splits in equal sizes.⁹

The fact that the exchange rate of the labeled homopolymers is not decreased by adding longer unlabeled homopolymers also implies that, at least for this C3M system, the protection of the cargo cannot be improved by adding longer polymers that have the same charge as the cargo. This is in line with a recent study on protein-containing C3Ms, where it was shown that adding a negatively charged homopolymer does not help in preventing the dissociation of the negatively charged proteins from the micelle at higher salt concentrations.³²

In addition to changing the total micelle concentration and the length of the unlabeled polymer, we can also change the ratio at which we mix the donor and acceptor micelles (Figure 6c). Rather than giving new insights into the exchange mechanisms themselves, this can give additional information on the fluorescence properties of the system. As mentioned before, these fluorescence properties are important to interpret the observed increase in normalized FRET efficiencies in terms of micelle exchange rates. The relatively low N and ν values we obtained from studying equilibrated micelles suggest that differences in E(t)/E(∞) are mainly caused by changes in the exchange rate and not by other factors. Changing the ratio of donor and acceptor micelles can help in checking whether this is indeed the case: for low N and ν values, changes in the donor fraction f_D should only have little effect on the normalized FRET efficiency increase (Figure 3c), while for larger N and ν this effect is larger (Figure 4c,f). In this case, we observe some differences in normalized FRET increase, especially at the start of the mixing experiment. However, these differences do not follow a general trend, as the normalized FRET first seems to decrease when going from f_D = 0.25 to 0.5 and subsequently seems to increase again when going to f_D = 0.75. Based on our model, we would expect a decrease in both E(t) and E(t)/E(∞) for increasing donor fractions. For E(t), this is indeed the case (Figure S6), but the normalized FRET efficiency deviates from this prediction. Presumably, this deviation is caused by experimental uncertainties in the determination of the end FRET efficiency and the correction for direct acceptor excitation. Since we work at relatively low FRET efficiencies, small deviations might already affect the normalized FRET efficiency. This is especially the case for the highest donor fraction since this gives the lowest FRET efficiency. Due to these experimental uncertainties, we cannot conclude whether the donor fraction indeed has a negligible effect on the increase in FRET efficiency. However, its effect is at least smaller than the experimental uncertainty in the determination of E(t)/E(∞).

Ionic Strength Effect

In the previous section, we concluded that the chain expulsion from the core is probably the rate-limiting step of the exchange. The exchange rate should thus be affected by changing the electrostatic attraction in the core. Therefore, we continue by measuring the C3M exchange at different ionic strengths. Again, we first check the fluorescence properties of equilibrated micelles before we focus on the exchange itself.

An increase in the ionic strength decreases the FRET efficiency (Figure 7a). The FRET efficiency can be decreased by an increase in the fraction of fluorophores free in solution and by a decrease of fluorophore volume fraction within the micelle core. Even at 400 mM KCl, the fraction of free fluorophores is only about 2% (Figure S7). The decrease in FRET efficiency is thus mainly the result of a decrease in the fluorophore volume fraction. This means that the polyelectrolyte volume fraction in the coacervate phase decreases with increasing salt concentration, which has also been observed for the macroscopic phase separation of complex coacervates.^33,34 The decrease in FRET efficiency is accompanied by a decrease in micelle aggregation number (Table 1). This agrees with recent thermodynamic calculations, which also showed that the equilibrium micelle aggregation number decreases with the increasing salt concentration.⁹

Figure 7.

Effect of the ionic strength on the micelles. (a) FRET efficiency of the mixed micelles as a function of label fraction for different salt concentrations. FRET efficiencies are corrected for differences in donor and acceptor self-quenching. Solid lines are model predictions with N_D, N_A, and ν values as indicated in Table 1. (b) Micelle exchange experiments: normalized FRET efficiency E(t)/E(∞) as a function of time after mixing t at different salt concentrations. (c) Time t_x at which E(t_x)/E(∞) = 0.75, as a function of the square root of the salt concentration. Filled symbols are obtained from the experimental data. The open symbol is estimated from extrapolation exchange measurement of 16.7 h at c_s = 10 mM, assuming the same logarithmic time dependence as the final measured 3.3 h. (d) Estimated fraction of exchanged acceptor chains at t = 0.1 and 16 h as a function of salt concentration. The borders of the shaded regions correspond to the lower and upper limit of the estimated exchanged fraction.

From the measured FRET efficiencies and the estimated donor and acceptor numbers (Table 1), we can again estimate the experimental constant ν for the different salt concentrations. Only minor changes in ν take place (Table 1). The decrease in FRET efficiency is thus mainly the result of the decrease in the number of fluorophores per micelle.

The exchange rate is strongly increased by increasing the salt concentration (Figure 7b). Micelles at the lowest salt concentrations have the lowest normalized FRET efficiency after the first minute and also show the slowest increase for the next 16 h. At 400 mM KCl, the exchange is fast and within a few minutes the micelles reach the FRET efficiency of the completely mixed micelles E(∞). In fact, they even seem to reach an FRET efficiency slightly above E(∞) and, subsequently, their FRET efficiency slightly decreases. This might indicate that some of the fluorophores bleach, even though the majority of the fluorophores are stable against bleaching as we have shown by measuring the FRET efficiency of the mixed micelles over 16 h (Figure S8). The fast exchange indicates that the micelles at 400 mM KCl might be less effective encapsulators than one would expect based on their static properties: their monomer concentration is well above the critical micelle concentration of ∼20 μM (Figure S7) and the salt concentration is well below the critical salt concentration of ∼790 mM KCl (Figure S4) and still all chains exchange within a few minutes.

The strong salt dependence indicates that the micelle exchange rate is largely governed by the dissociation of electrostatic bonds. This dissociation is often treated as an activated process with an energy barrier that decreases linearly with the square root of the salt concentration.³⁵⁻³⁸ In this approach, the energy of the bound ion groups is calculated from Coulomb interactions, while the calculation of the energy of the unbound ion groups is based on the Debye–Hückel approximation. The last-mentioned gives the square root salt term in the energy barrier. To see whether the micelle exchange can also be described in this way, we compared for different salt concentrations the time t_x at which the normalized FRET efficiency equals 0.75 (Figure 7c). Here, we make use of the fact that for these micelles the normalized FRET efficiency is little affected by small changes in N and ν and, therefore, in all cases E(t)/E(t_x) = 0.75 corresponds to approximately the same fraction of exchanged chains. In the first approximation, the time t_x can thus be used as a direct measure of the micelle exchange rate.

The exchange times at 100, 200, and 300 mM KCl seem to show the expected square root salt dependence (Figure 7c). However, the exchange time that is obtained from extrapolating the exchange data at 10 mM KCl deviates from this trend and is larger than expected. This might mean that the electrostatic dissociation has a stronger salt dependence, as was also suggested by Marciel et al.³⁹ Another possibility is that inaccuracies in the extrapolation resulted in an overestimation of the exchange time. We assumed that the exchange continues with the same logarithmic increase, but the exchange might also show an upturn at later times. In addition, due to the slow increase in FRET efficiency, small errors in the E(t)/E(∞) determination have a major effect on the determination of t_x. To further determine the salt dependence, it would help if the exchange can be determined over a broader time range so that extrapolation is no longer necessary. A decrease in the time to measure the first data point would especially be helpful. Here, this time was set by the time needed to mix the micelle solutions and to record a full spectrum, which together took about 40 s. A broader time range would also allow determining the exchange times for different exchanged chain fractions. In this way, it would be possible to check whether the exchange of the first chains follows the same salt dependence as the later exchanging chains, which will help in determining whether all chains exchange by the same mechanism.

Although we cannot easily compare the exchange time for a given fraction of exchanged chains at all different salt concentrations, we can make the comparison the other way round and for a given time point determine which fraction of chains has exchanged. For this, we compare the experimentally normalized FRET efficiency at a given time point to the model predictions of the normalized FRET efficiency for the obtained N and ν values (Table 1). The increase in normalized FRET efficiency differs when the donors and acceptors exchange with other rates. Since we do not know how much the donor and acceptor exchange rate differs from each other, we cannot determine the fraction of exchanged chains exactly. Instead, we estimate a lower and upper limit of the exchanged acceptor chain fraction. The acceptor chain is on average shorter. Therefore, if the donors and acceptors show any difference in the exchange rate, we expect that the acceptor exchange is faster. To calculate the lower limit, we thus assume that the donor and acceptor have equal exchange rates, and to calculate the upper limit, we set the donor exchange rate to zero and let only the acceptors exchange. Here, we make use of the fact that for a given fraction of exchanged acceptors, the distribution of acceptors in the micelles is the same, irrespective of the acceptor exchange rates. The same applies to the donors. To determine the fraction of exchanged acceptor chains, we can thus use arbitrary exchange rates for the model predictions. The only restriction is that the donor and acceptor rates have to be the same to determine the lower limit and the donor exchange rate has to be zero to determine the upper limit. In this way, we find that even at the lowest salt concentration, at least 18% of the chains has already exchanged within 0.1 h (Figure 7d). On the other hand, more than 60% of the chains did not exchange within 16 h. This again shows the broad time range over which the exchange takes place. Increasing the salt concentration affects both the fraction of chains that exchanges at short times and at long times. Electrostatic interactions thus play a role both for the fastest 20% of the exchanging chains and for the slower exchanging chains.

Comparison to Literature Models of Exchange Rates

We now return to a broad range of the exchange rates and the role that the polymer polydispersity might have played in this. This requires a description of how the exchange rate k depends on the polymer length W. We know that the expulsion of chains from the core is probably the rate-limiting step in the exchange and that for this expulsion, electrostatic bonds have to be broken. Therefore, we compare our experimental data to three literature models predicting how the chain expulsion rate depends on the polymer length and one literature model predicting how the relaxation rate in complex coacervates depends on the polymer length.

To fit the different literature predictions to our experimental data, we first bin the exchange data in time steps that are evenly spaced on a logarithmic time scale. In this way, we give the data at short and long time scales similar weighting. Subsequently, we perform the fit. We first calculate the distribution of exchange rates k_i based on the literature model and on the polymer length W_i distribution. We approximate the experimental polymer length distribution with a Schulz–Zimm distribution. Based on GPC measurements, these distributions have a number average chain length of 110 and 71 and a weight average chain length of 189 and 115 for the donor and acceptor polymers, respectively. We split the donor and acceptor polymer distribution both in 100 fractions, each fraction having the same probability of 0.01. For every fraction i, we use its median polymer length as the characteristic polymer length W_i of this fraction. Subsequently, we use the literature predictions to calculate the corresponding exchange rate k_i for every fraction. Next, we use eqs 18 and 19 to calculate the average fluorophore numbers per micelle, where every time N_i is given by 0.01N, with N being the initial average number of donors per donor micelle (N = 6.6 for 100 mM KCl) or the initial average number of acceptors per acceptor micelle (N = 11 for 100 mM KCl). The substitution of this expression in eqs 14 and 16 gives the fluorophore distributions. Finally, we use these distributions and the obtained value for ν (Table 1) to calculate the average FRET efficiency in time (eq 12) and compare this to the experimental data. In this fit procedure, the parameters of the literature exchange rate equations are thus the only fit parameters. The other parameters are estimated from GPC measurements or are obtained from Table 1.

The first model that we consider is the sticky Rouse model that was also used to describe the relaxation of complex coacervates in rheology experiments.³⁶ In this description, the total relaxation rate scales with W^–2

20

Here, τ₀ is the relaxation time of a single monomer and is determined by the electrostatic attraction and, thus, the salt concentration. The sticky Rouse model cannot accurately describe the experimental data: it predicts an FRET efficiency increase over a much smaller range of time scales than for the experimental FRET efficiency increase (Figure 8a). The C3M exchange can thus not be described by only a combination of sticky Rouse relaxation and chain polydispersity.

Figure 8.

Model fits to the FRET micelle exchange data. (a) Fits of the different literature models for the exchange rate to the FRET micelle exchange data at 100 mM KCl. The obtained fit values are τ₀ = 1.0 s for the Sticky Rouse model (eq 20), ω₀ = 3.6 × 10² Hz and aE_a = 0.3 k_BT for the activated process with a linear dependence of the energy barrier on the polymer length (eq 21), ω₀ = 2.9 × 10⁵ Hz and aE_a = 1.6 k_BT for the activated process with a 2/3 power dependence of the energy barrier on the polymer length (eq 22) and αχ= 0.36 for the activated process with the polymer length included in the energy barrier and in the prefactor (eq 23). (b) Fit values of the activation energy of a single monomer aE_a for the activated processes (eqs 21 and 22) as a function of the square root of the salt concentration. Dashed lines are linear fits of the data.

The second approach to describe the exchange rate is based on a common description for the expulsion of chains from amphiphilic diblock copolymer micelles. Here, the expulsion is treated as an activated process where the energy barrier depends on the polymer length. For short chains, the energy barrier is assumed to scale linearly with the polymer length,⁴⁰ while for longer chains the energy barrier is to assumed to scale with W^2/3 because these chains are expected to be expelled as a globule.¹⁵ Only the interactions of the outer globule monomers have to be broken to expel the chain, which gives the W^2/3 dependence. For short chains, the exchange rate is thus given by

21

and for long chains by

22

Here, E_a is the activation energy required to break the interaction of a single monomer, a is a numerical prefactor, and ω₀ is the dissociation rate in the absence of an energy barrier. Fits of these models to the experimental data give average ionic bond-breaking activation energies of aE_a = 0.3 and 1.6 k_BT for the linear and power-law polymer length dependence, respectively. These values are smaller than an earlier estimated bond dissociation activation energy, which was ∼5 k_BT at a 100 mM ionic strength.³⁷ In addition, the ω₀ values are larger than earlier determined.³⁷ This might mean that different coacervate systems have different bond dissociation times and activation energies. Alternatively, the numerical prefactor a in C3Ms might be relatively small. Another possibility is that this activated process is actually not an accurate description of the micelle exchange rates and, therefore, result in apparent lower dissociation energies and shorter bond dissociation times.

Apart from evaluating the absolute value of E_a at a single ionic strength, we can also evaluate how E_a varies with ionic strength. For this, we fit these simple activated process models to the FRET micelle exchange data at different salt concentrations using ω₀ as the shared fit parameter (Figure S9). As explained in the previous section, we would expect that the activation energy E_a depends linearly on the square root of the salt concentration for an electrostatic activated expulsion process. This indeed seems to be the case (Figure 8b). A simple, purely electrostatic activated expulsion process thus seems to describe the C3M exchange data reasonably well.

The final model is based on another description of the exchange of amphiphilic diblock copolymer micelles, which was used to explain their logarithmic relaxation.¹⁸⁻²⁰ In this case, the exchange is again described as an activated process, but now with a Rouse type of relaxation included in the prefactor. The prefactor thus has a W^–2 dependence. The energy barrier is assumed to scale linearly with W in this approach

23

The B-term in the prefactor can be estimated based on the polymer characteristics, and this gives B ≈ 1.4 × 10⁷ Hz. Fitting this model to the experimental data gives a too slow increase in the normalized FRET efficiency (Figure 8a). In this model, the exchange rate thus depends too strongly on the polymer length to describe the experimental data.

In summary, of the four models, the simple activated processes (eqs 21 and 22) give the best agreement with the experimental data. However, these models require activation energy that is lower than expected for an electrostatic process, especially when the activation energy barrier depends linearly on the polymer length W. This might mean that for this complex coacervate system, the energy needed to dissociate a single ionic bond is smaller than for other complex coacervate systems or that the numerical prefactor in the activation energy barrier is relatively small. Alternatively, additional factors have to be taken into account apart from the polydispersity of the homopolymer. For example, the length and polydispersity of the oppositely charged block might also play a role, giving a double polydispersity effect that is not included in one of the models. In addition, the broad range of exchange rates might not only be caused by polydispersity of the chains. Computer simulations on amphiphilic block copolymer micelles have suggested that logarithmic relaxation can even occur for monodisperse chains,³¹ although in experiments with monodisperse core blocks, this logarithmic relaxation has not been observed.^19,41,42 The logarithmic relaxation in the computer simulations was explained by degeneracy of the energy states of the core blocks, which is broken when the chain leaves the core. If these degeneracy effects indeed could play a role in the exchange of amphiphilic diblock copolymer micelles, they might also play a role here. For example, a homopolymer that binds to complete positive blocks only can more easily be expelled than a homopolymer that binds to only parts of different positive blocks, even though both homopolymers have the same number of ionic bonds: in the first case, only nonelectrostatic interactions have to be broken, whereas in the second case the ionic bonds first have to rearrange before expulsion can occur. It would be interesting to follow the exchange of C3Ms with less polydisperse components over a broad range of time scales to determine whether the broad distribution of exchange rates is mainly caused by the chain polydispersity or that other effects play a role as well. Protein-containing C3Ms would be a good system for this since the proteins are monodisperse and, therefore, only the diblocks introduce polydispersity effects in this system. However, the exchange of these protein-containing C3Ms can be fast.⁶ Faster measurements are thus required to determine the initial exchange as well.

Conclusions

In conclusion, we have shown that the expulsion of chains from the core is probably the rate-limiting step in the exchange of equilibrated C3Ms and that their exchange is largely governed by electrostatic interactions. This expulsion-based exchange implies that the exchange rate of C3M components of interest cannot be decreased by adding more stable components with the same charge, which is illustrated by the fact that the exchange rate of the labeled homopolymers was not decreased by replacing the shorter unlabeled homopolymers by longer ones.

We have also demonstrated that the C3M exchange can occur over a broad range of time scales. With the help of our analytical model, we have shown that this broad range of time scales indicates the presence of different homopolymer types, each with their own exchange rate. These different types might be polymers with different lengths. Of the four different literature models that relate the exchange rate to the polymer lengths, the two simple activated process models give the best agreement to the experimental data. However, these models do not include any other factors apart from polydispersity, while these other factors might also have played a role in the broad distribution of exchange rates. To further elucidate the exact origin of this broad distribution, further experiments are needed.

Any future FRET-based micelle exchange experiment can benefit from our analytical model as it can help us to relate the observed FRET increase to the underlying micelle exchange rate. Both our experimental observations and analytical model thus help us to further unravel the C3M exchange mechanisms and in this way can help in designing more stable C3M encapsulators.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.0c02387.

• ¹H NMR spectra; light scattering experiments; deconvolution of the emission spectrum; FRET intensity E(t) as a function of time after mixing t; estimation of the free polymer fraction; bleaching test of equilibrated mixed micelles; fits of the activated process models to the FRET micelle exchange data at different salt concentrations; and analytical solution of the differential equation for P(n,t) (PDF)

The authors declare no competing financial interest.