Latent class mediation: A comparison of six approaches

Abstract

Latent class mediation modeling is designed to estimate the mediation effect when both the mediator and the outcome are latent class variables. We suggest using an adjusted one-step approach in which the latent class models for the mediator and the outcome are estimated first to decide on the number of classes, then the latent class models and the mediation model are jointly estimated. We present both an empirical demonstration and a simulation study to compare the performance of this one-step approach to a standard three-step approach with modal assignment (modal) and four different modern three-step approaches. Results from the study indicate that unadjusted modal, which ignores the classification errors of the latent class models, produced biased mediation effects. On the other hand, the adjusted one-step approach and the modern three-step approaches performed well with respect to bias for estimating mediation effects, regardless of measurement quality (i.e., model entropy) and latent class size. Among the three-step approaches we investigated, the maximum likelihood method with modal assignment and the BCH (Bolck, Croon, & Hagenaars, 2004) correction with robust standard error estimators are good alternatives to the adjusted one-step approach, given their unbiased standard error estimations.

Mediation analyses are commonly employed in the field of psychology to gain a better understanding of why specific experimental manipulations, prevention programs, or treatments are effective in mobilizing change in psychological phenomenon. The landmark Baron and Kenny (1986) paper that described a step-by-step approach to testing mediation was listed among the top 100 papers in a study published in Nature (Van Noorden, Maher, & Nuzzo, 2014) and has been cited over 90,000 times in Google Scholar (last accessed February 12, 2020). There are, however, more accurate methods to test mediation using a variety of different approaches, such as the difference in coefficients, product of coefficients (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002) and methods from the causal inference literature (Imai et al., 2010; VanderWeele, 2010).

Mediation models are commonly used to examine how a specific treatment, experimental manipulation, or prevention program (i.e., the independent variable) affects some outcome (i.e., the dependent variable) via some mediating process (i.e., the mediator). Testing mediation allows investigators to understand why and how specific independent variables affect outcomes, which is critically important for understanding the mechanisms of change in the outcome (Kazdin, 2007; Kraemer et al., 2002; MacKinnon and Dwyer, 1993; Weersing & Weisz, 2002). This is particularly important in the fields of community and clinical psychology, as researchers are often interested in understanding how specific interventions (treatment and prevention programs) may impact outcomes (MacKinnon, 2008). Understanding the mechanisms by which interventions impact outcomes can also be used to refine interventions (Huebner and Tonigan, 2007; Kazdin and Nock, 2003; Longabaugh and Magill, 2011). For example, the development and deployment of coping skills is often considered an essential component of cognitive-behavioral treatment (CBT). Thus, coping would be expected to mediate the effect of CBT on outcomes, however findings have been mixed in this area (Kiluk et al., 2010; Litt et al., 2003; Morgenstern and Longabaugh, 2000; Roos, Maisto, & Witkiewitz, 2017).

Importantly, mediation modeling approaches typically assume independent observations of the mediators and outcomes, but there are many cases in psychology where the assumption of independent observations is violated. One particularly challenging example is the heterogeneity among participants that is often observed in the study of psychological disorders and behavioral symptoms related to disorders (Wardenaar and de Jonge, 2013). For example, in examining diagnosis of alcohol use disorder in the Diagnostic and Statistical Manual for Mental Disorders, 5^th edition (American Psychiatric Association, 2013), a diagnosis is made when an individual patient endorses 2 or more of 11 possible symptoms. This works out to 2048 possible symptom combinations for meeting criteria for an alcohol use disorder, of which 548 actual symptom combinations have been measured in a large national epidemiological sample of individuals with alcohol use disorder (Lane and Sher, 2015). Moreover, Witkiewitz and colleagues (2007) noted excessive heterogeneity in alcohol use outcomes following treatment for an alcohol use disorder. Therefore, instead of being independent observations of drinking outcomes, the observations may be “conditionally independent” on some subgroups (e.g., abstinent subgroup, heavy drinking subgroup). Identifying subpopulations among observations has become an important priority in psychological research.

The heterogeneity of psychological symptoms and disorders has led many researchers to pursue mixture modeling approaches (McLachlan and Peel, 2000). For example, latent class modeling has been used to distinguish subtypes of depression (Sullivan et al., 1998), obsessive-compulsive symptoms (Scherrer et al., 2015), psychotic experiences (Jones et al., 2018), coping skills among those with alcohol use disorder (Roos and Witkiewitz, 2016), tobacco use during cessation attempts (McCarthy et al., 2015), and the developmental progression of heavy drinking in young adulthood (Lanza and Collins, 2006), among many other applications (Wardenaar and de Jonge, 2013). A brief review of articles in two flagship clinical psychology journals (the Journal of Consulting and Clinical Psychology; JCCP and the Journal of Abnormal Psychology; JAP) from March 2013 until March 2018 identified 25 papers using latent class models. Yet, none of these papers have used latent class models to examine mediation, which is common in the field of clinical psychology.

The current paper focused on investigating the potential methods for estimating latent class mediation. We first review latent class modeling and applications of latent class modeling approaches in the field of clinical psychology. We then introduce the latent class mediation model and apply the latent class mediation model to empirical data. Next, we describe the current simulation study to assess six different approaches, including the adjusted one-step approach, standard three-step approach, and four different modern three-step approaches, to latent class mediation modeling. We end with a discussion of the limitations of the current findings and future research examining latent class mediation.

Latent Class Mediation Model

Latent class modeling (McCutcheon, 1987; Vermunt & Magidson, 2002) is designed to find the implicit subgroups (classes) among heterogeneous individuals based on their response to multiple manifest variables or indicators. Latent class models have been widely used in several research fields, such as psychology (e.g., Gabriel, Daniels, Diefendorff, & Greguras, 2015), medicine (e.g., Calfee et al., 2014), human ecology (e.g., Byles et al., 2018), environmental science (e.g., Chikaraishi et al., 2015), and business (e.g., Baum, Schwens, & Kabst, 2015). Several latent class models have been developed based on the scale of the indicators, such as categorical variables (Lazarsfeld, 1950; Lazarsfeld & Henry, 1968), continuous variables (Gibson, 1959), and polytomous variables (Haberman, 1979). In the present study, we will be focusing on latent class mediation models with categorical indicators.

Mediation with Counterfactual Approach

We assume a correctly specified mediation model with one antecedent (X), one mediator (M), and one outcome variable (Y), and that X denotes a binary treatment condition. Both M and Y are latent class variables each with 2 classes where the second class is the reference category. Also, we assume there is no unmeasured confounder and no interaction effect between X and M in predicting the outcome. The mediation model is represented by two logistic regressions as follows:

$$log[\frac{P(M=1\mid X=x)}{P(M=2\mid X=x)}]={\beta }_0+{\beta }_{1}x$$ (1)

$$log\left[\frac{P(Y=1\mid X=x,M=m)}{P(Y=2\mid X=x,M=m)}\right]={\gamma }_0+{\gamma }_{1}x+{\gamma }_{2}m$$ (2)

where P(M = m∣X = x) denotes the probability of the mediator being in the m^th class (m=1 or 2) given X = x. P(Y = y∣X = x, M = m) denotes the probability of the outcome being in the y^th class (y=1 or 2) given X = x and M = m. β₀ and γ₀ are the intercepts which represent the predicted logit (i.e., log odds) when X and M are in the reference group (group coded 2). β₁, γ₁, and γ₂ indicate the change in the predicted logit with 1 unit increases in the corresponding variables adjusted for other predictors in the model. β₁ corresponds to the association between X and M (a-path), γ₂ corresponds to the association between M and Y (b-path), and γ₁ corresponds to the association between X and Y (c-path).

The mediation (indirect) effect is defined by using the counterfactual approach (Pearl, 2001; Robins & Greenland, 1992) and quantified on the odds ratio (OR) scale (MacKinnon, forthcoming, Valeri & VanderWeele, 2013; VanderWeele & Vansteelandt, 2010; VanderWeele, 2015):

$$O{R}^{NIE}=\frac{\{1+\text{exp}({\beta }_0+{\beta }_1{a}^{\ast })\}\{1+\text{exp}({\gamma }_2+{\beta }_0+{\beta }_{1}a)\}}{\{1+\text{exp}({\beta }_0+{\beta }_{1}a)\}\{1+\text{exp}({\gamma }_2+{\beta }_0+{\beta }_1{a}^{\ast })\}},$$ (3)

where a* = 0 and a = 1 are the two levels of the binary treatment condition X. Using a counterfactual approach, the natural indirect effect (NIE) captures the average change in the outcome caused by the treatment while manipulating the level of the mediator (VanderWeele, 2015, p. 23). The standard error (SE) and 95% confidence interval (CI) for the NIE can be estimated by using the Monte Carlo method (MacKinnon, Lockwood, & Williams, 2004; Tofighi and MacKinnon, 2011, 2016).

Approaches for estimating LCA mediation models

Given the lack of literature on testing LCA mediation models, we reviewed several approaches which are used to investigate the relationship between the latent class variable and outcome variables as potential examples for examining the association between the latent class mediator and latent class outcome. One approach to examine the relationship between latent class variables and outcomes is the one-step approach (Bandeen-Roche, Miglioretti, Zeger, & Rathouz, 1997). In this approach, the latent class model and the path from the latent class variables to outcomes (the regression model) are estimated at the same time. However, the one-step approach could be limited in that the latent class model estimation would be influenced by the regression model, which may lead to different latent class results (Asparouhov & Muthén, 2014; Vermunt, 2010). Therefore, an adjusted one-step approach has recently been suggested (Kim et al., 2016; Lanza, Tan, & Bray, 2013; Masyn, 2017). The two latent class models, one for the latent mediator and one for the latent outcome, are first estimated separately. The number of latent classes are determined separately for both latent class models in this step. Next, the latent class models and the mediation model are estimated simultaneously, with the presumption that the number of classes is known from the previous step. Note that although the number of classes is fixed, it is recommended to double-check the class interpretations in the full latent class mediation model to evaluate whether including the treatment and mediator in the model changes class interpretations.

Another approach is the classify-analyze approach (Clogg, 1995), also known as the standard three-step approach which consists of: 1) the latent class models for both the mediator and the outcome are estimated separately; 2) individuals are assigned to a class based on their posterior probabilities; and 3) the latent class membership is treated as an observed variable in subsequent mediation analyses (Figure 1). Two class membership assignments can be used in the standard three-step approach. One is called modal assignment (Vermunt, 2010), in which the class membership for individual i is based on that individual’s maximum posterior probability (p_ic). The other is called multiple pseudo-class draw, in which the class membership is assigned based on a pre-specified number of draws (usually 20) from the individual’s posterior probability distribution for class membership, and the results are summarized across all draws. (Asparouhov & Muthen, 2014; Bray, Lanza, & Tan, 2015; Wang, Brown, & Bandeen-Roche, 2005). A simpler alternative to the pseudo-class draw, called proportional assignment, assigns each individual to each class membership, with a weight given by the posterior probability. Therefore, instead of assigning individuals to classes multiple times, only one assignment is needed while using the proportional assignment (Bakk & Vermunt, 2016).

Figure 1.

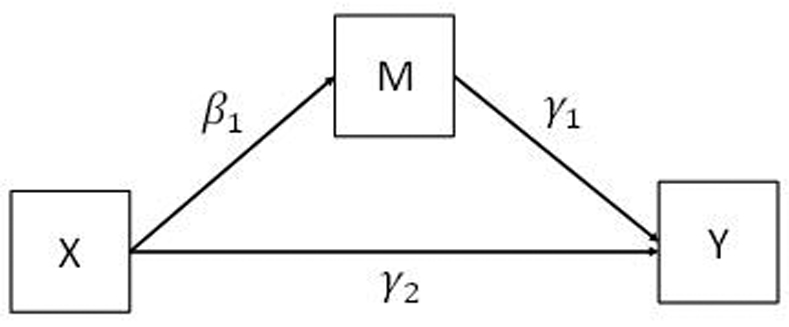
The mediation model with single binary predictor variable (X), single binary mediator (M), and single binary outcome (Y).

The standard three-step approach has been criticized for not accounting for classification errors of the latent class models, which typically attenuates the path coefficients from the latent class variables to the distal outcomes (Bakk, Tekle, & Vermunt, 2013; Bray et al., 2015; Gudicha & Vermunt, 2013; Vermunt, 2010). Although the multiple pseudo-class draw assignment was once believed to account for such errors by utilizing the individual’s posterior probability distribution, researchers have found that the multiple pseudo class draw performs no better than the modal assignment; and may perform even worse in some simulation conditions (Peterson, Bandeen-Roche, Budtz-Jørgensen, & Jarsen, 2012; Bray et al., 2015; Lanza et al., 2013).

Given these drawbacks, two correction methods have been developed to improve the standard three-step approach: the maximum likelihood (ML: Vermunt, 2010) and the BCH (Bolck, Croon, & Hagenaars, 2004) methods. Unlike the standard three-step approach, both the ML and the BCH methods can be used to account for the classification errors in latent class mediation analysis. In the ML approach, similar to the one-step approach, both the latent class and regression models are estimated at the same time. However, the latent class model is specified as a single-indicator model, in which the indicator is now the assigned class membership created from step 2 in the three-step approach. Additionally, the classification error probabilities are treated as known and the values are taken from step 1 in the three-step approach (Vermunt, 2010). In the BCH approach, the association between the latent class variable and the distal outcome is computed by using the joint probability distribution of the assigned class membership and the distal outcomes, weighted by the inverse of the classification error probabilities (Bakk et al., 2013; Bolck et al., 2004). A robust standard error estimator is recommended along with the BCH approach to produce unbiased standard error estimates (Bakk & Vermunt, 2016; Bolck et al., 2004; Vermunt, 2010).

The modern three-step approach with the ML and BCH corrections have been shown to outperform the standard three-step approach for predicting distal outcomes in LCA (Asparouhov & Muthén, 2014; Bakk & Vermunt, 2016; Bray et al., 2015). However, the standard three-step approach with modal assignment is still one of the most prevailing methods in clinical psychology. In our 5-year literature review in JCCP and JAP, 19 out of the 25 articles still used this approach to examine the association between latent class variables and distal outcomes. The adjusted one-step approach also has the potential to be a better choice than the standard three-step approach. But to our knowledge, the adjusted one-step approach has been used in only one empirical study (Witkiewitz, Roos, Tofighi, & Van Horn, 2018). Additionally, how these methods perform in a latent class mediation model, which contains two latent class variables in the mediation analysis, has yet to be studied.

In the present study, we investigate the performance of estimating the mediation effects in latent class mediation models across six approaches: (a) the adjusted one-step approach, (b) the standard three-step approach using model assignment (we call it the “modal” approach in this article), (c) the modern three-step approach using the modal assignment and the ML correction (ML modal), (d) the modern three-step approach using the proportional assignment and the ML correction (ML proportional), (e) the modern three-step approach using the modal assignment and the BCH correction (BCH modal), (f) the modern three-step approach using the proportional assignment and the BCH correction (BCH proportional). Despite being shown to produce biased estimates in previous simulation studies, we included the modal approach as it is still the most prevailing method in the clinical psychology literature.

Empirical Demonstration

We demonstrate the six approaches using an empirical case of one predictor, one latent class mediator and one latent class outcome. Data were collected from the COMBINE study [“Combined Pharmacotherapies and Behavioral Interventions for Alcohol Dependence” (The COMBINE Study Research Group, 2006). The predictor was defined as a randomization procedure to receive any form of active medication (naltrexone or acamprosate) or placebo equivalents (n=1226) versus a condition that did not receive any pills (n=157) coded as 1=received pills and 0=did not receive pills in the COMBINE study. Three manifest variables of negative mood, including tension, anger, and depression (each coded as 0=low negative mood, 1=moderate negative mood, and 2=high negative mood), at week 8 of treatment were used as indicators of the latent class mediator. Three drinking outcome variables, including drinking frequency and drinking quantity (each coded as 0=abstinence, 1=low risk/infrequent drinking, 2=heavy/frequent drinking) and drinking-related problems (coded as 0=no problems, 1=problems), at week 16 of treatment were used as indicators of the latent class outcome. All the indicators were categorical variables. The goal of the empirical example was to test whether randomization to receive a pill would be associated with better outcomes via improvements in negative mood. To simplify the example, we tested a model with two negative mood latent classes: low negative mood and high negative mood, and two drinking classes: abstinence with few problems and drinking with some problems. We hypothesized that individuals who received a pill would have a lower likelihood of expected classification in the high negative mood class (Szabo, Jobbagy, & Koteles, 2018) and that greater likelihood of expected classification in the high negative mood class would a predict a lower likelihood of expected classification in the abstinence class (Witkiewitz & Villarroel, 2009).

Analysis

Latent class analysis (LCA) was first conducted to confirm that the two-class model fit the data better than the one-class model for both the latent class mediator and the latent class outcome. Then, we performed the adjusted one-step approach, standard three-step with modal assignment (modal), and the four modern three-step approaches. These approaches were compared in terms of parameter estimates of the mediation effects. The adjusted one-step approach and the modal approach were performed by using Mplus 8.2 (Muthén & Muthén, 1998-2018); the modern three-step approaches were conducted by using Latent GOLD 5.1 (Vermunt & Magidson, 2016).

Results

First, LCAs with one or two classes were compared based on the Bayesian information criterion (BIC; Schwartz, 1978), sample-size adjusted BIC (a-BIC; Sclove, 1987), and the bootstrapped likelihood ratio test (BLRT; McLachlan & Peel, 2000). Compared with the one-class models, the two-class models yielded lower BIC and a-BIC estimates for both the mediator and the outcome classes. The BLRT results showed that the one-class model was inadequate. The entropy estimates for the two-class models were 0.75 and 0.99 for the mediator and the outcome latent classes, respectively.

For the latent mediator classes, the first class could be defined as a low negative mood class (approximately 46% of the sample). The response probabilities for the low negative mood class indicated the highest probability of endorsing the first category (low negative mood) for all the three indicators. On the other hand, the second class (approximately 54% of the sample) was labeled the high negative mood class, for the related response probabilities were the highest for either the second (moderate negative mood) or the third category (high negative mood). The latent outcome classes could be defined as abstinence (approximately 36% of the sample) and drinking (approximately 64% of the sample). The response probabilities for the drinking frequency and drinking quantity were 100% in the first category (abstinence) in the abstinence class, whereas these probabilities were both 0% in the first category (abstinence) in the drinking class. For the alcohol problems indicator, the probability of choosing the first category (no problems) was 96.4% for the abstinence class, which is larger than 78.6% endorsing the first category (no problems) for the drinking class.

Table 1 includes the coefficients of the logistic regression and the odds ratios of the natural indirect effects for the mediation model across six approaches. From the adjusted one-step approach, we found that receiving pills was associated with a higher probability of classification in the low negative mood class (odds ratio, OR=1.819); and being in the low negative mood class was associated with a higher probability of being in the abstinence class (OR=1.187). Using the counterfactual approach to calculate the mediation effect, we found the natural indirect effect of taking pills on being in the drinking class in comparison to the abstinence class was mediated by being in the low negative mood class (OR=1.126, 95% CI=[1.028, 1.250]). In other words, receiving pills was associated with lower negative mood and less negative mood was associated with a greater probability of abstinence.

Table 1.

The Mediation Effects of Medication Intake on Drinking Problems among Six LCA Approaches

	Logit (SE)			Odds ratio [95% CI]
	a-path	b-path	Intercept M	Natural indirect effect
Adjusted One-Step	0.598 (0.228)	0.829 (0.148)	−0.396 (0.251)	1.126 [1.028, 1.250]
Modal	0.447 (0.206)	0.684 (0.126)	−0.549 (0.196)	1.077 [1.006, 1.153]
ML Modal	0.520 (0.240)	0.862 (0.164)	−0.288 (0.227)	1.113 [1.009, 1.245]
ML Proportional	0.535 (0.262)	0.831 (0.171)	−0.301 (0.248)	1.112 [1.004, 1.254]
BCH Modal	0.510 (0.202)	0.859 (0.130)	−0.279 (0.192)	1.110 [1.022, 1.216]
BCH Modal & robust SE estimator	0.510 (0.241)	0.859 (0.164)	−0.279 (0.228)	1.110 [1.007, 1.241]
BCH Proportional	0.538 (0.203)	0.830 (0.130)	−0.305 (0.192)	1.112 [1.026, 1.217]
BCH Proportional & robust SE estimator	0.538 (0.230)	0.830 (0.150)	−0.305 (0.218)	1.112 [1.016, 1.234]

Note. Modal=standard three-step approach with modal assignment; ML Modal=modern three-step approach with modal assignment and maximum likelihood correction method; ML Proportional= modern three-step approach with proportional assignment and maximum likelihood correction method; BCH Modal=modern three-step approach with modal assignment and BCH correction method; modern three-step approach with proportional assignment and BCH correction method.

The modal approach yielded much smaller parameter estimates than to the adjusted one-step approach. As shown in Table 1, the odds ratio of the mediation effect was 1.077 (95% CI=[1.006, 1.153]) for the modal approach. Using the modern three-step approach with either the BCH or ML corrections also yielded smaller mediation effects (OR ranged from 1.110 to 1.113) than using the adjusted one-step approach. However, those estimates were larger than the ones produced by using the standard three-step approach. The largest SEs were observed for the ML proportional approach, followed by the BCH approaches with robust SEs which yielded comparable SE estimates to the modal ML and the adjusted one-step approaches. The modal approach yielded the smallest SE estimates, along with the BCH approaches with robust SE estimators. To further investigate the performance of the six approaches in latent class mediation models, we conducted a simulation study using the empirical demonstration as a basis for its design.

Monte Carlo Study: Latent Class Mediation Analysis with Categorical Indicators

The purpose of this simulation study was to compare the performance of the six latent class approaches: adjusted one-step, standard three step with modal assignment (modal), and four modern three-step approaches with the combinations of modal/proportional assignments and ML/BCH corrections, in latent class mediation estimates. We examined the performance of each approach for latent mediator with 2, 3, and 4 classes. We also examined whether the estimation of the mediation effects would be influenced by different measurement quality (weak vs. good). Mplus 8.2 (Muthén & Muthén, 1998-2018) and Latent GOLD 5.1 (Vermunt & Magidson, 2016) were used for model estimation. R-3.5.3 (R Core Team, 2019) was used to generate data. The R package MplusAutomation (Hallquist & Wiley, 2018) was used to organize simulation results generated via Mplus, and the R package RMediation (Tofighi and MacKinnon, 2011, 2016) were used to compute the 95% Monte Carlo CI for the mediation effects.

Generating Population Data

The data generation model (Figure 2) assumed a mediation model with one antecedent, one mediator, and one outcome variable. X was a binary antecedent representing treatment condition (0=control, 1=treatment) in a randomized controlled trial with the probability of being in either group was 50%. The mediator M and the outcome Y were each associated with six binary variables (coded as 0 or 1). We assume no X and M interaction and no confounding variables in the mediation model. For each combination of a mediator class and measurement quality condition, we generated one large data set (N = 1,000,000). We used these large data sets to provide population estimates for model parameters and entropy.

Figure 2.

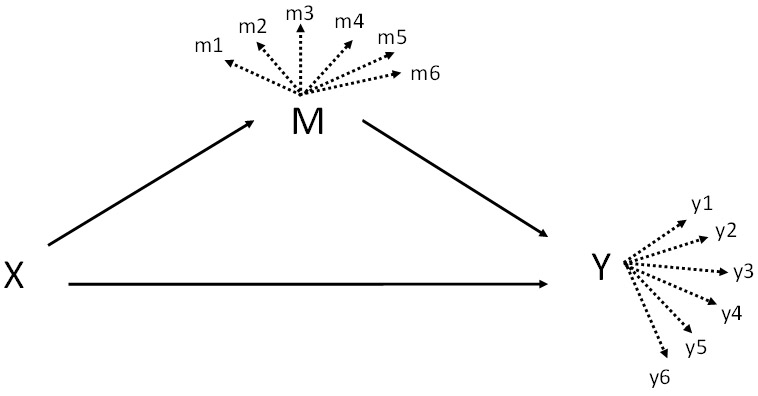
The model for generating population data. X, Y, mi, and yi are all binary variables. M is manipulated as either binary or categorical variable. The dot arrows indicate that M and Y are associated with mi and yi (i=1 to 6), respectively.

Number of mediator classes.

In the present study, we investigated conditions with 2 through 4 latent classes for the mediator, while both the treatment and outcome were binary. In the 2-class mediator conditions, we manipulated the corresponding ORs for β₁ (a-path) and γ₁ (b-path) equal to 2 (a small effect; Chen, Cohen, & Chen, 2010), which resulted in a natural indirect effect of 1.121 in OR (Equation 3), which was comparable to the effect size we observed from the previous empirical example. For the 3-class and 4-class mediator conditions, we set the last class (e.g., the 3^rd class in the 3-class condition) as the reference group. Hence, we specified two sets of logistic regression models in the 3-class mediator (M) conditions: one for M class 1 vs. M class 3 and the other for M class 2 vs. M class 3. The average of the two natural indirect effects corresponding to the two sets of logistic regression models were 1.101. For the 4-class mediator conditions, the average of the three natural indirect effects corresponding to the three sets of logistic regression models were 1.145.

Measurement Quality.

As can be seen in Figure 2, both M and Y were each measured with six binary indicators (coded as 0 or 1), namely, m1-m6 and y1-y6. The level of the associations between the class variables and indicators were defined as the measurement quality. To simplify the comparisons, only the conditions in which M and Y had the same measurement quality as measured by six binary indicators were included. To determine measurement quality for the latent class variables, we manipulated the probabilities for the endorsement of each item given the class membership (Table 2). For weak measurement quality, the scaled entropy (Ramaswamy, Desarbo, Reibstein, & Robinson, 1993) was approximately .71; for good measurement quality, the entropy was approximately .80. Such criteria to define measurement quality have been used in previous simulation studies (e.g., Dziak, et al., 2016).

Table 2.

Patterns of item-response probabilities under Different Measurement Quality and Class Number Conditions in the Simulation Study

		2 Class		3 Class			4 Class
		C1	C2	C1	C 2	C 3	C1	C2	C3	C4
Good	Item1	.79	.21	.87	.87	.13	.87	.87	.13	.13
	Item2	.79	.21	.87	.87	.13	.87	.87	.13	.13
	Item3	.79	.21	.87	.87	.13	.87	.87	.13	.13
	Item4	.79	.21	.87	.13	.87	.87	.13	.87	.13
	Item5	.79	.21	.87	.13	.87	.87	.13	.87	.13
	Item6	.79	.21	.87	.13	.87	.87	.13	.87	.13
		Entropy=.79		Entropy=.81			Entropy=.79
Weak	Item1	.76	.24	.83	.83	.17	.84	.84	.16	.16
	Item2	.76	.24	.83	.83	.17	.84	.84	.16	.16
	Item3	.76	.24	.83	.83	.17	.84	.84	.16	.16
	Item4	.76	.24	.83	.17	.83	.84	.16	.84	.16
	Item5	.76	.24	.83	.17	.83	.84	.16	.84	.16
	Item6	.76	.24	.83	.17	.83	.84	.16	.84	.16
		Entropy=.71		Entropy=.71			Entropy=.71

In the 2-class mediator conditions, all six indicators had the same high probabilities item endorsement in class-1 and the same low probabilities for item endorsement in class 2. For the 3-class mediator conditions, high probabilities for all the six indicators were specified in class 1; low probabilities were specified for all the six indicators in class 3; those in class 2 had high probabilities for the first three indicators and low probabilities for the last three indicators. For the 4-class mediator conditions, classes 1 through 2 followed the same manipulation as the 3-class mediator conditions. Those in class-3 had the first three indicators with low probabilities and the last three indicators with high probabilities. All the six indicators in class 4 had low probabilities of endorsement. Detailed information regarding the item probabilities, class membership, and the estimated entropy values are listed in Table 2.

Data Analysis Models

Five hundred sample data sets each with a sample size of 500 observations were drawn (without replacement) from each population data set (combination of number of mediator classes and measurement quality level). The sample size of 500 was chosen as a recommended minimal sample size for latent class analysis (Vermunt, 2010).

Each simulated data set was analyzed using each of the six approaches, including adjusted one-step, modal, ML modal, ML proportional, BCH modal, and BCH proportional. For each approach, m1-m6 and y1-y6 were specified as indicators for two latent class variables, CM and CY, respectively. 200 random sets of starting values for the initial stage were used for every latent class analysis. Given the indicators in latent class models being binary, the estimated thresholds for each indicator in each class would be positive for a high probability indictor or negative for a low probability indicator. Label switching for all the three step approaches were handled by checking the estimated thresholds in step 1 and labeling the classes based on the pattern of the thresholds. As for the adjusted one-step approach, because the class permutation and the mediation analysis were conducted simultaneously, we constrained the first threshold of the first indicator in each class to the population values to prevent label switching from happening. We then double-checked for the label switching and found no evidence of label switching among replications.

The natural indirect effect was estimated by using equation (3). As mentioned earlier, for the 3-class and 4-class mediator conditions, the mediation equations were specified by conducting two and three sets of logistic regression models, respectively. Taking the 3-class mediator conditions as an example, two mediation models: (1) from X (treatment vs. control) to Y (class 1 vs. class 2) via M (class 1 vs. class 3); and (2) from X (treatment vs. control) to Y (class 1 vs. class 2) via M (class 1 vs. class 3) would be conducted and two natural indirect effects would be produced. Likewise, three natural indirect effects would be produced for the 4-class mediator conditions.

The natural indirect effects were the focus of the simulation study. The four criterion for judging model performance in simulations were (1) standardized bias, (2) relative standard error (SE) bias, (3) 95% confidence interval (CI) coverage rate, and (4) root mean square error (RMSE). Raw bias was defined as the average difference between the sample estimates and the population parameters. Standardized bias was used to report the bias as a percentage of the standard error, which is the standard deviation of the sampling distribution of the estimates. Collins, Schafer, and Kam (2001) suggested that standardized bias above 0.40 in absolute value was considered markedly biased. In a well performing model the relative SE bias would be expected to be between −10% and 10% (Hoogland & Boomsma, 1998). Relative SE bias above 10% would indicate that the average SE of the mediation estimates was larger than the empirical standard deviation of the mediation estimates across replications. The 95% CI coverage rate larger than 91% is considered acceptable (Muthén & Muthén, 2002). RMSE is the square root of the average square difference between the sample estimates and the population parameters. Small RMSE values indicate small estimation error.

Results

Across simulation conditions, the convergence rate for the six approaches was 100%. No inadmissible solutions were generated for all six approaches.

Latent Class Models of the Mediator and the Outcome

For each of the measurement quality conditions, the entropy values of the samples were comparable to those yielded from the population data. For the mediator and outcome LCA models across replications, we further used BLRT to compare the target class solutions with a solution with one fewer latent class (C-1) and with a solution with one additional latent class (C+1). We found that the target class solutions were preferred over C-1 solutions across all the situations. These results indicated that there was sufficient power to detect the C-class model for all replications. On the other hand, when comparing the target solutions to the C+1 solutions, less than 10% of the replications incorrectly chose the C+1 solutions over the target solutions. Hence, we conclude that the target class solutions for the LCA models were correctly specified in the simulation.

2-class mediators and 2-class outcomes

Table 3 shows the simulation results for the cases in which both the mediator and outcome have 2 classes. Generally, larger biases in the indirect effects were produced when measurement quality was weak. In all cases the mean estimates of the indirect effects obtained by conducting the adjusted one-step approach were comparable to the true parameter estimates (i.e., standardized biases less than .40). On the contrary, markedly downward indirect effect estimates were observed when conducting the modal approach (standardized bias approximately −2.05 ~ −1.08). The standardized biases for the four modern three step approaches were all below .40 in high measurement quality conditions. In weak measurement quality conditions, the modern three step approaches yielded larger downward biases (standardized bias = −0.48 ~ −0.10), but still more accurate than the modal approach.

Table 3.

Results for Six Approaches in Estimating Mediation Effects in Mediation Models with 2-class Mediators and 2-class outcomes

	Measurement Quality	Std. bias	Rel SE bias (%)	95% CI coverage rate (%)	RMSE
Adjusted One-step	Good	−0.09	4.37	95.40	0.055
	Weak	−0.18	6.88	94.80	0.060
Modal	Good	−1.08	3.26	72.60	0.058
	Weak	−2.05	8.10	57.20	0.074
ML Modal	Good	−0.10	8.33	94.00	0.060
	Weak	−0.48	9.72	90.20	0.063
ML Proportional	Good	−0.12	21.00	98.40	0.054
	Weak	−0.24	33.46	97.60	0.059
BCH Modal	Good	−0.10	−17.98	88.40	0.060
	Weak	−0.48	−20.00	81.00	0.063
BCH Modal & robust	Good	−0.10	7.01	94.40	0.060
	Weak	−0.48	8.22	90.20	0.063
BCH Proportional	Good	−0.12	−9.72	90.20	0.054
	Weak	−0.24	−15.26	86.60	0.059
BCH Proportional & robust	Good	−0.12	5.22	95.20	0.054
	Weak	−0.24	6.74	93.00	0.059

Note. Modal=standard three-step approach with modal assignment; ML Modal=modern three-step approach with modal assignment and maximum likelihood correction method; ML Proportional= modern three-step approach with proportional assignment and maximum likelihood correction method; BCH Modal=modern three-step approach with modal assignment and BCH correction method; modern three-step approach with proportional assignment and BCH correction method. robust=robust standard error estimator. Values exceeding the recommended cutoffs are in boldface.

The standard error estimates for the adjusted one-step, the modal, the ML modal, and the BCHs with robust SE estimators were good approximations of the observed standard deviation of the parameter estimates. None of the SEs were substantially underestimated (relative SE bias ranged from 3.26% to 9.72%). ML proportional yielded substantially overestimated SE values (relative SE bias above 20%) whereas the BCH approaches without using robust SE estimators yielded substantially underestimated SE values (relative SE bias ranged from −20.00% to −15.26%), except for BCH proportional under good measurement quality conditions (relative bias = −9.72%).

As for 95% CIs, the coverage rate for the adjusted one-step, the BCH approaches with robust SE estimators, the ML modal, and the ML proportional were all over 91%, except for the BCH modal and ML modal under weak measurement quality conditions (both 90.20%). However, the coverage rate results for the ML proportional may be inflated due to the overestimated SEs. The BCH approach without using robust SE estimators yielded coverage rate ranged from 81.00% to 90.20%. The modal approach had the worst coverage rate among the six approaches (72.60% for good measurement quality and 57.20% for weak measurement quality)

RMSE values increased as the measurement quality decreased among the six approaches. The RMSE values were ranged from 0.054 to 0.060 for the good measurement quality conditions and from 0.059 to 0.074 for the weak measurement quality conditions. The RMSE value for the modal approach under weak measurement quality condition had the highest RMSE.

3- and 4-class mediators and 2-class outcomes

Table 4 and Table 5 list the performance of the six approaches in estimating the indirect effects in 3-class and 4-class mediator conditions, respectively. Given there are at least two indirect effects being estimated and the results are comparable, we report the average of the simulation results for multiple indirect effects. Across all the simulation conditions, the adjusted one-step approach and the four modern three-step approaches obtained unbiased indirect estimates (standardized bias ranged from −0.10 to 0.01), whereas the modal approach yielded markedly downward biases (standardized bias ranged from −1.21 to −0.55).

Table 4.

Results for Six Approaches in Estimating Mediation effects in Mediation Models with 3-class Mediators and 2-class Outcomes

	Measurement Quality	Std. bias	Rel SE bias (%)	95% CI coverage rate (%)	RMSE
Adjusted One-step	Good	−0.01	2.76	94.90	0.059
	Weak	0.01	4.84	95.30	0.069
Modal	Good	−0.55	3.66	89.50	0.049
	Weak	−0.84	3.52	85.30	0.052
ML Modal	Good	−0.02	3.52	95.30	0.059
	Weak	−0.06	3.50	94.40	0.069
ML Proportional	Good	−0.03	20.29	97.40	0.057
	Weak	−0.06	24.62	97.20	0.067
BCH Modal	Good	−0.02	−13.56	89.20	0.059
	Weak	−0.06	−23.86	85.80	0.069
BCH Modal & robust	Good	−0.02	3.78	95.20	0.059
	Weak	−0.06	3.95	94.30	0.069
BCH Proportional	Good	−0.04	−10.66	91.10	0.057
	Weak	−0.06	−21.32	87.10	0.066
BCH Proportional & robust	Good	−0.04	3.646	94.50	0.057
	Weak	−0.06	1.274	94.00	0.066

Note. Modal=standard three-step approach with modal assignment; ML Modal=modern three-step approach with modal assignment and maximum likelihood correction method; ML Proportional= modern three-step approach with proportional assignment and maximum likelihood correction method; BCH Modal=modern three-step approach with modal assignment and BCH correction method; modern three-step approach with proportional assignment and BCH correction method. robust=robust standard error estimator. Values exceeding the recommended cutoffs are in boldface.

Table 5.

Results for Three Approaches in Estimating Mediation effects in Mediation Models with 4-class Mediators and 2-class Outcomes

	Measurement Quality	Std. bias	Rel SE bias (%)	95% CI coverage rate (%)	RMSE
Adjusted One-step	Good	0.01	8.80	95.60	0.088
	Weak	0.01	7.62	95.33	0.112
Modal	Good	−0.81	7.39	87.77	0.086
	Weak	−1.21	7.77	77.53	0.099
ML Modal	Good	−0.03	4.54	95.03	0.097
	Weak	−0.06	3.16	93.87	0.111
ML Proportional	Good	−0.06	20.89	98.00	0.094
	Weak	−0.10	29.70	98.13	0.105
BCH Modal	Good	−0.02	−17.82	89.00	0.098
	Weak	−0.05	−28.60	83.73	0.113
BCH Modal & robust	Good	−0.02	4.06	94.60	0.098
	Weak	−0.05	2.76	93.73	0.113
BCH Proportional	Good	−0.06	−16.00	89.40	0.095
	Weak	−0.10	−25.09	84.53	0.106
BCH Proportional & robust	Good	−0.06	4.18	94.07	0.095
	Weak	−0.10	2.80	92.73	0.106

Note. Modal=standard three-step approach with modal assignment; ML Modal=modern three-step approach with modal assignment and maximum likelihood correction method; ML Proportional= modern three-step approach with proportional assignment and maximum likelihood correction method; BCH Modal=modern three-step approach with modal assignment and BCH correction method; modern three-step approach with proportional assignment and BCH correction method. robust=robust standard error estimator. Values exceeding the recommended cutoffs are in boldface.

Results for the 3- and 4-class mediator conditions in both the relative SE bias and 95% CI coverage rate were similar to the 2-class mediator conditions. The adjusted one-step, the modal, the ML modal, and the BCHs with robust SE estimators all yielded unbiased SE estimates. The BCH correction without using robust SE estimators substantially underestimated SEs. Overestimation of SEs was observed for the ML proportional approach. The biased estimation in SEs led to lower coverage (<91%) for the BCH modal and the BCH proportional approaches and inflated coverage rate for the ML proportional approach. The coverage rates for the modal approach were also below 91% even when the SE estimates were unbiased

It is worth noting that the pattern of the RMSE values in the 3- and 4-class mediator conditions were different from that in the 2-class mediator conditions. As can be seen in Table 4 and Table 5, across the six approaches, relatively smaller RMSE values were observed for the modal approach. These results suggested that accounting for the classification errors in the adjusted one-step approach and the modern three-step approaches may increase the variance of the sampling distribution of the indirect effects across replications.

Discussion

In psychological studies, researchers are interested in using analytic strategies that describe the heterogeneity both in the behavioral outcome and potential mediators of that outcome. However, models that combine both latent class analysis and mediation analysis have not been thoroughly evaluated. In this article, we propose a method to fit a latent class mediation model by using an adjusted one-step approach. We also compared the performance of the recommended adjusted one-step approach with that of the standardized three-step approach with modal assignment (modal) and modern three-step approaches in a simulation study of the latent class mediation model.

In this simulation, the latent class portion of the model was assumed to be correctly specified for both the mediator and outcome. Under this premise, the six approaches’ performance in terms of estimation accuracy varied. Simulation results suggested that the modal approach underestimated true population values, when compared to the adjusted one-step approach and the four modern three-step approaches. This finding validates previous findings, which have shown that ignoring classification errors results in underestimation when testing the association between latent class variables and continuous distal outcomes (Asparouhov & Muthén, 2014) or numeric covariates (Vermont, 2010). The result is also consistent with the findings of Bolck, Croon, and Hagenaars’s (2004), in which they show that a one-step approach accurately recovers the association between a latent class variable and a categorical predictor. Our findings in terms of bias are also consistent across 2-, 3-, and 4-class mediator conditions.

Measurement quality plays an important role in estimating the mediation effects in LCA. As shown in the simulation, the performance of the estimation get worse under the weak measurement quality conditions. However, the adjusted one-step and the four modern three-step approaches have shown robustness to weak measurement quality conditions. Again, the modal approach is influenced the most by the amount of classification errors when estimating the indirect effects.

Among the six approaches we compared, both the adjusted one-step approach and the four modern three-step approaches perform well in the simulation. Our results are in agreement with previous simulation research on estimating the association between latent class variables and numeric covariates (Bakk, Oberski, & Vermunt, 2014; Bakk & Vermunt, 2016) or group-level outcomes (Bennink, Croon, & Vermunt, 2015). However, the SE estimates for the ML proportional approach are overestimated and those are underestimated for the BCH three-step methods without using robust SE estimators. The adjusted one-step, the ML modal, and the BCHs with robust SE estimators yielded unbiased SE estimates in our simulation conditions. These results are consistent with the findings in a previous LCA simulation study (Vermunt, 2010).

One advantage of the adjusted one-step approach is that it can be easily implemented in several software programs for latent class analysis. However, conducting latent class mediation analysis with the adjusted one-step approach requires fitting both the latent class models and the mediation model simultaneously. Such practice may increase the risk of model non-convergence, although we did not find any examples in our simulations. On the other hand, implementing modern three-step approaches may reduce the risk of model non-convergence; but currently only Latent GOLD can handle models with two or more latent class variables in a regression model. Taking into account the performance of the SE estimates, for researchers who intend to reduce model complexity in the analysis, the ML modal and the BCH with robust SE estimators (for both modal and proportional) are reasonable alternatives to the adjusted one-step approach.

Both a-path (from predictor to mediator) and b-path (from mediator to outcome) are key elements when estimating mediation effects. Compared to the a-path, we found that the b-path and the mediation effect are more sensitive to the weak measurement quality conditions. Given the estimation in a latent class mediation model includes two latent class variables, and therefore is dependent on errors from both the mediator and the outcome, the impact of ignoring classification errors on the estimation accuracy is compounded. We also note that the adjusted one-step approach and the modern three step approaches had higher estimation variations in some simulation conditions. One explanation for this finding is the bias-variance tradeoff (Dziak, et al., 2016). The downward bias toward 0 in the parameter estimates for the modal approach reduced the chance for extreme estimates of the indirect effect to occur. On the other hand, those unusual estimates may be more likely to occur when accounting for classification errors in the adjusted one-step approach and the modern three-step approaches.

Limitations and Future Directions

We simplified our empirical example to only two latent classes for the mediator and only two latent classes for the outcome. Empirical examples with more classes for the mediator and outcome variables would be helpful for substantive researchers. We included a scenario with three and four latent classes for the mediator in the simulation study and found consistent results with the 2-class mediator conditions. In our simulation, we constrained one parameter per class to its true value to overcome label switching in the adjusted one-step approach. This may give the adjusted one-step approach some advantage over the other approaches. We note that the remaining latent class parameters (more than 90% of the total parameters) were freely estimated. The simulated data were also generated through defining the associations among mediator/outcome and their corresponding indicators, not through a latent class mediation model to favor the adjusted one-step approach. Additionally, conclusions in regards to the performance of the six approaches were consistent from the empirical study to the simulation studies. Thus we argue that the impact of this constraint on simulation results is likely to be small.

This study covered the categorical indicator case, but did not address the case where observed indicators are continuous. Achieving model convergence with continuous indicators is more complex than binary or categorical indicators. Other issues such as how non-normal indicators affect class enumeration (Bauer & Curran, 2003) and estimation accuracy (Dziak, et al., 2016) also need to be considered when using continuous indicators. Previous simulation research in latent profile analysis has shown that the BCH three step yielded is more robust to violating non-normality assumption than the ML three step. Therefore, additional research comparing potential approaches for a latent class mediation model with continuous indicators is required before the current results can be generalized to the use of continuous indicators.

Conclusion

Employing the adjusted one-step latent class mediation approach leads to more accurate mediation estimates. The advantage of the adjusted one-step approach over the modal approach was greatest as the measurement quality of the latent class models decreased. Our simulation results show that the modal approach should not be considered as it substantially attenuates the mediation effects. The modern three-step approaches also yielded unbiased estimates of the mediation effects. If model convergence is of concern, the ML modal and the BCHs with robust SE estimators are good alternatives to the adjusted one-step approach. A fuller understanding of the performance of the adjusted one-step approach and modern three-step approaches under conditions of continuous latent class indicators will require further study.