Reaction prediction via atomistic simulation: from quantum mechanics to machine learning

Summary

It is an ultimate goal in chemistry to predict reaction without recourse to experiment. Reaction prediction is not just the reaction rate determination of known reactions but, more broadly, the reaction exploration to identify new reaction routes. This review briefly overviews the theory on chemical reaction and the current methods for computing/estimating reaction rate and exploring reaction space. We particularly focus on the atomistic simulation methods for reaction exploration, which are benefited significantly by recently emerged machine learning potentials. We elaborate the stochastic surface walking global pathway sampling based on the global neural network (SSW-NN) potential, developed in our group since 2013, which can explore complex reactions systems unbiasedly and automatedly. Two examples, molecular reaction and heterogeneous catalytic reactions, are presented to illustrate the current status for reaction prediction using SSW-NN.

Graphical abstract

Highlights

• •Brief history of chemical reaction prediction
• •Theory and methods for reaction prediction via atomistic simulation
• •Architecture of SSW-NN method for reaction prediction
• •Case studies of SSW-NN simulation for reaction prediction

Introduction

Chemistry aims to synthesize new matter, where the theory of chemical reaction develops constantly to better understand and even guide the synthesis. As early as 1880s, Arrhenius equation was summarized from experiment to correlate reaction rate with temperature, the key controlling factor of reaction. After the establishment of quantum mechanics (QM), the absolute rate theory, also known as transition state theory (TST), was also developed in 1930s (Eyring, 1935), which laid the foundation of modern kinetics theory. As shown in Equation 1, TST states that the rate constant k_TST of elementary reaction is exponentially related to its free energy barrier, ΔG_TS⁰, which is the free energy difference between the transition state (TS), and the initial state (IS). TS by definition is a saddle point on potential energy surface (PES).

$$k_{TST}=\frac{k_{B}T}{h}{e}^{-\Delta G_{TS}^o/k_{B}T}$$ (Equation 1)

The TST is most powerful in the form of variational transition state theory (VTST) as well practiced in 1980s, which is able to provide more accurate rate constant for elementary reaction (Truhlar and Garrett, 1984). The VTST, requiring extensive statistics of states on PES, is often too demanding to compute in complex reactions.

For a long period, conceptually simple and less computational extensive models for understanding chemical reaction are much welcomed by chemists. Fukui et al. (1952) first noticed the prominent roles of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) in governing chemical reaction activity, and led to the frontier molecular orbital theory, which understands better Woodward–Hoffmann rules on pericyclic reactions. Beyond the HOMO-LUMO concept for reactivity prediction, the hard and soft acids and bases (HSABs) theory (Pearson, 1963) encapsulates both thermodynamic and kinetic propensities of molecules and can be utilized for reactivity prediction of a wide range of reactions. The HSAB theory was first summarized from the rate data of generalized nucleophilic displacement reaction and later rooted on density functional theory (DFT) (Parr and Pearson, 1983). These conceptual indices offer practical and insightful ways for understanding and even predicting chemical reactions, particularly in organic chemistry.

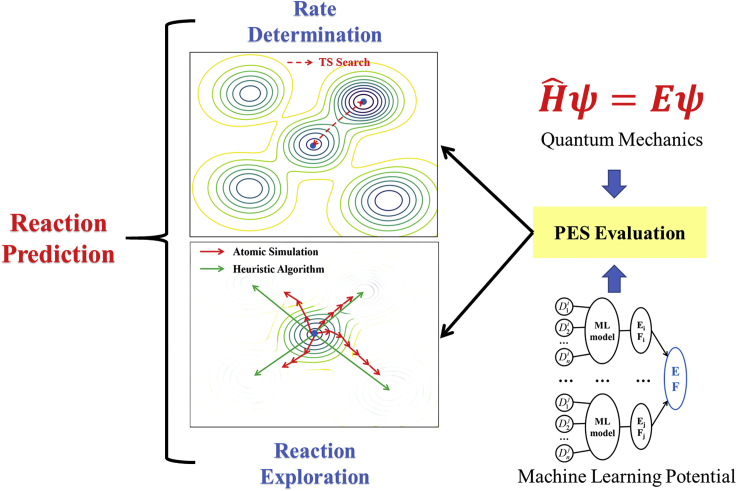
With the ever-increasing computational power, QM calculations, particularly in DFT framework, emerged as the main theoretical tool for investigating chemical reactions since 1990s (Friesner, 2005; Zhao and Truhlar, 2008). Being able to compute the electronic structure with high accuracy, QM methods can be utilized to locate the TS and thus evaluate the reaction rate provided with the correct reaction coordinate (Figure 1). For complex reactions with unknown pathways, an exhaustive exploration of reaction space would be mandatory and the QM-based methods become intractable due to the too high computational cost. Consequently, the low-cost approaches have been designed, either to avoid the reaction pathway exploration or to reduce the cost of PES evaluation. For example, it has been popular to fast estimate the reaction barrier using Evans–Polanyi principles (Evans and Polanyi, 1938), see Equation 2, which establishes the linkage between reaction enthalpy ΔH and reaction barrier E_a.

$$E_a=E_0+\text{ αΔH}$$ (Equation 2)

Figure 1.

Current status of reaction prediction

Reaction prediction not only involves the rate determination between known initial and final states but also demands the reaction space exploration to reveal new reaction patterns.

The pre-factor $\text{α}$ is reaction dependent but often regarded to be around 0.5; and E₀ is the barrier of the putative thermal-neutral reaction, the so-called identity reaction. The approach replaces the difficult reaction pathway exploration by the much straightforward computation of the binding energy of atoms and molecules, and has be applied to organic reactions (Broadbelt et al., 1994) and heterogeneous catalysis (Bligaard et al., 2004; Michaelides et al., 2003).

The low-cost PES evaluation methods are more attractive and desirable for the future of atomistic simulation. Developed upon the classical force field, many reactive force field methods have been continuously developed through the years aiming to describing the bond making/breaking during the atomistic simulation, such as empirical valence bond approach (Warshel and Weiss, 1980), modified embedded atom method (Baskes, 1997), ReaxFF (Van Duin et al., 2001), reactive empirical bond order (Brenner et al., 2002) and more recently, adiabatic reactive MD (Danielsson and Meuwly, 2008). These approaches are often fitted to one class of reactions involving specific bonds since the analytic functions in these methods are relatively simple and not adequate for describing in general the multidimensional reaction space. In recent years, machine learning (ML) potential method demonstrates the great potential to replace QM calculations in large-scale atomistic simulation. Instead of solving Schrodinger equation directly, ML-based simulations rely on a large data set of accurate PES and complex numerical models to predict the total energy, featuring both high speed and high accuracy in computing large systems. Importantly, as long as reaction data is included in learning, ML potential can be used to explore the reaction space and identify unknown reactions (Figure 1). The ML methods for fitting reaction PES may be divided into three types according to their applications. The first type is for polyatomic reactions in the gas phase or at gas-surface interface with limited degrees of freedom, where neural network techniques are utilized to achieve a very high accuracy of PES (Koner et al., 2019; Hong et al., 2020). The second type, i.e. the delta-ML model, is utilized to train the high-accuracy QM data to provide a correction to energy and force of low-accuracy method (force filed or low-level QM calculation) (Brunken and Reiher, 2020; Sun and Sautet, 2019). The third type, also the one most widely adopted, utilizes ML models to directly simulate reaction systems with many degrees of freedom. In this type, many excellent ML models with different architectures have been proposed to describe the high-dimensional PES, e.g. the high-dimensional neural network (HDNN) framework with atomic centered symmetry functions proposed by Behler and Parrinello (Behler and Parrinello, 2007; Behler, 2017), the smooth overlap of atomic positions (Bartók et al., 2013), and the graph convolutional neural networks (Schutt et al., 2017, 2018; Unke and Meuwly, 2019), the Coulomb matrix descriptor (Chmiela et al., 2017), and its variants (Christensen et al., 2020). We proposed the stochastic surface walking neural network (SSW)-NN method in 2017 (Huang et al., 2017, 2018), which integrates the SSW global optimization method (Shang and Liu, 2013) with HDNN framework for predicting the global PES of complex materials and reactions. A main purpose of this review serves to introduce the recent progress of SSW-NN method on reaction prediction.

Reaction prediction via atomistic simulation: theory and methods

Master equation and current methods for pathway sampling

The chemical process can be modeled by a continuous time Markov chain, where the transition between adjacent states is Markovian so that the transition is stochastic without the previous memory. This can be visualized as Figure 2A, where each circle represents a basin with a group of fast interchangeable states (small rectangular), and the line linkage between circles indicate the slow reaction pathways. Chemical reaction often refers to slow reactions occurring near or above ambient temperatures. The kinetics of chemical process is governed by the Master Equation (Equation 3) (Van Kampen, 1992).

$$\frac{d{p}_{\alpha }\left(t\right)}{dt}=\sum _{\beta \ne \alpha }\left[k_{\alpha \beta }{p}_{\beta }\left(t\right)-k_{\beta \alpha }{p}_{\alpha }\left(t\right)\right]$$ (Equation 3)

where k_αβ is the rate constant from state β to state α and p_α(t) is the population of state α, being a function of time t. The sums are over all possible transitions. To compute the overall rate of chemical process, it is therefore essential to obtain both the population of all states and the rate constant between them. By establishing the rate equations for each state, the overall rate of the chemical system can be solved by kinetics Monte Carlo simulation (Bortz et al., 1975) or simply by mean field microkinetics. For complex systems the possible states and reactions could easily reach to an astronomical number, which leads to the rate being virtually impossible to determine exactly.

Figure 2.

Configuration complexity encountered in reaction prediction

(A) Scheme for complex reaction network with many intermediates as labeled by a, b, c, and d (large circles) and a number of possible configurations (small squares) for each intermediate.

(B) Reaction snapshots of ring opening of β-D-glucose starting from two different configurations, which illustrates the critical role of configuration sampling to identify the lowest energy pathway. The reaction barrier of pathway (i) is 1.35 eV and that of pathway (ii) is 2.06 eV, both with respect to the most stable conformation of β-D-glucose. Gray balls: C; red balls: O; white stick: H; yellow balls: the reacting (H)

In fact, it is the common practice to focus on a few slowest reaction steps (e.g. rate-determining step) in reaction network, i.e. to determine their rate constant and the population of the associated precursor states. This may still be challenging. In molecular systems, for example, the presence of the H-bonding network and the soft rotation in molecular side-chains results in many energy-degenerate configurations, but typically only one of them has the low energy pathway to the observed product. As illustrated in Figure 2B, we show two pathways of the ring opening of β-D-glucose (Zhang et al., 2017; Kang et al., 2019). The pathway (i), the lowest energy pathway, has the H transfer via an H-bonding network involving three neighboring hydroxy groups. In contrast, the pathway (ii) has the direct H atom transfer with a much higher barrier, 0.7 eV higher than that of pathway (i).

If the reaction mechanism is known, the most straightforward way to compute reaction rate is via the TS search, which exploits the local curvature (the second derivative of energy with respect to coordinate) information to guide the structure toward to the desired saddle point. Many efficient TS search methods have been developed since 1990s, and depending on whether the coordinate of the final product is required, they can be classified as the single-ended and the double-ended approaches. The single-ended method starts from the pre-guessed TS structure and relies on the identified negative normal mode (eigenvector of the second derivative matrix) to locate TS. The typical methods are Berny geometry optimization (Peng et al., 1996), dimer method (Henkelman and Jónsson, 1999; Olsen et al., 2004), and its improved versions(Shang and Liu, 2010). By contrast, the double-ended approach utilizes the coordinates of the initial and final states for generating the reaction coordinate or building a pseudo-pathway. The TS can then be searched by optimizing the reaction coordinate or the pseudo-pathway. The representative methods include nudged elastic band method (Henkelman et al., 2000; Henkelman and Jónsson, 2000), freezing string method (Behn et al., 2011), growing string method (Zimmerman, 2013b) and double-ended surface walking (DESW) (Zhang et al., 2013).

The TS search becomes frustrated for complex reactions with numerous pathways where the reaction mechanism is often uncertain, such as those involved in phase restructuring and with unknown intermediates in reaction network. In addition, due to the lack of proper PES sampling, the TS search also fails to resolve the population of key reaction states, which can be critical when the configurational space is huge. To solve these problems, advanced PES sampling methods were developed to explore the reaction space. Generally speaking, there are two different ways to detect reaction (see Figure 1): (i) via the heuristics algorithms; (ii) via the atomistic simulation using local curvatures.

In organic chemistry, the heuristics algorithm for reaction exploration is popular since the rules governing organic reactions can be extracted from the experimental database of organic reactions and the concept of bond order and valence is generally valid in organic chemistry. These rules are utilized to rapidly derive potential products based on the initial structure and then the low energy pathway can be searched directly using TS search methods. The reaction pattern generation packages, such as Netgen (Broadbelt et al., 1994), Reaction mechanism generator (Gao et al., 2016), ZStruct (Zimmerman, 2013a), are now available to formulate rules of reaction that create products based on the graph representation of the reacting molecules. One step further, ML techniques are utilized recently to speed up the exploration of complex reaction network and facilitate the design of synthetic routes (Wei et al., 2016; Coley et al., 2019; Segler et al., 2018; Pattanaik and Coley, 2020).The heuristics approaches are however not available for many other types of reactions, e.g. those in heterogeneous catalysis. Furthermore, the completeness of the transformation patterns cannot be guaranteed even for organic reactions with a large reaction library, which limits the approach to discover new synthetic routes.

The reaction exploration via atomistic simulation is a more general approach. The MD-based enhanced sampling techniques, such as umbrella-sampling MD (Torrie and Valleau, 1977), metadynamics (Laio and Parrinello, 2002; Ensing et al., 2006), local elevation (Huber et al., 1994), and interactive MD (Haag et al., 2014), can all be regarded as the PES sampling method using the local curvature information, either explicitly or implicitly, which drives reaction to occur along certain pre-defined directions, often known as collective variables. In parallel with them, the transition path sampling (Bolhuis et al., 2002) and discrete path sampling (Wales, 2002) methods are able to compute the reaction rate between the predefined reactant and product. Since the pre-knowledge on reaction, such as the collective variable and the product, is imposed as constraint in simulation, all these methods cannot be utilized as a tool for automated reaction exploration, but mainly for pathway exploration and rate determination. Ideally, a reaction explorer should start from a known reactant and be able to scan the whole reaction space automatically, which leads to the finding of new products and the low energy pathways connecting to them. Toward this ultimate goal were the methods developed by automatically selecting likely reaction directions during the reaction search, such as gradient extremal following method (Schlegel, 1992), reduced gradient following method (Quapp et al., 1998), anharmonic downward distortion following (ADDF) method (Luo et al., 2009), artificial force induced reaction (AFIR) method (Sameera et al., 2016; Hatanaka et al., 2013), and SSW method (Shang and Liu, 2013; Zhang and Liu, 2015a).

It should be emphasized that due to the heavy computational cost in reaction sampling, the current methods are generally based on the knowledge of PES calculated from DFT. In reality, the chemical environment and the associated free energy contribution, e.g. solvent, temperature and pressures, could be extremely important and thus have to be considered properly to predict the realistic rate. For example, there is often a huge difference in free energy between the gaseous and the adsorbed states for molecules in heterogeneous catalysis and these entropy terms must be corrected in the microkinetics simulation (Ma et al., 2019). In general, the knowledge from sampled reactions could be used to define the reaction coordinate (collective variables) and thus the enhanced MD (umbrella-sampling and metadynamics) can be utilized to evaluate the reaction free energy. For polyatomic reactions, it is already possible to utilize ML approach to train and predict bimolecular thermal rate constants over a large temperature range (Houston et al., 2019). Similarly, the multi-reference effects in electronic structure calculation may well be critical for strongly-correlated systems, such as the metal-containing proteins where the metal-center commonly has the strong multireference character. To better take these effects into account, it would be necessary to recalculate the sampled reactions with more accurate multi-reference methods or to use directly the high accuracy PES that are constructed by force-field and ML methods (Danielsson and Meuwly, 2008; Koner et al., 2019).

In general, the reaction exploration to identify saddle points and reveal low energy pathways are considerably more demanding in computation compared to the minimum search of structure, and the slow PES evaluation by QM calculations further dooms the viability. Not surprisingly, the applications of transition path sampling and discrete path sampling were generally based on empirical force field, such as H₂O clusters and peptides (Geissler, 1999; Evans and Wales, 2003); The state-of-the-art AFIR and SSW methods, although have been utilized in combination with QM calculations of PES, were applied only to the reaction of small molecules (e.g. < 20 atoms) and solid phase transition in small cells. In 2017, we proposed the global neural network (G-NN) potential method (Huang et al., 2017), which builds the G-NN potential by learning iteratively the global PES data set from SSW sampling (SSW-NN). Because G-NN potential can describe unknown minima and reaction pathways thanks to the unbiased SSW global sampling, SSW-NN method turns out to be a powerful tool for reaction exploration, which improves significantly both the speed of PES evaluation and the efficiency of reaction exploration compared to traditional methods. In the following sections, we will elaborate the methodology of SSW-NN and discuss its key features in reaction exploration.

SSW-NN for reaction prediction

A. SSW method for reaction exploration

The SSW method(Shang and Liu, 2013; Shang et al., 2014) was initially developed for global optimization and pathway search of aperiodic systems, such as molecules and clusters, and then extended to periodic crystals(Ma et al., 2019). Compared to other global optimization methods with aggressive structure perturbation, SSW method visits PES with a small step-size by exploiting the local curvature information and thus can be utilized both for structure and reaction exploration. SSW method combines the features of bias-potential-driven dynamics and Metropolis Monte Carlo (MC). The former is a technique utilized to overcome high barriers between minima on PES by adding bias potentials, and the latter is a common method in PES sampling to select state according to the Boltzmann distribution. SSW method adopts a random mode generation and a constrained softening technique to refine the random mode, along which the bias potentials are added. With consecutive bias potentials (Gaussian function) addition, the structural configuration can move gradually from minima to a high energy position on PES.

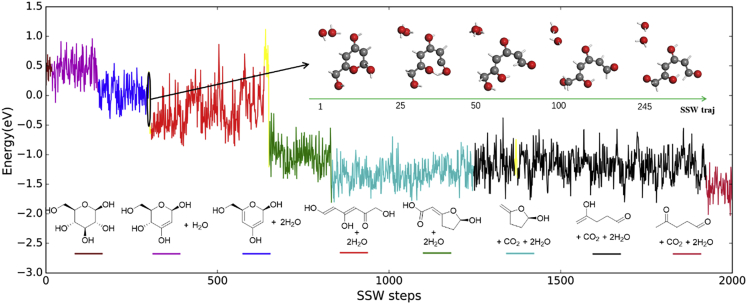
To illustrate the reaction exploration of SSW method, we show a typical SSW trajectory starting from β-D-glucose in Figure 3 (Kang et al., 2019). Within a 2000 step SSW sampling, 31 different molecules are encountered, which can be divided into 8 main minimum domains (marked by different color lines) and many other minority minimum structures (marked by yellow lines). In each minimum domain the diversity of conformations is also evident from the large oscillation in the energy scale. The entire trajectory gradually changes from six-member ring to dehydration products and finally to short-chain molecules. In the meantime, different functional groups emerge, e.g. the common alcohol, ether, alkenyl and aldehyde groups, together with some exotic structures (e.g. with uncommon coordination). As a representative, the inset indicated by the dashed arrow in Figure 3 illustrate the structure snapshots in one step SSW, which transform 6-(hydroxymethyl)-2H-pyran-2,4-diol (blue line) to 3,5,6-trihydroxyhexa-2,4-dienal (minority minimum, yellow line), which is the enol-keto tautomeric precursor of 1,4,6-trihydroxyhexa-3,5-dien-2-one (red line). With such a process, the reaction space with the simultaneous O-H bond formation and C-O bond rupture is captured by SSW sampling. Not limited to molecular reactions, SSW method can be applied generally to many reaction systems, ranging from surface reactions to solid phase transition (Zhang et al., 2017; Guan et al., 2015). In short, SSW trajectories constitute a representative global PES data set with both minima and transition regions, and thus are well suited for constructing ML potentials for atomistic simulation (Huang et al., 2017, 2018).

Figure 3.

A typical 2000-step SSW trajectory where a β-D-glucose molecule evolves into different products

The color of lines represents major intermediate molecules evolved in the trajectory (also see the plotted molecular structure), except that yellow lines represent various products that appear only occasionally. The 3D structural changes in one step SSW step between two specific minima are also highlighted in the inset as indicated by the dashed arrow. Energy zero is defined by the lowest energy conformation of β-D-glucose. Gray balls: C; red balls: O and white stick: H. Reproduced with permission from ref (Kang et al., 2019), Copyright (2019) American Chemical Society.

B. Global neural network potential

Our G-NN potential follows the HDNN framework proposed by Behler and Parrinello (2007), in which the total energy is written as the summation of individual atomic energy in Equation 4 (also see Figure 1).

$$E=\sum _i{E}_i$$ (Equation 4)

$$f_c\left(r_{ij}\right)=\{\begin{array}{l}0.5\times \tan h^3\left[1-\frac{r_{ij}}{r_c}\right],for{r}_{ij}\le r_c\hfill \\ 0for{r}_{ij}>r_c\hfill \end{array}$$ (Equation 5)

$$R^n\left(r_{ij}\right)=r_{ij}^n\cdot f_c\left(r_{ij}\right)$$ (Equation 6)

$$S_i^1=\sum _{j\ne i}{R}^n\left(r_{ij}\right)$$ (Equation 7)

$$S_i^2={\left[\sum _{m=-L}^L{\left|\sum _{j\ne i}{R}^n\left(r_{ij}\right)Y_{Lm}\left({\mathit{r}}_{ij}\right)\right|}^2\right]}^{\frac{1}{2}}$$ (Equation 8)

$$S_i^3=2^{1-\zeta }\sum _{j,k\ne i}{\left(1+\lambda cos{\theta }_{ijk}\right)}^{\zeta }\cdot R^n\left(r_{ij}\right)\cdot R^m\left(r_{ik}\right)\cdot R^p\left(r_{jk}\right)$$ (Equation 9)

$$S_i^4=2^{1-\zeta }\sum _{j,k\ne i}{\left(1+\lambda cos{\theta }_{ijk}\right)}^{\zeta }\cdot R^n\left(r_{ij}\right)\cdot R^m\left(r_{ik}\right)$$ (Equation 10)

$$S_i^5={\left[\sum _{m=-L}^L{\left|\sum _{j,k\ne i}{R}^n\left(r_{ij}\right)\cdot R^m\left(r_{ik}\right)\cdot R^p\left(r_{jk}\right)\cdot \left(Y_{Lm}\left({\mathit{r}}_{ij}\right)+Y_{Lm}\left({\mathit{r}}_{i\text{k}}\right)\right)\right|}^2\right]}^{\frac{1}{2}}$$ (Equation 11)

$$S_i^6=2^{1-\zeta }\sum _{j,k,l\ne i}{\left(1+\lambda cos{\delta }_{ijkl}\right)}^{\zeta }\cdot R^n\left(r_{ij}\right)R^m\left(r_{ik}\right)R^p\left(r_{il}\right)$$ (Equation 12)

where $E_i$ for each atom is the output of a standard feedforward NN. The input of NN is a set of structural descriptors to describe the atomic chemical environment and the parameters in NN can be trained using the PES data set from accurate QM calculations. G-NN potential utilizes a more sophisticated power-type structure descriptors (PTSDs) as the input of NN (Huang et al., 2018), as shown in Equations (Equation 5), (Equation 6), (Equation 7), (Equation 8), (Equation 9), (Equation 10), (Equation 11), (Equation 12) (r_ij is the internuclear distance between atom i and j, θ_ijk is the angle centered at i atom with j and k being neighbors; i, j, and k are atom indices), which is developed to best discriminate the SSW global data set. In PTSD, not only the traditional two-body and three-body terms but also the four-body terms are added, and the spherical functions are introduced to enhance the angular resolution of chemical environment. In PTSDs ((Equation 5), (Equation 6), (Equation 7), (Equation 8), (Equation 9), (Equation 10), (Equation 11), (Equation 12)), the key ingredients are the cutoff function f_c that decays to zero beyond the r_c (Equation 5), the power-type radial function, the trigonometric angular functions, and the spherical harmonic function, which constitute the two-body functions S¹ and S², the three-body functions S³, S⁴, and S⁵, and the four-body function S⁶.

In practice, to start off, the G-NN potential is obtained by first learning a small data set (typically less than one thousand structures) collected from short-time DFT-based SSW sampling, which is often restricted to small systems (below 20 atoms) starting from known configurations. The data set needs to be calculated by DFT with a high accuracy setup. Next, the SSW global optimization based on NN potential will be carried out extensively, starting from a variety of initial structures, mainly randomly constructed, with different morphology, including bulk, surface, and clusters, different chemical compositions, and different number of atoms per cell. After each iteration of global optimization, a small data set with diverse structures on PES is screened out by selecting either randomly or from those exhibiting new atomic environment (e.g. out-of-bounds in structural descriptors, unrealistic energy/force/curvature). These additional data will be calculated by DFT with the same high accuracy setup, and then added to the training data set for a new iteration of NN potential update. Typically, more than ∼100 iterations are required to finally obtain a transferable G-NN potential. Approximately 200,000–300,000 CPU core-hours (1000 CPU cores for two weeks) were needed for the iterated training process of a robust global NN potential and the final data set is usually in the range of 30,000 to 100,000 structures. The accuracy for G-NN potential is typically 5–10 meV/atom for the root mean square error (RMSE) of energy and 0.1∼0.2 eV/ Å for RMSE of force.

C. SSW reaction sampling based on G-NN potential

The SSW global optimization can be extended for automated reaction sampling, i.e. SSW-RS method (Zhang and Liu, 2015a; Zhang et al., 2017). The SSW-RS simulation targets to explore the likely reaction pathways nearby a predefined reactant and identify the lowest energy pathway leaving it (also see Figure 1). The method was initially utilized for single-step reactions and solid phase transitions in small cells. With the advent of G-NN potential, SSW-RS is now capable to explore complex reaction network.

There are two stages in SSW-RS simulation. (i) Reaction pair collection via extensive SSW global pathway search. In reaction sampling, the structure selection module no longer follows Metropolis MC scheme but makes judgment based on whether a chemical reaction occurs. It can be done by comparing the bond matrix and the chirality of minima; (ii) Pathway building and TS determination via DESW method (Zhang et al., 2013; Zhang and Liu, 2015b). Using the reaction pairs collected in step (i), the saddle point along the pathway is identified first and the extrapolation from the saddle point to nearby minima is performed to confirm the reaction. If it is not an elementary reaction, an iterative procedure is invoked to connect each segment and identify the pathway for each elementary reaction. Once the pathway is finally completed, the reaction barrier can be obtained with respect to the energy of the global minimum configuration of reactant, which will be utilized as the quantitative measure to compare different pathways and to select the lowest energy pathway.

Case studies of SSW-NN simulation for reaction prediction

To illustrate the reaction prediction using SSW-NN, we here show two examples, water gas shift reaction (WGSR) on Cu (111) and glucose pyrolysis. Both systems were simulated using LASP code (Large-scale Atomic Simulation with neural network Potential, www.lasphub.com) developed in our group (Huang et al., 2019), where a large set of G-NN potentials is available. The CuCHO potential and the CHON potential utilized in the examples below are able to describe catalytic reactions on Cu surfaces and organic reactions in the gas phase, respectively. The CuCHO potential was trained using a data set of 68440 structures, reaching to a RMSE of 4.60 meV/atom for energy and 0.106 eV/Å for force. The data set for training CHON potential has 94854 structures, containing nearly all (78 of 79) bonding patterns with C-H-O-N four elements. The RMSE of CHON potential is 10.05 meV/atom for energy and 0.242 eV/Å for force.

Water gas shift reaction on Cu (111)

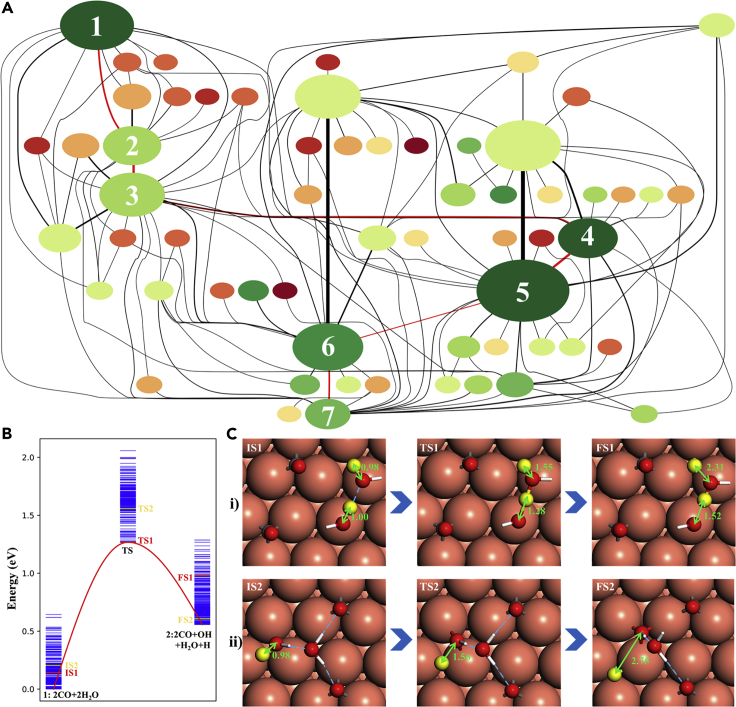
Figure 4 plots the reaction network map for WGSR on Cu (111) from SSW-NN, which is simulated using two CO and two H₂O molecules on Cu (111) surface (p(3x3) supercell). Each circle represents a state and its area indicates the frequency of the state encountered in collected reaction pairs. The system was initially studied by DFT (Zhang et al., 2017) driven by preconfigured reaction directions, and can now be performed unbiasedly with CuCHO G-NN potential. The total sampling contains 375,000 minima and collects more than 10,000 reaction pairs. After removing duplicate reactions and recording only the lowest barrier connection between pairs, the final reaction database contains 290 different reactions and 143 different intermediates. Figure 4A plots 60 low energy intermediates and their associated 127 reactions. From the reaction network, the lowest energy pathway of WGSR is identified to pass through the HCOOH intermediate, i.e. CO+H₂O→CO+OH+H→COOH+H→ HCOOH→HCOO+H→CO₂+H+H→CO₂ +H₂ as shown in the route 1→7 marked by red lines of Figure 4. These intermediates along the lowest energy pathway are frequently visited by SSW-RS with relatively large area in the map, while the intermediates along high energy pathways are much less visited. This result is consistent with experiment that formic acid and formate are major intermediates at low temperatures (Fishtik and Datta, 2002).

Figure 4.

SSW-NN applied to predict heterogeneous catalytic reaction network

(A) Reaction network map for water gas shift reaction (WGSR) on Cu(111) from G-NN-based SSW-RS simulation. The system starts from two CO and two H2O molecules on Cu (111) surface (p(3x3) supercell). The key intermediates along the WGSR pathway are marked by red lines, e.g. 1: 2CO+2H2O; 2: 2CO + H2O + OH + H; 3: COOH + CO + H2O + H; 4: HCOOH + CO + H2O; 5: HCOO + CO + H2O + H; 6: CO2+CO + H2O + H + H; 7: CO2+CO + H2O + H2. The color of circle from dark green to dark red indicates the energy from low to high; the area of circle represents the frequency of the state encountered in collected reaction pairs; the width of line corresponds to the occurrence number of the transformation in simulation.

(B) Energy profile of the water splitting step on Cu (111) revealed by the SSW-RS method. The possible configurations of each state as identified from simulation is shown by the blue spectrum.

(C) Reaction snapshots of the water splitting step on Cu (111), which illustrates the critical role of H-bonding network and the molecular configuration. The reaction barrier of pathway (i) is 1.28 eV, while that of pathway (ii) is 1.57 eV. Energy zero is defined by the lowest energy conformation of 2CO+2H2O on Cu (111). Gray balls: C; red balls: O; white stick: H; brick red balls: Cu; yellow balls: the reacting (H)

Figures 4B and C show the energy profile and the reaction snapshots for the water splitting step (1→2), the rate-determining step, which illustrate the key feature of SSW-RS to simultaneously sample both the reactant space of conformations and the pathway space. Among 247 reactions sampled, the lowest energy pathway has a barrier of 1.28 eV, which corresponds to the reaction starting from a metastable IS (IS1) and having the H₂O dissociation with the help of another H₂O (Figure 4C). For comparison, a less favored pathway where H₂O splits directly is also shown, which has a barrier of 0.3 eV higher.

Glucose pyrolysis

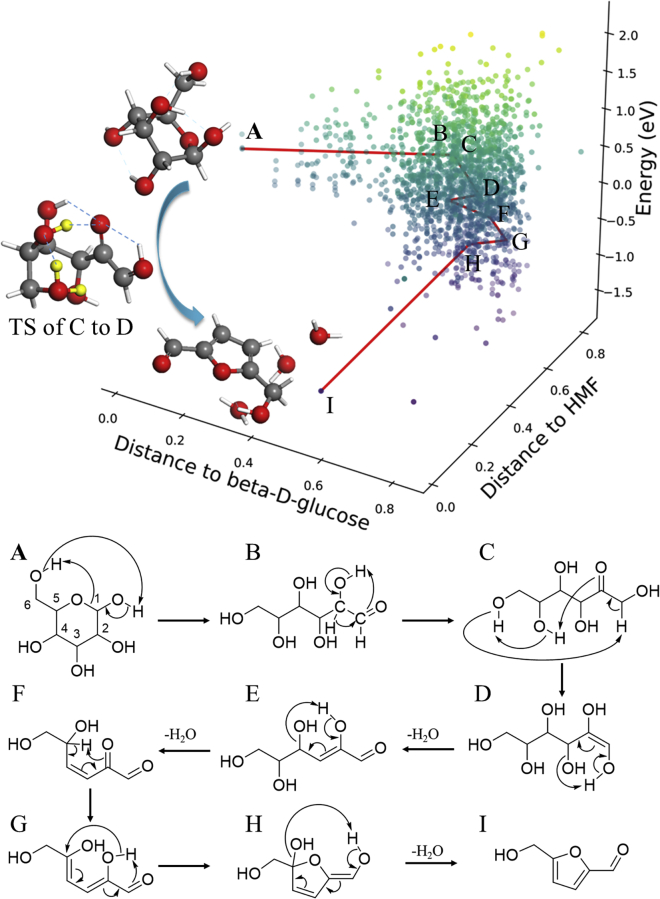
Figure 5 shows the glucose pyrolysis reaction network data generated from SSW-NN simulation (Kang et al., 2019). Benefited from the low cost of G-NN PES, we can achieve a deep exploration of the reaction tree starting from β-D-glucose. In total, we managed to sample 1.2 million minima and collected more than 150,000 reaction pairs. After removing duplicate reactions and recording only the lowest barrier connection between pairs, the final reaction database, as shown in Figure 5, contains 4455 unique molecules, 6407 different reactions. We have analyzed carefully the pathways in our reaction database to identify the pathways to 5-Hydroxymethylfurfural (HMF), a major and valuable product observed in experiments (Fang et al., 2018; Patwardhan et al., 2009; Mayes et al., 2014). It should be mentioned that these pathways belong to gas phase reactions mimicking the pyrolysis condition.

Figure 5.

Reaction database and the lowest energy pathway in glucose pyrolysis from SSW-NN simulation

The x and y axis are the similarity distances of intermediates with respect to β-D-glucose and HMF, respectively. The similarity distances are calculated using the fingerprint algorithm in RDkit using the Tanimoto similarity (Landrum, 2006). The lowest energy pathway from beta-D-glucose to HMF is marked by red line and the reactions along the lowest energy pathway, from A to I, are shown below.

In the lowest energy pathway (A to I in Figure 5), β-D-glucose undergoes sequentially ring-opening, isomerization, tautomerization, dehydration, and cyclization to HMF. The rate-determining step belongs to the enol-keto tautomerization (TA) reaction (C→D), with a barrier of 1.91 eV (with respect to the most stable configuration of β-D-glucose hereafter), which is 0.19 eV lower than the previous proposed pathways (2.10 eV via β-H elimination). The TA reaction opens the retro-Michael reaction (RM) route in the subsequent dehydration reactions and avoids the direct β-H elimination. Again, the TA step (C→D) benefits from a highly sophisticated H-bonding network for H atom transfer. This new mechanism for 5-HMF production supports the observed glucose pyrolysis phenomena and provides important insights int to the catalytic glucose conversion. A recent NMR experiment in catalytic carbohydrate dehydration does reveal 3-deoxyglucos-2-ene (3-DGE, E) as an on-pathway intermediate (Jensen and Meier, 2020).

Conclusions

Reaction prediction is a central task in chemistry. The traditional atomistic simulation methods, such as QM-based MD, are not efficient enough to meet the purpose. We have shown that the global PES sampling based on ML potential, as represented by SSW-NN method, provides a new route for reaction prediction. Two examples of SSW-NN applications, WGSR on Cu and glucose pyrolysis, demonstrate that both the right configuration of reactant and the correct reaction pattern are critical in achieving the lowest energy pathway, which emphasizes the key contributions of SSW-NN for reaction prediction: G-NN potential speeds up PES evaluation and SSW efficiently samples global PES. Because the degrees of freedom increase rapidly with the increase of system size, and the difficulties to construct G-NN potential grow markedly in complex reaction systems (e.g. number of elements, complexity of reaction network), it remains early at the current stage to foresee how far SSW-NN can be applied to different fields of chemistry. The true battle for reaction prediction just starts.