Evidence for S2 flexibility by direct visualization of quantum dot–labeled myosin heads and rods within smooth muscle myosin filaments moving on actin in vitro

Brizendine et al. directly visualized quantum dot–labeled myosin heads and rods in vitro to understand the flexibility of the S2 subdomain. Their results confirm theoretical predictions about the range of motion of S2 and its effect on the relative movement of myosin on actin in vitro.

Abstract

Myosins in muscle assemble into filaments by interactions between the C-terminal light meromyosin (LMM) subdomains of the coiled-coil rod domain. The two head domains are connected to LMM by the subfragment-2 (S2) subdomain of the rod. Our mixed kinetic model predicts that the flexibility and length of S2 that can be pulled away from the filament affects the maximum distance working heads can move a filament unimpeded by actin-attached heads. It also suggests that it should be possible to observe a head remain stationary relative to the filament backbone while bound to actin (dwell), followed immediately by a measurable jump upon detachment to regain the backbone trajectory. We tested these predictions by observing filaments moving along actin at varying ATP using TIRF microscopy. We simultaneously tracked two different color quantum dots (QDs), one attached to a regulatory light chain on the lever arm and the other attached to an LMM in the filament backbone. We identified events (dwells followed by jumps) by comparing the trajectories of the QDs. The average dwell times were consistent with known kinetics of the actomyosin system, and the distribution of the waiting time between observed events was consistent with a Poisson process and the expected ATPase rate. Geometric constraints suggest a maximum of ∼26 nm of S2 can be unzipped from the filament, presumably involving disruption in the coiled-coil S2, a result consistent with observations by others of S2 protruding from the filament in muscle. We propose that sufficient force is available from the working heads in the filament to overcome the stiffness imposed by filament-S2 interactions.

Introduction

Myosin II is a class of molecular motors found in all muscles, as well as nonmuscle cells. During the actomyosin adenosine triphosphatase (ATPase) cycle (Fig. 1 A; Lymn and Taylor, 1971), ATP hydrolysis within the two motor domains is coupled to work done against actin within the thin filament. Myosin generates force and motion through a discrete rotation of part of the head domain, the lever arm, when bound to actin, which moves myosin a distance d called the step size (∼10 nm; Molloy et al., 1995; Warshaw et al., 2000; Baker et al., 2002). It is necessary to understand how myosin couples this chemical energy (ATPase activity) to motion to describe how muscle fundamentally operates in both normal and disease states.

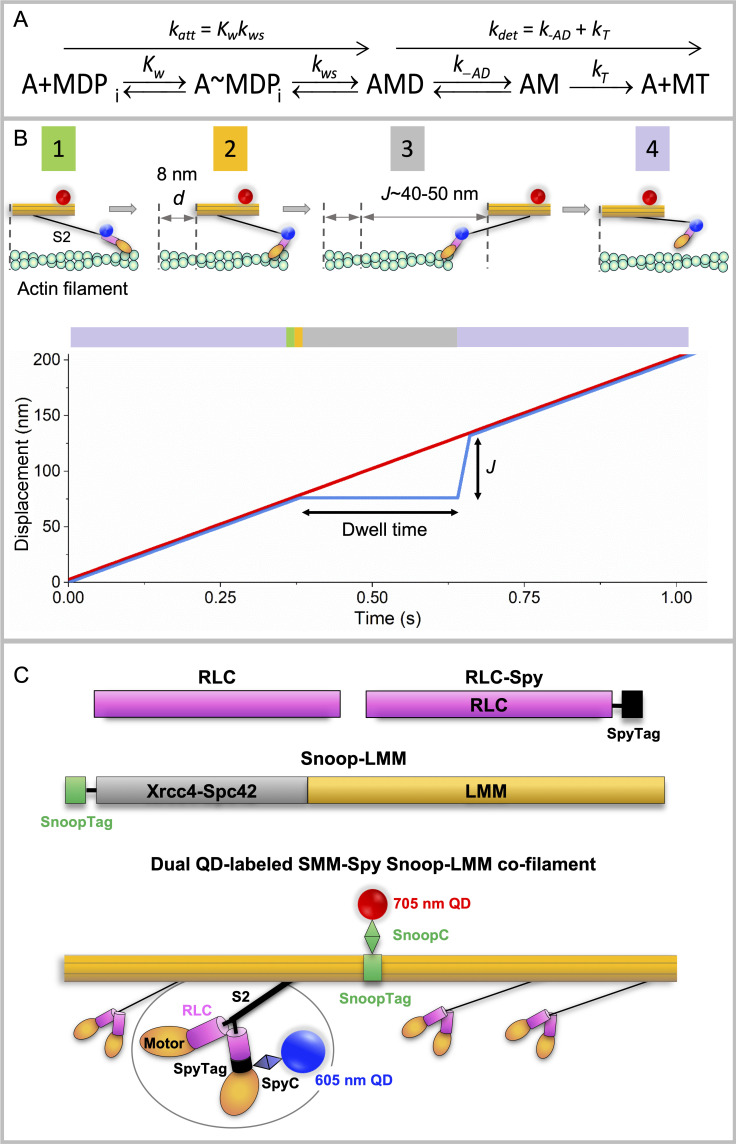
Figure 1.

Summary of actomyosin kinetics and experimental system. (A) Kinetic scheme for myosin (M) attachment to actin (A). D, ADP; T, ATP; Pi, phosphate. K_w, equilibrium constant for weak binding of myosin to actin; k_ws, forward rate constant for the weak to strong transition. We assume that k_-ws is insignificant. See text for other rate constants. (B) Top: M_f/A assay showing SMM-Spy Snoop-LMM (RLC-LMM) cofilament (orange) labeled with QD-SpyC (blue dot) attached to the RLC in the lever arm domain (pink) and QD-SnoopC (red dot) moving over biotinylated actin (green) attached to PEG brush-coated coverslip (not shown). Filaments are shown widely separated for clarity with S2 (black) detached completely from the filament backbone, which may not reflect the actual process (see text). Pre-working step, green box 1; post-working step, gold box 2; and after full extension of S2, gray box 3, by other working heads (not shown) giving L = 40–50 nm. The myosin head then must return to its starting position relative to the filament backbone, purple box 4. Bottom: Graph of mixed-kinetic model predictions of single head behavior in a filament. Black arrows indicate approximate predicted dwell time and J value (see text) predictions at 10 µM [ATP]. Red line, filament backbone trajectory. Blue line, predicted single myosin head behavior. Lines are shown nearly coincident for clarity but could be separated depending upon the relative positions of the two QDs. Colors in the bar above the graph correspond to the state of the myosin head. The entire cycle time is not shown for clarity. (C) Expressed constructs and proteins. Pink, RLC (UniProtKB, P02612). Black, SpyTag002 (VPTIVMVDAYKRYK; Keeble et al., 2017). Gray, Xrcc4-Spc42 (Andreas et al., 2017; Drennan et al., 2019). Green, SnoopTag (KLGDIEFIKVNK; Hatlem et al., 2019). Thin black line, GSGESG linker. Lengths reflect approximate relative sequence lengths. RLC-Spy, SpyTag on C terminus of RLC. Snoop-LMM, SnoopTag on the N terminus of the Xrcc4-Spc42 domain, then LMM 1728–1979 (National Center for Biotechnology Information accession no. NP_990605.2). In RLC-LMM cofilament, colors match constructs above. Backbone formed by assembled LMM domains (orange), two heads (orange) and S2 domain (black); Xrcc4-Spc42 domain is not visible. 705 nm QD (red dot) chemically coupled to a SnoopC (green diamond) interacting with SnoopTag (green box) of LMM construct (orange). Enlarged region shows 605 nm QD (blue dot) chemically coupled to SpyC (blue diamond) interacting with SpyTag of RLC construct in myosin head (orange). See Materials and methods for details.

Myosin IIs operate in vivo as macromolecular assemblies of monomers that are stabilized through intermolecular ionic interactions between the C-terminal coiled-coil rod domains. This assembly allows multiple myosin heads (motor domains) to interact with a single actin filament. To understand how and if filaments operate in a fundamentally different manner from soluble subfragments of myosin, we have been working to bridge the gap between solution kinetics and muscle mechanics using in vitro assays designed to directly observe the relative motion between myosin and actin filaments.

Using data from in vitro motility assays that allow measurement of unloaded velocity (V) of fluorescent myosin filaments moving along fixed fluorescent actin filaments (M_f/A assay; Fig. 1 B; Haldeman et al., 2014), we developed the mixed kinetic (MK) model (Brizendine et al., 2015; Brizendine et al., 2017) that describes V as being influenced by not only the rate of actin detachment but also the rate of actin attachment (k_att). The model was developed from data collected for three different myosin II isoforms, smooth, skeletal, and cardiac muscle myosins. It was consistent with known kinetic parameters but required an additional mechanical feature to be accounted for that we believe is important to how filaments move along actin.

Fig. 1 B illustrates this key mechanical feature of the model. A single head within a myosin filament is shown moving relative to an actin filament. Between the head and the filament backbone is the relatively flexible subfragment 2 or ∼1/3 of myosin tail proximal to the heads (S2) domain shown projecting from the filament surface. After actin attachment and the working stroke, which translates the myosin filament a distance d, other heads (not shown) continue to move the myosin filament to the right. During this time, if the head remains bound to actin, it is pulled backward a given distance permitted by the flexibility of the S2 domain.

At low numbers of available myosin heads in the filament (N), V is slow, and the attached head is likely to detach before it places a drag load on the working heads so that V is influenced primarily by the rate of attachment of myosin to actin (k_att; Fig. 1 A). With increasing N, V becomes fast enough to allow a head to reach the end of its S2 tether before it has had time to detach from actin (Fig. 1 B, upper), resulting in a drag load that resists the working heads. These drag heads must detach from actin before the working heads can further move the filament. This leads to V being influenced by both attachment and detachment kinetics. Here, detachment kinetics are affected not by d, but by the distance parameter, L, related to the distance the filament can travel without placing a drag load on the moving filament. L is influenced by the mechanical behavior of the proximal rod called S2 (Fig. 1 B).

We can make predictions about the behavior of individual myosin heads within a moving filament (Fig. 1 B, lower). A given head will move along the same trajectory as the filament backbone until it attaches to actin. While attached, the head will appear stationary relative to the backbone for a dwell time (t_on = k_det⁻¹; Fig. 1 A), followed by a jump forward a distance J upon detachment. The observed jump distance, J, is related to the distance parameter L (Fig. 1 B, lower). The actual measured jump height, J, can only approach the predicted L in the extreme case where motion is essentially completely detachment limited. Under these conditions, a head will be pulled to the end of its S2 tether (low [ATP] or high N). Based on fits of the MK model to V versus N data, we estimated L to be ∼59 ± 3 nm for smooth muscle myosin (SMM) filaments (Brizendine et al., 2017).

The aim of this study is to test model predictions by simultaneously tracking, with high temporal and spatial resolution, the motion of a single head relative to the motion of the filament backbone while moving along actin. SMM was chosen for this study because, of the three myosin IIs mentioned above, it has the longest L and the slowest rate of ADP release (k_-AD). These two parameters are important to be able to reliably detect events, i.e., dwells followed by jumps.

SMM cofilaments were prepared with quantum dots (QD) of two different colors (Fig. 1 C). The approach requires that the QDs are attached specifically, covalently, and with the correct stoichiometry after the filament is formed, because we have previously shown that the presence of the QD disrupts normal filament assembly (Brizendine et al., 2019). To monitor head motion, we used the SpyCatcher (SpyC)/SpyTag system (Keeble et al., 2017) to attach a QD to the regulatory light chain (RLC) in the lever arm domain of the head, as we described previously (Brizendine et al., 2019). To monitor filament backbone motion, we used a complementary but non–cross-reactive SnoopCatcher (SnoopC)/SnoopTag system (Veggiani et al., 2016) to attach a QD to the light meromyosin, C-terminal portion of the myosin tail excluding S2 (LMM), subdomain of the rod.

We have detected events in filament trajectories that match the behavior predicted by the MK model, with dwell times and values of J that are consistent with our prior estimates of L and other measured kinetic parameters for SMM that define t_on. We also have shown that the frequency of observed events and the time between events are consistent with the model. Our data suggest that the S2 domain of myosin can move independently from the filament backbone and is a key mechanical feature of unloaded motility of myosin filaments.

Materials and methods

Buffers and proteins

Filament buffer contained 10 mM NaPi, pH 7.0, 5 mM MgCl₂, 125 mM NaCl, 0.1 mM EGTA, 1 mM dithiothreitol (DTT), and 30 nM NaN₃. Conjugation buffer contained 20 mM HEPES, pH 7.2, 0.5 M NaCl, 0.1 mM EGTA, 5 mM DTT, and 30 nM NaN₃. Exchange buffer contained 20 mM NaPi, pH 7.5, 0.5 M NaCl, 5 mM EGTA, 2 mM EDTA, 1 mM DTT, and 30 nM NaN₃. Actin, Alexa Fluor 488–labeled actin (Thermo Fisher Scientific), tetramethylrhodamine isothiocyanate–labeled actin, and biotin-labeled actin (5%) were prepared as described (Haldeman et al., 2014; Brizendine et al., 2015). Chicken gizzard SMM was prepared and labeled with N-hydroxysuccinimide (NHS)–rhodamine as described (Haldeman et al., 2014). The following extinction coefficients (0.1% wt/vol) were used to determine protein concentrations at 280 nm: SMM, 0.56; RLC-Spy, 0.341; RLC-SpyC, 0.547; His-Cys-SpyC, 1.02; His-Cys-SnoopC, 0.776; and Snoop-LMM, 0.385. Protein molecular weights were as follows: SMM, 480 kD; RLC-Spy, 21.85 kD; RLC-SpyC, 34.59 kD; His-Cys-SpyC, 15.9 kD; His-Cys-SnoopC, 15.4 kD; and Snoop-LMM, 47.9 kD (monomer) and 95.8 kD (dimer).

Protein expression and purification

His₆-Cys-SpyC002 protein expression was as described in Keeble et al. (2017). pDEST14-Cys-SpyC002 was a gift from M. Howarth (University of Oxford, Oxford, UK; Addgene; plasmid #102829). Briefly, the plasmid was amplified in DH5α Escherichia coli by overnight Luria-Bertani (LB) culture with 50 µg ml⁻¹ ampicillin and purified using a Monarch Plasmid Miniprep kit (NEB). The plasmid was then transformed into BL21 DE3 pLysS competent E. coli. (Invitrogen). For protein expression, transformed bacteria were grown in LB with 50 µg ml⁻¹ ampicillin and chloramphenicol to OD₆₀₀ 0.5–0.7 at 37°C while shaking at 250 rpm. To induce expression, isopropyl-β-D-thiogalactoside (IPTG) was added to a final concentration of 0.4 mM and incubated for 4 h at 37°C and 225 rpm. His₆-Cys-SpyC002 was purified using an AKTA explorer and a 5 ml HiTrap Chelating HP column (GE Healthcare) charged with 100 mM NiSO₄. The buffer was exchanged by dialysis into conjugation buffer, and the protein was stored at −80°C.

His₆-Cys-SnoopC (Veggiani et al., 2016) DNA was synthesized by Eurofins Genomics. The DNA sequence was modified to include a cysteine after the His tag to allow coupling to QDs and the necessary complementary overhangs for ligation-independent cloning using the aLICator expression system (Thermo Fisher Scientific). The amino acid sequence was as follows: MHHHHHHSCSGLVPRGSHMKPLRGAVFSLQKQHPDYPDIYGAIDQNGTYQNVRTGEDGKLTFKNLSDGKYRLFENSEPAGYKPVQNKPIVAFQIVNGEVRDVTSIVPQDIPATYEFTNGKHYITNEPIPPKYNDFPS. After the construct, DNA was ligated into pLATE11 according to the manufacturer’s protocol, and the vector was transformed into chemically competent E. coli NEB5α cells (NEB), amplified, and purified as above. The plasmid was then transformed into BL21 DE3 pLysS competent E. coli (Invitrogen). For protein expression, transformed bacteria were grown in LB with 100 µg ml⁻¹ ampicillin and grown to OD₆₀₀ 0.5–0.7 at 37°C while shaking at 250 rpm. To induce protein expression, IPTG was added to a final concentration of 0.4 mM and incubated for 4 h at 37°C and 225 rpm. His₆-Cys-SnoopC was purified identically to His₆-Cys-SpyC002.

Chicken smooth muscle RLC (UniProtKB-P02612) and SpyTag002 (RLC-Spy) construct was expressed and purified as described (Brizendine et al., 2019).

SnoopTag-LMM and SpyTag-LMM DNA was synthesized by Integrated DNA Technologies with the necessary complementary overhangs for ligation-independent cloning using the aLICator expression system (Thermo Fisher Scientific) into pLATE11 vector. These constructs included the following domains from N to C: SnoopTag or SpyTag, GS linker, Xrcc4 1–135, Spc42 72–86, and LMM 1728–1979. The amino acid sequences were as follows: SnoopTag, KLGDIEFIKVNK (Hatlem et al., 2019); SpyTag, VPTIVMVDAYKRYK (Veggiani et al., 2016); GS linker, GSGESG; and Xrcc4-Spc42 domain, added to increase solubility and ensure correct coiled-coil formation (Andreas et al., 2017; Drennan et al., 2019), ERKISRIHLVSEPSITHFLQVSWEKTLESGFVITLTDGHSAWTGTVSESEISQEADDMAMEKGKYVGELRKALLSGAGPADVYTFNFSKESRYFFFEKNLKDVSFRLGSFNLEKVENPAEVIRELIDYALDTTAELNFKLREKQNEIFE. Finally, the LMM sequence was the last 254 amino acids from chicken gizzard SMM heavy chain (National Center for Biotechnology Information accession no. NP_990605.2): ANSGRTSLQDEKRRLEARIAQLEEELDEEHSNIETMSDRMRKAVQQAEQLNNELATERATAQKNENARQQLERQNKELRSKLQEMEGAVKSKFKSTIAALEAKIASLEEQLEQEAREKQAAAKTLRQKDKKLKDALLQVEDERKQAEQYKDQAEKGNLRLKQLKRQLEEAEEESQRINANRRKLQRELDEATESNDALGREVAALKSKLRRGNEPVSFAPPRRSGGRRVIENATDGGEEEIDGRDGDFNGKASE. After the construct DNA was ligated into pLATE11 per the manufacturer’s protocol, the vector was transformed into chemically competent E. coli NEB5α cells (NEB), amplified, and purified as above. The plasmid was then transformed into BL21 DE3. For expression, transformed bacteria were grown in LB with 100 µg ml⁻¹ ampicillin and grown to OD₆₀₀ 0.5–0.7 at 37°C while shaking at 250 rpm. To induce protein expression, IPTG was added to a final concentration of 0.4 mM and incubated for 5 h at 37°C and 225 rpm. Protein was purified by one round of high to low salt clarification followed by size exclusion chromatography. Briefly, after the cells were lysed by addition of lysozyme to 0.2 mg ml⁻¹ in 50 mm NaPO₄, pH 7.4, 5 mM DTT, and 1 mM EDTA, NaCl was added to 0.5 M, and the lysate was centrifuged at 12,000× g at 4°C for 20 min. The supernatant was removed and concentrated by dialysis against solid 20,000 molecular weight polyethylene glycol (PEG; Sigma-Aldrich; 81300) in 10,000 molecular weight cut-off snakeskin dialysis tubing (Thermo Fisher Scientific; 88245) until the final volume was ∼10-fold reduced. The solution was then dialyzed against 4 L of the above lysis buffer overnight, then centrifuged at 14,000× g at 4°C for 30 min. The pellet was then resuspended in 5 ml of conjugation buffer. Any insoluble material was removed by centrifugation at 126,000× g at 4°C for 15 min. Final polishing of the LMM construct was done by gel filtration in conjugation buffer on a XK16/60 column packed with Superdex 200 prep grade (GE Healthcare). Fractions were analyzed by SDS-PAGE and pooled for purity. The protein was stored at −80°C.

Modification of QDs with maleimide functional groups

Modification of QDs was performed similar to that described in Brizendine et al. (2019). Briefly, amine QDs (Invitrogen; 50 µl of 605 or 705 nm; 8 µM) were centrifuged for 3 min at 2,400× g and washed twice in a 100 kD cutoff centrifugal filter unit (Millipore) in DTT-free conjugation buffer. The final volume was adjusted with DTT free conjugation buffer so that the [QD] = 4 µM. Maleimide-PEG₆-NHS (SM[PEG]₆; Thermo Fisher Scientific) was added to the QDs to a fourfold molar excess (16 µM) and allowed to react for 30 min at room temperature (RT). Unreacted amines on the QD were blocked with the addition of 2 mM NHS-acetate (Thermo Fisher Scientific) for 30 min at RT. The NHS reactions were quenched with 4 mM hydroxylamine (Sigma-Aldrich). Excess reactants and side products were removed with a NAP-5 desalting column (GE Healthcare) equilibrated in DTT-free conjugation buffer.

Coupling QDs to SpyC and SnoopC

Protein cysteines were reduced (5 mM DTT, 1 h on ice), and excess DTT was removed with a PD minitrap G-10 column (GE Healthcare) equilibrated in DTT-free conjugation buffer. A fourfold molar excess of the reduced protein was added to the modified QDs (SpyC to 605 nm QDs and SnoopC to 705 nm QDs) and reacted for 2 h at RT, then overnight on ice. The reaction was quenched with 5 mM DTT. Unreacted protein was removed through a 100 kD cutoff centrifugal filter unit (Millipore) by suspending five times in filament buffer and stored on ice until use. QDs were assumed to be coupled to SpyC or SnoopC on the sole Cys engineered near the N terminus.

RLC-Spy exchange

RLC-Spy (Fig. 1 C) was exchanged onto SMM as described (Ellison et al., 2000). Briefly, the exchange reaction was performed in exchange buffer at 4.2 µM SMM (8.4 µM SMM heads) with an equimolar ratio of RLC-Spy to SMM heads with additional 10 mM DTT and 1 mM ATP. The mixture was heated to 42°C for 30 min. The sample was then allowed to cool at RT for 10 min, followed by addition of MgCl₂ to 20 mM, and placed on ice for 2 h to allow RLC-Spy to bind to the denuded myosin. Precipitated protein was removed by centrifugation for 5 min at 16,100 g at 4°C in a refrigerated microcentrifuge (Eppendorf 5415R), and the pellet was discarded. Excess RLC was removed from SMM with a prespun (150 g, 2 min) 10 ml Sephacryl S-400 HR (GE Healthcare) spin column equilibrated in exchange buffer. The exchange efficiency of RLC-Spy was determined by SDS-PAGE and gel densitometry after staining with Coomassie blue. Gels were imaged with a Bio-Rad ChemiDoc XRS Imaging system and analyzed with ImageLab 3.0 software (Bio-Rad). Exchange efficiency was generally ∼30–35%.

Preparation of SMM-Spy Snoop-LMM (RLC-LMM) cofilaments

After the RLC was exchanged into SMM, the product was mixed with rhodamine-labeled SMM and Snoop-LMM (Fig. 1 C) so that the final SMM-Spy heads were 3% (wt/wt) and the final concentration of Snoop-LMM was 3% (wt/wt) of the total protein at a final concentration of 4.2 µM. RLC-LMM cofilaments (Fig. 1 C) were formed by O/N dialysis into filament buffer and cross-linked with 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide hydrochloride as described (Haldeman et al., 2014; Brizendine et al., 2015; Brizendine et al., 2017).

Preparation of SMM Spy-LMM Snoop-LMM (LMM-LMM) cofilaments

Rhodamine-labeled SMM was mixed with Snoop-LMM and Spy-LMM so the final concentration of Snoop-LMM was 3% (wt/wt) and of Spy-LMM was 3% (wt/wt) at a total protein concentration of 4.2 µM. Filaments were formed and cross-linked as above.

Cofilament phosphorylation

Filaments were phosphorylated by myosin light chain kinase as previously described (Haldeman et al., 2014; Brizendine et al., 2015). Phosphorylation of the Spy-RLC and native RLC was detected by urea gel electrophoresis.

Attaching SpyC-QDs and SnoopC-QDs to phosphorylated cofilaments

Phosphorylated cofilaments at 1 µM were reacted with 60 nM QD-SpyC and 60 nM QD-SnoopC at 4°C overnight.

Motility assays and TIRF imaging

M_f/A motility assays were essentially as described (Brizendine et al., 2015; Brizendine et al., 2017). Briefly, experiments were at 30°C in filament buffer without NaN₃ plus 0.5% methylcellulose and 32 mM glucose, 0.2 µM (5 U ml⁻¹) glucose oxidase, 0.18 µM (90 U ml⁻¹) catalase, and indicated ATP. Imaging was performed with a Nikon TE2000 inverted microscope, 100× plan apo Nikon objective (NA 1.45), and a 1.5× tube lens. TIRF excitation was controlled with a Cairn Optics OptoTIRF module. Alexa Fluor 488 actin containing 5% biotin was attached to a PEG surface, and the QD-labeled cofilaments were observed moving along the actin. Alexa Fluor 488 actin was imaged with a 488-nm excitation laser (QiOptiq), and QDs were excited with a 405-nm laser (QiOptiq) using a custom filter cube with no excitation or emission filters and a ZET 405/488 dichroic. Two emission filters (600/50 and 706/95; Chroma) were mounted in a double-channel beam splitter (Cairn Optics) set up with a 630 long-pass dichroic (Chroma). The individual channels were aligned by imaging TetraSpeck beads (Thermo Fisher Scientific) and the SplitView module in Metamorph to overlay the channels. The beamsplitter mirrors were adjusted until the beads in each channel were overlapping. The Alexa Fluor 488 actin was imaged using the bleed-through on the 600/50 channel when excited by the 488-nm laser. An Andor iXon 888 Ultra camera was controlled using Metamorph (Molecular Devices). Images were collected using center cropped mode (515 × 512 pixel sensor) at 20-ms exposure times in overlapped data acquisition mode with EM gain set to 800, 30 MHz 16 bit analog-to-digital conversion, vertical shift speed set at 1.67 MHz, and vertical clock voltage at +2. This resulted in an imaging speed of 50 frames s⁻¹, with a field of view of 44.4 µm × 22.2 µm (512 × 256 pixels) at 86.7 nm per pixel. Typical video lengths were 1,500 frames (30 s).

Image analysis and QD tracking

The individual channels were separated into stacks, and an aligned overlay was created using the Cairn Image Splitter plugin for ImageJ (Cairn Optics). The alignment of the overlay was checked using images of TetraSpeck beads taken before and after each experiment. Any necessary further alignment of the channels was done using the Cairn Image Splitter plugin. Stacks of the moving QDs were cropped to a smaller size to include only one QD per stack. Noticeably brighter QD signals were observed and were likely due to two or more QDs within a diffraction-limited spot and were not further analyzed. A MATLAB program generously provided by Paul Selvin (University of Illinois, Urbana-Champaign, IL) was used to find the center of the QD intensity profile (i.e., point spread function) by fitting to a 2-D Gaussian distribution (Yildiz and Selvin, 2005), to remove outliers, and to align the displacement trajectory along the axis of the actin filament. The displacement trajectories were median-filtered with a window width of 3 points. The typical precision of localization (Thompson et al., 2002; Yildiz et al., 2003) was ∼6 nm for 605-nm QDs and ∼11 nm for 705-nm QDs.

Portions of some trajectories could not be further analyzed due to filament behaviors that have been previously described (Haldeman et al., 2014). Transient loss of signal from one or both QDs leaving the TIRF field occurs when portions of moving filaments are no longer oriented parallel to actin. This can lead to large shifts (greater than several hundred nanometers) in trajectories of one QD relative to another if both QDs remain in the TIRF field. Most of these shifts are evident in both the QD-LMM and QD-RLC trajectories.

Dwells followed by jumps (together called events) were identified using a custom MATLAB program to perform a simple geometrical analysis. A sliding window equal to approximately half the predicted dwell time was used to measure the slope of both the reference trace and the analyzed trace. Window widths were 8, 8, 7, 6, 5, and 5 frames for 5, 7.5, 10, 12.5, 15, and 20 µM ATP, respectively. The analyzed trace is the one that is being analyzed to contain events. Dwells ≥6 frames in the analyzed trace were identified when the slope of the analyzed trace was greater than −40, while the slope of the reference trace was positive, and the difference between the two slopes was greater than two. Jumps following the dwell were identified when the difference between the two slopes changed to negative with no gap in between. Since the variation in displacement during the dwell was not stipulated, the algorithm identified events that were later rejected as noise by the user and were therefore not included in the data presented.

Online supplemental material

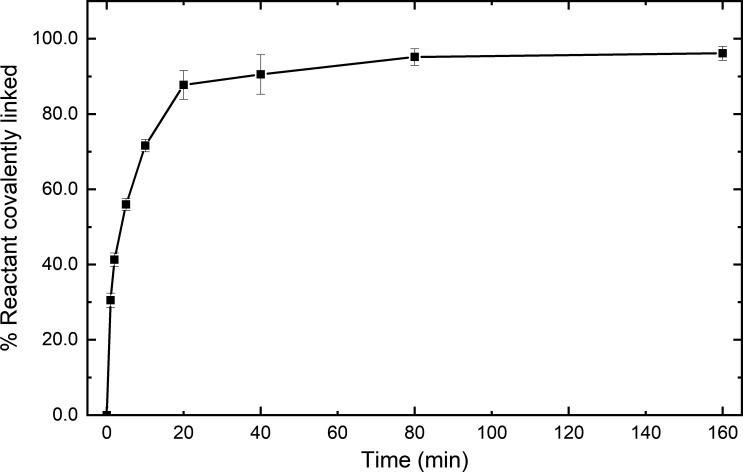
Fig. S1 shows data illustrating that the Snoop-LMM construct reacts spontaneously with SnoopC. In Fig. S2, are TIRF microscopy images that show Snoop-LMM SMM cofilaments that are stable and can be labeled with SnoopC-QDs. Fig. S3 display representative false-positive events from LMM-LMM trajectories. Video 1 and Video 2 are examples of moving QD-labeled filaments.

Figure S1.

Snoop-LMM reacts spontaneously with SnoopC. Reaction time course of 0.5 µM Snoop-LMM mixed with 1 µM SnoopC in filament buffer. Percent reactants covalently linked was determined by SDS-PAGE and gel densitometry. Error bars are SD; n = 3.

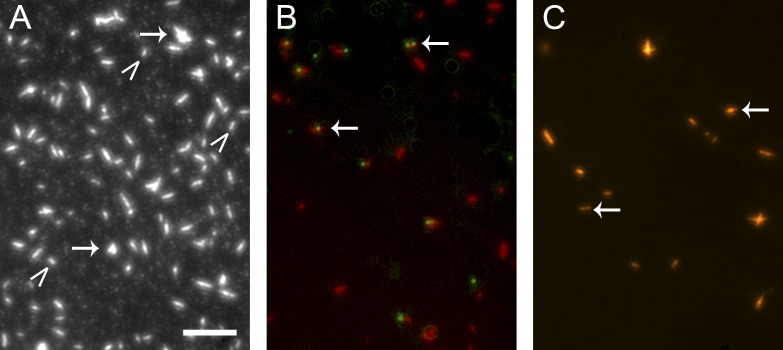
Figure S2.

Snoop-LMM SMM cofilaments are stable and can be labeled with SnoopC-QDs. TIRF microscopy images of various rhodamine labeled SMM filament preparations in filament buffer. Scale bar, 5 µm. (A) Control 20 µg ml⁻¹ SMM filaments on a glass coverslip. Arrows indicate aggregates of filaments; carrots indicate single filaments. (B) Overlaid image of 20 µg ml⁻¹ 95% SMM 5% Snoop-LMM cofilaments (red) reacted at 1 µM with 0.12 µM 585 nm QD-SnoopC overnight at 4°C. (C) Same as B, except with 0.12 µM 655 nm QD-SnoopC. For B and C, arrows point to colocalized filaments and QDs.

Figure S3.

Representative false-positive events from LMM-LMM trajectories. The horizontal black line is the estimated time the black trace pauses (dwell time) while the reference trace rises, and the vertical black line is the estimated jump distance (J). All data were collected at 10 µM [ATP] (see Fig. 4, A and B).

Video 1.

Representative video of RLC-LMM cofilaments labeled with 605 nm QD-SpyC and 705 nm QD-SnoopC moving along actin filaments. 605 nm QD-SpyC (green) and 705 nm QD-SnoopC labeled (red) SMM filaments are seen moving on surface-attached actin filaments (blue). Field is 503 × 234 pixels, 1,500 frames acquired at 20-ms exposure time. Playback is set at 200 frames s⁻¹. Each pixel is 86.7 × 86.7 nm. [ATP] = 10 µM.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012751.v1.mp4/source

Video 2.

Representative video showing a region of interest that was tracked. White box shows the two QDs of different color attached to the same filament moving along actin that provided the data in Fig. 2. Field is 503 × 192 pixels, 1,500 frames acquired at 20-ms exposure time. Playback is set at 200 frames s⁻¹. Each pixel is 86.7 × 86.7 nm. [ATP] = 10 µM.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012751.v2.mp4/source

Results

Preparation of dual-QD-labeled SMM cofilaments

To detect the behavior of myosin heads relative to the global motion of the filament, we simultaneously monitored fluorescence of SMM cofilaments containing on average one QD attached to the RLC in the lever arm and one QD of another color attached to the LMM region of the rod (Fig. 1 C).

To monitor the global filament motion, we initially tried to chemically couple a QD to LMM prepared by proteolysis, then used the QD-LMM to form cofilaments. This approach resulted in low incorporation of the QD-LMM into filaments (data not shown). Instead, we chose a system similar to that used for the RLC labeling, the SnoopC/SnoopTag system, which can be used in the presence of the SpyC/SpyTag with no cross-reactivity (Veggiani et al., 2016). An N-terminal SnoopTag was engineered onto the folding domain Xrcc4 1–135–Spc42 72–86 followed by the final 254 amino acids from chicken gizzard SMM heavy chain (Fig. 1 C), which is ∼24% of the length of LMM. The Xrcc4 and Spc42 domains were included to improve solubility and to ensure the LMM construct was a dimer and formed in-frame coiled-coil heptad repeats (Andreas et al., 2017; Drennan et al., 2019). The Snoop-LMM construct reacted as expected with SnoopC, with the reaction going to completion within 1 h (Fig. S1). To form SMM Snoop-LMM cofilaments, Snoop-LMM was mixed with rhodamine-labeled SMM at high ionic strength before lowering the ionic strength by dialysis to promote filament formation. To determine if the Snoop-LMM construct incorporated into the filaments, we tested whether QD-SnoopC could efficiently label SMM Snoop-LMM cofilaments. Fig. S2 A shows the control rhodamine-labeled SMM filaments. Filaments appear as bright oblong shapes that we have previously characterized (Haldeman et al., 2014; Brizendine et al., 2015; Brizendine et al., 2017). The majority were single filaments (Fig. S2 A, carets), but some filaments in small aggregates were also evident (arrows). Fig. S2 B shows a composite image of 95% SMM 5% Snoop-LMM cofilaments (rhodamine, red) and QD (green) fluorescence from an overnight reaction of 0.12 µM 585 nm QD-SnoopC with 1 µM 95% SMM 5% Snoop-LMM cofilaments. Fig. S2 C shows the same except the cofilaments were reacted with 655 nm QD-SnoopC. In both images, the arrows indicate filaments that colocalized with a QD. Importantly, the filaments appear similar to control filaments (Fig. S2 A), suggesting that the Snoop-LMM construct did not significantly interfere with filament formation. In a representative field (not shown), ∼90% of the filaments appeared to be colocalized with a single QD and ∼5–10% colocalized with two QDs, indicating that the filaments were incorporated with the Snoop-LMM construct with reasonably good efficiency.

To monitor the myosin head motion, we used a QD attached to the RLC. The SMM RLC is an attractive place to attach a QD because constructs can be easily exchanged for the native subunit under mild conditions. We used a previously characterized approach in which a RLC with a C-terminal SpyTag was exchanged onto SMM monomers (Brizendine et al., 2019). We mixed these SMM-Spy monomers with rhodamine-labeled untagged SMM (to visualize filaments) and Snoop-LMM in high salt, then dialyzed this mixture into filament buffer to form RLC-LMM cofilaments (named for the labeling sites). Prior to imaging, a QD-labeled SpyC was added to attach a QD to the RLC-Spy, and a QD-labeled SnoopC was added to attach a QD to the Snoop-LMM (Fig. 1 C). This allowed us to simultaneously monitor myosin head motion and global myosin filament motion.

M_f/A motility assays with dual-color QD-labeled RLC-LMM cofilaments

M_f/A motility assays with RLC-LMM cofilaments labeled with 605 nm QD-SpyC and 705 nm QD-SnoopC (Fig. 1 C, see example Video 1) were performed at various ATP concentrations. Occurrences of moving dual-labeled filaments were cropped and tracked (see example Video 2), and then tracks were reoriented along the axis of motion to create a displacement trajectory. Fig. 2 shows a representative displacement trajectory at 10 µM ATP. As expected, the overall trajectory of the QD on the RLC (black) is similar to the QD on the LMM (red trace). The average velocity estimated from the slopes of the QD trajectories (76 nm s⁻¹ ± 40 SD) is similar to but lower than previously measured at this [ATP] (330 nm s⁻¹; Brizendine et al., 2015). The significance of this difference in velocity is likely due to major differences in samples (LMM constructs and QDs), laser illumination wavelengths (currently 405 versus 532 nm), and the method of determining velocity of the two studies (transformed QD trajectories versus filament centroid and different frame rates). The RLC trace appears to be noisier as might be expected because the QD is attached to the head, which is known to be linked to the rod at a flexible hinge at the head–rod junction.

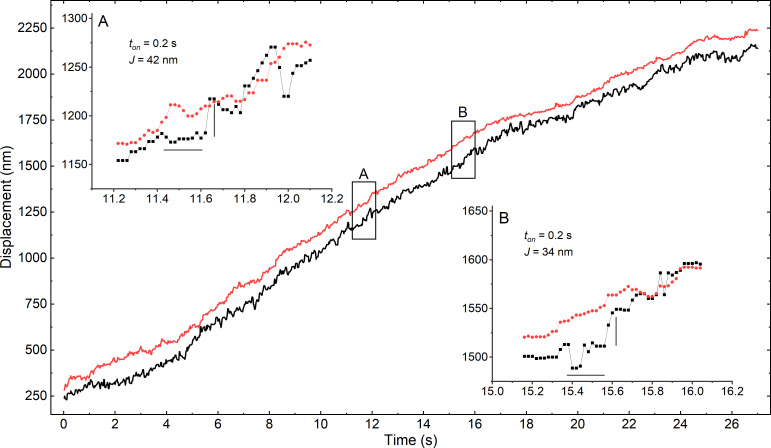
Figure 2.

Representative displacement trajectory of SMM filament moving on stationary actin filament. Fluorescence of 605 nm QD on RLC (black trace) and 705 nm QD on LMM (red trace) incorporated into RLC-LMM cofilament was simultaneously acquired, tracked, and reoriented along the axis of motion. [ATP] = 10 µM. (A and B) Insets reveal dwells (horizontal lines) followed by jumps (vertical lines) in the RLC trace. The LMM traces were translated from the RLC traces by −80 nm in the insets for better comparison.

To analyze the trajectories, we could not use prior step-finding methods that were developed for myosin V (Yildiz et al., 2003; Warshaw et al., 2005; Lu et al., 2010) and kinesin (Yildiz et al., 2004; Pierobon et al., 2009) such as velocity calculation and thresholding (Hua et al., 1997), two-sample Student's t test (Carter and Cross, 2005), wavelet transform multiscale products (Sadler and Swami, 1999), and χ²-reduction methods (Kerssemakers et al., 2006; see Carter et al., 2008 for a comparison). Such methods work well for these slow and high duty ratio processive single-molecule motors that do not form filaments and must step to move forward. In contrast, SMM is a low duty ratio motor that does not move processively. Therefore, many molecules are required to generate processive filament motion. A given head within a moving filament spends most (∼95%) of the ATPase cycle detached from actin (Harris and Warshaw, 1993; Cremo and Geeves, 1998). Therefore, there will be two general types of motion possible for a QD attached to the head. Most of the time it will be similar to the filament backbone motion, as it is carried along by the action of the other heads. We are interested in finding relatively rare events that represent binding and detachment from actin that are coupled to the ATPase cycle (Fig. 1 A). Because of the rarity of events, and frame rate considerations, a statistical comparison of noise in detrended trajectories across a sliding window width between the RLC-QD and the LMM-QD is not a reliable method to find events. Therefore, we developed an algorithm that is designed to compare a trajectory for global filament motion where actin interactions are not possible (e.g., Fig. 2, red) to the trajectory representing head motion for actin interactions (Fig. 2, black). The Fig. 2, A and B insets show the two events identified by our algorithm from this trajectory, which are instances where the RLC trajectory stops relative to the LMM trajectory (dwell time estimated indicated by the horizontal line), then returns to a position close to its starting point relative to the LMM trajectory (J, jump height estimated indicated by the vertical line). In the insets of Fig. 2, A and B, the dwell time is estimated to be 0.2 s, while the J values were estimated to be 42 and 34 nm, respectively.

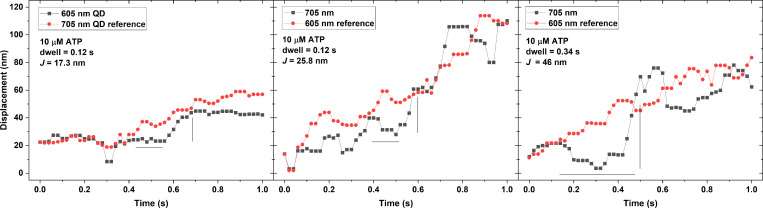
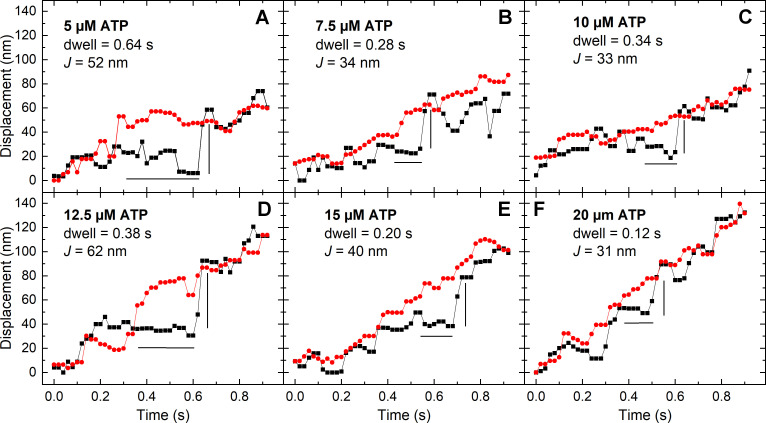
The panels in Fig. 3 shows representative events from different trajectories at varying [ATP]. The black and red points show the trajectories of the RLC and filament backbone, respectively, along with estimated dwell time and J for selected events. As the ATP concentration increases, the overall slopes of both trajectories increase as expected.

Figure 3.

Representative events showing dwell times followed by jumps at varying [ATP]. For all panels, the black squares and line are the displacement of the SpyC-605QD (RLC), and the red circles and line are the displacement of the SnoopC-705QD (LMM). The horizontal black line is the estimated time that the RLC trace pauses (dwell time) while the LMM traces rises, and the vertical black line is the jump distance (J). (A) 5 µM ATP. (B) 7.5 µM ATP. (C) 10 µM ATP. (D) 12.5 µM ATP. (E) 15 µM ATP. (F) 20 µM ATP.

If events observed in the RLC trajectory actually represent actin interactions related to the ATPase cycle rather than nonstereospecific actin binding/detachment, the dwell times should become shorter with increasing [ATP] according to Eq. 1 corresponding to the mechanism in Fig. 1 A.

$$t_{on}=k_{\det }{}^{-1}={\left(k_{-AD}\right)}^{-1}+{\left(k_T\left[ATP\right]\right)}^{-1}$$ (1)

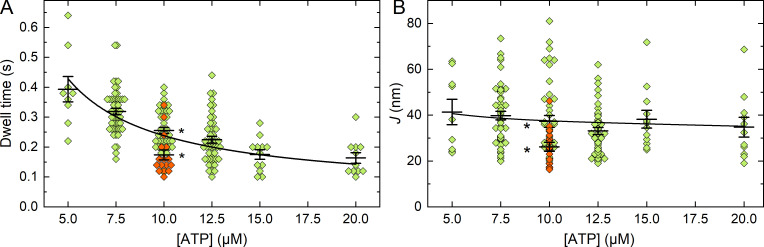
Fig. 4 A shows the relationship between dwell times and [ATP] for all events (green points). Outliers were not removed from the dataset. The black line is a fit of Eq. 1 to the mean of the data for each [ATP], where k_-AD was fixed to 21 s⁻¹ (Brizendine et al., 2015). This resulted in k_T = 0.52 ± 0.02 µM⁻¹ s⁻¹, in good agreement with our published value of 0.50 ± 0.01 µM⁻¹ s⁻¹ (Haldeman et al., 2014). This result strongly suggests that the dwell times for the events identified decrease with increasing ATP according to Eq. 1.

Figure 4.

Dwell times (t_on) and jump lengths (J) at varying [ATP]. (A) Dwell times identified before the jump at varying [ATP]. Green diamonds, RLC-LMM cofilaments, 5 µM ATP, n = 9; 7.5 µM ATP, n = 50; 10 µM ATP, n = 45; 12.5 µM ATP, n = 46; 15 µM ATP, n = 12; 20 µM ATP, n = 11. Red diamonds, LMM-LMM cofilaments, 10 µM ATP, n = 16. The asterisks for the 10 µM ATP condition indicate the two means are statistically significantly different using a two-sample t test with P = 0.000645. The black line is a fit of Eq. 1 to the means. (B) Jump lengths (J) following the dwell times identified in A. The asterisks for the 10 µM ATP data indicate the means are statistically significantly different with P = 0.01. For A and B, the black vertical whiskers indicate SEM; the longer black horizontal line is the mean.

Fig. 4 B (green points) shows the relationship between J and [ATP]. Note that J will by definition be less than L. L is a constant that is predicted from the MK model. It represents the maximum distance a filament could move while a head is attached to actin (Fig. 1 B), whereas J is directly measured under the given conditions. If the filaments are in the fully detachment-influenced regimen, then J will approach L. In these experiments, the average filament length measured from static filaments attached to a coverslip was 469 ± 134 nm, which corresponds to an average N of 131 ± 37. At this N and range of [ATP], the MK model predicts that the filaments are not operating under fully detachment-limited conditions, so we expect J to be less than L. A fit of the data in Fig. 4 B to the MK model (black line) resulted in L of 52 ± 1 nm (fixed parameters: k_att = 0.5 s⁻¹, d = 8, k_-AD = 21 s⁻¹, and k_T = 0.5 µM⁻¹s⁻¹). Our previous estimate of L from fits of the MK model to V versus N and V versus ATP data are 59 ± 3 nm (Brizendine et al., 2015; Brizendine et al., 2017) and k_att = 0.6 s⁻¹. Therefore, the values of J and the fit of the MK model to the ATP dependence of J are in good agreement with our prior estimates of L.

As a control, cofilaments were made with QDs attached only to the filament backbone using Spy-LMM and Snoop-LMM (LMM-LMM cofilaments), and trajectories were collected at 10 µM ATP. Trajectories were analyzed as above but twice, changing the trajectory used as the reference. Any events identified are false positives and likely to be related to noise. As expected, the algorithm detected events (Fig. 4, A and B, red diamonds), but the shorter dwell times and smaller J values were statistically significantly different from corresponding data for the RLC-LMM cofilaments. See Fig. S3 for examples of representative false-positive events.

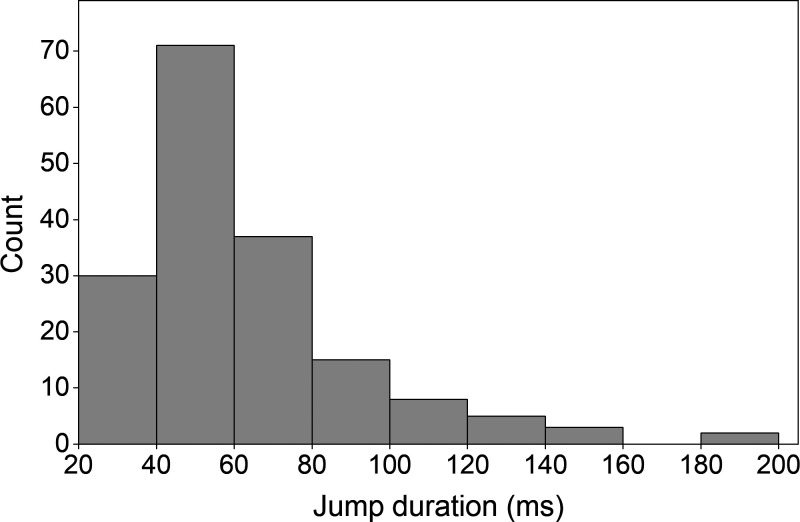
Jump duration

Fig. 5 shows the distribution of the jump duration, or the time it took for the head trajectory to return to the LMM trajectory following the dwell. The average jump duration was 52.9 ± 2.3 ms. No correlation was found between the dwell time or J (data not shown).

Figure 5.

Distribution of jump durations. Histogram showing the distribution of the time each jump took from the end of the dwell to where it returned to the LMM trace. The average = 52.9 ± 2.3 ms (SE), n = 171.

Frequency of observed events

If events identified are related to acto-myosin interactions coupled to ATP hydrolysis, they should have a predicted frequency of occurrence related to the kinetics of the system. The overall ATPase rate determines the expected number of events per unit time. The probability of n events happening in a given time can be estimated by a Poisson distribution (Eq. 2),

$$y=y_0+\frac{e^{-\lambda }{\lambda }^x}{x!},$$ (2)

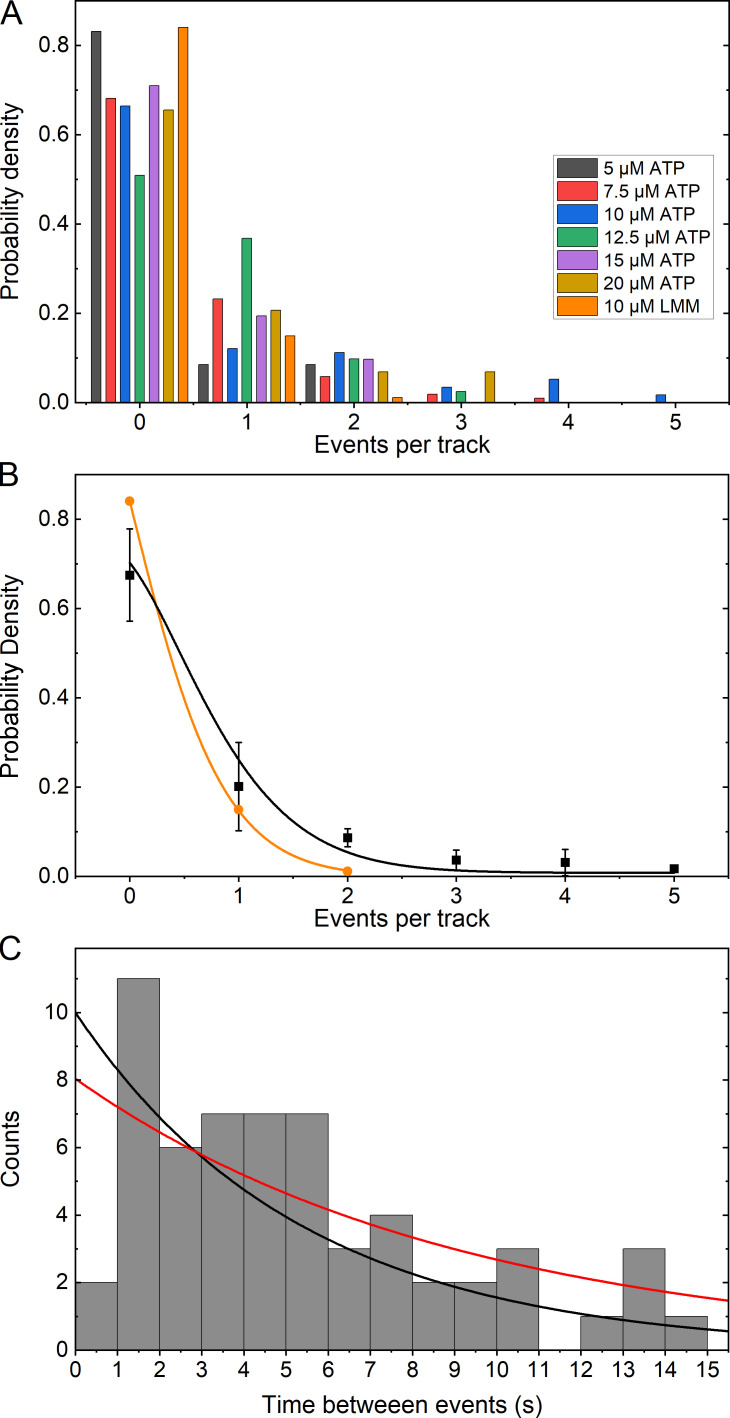
where x is the number of events, y₀ is the offset, and λ is the rate multiplied by the time interval.SMM filaments are side-polar (Craig and Megerman, 1977; Cross and Engel, 1991; Haldeman et al., 2014; Brizendine et al., 2015), meaning that all heads on one side are projecting in the same direction. For a given moving filament, if the QD on the RLC happens to be on the side not interacting with actin, no events should be detected, assuming heads on only one side are close enough to engage actin during the whole track. Therefore, at least 50% of trajectories should have zero events due only to the experimental constraints. Fig. 6 A shows the probability density of a trajectory containing an event at each [ATP], after removing half of the trajectories that contained zero events. Overall, for the RLC-LMM cofilaments, the probability of a trajectory containing an event did not depend strongly on [ATP], and the LMM-LMM cofilaments (orange) were similar to the RLC-LMM cofilaments.

Figure 6.

Frequency of events per track and distribution of time between events. (A) Histogram of the frequency of detected events as a probability density given the total number of trajectories. All data refer to RLC-LMM except that indicated as LMM (orange) for the LMM-LMM data. Half of the tracks that contained zero events were removed from the probability calculation (see text). (B) Plot of the mean probability density (black squares) for each [ATP] from data shown in A, excluding the LMM-LMM data. The LMM-LMM data are shown in orange circles. The color-coded lines show a fit to Eq. 2. (C) Histogram showing the distribution of the time between events for all tracks that contained multiple events. The black line is an exponential distribution with the mean time between events equal to that of the data and the amplitude equal to the maximum of the data. The red line is a fit to Eq. 3.

Fig. 6 B shows the average probability density of events per track for data collected at all [ATP] combined for the RLC-LMM cofilaments. The red line is a fit of Eq. 2, resulting in y₀ = 0.01 ± 0.02, λ = 0.37 ± 0.05, and R² = 0.98. In a Poisson distribution, λ is the rate of observed events multiplied by the time interval. Therefore, since we know the approximate ATPase rate and that each track is 30 s long, we can estimate the expected λ if all events are observable. At 10 µM ATP, v ~ 0.2 s⁻¹ (Haldeman et al., 2014), so the predicted λ = 6. The fit of the Poisson equation to the points in Fig. 6 B resulted in a λ = 0.37 ± 0.05, suggesting that we are discovering ∼6% of all possible events using our experimental approach and method of analysis. In SMM filaments, the heads are spaced every 14.3 nm (Cross and Engel, 1991; Cross et al., 1991), and best estimates are that four heads are at every interval on a given side of the filament (Tonino et al., 2002). This would suggest that even if a labeled myosin head is on the correct side of the filament, the chance of it interacting with a single actin filament may be as low as ∼25%. If this were true, we are discovering 6/25 or 24% of the expected events. Importantly, this analysis suggests that we are not detecting more events than expected for a Poisson process.

The probability density data for LMM-LMM are shown in Fig. 6 B (orange). Overall, events were less frequent that for the RLC-LMM with 84% of all tracks lacking any events, and only 15% containing two events. In contrast to the RLC-LMM data, no tracks were found to contain three, four, or five events.

Time between events or waiting time

In a Poisson process, the distribution of time between events, y, decays exponentially, where t is time, A is the initial amplitude, and r is the rate of decay (Eq. 3).

$$y=A{e}^{-rt}$$ (3)

On average, a myosin head should step with a frequency equal to the rate of the ATPase activity (Fig. 1 C). The distribution of time between events for all RLC-LMM tracks where multiple events were detected is shown in Fig. 6 C. The general shape of the data is exponential with a mean of 5.3 ± 3.7 s. The black line is an exponential distribution with the mean equal to that of the data and the amplitude equal to the maximum of the data = 10. This results in r = 0.19 s⁻¹. The red line is a fit to Eq. 3 resulting in A = 8.1 ± 1.5, r = 0.11 ± 0.04 s⁻¹, and R² = 0.54. Both of these rate constants are in good agreement with the predicted value of ∼0.2 s⁻¹ (Haldeman et al., 2014). A similar analysis could not be done for the LMM-LMM tracks because there were insufficient tracks with more than one event.

Discussion

In this study, we used QD fluorescence to observe the trajectory of a single head in an SMM filament moving on actin, while at the same time observing the trajectory of the filament backbone. By comparing the two trajectories, which usually mimicked each other, we detected rare events comprised of two parts. First, the head dwells for a time without making the forward progress seen in the backbone trajectory. Second, the dwell ends followed by a return of the head (jump in nanometers, J) to match the backbone trajectory once again. We propose that the dwells are times when the head is attached to actin, and the jumps are when it releases from actin.

Usually, we imagine that during the time a head is bound to actin, the filament velocity would go to zero because the other heads trying to undergo the powerstroke experience a load from the attached head that is very stiff. In contrast, during the events described above, the filament does not stop moving. This behavior arises because myosin heads are attached to the filament backbone by a tether, the S2 region of the rod, which is much more flexible than the head. As the filament moves past the attached myosin head, the tether is pulled in the opposite direction of filament movement while exerting little opposing force. If it detaches from actin before all the slack is taken up, the other myosin heads continue to move the filament. If the end of the tether is reached, the load would become high because the rod is not flexible in the axial direction, and the filament would stop.

Our MK model describing the velocity of in vitro filaments moving on actin incorporates the variable L, which is the maximum distance working heads can move a filament unimpeded by an actin-attached head. This distance is related to the properties of S2 but also to the kinetics of the system. By measuring the jump distance, J, we were able to estimate the value of L. By fitting the MK model to the dependence of J on [ATP], L was estimated to be 52 ± 1 nm, in good agreement with our previous estimate of 59 ± 3 nm. The observed average dwell times were consistent with known kinetics of actin-attached time (t_on). The time it took to undergo the jump was on average 53.9 ± 2.3 ms. The distribution of the waiting time between observed events was consistent with a Poisson process and the expected ATPase rate. The distribution of the number of events per track indicated that the method did not detect more events than predicted. These results provide direct evidence of a flexible S2 as an important mechanical feature affecting movement of myosin filaments on actin.

An important aspect of the MK model is its dependence of V on N, which should hold true for all myosin IIs. We previously showed that the model fit well to V versus N data for smooth, skeletal, and cardiac myosin filaments (Brizendine et al., 2015; Brizendine et al., 2017). Similar experiments with nonmuscle myosin IIB (Melli et al., 2018) showed little dependence of V on N. However, considering the long t_on and very slow k_-AD of this myosin (Rosenfeld et al., 2003; Wang et al., 2003; Ramamurthy et al., 2004; Kim et al., 2005; Kovács et al., 2007; Nagy et al., 2013), the MK model would predict little N-dependence of V above approximately five or six heads, consistent with the data. In this analysis, L would be ∼30 nm. However, to explain the velocities observed by Melli et al. (2018), the MK model requires k_att to be ∼3.7 s⁻¹, a value that is ∼10-fold faster than the measured kinetics of NMII-B would suggest, but is consistent with observations of high duty ratios (Rosenfeld et al., 2003) and processivity of a single NMII-B (Norstrom et al., 2010; but not observed in other similar experiments, such as Nagy et al., 2013). However, it is worth noting that the detachment-limited Uyeda–Spudich model (Uyeda et al., 1990; Harris and Warshaw, 1993) cannot account for the Vs observed by Melli et al. (2018) without a k_AD ∼10-fold faster than measured.

The results of this study and previous studies (Baker et al., 2002; Baker et al., 2003; Hooft et al., 2007; Haldeman et al., 2014; Brizendine et al., 2015; Brizendine et al., 2017) suggest that different muscles may operate primarily in different kinetic regimes depending on N, which is related to the number of activated heads and the filament length. In smooth muscle, the length of filaments is debated. Filaments in sheep trachealis, sheep pulmonary artery, and rabbit carotid artery smooth muscle cells had variable lengths with most being shorter, around 100–500 nm (Liu et al., 2013), while in rabbit portal mesenteric vein (Ashton et al., 1975) and in pig trachealis (Herrera et al., 2005), lengths were 1.8–2.4 µm. Additionally, the length of filaments was shown to be variable depending on the activation state of the muscle (Liu et al., 2013). This suggests that N could be a changeable parameter within smooth muscle, tuning the muscle to operate in either an attachment- or detachment-influenced state.

It is of interest to consider what is known about the myosin S2 domain and its interactions with the filament backbone to place our results into context. The myosin rod (also known as the tail) is C-terminal to the two myosin heads, is ∼1,100 amino acids long, and extends ∼150 nm. It is predicted by sequence alone to be stable α-helical coiled-coil, excepting the first two heptad repeats (Blankenfeldt et al., 2006) and a C-terminal small tailpiece. S2 was originally identified by proteolysis and is generally defined as the N-terminal approximately one third of the rod beginning immediately after the RLC binding region on the heavy chain within the head at an invariant proline residue. The exact length of S2 depends upon the myosin isoform and the proteolytic conditions used. The remainder of the rod is called LMM.

Our results suggest that S2 must be flexible to bend or buckle and have freedom to deviate away from the filament backbone while being pulled in the opposite direction of motion, potentially overcoming filament backbone interactions (Kaya and Higuchi, 2010). Although both S2 and LMM are coiled-coils, S2 is generally soluble under physiological ionic strength conditions (depending on its length and source; Sutoh et al., 1978), while LMM and full-length myosin self-aggregate into filaments (Lowey et al., 1967; Lowey et al., 1969; Weeds and Pope, 1977). This suggests that the interactions of S2 with the filament backbone are weaker than those of LMM.

The spacing between actin and myosin filaments in relaxed muscle is relatively short, but as muscle contracts, the spacing increases. Relatively weak ionic interactions with the filament backbone may allow S2 to be unzipped from the filament surface by forces initiated from subfragment 1 or head domain of myosin (S1)–actin interactions initiated upon muscle activation. This would allow stereospecific S1-actin interactions to continue to take place over a wide range of inter-filament spacing (Huxley, 1969).

Is all or only part of S2 able to be freed from filament packing constraints in muscle? Tomograms of swollen insect flight muscle in rigor show S2 projecting 10 nm from the main shaft, where thick filament diameter is constant (Liu et al., 2006). Interestingly, longer lengths of exposed S2 (26.6 ± 8.3 nm) were common toward the tips of the filaments, where there is a reduced packing density within the thick filament shaft. Throughout the filament length, projection angles were highly variable both azimuthally and axially relative to the filament axis (Liu et al., 2006). These results strongly suggest that S1-actin interactions can lead to unzipping of S2 off the myosin filament backbone in insect flight muscle. The fact that bends at acute angles are seen suggests that the direction of the pull on the unzipped section causes crumpling of S2, presumably at a point of disruption in the coiled-coil structure, but the exact point of crumpling is variable and is affected by preexisting interactions with the filament surface. It is possible that the points of disruption along S2 are not preexisting as in the notion of a hinge, but rather reflect a balance between the forces required to break the bonds stabilizing the coiled-coil and the forces required to disrupt ionic interactions with the filament backbone.

Interestingly, the structure of myosin filaments from relaxed Lethocerus indicus flight muscle by cryo-EM shows a similar length of S2 (∼11 nm long and 2 nm wide) projecting from the filament backbone at an 11° angle and connecting to the heads that are in the interacting heads motif (Hu et al., 2016). A similar arrangement of S2 is found in tarantula muscle filaments (Woodhead et al., 2005; Alamo et al., 2016) and in Drosophila melanogaster flight muscle (Daneshparvar et al., 2020).

Two parameters will govern the effective stiffness of S2 as it is being pulled backward, bonding to the filament backbone and bending stiffness of the unzipped portion as the other heads move the filament along. An in vitro experiment with rabbit skeletal myosin reveals the combined forces that must be overcome to pull the tip of a myosin head that is incorporated into a filament backward toward the direction of the M line (Kaya and Higuchi, 2010). This closely matches how we expect the process to occur in our experiments. The initial ∼60 nm region of the force versus displacement curve is linear with a stiffness of 0.037 pN nm⁻¹. This is higher than estimates of S2 stiffness by equilibrium molecular dynamics simulations of ∼0.010 pN nm⁻¹ (Adamovic et al., 2008). The next ∼15-nm region has an intermediate stiffness of ∼0.17 pN nm⁻¹ before reaching the high stiffness of the S1 domain.

We can use a simple calculation to determine how much of S2 would be unzipped from the filament surface if L = 55 nm. A surface-to-surface filament distance of 20 nm was chosen for the calculation, but of course the actual distance is not known, and in vitro it may be different from muscle. Assuming that all but 6 nm of S2 begins on the filament surface, we estimate that pulling S1 back a distance of 55 nm along the filament axis will unzip an additional 26 nm of S2 from the backbone. This is close to the maximal observed length of S2 seen projecting off the filament backbone in flight muscle (Liu et al., 2006). Interestingly, 26 nm is very close to a site of occasional bending at 28 nm seen in images of single SMM molecules obtained by cryo-atomic force microscopy (Zhang et al., 1997; Sheng et al., 2003).

It is important to note that the unzipped portion of S2 probably does not reach the C terminus of short S2, a site of proteolytic susceptibility (Cross et al., 1984) near the first skip residue corresponding to a bend observed by EM (Elliott and Offer, 1978; Walker et al., 1985) at ∼42–44 nm from the S1/S2 junction. It is interesting that even this site is probably not a preexisting molecular hinge but rather is a stable conformational state in which the coiled-coil partially unwinds for a region of ∼29 amino acid residues over which the α-helices run approximately parallel to each other (Taylor et al., 2015). This is in agreement with the structure of the corresponding region from L. indicus flight muscle myosin (Hu et al., 2016).

We do not have any information about the structural mechanism of deformation of the coiled-coil. It may not require a single point of weakness or a preexisting hinge. If we use previous estimates of myosin force of 1.5–3.7 pN head⁻¹ (Guilford et al., 1997) and estimate that there are ∼10 working heads in our system, the total available force would be ∼15–37 pN. This would be sufficient force to detach and bend 26 nm of S2 at an effective stiffness of 0.037 pN nm⁻¹ or ∼1 pN. This is probably not enough force to break the hydrophobic contact seam in the coiled-coil, which would require >100 pN (Yogurtcu et al., 2010). We estimate that the time it takes to restore the starting conformation of S2 once the head detaches from actin is ∼50 ms. This time scale does not necessarily inform the mechanism because coiled-coils do not behave as a simple elastic rods and can show complex nonlinear responses to forces (Gao et al., 2011).

We found previously that both skeletal and cardiac myosin have a significantly shorter L than SMM. One interpretation is that muscles with fast ADP release rates do not need long Ls to allow for attachment-limited motion at low loads. It is the muscles with slow ADP release rates that benefit from longer Ls to remain in the attachment-limited regimen. We do not know whether the isoform-specific differences in L are influenced by differences in the mechanics of the S2 subdomain. For rabbit skeletal and bovine cardiac myosin, L is ∼22 nm, whereas SMM kinetics allow L to be much longer, 59 ± 3 nm (Brizendine et al., 2017) or 52 ± 1 nm (this work), and our estimate for nonmuscle myosin IIB is ∼30 nm. These are all well within the region of the lowest effective stiffness measured by Kaya and Higuchi (2010).

In summary, based upon several experimental results and lines of evidence, there is strong evidence that the system can provide sufficient force to overcome S2 interactions with the filament backbone to bend it in the opposite direction of motion a distance indicated by our results.