Abstract
Rattling phenomena have been observed in materials characterized by a large cage structure but not in a simple ABO3-type perovskite because the size mismatch, if it exists, can be relieved by octahedral rotations. Here, we demonstrate that a stoichiometric perovskite oxide NaWO3, prepared under high pressure, exhibits anharmonic phonon modes associated with low-energy rattling vibrations, leading to suppressed thermal conductivity. The structural analysis and the comparison with the ideal perovskite KWO3 without rattling behavior reveal that the presence of two crystallographic Na1 (2a) and Na2 (6b) sites in NaWO3 (space group Im) accompanied by three in-phase WO6 octahedral (a+a+a+) rotations generates an open space Δ ~ 0.5 Å for the latter site, which is comparable with those of well-known cage compounds of clathrates and filled skutterudites. The observed rattling in NaWO3 is distinct from a quadruple perovskite AA′3B4O12 (A, A′: transition metals) where the A (2a) site with lower multiplicity is the rattler. The present finding offers a general guide to induce rattling of atoms in pristine ABO3 perovskites.
Graphical Abstract
INTRODUCTION
Inorganic solids with a network of polyhedral cages that host guest cations show interesting properties associated with characteristic phonon modes.1–4 When guest cations are smaller relative to the space inside the cage, a local and anharmonic vibration, or “rattling”, occurs, leading to strong scattering of long wavelength acoustic phonons in clathrates (e.g., Sr8Ga16Ge30),5,6 superconductivity with strong electron–phonon coupling in β-pyrochlore IKOs2O6,7–9 and heavy Fermion states in filled skutterudites (e.g., SmOs4Sb12).10–13 It has been widely believed that the rattling vibration suppresses the lattice thermal conductivity, κL, resulting in the enhancement of thermoelectric efficiency.14–16 Quasi-harmonic interaction between the cage and guest cation is also proposed.17 These features have stimulated numerous studies toward exotic physical properties coupled with rattling vibrational modes, such as high efficiency thermoelectric materials with low κL.
Perovskite ABO3 is the most studied system in materials science because of the richness in chemical and physical properties including superconductivity,18 colossal magneto-resistivity,19 and ferroelectricity.20 The diversity of properties arises from the ability of perovskite compounds to take various cations at the A and B sites,21 along with the substitution of oxide site by other anions.22 In addition, octahedral rotation of various patterns causes the deviation of ∠B–O–B angle from 180° in the ideal perovskite, which influences orbital overlap, superexchange interactions, and electron hopping between neighboring B sites. Here, the relief of size mismatch is the origin of octahedral rotations: when the Goldschmidt tolerance factor is smaller than 1, BO6 octahedra rotate to satisfy the necessary the A site cation environment, leading to structural distortion from a cubic perovskite (space group: Pmm).21 Octahedral rotations match almost any A site sizes, leading to dense structures and therefore leaving little “open space” for rattling to occur. Recently, Tanaka et al. reported several quadruple perovskite oxides, ACu3V4O12 (A = Mn, Cu).23,24 In general, the A′ ions in AA′3B4O12 are Jahn–Teller active transition metals (e.g., Cu2+ and Mn3+), and extensive BO6 octahedral tilting permits square-planar A′O4 coordination.25 The resultant A site is 12-fold coordinated typically occupied by large alkaline earth metals (e.g., La), but when it is occupied by small transition metal ions, a rattling phenomenon emerges, as seen from a large atomic displacement parameter (ADP) and Einstein-like specific heat.23,24
In this paper, we report the high-pressure synthesis of a stoichiometric tungsten bronze NaxWO3 (x = 1). NaxWO3 has been extensively studied for decades, and a perovskite structure with a+a+a+ octahedral rotation (space group: Im) is found in a high concentration regime (x ≥ 0.8).26–29 However, there remains an uncertainty about its Na composition, as will be shown later. The present study follows our recent work on KxWO3, where the high-pressure method expanded the x amount, forming a stoichiometric tetragonal phase K0.6WO3 and a cubic (perovskite) one KWO3.30 Quite unexpectedly, we observed rattling behavior in this pristine perovskite NaWO3 but not in KWO3. We discuss the origin of the rattling phenomenon in NWO3 by considering crystal structures and physical properties, in comparison with the 1:3 ordered quadruple perovskite AA′3B4O12. A general guideline to the rattling phenomenon in perovskite is presented.
EXPERIMENTAL PROCEDURE
Polycrystalline samples of NaxWO3 (x = 0.5, 0.6, 0.75, 0.8, 1.0) were prepared using a high-pressure (HP) technique. Stoichiometric mixtures of Na2WO4, WO2 (99%, Rare Metallic), and WO3 (99.999%, Rare Metallic) were ground in a mortar for 30–60 min and pressed into a pellet. The pellets were sealed in a platinum capsule, inserted in a graphite tube heater, and enclosed in a pyrophyllite cube. These procedures were carried out in a N2-filled groove box. The Na2WO4 precursor was prepared by heating Na2WO4·2H2O (99.8%), Alfa Aesar) in air at 400 °C for 24 h; a complete loss of water was checked by infrared spectroscopy.31 The HP reactions were performed at 1000 °C for 30 min under pressures of 5–8 GPa. The samples were characterized through powder X-ray diffraction (XRD) with Cu Kα radiation at room temperature (RT). Synchrotron powder X-ray diffraction (SXRD) measurements were performed at RT on the BL02B2 beamline at SPring-8. The wavelengths employed were λ = 0.42044 Å for x = 0.5, 0.6, 0.75, 1.0 and λ = 0.41914 Å for x = 0.8. A glass capillary with a 0.2 mm inner diameter was used. The SXRD patterns were analyzed by the Rietveld refinement method using the program JANA2006.32,33 Reaction procedures were similar to those followed for the synthesis of Li0.5WO3, with stoichiometric mixtures of Li2WO4 (99%, Kojundo Chemical), WO2 (99%, Rare Metallic), and WO3 (99.999%, Rare Metallic). Neutron diffraction (ND) measurements (λ = 1.5397 Å) for Li0.5WO3 were carried out using the high-resolution powder diffractometer BT-1 at the NIST Center for Neutron Research. The sample was loaded into a vanadium cell. The collected neutron data were analyzed by the program JANA2006.
Specific heat, Cp, was measured with a commercial calorimeter (Quantum Design PPMS) in a temperature range from 200 to 2 K. Thermal conductivity, κ, was measured by a standard four-contact method at temperatures between 300 and 100 K. Electrical resistivity, ρ, was measured with a four-probe method using a commercial apparatus (Quantum Design PPMS) equipped with an adiabatic demagnetization refrigerator. We used rectangular-shaped samples cut out from the pellets. Gold wires were attached to the samples with silver paste. Magnetization was measured with a SQUID magneto-meter (Quantum Design, MPMS).
RESULTS AND DISCUSSION
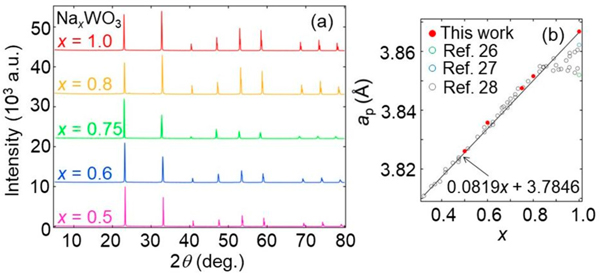
Figure 1a shows powder XRD patterns for a series of NaxWO3 at RT, which are indexed with a tetragonal supercell of a perovskite structure (2ap × 2ap × 2cp) for x ≤ 0.75 and a cubic supercell (2ap × 2ap × 2ap) for x ≥ 0.8, as indicated previously.28,29 No impurity phases were detected for all samples. In Figure 1b, we plotted the x dependence of the reduced cell parameters, ap, along with those of previous reports, where the samples were prepared by solid-state reaction at ambient pressure.26–28 The results for x ≤ 0.8 agree with the previous results. Whereas the reported data show a deviation from the Vegard law above x = 0.85, our samples follow a linear evolution in the entire range up to x = 1. Extrapolating the proposed relation, ap = 0.0819x + 3.7846,28 to x = 1 gives ap = 3.8665 Å, which is fairly consistent with the experimental value of 3.86596(1) Å. This fact strongly suggests that previous studies overestimated the Na content for x > 0.85.26–28 Deviation from the nominal values in earlier works may be due to Na evaporation. The use of high pressure prevented such undesirable evaporation. Higher compressibility of alkali metal may can also help Na ions be incorporated in the perovskite lattice.
Figure 1.
(a) Powder XRD patterns of NaxWO3 measured at RT. (b) Pseudocubic (normalized) lattice parameters, ap, plotted as a function of x, where data from previous studies26–28 are included. The solid line represents the proposed relationship, ap(x) = 0.0819x + 3.7846.28
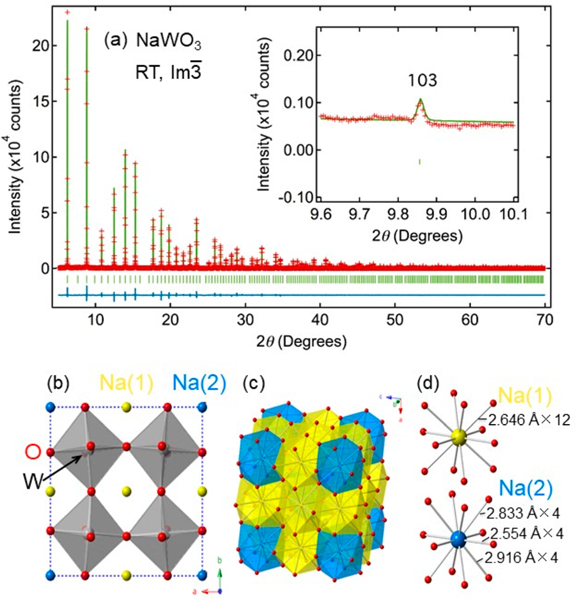
A Rietveld refinement for the x =1 data assuming the Im structure confirmed the full stoichiometry of our specimen, with reasonable reliability factors of Rwp= 7.37% and Rp = 5.70% and goodness-of-fit of 2.22 (Figure 2a and Table 1). Rietveld analyses for other NaxWO3 samples gave results consistent with nominal Na compositions (Figure S1 and Table S1). It is remarkable that ADP of the Na2 site for NaWO3 (x = 1) is 2.23(15) × 10−2 Å2. This value corresponding to the isotropic root-mean-square displacement (rmsd) of 0.15(1) Å implies unusually large thermal vibration of sodium ions at the Na2 (6b) site. No anomaly is observed for the Na1 (2a) site (ADP = 7 × 10−3 Å2).
Figure 2.
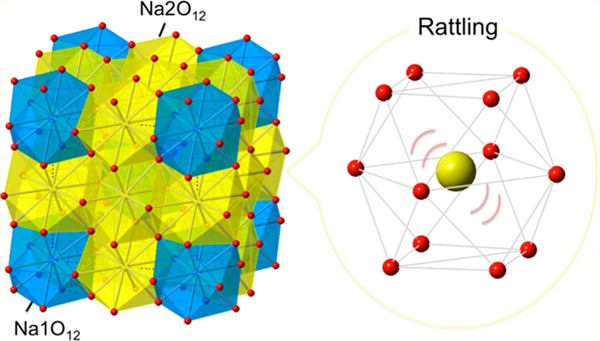
(a) Rietveld refinement of SXRD of NaWO3 at RT. Red crosses, green solid line, and blue solid line represent observed, calculated, and difference intensities, respectively. The green ticks are the position of Bragg peaks. The inset shows the (103) reflection. (b) Crystal structure of NaWO3 (Im) with octahedral rotation of a+a+a+. Blue, yellow, gray, and red spheres denote Na1 (2a), Na2 (6b), W (8c), and O (24g), respectively. The dotted lines show a 2ap × 2ap × 2ap cell. (c) Two nonequivalent cuboctahedral units of NaO12 around Na1 (yellow) and Na2 (blue). (d) Coordination geometry around Na1 (top) and Na2 (bottom).
Table 1.
Refined Structural Parameters of NaxWO3 (x = 1.0) at RT (Space Group: Im (No. 204), a = 7.731934(8) Å)
| atom | site | x | y | z | Uiso (×10−2 Å2) |
|---|---|---|---|---|---|
| Na | 2a | 0 | 0 | 0 | 0.7(2) |
| Na | 6b | 0 | 1/2 | 1/2 | 2.23(15) |
| W | 8c | 1/4 | 1/4 | 1/4 | 0.238(2) |
| O | 24g | 0 | 0.263(2) | 0.230(2) | 0.77(7) |
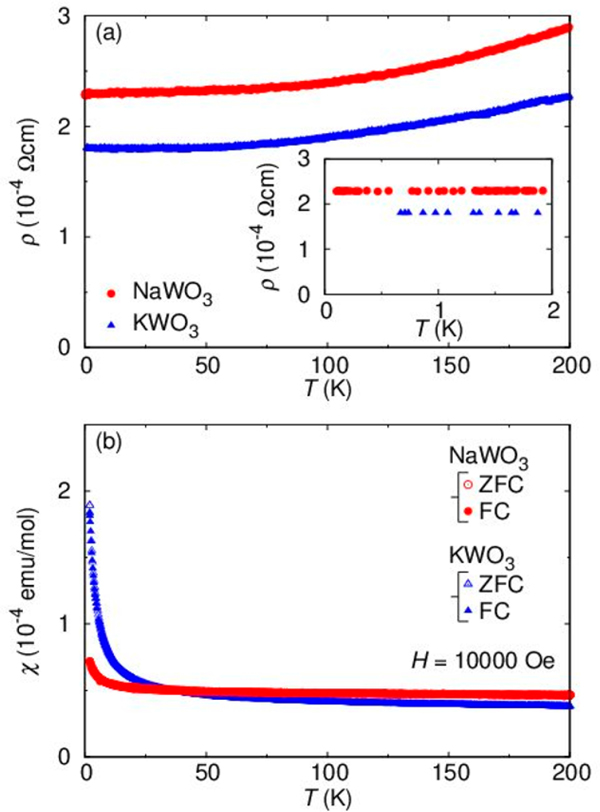
Together with our previous report,30 we have two isoelectric (d1) compounds, NaWO3 (Im) with a+a+a+ rotations and KWO3 (Pmm) with a0a0a0 rotations. This offers an ideal opportunity to clarify the effect of WO6 octahedral rotation on physical properties. First, let us present the temperature variation of resistivity, ρ, and magnetic susceptibility, χ (=M/H), in Figure 3. Both compounds exhibit metallic temperature dependence and almost the same ρ values in a whole temperature range examined (Figure 3a), where no signature of phase transition is observed. This behavior is paralleled with T-independent χ (Figure 3b), and hence, both compounds can be attributed to a Pauli paramagnetic metal. The Curie-type increases in χ at low temperatures below 20 K come from a small amount of free impurity spins (0.01–0.1%).
Figure 3.
(a) Temperature dependence of electrical resistivity, ρ, for 0.1 K < T < 200 K in NaWO3 and 0.6 K < T < 200 K in KWO3. The low-T region is magnified in the inset. (b) Temperature dependence of magnetic susceptibility, χ, for NaWO3 and KWO3 in the zero-field-and field-cooling process.
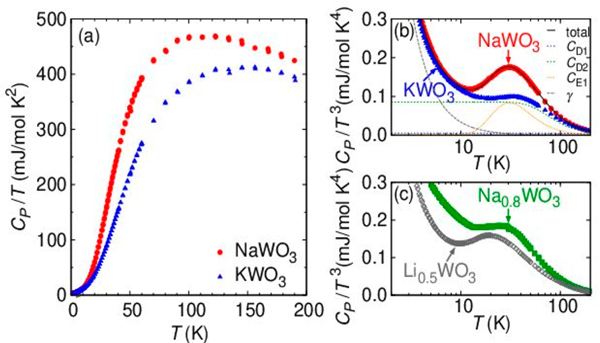
On the contrary, heat capacities of the two compounds behave differently, as shown in Figure 4a (CP/T versus T). This difference can be highlighted for the CP/T3–T plot (Figure 4b). A broad peak is observed at 30 K only for NaWO3, suggesting the presence of a low-energy optical phonon. A similar peak in the CP/T3 versus T curve has been known to appear in cage compounds having large ADPs:9,34,35 these two features, namely, CP/T3 peak and large ADPs, are hallmarks of local vibrational mode (or rattling) associated with guest cations inside cages.3,4 Thus, the observed broad peak of NaWO3 is most likely attributed to Na2 (6b) ions with the large ADP.
Figure 4.
(a) Temperature dependence of (a) CP/T and (b) CP/T 3 for NaWO3 and KWO3. Lines are fitting results (see the text for detail). (c) CP/T 3 versus T plot for Na0.8WO3 and Li0.5WO3.
The CP/T3 peak of cage compounds is typically characterized by Einstein specific heat within the “harmonic” approximation.9,34,35 To do this, we analyzed our raw data of NaWO3 by a combination of Debye and Einstein specific heats, along with an electronic specific heat of Ce(T) = γT (where γ is the electronic specific heat constant), which is given by
| (1) |
where fD,i and fE,j represent the number of the Debye and Einstein modes for the ith and jth contributions, respectively, all of which were determined by fitting. The sum of these is nothing but the total number of phonon modes in the unit cell, that is, and CE,j(T) denote, respectively, Debye and Einstein specific heat, which are expressed as follows:
| (2) |
| (3) |
Here, R is the gas constant and and are Debye and Einstein temperatures, respectively, that were also used as fitting parameters. The least-squares fitting was carried out using the data in the temperature range of 2 K < T < 200 K. A reasonable agreement was obtained for NaWO3 when we assume two Debye and one Einstein modes (i = 2, j = 1) and for KWO3 with two Debye modes only (i = 2, j = 0) (see Figure 4b and Table 2). It is clear that the additional Einstein term can reproduce the main feature of the CP/T3 peak in NaWO3, suggesting rattling-like local vibrational mode. It is noteworthy that the introduction of Na site deficiency (i.e., Na0.8WO3) substantially suppresses the CP/T3 peak, as shown in Figure 4c. This implies that the effect of lattice defect and disorder is not the origin of the peak, as opposed to random or disordered systems such as those containing Bi or Pb with 6s lone pair electrons.36,37
Table 2.
Parameters Obtained by Fitting the Specific Heat Data of NaWO3 to Equation 1, Where a Model with Two Debye and One Einstein Mode Was Useda
| mode | fD,i, fE,j | |
|---|---|---|
| D1 | 962 | 6.62 |
| D2 | 371 | 6.74 |
| E1 | 151 | 1.64 |
The terms of the Debye and Einstein modes are Di (i = 1, 2) and E1. The γ value was obtained as γ = 3.34 mJ/K2.
The observed rattling phenomenon in NaWO3 is unprecedented because the simple ABO3 perovskite can be described by cubic closed-packed arrangement of AO3 layers with B cations occupied at the interstitial octahedral site, and if the A cation is smaller, BO6 octahedral rotation takes place to adjust and optimize the local coordination environment around A. In NaWO3, however, the a+a+a+ rotation generates nonequivalent Na sites, Na1 (2a) and Na2 (6b) (Figure 2b,c). This necessarily leads to a situation that both sites cannot be simultaneously optimized in terms of the local environment, yielding relatively large guest-free-space Δ around the Na2 ion. The value of Δ can be roughly estimated by taking the difference between the cage distance dcage (from the center) and ionic radius of a guest cation: Δ = dcage – r(Na+). Our structural analysis indicates that Na1 has 12 equidistant Na1–O bonds (2.701(18) Å), whereas Na2 has four short (2.552(17) Å), four medium (2.778(17) Å), and four long (2.916(17) Å) bonds (Figure 2d). The available space of Na1 and Na2 is estimated by calculating dcage = d – r(O2–),9,24,34,35,38 where d is the Na–O bond length and r(O2–) refers to the ionic radius of O2– (=1.4 Å).39 This yielded dcage = 1.301 Å for Na1 and 1.152, 1.378, and 1.516 Å for Na2. Subsequently, using r(Na+) ~ 1 Å,33 we obtained Δ ~ 0.3 Å for Na1O12 and Δ ~ 0.5 Å for Na2O12. The Δ value of Na2O12 is parallel with those in the known cage compounds: Δ = 0.5–0.9 Å for filled skutterudites,35,38 Δ = 0.3–0.4 Δ for A-site-ordered quadruple perovskites,23,24 and Δ = 1–3 Å for clathrates and β-pyrochlores.3,4,9,34 Together with the large rmsd of 0.15 Å, the large value of Δ for Na2 led us to conclude that the Na2 site is responsible for rattling local vibration.
A comparison with the A-site-ordered quadruple perovskite CuCu3V4O12 further revealed that the coefficient of the Einstein specific heat, fE,1 = 1.64 per the NaWO3 formula, is larger than 0.27 per the “CuVO3” formula (i.e., 1/4 × CuCu3V4O12).24,33 This result is fairly consistent with the difference in the rattling site: CuCu3V4O12 has a rattler at the A site (2a) with the 2-fold multiplicity, whereas NaWO3 has a rattler at the A′ site (6b) with 6-fold multiplicity. Another prominent feature that differentiates NaWO3 from CuCu3V4O12 is the degree of octahedral tilting. Although both compounds are isostructural, the octahedral (a+a+a+) tilting in CuCu3V4O12 is very extensive and gives the ∠V–O–V bridging angle of ~140°, which forces the A′ site transition metal to adopt the square-planar coordination. As a result, the A site can be a rattler. In contrast, the ∠W–O–W angle for NaWO3 is ~169°, meaning that moderate octahedral rotation makes the A′ site a rattler.
One can generalize a strategy to find rattling phenomena in the pristine ABO3 perovskite. Among 15 tilting systems in perovskite,26,40–42 four systems (a+a+a+, a0b+b+, a0b+c–, and a+a+c–) have nonequivalent A sites. Examples include LixWO3 (x ≤ 0.5) and Li0.2ReO3 with a+a+a+,43 NaTaO3, NaNbO3, SrZrO3, and SrHfO3 with a0b+c–,41,44 and NH4MnCl3 with a0b+c–.41 Unfortunately, most of them exist as an intermediate phase (e.g., 803–893 K for NaTaO3). As far as we are aware, Li0.5WO3 with a+a+a+ is stable at RT,33 so we prepared the phase-pure Li0.5WO3 under high pressure and measured CP. As expected, a CP/T3 peak is found at 20 IK, which can be fitted by introducing the Einstein specific heat with (Figure 4c and Figure S4 and Table S4). Extensive research on rattling compounds has shown that decreases with increasing the cage size.3,4,34,35,38 In fact, the smaller value for Li0.5WO3 (versus 151 K for NaWO3) could be related to a larger Δ value of ~1 Å.
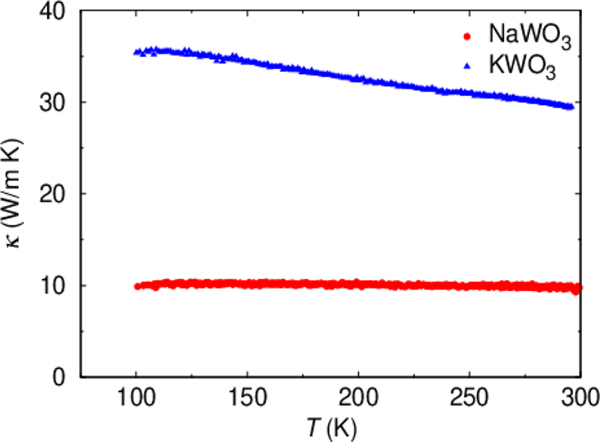
In order to see the effect of rattling on physical properties, we measured κ for NaWO3, the result of which is plotted in Figure 5, together with the data for KWO3. The κ for NaWO3 is clearly larger than that for KWO3 in the whole temperature range measured. The Wiedemann–Franz law was used to extract the electronic contribution of thermal conductivity κe. Using the 200 K data of ρ, we obtained κe = 1.6 W/m·IK for NaWO3 and κe = 2.2 W/m·K for KWO3. Hence, the difference in κ is ascribed to that of lattice thermal conductivity, κL, but is different from what can be expected from the weight difference of K+ and Na+ ions.45,46 We thus conclude that rattling vibration of Na+ ions largely suppresses κL for NaWO3. The suppression of κL is discussed for cage compounds in the context of the rattling effect.13–15,46 More recently, the rattling and its relation with the suppression of κL are discussed in compounds without cage structure47,48 such as LaOBiS2–xSex, where rattling-like local vibration is found in a cation at the planar coordination geometry with lone pair electrons. These findings give us hope to explore compounds beyond well-known cage systems toward finding low κL.
Figure 5.
Temperature dependence of thermal conductivity κ of NaWO3 and KWO3.
CONCLUSION
We have extended the solubility limit of NaxWO3 to the full stoichiometry (x = 1) by exploiting a high-pressure route. NaWO3 crystallizes in a perovskite structure with all in-phase octahedral rotations (a+a+a+). Despite the pristine perovskite phase, the specific heat measurement on NaWO3 exhibits anharmonic phonon modes associated with low-energy rattling vibrations, which is absent in the ideal cubic perovskite KWO3. The rattling behavior in NaWO3 is caused by the presence of distinct crystallographic Na sites. The structural analysis revealed that the Na2 (6b) site is a rattler, as opposed to the isostructural quadruple AA′3B4O12 perovskite, where the rattling site is the A (2a) cation. The present finding suggests that rattling phenomenon will be available for other ABO3 perovskites with nonequivalent A sites. Conversely, a cation order may be possible by introducing different alkali metals (e.g, A = Na, A′ = K) in this structural type. Together with our recent study on stoichiometric phases of K0.6WO3 and KWO3,29 the high-pressure method turned out to be highly efficient: LixWO3 (0.5 ≤ x ≤ 1) in the LiNbO3 structure is also isolated.
Supplementary Material
ACKNOWLEDGMENTS
Synchrotron and neutron experiments were performed at SPring-8 BL02B2 of JASRI and BT-1 of the NIST Center for Neutron Research. We thank Dr. K Fujita for giving us heat capacity data of CuCu3V4O12. The work was supported by CREST (JPMJCR1421) and JSPS KAKENHI (JP16H6439, 17H04849).
Footnotes
The authors declare no competing financial interest.
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACSPublicationswebsite at DOI: 10.1021/acs.inorgchem.9b00248.
Detailed information on sample preparation, measurements of physical properties (electrical resistivity, specific heat, and thermal conductivity), and analysis of specific heat (PDF)
Accession Codes
CCDC 1893481 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.
REFERENCES
- (1).Nolas GS; Morelli DT; Tritt TM SKUTTERUDITES: A Phonon-Glass-Electron Crystal Approach to Advanced Thermoelectric Energy Conversion Applications. Annu. Rev. Mater. Sci 1999, 29, 89–115. [Google Scholar]
- (2).Sato H; Sugawara H; Aoki Y; Harima H. Handook of Magnetic Materials; Elsevier: Amsterdam, 2009; Vol. 18, Chapter 1, p 1. [Google Scholar]
- (3).Takabatake T; Suekuni K; Nakayama T; Kaneshita E. Phonon-glass Electron-crystal Thermoelectric Clathrates: Experiments and Theory. Rev. Mod. Phys 2014, 86, 669–716. [Google Scholar]
- (4).Hiroi Z; Yamaura J; Hattori K. Rattling Good Super-conductor: β-Pyrochlore Oxides AOs2O6. J. Phys. Soc. Jpn 2012, 81, 011012. [Google Scholar]
- (5).Nolas GS; Cohn JL; Slack GA; Schujman SB Semiconducting Ge Clathrates: Promising Candidates for Thermoelectric Applications. Appl. Phys. Lett 1998, 73, 178–180. [Google Scholar]
- (6).Nolas GS; Poon J; Kanatzidis M. Recent Developments in Bulk Thermoelectric Materials. MRS Bull. 2006, 31, 199–205. [Google Scholar]
- (7).Yonezawa S; Muraoka Y; Matsushita Y; Hiroi Z. Superconductivity in a Pyrochlore-related Oxide KOs2O6J. Phys. J. Phys.: Condens. Matter 2004, 16, L9–L12. [Google Scholar]
- (8).Brühwiler M; Kazakov SM; Karpinski J; Batlogg B. Mass Enhancement, Correlations, and Strong-Coupling Superconductivity in the β-Pyrochlore KOs2O6. Phys. Rev. B: Condens. Matter Mater. Phys 2006, 73, 094518. [Google Scholar]
- (9).Hiroi Z; Yonezawa S; Nagao Y; Yamaura J. Extremely Strong-coupling Superconductivity and Anomalous Lattice Properties in the β-Pyrochlore Oxide KOs2O6. Phys. Rev. B: Condens. Matter Mater. Phys 2007, 76, 014523. [Google Scholar]
- (10).Sanada S; Aoki Y; Aoki H; Tsuchiya A; Kikuchi D; Sugawara H; Sato H. Exotic Heavy-Fermion State in Filled Skutterudite SmOs4Sb12. J. Phys. Soc. Jpn 2005, 74, 246–249. [Google Scholar]
- (11).Hattori K; Hirayama Y; Miyake K. ILocal Heavy Quasiparticle in Four-Level Kondo Model. J. Phys. Soc. Jpn 2005, 74, 3306–3313. [Google Scholar]
- (12).Hotta T. Effect of Rattling Phonons on Sommerfeld Constant. J. Phys. Soc. Jpn 2008, 77, 103711. [Google Scholar]
- (13).Hotta T. Inverse Isotope Effect on Kondo Temperature in Electron-Rattling System. J. Phys. Soc. Jpn 2009, 78, 073707. [Google Scholar]
- (14).Nolas GS; Slack GA; Morelli DT; Tritt TM; Ehrlich AC The effect of Rare-earth Filling on the Lattice Thermal Conductivity of Skutterudites. J. Appl. Phys 1996, 79, 4002–4008. [Google Scholar]
- (15).Sales BC; Mandrus D; Williams RK Filled Skutterudite Antimonides: A New Class of Thermoelectric Materials. Science 1996, 272, 1325–1328. [DOI] [PubMed] [Google Scholar]
- (16).Keppens V; Mandrus D; Sales BC; Chakoumakos BC; Dai P; Coldea R; Maple MB; Gajewski DA; Freeman EJ; Bennington S. Localized Vibrational Modes in Metallic Solids. Nature 1998, 395, 876–878. [Google Scholar]
- (17).Koza MM; Johnson MR; Viennois R; Mutka H; Girard L; Ravot D. Breakdown of Phonon Glass Paradigm in La- and Ce-filled Fe4Sb12 Skutterudites. Nat. Mater 2008, 7, 805–810. [DOI] [PubMed] [Google Scholar]
- (18).Sleight AW; Gillson JL; Bierstedt PE High-temperature superconductivity in the BaPb1-xBixO3 systems. Solid State Commun. 1975, 17, 27–28. [Google Scholar]
- (19).Kuwahara H; Tomioka Y; Asamitsu A; Moritomo Y; Tokura Y. A First-Order Phase Transition Induced by a Magnetic Field. Science 1995, 270, 961–963. [Google Scholar]
- (20).Megaw HD Origin of ferroelectricity in barium titanate and other perovskite-type crystals. Acta Crystallogr. 1952, 5, 739–749. [Google Scholar]
- (21).Tilley RJD Perovskites: Structure–Property Relationships; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar]
- (22).Kageyama H; Hayashi K; Maeda K; Attfield JP; Hiroi Z; Rondinelli JM; Poeppelmeier KR Expanding frontiers in materials chemistry and physics with multiple anions. Nat. Commun 2018, 9, 772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Akizuki Y; Yamada I; Fujita K; Nishiyama N; Irifune T; Yajima T; Kageyama H; Tanaka K. A-Site-Ordered Perovskite MnCu3V4O12 with a 12-Coordinated Manganese(II). Inorg. Chem 2013, 52, 11538–11543. [DOI] [PubMed] [Google Scholar]
- (24).Akizuki Y; Yamada I; Fujita K; Taga K; Kawakami T; Mizumaki M; Tanaka K. Rattling in the Quadruple Perovskite CuCu3V4O12. Angew. Chem., Int. Ed 2015, 54, 10870–10874. [DOI] [PubMed] [Google Scholar]
- (25).Shimakawa Y. A-Site-Ordered Perovskites with Intriguing Physical Properties. Inorg. Chem 2008, 47, 8562–8570. [DOI] [PubMed] [Google Scholar]
- (26).Straumanis ME The Sodium Tungsten Bronzes. I., Chemical Properties and Structure. J. Am. Chem. Soc 1949, 71, 679–683. [Google Scholar]
- (27).Brimm EO; Brantley JC; Lorenz JH; Jellinek MH Sodium and Potassium Tungsten Bronzes. J. Am. Chem. Soc 1951, 73, 5427–5432. [Google Scholar]
- (28).Brown BW; Banks E. The Sodium Tungsten Bronzes. J. Am. Chem. Soc 1954, 76, 963–966. [Google Scholar]
- (29).Clarke R New Sequence of Structural Phase Transitions in NaxWO3. Phys. Rev. Lett 1977, 39, 1550–1553. [Google Scholar]
- (30).Ikeuchi Y; Takatsu H; Tassel C; Goto Y; Murakami T; Kageyama H. High-Pressure Synthesis of Fully Occupied Tetragonal and Cubic Tungsten Bronze Oxides. Angew. Chem., Int. Ed 2017, 56, 5770–5773. [DOI] [PubMed] [Google Scholar]
- (31).Fortes AD Crystal Structures of Spinel-Type Na2MoO4 and Na2WO4 Revisited using Neutron Powder Diffraction. Acta Cryst. E 2015, 71, 592–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Petříček V; Dušek M; Palatinus L. Crystallographic Computing System JANA2006: General Features. Z. Kristallogr. - Cryst. Mater 2014, 229, 345–352. [Google Scholar]
- (33). [See the Supporting Information for powder XRD and SXRD data of NaxWO3, the detailed structure analysis, and the analysis of the specific heat of NaxWO3, LixWO3, and KWO3.]
- (34).Suekuni K; Avila MA; Umeo K; Fukuoka H; Yamanaka S; Nakagawa T; Takabatake T. Simultaneous Structure and Carrier Tuning of Dimorphic Clathrate Ba8Ga16Sn30. Phys. Rev. B: Condens. Matter Mater. Phys 2008, 77, 235119. [Google Scholar]
- (35).Matsuhira K; Sekine C; Wakeshima M; Hinatsu Y; Namiki T; Takeda K; Shirotani I; Sugawara H; Kikuchi D; Sato H. Systematic Study of Lattice Specific Heat of Filled Skutterudites. J. Phys. Soc. Jpn 2009, 78, 124601. [Google Scholar]
- (36).Melot BC; Tackett R; O’Brien J; Hector AL; Lawes G; Seshadri R; Ramirez AP Large Low-temperature Specific Heat in Pyrochlore Bi2Ti2O7. Phys. Rev. B: Condens. Matter Mater. Phys 2009, 79, 224111. [Google Scholar]
- (37).Takatsu H; Hernandez O; Yoshimune W; Prestipino C; Yamamoto T; Tassel C; Kobayashi Y; Batuk D; Shibata Y; Abakumov AM; Brown CM; Kageyama H. Cubic Lead Perovskite PbMoO3 with Anomalous Metallic Behavior. Phys. Rev. B: Condens. Matter Mater. Phys 2017, 95, 155105. [Google Scholar]
- (38).Yamaura J; Hiroi Z. Rattling Vibrations Observed by Means of Single-Crystal X-ray Diffraction in the Filled Skutterudite ROs4Sb12 (R = La, Ce, Pr, Nd, Sm). J. Phys. Soc. Jpn 2011, 80, 054601. [Google Scholar]
- (39).Shannon RD Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr., Sect. A: Cryst. Phys. Diffr., Theor. Gen. Crystallogr 1976, 32, 751–767. [Google Scholar]
- (40).Woodward PM Octahedral Tilting in Perovskites. I. Structure Stabilizing Forces. Acta Crystallogr., Sect. B: Struct. Sci 1997, 53, 32–43. [Google Scholar]
- (41).Woodward PM Octahedral Tilting in Perovskites. II. Structure Stabilizing Forces. Acta Crystallogr., Sect. B: Struct. Sci 1997, 53, 44–66. [Google Scholar]
- (42).Howard CJ; Stokes HT Group-Theoretical Analysis of Octahedral Tilting in Perovskites. Acta Crystallogr., Sect. B: Struct. Sci 1998, 54, 782. [DOI] [PubMed] [Google Scholar]
- (43).Cava RJ; Santoro A; Murphy DW; Zahurak SM; Roth RS The Structures of the Lithium Inserted Metal Oxides Li0.2R.eO3 and Li0.36WO3. J. Solid State Chem 1983, 50, 121–128. [Google Scholar]
- (44).Kennedy BJ; Howard CJ; Chakoumakos BC High-Temperature Phase Transitions in SrHfO3. Phys. Rev. B: Condens. Matter Mater. Phys 1999, 60, 2972–2975. [Google Scholar]
- (45).Tritt TM Thermal Conductivity: Theory, Properties, and Applications; Springer Science & Business Media: New York, 2005. [Google Scholar]
- (46).Rowe DM CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, 1995. [Google Scholar]
- (47).Suekuni K; Lee CH; Tanaka HI; Nishibori E; Nakamura A; Kasai H; Mori H; Usui H; Ochi M; Hasegawa T; Nakamura M; Ohira-Kawamura S; Kikuchi T; Kaneko K; Nishiate H; Hashikuni K; Kosaka Y; Kuroki K; Takabatake T. Retreat from Stress: Rattling in a Planar Coordination. Adv. Mater 2018, 30, 1706230. [DOI] [PubMed] [Google Scholar]
- (48).Lee CH; Nishida A; Hasegawa T; Nishiate H; Kunioka H; Ohira-Kawamura S; Nakamura M; Nakajima K; Mizuguchi Y. Effect of Rattling Motion without Cage Structure on Lattice Thermal Conductivity in LaOBiS2-xSex. Appl. Phys. Lett 2018, 112, 023903. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.