Abstract
Alzheimer’s disease (AD) is linked to changes in fMRI task activations and fMRI resting-state functional connectivity (restFC), which can emerge early in the illness timecourse. These fMRI correlates of unhealthy aging have been studied in largely separate subfields. Taking inspiration from neural network simulations, we propose a unifying mechanism wherein restFC alterations associated with AD disrupt the flow of activations between brain regions, leading to aberrant task activations. We apply this activity flow model in a large sample of clinically normal older adults, which was segregated into healthy (low-risk) and at-risk subgroups based on established imaging (positron emission tomography amyloid) and genetic (apolipoprotein) AD risk factors. Modeling the flow of healthy activations over at-risk AD connectivity effectively transformed the healthy aged activations into unhealthy (at-risk) aged activations. This enabled reliable prediction of at-risk AD task activations, and these predicted activations were related to individual differences in task behavior. These results support activity flow over altered intrinsic functional connections as a mechanism underlying Alzheimer’s-related dysfunction, even in very early stages of the illness. Beyond these mechanistic insights, this approach raises clinical potential by enabling prediction of task activations and associated cognitive dysfunction in individuals without requiring them to perform in-scanner cognitive tasks.
Keywords: Functional connectivity, Task activation, fMRI, Alzheimer’s, Aging
1. Introduction
Analyzing the synchronization of activity fluctuations in task-free rest is thought to provide insight into the brain’s intrinsic network organization (Raichle, 2010; Petersen and Sporns, 2015). Formalized in the subfield of resting-state functional connectivity (restFC), such approaches have primarily been applied to human functional magnetic resonance imaging (fMRI) data. As testament to the reproducibility of restFC, convergent network topologies have been recovered across different regional atlases (Power et al., 2011; Ji et al., 2019), non-fMRI human imaging modalities (Brookes et al., 2011; Kucyi et al., 2018) and non-human animals (Wang et al., 2013; Stafford et al., 2014). Whilst these findings highlight that restFC is reliably observed, debate persists over its cognitive relevance, given that the experimentally unconstrained nature of rest raises practical difficulties in separating signal from noise (Power et al., 2012; Laumann et al., 2016), as well as theoretical difficulties in moving from an exploratory to explanatory understanding of brain network function (Mill et al., 2017).
Evidence of restFC’s cognitive relevance comes from clinical research linking restFC alterations to pathology (Buckner et al., 2008; Buckholtz and Meyer-Lindenberg, 2012). Given the severe prognosis and societal burden of Alzheimer’s disease (AD), much of this work has interrogated restFC changes characterizing various forms of healthy and unhealthy aging (Andrews-Hanna et al., 2007; Sorg et al., 2007; Ferreira and Busatto, 2013; Geerligs et al., 2015a; Ferreira et al., 2016). Burgeoning research focuses on restFC changes in early at-risk stages of AD (Hedden et al., 2009; Sheline and Raichle, 2013; Schultz et al., 2017), as neurobiological abnormalities such as elevated positron emission tomography (PET) measures of amyloid beta may precede clinical impairment by many years (Jack et al., 2010; Sperling et al., 2011). Alzheimer’s-related alterations of restFC emerge around the same time as elevated amyloid (Sheline and Raichle, 2013) and have been associated with presence of the genetic apolipoprotein (APOE) ε4 allele (Sheline et al., 2010), suggesting utility of restFC in developing imaging biomarkers to expedite diagnosis and intervention.
Recent reports have extended towards using restFC to quantitatively predict or classify age-related conditions (Dosenbach et al., 2010; Woo et al., 2017; Du et al., 2018). However, reported failures of predictive models in generalizing out-of-sample (Onoda et al., 2017; Teipel et al., 2017; Fountain-Zaragoza et al., 2019) highlight limitations of entirely data-driven approaches to predicting Alzheimer’s-related pathologies, especially as artifactual contaminants of restFC can drive clinical group differences (Siegel et al., 2016; Hodgson et al., 2017). These findings again call for increased efforts to clarify the cognitive relevance of restFC, so as to identify clear mechanisms by which restFC alterations impact on AD and other pathologies.
To this end, we recently developed an approach inspired by neural network simulations to mechanistically predict task activations from restFC via the concept of activity flow (the propagation of task-evoked activity between neural populations; Cole et al., 2016; Ito et al., 2017). This approach directly interrogates the cognitive relevance of restFC, given that tasks are designed to elicit particular cognitive processes. Furthermore, in addition to restFC, fMRI task activations are disrupted in various forms of aging (Grady, 2012; Campbell and Schacter, 2017), raising the potential for age-related alterations of restFC and task activations to arise from a common activity flow mechanism.
The present report sought empirical evidence for this mechanism (Fig. 1). We hypothesized that unhealthy age-related restFC alterations disrupt the ability for activity to flow between brain regions, leading to the emergence of dysfunctional task activations. We tested this framework in clinically normal older adults, a subset of whom presented positively for PET amyloid or APOE risk factors for AD, which were separately used to define ‘at-risk’ subjects. We found that activity flow mapping reliably predicted task activations in held-out at-risk AD subjects from their pattern of restFC. We extended the approach to accurately predict individual differences in task behavior from the model’s predicted activations, observing superior performance to using ‘raw’ restFC features that had not been passed through the model. These results support activity flow alterations as a mechanism underlying age-related dysfunction, even in the earliest stages of AD.
Fig. 1.
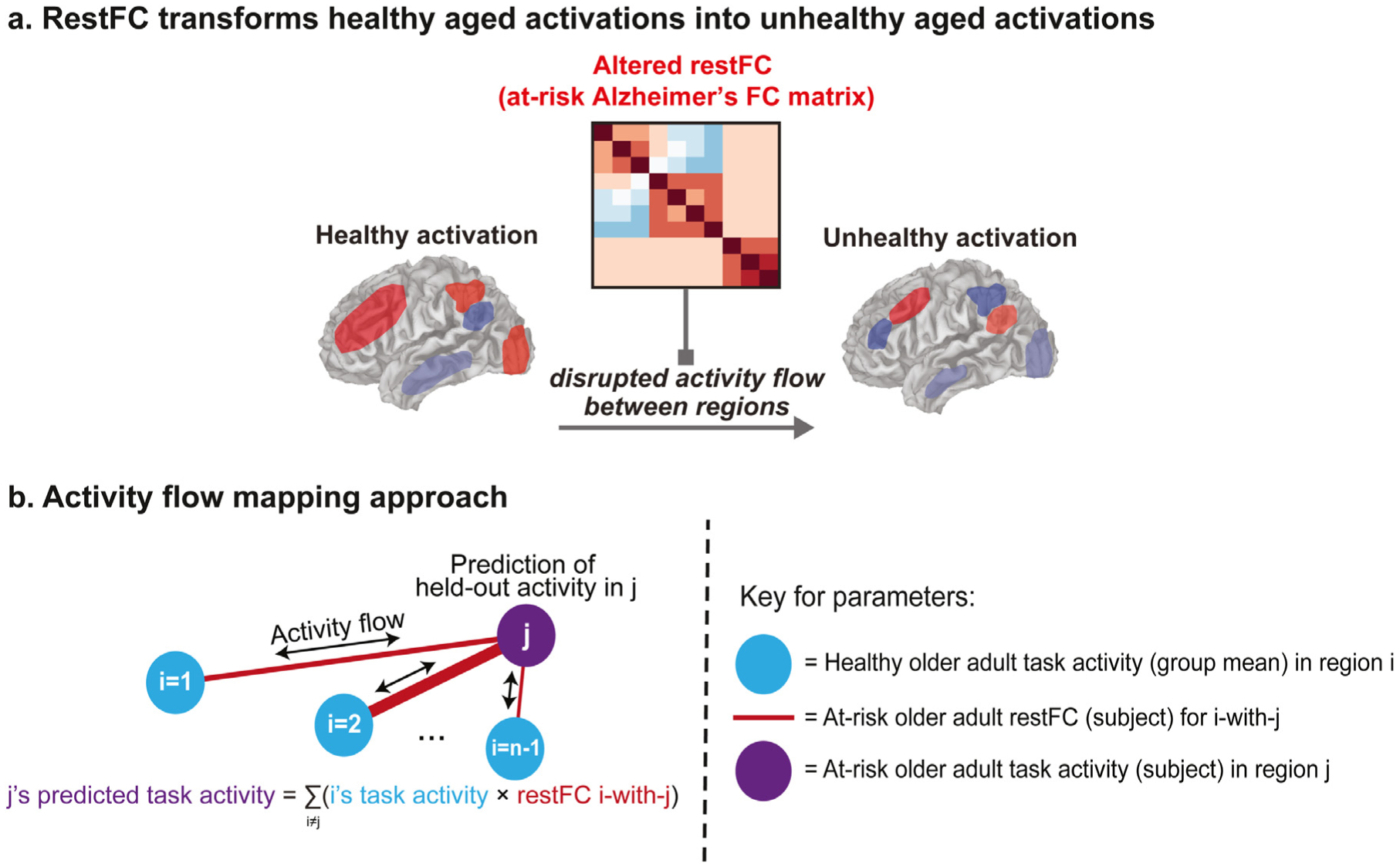
Theoretical and methodological principles underlying application of activity flow mapping in an integrated connectivity-activity account of at-risk Alzheimer’s disease (AD). a) Abstract theoretical underpinnings of activity flow mapping – which is based on the core mechanism underlying neural network simulations – in a clinical context. A ‘healthy’ aged task activation pattern is transformed into an ‘unhealthy’ aged activation (i.e. one associated with being at-risk for developing AD) by an altered pattern of resting-state functional connectivity (restFC) in at-risk subjects disrupting the ability for task activations to flow between brain regions. b) Methodological formalization of the activity flow mapping approach. Task activation in a held-out brain region (j) in a held-out at-risk AD subject is predicted from the dot product between the healthy activation state of the rest of the brain (regions i, estimated as the mean activation in the healthy group) and the restFC between i and j (estimated from the to-be-predicted at-risk subject). See Methods for further details.
2. Materials and methods
2.1. Participants
The sample comprised 101 right-handed elderly subjects (age mean = 65.1 years, age range = 42–82 years, 63 female) collected as part of the Adult Children Study at the Knight Alzheimer’s Disease Research Center at Washington University in St Louis (Knight ADRC, https://knightadrc.wustl.edu/). All participants gave their informed consent in compliance with Washington University’s human subjects guidelines. Full details of behavioral and neuroimaging measures acquired by the Knight ADRC project are available in Gordon et al. (2015). Subjects included in our sample underwent behavioral (Mini Mental State Exam, MMSE; Folstein et al., 1975) and neuropsychological (Clinical Dementia Rating, CDR; Morris, 1993) assessment, rest and task fMRI scans, structural MRI scans, 11 [C] Pittsburgh Compound B (PiB)-PET imaging for high levels of amyloid beta uptake, and a DNA swab testing for presence of the apolipoprotein (APOE) ε4 allele. All subjects were assessed as clinically ‘normal’ at the time of recruitment (Mini Mental State Exam, MMSE score > 24; Clinical Dementia Rating, CDR=0). All subjects passed the exclusion criteria of high motion across runs (subjects with an average absolute movement > 1.50 mm or an average relative movement of 0.5 mm were excluded from our sample), presence of neurological damage (stroke or traumatic brain injury), and a lag between their fMRI and PiB-PET imaging sessions greater than 90 days. Note that this Knight ADRC sample was the largest AD-related sample available at the time of analysis that had both a sufficient amount of resting-state data, and data collected from multiple cognitive tasks (both integral to our analyses; see Discussion for further on issues relating to sample size in AD research).
2.2. Segregation of sample into at-risk and healthy aged groups
We binarized the APOE ε4 and PiB-PET amyloid beta measures separately to provide distinct methods of segregating our sample into ‘at-risk AD’ (i.e. ‘unhealthy’) and ‘healthy’ subject groups. This enabled us to test the generalizability of the activity flow mapping approach across different ways of identifying at-risk subjects. The APOE segregation was created by labeling any subject with at least one APOE ε4 allele as at-risk, and all other subjects as healthy (see Table 1 for demographic information). At-risk subjects were identified in the amyloid segregation on the basis of a standardized PiB uptake ratio (SUVR) greater than 1.42 (following Jack et al., 2017; Vlassenko et al., 2018; see Section 2.3 for details), with the remaining subjects classified as healthy. Note that our definition of at-risk AD encompasses both previously adopted at-risk (APOE ε4 genotype) and preclinical (elevated PET amyloid) AD categorizations. For brevity, the Results section focuses primarily on the APOE segregation due to the larger at-risk group obtained compared to the amyloid segregation (see Table 1). However, the pattern of observed results is virtually identical for both segregation types (see Supplementary Information section 1.1).
Table 1.
Demographic information for the two at-risk AD segregation approaches: APOE and amyloid. MMSE = Mini Mental State Exam scores; Std = standard deviation; RT = mean cross-task reaction time (in ms); zRT = mean cross-task reaction time after z-scoring across trials; Acc = task accuracy (in%).
| Segregation type | |||||
|---|---|---|---|---|---|
| APOE | Amyloid | ||||
| Group | At-risk | Healthy | At-risk | Healthy | |
| Size (n) | 33 | 68 | 20 | 81 | |
| Age (years) | Mean | 64.67 | 64.76 | 70.30 | 63.36 |
| Range | 53–78 | 42–82 | 55–82 | 42–79 | |
| Gender (n female) | 20 | 43 | 15 | 48 | |
| MMSE | Mean | 28.97* | 29.50* | 28.80* | 29.46* |
| Std | 1.51 | 0.91 | 1.58 | 1.00 | |
| Cross-task RT | Mean | 859.65 | 868.88 | 876.68 | 863.19 |
| Std | 108.26 | 97.10 | 121.99 | 95.07 | |
| Cross-task zRT | Mean | −0.0074 | −0.0073 | −0.0069 | −0.0074 |
| Std | 0.021 | 0.012 | 0.019 | 0.014 | |
| Cross-task Acc | Mean | 96.63* | 97.63* | 96.28* | 97.56* |
| Std | 2.91 | 1.43 | 3.42 | 1.50 | |
= at-risk versus healthy group comparison is significant at p < .05 (via paired ttest computed for a given segregation type).
2.3. Data acquisition and preprocessing
MRI data was collected on a Siemens Trio 3T scanner. Anatomical T1-weighted images were acquired via a magnetization-prepared rapid gradient-echo sequence (MPRAGE; TR = 2400 ms, TE = 3.16 ms, flip angle = 8°, field of view = 256 mm, 1 mm isotropic voxels, sagittal orientation). Task fMRI images were acquired using an interleaved whole-brain echo planar imaging (EPI) sequence (TR = 2000 ms, TE = 25 ms, flip angle=90°, field of view=256 mm, 4 mm isotropic voxels, 36 slices in interleaved sagittal orientation). Task fMRI data was collected for two tasks (see next section for paradigm details): semantic animacy (2 runs, 303 volumes each) and color Stroop (2 runs, 295 volumes each). Resting-state fMRI images were acquired using a similar EPI sequence (TR = 2200 ms, TE = 27 ms, flip angle = 90°, field of view = 256 mm, 4 mm isotropic voxels, 36 slices in interleaved sagittal orientation; 2 runs, 164 volumes each). Separate dual-echo gradient-recalled echo (GRE) fieldmaps were also acquired to correct b0 distortions in the task and rest EPI images respectively.
The full analysis pipeline is depicted in the flowchart in Fig. 2. T1 images were segmented using Freesurfer (Fischl, 2004). fMRI preprocessing was conducted in FSL using the FEAT toolbox (Woolrich et al., 2001). Subjects’ task and rest fMRI images underwent motion correction, fieldmap b0 unwarping, slice timing correction, linear coregistration to their anatomical T1 and non-linear normalization to an age-appropriate MNI template (created from a separate large sample of demographically matched older adults; Gordon et al., 2015). Subsequent analyses were conducted at both the regionwise and voxelwise levels. For the regionwise analyses, task and rest timeseries were extracted from 264 regions from the Power functional atlas (Power et al., 2011). For the voxelwise analyses, timeseries were extracted from all gray matter voxels. Nuisance regression was performed for the regionwise/voxelwise timeseries via general linear models (GLMs), which included regressors for 6 motion parameters, white matter and ventricular timeseries, and their temporal derivatives. The GLM fit to the task fMRI data also included regressors for the two tasks (see next section for details). Note that the main results were virtually identical if a regressor modeling the global signal (GSR) was included in the task and rest GLM, and if high motion timepoints were scrubbed from the rest GLM (see Supplementary Information section 1.1.; note that high motion subjects were also excluded from the sample, see Section 2.1). The residual timeseries from the rest GLM and the beta activation amplitudes from the task GLM were used for the main activity flow mapping analyses. The voxelwise beta activation maps were spatially smoothed using non-Gaussian nearest-neighbor averaging (at 4 mm), which reduces spatial autocorrelation compared to Gaussian smoothing.
Fig. 2.

Flowchart depicting full analysis pipeline. Relevant Results section numbers are also provided. Note that generating predicted activations via the main activity flow mapping procedure is the basis for the majority of presented analyses. “regs ”=regressors; “ML ”=machine learning; “pred ”= predicted; “RT = reaction time ”; “alt. ”=alternative.
Full details about PiB-PET acquisition in the Knight ADRC project was provided previously (Su et al., 2013). Briefly, after injection of the PiB tracer subjects underwent 60 min dynamic PET imaging scans using a Siemens 962 HR+ ECAT scanner. A summary measure of whole-brain PET amyloid was estimated from anatomical atlas regions identified from Freesurfer segmentations of each subject’s T1 image (using the ‘wmparc’ segmentation; Fischl, 2004). Errors in the Freesurfer segmentation were identified and corrected manually. The Freesurfer regions of interest were then aligned to the native PET images, and the standardized uptake value ratio (SUVR) was computed as the median PiB uptake at each region relative to a cerebellar reference (following Rousset et al., 2008; Su et al., 2015). SUVR was averaged across regions to provide a summary measure of whole-brain PET amyloid deposition, which was then binarized to label at-risk AD and healthy subjects for the Amyloid segregation (whole-brain SUVR > 1.42 = at-risk; Vlassenko et al., 2018).
2.4. Experimental design and fMRI task activation estimation
The design of the two tasks is depicted in Fig. 3a. Each task was briefly practiced by subjects just prior to their fMRI sessions. Both tasks involved word stimuli presented in a block design, with the presentation format and durations matched closely across them. There were 2 runs of each task, each alternating between 4 task blocks (containing 24 trials with jittered intertrial intervals) and 5 rest intervals. The semantic animacy task preceded the color Stroop task, and required subjects to judge whether individually presented words referred to living or nonliving things. Words used in this task were balanced across living/nonliving categories in terms of length, orthographic neighborhood and frequency. The color Stroop task required participants to judge whether words were presented in a red or blue font; the words’ meaning was either ‘congruent’ with the font color (e.g. the word ‘red’ in red font), ‘incongruent’ (e.g. the word ‘blue’ in red font), or ‘unrelated’ to color (e.g. the word ‘deep’ in red font). Stimulus classes for both tasks were balanced within task blocks (e.g. equal numbers of living and non-living words were presented for each animacy task block, in a randomized order). For the resting-state fMRI scans, subjects lay passively in the scanner with their eyes open. fMRI task activation amplitudes were estimated via GLM in Matlab. In addition to nuisance regressors (see previous section), the task GLM included two regressors modeling blocks for each task as box-cars convolved with the canonical hemodynamic response function (using the ‘spm_hrf’ function from the SPM toolbox). GLMs were fit to the regionwise and voxelwise timeseries data separately, and the resulting beta amplitude estimates were used in all analyses involving fMRI task activations.
Fig. 3.

Task design, restFC estimation and activity flow mapping implementation. a) Design schematic for the two fMRI tasks: semantic animacy and color Stroop. See Methods for a detailed description. Example trials are depicted for each task, with the hand symbol denoting the correct response. ‘ITI jitter’ = intertrial interval jitter, which ranged from 1 to 9 s in increments of 2 s. b) Approach to estimating restFC for each subject using an ‘optimized’ form of multiple linear regression with PCA dimensionality reduction. After extraction of BOLD rest timeseries from functional regions-of-interest (panel i, color-coded according to network affiliations from the Power et al., 2011), restFC was estimated for each subject via a regression model predicting target j region timeseries from the principal components of the remaining source i region timeseries (panel ii). The stability (i.e. matrix similarity) of the restFC solutions across the 2 runs was optimized for each subject via a cross-validation scheme that is described in Method Section 2.5 . ‘ncomps’ = the number of principal components from the PCA of the source i timeseries included in the regression model predicting j. This is the term that is varied as part of the restFC optimization. c) Practical implementation of activity flow mapping approach. Note that the restFC term used to generate the activity prediction for a given region/voxel j is a single row from that at-risk AD subject’s restFC matrix (color-coded in the Figure according to the Power network affiliations). ‘subject RFX’ = quantification of prediction accuracy via a subject-level random effects approach (see Methods for details).
2.5. Resting-state functional connectivity estimation
The residual timeseries from the rest fMRI GLM were used to estimate restFC. Fig. 3b illustrates the approach, which involves an optimized form of multiple linear regression with principal component analysis (PCA) dimensionality reduction. Multiple linear regression has been used for activity flow mapping previously (Cole et al., 2016), with a primary benefit over alternative FC estimation methods being the removal of indirect connections. For example, an underlying ground truth FC pattern with connectivity between regions A-B-C would incorrectly yield connections between A-C if using Pearson correlation, but not multiple linear regression.
The optimization of multiple linear regression FC was performed for each individual subject, with the goal of maximizing the inter-session stability of restFC, and hence prevent overfitting to noise. The latter may arise from multiple linear regression using the maximum number of principal components permitted by the data, given that some components will reflect noise rather than neural signal. Our optimization approach varied the number of principal components included in the regression in a cross-validation scheme that maximised the similarity of the restFC pattern across the two resting-state runs for each subject.
Specifically, for a ‘target’ brain region j (see Fig. 3b), a PCA projection was performed for all ‘source’ regions i→n excluding that target (i.e. spatial PCA on an input matrix where timepoints = observations and source regions = variables). The number of principal component scores (ncomps) retained after this step was iteratively varied from 1 to the maximum permitted (i.e. 164 timepoints per rest run minus 1 = 163 max ncomps). The retained PCA scores were then used in a multiple linear regression predicting the target j timeseries, with the resulting coefficients multiplied by the PCA loadings to obtain betas capturing resting-state connectivity between region j and all other regions i (pcaβij in Fig. 3b). This process was repeated for all target regions j to populate the (asymmetric) region x region restFC matrix for each rest run. The similarity between the run 1 and run 2 restFC matrices was finally calculated as the Pearson correlation between all off-diagonal matrix elements, with this entire process repeated on each ncomps cross-validation loop. The optimized ncomps value was chosen as that yielding the maximum FC similarity between rest runs, whilst also accounting for greater than 50% of the variance explained in the source region PCA (averaged across all PCAs performed for each target region, for each optimization loop). This PCA variance explained constraint served as a hyperparameter ensuring that FC stability was maximized without excluding signal components accounting for meaningful variance. Note that we did not explore any other values for this hyperparameter to reduce the chance of overfitting to noise in the data. Hence, each subject had a different optimized ncomps value (mean ncomps across subjects = 10.26, std = 6.88; mean restFC similarity = 0.58, std = 0.09; mean source PCA variance explained = 63.90%, std = 10.85). This optimized ncomps value was entered when computing the final restFC estimates for each target region for that individual subject, with the resulting restFC matrix used for further analyses.1
A separate restFC optimization was performed for the voxelwise analyses following an almost identical approach, wherein target voxels j were predicted by the PCA projection of source voxels i. The only modifications were the exclusion of spatially proximal voxels from the source voxel set (i) i.e. voxels from the same functional region as the target voxel and all voxels within 9 mm of that functional region were excluded. Functional region affiliations were identified from the Gordon functional atlas (Gordon et al., 2016), as this parcellation provides regional affiliations for every gray matter voxel in the brain, unlike the Power functional atlas which only provides affiliations for 10 mm diameter spheres. This exclusion step reduced the inflation of activity flow mapping predictions by spatial autocorrelation of the fMRI BOLD response.2
2.6. Machine learning classifications using restFC and task activation features
We trained multivariate machine learning classifiers to distinguish between healthy and at-risk subjects, separately on the basis of regional restFC and regional task activation features. We employed a minimum-distance classification approach, which is related to representational similarity analysis (Kriegeskorte et al., 2008; Mur et al., 2009; Diedrichsen and Kriegeskorte, 2017; Hebart and Baker, 2018; Spronk et al., 2018). To increase the sample size for classifier training, we concatenated at-risk subjects across both APOE and amyloid segregation types, yielding a combined at-risk group size of 40. Given that the healthy group was larger (n = 61), we selected a random subset of 40 subjects from the healthy group to ensure that training was performed on balanced group sizes (as recommended e.g. in Poldrack et al., 2019). To probe the robustness of the classification results, we employed two distinct approaches to cross-validation: a k-folds approach (90% of subjects assigned to training and 10% to testing over 10 folds, with each test fold containing equal numbers of healthy/at-risk subjects uniquely assigned to each fold) and a leave-two-subjects-out approach (two unique subjects assigned to testing on each loop, one from each healthy/at-risk group to ensure perfectly balanced group sizes during training, as recommended e.g. in Poldrack et al., 2019). These cross-validation approaches yielded an identical pattern of classification results, highlighting robustness of the between-group differences (see Results).
Features for the restFC classification were the off-diagonal elements from each subject’s restFC matrix (264 × 264 regionwise connections), as estimated via the optimized regression approach described above. Features were first z-scored within subjects. Given the high dimensionality of restFC (69,432 connections), we performed a feature selection step at the start of each training/testing loop to remove outlier connections (i.e. features contributing noise to the classification of AD group status; Thung et al., 2018). Consistent with statistical outlier identification approaches, noisy connections were identified from the z-scored standard deviations of each connection across training set subjects (i.e. connections with z-score standard deviation > 4.5 were removed). The held-out test subjects were excluded from this step to prevent circularity. Note that the pattern of classification results was highly similar when varying this z-score threshold hyperparameter at > 4 or > 5. After feature selection, at-risk and healthy group restFC templates were computed by averaging features for each group separately (again, excluding the held-out test subjects). Pearson correlation was used as a distance metric to assess the similarity between the test subjects and both templates, with binary classification decisions set by comparing whether the test subjects’ restFC was more similar to the unhealthy group (yielding an ‘unhealthy’ classification) or healthy group (‘healthy’ classification) template. Decisions were averaged across test subjects to estimate classification accuracy.
The approach to the machine learning classification using task activations was almost identical to the restFC classification. Given the low dimensionality of the regional activations, we used all 264 activation features without performing feature selection. Separate classifications were performed for the two fMRI tasks, as well as after averaging activations across the two tasks for each subject to promote ‘task general’ activation features.
In all cases, significance of the classification accuracies was assessed by a permutation testing approach, wherein the observed accuracy for a given classifier was compared to a permuted null distribution of classification accuracies generated from scrambled group labels (over n = 1000). P values were generated as the proportion of permuted accuracies that exceeded the observed ones (alpha = 0.05). This permutation testing approach ensured that significantly above-chance classification performance was not driven by random noise in the sample, increasing confidence that the groups meaningfully differed in terms of their restFC and activation patterns. Note that the pattern of classification accuracies was identical when using binomial tests against 50% chance.
2.7. Activity flow mapping approach
Fig. 1b provides an abstract depiction of our activity flow mapping approach that predicted task activations in at-risk AD subjects. Fig. 3c provides a more practical guide to implementing the procedure, which can also be formalized as a matrix equation:
where i and j index source (predictor) and target (to-be-predicted) regions respectively, Pj is the predicted task activation for an at-risk subject at a target j, Ai is the healthy group activation for the same task (the average over GLM betas estimated for the healthy subjects) at a source i, and Fij is the restFC between i and j. Hence, for an at-risk subject, task activations in target regions j were predicted by the dot product of two vectors (both of length n regions - 1): the healthy group activation in the sources i (which excludes j) and the at-risk subject’s restFC between j and i. To clarify, the Fij vector is taken from the subject’s full restFC matrix estimated via the PCA multiple regression approach (described in Section 2.5), which excludes self-connections on the diagonal and is oriented appropriately to capture the influence of sources i predicting the resting-state timeseries of the target j (rather than vice versa, given the asymmetry of the regression-based restFC matrix). The restFC estimates thus weight the ability for activity to flow between regions, as indicated by the variable width of the red lines in Fig. 1b. Iterating through all target brain regions populated a predicted task activation vector for each at-risk AD subject (see Fig. 3c). The accuracy of the activity flow predictions was then assessed by computing the overlap (Pearson correlation) between the predicted task activation vector and the actual activation vector. This was done both after averaging predicted and actual activations across subjects (group-level overlap) and for each subject’s individual vectors (subject-level overlap).
Statistical significance of the prediction accuracy was assessed in both parametric and non-parametric fashion. For parametric statistics, the significance of the group-level overlap was indexed by the p value accompanying the Pearson correlation. The subject-level significance was assessed in a random effects approach, with the overlap r values for each subject transformed to Fisher-z values and submitted to a one-sample t-test against 0. We also conducted non-parametric permutation tests to: i) demonstrate the importance of region-to-region correspondence between the healthy group activation and at-risk subject restFC terms to the prediction accuracy, and ii) deal with any violation of the independence assumption in the parametric statistics. The latter is a possibility given that each region’s activation prediction is made on the basis of dot product operations between task activation and restFC terms, which involve overlapping regions that could introduce dependency. Hence for 1000 permutations, the group healthy activation term and the rows of each at-risk subject’s restFC matrix were shuffled. Activity flow predictions were then computed from the dot product of these shuffled terms as described above, ultimately generating permuted group-level and subject-level overlap r values. Significance was assessed by calculating the proportion of permuted r values that were higher than the observed values (group- and subject-level), at an alpha threshold of 0.05.
Activity flow mapping was applied separately for each task and at-risk AD group segregation type (APOE and amyloid; see Table 1). The procedure was virtually identical for both the regionwise and voxelwise analyses (i.e. replace ‘region’ with ‘voxel’ in the matrix equation above). For the voxelwise analyses, accompanying the exclusion of nearby voxels from the restFC estimation for a given voxel (see Section 2.5), we also excluded the same set of source voxels from the group healthy activation vector when computing the activity flow prediction for that target voxel. Combined with use of non-Gaussian smoothing, this step prevented inflation of activity flow predictions by fMRI BOLD spatial autocorrelation amongst proximal voxels.
We also applied a ‘two-cycle’ variant of this general approach, wherein the predicted at-risk task activations obtained from the standard ‘one-cycle’ approach described above were multiplied by subjects’ restFC a second time (see Supplementary Information section 1.4 and Figure S3). This was theoretically motivated to enhance the ability for activity flow mapping to transform the healthy activation state to an at-risk AD (unhealthy) activation state (see Fig. 1a), and hence improve the prediction accuracy.
To clarify, the task activation term for this activity flow model is taken from the healthy group, whereas the restFC term is taken from each to-be-predicted at-risk AD subject (see Fig. 1b and Fig. 3c). This represents a modification to the original activity flow mapping approach (Cole et al., 2016), wherein both activation and restFC terms were taken from the to-be-predicted subject. This modification permits application of the procedure in cases where task fMRI data is unavailable or difficult to acquire for a given subject, which raises clinical utility. The fact that the activation and FC terms are derived from separate subjects (as well as separate task/rest sessions) also avoids any direct correspondence of the first-order activation and second-order FC moments.
2.8. Activity flow prediction of dysfunctional activations: regressing-out approach
The previous section describes our approach to using activity flow mapping to predict task activations in at-risk subjects. We also extended the approach to more directly model AD dysfunction i.e. task activation differences between the at-risk and healthy groups. To achieve this, we used a regression approach in which we took the activity flow-predicted activations for each at-risk subject, and regressed out the group healthy task activation from each one (see flowchart Fig. 2, and commented analysis code provided via Section 2.11). After this operation, the residual activation vector reflects differences between the healthy group and that at-risk subject (scaled by the constant in the regression). We also regressed out the group healthy activation from the actual activation for the same at-risk subject. This enabled comparison (via Pearson correlation) of the overlap between the predicted and actual dysfunctional activation vectors. Statistical significance of the overlap was assessed by both parametric and non-parametric (permutation) tests, applied to the group-level and subject-level overlap. This approach was repeated for both the regionwise and voxelwise data (again, excluding nearby voxels from the activation and restFC terms that generate the voxelwise predictions).
The permutation test approach was similar to that described in the previous section: scrambled group healthy activation and subject at-risk restFC vectors were generated for each to-be-predicted at-risk subject. Activity flow was then computed from these terms, with the same unscrambled group healthy activation vector regressed out of the predicted and actual activations prior to computing their overlap at both the group level (after averaging activations across subjects) and the subject level (for each individual subject). This generated a permuted distribution of activity flow mapping prediction overlap (over 1000 permutations), to which the observed group-/subject-level overlap was compared at an alpha threshold of 0.05.
2.9. Activity flow prediction of dysfunctional activations: contrast image approach
As an alternative method of predicting dysfunctional task activations (to the regressing-out approach described in Section 2.8), we used activity flow mapping to generate a predicted between-group contrast image that captured activation differences between the at-risk and healthy groups (see flowchart Fig. 2). We focused on the voxelwise data for this analysis as this spatial scale provides the most visually interpretable results, and as this is typically the scale at which between-group contrast images are analyzed in fMRI research. The actual healthy task activations and the predicted at-risk activations were firstly z-scored (within subjects) to more clearly recover the activation patterns. The average of the healthy activations was then subtracted from the average of the predicted at-risk activations. The resulting ‘predicted contrast image’ directly indexed how activations at each brain voxel differed in the at-risk relative to the healthy group. This predicted contrast image was correlated with the ‘actual contrast image’ (the averaged actual at-risk activation minus the averaged healthy activation) to assess how accurately task activation dysfunction was captured.
To correct for any inflation of the contrast image overlap induced by subtracting the same vector (healthy group activation) from two other vectors (predicted and actual at-risk group activations) that are subsequently correlated, we used a non-parametric permutation approach to generate a more appropriate null than overlap r = 0. Over 1000 permutations, we generated activity flow-predicted task activations based on scrambled group-averaged healthy activation and scrambled at-risk subject restFC terms (as per the permutation tests described in previous sections). From the resulting scrambled predicted group at-risk activation, we subtracted the unscrambled group healthy activation. This permuted predicted contrast image was correlated with the observed (unscrambled) actual contrast image. Significance of the observed overlap values was assessed against this permuted null distribution at an alpha threshold of 0.05.
We also conducted a thresholded version of the voxelwise contrast image analyses. A 2-sample t-test contrasting the actual at-risk activations versus the actual healthy activations was used to identify the most highly dysfunctional voxels in the actual data. A ‘predicted’ version of this 2-sample t-test was also computed by contrasting predicted at-risk activations versus the healthy activations. Prediction overlap was assessed by correlating the actual at-risk t-statistic vector with the predicted t-statistic vector, after confining to the most highly dysfunctional voxels in the actual data (identified by thresholding the actual t-statistic vector at p <.001 uncorrected). Significance was assessed by a non-parametric permutation approach, wherein a null overlap distribution was generated by randomly selecting a matched number of voxels from the predicted t-statistic vector and correlating with the (unscrambled) actual thresholded t-statistic vector over 1000 iterations. Significance of the observed overlap r values was assessed against this null distribution at an alpha level of 0.05.
2.10. Using the activity flow-predicted activations to model individual differences in task behavior
We assessed whether task activations predicted by the activity flow approach were able to accurately model individual differences in task behavior (see flowchart Figs. 2 and 4). To increase the sample size for this analysis (as recommended for individual differences research, Brydges, 2019), we used activity flow mapping to generate predicted task activations for the healthy subjects in analogous fashion to the procedure for at-risk subjects. Specifically, a group activation template was created by averaging the healthy group excluding the to-be-predicted healthy subject, and the dot product was computed between this activation template and that healthy subject’s restFC. The resulting predicted healthy task activations were concatenated with the predicted at-risk task activations to increase the sample size to 101.
Fig. 4.
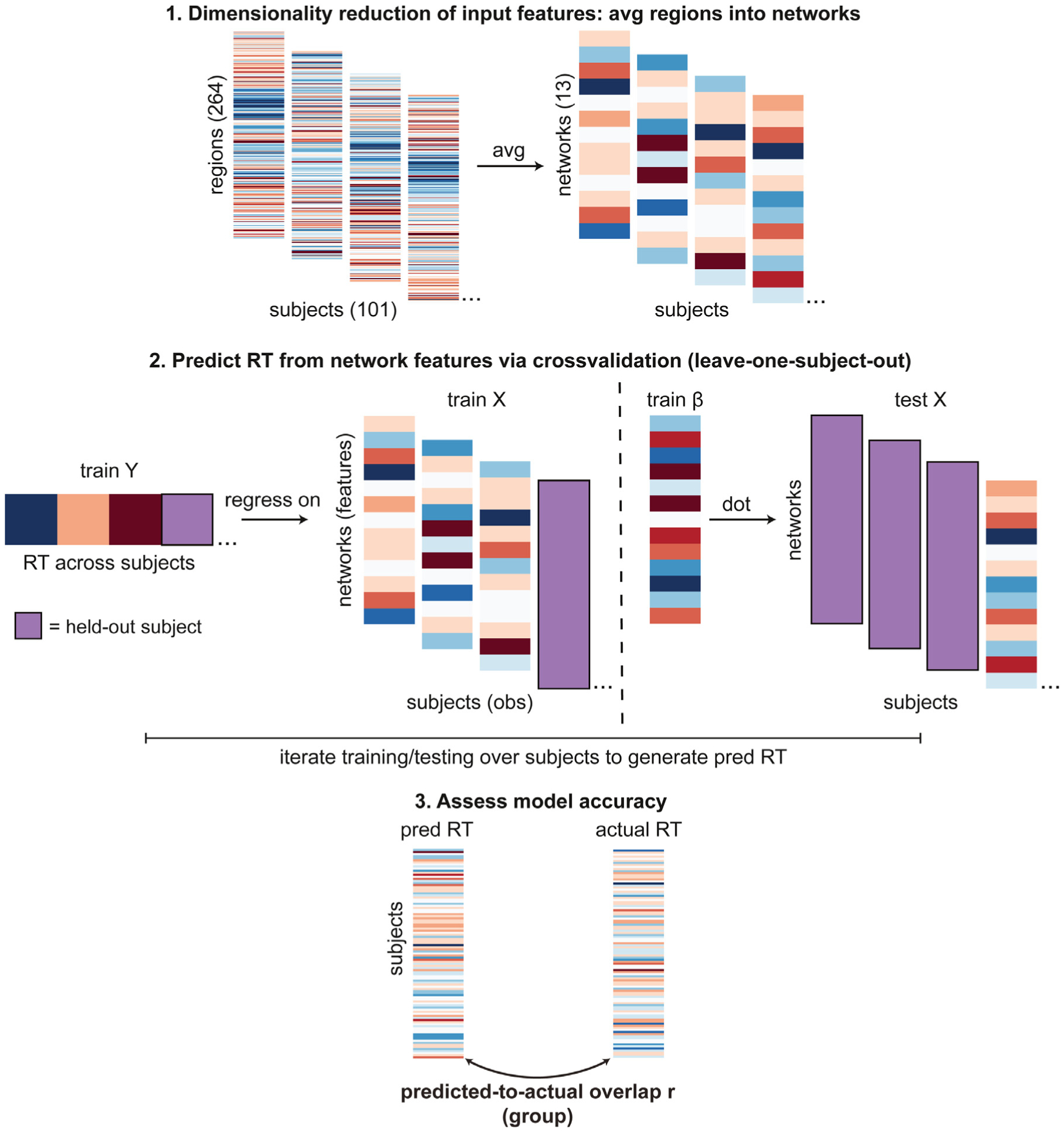
Procedure for modeling individual differences in task behavior (reaction time, RT). Note that this approach was applied for the model of primary interest that used activity flow-predicted task activations as input features, as well as for the alternative models it was compared to (i.e. the actual activation features model, and the ‘raw’ restFC features model; see Methods 2.10 for details). “obs ”= observations, “pred ”= predicted.
We then trained a regression model to predict task behavior from the activity flow-predicted activations (see Fig. 4). We used cross-task reaction time as the behavioral outcome measure for these analyses (see Table 1 for cross-task RT and accuracy information). We began by z-scoring RT across trials for each subject, as recommended previously to account for each subject’s characteristic processing speed (Faust et al., 1999). These z-scored RT values were then averaged across all trials (correct and incorrect) for each subject, for each task separately. To focus the model on prediction of cross-task RT, the first principal component across RT for the two tasks was estimated for a given subject and this was used as their final behavioral outcome measure.
After these preprocessing steps, leave-one-subject-out cross-validation was used for model training. Given that the number of features (264 regional activations) exceeded the number of subjects (100 in each training set), we first performed feature dimensionality reduction by averaging the regional activations according to each region’s network affiliation (determined by the Power functional atlas, Power et al., 2011), yielding 13 network-averaged activation features for each task, for each subject. These dimensionality reduction steps circumvented rank deficiency problems that would arise if the number of features was greater than the number of subjects (i.e. observations). The first principal component across the two task activation vectors was taken for each subject, meaning that cross-task RT (1st component across animacy and stroop tasks, PCA estimated across all 101 subjects) was predicted from cross-task predicted activations (1st component across animacy and Stroop task activations, PCA estimated separately for each subject).
Within each training loop, the activation features and behavioral RT outcomes were z-scored using the means and standard deviations from the training set (to prevent circularity). The RT scores (Y) were then regressed onto the activation features (X) in the training set, with the beta coefficients of the resulting model used to predict the held-out test subject’s RT. Behavioral prediction accuracy was finally quantified as the Pearson correlation between the predicted and actual RT scores, with significance assessed via the accompanying p values (alpha = 0.05 uncorrected). To demonstrate robustness of the approach, separate models were trained across all ways of identifying at-risk subjects: amyloid, APOE, and the concatenation of at-risk subjects across amyloid and APOE.
For comparison, the above regression approach was repeated to generate behavioral predictions using i) the actual task activations as features (network-averaged, as with the predicted activations), and ii) ‘raw’ restFC features that had not been passed through the activity flow model to simulate task activations. For the latter, an analogous feature dimensionality reduction approach to that used for the predicted/actual activations was devised, wherein restFC was averaged across all connections for each individual network. This graph theoretic measure has previously been described as ‘global brain connectivity’ (GBC; Cole et al., 2012) or ‘unthresholded weighted degree centrality’ (Rubinov and Sporns, 2011). In this case, GBC was averaged across regions within each network to yield 13 restFC features in total (identical to the number of features in the activation-based behavior models).
2.11. Data and code availability
Analysis code used in the present report is available from the following public repository: https://github.com/ColeLab/AgingActflow_release. This includes the Matlab functions used for estimation of multiple regression FC (with PCA optimization, Section 2.5), prediction of task activations via activity flow mapping (Section 2.7; which also optionally applies the ‘regressing-out’ dysfunction prediction approach described in Section 2.8), and modeling of individual differences in behavior (Section 2.10). Requests for neuroimaging and clinical data should be submitted to the Knight ADRC (as described here https://knightadrc.wustl.edu/Research/ResourceRequest.htm).
3. Results
3.1. Evidence of at-risk Alzheimer’s-related dysfunction: behavioral
To reiterate our sample’s screening criteria, none of the included subjects met clinical criteria for full Alzheimer’s-related behavioral impairment: Mini Mental State Exam (MMSE) scores were greater than 24, and Clinical Dementia Ratings (CDR) were 0 (negative dementia diagnosis). However, analysis of the MMSE scores revealed that the at-risk group was behaviorally impaired compared to the healthy group, even in this sub-clinical range (see Table 1 for MMSE means and standard deviations across groups). MMSE scores were significantly lower for the at-risk group across both APOE (2-sample t-test healthy > at-risk: t(99) = 2.20, p =.030) and amyloid (t(99) = 2.32, p =.022) segregation types.3 Overall, these results support the presence of sub-clinical Alzheimer’s-related behavioral dysfunction in the at-risk AD subjects, which activity flow mapping attempted to capture.
3.2. Evidence of at-risk Alzheimer’s-related dysfunction: restFC and task activation classifications
To further demonstrate dysfunction in the at-risk versus healthy group, we trained multivariate machine learning classifiers to discriminate between the two groups separately on the basis of regional restFC and regional task activation features. We used a minimum-distance classifier with two distinct forms of cross-validation to demonstrate robustness (see Methods; Poldrack et al., 2019). To increase the sample size for classifier training, these analyses collapsed across at-risk subjects identified in either APOE or amyloid segregation types (yielding at-risk n = 40).
The restFC classifier achieved significantly above-chance accuracy in discriminating between at-risk and healthy groups via k-folds cross-validation (60% mean accuracy; 62.5% sensitivity in classifying ‘at-risk’, 57.5% specificity in classifying ‘healthy’; p =.021 via permutation test, null classification mean = 50.1%). Classifiers trained via k-folds to discriminate based on task activation features yielded above-chance accuracy for the animacy task (68.8% accuracy; 72.5% sensitivity, 65% specificity; p <.001, null mean = 50%) but not the Stroop task (53.8% accuracy; 60% sensitivity, 47.5% specificity; p =.253, null mean = 49.9%). A separate classifier was trained to discriminate on the basis of ‘task general’ activation features identified by averaging across the two tasks for each subject, yielding significantly above-chance accuracy (62.5% accuracy; 65% sensitivity, 60% specificity; p =.005, null mean = 50.1%). Note that the pattern of performance was identical when using a distinct leave-two-subjects-out cross-validation approach: restFC classification mean accuracy = 61.3%, p =.016; animacy task activation accuracy = 66.3%, p <.001; Stroop task activation accuracy = 56.3%, p =.097; task general activation accuracy = 66.3%, p =.002.
Overall, the classification results revealed reliable differences between the at-risk and healthy groups in terms of their restFC and task activations. Taken in isolation, these findings help to address the previously highlighted dearth of machine learning classification/prediction approaches applied to at-risk Alzheimer’s samples versus more commonly studied mild cognitive impairment (MCI) samples (Rathore et al., 2017; Liu et al., 2018). Our results demonstrate statistically reliable between-group classification even at this earlier stage of AD. Considered with the between-group MMSE differences reported above, this validates the presence of meaningful dysfunction in the at-risk AD group. This supports the ensuing analyses of primary interest, in which we apply our theory-driven activity flow mapping approach to model this AD-related dysfunction.
3.3. Activity flow mapping accurately predicts task activation patterns in held-out at-risk AD subjects
Activity flow mapping was firstly applied to predict at-risk AD task activations at the region level (Fig. 5a). For the APOE segregation, the group-level predicted-to-actual activation overlap was significant for both the animacy task (Pearson r = 0.68, p <.00001) and the Stroop task (r = 0.70, p <.00001). Significance was maintained when computing the overlap at the subject level (treating subjects as a random effect, see Methods) for both the animacy task (mean r = 0.24, t(32) = 7.80, p <.00001) and the Stroop task (mean r = 0.18, t(32) = 6.84, p <.00001).4 Visual inspection of the commonalities across the predicted and actual regional vectors (see Fig. 5a) highlights the cross-task recovery of the canonical task-negative deactivation of the default mode network (DMN) and task-positive activation of the cognitive control networks (CCNs; including the frontoparietal control network, FPN, cingulo-opercular network, CON, dorsal and ventral attention networks, DAN and VAN).
Fig. 5.
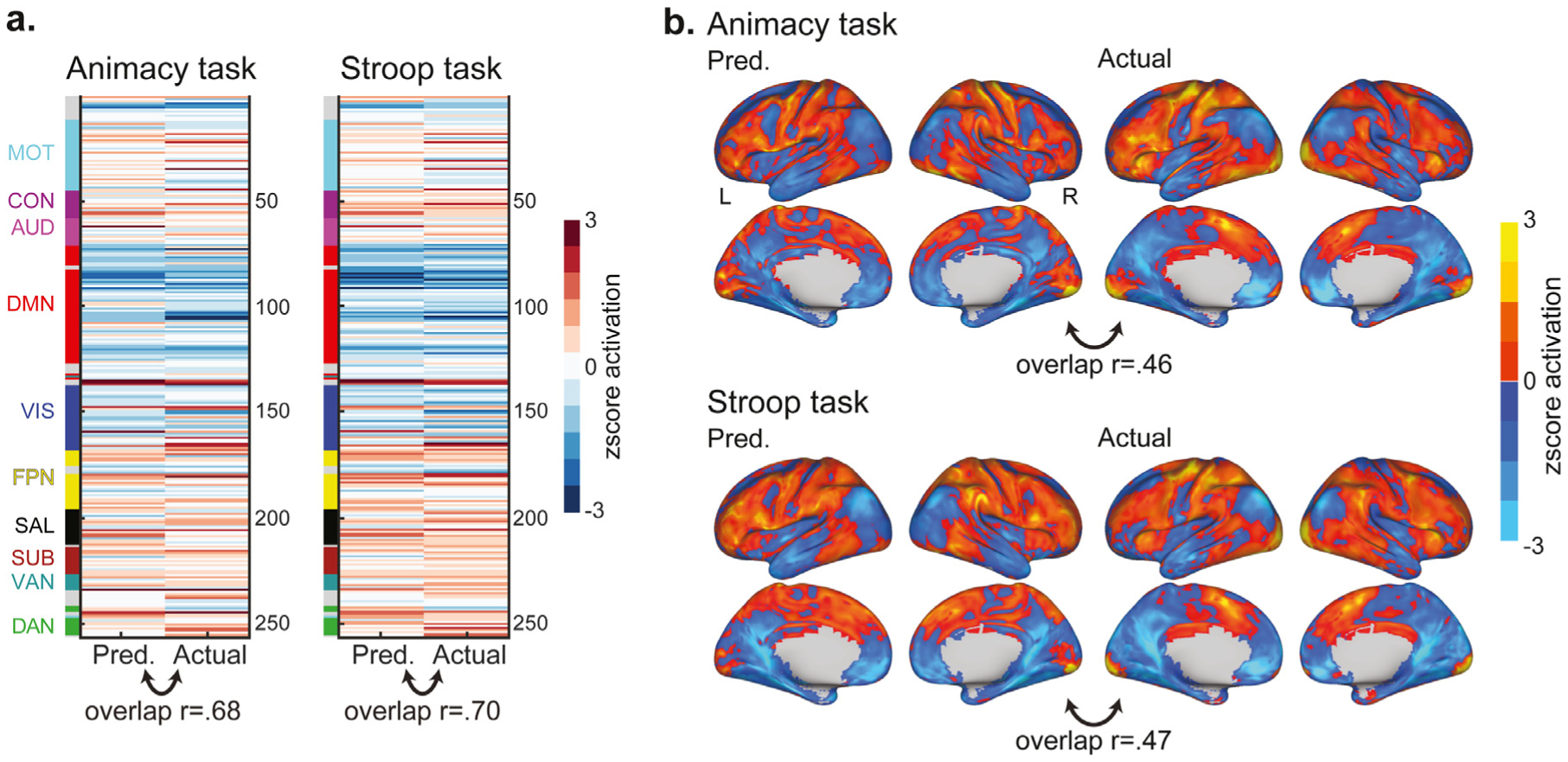
Activity flow mapping results for the prediction of task activations in at-risk AD subjects, as identified by the APOE segregation. a) Group-averaged predicted and actual task activation vectors for the regionwise analysis, and their overlap (Pearson r). Network affiliations for each region from the Power et al. (2011) atlas are provided in the color-coded bar to the left: MOT = motor network, CON = cingulo-opercular network, AUD = auditory network, DMN = default mode network, VIS = visual network, FPN = fronto-parietal control network, SAL = salience network, SUB = subcortical network, VAN = ventral attention network, DAN = dorsal attention network. b) Group-averaged predicted and actual task activation brain maps for the voxelwise analysis, and their overlap (Pearson r). All regionwise and voxelwise activations were z-scored for visualization purposes.
Non-parametric permutation tests were also conducted to demonstrate the importance of region-to-region correspondence between the activation and restFC terms to the activity flow predictions, and deal with any violation of the independence assumption in the parametric tests (see Methods). The pattern of results obtained with this non-parametric approach was identical to that obtained with parametric methods: for the APOE segregation, prediction overlap was significant at both the group level (p <.001 for both tasks) and the subject level (p <.001 for both tasks).
Activity flow mapping was extended to predict task activations at every voxel in the brain (Fig. 5b). To prevent circularity arising from spatial autocorrelation of fMRI data, voxels within the same functional region as the to-be-predicted region were excluded as well as all voxels within a 9 mm radius of that region (see Methods). The overlap between the group-averaged predicted and actual voxelwise activations was significant for both tasks: animacy r = 0.46, p <.00001; Stroop r = 0.47, p <.00001. Significant prediction accuracy was maintained when computing the voxelwise overlap at the subject level (as per the regionwise analyses above): animacy r = 0.13, t(32) = 6.20, p <.00001; Stroop r = 0.09, t(32) = 4.76, p <.0001. We also conducted permutation tests for the voxelwise analyses following the same rationale as the regionwise results. This yielded an identical pattern as the parametric voxelwise results: prediction overlap was significant at both the group level (p <.001 for both tasks) and the subject level (p <.001 for both tasks). Visual inspection of the common activation patterns across the predicted and actual voxelwise brainmaps (see Fig. 5b) again demonstrates cross-task recovery of canonical task negative (DMN regions e.g. bilateral precuneus, posterior cingulate, angular gyrus and ventromedial prefrontal cortex) and task positive (CCN regions e.g. bilateral anterior cingulate, superior frontal gyrus, lateral prefrontal cortex and inferior parietal cortex) activations by the activity flow mapping procedure.
Similarly high prediction accuracy was obtained when activity flow was applied to at-risk AD subjects identified by the amyloid segregation (see Supplementary Information section 1.1). In the Supplementary Information (see section 1.2), we also report a “pairwise network ” variation of the approach that generated task activation predictions from specific networks one at a time, which highlighted prominent involvement of DMN and FPN networks in driving activity flow in these at-risk subjects. Overall, the results demonstrate accurate prediction of task activations in held-out at-risk subjects by activity flow mapping, as estimated at the group and subject level, at regionwise and voxelwise spatial scales, across two distinct cognitive tasks and across two distinct ways of identifying at-risk AD subjects.
3.4. Activity flow over at-risk AD restFC transforms a healthy aged activation state into an unhealthy one
We next sought more direct evidence that activity flow over an at-risk pattern of restFC transforms a healthy activation state into an at-risk one (see Fig. 1a). To clarify, the extent to which the activity flow model makes accurate predictions of at-risk AD activations is determined by how successfully the model transforms the healthy activation template (via at-risk restFC) into the actual at-risk activation (see Fig. 6a). We formally tested this transformation hypothesis by comparing the similarity between each at-risk subject’s predicted activation with i) the group healthy activation versus ii) the actual group at-risk activation. If the similarity of the predicted-to-actual at-risk activation was reliably greater than the similarity of the healthy-to-actual at-risk activation, this would support a mechanistic link between altered restFC and the emergence of dysfunctional task activations. The actual group at-risk activations were averaged after excluding the to-be-compared at-risk subject. The analysis yielded a pair of Pearson r values for each subject (at-risk task similarity r and healthy task similarity r, averaged across the two tasks), which were Fisher-transformed and contrasted via a paired-sample t-test.5
Fig. 6.

Activity flow mapping recovers salient task activation properties in at-risk AD subjects. a) Schematic demonstration of the transformation analysis: operation with at-risk subject restFC transforms a healthy task activation into an at-risk (unhealthy) one. This is formalized as the at-risk predictions having greater similarity with the actual at-risk group template versus the healthy group template. Panels b-d follow a similar approach of computing the Pearson r similarity between the predicted at-risk subject activations with two activation templates (denoted for each analysis by the panel legends), followed by group-level contrasts of the resulting two similarity values (after Fisher-z transform) via paired t-test. All plots represent the mean +/− the standard error of the paired similarity r difference values (the box) and the minimum/maximum (the whisker), with individual data points overlaid (r difference values for each at-risk subject). All panels depict results across the APOE (left plot) and amyloid (right plot) segregation types. Difference r values with boxes above zero suggest recovery of effects in the anticipated direction for each panel. P-values reflect paired t-tests contrasting the similarity r values across conditions (equivalent to one-sample t-tests contrasting the paired difference r values against 0). b) Activity flow mapping transforms healthy into at-risk activations: the similarity between the predicted at-risk activations for each subject was compared with group-averaged templates of the actual at-risk and actual healthy activations. c) Activity flow mapping captures activation patterns that are specific to a given task. Similarity of predicted at-risk activations to actual at-risk activations from the same task was compared to similarity with the actual at-risk activation from the other task (both group templates). d) Activity flow mapping captures activation patterns that are specific to a given subject. Similarity of the predicted activations for a given at-risk subject to the actual activations for that subject was contrasted with similarity to the actual activations for the other at-risk subjects (averaging the r values across these other subjects).
As expected, the predicted at-risk activations were significantly more similar to the actual at-risk group activation than to the actual healthy group activation (Fig. 6b displays the Pearson r difference values). This held for both the APOE segregation (actual at-risk > actual healthy similarity, paired-sample t(32) = 4.74, p <.001) and the amyloid segregation (t(19) = 2.41, p =.026). These results are noteworthy given that the group healthy activation vector is the only activation term the model has access to when predicting at-risk AD subject activations (see Fig. 1b). That the activity flow-predicted activations are actually more similar to the actual at-risk group activation hence provides compelling evidence of the power of restFC alone in transforming healthy into unhealthy activation states. In the Supplementary Information (section 1.4), we demonstrate that this transformation can be further enhanced by implementing two cycles of multiplying the healthy activation template with the at-risk subject’s restFC.
3.5. Activity flow mapping activation predictions are task-specific
To further validate the accuracy of activity flow mapping, we interrogated whether the predicted activations captured features specific to the to-be-predicted task. This property is particularly desirable when applied in clinical contexts, as it enables prediction of brain activations in different tasks designed to isolate different cognitive processes and associated impairment (rather than solely capturing task-general activation patterns).
For each at-risk AD subject, we compared the similarity (Pearson r) of their predicted activations to i) the group actual at-risk activation for the same task versus ii) the similarity to the group actual at-risk activation for the other task. To clarify, to conduct the analysis for the animacy task, we would compute the similarity of the predicted animacy activation for an at-risk subject to the group-averaged actual at-risk animacy activation (same task), and compare this to the similarity to the group-averaged actual at-risk Stroop activation (other task). Both at-risk group activation templates (same task and other task) excluded the at-risk subject from which the predicted activation is taken. This yielded a pair of Pearson r values for each subject (same task similarity r and other task similarity r, each averaged across the two tasks), which were Fisher-transformed and contrasted via paired-sample t-test.
The results reveal that the activity flow-predicted at-risk subject activations were significantly more similar to the actual at-risk group activation for the same task than the other task (Fig. 6c displays the Pearson r difference values). This held for both the APOE segregation (same > other task similarity, paired-sample t(32) = 5.80, p <.001) and the amyloid segregation (t(19) = 5.89, p <.001).
3.6. Activity flow mapping activation predictions are subject-specific
As another demonstration of prediction accuracy and potential clinical utility, we sought evidence that the activity flow-predicted activation for a given at-risk subject was more similar to i) the actual activation for that same subject versus ii) the activation of other at-risk subjects in the sample. For each at-risk AD subject we compared the similarity between their predicted task activation and their actual task activation (same subject similarity) versus the similarity with the actual task activations of all other at-risk subjects (other subject similarity). The similarity r values computed with the other subjects were averaged to yield one ‘other subject’ similarity r value, which was contrasted with the ‘same subject’ similarity r value via paired t-test (after Fisher-z transform).
The results confirmed that the activity flow-predicted task activation for a given at-risk subject was significantly more similar to their own actual activation pattern (Fig. 6d displays the Pearson r difference values): APOE segregation (same > other subject similarity, paired t(32) = 2.85, p =.008), amyloid segregation (t(19) = 3.04, p =.007). This illustrates the ability of the activity flow framework to capture individualized aspects of at-risk AD task activation patterns. This again enhances the framework’s potential clinical utility, given considerable recent biomedical research interest in modeling individual differences to develop personalized medicine interventions (Matthews and Hampshire, 2016). Consistent with the mechanism proposed to underlie our framework, we employed a similar approach to demonstrate the particular utility of subject-specific restFC in generating accurate individualized task activation predictions (see Supplementary Information section 1.3).
3.7. Isolation of dysfunctional task activation predictions by regressing out healthy activations
Thus far, we have demonstrated high accuracy of activity flow mapping when used to predict task activations in at-risk AD subjects. This prediction did not directly characterize how the activation patterns differed between at-risk and healthy subject groups. Demonstrating that activity flow mapping is able to accurately capture such differences is desirable for the aim of modeling dysfunction in AD (and other pathologies). To achieve this, we regressed out the actual group healthy task activation from both the predicted and actual task activations for each at-risk subject (see Methods 2.8 and flowchart Fig. 2). The overlap computed between the predicted and actual residual vectors hence indexed the ability for activity flow to capture differences between the healthy group and that at-risk subject.
For the APOE segregation, group overlap between predicted and actual dysfunctional activations was significant for both the animacy task (Pearson r = 0.35, p <.00001) and the Stroop task (r = 0.32, p <.00001). Significant overlap was maintained when treating the subjects as a random effect, for both the animacy task (mean r = 0.13, p <.00001) and the Stroop task (mean r = 0.07, p =.004).6 As with the main activity flow mapping results (Section 3.3), we also assessed the significance of the ‘dysfunction’ predictions via non-parametric permutation tests (see Methods 2.8). This yielded an identical pattern of results to the parametric statistics: dysfunctional prediction overlap was significant at the group level (p <.001 for both tasks) and the subject level (p <.001 for the animacy task, p =.005 for the Stroop task). The pattern of results was identical for the amyloid segregation type (see Supplementary Information section 1.1).
We also predicted task activation dysfunction at every gray matter voxel in the brain. The voxelwise overlap between predicted and actual dysfunctional activations was significant for both the animacy task (Pearson r = 0.29, p <.00001) and the Stroop task (r = 0.18, p <.00001). Significant overlap was maintained when treating the subjects as a random effect for both the animacy task (mean r = 0.09, p <.00001) and the Stroop task (mean r = 0.07, p <.001). The pattern of significance was identical via non-parametric permutation tests (following the same rationale as the regionwise analyses), for both the group-level (p <.001 for both tasks) and subject-level overlap (p <.001 for both tasks). Overall, these findings support the ability of activity flow mapping to capture activation differences between the at-risk and healthy groups, suggesting utility in modeling AD-related dysfunction.
3.8. Prediction of between-group contrast images also captures task activation dysfunction
The preceding section described our use of activity flow mapping to predict at-risk AD task activations directly linked to clinical dysfunction. As an alternative to the regressing-out approach, we generated between-group contrast images capturing voxelwise task activation differences between the at-risk and healthy subjects (see Methods 2.9 and flowchart Fig. 2). This was done both using the activity flow-predicted at-risk activations (predicted contrast image = group predicted at-risk minus group healthy) and the actual at-risk activations (actual contrast image = group actual at-risk minus group healthy). The predicted-to-actual contrast image overlap was quantified via Pearson correlation as before. A non-parametric permutation approach was used to assess significance whilst controlling for any inflation of the overlap correlation by the subtraction of the group healthy activation (see Methods 2.9).
For the APOE segregation, the overlap between the predicted and actual contrast images was r = 0.39 and r = 0.30 for the animacy and Stroop tasks respectively (see Fig. 7). Both overlap correlations were significant versus the permuted null (p <.001 for both tasks). A thresholded version of these analyses confined the predicted-to-actual contrast image overlap to only those voxels that significantly differed in the actual contrast image map (via 2-sample t-test at p <.001 uncorrected, see Methods 2.9 for details). This also yielded significant overlap: animacy r = 0.53, p <.001 (via non-parametric permutation test, see Methods 2.9); Stroop r = 0.67, p <.001. This demonstrates that activity flow mapping is able to accurately predict the multivariate pattern amongst the most highly dysfunctional voxelwise task activations in the at-risk AD subjects. Overall, the generation of between-group contrast images via activity flow mapping raises another potentially fruitful clinical application by providing visually interpretable activation dysfunction brain maps. However, in the Supplementary Information we report only modest overlap in peak dysfunctional loci identified across the actual and predicted images. This highlights a limitation in a univariate extension of our model that will need to be addressed by future refinements (see Supplementary Information section 1.5 and Figure S4 for more details).
Fig. 7.

Generation of between-group activation contrast images via activity flow mapping. Predicted (left panel) and actual (right panel) contrast images for the animacy task (upper panel) and Stroop task (lower panel) are depicted for the APOE segregation, along with the predicted-to-actual contrast image overlap (both r values p < .001 via permutation test, see Results for details). Activation differences were generated as group averaged predicted/actual at-risk AD minus group averaged healthy, and were z-scored for visualization purposes.
3.9. Activity flow-predicted activations capture individual differences in task behavior
Thus far we have demonstrated the ability of the activity flow model to accurately predict task activations and task activation dysfunction in at-risk AD subjects. Critically, applying the model does not require in-scanner task performance from those individual subjects. We extended the approach by using the activity flow-predicted task activations to model individual differences in behavior (i.e. task reaction time, RT; see Fig. 2). Linking imaging measures to behavior (and behavioral impairment) is increasingly recognized as integral to clinical biomarker development (Rosenberg et al., 2016; Woo et al., 2017).
We first adapted activity flow mapping to generate predicted activations for the healthy subjects (see Methods 2.10 for details), so as to increase our sample size as recommended for individual differences analyses (Brydges, 2019). This yielded accurate predictions of task activations in the healthy group, both for the APOE (animacy group overlap r = 0.65, Stroop group r = 0.71, both p <.00001) and amyloid (animacy group r = 0.66, Stroop group r = 0.72, both p <.00001) segregations.
After concatenating activity-flow predicted activations across the healthy and at-risk groups, we next trained regression models to predict cross-task behavioral RT from cross-task predicted activation features (after averaging regional activations into networks; see Methods Section 2.10 and Fig. 4 for details). The accuracy of the behavioral predictions was assessed by computing the overlap (Pearson r) between the predicted and actual RT scores. Regression models trained on activity-flow predicted activations were able to reliably model behavior and this held across different approaches to segregating at-risk subjects: amyloid overlap r = 0.20 (p =.041), APOE overlap r = 0.19 (p =.055), concatenated (amyloid or APOE) overlap r = 0.21 (p =.038). The results using the predicted activations are comparable (albeit numerically weaker) to those obtained when using the actual activations as features in the regression: actual activation overlap r = 0.31 (p =.002). Notably, when the regression approach was adapted to use the actual restFC information as features (using a network-averaged GBC measure of restFC, see Methods), no reliable prediction of behavioral RT was observed: restFC overlap r = 0.05 (p =.600).
Overall, this demonstrates the utility of the activity flow approach in reliably modeling individual differences in task behavior from subjects’ predicted activations. Again, critically, this link to task behavior was achieved without requiring the model to have access to the subjects’ actual fMRI task activations (rather, only their restFC). This highlights an optimal use-case for applying the activity flow approach in clinical contexts: when actual task fMRI data was not collected for a given subject/s, yet modeling their activations on that task and how they relate to behavior (and associated cognitive deficits) is desired. This raises clinical potential as the absence of fMRI data for a specific task (indeed, often any task) is a common occurrence in clinical datasets, given the need to minimize overall scan time to ensure participant comfort and lower costs. We demonstrate here that modeling of behavioral performance in such cases can be improved when using activity flow-simulated activation features rather than the ‘raw’ restFC features. Note that even though behavioral prediction accuracy was qualitatively similar when using predicted or actual task activation features (in that both surpassed statistical significance thresholds), future refinements of the activity flow approach should target quantitative improvements to reach the higher accuracy of the actual activation model (see Discussion for future directions for activity flow model refinement).
4. Discussion
We report the first extension of the activity flow framework (Cole et al., 2016) to a clinical context: modeling dysfunction in individuals at risk for Alzheimer’s disease. The framework was applied in an elderly sample segregated into at-risk and healthy subgroups based on established AD risk factors (presence of APOE ε4 or high PET amyloid). These group definitions were validated by demonstration of reliable group differences in behavior (MMSE) and reliable multivariate machine learning classifications of group status based on restFC and regional task activations. To model the emergence of this observed dysfunction, activity flow mapping was used to predict activations in held-out at-risk subjects (and held-out brain regions/voxels) from their individual pattern of restFC altering a healthy task activation template. This procedure accurately predicted at-risk AD activations across different cognitive tasks, neural spatial scales, and at-risk segregation types, illustrating its robustness. Follow-up analyses confirmed key mechanistic properties of our framework: healthy activations were transformed by the individual pattern of at-risk restFC alone, and this transformation was improved by a second cycle (see Supplementary Information 1.4). In support of the framework’s clinical utility, activation predictions were statistically reliable at the individual level, and captured task-specific and subject-specific signatures. Activity flow mapping remained accurate when predicting overtly dysfunctional activations (those that differed for at-risk versus healthy subjects), and was extended to reliably model individual differences in task behavior using the predicted task activations.
Our findings have three broad implications. Firstly, the success of activity flow mapping provides empirical evidence for a mechanistic role of restFC in defining the pathways over which activity flows across the brain and, therefore, pathways underlying activity dysfunction. Secondly, our findings highlight the potential of applying activity flow mapping to predict features of AD-related pathology. Thirdly, these results provide theoretical insights that can guide ongoing efforts to optimize the use of restFC to predict/classify disease features more generally.
The first implication relates to much needed insight into the cognitive relevance of restFC, which has been questioned given the experimentally unconstrained nature of rest (Mill et al., 2017). A role for connectivity in driving the emergence of task activations has long been formalized in computational models (Hodgkin and Huxley, 1952), and empirically demonstrated by local circuit neurophysiology linking connectivity to synaptic modulation of action potentials (Laughlin and Sejnowski, 2003; Fries, 2005). A similar role for synaptic connectivity in weighting paths of information propagation across computational ‘layers’ has been a unifying property of neural network simulations of cognitive function (McClelland and Rogers, 2003; Battaglia et al., 2012).Importantly, the success of activity flow mapping suggests restFC as a large-scale analogue of such synaptic processes, corroborating its utility in mapping intrinsic network organization (Raichle, 2010). By extension, incorporating network connectivity is likely central to achieving a full theoretical understanding of how the brain activates during cognitive processing. This goes against the historical isolation of connectivity and task activation studies into separate neuroscientific subfields, and instead promotes their mechanistic unification via activity flow. Future research applying activity flow mapping to more direct measures of neural activity than the fMRI BOLD response (e.g. human electrocorticography or source-modeled electro-/magnetoencephalography) could substantiate this association between restFC and synaptic processes.
Our findings build on previous successful demonstrations of activity flow mapping (Cole et al., 2016; Ito et al., 2017) by extending the approach to a clinical context. Our focus on AD was motivated by its grim prognosis, raising an urgent need to develop imaging biomarkers that can aid early diagnosis and intervention. It was also motivated by the strong evidence base (relative to other disorders; Fox and Grecius, 2010; Woo et al., 2017) characterizing restFC and task activation alterations in at-risk (Hedden et al., 2009; Sheline and Raichle, 2013; Oh et al., 2016) and later stages of AD (Grady, 2012; Ferreira and Busatto, 2013; Campbell and Schacter, 2017). Considered with the accuracy of our restFC-based machine learning classification of at-risk subjects (previously highlighted as an understudied AD group compared to later-emerging MCI samples; Liu et al., 2018), the success of activity flow in the present sample strengthens previous staging models of AD risk factors (Jack et al., 2010;Sheline and Raichle, 2013). These suggest that restFC alterations emerge many years prior to clinical impairment.
Critically, rather than studying restFC alterations separately from task activations, the activity flow framework unifies both measures mechanistically (Fig. 1). The notion that individual variation in task activations is associated with individual variation in restFC has been raised previously (Chan et al., 2017), and we extend this theoretical association towards a formalized computational model that generates accurate task activation predictions in held-out subjects. The model affords a synthesis of the practical benefits of acquiring resting-state data (e.g. reducing overall scanner time, enabling imaging assays for clinical samples unable to perform in-scanner tasks) with clearer theoretical grounding via linking to task activations and associated cognitive function.
The practical benefits of using restFC in the activity flow approach extends to not requiring FC weights in our model to be estimated from task data (i.e. taskFC). Our present use of restFC over taskFC is further motivated by documented methodological issues in separating real taskFC from spurious coactivation effects (Cole et al., 2019), as well as overall modest influences of task states in explaining FC network topology versus larger influences of stable group and individual factors captured by restFC (Gratton et al., 2018; see also Geerligs et al., 2015b). Nevertheless, it remains to be seen whether taskFC when available, and when correctly estimated from task fMRI data of sufficient quality (Gratton et al., 2018), can improve prediction accuracy of the activity flow model.
Future research will also need to clarify the chronology of restFC alterations relative to the emergence of PET amyloid and other AD signatures (e.g. tau deposition; Jones et al., 2016, 2017). Relatedly, recent demonstration that connectivity at an earlier timepoint (5 years of age) predicts the location of fMRI task activations associated with later development of reading ability (assessed at 8 years of age; Saygin et al., 2016), suggests potential to use activity flow to predict task activation dysfunction well in advance of its actual emergence. This would have clear clinical utility, and calls for the extension of the activity flow framework to predict timecourse features of AD (i.e. onset, prognosis). A prerequisite to this endeavor is the furthering of recent attempts (e.g., the Alzheimer’s Disease Neuroimaging Initiative, ADNI) to collect longitudinal data in larger elderly samples spanning the full spectrum of AD-related pathology: healthy aged, at-risk, MCI, and post-AD onset. The latter point is pertinent given recent work highlighting the utility of training predictive models in larger samples to ensure their generalizability (Poldrack et al., 2019). This recommendation is at odds with the present paucity of large AD neuroimaging datasets that also collect sufficient resting-state and multi-task data. Indeed, the present Knight ADRC sample was the largest AD-related sample available to us at project commencement that had both sufficient amounts of resting-state fMRI data and data from multiple tasks (both prerequisites for our analyses). Hence, despite the inherent difficulties in collecting elderly/AD-related samples, improving data collection practices should be prioritized moving forwards.
In interrogating the general utility of activity flow for clinical neuroscience, another promising avenue would be to extend the approach to pathologies beyond AD. Theoretically, activity flow modeling can be applied to any meaningful categorization of unhealthy and healthy subgroups, given that it makes predictions on the basis of the unhealthy subjects’ restFC altering a healthy group activation template. Notably, the mechanistic basis of the activity flow framework (Cole et al., 2016) differentiates it from other more data-driven ‘fingerprinting’ approaches with similar predictive aims (Rosenberg et al., 2016; Saygin et al., 2016; Tavor et al., 2016; Lin et al., 2018). These approaches use abstract coefficients to translate an individual’s connectivity profile into predicted task activations (or behavior), as estimated via intensive optimization/cross-validation during model training. Such abstract data-driven provisions risk a lack of theoretical grounding (‘neuroscientific validity’), which has been highlighted as an obstacle to integrating connectivity-based predictive models into clinical practice (Stephan et al., 2015; Matthews and Hampshire, 2016; Woo et al., 2017). In contrast, the activity flow model assumes that the whole-brain activation state translates a connectivity profile into a task activation, consistent with the proposed mechanism of neural activity (and associated cognitive information) propagating across paths defined by restFC. Another limitation to a reliance on data-driven optimization is the evidenced risk of overfitting to noise in the training set (Onoda et al., 2017; Teipel et al., 2017; Fountain-Zaragoza et al., 2019). Whilst the need to test the generalizability of connectivity-based predictive models across out-of-set samples and scanner sites also applies to activity flow, it is possible that an increased emphasis on neuroscientific theory (e.g. use of the healthy activation template rather than abstract coefficients) will not only ease translation of models to the clinic, but also quantitatively improve their generalizability.
Nevertheless, it is worth highlighting that the reported activity flow results serve more as a proof-of-concept at this stage rather than a ready-to-implement clinical protocol. Future extensions specifically targeting improvement in the individualized (subject-level) prediction accuracy will be necessary to elevate variance explained to clinically useful thresholds. To this end, some of the optimization methods adopted in the more data-driven fingerprinting approaches cited above may be integrated with activity flow mapping (e.g. nested cross-validation of restFC estimation parameters to optimize prediction accuracy). Critically, such optimization is only advocated if it complements the model’s underlying theory. Indeed, the observed improvement in subject-level prediction accuracy with the two-cycle activity flow approach (see Supplementary Information 1.4) highlights potential for future optimization that is theoretically grounded (in this case, by similar transformations operationalized in neural network models). Collecting higher quality fMRI data (e.g. higher spatiotemporal resolution sequences, Smith et al., 2013), longer resting-state scan durations per subject (Gordon et al., 2017) and encompassing multiple scanner sites (Woo et al., 2017), all serve as important data acquisition refinements that may also improve individualized prediction accuracy. Overall, the present findings favor a synergistic approach, wherein the theoretical constraints imposed by the activity flow framework allow for considered optimization of predictive frameworks whilst mitigating the risk of overfitting, potentially enabling better generalization in large out-of-set populations.
In pursuing these extensions of activity flow mapping, it is worth reiterating the practical benefits of the approach: predictions of cognitive task activations (and associated dysfunction) are made without having subjects actually perform in-scanner tasks. The resulting task activation predictions show promise for use in a variety of clinical contexts: to expedite diagnosis, identify targets for stimulation-based intervention (Fox et al., 2014; Reinhart and Nguyen, 2019), and for longitudinal assessment of prognosis/response to intervention (He et al., 2007). The reported preliminary success of activity flow mapping hence provides a theoretical foundation for future developments in the use of restFC as a clinical biomarker, aiding the realization of long-upheld goals of incorporating functional neuroimaging measures in personalized medicine applications.
Supplementary Material
Acknowledgements
The authors acknowledge support by the US National Institutes of Health under awards R01 AG055556 and R01 MH109520 to MWC, awards P50 AG005681 and P01 AG026276 that enabled data collection by the Adult Children Study at the Knight Alzheimer’s Disease Research Center at Washington University in St Louis (Knight ADRC), and the K01 AG053474 awarded to BAG. The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies. The authors would like to thank John C. Morris and Tammie L.S. Benzinger for their involvement in the Knight ADRC project, which facilitated the present report. The authors would also like to thank Jeffrey M. Zacks for helpful feedback. The authors acknowledge the Office of Advanced Research Computing (OARC) at Rutgers, The State University of New Jersey for providing access to the Amarel cluster and associated research computing resources that have contributed to the results reported here.
Footnotes
Declaration of Competing Interest
The authors declare no competing financial interests.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2020.117167.
Note that the final restFC matrix for each subject was computed after concatenating timeseries across both resting-state runs. This step is non-circular, given that the optimization across sessions was performed as a preliminary step to maximize restFC stability for each subject, rather than to directly optimize any analyses that we report inferential statistics for (e.g. the strength of the activity flow mapping predictions).
Note that applying this PCA regression FC approach at the voxel scale was computationally intensive: 32424 gray matter voxels * 2 rest runs * 163 PCA ncomps = 10570224 regressions for the initial optimization process; followed by 32424 gray matter voxels * 1 concatenated rest run * 1 optimal PCA ncomps = 32424 regressions to estimate the final FC matrix; applied to each subject separately. The procedure therefore required parallel computation of individual subjects using a high performance computing cluster.
Note that these between-group MMSE differences were only marginally significant when using the more conservative Wilcoxon ranksum test: z = 1.68, p =.093 (collapsed across segregation types).
Note that the lower subject-level prediction accuracy for the Stroop versus the animacy task was found to be statistically significant (via paired ttest of the fisher-transformed r values): t(32) = 2.39, p =.023. This is consistent with the Stroop activations being less related to AD dysfunction in this cohort, as suggested by the lower accuracy obtained when classifying group status from the actual Stroop activations (see section 3.2).
Note that this corresponds to a random effects (subject RFX) approach to significance assessment that takes subject variance into account. The same approach was employed for the conceptually similar analyses detailed in Sections 3.5 and 3.6.
Note that the lower subject-level accuracy in predicting dysfunctional activations for the Stroop versus the animacy task was found to be statistically significant (via paired ttest of the fisher-transformed r values): t(32) = 2.39, p =.023. Extending the significant cross-task differences in the main activity flow predictions (see footnote Section 3.3), this suggests the Stroop activations were less related to AD dysfunction in this cohort, consistent with the lower accuracy obtained when classifying group status from the actual Stroop activations (see Section 3.2).
References
- Andrews-Hanna JR, Snyder AZ, Vincent JL, Lustig C, Head D, Raichle ME, Buckner RL, 2007. Disruption of large-scale brain systems in advanced aging. Neuron 56, 924–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battaglia D, Witt A, Wolf F, Geisel T, 2012. Dynamic effective connectivity of inter-areal brain circuits Sporns O, ed. PLoS Comput. Biol 8, e1002438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookes MJ, Woolrich M, Luckhoo H, Price D, Hale JR, Stephenson MC, Barnes GR, Smith SM, Morris PG, 2011. Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proc. Natl Acad. Sci 108, 16783–16788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brydges CR, 2019. Effect size guidelines, sample size calculations, and statistical power in gerontology sands LP. Innovation in Aging, 3 Available at: https://academic.oup.com/innovateage/article/doi/10.1093/geroni/igz036/5560156. (Accessed 9 October 2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckholtz JW, Meyer-Lindenberg A, 2012. Psychopathology and the human connectome: toward a transdiagnostic model of risk for mental illness. Neuron 74, 990–1004. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Andrews-Hanna JR, Schacter DL, 2008. The brain’s default network: anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci 1124, 1–38. [DOI] [PubMed] [Google Scholar]
- Campbell KL, Schacter DL, 2017. Ageing and the resting state: is cognition obsolete? Lang. Cognit. Neurosci 32, 661–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan MY, Alhazmi FH, Park DC, Savalia NK, Wig GS, 2017. Resting-state network topology differentiates task signals across the adult life span. J. Neurosci. Off. J. Soc. Neurosci 37, 2734–2745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Ito T, Bassett DS, Schultz DH (2016) Activity flow over resting-state networks shapes cognitive task activations. Available at: http://biorxiv.org/lookup/doi/10.1101/055194 [Accessed August 28, 2016]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Ito T, Schultz D, Mill R, Chen R, Cocuzza C, 2019. Task activations produce spurious but systematic inflation of task functional connectivity estimates. Neuroimage 189, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Yarkoni T, Repovs G, Anticevic A, Braver TS, 2012. Global connectivity of prefrontal cortex predicts cognitive control and intelligence. J. Neurosci 32, 8988–8999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diedrichsen J, Kriegeskorte N, 2017. Representational models: A common framework for understanding encoding, pattern-component, and representational-similarity analysis Cichy R, ed. PLoS Comput. Biol 13, e1005508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NUF, Nardos B, Cohen AL, Fair DA, Power JD, Church JA, Nelson SM, Wig GS, Vogel AC, Lessov-Schlaggar CN, Barnes KA, Dubis JW, Feczko E, Coalson RS, Pruett JR, Barch DM, Petersen SE, Schlaggar BL, 2010. Prediction of individual brain maturity using fMRI. Science 329, 1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Y, Fu Z, Calhoun VD, 2018. Classification and prediction of brain disorders using functional connectivity: promising but challenging. Front. Neurosci 12, 525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust ME, Balota DA, Spieler DH, Ferraro FR, 1999. Individual differences in information-processing rate and amount: implications for group differences in response latency. Psychol. Bull 125, 777–799. [DOI] [PubMed] [Google Scholar]
- Ferreira LK, Busatto GF, 2013. Resting-state functional connectivity in normal brain aging. Neurosci. Biobehav. Rev 37, 384–400. [DOI] [PubMed] [Google Scholar]
- Ferreira LK, Regina ACB, Kovacevic N, Martin M.da G.M., Santos PP, Carneiro C, de G, Kerr DS, Amaro E, McIntosh AR, Busatto GF, 2016. Aging effects on whole-brain functional connectivity in adults free of cognitive and psychiatric disorders. Cereb. Cortex 26, 3851–3865. [DOI] [PubMed] [Google Scholar]
- Fischl B, 2004. Automatically parcellating the human cerebral cortex. Cereb. Cortex 14, 11–22. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR, 1975. “Mini-mental status ”. A practical method for grading the cognitive state of patients for the clinician. J. Psychiatr. Res 12, 189–198. [DOI] [PubMed] [Google Scholar]
- Fountain-Zaragoza S, Samimy S, Rosenberg MD, Prakash RS, 2019. Connectome-based models predict attentional control in aging adults. Neuroimage 186, 1–13. [DOI] [PubMed] [Google Scholar]
- Fox MD, Buckner RL, Liu H, Chakravarty MM, Lozano AM, Pascual-Leone A, 2014. Resting-state networks link invasive and noninvasive brain stimulation across diverse psychiatric and neurological diseases. Proc. Natl. Acad. Sci. U. S. A 111, E4367–E4375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Grecius M, 2010. Clinical applications of resting state functional connectivity. Front. Syst. Neurosci Available at: http://journal.frontiersin.org/article/10.3389/fnsys.2010.00019/abstract. (Accessed 24 April 2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, 2005. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cognit. Sci 9, 474–480. [DOI] [PubMed] [Google Scholar]
- Geerligs L, Renken RJ, Saliasi E, Maurits NM, Lorist MM, 2015a. A brain-wide study of age-related changes in functional connectivity. Cereb. Cortex 25, 1987–1999. [DOI] [PubMed] [Google Scholar]
- Geerligs L, Rubinov M, Cam-CAN HRN, 2015b. State and trait components of functional connectivity: individual differences vary with mental state. J. Neurosci 35, 13949–13961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon BA, Zacks JM, Blazey T, Benzinger TLS, Morris JC, Fagan AM, Holtzman DM, Balota DA, 2015. Task-evoked fMRI changes in attention networks are associated with preclinical Alzheimer’s disease biomarkers. Neurobiol. Aging 36, 1771–1779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, et al. , 2017. Precision functional mapping of individual human brains. Neuron 95, 791–807 e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE, 2016. Generation and evaluation of a cortical area parcellation from resting-state correlations. Cereb. Cortex 26, 288–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grady C, 2012. The cognitive neuroscience of ageing. Nat. Rev. Neurosci 13, 491–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton C, Laumann TO, Nielsen AN, Greene DJ, Gordon EM, Gilmore AW, Nelson SM, Coalson RS, Snyder AZ, Schlaggar BL, Dosenbach NUF, Petersen SE, 2018. Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation. Neuron 98, 439–452 e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He BJ, Snyder AZ, Vincent JL, Epstein A, Shulman GL, Corbetta M, 2007. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficits in spatial neglect. Neuron 53, 905–918. [DOI] [PubMed] [Google Scholar]
- Hebart MN, Baker CI, 2018. Deconstructing multivariate decoding for the study of brain function. Neuroimage 180, 4–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedden T, Van Dijk KRA, Becker JA, Mehta A, Sperling RA, Johnson KA, Buckner RL, 2009. Disruption of functional connectivity in clinically normal older adults harboring amyloid burden. J. Neurosci 29, 12686–12694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF, 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol 117, 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgson K, Poldrack RA, Curran JE, Knowles EE, Mathias S, Göring HHH, Yao N, Olvera RL, Fox PT, Almasy L, Duggirala R, Barch DM, Blangero J, Glahn DC, 2017. Shared Genetic Factors Influence Head Motion During MRI and Body Mass Index. Cereb Cortex N Y N 27, 5539–5546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito T, Kulkarni KR, Schultz DH, Mill RD, Chen RH, Solomyak LI, Cole MW, 2017. Cognitive task information is transferred between brain regions via resting-state network topology. Nat. Commun 8 Available at: http://www.nature.com/articles/s41467-017-01000-w (Accessed 4 November 2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Knopman DS, Jagust WJ, Shaw LM, Aisen PS, Weiner MW, Petersen RC, Trojanowski JQ, 2010. Hypothetical model of dynamic biomarkers of the Alzheimer’s pathological cascade. Lancet Neurol. 9, 119–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Wiste HJ, Weigand SD, Therneau TM, Lowe VJ, Knopman DS, Gunter JL, Senjem ML, Jones DT, Kantarci K, Machulda MM, Mielke MM, Roberts RO, Vemuri P, Reyes DA, Petersen RC, 2017. Defining imaging biomarker cut points for brain aging and Alzheimer’s disease. Alzheimers Dement 13, 205–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji JL, Spronk M, Kulkarni K, Repovš G, Anticevic A, Cole MW, 2019. Mapping the human brain’s cortical-subcortical functional network organization. Neuroimage 185, 35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Graff-Radford J, Lowe VJ, Wiste HJ, Gunter JL, Senjem ML, Botha H, Kantarci K, Boeve BF, Knopman DS, Petersen RC, Jack CR, 2017. Tau, amyloid, and cascading network failure across the Alzheimer’s disease spectrum. Cortex 97, 143–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Knopman DS, Gunter JL, Graff-Radford J, Vemuri P, Boeve BF, Petersen RC, Weiner MW, Jack CR, 2016. Cascading network failure across the Alzheimer’s disease spectrum. Brain 139, 547–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Mur M, Bandettini P, 2008. Representational similarity analysis - connecting the branches of systems neuroscience. Front. Syst. Neurosci 2, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucyi A, Schrouff J, Bickel S, Foster BL, Shine JM, Parvizi J, 2018. Intracranial electrophysiology reveals reproducible intrinsic functional connectivity within human brain networks. J. Neurosci 38, 4230–4242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laughlin SB, Sejnowski TJ, 2003. Communication in neuronal networks. Science 301, 1870–1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumann TO, Snyder AZ, Mitra A, Gordon EM, Gratton C, Adeyemo B, Gilmore AW, Nelson SM, Berg JJ, Greene DJ, McCarthy JE, Tagliazucchi E, Laufs H, Schlaggar BL, Dosenbach NUF, Petersen SE, 2016. On the Stability of BOLD fMRI Correlations. Cereb. Cortex Available at: http://cercor.oxfordjournals.org/cgi/doi/10.1093/cercor/bhw265 (Accessed 26 January 2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Q, Rosenberg MD, Yoo K, Hsu TW, O’Connell TP, Chun MM, 2018. Resting-state functional connectivity predicts cognitive impairment related to Alzheimer’s disease. Front. Aging Neurosci 10, 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Chen K, Wu T, Weidman D, Lure F, Li J, 2018. Use of multimodality imaging and artificial intelligence for diagnosis and prognosis of early stages of Alzheimer’s disease. Transl. Res 194, 56–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PM, Hampshire A, 2016. Clinical concepts emerging from fMRI functional connectomics. Neuron 91, 511–528. [DOI] [PubMed] [Google Scholar]
- McClelland JL, Rogers TT, 2003. The parallel distributed processing approach to semantic cognition. Nat. Rev. Neurosci 4, 310–322. [DOI] [PubMed] [Google Scholar]
- Mill RD, Ito T, Cole MW, 2017. From connectome to cognition: The search for mechanism in human functional brain networks. Neuroimage 160, 124–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris JC, 1993. The clinical dementia rating (CDR): current version and scoring rules. Neurology 43, 2412–2414. [DOI] [PubMed] [Google Scholar]
- Mur M, Bandettini PA, Kriegeskorte N, 2009. Revealing representational content with pattern-information fMRI–an introductory guide. Soc. Cognit. Affect. Neurosci 4, 101–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh H, Steffener J, Razlighi QR, Habeck C, Stern Y, 2016. β-Amyloid deposition is associated with decreased right prefrontal activation during task switching among cognitively normal elderly. J. Neurosci. Off. J. Soc. Neurosci 36, 1962–1970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onoda K, Yada N, Ozasa K, Hara S, Yamamoto Y, Kitagaki H, Yamaguchi S, for the Alzheimer’s Disease Neuroim, 2017. Can a resting-state functional connectivity index identify patients with Alzheimer’s disease and mild cognitive impairment across multiple sites? Brain Connect. 7, 391–400. [DOI] [PubMed] [Google Scholar]
- Petersen SE, Sporns O, 2015. Brain networks and cognitive architectures. Neuron 88, 207–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Huckins G, Varoquaux G, 2019. Establishment of best practices for evidence for prediction: a review. JAMA Psychiatry Available at: https://jamanetwork.com/journals/jamapsychiatry/fullarticle/2756204 (Accessed 9 February 2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE, 2012. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59, 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE, 2011. Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, 2010. Two views of brain function. Trends Cognit. Sci 14, 180–190. [DOI] [PubMed] [Google Scholar]
- Rathore S, Habes M, Iftikhar MA, Shacklett A, Davatzikos C, 2017. A review on neuroimaging-based classification studies and associated feature extraction methods for Alzheimer’s disease and its prodromal stages. Neuroimage 155, 530–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhart RMG, Nguyen JA, 2019. Working memory revived in older adults by synchronizing rhythmic brain circuits. Nat. Neurosci 22, 820–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg MD, Finn ES, Scheinost D, Papademetris X, Shen X, Constable RT, Chun MM, 2016. A neuromarker of sustained attention from whole-brain functional connectivity. Nat. Neurosci 19, 165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset OG, Collins DL, Rahmim A, Wong DF, 2008. Design and implementation of an automated partial volume correction in PET: application to dopamine receptor quantification in the normal human striatum. J. Nucl. Med 49, 1097–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O, 2011. Weight-conserving characterization of complex functional brain networks. Neuroimage 56, 2068–2079. [DOI] [PubMed] [Google Scholar]
- Saygin ZM, Osher DE, Norton ES, Youssoufian DA, Beach SD, Feather J, Gaab N, Gabrieli JDE, Kanwisher N, 2016. Connectivity precedes function in the development of the visual word form area. Nat. Neurosci 19, 1250–1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz AP, Chhatwal JP, Hedden T, Mormino EC, Hanseeuw BJ, Sepulcre J, Huijbers W, LaPoint M, Buckley RF, Johnson KA, Sperling RA, 2017. Phases of hyperconnectivity and hypoconnectivity in the default mode and salience networks track with amyloid and tau in clinically normal individuals. J. Neurosci 37, 4323–4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheline YI, Morris JC, Snyder AZ, Price JL, Yan Z, D’Angelo G, Liu C, Dixit S, Benzinger T, Fagan A, Goate A, Mintun MA, 2010. APOE4 allele disrupts resting state fMRI connectivity in the absence of amyloid plaques or decreased CSF A 42. J. Neurosci 30, 17035–17040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheline YI, Raichle ME, 2013. Resting state functional connectivity in preclinical Alzheimer’s disease. Biol. Psychiatry 74, 340–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JS, Mitra A, Laumann TO, Seitzman BA, Raichle M, Corbetta M, Snyder AZ, 2017. Data Quality Influences Observed Links Between Functional Connectivity and Behavior. Cereb Cortex 27, 4492–4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, et al. , 2013. Resting-state fMRI in the human connectome project. Neuroimage 80, 144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorg C, Riedl V, Muhlau M, Calhoun VD, Eichele T, Laer L, Drzezga A, Forstl H, Kurz A, Zimmer C, Wohlschlager AM, 2007. Selective changes of resting-state networks in individuals at risk for Alzheimer’s disease. Proc. Natl Acad. Sci 104, 18760–18765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling RA, et al. , 2011. Toward defining the preclinical stages of Alzheimer’s disease: recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimers Dement. J. Alzheimers Assoc 7, 280–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spronk M, Kulkarni K, Ji JL, Keane B, Anticevic A, Cole MW (2018) A whole-brain and cross-diagnostic perspective on functional brain network dysfunction. Available at: http://biorxiv.org/lookup/doi/10.1101/326728 [Accessed 4 November 2018]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafford JM, Jarrett BR, Miranda-Dominguez O, Mills BD, Cain N, Mihalas S, Lahvis GP, Lattal KM, Mitchell SH, David SV, Fryer JD, Nigg JT, Fair DA, 2014. Large-scale topology and the default mode network in the mouse connectome. Proc. Natl Acad. Sci 111, 18745–18750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan KE, Iglesias S, Heinzle J, Diaconescu AO, 2015. Translational perspectives for computational neuroimaging. Neuron 87, 716–732. [DOI] [PubMed] [Google Scholar]
- Su Y, et al. , 2015. Partial volume correction in quantitative amyloid imaging. Neuroimage 107, 55–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Y, D’Angelo GM, Vlassenko AG, Zhou G, Snyder AZ, Marcus DS, Blazey TM, Christensen JJ, Vora S, Morris JC, Mintun MA, Benzinger TLS, 2013. Quantitative Analysis of PiB-PET with FreeSurfer ROIs Chen K, ed. PLoS One 8, e73377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavor I, Jones OP, Mars RB, Smith SM, Behrens TE, Jbabdi S, 2016. Task-free MRI predicts individual differences in brain activity during task performance. Science 352, 216–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teipel SJ, Wohlert A, Metzger C, Grimmer T, Sorg C, Ewers M, Meisenzahl E, Klöppel S, Borchardt V, Grothe MJ, Walter M, Dyrba M, 2017. Multicenter stability of resting state fMRI in the detection of Alzheimer’s disease and amnestic MCI. NeuroImage Clin. 14, 183–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung K-H, Yap P-T, Adeli E, Lee S-W, Shen D, 2018. Conversion and time-to–conversion predictions of mild cognitive impairment using low-rank affinity pursuit denoising and matrix completion. Med. Image Anal 45, 68–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlassenko AG, Gordon BA, Goyal MS, Su Y, Blazey TM, Durbin TJ, Couture LE, Christensen JJ, Jafri H, Morris JC, Raichle ME, Benzinger TL-S, 2018. Aerobic glycolysis and tau deposition in preclinical Alzheimer’s disease. Neurobiol. Aging 67, 95–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Chen LM, Négyessy L, Friedman RM, Mishra A, Gore JC, Roe AW, 2013. The relationship of anatomical and functional connectivity to resting-state connectivity in primate somatosensory cortex. Neuron 78, 1116–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo C−W, Chang LJ, Lindquist MA, Wager TD, 2017. Building better biomarkers: brain models in translational neuroimaging. Nat. Neurosci 20, 365–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich MW, Ripley BD, Brady M, Smith SM, 2001. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage 14, 1370–1386. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Analysis code used in the present report is available from the following public repository: https://github.com/ColeLab/AgingActflow_release. This includes the Matlab functions used for estimation of multiple regression FC (with PCA optimization, Section 2.5), prediction of task activations via activity flow mapping (Section 2.7; which also optionally applies the ‘regressing-out’ dysfunction prediction approach described in Section 2.8), and modeling of individual differences in behavior (Section 2.10). Requests for neuroimaging and clinical data should be submitted to the Knight ADRC (as described here https://knightadrc.wustl.edu/Research/ResourceRequest.htm).


