Abstract
Aim:
In some situations of radiotherapy treatments requiring application of tissue-equivalent bolus material (e.g., gel bolus), due to material's rigid/semi-rigid nature, undesirable air gaps may occur beneath it because of irregularity of body surface. The purpose of this study was to evaluate the dosimetric parameters such as surface dose (Ds), depth of dose maximum (dmax), and depth dose along central axis derived from the percentage depth dose (PDD) curve of a 6 MV clinical photon beam in the presence of air gaps between the gel bolus and the treatment surface.
Materials and Methods:
A bolus holder was designed to hold the gel bolus sheet to create an air gap between the bolus and the radiation field analyzer's (RFA-300) water surface. PDD curves were taken for field sizes of 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm, and 25 cm × 25 cm, with different thicknesses of gel bolus (0.5, 1.0, and 1.5 cm) and air gap (from 0.0 to 3.0 cm), using a compact ionization chamber (CC13) with RFA-300 keeping 100 cm source-to-surface (water) distance. The dosimetric parameters, for example, “Ds,“ “dmax,“ and difference of PDD (maximum air gap vs. nil air gap), were analyzed from the obtained PDD curves.
Results:
Compared to ideal conditions of full contact of bolus with water surface, it has been found that there is a reduction in “Ds“ ranging from 14.8% to 3.2%, 14.9% to 1.1%, and 12.6% to 0.7% with the increase of field size for 0.5, 1.0, and 1.5 cm thickness of gel boluses, respectively, for maximum air gap. The “dmax“ shows a trend of moving away from the treatment surface, and the maximum shift was observed for smaller field size with thicker bolus and greater air gap. The effect of air gap on PDD is minimal (≤1%) beyond 0.4 cm depth for all bolus thicknesses and field sizes except for 5 cm × 5 cm with 1.5 cm bolus thickness.
Conclusions:
The measured data can be used to predict the probable effect on therapeutic outcome due to the presence of inevitable air gaps between the bolus and the treatment surface.
Keywords: Air gap, bolus, buildup, surface dose
INTRODUCTION
In some clinical radiation oncology treatments involving megavoltage (MV) photon beam, it is important to use tissue-equivalent material (bolus) on treatment surface to enhance the surface dose (Ds) if the tumor or fungating lymph node extends upto the skin.[1] Precise measurement of “Ds“ will provide useful information for clinical use, to prevent superficial and near-surface recurrences (e.g., subcutaneous recurrence of tumor and flap recurrences in postoperative head-and-neck cancer patients) while reducing extreme skin toxicity at the same time.[2,3] Because of the rigid/semi-rigid nature of the bolus and irregularity of body surface of the patient in the treatment region (especially in head-and-neck or chest wall irradiation), inadequate uniform contact with the skin surface may occur during bolus application, which may create small air gaps of the order of a few millimeters below it.[4,5,6] Such air gaps may alter the “Ds“ value, adversely affecting the treatment outcome. The Ds due to bolus-emitted electrons depends on the energy of the photon, presence and dimensions of air gaps, field sizes, and bolus thickness.[7,8,9,10,11] Effect of bolus without air gaps on a Ds is well documented in high-energy photon beams.[12,13]
Apipunyasopon et al.[5] investigated the central axis percentage depth dose (PDD) of 6 MV photon beam in the buildup region and “Ds“ using four different detectors (CC13 ionization chamber, P-type photon semiconductor dosimeter, Markus chamber, and thermoluminescence dosimeter) in Blue Phantom radiation field analyzer (RFA) and compared their results with Monte Carlo simulations.
Khan et al.[7] investigated the influence of air gaps (of 0.0–5.0 cm) on “Ds“ and depth of dose maximum (dmax) in a solid water phantom using Gafchromic® EBT films under 6 MV photon beam for different field sizes using 1.0 cm thickness bolus. Chung et al.[13] used the Markus chamber, metal–oxide–semiconductor field-effect transistor (MOSFET) to analyze the Ds effects in the presence of air gaps (0.2, 0.5, and 1.0 cm thickness) below the bolus (0.5 and 1.0 cm thickness), and detector in oblique photon beam incidence. The dose variations were demonstrated for different field sizes of 6 MV and 15 MV photon beams at 100 cm source-to-surface distance (SSD). Sroka et al.[4] studied the influence of the bolus–surface distance on the dose distribution in the buildup region using Markus chamber with 1.5 cm and 2.5 cm thickness of bolus for 6 MV and 15 MV photon beams, respectively. Sharma and Johnson,[6] investigated the influence of air gap (up to 3.0 cm thickness) under the bolus of thickness 0.5 and 1.0 cm on dose perturbation at skin surface, for different energies of electron beam with various field sizes. Kong and Holloway,[14] investigated the effect on the central axis dose distribution of electron beams with semi-infinite air gap between the gel bolus and the water surface, using a locally fabricated bolus holder that was fitted to the RFA.
As can be inferred from literature survey, not all authors have addressed the issues of field sizes, bolus thickness, and air gaps in a systematic ascending or descending order; in some of these studies, the dimensions of several of these parameters which are of significant practical clinical relevance have not been taken into account at all. Hence, there is a need to examine the effect of air gap under bolus on clinical photon beam dosimetric parameters, under which the data collected can be useful in determining the impact of unavoidable air gaps between bolus and patient, influencing the radiotherapy treatment outcome. Our study aims at seeking a consolidated answer to all these cumulative shortcomings and comes up with a data set that shall be relevant for nearly all common clinical scenarios. The aim of this study is, therefore, to investigate the influence of central axis dosimetric parameters of 6 MV photon beam such as Ds, depth of dmax, and PDD in the presence of air gaps that occurred between the bolus and the treatment surface.
MATERIALS AND METHODS
Subjects of study
To assess the effect on central axis dose parameters by varying air gap between bolus and treatment surface, a series of experimental steps were undertaken in this study. Measurements were performed using two calibrated ionization chambers (Model CC13, from IBA Dosimetry, Germany) as reference and field detectors in RFA (Model RFA-300, IBA Dosimetry GmbH, Schwarzenbruck, Germany) and software (OmniPro-Accept v7, IBA Dosimetry GmbH, Schwarzenbruck, Germany), under 6 MV medical linear accelerator (Model: Compact, Elekta Ltd., Crawley, UK), maintaining source-to-water surface distance as 100 cm. The machine was calibrated to deliver 1 cGy/MU for a field size of 10 cm × 10 cm with a dose rate of 350 MU/min using the calibration conditions stated in the International Atomic Energy Agency dosimetry code of practice (TRS-398).[15] Commercially available Superflab bolus (a flexible tissue-equivalent material made from proprietary synthetic gel, ρ ≅ 1.03 g/cc) sheets of thickness 0.5, 1.0, and 1.5 cm (size 30 cm × 30 cm) were used. An in-house bolus holder with height-adjustable mechanism was designed and fabricated to facilitate measurements with different air gap sizes between the bolus and the water phantom surface which can be fitted on top of the RFA-300. Figure 1 shows the schematic diagram of experimental measurement setup.
Figure 1.
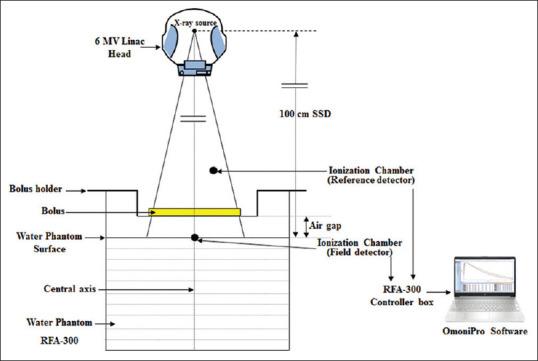
Schematic diagram of the measurement setup
Design and fabrication of bolus holder with height adjustable mechanism
The bolus holder consisted of four major components that included an acrylic plate, acrylic spacers, threaded rods, and wooden bars. The acrylic plate is 0.2 cm thick, with dimension of 35 cm × 35 cm with a cutout of size 25 cm × 25 cm at its center, and is held with the help of 4 threaded rods attached to the wooden frame. A thin transparent Mylar sheet (polyester film or plastic sheet about 100-micron thickness) is fitted around the middle open portion of acrylic sheet to provide stiff support when bolus sheet is placed on top of it. Figure 2 shows the schematic diagram (design) showing the wooden frame assembly. The bolus holder's wooden bars fastened to the water tank ends are to be mounted on top of the RFA-300, holding the acrylic plate with gel bolus. The panel can be raised from the water phantom surface with the help of acrylic spacers placed on top of wooden bars along rods [Figure 2], so that an air gap could be created between the bolus and the water phantom surface. A summary of materials employed in this study are mentioned in Table 1.
Figure 2.
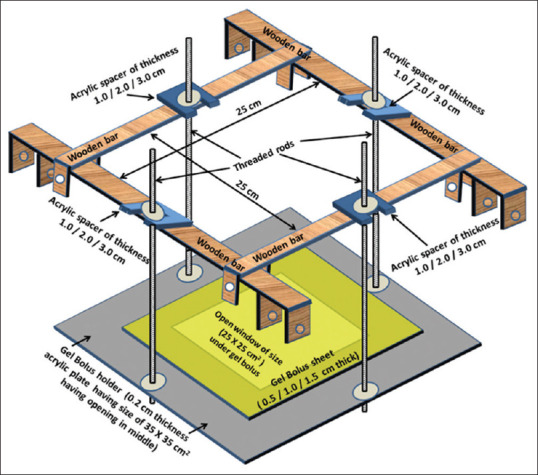
Schematic diagram showing perspective view of wooden frame (with dimensions), to be mounted on top of RFA-300, carrying the acrylic plate (having middle opening) held with threaded rods. Acrylic spacers (of thickness 1.0/2.0/3.0 cm) on top of wooden frame fixed along length of rod provided air gap between the gel bolus and the water surface when gel bolus sheet (of thickness 0.5/1.0/1.5 cm) was placed on top of plate
Table 1.
A summary of materials employed in this study
| Linear accelerator | Elekta compact (# 20177) |
|---|---|
| Photon energy | 6 MV |
| Radiation field analyzer | RFA-300 |
| Detectors | CC13 (Field and Reference) |
| Software | OmniPro v. 7 |
| Gel bolus (Superflab) thicknesses; density | 0.5, 1.0, and 1.5 cm;ρ=1.03gm/cc |
| Field sizes | 5 × 5, 10 × 10, 15 × 15, 20 × 20, and 25 × 25 cm2 |
| Air gap thicknesses | 1.0, 2.0 and 3.0 cm. |
Depth dose measurements with bolus and air gap
Field and reference detectors (CC13) were placed inside RFA-300 with the fabricated bolus holder assembly fixed on top of it, as shown in Figure 3a. With this setup, central axis depth dose measurements were carried out, using OmniPro-Accept software, at a 0.25 cm step increment from the depth of 20 cm to the surface of water phantom for field sizes of 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm, and 25 cm × 25 cm, with no bolus, 0.5, 1.0, and 1.5 cm thicknesses of gel bolus sheets providing an air gap (of thickness 0, 1.0, 2.0, and 3.0 cm) between bolus and water surface. The experimental setup under 6 MV linac (RFA-300 having bolus holder assembly and detectors) is shown in Figure 3b.
Figure 3.

(a) Wooden frame with acrylic plate holding gel bolus sheet fitted on top of RFA-300 with CC13 (field and reference) detectors fixed inside. (b) Experimental setup with RFA-300 having wooden frame under 6 MV linac to determine the influence on dosimetric parameters along the central axis in the presence of air gap between the bolus and the water surface
Depth dose curves were normalized to its maximum readings. Parameters such as Ds, depth of maximum dose (dmax), and dose values till 10 cm depth from the PDD curves were noted. As the measurements were performed with CC13 ionization chamber, to correct for overestimation of Ds (for without bolus condition), a detector correction factor (Ci) is multiplied to the obtained “Ds“ values, as suggested by Apipunyasopon et al.[5] The correction factor “Ci (L)“ is calculated using the empirical relation (Equation 1).
Ci (L) = ai (L)2 + bi (L) + di (1)
where Ci (L) is the correction (labeled by an index “i“) which is a function of the length of square field's side (L) and ai, bi, and di are arbitrary constants which depend on the type of detector. For CC13 ionization chamber, these constants were ai= −0.0002, bi= 0.0198, and di= 0.1091, and the obtained “Ci“ values for the field sizes 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm, and 25 cm × 25 cm were 0.2031, 0.2871, 0.3611, 0.4251, and 0.4791, respectively.
RESULTS
Effect on surface dose for different air gaps, bolus thicknesses, and field sizes
Figure 4 shows the measured PDD curves of 6 MV photon beam for field size (a) 5 cm × 5 cm and (b) 25 cm × 25 cm obtained under no bolus condition and with 0.5 cm, 1.0 cm, and 1.5 cm gel bolus sheets without (0.0 cm) and maximum (3.0 cm) air gap below bolus and water surface of RFA-300.
Figure 4.
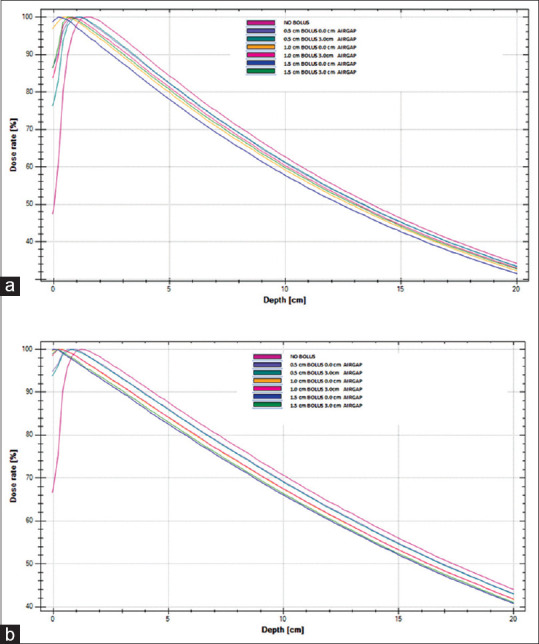
Percentage depth dose curves of 6 MV photon beam for field size (a) 5 cm × 5 cm and (b) 25 cm × 25 cm obtained under no bolus condition and with 0.5 cm, 1.0 cm, and 1.5 cm gel bolus sheets without (0.0 cm) and maximum (3.0 cm) air gap below bolus and water surface of RFA-300
Table 2 illustrates the percentage Ds values without and with the presence of air gaps between different thicknesses of gel bolus and water surface of RFA-300, obtained from central axis PDD curves for different field sizes of 6 MV photon beam. The corrected “Ds“ values (for no bolus and with 0 cm air gap) for field sizes 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm, 20 cm × 20 cm, and 25 cm × 25 cm were 9.9%, 15.6%, 21.6%, 27.2%, and 32.4%, respectively.
Table 2.
Surface dose (Ds) values (%) in the presence of air gaps under different thicknesses of gel bolus and water surface of radiation field analyzer-300, obtained from central axis depth dose curve of 6 MV clinical photon beam for different field sizes
| Bolus thickness (cm) | Field size (cm2) | Air gap (cm) | Reduction in “Ds”** | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 1.0 | 2.0 | 3.0 | ||||
| No bolus | 5 × 5 | 48.7 | 9.9* | - | - | - | - |
| 10 × 10 | 54.2 | 15.6* | - | - | - | - | |
| 15 × 15 | 59.9 | 21.6* | - | - | - | - | |
| 20 × 20 | 64.1 | 27.2* | - | - | - | - | |
| 25 × 25 | 67.7 | 32.4* | - | - | - | - | |
| 0.5 | 5 × 5 | 92.0 | 87.0 | 83.6 | 77.2 | 14.8 | |
| 10 × 10 | 93.9 | 90.0 | 88.9 | 87.3 | 6.6 | ||
| 15 × 15 | 95.3 | 92.1 | 91.5 | 90.9 | 4.4 | ||
| 20 × 20 | 96.6 | 94.0 | 93.4 | 92.9 | 3.7 | ||
| 25 × 25 | 97.4 | 95.1 | 94.5 | 94.2 | 3.2 | ||
| 1.0 | 5 × 5 | 99.4 | 97.3 | 92.4 | 84.5 | 14.9 | |
| 10 × 10 | 99.8 | 98.2 | 97.4 | 94.9 | 4.9 | ||
| 15 × 15 | 99.9 | 99.2 | 98.4 | 97.4 | 2.5 | ||
| 20 × 20 | 99.9 | 99.4 | 99.0 | 98.3 | 1.6 | ||
| 25 × 25 | 99.9 | 99.8 | 99.3 | 98.8 | 1.1 | ||
| 1.5 | 5 × 5 | 99.8 | 99.1 | 95.2 | 87.2 | 12.6 | |
| 10 × 10 | 99.9 | 99.5 | 95.2 | 96.5 | 3.4 | ||
| 15 × 15 | 99.8 | 99.7 | 99.2 | 98.5 | 1.3 | ||
| 20 × 20 | 100.0 | 99.9 | 99.4 | 98.8 | 1.2 | ||
| 25 × 25 | 99.9 | 100.0 | 99.5 | 99.2 | 0.7 | ||
*Value after application of correction factor (Ci [L]),[5] **Value obtained by subtracting the Ds value without (0.0 cm) and with 3.0 cm air gap
For a specific field size, the reduction in “Ds“ (i.e., the difference of “Ds“ value without and with air gap) was observed with the increase of air gap from 0 to 3.0 cm irrespective of bolus thickness. This reduction for maximum air gap of 3.0 cm for 0.5, 1.0, and 1.5 cm thick gel boluses was 14.8%, 14.9%, and 12.6% (for 5 cm × 5 cm); 6.6%, 4.9%, and 3.4% (for 10 cm × 10 cm); 4.4%, 2.5%, and 1.3% (for 15 cm × 15 cm); 3.7%, 1.6%, and 1.2% (for 20 cm × 20 cm); and 3.2%, 1.1%, and 0.7% (for field size 25 cm × 25 cm), respectively.
From these values, the maximum reduction in the “Ds“ was observed with smaller field size and was minimal for larger field sizes irrespective of bolus thickness and air gap.
Depth of dose maximum in the presence of air gap
Table 3 shows the dmax values (in cm) in the presence of air gaps between different thicknesses of gel bolus and water surface of RFA-300, obtained from central axis PDD curve for different field sizes. It is observed that dmax was shifting away from surface with increase of air gap under specific thickness of bolus and field size. This shift (i.e., the difference of dmax value without and with maximum air gap) for 0.5, 1.0, and 1.5 cm thick gel boluses was 0.1, 0.4, and 0.6 (for 5 cm × 5 cm); 0.1, 0.2, and 0.4 (for 10 cm × 10 cm); 0.1, 0.4, and 0.3 (for 15 cm × 15 cm); 0.1, 0.4, and 0.3 (for 20 cm × 20 cm); and 0.2, 0.3, and 0.3 (for field size 25 cm × 25 cm), respectively. From these values, the maximum shift in the dmax was observed for smaller field size with thicker bolus and greater air gap. However, with increase of field size, the dmax was moving toward the surface irrespective of bolus thicknesses and air gap.
Table 3.
Depth of dose maximum (dmax) values (cm) in the presence of air gaps between different thicknesses of gel bolus and water surface of radiation field analyzer- (RFA- 300), obtained from central axis depth dose curve of 6 MV clinical photon beam for different field sizes
| Bolus thickness (cm) | Field size (cm2) | Air gap (cm) | Shift of “Dmax”* | |||
|---|---|---|---|---|---|---|
| 0 | 1.0 | 2.0 | 3.0 | |||
| No bolus | 5 × 5 | 1.4 | - | - | - | - |
| 10 × 10 | 1.4 | - | - | - | - | |
| 15 × 15 | 1.4 | - | - | - | - | |
| 20 × 20 | 1.2 | - | - | - | - | |
| 25 × 25 | 1.2 | - | - | - | - | |
| 0.5 | 5 × 5 | 1.2 | 1.2 | 1.2 | 1.3 | 0.1 |
| 10 × 10 | 1.2 | 1.2 | 1.3 | 1.3 | 0.1 | |
| 15 × 15 | 1.1 | 1.1 | 1.2 | 1.2 | 0.1 | |
| 20 × 20 | 1.0 | 1.0 | 1.1 | 1.1 | 0.1 | |
| 25 × 25 | 0.8 | 0.9 | 0.9 | 1.0 | 0.2 | |
| 1.0 | 5 × 5 | 0.4 | 0.4 | 0.6 | 0.8 | 0.4 |
| 10 × 10 | 0.4 | 0.4 | 0.4 | 0.6 | 0.2 | |
| 15 × 15 | 0.0 | 0.4 | 0.4 | 0.4 | 0.4 | |
| 20 × 20 | 0.0 | 0.2 | 0.4 | 0.4 | 0.4 | |
| 25 × 25 | 0.0 | 0.2 | 0.2 | 0.3 | 0.3 | |
| 1.5 | 5 × 5 | 0.0 | 0.2 | 0.4 | 0.6 | 0.6 |
| 10 × 10 | 0.0 | 0.2 | 0.4 | 0.4 | 0.4 | |
| 15 × 15 | 0.0 | 0.2 | 0.2 | 0.3 | 0.3 | |
| 20 × 20 | 0.0 | 0.2 | 0.2 | 0.3 | 0.3 | |
| 25 × 25 | 0.0 | 0.2 | 0.3 | 0.3 | 0.3 | |
*Shift of dmax value obtained by subtracting the value of dmax without (0.0 cm) and with (3.0 cm) air gap
Effect of air gap on percentage depth dose
The influence of air gap on PDD up to 10 cm depth was noted for varied bolus thicknesses and field sizes. Figure 5a-c represents the graphical representation of the difference of PDD (with 0.0 cm and 3.0 cm air gap) below the 0.5, 1.0, and 1.5 cm of gel bolus, respectively. These graphs represent the reduction in PDD for maximum air gap of 3.0 cm under gel bolus for different field sizes. The maximum reduction was observed in the first few millimeters for all field sizes and is predominant for smaller field size. As seen from these graphs, for the field size 5 cm × 5 cm, the difference of PDD values was 15%–1.1% up to the depth of 0.6 cm, 14.9%–2.3% up to the depth of 0.4 cm, and 12.5%–1.9% up to the depth of 10.0 cm with 0.5, 1.0, and 1.5 cm gel bolus, respectively.
Figure 5.
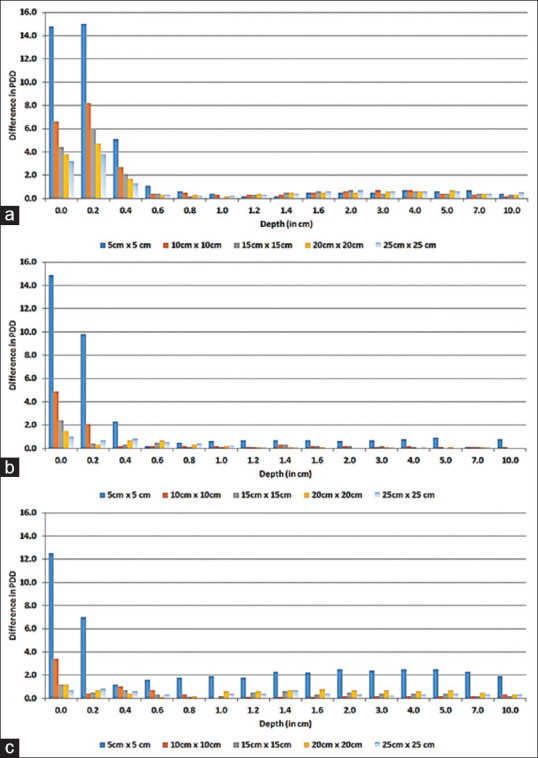
Difference in percentage depth dose (up to 10 cm depth) with and without air gap of 3.0 cm below (a) 0.5 cm, (b) 1.0 cm, and (c) 1.5 cm gel bolus for different field sizes
Furthermore, as observed, the effect of air gap on PDD is minimal (≤1%) beyond 0.4 cm depth for all bolus thickness and field sizes except for 5 cm × 5 cm with 1.5 cm bolus thickness [Figure 5c].
DISCUSSION
In this study, the influence of air gap between bolus and surface on central axis dosimetric parameters, for example, Ds, depth of dmax, and dose at shallow depth (up to 10 cm), for varied thickness of bolus and field size of 6 MV clinical photon beam was investigated. Bilge et al.[16] and Akbas et al.[17] recorded Ds measurements with parallel-plate chamber using 6 MV photon beam at 100 cm SSD under normal incidence condition and the values were 10%, 15%, and 23% and 10.8%, 16.6%, and 28.1% for field sizes of 5 cm × 5 cm, 10 cm × 10 cm, and 20 cm × 20 cm, respectively. Apipunyasopon et al.[5] studied depth doses near the surface by Monte Carlo simulated techniques for 6 MV photon beam and the values were 10.3%, 16.5%, and 22.2% for field size of 5 cm × 5 cm, 10 cm × 10 cm, and 15 cm × 15 cm, respectively. The comparison of Ds values for different field sizes obtained from this study with the published literature is mentioned in Table 4 which is well in agreement. At this juncture, it is highlighted that CC13 cylindrical compact chamber with necessary corrections done in this study was well in agreement with the Markus chamber measurements.
Table 4.
Comparison of surface dose (Ds) values (%) of 6 MV photon beam for various field sizes cited in the literature with the present study
| Study | Field size (cm2) | ||||||
|---|---|---|---|---|---|---|---|
| 5 × 5 | 8 × 8 | 10 × 10 | 10 × 20 | 15 × 15 | 20 × 20 | 25 × 25 | |
| Bilge et al.[16]a | 10.0 | * | 15.0 | * | * | 23.0 | * |
| Akbas et al.[17]a | 10.8 | * | 16.6 | * | * | 28.1 | * |
| Devic et al.[18]b | 10.5 | * | 16.0 | * | 21.7 | * | * |
| Sigamani et al.[19]b | 12.0 | * | 18.0 | * | 22.0 | 27.0 | 31.5 |
| Butson et al.[20]a,b | * | 14.0 | * | 21.0 | * | * | * |
| Ishmael Parsai et al.[21]c | 10.5 | * | 16.0 | * | 21.5 | * | 31.5 |
| Ishmael Parsai et al.[22]d | 10.3 | * | 16.1 | * | 21.9 | * | 32.2 |
| Apipunyasopon et al.[5]e | 10.3 | * | 16.5 | * | 22.2 | * | 30.9 |
| Present studyf | 9.9 | * | 15.6 | * | 21.6 | 27.2 | 32.4 |
*Not quoted/measured. Measurements were done with following instruments/methods. aMarkus parallel plate chamber, bRadiochromic film, cExtrapolation chamber, dParallel plate chamber (readings applied with correction factor), eMonte Carlo simulation techniques, fCylindrical (CC13) chamber after applying the correction factor (“Ci [L]”)
The percentage increment of Ds observed in this study with the application of 0.5 cm and 1.0 cm gel bolus was 47.1%, 42.3%, and 37.1% and 51.0%, 45.7%, and 40.0% and the corresponding values observed by Chung et al.[13] were 54.2%, 52.0%, and 49.9% and 63.4%, 60.6%, and 57.9%, respectively, for the field sizes 5 cm × 5 cm, 10 cm × 10 cm, and 15 cm × 15 cm.
On measuring Ds with air gap of 1.0 cm under bolus of thickness 1.0 cm using parallel plate ionization chamber, Butson et al.[20] observed a reduction of 6% and 2% in Ds for 8 cm × 8 cm and 10 cm ×20 cm (equivalent square field size @ 13.14 cm2) field sizes, respectively. In the current study, with similar air gap and bolus thickness Table 2, a 2.1% (difference of values in the third and fourth columns, i.e., 99.4–97.3 = 2.1%) and 1.6% (difference of values in the third and fourth columns, i.e., 99.8–98.2 = 1.6%) reduction of Ds was observed, respectively, for 5 cm × 5 cm and 10 cm × 10 cm field sizes. It is clear from Table 2 that the reduction in Ds predominates for smaller field sizes and bolus thickness as opposed to larger field sizes and bolus thickness in the presence of air gaps.
Table 5 represents the percentage reduction of Ds values published in literature under 1.0 cm bolus application for different field sizes and air gap thicknesses. It is observed that the trend of maximum reduction of Ds was predominant for smaller field sizes having larger air gap in all these studies.
Table 5.
Trends of percentage reduction of surface dose under 1.0 cm gel bolus for different field sizes and air gaps
| Field size (cm2) Air gap (cm) |
5 × 5 | 10 × 10 | 15 × 15 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| Shaw[22]a | * | * | * | 1.0 | 5.0 | 9.0 | * | * | * |
| Shaw[22]b | * | * | * | 3.0 | 8.0 | 15.0 | * | * | * |
| Shaw[22]c | 15.0 | 31.0 | 47.0 | 5.0 | 11.0 | 20.0 | 5.0 | 9.0 | 12.0 |
| Khan et al.[7]b | 8.0 | 18.0 | 26.0 | 2.0 | 4.0 | 8.0 | 2.0 | 2.1 | 2.2 |
| Chung et al.[13]a | * | * | * | 4.2 | * | * | * | * | * |
| Chung et al.[13]e | * | * | * | 4.5 | * | * | * | * | * |
| Present studyf | 2.7 | 7.6 | 15.5 | 1.8 | 2.6 | 5.1 | 0.8 | 1.6 | 2.6 |
*Not quoted. aMarkus chamber, bRadiochromic film, cMonte Carlo simulation techniques, dParallel plate chamber (readings applied with correction factor), eMOSFET, fCylindrical (CC13) chamber
Referring Table 3, the shift of dmax away from the surface with the increment of air gap for different thicknesses of boluses for a particular field size is observed in which the similar observations were made by Khan et al.,[7] Shaw,[22] and Sroka et al.[4]
The physics behind the observations/findings of this study can be explained by the interaction of photons with bolus atoms. When the bolus is introduced in the path of the photon beam, the low-energy secondary electrons generated by the photon interactions, which have a limited range, are added on to the photon beam. These electrons affect the dose only close to the phantom surface and up to dmax.[23] With the increase in the thickness of the bolus and the field size, the generation of this electron fluence from the bolus increases. Hence, a higher dose is deposited on the phantom surface when the bolus is in contact with the phantom surface. When the bolus moves progressively away from the phantom surface, i.e., in the presence of an increasing air gap between the bolus and the phantom surface, influence of the electron stream formed in the bolus on the absorbed dose on the phantom surface decreases due to the partial attenuation of these particles within the air gap.[22,23] When the thickness of bolus and build-up region for a relevant photon energy are equal and, at the same time, the bolus lies directly on the surface of the phantom, the buildup region does not appear and the depth of maximum dose moves to the surface of the phantom (dmax= 0.0 cm). If the bolus is now moved progressively away from the surface of the phantom, the maximum dose reaches a greater depth in the phantom (i.e., dmax moves away from the phantom surface) until this value reaches the same as that of the open beam for the collative bolus–surface distance.[4] This is due to very few of the secondary electrons reaching the phantom surface and the predominant dose being delivered by the incident photon beam.
Care needs to be taken while treating the superficial tumors by fully utilizing the need of bolus to get adequate dose. Thus, it is suggested, while in clinical radiotherapy planning process, the use of bolus (if required for specific treatment) during computed tomography simulation process is encouraged and the use of virtual bolus should be avoided in treatment planning system as it fails to account for the possible air gap that occurs during actual treatment which might result in the variation in planned and delivered dose. As the field sizes employed for clinical radiotherapy will be usually broad, our results show confidence that, in most of the clinical circumstances, patients are not underdosed because air gaps of 1.0 cm and above may not be encountered in treatment setups.
CONCLUSIONS
Radiotherapy has undergone significant improvement in terms of dose administration precision and monitoring and the sophistication of delivery methods. Bolus use in radiotherapy has a long tradition, and the general concept of changing the maximum dose point by adding bolus to the treatment surface has not changed. The re-examination of time-tested approaches in light of new methods is, therefore, a significant challenge.
Although this study basically analyzed the effect of air gaps present between the bolus and the treatment surface on dosimetric parameters along central axis PDD of a 6 MV photon beam with different thicknesses of gel bolus and field sizes under normal incidence condition, in reality, the radiotherapy treatment planning involves beam incidence with varied gantry angles. Thus, the effect of air gap occurred under the bolus and curved surface with different gantry angles needs to be investigated.
As the linac used in this study has no electron beam mode but only 6 MV photon beam, the authors did not have the facility of parallel plate chamber in their institutional setup. Hence, the measurements carried out in this study used miniature ionization chamber (CC13). This issue warrants further investigation, and these experiments/methods can be repeated with different beam qualities and are intended to promote further analysis of the effects of bolus in modern radiotherapy, discussing in particular the presence of air gaps between the bolus applications and the skin of a patient to obtain more comprehensive data. We hope that this study will inspire further research into bolus and its effects on effective dose delivery control in radiotherapy. The measured data in this study can be used to determine the probable degree of impact on therapy due to inevitable air gaps occurring between bolus and treatment surface. As a general rule, air gaps between bolus and treatment surface should be avoided to the extent practically possible.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
REFERENCES
- 1.Hsu SH, Roberson PL, Chen Y, Marsh RB, Pierce LJ, Moran JM. Assessment of skin dose for breast chest wall radiotherapy as a function of bolus material. Phys Med Biol. 2008;53:2593–606. doi: 10.1088/0031-9155/53/10/010. [DOI] [PubMed] [Google Scholar]
- 2.Hsu SH, Kulasekere R, Roberson PL. Analysis of variation in calibration curves for Kodak XV radiographic film using model-based parameters. J Appl Clin Med Phys. 2010;11:3172. doi: 10.1120/jacmp.v11i4.3172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kassaee A, Bloch P, Yorke E, Altschuler MD, Rosenthal DI. Beam spoilers versus bolus for 6 MV photon treatment of head and neck cancers. Med Dosim. 2000;25:127–31. doi: 10.1016/s0958-3947(00)00038-8. [DOI] [PubMed] [Google Scholar]
- 4.Sroka M, Reguła J, Łobodziec W. The influence of the bolus-surface distance on the dose distribution in the build-up region. Rep Pract Oncol Radiother. 2010;15:161–4. doi: 10.1016/j.rpor.2010.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Apipunyasopon L, Srisatit S, Phaisangittisakul N. An investigation of the depth dose in the build-up region, and surface dose for a 6-MV therapeutic photon beam: Monte Carlo simulation and measurements. J Radiat Res. 2012;54:374–82. doi: 10.1093/jrr/rrs097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sharma SC, Johnson MW. Surface dose perturbation due to air gap between patient and bolus for electron beams. Med Phys. 1993;20:377–8. doi: 10.1118/1.597079. [DOI] [PubMed] [Google Scholar]
- 7.Khan Y, Villarreal-Barajas JE, Udowicz M, Sinha R, Muhammad W, Abbasi AN, et al. Clinical and dosimetric implications of air gaps between bolus and skin surface during radiation therapy. J Cancer Ther. 2013;4:1251–5. [Google Scholar]
- 8.Nilsson B, Sorcini B. Surface dose measurements in clinical photon beams. Acta Oncol. 1989;28:537–42. doi: 10.3109/02841868909092265. [DOI] [PubMed] [Google Scholar]
- 9.O'Shea E, McCavana P. Review of surface dose detectors in radiotherapy. J Radiother Pract. 2003;3:69–76. [Google Scholar]
- 10.Kry S, Smith S, Weathers R, Stovall M. SU-GG-T-610: Skin dose during radiotherapy: A summary and general estimation technique. Med Phys. 2010;37:3327–8. doi: 10.1120/jacmp.v13i3.3734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Attalla EM, El-Sayed AA, Hessein H, Abouelenein HS, Ashour EF. Surface Dose Assessment for Different Clinical set up Parameters from High Energy Photon Beams. Adv Practice Nurs. 2017;2:133. [Google Scholar]
- 12.Andic F, Ors Y, Davutoglu R, Baz Cifci S, Ispir EB, Erturk ME. Evaluation of skin dose associated with different frequencies of bolus applications in post-mastectomy three-dimensional conformal radiotherapy. J Exp Clin Cancer Res. 2009;28:41. doi: 10.1186/1756-9966-28-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chung JB, Kim JS, Kim IA. Surface dose measurements from air gaps under a bolus by using a MOSFET dosimeter in clinical oblique photon beams. J Korean Phys Soc. 2012;61:1143–47. [Google Scholar]
- 14.Kong M, Holloway L. An investigation of central axis depth dose distribution perturbation due to an air gap between patient and bolus for electron beams. Australas Phys Eng Sci Med. 2007;30:111–9. doi: 10.1007/BF03178415. [DOI] [PubMed] [Google Scholar]
- 15.IAEA Technical Reports Series No.398. Absorbed Dose Determination in External Beam Radiotherapy. Vienna: International Atomic Energy Agency; 2000. [Google Scholar]
- 16.Bilge H, Cakir A, Okutan M, Acar H. Surface dose measurements with GafChromic EBT film for 6 and 18 MV photon beams. Phys Med. 2009;25:101–4. doi: 10.1016/j.ejmp.2008.05.001. [DOI] [PubMed] [Google Scholar]
- 17.Akbas U, Donmez Kesen N, Koksal, Bilge H. Surface and Buildup Region Dose Measurements with Markus Parallel-Plate Ionization Chamber, GafChromic EBT3 Film, and MOSFET Detector for High-Energy Photon Beams. Advances in High Energy Physics. 2016;2016:1–10. [Google Scholar]
- 18.Devic S, Seuntjens J, Abdel-Rahman W, Evans M, Olivares M, Podgorsak EB, et al. Accurate skin dose measurements using radiochromic film in clinical applications. Med Phys. 2006;33:1116–24. doi: 10.1118/1.2179169. [DOI] [PubMed] [Google Scholar]
- 19.Sigamani A, Nambiraj A, Yadav G, Giribabu A, Srinivasan K, Gurusamy V, et al. Surface dose measurements and comparison of unflattened and flattened photon beams. J Med Phys. 2016;41:85–91. doi: 10.4103/0971-6203.181648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Butson MJ, Cheung T, Yu P, Metcalfe P. Effects on skin dose from unwanted air gaps under bolus in photon beam radiotherapy. Radiat Meas. 2000;32:201–4. [Google Scholar]
- 21.Ishmael Parsai E, Shvydka D, Pearson D, Gopalakrishnan M, Feldmeier JJ. Surface and build-up region dose analysis for clinical radiotherapy photon beams. Appl Radiat Isot. 2008;66:1438–42. doi: 10.1016/j.apradiso.2008.02.089. [DOI] [PubMed] [Google Scholar]
- 22.Shaw A. Evaluation of the effects of bolus air gaps on surface dose in radiation therapy and possible clinical implications, Doctoral dissertation University of British Columbia. 2018. pp. 71–94. Available from (https://openlibraryubcca/cIRcle/collections/ubctheses/24/items/10371864) doi:1014288/10371864.
- 23.Kassaee A, Xiao Y, Bloch P, Goldwein J, Rosenthal DI, Bjarngard DI. Doses near the surface during total-body irradiation with 15 MV X-ray. Med Dosim. 2000;25:127–31. doi: 10.1002/ijc.10349. [DOI] [PubMed] [Google Scholar]


