Pathway crosstalk effects: Shrinkage and disentanglement using a Bayesian hierarchical model

Abstract

Identifying the biological pathways that are related to various clinical phenotypes is an important concern in biomedical research. Based on estimated expression levels and/or p-values, over-representation analysis (ORA) methods provide rankings of pathways, but they are tainted because pathways overlap. This crosstalk phenomenon has not been rigorously studied and classical ORA does not take into consideration: (i) that crosstalk effects in cases of overlapping pathways can cause incorrect rankings of pathways, (ii) that crosstalk effects can cause both excess type I errors and type II errors, (iii) that rankings of small pathways are unreliable and (iv) that type I error rates can be inflated due to multiple comparisons of pathways.

We develop a Bayesian hierarchical model that addresses these problems, providing sensible estimates and rankings, and reducing error rates. We show, on both real and simulated data, that the results of our method are more accurate than the results produced by the classical over-representation analysis, providing a better understanding of the underlying biological phenomena involved in the phenotypes under study.

The R code and the binary datasets for implementing the analyses described in this article are available online at: http://www.eng.wayne.edu/page.php?id=6402.

1. Introduction

Identifying the biological pathways that are significantly impacted in a given phenotype is a crucial step in understanding disease mechanisms. For the purpose of this paper, we will consider a pathway as a set of genes that are involved in the same biological process, disregarding the interactions among genes. Pathway data are typically retrieved from databases such as KEGG or Reactome; in this work we will use KEGG. The phenotype is typically characterized by a set of differentially expressed (DE) genes, as determined by using one of many available techniques (e.g. linear models [45]).

Although several alternative methods have been proposed ([4],[14],[28],[30], [39], [40]) ORA remains a mainstream approach used to find the signaling pathways that are impacted in a given experiment ([12],[23], [30]). The underlying assumption of ORA is that pathways with an unusually high number of DE genes are more related to the phenotype than pathways that contain fewer such genes. We will focus on Fisher’s exact test because it is the most common statistical test used for over-representation analysis ([30]). For a given pathway, the null hypothesis is that the proportion of DE genes inside the pathway is no different from the proportion of DE genes outside. The p-value calculated by ORA is the probability of observing the actual number or a higher number of DE genes belonging to a pathway, under the null hypothesis.

As in classic ORA, we will consider a pathway as a set of genes that are involved in the same biological process, disregarding the interactions among genes. A gene can be found to be either differentially expressed (DE) or not in the comparison between the two phenotypes. The level and direction of differential expression is not considered for our analysis, although the general model presented here can be extended to a continuous case. While use of directional information may be helpful, our research is couched within the stream of ORA-related research that uses only binary DE/non DE gene classifications; see [30].

A problem with ORA is that it produces contaminated p-values when some pathways share genes with other pathways, a phenomenon referred to as crosstalk. The effects of crosstalk on p-values has been studied in [9]. These p-values translate into reporting both false positives (Type I errors) and false negatives (Type II errors) unrelated to the multiplicity issue. Our proposed model reduces both error rates because it disentangles these effects as it assigns a gene to only one true, or latent pathway. The real proportion of DE genes is the latent, pathway-specific gene expression probability.

While our main competitor is ORA, there are other approaches to gene set analysis. Gene Set Enrichment Analysis (GSEA) [46], and its enhanced version [13] ranks all genes based on the correlation between their expression and the given phenotype, and calculates a score that reflects the degree to which a given pathway is represented at the extremes of the ranked list. Like ORA, these methods still do not address the overlap effects. Overlap issues are addressed by Newton at al. [43], but our approach differs in that we use a Bayesian latent pathway modeling approach to specifically disentangle the pathway effects.

Type I errors in ORA are also a problem because of the multiplicity issue: when many pathways are tested at the 5% level, there is a chance of spurious false positive tests ([29], [12],[11]). Often frequentist multiple comparison correction methods, such as familywise error rate controlling or false discovery rate controlling methods are used ([44], [52]). While correction for multiple comparisons is not the main focus of this paper, our method produces p-values that implicitly correct for the multiple comparison problem via Bayesian shrinkage ([31]).

The proposed method reduces the negative effects of both pathway size and pathway overlap on the estimated pathway-specific gene expression probabilities. The result is that the Bayesian posterior probability estimates are not as extreme as the raw probabilities, especially when the probabilities differ little, and the potential for false positives is thus reduced.

Our method estimates the quantity “true proportion of differentially expressed genes on a pathway.” As long as the imperfection (due to random noise) of the experiment is acknowledged, the empirical percentages are bound to differ from the “true” values. And it is factual that the size of the error is related to sample size; pathway size in our case. By analogy, any athlete’s performance statistic based on a small size is generally less accurate as a measure of true ability than one based on a larger sample size. For example, a major league baseball player’s batting average may easily be .450 after 20 at bats, but it is nearly unthinkable that it could be so large at the end of the season with 500 or more at bats. Pathway size influence also has been discussed by other researchers as a concern ([7]). In an analogous situation, [21] address the issue of customer-provided online product ratings, and make the point that a high average rating score from a small number of reviewers should be given less credence than a lower average rating from a large number of reviewers. The shrinkage property of our model sensibly discounts the raw proportions in small pathways, and thus gives greater credence to the raw proportions from larger pathways.

Others have addressed the disentanglement problem in different ways. In [10], methods are developed to identify and rank “modules”, or combinations of pathways. Our approach differs in that the emphasis is on the given pathways themselves, not modules. In [49], methods are proposed that downweigh the overlapped pathways and provide alternative rankings. Our method can be considered similar to [10] and [49], albeit with a more rigorous foundation in two ways. First, we provide a statistical model for gene expression percentages that automatically disentangles the results from the overlapping pathways: the proposed model considers gene expression to be a random variable as the phenotype is the result and not the cause of the genotype. Similar models have been developed before, such as regression models where pathway membership is a predictor [24] or models that apply learning techniques related to regression directly to pathway analysis [37]. Second, we attach to this model a Bayesian prior that produces pathway size-related shrinkage in addition to the disentanglement.

In [2], an alternative Bayesian method is provided for this type of analysis; however, our method differs in that the primary output of the analysis is gene expression probability, which might be considered more easily interpreted (being related to simple r/n proportions) than their “probability of involvement” measure. In addition, in comparing analyses of our data sets using the two methods, we found problems with [2] in that there was less than desired disentanglement, as well as frequent failure to converge, which yielded uninterpretable results with no warning message. Early versions of our algorithm produced similar difficulties in convergence; however, the methodology which we ultimately adopted as described in this article provided a more robust computational solution.

Our method is based on Bayesian hierarchical modeling in terms of latent pathways; disentanglement is accomplished using a model in which latent pathways do not overlap. We use a data augmentation approach to simulate latent pathways, using [48] and [1] to obtain posterior distributions of the parameters of the Bayesian hierarchical model. Loosely related latent variable formulations are given by [51] and [15]. Using this model, shrinkage towards a global mean is found to be especially prominent in cases where there is much overlap, since the latent pathway sizes tend to be smaller in such cases. This additional shrinkage, in cases of overlap, is a desirable outcome for such ambiguous cases.

2. The statistical model

We consider the binary gene expression indicator to be a dependent random variable. Similar approaches in the literature have regarded pathway membership as a predictor ([24]), or have applied learning techniques related to regression directly to pathway analysis ([37]).

Our proposed model is inspired by the one presented in [17], p. 109–111, who analyzed toxicity experiments performed on rodents. The rodents were separated into k distinct groups with n_j in group j, and the goal was to estimate the treatment-specific tumor development probabilities π_j. Let $g={\mathrm{\Sigma }}_j{n}_j$ denote the total number of rodents (the symbol “g” is used to anticipate its later use as number of genes), and let Y_i denote rodent i’s binary tumor development indicator, i = 1,...,g. Let Π = (π₁ π₂ ... π_k)^′ denote the k-column vector of treatment specific tumor development probabilities, and let Z_i be a row vector with 1 in the jth column if rodent i is in group j, 0 otherwise. Note that Z_i has only one “1” and all the rest zeros because a rodent can belong to only one treatment group. Let Z denote the vertically stacked Z_i, a standard ANOVA design matrix indicating group membership for each rodent. Then the probability of tumor development for rodent i is Z_iΠ, and the vector of probabilities for all g rodents is ZΠ.

The hierarchical model in [17], stated in the terms given above is as follows:

$$\begin{gathered} Y_i|{\mathbf{Z}}_i,\Pi {~}_{ind}\text{Bernoulli}\left({\mathbf{Z}}_i\Pi \right),\text{for}i=1,\dots ,g \\ {\pi }_j|\alpha ,\beta {~}_{ind}\mathrm{Beta}(\alpha ,\beta ),\text{for}j=1,\dots ,k \\ p(\alpha ,\beta )\propto (\alpha +\beta {)}^{(-5/2)} \end{gathered}$$ (1)

[17] chose the hyperprior p(α, β) ∝ (α + β)^(−5/2) as a “diffuse” distribution for (α, β) that is proper and dominated by the likelihood. They go on to provide a robust solution to obtaining a posterior sample from Π|{y₁,...,y_g}. Our model for the genomic pathway analysis is inspired by this model for tumor development, with modifications that allow it to take into account overlapping pathways, as we now show.

Assume the gene expression data are organized as in Table 1. The “Observed Expression” column is an indicator variable for gene differential expression: Y_i = 1 if the gene is differentially expressed and it is 0 if not, analogous to rodent i having a tumor or not in Equation 1. There are k pathways, analogous to k treatment groups in the rodent experiment, and g genes, analogous to the g rodents.

Table 1:

Gene expression and pathway indicators

Gene Label	Observed Expression (binary)	Pathway 1 Indicator (binary)	Pathway 2 Indicator (binary)	$\dots$	Pathway k Indicator (binary)
1	Y1	X11	X12	$\dots$	X1k
$⋮$	$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
g	Yg	Xg1	Xg2	$\dots$	Xgk

Row ${\mathbf{X}}_i=\left(X_{i1},\dots ,X_{ik}\right)$ is a binary row vector that represents the pathway membership information for gene i, analogous to the Z_i in the rodent model, except that X_i can have multiple 1’s because a gene can belong to more than one pathway. For example a membership vector X_i = (0, 1, 1) for a certain gene would indicate that we consider a total of three pathways and the gene is shared by the last two pathways. In general, gene i is shared by more than one pathway if ${\sum }_j{X}_{ij}>1$, or, in vector form, if ${\mathbf{X}}_i\mathbf{1}>1$, where 1 is the column vector of 1’s.

While multiple pathways can have effects, our model disentangles the effect of overlapping pathways by assuming that only one of these (latent) biological processes (pathways) is the main cause of the gene expression change for any gene i. The biological relevance of this assumption will be more relevant in some contexts than others; nevertheless, the disentanglement occurs in any case and is still useful, as we shall show. The latent process assumption gives rise to a matrix of Zs, many of which are unobserved, as shown in Table 2.

Table 2:

Gene expression and latent pathway indicators

Gene Label	Observed Expression (binary)	Latent P1 Indicator (binary)	Latent P2 Indicator (binary)	$\dots$	Latent Pk Indicator (binary)
1	Y1	Z11	Z12	$\dots$	Z1k
$⋮$	$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
g	Yg	Zg1	Zg2	$\dots$	Zgk

Now, with the vector Z_i representing the latent gene membership for gene i, the structure of the gene expression data is identical to the structure of the rodent tumor data in that each gene belongs to one and only one true pathway, just like each rodent belongs to one and only one treatment group. For genes that only belong to one pathway, ${\sum }_j{X}_{ij}=1$ and ${\mathbf{Z}}_i={\mathbf{X}}_i$. For genes that are common to multiple pathways, ${\sum }_j{X}_{ij}>1$, but ${\sum }_j{Z}_{ij}=1$ and Z_i is a binary vector such that all the elements of Z_i are zero, except for only one position that is 1, which is one of the positions where a 1 element of X_i occurs. As stated above, given the latent Z_i, which we assume are uniformly distributed on the 1’s in X_i (although allowing biologically relevant pathway specific weights is straightforward) we have:

$$\text{P}({\mathbf{Z}}_i=\mathbf{z}|{\mathbf{X}}_i)={({\mathbf{X}}_i\mathbf{1})}^{-1}\text{I}(\mathbf{z}{\mathbf{X}}_i^{\prime }=1),$$ (2)

where I(·) is the indicator function, and where z is a binary row vector with z1=1. For example, if X_i = (0 1 1), then the proposed model states that Z_i can take the vector values (0 1 0) or (0 0 1), each with 1/2 probability.

3. Estimation methods

3.1. Analysis conditional on latent pathways

The main tool used in our analysis is data augmentation, which involves simulating hypothetical realizations of the Z matrix; the “augmented” data is then (Y:X:Z). Standard MCMC methods were initially attempted, but experienced problems of failure to converge ([16], [5]); neither did improvements of this method ([22], [18]) work for our case. As stated by [48], data augmentation is useful when (a) it is easy to analyze the augmented data and (b) it is easy to generate the augmented data from its predictive distribution. Both these conditions are valid for our case: [17] provide a stable analysis of the augmented data, and we will show that (b) is easily accomplished as well. The following steps describe how to analyze the augmented data, where Z_i are known. The method of sampling from the posterior distribution described in [17] applies in this case.

In describing the various conditional distributions needed to describe the methods, the pathway incidence matrix X is assumed given and hence, this term will be dropped from all conditioning arguments for clarity except when absolutely needed. Let $f_j=\sum _{i=1}^g{Y}_i{Z}_{ij}$, the number of expressed genes on latent pathway j, let n_j = $\sum _{i=1}^g{Z}_{ij}$, the number of genes on latent pathway j, let $A_j=\alpha +f_j$, and let $B_j=\beta +n_j-f_j$. [17] give the posterior distribution p(Π|Y, Z) conveniently in two steps. First,

$$p(\alpha ,\beta |\mathbf{Y},\mathbf{Z})\propto p(\alpha ,\beta )\prod _{j=1}^k\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}\frac{\Gamma (A_j)\Gamma (B_j)}{\Gamma (A_j+B_j)},$$ (3)

and second,

$${\pi }_j|(\alpha ,\beta |\mathbf{Y},\mathbf{Z}){\sim }_{ind}\text{Beta}(A_j,B_j).$$ (4)

To sample from p(Π|Y, Z), one can first sample the vector (α*, β*) from (3); then, using this vector value for (α, β ), sample the ${\pi }_j^{*}$, j = 1,...k from (4). Repeating many times yields a sample from the joint k-dimensional posterior distribution p(Π|Y, Z).

Sampling from (4) is trivial but (3) has no closed-form solution. So [17] reparametrized equation (3) in terms of logit{α/(α + β)} = log(α/β) and log(α + β), the logit mean and the logarithm of the ‘sample size’ of the beta prior of the π’s, respectively.

They then suggested a grid-based approximation for the resulting density as a discrete two-dimensional distribution, with support determined by a well-chosen grid of transformed data points. The constant of proportionality can then easily be determined, as well as the finite set of joint probabilities, and values α*, β* are then sampled from the resulting bivariate discrete distribution.

While [17] suggest determining the range of grid values by trial and error, viewing contour plots and making a judgment as to whether the ranges for α, β are adequate, too narrow (missing important parts of the posterior), or too wide (including points with essentially zero probability in the grid), we automate the grid specification to simplify the application of the method. We use a 200×200 calculated grid to capture most of the posterior probability distribution of (3). Larger grids allow for better approximations of the continuous distribution. The grid is automatically determined as follows:

1. We first start with very imprecise boundaries [−10,10] on both axis log(α/β) and log(α + β).

2. We calculate the grid of proportional posterior probabilities.

3. The maximum probability is located.

4. We expand the grid boundaries to the points where the ratio of the maximum to minimum probability values is at least 10³.

Setting the initial boundaries to [−10,10] is mathematically justifiable as follows. The quantity $\log (\alpha +\beta )=\mathrm{logit}[\alpha /(\alpha +\beta )]$ is the logit of the mean for the beta distribution of the π’s. The boundaries [−10,10] on the logit scale correspond to the values 0.000045 to 0.9999 on the original scale; thus, our initial grid covers an almost exhaustive range of potential mean values. On the y-axis, log(α + β) is inversely proportional to the variance of the beta distribution of the π’s. By setting [−10,10] boundaries for log(α + β) the algorithm allows a wide range of posterior π distributions with very high precision or very low precision. Our algorithm has the advantage that it is easily implementable and it does not need any human intervention. The justification for the max/min ratio of 1,000 is that such a rectangle captures at least 99.9% of the bivariate normal distribution.

3.2. Data augmentation: Averaging over latent pathways

The desired posterior distribution is $p(\Pi |\mathbf{Y})$, not $p(\Pi |\mathbf{Y},\mathbf{Z})$, but they are related via $p(\Pi |\mathbf{Y})={\mathrm{\Sigma }}_{\mathbf{Z}}p(\Pi |\mathbf{Y},\mathbf{Z})p(\mathbf{Z}|\mathbf{Y})$ since Z is a discrete random variable. However, the sample space of Z has ${\prod }_{i=1}^g({\sum }_{j=1}^k{X}_{ij})$ elements, far too many to enumerate, and the simulation-based data augmentation analysis method of [48] is used instead. The algorithm requires Monte Carlo samples from p(Z|Y). Applying Bayes formula, the rows of Z are multinomial given $Y_i:p\left({\mathbf{Z}}_i|Y_i,\Pi \right)\propto \text{Bernoulli}\left(Y_i|{\mathbf{Z}}_i,\Pi \right)$, since ${\mathbf{Z}}_i|X_i$ is uniformly distributed.

As a simple example, assume only k = 3 pathways and that gene is shared by two pathways, the first and the third pathway. Then $p({\mathbf{Z}}_i=(1,0,0)|{\mathbf{X}}_i,Y_i=1,\Pi )={\pi }_1/({\pi }_1+{\pi }_3)$ and $p({\mathbf{Z}}_i=(0,0,1)|{\mathbf{X}}_i,Y_i=1,\Pi )={\pi }_3/({\pi }_1+{\pi }_3)$. If Y_i = 0, then the probabilities on (1,0,0) and (0,0,1) are $(1-{\pi }_1)/\{(1-{\pi }_1)+(1-{\pi }_3)\}$ and $(1-{\pi }_3)/\{(1-{\pi }_1)+(1-{\pi }_3)\}$, respectively.

The algorithm starts with an initial approximation g₀ (Π) to p(Π|Y) and consists of iterating two steps that use simulated data from p(Z|Y) and p(Π|Z, Y).

1. A grid of 200×200 values for $(\log (\alpha /\beta ),\log (\alpha +\beta ))$ and function (3) is calculated at each of the grid points.

2. Start with an initial guess g₀(Π) of p(Π|Y), using the standard posteriors using the raw DE proportions. (These posteriors are attenuated by crosstalk effects; the remaining steps of the algorithm disentangle these effects.)

3. Generate the Z matrix: draw a sample Π from the current p(Π|Y) and then draw the Z’s from the posterior distribution Z|{Y,Π}.

4. Sample one pair $(\log (\alpha /\beta ),\log (\alpha +\beta ))$ from the transformed (3) and transform it back to the original scale α, β. The α, β drawn at the previous step will completely specify the Π’s distribution according to equation (4).

5. Steps 3–4 are repeated m times.

6. Sample m Π’s from $m^{-1}{\mathit{\sum }}_{v=1}^{m}p(\Pi |{\mathbf{Z}}^{(v)},\mathbf{Y})$, the new approximation to $p(\Pi |\mathbf{Y})$.

7. Repeat steps 3–6. [48] suggest using anywhere from 15 to 70 iterations while varying m for some iterations. We used 25 iterations with a draw size m=500, finding acceptable convergence.

8. The last m Π samples will be considered a sample from the desired posterior distribution p(Π|Y).

3.3. Predicted probability and P-value calculation

A benefit of obtaining a sample from the posterior distribution $p(\Pi |\mathbf{Y})$ is that it is easy to construct various estimates and inferential statistics. We call the disentangled pathway effect estimates predicted probabilities (pred prob for short), and these are simply the averages of the posterior sampled Π vectors.

A Bayesian version of a p-value can also be constructed from these posterior samples. If the Z’s were known, then the Fisher p-value for pathway j would compare the proportion of DE genes inside pathway j with the proportion of DE genes of all the genes outside pathway j. With non-overlapping pathways, the comparison is between the DE proportion inside the pathway with a weighted average of the proportions outside. We use this logic to calculate the Bayesian posterior probability that the weighted average of the true pathway proportion inside a pathway determined by the latent Z is less than the weighted average outside.

For each pathway P_j we simulate the contrast between the latent pathway probability and the weighted average of the other pathways ‘ probabilities:

$$C_j={\pi }_j-\sum _{t=1,t\ne j}^k\frac{n_t}{n_j^c}{\pi }_t.$$

The C_j statistics are calculated for all m samples from the posterior. Then we estimate the p-value for each pathway j as:

$${\text{p-value}}_j=\left[\sum _{iter=1}^{m}I(C_{j,iter}\le 0)\right]/m.$$

The smaller the p-value_j, the higher the probability that latent pathway P_j’s DE gene proportion is more than the average DE proportion for all other latent pathways.

4. Applications to real experimental datasets

We illustrate the proposed approach using three real data sets and a number of simulations. The results on the real data presented in this section show that the proposed method provides reasonable results compared to ORA for the specific data sets, and the simulation results presented in the Discussion section show that our proposed method works more generally as well. The set of signaling pathways used for the data analyses was obtained from the KEGG database. For each dataset, we used Release 55 of the KEGG database. Newer releases of course give different, presumably more biologically relevant results.

4.1. Fat remodeling in mice

The first data set analyzed here comes from an experiment investigating cellular and metabolic plasticity of white adipose tissue (WAT). In this experiment, obese mice were treated with a low dose (0.75 nmol/hr) of CL 316243, and samples of WAT were collected before treatment (day 0), after 3 days, and after 7 days. The hypothesis is that the treatment would trigger the remodeling of WAT into a tissue resembling brown fat, a thermogenic organ ([19],[36],[41]).

The first comparison we discuss is the one between expression levels of genes at day 3 and 0, considering k = 101 pathways, with 5059 genes on these 101 pathways, of which 1390 are differentially expressed, 894 up and 496 down. As with the remaining two data sets, determination of DE was done by the experimenters using the top 5% of genes as ranked by p-value, see [47] and [25]. Also, in accordance with standard pathway analysis practices, only genes associated with pathways are included in our analyses, see [11], Section 24.5.3.

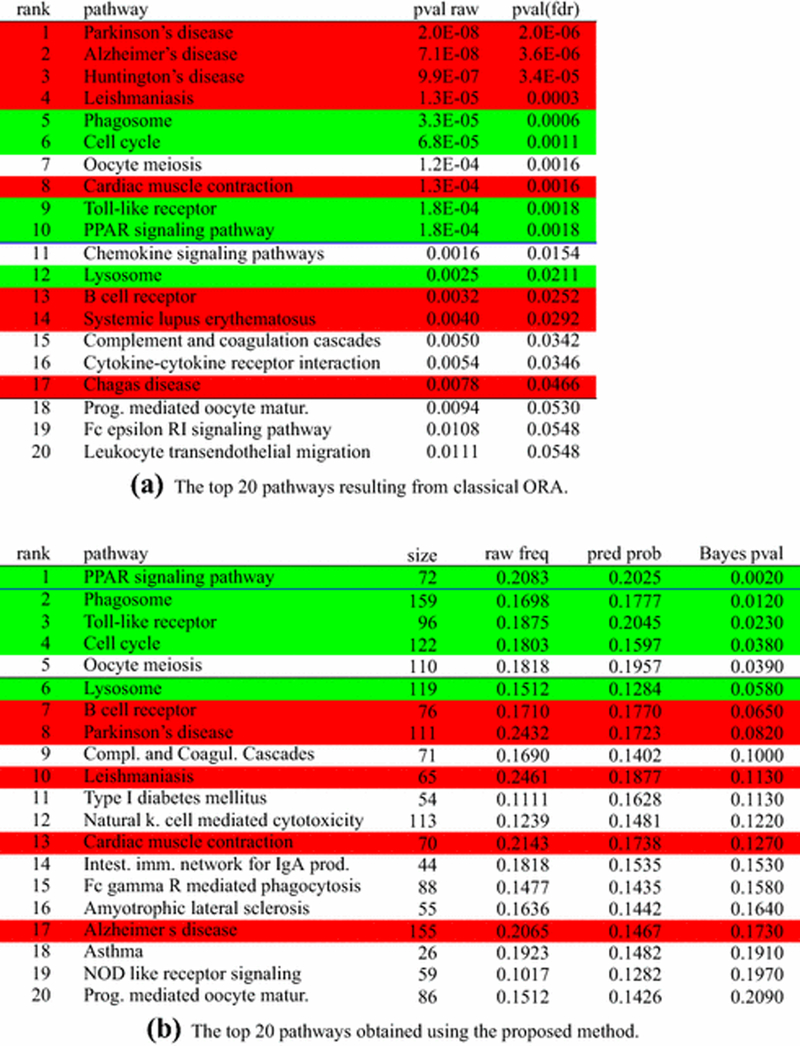
The top 20 pathways ranked by the classical ORA are shown in Figure 1a. In this figure, red background indicates pathways that are not related with the phenomenon of tissue remodeling, green background indicates pathways that, with reasonable confidence, we can associate with the phenomenon. White background indicates pathways for which we cannot draw any conclusion regarding their involvement in the phenomenon.

Fig. 1:

Analysis of the fat remodeling experiment for the comparison between days 3 and 0, with ORA, sorted by p-value after FDR correction (left), and with the proposed method, sorted by their Bayes p-values (right). Only the top 20 pathways are presented. The proposed algorithm gives the posterior mean of π_j in the “pred prob” column and it is different from the “raw freq” column which lists the proportion of DE genes for each pathway. The algorithm also calculates a Bayes p-value type of statistic that refers to the latent pathways (shown in the “Bayes pval” column) and is different from the FDR corrected Fisher p-value, shown in the “pval(fdr)” column, and calculated for the initial, non-latent pathways. Pathways highlighted in red represent pathways not related with the phenomenon in analysis, while pathways highlighted in green are those for which we know, with reasonable confidence, that they are involved in the given phenomenon. The white background indicates pathways for which we do not have conclusive information on their involvement (or lack of) with the phenomenon in analysis. Classical ORA yields a ranking in which the top 4 pathways are clearly false positives. Also, five out of 10 pathways significant at 1% are false positives. Using the 5% threshold, ORA yields 17 significant pathways, of which 8 are false positives, 6 are true positives and 3 are unknown. In contrast, the proposed approach reports 5 pathways as significant at 5%, where we do not have conclusive information about the involvement of only one, the Oocyte meiosis pathway. No clear false positives are reported at either 1% or 5% thresholds.

The top four pathways inFigure 1a, withp-values smaller than 0.01 (after correction using the standard FDR method [3]), are Parkinson’s, Alzheimer’s and Huntington’s diseases. The fourth pathway in the ranked list is Leishmaniasis. These disease pathways are unlikely to be related to the fat remodeling phenomenon analyzed: the first three describe degenerative diseases of the central nervous system, while the fourth is related to a disease transmitted by certain species of sand flies.

Even though the list presents several pathways that can be definitely be considered more related to the phenomenon of fat remodeling (Phagosome ([42]), PPAR Signaling ([19]), and Cell cycle ([32])), the abundance of false positives in the list (half of the 10 pathways significant at 1% can be safely considered false positive) shows that the classical ORA is unable to clearly identify the pathways that are related to the phenomenon in analysis.

The ranked list obtained with the method proposed here is shown in Figure 1b. This list is a clear improvement from the list obtained with classical ORA. The first notable difference is the absence of the Parkinson’s, Alzheimer’s, Huntington’s, and Leishmaniasis pathways. The top pathway, significant at 1% after the correction for multiple comparison, is the PPAR signaling pathway. The involvement of this pathway with the fat remodeling phenomenon has been demonstrated ([19]). Again, the involvement of the Phagosome and Cell cycle pathways in tissue remodeling is known ([42], [32]). The Toll-like receptor (TLR) pathway is related to generic immune response. The KEGG diagram shows that the TLR pathway is composed of two sub-pathways: one related to the response to the host genetic material, while the other sub-pathway is related to the response to foreign genetic material. In the process of fat remodeling, white fat cells die ([19]), triggering an immune system response to dispose of the dead cells ([35]), hence the presence of TLR in the list of significant pathways. Finally, the presence of the Lysosome pathway is explained by the role that lysosome enzymes play in the process of tissue destruction ([8]).

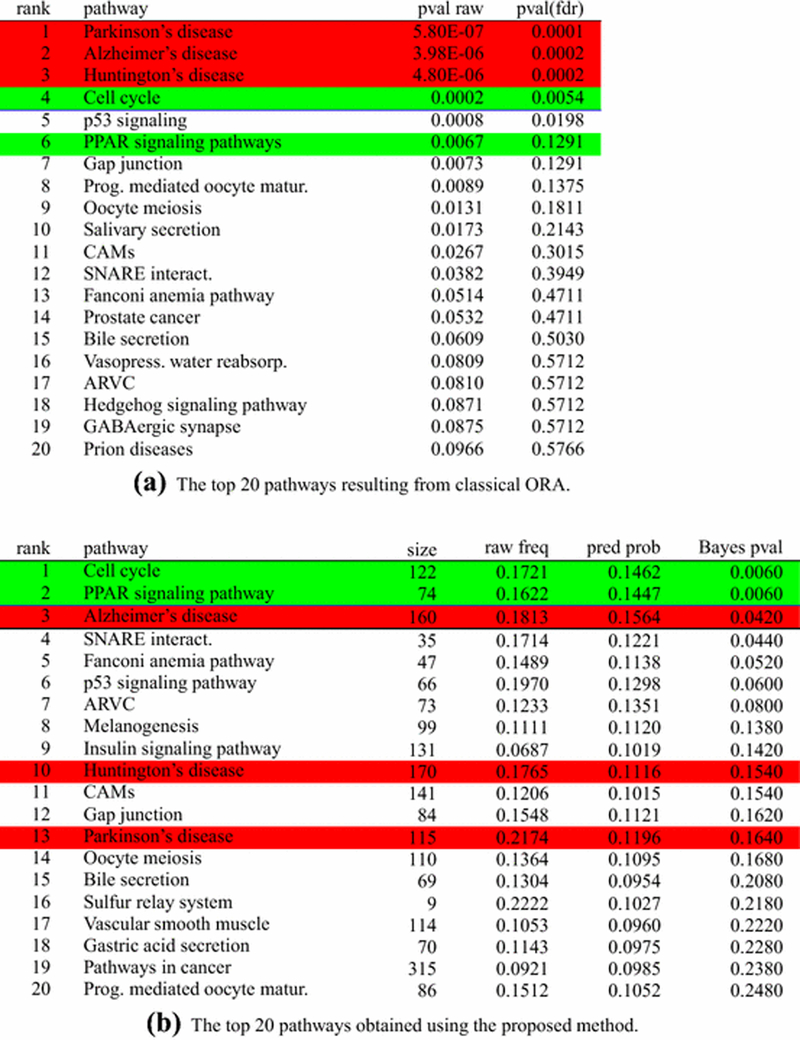
The complete results of ORA on the comparison between days 7 and 0 of the fat remodeling experiment (k = 124 pathways, with 5543 genes on these 124 pathways, of which 1379 are differentially expressed, 867 up and 512 down) are available in Figure 2b. Similar to the previous comparison, the three most significant pathways are Parkinson’s, Alzheimer’s and Huntington’s diseases. The Cell cycle pathway is the only clearly relevant pathway among the significant ones. The corrected ranked list obtained with the proposed method shows the Cell cycle pathway as the most significant, and PPAR signaling as second. Although the Alzheimer’s disease pathway is third in the list, its Bayes p-value is less significant than those of the first two pathways, suggesting a clear difference in the involvement of Alzheimer’s with respect to the others.

Fig. 2:

Day 7 vs day 0 mice fat dataset. Ranking of pathways resulting from the proposed algorithm, sorted by their Bayes p-values. Only the top pathways are presented. The proposed algorithm gives the posterior mean of π_j in the “pred prob” column and it is different from the “raw frequency” column which lists the proportion of DE genes for each pathway. The algorithm also calculates a “Bayes p-value” type of statistic that refers to the latent pathways and is different from the Fisher “p-value adjusted” calculated for the initial, non-latent pathways. Pathways highlighted in red represent pathways not related with the phenomenon in analysis, while pathways highlighted in green are those for which we know, with reasonable confidence, that they are involved in the given phenomenon. The white background indicates pathways for which we do not have conclusive information on their involvement (or lack of) with the phenomenon in analysis.

4.2. Cervical ripening

The second experiment analyzed here was obtained by a study investigating the processes involved in the ripening of the uterine cervix in human pregnancy ([20]), having k = 139 pathways, with 4113 genes on these 139 pathways, of which 91 are differentially expressed, 8 up and 83 down. Cervical ripening is a critical component of the processes related to parturition. The goal of this experiment was to investigate the relationship between cervical ripening and the cervical transcriptome, in order to understand the underlying biological phenomena. The study involves the comparison between gene expression levels of pregnant women with an unripe cervix and women with a ripe cervix.

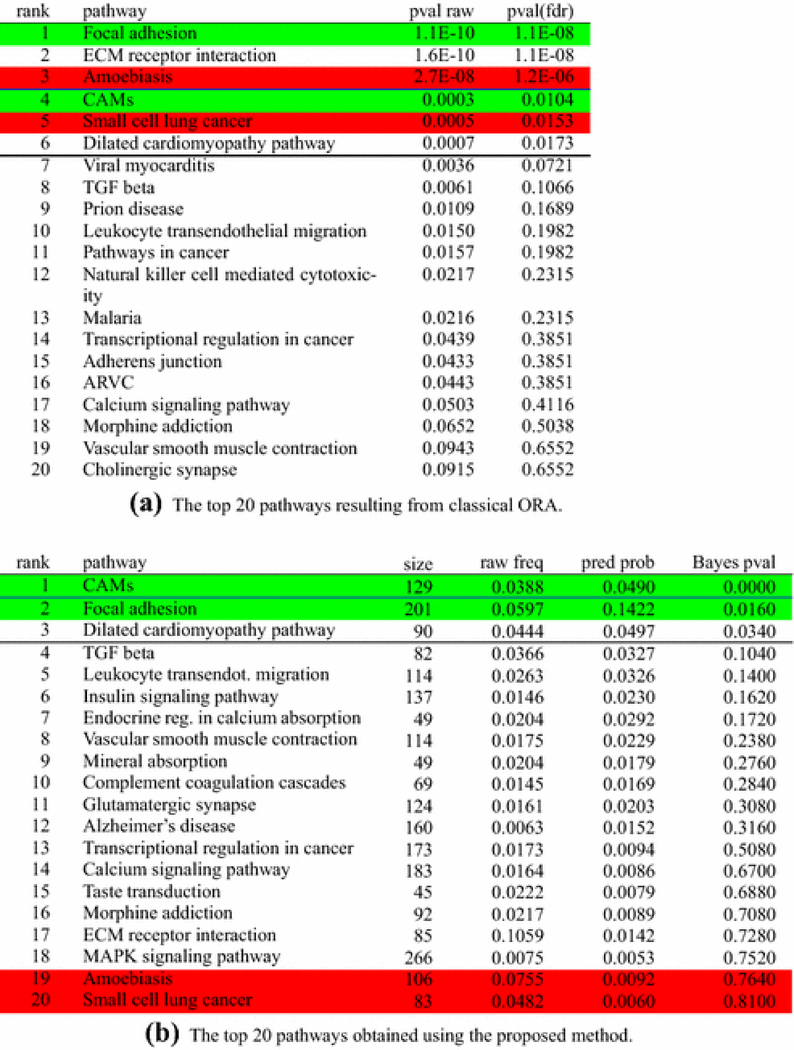
Figure 3a shows the results of ORA on the comparison. The significant pathways are Focal adhesion, ECM-receptor interaction, Amoebiasis, Cell adhesion molecules (CAMs), Small cell lung cancer, and Dilated cardiomyopathy. While Focal Adhesion, ECM-Receptor Interaction, and Cell Adhesion Molecules are definitely related to cervical ripening [33], [34], [38], [50], the list of significant pathways includes Amoebiasis, a pathway describing the process of infection from a parasite that invades the intestinal epithelium, and Small cell lung cancer, two pathways that are not related to cervical ripening.

Fig. 3:

Analysis of the cervical ripening experiment. Ranking of pathways resulting from the proposed algorithm, sorted by their Bayes p-values. Only the top pathways are presented. The proposed algorithm gives the posterior mean of π_j in the “pred prob” column and it is different from the “raw frequency” column which lists the proportion of DE genes for each pathway. The algorithm also calculates a “Bayes p-value” type of statistic that refers to the latent pathways and is different from the Fisher “p-value adjusted” calculated for the initial, non-latent pathways. Pathways highlighted in red represent pathways not related with the phenomenon in analysis, while pathways highlighted in green are those for which we know, with reasonable confidence, that they are involved in the given phenomenon. The white background indicates pathways for which we do not have conclusive information on their involvement (or lack of) with the phenomenon in analysis. The classical ORA reports 3 pathways as significant at 1%: one true positive, one false positive, and one for which the involvement with the phenomenon in analysis is unknown. When the threshold is 5%, one true positive, one false positive, and one pathway with unknown involvement are added to the list of significant pathways. The proposed approach reports a single pathway as significant at 1%, the Cell Adhesion Molecules, which is involved in the phenomenon of cervical ripening. Two other pathways are added at 5%, one true positive and one unknown. Both false positives reported by ORA are now placed towards the bottom, with p-values higher than 0.76.

The ranking of pathways resulting from the method proposed here is shown in Figure 3b. In this list, the Cell Adhesion Molecules and the Focal Adhesion pathways are at the top of the list, while the false positives are not reported as significant anymore. Although the Dilated Cardiomyopathy pathway is not directly related to the phenomenon, its presence in the list of significant pathways may be related to the fact that 10% – 15% of the uterine cervix tissue is composed of smooth muscle.

The pathway ECM receptor shares all of its DE genes with the pathway Focal adhesion. The proposed algorithm disentangles the common genes in a way that reallocates them to the Focal adhesion pathway, so that the true DE gene proportion for Focal adhesion gets enhanced. The final ranking shows Focal adhesion getting promoted towards the top position of the hierarchy and the ECM receptor getting demoted.

5. Discussion

In this section, we first give an example to emphasize gene disentanglement, then we show how the method behaves in case of pure noise, and finally we describe an example for which our method provides better power than ORA.

5.1. Disentanglement

Here, we show how the method is able to correctly disentangle the overlap between pathways. In our simple example, two pathways are considered. Let each pathway have n_t genes and let the two pathways share n_c genes. Of the n_u unique genes that belong exclusively to pathway X₁, 80% are DE, and only 40% of the genes that belong exclusively to X₂ are DE. We also suppose that half of the overlapping genes truly belong to X₁ and thus, they have an expression level of 80%. The other half’s true pathway membership is X₂ and their expression level is 40%; therefore, the overlap is 60% expressed.

To show that the algorithm is stable around the convergence values, assume 80% for the predicted probability for pathway X₁ and 40% for X₂. In the data augmentation algorithm, the Z’s are then sampled from the conditional distributions $p(Z=(1,0)|Y=1)=0.8/(0.4+0.8)=2/3$, $p(Z=(0,1)|Y=1)=0.4/(0.4+0.8)=1/3$ ; also p(Z|Y = 0) are 0.25 and 0.75, respectively. A large-sample approximation of the expected value for the probability of expression of X₁ is then $f_1/n_1=(0.8n_u+(2/3)0.6n_c)/\left(n_u+(2/3)0.6n_c+(0.25)(0.4)n_c\right)=\left(0.8n_u+0.4n_c\right)/\left(n_u+0.5n_c\right)=0.8$. This shows that the algorithm is stable at the convergence point: by starting with a guess equal to the true proportions, it was able to produce the correct predictions. Use of proportions other than 0.8 and 0.4 provides identical results.

These details only provide an intuitive explanation of the behavior of the algorithm. A full proof, available in [48], shows the data augmentation algorithm guarantees the simulated posterior distributions will converge to the true posterior distributions. [48] also give an upper bound for the convergence speed.

5.2. Shrinkage

In general, shrinkage to an overall mean is a result of Bayesian hierarchical modeling using a vague hyperprior, as is the case in (1). In particular, an estimate that is below the mean is estimated to be higher following the Bayesian analysis, closer to the overall mean. Similarly, an estimate that is above the overall mean is moved downward. This phenomenon is called “shrinkage”, and the degree of shrinkage depends on the reliability of the standard estimate.

In our case, reliability of the standard pathway-specific gene expression proportions depends on pathway size. Since $(\alpha +f_j)/(\alpha +\beta +n_j)$ is the expected posterior value of the pathway j probability, there will be little shrinkage for large n_j since $(\alpha +f_j)/(\alpha +\beta +n_j)=(\alpha /n_j+f_j/n_j)/(\alpha /n_j+\beta /n_j+1)\approx f_j/n_j$. For small n_j, the shrinkage will be large: assuming α = 10 and β = 90, corresponding to an overall expression level 10/(10 + 90) = 0.10, a pathway with n_j = 1 expressed genes (so f_j = 1) will have a raw estimate of 100% expressed, but a Bayes estimate of (10 + 1)/(10 + 90 + 1) = 0.109, or 10.9% expressed. Similarly, apathway with n_j = 1 non-expressed genes (f_j = 0) will have a raw estimate of 0% expressed, but a Bayes estimate of (10 + 0)/(10 + 90 + 1)= 0.099, or 9.9% expressed.

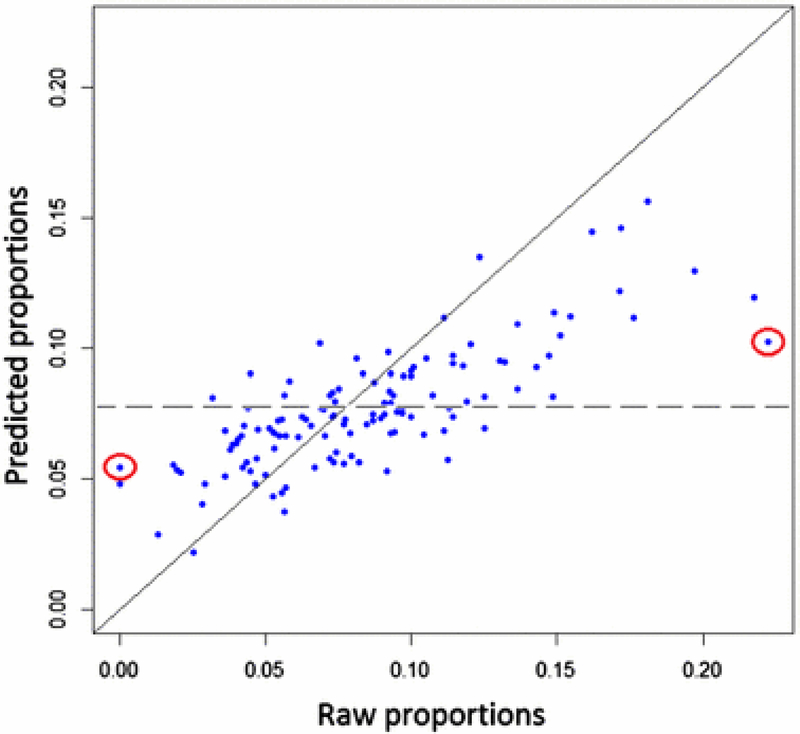
The analysis of the days 7 and 0 fat remodeling experiment provides a clear instance of shrinkage and Figure 4 shows how the predicted probabilities are shrunk toward the overall mean. Points situated close to the diagonal in Figure 4 indicate pathways for which the predicted proportions are similar to the original raw DE gene proportions. The highlighted points in Figure 4 correspond to pathways Sulfur relay system and Regulation of autophagy that experienced shrinkage in opposite directions: Sulfur relay system had a raw proportion of 0.2222 that was pushed down to a predicted proportion of 0.1027, while Regulation of autophagy was shrunk up from 0.00 to 0.1019. Sulfur relay system is a small pathway, composed of only 9 genes and its predicted probability was dominated by the overall expression level. Pathway Regulation of autophagy is an interesting case also: it is a relatively small pathway with 0 DE genes and its predicted probability will also be highly influenced by the overall DE proportion.

Fig. 4:

Shrinkage. The algorithm shrinks the predicted probabilities towards the overall DE gene proportion, represented by the dotted line. Shrinkage is apparent for low raw probability pathways points that are above the diagonal line and for high raw probability points that are below. Points situated close to the diagonal in Figure 4 indicate pathways for which the predicted proportions are similar to the original raw DE gene proportions. The highlighted points in Figure 4 correspond to pathways Sulfur relay system and Regulation of autophagy that experienced shrinkage in opposite directions: Sulfur relay system had a raw proportion of 0.2222 that was pushed down to a predicted proportion of 0.1027, while Regulation of autophagy was shrunk up from 0.00 to 0.1019.

5.3. Pure noise simulation

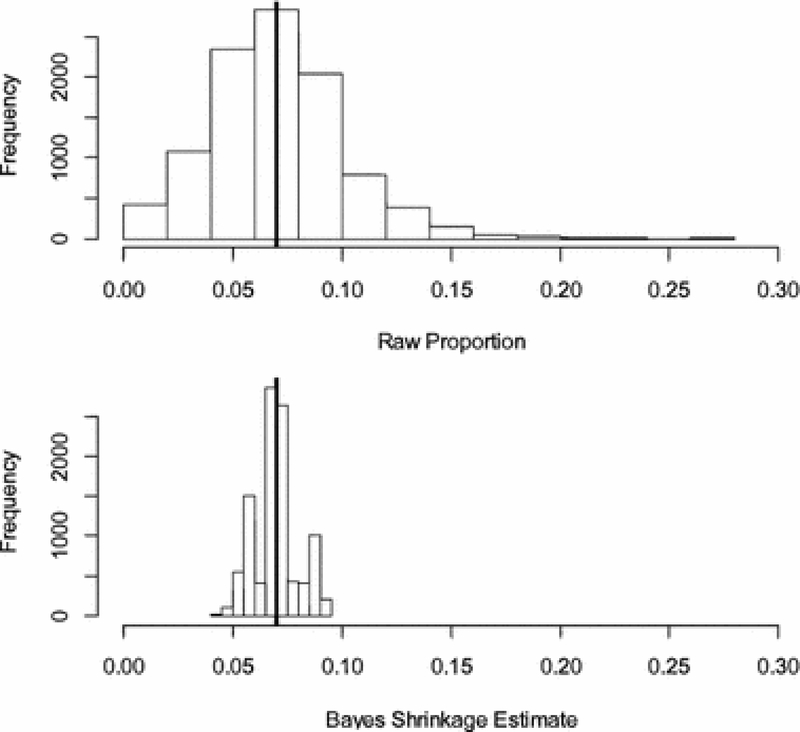
We simulated data where there were truly no differences in expression probabilities, using the set of pathways used in the day 3 vs day 0 comparison of the fat remodeling experiment. The original data set had an approximate 7% proportion of DE genes, therefore we simulated the entire expressed column as a Bernoulli random vector with a probability of success of 0.07. We ran the simulation generating 100 different data sets, and for each data set we ran the data augmentation algorithm with a sample size of 500 and for 25 iterations. There are 101 pathways in the data set; Figure 5 compares the histograms for the 100*101 raw (ORA) proportions and our Bayesian probability estimates. It is clear that the Bayesian estimates are much closer to the target 0.07; the average of our Bayesian estimates is 0.06966 with a standard deviation of 0.0099; the corresponding figures for the raw (ORA) proportions are 0.07029 and 0.0311.

Fig. 5:

Comparison of estimates of pathway-specific gene expression probabilities in the pure noise case where the true probabilities are identically 0.07 (vertical lines in the histograms). Each histogram displays (100 simulations)*(101 Pathways) probability estimates.

The unadjusted Fisher p-values in the simulation showed that, out of the 100 simulations, 93 had at least one p-value 0.05 for an estimated familywise error rate (FWER) of 0.93. The false discovery rate adjustments gave no significances in all 100 studies for an estimated FWER of 0.00. This figure is lower than the expected 0.05 because the Fisher exact tests, being discrete, are conservative. The Bayesian posterior probabilities show one study out of 100 with a Bayes p-value less than 0.05 for an estimated FWER of 0.01, acceptably small. Thus our algorithm correctly shrinks the predicted probabilities towards the overall probability, unlike the classical ORA probability estimates with FDR correction.

5.4. A power comparison

Like multiple comparisons adjustments (whether fdr or fwer controlling) the effect of Bayesian shrinkage is usually to make the tests less powerful than tests based on unadjusted methods. However, because of disentanglement, our algorithm can in some cases provide higher power than even the unadjusted ORA, despite the shrinkage effects embedded in our proposed method. To illustrate, we simulate 1000 genes and 10 pathways, X₁ through X₁₀. All the pathways’ sizes are 10% of the total number of genes. Pathways X₁ and X₂ share 50% of their genes and we use a 21% level of differential expression for X₁ and 15% for X₂. The rest of the pathways X₃ through X₁₀ are 7% differentially expressed. For the power calculations, 100 datasets are simulated and a Bayesian p-value and a FDR adjusted Fisher right-sided p-value are calculated for pathway X₁ . The algorithm is run for each simulated dataset for 10 iterations and we use a sample size of 100.

By counting the cases where the p-values where smaller than 0.05, we obtained a power of 0.67 for the algorithm we propose, 0.64 for the raw p-value ORA and 0.23 for the FDR adjusted p-value ORA. These results show that, under the specified simulated conditions, our algorithm is better at correctly estimating significance for pathway X₁, even compared to ORA using the unadjusted, raw p-values.

5.5. Demonstrating consistency of the estimates via simulation

To show that the method works, we ran large simulation study with the following specifications:

• -There are ten true pathways
• -True pathway expression probabilities are either close (0.20, 0.18, . . . , 0.02) or
• -spread(0.50, 0.45, . . . , 0.05)
• -Number of genes per path is either 10, 50, 100, 500, or 1000
• -Each gene is associated with both the given pathway, and one other randomly selected pathway (creating the crosstalk effects)

We simulated 100 data sets under each configuration, calculated the raw probabilities corresponding to expression of genes on a pathway (which is biased by crosstalk), our predicted probabilities, and the sample estimates using the latent true pathways (which are unknown in practice but form a useful comparison. To evaluate the quality of the estimates, we calculated the average root mean squared deviation of the estimates from the true probabilities $RMS=(1/100){\sum }_{j=1}^{100}\sqrt{{\sum }_{i=1}^{10}{({\widehat{\pi }}_{ij}-{\pi }_{ij})}^2/10}$ where ${\widehat{\pi }}_{ij}$. is one of the three estimates of pathway-specific probability i in simulation j. Table 3 presents the results.

Table 3:

Average RMS deviations of estimates from true probabilities

		RMS differences
Pathway size	TRUE Probabilities	Z Proportions	ORA Raw Proportions	Bayesian Estimates
10		0.1025	0.0618	0.0682
50		0.0179	0.0197	0.0239
100	Close	0.0097	0.0148	0.0151
500		0.0021	0.0112	0.004
1000		0.0009	0.0108	0.0019
10		0.1698	0.1590	0.2175
50		0.0362	0.0820	0.0632
100	Spread	0.0182	0.0732	0.0359
500		0.0038	0.0655	0.0089
1000		0.0015	0.0636	0.0046

As can be seen in Table 3, the method successfully targets the true probabilities with larger pathway sizes, while the classic ORA proportions are inconsistent. While it may seem that the ORA proportions are better for small pathways (even compared to the correct “I” proportions), this is a function of reduction in variability of estimates due to larger sample sizes. The problem is that much of these larger sample sizes reflects incorrect pathways, giving bias.

6. Conclusion

The Bayesian model we presented produces an algorithm that ranks pathways according to their estimated true DE proportions and provides Bayesian p-values for making comparisons. The method disentangles the pathway estimates in the case of crosstalk, and shrinks the estimates based on pathway size. In real data examples, the method was shown to identify pathways that have been biologically confirmed. Also, the method was able to eliminate irrelevant pathways from the top of the ranking: this is very useful for biological research purposes and it is a definite improvement over ORA. We also showed, via simulation and analytic calculations, that the method effectively disentangles crosstalk effects and reduces both type I error and type II error rates.

We recommend our method for pathway analysis research especially for cases when there is a high level of pathway overlap (e.g. pathways from KEGG ([26],[27]) or Reactome ([6]), overlap that leads to the wrong pathways being considered significant.