Abstract
The growth of COVID-19 pandemic throughout more than 213 countries around the world have put a lot of pressures on governments and health services to try to stop the rapid expansion of the pandemic. During 2009, H1N1 Influenza pandemic, statistical and mathematical methods were used to track how the virus spreads around countries. Most of these models that were developed at the beginning of the XXI century are based on the classical susceptible–infected–recovered (SIR) model developed almost a hundred years ago. The evolution of this model allows us to forecast and compute basic and effective reproduction numbers (Rt and R0), measures that quantify the epidemic potential of a pathogen and estimates different scenarios.
In this study, we present a traditional estimation technique for with statistical distributions by best fitting and a Bayesian approach based on continuous feed of prior distributions to obtain posterior distributions and computing real time . We use data from COVID-19 officially reported cases in Ecuador since the first confirmed case on February 29th. Because of the lack of data, in the case of we compare two methods for the estimation of these parameters below exponential growth and maximum likelihood estimation. We do not make any assumption about the evolution of cases due to limited information and we use previous methods to compare scenarios about and in the case of we used Bayesian inference to model uncertainty in contagious proposing a new modification to the well-known model of Bettencourt and Ribeiro based on a time window of days to improve estimations.
Ecuadorian with exponential growth criteria was 3.45 and with the maximum likelihood estimation method was 2.93. The results show that Guayas, Pichincha and Manabí were the provinces with the highest number of cases due to COVID-19. Some reasons explain the increased transmissibility in these localities: massive events, population density, cities dispersion patterns, and the delayed time of public health actions to contain pandemic.
In conclusion, this is a novel approach that allow us to measure infection dynamics and outbreak distribution when not enough detailed data is available. The use of this model can be used to predict pandemic distribution and to implement data-based effective measures.
Keywords: Bayesian inference, R0, COVID-19, Real time reproduction factor, Basic reproduction factor, Ecuador
1. Introduction
In March 2020, the new coronavirus disease (COVID-19) was defined as the first pandemic of this century (C. Zhang et al., 2020a). A newly discovered zoonotic coronavirus named SARS-CoV-2 was responsible for the rapid spread of the disease putting the entire world under partial or total lockdowns(Ishii, 2020). In this regard, COVID-19 presents certain characteristics that hinder its control and facilitate its spread, such as the lack of knowledge about it, the absence of any related vaccine, the lack of a recognized treatment and the high transmission rate due to aerosol transmission (Mandal et al., 2020; Ortiz-Prado, Simbaña-Rivera et al., 2020).
At the beginning of this pandemic, governments, researchers and health care providers relied on several mathematical models that were founded on the basic reproduction number of the virus in order to obtain a reliable value of 1.4–2.5 for the SARS-CoV-2 virus (Wu et al., 2020). This approach was used previously in similar epidemiological scenarios to adopt adequate health policies trying to control diseases. For example, the 2003 Severe Acute Respiratory Syndrome (SARS) affected at least 37 countries and the estimated was set at 2.2–3.7, meanwhile the 2012, Middle Eastern Respiratory Syndrome (MERS) had a of 0.29–0.80 around 27 countries (Breban et al., 2013; Cauchemez & Fraser, 2014; Wu et al., 2020).
-derived estimations has become widely used, since Kermack and McKendric developed its transmission model in 1920 after getting inspired by Ross’s model for Malaria (Kermack & Mckendrick, 1991; Kucharski, 2020). The basic reproduction number and the real-time estimation of the basic reproduction number are measures that quantifies the epidemic potential of a pathogen. is defined as the average number of people that an infected person can spread the virus; however, cannot reflect the time-varying nature of an epidemic. For this reason, a time-varying effective reproductive number provides more temporal information. Nevertheless, one of the main issues about giving real time track for is the quality of estimations. Methods used for this value range from using specific distributions for the volume of daily cases to stochastic models and even statistical inference of chains of transmission (Yuan et al., 2020). The optimal population tracking for a pandemic in any country can be done with solid following for the evolution of and across days. Based on standard epidemics, both values and over the unit lead to an epidemic spread behavior, thus is desired to have both below one which means epidemic is being controlled and close to zero which is translated into eradication state. It’s also necessary to highlight that tracks the evolution of pandemic in continuous way and it’s a more accurate indicator of how viral spreading process is changing below public health policies (Yuan et al., 2020). On the other side, is a static quantity that principally explains what happens with pandemic when no public health policies are adopted (Yuan et al., 2020). During the early phase of rapid growth in any epidemic, a delay in the results (positive cases) could be determined by the lack of response regarding the availability of screening tests. Consequently, the growth rate of cases could be altered again because of a number of cases that exceeds the maximum number of results that are available in one day. As a result, this could be identified as a constant number of cases and is plotted as an altered curve with the presence of decreases or unreal plateaus. These typical difficulties of disease and health systems inevitably lead to changes the values of (Omori et al., 2020).
Concerning , it can be modeled behind SIRS model context (a generic epidemiological model of an infectious disease transmission through individuals that pass through the states: susceptible, infectious, recovered, and susceptible) with the assumption of exponential growth and using as reference mean and standard deviation according to confirmed cases reporting dates (Ma, 2020; Zhao et al., 2020). Another, Static for COVID-19 spread in Diamond princess cruise ship was computed with maximum likelihood estimation using the serial interval distribution of gamma distribution (S. Zhang et al., 2020b). Also, can be estimated with removal method based on bias corrected maximum likelihood estimation obtained from chain binomial models (Ferrari et al., 2005). Additionally, a connection between classic and modern statistics was developed during the H1N1 influenza pandemic, combining regularization, penalized likelihood and assumptions about serial interval with a Weibull distribution in order to determine the distribution of (Hens et al., 2011). Modern approaches use Bayesian methods to quantify possible heterogeneities in the spread of the disease.
Ecuador, suffered arguably one of the worst COVID-19 scenario during the first stage of the pandemic in the region, with a death toll that is 15 times higher than its official tally of coronavirus related deaths(Ortiz-Prado, Diaz, et al., 2020). No mathematical estimations were given prior the arrival of COVID-19 in the country, neither any study is available in Ecuador regarding previous outbreaks. In this sense, the aim of this model is to provide the evidence of the transmission dynamics of SARS-CoV-2 in Ecuador in order to track the evolution of COVID-19 pandemic in a continuous way and to evaluate the development of public health policies in Ecuador.
2. Methods
2.1. Study setting
Ecuador is multiethnic country with more than 17 million inhabitants and is located in the South America, pacific coast. A country that borders Colombia to the north, Peru to the south/east and the Pacific Ocean to the west. The current administrative political division is divided into four regions (Coastal, Andes, Amazon and Galapagos Islands), which are organized in 24 provinces and 221 territorial constituencies called cantons (Instituto Nacional de Estadística y Censos, 2019).
2.2. COVID-19 data
Daily confirmed cases reported in Ecuador due to COVID-19 pandemic was analyzed from National Emergency Operations Committee registries. Data was available from February 28th to May 5th, 2020. Demographic features as provinces and cantons were included. The information was transferred to our research team after presenting a formal petition and signing a confidentiality agreement with the Ministry of Health (MoH) to protect patient’s rights. This secondary data analysis of anonymized, un-identifiable information received ethical approval from the Universidad de las Americas Ethics Committee CEISH on March 10th, 2020.
2.3. Probabilistic model calculation
The present work use Bayesian inference to determine the full probability distribution of and . The method consists on formulating a probabilistic scheme by confirmed cases time series data. Then, the Bayesian procedure translates the time series data into a probability distribution for the parameter R.
2.3.1. Quantifying the static transmission dynamics
In order to estimate , two methods will be considered: exponential growth (EG) and maximum likelihood estimation (MLE).
-
•
Exponential growth rate is defined as the per capita change in number of new cases per unit of time. During the outbreak of a pandemic exponential growth rate is linked to reproduction ratio. Poisson regression is indicated to estimate this parameter (Wallinga & Lipsitch, 2007). Therefore, the reproduction number is computed as:
| (1) |
Where is the moment generating function of the generation time distribution belonging to contagious data series.
-
•
Maximum likelihood estimation method, this model makes the assumption that the number of secondary cases during a virus spread stage is Poisson distributed with expectation (Forsberg White & Pagano, 2008). Given a series of confirmed cases over a consecutive time period, and a generation time distribution , is estimated by maximizing the log-likelihood:
| (2) |
Where .
Due to the nature of data for Ecuadorian case, only the exponential and maximum likelihood estimation methods were available. There are different settings for the computing of in order to determine the behavior in contagious growth but they require more variables which are not present in our dataset.
2.3.2. Quantifying the temporal transmission dynamics
2.3.2.1. Bettencourt model
Bettencourt’s original model considers a Bayesian framework to feed dynamically the posterior distribution of parameter at time as new prior so that it is possible to consider previous evidence (Bettencourt & Ribeiro, 2008). The concept of the model uses Poisson distribution to model the number of contagious:
| (3) |
Then, the likelihood distribution has the same style as the adjusted model in order to compute :
| (4) |
At this point, values are estimated but the accuracy and quality of last expression could be affected by delays in the test results. That is why same author suggests approaches to amend this issue by considering windows of time and methods to avoid the estimation of additional parameters.
2.3.2.2. Proposed model
In order to develop the methodology for calculated, a Bayesian statistical framework was used to derive the full distribution of the parameter (Bettencourt & Ribeiro, 2008). It must be considered how to model the number of infections inside population. One way to do this, is to model the number of contagious with a Poisson distribution.
| (5) |
Where is the average rate of infections per day, and is the number of contagious expected to have in one day. Now, based on data records it’s only observed the number of cases produced each day. It’s desired to define the distribution for the parameter. This can be done using the likelihood of its poisson probability distribution.
| (6) |
It’s looked for a connection between parameter and the infection rate . The relationship after deriving some math is the next:
| (7) |
The parameter in last expression is about 4 days, the inverse of the serial interval (Du et al., 2020) The value is the number of new contagious in time . According to this, it is possible to reformulate the likelihood in terms of .
| (8) |
With this, it can be explained how to estimate using bayesian inference. The probability distribution of in terms of Bayes rule can be defined as:
| (9) |
Where is the prior distribution for . is the likelihood of having cases given and is the distribution of seeing cases. is known as the posterior distribution of given that cases have appeared. The equation can be rewritten in next form, using the posterior distribution from previous period as new prior:
| (10) |
Setting for all periods, since start , it is reached:
| (11) |
Finally, defining an uniform prior for , leads to:
| (12) |
Last equation is the mathematical expression that allows to compute in dynamic way for all days in an outbreak. It’s highlighted that a concern in estimation can be the lag in test results (Bettencourt & Ribeiro, 2008). For this reason, the probability distribution of can be shifted to consider periods and make estimates more robust:
| (13) |
Previous equation constitutes the improvement to the model proposed by Bettencourt and Ribeiro. Last authors model considering the daily flow of contagious into the likelihood function. Using static cases into the modeling process could produce inappropriate estimations as mentioned by Gostic et Al. in an early preprint. That is why we reformulate the likelihood for posterior estimation of to only consider a period of days. With this is possible to feed the likelihood with proper values that can compile elements like lags in reporting or new cases that can appear due to failures in public health management.
In simulation studies, it is common to use a Montecarlo approach to replicate the behavior of parameters and estimators. After doing a number of simulations, the results are stored in matrices, arrays or vectors. According to central limit theorem, the estimates would be normally distributed around the mean . Having of such as measures , a measure of performance in the estimation of is:
Where:
And:
Based on large numbers theorem and when is large enough so that it tends to , we have:
Last expression was used in our document as performance measure. After simulating epidemic curves, as our parameters and those from original model are estimated at daily level, they were stored in arrays so that it was possible to compute the Montecarlo error below previous definition and show that our proposed method has better performance than Bettencourt’s model(Efron & Tibshirani, 1994).
2.4. Modeling process
Confirmed cases were separated for the following demographic features: overall country, provinces and cantons. All data analysis was conducted on R software version 3.6.2. This information was used to calculate and with its confidence interval and high-density intervals, respectively, as follows:
For estimation as a static quantity, it was estimated the parameters through the methods of exponential growth and maximum likelihood estimation with each confirmed series (using equations from previous section) (Obadia et al., 2012). Finally, confidence intervals were calculated.
For , using each confirmed case,in order to fit an initial overall distribution, likelihood was determined, then the posterior daily probabilities for confirmed cases were obtained, and finally using equations from previous section, the values of at daily level was computed. The shifting process in the estimation of Rt considered adjusting the confirmed cases series with m equals seven in order to avoid lags such as results in new tests. Additionally, to provide quality results, high density intervals (HDI) were derived for all estimates. These intervals are similar to confidence intervals in the frequentist approach but they use Bayesian principles to be shorter and more accurate (Gelman et al., 2013).
In order to contrast our results, we estimate without considering the days period into the likelihood function which belongs to the original concept of Bettencourt and Ribeiro.
To confirm that our method compares well, we have tested our model against the original Bettencourt’s model to estimate . In order to test the performance for estimating , we have conducted a simulation study comparing the two methods (supplementary file 1). The attached simulation generated 105 epidemic curves (samples) for each setting belonging to the set of values defined in 1.5, 2.25, 3 and 4. These quantities are considered as real and based on this parameter each epidemic curve will be generated using a Poisson distribution. Please refer to supplementary file 1 for additional information in this simulated data analysis.
3. Results
Since COVID-19 pandemic outbreak until May 5th, 20 483 cases have been diagnosed in Ecuadorian territory by Reverse Transcriptase Polymerase Chain Reactions (RT-PCR). The mean of daily confirmed cases during this period was 301 infected people per day with a maximum of 1682 cases on April 9th. At province level most of them presented few daily cases but some locations were more affected, such as Guayas reaching a mean of 203 daily confirmed cases (peak: 1462), followed by Pichincha with a mean of 35 cases (peak: 92), Manabí with 19 cases (peak: 66) and Los Ríos with 18 cases (peak: 52).
3.1. National real time reproduction number
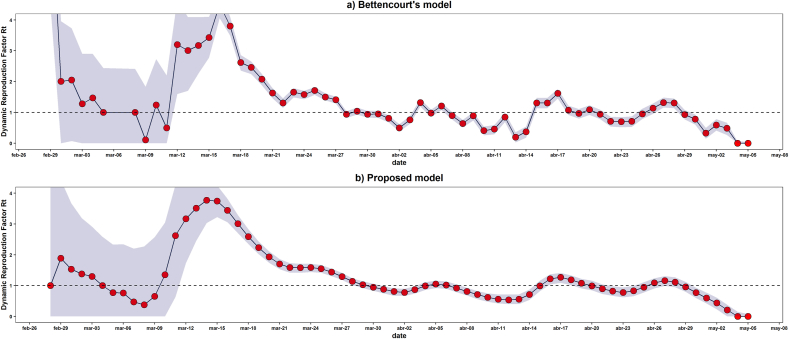
The factor for the global confirmed cases across all dates showed its highest level at March 14th, 2020, where an infected person could spread the virus until 3.77 people (95%HDI: 3.01–4.47) with the proposed model, meanwhile a value of 4.50 people (95%HDI: 4.06–4.91) with Bettencourt’s model was reached at March 16th, 2020. Since that date, estimates started to decrease to final fall below one for the first time at March 30th, 2020 with an estimate of 0.95 (95%HDI: 0.83–1.06) with the proposed model and 0.94 people (95%HDI: 0.83–1.05) with Bettencourt’s model (Fig. 1). Besides, maximum values differences, trends observed with both models’ estimations are quite similar (Fig. 1). In addition, below Pearson scheme there is a correlation of 0.713 which a significant p-value of 2.67^{−11}. In the case of Spearman context, there is a correlation of 0.877 which is significant p-value of 1.01^{−21}. To complement previous results, for all Ecuador with exponential growth criteria was 3.45 (95%CI: 3.37–3.54) and with the maximum likelihood estimation method was 2.93 (95%CI: 2.83–3.04) (Fig. 1).
Fig. 1.
Daily Rt estimation for Ecuador. a) Calcid Rt factor sequence using the Bettencourt’s model, from February 28th to May 5th, 2020, shows its highest peak on March 16 (Rt: 4.50, 95% HDI: 4.06–4.91). b) Rt factor sequence calculated using the proposed model from February 28th to May 5th, 2020, shows its highest peak on March 14 (Rt: 3.77, 95% HDI: 3.01–4.47). The trend followed by the daily recommendations in both models, represent a similar behaviour, however, the recommendations from the Bettencourt model are plotted with the most exaggerated main Rt values compared to those belonging to the proposed model.
3.2. Age and gender analysis
According to estimates by age group and gender in Ecuador, the most prevalent groups were 15–19 years, followed by 20–49 years and 50–64 years that reached highest estimates of 3.77, 3.77 and 3.6, respectively. In the case of gender, female population had of 3.85 while male had 3.58.
3.3. Province estimations
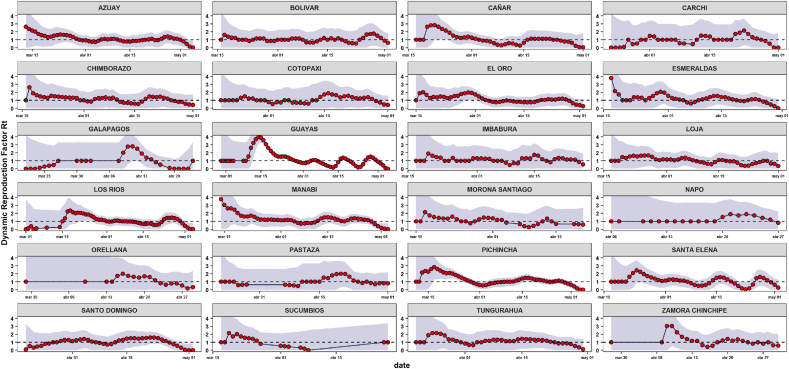
Regarding to provinces in Ecuador, Guayas reached the highest at March 14th, 2020 with 3.96 (95%HDI: 3.07–4.76) people being infected by one sick person with the proposed method and 4.91 (95%HDI: 4.4–5.39) with Bettencourt’s method. There was a similar situation with Pichincha and Manabí with values of 2.83 (95%HDI: 1.32–4.22) and 3.77 (95%HDI: 0–7.5) with the proposed method on March 17th and 14th, respectively. For the rest of provinces, the maximal was close to two. Furthermore, Guayas had a sharp decline in the value of its estimates after reaching the highest value, while Pichincha and Manabí showed a slight drop (Fig. 2).
Fig. 2.
Daily Rt estimation for Ecuadorian Provinces by proposed model.
Similar trends were observed with Bettencourt estimations in (Supplementary file 1). The estimated results of at Province level showed that the most affected provinces with exponential growth method would be Zamora Chinchipe, Guayas and Esmeraldas with 3.95 (95%CI: 2.29–6.92), 3.66 (95%CI: 3.55–3.77) and 3.5 (95%CI: 2.44–4.94). Furthermore, regarding below the maximum likelihood method, would be Zamora Chinchipe, Esmeraldas, Sucumbíos with 4.91 (95%CI: 2.11–9.49), 3.45 (95%CI: 2.28–4.97), 3.29 (95%CI: 1.5–6.13) (Table 1).
Table 1.
R0 and Rt estimates for provinces in Ecuador.
| Province | R0 EG (95%CI) | R0 MLE (95%CI) | Max Rt proposed model (95%HDI) | Max Rt Bettencourt model (95%HDI) |
|---|---|---|---|---|
| Azuay | 1.08 (1.04–1.12) | 1.18 (1.05–1.33) | 2.62 (0–5.81) | 5.71 (3.24–7.63) |
| Bolivar | 1.02 (0.94–1.10) | 1.2 (0.95–1.49) | 1.76 (0.31–3.04) | 2.75 (1.2–4.01) |
| Cañar | 2.36 (2.03–2.74) | 2.25 (1.82–2.75) | 2.84 (0.95–4.45) | 4.05 (2.58–5.42) |
| Carchi | 1.36 (1.16–1.57) | 1.6 (1.1–2.25) | 2.15 (0.44–3.75) | 2.24 (0.24–3.91) |
| Chimborazo | 2.16 (1.44–3.1) | 2.45 (1.59–3.56) | 2.62 (0–5.81) | 2.88 (0.17–4.99) |
| Cotopaxi | 1.26 (1.1–1.44) | 1.49 (1.1–1.96) | 1.89 (0.02–3.41) | 2.52 (0.68–4.21) |
| El Oro | 3.16 (2.61–3.82) | 3.14 (2.5–3.89) | 2.01 (0–3.95) | 2.67 (1.93–3.36) |
| Esmeraldas | 3.5 (2.44–4.94) | 3.45 (2.28–4.97) | 3.77 (0–7.43) | 3.87 (2.6–4.97) |
| Galapagos | 2.12 (1.72–2.63) | 2.95 (1.93–4.27) | 2.81 (1.01–4.34) | 5.12 (3.85–6.25) |
| Guayas | 3.66 (3.55–3.77) | 3.08 (2.94–3.22) | 3.96 (3.11–4.76) | 4.91 (4.4–5.39) |
| Imbabura | 1.27 (1.12–1.44) | 1.39 (1.02–1.85) | 1.89 (0–4.49) | 2.62 (0–4.94) |
| Loja | 1.81 (1.55–2.11) | 1.9 (1.49–2.37) | 1.67 (0.4–2.83) | 5.39 (0.55–8.7) |
| Los Rios | 1.28 (1.24–1.33) | 1.2 (1.09–1.32) | 2.35 (0.61–3.88) | 2.36 (1.08–3.43) |
| Manabí | 1.33 (1.27–1.4) | 1.43 (1.28–1.6) | 3.77 (0–7.44) | 3.77 (0.87–6.22) |
| Morona Santiago | 1.57 (1.21–1.99) | 1.84 (1.13–2.8) | 2.15 (0–4.96) | 3.77 (0–7.45) |
| Napo | 1.86 (1.43–2.42) | 1.93 (1.09–3.13) | 1.89 (0–3.43) | 1.95 (0.22–3.46) |
| Orellana | 2.08 (1.63–2.68) | 2.25 (1.34–3.5) | 2.01 (0–3.96) | 2.62 (0–5.76) |
| Pastaza | 1.64 (1.34–2.01) | 2.08 (1.37–2.99) | 2.01 (0.12–3.48) | 3.04 (1.14–4.64) |
| Pichincha | 1.26 (1.23–1.29) | 1.32 (1.23–1.4) | 2.83 (1.27–4.14) | 3.04 (1.75–4.08) |
| Santa Elena | 1.44 (1.3–1.59) | 1.53 (1.31–1.78) | 2.43 (0.97–3.84) | 3.77 (2.33–5.05) |
| Santo Domingo | 1.5 (1.38–1.63) | 1.64 (1.37–1.94) | 1.6 (0.75–2.32) | 2.23 (1.22–3.18) |
| Sucumbíos | 3.44 (2.19–5.62) | 3.29 (1.5–6.13) | 2.15 (0–5.02) | 3.77 (0.48–6.3) |
| Tungurahua | 1.46 (1.26–1.67) | 1.61 (1.23–2.07) | 2.15 (0.11–3.92) | 2.62 (0.7–4.26) |
| Zamora Chinchipe | 3.95 (2.29–6.92) | 4.91 (2.11–9.49) | 3.04 (0.35–5.03) | 7.16 (4.89–9.1) |
MLE: Maximum likelihood estimation; EG: Exponential growth; Max: Maximum, CI: confidence interval; HDI: High density interval.
3.4. Cantons estimations
As mentioned before, most affected provinces due to the highest number of confirmed cases of COVID-19 were Guayas, Pichincha and Manabí. In Guayas, the cantons with the highest with the proposed model were Samborondón with 5.39 (95%HDI: 1.86–8.28), Daule with 4.39 (95%HDI: 1.06–6.83) and Milagro with 4.39 (95%HDI: 1.07–6.94). Contrasting with the cantons of Pichincha, Quito got 2.83 (95%HDI: 1.31–4.18), Rumiñahui 1.53 (95%HDI: 0–3.65) and Mejía 1.01 (95%HDI: 0–3.28). Finally, in Manabí were Sucre 3.77 (95%HDI: 0–7.44), Jipijapa 2.62 (95%HDI: 0–5.72), Manta 2.62 (95%HDI: 0–4.99). On the other hand, estimations were replicated for cantons (Supplementary file 1). Below exponential growth criteria, the most affected cantons would be Samborondón with 23.42 (95%CI: 14.6–39) and El Triunfo with 15.49 (95%CI: 3.99–51.06). Whilst below maximum likelihood estimation would be El Triunfo and Samborondón with 14.09 (95%CI: 6.44–26.23) and 12.77 (95%CI: 9.55–16.65), respectively.
4. Discussion
From the first case of COVID-19 reported in Wuhan China in December 2019, the disease spread globally easily, for this reason, on March 11th 2020 was declared a pandemic(C. Zhang et al., 2020b). During the initial growth phases of viral transmission, sanitary control measures would determinate population final outcome (Omori et al., 2020). For a comprehensive evaluation of pandemic trends, some static measures (and time dynamic models had been developed (Forsberg White & Pagano, 2008; Ridenhour et al., 2018; Wallinga & Lipsitch, 2007). In this study, Ecuadorian COVID-19 onset with two described methods and two models was evaluated, one of them previously described by Bettencourt et al. (Bettencourt & Ribeiro, 2008) and a novel proposed method.
Present study has an improvement and shift for seminal research in Bayesian methods used for estimation. Instead of formulating complex likelihood function of , we use the direct relationship between and the Poisson distribution, avoiding the addition for new parameters in the distribution setting. Moreover, the possible approximation to one of posterior distribution is amended configuring the likelihood for posterior computing to consider only last m days. This approach makes estimates more sensitive around the behavior of parameters considered inside formulation giving a better view of how estimates will evolve during the outbreak. Last, Pearson and Spearman framework demonstrated a strong correlation between two models. For instance, adding parameters, the evaluation of adopted public health policies could be possible (Yuan et al., 2020).
The average for Ecuador in the period February 28th, 2020 to May 5th, 2020 is 1.26 which is far from estimates from exponential growth and maximum likelihood method with 3.45 and 2.93, respectively. This could mean that despite of estimates are below one, the global situation of Ecuador is still not controlled because the average is over one and the directions from show also over the unit. To contrast, epidemiological data in COVID-19 outbreak in Latin American countries is limited(Simbana-Rivera et al., 2020). However, Caicedo-Ochoa et al. using Li (Li et al., 2020) and Nishiura (Nishiura et al., 2020) methods compared for some Latin American and European countries in the early stage of COVID-19 pandemics. This data demonstrated a median of 3.95 and 12.86 with Nishiura and Li methods, respectively for Ecuador, which compared which were the highest between the nine countries studied (Effective Reproductive Number Estimation for Initial Stage of COVID-19 Pandemic in Latin American Countries - International Journal of Infectious Diseases, n.d.). Additionally, in the same study, Ecuador, Panama and Brazil obtained values over Spain and Italy on the first 10 days of outbreak. Those results demonstrated a near approach between Nishiura methodology and our new proposed framework. This could be due to both approximations are based on a more conservative data management but differs in the use of the distribution for the parameter in their calculation.
In Ecuador, the first confirmed case of COVID-19 was reported on February 29th, then the number of infections increased dramatically, however only local measures were adopted, thus a consequence of was evident until reach its peak on the second week of March 2020 (Ortiz-Prado, Diaz, et al., 2020). Just one day before, on March 13th, the first death related to pandemic was confirmed (Ministerio de Salud Pública, n.d.) and at that time all events over 1000 people and classes were suspended in the nation ((Metro, n.d.)-(Ecuador Suspende Todas Las Clases Por COVID-19 - Educación - Vida - ELTIEMPO.COM, n.d.)). As of March 17th, measures of social isolation began, taking compulsory quarantine as the main action (El Universo, 2020). The sum of both interventions are highly related to the evident continuous decrease in the values of since March 18th, which mostly show a decrease from the beginning of the quarantine state. This study also evidenced that it took almost 2 weeks to get a value of around the unit, which finally keeps with no great variations until end of April.
In terms of and by provinces, the trends are similar to the whole nation but provinces which surpass the maximum whole nation as Guayas, Esmeraldas and Manabí, all of them located in coastal region and related geographically. This findings are in current with local newspaper that reports a high mortality in Guayas (CNN Latinoamérica, 2020; España, 2020). This situation could be most severe in this province due to high population concentration over four million inhabitants in the 2020 projection (Instituto Nacional de Estadística y Censos, n.d.). Concerning to Manabí on April 24th, became the province with more daily confirmed cases in the nation (El Telégrafo-Noticias del Ecuador y del mundo, 2020; Primicias, n.d.; Servicio Nacional de Gestión de Riesgos y Emergencias, n.d.), however mortality at that time was 5 times less than Guayas. In contrast, provinces with a maximum lower than two were Santo Domingo, Loja, Bolivar and Cotopaxi. This could be due to geographical location and adequate temporal control of the outbreak. Finally, Quito, capital of Ecuador, had a population of almost three million inhabitants, showed a maximum of 2.83 and a around of 1.3. This means that the situation became more controlled and the local decisions performed since March 12th were temporally adequate (El Comercio, n.d.-a). Another reason that explains the increased transmissibility in these localities are cities dispersion patterns, on one hand, could be observed a radial configuration like in the lower basin of Guayas river, whilst, in a linear configuration in most of the valleys cities of highlands could be responsible of a different kind of flow of mobility, contiguity and neighborhood (ARO, 2020; “Así se propagó el coronavirus en la provincia de Guayas,” n.d.; El Comercio, n.d.-b; COE NACIONAL, MINISTERIO DE GOBIERNO ECUADOR, 2020).
Regarding cantons, Samborondón despite not having much population density, some massive events took place that allowed the spread and contagion (“Así se propagó el coronavirus en la provincia de Guayas,” n.d.). This canton had the highest contagion rate in the country for April 9th, with 254 inhabitants infected for every 100 000 inhabitants (“Así se propagó el coronavirus en la provincia de Guayas,” n.d.). In concordance, with our findings this canton had the highest in the whole nation followed by Daule and Milagro.
In conclusion, the proposed model in this study estimates a similar trend of the contagion’s behavior within the population, in relation to the models proposed by other authors. Additionally, it demonstrated smaller high density intervals and a dismiss number of needed covariates, thus this novel approach could be an appropriate tool to measure dispersal outbreak with low access data. Related to Ecuador, adequate reproductive number modelling allows a better understanding of local transmission and temporal decision analysis. Lastly, an adequate public health valuation of this estimations could further intensify health local measures.
5. Limitations
The most important limitation of these data-driven estimations are the quality of national confirmed cases reports that was caused by a delayed processing test as was reported by Ecuadorian Minister of Health (Los Casos Se Duplican En Ecuador, Pero Todavía Hay Déficit de Pruebas, n.d.). Additionally, the fact that other countries had publicized a more detailed database has allowed to compute confirmed cases series by clusters, according to potential points of contagious which is the best modelling of reproductive number available (Wu et al., 2020). However, it was not possible to calculate because of the basic database information available.
Due to the limited information (only one data series of confirmed cases), it was not possible to determine the nature of confirmed cases growth. That is why we modified the formulation of Bettencourt and Ribeiro in order to have an approach for based on Bayesian inference to obtain more accurate estimations and for we showed the results from two known estimation methods in order to give a summary about the contagious situation if no health policies were adopted.
Funding
The author(s) disclosed receipt the financial support for the research and publication of this article from Universidad de Las Américas through their annual general research projects funds.
Declaration of competing interest
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Acknowledgements
We would like to Thank Universidad de las Americas for providing the funds to complete this investigation.
Handling editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.idm.2020.12.012.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- ARO . Diario El Mercurio; 2020, April 6. Los posibles escenarios del coronavirus en Ecuador creados con datos de movilidad.https://ww2.elmercurio.com.ec/2020/04/06/los-posibles-escenarios-del-coronavirus-en-ecuador-creados-con-datos-de-movilidad/ [Google Scholar]
- Así se propagó el coronavirus en la provincia de Guayas. (n.d.). Primicias. Retrieved May 30, 2020, from https://www.primicias.ec/noticias/sociedad/propagacion-coronavirus-provincia-guayas/.
- Bettencourt L.M.A., Ribeiro R.M. Real time bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS One. 2008;3(5):e2185. doi: 10.1371/journal.pone.0002185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breban R., Riou J., Fontanet A. Interhuman transmissibility of Middle East respiratory syndrome coronavirus: Estimation of pandemic risk. The Lancet. 2013;382(9893):694–699. doi: 10.1016/S0140-6736(13)61492-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauchemez S., Fraser C. 2014. Middle East respiratory syndrome coronavirus: Quantifi cation of the extent of the epidemic, surveillance biases, and transmissibility. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CNN Latinoamérica . CNN; 2020, April 2. Coronavirus en Ecuador: Cuerpos en las calles de Guayaquil en medio de la pandemia.https://cnnespanol.cnn.com/video/guayaquil-coronavirus-ecuador-cuerpos-muertos-calle-pandemia-pkg-kay-guerrero-reporte-k-conclusiones/ [Google Scholar]
- COE NACIONAL, Ministerio DE Gobierno Ecuador . 2020. COVID-19 EN EL Ecuador. TENDENCIA TEMPORO ESPACIAL DE LA PANDEMIA del 27 de febrero al 19 de abril del 2020. [Google Scholar]
- Du Z., Xu X., Wu Y., Wang L., Cowling B.J., Meyers L.A. The serial interval of COVID-19 from publicly reported confirmed cases. MedRxiv. 2020 doi: 10.1101/2020.02.19.20025452. 2020.02.19.20025452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecuador suspende todas las clases por COVID-19—Educación—Vida—ELTIEMPO.COM. (n.d.). Retrieved May 30, 2020, from https://www.eltiempo.com/vida/educacion/ecuador-suspende-todas-las-clases-por-covid-19-472146.
- Effective Reproductive Number estimation for initial stage of COVID-19 pandemic in Latin American Countries—International Journal of Infectious Diseases. (n.d.). Retrieved May 25, 2020, from https://www.ijidonline.com/article/S1201-9712(20)30285-X/fulltext. [DOI] [PMC free article] [PubMed]
- Efron B., Tibshirani R.J. CRC press; 1994. An introduction to the bootstrap. [Google Scholar]
- El Telégrafo-Noticias del Ecuador y del mundo Manabí supera en contagios por covid-19 a Pichincha. El Telégrafo - noticias del Ecuador y del mundo. 2020, April 24. https://www.eltelegrafo.com.ec/noticias/sociedad/6/manabi-contagios-pichincha-coronavirus
- El Universo D. Las medidas que toma Ecuador, en emergencia sanitaria por coronavirus: Cuarentena de pasajeros internacionales, suspensión de clases y eventos masivos. El Universo. 2020, March 12. https://www.eluniverso.com/noticias/2020/03/12/nota/7778376/coronavirus-ecuador-viaje-restriccion-vuelos-pasajeros-aeropuertos
- El Comercio. (n.d.-b, El Comercio. (n.d.-b). Retrieved May 30, 2020, from https://www.elcomercio.com/tag/covid-19/278.
- España S. El coronavirus desborda Ecuador y abruma a su población por la acumulación de cadáveres en casas. EL PAÍS. 2020, April 1. https://elpais.com/sociedad/2020-04-01/el-coronavirus-desborda-ecuador-y-abruma-a-su-poblacion-por-la-acumulacion-de-cadaveres-en-casas.html
- Ferrari M.J., Bjørnstad O.N., Dobson A.P. Estimation and inference of R0 of an infectious pathogen by a removal method. Mathematical Biosciences. 2005;198(1):14–26. doi: 10.1016/j.mbs.2005.08.002. [DOI] [PubMed] [Google Scholar]
- Forsberg White L., Pagano M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Statistics in Medicine. 2008;27(16):2999–3016. doi: 10.1002/sim.3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A., Carlin J.B., Stern H.S., Dunson D.B., Vehtari A., Rubin D.B. 3rd ed. CRC Press; 2013. Bayesian data analysis. [Google Scholar]
- Hens N., Van Ranst M., Aerts M., Robesyn E., Van Damme P., Beutels P. Estimating the effective reproduction number for pandemic influenza from notification data made publicly available in real time: A multi-country analysis for influenza A/H1N1v 2009. Vaccine. 2011;29(5):896–904. doi: 10.1016/j.vaccine.2010.05.010. [DOI] [PubMed] [Google Scholar]
- Instituto Nacional de Estadística y Censos. (n.d.). Proyecciones Poblacionales. Instituto Nacional de Estadística y Censos. Retrieved June 5, 2020, from https://www.ecuadorencifras.gob.ec/proyecciones-poblacionales/.
- Instituto Nacional de Estadística y Censos . Instituto Nacional de Estadística y Censos; 2019. Actividades y recursos de Salud.https://www.ecuadorencifras.gob.ec/actividades-y-recursos-de-salud/ [Google Scholar]
- Ishii T. 2020. Measures against the spread of COVID-19: Simultaneous international action and lockdown postponement. Available at: SSRN 3572862. [Google Scholar]
- Kermack W.O., Mckendrick A.G. Laboratory of the Royal College of Physicians; Edinburgh, U.K: 1991. Contributions to the mathematical theory OF epidemics--I∗. [Google Scholar]
- Kucharski A. 2020. The rules of contagion: Why things spread-and why they stop. [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Wong J.Y., Xing X., Xiang N., Wu Y., Li C., Chen Q., Li D., Liu T., Zhao J., Liu M.…Feng Z. Early transmission dynamics in wuhan, China, of novel coronavirus–infected pneumonia. New England Journal of Medicine. 2020;382(13):1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Los casos se duplican en Ecuador, pero todavía hay déficit de pruebas El Comercio. http://www.elcomercio.com/actualidad/ecuador-deficit-pruebas-coronavirus-covid19.html n.d. Retrieved May 30, 2020, from.
- Ma J. Estimating epidemic exponential growth rate and basic reproduction number. Infectious Disease Modelling. 2020;5:129–141. doi: 10.1016/j.idm.2019.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandal M., Jana S., Nandi S.K., Khatua A., Adak S., Kar T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos, Solitons & Fractals. 2020;136:109889. doi: 10.1016/j.chaos.2020.109889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metro, E. (n.d.). Medidas del Gobierno ante coronavirus en Ecuador: Se suspenden eventos públicos masivos. Metro Ecuador. Retrieved June 5, 2020, from https://www.metroecuador.com.ec/ec/noticias/2020/03/12/medidas-del-gobierno-ante-coronavirus-en-ecuador-se-suspenden-eventos-masivos.html.
- Ministerio de Salud Pública, E. (n.d.). Ministra de Salud confirma muerte de paciente por COVID-19. Retrieved June 5, 2020, from https://www.salud.gob.ec/ministra-de-salud-confirma-muerte-de-paciente-por-covid-19/.
- Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. International Journal of Infectious Diseases. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obadia T., Haneef R., Boëlle P.-Y. The R0 package: A toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Medical Informatics and Decision Making. 2012;12(1):147. doi: 10.1186/1472-6947-12-147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omori R., Mizumoto K., Chowell G. Changes in testing rates could mask the novel coronavirus disease (COVID-19) growth rate. International Journal of Infectious Diseases. 2020;94:116–118. doi: 10.1016/j.ijid.2020.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortiz-Prado E., Diaz A.M., Barreto A., Moyano C., Arcos V., Vasconez-Gonzalez E.…Fernandez-Naranjo R. Epidemiological, socio-demographic and clinical features of the early phase of the COVID-19 epidemic in Ecuador. MedRxiv. 2020 doi: 10.1371/journal.pntd.0008958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortiz-Prado E., Simbaña-Rivera K., Gómez-Barreno L., Rubio-Neira M., Guaman L.P., Kyriakidis N.C.…Cevallos-Robalino D. Diagnostic Microbiology and Infectious Disease; 2020. Clinical, molecular and epidemiological characterization of the SARS-CoV2 virus and the Coronavirus disease 2019 (COVID-19), a comprehensive literature review; p. 115094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Primicias 24 de abril: Los casos de Covid-19 registrados en Ecuador son 22.719. Primicias. https://www.primicias.ec/noticias/sociedad/24-abril-casos-covid-registrados-ecuador/ n.d. Retrieved June 5, 2020, from.
- Ridenhour B., Kowalik J.M., Shay D.K. El número reproductivo básico (R0): Consideraciones para su aplicación en la salud póblica. American Journal of Public Health. 2018;108(S6):S455–S465. doi: 10.2105/AJPH.2013.301704s. [DOI] [PubMed] [Google Scholar]
- Servicio Nacional de Gestión de Riesgos y Emergencias Informes de Situación e Infografias – COVID 19 – desde el 29 de Febrero del 2020. https://www.gestionderiesgos.gob.ec/informes-de-situacion-covid-19-desde-el-13-de-marzo-del-2020/ n.d. Retrieved June 5, 2020, from.
- Simbana-Rivera K., Gomez-Barreno L., Guerrero J., Simbana-Guaycha F., Fernandez R., Lopez-Cortes A., Lister A., Ortiz-Prado E. Interim analysis of pandemic coronavirus disease 2019 (COVID-19) and the SARS-CoV-2 virus in Latin America and the caribbean: Morbidity, mortality and molecular testing trends in the region. MedRxiv. 2020 doi: 10.1101/2020.04.25.20079863. 2020.04.25.20079863. [DOI] [Google Scholar]
- Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences. 2007;274(1609):599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in wuhan, China: A modelling study. The Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J., Li M., Lv G., Lu Z.K. Monitoring transmissibility and mortality of COVID-19 in Europe. International Journal of Infectious Diseases. 2020;95:311–315. doi: 10.1016/j.ijid.2020.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S., Diao M., Yu W., Pei L., Lin Z., Chen D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond princess cruise ship: A data-driven analysis. International Journal of Infectious Diseases. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C., Huang S., Zheng F., Dai Y. Controversial treatments: An updated understanding of the coronavirus disease 2019. Journal of Medical Virology. 2020 doi: 10.1002/jmv.25788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S., Lin Q., Ran J., Musa S.S., Yang G., Wang W., Lou Y., Gao D., Yang L., He D., Wang M.H. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. International Journal of Infectious Diseases. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.