Spatial Agreement of Brainstem Dose Distributions Depending on Biological Model in Proton Therapy for Pediatric Brain Tumors

Abstract

Purpose

During radiation therapy for pediatric brain tumors, the brainstem is a critical organ at risk, possibly with different radio-sensitivity across its substructures. In proton therapy, treatment planning is currently performed using a constant relative biological effectiveness (RBE) of 1.1 (RBE_1.1), whereas preclinical studies point toward spatial variability of this factor. To shed light on this biological uncertainty, we investigated the spatial agreement between isodose maps produced by different RBE models, with emphasis on (smaller) substructures of the brainstem.

Methods and Materials

Proton plans were recalculated using Monte Carlo simulations in 3 anonymized pediatric patients with brain tumors (a craniopharyngioma, a low-grade glioma, and a posterior fossa ependymoma) to obtain dose and linear energy transfer distributions. Doses and volume metrics for the brainstem and its substructures were calculated using a constant RBE_1.1, 4 phenomenological RBE models with varying (α/β)_x parameters, and with a simpler linear energy transfer-dependent model. The spatial agreement between the dose distributions of constant RBE_1.1 versus the variable RBE models was compared using the Dice similarity coefficient.

Results

The spatial agreement between the variable RBE dose distributions and RBE_1.1 decreased with increasing isodose levels in all patient cases. The patient with ependymoma showed the greatest variation in dose and dose volumes, where V_50Gy(RBE) in the brainstem increased from 32% (RBE_1.1) to 35% to 49% depending on the applied model, corresponding to a spatial agreement (Dice similarity coefficient) between 0.79 and 0.95. The remaining patients showed similar trends, however, with lower absolute values due to lower brainstem doses.

Conclusions

All phenomenological RBE models fully enclosed the isodose volumes of the constant RBE_1.1, and the volumes based on variable RBE spatially agreed. The spatial agreement was dependent on the isodose level, where higher isodose levels showed larger expansions and less agreement between the variable RBE models and RBE_1.1.

Introduction

Pediatric patients with brain tumors are often referred to proton therapy instead of photon-based radiation therapy with the aim of reducing doses to normal tissues. Whereas proton therapy has the potential to increase the conformity of the physical dose deposition, there is considerable uncertainty connected to its relative biological effectiveness (RBE). In current treatment planning practice, protons are assumed to be uniformly 10% more effective than photons, expressed as a constant RBE of 1.1 (RBE_1.1). However, the RBE is known to vary depending on several factors, such as the linear energy transfer (LET), physical dose per fraction, tissue fractionation sensitivity (ie, [α/β]_x ratio in the linear quadratic model), and clinical endpoint.^1,2

Brainstem injury after cranial radiation therapy is a rare but serious side effect^3,4 and is a particular concern for patients with tumors located in the vicinity of the brainstem.⁵ During treatment planning, maintaining the brainstem dose below established tolerance levels has the highest priority. Substructures of the brainstem may, in addition, have different radio-sensitivities,^6,7 and to enable further risk mitigation, smaller structures could benefit from being constrained by separate tolerance dose levels. To detect and apply dose limitations to substructures, accurate modeling of the RBE is a prerequisite.

The RBE depends on the plan configuration, and the LET distribution in the brainstem can be substantially different depending on tumor location and field configuration.⁸ The brainstem is furthermore recognized to have a low (α/β)_x ratio, which has been associated with higher RBE.^9,10 Clinical evidence of variable RBE is starting to emerge; a recent study of pediatric patients with medulloblastoma who experienced brainstem morbidity after proton therapy reported slightly elevated LET values in areas of symptomatic image changes.¹¹ Indications of variable RBE in proton therapy have also been observed in pediatric patients with ependymoma¹² and glioma.^13,14

Whereas proton treatment plans are commonly evaluated based on dose-volume histograms, there has so far been no systematic investigation of the spatial agreement of different RBE models, nor has there been any examination of how variable RBE models would influence the brainstem and substructures in pediatric patients with brain tumors. Considering that all clinical data from proton therapy are based on an RBE of 1.1, an important step toward including this biological uncertainty is to identify how the isodose maps from different variable RBE models spatially correlate to volumes from constant RBE. If variable RBE models scale incoherently in regard to dose level, (α/β)_x ratios, and LET, it could lead to conflicting criteria during treatment planning depending on the RBE model, in addition to complicating the evaluation of dose-volume constraints based on variable RBE in a clinical setting.

The main objective of this study was therefore to investigate how different variable RBE models influence isodose volumes in the brainstem and substructures for typical pediatric brain tumor entities, and in particular to identify potential spatial shifts between the isodose volumes using variable and constant RBE models.

Methods and Materials

Patient materials and treatment plans

The patient material included computed tomography and magnetic resonance imaging scans with structure delineations for 3 anonymized pediatric patients with brain tumors, with craniopharyngioma, a low-grade glioma, and a posterior fossa ependymoma (located in vicinity of the brainstem) (Fig E1). The full brainstem, brainstem surface (outer 3 mm), and brainstem core (brainstem cropped by 3 mm), in addition to the clinical target volumes (CTVs) and planning target volumes (PTVs) from the clinical structure set, were delineated for treatment planning. The PTV was defined using a 3-mm margin for the CTV. For the purpose of this study, fused computed tomography–magnetic resonance imaging scans were used to further delineate the 3 main substructures of the brainstem: the midbrain, pons, and medulla oblongata.

The intensity modulated proton therapy (IMPT) plans for the patients used 3 fields (1 vertex and 2 lateral oblique fields) and a dose of 54 Gy(RBE) over 30 fractions to the PTVs. For the patient with ependymoma, an additional 3-fraction boost for a total of 5.4 Gy(RBE) was delivered to the center of the PTV using 2 lateral opposing fields. The IMPT plans were multifield optimized based on an RBE of 1.1 in the Eclipse (Varian Medical Systems, Palo Alto, CA) treatment planning system.

Monte Carlo simulations

The IMPT plans were recalculated using the FLUKA Monte Carlo code^15,16, 17 and Flair¹⁸ to obtain biological doses, dose-averaged LET (LET_d) distributions, and LET spectra (details found in reference 8). Each treatment field was simulated with 50 million primary particles to obtain statistical uncertainties below 0.5% in the target volume. The physical dose was scored for all particles, whereas the LET was scored for primary and secondary protons only. The quantities were scored in the patient geometries employing Hounsfield units to material density conversions as described by Schneider et al¹⁹ and Parodi et al.²⁰ The dose and LET were further converted to their water equivalent quantities using density ratios, resulting in dose-to-water and LET-in-water. The scoring was done on a voxel-by-voxel basis using the same grid and voxel size (1.95 × 1.95 × 1.00 mm³) that were used during the IMPT plan optimization.

RBE models

To evaluate variable RBE-weighted dose distributions we used 4 phenomenological RBE models: the Wedenberg (WED),²¹ McNamara (MCN),²² and Carabe-Fernandez (CAR)²³ models (based on a linear relation between RBE and LET). In addition, we used a model developed by Rørvik et al (ROR)²⁴ based on a nonlinear relationship between RBE and LET. These models were selected because they are based on a high number of experimental data points for low (α/β)_x ratios and LET values, while at the same time predicting different RBEs based on the remaining model dependencies. Further details on the different models are described elsewhere.²⁵

Well-established data on (α/β)_x ratios for the brain and brainstem are limited and the uncertainties are large. To evaluate the effect of variation in these parameters, the patients were simulated using 3 different ratios²⁶ of 2.1,⁷ 2.5,²⁷ and 3.3 Gy²⁸ for the entire brain, including the brainstem and its substructures.

Owing to the (α/β)_x ratio uncertainties, we also used the LET-weighted dose (LWD),²⁹ which represents RBE variations exclusively depending on LET_d, disregarding biological aspects such as the (α/β)_x ratio. The LWD was initially designed for LET_d optimization of proton plans and was normalized with a factor such that the RBE in the center of a spread-out Bragg peak (range, 10 cm; modulation width, 5 cm) equals 1.1.^2,29 We therefore scaled the LWD such that the median RBE was equal to 1.1 in the CTV of the patient.

Analysis

The 3-dimensional spatial agreement of the isodose volumes from the RBE models was compared using the Dice similarity coefficient (DSC),³⁰ that is, with DSC = 1 representing full overlap between isodose volumes and DSC = 0 representing no overlap (Fig E2). The DSCs were calculated for biological isodose volumes in 5 Gy(RBE) steps within the brainstem and its substructures for each model relative to the RBE_1.1 isodose volumes. By employing logical relations, we also investigated whether isodose volumes from the variable RBE models would fully encompass the RBE_1.1 volumes or if, in certain cases, the isodose volumes would be shifted and only partially overlap.

Results

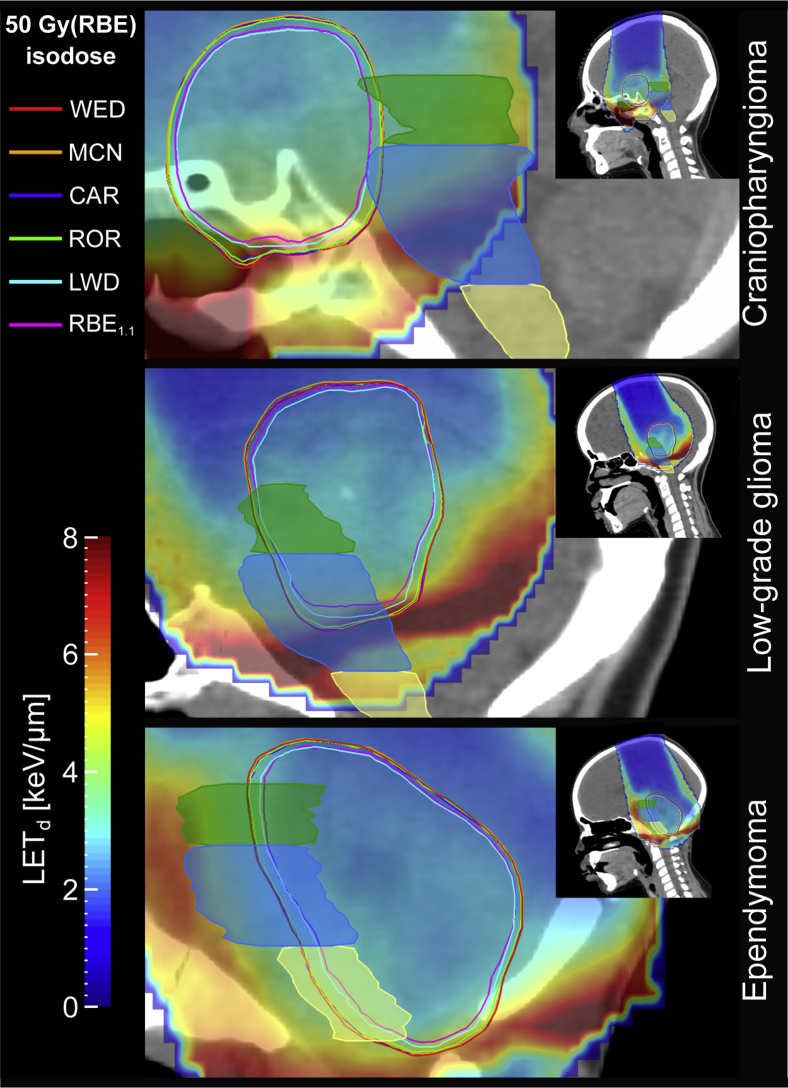
The biological isodose volumes from the 4 phenomenological RBE models were systematically larger than when calculated using LWD and RBE_1.1 for all patients and structures, and thereby extended further into the brainstem. RBE_1.1 and LWD showed similar isodose volumes; however, for regions with higher LET_d the distance between the isodose curves increased (Fig 1). In all cases, the isodose volumes from the 4 phenomenological RBE models fully enclosed the RBE_1.1, whereas the LWD was shifted by a negligible amount relative to RBE_1.1 for a few isodose levels and structures. The largest shift resulted in an RBE_1.1 volume of only 0.05 cm³ that was not included in the LWD volume.

Figure 1.

50 Gy(RBE) isodose curves ([α/β]_x = 2.1 Gy) and LET_d distributions for the 3 patients. Delineated structures are midbrain (green), pons (blue), and medulla oblongata (yellow). The LET_d in voxels receiving doses below 0.1 Gy(RBE) according to the RBE_1.1 dose is set transparent. Abbreviations: CAR = Carabe; LET_d = dose-averaged linear energy transfer; LWD = LET-weighted dose; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg. (A color version of this figure is available at https://doi.org/10.1016/j.adro.2020.08.008.)

The V_50Gy(RBE) of the brainstem and its substructures was higher when calculated with the 4 phenomenological RBE models than according to the LWD model and with RBE_1.1 (Fig 2). For the patient with ependymoma, the V_50Gy(RBE) increased from 32% with RBE_1.1 to 35% with LWD (DSC, 0.95), 46% with ROR (DSC, 0.83), 48% with CAR (DSC, 0.81), 49% with MCN (DSC, 0.80), and 49% with WED (DSC, 0.79). The trends were similar for the other patients, however, with different absolute values.

Figure 2.

V_50Gy(RBE) metrics and corresponding Dice similarity coefficients within the brainstem and substructures for the 3 patients. (α/β)_x = 2.1 Gy was used for the phenomenological RBE models. Abbreviations: CAR = Carabe; DSC = dice similarity coefficient; LWD = LET-weighted dose; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg.

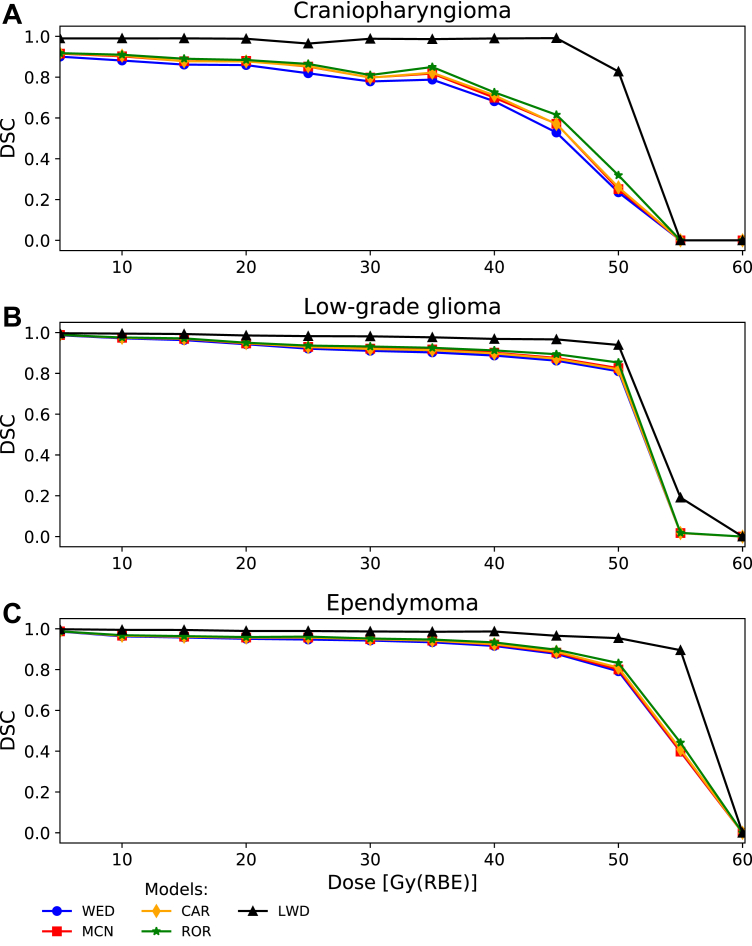
The dose distributions found with the LWD model showed better spatial agreement in the brainstem with the RBE_1.1 dose than the 4 phenomenological RBE models at all dose levels (Fig 3). The LWD also had the least increase in RBE with respect to LET_d (Fig E3). The spatial agreement between the RBE_1.1 isodoses and the 4 phenomenological RBE models showed the same trends at all dose levels, with marginally higher DSCs for the ROR model and marginally lower DSCs for the WED model (Fig 3). Across the models the DSCs were relatively high for lower isodose levels but decreased rapidly for higher doses (Fig 3). The dose level at which the decrease occurred was dependent on the evaluated patient, but the trends seen in the entire brainstem were also apparent for the midbrain and pons (Fig E4).

Figure 3.

Dice similarity coefficients relative to RBE_1.1 for every 5 Gy(RBE) isodose step in the brainstem for the 3 patients. (α/β)_x = 2.1 Gy was used for the phenomenological RBE models. Abbreviations: CAR = Carabe; DSC = dice similarity coefficient; LWD = LET-weighted dose; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg.

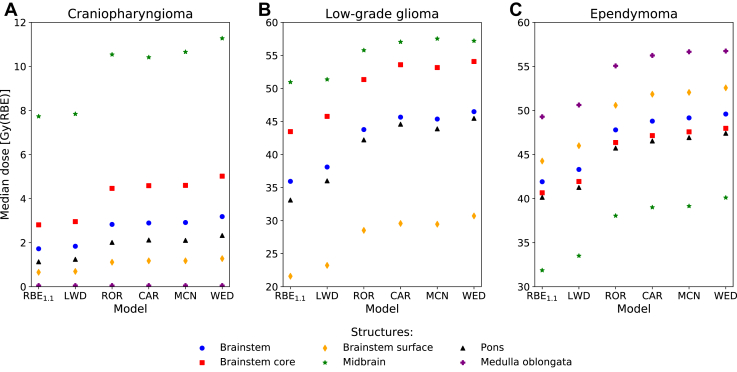
The trends for the variation in the median doses were similar for all patients, typically with WED, MCN, and CAR calculating the highest doses, followed by ROR, LWD, and RBE_1.1, respectively. In the patient with ependymoma, the medulla oblongata received the highest median dose of 49.3 Gy(RBE) using RBE_1.1, increasing up to 56.7 Gy(RBE) for the WED model. For the patient with craniopharyngioma, the highest median dose was observed in the midbrain (RBE_1.1: 7.7 Gy[RBE] up to WED: 11.3 Gy[RBE]). Similarly, the midbrain in the patient with glioma also reported the highest median dose of 51.0 Gy(RBE) from RBE_1.1, increasing up to 57.5 Gy(RBE) for the MCN model (Fig 4). Overall, the WED model estimated the largest increase in the median biological dose of the full brainstem relative to RBE_1.1 in all patients, up to 10.5 Gy(RBE). For the substructures, the same model showed the largest increase in the pons of 12.4 Gy(RBE) for the patient with glioma (Table E1).

Figure 4.

Median dose (D_50%) in the brainstem and substructures for the 3 patients. (α/β)_x = 2.1 Gy was used for the phenomenological RBE models. The medulla oblongata for the patient with glioma is not shown due to doses of 0 Gy(RBE). Abbreviations: CAR = Carabe; LWD = LET-weighted dose; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg.

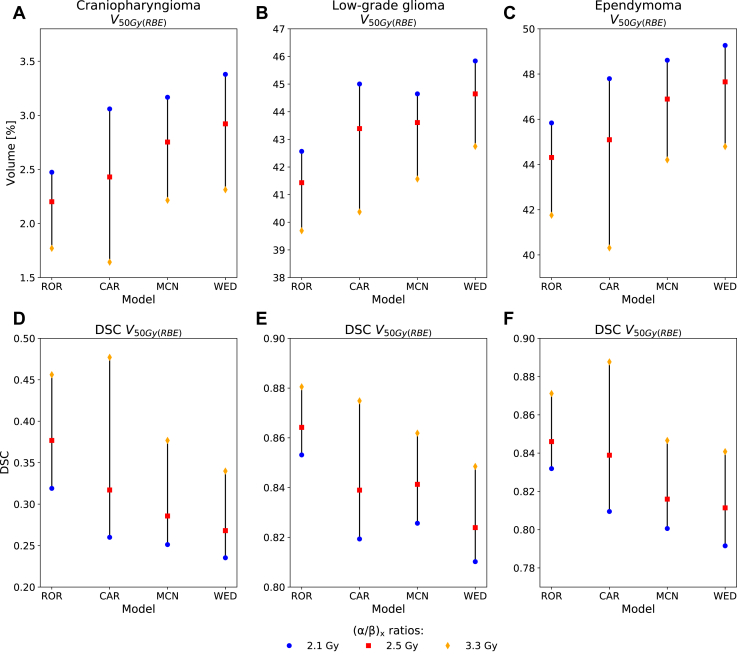
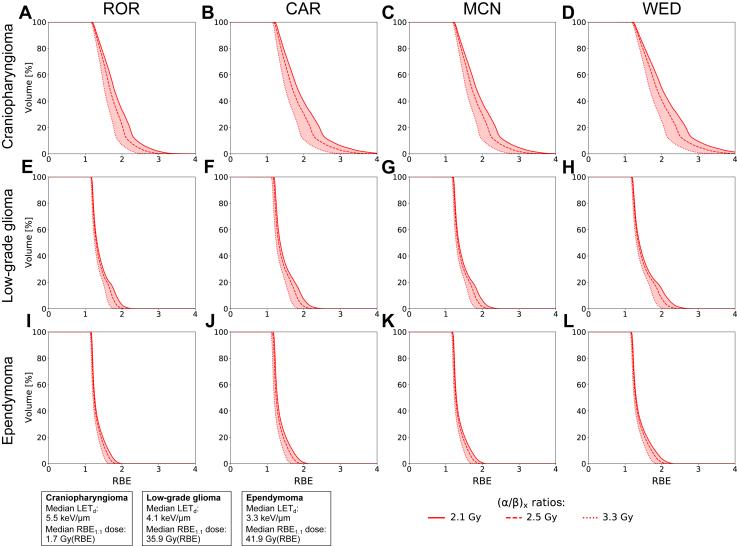
By changing the (α/β)_x ratios from 2.1 to 2.5 and 3.3 Gy, the CAR model showed the largest variations in the V_50Gy(RBE), declining by 1.5% to 7.5% depending on the patient, with the DSC consequently increasing. The WED, MCN, and ROR models showed smaller variations (Fig 5). Among the 3 patients, the patient with craniopharyngioma showed the largest variations in RBE depending on the (α/β)_x ratios (Fig 6); this was also the patient with the highest LET values (Fig E5) and the overall lowest doses in the brainstem (Fig 4).

Figure 5.

V_50Gy(RBE) and corresponding Dice similarity coefficients in the brainstem for the 3 patients using (α/β)_x = 2.1, 2.5, and 3.3 Gy. Abbreviations: CAR = Carabe; DSC = dice similarity coefficient; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg.

Figure 6.

RBE volume histograms comparing differences between (α/β)_x = 2.1, 2.5, and 3.3 Gy for the brainstem. For reference, the median LET_d and dose from RBE_1.1 in the brainstem for each patient are shown in the boxes in the bottom left corner. Abbreviations: CAR = Carabe; LET_d = dose-averaged linear energy transfer; MCN = McNamara; RBE = relative biological effectiveness; ROR = Rørvik; WED = Wedenberg.

Discussion

In this study, we investigated how biological isodoses from published variable RBE models spatially correlated in the brainstem and its substructures for typical pediatric brain tumor entities, accounting also for variation in the tissue-dependent model parameters. There were variations in absolute dose levels depending on the RBE model as well as in how the biological isodose curves coincided. The phenomenological RBE models (dependent on [α/β]_x, LET, and physical fraction dose) resulted in the highest biological dose and the least spatial agreement with the RBE_1.1 isodose volumes. Furthermore, the DSCs, and thereby spatial agreement, were seen to rapidly decrease for higher isodose levels while the DSCs increased when applying higher (α/β)_x ratios.

Across the 3 patients, there were large differences in which brainstem structure showed the highest and lowest increase in biological dose when comparing variable RBE models to RBE_1.1. These differences can mainly be attributed to the variations of the patient cases. When applying the same (α/β)_x ratio for the brainstem and the substructures, the difference in biological dose from variable RBE models relative to RBE_1.1 dose will solely depend on the LET and physical dose distribution within the brainstem. An increase in biological dose depends on the combined effect of elevated LET and physical dose. Although the patients with craniopharyngioma and glioma had high LET_d values in the medulla oblongata (Fig E5), the physical dose was so low that it resulted in a modest to no increase in absolute biological dose.

It has previously been demonstrated that variable RBE models typically estimate higher biological dose compared with RBE_1.1.^10,25,31, 32, 33 Depending on the tumor site and location relative to organs at risk, as well as the treatment regime, variable RBE models may violate established dose constraints. Because dose calculation using variable RBE models is not particularly common in clinical settings, having elemental knowledge on how these models behave in different treatment scenarios is therefore important, in particular when the RBE_1.1 dose is near organ dose limits. In a recent clinical investigation by Gentile et al,³⁴ it was suggested to keep V_55Gy(RBE) (for RBE_1.1) in the brainstem below 6% for pediatric patients with posterior fossa tumors. In our results, we showed that the spatial agreement between isodose volumes from the variable RBE models and RBE_1.1 was lower for increasing isodose levels, with an increased rate of change for doses typically above 30 to 50 Gy(RBE) depending on the patient case (Fig 3 and Fig E4). When comparing the RBE_1.1 isodose to a variable RBE model estimating a larger isodose volume, the absolute difference between the RBE_1.1 and variable RBE volumes will be more or less constant for different dose levels (Fig E6). However, the ratio between the volumes increases rapidly when the RBE_1.1 volume approaches zero, thus leading to a decrease in the spatial agreement. As a consequence, this effect is most crucial near high-dose constraints of smaller structures.

Although the increase in variable RBE dose relative to RBE_1.1 dose was pronounced, the differences among the variable RBE models were limited and likely within the uncertainties of the models.^9,35 Furthermore, a limitation of the phenomenological RBE models is that they are purely based on in vitro cell survival data, and it is uncertain if this survival relationship can be directly translated to in vivo endpoints.³⁶ RBE models in general are also based on different data sets, complicating the task of discriminating between differences in biological dose due to applied data sets or differences in modeling approaches.²⁵

Literature on (α/β)_x ratios for the brainstem is limited, and the few reported ratios are not particularly well established. We calculated substantially different spatial agreement between the biological models and RBE_1.1 depending on the applied (α/β)_x ratios, and thus the choice of this ratio must be carefully considered in RBE modeling. By including several values reported in the literature, it may be possible to bound a plausible interval of RBE values. It should furthermore be acknowledged that (α/β)_x ratios are highly endpoint specific and may slightly differ across the various substructures. The majority of our presented results were calculated using (α/β)_x = 2.1 Gy, a value frequently applied for the brainstem in literature.^9,11,37 This value originates from an examination of normal tissue complication probability for the brainstem in patients treated with radiosurgery for acoustic neuroma,⁷ and the (α/β)_x ratios may therefore be correlated to that particular treatment modality. The 2 remaining (α/β)_x ratios we applied were 2.5 and 3.3 Gy. The former was primarily intended for comparison of dose-fractionation schedules,²⁷ whereas the latter is from a study where they converted the reported ratio from a linear quadratic model equivalent (α/β)_x ratio of approximately 4.2 Gy³⁸ to fit their model.²⁸

In conclusion, for the 3 tumor entities we have explored in this study, the biological isodose surfaces derived when using the variable RBE models extended further into the brainstem compared with the RBE_1.1 dose. The doses calculated with the different phenomenological RBE models fully surrounded the RBE_1.1 isodose volumes in all cases, and the shapes of the isodose volumes from the phenomenological RBE models agreed spatially. The spatial agreement between the variable RBE models and RBE_1.1 was highly dependent on the evaluated isodose level, where higher doses led to larger isodose expansions and less agreement. In a clinical setting, the RBE effect may therefore particularly affect constraints regarding high doses and small volumes such as V_55Gy(RBE). It is furthermore important to keep in mind that current dose constraints are based on RBE = 1.1, and therefore derived dose constraints obtained through variable RBE models are crucial for future RBE optimization paradigms.