Low-complexity and highly robust barcodes for error-rich single molecular sequencing

Abstract

DNA barcodes are frequently corrupted due to insertion, deletion, and substitution errors during DNA synthesis, amplification and sequencing, resulting in index hopping. In this paper, we propose a new DNA barcode construction scheme that combines a cyclic block code with a predetermined pseudo-random sequence bit by bit to form bit pairs, and then converts the bit pairs to bases, i.e., the DNA barcodes. Then, we present a barcode identification scheme for noisy sequencing reads, which uses a combination of cyclic shifting and traditional dynamic programming to mark the insertion and deletion positions, and then performs erasure-and-error-correction decoding on the corrupted codewords. Furthermore, we verify the identification error rate of barcodes for multiple errors and evaluate the reliability of the barcodes in DNA context. This method can be easily generalized for constructing long barcodes, which may be used in scenarios with serious errors. Simulation results show that the bit error rate after identifying insertions/deletions is greatly reduced using the combination of cyclic shift and dynamic programming compared to using dynamic programming only. It indicates that the proposed method can effectively improve the accuracy for estimating insertion/deletion errors. And the overall identification error rate of the proposed method is lower than ${10}^{-5}$ when the probability of each base mutation is less than 0.1, which is the typical scenario in third-generation sequencing.

Introduction

Next-generation sequencing technologies require to improve in cost, quality and capacity, thereby facilitating versatile applications in nucleotide research (Lyons et al. 2017; Larsson et al. 2018; Minoche et al. 2011). Similar as the development of the second-generation sequencing, the sequencing throughput of the third-generation sequencing technologies for long reads is also increasing. For example, Pacific Biosciences (PacBio) has stated that its Sequel II instrument can generate up to 320 gigabases per sequencing cell within 30 h. Oxford Nanopore Technology (ONT) has released the PromethION, which can run either 24 or 48 flow cells in a single experiment, enabling users to collect several terabases per experiment (Ardui et al. 2018; Eisenstein 2019). However, many users do not need so high a sequencing depth for a single sample, especially sequencing plasmids or the genomes of viruses or bacteria. To efficiently share the rising sequencing capacity, multiplexed sequencing is adopted to pool different samples into batches and then sequence in parallel in a single sequencing run. To do so, a specific DNA barcode is attached to an amplification or sequencing primer to discriminate samples in the mixture (Parameswaran et al. 2007; Wand et al. 2019). After sequencing, reads can be identified via decoding the barcodes and the identification robustness generally relies on the error-tolerant properties of the barcodes (Tambe and Pachter 2019; Somervuo et al. 2018). It is similar with the oligo identification in DNA storage (Chen et al. 2020a).

However, insertion, deletion, and substitution errors are often introduced during the biochemical manipulations including DNA synthesis, amplification, and sequencing, leading to the index hopping problem (Vodák et al. 2018). The insertions and deletions (indels) are the most common types of errors in DNA synthesis while next-generation sequencing by synthesis (SBS) method has an error rate of ${10}^{-3}$–${10}^{-4}$ (Hawkins et al. 2018). A contamination rate of 1–7% is reported when using Illumina's platforms, especially for ExAmp amplification, such as HiSeq 3000/4000, HiSeq X Ten and NovaSeq (Costello et al. 2018; Griffiths et al. 2018). In comparison, for some typical three-generation sequencing platforms, such as Nanopore or PacBio sequencing, DNA sequencing reads are considerably longer, and unfortunately corrupted at very high rates of 15%, where the insertions and deletions are the dominant types of errors class (10% each) while the substitutions are followed (5%) (Jain et al. 2018). Therefore, there is great demand to design DNA barcodes resistant to various types of errors, and this is of great significance for reducing index hopping in high-throughput sequencing.

Recently, different constructions of DNA barcodes using error-correcting codes have been proposed. The first attempt to create a systematic error-correcting code for DNA barcodes was made by Hamady et al., based on binary Hamming code (Hamady et al. 2008). Furthermore, Krishnan et al. proposed using Bose–Chaudhuri–Hocquen–ghem (BCH) codes for DNA barcodes, which provided larger Hamming distance and better error-correcting capacity (Krishnan et al. 2011). The constructions mentioned above are designed to correct substitution errors only. To correct insertion and deletion errors, Adey et al. made the first attempt to find robust barcodes based on Levenshtein distance (Adey et al. 2010). So far, there is no explicit code-construction method to give optimal codes for edit metrics. Although greedy algorithms were proposed in literature (Ashlock et al. 2002) to find sets of barcodes with different choices of word lengths and minimum edit distances, the integration of barcodes into DNA context remained unsolved. Buschmann and Bystrykh presented an adaptation of Levenshtein-based codes to DNA contexts, called "Sequence-Levenshtein" code (Buschmann and Bystrykh 2013). This improved method is capable of recovering the length of corrupted barcodes and correcting on average more random mutations than traditional codes using Levenshtein distance (Levenshtein 1966; Likhitha et al. 2016). Kracht and Schober (2015) proposed an adaption of the watermark codes of Davey and Mackay (2001), which are capable of correcting insertion, deletion and substitution errors together. This approach has the advantage of recovering the barcode boundaries in sequencing reads (Haughton and Balado 2013). However, this method is not so efficient for short length barcodes due to the limited error correction capability. Furthermore, we have proposed a novel barcode construction method based on the block error correction code and the predetermined pseudorandom sequence (Chen et al. 2020b). However, the identification method using the forward–backward (FB) algorithm (Liu and Chen 2016, 2018) has relatively high decoding complexity.

In this paper, we propose a barcode construction scheme that combines a special type of error-correction codes, cyclic block codes with a predetermined pseudo-random sequence, and then converts to the barcodes. Furthermore, we propose a barcode identification scheme with low complexity and high robustness that uses the combination of cyclic shifting and dynamic programming to mark the insertion and deletion positions, and then performs modification and decoding on the corrupted cyclic block codes. The proposed schemes show superior error correction capabilities for various sequencing error scenarios, including the scenario in which the barcode is embedded in DNA context and its length is changed unpredictably due to insertion/deletion errors. The processing method is different with the forward–backward algorithms in Chen et al. (2020b) and in that contribution, we used the general block error correction codes and thus we could not use cyclic shifting and dynamic programming in this paper to identify the insertions and deletions and we used the forward–backward algorithm. Cyclic shifting and dynamic programming schemes only need processing on the characters and does not use the probabilities, which presents lower processing complexity.

Materials and methods

System model

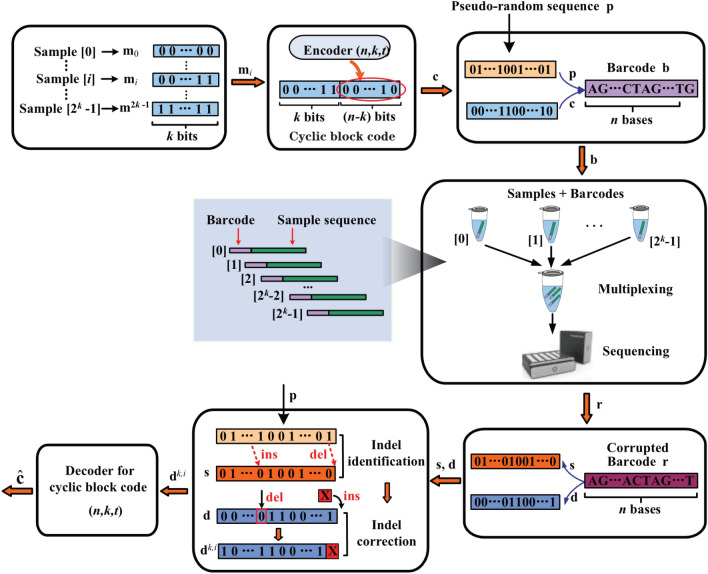
Figure 1 presents an overall description of the system model for the proposed robust barcodes used in multiplexed sequencing.

Fig. 1.

Schematic representation of barcode application in multiplexed sequencing. The system model consists of three steps. (i) The sequencing barcodes are first generated using combination of pseudorandom sequence and cyclic block codes. (ii) The barcodes are attached to the amplification or sequencing primer of different samples for multiplexed sequencing. (iii) After pooled sequencing, the barcodes are identified using the proposed identification method to recover the sample index

Barcode construction

To construct barcodes for multiplexed sequencing, a series of parallel DNA samples with the maximum number of $2^k$ are first represented by different information vectors with length $k$. Then, $k$-bit information vector ${\mathbf{m}}_{\text{i}}$, representing a particular sample number $i(i=0,1,\dots ,2^k-1)$, is sent to the encoder of a cyclic block code $\left(n,k,t\right)$ to obtain a codeword $\mathbf{c}$, where $n$ is the length of the codeword, $k$ is the length of the information vector and $t$ is the error correction capability of the cyclic block code (Lin and Costello 2001). Finally, we combine the cyclic block codeword $\mathbf{c}$ with a predetermined pseudo-random sequence $\mathbf{p}$ of the same length into bit pairs, which are mapped into a DNA barcode $\mathbf{b}$. In this way, a set of $2^k$ candidate barcodes can be obtained.

DNA library preparation and sequencing

To start multiplexed sequencing, each sample is prepared separately by embedding barcodes in DNA context through ligation with indexed adapters or polymerase chain reaction (PCR) amplification with indexed primers. Then, different samples are mixed together and sequenced in one run. Due to defects in sequence synthesis, ligation process, sample amplification, cluster generation, sequencing and final base calling (Minoche et al. 2011; Lyons et al. 2017), sequencing reads are often corrupted by multiple types of errors including insertions (ins), deletions (del), and substitutions (sub).

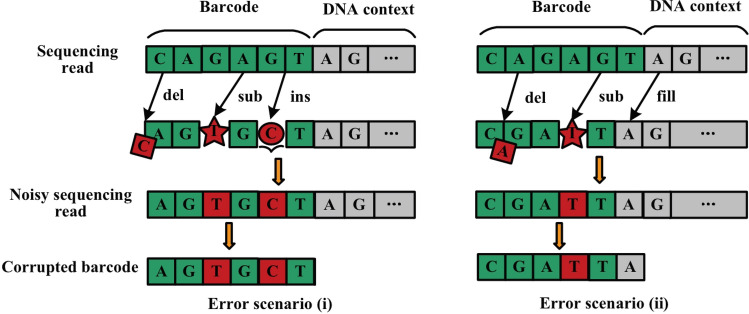
For a barcode embedded in DNA context, all the three types of errors may occur. The substitution errors are relatively easy to handle while the insertion and deletion errors can cause the length of barcode to change unpredictably because there is no "stop word" to separate the barcode from the sequence of context sample. To illustrate this, Fig. 2 presents two error scenarios for insertions and deletions, with the use of "CAGAGT" as an example of barcode. For the error scenario (i), the base "C" at the first position of the barcode is deleted, the base "A" at the fourth position is substituted with "T", and a base "C" is inserted after the fifth position of the base "G". The corrupted barcode "AGTGCT" is obtained, leading to five burst errors. For the error scenario (ii), the base "A" at the second position of the barcode is deleted, the base "G" at the fifth position is substituted with "T", and the first base "A" of the DNA context succeeds the base at the sixth position taken originally by the base "T". The corrupted barcode "CGATTA" is obtained, leading to five burst errors.

Fig. 2.

Two error scenarios in DNA context for insertions/deletions and substitutions. For the error scenario (i), the length of the barcode remains unchanged. For the error scenario (ii), the barcode is shortened due to deletion(s), the head of the succeeding sequence of the DNA context may be filled into the region of the corrupted barcode

The two error scenarios are summarized as follows: for the scenario (i), the barcode is corrupted by the same number (one or more) of insertion and deletion errors, and the length of the barcode thus remains unchanged. In this scenario, the two adjacent insertion and deletion errors are close to each other, short burst errors occur. In real case, they may be far apart, long burst errors unfortunately come up, and are difficult to deal with. For the scenario (ii), the barcode is corrupted by either insertion or deletion error(s), and the length of the barcode is thus changed. In this scenario, the barcode is shortened due to deletion(s), the head of the succeeding sequence of the DNA context may be filled into the region of the corrupted barcode. When the barcode is elongated due to insertions, the tail base(s) of the barcode may be dropped out.

Barcode identification

After sequencing, the corrupted barcode $\mathbf{r}$ is identified based on the primer position in noisy sequencing reads. To decode the corrupted barcode for the assignment of reads to their respective samples, an efficient barcode identification scheme is presented in this research. Specifically, the corrupted barcode $\mathbf{r}$ is first demapped to obtain the corrupted pseudo-random sequence $\mathbf{s}$ and the corrupted cyclic block code $\mathbf{d}$. Then, a combination of cyclic shifting and dynamic programming is used to calculate the Levenstein distance and to mark the insertion and deletion positions between the pseudo-random sequence $\mathbf{p}$ and the corrupted sequence $\mathbf{s}$. Then, the corrupted cyclic block code is modified using the marked positions. Finally, the modified cyclic block code is sent to the algebraic decoder for erasure-and-error-correcting decoding to obtain the final decoded codeword $\widehat{\mathbf{c}}$, which is then used to yield the estimated information vector, i.e., the decoded index $\widehat{\mathbf{m}}$ for the assignment of reads to their respective samples.

Proposed barcode construction scheme

Aiming at the insertion, deletion and substitution errors introduced during multiplexed sequencing, we propose a new construction of barcodes based on the combination of the pseudo-random sequence $\mathbf{p}$ and the cyclic block codeword $\mathbf{c}$. To construct a set of candidate barcodes capable of supporting multiple parallel samples, we use a $k$-bit information vector ${\mathbf{m}}_{\text{i}}$ as an index of the sample $i$, thus the generated $2^k$ different information vectors can support up to $2^k$ different samples. Then, the information vectors are encoded into different cyclic block codewords. Finally, we combine different cyclic block codewords with a predetermined pseudo-random sequence to generate different candidate barcodes. The predetermined pseudo-random sequence is fixed for $2^k$ different barcodes and is known in the identification process. The candidate barcodes can be further optimized according to some biochemical constraints, resulting in the number of samples less than $2^k$.

Figure 3 illustrates the specific construction process in detail. Here, the pseudo-random sequence is used for insertion and deletion identification. Specifically, the pseudo-random sequence is a hidden component of the barcode, the insertions/deletions for both the pseudo-random sequence and the barcode are consistent, i.e., when insertions and deletions occur in the pseudo-random sequence, these operations will occur at the same positions of the barcode. Moreover, since the pseudo-random sequence is known for the barcode identification, we can compare the original pseudo-random sequence and the corrupted pseudo-random sequence to estimate the insertion/deletion positions. Then, using the estimated positions of insertion/deletion, the codeword can be modified, converting the insertions/deletions into substitutions.

Fig. 3.

A construction method for DNA sequencing barcode based on a predetermined pseudo-random sequence and a cyclic block code. The method consists of three steps. (i) Using a $k$-bit information vector ${\mathbf{m}}_{\text{i}}$ as an index of the sample $i$. (ii) Encoding the information vectors into different cyclic block codewords. (iii) Combining different cyclic block codewords with a predetermined pseudo-random sequence to generate different candidate barcodes

Furthermore, the cyclic block code $\left(n,k,t\right)$ adds $(n-k)$ redundant bits to a $k$-bit information vector ${\mathbf{m}}_{\text{i}}(i\in \{0,1,...,2^k-1\})$ to protect it against the substitution errors. The cyclic block codes used in this paper, i.e., the BCH codes, as a kind of important error-correction codes, have the advantages of relatively strong error correcting capability and low encoding and decoding complexity (Lin and Costello 2001). Therefore, when designing the barcode, the characteristics of the predetermined pseudo-random sequence (such as repeatability and run length) and the code rate $R=k/n$ of the cyclic block code are both important factors that determine the error correction capability of the constructed barcode. The barcode construction algorithm is presented as Table 1.

Table 1.

Barcode generation method

Proposed barcode identification scheme

To decode a barcode $\mathbf{r}$ corrupted by various types of errors, a barcode identification method based on a combination of cyclic shifting and dynamic programming is presented for the proposed robust barcodes. First, the corrupted barcode $\mathbf{r}$ is demapped to obtain the corrupted codeword $\mathbf{d}$ and the corrupted pseudo-random $\mathbf{s}$. Second, by comparing the corrupted sequence $\mathbf{s}$ with the pseudo-random sequence $\mathbf{p}$, a novel scheme including cyclic shifting and dynamic programming is proposed for insertion/deletion identification. Based on the identified insertion/deletion positions, the corrupted cyclic block code $\mathbf{d}$ can then be aligned, therein converting insertions/deletions into random or burst substitution errors or erasures. Finally, erasure-and-error-correcting decoding is performed to correct the remaining substitutions and erasures.

For the insertion/deletion identification, it is known that dynamic programming can be used to calculate the Levenstein distance $d(\mathbf{p},\mathbf{s})$ and output the optimum alignment ${\mathbf{l}}_{\text{path}}\left(\mathbf{p},\mathbf{s}\right)$ for the sequences $\mathbf{p}$ and $\mathbf{s}$. Using the optimum alignment ${\mathbf{l}}_{\text{path}}\left(\mathbf{p},\mathbf{s}\right)$, the insertion, deletion, and substitution positions from $\mathbf{p}$ to $\mathbf{s}$ can be marked (Kruskal 1983). The marker vector is denoted as ${\mathbf{l}}_{\text{mark}}\left(\mathbf{p},\mathbf{s}\right)$.

Furthermore, since the cyclic block codes are used in the barcode construction, the codewords can be correctly decoded after cyclic shifting. In addition, cyclic shifting can reduce the difficulty of insertion/deletion identification. Specifically, by cyclic shifting, the deletion or insertion can be moved to the tail of the barcode, which can cancel the occurrence of long burst errors due to base shifts caused by insertion/deletion. This insertion/deletion at the tail can be viewed as a substitution. Moreover, regardless of where insertions or deletions occur in the sequence, each one can always be moved to the tail of the sequence by cyclic shifting to be converted to a single substitution. Therefore, we propose a barcode identification method based on the combination of cyclic shifting and dynamic programming. The specific steps are explained as follows:

1. To decode a corrupted barcode $\mathbf{r}$, we first need to demap $\mathbf{r}$ into a corrupted codeword $\mathbf{d}$ and a corrupted pseudo-random $\mathbf{s}$.

2. To reduce the number of burst substitution errors caused by insertion/deletion with the method of moving the insertion or deletion error to the tail, we cyclically shift the corrupted sequence $\mathbf{s}$, the corrupted codeword $\mathbf{d}$, and the predetermined pseudo-random sequence $\mathbf{p}$. Specifically, shift cyclically $\mathbf{s}$ and $\mathbf{d}$ to the left by $i$ times ($0\le i<n$), denoted as ${\mathbf{s}}^{(i)}$ and ${\mathbf{d}}^{(i)}$. Simultaneously, shift cyclically $\mathbf{p}$ to the left by $k$ times ($i-c\le k\le i+c$,$c$ is a constant), denoted as ${\mathbf{p}}^{(k)}$.

3. Use dynamic programming to calculate the optimum alignment ${\mathbf{l}}_{\text{path}}({\mathbf{p}}^{(k)},{\mathbf{s}}^{(i)})=$$\left({(u,v)}_j\right)$ for ${\mathbf{p}}^{(k)}$ and ${\mathbf{s}}^{(i)}$. Then, the vector ${\mathbf{l}}_{\text{mark}}({\mathbf{p}}^{(k)},{\mathbf{s}}^{(i)})=\left(l_0,...,l_{n-1}\right)$ that marks the insertion and deletion positions is obtained using ${\mathbf{l}}_{\text{path}}({\mathbf{p}}^{(k)},{\mathbf{s}}^{(i)})$, which can be expressed as

   $$l_j=\left\{\begin{array}{cc}1,\hfill & {(u,v-1)}_{j-1}\to {(u,v)}_j(\text{insertion}),\\ \hfill & \\ 2,\hfill & {(u-1,v)}_{j-1}\to {(u,v)}_j(\text{deletion}),\\ \hfill & \\ 3,\hfill & {(u-1,v-1)}_{j-1}\to {(u,v)}_j\text{and}{p}_{u-1}^{(k)}\ne s_{v-1}^{(i)}\\ \hfill & (\text{substitution}),\end{array}j=0,1,...,n-1,0\le u,v\le n.\right)$$ 1
4. Based on the marker vector ${\mathbf{l}}_{\text{mark}}({\mathbf{p}}^{(k)},{\mathbf{s}}^{(i)})$, the codeword ${\mathbf{d}}^{(i)}$ can be modified to obtain ${\mathbf{d}}^{k,i}$. Specifically, if the $j$-th element of ${\mathbf{l}}_{\text{mark}}$ is an insertion, delete the $j$-th bit of ${\mathbf{d}}^{(i)}$. If the $j$-th element of ${\mathbf{l}}_{\text{mark}}$ is a deletion, insert the bit ‘X’ as an erasure to the $j$-th position of ${\mathbf{d}}^{(i)}$, written as

   $$d_j^{k,i}=\left\{\begin{array}{cc}\mathrm{\varnothing },\hfill & l_j=1,\\ {}^{\prime }{\text{X}}^{\prime },\hfill & l_j=2,\\ d_j^{\left(i\right)},\hfill & \text{others},\end{array}\right)j=0,1,...,n-1.$$ 2

5. Perform erasure-and-error-correcting decoding $\left(n,k,t\right)$ to the modified codewords ${\mathbf{d}}^{k,i}$ for correcting residual errors, obtaining the decoded codewords ${\widehat{\mathbf{c}}}^{k,i}$. Then, the decoded codeword satisfying the syndrome is considered to be decoded successfully, thus this decoded codeword is selected as the final decoding result ${\widehat{\mathbf{c}}}^{\prime }$.

6. Since the decoding result ${\widehat{\mathbf{c}}}^{\prime }$ is a codeword that has undergone cyclic shifting, thus the decoding result needs to be cyclically reverse-shifted to recover the original codeword. Specifically, the final decoded result ${\widehat{\mathbf{c}}}^{\prime }$ is cyclically shifted to the right by $k$ times, obtaining $\widehat{\mathbf{c}}$, and the information vector $\widehat{\mathbf{m}}$ of $\widehat{\mathbf{c}}$ is the decoded index. It can be used to discriminate the reads.

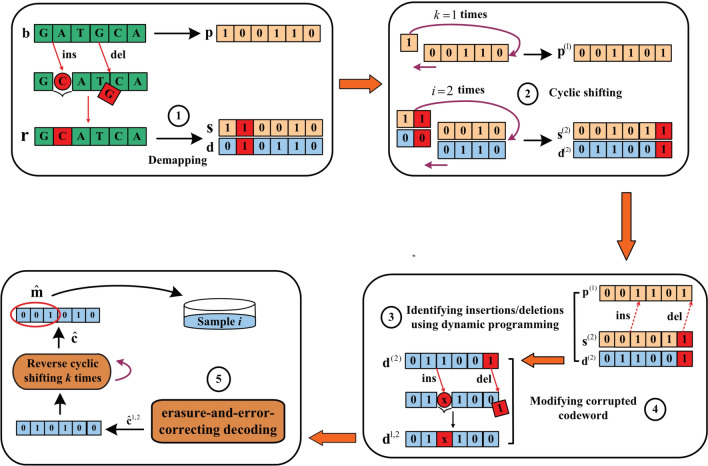
Figure 4 gives an example of insertion/deletion identification with a barcode $\mathbf{b}=$ "GATGCA", which is constructed by a predetermined pseudo-random sequence $\mathbf{p}=$ "100,110". Suppose that the base "C" is inserted at the position 2 and that the base "G" at the position 4 is deleted during sequencing, obtaining the corrupted barcode $\mathbf{r}=$"GCATCA". To decode the corrupted barcode $\mathbf{r}$, we first convert $\mathbf{r}$ to a corrupted sequence $\mathbf{s}=$ "110,010" and a corrupted codeword $\mathbf{d}=$ "010,110". Then, using the proposed method for insertion/deletion identification, it can be observed that when $\mathbf{s}$ and $\mathbf{d}$ are cyclically shifted to the left by $i=2$ times, obtaining ${\mathbf{s}}^{(2)}=$ "001,011" and ${\mathbf{d}}^{(2)}=$ "011,001", the inserted base "C" is moved to the tail. At this time, when $\mathbf{p}$ is cyclically shifted to the left by $k=1$ time, obtaining ${\mathbf{p}}^{(1)}=$"001,101", dynamic programming can identify an insertion of "1" at position 2 and a deletion of "1" exactly at the tail by comparing ${\mathbf{s}}^{(2)}=$"001,011" and ${\mathbf{p}}^{(1)}=$"001,101". The barcode identification method is summarized as Table 2.

Fig. 4.

The identification method for sequencing barcodes using a combination of cyclic shifting and dynamic programming. First, converting $\mathbf{r}$ to a corrupted sequence $\mathbf{s}$ and a corrupted codeword $\mathbf{d}$. Then, using a combination of cyclic shifting and dynamic programming to mark the insertion and deletion positions and modify corrupted codeword. Finally, performing erasure-and-error-correcting decoding

Table 2.

Barcode identification

Results and discussion

To assess the performance of the proposed barcode construction and identification schemes, we chose Bose–Chaudhuri–Hocquenghem (BCH) codes (Lin and Costello 2001) as the cyclic block codes and validated the proposed barcode identification scheme by evaluating the identification error rate $P_{\text{e}}$ (i.e., the probability of incorrectly decoding a corrupted barcode) as a function of the per-base mutation probability $P_{\text{mut}}$. Here, $P_{\text{mut}}$ denotes the probability that every base is mutated, and is calculated by $P_{\text{mut}}=N_{\text{mut}}/n$, where $N_{\text{mut}}$ is the number of mutations for each barcode of length $n$. The number of mutations $N_{\text{mut}}$ is obtained by $N_{\text{mut}}=N_{\text{i}}+N_{\text{d}}+N_{\text{s}}$, and $N_{\text{i}}$, $N_{\text{d}}$ and $N_{\text{s}}$ are the numbers of insertions, deletions and substitutions in a barcode, respectively. To simulate various errors introduced during sequencing, we attached a sample sequence of random bases to each barcode. The barcode within each of these sample sequences was then mutated with the insertions, deletions and substitutions based on a certain probability. As the length of the received barcode was unknown, the barcode with an equal length as the corrupted barcode was used. At this time, the number of insertions, deletions and substitutions in the barcode are $N_{\text{i}}=P_{\text{i}}\times n$, $N_{\text{d}}=P_{\text{d}}\times n$ and $N_{\text{s}}=P_{\text{s}}\times n$, respectively. Here, $P_{\text{i}}$, $P_{\text{d}}$ and $P_{\text{s}}$ denote the probabilities of insertion, deletion and substitution in a barcode and $P_{\text{mut}}=P_{\text{i}}+P_{\text{d}}+P_{\text{s}}$.

Performance analysis for two error scenarios

To verify the performance of the proposed barcodes in two sequencing error scenarios, we simulated the identification error rates of 31-nt barcodes constructed with BCH(31, 11, 5) and 15-nt barcodes constructed with BCH(15, 5, 3) in two error scenarios. The simulation results are depicted in Fig. 5. The figure shows that $P_{\text{e}}$ for error scenario (ii) is slightly lower than that of error scenario (i) when considering $P_{\text{mut}}\in \left[0.12,0.33\right]$$\left(P_{\text{i}}=P_{\text{d}}=P_{\text{s}}\right)$. Therefore, the simulation results reveal that the proposed barcodes can work in both random and context scenarios.

Fig. 5.

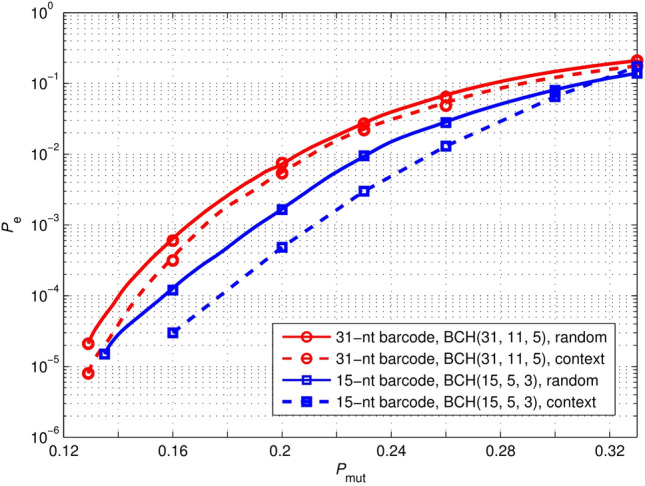
Performance comparison of 31-nt and 15-nt barcodes for two error scenarios. $P_{\text{mut}}$ represents the probability that every base is mutated. $P_{\text{e}}$ indicates the probability of incorrectly decoding a corrupted barcode. The $P_{\text{e}}$ for context scenario is slightly lower than that of random scenario when considering $P_{\text{mut}}\in \left[0.12,0.33\right]$$\left(P_{\text{i}}=P_{\text{d}}=P_{\text{s}}\right)$

Specifically, we analyzed the accuracy of insertion/deletion identification using a combination of cyclic shifting and dynamic programming to be higher than that using dynamic programming only under two error scenarios. For a predetermined pseudo-random sequence $\mathbf{p}$ and a corrupted sequence $\mathbf{s}$ of the 31-nt barcode constructed with BCH(31, 11, 5), we can first calculate ${\mathbf{l}}_{\text{mark}}$ using two methods: (i) dynamic programming and (ii) cyclic shifting + dynamic programming. Then, the corrupted codeword $\mathbf{d}$ is modified with ${\mathbf{l}}_{\text{mark}}$. We verify the accuracy of insertion/deletion identification by measuring the bit error rate of the modified codeword. For this simulation, $P_{\text{i}}=P_{\text{d}}=P_{\text{s}}=0.033$ and $P_{\text{i}}=P_{\text{d}}=P_{\text{s}}=0.066$ for two error scenarios are considered. The simulation result is depicted in Fig. 6. Apparently, the bit error rate for identifying insertions/deletions using a combination of cyclic shift and dynamic programming is lower, which indicates that the proposed method can effectively improve the accuracy for estimating insertion/deletion errors.

Fig. 6.

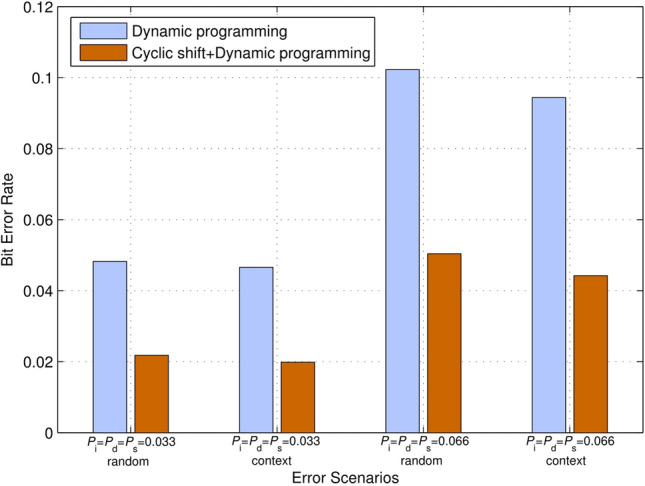
Comparison of bit error rate for insertion and deletion identification using two methods. The bit error rate of identifying insertions/deletions using a combination of cyclic shift and dynamic programming is lower than that of using dynamic programming

Robustness verification for barcodes with different error-correcting capabilities

To verify the robustness of the proposed barcodes in DNA context, we compared the identification error rate $P_{\text{e}}$ of 12-nt barcodes constructed using the proposed scheme and Sequence-Levenshtein codes under different $P_{\text{mut}}$ ($P_{\text{i}}=P_{\text{d}}=P_{\text{s}}$) in error scenario (ii). Sequence-Levenshtein-based barcodes of length 12 are constructed by Sequence-

Levenshtein codes with a minimum distance $d_{\text{SL}}^{min}=5$, which can support $N=232$ parallel samples (Buschmann and Bystrykh 2013). The proposed barcodes of length 12 are constructed with BCH(12, 8, 1) and BCH(12, 4, 2), respectively, where BCH(12, 8, 1) and BCH(12, 4, 2) are the shortened cyclic BCH codes. Specifically, the information vectors with the first three bits of ‘0′ are encoded using BCH(15, 11, 1) to generate the codewords, and then the corresponding three bits of ‘0′ in the codewords are removed to obtain the shortened cyclic block codewords BCH(12, 8, 1). Similarly, the shortened.

cyclic block codes BCH(12, 4, 2) are generated using BCH(15, 7, 2). The simulation results are depicted in Fig. 7. The proposed barcodes with $N=256$ have similar error correction capability to Sequence-Levenshtein codes with $N=232$. Moreover, the proposed barcodes with $N=16$ outperform the Sequence-Levenshtein barcodes in a context scenario. In addition, it should be noted that the shortened cyclic block codes can be used to construct barcodes with flexible lengths.

Fig. 7.

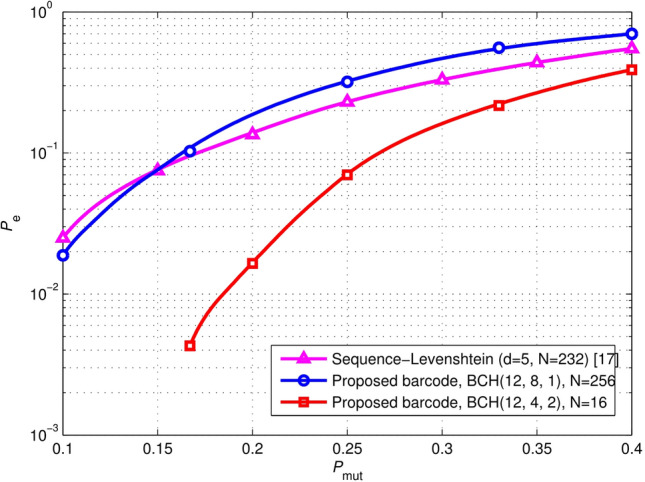
Performance comparison for 12-nt barcodes constructed using the proposed scheme and Sequence-Levenshtein codes in DNA context. $P_{\text{mut}}$ represents the probability that every base is mutated. $P_{\text{e}}$ indicates the probability of incorrectly decoding a corrupted barcode. The proposed barcodes with $N=256$ have similar error correction capability to the Sequence-Levenshtein codes with $N=232$. Moreover, the proposed barcodes with $N=16$ outperform the Sequence-Levenshtein barcodes in a context scenario

Furthermore, compared with Sequence-Levenshtein codes, our proposed method can be easily generalized to construct long barcodes which may be used in scenarios with many errors. For the Sequence-Levenshtein codes, constructing longer barcodes with larger distances is difficult to achieve. Therefore, we additionally simulated 15-nt and 31-nt barcodes with different values of $k$, which can support different numbers of multiplexed samples. The 31-nt barcodes are constructed with BCH(31, 11, 5) and BCH(31, 16, 3), and the 15-nt barcodes are constructed with BCH(15, 5, 3) and BCH(15, 7, 2). In this simulation, the mutation probability $P_{\text{mut}}\in \left[0.1,0.33\right]$$\left(P_i=P_d=P_s\right)$ is considered. Figure 8 gives the identification error rate $P_{\text{e}}$ under different $P_{\text{mut}}$. Apparently, the 31-nt barcodes constructed by BCH(31, 11, 5) and the 15-nt barcodes constructed with BCH(15, 5, 3) perform better, and the identification error rates are lower than ${10}^{-5}$ for $P_{\text{mut}}<0.10$. Obviously, the proposed barcodes are highly robust to high mutations in the barcode.

Fig. 8.

Performance comparison of barcodes with different lengths and different values of $k$. $P_{\text{mut}}$ represents the probability that every base is mutated. $P_{\text{e}}$ indicates the probability of incorrectly decoding a corrupted barcode. The 31-nt barcodes constructed by BCH(31, 11, 5) and the 15-nt barcodes constructed with BCH(15, 5, 3) perform better when considering $P_{\text{mut}}\in \left[0.1,0.33\right]$$\left(P_{\text{i}}=P_{\text{d}}=P_{\text{s}}\right)$, and the identification error rates are lower than ${10}^{-5}$ for $P_{\text{mut}}<0.10$

Properties of barcodes with different pseudo-random sequences

The performance of the proposed barcodes is related to the pseudo-random sequence, thus we simulated three barcodes constructed with the same BCH(31, 11, 5) and three different pseudo-random sequences under $P_{\text{mut}}\in \left[0.12,0.26\right]$ in error scenario (i). Three pseudo-random sequences are designed with different repeatability and run lengths. The first pseudo-random sequence is an m-sequence with long runs of zeros or ones. The second pseudo-random sequence is designed with a maximum run length of 3. The third pseudo-random sequence has a maximum run length of 3, and every two adjacent sets of 3-bit are not repeated. We compared the performances of these barcodes for two cases of $P_{\text{i}}=P_{\text{d}}=0.033$ and $P_{\text{i}}=P_{\text{d}}=0.066$. The simulation result is depicted in Fig. 9. It can be observed that under a fixed $P_{\text{mut}}$, the performances of the barcodes for the two cases of $P_{\text{i}}=P_{\text{d}}=0.033$ and $P_{\text{i}}=P_{\text{d}}=0.066$ are similar. The barcode using a pseudo-random sequence with limited run-length and low repeatability can obtain the best error correction capability.

Fig. 9.

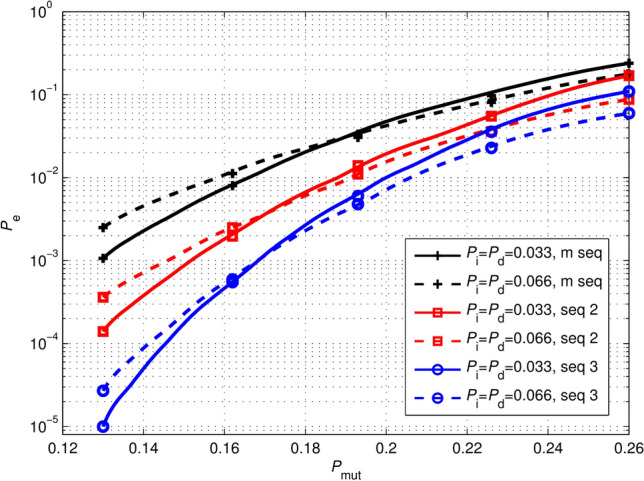
Performance comparison of 31-nt barcodes constructed by different pseudo-random sequences and BCH(31, 11, 5). $P_{\text{mut}}$ represents the probability that every base is mutated. $P_{\text{e}}$ indicates the probability of incorrectly decoding a corrupted barcode

Conclusions

In this paper, we propose a new construction method for robust sequencing barcodes based on a combination of a cyclic block code and a predetermined pseudo-random sequence. For this construction, we present an efficient barcode identification scheme based on a combination of cyclic shifting and dynamic programming to mark the insertion and deletion positions based on the known pseudo-random sequence. Then, using the marked positions, the corrupted codeword can be modified. Finally, erasure-and-error-correcting decoding is performed to correct residual errors. The simulation results show that the proposed method can be easily generalized for constructing longer barcodes, which may be used in scenarios with many errors, and that the barcodes are highly robust to a large number of insertions, deletions, and substitutions in the process of DNA library preparation, cluster generation, sequencing, and base calling. In addition, for various sequencing error scenarios, the error correction capability of the proposed barcode is superior.

Author contributions

W.C. designed the study. W.C., P.W., L.W., D.Z., and M.H. performed bioinformatic analyses. P.W. and L.W. performed the simulations, and wrote the manuscript. L.W. and M.H. validated the results. W.C., D.Z., M.H., and L.S. supervised the results, and revised the manuscript. All authors read and approved the final manuscript.

Compliance with ethical standards

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.