Increased wiring cost during development is driven by long-range cortical, but not subcortical connections

Abstract

The brain undergoes a protracted, metabolically expensive maturation process from childhood to adulthood. Therefore, it is crucial to understand how network cost is distributed among different brain systems as the brain matures. To address this issue, here we examined developmental changes in wiring cost and brain network topology using resting-state functional magnetic resonance imaging (rsfMRI) data longitudinally collected in awake rats from the juvenile age to adulthood. We found that the wiring cost increased in the vast majority of cortical connections but decreased in most subcortico-subcortical connections. Importantly, the developmental increase in wiring cost was dominantly driven by long-range cortical, but not subcortical connections, which was consistent with more pronounced increase in network integration in the cortical network. These results collectively indicate that there is a non-uniform distribution of network cost as the brain matures, and network resource is dominantly consumed for the development of the cortex, but not subcortex from the juvenile age to adulthood.

1. Introduction

The mammalian brain undergoes protracted development from childhood to adulthood. This developmental process can greatly determine the mental health of an individual, and many psychiatric disorders are attributed to atypical development during this period (di Martino et al., 2014; Insel, 2010; Menon, 2013; Paus et al., 2008; Shaw et al., 2010).

An interesting and important phenomenon in brain development is that timelines can be considerably different among separate brain regions and circuits/networks. At the regional level, the ontogeny of the development of the sensory cortex is typically earlier than the high-tier associate cortex like the prefrontal cortex (Blakemore, 2012; Bourgeois et al., 1994; Gogtay et al., 2004). At the circuit/network level, over development brain networks tend to involve more long-distance connections but less short-range connections (di Martino et al., 2014; Fair et al., 2009; Gao et al., 2011; Ma et al., 2018a). For instance, the anterior-to-posterior connectivity in the default mode network (DMN) is missing at early age but emerges after adolescence in both humans (Fair et al., 2008; Kelly et al., 2009; Supekar et al., 2010) and animals (Choi et al., 2015; Ma et al., 2018a). Consistent with this notion, the topological architecture of brain networks exhibits age-dependent decrease in local clustering and increase in communication efficiency (Ma et al., 2018a; Stevens et al., 2009).

Considering that forming long-distance connections between distal regions is energetically demanding, understanding how network cost is spatiotemporally distributed during brain development is critical. In addition, previous research in brain development primarily focuses on cortical regions, while our knowledge of the developmental trajectory of the subcortex remains sparse. Interestingly, some subcortical regions show differential developmental patterns from cortical regions. For instance, the volumes of the thalamus and brainstem increase with age (Muftuler et al., 2011), whereas the cortex typically exhibits reduced thickness/volume during development (Ostby et al., 2009). In addition, cortico-cortical functional connectivity generally increases as the brain matures, while subcortico-subcortical connectivity mostly decreases (Niessen et al., 2018; Sawiak et al., 2018). The developmental timelines can also be different between the subcortex and cortex. Subcortical regions exhibit prominent changes during early developmental stages including pre-puberty and puberty, but cortical regions can continue to develop post puberty (Ostby et al., 2009; Raznahan et al., 2014). Taken together, these data suggest that the subcortex and cortex might have distinct development profiles and different energy requirement at each stage.

To elucidate the difference of developmental change in network cost between the cortex and subcortex, we reanalyzed the whole-brain resting-state functional magnetic resonance imaging (rsfMRI) data previously collected (Ma et al., 2018a) for the purpose of the present study. We longitudinally acquired rsfMRI data in awake rats at five developmental stages: juvenile (P30-P31), early adolescence (P34-P35), adolescence (P41-P42), late adolescence (P48-P49) and adulthood (P70-P90). In our published study (Ma et al., 2018a), we demonstrated significant spatiotemporal heterogeneity of individual neural circuits over development in the rodent brain. Specifically, significant FC increase in cortico-cortical connections and FC decrease in subcortico-subcortical connections were observed. In the present study, we further investigate the development of the cortex and subcortex using two metrics, wiring cost and network topology. Wiring cost, defined by the product of functional connectivity and physical distance between regions, is a key measure that provides insight into brain metabolism during development as higher energy costs are typically required for regions with dense (Chklovskii et al., 2002; Chklovskii and Koulakov, 2004) and distributed (Kaiser and Hilgetag, 2006; Sporns, 2011a) connections. The topological organization can assess information specialization and integration in brain networks (Menon, 2013; Sporns, 2011b). We find that the increase in mean wiring cost is more prominent in cortical regions than subcortical regions. Importantly, the wiring cost increase during development is dominated by long-range cortical, but not subcortical connections. Consistently, the cortical network also becomes more globally integrated with reduced local clustering over development. Taken together, this study provides important evidence suggesting that brain development is accompanied by a non-uniform distribution of network cost between the cortical and subcortical systems.

2. Methods

We reanalyzed data collected in our previous publication (Ma et al., 2018a) for the purpose of the present study.

2.1. Animals

Data from 43 male Long Evans (LE) rats were used in the present study. Singly housed pregnant LE rats at embryonic day 15 (E15) were obtained from Charles River Laboratory (Wilmington, MA). The off-spring was housed in the same Plexiglas cage with the mother until P21. Food and water were provided ad libitum. Room temperature of 22–24 °C and a 12 h light: 12 h Dark cycle were maintained. All experiments were approved by the Institutional Animal Care and Use Committee of the Pennsylvania State University.

2.2. Acclimation

To minimize motion and stress during awake MR imaging, animals were acclimated to the scanning environment and noise for seven consecutive days (Dopfel and Zhang, 2018; Gao et al., 2017). The acclimation time was gradually increased each day up to 60 min per day (i.e. 15, 30, 45, 60, 60, 60 and 60 min/day, respectively). To achieve optimal adaptation, the design of the acclimation restrainer was modified according to the size and shape of head and body weight of rats of each age. More detailed description of the acclimation procedure can be found from our previous publications for adult (Dopfel et al., 2019; Liang et al., 2011; Zhang et al., 2010) and young rats (Ma et al., 2018a). It has been confirmed that this procedure provides adequate habituation in animals during awake fMRI imaging (King et al., 2005). Similar approaches have also been adopted by other research groups (Becerra et al., 2011; Bergmann et al., 2016; Chang et al., 2016; Yoshida et al., 2016).

2.3. fMRI experiments

Each rat was longitudinally imaged at the fully awake state during five different developmental stages: juvenile age (P30-P31), early adolescence (P34-P35), adolescence (P41-P42), late adolescence (P48-P49) and adulthood (P70-P90). Each stage, except for adulthood, included an age range of 2 days, which was the time needed to scan a batch of (typically 8) animals. The age range for adulthood was larger considering that the brain maturation already reached a plateau. Fig. S1A shows the distribution of age at which animals were scanned during adulthood, demonstrating that ~80% scans were imaged during P70–71. In addition, the wiring cost matrix measured during P70–71 was almost identical to that measured during P74–90 (Fig. S1B,C), suggesting that the wider age range in the adulthood group did not substantially impact our results.

All rsfMRI experiments were performed on a 7T Bruker scanner (Bruker, Germany) using a birdcage coil at the High Field MRI Facility at the Pennsylvania State University. T2 * -weighted single-shot gradient-echo echo-planner-imaging (GE-EPI) images were obtained using the following parameters: repetition time = 1000 ms, echo time = 15 ms, flip angle = 60°, FOV = 3.2 × 3.2 cm², slice thickness = 1 mm, number of slices = 20, matrix size = 64 × 64, 600 volumes each scan. Two scans were acquired in each rsfMRI session.

2.4. Data preprocessing

rsfMRI data preprocessing was performed using a MATLAB-based pipeline described in previous publications (Liang et al., 2013, 2012a; Ma et al., 2018a). To ensure steady-state MR signal, the first 10 volumes of each scan were removed. Motion was estimated by calculating the relative framewise displacement (FD) for each scan (Ma et al., 2018b). FD was estimated using the method described in (Power et al., 2012) with the parameters adjusted for the rat brain size. Specifically, for a given EPI volume, the Matlab image intensity-based geometric transformation function (‘imregtform’) was used to obtain both the translation (x_i, y_i, z_i) and rotation (α_i, β_i, γ_i) parameters of the geometric transformation. FD was calculated using the following equation based on these parameters:

$$FD=\left|\Delta x_i\right|+\left|\Delta y_i\right|+\left|\Delta z_i\right|+\left|\Delta l_{{\alpha }_i}\right|+\left|\Delta l_{{\beta }_i}\right|+\left|\Delta l_{{\gamma }_i}\right|$$

where Δ x_i, Δ y_i, Δz_i are translational displacement for frame i in three axes, and α_i, β_i, and γ_i are rotations around the three axes. $\Delta l_{{\alpha }_i}=\left|\left({\alpha }_{i-1}-{\alpha }_i\right)*r\right|$. Here r was set at 5 mm, which is the approximate distance from the cortex to the center of the rat head. Volumes with FD > 0.25 mm and their adjacent volumes were removed. Scans with more than 5% volumes removed were excluded for further analysis. Subsequently, manual co-registration of rsfMRI images to a defined template for each age was performed using Medical Image Visualization and Analysis software (MIVA, http://ccni.wpi.edu), which involved rigid-body transformation only. This is based on the prior knowledge that the rodent brain shape is virtually identical, particularly after P30 (Chen et al., 2016). The templates were developed based on Swanson atlas for the adult rat (P70), and the histology atlas (Calabrese et al., 2013) for younger groups (P31, 35, 41, and 49). At last, motion correction (SPM12), spatial smoothing (Gaussian kernel, FWHM 1 mm, twice of the in-plane voxel size), nuisance regression of motion parameters and signals from the white matter and ventricle, as well as band-pass filtering (0.01–0.1 Hz) were performed. The CSF/WM masks were eroded to avoid any partial volume contamination from the gray matter.

2.5. Data analysis

The whole brain was parcellated into 134 unilateral regions of interest (ROIs) based on anatomical definition. ROIs were then grouped into 9 brain systems including the sensorimotor cortex, polymodal association cortex, hippocampus, retrohipoocampus, amygdala complex, striatum, pallidum, thalamus and hypothalamus (Liang et al., 2012b).

The wiring cost between two ROIs was calculated as the product of the functional connectivity (FC) and their physical distance. FC between each ROI pair was determined by Pearson correlation coefficient between the two ROI time courses. Pearson correlation coefficients were converted to z scores using Fisher’s z transformation. The sign of FC was maintained in the calculation of wiring cost so that the sign of wiring cost represented the sign of FC. Notably, the vast majority of connections showed positive FC (Ma et al., 2018a). Physical distance between ROIs was estimated by calculating the Euclidean distance between their centroids. The partitioning of the brain (i.e. ROI definition) balanced the ROI size, limited by the spatial resolution of rsfMRI images, as well as ROI compactness which affected the accuracy of physical distance estimation. Higher ROI compactness provides a more accurate measure of physical distance between ROIs. The compactness for each ROI was assessed by its sphericity (Ψ) (Wadell, 1935):

$$\Psi =\frac{{\pi }^{\frac{1}{3}}{\left(6V_p\right)}^{\frac{2}{3}}}{A_p}$$

where V_p is the volume of the ROI and A_p is the surface area of the ROI. Table S1 shows that only 3 ROIs had a sphericity less than 0.5 (i.e. piriform area, CA1 and endopiriform nucleus), suggesting that the vast majority of ROIs are relatively compact. These data confirm that our estimation of physical distance was not adversely affected by ROI compactness.

To examine the developmental change on wiring cost, the age-related effect was tested using mixed-effect ANOVA with wiring cost at each age as the dependent variable. The slope of wiring cost against age was also calculated using linear regression.

The graph theory analysis was applied to all ROIs (134 ROIs), cortical ROIs (48 ROIs) and subcortical ROIs (56 ROIs), respectively, to examine the developmental change in the topology of each system. Topological parameters including the node degree, modularity and rich club coefficient were calculated based on binarized networks at the graph density of 0.15, 0.2, 0.25 and 0.3, respectively, using the brain connectivity toolbox (Rubinov and Sporns, 2010). At each density, modularity and rich club coefficient were normalized to a random network with same degree distribution. The randomization process was repeated 1000 times. These topological measures provide information regarding individual nodes, local clustering and distant integration. Node degree quantifies the number of connections emanated from a node. Modularity detects the modular organization of a network, and is often used for identifying the network’s community structure. Rich-club measures the extent to which well-connected nodes are connected to each other. It assesses information transfer between communities and distant hubs. Mathematical definitions of these topological parameters are described below:

Modularity (Newman, 2004):

$$Q=\sum _{i\in M}\left[e_{ii}-{\left(\sum _{j\in M}{e}_{ij}\right)}^2\right]$$

where M represents a set of non-overlapping modules. e_ij and e_ij represent within-module connections and between-module connections, respectively.

Rich club (Colizza et al., 2006):

$$\Phi (k)=\frac{2E_{>k}}{N_{>k}\left(N_{>k}-1\right)}$$

where E_>k denotes the number of edges connecting nodes with a degree greater than or equal to k and N_>k denotes the number of nodes with a degree greater than or equal to k.

We also generated the community structure for the whole-brain network at each age. To avoid the potential issue of degeneracy in modularity-based network partitioning (Good et al., 2010), we adopted the within-module connectivity method to identify consistent modular structures for each age’s network (Rubinov and Sporns, 2011). Specifically, for each network we applied the conventional modular-based algorithm to generate network partitions across a range of graph densities from 0.1 to 0.6 with the step size of 0.05. For each network partition a likelihood matrix was calculated, in which each entry was assigned to 1 when the two nodes (the column and row of the entry) belonged to the same module and 0 otherwise. This process was repeated 100 times. A mean likelihood matrix was then generated by averaging likelihood matrixes across all repetitions, network densities and subjects. The final community structure for the age was obtained by thresholding the mean within-module likelihood matrix at 0.75.

3. Result

In the present work, we investigated the developmental profiles of the cortex and subcortex using wiring cost and network topology (Fig. 1). We previously showed that the motion level of the dataset was low and consistent across all age groups (see Fig. 1 in (Ma et al., 2018a) for details). We have also ruled out the desensitization effect due to repeated imaging on our rsfMRI data (Ma et al., 2018a).

Fig. 1.

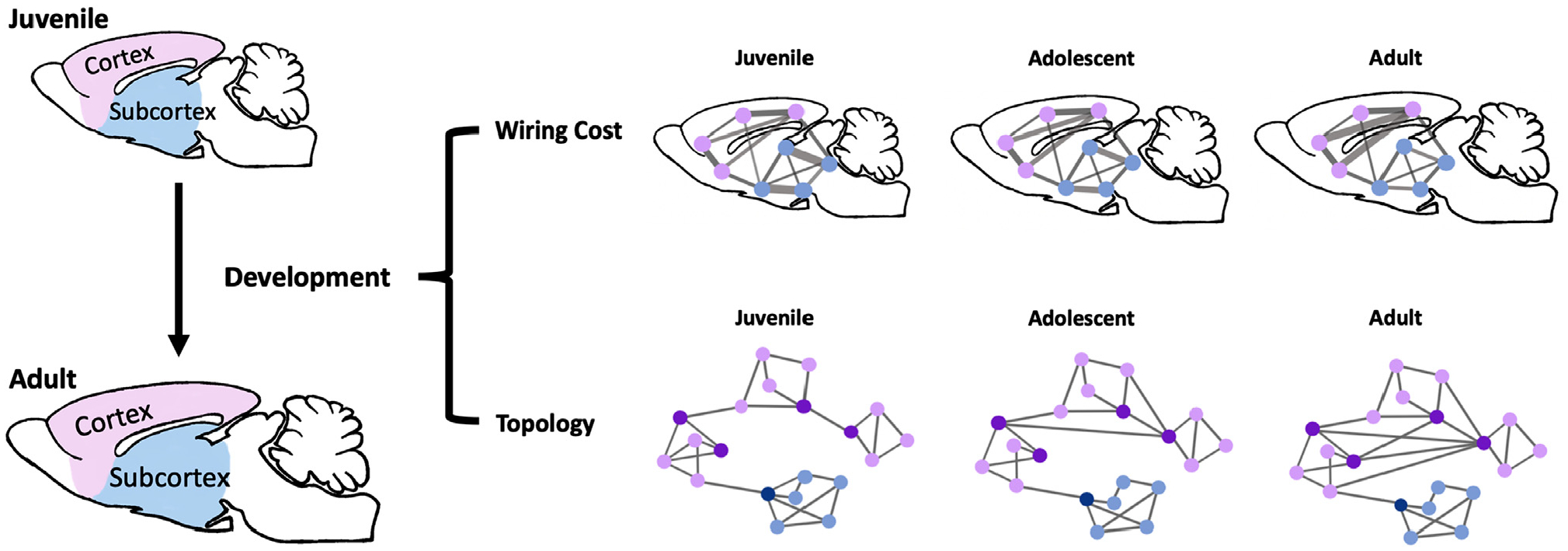
Schematic illustration of the analyses and main findings in the present study. Top: schematic illustration of wiring cost changes over development. Purple dots: cortical nodes. Blue dots: subcortical nodes. Edge thickness: magnitude of wiring cost. Bottom: schematic illustration of topology changes over development. Purple dots: cortical nodes. Blue dots: subcortical nodes. Dark purple nodes: hub nodes that form a rich-club core.

3.1. Regional mean wiring cost increase was more prominent in cortical regions

We first examined the developmental change in wiring cost at the regional level, which measures the averaged wiring cost across all connections involving a defined ROI. Specifically, for each ROI, we calculated its mean wiring cost by averaging its wiring costs with all other ROIs at each age, as shown in Fig. 2 A. Our data indicate that although the mean wiring cost of both cortical and subcortical regions increased as the animal matured, this increase was more prominent in the cortex relative to the subcortex. Fig. 2B shows regions displaying significant mean wiring cost change over the five developmental stages (mixed-effect ANOVA, p < 0.05, Bonferroni corrected), suggesting that most of these regions are located in the cortex. To further elucidate these changes, we averaged the mean wiring cost across ROIs in the cortex (48 ROIs) and subcortex (56 ROIs), respectively (Fig. 2C). The result shows that the regional mean wiring cost was comparable between the cortex and subcortex during the juvenile period (P31). The subcortical mean wiring cost increased moderately at early developmental stages and plateaued at P41. In contrast, the regional mean wiring cost of the cortex displayed a faster increase from the juvenile period to early adolescence and continued to increase after adolescence, albeit at a slower rate (Fig. 2C).

Fig. 2.

Developmental change in regional mean wiring cost. (A) Maps of regional mean wiring cost for all ages. (B) Regions exhibiting significant change in mean wiring cost over development (Mixed-effect one-way ANOVA, p < 0.05, Bonferroni corrected). (C) Developmental trajectories of mean wiring cost for the cortex and subcortex. (D) Developmental trajectories of mean wiring cost for cortical systems including the sensory-motor and polymodal association cortices. Significant age-related changes were found for both systems (one-way ANOVA, p < 0.05). (E) Developmental trajectories of mean wiring cost for subcortical brain systems including the striatum, hippocampus, retrohippocampus, thalamus, pallidum, and hypothalamus. Significant age-related changes were found for the striatum, hippocampus, retrohippocampus, and thalamus (one-way ANOVA, p < 0.05), but not the pallidum and hypothalamus (one-way ANOVA, p = 0.97 and 0.12, respectively). Bars: SEM.

Similar trajectories were found at the brain system level, obtained by averaging the mean wiring cost across all ROIs within each system at each age (Figs. 2D–2E). Pronounced increases in mean wiring cost were found in both the sensorimotor and polymodal association cortices (one-way ANOVA, p < 0.05, Fig. 2D), with a continuous increase after adolescence. In contrast, mean wiring cost in subcortical systems such as striatum, hippocampus, and thalamus showed a more moderate increase and plateaued at P41 (one-way ANOVA, p < 0.05). No significant change was found in the pallidum and hypothalamus (one-way ANOVA, p = 0.97 and 0.12, respectively). These data suggest that the spatial distribution of network cost might be non-uniform during development, with significantly more network resource dedicated to the cortex than the subcortex.

3.2. Cortical and subcortical connections exhibited different developmental wiring cost changes

To investigate the developmental change in wiring cost for individual connections, we first identified connections with significant wiring cost change over age (Fig. 3A, 1707 connections, mixed-effect ANOVA, p < 0.01, Bonferroni corrected). For these connections we regressed their wiring cost against age (in postnatal day), and used the slope of regression as a measure of developmental wiring cost change (Fig. 3A). All these connections were overlaid on a glass rat brain. The majority of these connections exhibited increased wiring cost over development (1057 connections), reflected by positive linear regression slopes. In addition, developmental wiring cost change showed strong bias across different anatomical systems between the cortex and subcortex. Specifically, wiring cost in cortico-cortical connections involving sensorimotor (SM) and polymodal-association (PA) cortices, as well as in cortico-subcortical connections was dominantly increased with age (i.e. positive slopes), but that in subcortico-subcortial connections including retrohippocampal, hippocampal, thalamic, striatum, and hypothalamic regions was mostly decreased (i.e. negative slopes). 77% of cortico-cortical connections with significant wiring cost change showed positive slopes, whereas only 26% of subcortical-subcortical connections with significant wiring cost change showed positive slopes. In addition to the bias in the sign of wiring cost change between the cortex and subcortex, the magnitude of age-related wiring cost change, measured by the amplitude of the slope, varied considerably across connections. The wiring cost of cross-hemisphere cortico-cortical connections showed a stronger increase than that of within-hemisphere cortico-cortical connections (Fig. 3B, two-sample t-test, p = 8.7 × 10⁻⁴). Also, the wiring cost of contralateral subcortical-subcortical connections showed a larger decrease than that of ipsilateral subcortical-subcortical connections (two-sample t-test, p = 0.0032).

Fig. 3.

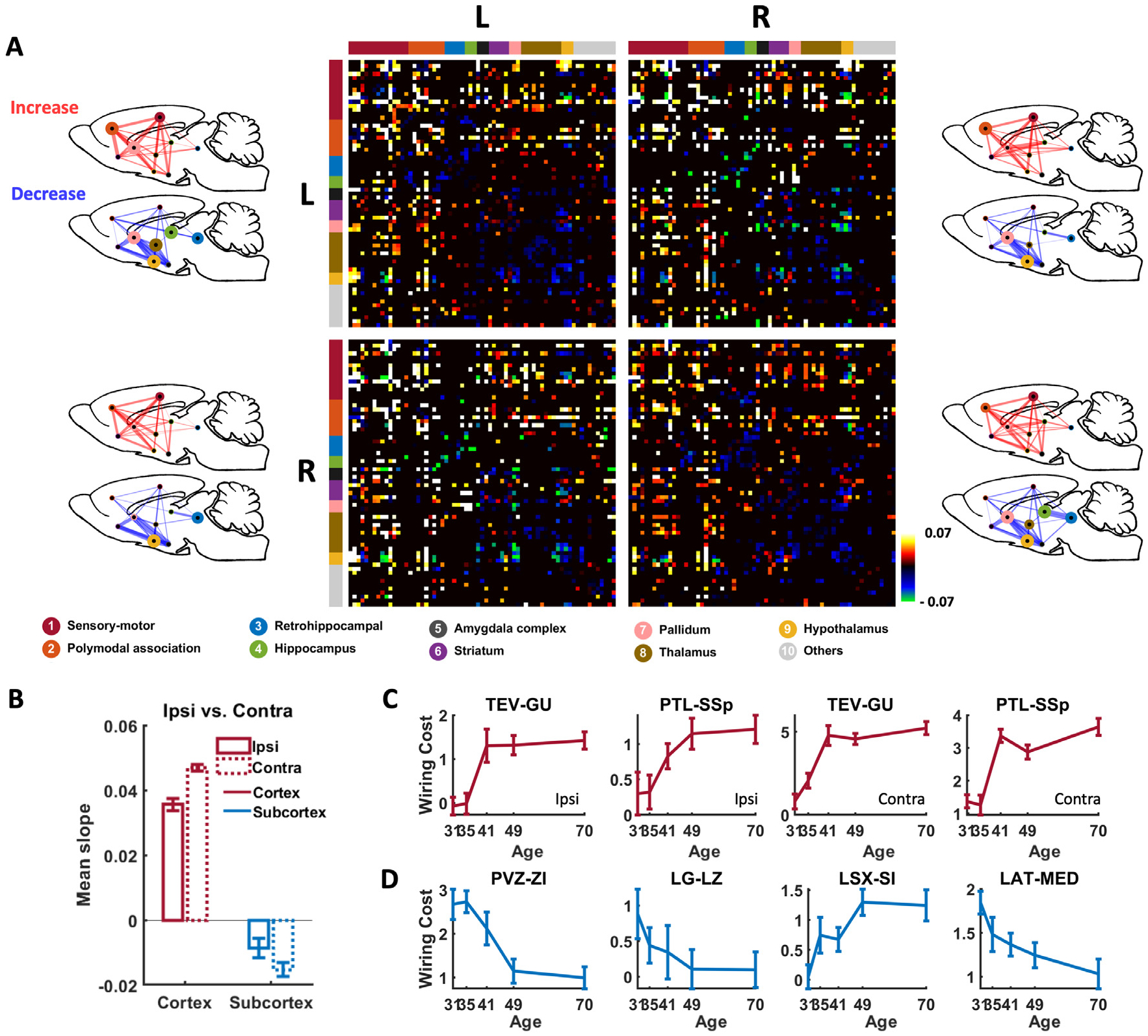
Developmental wiring cost changes for individual connections. (A) Connections exhibiting significant wiring cost change over age (mixed-effect one-way ANOVA, p < 0.01, Bonferroni corrected). Colors indicate the slope of linear regression of wiring cost against age. ROIs in the matrix were organized by left/right hemisphere and by 9 brain systems based on anatomical definition. Red: sensorimotor cortex; orange: polymodal association cortex; blue: retrohippocampus; green: hippocampus; black: amygdala complex; purple: striatum; pink: pallidum; brown: thalamus; yellow: hypothalamus; gray: all other ROIs. Wiring cost changes in each quadrant were overlaid on to a glass rat brain. Top left: Left to left hemisphere. Top right: Left to right hemisphere. Bottom left: Right to left hemisphere. Bottom right: Right to right hemisphere. The node size is proportional to the number of connections with significant wiring cost change normalized to the number of all possible connections within the system. The edge thickness is proportional to the number of connections with significant wiring cost change normalized to the number of all possible connections between the two systems. (B) Age-related change in wiring cost separately averaged from all cross-hemispheric connections and within-hemispheric connections in the cortex and subcortex, respectively. (C-D) Wiring cost trajectories in representative connections in the cortex (C) and subcortex (D). Bars: SEM.

In addition to the sign and strength of developmental wiring cost changes, individual connections exhibited distinct time profiles of ontogeny. Figs. 3C and 3D display the developmental trajectories of wiring cost in 4 representative connections in the cortex (Fig. 3C) and subcortex (Fig. 3D), respectively, demonstrating a variety of developmental patterns.

3.3. Wiring cost increase during development was dominated by long-range cortical, but not subcortical connections

As wiring cost directly depends on the physical distance of the connection, we investigated the developmental change of wiring cost for short- and long-distance connections in the cortex and subcortex, respectively. Fig.4A shows that the magnitude of age-related wiring cost change was overall strongly dependent on the physical distance across all connections. Interestingly, when we separated connections between cortical ROIs and subcortical ROIs, we found that short-distance connections in both the subcortex and cortex showed decreased wiring cost with age. However, as the connection distance became longer, cortical connections displayed a dramatic increase in wiring cost over age whereas subcortical connections showed virtually no change.

Fig. 4.

Relationship of regional mean wiring cost and node degree. (A) Scattered plot of regional mean wiring cost and node degree for 134 unilateral ROIs at all ages. (B) Slope of linear regression between regional mean wiring cost and node degree is significantly different between early and late developmental stages (one-way ANOVA, p = 1.32 × 10⁻⁷, eta-squared effect size η=0.11). Error bars represent variability (S.E.M.) across rats.

To further confirm these relationships, we divided all cortical and subcortical connections into short-distance (physical distance < 8 mm) and long-distance connections (physical distance > 8 mm). We chose this cutoff because 8 mm was the transition point of wiring cost/age slope vs. physical distance at the whole brain level. Fig. 4B shows moderate decrease in wiring cost over development for short-distance connections in both the cortex (one-way ANOVA, p = 0.0056) and subcortex (one-way ANOVA, p = 9.2 × 10⁻¹⁷). In contrast, the wiring cost for long-distance cortical connections sharply increased during development (one-way ANOVA, p = 9.5 × 10⁻⁶), whereas this trend was absent in long-distance subcortical connections (one-way ANOVA, p = 0.63, Fig. 4C). These results collectively indicate that wiring cost increase during development was dominantly driven by long-range cortical, but not subcortical connections.

The remarkable difference in wiring cost changes between short- and long-distance cortical and subcortical connections resulted from differential FC changes for different types of connections in relation to physical distance increase due to growth (Fig. S2). For short-distance connections in both the subcortex and cortex, the FC decreased as the brain matured (i.e. negative slope between FC and age, Fig. S2A), which offset relatively small increases in physical distance (Fig. S2B) and led to moderate decreases in wiring cost (Fig. 4B). Similarly, the reduction of FC in long-distance subcortical connections counteracted their increase of physical distance (Fig. S2), resulting in virtually no change in wiring cost (Fig. 4C). In contrast, long-distance cortical connections displayed increased FC and increased physical distance, producing a strong increase in wiring cost during brain development.

3.4. Cortex and subcortex showed different topological change over development

The mammalian brain network is organized by balanced clustered local processing, which minimizes wiring cost, and long-range connections between connector hubs (Bullmore and Sporns, 2012, 2009), which enable efficient distal communication (Liang et al., 2011; Vincent et al., 2007). However, developmental changes in brain network topology in relation to wiring cost are not well understood.

To examine this issue, we plotted mean wiring cost against node degree (network density = 0.15) for all 134 ROIs across five developmental stages. A strong positive linear relationship was observed between these two measures (Fig. 5A). In addition, this linear dependency became stronger as the brain matured, reflected by significantly higher slope of wiring cost against node degree between early (juvenile and early adolescent periods, P31-P35) and late (adolescence to adulthood P41-P70) development stages (one-way ANOVA, p = 1.32 × 10⁻⁷). These data demonstrate the relationship between wiring cost and brain topology, and this relationship can change during development.

Fig. 5.

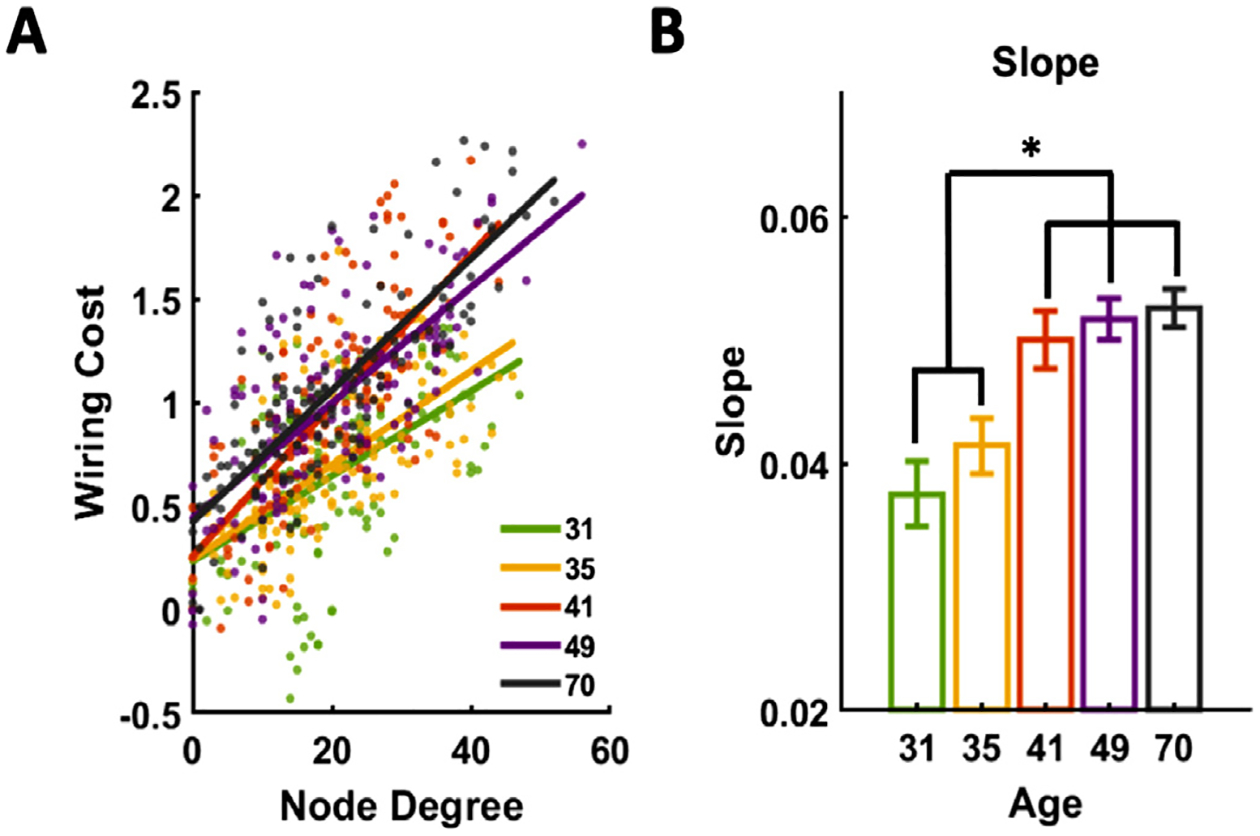
Relationship between age-related wiring cost change and physical wiring distance. (A) Whole-brain, cortical and subcortical connections with significant age-related wiring cost change, plotted against their physical distance. (B) Developmental trajectories of wiring cost for short-distance connections (physical distance < 8 mm) in the cortex and subcortex, respectively. Significant age-related change in wiring cost is observed for both the cortex (one-way ANOVA, p = 0.0056) and subcortex (p = 9.17 × 10⁻¹⁷). (C) Developmental trajectories of wiring cost for long-distance connections (physical distance > 8 mm) in the cortex and subcortex. Significant age-related change in wiring cost is observed only for the cortex (p = 9.53 ×10⁻⁶) but not the subcortex (p = 0.63). Bar: SEM.

To further elucidate development-related topological changes in the cortex and subcortex, cortical and subcortical networks were constructed based on cortical only ROIs (48 ROIs) and subcortical only ROIs (56 ROIs), respectively. Topological parameters including node degree, modularity and rich club coefficient were calculated as a function of age at the network density of 0.15, 0.2, 0.25 and 0.3, respectively.

The mean node degree was found to increase in the cortical network (one-way ANOVA, p = 1.49 × 10⁻⁵, p = 8.14 × 10⁻⁷, p = 3.34 × 10⁻⁸, p = 1.99 × 10⁻⁹ at graph density 0.15, 0.2, 0.25 and 0.3 respectively) but decrease in the subcortical network (one-way ANOVA, p = 3.34 × 10⁻⁵, p = 6.09 × 10⁻¹⁰, p = 1.32 × 10⁻¹⁰, p = 1.80 × 10⁻¹⁰ at graph density 0.15, 0.2, 0.25 and 0.3 respectively) (Fig. 6 A), which suggests that during development cortical regions tend to form more connections with other cortical regions, but subcortical regions generally reduced the number of connections with other subcortical regions.

Fig. 6.

Developmental changes in network topology. Developmental trajectories of topological measurements as a function of age. (A) node degree, (B) modularity, (C) rich club coefficient.

The developmental change in local information processing was assessed by modularity. At the juvenile stage, the modularity was similar between the cortical and subcortical networks. Over development the modularity considerably decreased in the cortical network until late adolescence (one-way ANOVA, p = 3.16 × 10⁻¹⁹, p = 1.81 × 10⁻²², p = 2.66 × 10⁻²⁵, p = 3.58 × 10⁻²⁶ at graph density 0.15, 0.2, 0.25 and 0.3 respectively), but changed less significantly in the subcortical network (one-way ANOVA, p = 1.89 × 10⁻⁵, p = 4.02 × 10⁻⁶, p = 5.92 × 10⁻⁷, p = 2.08 × 10⁻⁷ at graph density 0.15, 0.2, 0.25 and 0.3 respectively). This result suggests reduced local processing in the cortical network during development.

Information integration was assessed by rich club coefficient. Similar to modularity, rich club coefficient was similar between the cortical and subcortical networks at the juvenile age. It increased in the cortical network (one-way ANOVA, p = 0.12, p = 0.026, p = 0.047, p = 0.019 at graph density 0.15, 0.2, 0.25 and 0.3 respectively) but decreased in the subcortical network (one-way ANOVA, p = 0.079, p = 0.248, p = 0.083, p = 0.025 at graph density 0.15, 0.2, 0.25 and 0.3 respectively) over development. These data suggest that the global integration is increased in the cortical network, consistent with the result of increased long-range cortical connections as the brain matures.

We also mapped the community structure for the whole-brain network for each age (Fig. 7). Communities were organized and color coded according to their sizes. It appears that regions in the separate communities were significantly reorganized over development.

Fig. 7.

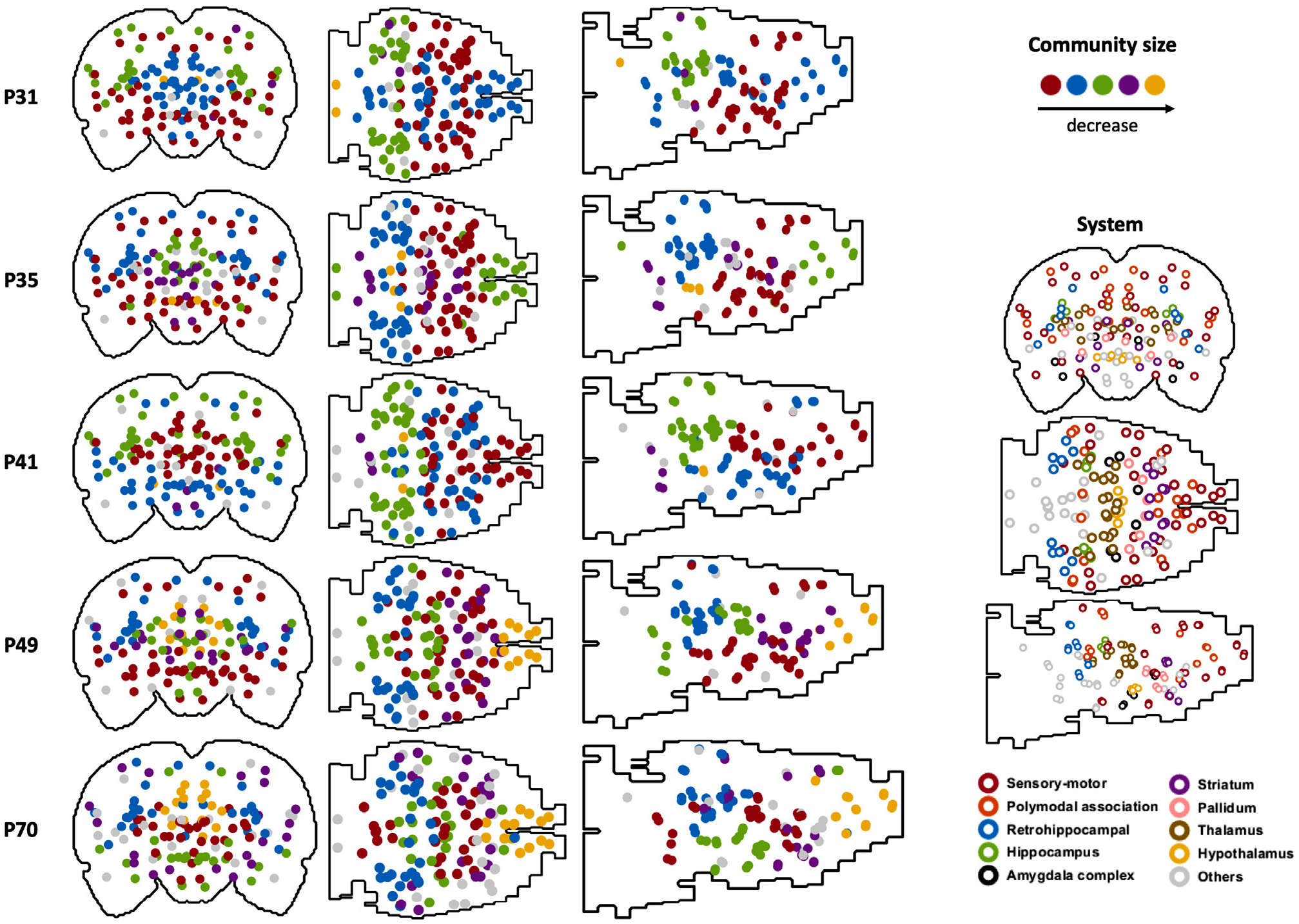
Community structure at each age (graph density = 0.15). Each dot represents one ROI. Left: solid dots represent the community structure. Dots with the same color belong to the same community, and the color indicates the community size. The largest 5 communities are displayed. Right: open circles represent the corresponding brain systems of ROIs.

Taken together, these topological measurements suggest that distal information integration is strengthened but clustered local processing is weakened in the cortical network over development. This result is consistent with our observation of increased wiring cost for long-distance connections but decreased wiring cost for short-distance connections in the cortex (Fig. 4).

4. Discussion

Brain development is a metabolically expensive process. Therefore, understanding how network cost is distributed among separate brain systems during development is critical. Using rsfMRI data longitudinally collected in the awake rat brain, here we investigated the developmental changes of wiring cost and network topology in both the cortex and subcortex. Our data showed that at the regional level, the mean wiring cost generally increased in both the cortex and subcortex during development, but the increase in cortical regions was disproportionally larger. When examining individual connections, the wiring cost significantly increased in cortical connections but decreased in subcortico-subcortical connections as the brain matured. We further found that the wiring cost increase during development was dominantly driven by long-range cortical, but not subcortical connections, consistent with increased network integration in the cortex revealed by graph analysis. Taken together, our results have provided evidence suggesting that there is a non-uniform distribution of network cost between the cortex and subcortex during brain development, and increase of network integration as the brain matures is mainly contributed by long-distance cortical connections.

4.1. Brain development is spatiotemporally heterogeneous and system specific

Our data show that during development, the increase of regional wiring cost was appreciably larger in cortical regions than subcortical regions. Considering that the energy needed for wiring cost change is high (Martin, 1996), our result is consistent with the report of high wiring cost and high metabolism in DMN-related cortical but not subcortical regions in rats (Liang et al., 2018). PET studies in humans and rodents also revealed linear increases in the metabolism of the bilateral prefrontal and orbitofrontal cortices during brain maturation (Choi et al., 2015; Kang et al., 2004). These results suggest that developmental change in regional wiring cost is dominant in cortical regions.

In addition to non-uniform regional-level changes, the cortex and subcortex exhibited distinct developmental profiles in wiring cost in individual connections. Of all cortico-cortical connections that showed significant wiring cost change over development, 77% had positive slopes, and this number in subcortical connections was only 26%. This remarkable contrast agrees well with the human literature reporting stronger cortico-cortical but weaker subcortical functional connectivity in adults compared to children (Power et al., 2010; Supekar et al., 2009). Similarly, metabolic connectivity, quantified by correlations between regional F-Fluorodeoxyglucose levels measured by PET, increases in connections between retrosplenial, medial prefrontal, and sensorimotor cortices from postnatal 5 to 10 weeks in rats, while metabolic connectivity involving limbic regions did not change during these development periods (Choi et al., 2015).

Individual connections also exhibited heterogeneous ontogeny in wiring cost. Most connections continued to develop during early developmental ages until adolescence or late adolescence (P41 or P49). These changes can persist into adulthood in some connections. These differences echo heterogeneous maturation timelines in separate brain structures. For instance, structural studies in humans have demonstrated differential developmental changes in the gray matter volume of the cortex and subcortex (Sowell et al., 2003). A nonlinear reduction in cortical gray matter volume was observed, whereas most subcortical regions including the pallidum and striatum displayed a linear decrease in gray matter volume with age. The hippocampus and amygdala showed a slight nonlinear increase in gray matter volume over human brain development (Ostby et al., 2009). Taken together, these data confirm that brain development is spatiotemporally heterogeneous and system specific.

4.2. Adolescence is a key transition stage for postnatal brain development

Our data show that regional wiring cost significantly increased during early developmental periods but plateaued during P41 - P49 for both cortical and subcostal regions. These data are consistent with our previously reported maturation timelines of brain-wide functional connectivity (Ma et al., 2018a), as well as the development of brain microstructure measured by diffusion tensor imaging (DTI). In white matter regions including the anterior commissure, cingulum, corpus callosum and optical pathways, the fractional anisotropy (FA) was found to increase starting from birth and reach a maximum around adolescence for both rats (Bockhorst et al., 2008; Calabrese et al., 2013) and mice (Chuang et al., 2011). Depending on the region, the white matter FA either remains the same or decreases slightly until P80. This trajectory can be explained by a few neurobiological maturation processes including synaptic overproduction, pruning and myelination of axons. During brain development, neurons undergo synaptogenesis and then network refinement through synaptic pruning and myelination (Flechisg, 1901; Huttenlocher, 1979; Huttenlocher et al., 1982). Synaptic overproduction still exists during adolescence, but is significantly slower (Huttenlocher, 1979). Meanwhile, synaptic pruning starts to increase during this period. We speculate that the combined effect of decreased synaptic overproduction and increased pruning may lead to stable wiring cost, FC and FA during adolescence.

After adolescence, regional wiring cost was seen to increase again in the cortex but not in the subcortex (Fig. 2 C&D). This can be attributed to continuous synaptic pruning and myelination but limited synaptic overproduction during this period (Juraska and Willing, 2017), which result in more efficient functional communication between cortical regions. Another factor that can contribute to post-adolescence cortical wiring cost increase is rostral/caudal expansion in the rat cortex, which continues after adolescence until around P60 (Mengler et al., 2014; Shaw et al., 2008). Rostral/caudal expansion of the cortex produces more long-distance connections between anterior and posterior ROIs, which can increase wiring cost in the cortex. These factors may collectively contribute to the continuous increase of wiring cost in the cortex from late adolescence into adulthood.

4.3. Wiring cost increase during development is dominated by long-range cortical, but not subcortical connections

We found that the wiring cost of short-distance connections, both in the cortex or subcortex, moderately decreased over development. In contrast, the wiring cost of long-distance connections in the cortex, but not the subcortex, dramatically increased during brain maturation. A similar relationship between FC strength and wiring distance was also reported during the development of DMN in human (Fair et al., 2008; Kelly et al., 2009) and animals (Choi et al., 2015; Ma et al., 2018a). Distributed regions in DMN were sparsely connected at young age, but long-distance, anterior-to-posterior connections substantially increase during development. In addition, metabolic connectivity between these distal regions was significantly increased from childhood to adolescence (Choi et al., 2015). These data also well agree with the topological measures we obtained. In the cortical network, we observed increased nodal degree and rich club coefficient but decreased modularity during brain development. This suggests that brain development is accompanied by the formation of rich-club cores, which requires long-range, metabolically expensive connections that integrate centralized network hubs from distributed communities (Liang et al., 2013; van den Heuvel et al., 2012). Indeed, PET data showed that the increase in metabolic connectivity strength was coupled to increased energy efficiency in hub regions such as the medial prefrontal and retrosplenial cortices from childhood to early adulthood in the rat brain (Choi et al., 2015). In contrast, the subcortical network exhibited reduced node degree, subtle changes in modularity and decreased rich club coefficient, implying that the subcortical network most likely did not contribute to increased network integration during brain development. In addition, nodes that were highly involved in mediating communication between functional specialized regions were found to have much higher wiring cost compared to other nodes (Rubinov et al., 2015). Most of these nodes also closely corresponded to distributed regions in the DMN.

These data collectively indicate that resource is primarily used for the development of the cortex, but not subcortex from the juvenile stage to adulthood. They also provide strong evidence supporting that enhanced distant integration during brain development might be dominated by increases in long-range cortico-cortical connections.

4.4. An evolutionary view of brain development

Among different species, brain to body size scales allometrically (Rilling, 2006; Shingleton, 2010): animals with larger body sizes in general have larger brains, albeit following an allomeric scaling law. This means that the increase of brain size is slower than that of body size across species. One of the key constraints of brain size is the energy cost (Martin, 1996), as a larger brain needs a greater number of connections, especially long-range connections between distant brain regions. During the process of evolution, the increase in brain to body size is accompanied by increase in the complexity of brain structure and function. At the early stages of brain evolution, the ‘old brain’ forms, including the brain stem, medulla, pons, thalamus, and hypothalamus (Stangor and Walinga, 2010), which are responsible for sustaining fundamental homeostatic functions such as breathing, moving, resting and feeding. A ‘new brain’ that provides more advanced functions mediating sexual, emotional and fighting behaviors develops after the appearance of the ‘old brain’. It is mainly comprised of the olfactory system and part of the limbic system including amygdala and hippocampus, but also includes the earliest section of cerebral cortex. The most advanced, largest, and evolutionarily young part of the cerebral cortex to evolve is the neocortex. Regions in the neocortex are involved in higher-order brain functions such as cognition, language, sensory perception and motor command generation. With increased brain to body size as well as brain complexity, there is an increase in metabolic cost to maintain sufficient functionality (Martin, 1996). In addition, the neocortex is spatially the outmost layer of the brain. Therefore, it is the structure that contains the most long-range connections and thus requires the highest wiring cost. This is supported by the finding that the increase of gray matter volume lags behind the increase of white matter volume that contains long-distance connections for integrative processing (Zhang and Sejnowski, 2000). Notably, white matter fibers play a major role in connecting cortical to cortical regions, suggesting that increased wiring cost is dominantly in neocortex. These evolutionary processes are consistent with the developmental processes that cortical regions and connections exhibit greater wiring cost change. Another important evolutionary process of the brain, the neocorticalization, describes a gradual enlargement of neocortex relative to subcortex (Changizi, 2001). This process shows a trend of evolution toward a higher cognitive function that requires better integrative processing and communication efficiency. Comparably, the level of brain integrative ability reflects the degree of maturity over development. Taken together, the network resource distribution during brain development to a certain extent mimics the process of the evolution of the brain.

4.5. Potential pitfalls

There are a couple of potential pitfalls in the present study. First, the wiring cost was defined as the product of the FC and the physical distance between two nodes. Physical distance was estimated by the Euclidean distance between ROI centroids. This will result in an underestimate of wiring cost for most connections as the length of axonal projections are typically longer than the Euclidean distance. Another confounding factor is that rats could have different hemodynamic response function (HRF) at different developmental stages. However, the previous literature has demonstrated that rat local field potential (LFP) and BOLD signal are already adult-like by the age of P30 (Arichi et al., 2012). The earliest time point in this study was P31. Therefore, subtle difference in the HRF should not significantly affect the quantification of FC and wiring cost. Lastly, it needs to be recognized that subcortical to cortical connections are also important to understand the developmental processes in the brain, although data related to these connections were not specifically examined in the present study.