Abstract
In the context of radioimmunotherapy of cancer, there is a need for continued improvement of dosimetry of radionuclides localized in tumors. Current methods assume uniform distribution of radionuclides in the tumor despite experimental evidence indicating nonuniformity. We have developed a model in which nonuniform distribution of radioactivity in the tumor is taken into account. Spherically symmetric radionuclide distributions, depending linearly and exponentially on the radial position, are considered. Dose rate profiles in the tumor are calculated for potentially useful beta-emitting radionuclides, including 32P, 67Cu, 90Y, 111Ag, 131I, and 188Re, and for 193mPt, an emitter of conversion electrons and low-energy Auger electrons. For the radionuclide distributions investigated, high-energy beta emitters, such as 90Y, are most effective in treating large tumors (diameter, d ≳, 1 cm), whereas for small tumors (d ∼ 1 mm), medium energy beta emitters such as 67Cu are better suited. Very small tumors (d < 1 mm), and micrometastases are best handled with low-energy electron emitters such as l93mPt.
Keywords: radionuclides, dosimetry, radioimmunotherapy
1. Introduction
The advent of radiolabeled monoclonal antibodies (MAb's) has elicited much interest in the possibility of developing cancer cell specific radiopharmaceuticals for therapeutic purposes. It is generally believed that radioimmunotherapy (RIT) may be effective in treating metastases and small tumors, where surgery may not be feasible, by suitable combinations of MAb's and radioisotopes. Numerous factors dictate the choice of both the MAb and the radionuclide. DeNardo et al.1 considered some of the biological questions concerning MAb's and appropriate targets, as well as radionuclide selection based on absorbed doses around point sources. Jungerman et al.2 have performed similar calculations. Wessels and Rogus3 have noted several of the biological and physical factors that determine the tumor dose relative to the liver and whole body. These studies do not address the radionuclide distribution in the tumor.
Current Medical Internal Radiation Dose (MIRD) guidelines4 for estimating doses to individual organs are based on uniform radionuclide distribution in homogeneous media5 of varying shapes and sizes. The assumption of uniformity may be adequate for homogeneous normal tissue where the radioisotope carriers permeate the entire tissue. As tumor tissue undergoes microvascular changes during the various phases of malignant growth, the flow of blood to interior regions of some tumors may be inhibited, and necrosis may develop.6 Heterogeneities in blood flow may also cause nonuniform distributions of radioactivity in tumors. Kwok et al.7 recently considered this problem theoretically. They calculated the spatial dose rate distribution in a sphere of soft tissue containing 131I, 32P, and hypothetical sources of monoenergetic photons. Their convolution technique has the advantage of accepting any distribution of activity. Humm8 has employed a similar tumor model to calculate the absorbed doses using Charlton's influence functions.9 This method has not been adapted to handle inhomogeneous regions of activity. However, the effect of different size “cold regions” was investigated for 90Y, 77As, and 199Au, representing high-, medium-, and low-energy β particles, respectively. The results suggest that as the size of the cold region increases, correspondingly higher energy β emitters are required to sterilize the tumor.8 Based on calculations for spherical sources of uniformly distributed activity, Humm has also concluded that as the size of the tumor decreases it becomes more advantageous to use low-energy electron emitters in order to minimize the dose to the normal tissue, in agreement with an earlier observation of Sastry et al.10
In this work, we expand on the above findings by examining the radial dependence of the tumor dose on tumor size, activity distributions within the tumor, and radiation type and energy. Using spherically symmetric distributions of activity in homogeneous unit density spheres (diameters, d = 0.1 and 1.0 cm) as the model, the radial dependence of the dose rate for several β emitters has been determined. Three different hypothetical distributions of radionuclides are considered: (1) uniform, (2) linearly dependent on the radial position, and (3) an exponential radial dependence. For purposes of comparison with the work of Kwok et al.,7 a fourth activity distribution representing a tumor with a necrotic core is also considered. Finally, we calculate the dose to organs in the peritoneal cavity following intraperitoneal (ip) injection of radioactive material.
Radionuclides which decay by the emission ofβ-rays have been suggested for use in radioimmunotherapy1–3,8,10; hence 32P, 67Cu, 90Y, 111Ag, 131I, and 188Re are selected for these calculations. These β emitters are some of the potential candidates for RIT since their emissions have maximum ranges varying from 2 to 12 mm in soft tissue. Table I contains a summary of the properties of these radionuclides. In addition, results are obtained for 193mPt, a prolific Auger electron emitter by virtue of its decay almost entirely by internal conversion.11 About three conversion electrons and 26 Auger electrons are emitted by this radionuclide per decay.11 In view of the short range of the conversion electrons (see footnote, Table I), this radionuclide may be of special interest to RIT for treating small metastatic tumor cell clusters.
Table I.
Data on the radionuclides.
| β emitter | β-ray endpoint energy (MeV) | Maximum range (mm)c | Half-life |
|---|---|---|---|
| 32pa | 1.710 | 8.7 | 14.3 d |
| 67Cua | 0.576 | 2.2 | 61.7 h |
| 90Ya | 2.273 | 11.9 | 64.0 h |
| 111Agb | 1.035 | 4.8 | 7.45 d |
| 131Ia,d | 0.606 | 2.4 | 8.06 d |
| 188Rea | 2.132 | 11.1 | 16.8 h |
Calculated for unit density matter using Eq. (10).
The 0.806-MeV β group is very weak.
[193mPt (4 33.d half-life) emits conversion electrons with average energy (yield) of 57.1 (0.16), 126.0 (0.84), 10.0 (1.0), and 1.0 keV (1.0) per decay. The range of the highest energy group is about 0.2 mm. See Ref. 11 for more details and for data on other radiations.]
Our results show that medium-energy β emitters such as 67Cu may be well suited for therapy of tumors ∼ 1 mm in diameter regardless of activity distribution, while high-energy β emitters such as 90Y are more appropriate for larger tumors. In addition, the results suggest that 193mPt may be efficient in treating very small tumors (d < 1 mm) with minimal dose to the surrounding normal tissue.
II. Methods
A. Formulation of dose rates within the MIRD schema
The tumor model used in this work is a homogeneous sphere of unit density matter surrounded by healthy tissue of the same composition. Radioactivity is confined to the tumor. The spatial dependence of the dose rate to the tumor and surrounding tissue is found by computing the rate to 25 concentric shells of equal thickness. The geometry is indicated in Fig. 1. Per unit of radioactivity in the tumor, the total dose rate to the jth annular region, from all the different components of the emitted radiations, may be written in the MIRD formalism4 as follows:
Fig. 1.
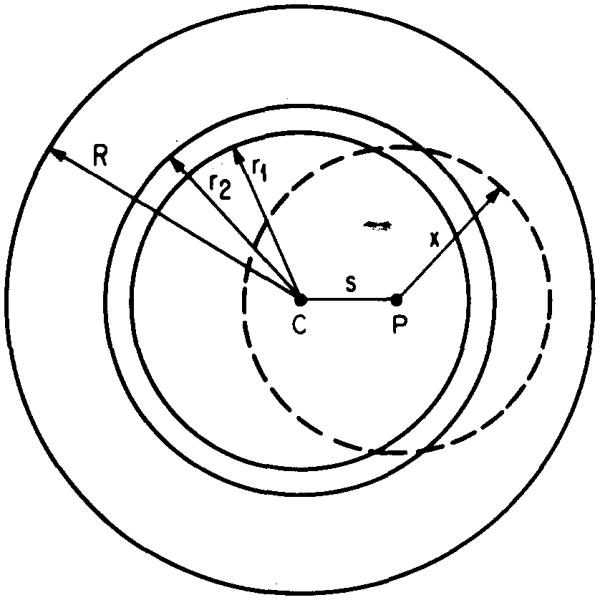
Geometry used for calculation of the absorbed fractions. The homogeneous unit density sphere (center C, radius R) represents a soft tumor tissue, containing a spherically symmetric distribution of radioactivity given by Eqs. (3)–(5). Located at a distance s from the center of the tumor is an arbitrary source point P. The variable x represents the distance traveled by radiation emanating from the source point. The annular region between the radii r1, and r2 is an example of the 25 target regions in which the dose rates are calculated. The fraction of energy emitted from all source points in the entire sphere and absorbed in each target region is calculated using Eq. (8) for photons, and Eq. (12) for electrons and for β particles (see text, Sec. II E).
| (1) |
where
Ḋ(j) = dose rate to jth annular region in Gy/h per MBq of activity in the tumor;
= fraction of energy of the ith radiation component absorbed in the jth annular region;
m(j) = mass of jth annular region in g;
Δi, = mean energy of the ith radiation emitted per unit cumulated activity in g Gy/MBq h; and
= specific absorbed fraction in the jth region for the ith radiation.
Average dose rates to the whole tumor (Ḋave) may be calculated using Eq. (2), where is the fraction of energy of the ith radiation absorbed by the entire sphere, and M is the total mass of the sphere:
| (2) |
B. Activity distributions
Formulation of an appropriate mathematical description which represents the in vivo temporal and spatial activity distribution in tumorous tissue following administration of radiolabeled MAb's requires consideration of the effective half-life of the MAb radioisotope complex, vascularity of tumor tissue, capillary and cell permeability, tumor geometry, and several other variables. In order to gain some insight into choosing appropriate radionuclides for RIT, we have used a simple model where the tumor is represented by a sphere of radius R containing a static and spherically symmetric activity distribution. If blood flow to the central region of the tumor is restricted due to modifications of the intratumor vascular network during growth,6 activity in the tumor may be expected to be localized predominantly in its peripheral regions. Accordingly, the radial dependence of the activity density ρA (s) is represented by a linear and an exponential function, with no activity at the center and increasing radially outward. These mathematically simple distributions result in concentration of the activity, in different degrees, toward the sphere's perimeter. For the sake of comparison, calculations are also performed for radioactivity uniformly distributed in the spheres. The activity distribution functions considered are given below:
Uniform: ρA (s) = A0/V,
| (3) |
| (4) |
| (5) |
In order to obtain dose rates per unit activity, each distribution is normalized according to Eq. (6), where A0 is the total activity in the tumor, and V, the tumor volume:
| (6) |
The choice of the constant a in Eq. (5) is arbitrary. A value of a = 5/R is used in this work, representing a rapid decrease in the density of activity as one proceeds from the perimeter to the center of the sphere.
For comparison with the results of Kwok et al.,7 we have considered an additional activity distribution given by Eq. (7), used in their work:
| (7) |
It represents a tumor where the central necrotic core (radius Rm = 2.2 mm) contains no activity. Equation (7) may also be applicable for organs surrounded by a sea of radioactivity. This situation may arise following ip injection of radiolabeled MAb's. Using this model, one may calculate dose rate distributions in healthy organs from activity in the ascitic fluid.
C. Photon absorbed fractions
Absorbed fractions for photons are computed using the point kernel – geometric reduction factor approach of Berger,12 with two modifications: (i) provision for nonuniform distribution of radioactivity, and (ii) the annular geometry of interest to this work. For the configuration shown in Fig. 1, the fraction of energy of the ith photon radiation absorbed in the jth annular region is given by the following:
| (8) |
Where
= geometric reduction factor for annular geometry;
Φ (x,Ei) = point isotropic specific absorbed fraction13;
Ei = energy of the ith photon;
ρm = mass density;
s = distance from center of sphere to source point;
= inner and outer boundaries of jth annular region;
and
x = distance from source point to target point.
The function Φ (x,Ei) is given by13
| (9) |
where μen and μ are the linear energy absorption and attenuation coefficients, respectively, for photons of energy Ei. The energy absorption buildup factor Ben is tabulated by Berger.13 The Φ's are normalized according to
The geometric factor may be understood as follows. Let an arbitrary source point P be located at a distance s from the center of the sphere of radius R containing radioactivity (Fig. 1). The variable x is the distance traveled by the radiation emanating from the source point. Consider a spherical shell of radius x, centered on P. If the annulus defined by r1, and r2 is the target region, then the geometric factor ψ is the fraction of the surface area of the spherical shell that lies within the annular target volume. By definition, 0 ≤ ψ ≤ 1, depending on the geometry. The equations defining ψ are presented in the Appendix for various contingencies arising from the geometry of Fig. 1.
D. Absorbed fractions for monoenergetic electrons
Computations of absorbed fractions for electrons are similar to the case of photons except that the point kernel is replaced by Cole's14 energy loss expression for electrons with appropriate normalization. For unit density matter, Cole has experimentally established that the electron energy E (in keV) and the range X (in μm) are related by
| (10) |
Differentiation of Eq. (10) yields Eq. (11) for dE/dX, the rate of energy expended as the electron traverses an infinitesimal path dX of its range in the continuously slowing down approximation (csda):
| (11) |
Using Eq. (11) and following Kassis et al.,15 we may write the absorbed fraction for the jth shell and ith electron of initial energy Ei as
| (12) |
In Eq. (12), x is the distance traveled by the electron from the source point P, and dE/dX is continuously reevaluated as the electron with initial energy Ei, and initial range X(Ei), undergoes loss of energy as it moves away from the source point. Cole's experimental data,14 available over energies from 20 eV to 20 MeV, provide maximum flexibility for use with Auger electrons, conversion electrons, and β rays. Care should be taken when considering electrons with very low energies since Eqs. (10) and (11) provide a poor fit to the experimental data below 0.4 keV. In this energy region, we have fitted Cole's experimental data to a power series expression for use in the computer dosimetry program. Recent Monte Carlo calculations confirm the adequacy of continuous slowing down approximation (csda) to spheres with radii > 10 nm.16
E. Beta radiation
The β spectrum is continuous up to the endpoint energy. For all the β emitters in Table I, except for 90Y, the spectra have the usual “allowed” shape associated with statistical sharing of available energy between the β particle, antineu-trino and the residual nucleus. The additional energy dependence17 for the 90Y unique once-forbidden transition is taken into account. The calculated spectrum is divided into a large number of energy intervals of equal width over the entire energy range, and the relative β particle yield per decay is calculated for each bin for the radionuclides of interest. Treatment of the β radiation in this fashion allows us to calculate absorbed fractions for β emitters using Eq. (12). For 67Cu, 111Ag, 131I, and 188Re, which have several different groups, a composite β spectrum, weighted appropriately by the branching ratios, is used.
F. Computations
Absorbed fractions given by Eqs. (8) and (12), and the dose rates given by Eqs. (1) and (2), are obtained numerically on a VAX-11/750 computer. Input data for all radiations, including yields and energies, are taken from the tables of Dillman and Von der Lage,18 with the exception of 111Ag and 193mPt. The data for 111Ag are from Martin and Blichert-Töft,19 and from Howell et al.11 for 193mPt. All radiations emitted by each radionuclide are included in the calculations. Possible corrections for bremsstrahlung are not included. The photon attenuation and energy absorption coefficients in water as well as the energy absorption buildup factors Ben, given by Berger,13 are used to calculate the functions Φ (x,Ei) in Eq. (9) for photons of various energies (Ei) emitted by the radionuclides.11,18,19 The energy dependent coefficients in the polynomial expression for Ben may be found in Table 4 of Ref. 13. Incidentally, we note that the algebraic signs of the first four coefficients (a0 through a3) given in this table for 0.015-MeV photons should be reversed.
III. Results and Discussion
The relevance of nonuniform distributions of radioactivity to the dosimetry problems encountered in RIT stems from tumor biology. Cells near the necrotic core are hypoxic as a result of reduced blood flow to the center of solid tumors.20,21 Sterilization of these hypoxic cells with RIT may be difficult since they are relatively radioresistant, and accumulation of radioactivity in this region is much less than desirable. Accordingly, radionuclide selection is governed by the need to deliver high enough doses to this central region while minimizing the dose to the surrounding tissue, and to critical organs. The results presented here are of interest in this context.
A. 90Y vs 193mPt
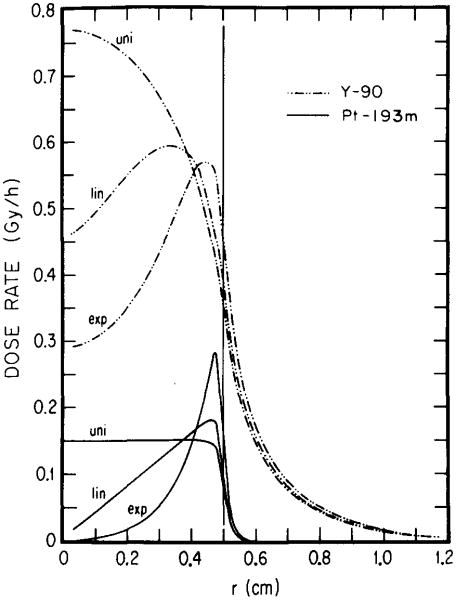
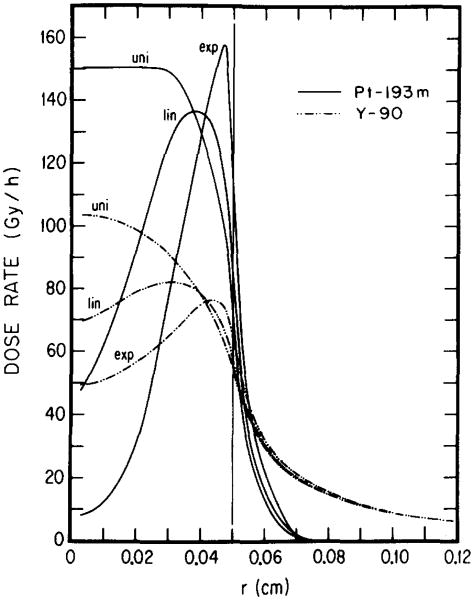
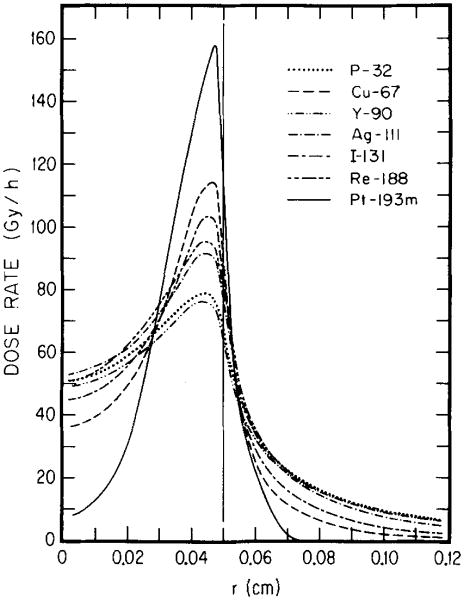
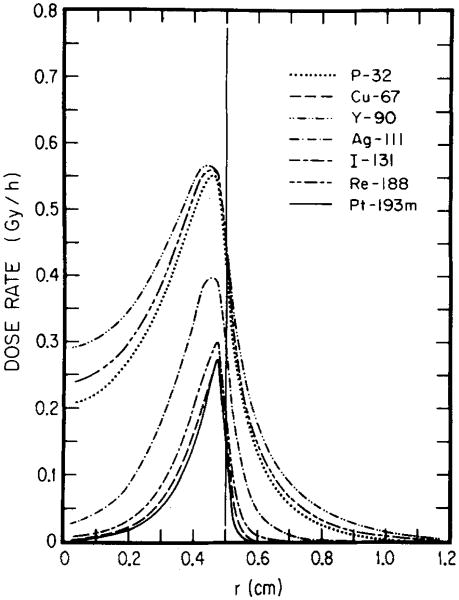
Figures 2 and 3 show dose rate distributions in spheres of diameters 1.0 and 0.1 cm, respectively, for 1 MBq of 193mPt and 90Y distributed uniformly, linearly, and exponentially. These results indicate the importance of choosing optimal electron energy toward achieving the above aims. The longest range of conversion electrons from 193mPt is about 0.2 mm, while the majority of the Auger elecrons have subcellular ranges. 11 Unlike 193mPt, 90Y emits energetic β rays with an endpoint energy of 2.27 MeV with the maximum range of 11.9 mm (Table I). The results in Fig. 2 indicate that, regardless of activity distribution, 90Y delivers a much larger dose than 193mPt throughout the 1.0-cm-diam tumor. It should be noted, however, that the ratio of tumor to healthy tissue dose rate is substantially greater for 193mPt than for 90Y. In the case of the smaller 0.1-cm-diam tumor (Fig. 3), the efficacy of l93mPt vs 90Y depends on the radionuclide distribution. Clearly, for both uniform and linear distributions, 193mPt is superior to 90Y since it delivers a higher dose rate throughout most of the tumor. It is also evident from Fig. 3 that the dose rate from the low-energy electron emitter, 193mPt, is more nonuniform than that from 90Y when the radioactivity is exponentially distributed. Even so, the dose rates from 193mPt and 90Y are equal at r = R/2, and for R/2< r≤R, values for 193mPt are considerably greater than for 90Y. While sterilization of the inner core may be a desirable goal, it is noteworthy that almost 90% of the total tumor volume, contained in the outer region (R/2 < r ≤ R), may be treated better with 193mPt than with 90Y in this case.
Fig. 2.
Dose rate profile for 90Y and 193mPt as a function of the radial coordinate r. Each radionuclide (1 MBq) is assumed to be localized uniformly (uni), linearly (lin), and exponentially (exp) in a tumor of 0.5-cm radius. Substantial tailing of the 90Y dose rate into healthy tissue regions (to the right of the vertical line at r = 0.5 cm) may be noted.
Fig. 3.
Radial dependence of dose rates for one MBq of 90Y and 193mPt. The results are given for uniform (uni), linear (lin), and exponential (exp) distributions of radioactivity in a tumor of 0.05-cm radius. To the right of the vertical line at r = 0.05 cm is the healthy tissue region. For any distribution, 193mPt is superior to 90Y.
Although the above comparisons are useful, estimates of the cumulated tumor dose are necessary to predict the effect of a given radiolabeled antibody. A quantitative comparison of the dose to the central core of a 0.1-cm tumor can be made by assuming an initial tumor uptake of 1 kBq and no biological elimination of the radionuclide from the tumor. These assumptions along with the results in Fig. 3 yield doses to the center of the tumor (d = 0.1 cm) of 1.0 and 4.3 Gy for exponential distributions of 193mPt and 90Y, respectively. The maximum doses for the two isotopes, which occur just inside the tumor surface, are 22 and 7.0 Gy, respectively. The actual doses, which take account of the biological clearance, may be significantly lower than the above.
Is 1 kBq a reasonable estimate of the uptake? Assume that the 0.1-cm-diam tumor is a cluster of 10-μm-diam cells in a close packed cubic geometry. Since the packing density for this geometry is 0.74, the cluster contains about 740 000 cells.10 Correspondingly, the cell density is 1.4 × 106 cells/mm.3 One kBq of carrier-free 90Y radioactivity (half-life = 64 h) contains 3.3 × 108 90Y atoms. If this activity is distributed exponentially in the tumor according to Eq. (5), then we can estimate the density of 90Y atoms at the periphery of the tumor. With s = R = 0.5 mm, and a = 5/R, Eq. (5) gives an activity density of 4.8 kBq/(mm)3 at the periphery. Correspondingly, the density of 90Y atoms in this region is about 1.6 × 109 atoms/mm.3 If each MAb, labeled with one 90Y atom, is bound to a cell surface antigen, the minimum number of such binding sites per cell is about 1.2 × 103 for localization of 1 kBq of activity in the 0.1-cm-diam tumor. A similar analysis for carrier-free 193mPt (4.33 d half-life) gives a required minimum of about 1.9 × 103 binding sites per cell. Both of these values are well below the 6.9 × 106 tumor-specific antigenic cellular binding sites on AKR virus-induced lymphoma cells, as reported by Boone et al.22 Thus, in principle, a 0.1-cm-diam tumor may be capable of an uptake of 1 kBq of radiolabeled MAb's exponentially distributed according to Eq. (5).
B. Comparison between different radionuclides
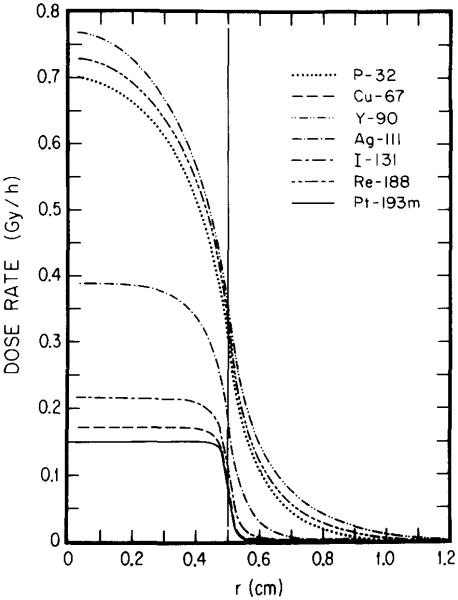
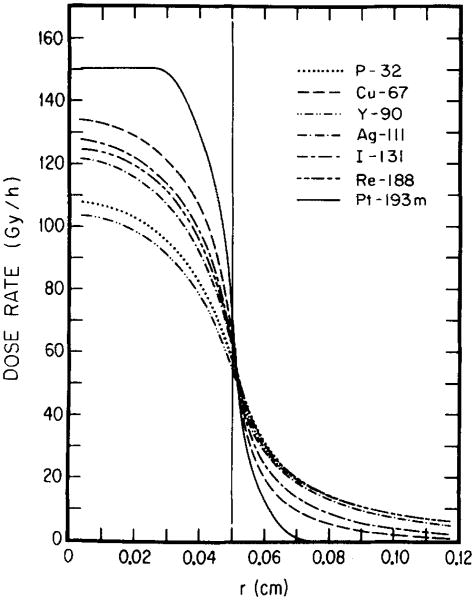
The nature of the radioisotope, its distribution within the tumor, and the tumor size all contribute to the dose rate profile. For each tumor size and radionuclide distribution there may be an optimal electron energy which yields the greatest dose rate to the tumor. This is illustrated by Figs. 4–7 where the dose rate is plotted as a function of radial position in the tumor for the β emitters 32P, 67Cu, 90Y, 111Ag, l31I, and l88Re, and for 193mPt in Table I. Figures 4 and 5 reemphasize that high-energy β emitters (i.e., 32P, 90Y, 188Re) provide the highest dose rates throughout large tumors (1-cm diameter); and 131I, 67Cu and 193mPt the least with 111Ag in between. For the 0.1-cm tumor (Figs. 6 and 7), the situation is once again different. For uniform distribution of activity, 193mPt yields the highest dose rate throughout the tumor and the lowest dose rate to healthy tissue (Fig. 6). When 193mPt is distributed exponentially (Fig. 7) in the 0.1-cm tumor, its electron emissions are not sufficiently penetrating to irradiate the tumor center; however, it provides the highest dose rate to about 90% of the tumor volume. Figure 7 also shows that, for exponential distribution, the medium-energy β emitter 67Cu yields the best dose rate profile within and external to the tumor, while 111Ag and 131I are not very different. Interestingly, 188Re, though a high-energy β emitter, also falls into this group by virtue of its conversion electron component.18 These results illustrate how the optimal electron energy and the optimal radionuclide for RIT depend on the size of the tumor and the distribution of the radiochemical in the tumor.
Fig. 4.
Radial dependences of dose rates from various radionuclides. The results are for 1 MBq of each activity uniformly distributed in a tumor (radius 0.5 cm). The curves show the advantages and drawbacks of medium-, high-, and low-energy emitters in the context of large tumors.
Fig. 7.
Relative efficacy of radionuclides distributed exponentially in a small tumor of 0.05-cm radius. Radial dependence of dose rates is shown for 1 MBq of 32P, 67Cu, 90Y, 111Ag, 131I, 188Re, or 193mPt. The highest dose rate to about 90% of the tumor volume is delivered by 193mPt.
Fig. 5.
Dose rate profiles for several radionuclides: 1 MBq of each is exponentially distributed in a 0.5-cm radius tumor.
Fig. 6.
Spatial dependence of dose rates: An intercomparison between several radionuclides. 1 MBq each of 32P, 67Cu, 90Y, 111Ag, 131I, l88Re, and 193mPt is assumed to be uniformly distributed in a small tumor (radius, 0.05 cm). Note that the high-energy β emitters (32P and 90Y) are not as effective as the radionuclides with medium- and low-energy particulate emissions.
C. Comparison with other work
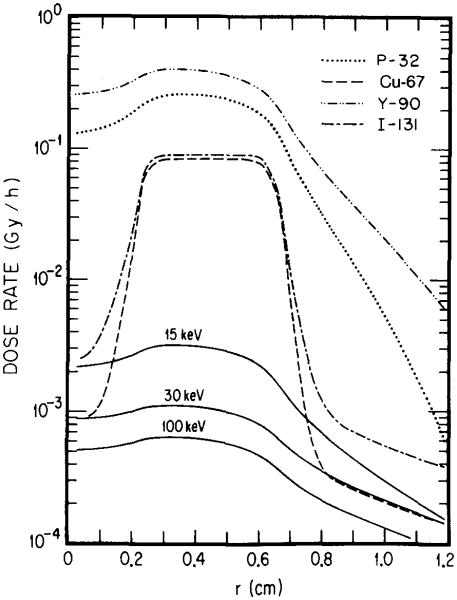
In this study, we have adopted a geometric approach to macroscopic dosimetry of tissue incorporated radionuclides. This is quite different from the method of Kwok et al.,7 who have used the fast Fourier transform as a computer algorithm for their convolution technique. In adopting Loevinger's23 formalism for beta-point-specific absorbed fractions, these investigators were limited to the use of average values of β-ray energies. Another inadequacy noted by them is that Loevinger's formula does not allow for the inclusion of monoenergetic electron groups in their dosimetry program. In contrast, our procedure explicitly allows for mono-energetic electrons and for the β continuum. In view of these differences, it is useful to compare results of calculations based on the present method with the approach of Kwok et al. For this purpose, we have used their model, represented by Eq. (7). The dose rate profiles for 32P, 131I, and for 15, 30, and 100 keV hypothetical photon emitters in Fig. 8 may be compared with the corresponding ones in their paper [Ref. (7), Fig. 4]. Although the agreement is quite good in general, some differences may be noted in passing. For the β emitters 32P and 13II, the maximum dose rates of Kwok et al.7 are higher by about 30% and 10%, respectively, compared to our values (Fig. 8). The dose rates in the central necrotic core are considerably higher, while the dose rates in the “healthy region” tail off more slowly in our approach compared to theirs. The most plausible reason for these differences is use of the complete β spectrum in this work. Another notable difference is in the dose rate profiles for mono-energetic photons shown in Fig. 8 to be compared with the corresponding results in Fig. 4 in Ref. 7. Photons of energies 15, 30, and 100 keV have linear energy absorption coefficients of 1.29, 0.140, and 0.0248 cm−1, respectively, in water.24 The corresponding mean free paths for energy exchange are about 0.8, 7, and 40 cm. Since these distances represent 1/e penetration depths for energy transfer in soft tissue, the photon dose rates should decrease gradually in the “healthy tissue region” (r > 6.6 mm). Results in Fig. 8 are in agreement with this expectation. In contrast, data presented by Kwok et al. (Figs. 4–6 in Ref. 7) show that photons of the above energies do not even penetrate into this region, as indicated by the abrupt cutoff in the dose rate at r = 6.6 mm, the boundary between the tumor and healthy tissue. Considering that the basic data on photon absorption are essentially the same in both calculations, this discrepancy is difficult to understand.
Fig. 8.
Spatial distribution of dose rates in the tumor model of Ref. 7 with a necrotic core. The tumor is a sphere of soft tissue, 0.66 cm in radius. The central region (0–0.22 cm) is necrotic with no uptake of radioactivity. Each one of the radionuclides, 32P, 67Cu, 90Y, and 131I, or a hypothetical monoenergetic photon emitter (either 15, 30, or 100 keV) is assumed to be uniformly distributed in the non-necrotic region of the tumor with a concentration of 1 MBq/ml. The region to the right of r = 0.66 cm is the normal tissue.
D. Dose to an organ in the peritoneal cavity
As noted in Sec. II B, the activity distribution given by Eq. (7) may represent a healthy organ surrounded by ascitic fluid containing radioactivity. This situation may occur in RIT of small metastatic tumors in the peritioneal cavity. Using this model, we have calculated the average doses to the human ovary. We assume that: (i) a 2-cm-thick shell of radioactive fluid surrounds the ovary, (ii) there is no uptake of radioactivity by the ovary, and (iii) the organ is spherical with a volume of 4.2 cm3 for a standard person.5 If τ1/2 is the effective half-life (in days) of the radiopharmaceutical in the peritoneal fluid, and κ is the activity concentration in the fluid in MBq/ml, then the average dose to the ovary is given by 7.6τ1/2κ Gy for 90Y, and 0.02τ1/2κ Gy for 193mPt. The dose to the surface of the ovary is 11.4τ1/2κ Gy and 1.6τ1/2κ Gy for 90Y and 193mPt, respectively. The surface dose to other organs is similar. The physical half-lives of 90Y and 193mPt (64 vs 104 h) are comparable. The half-times of biological clearance for either radionuclide, bound tightly enough to the same MAb species, may not be very different either. In that event, the above estimates suggest that small tumors may be treated with low-energy conversion electron emitters such as 193mPt with minimal dose to healthy organs near by. For large tumors, energetic β emitters may be appropriate despite an increased dose to surrounding organs.
IV. Concluding Remarks
This work is a contribution to tissue-incorporated radionuclide dosimetry of importance in the application of radiolabeled MAb's for diagnostic and therapeutic purposes. Our formalism, different from Kwok et al.7 and Humm,8 is an adaptation of the established approach of Berger.12 It facilitates estimation of dose rates for nonuniform radionuclide distributions with spherical symmetry. Notable in these calculations are the following: (i) inclusion of complete data on radiations from each radionuclide; (ii) appropriate treatment of β spectra; and (iii) use of experimental data, rather than theory, for range-energy relations and energy loss of electrons.14 There is general agreement in the literature13,24 regarding interactions of photons with matter. These considerations point to the quantitative nature of the results. The dose rate distributions given are valid for homogeneous soft tissues with a spherical geometry. The present formulation may be readily extended to organs of arbitrary shape and size but possessing axial symmetry.25 Model calculations involving discontinuities in soft tissue due to bone, pockets of air, etc., would be helpful.
Heterogenous distribution of radioactivity in tumors and the consequent inhomogeneity of dose are attracting attention recently.7,26–29 While the in vitro work of Sutherland et al.30 indicates a shell-type penetration of radiolabeled MAb's in tumor cell spheroids, quantitative data are needed to obtain functional dependence of activity distributions in tumors, especially in vivo. The nonuniform distributions considered here, and the diffusion limited distribution in the work of Kwok et al.,7 are plausible, and the dose rate profiles presented may shed some light on problems relevant to RIT. The targets of radiation action are the nuclei of cells containing the radiosensitive DNA. Hence, radionuclide dosimetry at the subcellular level is desirable. Such an approach is particularly necessary when the ranges of the particulate radiations are less than or of the order of cell dimensions.10 The macroscopic dosimetry considered here is valid and adequate since the ranges of the radiations (Table I) are by far larger than typical cell diameters (∼ 10 μm). The frequencies of hits suffered by the targets and dose rate fluctuations are, no doubt, important from a microdosimetric viewpoint. The dose rates given here are the mean values involving the decay of a large number of radionuclides.
The present results may serve as guidance in the optimal choice of radionuclides based on dosimetric considerations appropriate to various tumor sizes. The host of radionuclides examined here provide an arsenal for the radioimmunotherapist. Even if high-energy β emitters may be attractive in handling large tumors, the strategy needs modifications depending on tumor regression, and changing morphology, not to speak of various other parameters of an interacting nature.3 High-energy β emitters also contribute proportionately more bremsstrahlung photons than those of lower energy. The implications of these for healthy tissue, locally and farther away, need to be considered. These observations indicate that optimal treatment with RIT requires that each tumor be considered individually. Recent work by Hagan et al.,26 in the nude mouse–human tumor model, shows that specific radiolabeled MAb uptake per gram is inversely proportional to tumor size. Williams et al.27 have presented a model to explain such a dependence. While this behavior is presumably due to necrosis as tumors enlarge, Hagan et al. note that the above finding is independent of the radiolabel, antibody type, nature of the tumor, the target antigen or its mobility. Accordingly, it is plausible that smaller tumors in humans may accumulate greater concentrations of radiolabeled MAb's, and may be more amenable to RIT than larger ones. In this context, the medium- and low-energy electron emitters (e.g., 67Cu, 193mPt, etc.) should be useful as indicated by our results.
Inasmuch as minute cell clusters and individual cells are the ultimate limit of “very small” tumors, a few final remarks of a microscopic nature are in order. For radiolabeled MAb's localized on cell surfaces, the cellular RIT dosimetry model of Sastry et al.10 has indicated that about 20 keV is an optimal electron energy for an effective irradiation of radiosensitive targets in the nuclei of cells. The 38-h 119Sb almost uniquely satisfies this criterion. This has been corroborated by Huram.8 The conversion electron and Auger electron spectra given by Howell et al.11 for 193mPt indicate multiple utility of this radionuclide in RIT of small tumors as well as at the microscopic level when attached to MAb's binding to cell surfaces. Local and selective irradiation of intranuclear targets by the Auger electrons may be exploited if the MAb's labeled with this radionuclide internalize into the cells. Since platinum-coordinated complexes (e.g., cis-Platin II) are known to bind to nuclear DNA,11 such compounds containing 193mPt may offer new opportunities to induce critical molecular lesions in the DNA by the collective action31 of the numerous low-energy Auger electrons. Although this radionuclide is not regularly available at present, it can be produced in a carrier-free form by the (α, 3n) reaction on l92Os (natural abundance 41%) with a cross section of 0.5 b.11 In conclusion, we hope that the various considerations presented in this paper may be useful in radionuclide tumor therapy including RIT.
Acknowledgments
This work is supported by USPHS Grant No. CA-32877.
Appendix: Geometric Factor ψ
Case 1. s≤r1; r1 + s > r2 – s
Case 2. s≤r1; r1 + s≤r2 – s
Case 3. r1≤s≤r2; r1 + s≥r2 – s; s – r1≤r2 – s
Case 4. r1 ≤s≤r2; r1 + s≥r2 – s; s – r1≥r2 – s
Case 5. r1≤s≤r2; r1 + s≤r2 – s; s – r1≤r2 – s
Case 6. s≥r2
Contributor Information
Roger W. Howell, Department of Radiology, University of Medicine and Dentistry of New Jersey, Newark, New Jersey 07103
Dandamudi V. Rao, Department of Radiology, University of Medicine and Dentistry of New Jersey, Newark, New Jersey 07103
Kandula S. R. Sastry, Department of Physics and Astronomy, University of Massachusetts, Amherst, Massachusetts 01003
References
- 1.DeNardo SJ, Jungerman JA, DeNardo GL, Lagunas-Solar MC, Cole WC, Meares CF. Proceedings of the International Symposium on Shorter-Lived Radionuclides. Washington, D.C.: May, 1982. The choice of radionuclides for immunotherapy; pp. 401–414. DOE Conference, 820523 ORNL 1983. [Google Scholar]
- 2.Jungerman JA, Yu KP, Zanelli CI. Radiation absorbed dose estimates at the cellular level for some electron-emitting radionuclides for radioimmunotherapy. Int J Appl Isot. 1984;35:883. doi: 10.1016/0020-708x(84)90025-5. [DOI] [PubMed] [Google Scholar]
- 3.Wessels BW, Rogus RD. Radionuclide selection and model absorbed dose calculations for radiolabeled tumor associated antibodies. Med Phys. 1984;11:638. doi: 10.1118/1.595559. [DOI] [PubMed] [Google Scholar]
- 4.Loevinger R, Berman M. MIRD Pamphlet No 1, Revised. Society of Nuclear Medicine; New York: 1976. A revised schema for calculating the absorbed dose from biologically distributed radionuclides. [Google Scholar]
- 5.Snyder WS, Ford MR, Warner GG. MIRD Pamphlet No 5, Revised. Society of Nuclear Medicine; New York: 1978. Estimates of specific absorbed fractions for photon sources uniformly distributed in various organs of a heterogenous phantom. [Google Scholar]
- 6.Manz R, Otte J, Thews G, Vaupel P. Relationship between size and oxygenation status of malignant tumors. Adv Exp Med Biol. 1981;159:391. doi: 10.1007/978-1-4684-7790-0_34. [DOI] [PubMed] [Google Scholar]
- 7.Kwok CS, Prestwich WV, Wilson BC. Calculation of radiation doses for nonuniformly distributed β and γ radionuclides in soft tissue. Med Phys. 1985;12:405. doi: 10.1118/1.595752. [DOI] [PubMed] [Google Scholar]
- 8.Humm JL. Dosimetric aspects of radiolabeled antibodies for tumor therapy. J Nucl Med. 1986;27:1490. [PubMed] [Google Scholar]
- 9.Charlton DE. Energy dissipation near an interface: A more realistic approach to electron range and stopping power. Radiat Res. 1970;44:575. [PubMed] [Google Scholar]
- 10.Sastry KSR, Haydock C, Basha AM, Rao DV. Electron dosimetry for radioimmunotherapy: Optimal electron energy. Radiat Prot Dosim. 1985;13:249. [Google Scholar]
- 11.Howell RW, Sastry KSR, Hill HZ, Rao DV. Cis-193m Platinum: Its microdosimetry and potential for chemo-Auger combination therapy of cancer. In: Schlafke-Stelson AT, Watson EE, editors. Proceedings of the Fourth International Radiopharmaceutical Dosimetry Symposium; Oak Ridge, TN. November, 1985; DOE Conference, CONF-851113, (DE86010102); 1986. pp. 493–513. [Google Scholar]
- 12.Berger MJ. Beta-ray dosimetry calculations with the use of point kernels. In: Cloutier RJ, Edwards CL, Snyder WS, editors. Radiation Dose and Effects. U.S Atomic Energy Commission; Washington, D.C.: 1970. pp. 63–86. AEC Symposium Series No. 20. [Google Scholar]
- 13.Berger MJ. MIRD Pamphlet No 2. Suppl. 1. Society of Nuclear Medicine; New York: 1968. Energy deposition in water by photons from point isotropic sources. [PubMed] [Google Scholar]
- 14.Cole A. Absorption of 20-eV to 50,000-eV electron beams in air and plastic. Radiat Res. 1969;38:7. [PubMed] [Google Scholar]
- 15.Kassis AI, Adelstein SJ, Haydock C, Sastry KSR. Radiotoxi-city of 75Se and 35S: Theory and application to a cellular model. Radiat Res. 1980;84:407. [PubMed] [Google Scholar]
- 16.Sastry KSR, Howell RW, Rao DV, Mylavarapu VB, Kassis AI, Adelstein SJ, Wright HA, Hamm RN, Turner JE. Dosimetry of Auger-emitters: Physical and phenomenological approaches. In: Baverstock KF, Charlton DE, editors. DNA Damage by Auger Emitters. Taylor and Francis; London, England: 1988. pp. 27–38. [Google Scholar]
- 17.Langer LM, Price HC., Jr Beta-spectra of forbidden transitions. Phys Rev. 1949;76:641. [Google Scholar]
- 18.Dillman LT, Von der Lage FC. MIRD Pamphlet No 10. Society of Nuclear Medicine; New York: 1975. Radionuclide decay schemes and nuclear parameters for use in radiation-dose estimation. [PubMed] [Google Scholar]
- 19.Martin MJ, Blichert-Töft PH. Radioactive atoms, Auger-electron, α-, β-, γ-, and x-ray data. Nucl Data Tables. 1970;A8:1. [Google Scholar]
- 20.Hill RP, Pallavicini MG. Hypoxia and the radiation response of tumors. Adv Exp Med Biol. 1981;159:17. doi: 10.1007/978-1-4684-7790-0_3. [DOI] [PubMed] [Google Scholar]
- 21.Vaupel P. Oxygen supply to malignant tumors. In: Peterson HI, editor. Tumor Blood Circulation: Angiogenesis, Vascular Morphology, and Blood Flow of Experimental and Human Tumors. CRC; Boca Raton, FL: 1979. pp. 143–168. [Google Scholar]
- 22.Boone CW, Brandchaft PR, Irving DN, Gilden R. Quantitative studies on the binding of syngeneic antibody to the surface antigens of AKR virus-induced rat lymphoma cells. Int J Cancer. 1972;9:685. doi: 10.1002/ijc.2910090327. [DOI] [PubMed] [Google Scholar]
- 23.Loevinger R, Japha EM, Brownell GL. Discrete radioisotope sources. In: Hine GJ, Brownell GL, editors. Radiation Dosimetry. Academic; New York: 1956. pp. 693–799. [Google Scholar]
- 24.Storm E, Israel HI. Report LA-3753, UC-34, Physics, TID-4500, Los Alamos Scientific Laboratory. Clearing House for Federal Scientific and Technical Information; Springfield, VA: 1967. Photon Cross Section from 0.001 to 100 MeV for elements 1 through 100. [Google Scholar]
- 25.Rossi HH, Ellis RH., Jr Distributed beta sources in uniformly absorbing media. Nucleonics. 1950;7(No. 1):18. 7 (No. 2), 19 (1950) [PubMed] [Google Scholar]
- 26.Hagan PI, Halpern SE, Dillman RO, Shawler DL, Johnson DE, Chen A, Krishnan L, Frincke J, Bartholomew RM, David GS, Carlo D. Tumor size: Effect on monoclonal antibody uptake in tumor models. J Nucl Med. 1986;27:422. [PubMed] [Google Scholar]
- 27.Williams LE, Duda RB, Proffit RT, Beatty BG, Beatty JD, Wong JC, Shively JE, Paxton RJ. Tumor uptake as a function of tumor mass: A mathematical model. J Nucl Med. 1988;29:103. [PubMed] [Google Scholar]
- 28.Wessels BW, Griffith MH. Miniature thermoluminescent dosimeter absorbed dose measurements in tumor phantom models. J Nucl Med. 1986;27:1308. [PubMed] [Google Scholar]
- 29.Yorke ED, Griffith MH, Wessels BW. Computerized dose calculations for inhomogeneous activity distributions in RIT. Med Phys. 1987;14:456. Abstract. [Google Scholar]
- 30.Sutherland R, Buchegger F, Schreyer M, Vacca A, Mach JP. Penetration and binding of radiolabeled anticarcinoembryonic antigen monoclonal antibodies and their antigen binding fragments in human colon multicellular tumor spheroids. Cancer Res. 1987;47:1627. [PubMed] [Google Scholar]
- 31.Sastry KSR, Rao DV. Dosimetry of low energy electrons. In: Rao DV, Chandra R, Graham MC, editors. Physics of Nuclear Medicine: Recent Advances. American Institute of Physics; New York: 1984. pp. 169–208. Medical Physics Monograph No. 10. [Google Scholar]