Doping evolution of the Mott–Hubbard landscape in infinite-layer nickelates

Significance

Copper-based (cuprate) oxides are not only the original but also one of the best-studied families of “high-temperature” superconductors. With nominally identical crystal structure and electron count, nickel-based (nickelate) compounds have been widely pursued for decades as a possible analog to the cuprates. The recent demonstration of superconductivity in nickelate thin films has provided an experimental platform to explore the possible connections between the copper- and nickel-based superconductors. Here, we perform highly localized spectroscopic measurements to reveal a number of key differences between the two systems, particularly with regard to the hybridization between the O and metal (Cu or Ni) orbitals.

Abstract

The recent observation of superconductivity in ${\mathrm{N}\mathrm{d}}_{0.8}{\mathrm{S}\mathrm{r}}_{0.2}{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ has raised fundamental questions about the hierarchy of the underlying electronic structure. Calculations suggest that this system falls in the Mott–Hubbard regime, rather than the charge-transfer configuration of other nickel oxides and the superconducting cuprates. Here, we use state-of-the-art, locally resolved electron energy-loss spectroscopy to directly probe the Mott–Hubbard character of ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$. Upon doping, we observe emergent hybridization reminiscent of the Zhang–Rice singlet via the oxygen-projected states, modification of the Nd 5$d$ states, and the systematic evolution of Ni 3$d$ hybridization and filling. These experimental data provide direct evidence for the multiband electronic structure of the superconducting infinite-layer nickelates, particularly via the effects of hole doping on not only the oxygen but also nickel and rare-earth bands.

The discovery of copper oxide high-temperature superconductors (1) and subsequent realizations of non–copper-based compounds (2, 3) has spurred significant efforts not only to understand the mechanisms underlying superconductivity (4–7) but also to identify and realize new host materials. The recent discovery of superconducting nickel-based thin films (8) has opened an opportunity to explore a system that is closely related to the infinite-layer cuprates in both crystal structure and transition-metal electron count. Trading out the ${\mathrm{C}\mathrm{u}}^{2+}$ ions for ${\mathrm{N}\mathrm{i}}^{1+}$ preserves an isoelectronic formal 3$d^9$ state, raising the possibility of a nickel analog to the cuprates (9). At the same time, key differences between the systems have been proposed both early on (10) and more recently following the successful demonstration of nickelate superconductivity (11–20). Experimentally, however, direct measurements of the electronic landscape of hole-doped infinite-layer nickelates, particularly with variable band filling, are lacking.

In the family of superconducting cuprates, extensive spectroscopic characterization of bulk samples enabled a thorough understanding of their electronic structure, especially regarding the role of doped holes (6). Compared to such bulk phase systems, the successful realization of nickelate superconductivity in epitaxial thin films complicates their characterization by traditional bulk techniques, instead requiring local probes as well as measurements with high sensitivity due to the metastable nature of these compounds. Here, we directly probe the electronic structure across the doped ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_y$ ($y$ = 2, 3) family using locally resolved electron energy-loss spectroscopy (EELS) in the scanning transmission electron microscope (STEM) highly optimized for detection of subtle spectroscopic signatures. We identify a distinct prepeak feature in the ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ O-K edge, which disappears completely in ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$, consistent with the predicted Mott–Hubbard character of the infinite-layer parent compound (10, 18). Moreover, our systematic study across a series of superconducting hole-doped ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ ($x\le$ 0.225) films uncovers an emergent feature in the O 2$p$ band with hole doping, reminiscent of the Zhang–Rice singlet (ZRS) peak in the isostructural superconducting cuprates. Unlike the cuprates, however, the spectral weight of the O 2$p$ feature is small even at high doping levels, suggesting necessary involvement of other bands. Indeed, parallel spectroscopy of both Ni and Nd confirms contributions of the Ni 3$d$ and modification of the Nd 5$d$ states, demonstrating, in contrast to the superconducting cuprates, the multiband nature of this system.

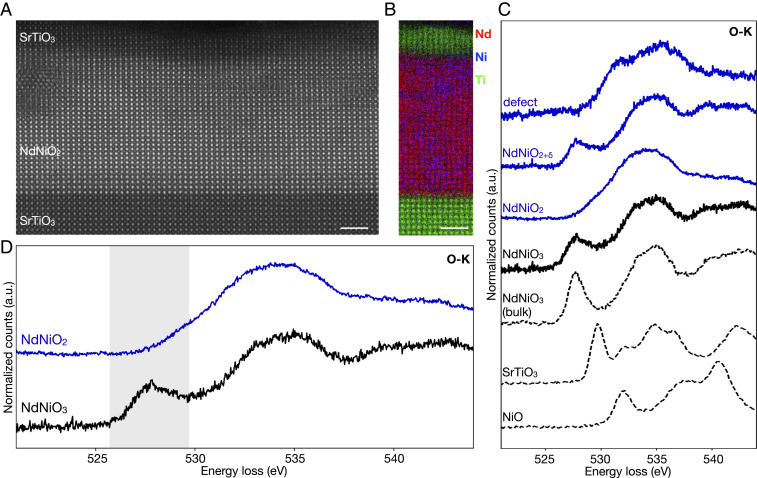
Infinite-layer nickelate thin films are stabilized by soft-chemistry topotactic reduction (21) of the perovskite phase grown epitaxially on ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ (001) substrates and capped with a thin layer of ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ by pulsed-laser deposition (PLD), as previously described (8, 22). Capping layers between 2 and 25 nm have been found to stabilize and support the infinite-layer structure during topotactic reduction, producing more crystallographically uniform films (22). STEM-EELS is therefore an ideal way to spectroscopically probe the nickelate thin film without contributions from the capping layer (or substrate). Starting with the undoped ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ film, atomic-resolution high-angle annular dark-field (HAADF) STEM imaging confirms the overall high crystalline quality of the film (Fig. 1a) after optimization of the epitaxial growth and subsequent reduction process as discussed elsewhere (22). Elemental EELS mapping performed in the STEM confirms the abruptness of the nickelate–${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ interface and shows no obvious impurity phases (Fig. 1b). Extended defects are, however, present and must be taken into account when interpreting more commonly used area-averaged spectroscopic measurements (SI Appendix, Figs. S1 and S2). Spatially resolved STEM-EELS reveals distinct O-K near-edge fine structures in different regions of the same film including some crystalline defects and small pockets that have not completely reduced to ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ (Fig. 1C and SI Appendix, Fig. S2). The intrinsically metastable nature of the infinite-layer compound (21) has required an empirical fine tuning of the conditions for maximal reduction without decomposition (22), so the presence of some unreduced pockets is likely unavoidable at this time. When averaging over the entire film, however, contributions from such variations can mask the electronic character of the pure nickelate phase. In this work, we extract the electronic signatures of the ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_y$ phases without contributions from extended defects by confining our spectroscopic measurements to crystallographically clean and fully reduced regions of each film using an angstrom-size STEM probe.

Fig. 1.

Lattice and electronic structure of ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_y$ thin films. (A) Atomic-resolution HAADF-STEM imaging of an undoped ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ film shows mostly well-ordered epitaxial structure with some visible crystalline defects. (B) STEM-EELS Nd, Ni, and Ti elemental mapping confirms an abrupt interface with ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$. (C) Observed variations in O-K near-edge fine structure across different regions in the same reduced nickelate film (blue) necessitate local measurements to avoid contributions from defects and partially unreduced regions. For comparison, reference spectra from bulk oxides are also shown. (D) EELS O-K edge of ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ and a ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ film before reduction to the infinite-layer phase. The disappearance of the first peak (highlighted in gray), ascribed to metal-oxygen hybridization, indicates filling of the Ni states upon reduction from $d^7$ to $d^9$. (Scale bars, 2 nm.)

The distinct characteristic shapes of EELS edges provide access to a wealth of rich chemical information (23–26). To first approximation, the energy loss near-edge structure (ELNES) of core-loss spectra (edges at more than $\sim$100 eV) reflects the local density of unoccupied states for a specific element and angular momentum. The dipole selection rule permits only transitions from states with orbital angular momentum $l$ to final states with $l\pm 1$, e.g., $s\to p$ or $p\to d$, such that different EELS edges for the same element will probe the unoccupied density of different states. Changes to ELNES shape therefore signify corresponding changes in the density of unoccupied states for a given element that may be affected by hybridization, atomic coordination, or other local bonding effects. Small shifts in the absolute position of the EELS edge can similarly point to shifts or redistribution of unoccupied states. Because EELS probes the energy separation of the unoccupied and the core states, however, shifts in the EELS spectrum can also arise from changes in the core (rather than the unoccupied) level (26, 27). Importantly, the effect of the core-hole created during the excitation process can significantly modify the ELNES and must be taken into account when considering comparisons to ground-state calculations. The interpretation of EELS fine structure provides, in general, similar information as other spectroscopic probes such as unpolarized X-ray absorption spectroscopy (XAS), and can be used to probe the local electronic landscape in great detail.

We first explore the electronic character of the parent infinite-layer compound, ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$. In 3$d$ transition metal oxides, the onset structure of the O-K edge is ascribed to hybridization between the O 2$p$ and metal 3$d$ states (28). For ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$, this hybridization results in a strong prepeak feature at $\sim$527 eV (28–30). Compared to the bulk compound, the prepeak in the ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ thin film is broadened, consistent with changes to local Ni–O coordination (29, 31) due to epitaxial strain imposed by the ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ substrate (Fig. 1C). Upon oxygen reduction from the perovskite ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ to the infinite-layer ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ phase, the prepeak disappears entirely (Fig. 1D). Here, the suppression of this peak reflects filling of the lower $d$ bands with the change in formal Ni configuration from 3$d^7$ to 3$d^9$ (29) (SI Appendix, Fig. S3). The undoped infinite-layer cuprates exhibit a similar suppression in spectral weight of the $d^9$ states compared to the perovskite phase (32). Notably, the cuprates also show an additional O-K prepeak observed $\sim$1.5 eV above the $d^9$ peak due to transitions into the $d^{10}$ upper Hubbard band (32, 33). In the nickelates, however, a similar second peak is not observed, suggesting that it falls within and is thus hidden by the bulk of the O-K edge. Compared to the cuprates, the reduction in nuclear charge from Cu to Ni greatly reduces the covalency of the $d^9$ state and pushes the $d^{10}$ states to higher energies (12, 14, 18, 34). A $d^{10}$ peak like that observed in the cuprates would therefore be much weaker and located several electron volts ($\sim$5 to 6 eV) higher in energy, overlapping with the rest of the O-K edge. The lack of a visible spectral peak thus suggests that the $d^{10}$ states sit at higher relative energies in the nickelates than in the cuprates. This experimental observation is consistent with theoretical predictions that the infinite-layer nickelates have a larger charge-transfer energy $\mathrm{\Delta }$ than the superconducting cuprates (17, 18).

For similar on-site Coulomb interactions $U$ (17, 18), these experiments suggest an electronic structure in the nickelates with a charge-transfer gap $\mathrm{\Delta }$ larger than $U$. Using the Zaanen–Sawatzky–Allen classification scheme (35), this places the parent infinite-layer compound in the Mott–Hubbard regime ($\mathrm{\Delta }>U$) (11, 17, 18, 36), in contrast to the charge-transfer ($\mathrm{\Delta }<U$) cuprates (33) (SI Appendix, Fig. S3). It is, however, likely that hybridization in the nickelates spreads out the distribution of the O 2$p$ bands (37), so that the system actually falls somewhere near the boundary between the two regimes (Mott–Hubbard and charge-transfer) (35). Additionally, while no spectroscopic prepeak is observed in the parent compound ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$, possible effects due to self-doping (17, 34, 38) that may play a role in the detailed electronic structure cannot be directly excluded from the data presented here. Previous results by XAS have similarly suggested the Mott–Hubbard nature of La-based nickelates (36).

XAS has also been used to probe the O-K near-edge fine structure of reduced ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ and unreduced ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ films on ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ (34, 36), but these measurements averaged over large parts of the films. The exclusion of defects and the stabilizing ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ capping layer in our spatially resolved approach explains the apparent discrepancy between these results. In particular, contributions from ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ or secondary phases in nonoptimized films (22) result in an additional peak at $\sim$530 eV in the unreduced film as well as a subtle but clear shoulder at the same energy in the reduced film (SI Appendix, Fig. S1). While differences in the perovskite phase are quite striking, below we show that even small contributions from this shoulder in the infinite-layer films can inhibit the ability to probe the effects of hole doping in this system.

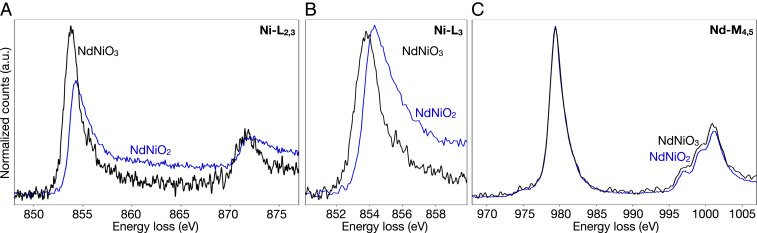
In addition to the O-K edge, EELS measurements provide simultaneous access to the Ni and Nd states in corresponding localized regions. We measure the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge (Fig. 2A) to probe the Ni 3$d$ states (39) across the same evolution from the perovskite to infinite-layer phase. A clear distinction can be made between the parent ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ and infinite-layer ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ thin films, particularly by a broadening and shift of the ${\mathrm{L}}_3$ edge at $\sim$854 eV (Fig. 2B). The redistribution of spectral weight to higher energies can be seen as a relative decrease in the peak intensity of the ${\mathrm{L}}_3$ peak when spectra are normalized by integration over the full ${\mathrm{L}}_{\mathrm{2,3}}$ edge (Fig. 2A) as well as by the increased width of the ${\mathrm{L}}_3$ peak when spectra are instead normalized by the maximum ${\mathrm{L}}_3$ peak intensity (Fig. 2B). A shift of the infinite-layer ${\mathrm{L}}_3$ peak to higher energies by $\sim$0.6 eV is also clearly apparent with the latter normalization. In more ionic systems, transition metal ${\mathrm{L}}_{\mathrm{2,3}}$ edges have been used to fingerprint valence states (32, 40–42). In nickel compounds, however, hybridization effects play an important role and are reflected in the fine structure of the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge (27, 39), complicating their physical interpretation. Comparing the two thin-film phases, the asymmetric broadening and long high-energy tails of the Ni-${\mathrm{L}}_3$ edge in the reduced ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ suggests increased $p$-$d$ hybridization (30, 39, 43) consistent with the larger ${\mathrm{N}\mathrm{i}}^{1+}$ ionic radius and straightening of the Ni–O–Ni bond angles (44) in the infinite-layer structure, as well as with theoretical predictions of strong Ni $d$ orbital hybridization (45). The energy shift of the ${\mathrm{L}}_3$ peak could be reflective of the change in Ni 3$d$ states in the infinite-layer compound, as has been described in other nickel-based systems, but EELS measurements alone cannot rule out the contribution of shifts of the core state (27). More direct interpretation of these spectral changes will require comparison with careful and thorough calculations. Similar to the O-K edge, the spectral differences between bulk and thin film ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ in the ${\mathrm{L}}_{\mathrm{2,3}}$ are likely due to strain effects imparted by the substrate (46). Unlike the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ and O-K, the Nd-${\mathrm{M}}_{\mathrm{4,5}}$ edge (4$f$ states) remains unchanged upon reduction from perovskite to infinite-layer (Fig. 2C), indicating a formal Nd valence of 3+ in both phases (SI Appendix, Fig. S4). This lack of change is consistent with the experimental demonstration of superconducting Pr-based infinite-layer nickelate films, suggesting that the specific configuration of the rare-earth 4$f$ state may be relatively unimportant for superconductivity (47).

Fig. 2.

Electronic evolution from perovskite ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ (black) to infinite-layer ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ (blue) phase for epitaxial thin films on ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$. (A) The Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge (3$d$ states) shows a clear change upon O reduction from ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ to ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$, including significant broadening and shift of the ${\mathrm{L}}_3$ edge (B). (C) The Nd-${\mathrm{M}}_{\mathrm{4,5}}$ edge (4$f$ states) shows little or no change between the two compounds. Spectra in A and C are normalized by integrated signal over the full energy ranges shown; the Ni-${\mathrm{L}}_3$ edges in B have been renormalized by maximum intensity for easier comparison.

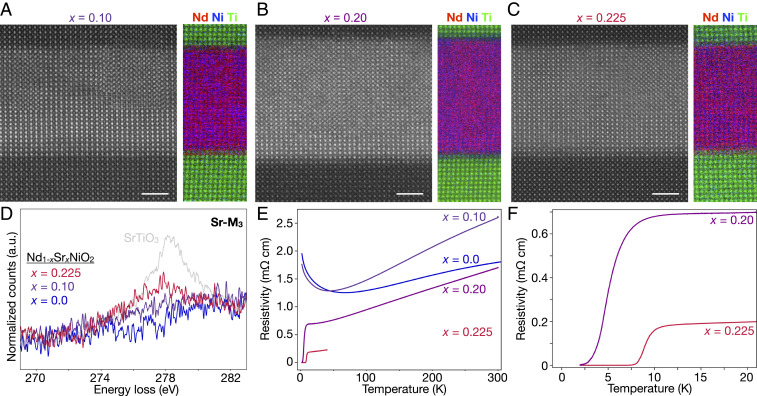
Having established the nature of the parent compounds, we systematically study the effect of hole doping in a series of superconducting infinite-layer ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ films. HAADF-STEM imaging and elemental EELS mapping (Fig. 3 A–C) confirm overall film quality across all samples with uniform distribution of Nd and Ni throughout the films. Summed spectra (Fig. 3D) from clean regions within the films show Sr-${\mathrm{M}}_3$ signals consistent with the relative nominal Sr doping expected in each case. Transport measurements for the infinite-layer films studied here (Fig. 3 E and F) show metallic temperature dependence of the low ($x$ = 0.0, 0.1) Sr (hole)-doped films down to about 50 to 70 K, below which a resistive upturn is observed. Upon increased hole doping ($x$ = 0.2, 0.225), the infinite-layer films become superconducting with transition temperatures $T_{\mathrm{\text{c, 90\%R}}}$ (the temperatures at which the resistivity is 90% that at 20 K) of 8 and 11 K, respectively (Fig. 3F). The relative values of $T_{\mathrm{\text{c}}}$ for these films are consistent with a recent investigation of the doping dependence of ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ establishing a superconducting dome spanning 0.125 $<x<$ 0.25 (48).

Fig. 3.

Structure and transport of ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ films with hole doping $x\le$ 0.225. (A–C) Atomic-resolution HAADF-STEM and elemental EELS maps of $x$ = 0.10, 0.20, and 0.225 samples, respectively. (D) Sr-${\mathrm{M}}_3$ EEL spectra from each film show a qualitative trend consistent with the expected nominal Sr doping in each sample. A similar spectrum from ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ is shown in gray for comparison. (E and F) Resistivity vs. temperature curves for the four ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ films studied here. Lightly Sr-doped ($x$ = 0.0, 0.1) films show metallic behavior with a resistive upturn near 50 to 70 K, while more strongly doped ($x$ = 0.2, 0.225) films show superconducting transitions (${\mathrm{T}}_{c,90\%R}$) at 8 and 11 K, respectively. Data for $x$ = 0.0 are from ref. 8.

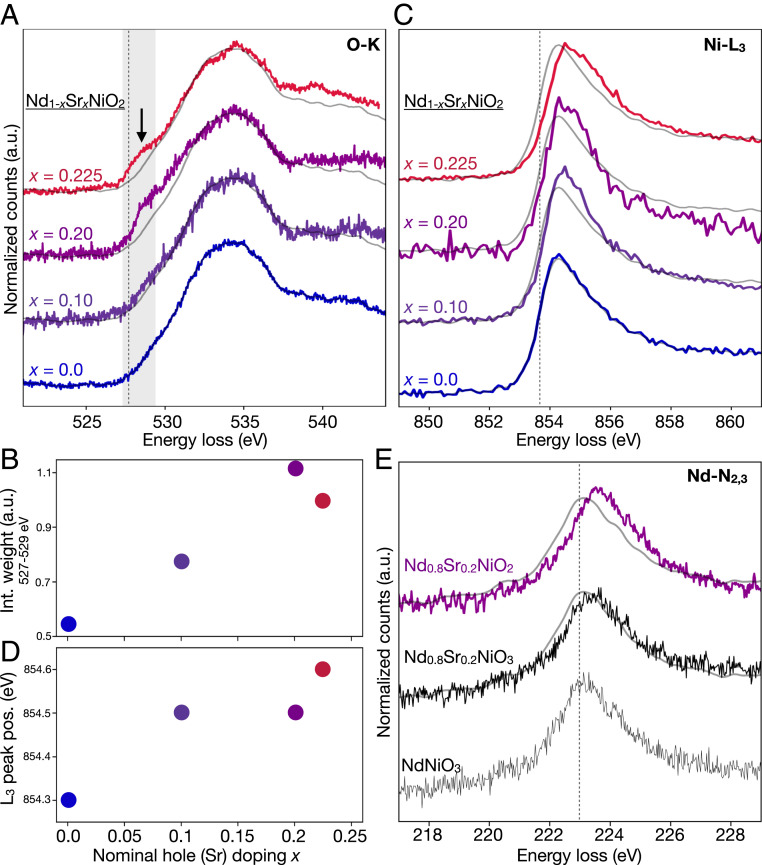
In the O-K edge, we observe an emergent feature at $\sim$528 eV as a function of Sr (hole) doping across the ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ films (Fig. 4A). The strength of this peak increases with hole doping (Fig. 4B), $x$, although the spectral weight of the $x$ = 0.2 sample is higher than the more strongly doped $x$ = 0.225 sample, likely due to the inclusion of some Ruddlesden–Popper fault regions (SI Appendix, Figs. S1 and S5). A similar spectral feature is also observed upon hole doping in the cuprates (33, 49). As in the cuprates, we attribute the emergent spectral feature to doped holes in the oxygen orbitals forming 3$d^9\underset{\_}{L}$ states, where $\underset{\_}{L}$ is the oxygen “ligand” hole (4, 49). The coordination of two such holes into a ZRS state is thought to reduce the cuprate system into an effective single-band model (4, 50). In nickelates the picture is less clear: despite the similarity in presence and doping dependence of this O-K edge feature in both systems, a few key spectroscopic differences are apparent. In the cuprates, hole doping results in a tradeoff of spectral weight from the $d^{10}$ upper Hubbard band into the emergent $d^9\underset{\_}{L}$ states (33). In the nickelates, we do not observe a similar trend, most likely due to shift of the $d^{10}$ band to much higher energy, as described by the Mott–Hubbard picture discussed above. Perhaps more importantly, the overall strength of the hole doping (3$d^9\underset{\_}{L}$) feature is significantly reduced in the nickelates compared to the cuprates, even for comparatively high levels of hole doping. The weak effect of doping on the O-K edge raises the question: where else do the holes go?

Fig. 4.

Electronic structure evolution of ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_2$ with hole doping $x\le$ 0.225. (A) A spectral feature at $\sim$528 eV emerges with increased Sr (hole) doping in the O-K edge, attributed to $d^9\underset{\_}{L}$ states. The dotted line marks the $d^9$ peak position in ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$. (B) The integrated signal over the $d^9\underset{\_}{L}$ feature spectral range (527 to 529 eV), highlighted gray in A, increases with hole doping. (C and D) The Ni-${\mathrm{L}}_3$ edge systematically shifts to high energies and broadens with hole doping. The dotted line marks the ${\mathrm{L}}_3$ peak position in ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$. (E) The Nd-${\mathrm{N}}_{\mathrm{2,3}}$ edge (5$d$ states) shows a small shift to higher energies upon Sr doping of the perovskite phase. A further shift is observed upon O reduction to infinite-layer ${\mathrm{N}\mathrm{d}}_{0.8}{\mathrm{S}\mathrm{r}}_{0.2}{\mathrm{N}\mathrm{i}\mathrm{O}}_2$. The dotted line marks the ${\mathrm{N}}_{\mathrm{2,3}}$ peak position in ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$. For comparison, reference spectra are plotted in gray for ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$ in A and C and for ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ in E.

The ability of EELS measurements to access several edges simultaneously allows us to consider the corresponding effects on the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge (3$d$ bands) (Fig. 4C). The Ni-${\mathrm{L}}_3$ peak position (Fig. 4D and SI Appendix, Fig. S6) shifts systematically to higher energies upon hole doping, with a total increase of $\sim$0.3 eV between the undoped $x$ = 0.0 and the $x$ = 0.225 films. We also observe the ${\mathrm{L}}_3$ edge broadening as an extended tail in the doped samples (SI Appendix, Fig. S5). When compared to previously reported spectra for various Ni formal valences (30, 39, 43, 44, 51), the changes in the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge may suggest increased hybridization and a mixed-valent Ni state. Similar to the evolution from perovskite to infinite layer, we interpret the doping-dependent broadening of the ${\mathrm{L}}_3$ edge as a sign of increasing hybridization of the Ni 3$d$ states with the introduction of more holes through Sr doping.

We also probe the Nd-${\mathrm{N}}_{\mathrm{2,3}}$ edge (5$d$ states) across the sample series (Fig. 4E). Given the extreme technical challenges due to the need for simultaneous high-spatial resolution, high-energy resolution, and high signal-to-noise ratio (SNR), current data are limited to only the compositions shown in Fig. 4E, although characterizing the full doping dependence of the ${\mathrm{N}}_{\mathrm{2,3}}$ edge is the subject of ongoing work. The $x$ = 0.2 hole-doped perovskite shows a $\sim$200-meV shift to higher energies compared to the parent compound. In the $x$ = 0.2 infinite-layer film, we observe a twofold increase in this energy shift as well as an increase in spectral intensity. We note that a number of complicating factors could also contribute to changes in the edge shape, such as hybridization with the O states and a modified Madelung potential, both of which may be dominated simply by the stark difference in the crystalline environment of Nd from the perovskite to infinite-layer phase. Calculations by Choi et al. (13) have also suggested that Nd 5$d$ bands may be broadened by disorder in the 4$f$ states in the hole-doped infinite-layer compound. Others have predicted that these small 5$d$ contributions can and, in fact, should be avoided by adjusting the choice of rare earth to shrink the corresponding Fermi pockets (11, 14). Given the ongoing theoretical debate about the importance of the parent cation 5$d$ bands (10, 19, 52), direct experimental measurements of these states provide valuable information, although full interpretation of the observed shifts in the Nd-${\mathrm{N}}_{\mathrm{2,3}}$ edge will require detailed calculations.

Together, the evolution of all three edges (O-K, Ni-${\mathrm{L}}_{\mathrm{2,3}}$, and Nd-${\mathrm{N}}_{\mathrm{2,3}}$) suggest markedly different behavior of doped holes in infinite-layer nickelates than in the cuprates. Rather than doping mostly onto O, our data are consistent with a picture in which the large charge-transfer energy $\mathrm{\Delta }>U$ of the Mott–Hubbard regime instead pushes holes also onto Ni, resulting in $d^8$-like states above the O 2$p$ band. Hybridization between the ligand holes and $d^8$ states results in the observed $d^9\underset{\_}{L}$ peak at $\sim$528 eV in the O-K edge. Hybridization with this $d^9\underset{\_}{L}$ pushes the $d^8$ state up toward the Fermi energy, resulting in a “mixed-valent metal” state, as also suggested by the observed broadening of the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ edge. Finally, the effects measured in the Nd-${\mathrm{N}}_{\mathrm{2,3}}$ edge illustrate some interaction with the doped holes in the Nd 5$d$ bands as well, consistent with a multiband system fundamentally different from the effective single-band superconducting cuprates, as previously proposed by theoretical models (12, 16, 20, 45) and Hall effect measurements (48).

Beyond hole doping, the large parameter space, including rare-earth cation (11, 14), epitaxial strain, reduction process, etc., yet to be explored for this new family of superconductors will provide a rich backdrop for future experiments. Especially in thin-film form, spatially resolved spectroscopy will be a powerful technique to not only minimize spectral signatures due to defects but also exclude contributions from stabilizing capping layers (22).

The data presented here are direct evidence of key differences between the electronic structures of two isostructural superconducting oxide families. Analysis of the parent perovskite and infinite-layer compounds establishes the Mott–Hubbard character of ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_2$, distinct from the charge-transfer cuprates. Within the doped infinite-layer series, we observe effects of hole doping in not just the O 2$p$ but also the Ni 3$d$ and Nd 5$d$ bands, drawing a further distinction between the nickelates and their isostructural cuprate cousins. Lacking both the charge-transfer character and magnetic order (53) of the cuprates, understanding the nature of superconductivity in this new family of nickelates will require new insights from both theory and experiment.

Materials and Methods

Thin Film Synthesis and Characterization.

Thin films of precursor perovskite nickelate ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_3$ 8 to 10 nm in thickness were fabricated by PLD on single-crystalline (001) ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ substrates. To synthesize crystalline uniform films and improve sample-to-sample reproducibility, we adopted the recently established “high-fluence” conditions using precise laser-imaging conditions (22). For all samples, a ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ epitaxial capping layer was subsequently deposited using conditions described previously (8). After the growth, an annealing-based topochemical reduction was then employed to achieve the infinite-layer phase using ${\mathrm{C}\mathrm{a}\mathrm{H}}_2$ as the reducing reagent. The annealing conditions were optimized, as described previously (22). In particular, for samples with a ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ cap layer of $\sim$25 nm, the reduction temperature $T_{\mathrm{\text{r}}}$ of $\mathrm{280}°$C and reduction time $t_{\mathrm{\text{r}}}$ of 4 to 6 h were used; for samples with a $\sim$2-nm ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ cap layer, $T_{\mathrm{\text{r}}}$ and $t_{\mathrm{\text{r}}}$ were $\mathrm{260}°$C and 1 to 3 h, to achieve a complete transformation to the infinite-layer phase. X-ray diffraction symmetric and asymmetric scans of the nickelate films were measured using a monochromated Cu ${\mathrm{K}}_{\alpha 1}$ ($\lambda$ = 1.5406 Å) source. The resistivity measurements were made using Al wire-bonded contacts.

Atomic-Resolution STEM and EELS.

Electron transparent TEM samples of each film were prepared on a Thermo Fischer Scientific Helios G4 X focused-ion beam (FIB) using the standard lift-out method. Samples were thinned to $<$30 nm with 2-kV Ga ions, followed by a final polish at 1 kV to reduce effects of surface damage. All specimens were stored in vacuum to prevent possible degradation in air.

HAADF-STEM was performed on an aberration-correction FEI Titan Themis at an accelerating voltage of 300 kV with a convergence angle of 30 mrad and inner and outer collection angles of 68 and 340 mrad, respectively. Elemental maps were recorded with a 965 GIF Quantum ER spectrometer and a Gatan K2 Summit direct electron detector operated in counting mode. All EELS experiments presented here were conducted with probe currents less than 20 pA to minimize radiation damage with the scan parameters used: ∼1-Å probe, ∼0.1-Ų scan pixel size, and 0.5 μs per pixel dwell time (SI Appendix, Fig. S7). One consequence of this low beam current is the need for long total acquisition times to achieve spectral SNR suitable for resolving subtle differences in the EELS fine structure.

Particularly for the O-K edge, acquisitions up to 2,000 s for a single $\sim$10- to 20-nm² region were needed in order to record spectra with sufficiently high SNR. To ensure low spatial drift over such long measurements, EELS experiments of the O-K edge were performed on a Nion UltraSTEM equipped with a high stability stage, an Enfinium ER spectrometer, and a Quefina 2 camera, operated at 100 kV with 12-pA beam current. The effective energy resolution measured by the full width at half-maximum of the zero loss peak was $\sim$0.39 eV. In each specimen, atomic-resolution STEM imaging was used to locate defect-free regions and eliminate contributions from ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ substrate and capping layers.

Most spectra presented here are the sum of multiple acquisitions. All individual spectra were aligned in energy based on cross-correlation of the large spectral features. In some cases (Ni-${\mathrm{L}}_{\mathrm{2,3}}$ and Nd-${\mathrm{M}}_{\mathrm{4,5}}$ edges from the ${\mathrm{N}\mathrm{d}\mathrm{N}\mathrm{i}\mathrm{O}}_3$ film; Fig. 2), a weighted moving average over a small window (three to five channels) has been applied for clarity of comparison between spectra. The energy dispersion of 0.025 eV per channel is significantly smaller than the instrumental energy resolution, so smoothing to this degree will not affect the overall interpretation of our data. Absolute energy alignment of the O-K edges of the ${\mathrm{N}\mathrm{d}}_{1-x}{\mathrm{S}\mathrm{r}}_x{\mathrm{N}\mathrm{i}\mathrm{O}}_y$ thin films are based on simultaneously recorded O-K spectra from the ${\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{i}\mathrm{O}}_3$ substrates, which serves as a consistent and well-documented reference. In each figure, spectra are normalized and shifted vertically for clarity and ease of comparison.

To obtain sufficient SNR of the high-energy edges (Ni-${\mathrm{L}}_{\mathrm{2,3}}$, Nd-${\mathrm{M}}_{\mathrm{4,5}}$), we took advantage of the low background and readout noise in the Gatan K2 Summit direct electron detector installed on the FEI Titan Themis system (54–56). The inherent energy spread of the high-brightness Schottky field emission gun (X-FEG) electron source on this system, however, required monochromation to obtain sufficient energy resolution. For these experiments, we used a monochromator excitation of 1.0 at an accelerating voltage of 120 kV to achieve measured energy resolution of $\sim$0.21 eV with a spectrometer dispersion of 0.025 eV per channel. Because of the point spread function of the K2 Summit detector (54–56), the 0.1 eV per channel dispersion used for the experiments preserved an effective energy resolution of $\sim$0.29 eV over a total energy range of 370 eV, enabling simultaneous acquisition of both the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ and the Nd-${\mathrm{M}}_{\mathrm{4,5}}$ edge used for absolute energy alignment (SI Appendix, Fig. S4). Ni and Nd spectra were acquired by the same process described for the O-K edge. The O-K signature was checked for each region before and after additional data collection to ensure proper phase identification (i.e., perovskite vs. infinite-layer) and to confirm that the results were not affected by radiation damage during the experiment (SI Appendix, Fig. S7). All spectra were aligned in energy based on a simultaneously recorded nearby standard edge: e.g., the Ni-${\mathrm{L}}_{\mathrm{2,3}}$ spectra were aligned by the Nd-${\mathrm{M}}_{\mathrm{4,5}}$, the Nd-${\mathrm{N}}_{\mathrm{2,3}}$ by the C-K edge.

Data Availability.

The spectral and image data reported in this paper have been deposited in the Platform for the Accelerated Realization, Analysis, and Discovery of Interface Materials (PARADIM) database (https://doi.org/10.34863/1lk1-pd01).