Estimating Local Cellular Density in Glioma Using MR Imaging Data

Abstract

BACKGROUND AND PURPOSE:

Increased cellular density is a hallmark of gliomas, both in the bulk of the tumor and in areas of tumor infiltration into surrounding brain. Altered cellular density causes altered imaging findings, but the degree to which cellular density can be quantitatively estimated from imaging is unknown. The purpose of this study was to discover the best MR imaging and processing techniques to make quantitative and spatially specific estimates of cellular density.

MATERIALS AND METHODS:

We collected stereotactic biopsies in a prospective imaging clinical trial targeting untreated patients with gliomas at our institution undergoing their first resection. The data included preoperative MR imaging with conventional anatomic, diffusion, perfusion, and permeability sequences and quantitative histopathology on biopsy samples. We then used multiple machine learning methodologies to estimate cellular density using local intensity information from the MR images and quantitative cellular density measurements at the biopsy coordinates as the criterion standard.

RESULTS:

The random forest methodology estimated cellular density with R² = 0.59 between predicted and observed values using 4 input imaging sequences chosen from our full set of imaging data (T2, fractional anisotropy, CBF, and area under the curve from permeability imaging). Limiting input to conventional MR images (T1 pre- and postcontrast, T2, and FLAIR) yielded slightly degraded performance (R² = 0.52). Outputs were also reported as graphic maps.

CONCLUSIONS:

Cellular density can be estimated with moderate-to-strong correlations using MR imaging inputs. The random forest machine learning model provided the best estimates. These spatially specific estimates of cellular density will likely be useful in guiding both diagnosis and treatment.

Increased cellular density (CD) is a hallmark of cancer and a key feature in histologic glioma analysis.¹ Mapping cellular density throughout a tumor would be a valuable tool to probe how tumors infiltrate and analyze the transition between diseased and healthy brain. However, measuring CD requires tissue, which entails additional risks and is expensive to obtain. There is no currently accepted clinical algorithm to translate imaging data into quantitative assessments of CD.

There is great need for a method to estimate CD noninvasively in human patients with gliomas. In this article, we describe the development of such a method using MR imaging data inputs by correlating with multiple biopsy specimens acquired during a prospective human clinical trial. We obtained comprehensive MR imaging, including conventional, diffusion, perfusion, and permeability imaging sequences. We used machine learning approaches to correlate imaging findings with CD measurements from pathology, devised an algorithm to estimate CD from MR imaging inputs, and generated CD maps for the visual display of the predictions. We identified the most informative imaging data subset. This work has multiple applications in the diagnosis and treatment of patients with gliomas: For example, the method can be used to guide biopsy, resection, and surgery and delineate tumor borderzones both pre- and postoperatively.²

MATERIALS AND METHODS

Data were collected as part of a Health Insurance Portability and Accountability Act–compliant institutional review board–approved imaging clinical trial protocol (NCT03458676) for adult, treatment-naïve patients with gliomas at MD Anderson Cancer Center. See Table 1 for demographics. We have previously reported results in the estimation of Ki-67 and tumor grade.^3,4 Up to 5 separate biopsies were collected per patient, which were targeted by 2 alternative methods:

• The conventional biopsy site was defined as enhancing tumor if present or T2 bright signal closest to an accessible brain surface

• The advanced biopsy site was defined, in order, by high relative CBV, high volume transfer constant, and/or restricted diffusion.

Table 1:

Patient demographics

Demographics
No. (Sex)	23 Patients (14 women, 9 men)
Age (mean) (range) (yr)	43.9 [SD, 16.9] range, 21–80
WHO grade (I/II/III/IV)	0/7/9/7
Biopsy samples/patient (mean)	2.26 [SD, 0.54]
No. of biopsy samples in final analysis	52 real + 52 virtual

Note:—WHO indicates World Health Organization.

Additional biopsies could be obtained en route to the sites defined above, with preference given to sampling normal brain and the brain-tumor interface when possible. Biopsy locations were sampled under stereotactic guidance using iPlan cranial neuronavigation software (Brainlab), and the final sampling coordinate locations were recorded. Tissue samples were sectioned at 4-μm thickness and stained with H&E. Some slides were also immunohistochemically stained with proliferation and vascularity markers, but these data were not used in the cell density measurement. The H&E-stained tissue was analyzed by a board-certified neuropathologist, and the cell density was measured semiautomatically in nuclei/square millimeter using Aperio ImageScope software (Leica Biosystems).

Image Acquisition

Four clinical categories of imaging were obtained for every patient on a Signa HDxt 3T or Discovery MR750 3T clinical MR imaging scanner (GE Healthcare): anatomic/conventional, diffusion, perfusion, and permeability. Detailed acquisition parameters are given in the Online Appendix and Online Tables 1 and 2. A total of 23 imaging parameters were acquired or generated.

Anatomic images were T1-weighted, T1 postgadolinium, T2-weighted, T2*/susceptibility, FLAIR, and T2*-weighted angiography (SWAN).

DWI and DTI were both acquired for each patient. They were then processed to generate maps of ADC, exponential ADC (eADC), and fractional anisotropy.^5,6

Finally, we acquired 2 image series using a dynamic acquisition after the injection of contrast. The dynamic contrast-enhanced (DCE) image series was acquired using a 0.1-mmol/kg contrast bolus, and this same bolus was used for the conventional T1 contrast-enhanced image. The raw data were processed using nordicICE (NordicNeuroLab) using the full extended Tofts model, including leakage correction^7-9 and arterial input deconvolution. This process yielded maps of forward and backwards transfer constants (K_trans and k_ep respectively), plasma and extravascular extracellular contrast fractions (v_p and v_e), time to peak enhancement (TTP), area under enhancement curve (AUC), and peak enhancement.^7-9 Later in the same study, a second bolus of contrast (again 0.1 mmol/kg) was injected to acquire dynamic susceptibility contrast image data. This time-series was similarly processed to yield maps of relative CBV, CBF, MTT, delay time, and leakage correction K2.^10-12

Image Normalization and Measurement

Anatomic images were normalized on the basis of patient-specific average tissue intensities. The T1-weighted, FLAIR, and T2*-weighted angiography images were linearly scaled so that white matter (WM) and CSF had average intensities of 1 and 0, respectively. Similarly, T2-weighted and T2*-weighted images were scaled with WM and CSF having average intensities of 0 and 1. T1 postcontrast was scaled using CSF and gray matter. Parametric maps from DWI, DSC, and DCE are quantitative and were used as provided. Although all images were acquired in the same study, we mutually coregistered them using a 6-df and 12-df affine registration in ANTs¹³ to correct for patient motion and geometric distortion.^14,15 For each biopsy, a 5-mm spheric VOI was placed at the sampling coordinates, and the average intensity in this VOI was recorded for each image parameter.

Cell Density in Control Regions

To record imaging characteristic in normal brain, a neuroradiologist placed an ROI in normal-appearing white matter contralateral to the location of each tissue biopsy, and the average image intensity was recorded. These “virtual biopsies” were assumed to have cell density equal to that of normal white matter. We used values provided by Roetzer et al¹⁶ and corrected the CD estimates for histologic section thickness using the Abercrombie method (see On-line Appendix).^17,18 We obtained a best estimate for normal white matter cell density of 2912 [SD, 673] nuclei/mm². Table 2 lists values reproduced from Roetzer et al,¹⁶ and the corrected values were used in our study.

Table 2:

Normal brain tissue cell density estimates (1/mm²)

	Mean	SD	Mean, Corrected to 4-μm Thickness	SD, Corrected to 4-μm Thickness
Cortex	2473a	716a	2011	582
White matter	3581a	828a	2912	673
Tumor	5714a	1786a	4646	1452

^aData reproduced from Table 1 with permission from Roetzer et al.¹⁶ Virtual biopsies used mean and SD for white matter.

Model-Building Procedure

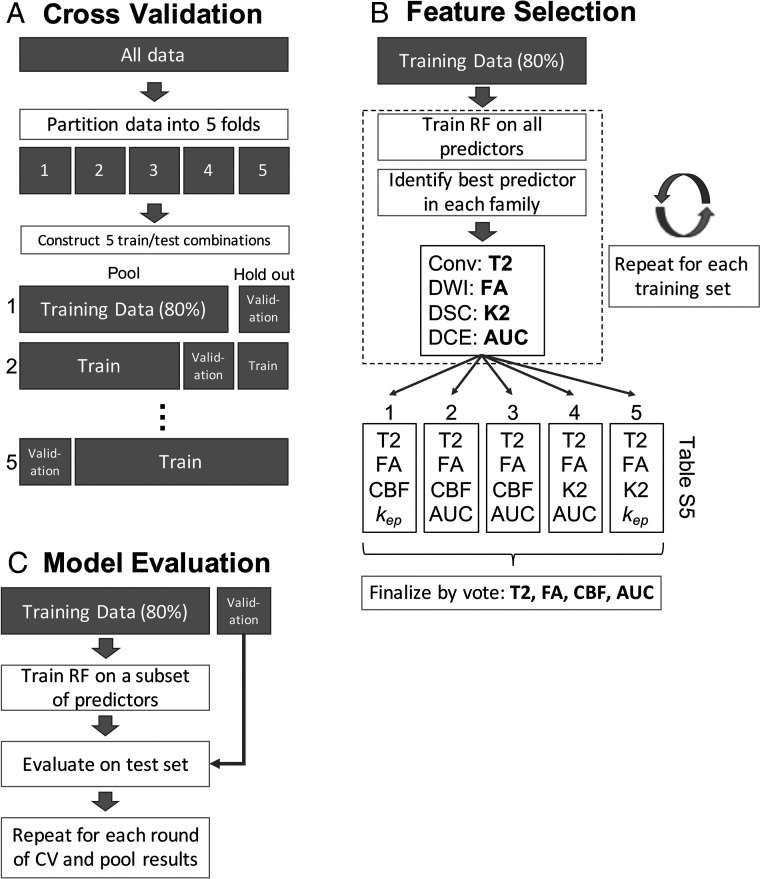
To avoid overfitting, we performed 5-fold cross-validation using disjoint training and testing subsets of the biopsy data within each round (Fig 1A). We partitioned our data into 5 groups, each containing about 20% of our data. To further preserve independence, we placed each sample in the same fold as its paired virtual biopsy.

FIG 1.

Schematic of each of the 3 main stages of the model-building procedure. A, The data are partitioned into 5 homogeneous folds, each comprising 80% of the data for training and 20% for validation, repeated 5 times. Within each round of cross-validation (CV) 1 fold is held out for validation while the other 4 (80%) are pooled to form a training set. B, A random forest (RF) model was fit to the training data, and the best predictor variable from each imaging family was selected. Because there are 5 rounds of CV, this procedure was repeated 5 times and the selections (listed in Online Tables 4 and 5) were combined by voting. C, Using the consensus subset of predictor variables after feature selection, we trained another random forest on each training set and made predictions on the corresponding holdout set. The average correlations between predicted and observed values across all rounds of CV are given in Table 4. K_ep indicates reverse transfer constant from DCE imaging.

Variable selection was performed to reduce the number of model inputs from the 23 available parameters to something more parsimonious and to reduce information redundancy among related imaging variables. Within each round of cross-validation, we fit a random forest model to the training subset (4 of 5 groups) using all input variables and computed a variable importance ranking on the basis of the permuted out-of-bag data.¹⁹ After the rankings were computed, the most important predictor from each imaging family was used to select 4 final predictors, 1 each from anatomic, diffusion, perfusion, and permeability.^3,20 Because this was repeated for each round of cross-validation, 5 variable selections resulted. When the 5 rankings gave different results regarding the most important imaging variable, simple voting was used to determine a consensus. This process is illustrated in Fig 1B and yielded a final set of imaging variables to include in the final model. To provide a fair comparison, we used the final 4-variable set in all model classes tested.

The cross-validation procedure was performed using both the selected variables within each round and the final 4 variables based on consensus among all rounds. The predicted estimates of CD were compared with the actual values known in the 20% validation set and assessed using the Pearson correlation (R²) between predicted and observed CD. This process is explained in Fig 1C. Figure 1 illustrates the full process with the random forest model (our eventual winner), but several models were tested (single decision tree, single-layer neural network, and linear regression). Model descriptions are given in Online Table 3. The model building process was implemented in R, Version 3.4.2 (http://www.r-project.org/).

RESULTS

Patient Data

Thirty-one patients were enrolled in the trial between 2013 and 2016 (mean age, 46 ± [SD, 16]  years). Patient demographics are summarized in Table 1. Tissue could not be harvested from 5 patients due to surgical complexity or technical difficulties. For another 3 patients, missing DCE imaging data (1 patient) or unanalyzable tissue samples (2 patients) excluded them from analysis. After exclusions, 23 evaluable patients with 52 image-guided biopsies remained in the final analysis. Of these patients, 7 had clinical grade II gliomas, 9 had grade III, and 7 had grade IV. Among the tissue samples themselves, 9 were collected from contrast-enhancing regions, 2 were collected from just outside the visible T2 hyperintensity, none were collected from necrotic regions, and the remainder were collected from the visible T2-hyperintense tumor. The cell density among all tissue samples increased with increasing sample grades as listed in Table 3.

Table 3:

Number of samples of each WHO grade^a

Sample Grade	No. of Samples	Cell Density (Mean) (SD)
Normalb	3	1777 [SD, 371]
II	39	5790 [SD, 2667]
II/III	3	6085 [SD, 2022]
IIIc	2	2584, 14,634
IV	5	11,547 [SD, 4252]

^aThe grade of a sample is not necessarily the same as the patient’s clinical grade. As expected, the cell density of the samples increases with increasing sample grade.

^bThese samples appeared histologically tumor-free but showed Ki-67-positive endothelial cells.

^cBecause only 2 samples were grade III, the values are listed.

Three samples were histologically graded as normal cortex and provide some comparison with the normal cell densities used for virtual biopsies. The recorded CD values were 2169, 1729, and 1432 nuclei/mm², comparing well with the CD values of Roetzer et al¹⁶ for normal cortex at 2011 [SD, 582] nuclei/mm². See Table 2 for the original estimates and corrected values comparable with our measurements.

Variable Selection and Predictive Modeling

The best predictor from each imaging sequence family for the random forest model was determined by the most votes from each fold of cross-validation and is summarized in Online Table 4. Combining the selections produced a 4-variable set: T2, fractional anisotropy, CBF, and AUC. Of these 4 predictors in the final model, the T2-weighted image intensity had the greatest importance as measured by the random forest with a 27% increase in mean-square error when variables are permuted. Fractional anisotropy and AUC have a smaller importance at 18.0% and 16.1%, respectively. Finally, CBF, despite being the best predictor from the DSC family in 3 of 5 folds of cross-validation, had only an importance of 11.3% increased mean-square error in the final model.

Similar magnitude variable importance was measured for the conventional-only model, ranging from 26.7% for the T2-weighted image down to 9.4% for the FLAIR image, shown in Online Table 5. While the importance measures provide some information about how each predictor relates to CD, they do not measure the combined nonlinear relationships modeled by the random forest.

We compared the reduced variable set selected with modeling done with no selection to show the effects of variable selection. We found comparable modeling performance using the random forest trained on all 23 variables and using the much smaller 4-variable set chosen by random forest importance (R² = 0.572 versus 0.586). The predicted-versus-observed R² values are given in Table 4 and Fig 2. Additionally, root-mean-square error values are listed in Online Table 6. Overall, the high average R² = 0.586 with 4 imaging variables and the random forest model suggest a strong ability to predict cell density with imaging data.

Table 4:

Average R² for predicted-versus-observed cell density for cross-validation^a

	All Variables (23 Inputs)	Variables Selected by RF Importance (4 Inputs)	All Conventional Variables (6 Inputs)	Variables Selected by RF Importance: Conventional Only (4 Inputs)
Random forest	0.572	0.586	0.513	0.523
Linear	0.542	0.572	0.444	0.475
Neural network	0.265	0.460	0.382	0.379
Decision tree	0.301	0.325	0.376	0.376

^aThe columns list variables used to train the predictive model. “All Variables” is simply using all 23 imaging parameters of all 6 conventional sequences, whereas “RF Importance” and “RF Importance, Conventional” use the final 4 variable sets shown in Online Tables 4 and 5. A larger average R² indicated better performance.

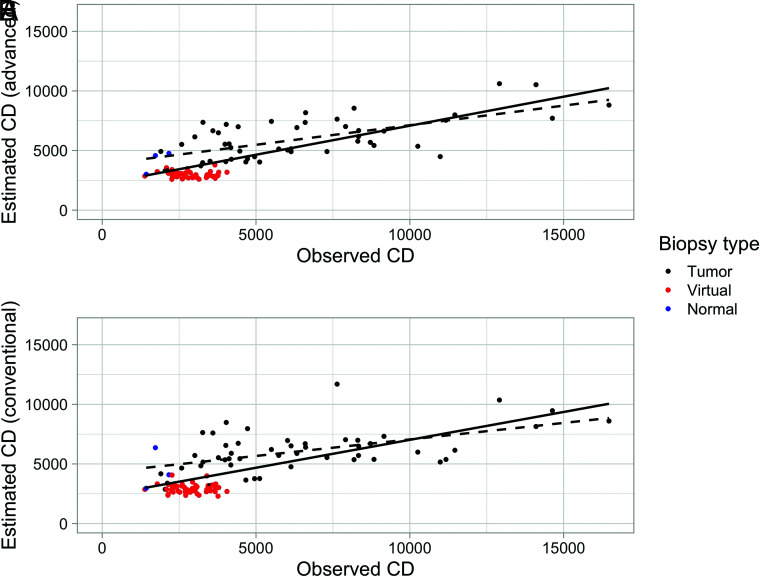
FIG 2.

Predicted and observed cell density (nuclei/square millimeter) for the random forest model using 4 fixed inputs from conventional-plus-advanced imaging. A, The solid line is the best fit for all predictions (R² = 0.56), and the dashed black line is the best fit for real-sample predictions only (R² = 0.39), that is, excluding virtual samples (red points). B, The predictions using conventional imaging only. The model performance decreased slightly with R² = 0.50 for all observations and R² = 0.30 for real observations only. Blue points are real tissue biopsies that were graded as histologically normal-appearing. The cell density for these points is generally lower than the CD for tumor samples and falls within the range of the virtual biopsies.

Using only conventional imaging variables yielded marginally lesser predictive performance. For conventional imaging only, the highest performance was also with all 6 conventional images as variables in a random forest model, and there was a small improvement made by reducing the number of input variables from 6 to 4 (R² = 0.513 versus 0.523). The 4-variable set consisted of T2, T1 postcontrast (T1C), FLAIR, and T1 (Online Table 5). These predictions also are strong enough to still be clinically meaningful. No other model tested using only conventional imaging performed better than the random forest.

Maps of cell density generated using the random forest model and the selected conventional and advanced imaging variables are shown in Figs 3 and 4. As expected, the estimated cell density is heightened in regions of increased blood flow, permeability, and contrast enhancement. The estimated CD is also increased in regions of T2 hyperintensity relative to the normal white matter, which may represent infiltrative tumor growth. By looking at a line profile in Fig 3, we observe how the estimates based on the final predictive model change with the input images across the tumor. The importance of AUC and CBF in predicting CD within the visible tumor can be visually appreciated by studying these plotted transects. Additionally, these maps demonstrate the increased CD and heterogeneity of high-grade gliomas (Fig 4), showing the potential value of making local predictions of cell density because such a map may be useful for guiding therapeutic interventions for a range of glioma grades.

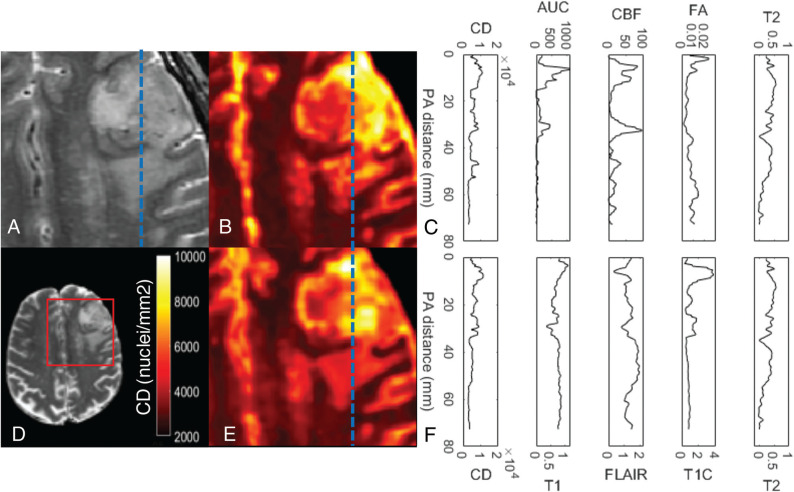
FIG 3.

Estimated map of cell density using machine learning models. A, The T2-weighted image of a glioblastoma. B, The estimated cell density map using the 4 inputs to the final model (T2, fractional anisotropy, CBF, and AUC) selected from all the available imaging data (conventional and advanced) and smoothed by a 1-mm radius filter. The profiles shown in C correspond to the dashed blue line in A, B, and E. We can see in C that the predicted CD is strongly related to the AUC and CBF within the tumor volume. E, The estimated cell density map using conventional imaging only with the analogous profiles shown in F. The model predicts less extreme values than seen with the model using advanced imaging. D, The whole axial section of the T2-weighted image for reference with the cropped area for A, B, and E is outlined in red. PA indicates posteroanterior distance.

FIG 4.

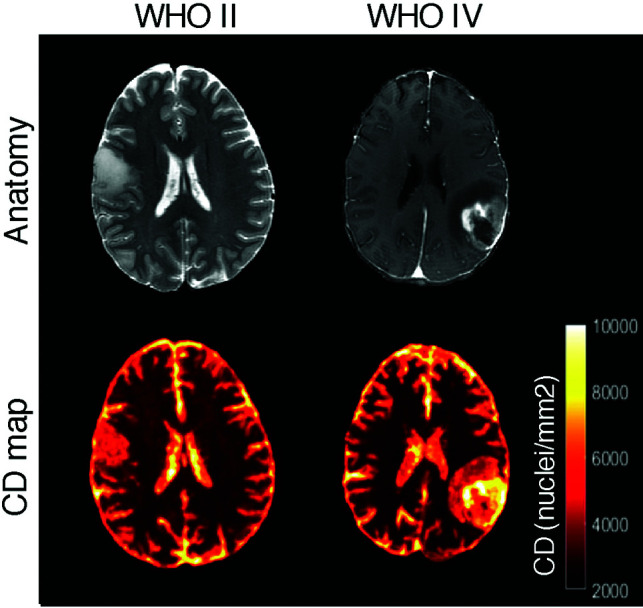
Sample cell density maps for a low-grade glioma (World Health Organization II, left images) and a high-grade glioblastoma (World Health Organization IV, images). The T2-weighted or T1-weighted postcontrast images are shown for reference. As expected, the low-grade tumor shows lower and more homogeneous cell density estimates.

DISCUSSION

We have derived an algorithm for the point-wise local estimation of CD in gliomas using MR imaging data. Using only conventional anatomic imaging sequences, T1, FLAIR, T1C, and T2, CD can be estimated to a R² of 0.523. When advanced imaging from diffusion tensor imaging, perfusion, and permeability sequences is also used, CD can be estimated to an R² of 0.586. The final inputs to these predictions are areas under the curve from DCE, cerebral blood flow, fractional anisotropy, and T2. This algorithm allows the construction of CD maps of the brain, translating imaging information into quantitative pathologic estimates that may be useful to guide biopsy and treatment.

Our work has avoided global-level image analysis, including “radiomics,”^20-22 due to biologic limitations imposed by histologic heterogeneity exhibited by gliomas.²³ Instead, we performed point-wise spatially specific analysis using tissue samples as the criterion standard, which allows local correlation with MR image characteristics and, in turn, point-wise estimates of CD. CD is 1 characteristic that varies considerably between tumor and healthy brain tissue^16,24 and also correlates with tumor aggressiveness, making it a useful target for predictive modeling.

In previous work, similar methods have shown effective correlation of imaging with proliferation, grade, and genetic heterogeneity.^3,4,25 We used a similar and effective methodology here to develop predictive models for CD as reported in our previous work.^3,4 However, estimating cell density represents a very different biologic target with different applications and stands separately from estimating proliferation or tumor grade. Our final model also takes advantage of different derivates of advanced imaging sequences.

Other previous studies have also estimated glioma cell density with spatially specific tissue samples. These studies are characterized by similar imaging protocols, including DTI or DSC, and generally find correlations with CD.^24,26 However, the exact image features like CBV versus CBF, ADC versus fractional anisotropy, or mean intensity versus 90th percentile intensity vary. Possible explanations for these discrepancies are differences in sample grades, such as only including samples from glioblastoma,²⁷ or subtle differences in measurement methods for imaging or cell density, cellularity, or related quantities. Overall, our work finds similar results and includes the addition of imaging features from DCE, a greater number of samples, advanced machine learning modeling via random forest, and a smaller number of variables included in the final model.

Our study confirmed the relationship between nuclear density and fractional anisotropy,²⁴ which is a natural expectation, considering that increased nuclei mean increased cell packing. This reduces water movement and affects diffusion parameters. While not used in the final predictive model, we also observed the well-established correlation between ADC and cell density.²⁷ The selection of fractional anisotropy over ADC within the 5 folds of cross-validation does not exclude ADC as a strong predictor of CD; it means simply that FA was a stronger predictor and we chose a priori to include only 1 diffusion parameter in the final model to reduce redundancy. There are many strongly correlated quantities derived from similar source data that are equally useful for predictive modeling and could be substituted with similar performance.

These correlations among sequences may also explain our success in predicting CD (R² = 0.523) using only conventional imaging sequences: T1, T1 postcontrast, T2, and FLAIR. The DCE parameter AUC is a rough measure of total blood-brain-barrier disruption;²⁸ thus, we would expect similar information to be contained in the T1 postcontrast image data. Correlating imaging with pathology (like cell density) is a rich way to help understand the degree to which these advanced sequences and their similar conventional sequences may probe the same underlying biologic processes. Such sequences have evolved in clinical practice because they are informative of biology and highlight pathology (ie, heightened CD).

The technical demands of collecting spatially specific tissue samples and comprehensive preoperative imaging with diffusion-weighted, DSC, and DCE imaging mean that our study is somewhat limited by the small sample size. However, the 52 samples used in the final analysis and the additional 52 corresponding virtual controls were sufficient to make useful estimates of cell density. Increased sample size would help improve model confidence and would likely help stabilize some of the variable selections that changed between cross-validation folds. An additional limitation is the assumption of cell density for normal white matter. Ethical constraints prohibit sampling healthy brain, so we must impute values for normal tissue on the basis of literature values.^16,17 The values we used from Roetzer et al¹⁶ do appear to agree with our values in both normal samples and tumor.

CONCLUSIONS

Our methodology allows noninvasive estimation of CD at points in the gliomatous brain with clinically useful accuracy using a combination of MR imaging sequences that are already in wide clinical use. CD estimates can be used to generate a map of estimated cell density for the whole brain. Our work is consistent with previous studies^3,24 and with clinical intuition. Maps of CD could be a useful clinical tool to guide biopsies and resections, measure the extent of resection, or plan radiation treatments. Additional trials to prospectively validate our estimating algorithms are justified.

ABBREVIATIONS:

AUC

area under the curve

CD

cellular density

DCE

dynamic contrast-enhanced

RF

random forest

T1C

T1 postcontrast