Amplitude modulation encoding in the auditory cortex: comparisons between the primary and middle lateral belt regions

Abstract

In macaques, the middle lateral auditory cortex (ML) is a belt region adjacent to the primary auditory cortex (A1) and believed to be at a hierarchically higher level. Although ML single-unit responses have been studied for several auditory stimuli, the ability of ML cells to encode amplitude modulation (AM)—an ability that has been widely studied in A1—has not yet been characterized. Here, we compared the responses of A1 and ML neurons to amplitude-modulated (AM) noise in awake macaques. Although several of the basic properties of A1 and ML responses to AM noise were similar, we found several key differences. ML neurons were less likely to phase lock, did not phase lock as strongly, and were more likely to respond in a nonsynchronized fashion than A1 cells, consistent with a temporal-to-rate transformation as information ascends the auditory hierarchy. ML neurons tended to have lower temporally (phase-locking) based best modulation frequencies than A1 neurons. Neurons that decreased their firing rate in response to AM noise relative to their firing rate in response to unmodulated noise became more common at the level of ML than they were in A1. In both A1 and ML, we found a prevalent class of neurons that usually have enhanced rate responses relative to responses to the unmodulated noise at lower modulation frequencies and suppressed rate responses relative to responses to the unmodulated noise at middle modulation frequencies.

NEW & NOTEWORTHY ML neurons synchronized less than A1 neurons, consistent with a hierarchical temporal-to-rate transformation. Both A1 and ML had a class of modulation transfer functions previously unreported in the cortex with a low-modulation-frequency (MF) peak, a middle-MF trough, and responses similar to unmodulated noise responses at high MFs. The results support a hierarchical shift toward a two-pool opponent code, where subtraction of neural activity between two populations of oppositely tuned neurons encodes AM.

INTRODUCTION

The middle lateral belt area of the auditory cortex (ML) is a region in the auditory belt adjacent to the primary auditory cortex (A1) that is considered to sit at a higher level of the auditory hierarchy due to its sparse lemniscal input from the ventral medial geniculate nucleus of the thalamus (Kaas and Hackett 2000). Given its location on the cortical sheet, as well as its connections (Romanski et al. 1999), latency (Camalier et al. 2012), and tuning properties to auditory objects and spatial location (Rauschecker and Tian 2000; Tian et al. 2001; Woods et al. 2006), ML appears to straddle the proposed “what” and “where” pathways in the auditory cortex. Although it is tonotopic like A1 (Rauschecker et al. 1995), it is more responsive to complex stimuli such as bandpass noise (Rauschecker et al. 1995; Rauschecker and Tian 2004) and frequency-modulated sweeps (Tian and Rauschecker 2004) than to pure tones.

Although there is a rudimentary knowledge of ML response properties, a detailed examination of ML responses to many basic auditory stimuli is still lacking. In particular, ML responses to amplitude-modulated stimuli remain largely uncharacterized. Amplitude modulation (AM) is a common feature of sound and an important information-conveying parameter for natural sounds, including animal vocalizations and speech (e.g., Cohen et al. 2007; Drullman et al. 1994; Elliott and Theunissen 2009; Geffen et al. 2011; Gervain and Geffen 2019; Jin and Nelson 2006; Liu et al. 2003; Narayan et al. 2006; Rosen 1992; Shannon et al. 1995; Singh and Theunissen 2003; Xiang et al. 2013; Zeng et al. 2005), as well as a feature useful for segregating and attending to sounds, more commonly referred to as the cocktail party problem (Bohlen et al. 2014; Bregman 1990; Grimault et al. 2002; Hershenhoren and Nelken 2017; Itatani and Klump 2009; Steinschneider et al. 2003; Yamagishi et al. 2017; Yost 1991). Despite its importance in auditory scene analysis, we know very little about how higher areas of cortex process AM.

AM stimuli are one of the simplest tools for investigating the temporal aspects of auditory processing. AM stimuli have been used to characterize every stage of the auditory system from auditory nerve to A1 in various animal models (reviewed in Joris et al. 2004). A1 in the nonhuman primate has been particularly well studied with AM stimuli (e.g., Bendor and Wang 2007, 2008; Bohlen et al. 2014; Hoglen et al. 2018; Johnson et al. 2012; Liang et al. 2002; Malone et al. 2007, 2013; Overton and Recanzone 2016; Scott et al. 2011; Yin et al. 2011), establishing the opportunity for the characterization of ML compared with A1. Recent reports have pointed to differences in the processing of AM noise stimuli in A1 and ML with regard to higher-level processes such as task engagement (Niwa et al. 2015) and decision-making (Niwa et al. 2013), but there remains a gap in our knowledge of simpler, more fundamental response properties to AM stimuli in ML.

One consistent finding in studies of neural responses to AM stimuli is that there is a temporal-to-rate transformation as the auditory hierarchy is ascended. The high-frequency phase-locking cutoff gradually decreases and a class of cells that responds to AM with changes in spike rate but does not phase lock to the stimulus itself emerges (e.g., Bendor and Wang 2007; Gao and Wehr 2015; Lu and Wang 2004; Lu et al. 2001; Schreiner and Urbas 1988). Because ML is putatively at a higher level than A1 in the auditory hierarchy, a continuation of this temporal-to-rate transformation from A1 to ML would be consistent with the hierarchical placement of ML.

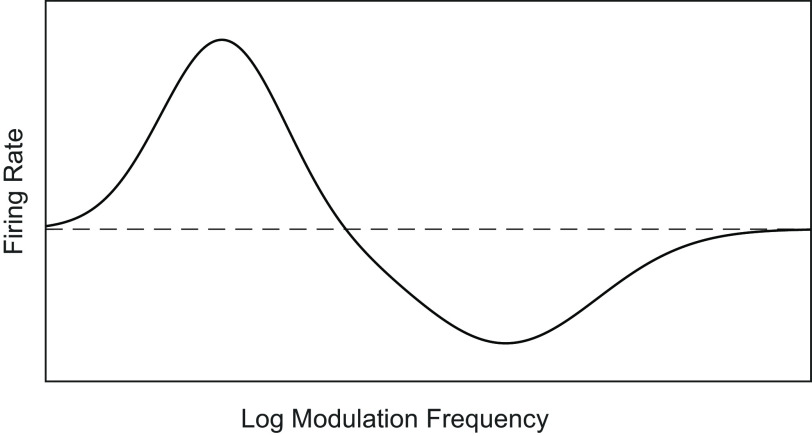
In this study, we compared various aspects of AM noise processing in A1 and ML of the awake nonbehaving macaque. We found much in common between the two areas, but the results indicated a shift away from temporal coding at the level of ML, consistent with an ascending temporal-to-rate transformation. A previous report in behaving macaques (Niwa et al. 2013) demonstrates that the proportion of cells that detect an increase in AM depth by decreasing (instead of increasing) their firing rates becomes greater in ML than in A1. Further results suggested that this greater proportion of “decreasing” cells in ML holds for the nonbehaving macaque as well (Niwa et al. 2015) and may point to a shift in higher auditory cortical areas toward a two-pool opponent code. A two-pool opponent code refers to a code where a subtraction of neural activity between two populations of oppositely tuned neurons can be used to determine the degree or presence of a stimulus property (Susilo et al. 2010)—for example, how far contralateral (Stecker et al. 2005) or how modulated a sound is. Additionally, in both A1 and ML, we found an abundant class of cells not widely reported in the cortex that we refer to as peak/trough (P/T) cells (schematic in Fig. 1). P/T cells typically had enhanced rate responses that were greater than the unmodulated noise response at lower modulation frequencies (MFs), suppressed rate responses relative to responses to the unmodulated noise at middle MFs, and returned to baseline (i.e., firing rate to unmodulated noise) at higher MFs, suggesting that at sufficiently high MFs many of these cells may have responded to the noise but may have been blind to the modulation. Responses in the excitatory region at low MFs were typically phase-locked, but responses in the high-MF region were typically not phase-locked.

Fig. 1.

Schematic of idealized peak/trough (P/T) cell. Dashed line indicates firing rate to an unmodulated stimulus. The idealized P/T cell has a low-MF peak with enhanced responses relative to the unmodulated response, a middle-MF trough with suppressed responses relative to the unmodulated response, and returns to roughly the level of the unmodulated response at high MFs. At modulation frequencies near the low-frequency peak, the neurons typically phase lock to the AM. AM, amplitude-modulated; MF, modulation frequency.

MATERIALS AND METHODS

Subjects

In this study, data were collected from the right hemispheres of three adult rhesus macaque monkeys, two females (monkey V, age 11–12, and monkey W, age 10–14) and one male (monkey X, age 13–16). A1 single neuron recordings were collected from all three monkeys. ML single neuron recordings were collected from monkeys W and X. The recordings analyzed in this study were made in conjunction with recordings analyzed in prior publications (Downer et al. 2017; Niwa et al. 2013, 2015). In those publications, these modulation transfer functions (MTFs) were used only to determine the modulation frequencies for collecting firing rate versus modulation depth functions. The data presented in this study have not previously been published. All procedures conformed to the US Public Health Service (PHS) policy on experimental animal care and were approved by the UC Davis Animal Care and Use Committee.

Identification of Cortical Fields

The assignment of recording site to cortical field was made on the basis of physiological measurements as described in Niwa et al. (2012a, 2013, 2015). Briefly, the best frequency (BF) of the recording site was determined from a frequency-tuning curve (100-ms tones limited between 125 Hz and 32 kHz, spanning three octaves around a manually determined BF estimate in 1/5 octave steps, sound level varying between 10 and 90 dB SPL in 10 dB steps). In each animal, a tonotopic map was created from the BFs in all recordings, and the location of A1 was determined on the basis of a systematic anterior-to-posterior increase in BF together with nearly constant BFs on the medial-to-lateral axis (Niwa et al. 2012a). The border of A1 and ML was based on ML’s lack of robust responses to tones, longer tone response latency, and wider frequency-tuning widths (Kosaki et al. 1997; Merzenich and Brugge 1973; Morel et al. 1993; Rauschecker 1997; Recanzone et al. 2000). Identified ML comprised a narrow strip 2–3 mm wide lateral to the A1-ML border. When recording time permitted, the BF of recording sites in ML was determined with a frequency-tuning curve collected using bandpass noise (100-ms bandpass noise, various center frequencies between 125 Hz and 32 kHz, bandpass filter widths of 1/3, 1/2, 1, and 2 octaves and sound level varying between 10 and 90 dB SPL in 10 dB steps). A tonotopic map was created from the BFs and the systematic change in BF was used to estimate the anterior border with AL and the posterior border with CL. In this study, BFs were used only for identification of cortical fields; the properties of modulation transfer functions with respect to BF were not analyzed.

Stimulus Generation and Presentation

Acoustic stimuli were 800-ms sinusoidally amplitude-modulated (AM) non-bandlimited broadband Gaussian noise bursts created digitally at 100 kHz. AM stimuli had modulation frequencies (MFs) of 2.5, 5, 10, 15, 20, 30, 60, 120, 250, 500, and 1,000 Hz and were at 100% modulation depth. In addition, an unmodulated version of the broadband noise burst was used. All stimuli were created from a single noise stimulus generated by the same random number sequence (“frozen” noise) and were thus identical before the application of the modulation envelope.

The digital version of each stimulus was created in MATLAB (MathWorks) and was given a 5-ms 1-cosine² ramp at onset and offset. Digital-to-analog conversion was performed at a sampling rate of 100 kHz with a digital-to-analog converter (Power1401; Cambridge Electronic Design). The resulting analog signal was passed through both a programmable attenuator (PA5; Tucker-Davis Technologies) and a passive attenuator (LAT-45; Leader) before being amplified (MPA-200; Radio Shack) and output to a speaker inside a sound booth. We used two different sound booths (both manufactured by IAC) with different speakers. One booth had dimensions of 2.9 × 3.2 × 2.0 m and had a Radio Shack PA-110 speaker (10-in. woofer with piezo-horn tweeter, 0.038–27 kHz) positioned 1.5 m in front of the subject; the other booth had dimensions of 1.2 × 0.9 × 2.0 m and had a Radio Shack Optimus Pro-7AV speaker positioned 0.8 m in front of the subject. In both cases, the speaker was positioned at ear level. Stimulus level was calibrated (without the animal in position) to 63 dB sound pressure level using a sound level meter (model 2231; Brüel & Kjær) with the microphone in a position corresponding to the subjects’ interpinnae point.

Behavioral Procedure

During the period of this study, the animals were maintained on fluid regulation. For the recording sessions used here, the animals alternated between passive blocks (no task) with alertness maintained by occasional liquid reward and active blocks during which the animals were given liquid rewards for correctly discriminating AM stimuli from unmodulated stimuli as a function of modulation depth. Whereas Niwa et al. (2012a, 2012b, 2013, 2015) used depth functions and reported some results from active block data, only data from MTF collection in the passive blocks were used in this study.

Physiological Recording

Each animal was chronically implanted with a titanium head post and a CILUX recording chamber (Crist Instruments) which was located over parietal cortex for access to A1 and ML. A plastic grid with 27-gauge holes arranged over a 15 × 15 mm area in 1 mm intervals was mounted on the recording chamber. For each recording, a stainless steel transdural guide tube was inserted through the grid. A high impedance tungsten microelectrode (1–4 MΩ, FHC; 0.5–1 MΩ, Alpha-Omega) was inserted into the guide tube and lowered through parietal cortex into A1 or ML with a hydraulic microdrive (FHC). Recordings were made while the animal was head-restrained by the head post in an “acoustically transparent” custom-made primate chair made of wire.

Electrophysiological signals were passed through an amplifier (A-M Systems model 1800) and filtered (0.3–10 kHz; A-M Systems model 1800 and Krohn–Hite model 3382) before being sent to an analog-to-digital converter (Power 1401; Cambridge Electronic Design), sampled at a rate of 50 kHz and saved to hard disk. Action potentials were spike-sorted offline, first using a waveform-matching algorithm (Spike2; Cambridge Electronic Design). The results of the waveform matching were visualized in a three-dimensional principal component analysis (PCA) space. Units that formed well-isolated clusters were confirmed as single units. Clusters that had any overlap in PCA space were run through a k-means clustering algorithm (Spike2; Cambridge Electronic Design). If the centers of the k-means-identified clusters matched the high-density centers in PCA space, waveform templates were made from the k-means-identified cluster, and waveform matching was performed again. If not, the unit was discarded.

Data Analysis

All data analysis was performed using MATLAB (MathWorks). All statistical comparisons between counts or percentages were performed with a z-test for independent proportions.

Measures of phase locking.

We used phase-projected vector strength (VS_PP) as our primary measure of phase locking. Conceptually, VS_PP is a trial-based measure of synchrony which penalizes trial-based vector strength (VS) values for having a mean phase which is misaligned with the cell’s overall mean phase (Yin et al. 2011). The standard formula for vector strength is

$$VS=\frac{\sqrt{{\left({\displaystyle \sum _{i=1}^n\cos {\theta }_i}\right)}^2+{\left({\displaystyle \sum _{i=1}^n\sin {\theta }_i}\right)}^2}}{n}$$ (1)

where VS is the vector strength, n is the number of spikes, and θ_i is the phase of each spike in radians, calculated by

$${\theta }_i=2\pi \frac{\left(t_i\text{ modulo }p\right)}{p}$$ (2)

where t_i is the time of the spike in ms relative to the onset of the stimulus and p is the modulation period of the stimulus in ms (Goldberg and Brown 1969; Mardia and Jupp 2000).

Phase-projected vector strength (VS_PP) was calculated on a trial-by-trial basis as follows:

$$V{S}_{pp}=V{S}_t\mathrm{\hspace{0.17em}\hspace{0.17em}cos}({\phi }_t-{\phi }_c)$$ (3)

where VS_PP is the phase-projected vector strength per trial, VS_t is the vector strength per trial, calculated as in Eq. 1, and φ_t and φ_c are the trial-by-trial and mean phase angle in radians respectively, calculated for each stimulus condition as follows:

$$\phi =\arctan \mathrm{\hspace{0.17em}2}\frac{{\displaystyle \sum _{i=1}^n\sin {\theta }_i}}{{\displaystyle \sum _{i=1}^n\cos {\theta }_i}}$$ (4)

where n is the number of spikes per trial (for φ_t) or across all trials (for φ_c) and arctan2 is a modified version of the arctangent that determines the correct quadrant of the output based on the signs of the sine and cosine inputs (MATLAB, atan2). A cell that fired no spikes was assigned a VS_PP of zero.

We also calculated cycle-by-cycle vector strength (VS_CC) to estimate the reliability of phase locking (Yin et al. 2011). VS_CC combines measures of how precise the timing of a neuron’s firing is and how often a neuron successfully responds to an AM cycle. To calculate VS_CC, one VS_PP value is calculated for each complete AM cycle of the stimulus and then all these values are averaged together to give VS_CC for a given trial. If no spike is fired for a given cycle, a value of 0 is used for that cycle. As such, VS_CC is a measure that incorporates reliability of the phase locking on a cycle-by-cycle basis. A cell that fires at exactly the same time within a cycle, but fails to fire on half of the cycles, will have a VS_PP of 1.0, but a VS_CC of 0.5.

Determining significance of phase locking and firing rate.

To determine whether firing rate or phase locking of a cell was affected by AM, we performed a statistical analysis. Significance of phase locking was calculated for each cell at each recorded modulation frequency (MF) with a two-tailed t test (P < 0.05, corrected for 11 multiple comparisons) evaluating the null hypothesis that the distribution of VS_PP values in response to AM was not different than the distribution of VS_PP values in response to unmodulated noise. Rate significance was calculated in the same fashion, but using the distributions of firing rates. A cell was considered to “detect” AM if there was a significant difference for at least one MF. If a neuron failed this test, it was classified as nonresponsive (NR). Each neuron was evaluated separately for AM responsiveness based on phase locking or firing rate. For any measure for which the neuron was responsive, a curve fit (see Eqs. 5–7) was performed on the modulation transfer function (MTF). If the neuron was NR for a measure, the MTF was not fit for that measure. Analogous tests to those performed against unmodulated noise were also performed against a 200-ms period of spontaneous activity preceding each stimulus to determine whether the distributions of VS_PP values and firing rates obtained during the AM stimulus were different from those obtained during the absence of any stimulus.

Fitting temporal modulation transfer functions.

For neurons whose VS_PP-based phase locking was not classified as NR, curve fits were used to place the temporal modulation transfer function (tMTF) into one of four categories: low pass (LP), bandpass (BP), high pass (HP), or No Fit. To achieve this classification, responsive tMTFs were separately fitted (MATLAB “fmincon” function) with three functions; a (logistic) sigmoid (Eq. 5), a Gaussian (Eq. 6), and a log-transformed Gaussian function (Eq. 7). All three functions have four free parameters determining the y-offset (a), the height (b), the x-center (µ), and the slope (s). Because they had the same number of free parameters, error minimization (see section Determining best fit function and classifying tMTFs) could be used to determine which function (if any) was the best fit.

$$y=a+\frac{b}{1+e^{-(x-\mu )*s}}$$ (5)

$$y=a+b{e}^{-\frac{{(x-\mu )}^2}{2s^2}}$$ (6)

$$y=a+b{e}^{-\frac{{(\ln (x)-\ln (\mu ))}^2}{2s^2}}$$ (7)

The constraints on the parameters were set as follows:

For all fits: 0.9 × (min of data) ≤ a ≤ 1.1 × (min of data); 0 ≤ b ≤ 1.03 × (max-min of data); 0 ≤ µ ≤ 2,000 Hz. The constraint on the height parameter prevented excessively high amplitude extrapolations.

Logistic: −1 ≤ s ≤ 1. The slope factor restricted the 90% width of the logistic to be ∼6 Hz or greater. A negative slope parameter allows the logistic to fit a LP MTF, whereas a positive slope parameter allows it to fit a HP MTF.

Gaussian: 3 ≤ s ≤ 213. The slope factor restricted the full width at half height (FWHH) of the Gaussian fit to lie between ∼7 and 500 Hz.

Log-transformed Gaussian: 0.05 ≤ s ≤ 2.36. The slope factor restricted the FWHH of the log-transformed Gaussian fit to a minimum of ∼1/6 of an octave and a maximum of ∼8 octaves.

Determining best fit function and classifying tMTFs.

A minimization was used to determine which of the three functions provided the best fit to the tMTF. The minimization in the tMTF fit procedures was weighted by the synchronized spike count (SSC, = VS × spike count) at each MF to emphasize fitting to the more reliable points in the tMTF. The coefficient of determination (CoD) was calculated for each fit as follows

$$CoD=1-\frac{{\displaystyle \sum _n{(O-F)}^2}}{{\displaystyle \sum _n{(O-mean(O))}^2}}$$ (8)

where O is the set of n observed points in the MTF and F is the corresponding set of n points from the resulting fitted function. The CoD is bounded by 1 on the high end, which indicates that all fitted points match the observed points exactly, but is unbounded on the low end. A CoD of zero indicates that the fit is equally good to a horizontal line plotted through the mean of the observed values. tMTFs for which none of the three fits (logistic, Gaussian, log-transformed Gaussian) had a CoD greater than 0.5 were categorized as No Fit (note that this is different from NR, because there were significant spike rate responses or phase locking to AM). tMTFs with at least one CoD greater than 0.5 which were best fit (i.e., had the highest CoD) by a sigmoid function were categorized as LP or HP based on the direction of the sigmoid’s inflection (in our data set we did not observe any HP tMTFs). tMTFs that were best fit by one of the Gaussian functions were categorized as BP, unless the VS_PP value at the lowest MF (or highest MF) was at least 90% of the highest VS_PP value found in that neuron, in which case the tMTF was categorized as LP (or HP) for lack of sufficient evidence of a downturn.

Classifying rate-based modulation transfer functions.

The same categorization that was done on tMTFs was initially performed on rate-based modulation transfer functions (rMTFs). However, we observed that a large number of our rMTFs did not fit neatly into the categories defined for tMTFs above. Specifically, many had multiple peaks or dips, so we modified the fitting procedure to objectively classify these rMTFs.

Therefore, all rMTFs were also fit in a separate multistep procedure with a two-curve fit. The first step of the two-curve fit was to fit the rMTF with the best of a Gaussian or log-transformed Gaussian, with the minimization weighted by the synchronized spike count (SSC), which emphasizes fitting synchronized and/or higher spike count regions of the MTF. This first fit was constrained to have a floor at the spontaneous firing rate of the cell. The result of this fit was subtracted from the rMTF to obtain a residual MTF, and the residual MTF was subsequently fit with the best of a Gaussian or log-transformed Gaussian, with the minimization weighted by the quantity max(SSC) − SSC_n at each MF n, so the weighting is higher for MFs with less synchronization [Max(SSC) is the point on the MTF with the maximum synchronized spike count]. This second fit was additionally constrained to have a floor of zero. These two fits were added together to obtain the two-curve fit. SSC weighting of the fits was done only on the two-curve fits, and not on any corresponding single-curve rate fits. We implemented the weighting procedure on the two-curve fits because we found that unweighted two-curve fits frequently resulted in two largely overlapping curves that did not capture the structure of the rMTF at high modulation frequencies. SSC was used to weight the fits due to the observation that for rMTFs that seemed to be good two-curve fit candidates, the low-MF region was usually synchronized, and the high-MF region was usually not synchronized. SSC weighting thus allowed us to encourage segregation of the curves in the two-curve fit based on the response properties of the individual cell rather than resorting to an arbitrary MF cutoff. The two-curve fit aided identification of a commonly observed rMTF shape that we refer to as peak/trough (P/T, Fig. 1) rMTFs.

As with tMTFs, rMTFs without any responses significantly different from the response to unmodulated noise at any modulation frequency were categorized as NR, and rMTFs for which none of the four fits (logistic, Gaussian, log-transformed Gaussian, and two-curve) had a CoD greater than 0.5 were categorized as No Fit. rMTFs that were best fit (i.e., had the highest CoD) by a function other than the two-curve fit were categorized using the same method as tMTFs; only rMTFs that were best fit by the two-curve fit were considered potential P/T rMTFs. Although P/T rMTFs typically had a peak at low MFs and a trough at middle MFs (Fig. 1), in practice, we categorized P/T rMTFs based on our two-curve fit, where both Gaussians were positive going. Potential P/T rMTFs were subjected to three tests to discourage “overfitting” with our two-curve fit when a one-curve fit would have been sufficient. First, we required that the two-curve fit clearly be the best fit. Our criterion here was that the CoD of the two-curve fit must be at least 0.02 greater than the CoD of the best one-curve fit. Second, we required that the two-curve fit consist of largely nonoverlapping curves. Here, we defined the half height as the cutoff for each curve. We required that these cutoffs not overlap in MF, and additionally that at least one collected MF data point fall between the two cutoffs (i.e., high cutoff of curve 1 < MF of a collected data point < low cutoff of curve 2). Third, we required that neither curve could be more than four times the height of the other, which prevents solutions that overfit a noisy tail of a one-curve solution. MTFs that met all three of these criteria were considered P/T, otherwise they were classified based on their best one-curve fit. Although in the results we describe the firing rate properties of P/T cells relative to the response to the unmodulated stimulus, these properties were not used as criteria for classifying P/T cells; the curve-fitting procedure in Eqs. 5–7 was the only method used for classifying P/T cells.

Categorizing whether neurons increase or decrease activity in response to modulation.

We defined increasing and decreasing cells somewhat differently than in Niwa et al. (2013). Although the terms increasing and decreasing were originally based on the rate depth function shapes (Niwa et al. 2012b, 2013, 2015), here they were applied to compare the response to 100% depth and the response to the unmodulated stimulus. For nearly every recording from the previous data (Niwa et al. 2012b, 2013, 2015), the rate-depth trend corresponded to the difference between 0 and 100% modulation, so the terms increasing and decreasing still reflect the presumed characteristics of the rate-depth functions. For each MF in the MTF, we compared the trial-by-trial spike count or VS_PP for the 100% depth AM-noise against the trial-by-trial spike count or VS_PP for the unmodulated noise to determine if the response was greater than or less than the response to unmodulated noise (one-sided t test for each comparison, corrected for 11 MFs). Cells with a response for at least one MF significantly greater than the response to unmodulated noise and a response for at least one MF significantly less than the response to unmodulated noise were classified as “mixed,” otherwise a cell was classified as “increasing” if the response for at least one MF was significantly greater than the response to unmodulated noise or “decreasing” if the response for at least one MF was significantly less than the response to unmodulated noise. A recent paper (Kim et al. 2015) uses the terminology “band-enhanced” and “band-suppressed” to describe MTFs and the relation to unmodulated noise in the inferior colliculus. For this paper, we prefer to use two different terminologies: one to describe the comparison with unmodulated noise (increasing/decreasing), and one to describe the shape of the MTF (BP, LP, HP, and P/T). This is consistent with the terminology used in our previous papers comparing A1 and ML (Niwa et al. 2013, 2015).

Cutoff frequencies and bandwidths.

For logistic fits, the high-frequency cutoff was calculated as the half-height point of the curve. For both Gaussian fits, low-frequency (f1) and high-frequency (f2) cutoffs were selected as the two half-height points on the curve, and the bandwidth was calculated as the full width at half height (FWHH) and expressed in octaves [log2(f2/f1)]. Low-frequency cutoff and bandwidth values were rejected for any Gaussian fit where the low-frequency cutoff was less than zero. In the two-curve fits, cutoffs and bandwidths were calculated for each curve individually.

To allow comparison with a different measurement of bandwidth, we include in the text the Q factor [best modulation frequency/(f2-f1)]. When bandwidth is calculated from a Gaussian fit that is linear in frequency, as here, the Q factor can be calculated from octaves (N) using the equation:

$$Q=\frac{\sqrt{2^N}}{2^N-1}$$ (9)

RESULTS

We recorded spiking activity from 250 single neurons in the primary auditory cortex (A1) of three macaques (monkey V, 21 units; monkey W, 120 units; and monkey X, 109 units) and from 138 single neurons in the middle lateral auditory cortex (ML) of two macaques (monkey W, 68 units; monkey X, 70 units) while the animals were awake and presented with unmodulated noise and 100% amplitude-modulated (AM) noise.

Modulation Transfer Functions

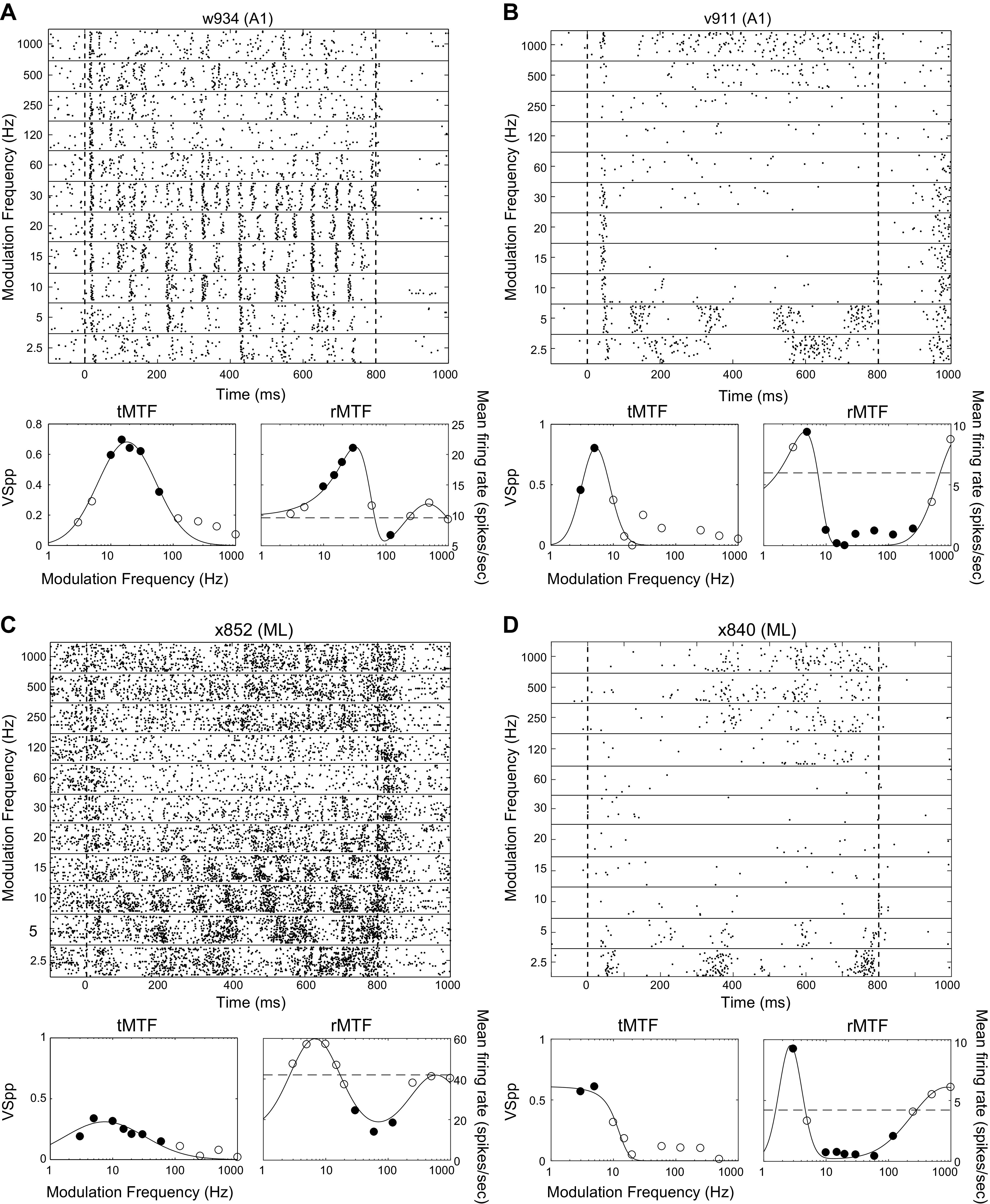
Responses to AM for four ML neurons exemplify their heterogeneity (Fig. 2). Figure 2A depicts a neuron that phase locks to the AM stimulus with a high firing rate up to MFs of 30 Hz and then continues to phase lock well with a lower cycle-by-cycle reliability up to 250 Hz. Note that for 60–250 Hz the neuron significantly phase locks (filled circles on temporal modulation transfer function, tMTF), although the firing rate does not differ from the unmodulated noise response (unmodulated noise response is dashed horizontal line on rate modulation transfer function, rMTF). Figure 2B depicts another phase-locking cell that typically fires only one spike per AM cycle and phase locks up to 250 Hz. Figure 2, C and D, shows two neurons that only produce nonsynchronized responses to AM noise, one with a narrow rate-based modulation transfer function (rMTF) and the other with a much broader rMTF. The AM responses are greater than the response to the unmodulated noise from 2.5 to 30 Hz for the neuron in Fig. 2C, and from 2.5 to 120 Hz for the neuron in Fig. 2D.

Fig. 2.

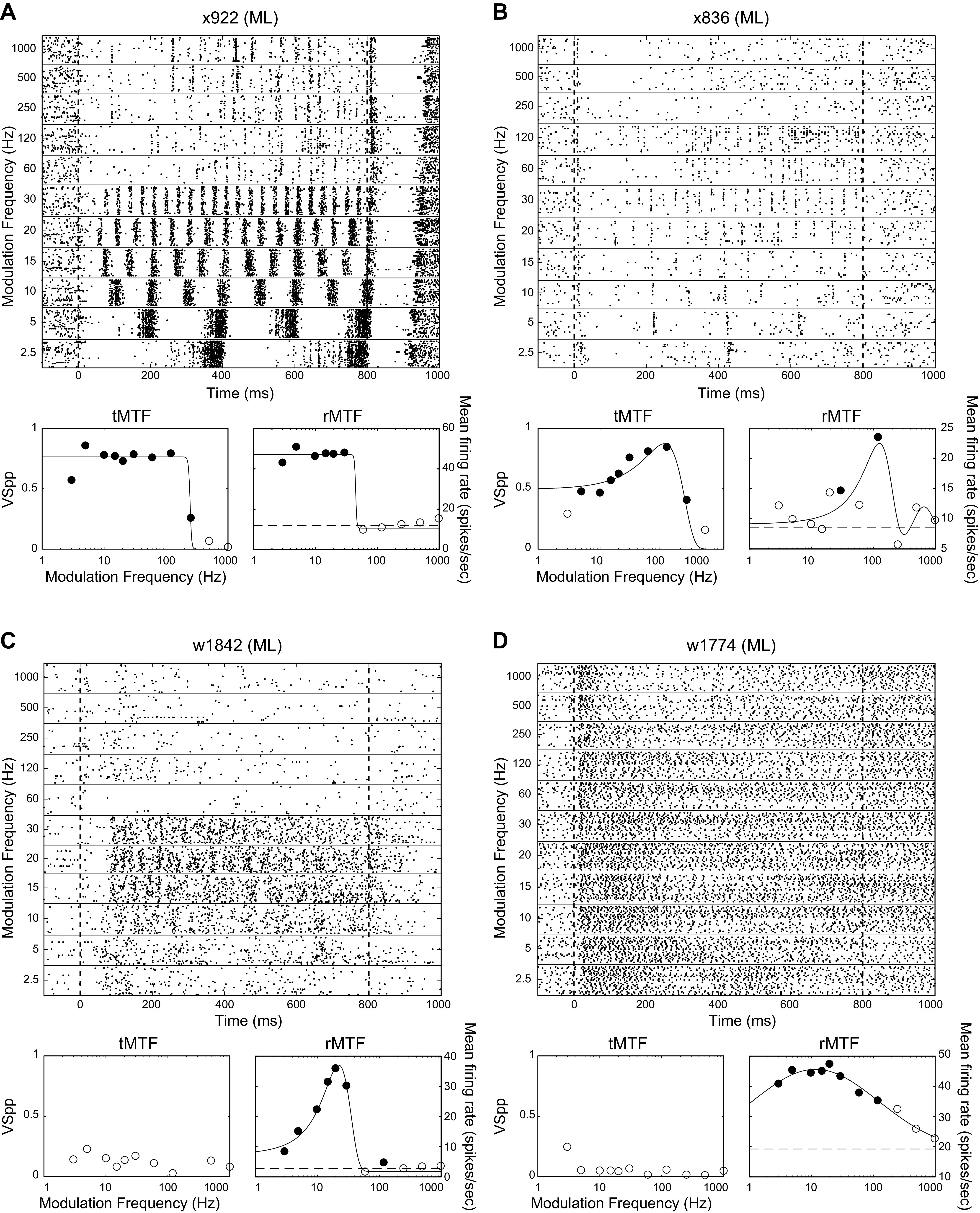
Example responses of ML neurons to AM noise. The responses to AM noise, and the modulation transfer functions are shown for four different example neurons (A–D). For each neuron, we show the responses to the 11 tested modulation frequencies with raster plots on the top. Below each raster plot are temporal (left, tMTF) and rate (right, rMTF) modulation transfer functions (MTFs) for the same neurons. Filled dots on the tMTFs indicate modulation frequencies at which there is significant phase locking (t test, P < 0.05 corrected for 11 comparisons), filled dots on the rMTFs indicate modulation frequencies at which the firing rate differed from the firing rate to the unmodulated stimulus (t test, P < 0.05 corrected for 11 comparisons). Dashed line on rMTFs indicates the firing rate to the unmodulated noise stimulus. For all four examples, the only points on the rMTF with significant response differences from the response to unmodulated noise (filled circles) were above the unmodulated noise response (dashed line), so they were all classified as increasing for Table 2. Best frequencies of cells depicted, by panel: A, 6 kHz; B, 11 kHz; C, 1.7 kHz; and D, 31 kHz.

We attempted to categorize all of our MTFs by shape into various classes, including low-pass (LP), bandpass (BP) and high-pass (HP) classes, using an automated fitting procedure (see methods). Cells that had a significant response for at least one modulation frequency (MF) but that did not achieve a significant fit for any MTF class were categorized as “no fit.” Unlike temporal-based MTFs (tMTFs), rMTFs (including the one in Fig. 2B) were often best fit by a two-curve fit and had a low-MF peak and a middle-MF trough. We called these peak/trough (P/T) MTFs, and they are described in more depth later in this paper.

There were some differences in temporal MTFs and response properties between ML and A1 neuronal populations (Table 1). The proportion of cells that phase locked to AM noise was lower in ML than in A1 (66/138, 48% in ML; 172/250, 69% in A1; z-test for independent proportions, P = 5 × 10⁻⁵). Among cells that phase locked to AM, HP tMTFs were not found in A1 or ML and BP was the most common tMTF class in both areas. However, there was a much higher percentage of neurons with LP tMTFs in ML than in A1 (ML = 27%, A1 = 7%; z-test for independent proportions, P = 2 × 10⁻⁵) and concomitantly more BP tMTFs in A1 than in ML (A1 = 79%, ML = 50%; z-test for independent proportions, P = 1 × 10⁻⁵). All of these observations support a reduction in phase-locking ability in ML consistent with a temporal-to-rate transformation from A1 to ML.

Table 1.

MTF-shape classification

	Temporal		Rate
	A1	ML	A1		ML
			Total	% that Synch	Total	% that Synch
Peak/Trough (P/T)	Not Applicable	Not Applicable	73/178 41.0%	Low: 58/73 79.5% High: 2/73 2.7%	34/88 38.6%	Low: 29/34 85.3% High: 2/34 5.9%
Bandpass	136/172 79.1%	33/66 50.0%	71/178 39.9%	43/71 60.6%	21/88 23.9%	10/21 47.6%
Low-pass	12/172 7.0%	18/66 27.3%	3/178 1.7%	1/3 33.3%	5/88 5.7%	4/5 80.0%
High-pass	0/172 0%	0/66 0%	8/178 4.5%	0/8 0%	5/88 5.7%	1/5 20.0%
No fit	24/172 14.0%	15/66 22.7%	23/178 12.9%	1/23 4.3%	23/88 26.1%	1/23 4.3%
Not responsive	78/250 31.2%	72/138 52.2%	72/250 28.8%	0/72 0%	50/138 36.2%	0/50 0%

Values on the left are in cell count, values on the right are in percentage. Denominator for “not responsive” cells is total cells recorded. Denominator for all others is total responsive cells (or for “synch” columns, total responsive cells within the given MTF class). “Synch” columns indicate a “synchronized rate” response—neurons that have at least one modulation frequency with both significant phase locking and a firing rate that was at or above the half height of the fitted Gaussian/sigmoid function for the MTF. Those neurons that do not exhibit changes in firing rate do not have synchronized rate responses by this definition, even if they exhibit some significant phase locking. A1, primary auditory cortex; ML, middle lateral auditory cortex; MTF, modulation transfer function.

There were also some differences in rate MTF and response properties between ML and A1 neuronal populations (Table 1). The proportion of cells that changed their firing rate to AM was not significantly different between the two areas (178/250, 71% in A1; 88/138, 64% in ML; z-test for independent proportions, P = 0.13). For rMTF shape classification, there were only a few salient differences between the A1 and ML populations. For one, ML showed an increase in the number of responsive cells that were not well fit (ML = 26%, A1 = 13%; z-test for independent proportions, P = 7 × 10⁻³), which could reflect an increase in the complexity of MTFs in higher levels of the auditory system. There were also fewer BP rMTFs in ML than in A1 (ML = 48%, A1 = 61%; z-test for independent proportions, P = 0.01), which seems to roughly correspond to the increase in no-fit rMTFs. We performed a separate analysis of rate-responsive cells that also synchronized to AM. Here, rate-responsive cells were considered to have a “synchronized rate” response if they also exhibited significant phase locking for at least one MF within the cutoffs of the rMTF fit (defined as the MFs corresponding to the half-max of the rMTF fit). Between A1 and ML, there was no significant difference in the proportion of cells having synchronized rate responses for any rMTF class. BP, LP, and P/T rMTFs were the only classes that commonly had synchronized rate responses.

Response Magnitudes Relative to the Unmodulated Noise

One way to evaluate the relationship of the MTF to the unmodulated noise response is to look at z-scored responses from key points on the MTF. In this section, we will describe this relationship for BP, LP, and HP MTFs, and later in the manuscript, we will perform a more detailed description of P/T MTFs.

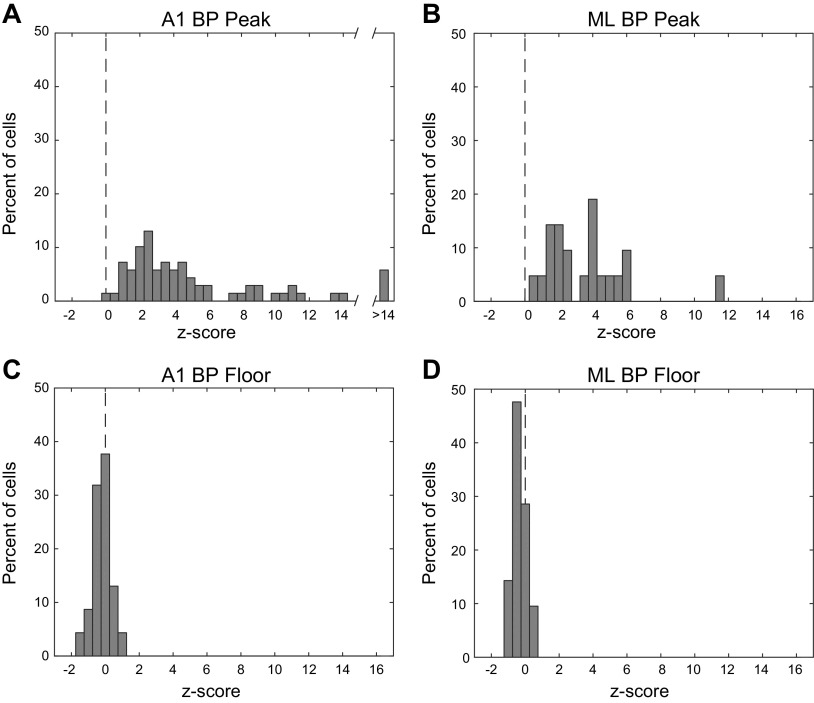
In general, for BP neurons, the response to the best modulation frequency (BMF) was greater than the response to unmodulated noise. The mean z-scored change in firing rate at BMF (difference between BMF and unmodulated noise responses divided by the standard deviation) in A1 was 6.4 and in ML was 3.6 (Fig. 3). These means were not significantly different (two-tailed t test, P = 0.23). There was also no difference between A1 and ML in the mean z-scored change in firing rate at the floor of the function—the minimum value found in the rMTF (A1 z-score = −0.22; ML z-score = −0.32; two-tailed t test, P = 0.46). However, the mean z-scored change in firing rate at the floor was significantly different from zero in both A1 and ML (two-tailed t test; A1, P = 0.001; ML, P = 0.001) though the magnitude of all floor z-scores was <2 in A1 and <1 in ML (Fig. 3, C and D).

Fig. 3.

Firing rate z-scored with respect to the response to unmodulated noise at peak and floor of bandpass cells. Top row, peak of rMTF (A and B). Bottom row, floor (minimum value) of rMTF (C and D). Left column, A1. Right column, ML. Dashed vertical line denotes a z-score of zero. Note that the x-axis in A is broken due to highest values. A1, primary auditory cortex; ML, middle lateral auditory cortex.

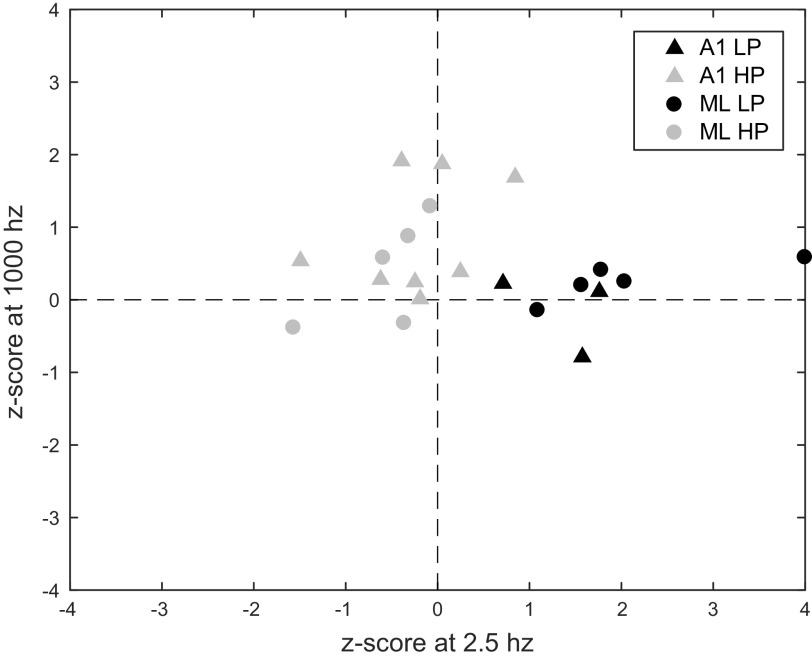
We did not find enough neurons with LP and HP MTFs to make histograms, but these neurons showed interesting potential differences in the relationship of their MTFs to the unmodulated noise response. HP neurons tended to have high-frequency responses above the unmodulated noise response and low-frequency responses below the unmodulated noise response. LP neurons tended to have low-frequency responses above the unmodulated noise response but high-frequency responses that were similar to the unmodulated noise response (Fig. 4).

Fig. 4.

Firing rate of individual cells z-scored with respect to the response to unmodulated noise at 2.5 Hz and 1,000 Hz for LP and HP cells. Triangles indicate A1, circles indicate ML. Black symbols indicate LP cells, gray symbols indicate HP cells. One value for ML LP truncated at 4.0. A1, primary auditory cortex; HP, high-pass; LP, low-pass; ML, middle lateral auditory cortex.

The most responsive parts of LP and HP MTFs (low frequency for LP MTFs and high frequency for HP MTFs) tended to have firing rates above that to the unmodulated noise. The combined mean z-score for the highest tested MF in HP cells was 0.69 with a standard error of the mean (SE) of 0.22. The mean in ML for high-frequency responses of HP MTFs of 0.41 was lower than the corresponding mean in A1 of 0.87, but this was not significant (two-tailed t test, P = 0.32, ns). Neurons with LP MTFs had significantly higher responses relative to the unmodulated noise at the lowest tested MF than neurons with HP MTFs (elongation of black symbols along the x-axis of Fig. 4 is larger than elongation along y-axis of gray symbols). Across both cortical areas, for LP neurons, the mean z-scored firing rate comparing the response to the lowest MF to the unmodulated noise was 2.01 with an SE of 0.52, which was significantly higher than the HP responses (gray symbols) at the highest MFs (y-axis) mean of 0.69 with an SE of 0.22 (two-tailed t test, P = 0.015). The mean in ML for low-frequency responses of LP MTFs (mean value of black symbols along x-axis) was 2.40, and the corresponding mean in A1 was 1.35 (two-tailed t test, P = 0.37, ns). Note that the mean responses relative to unmodulated at the preferred modulation frequencies for both LP and HP MTFs appeared to be less than the mean z-score at the BMF for BP MTFs but, due to small sample sizes, LP/HP neurons did not reach statistical significance unless LP and HP neurons were pooled (LP mean = 2.01, HP mean = 0.69, LP + HP mean = 1.19, BP mean = 5.73; two-tailed t test: LP vs. BP, P = 0.27 ns; HP vs. BP, P = 0.056 ns; LP + HP vs. BP, P = 0.029).

For HP neurons, there was a tendency to respond at the lowest MF at a lower firing rate than the response to the unmodulated noise. This is seen in Fig. 4 as HP neurons (gray symbols) having negative z-scores at 2.5 Hz. The combined A1/ML mean was −0.36, with an SE of 0.18. A1 and ML were similar (A1 mean = −0.22; ML mean = −0.58; two-tailed t-test, P = 0.35, ns).

In contrast, for LP neurons, the responses to 1,000 Hz AM were similar to the unmodulated noise response. This is seen in Fig. 4 as LP neurons (black symbols) having z-scores centered around the horizontal axis. The combined A1/ML mean was 0.11, with an SE of 0.15. The small sample size of LP neurons in A1 makes comparing the two areas difficult (A1 mean = −0.15, ML mean = 0.26).

Together, these results suggest that the responses relative to unmodulated were similar in A1 and ML, and that BP neurons responded more distinctly above the unmodulated response than neurons with HP or LP MTFs.

Best Modulation Frequencies

The distribution of best modulation frequencies (BMFs) for both rate (rBMF, spike count) and temporal (tBMF, VS_PP) measures can be greatly influenced by the range of modulation frequencies tested (Fig. 5, top and middle). The top panel depicts the A1 BMF histogram in the present data looking only at the frequencies that were tested in a previous report of A1 BMFs (Yin et al. 2011). The distribution of tBMFs was similar to that found previously. The distribution of rBMFs was different; in the current sample, about half of the cells would have had an rBMF of 5 Hz if based on only the previously tested frequencies, whereas in the previous report about one quarter of the cells had rBMFs at the lowest tested frequency. Much of this disparity was likely due to testing at an extended range of MFs. Cells with rBMFs outside of the range of MFs previously tested made up ∼40% of our sample, and many of these might not have registered sufficient activity in an AM search using the previous range of MFs to be further analyzed in the earlier experiment.

Fig. 5.

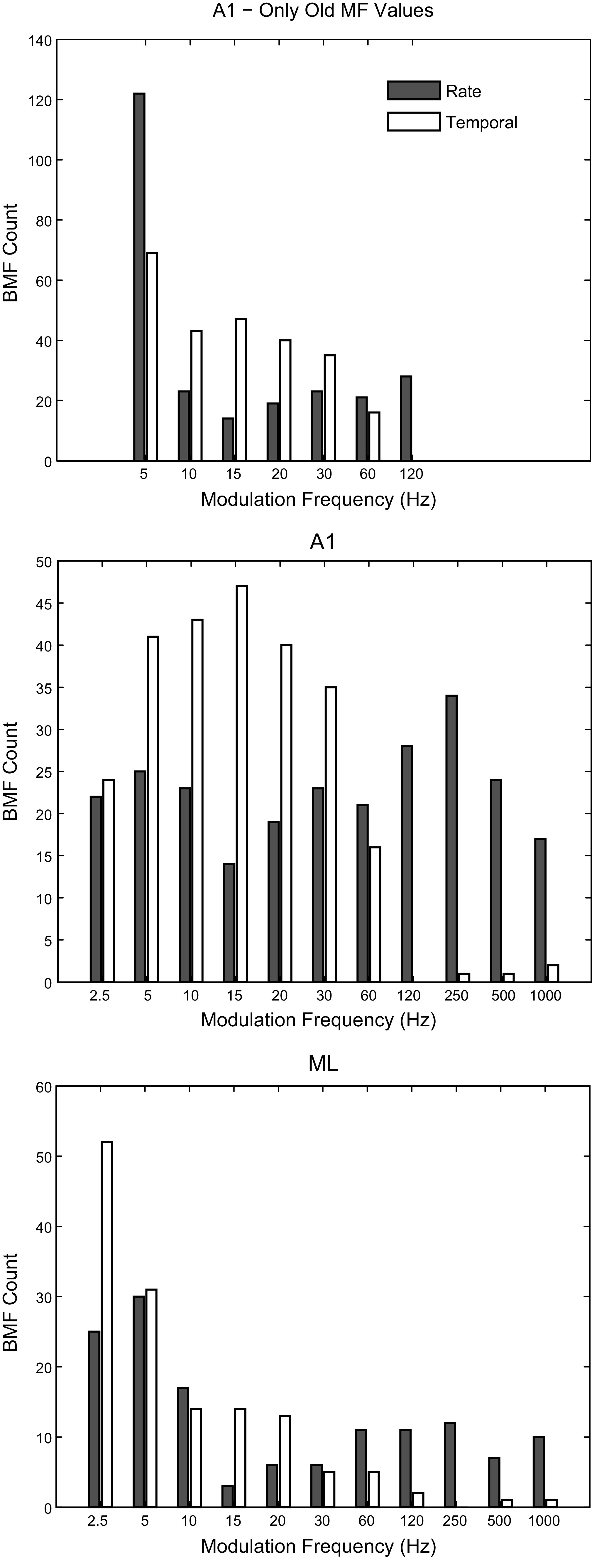
Best modulation frequencies. Top: best modulation frequencies (BMFs) for rate (shaded) and temporal (open) measures in A1 calculated using only the modulation frequencies tested in a previous report (Yin et al. 2011). Middle: BMFs for A1 calculated using all frequencies tested in this study. Bottom: BMFs for ML calculated using all frequencies tested in this study. A1, primary auditory cortex; ML, middle lateral auditory cortex.

Because of the wider range of modulation frequencies used for ML in this study, it was important to compare these ML data to A1 data collected with the same range of modulation frequencies (i.e., the comparison with Yin et al. 2011 would not be a fair comparison). When looking at the fuller range of MFs (Fig. 5, middle), rBMF distributions in A1 were not significantly different from a flat distribution across modulation frequency (Kolmogorov–Smirnov test with counts adjusted for uneven sampling in log space, P = 0.07, ns), despite a small dip around 15 Hz (which may be expected as our sampling density was increased on the log scale between 10 and 30 Hz) and a small peak around 250 Hz. tBMFs were clustered between 2.5 and 60 Hz, as strong phase locking to higher modulation frequencies is rare in A1. In ML (Fig. 5, bottom), both rBMFs and tBMFs showed a shift toward lower frequencies relative to A1, with the vast majority of tBMFs at 20 Hz or below.

Bandwidths

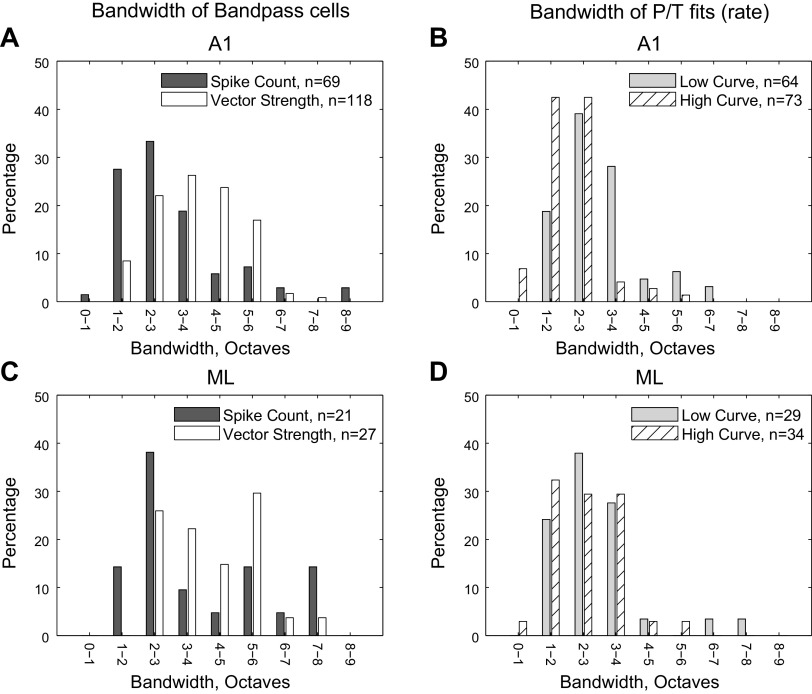
For all bandpass (BP) fits, we calculated the associated bandwidths (BWs), defined as the full width of the fit at half height. Some of our full widths extended below the lowest tested MF (2.5 Hz), and because we measured bandwidth in octaves, this could occasionally result in very high-octave bandwidths where a large portion of the width lay outside of the tested MFs. To avoid this, we assigned a low-frequency cutoff floor at 1.25 Hz and a high-frequency cutoff ceiling of 2,000 Hz (both one octave from the most extreme tested MFs) to ensure that the bandwidth values we calculated did not include excessive contributions from fits to untested MFs.

In general, we found a wide range of bandwidths. For A1 MTFs that were classified as BP (Fig. 6A), the distribution of BWs was skewed toward lower widths [centered around 1–4 octaves (Q factor 1.4–0.27) for spike count, mean of 3.0 octaves (Q factor 0.40)] and wider [centered around 1–6 octaves (Q factor 1.4–0.13), mean of 3.7 octaves (Q factor 0.30)] for vector strength. Vector strength bandwidths were significantly wider than spike count (two-tailed t test, P = 6 ×10⁻⁴).

Fig. 6.

Distributions of bandwidths. Bandwidths are calculated as the octave width of the fitted curve at half height (see methods), constrained by upper and lower limits that are one octave outside of the range of tested modulation frequencies (MF). Top plots (A and B) are A1 and bottom plots (C and D) are ML. Left: bandwidths of bandpass cells for both rate and temporal measures. Right: rate bandwidths for the lower-MF peak (gray) and the higher-MF peak (hatched) for peak/trough cells. A1, primary auditory cortex; ML, middle lateral auditory cortex.

ML BP MTF bandwidths (Fig. 6C) were similar to those in A1. The mean spike count bandwidth was 3.8 octaves (Q factor 0.29), and the mean vector strength bandwidth was 4.1 octaves (Q factor 0.26) and did not differ significantly in ML (two-tailed t test, P = 0.53). Unlike A1, there were several cells with extremely large bandwidths in ML. There was no significant difference between the bandwidth distributions in ML and A1 for either spike count (two-tailed t test, P = 0.06) or vector strength (two-tailed t test, P = 0.13) though the trend in both cases was for wider fits in ML.

The bandwidth distribution of P/T fits (Fig. 6, B and D) will be discussed in a later section devoted to this class (Figs. 10–12) but is included in Fig. 6 to allow for direct comparison between the bandwidths of those fits and BP fits.

Fig. 10.

Example responses from peak/trough (P/T) cells. Plots as in Fig. 2. All examples are best fit by the P/T fit (see methods). Filled dots on the tMTFs indicate modulation frequencies at which there is significant phase locking (t test, P < 0.05 corrected for 11 comparisons). Filled dots on the rMTFs indicate modulation frequencies at which the firing rate differed from the firing rate to the unmodulated stimulus (t test, P < 0.05 corrected for 11 comparisons). Dashed line on rMTFs indicates the firing rate to the unmodulated stimulus. Neurons with significant firing rate differences both greater than the response to unmodulated noise at some MFs and less than the response to unmodulated noise at other MFs (A, B, and D) were classified as “mixed” in Table 2. The neuron in C only had significant firing rate differences that were less than the unmodulated noise response and was classified as “decreasing” in Table 2. BFs of cells depicted, by panel: A, 5.5 kHz; B, 11 kHz; C, 2.4 kHz; and D, 27 kHz. MF, modulation frequency; rMTF, rate-based modulation transfer function; tMTF, temporal-based modulation transfer function.

Fig. 12.

Firing rate z-scored with respect to the response to unmodulated noise at low-frequency peak, mid-frequency trough, and high MF. Top row (A–C) is A1, bottom row (D–F) is ML. Left column, firing rate for peak/trough (P/T) cells at low-MF peak, z-scored with respect to the response to unmodulated noise. Middle column, same as left column, for P/T cell firing rate at middle-MF trough. Right column, same as left column, for P/T cell firing rate at 1,000 Hz. A1, primary auditory cortex; MF, modulation frequency; ML, middle lateral auditory cortex.

Mean Modulation Transfer Functions

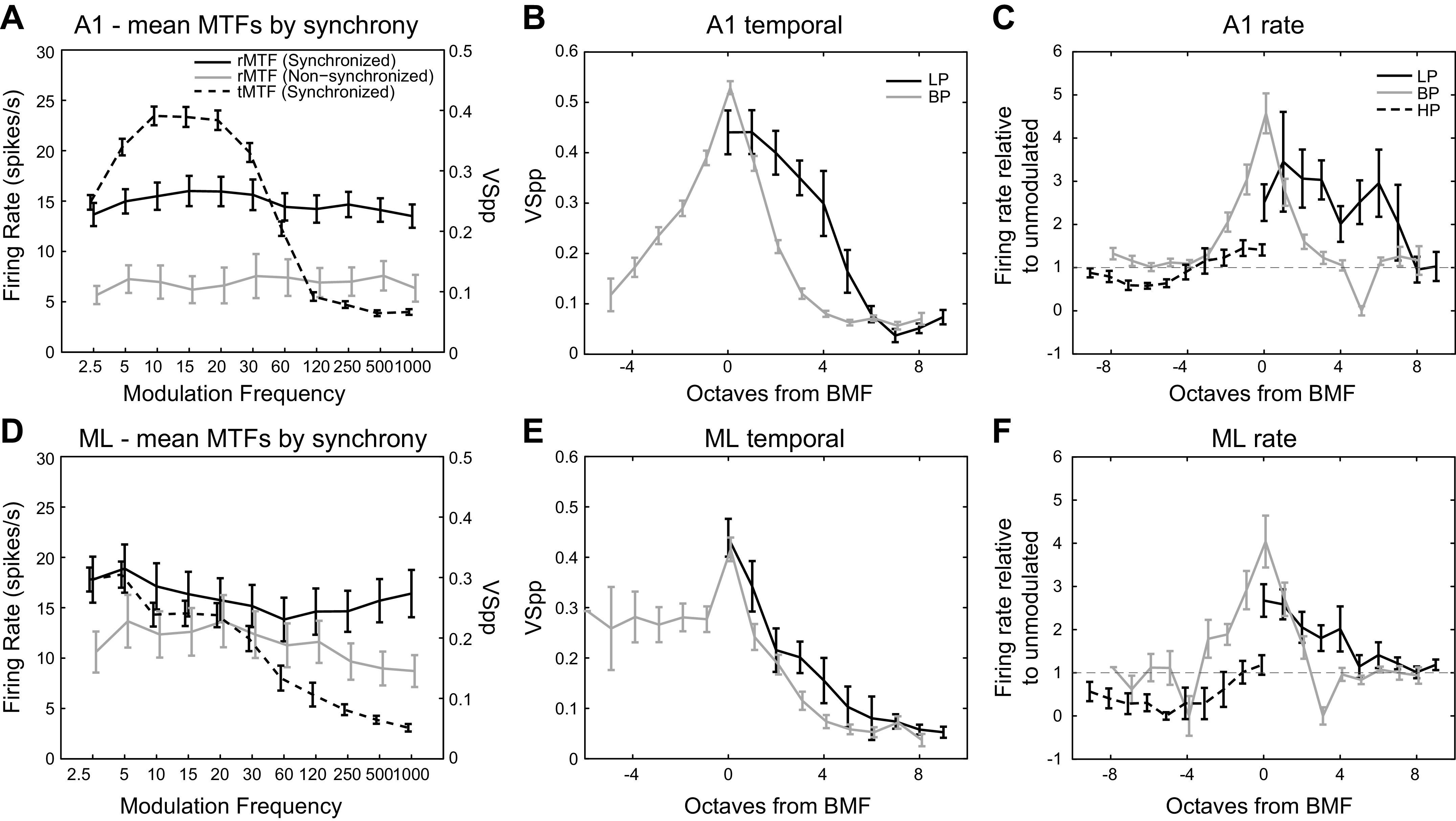
To estimate the overall representation of different modulation frequencies, and any roll-off of the population of neurons at higher frequencies, we calculated mean modulation transfer functions regardless of MTF class, broken down by synchronized and nonsynchronized cells (Fig. 7, A and D). Psychophysically, modulation frequency sensitivity for the macaque monkey rolls off sharply between 250 and 1,000 Hz (O’Connor et al. 2000, 2011). In A1, the mean rMTF of nonsynchronized and synchronized responses showed little MF dependence below 1,000 Hz (Fig. 7A, solid lines). In ML, it was difficult to determine whether the mean nonsynchronized and synchronized rMTFs were flat (Fig. 7D, solid lines), but combining nonsynchronized and synchronized neurons flattens the curve even more.

Fig. 7.

Mean modulation transfer functions (MTFs). Top row (A–C) is A1, bottom row (D–F) is ML. Mean MTFs are calculated by taking the mean response (firing rate or vector strength) or the geometric mean response (firing rate relative to unmodulated, right column) of all cells at each MF. Error bars indicate standard error of the mean (right column, standard error of the geometric mean). x-axis values are slightly offset to increase visibility of error bars. Only responsive cells are included. For left column, rate MTFs (rMTFs, solid lines) are referred to the left y-axis and broken down into synchronized and nonsynchronized cells. For left column, temporal MTFs (tMTFs, dotted lines) are referred to the right y-axis. Middle column, tMTFs for low-pass (LP) and bandpass (BP) classes; high-pass (HP) tMTFs were not observed in our data set. x-axis is in octaves from BMF (BP) or octaves from 2.5 Hz (LP). Right column, rMTFs for LP, BP, and HP classes. Firing rate relative to unmodulated is the firing rate to 100% AM divided by the firing rate to unmodulated noise. x-axis is in octaves from BMF (BP) or from 2.5 Hz (LP) or 1,000 Hz (HP). AM, amplitude-modulated.

The mean tMTFs rolled off more steeply at high modulation frequencies than the mean rMTFs. A1 showed a sharp roll-off beginning between 30 and 60 Hz (Fig. 7A, dashed line), and the mean ML rMTF showed a more gradual roll-off starting at 5 Hz (Fig. 7D, dashed line).

We also created mean MTFs broken down by LP, BP, and HP classes (Fig. 7, B, C, E, and F). We referred these mean MTFs to either the BMF of the cell (for the BP class) or to the lowest (for the LP class, 2.5 Hz) or highest (for the HP class, 1,000 Hz) recorded MF.

The middle column of Fig. 7 depicts mean tMTFs for A1 (Fig. 7B) and ML (Fig. 7E) for LP and BP neurons. In our sample, we did not observe any HP tMTFs in either cortical area. Figure 7, B and E, reinforces that phase locking is generally lower in ML than in A1.

For LP neurons, at the lowest tested modulation frequency (2.5 Hz, corresponding to 0 octaves from BMF in Fig. 7), phase locking was similar between A1 and ML (A1 LP mean VS_PP @ 2.5 Hz = 0.440; ML LP mean VS_PP @ 2.5 Hz = 0.439; not significant by two-tailed t test). However, for the LP population MTFs, the roll-off at higher MFs is steeper in ML than in A1 leading to lower vector strength values (compare Fig. 7, B and E).

For BP neurons at the BMF, A1 phase locked better than ML (A1, mean VS_PP = 0.545; ML, mean VS_PP = 0.444; two-tailed t test, P = 0.002). The ML curve then remains below the A1 curve at higher modulation frequencies (compare Fig. 7, B and E). However, there appears to be less drop-off in phase locking for BP cells at MFs below the BMF in ML than there is in A1 (compare left sides of Fig. 7, B and E).

Comparing LP to BP population tMTFs, A1 shows an interesting difference. LP MTFs roll off more gradually at higher MFs than in BP MTFs (Fig. 7B, right). In fact, the shape of the high-frequency roll-off part of the population MTFs looks quite different between LP and BP MTFs, with the LP MTF roll-off having an inflection point at ∼4 octaves from the BMF. In ML, the shape of the high frequency roll-off of the population MTF was similar for LP and BP population MTFs (Fig. 7E, right).

The right column of Fig. 7 depicts the geometric means of the rMTFs for A1 (Fig. 7C) and ML (Fig. 7F) normalized by their respective firing rates to the unmodulated stimulus (AM response divided by response to the unmodulated stimulus). Mean rMTF shapes were not as regular as tMTF shapes, but mean BP and HP rMTFs in both areas, as well as the mean LP rMTF in ML, suggest the general shape of the underlying class despite small sample sizes (Table 1). Unlike BP and LP classes, the HP class firing rates were generally suppressed below the firing rate to the unmodulated stimulus except at the highest modulation frequencies in both A1 and ML (also see Fig. 4).

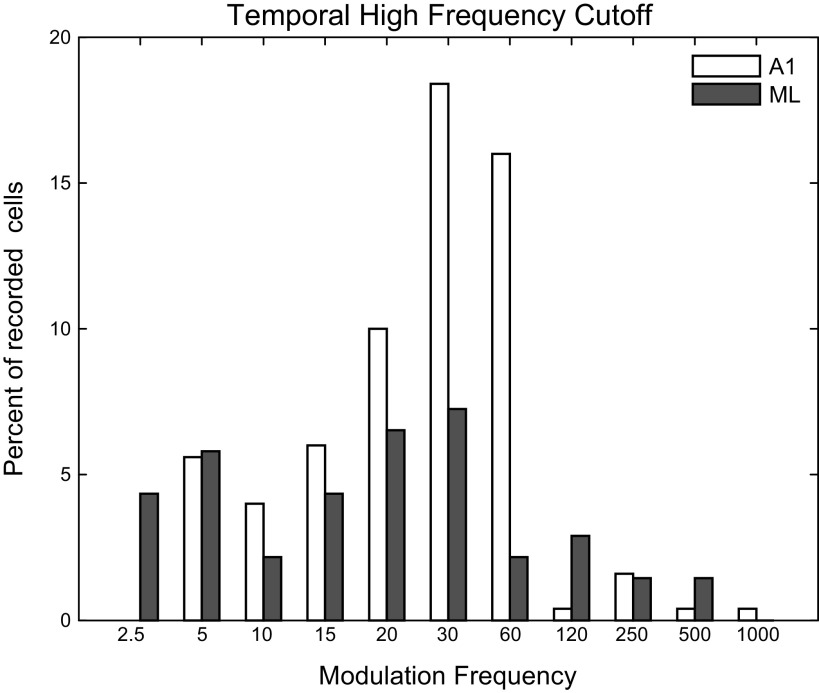
Temporal High-Frequency Cutoffs

A common measure of phase-locking ability is the temporal high-frequency cutoff, defined as the highest modulation frequency at which a cell is significantly phase locked to an AM stimulus. We determined the temporal high-frequency cutoff for both A1 and ML neurons, plotted in Fig. 8 as the percentage of recorded cells in each area with a cutoff at each tested MF. Because some cells did not significantly phase lock at all, the values in Fig. 8 do not add up to 100%. In addition to the reduction in number of cells that significantly phase locked in ML relative to A1 (see Table 1), there was also a downward shift in the mean temporal cutoff frequency in ML. To calculate the mean of the high-frequency cutoffs, we used the geometric mean. Because MF is a nonlinear octave-based measure, values to be averaged were first transformed into an octave representation, with the resulting mean transformed back into frequency, which is mathematically equivalent to taking the geometric mean of the frequency values. The mean A1 temporal high-frequency cutoff was 27.7 Hz, significantly higher than the mean ML temporal high-frequency cutoff of 19.5 Hz (two-tailed t test, P = 0.034).

Fig. 8.

Temporal high-frequency cutoffs. The temporal high-frequency cutoff is defined as the highest modulation frequency that results in a response with significantly greater phase locking relative to the response to an unmodulated stimulus. Percentages do not add up to 100 because some cells do not phase lock.

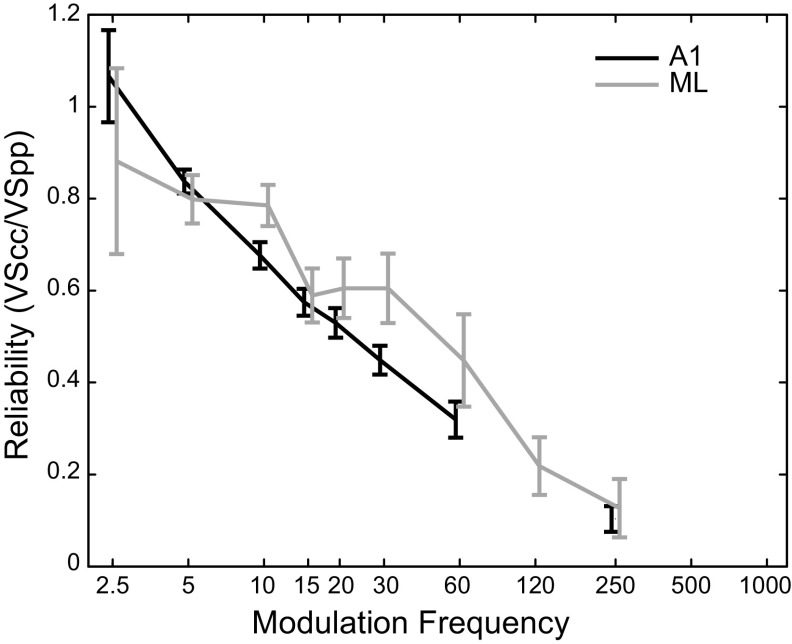
Reliability of Phase Locking

In A1, it has been shown that at higher MFs, the reliability of phase locking—the likelihood that a neuron will fire synchronously on any given cycle—decreases even for cells with strong phase locking (Yin et al. 2011). Although some cells continue to fire in a temporally precise fashion to high MFs, they are unable to follow each AM cycle, as the cycles get closer in time. Because reliability of phase locking drops off at higher MFs, it may be related to a neuron’s high-frequency temporal cutoff, which would suggest that ML neurons would show lower reliability than A1 neurons. In Fig. 9, we plot the average reliability at MFs where there was significant phase locking for A1 and ML neurons (e.g., if a given cell significantly phase locked to 15 Hz but not to 20 Hz, its 15 Hz responses were included in the calculated mean, but its 20 Hz responses were not). Any MF with fewer than four significantly phase-locking cells was excluded from this analysis. Our measure of reliability used cycle-by-cycle vector strength (VS_CC, see methods) and was calculated as VS_CC/VS_PP. This measure approximates the proportion of cycles that exhibit phase-locked firing. Although it might appear that Fig. 9 shows that ML neurons might be more reliable than A1 neurons on a cycle-by-cycle basis, this effect was not significant (two-sided t test corrected for multiple comparisons, no values significant at P = 0.05). The similarity of ML and A1 cycle-by-cycle reliability, despite the fact that the strength of phase locking (Fig. 7) and the high-frequency cutoffs (Fig. 8) were lower in ML than in A1, suggests that the weaker phase locking in ML is not solely due to a reduction of ML neurons’ ability to follow each cycle of modulation.

Fig. 9.

Reliability of synchronized firing. Mean reliability of synchronized firing in A1 (black) and ML (gray) is estimated by the ratio of VS_CC to VS_PP. Mean values are calculated only from modulation frequencies (MFs) that significantly phase lock; if fewer than four recorded cells significantly phase locked at a particular MF that point was omitted from the plot (120 Hz in A1). Values above 1.0 (e.g., A1 at the 2.5 Hz MF) are due to fact that cycles that include the 70 ms onset response window are excluded from the VS_CC analysis but the corresponding times are not excluded from the VS_PP analysis. Plots are offset slightly left and right to allow better visibility of overlapping error bars. Error bars show standard error of the mean. A1, primary auditory cortex; ML, middle lateral auditory cortex; VS_CC, cycle-by-cycle vector strength; VS_PP: phase-projected vector strength.

Peak/Trough (P/T) Cells

As mentioned earlier, in both areas, we found a class of cells that has previously not been widely reported in the cortex—the cells with P/T rMTFs. These cells had two distinct regions of response—one “peak” region at low-modulation frequencies, which was usually synchronized (at a rate of ∼80% in both A1 and ML, Table 1) and another region at high-modulation frequencies, which was rarely synchronized (∼5% in both A1 and ML, Table 1) separated by a “trough” region that was typically suppressed below the firing rate in response to unmodulated noise. In our previous report on A1 MTFs, we were not able to effectively observe this class of cells because our tested MFs did not go high enough (only to 120 Hz; however, note that the cell in Fig. 2A of Yin et al. (2011) also appears to be of this class but with a second response region that starts at lower MFs than commonly found). Because our tested MFs in the current experiment extended up to 1,000 Hz, this class of cells became evident, and we developed new analyses (see methods) to characterize them.

The P/T cells were found in high proportions in both A1 and ML, accounting for ∼40% of all rate-responsive cells in each area. Figure 10 depicts four examples of this class of P/T cells, two from A1 and two from ML. The cells depicted in Fig. 10, A, B, and D, show corresponding synchrony and firing rate in the lower-MF range and rate suppression over a mid-MF range. This was followed by nonsynchronized firing at MFs of 250 Hz and above that returned to approximately the same level as the cell’s firing rate to the unmodulated stimulus. The cell depicted in Fig. 10C phase locked in the lower-frequency response region but did not significantly increase its firing rate above the firing rate to the unmodulated stimulus.

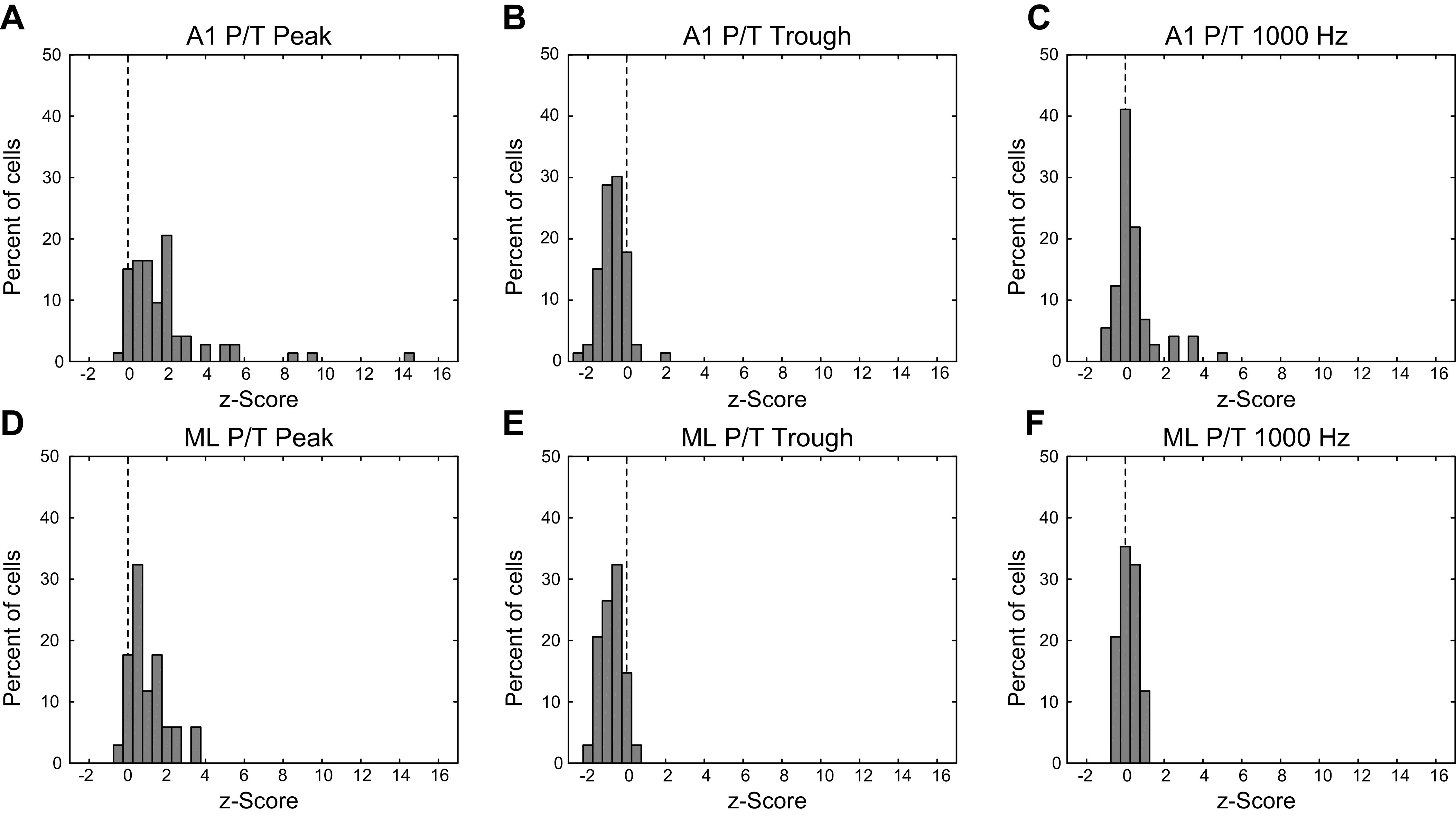
Examining a cell’s ability to detect modulation is particularly instructive with respect to firing rate measures in P/T cells. The firing rate at the lower-MF peak in P/T cells was almost exclusively higher than the firing rate to the unmodulated stimulus in both A1 and ML. This can be seen as points above and to the left of the unity line in Fig. 11, A and E, and neurons with z-score values greater than 0 in Fig. 12, A and D. At the same time, the firing rate at the suppressive trough was reduced below the firing rate to the unmodulated stimulus in both A1 and in ML. This can be seen as points below and to the right of the unity line in Fig. 11, B and F, and neurons with z-score values less than 0 in Fig. 12, B and E. Although we modeled the P/T cells as the sum of two positive peaks, the data were more suggestive of an excitatory peak at low MFs, followed by an inhibitory region at middle MFs, followed by a return to the level of firing rates to unmodulated stimuli at the highest MFs. Firing rates of the P/T cells to the highest tested MF of 1,000 Hz were generally similar to the rates in response to unmodulated stimuli. This can be seen as clustering around the diagonal in Fig. 11, C and G and z-scores near 0 in Fig. 12, C and F. The right panels in Fig. 11 illustrate the average (geometric mean) of the P/T rMTFs for A1 (Fig. 11D) and ML (Fig. 11H) normalized by their respective firing rates to the unmodulated stimulus. In both areas, the “average” P/T cell shows both a peak enhanced above the unmodulated response at low MFs (relative firing rate > 1) and a trough suppressed below the unmodulated response at middle MFs (relative firing rate < 1), but in ML, both peak and trough appear to be shifted toward lower MFs. In ML, the firing rate at the highest modulation frequencies returns to the level of the firing rate evoked by the unmodulated stimulus (relative firing rate ∼ = 1), whereas in A1, this firing rate slightly exceeds the firing rate to unmodulated noise. It appears that individual ML P/T neurons did not indicate the presence of high frequency (1,000 Hz) AM by changing their firing rate but rather responded at the highest MFs as if to unmodulated noise.

Fig. 11.

Firing rate relative to the response to unmodulated noise at low-frequency peak, middle-frequency trough, and high MF region. A–C, E–G: cell-by-cell scatter of firing rate to unmodulated noise (x-axis) against firing rate to AM for various conditions. Top row, A1. Bottom row, ML. A and E: firing rate of peak/trough (P/T) cells at the first P/T peak. B and F: firing rate of P/T cells at the P/T trough. C and G: firing rate of P/T cells at the 1,000 Hz modulation frequency (MF). Closed symbols represent cells for which the two firing rates significantly differ (t test, P < 0.05 after correction for multiple comparisons). Open symbols represent cells for which firing rates do not significantly differ. Diagonal line is a unity line. D and H: mean normalized rMTF of P/T cells (calculated as the geometric mean of P/T rMTFs normalized by their respective firing rate to unmodulated stimuli; error bars are standard error of the geometric mean). A1, primary auditory cortex; AM, amplitude-modulated; ML, middle lateral auditory cortex; rMTF, rate-based modulation transfer function.

The mean z-scored firing rate of P/T neurons at the low-MF peak (Fig. 12, A and D; combined across A1 and ML, mean = 1.60) was not significantly different than either the z-scored firing rates of the LP neurons at 2.5 Hz (LP mean = 2.01, P = 0.58, two-tailed t test) or the z-scored firing rates of the HP neurons at 1,000 Hz (HP mean = 0.69, P = 0.12, two-tailed t test). However, the mean z-scored firing rate of the P/T neurons at the low-MF peak was significantly less than the z-scored firing rate at the peak of the BP neurons (BP mean = 5.37, P = 1.4 × 10⁻⁵, two-tailed t test). This suggests that at the single unit level, the BP cells were sending a stronger signal with respect to modulation than the low-MF peak of the P/T cells.

In terms of mean z-scored firing rate, P/T neurons were relatively similar between A1 and ML. Although the mean z-scored firing rate for the low-MF peak was somewhat higher in A1 than in ML (Fig. 12, A and D; A1 mean = 1.87, ML mean = 1.01, P = 0.044, two-tailed t test), neither the middle-MF trough (Fig. 12, B and E; A1 mean = −0.69, ML mean = −0.82, P = 0.34, two-tailed t test) nor the response at 1,000 Hz (Fig. 12, C and F; A1 mean = 0.44, ML mean = 0.12, P = 0.093, two-tailed t test) differed in mean z-scored firing rate between A1 and ML.

Compared with the bandwidths of the purely BP cells, we also show the rate-based bandwidths of the cells categorized as P/T fits (Fig. 6, B and D). In both A1 and ML, the bandwidths of both the low-MF peak and the high-MF peak were as narrow or narrower than the rate bandwidth of the purely BP cells. For A1, the mean bandwidth of the low-MF peak was 3.0 octaves (Q factor 0.40), the same value as seen for BP cells. The high-MF peak was 2.1 octaves (Q factor 0.63) and was significantly narrower than the low-MF peak (two-tailed t test, P = 7 × 10⁻⁶).

In ML, the mean bandwidth of the low-MF peak was 2.9 octaves [Q factor 0.42; compare with 3.8 octaves (Q factor 0.29) for BP cells in ML], whereas the mean bandwidth of the high-MF peak was 2.6 octaves (Q factor 0.49)—here the low-MF peak and the high-MF peak did not have significantly different bandwidths (two-tailed t test, P = 0.21). Although the mean bandwidth of the low-MF peak did not change between A1 and ML (two-tailed t test, P = 0.85), the mean high-MF peak was wider in ML than in A1 (two-tailed t test, P = 0.04).

Although P/T cells are defined by their rate responses (we observed no tMTFs with similar properties), they often exhibit phase locking in the low-MF rate peak. This phase locking becomes weaker in ML (A1, mean VS_PP at tBMF = 0.507; ML, mean VS_PP at tBMF = 0.385; two-tailed t test, P = 0.0004), consistent with the general trend seen here.

One potential concern is that the cells identified as P/T might instead comprise two cells with different BMFs that were not appropriately segregated by our cell-sorting analysis. To determine if this might be the case, as a measure of isolation quality, we calculated for each cell the proportion of spikes that fell within a 1-ms refractory period. We then compared these values between our P/T cells and our other well-fit cells combined (LP, BP, and HP). In A1, the mean proportion of refractory spikes in P/T cells was 0.0034, whereas the mean proportion of refractory spikes in other well-fit cells was 0.0036 (two-tailed t test, P = 0.88, not significant), and in ML, the mean proportion of refractory spikes in P/T cells was 0.0039, whereas the mean proportion of refractory spikes in other well-fit cells was 0.0031 (two-tailed t test, P = 0.59, not significant), suggesting that the isolation of our P/T cells was not worse than the isolation of our other well-fit cells.

Categorizing Cells by their Firing Rate Relative to Unmodulated Noise

Both increases and decreases in spike rate relative to the unmodulated noise were observed. A small number of cells (“Mixed Inc/Dec”) showed increases in spike rate at some MFs but decreases at other MFs. However, most cells were classified as either increasing or decreasing. Increasing neurons are defined as neurons that, when significantly differing in firing from the unmodulated noise response, only increase firing rate relative to the unmodulated noise. Decreasing neurons are defined as neurons that, when significantly differing in firing from the unmodulated noise response, only decrease firing rate. The terms increasing and decreasing were used in earlier studies to describe the rate-depth functions (Niwa et al. 2012a, 2013, 2015), but as nearly all depth functions were monotonic, it can safely be implied that this nomenclature also applies to comparisons to the unmodulated noise [used as 0% depth in Niwa et al. (2012a, 2013, 2015) fits]. In the midbrain, the terminology “band-enhanced,” “band-suppressed,” and “hybrid” has been used (e.g., Kim et al. 2015) in studies of distance encoding and reverberation. For example, band-enhanced describes a neuron where the response at the peak of the MTF was greater than the response to the unmodulated stimulus. In this way, a band-enhanced neuron would likely be classified as “increasing” in our study. Similar relationships may be found between band-suppressed and decreasing cells, and between hybrid and mixed cells.

The increasing/decreasing/mixed classification, which is based on a comparison against the spike rates evoked by the unmodulated stimulus, was made independently of the earlier LP, BP, HP, and P/T classification, which is based on MTF shape. About half of the cells classified as mixed based on comparisons of responses to unmodulated noise had P/T MTFs (17 of 31 in A1, 6 of 11 in ML), but because for mixed cells both an increase and a decrease had to be significant, a smaller proportion of neurons with P/T MTFs were in the mixed classification (17 of 73 in A1, 6 of 34 in ML).

Among cells that were exclusively nonsynchronized (Table 2), increasing cells were more common than either decreasing or mixed cells in both A1 and ML (both comparisons of increasing vs. decreasing + mixed Inc/Dec were significant at P < 0.01, z test for independent proportions). Among synchronizing cells, the greater proportion of increasing cells in A1 was similar to that found for exclusively nonsynchronizing cells (z test for independent proportions, P < 0.001), but at the level of ML there was a shift to a nearly equal representation of increasing and decreasing cells (z test for independent proportions, P = 0.69, ns), consistent with the findings of Niwa et al. (2013) in ML under active conditions. Thus, for synchronized cells, when ascending from the level of A1 to ML, the ratio of increasing and decreasing cells in the population approached equality. This increase in the proportion of decreasing cells suggests that a two-pool opponent-coding scheme may provide an advantage in the detection of AM.

Table 2.

Percentage of AM cells detecting AM with increases and decreases in activity

	A1		ML
	Nonsynchronized	Synchronized	Nonsynchronized	Synchronized
Increasing (AM)	21/32 65.6%	87/146 60.0%	24/37 64.9%	21/51 41.2%
Decreasing (AM)	7/32 21.9%	32/146 21.9%	13/37 35.1%	19/51 37.2%
Mixed Inc/Dec (AM)	4/32 12.5%	27/146 18.5%	0/37 0%	11/51 21.6%

Values on the left are count of cells that detect AM by changing firing rate or phase locking, values on the right are in percentage. Cells in each area are broken down into synchronized and exclusively nonsynchronized categories. Detection of AM is also broken down into cells that show an increase or decrease in firing rate for AM relative to firing rate to unmodulated stimuli, and “mixed” cells, which exhibit both increases and decreases in rate at different modulation frequencies. To aid in comparisons to more recently used nomenclature from the midbrain, increasing and decreasing cells correspond to band-enhanced (AM responses greater than the unmodulated noise response) and band-suppressed (AM responses less than the unmodulated noise response) of Kim et al. (2015). AM, amplitude-modulated; A1, primary auditory cortex; ML, middle lateral auditory cortex.

Encoding of AM versus Responding to the Unmodulated Noise

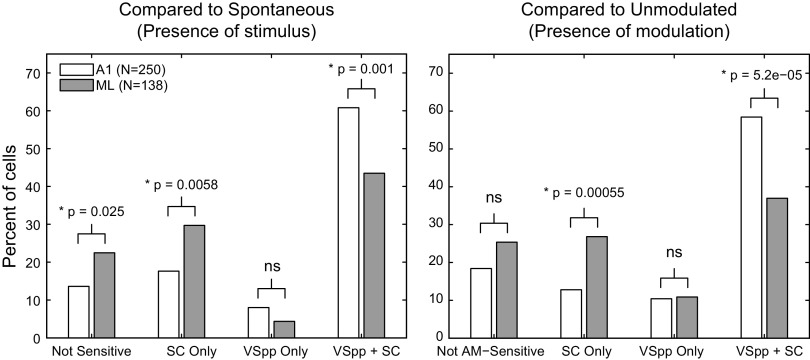
Modulation transfer functions describe, in terms of general shape, how a neuron responds to sounds with various modulation frequencies, but they do not inherently speak to a neuron’s ability to detect a stimulus or a stimulus feature. Spiking activity can be used to detect the presence of a stimulus or stimulus feature only if it differs from spiking activity when the stimulus or feature is not present. When neurons are presented with AM sounds, we can define two kinds of detection. First, the neuron can detect the presence of a sound as compared with the absence of a sound; this is stimulus detection, and the appropriate comparison is with the neuron’s spontaneous firing. Alternatively, the neuron can detect the presence of AM in a sound as compared with the absence of AM in a sound; this is modulation detection, and the appropriate comparison is with the neuron’s response to an unmodulated stimulus.

Although we have focused on modulation detection, our data show important differences between modulation detection and stimulus detection. Figure 13 demonstrates these detection differences in A1 and ML. The left panel depicts the percentage of cells exhibiting stimulus detection, whereas the right panel shows the extent of AM detection. When compared with A1, ML exhibited a decrease in the ability to use synchronized responses (VS_PP + SC) for detection, but an increase in the ability to use exclusively nonsynchronized responses (SC Only)—those that exhibited a change in firing rate without phase locking to the stimulus. This shift from temporal to rate coding in ML was consistent with a move up in the auditory hierarchy. In addition, there was an increase in the percentage of cells that did not detect the stimulus in ML compared with A1, but the percentage of cells that detected modulation was not significantly different between the two areas. There was no change across area in the percentage of exclusively synchronized cells (VS_PP Only), and these cells only accounted for 10% or less of the population.

Fig. 13.

Detection of a stimulus and detection of modulation. Left, percent of cells in A1 (open) and ML (shaded) that detect the stimulus (compared against spontaneous firing). Cells that failed to detect the presence of a stimulus with both spike count and vector strength are labeled as Not Sensitive. Cells that could detect the presence of a stimulus (relative to spontaneous) with spike counts, but not with vector strength are labeled SC Only. Cells that could detect the presence of a stimulus (relative to spontaneous activity) with vector strength, but not with spike counts are labeled VS_PP Only. Cells that had responses that significantly differed from the spontaneous firing rate for both spike counts and vector strength are labeled as VS_PP + SC. For each category, an A1/ML comparison was made using a z test for the difference of independent proportions (P value noted above bars). Right, same as left, except the comparison was made against the response to the unmodulated stimulus and represents detection of amplitude modulation at 100% depth. A1, primary auditory cortex; ML, middle lateral auditory cortex; SC, spike count; VS_PP: phase-projected vector strength.

The general pattern for both detection of a stimulus and detection of AM was very similar. The only statistically significant difference in detection in either area was an increase in ML of exclusively synchronized cells (VS_PP Only) detecting AM relative to those detecting the stimulus (z-test for independent proportions, P = 0.04). However, the VS_PP Only cells were the smallest class (4% of cells detecting the stimulus and 11% of cells detecting modulation), and therefore whether this difference is important is hard to determine.

DISCUSSION

AM Processing in Different Monkey Cortical Fields

We compared basic neural response properties to AM noise in macaque cortical areas A1 and ML and found several similarities between the areas. The proportion of cells that encoded AM by changing their firing rate was similar across the two areas, as were rMTF shapes. Response bandwidths were not statistically different across the two areas, though there was a slight trend for wider bandwidths in ML.

A1 and ML responses differed primarily in phase locking. We found several lines of evidence that suggested, in line with the typical temporal-to-rate transformation seen in the ascension of the auditory system, that phase locking was better in A1 than in ML—the proportion of cells that phase locked was higher in A1 (Table 1; Fig. 13); temporal BMFs were higher in A1 (Fig. 5); mean VS_pp was higher in A1, particularly at lower MFs (Fig. 7); and high-frequency phase-locking cutoffs were higher in A1 (Fig. 8). However, rate-based processing appeared to be relatively similar in the two areas, suggesting that the proposed temporal-to-rate transformation with auditory system ascension (e.g., Bendor and Wang 2007; Gao and Wehr 2015; Lu and Wang 2004; Lu et al. 2001; Schreiner and Urbas 1988) may largely reflect a loss in temporal resolution, rather than increasing nonsynchronous activity for higher modulation frequencies.

A few studies have examined AM processing in cortical regions outside of A1 in monkeys. These have supported a nonstandard, nonhierarchical view of the auditory cortex with regard to integration times and ability to phase lock. These studies suggest a possible integration time and corresponding phase-locking gradient in the caudomedial (short integration time, good phase locking) to anterolateral (long integration time, poor phase locking) direction; using a tone carrier, Scott et al. (2011) found that R, ML/AL (anterior lateral belt of the auditory cortex), and RM (rostromedial cortical field)/MM (middle medial cortical field) had similar phase-locking cutoff frequencies, which were lower than in A1. The caudomedial cortical field (CM), however, had phase locking similar to or better than A1. As ML is both hierarchically higher than A1 and lateral, our data are consistent with both current hypotheses, i.e., it might have lower frequency cutoffs and longer integration times because it is hierarchically higher than A1 or because it is more lateral in the caudomedial-to-anterolateral direction.

It is worthwhile to note that the auditory cortex has also been suggested to have additional gradients, including a rostrolateral-to-caudomedial gradient in the influence of somatosensory information with the caudomedial direction having the strongest somatosensory influence (Fu et al. 2003), as well as a caudal-to-rostral axis for spatial (caudal) versus nonspatial (rostral) processing (Camalier et al. 2012; Rauschecker and Tian 2000; Romanski et al. 1999). The degree to which these functional axes interact to create a functional organization of the auditory cortex has not yet been resolved.

The A1 population mean MTF data (Fig. 7) were qualitatively similar to that obtained by Scott et al. (2011), who measured the percentages of cells with significant firing rate or phase locking at each modulation frequency for tone-carrier sine-AM in both A1 and the core field R. They found a flat population rate function and a temporal MTF with a sharp roll-off in A1. However, the slope of the population tMTF roll-off in A1 was slightly shallower in Scott et al. (2011) than what we observed. R also had a flat population rMTF, but R’s population tMTF had a much sharper roll-off than what we observed in ML—sharp temporal roll-offs in the population response appear to be a feature of the auditory core, but not of the auditory belt.

Ultimately, the cortical representation of AM probably cannot be fully accounted for by rate responses alone nor by temporal responses alone. Both the current study and Scott et al. (2011) suggest that the phase-locking cutoff in cortical cells is lower than the behavioral limit for the detection of AM (macaque AM detection is demonstrated for 1 kHz in O’Connor et al. 2000, 2011). The presence of relatively flat population rate MTFs in A1 and ML suggests that sufficient nonsynchronized units responsive to AM at higher modulation frequencies exist to allow rate coding to contribute to AM perception, but the flatness of the population rMTF would mean that a labeled-line approach would be required for encoding AM via rate responses.

Species and Stimulus Effects

AM has been studied in many species (reviewed in Joris et al. 2004). Across a wide range of measures, such as MTF tuning, temporal following at different levels of the auditory hierarchy, sensitivity of temporally phase-locked versus rate codes, and emergence of rate codes with auditory system ascension, qualitative results are similar across species (e.g., Hoglen et al. 2018; Liang et al. 2002; Nelson and Carney 2007; Rosen et al. 2010; Ter-Mikaelian et al. 2007). However, there are many specific quantitative differences in these measures. The sensitivity and ability to temporally follow AM frequency in macaques from this study falls somewhere between rodents, which are less sensitive with less precise temporal following (e.g., Hoglen et al. 2018; Rosen et al. 2010; Ter-Mikaelian et al. 2007), and New World monkeys (e.g., Hoglen et al. 2018; Liang et al. 2002) which are better at both.

The type of stimulus used has particular relevance when studying temporal processing. We used sinusoidal AM noise. Most other studies of temporal processing have used different stimuli, including AM tones as well as click trains. Malone et al. (2013) showed that the type of stimulus could have large effects on single neuron responses, but little effect on population statistics. The results with clicks are more problematic to interpret in relation to AM. Clicks are fundamentally different stimuli, even though they have a broadband power spectrum as do our AM noise stimuli. Click trains comprise repeated discrete pulses whose power is restricted to (more or less) precise times. In contrast, sine-AM combines gradual temporal envelope fluctuations and periodicity, and it is well established that auditory cortical neurons are highly sensitive to envelope properties (Heil 2003). Click trains tend to yield a higher proportion of nonsynchronized responses at fast click rates than is observed with AM (e.g., Gao and Wehr 2015; Liang et al. 2002; Lu et al. 2001; Yin et al. 2011), possibly as a result of limited temporal resolution (similar to flicker fusion in vision, or what we observed at higher modulation rates). There have been studies attempting to bridge the gap between clicks and AM by using stimuli constructed to be intermediate between sinusoidally modulated amplitude modulation and click trains by varying duty cycle and envelope (e.g., Krebs et al. 2008; Lee et al. 2016; Osman et al. 2018). Lee et al. show a loss of temporal precision for high rates/envelopes, but they did not address whether this was due to a concomitantly improved rate code or simply a loss of fidelity. An intracellular study (Gao and Wehr 2015) has shown that fast click trains in rat auditory cortex cause intracellular depolarized plateaus (∼20 mV) with very low voltage click following (∼0.2 mV). By comparing currents under voltage clamp to voltage changes over time, the authors concluded that low-pass filtering by membrane capacitance cannot account for the nonsynchronized responses at high click repetition rates. This suggests that there is some specialized mechanism for processing rapid discrete events. However, these results are difficult to compare with ours as for click trains there is no continuously present sound analogous to unmodulated noise, and mechanisms other than membrane capacitance could make it impossible for cells to temporally follow rapid discrete events with fast rise time.

Two-Pool Opponent Coding of AM

Niwa et al. (2015) investigated the effects of attention on AM encoding and found that with attention, neurons in A1 with decreasing rate-depth functions had a reduced ability to detect AM (higher firing rate for AM during attention, making the slope of the rate-depth function shallower), but neurons in ML with decreasing rate-depth functions improved their ability to detect AM (lower firing rate for AM during attention, making the slope of the rate-depth function decrease steeper). This, together with a rise in the proportion of decreasing cells in ML, suggests that decreasing cells may play a more important role in AM processing at the level of ML than they do in A1.

One potential framework in which both cells that increase firing rate to AM and cells that decrease firing rate to AM may contribute to AM processing is a “two-pool opponent” code, where the difference in activity between cells that increase firing rate to AM and cells that decrease firing rate to AM is used to determine if a sound is modulated. The idea that the difference in activity of separate populations of oppositely tuned sensory neurons—one that increases activity and one that decreases activity—can encode stimulus properties is not new (e.g., De Valois and De Valois 1993). This idea has also been applied to sound localization (Grothe et al. 2010; McAlpine et al. 2001; Stecker et al. 2005) and temporal modulation. Krishna and Semple (2000) found such oppositely tuned neurons in the inferior colliculus of gerbils when presenting AM tones. In somatosensory cortex of macaques using fluttering vibrotactile stimuli, Salinas et al. (2000) found a similar hierarchical progression of the prevalence of such oppositely tuned neurons to what we are reporting. Salinas et al. found a substantially higher proportion of oppositely tuned neurons in secondary somatosensory cortex (S2) than in primary somatosensory cortex (S1). Although in many studies populations of oppositely tuned neurons have been reported, not much is known about the practical advantages of such an encoding mechanism.

Recently, we have proposed that a two-pool opponent coding mechanism could make signal processing robust to changes in correlated noise (“r_noise”) among neurons (Downer et al. 2017). In pools of similarly tuned neurons (e.g., a pair of neurons that both increase firing with modulation depth), increases in r_noise generally decrease encoding accuracy. In contrast, decreases in r_noise can increase encoding accuracy for pools of similarly tuned neurons. In A1, attention can reduce r_noise leading to improved neural coding accuracy (Downer et al. 2017). However, higher-order variables related to attention, decisions, motor responses, and learning tend to increase r_noise (Cohen and Newsome 2008; Cumming and Nienborg 2016; Gu et al. 2011; Vinck et al. 2015). In higher areas where such signals become more prevalent (Cohen and Newsome 2008; Niwa et al. 2015), they would increase r_noise and decrease encoding accuracy if the neurons in the population have similar tuning. For pools of neurons with opposite tuning (such as one that increases firing rate with modulation depth and one that decreases), increases in r_noise tend to improve population coding accuracy (e.g., Averbeck et al. 2006; Ecker et al. 2011; Jeanne et al. 2013; Oram et al. 1998; Romo et al. 2003). Thus, one possible benefit of implementing a two-pool opponent code is that it would be robust to increases in r_noise caused by the need to encode both sensory and cognitive-/task-related variables in higher areas. By introducing a population of oppositely tuned neurons, the effect that increased r_noise has on similarly tuned neurons is mitigated or eliminated. A recent study (Downer et al. 2017) has found that on average r_noise in ML increases with attention but that this increase in r_noise does not affect coding accuracy, supporting the idea that a two-pool opponent code in ML could result in a more noise-robust representation of AM.

Another advantage of a two-pool opponent code or response heterogeneity is that it allows for better multiplexing or disambiguating of neural signals that would be more ambiguous if only increases in activity were allowed. For example, it could allow for easier extraction of two features within the same sound, such as modulation frequency and noise bandwidth (e.g., Downer et al. 2017), or could allow for easier extraction of an early sensory signal followed by a later cognitive signal (Niwa et al. 2013).

Peak/Trough (P/T) Cells and Faux AM Sensitivity

We have used the term P/T to describe neurons whose MTFs were best fitted by two Gaussians. Although two positive Gaussians were used, the dip in the middle of the double curve fit tended to be at a firing rate lower than the firing rate to unmodulated noise. Although the unmodulated noise responses were not used in fitting or classifying P/T cells, we found that P/T neurons tended to have a low-frequency peak with a firing rate exceeding that to unmodulated noise, a middle-frequency trough with a firing rate lower than that to unmodulated noise and, then a second high-frequency “peak” with firing rate similar to the firing rate to unmodulated noise (Figs. 10–12). We have used the term “peak/trough” (P/T) to describe these cells rather than “multipeaked” because the firing rate suppression below the firing rate to unmodulated noise in the mid-frequency ranges is a relatively uniform property not captured by the broader term. We also did not use the term “band-reject/band-suppressed” because the latter gives the impression that the primary response is a suppression, while not acknowledging the excitatory peak at lower modulation frequencies.

Cells with MTFs similar to our P/T cells have been previously characterized for AM tones in the inferior colliculus of rabbit (Nelson and Carney 2007) and gerbil (Krishna and Semple 2000; Krebs et al. 2008), for AM noise in the inferior colliculus of rabbit (Kim et al. 2015) and cat (Zheng and Escabí 2008), and for AM tones and AM noise in auditory thalamus of rat (Cai and Caspary 2015). Examples of this class of cell (often called “band-reject”) are not so widely reported in the cortex. Outside of Bieser and Müller-Preuss (1996), who reported that ∼20% of cells in the squirrel monkey auditory cortex were “multipeak,” most examples of these cells in the primate auditory cortex found in the literature have gone mainly unremarked upon (e.g., for AM tones in Barbour and Wang 2002; Liang et al. 2002; Lu and Wang 2004; for AM noise in Yin et al. 2011), perhaps because they were not prevalent enough to constitute a clearly defined category. Here, we found that in both A1 and ML, ∼40% of cells exhibit a P/T MTF, likely due to our expanded modulation frequency test range. This value of 40% is similar to the value found in auditory thalamus (Cai and Caspary 2015). Although the prevalence of the P/T class appears stable between thalamus, A1, and ML, which suggests that these cells are an exception to the transformation of AM coding that is found ascending the auditory system, the fact that the strength of phase locking in P/T cells drops off significantly between A1 and ML is consistent with these cells being part of that general transformation.

Similar ratios of P/T cells through thalamus and cortex are suggestive that the P/T property may be inherited from lower levels of the auditory hierarchy. However, it is also possible that input from band-reject/band-suppressed MTFs converges with BP MTFs in thalamus or cortex to create both the trough and the return to unmodulated responses at higher MFs, resulting in de novo construction in the cortex (or thalamus). At the same time, many neurons (e.g., Figs. 2B and 10A) appeared to have a downturn at 1,000 Hz, suggesting that some excitatory drive may exist in the region of the second peak; whether this is a second region of excitatory response to modulation or simply the remnants of a very wide lower peak emerging from a narrower suppression is not clear. We note that in A1, the average bandwidths of the BP cells and the lower band of the P/T cells were essentially the same, which might argue against the higher peak being the tail of a very wideband response emerging from a narrower suppression. On the other hand, we observed very wideband BP responses (e.g., Fig. 2D) so this is not out of the question. Unlike in A1, in ML, the average bandwidth of the lower band of the P/T cells was narrower than the bandwidth of the BP cells, which may suggest that in ML, inhibition in the middle MFs acted to sharpen MF tuning.

A resurgence of interest in neurons responding to fast components of time-varying signals led to the notion that single neurons with such properties were important as feature detectors for rapid acoustic events (Lu et al. 2001). This idea was expanded to AM, popularizing the idea that neurons that fired nonsynchronously to high MF AM were important as AM feature detectors (e.g., Liang et al. 2002; Niwa et al. 2015; Wang et al. 2005). However, the present results suggest that these cells might not be as useful as AM feature detectors as previously thought. This is consistent with the psychophysical findings that these MFs are difficult to detect and discriminate (O’Connor et al. 2000). For neurons with P/T and HP MTFs, there were nonsynchronized responses at the highest modulation frequencies tested. However, for neurons with P/T MTFs, the mean response to the 1,000 Hz MF was close to the response to unmodulated noise (Figs. 11 and 12), suggesting that these neurons are primarily responding to the unmodulated noise. For neurons with HP MTFs, the mean response to the 1,000 Hz MF was higher than the response to unmodulated noise, but 10/14 neurons had responses within a z-score of 1 (i.e., approximately within one standard deviation of the unmodulated noise responses; Fig. 4), indicating that most of these neurons either were not signaling modulation at these high MFs or were sending a weak signal about whether the sound was modulated. This likely went unnoticed in the past because very few physiological studies of AM processing have compared AM responses and responses to the unmodulated noise. The weak 1,000 Hz responses described above, combined with the fact that the BP peaks were generating much stronger responses relative to unmodulated noise (Fig. 3), suggests that neurons with nonsynchronized responses at very high MFs are signaling weakly, if at all, about modulation. This could explain why it is harder to discern AM at these high MFs.

Temporal Locking to Frozen Noise

In this study, we used frozen noise in stimulus construction. One potential issue with the use of frozen noise is that particular features in the noise may induce precisely timed firing in some neurons, which has been shown in the midbrain and brain stem (e.g., Keller and Takahashi 2000; Steinberg and Peña 2011; Woolley and Casseday 2004). When these features are repeated from trial to trial, they may result in firing that shows as vertical striping in raster plots. In a few of our example panels, most notably Fig. 2A, the presence of what might be noise-locked responses can be seen at the highest MFs. A concern is that these responses could potentially skew our phase-locking metric. We do not believe this is likely to be a major source of error in our phase-locking values. If noise locking occurs, it most likely occurs at random phases relative to the AM, and as such will cancel out in phase-locking calculations, as these calculations use responses averaged over cycles. As a result, noise lock is most likely to somewhat reduce vector strength values. Noise lock can only result in increased vector strength values if most or all noise-locked responses happen to be in phase with the cell’s preferred AM phase, but even in this event there should be no introduction of spurious statistical significance from noise lock in our temporal measures; when calculating the significance of phase locking at each MF, the comparison was to a phase-locking measurement made on the response to the unmodulated noise, which would also contain any feature in the frozen noise that resulted in noise-locked responses. Similarly, because the noise sample is the same for all MFs, in most cases, responses to precisely timed features will be similar across the different MFs rather than having an undue effect on only some portions of the MTF.

GRANTS

This work was funded by National Institutes of Health National Institute on Deafness and Other Communication Disorders Grant DC02514 (to M. L. Sutter).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.N., K.N.O., and M.L.S. conceived and designed research; M.N. and K.N.O. performed experiments; J.S.J. analyzed data; J.S.J. interpreted results of experiments; J.S.J. prepared figures; J.S.J. and M.L.S. drafted manuscript; J.S.J., K.N.O., and M.L.S. edited and revised manuscript; M.L.S. approved final version of manuscript.