Prediction of mild parkinsonism revealed by neural oscillatory changes and machine learning

Abstract

Neural oscillatory changes within and across different frequency bands are thought to underlie motor dysfunction in Parkinson’s disease (PD) and may serve as biomarkers for closed-loop deep brain stimulation (DBS) approaches. Here, we used neural oscillatory signals derived from chronically implanted cortical and subcortical electrode arrays as features to train machine learning algorithms to discriminate between naive and mild PD states in a nonhuman primate model. Local field potential (LFP) data were collected over several months from a 12-channel subdural electrocorticography (ECoG) grid and a 6-channel custom array implanted in the subthalamic nucleus (STN). Relative to the naive state, the PD state showed elevated primary motor cortex (M1) and STN power in the beta, high gamma, and high-frequency oscillation (HFO) bands and decreased power in the delta band. Theta power was found to be decreased in STN but not M1. In the PD state there was elevated beta-HFO phase-amplitude coupling (PAC) in the STN. We applied machine learning with support vector machines with radial basis function (SVM-RBF) kernel and k-nearest neighbors (KNN) classifiers trained by features related to power and PAC changes to discriminate between the naive and mild states. Our results show that the most predictive feature of parkinsonism in the STN was high beta (∼86% accuracy), whereas it was HFO in M1 (∼98% accuracy). A feature fusion approach outperformed every individual feature, particularly in the M1, where ∼98% accuracy was achieved with both classifiers. Overall, our data demonstrate the ability to use various frequency band power to classify the clinical state and are also beneficial in developing closed-loop DBS therapeutic approaches.

NEW & NOTEWORTHY Neurophysiological biomarkers that correlate with motor symptoms or disease severity are vital to improve our understanding of the pathophysiology in Parkinson’s disease (PD) and for the development of more effective treatments, including deep brain stimulation (DBS). This work provides direct insight into the application of these biomarkers in training classifiers to discriminate between brain states, which is a first step toward developing closed-loop DBS systems.

INTRODUCTION

The primary pathology linked to Parkinson’s disease (PD) is the death of dopaminergic neurons in the substantia nigra pars compacta and subsequent loss of their striatal projections. This loss leads to widespread changes in neural activity throughout the basal ganglia that have been linked, in turn, to the development and manifestation of PD motor signs (Bergman et al. 1994; Escobar Sanabria et al. 2017; Lozano et al. 1998; Wang et al. 2017; Wichmann et al. 2018). Such changes can be readily appreciated through invasive local field potential (LFP) recordings taken from multiple brain regions. Consistently, data support a link between parkinsonian motor signs and changes in the power of synchronized oscillatory activity within individual frequency bands (e.g., beta) (Avila et al. 2010; Weinberger et al. 2006) as well as across frequency bands, most notably in the form of phase-amplitude coupling (PAC) across the beta and gamma bands (de Hemptinne et al. 2013; Kondylis et al. 2016; Swann et al. 2015), respectively.

In recent years, efforts have been made to use such oscillatory changes for programming deep brain stimulation (DBS) therapies (Yoshida et al. 2010), titrating medications (Priori et al. 2004), or as control signals within closed-loop DBS systems (Little et al. 2013). In parallel, there is a growing interest in developing algorithms that are sensitive to changes in circuit dynamics and capable of further informing patient care (Bruffaerts 2018). As an initial step in this process, we applied supervised machine learning algorithms to discriminate parkinsonism based on power spectral density (PSD) and PAC metrics derived from LFP recordings taken from the primary motor cortex (M1) and subthalamic nucleus (STN) of a nonhuman primate rendered mildly parkinsonian through administration of the 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP) neurotoxin. We report the performance of both individual and composite features in the process of discriminating between the naive and parkinsonian states.

MATERIALS AND METHODS

Animal.

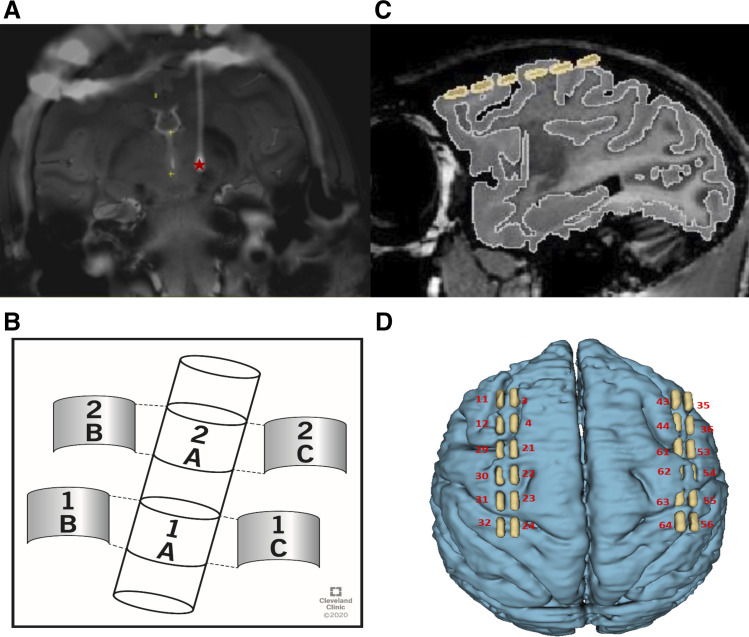
Animal care complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and procedures were performed under a protocol approved by the Institutional Animal Care and Use Committee of the Cleveland Clinic. A 14-yr-old adult female nonhuman primate (Macaca mulatta) underwent stereotaxic implantation of a six-contact directional deep brain stimulation (DBS) lead (Abbott Medical, Abbott Park, IL) in the area of the STN (Fig. 1A) by techniques described previously (Branco de Paiva et al. 2020). The lead consisted of two annular rows of contacts spaced 0.5 mm apart, with each ring separated into three directional contacts (i.e., 120° spacing) that were 0.76 mm in length (Fig. 1B). The animal was further implanted bilaterally with 12-contact electrocorticography (ECoG) arrays spanning from medial somatosensory cortex to prefrontal cortex (Fig. 1C). The M1 region was operationally identified as the contact(s) showing the lowest threshold for corticospinal activation and further confirmed by three-dimensional (3-D) reconstruction of the coregistered preoperative MRI and postoperative computer tomography (CT) (Fig. 1D) (Fedorov et al. 2012). Finally, a stainless steel headpost was implanted to allow for head fixation (Graymatter Research, Bozeman, MT).

Fig. 1.

Electrode configuration. A: coregistered preoperative MRI and postoperative computer tomography (CT) depicting the trajectory and location of the deep brain stimulation (DBS) lead targeting the subthalamic nucleus (STN) (coronal view, center of contact region of DBS lead marked with a red star). B: lead that was placed in STN. C: the relative location of the electrocorticography (ECoG) array over the ipsilateral hemisphere (sagittal view, contacts highlighted in yellow). Both images reflect coregistration of preoperative MRI and postoperative CT. D: 3-dimensional (3-D) reconstruction of cortex and ECoG array [primary motor cortex (M1) local field potentials (LFPs) were derived from bipolar rereferencing of sites 31 and 23].

After recordings made in the naive condition, the animal was rendered mildly parkinsonian by a series of systemic injections of the MPTP neurotoxin over three consecutive days (0.5, 0.3, and 0.2 mg/kg im, respectively). Bradykinesia, akinesia, tremor, and other PD motor signs were quantified by a blinded rater using a videotape-based rating scale system (Potts et al. 2015). A typical naive animal will score 0 across all categories, with increasing scores denoting the presence of mild (1–15), moderate (16–26), and severe (27–39) motor signs.

Electrophysiology.

Figure 2 summarizes the data acquisition and processing approach. Spontaneous electrophysiological data were recorded, referenced to the cranial headpost, and digitized (Fs ∼24 kHz) with a TDT workstation (Tucker Davis Technologies, Alachua, FL) with the awake animal seated in a commercial primate chair. The data were band-pass filtered (0.5–500 Hz) and downsampled to 2 kHz for analysis. Vertically aligned contacts were subtracted to yield LFPs such as 1a-2a yielding bipolar STN contacts. For M1, bipolar referencing was achieved by subtracting adjacent contacts 31 and 23 of the cortical array ipsilateral to the implanted STN lead. A moving window line noise (60 Hz) subtraction approach was applied and artifact detection algorithms used to identify and exclude segments with electronic jump or clipping artifacts and movement-related artifacts (Oostenveld et al. 2011). In addition to continuous direct or CCTV monitoring of the animal during each recording session to ensure that data were collected only during wakefulness, data were discarded if the monkey fell asleep (as defined by slow-wave LFPs in M1 and STN while the animal closed its eyes). All data processing and analysis was performed in MATLAB (r2019b; MathWorks) with customized scripts, the machine learning toolbox, and the FieldTrip toolbox (Oostenveld et al. 2011).

Fig. 2.

Procedure of data analysis. A: we record local field potentials (LFPs) from the cortex and the subthalamic nucleus (STN), after which these data are preprocessed by bipolar rereferencing, band-pass filtering, and artifact rejection. B: feature extraction via phase-amplitude coupling (PAC) and power spectral density (PSD) of specific frequency bands is performed. PD, parkinsonian. C: features are used for PSD and PAC-based classifier training [support vector machines with radial basis function (SVM-RBF) kernel and k-nearest neighbors (KNN)]. D: finally, classification accuracy is evaluated.

Feature extraction.

For each brain region, the relative power in each frequency band [delta (1–3 Hz); theta (4–7 Hz); alpha (8–12 Hz); low beta (13–20 Hz); high beta (21–35 Hz); low gamma (36–70 Hz); high gamma (71–200 Hz)] and high-frequency oscillations (HFO) (201–400 Hz) was calculated as one average value per band with the Welch algorithm (Welch 1967). Moreover, we evaluated PAC between beta and gamma frequency bands and also between beta and HFO frequency bands. Specifically, PAC between the low-frequency (f_p) “phase-modulating” and the high-frequency (f_A) “amplitude-modulated” bands was calculated via the modulation index (MI) method presented by Tort et al. (2010). Each segmented LFP sample was band-pass filtered (Butterworth 2nd order, zero phase forward and reverse filtering) with a center frequency f_p and bandwidth of 1 Hz so as to get the low-frequency component. Note that this narrow bandwidth of the filter was selected because it enabled the accurate calculation of the phase of the low-frequency component. A bandwidth of 2f_p was utilized to get the high-frequency component, considering that a value of 2f_p or higher is required to retain the envelope information of the high-frequency oscillations and thus calculate PAC accurately (Aru et al. 2015). Hilbert transform was then applied to extract the instantaneous phase of the low-frequency signal and the instantaneous amplitude of the high-frequency signal.

Comodulograms (rectangular maps) were used to examine the MI values. These were created at low frequencies for phase with 1-Hz increments across the beta band (13–30 Hz) and high frequencies for amplitude with 5-Hz increments across the gamma band (50–200 Hz) for each data segment. For detailed visualization (Fig. 2B), the comodulogram was displayed only within the subset of frequencies where PAC was observed (Escobar Sanabria et al. 2017). Note that the power in each frequency band along with the MI values for STN represent the average from all the bipolar pairs, since it was pointless here to include directional contacts where features contributed relatively little to classification (Khawaldeh et al. 2020).

Classification.

Supervised machine learning classifiers were used to identify discriminant features of the M1 and STN LFPs consistent with the parkinsonian state. The individual PSDs within each band, beta-gamma PAC, along with the combination of these features were used to train the classifiers. Consequently, we investigated which features provided a general improvement in accuracy in order to elucidate the relation between the selected features, the machine learning algorithms, and the electrophysiological phenomena. KNN and SVM using a radial basis function (RBF) kernel were considered as classifiers (Vapnik 2000), and their hyperparameters were optimized via the Bayesian approach (Snoek et al. 2012). SVM performs binary discrimination by projecting the feature set into a high-dimensional space where there exists a linear separation (i.e., the hyperplane) between the two groups, whereas KNN relies on feature similarity (how similar out-of-sample features look relative to the training set) to perform the discrimination between two groups (Altman 1992).

A 10-fold cross-validation strategy was used to evaluate each classifier (Dietterich 1998), such that the entire data set was partitioned into 10 subsets, each of which represented 10% of the whole data set. For each of the 10 subsets, we used 90% for training and the remaining 10% for testing. This cross-validation was performed 10 times to account for variability in random subset selection. Accuracy was summed across the 10 subsets for each cross-validation run, divided by the total number of observations, and then averaged across the 10 repetitions.

RESULTS

Behavioral scoring.

After MPTP induction, the animal demonstrated cardinal signs of parkinsonism, including bradykinesia and akinesia. Scores during the 3-mo period in the naive state were consistently 0, whereas those for the 4-mo experimental window following MPTP administration averaged 2.5 (±1.8).

Changes in spectral and PAC features during parkinsonism.

A total of 45 LFP samples (3 min each) were recorded in the naive state over a period of 3 mo, and 50 samples were collected in the parkinsonian state over a period of 4 mo. These were further split into shorter segments 15 s in duration before feature extraction. Figure 3 shows the M1 and STN LFP spectral power changes from the naive to the parkinsonian states. We compared differences in the scalar measurements of power and PAC between the naive and PD states with nonparametric Mann–Whitney–Wilcoxon statistical inference testing (significance threshold: P < 0.05). P values from this test were corrected for multiple comparisons with the false discovery rate (FDR) method. As detailed in Fig. 4 and Table 1, STN changes in the PD state included significant increases in LFP power across the alpha, low beta, high beta, high gamma, and HFO bands as well as significant decreases in power in the delta and theta bands. For M1, there was a significant increase in low beta, high beta, high gamma, and HFO band power as well as significant decreases in power in the delta band. Notably, although elevated across both brain regions, changes in PAC only reached statistical significance in the case of beta-HFO PAC from the STN area.

Fig. 3.

Local field potential (LFP) power spectra in the low- and high-frequency bands: primary motor cortex (M1) LFP data (A) and subthalamic nucleus (STN) LFP data (B) in both the naive and parkinsonian (PD) states.

Fig. 4.

Summary statistics of the changes in oscillatory activity and phase-amplitude coupling (PAC) due to parkinsonism. A: effect of parkinsonism on the power spectral densities (PSDs) and PAC in subthalamic nucleus (STN). B: effect of parkinsonism on the PSDs and PAC in primary motor cortex (M1). ***Significance bars represent P < 0.05, Mann–Whitney–Wilcoxon test, corrected for multiple comparisons. HFO, high-frequency oscillation; PD, parkinsonian; STN, subthalamic nucleus.

Table 1.

Summary of the variations of features from LFPs recorded in the M1 and STN across conditions

	Delta-PSD	Theta-PSD	Alpha-PSD	Low Beta-PSD	High Beta-PSD	Low Gamma-PSD	High Gamma-PSD	HFO-PSD	Beta-HFO PAC	Beta-Gamma PAC
STN	−	−	+	+	+	Not significant	+	+	+	Not significant
M1	−	Not significant	Not significant	+	+	Not significant	+	+	Not significant	Not significant

HFO, high-frequency oscillation; LFP, local field potential; M1, primary motor cortex; PAC, phase-amplitude coupling; PSD, power spectral density; STN, subthalamic nucleus. +, Significant increase; −, significant decrease.

Classification accuracy for the eight different features is depicted individually for M1 and STN in Fig. 5, A and B, respectively. Figure 5, C and D, show the receiver operating characteristic (ROC) curves (both KNN and SVM-RBF) for the STN and M1 pooled features that attained the highest classification (naive vs. parkinsonian) discrimination accuracy among all comparisons. Notably, by emphasizing features exhibiting significant differences between the two groups, the feature fusion approach (pooled features) markedly outperforms each individual feature-based approach across both recording sites, indicating that the different features provide complementary information that improves classification accuracy (Sun and Lee 2006).

Fig. 5.

Classification results. A and B: the results of the support vector machines with radial basis function (SVM-RBF) and k-nearest neighbors (KNN) classifiers for the discrimination of various features in the naive and parkinsonian (PD) states based on local field potential (LFP) recordings from primary motor cortex (M1, A) and subthalamic nucleus (STN, B) brain areas. Error bars indicate the 95% confidence interval. C and D: receiver operating characteristic (ROC) curves for both KNN and SVM-RBF for the STN (C) and M1 (D) pooled features that attained the highest classification accuracy among all the comparisons in discriminating between the naive and PD states. HFO, high-frequency oscillation; PAC, phase-amplitude coupling; PSD, power spectral density.

DISCUSSION

LFP spectral changes and PAC in mild parkinsonism.

Despite the relatively mild parkinsonian state of the animal studied, we have demonstrated that LFP recordings from both the M1 and STN show increased low-beta and high-gamma PSD changes relative to the naive state. Although these data are consistent with prior findings in patients with PD, those data typically were derived from individuals with well-established, moderate to severe disease (Brittain and Brown 2014). The balance between beta and gamma oscillations has been postulated to determine the effects of basal ganglia-thalamocortical projections on the motor areas of the cortex (Brown 2003), and a negative correlation between beta and gamma oscillations has previously been found to occur after treatment with dopaminergic medications (Alonso-Frech et al. 2006; Fogelson et al. 2005). Notably, however, PAC was not found to be significantly elevated, which may reflect the rather mild disease state in the present animal compared with prior studies (de Hemptinne et al. 2013; Escobar Sanabria et al. 2017; Kondylis et al. 2016). We only observed a significant increase in beta-HFO PAC in STN, and the individual classification accuracies of the PAC features were lower than the rest of the features, which may raise the question of whether this feature provides sufficient gains to the classification, but this is beyond the scope of this work and warrants further research. Our data support further widespread PSD changes across the delta, low beta, high beta, high gamma, and HFO bands in the mild parkinsonian state for LFP recordings made from the STN and M1. It is again notable that these changes were present at this relatively mild disease state, and their evolution, within both the STN as well as M1 and other cortical regions as a function of model severity progression, certainly warrants further investigation.

Despite the fact that adaptive deep brain stimulation (aDBS) has recently been developed to improve the efficacy of traditional open-loop stimulation paradigms, nevertheless, current aDBS methods are majorly based on a single-feature thresholding such as beta-band power. Although in the study from our animal we see that high beta-band power produces a relatively high classification accuracy, it is still necessary to consider all other features particularly given the variability reported in some previous studies. For example, large beta-band oscillations were observed in 100% of one cohort of STN-DBS lead implants (Little et al. 2012), yet other studies found beta peaks in ∼70% of cases (Bronte-Stewart et al. 2009) and others found beta-band peaks in <50% of all cases (Rosa et al. 2011). Consequently, this variability indicates that a single oscillatory feature may not be robust across animals or patients, rendering it inadequate in clinical applications, thus the necessity for a combination of features.

Application of machine learning.

In recent years machine learning algorithms have gained increasing attention not only as a means of better characterizing pathophysiology but also as a potential tool to guide therapy, including intraoperative lead placement (Guillén et al. 2011; Wong et al. 2009). In a previous study machine learning was applied to discriminate the healthy state from the parkinsonian state with LFP signals from the rat model (Amoozegar et al. 2019), whereas in yet another study its use was limited to the detection of tremors in parkinsonian patients (Yao et al. 2019). Despite these efforts, more work is needed before these can be fully implemented in the clinical setup and for closed-loop DBS. Although these studies focused on different features, they did not look into the individual frequency bands’ PSD (such as beta band) and PAC as features, yet these are the key features that have recently been explored in works such as beta bursts and closed-loop DBS. In other studies, SVMs and Bayesian classifiers were trained on structural MR images to distinguish between essential tremor and PD patients (Cherubini et al. 2014) and to identify PD patients who faced the risk of dementia (Morales et al. 2013). Here, machine learning algorithms (SVM-RBF and KNN) were able to classify the naive and mildly parkinsonian conditions from LFP spectral (primary features) and PAC (secondary features) with a high degree of accuracy. In M1, the feature that showed the highest accuracy was the HFO-PSD (Fig. 5A), whereas high beta-PSD was a major feature derived from the STN (Fig. 5B). It is noteworthy that the multiple features (pooled) classifiers achieved the highest accuracies in the discrimination between the naive and parkinsonian states. Overall, our data reveal the feasibility of reducing the number of features to 10 while still attaining satisfactory accuracy in the discrimination between states despite the animal only being in the mild parkinsonian state, which is important in engineering clinical applications with efficient processing time and adequate energy consumption for implantable devices. It is also noteworthy that some highly significant variables (Fig. 4) were not found to be good predictors (Fig. 5). Although it would seem intuitive that inclusion of information derived from variables observed to show higher statistical significance should increase prediction powers, it has been shown previously that the power is not inherently increased by the addition of significant variants to classical significance test-based approaches (Clayton 2009; Jakobsdottir et al. 2009; Janssens and van Duijn 2008; Lo et al. 2015). This is because what makes variants good for prediction versus significance depends on various properties of the underlying distributions, and a possible shortcoming of applying only the classical significance is that it considers marginal significance and does not take into account the possible interaction effects of groups of variants.

Future directions.

Future work will involve characterization of the important features in the naive and PD states in relation to movement disorders, establishing the relative contribution of different feature sets as a function of increasing parkinsonian severity, and developing methodologies for adaptive closed-loop deep brain stimulation (Swann et al. 2018). Another important future improvement will involve incorporation of deep learning (Zhu et al. 2019) for more efficient processing of raw data, thus unraveling avenues to perform binary classification based on multiple LFP channels and hence to the effects of parkinsonism on brain network (Bore et al. 2019, 2020; Li et al. 2020).

Limitations.

Notwithstanding, some limitations in the present work will need to be taken into account in future studies. Limited statistical power in macaque studies (Wakabayashi et al. 2018) may be complemented by larger-sample size studies in the primate model or by recording LFPs in patients undergoing DBS. In addition, considering the variability in parkinsonian pathophysiology, classifiers trained on one animal or patient may or may not accurately predict the state in another subject, yet again this could be resolved by employing subject-specific classifiers. It is also worth noting that although the rhesus macaque develops akinetic-rigid parkinsonism, it does not develop the dominant tremor usually observed in many patients. Beta-band power in the naive state is viewed to be associated with intention to move (Riehle et al. 1997). Nevertheless, we could not control for this intention in the present work and have included only spontaneous recordings during which the animal was at rest.

Conclusion.

In this study, features related to LFP spectral and PAC were extracted from M1 and STN LFPs and used to train machine learning algorithms with the aim of discriminating between normal and mildly parkinsonian conditions. Feature fusion (pooled) led to improved classification accuracies. Our findings support the view that multiple features may be beneficial in characterizing parkinsonism as opposed to use of a single unique feature.

GRANTS

Research reported in this publication was funded by NIH (R01 NS-092730).

DISCLOSURES

A. G. Machado is a consultant with St Jude Medical. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.

AUTHOR CONTRIBUTIONS

J.C.B., A.G.M., and K.B.B. conceived and designed research; J.C.B., B.A.C. and H.C. performed experiments; J.C.B., B.A.C., and K.B.B. analyzed data; J.C.B., B.A.C., H.C., R.G., A.G.M., and K.B.B. interpreted results of experiments; J.C.B. prepared figures; J.C.B. drafted manuscript; J.C.B., B.A.C., R.G., A.G.M., and K.B.B. edited and revised manuscript; J.C.B., B.A.C., H.C., R.G., A.G.M., and K.B.B. approved final version of manuscript.