Abstract
When a person tries to press with a finger, other fingers of the hand produce force unintentionally. We explored this phenomenon of enslaving during unintentional force drifts in the course of continuous force production by pairs of fingers of a hand. Healthy subjects performed accurate force production tasks by finger pairs Index-Middle, Middle-Ring, and Ring-Little with continuous visual feedback on the combined force of the instructed (master) fingers or of the noninstructed (enslaved) fingers. The feedback scale was adjusted to ensure that the subjects did not know the difference between these two, randomly presented, conditions. Across all finger pairs, enslaved force showed a drift upward under feedback on the master finger force, and master force showed a drift downward under feedback on the enslaved finger force. The subjects were unaware of the force drifts, which could reach over 50% of the initial force magnitude over 15 s. Across all conditions, the index of enslaving increased by ∼50% over the trial duration. The initial moment of force magnitude in pronation-supination was not a consistent predictor of the force drift magnitude. These results falsify the hypothesis that the counter-directional force drifts reflected drifts in the moment of force. They suggest that during continuous force production, enslaving increases with time, possibly due to the spread of excitation over cortical finger representations or other mechanisms, such as increased synchronization of firing of α-motoneurons innervating different compartments of extrinsic flexors. These changes in enslaving, interpreted at the level of control with referent coordinates for the fingers, can contribute to a variety of phenomena, including unintentional force drifts.
NEW & NOTEWORTHY We report a consistent slow increase in finger enslaving (force production by noninstructed fingers) when visual feedback was presented on the force produced by either two instructed fingers or two noninstructed fingers of the hand. In contrast, force drifts could be in opposite directions depending on the visual feedback. We interpret enslaving and its drifts at the level of control with referent coordinates for the involved muscles, possibly reflecting spread of cortical excitation.
Keywords: activation spread, force drift, moment of force, referent coordinate
INTRODUCTION
When a person tries to move one finger of a hand, other fingers move unintentionally. Similar effects are seen during force production in isometric conditions: Trying to press with one finger leads to unintentional pressing by other fingers of the hand. These phenomena, referred to as lack of independence or “enslaving” (Kilbreath and Gandevia 1994; Lang and Schieber 2003; Li et al. 1998; Zatsiorsky et al. 2000), have been discussed as consequences of many factors from connective tissue links, to the presence of multitendon extrinsic muscles, and to overlapping cortical representations (reviewed in Schieber and Santello 2004; van Duinen and Gandevia 2011). A number of studies have emphasized the importance of neural factors. These studies included analysis of enslaving during force production at proximal phalanges, where finger-specific intrinsic muscles play the role of prime movers (Latash et al. 2002), analysis of the patterns of finger force responses induced by transcranial magnetic stimulation of the motor cortex (Danion et al. 2003b), and changes in indices of enslaving over relatively short time intervals (Reschechtko et al. 2014; Wu et al. 2012, 2013).
Enslaving has been viewed as a potentially important factor for hand function. It is higher in the nondominant hand, under fatigue, and in certain groups of neurological patients (Danion et al. 2000, 2001; Park et al. 2012). On the other hand, indices of enslaving were reported to be lower in healthy older persons (Kapur et al. 2010; Shinohara et al. 2003). Patterns of enslaving have been seen as stabilizing the pronation-supination moment of force and as potential contributors to the synergic behavior of the hand in prehensile tasks (Zatsiorsky et al. 2000; Winges and Santello 2004; Zatsiorsky and Latash 2008).
Methods of estimating enslaving quantitatively during finger force production varied from performing one-finger maximal voluntary contraction (MVC) tasks (Li et al. 1998), to using neural network approach over MVC tasks with different finger combinations (Zatsiorsky et al. 1998, 2000), and to using one-finger submaximal tasks (Latash et al. 2001; Park et al. 2012). The results obtained in those studies were similar and allowed to combine them into a single equation:
| (1) |
where F is a four-dimensional finger force vector, |E| is a 4 × 4 enslaving matrix, m is a four-dimensional vector of hypothetical commands (“modes”) to individual fingers, n is the number of explicitly instructed (“master”) fingers, a is an empirically defined constant close to 0.7, and T is the sign of transpose (Danion et al. 2003a). The term 1/na reflects another phenomenon of finger interaction, force deficit, a drop in individual finger force when it acts together with other fingers of the hand (Li et al. 1998; Ohtsuki 1981). Equation 1 assumes that enslaving is a robust phenomenon and does not change across tasks and conditions. It showed changes with lengthy specialized training, for example, in professional musicians (Slobounov et al. 2002).
Robustness of enslaving has been challenged in several recent studies. In particular, several studies have documented a significant increase in indices of enslaving (such as the relative amount of force produced by noninstructed fingers) after relatively brief practice of ∼30 min (Wu et al. 2012). Steady-state force production by a subset of fingers of a hand with a brief perturbation led to higher indices of enslaving within a single trial over 20 s (Reschechtko et al. 2014). In a recent study (Hirose et al. In press), an increase in enslaving has been reported across conditions when the subjects had visual feedback on either master finger force or slave finger force. In the former condition, slave finger force drifted upward by over 30%; in the latter condition, master finger force drifted down, also by ∼30%, both leading to increased relative amounts of slave finger forces, i.e., to higher enslaving.
Changes in enslaving in the latter study are closely related to the phenomenon of force drifts observed when visual feedback on the force magnitude becomes unavailable (Ambike et al. 2015; Vaillancourt and Russell 2002). This phenomenon has been interpreted within the physical approach to motor control as a consequence of drifts in the referent coordinates (RCs) for the agonist and antagonist muscle groups toward actual muscle length values (Ambike et al. 2016; Latash 2016). At the level of a finger or a hand viewed as a single effector, this is expected to lead to drifts in RC for the effector to its actual coordinate and/or its apparent stiffness, k toward lower magnitudes. Both have been confirmed in experiments (Ambike et al. 2016; Reschechtko and Latash 2017). Understanding the nature of unintentional force drifts and unintentional finger force production (enslaving) within a single conceptual framework would advance our current understanding of the neural control of intentional and unintentional actions. This would have both basic and clinical implications, in particular, as related to unintentional movements after stroke and in subcortical disorders (Ejaz et al. 2018; Latash 2019; Latash and Huang 2015).
Note that force is not the only variable that shows unintentional drifts in the absence of visual feedback. In particular, large drifts have been also reported for the total moment of force in pronation-supination (MPS) produced in pressing tasks by the normal finger forces (Parsa et al. 2016; Reschechtko and Latash 2017). Similar to the aforementioned interpretation of force drifts, MPS drifts have been interpreted as consequences of drifts in the referent hand orientation and rotational stiffness. Such drifts have been invoked as possible reasons for the counter-directional drifts in the forces produced by the master and slave fingers (Hirose et al. In press).
In the study by Hirose et al. (2020), the instructed finger pairs were the index and ring (IR) and middle and little (ML) fingers. These finger combinations were selected to increase the effects of enslaving (cf. Zatsiorsky et al. 2000) and thus facilitate providing feedback to subjects on either master fingers force or slave finger force without subject’s knowledge. Note that both finger pairs are associated with producing a substantial non-zero MPS because of the difference in the lever arms between the “lateral” (I and L) and “central” (M and R) fingers within each pair. In the current study, we used a similar design to test three finger pairs associated with drastically different initial magnitudes of MPS: IM, RL, and MR. Note that IM and RL involve fingers with moment production in the same direction and, hence, are expected to produce large initial MPS magnitudes with plenty of room for MPS drift. In contrast, MR includes two fingers that are comparably strong (cf. Li et al. 1998), have similar lever arms with respect to the longitudinal forearm axis, and act in opposite directions. So, the initial MPS magnitude was expected to be low and lead to little drift, if any. If indeed MPS drift was the main factor leading to the observed counter-directional drifts in the forces produced by the master and slave fingers, much smaller finger force drifts were expected in the MR task, as compared with IM and RL tasks (Hypothesis 1).
We also considered an alternative hypothesis that the phenomena of unintentional force changes (drifts) and unintentional force production (enslaving) were reflections of related mechanisms, which we associated with spread of excitation to cortical finger representations of slave fingers leading to unintentional changes in spatial RCs for the fingers (cf. the “cortical piano” concept of Schieber 2001; see discussion for more detail). Hence, our Hypothesis 2 was that the amount of enslaving would show a significant increase over the trial duration invariant with respect to the task and feedback conditions.
METHODS
Subjects
Seven subjects (four men and three women, 20–28 yr old, mass 82.5 ± 12.54 kg, height 1.79 ± 0.08 m) participated in this study. The number of subjects was defined on the basis of power analysis of results from the previous study of similar phenomena (Hirose et al. In press), which showed large size effects in all major comparisons. All subjects self-identified as right-handed, according to the preferred hand used during writing and eating. The subjects were healthy, had no history of hand injury or neuromotor disorder, and provided written informed consent in accordance with procedures approved by the Office for Research Protections of The Pennsylvania State University.
Equipment
Subjects pressed with the four fingers of the right hand on four Nano-17 six-axis force/torque transducers (ATI Industrial Automation, Apex, NC). The sensors’ top surfaces were covered with 320-grit sandpaper. The sensors were mounted on a slotted aluminum plate, which allowed the sensors to be moved in the anterior-posterior direction to accommodate digits of different lengths. The sensors on each plate were spaced 3.0 cm from center-to-center in the medial-lateral direction. The sensors were powered and amplified by multisensor interface boxes (ATI Industrial Automation), which were factory-calibrated for the individual sensors used. Data were sampled at 1,000 Hz with a PCI-6225 16-bit analog-to-digital card (National Instruments, Austin, TX). A custom application built in the LabVIEW programming environment logged data for offline analysis and provided visual feedback to the experimenter and to the subjects. Subjects viewed any available visual feedback on their performance via a 20” monitor placed 1 m from their heads at eye level (Fig. 1A). The feedback represented a one-dimensional mapping of the sum of two finger forces, which differed across conditions (see later).
Fig. 1.

A: schematic illustration of the experiment setup. B: conditions used during the experiment. The instructed (master) fingers for the three conditions of the experiment are shown in gray. This panel also shows the finger pairs that produced forces, which were used to provide visual feedback across conditions. IM, Index + Middle; MR, Middle + Ring; RL, Ring + Little.
Procedure
The experimental procedure consisted of two main parts: maximal voluntary contraction (MVC) and submaximal accurate finger force production trials.
At the beginning of the experiment, the force sensors were adjusted according to the subject’s finger’s length, such that the right hand formed a natural dome, with the fingers in a slightly flexed position (Fig. 1A). The right forearm was aligned with the hand with the natural wrist position in the ulnar-median deviation. At the beginning of each trial, the subject rested the fingers on the force sensors, and the sensor readings were set to zero; as a result, the sensors measured only active downward pressing forces during the trials. Across trials, the subjects were asked to press downward with the fingers without changing the hand/arm configuration (monitored by an experimenter). The experiment was performed in a single 1-h session.
Maximal voluntary contraction task.
First, subjects were instructed to press on the force sensors with all four fingers as hard as possible during a 4-s time window. The sum of the four fingers forces was shown by a cursor on the feedback monitor; the cursor moved upward with force increase. This task was repeated twice, with a 30-s rest period in-between. The highest total maximum voluntary contraction (MVC) force across the two trials was used to set other tasks.
Submaximal accurate finger force production task.
During this task, subjects were asked to press on the force sensors with different instructed finger combinations, referred to as “master” finger pairs: Index-Middle (IM), Middle-Ring (MR), or Ring-Little (RL) (Fig. 1B). Note that the IM and RL pairs involve master fingers with moment production in the same direction, pronation or supination, respectively. Hence, these conditions were expected to be associated with large initial MPS magnitudes with plenty of room for MPS drift. In contrast, the MR condition includes two fingers that are comparably strong (cf. Li et al. 1998), have similar lever arms with respect to the longitudinal forearm axis, and act in opposite directions. So, the initial MPS magnitude was expected to be low and lead to little drift, if any. Note also that two other finger combinations, IR and ML, were explored in an earlier study (Hirose et al. In press).
The instruction was “Press with the instructed fingers to match the target on the screen with the cursor throughout the whole trial. Do not pay attention to possible force production by other fingers of the hand. Keep the cursor in the target accurately until the end of the trial. Never lift any finger off the sensor.” The subjects were at all times watched by an experimenter to ensure compliance with the instruction. In cases a finger was lifted off its sensor, the trial was stopped and repeated. Prior to the experiment, the subjects performed at least three practice trials with each instructed finger pair. During those trials, the target force was set at 25% of the instructed finger-pair MVC. The force produced by the other two (slave) fingers was not shown to the subject, but it was measured during the initial steady-state part of the trial and used to set targets for trials with feedback on slave force (see later).
The target force was set either at 25% of the instructed finger-pair MVC or at the level measured in the practice trials for the slave fingers during that finger-pair trial. This was done to ensure that the subjects were unaware of the feedback manipulation and produced, on average, similar magnitudes of finger forces under the two feedback conditions (see Fig. 2 in results). The feedback signal represented the sum of the master finger forces (for the former target) or the sum of the slave finger forces (for the latter target). The subjects were unaware of the feedback manipulations (presented in random order) and thought that they always pressed with the master fingers to reach the target, as confirmed by the postexperiment interview. Overall, the experimental design included two factors: Finger-pair (IM, MR, and RL) and Feedback (master and slave).
Fig. 2.
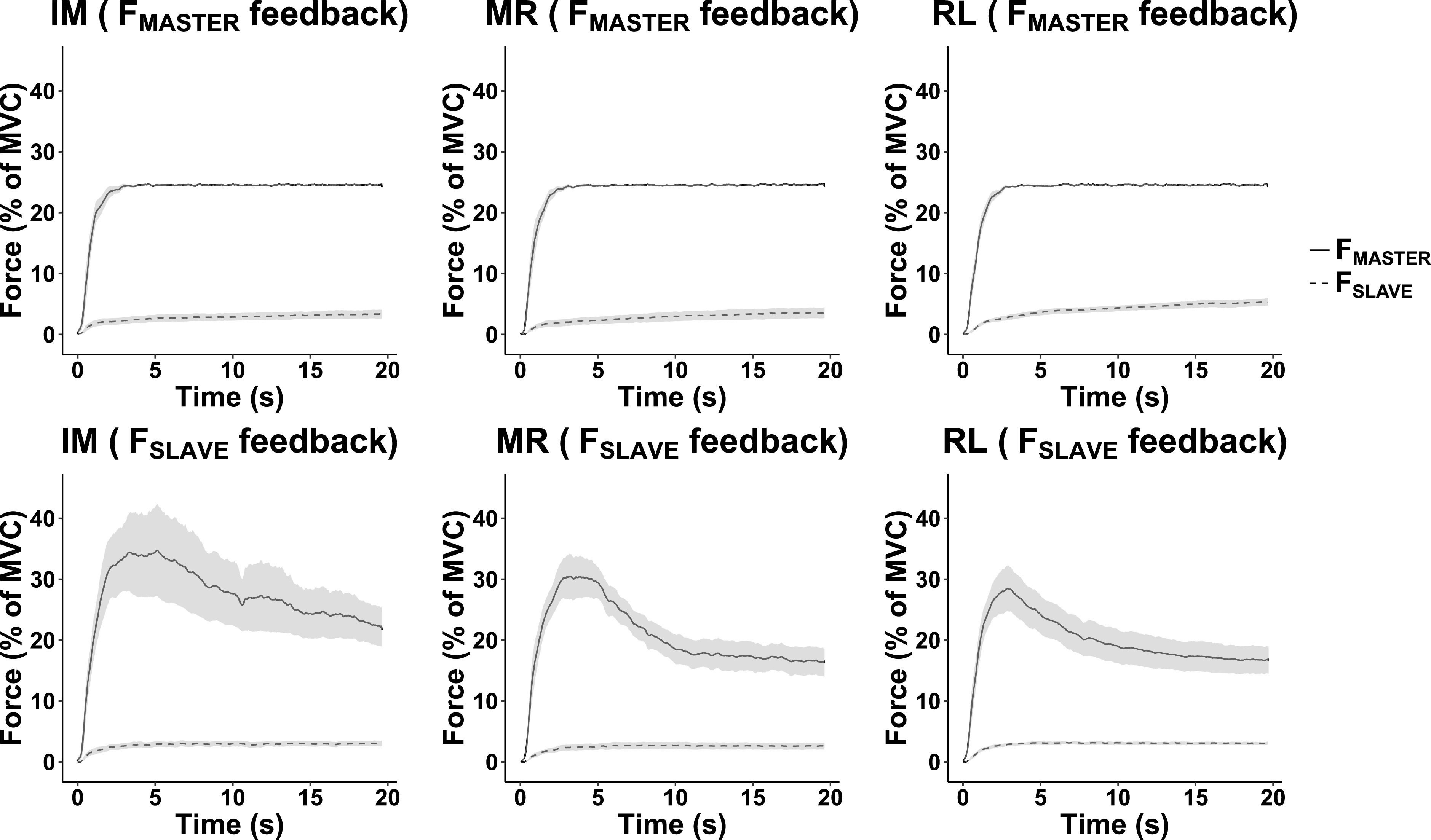
The time series of forces averaged across subjects with standard error shades for the FMASTER (solid lines) and FSLAVE (dashed lines). Top: trials when visual feedback was on FMASTER. Bottom: trial when visual feedback was FSLAVE. IM, Index + Middle; MR, Middle + Ring; RL: Ring + Little.
Each trial lasted 20 s with 8-s rest intervals between trials. Subjects performed 24 trials in a row for each of the master finger pairs, 12 with master finger force feedback and 12 with slave finger force feedback (in a random order). Additional 1-min rest was given to subjects after each 12-trial block. The order of instructed finger pairs was random across subjects.
Data Analysis
Data were processed off-line using routines written in R, version 3.6.1 (R Development Core Team 2019). Before analysis, all force data were low-pass filtered using a fourth-order, zero-delay Butterworth filter with a cutoff frequency of 10 Hz.
Force analysis.
Most of the analysis was performed at the level of finger pairs, master and slave. For each master finger pair, IM, MR, and RL, we computed the average of the sum of the two master finger forces (FMASTER) and two slave finger forces (FSLAVE) over two 500-ms time intervals early in the trial and before the end of the trial. These intervals were selected as 4–4.5 s and 19–19.5 s from the beginning of the trial. These intervals were selected to give subjects enough time to reach steady-state performance early in the trial (4–4.5 s) and to avoid edge effects at the end of the trial (19–19.5 s). We also computed the changes in these forces between the two time intervals as ΔFMASTER and ∆FSLAVE. Negative values of ∆F indicate a drop of force over time, while positive values of ∆F indicate an increase in force over time. Relative force changes were computed as fractions of ∆F with respect to the force value in the early time interval (4–4.5 s). Similar analyses were also performed for the forces produced by individual fingers.
Moment of force analysis.
We computed moment of force produced by the normal finger forces about the axis passing in-between the middle and ring finger sensors in pronation-supination. This variable, MPS, was considered positive for forces by the Index and Middle fingers and negative for forces by the Ring and Little fingers. We assumed no change in the lever arms and used nominal values of ± 1.5 cm for the Middle and Ring fingers and ± 4.5 cm for the Index and Little fingers. Changes in the moment over the trial duration, ∆MPS, were computed similarly to the changes in force between the two time intervals, 4–4.5 s and 19–19.5 s.
Analysis of enslaving.
Enslaving was quantified using an index reflecting the fraction of total force produced by the slave finger pair: E = FSLAVE/FTOT. We also performed analysis of enslaving at the level of individual fingers using the same equation: Ei = Fi/FTOT, where i = I, M, R, and L slave finger. Changes in enslaving were computed between the two time intervals, 4–4.5 s and 19–19.5 s, resulting in ∆E and ∆Ei indices expressed in relative units with respect to their initial values within the first time interval (4–4.5 s).
Statistics
Unless otherwise stated, all data presented in the text and figures are in the format means ± SE. We tested statistical significance at P < 0.05. To test the specific hypotheses, ANOVAs with repeated measures (using a mixed-model method) was used as appropriate to explore the changes in force, moment of force, and enslaving indices. The factors were instructed Finger-pair (IM, MR, and RL) and Feedback (master and slave). We tested the following specific hypotheses. Hypothesis 1 (H1): Master finger force will drift downward under feedback on slave finger force. Hypothesis 2 (H2): Slave finger force will drift upward under feedback on master finger force. Hypothesis 3 (H3): The drifts will be smaller for the MR pair compared with the IM and RL pairs. Hypothesis 4 (H4): Moment of force will drift to lower magnitudes across all conditions. Hypothesis 5 (H5): Enslaving index will increase under all conditions. Pearson correlation analysis was performed to test the following hypothesis: Hypothesis 6 (H6): Force drift magnitude will increase with the initial moment of force magnitude.
Additional analyses were run at the individual finger level. In particular, we tested H1 and H2 for each finger individually. In addition, we tested Hypothesis 7 (H7): Changes in the enslaving index will be larger in the “lateral fingers” (I and L) compared with the “central fingers” (M and R). In this analysis, an additional factor Finger was used.
Significant effects were further explored with pairwise contrasts with Bonferroni corrections. ANOVA model residuals were assessed for normality via quantile-quartile plots and transformed as necessary. All statistical tests were run in R, version 3.6.1 (R Development Core Team 2019).
RESULTS
Force Drifts
All subjects showed consistent patterns of force changes over the course of individual trials, which depended on visual feedback. In particular, when visual feedback on the master finger force (FMASTER) was provided, FMASTER showed minor deviations from the target and the force produced by the slave fingers (FSLAVE) increased gradually. These results are illustrated in Fig. 2 for each of the master finger pairs, IM, MR, and RL, and each feedback condition. Note the increase in FSLAVE (dashed lines) under FMASTER feedback (Fig. 2, top). The same Figure 2, bottom, illustrates a drop in FMASTER (solid lines) under FSLAVE feedback. Note that the initial force magnitudes produced by the master fingers were similar between the two feedback conditions, which was also true for the force magnitudes produced by the slave fingers (compare top and bottom panels). In particular, the mean initial force magnitude of the slave fingers measured between 4 and 4.5 s from the trial initiation was 2.7 ± 0.31% MVC under the slave finger force feedback and 2.8 ± 0.24% MVC under the master finger force feedback.
While the absolute changes in force were much smaller for the slave fingers under the FMASTER feedback, their relative to the initial magnitude changes were comparable to those for the master fingers. This is illustrated in Fig. 3, which shows the average across subjects changes in FMASTER and FSLAVE for the three conditions. On average, FMASTER dropped by ∼35% (F1,36 = 57.382; P < 0.001), and FSLAVE increased by over 50% (F1,36 = 14.437; P < 0.001).
Fig. 3.
The averaged force change relative to its initial magnitude with standard error bars for the master fingers (FMASTER, light gray bars) and slave fingers (FSLAVE, dark gray bars) are shown across subjects for each of the conditions. *P < 0.01, significant effects. IM, Index + Middle; MR, Middle + Ring; RL: Ring + Little.
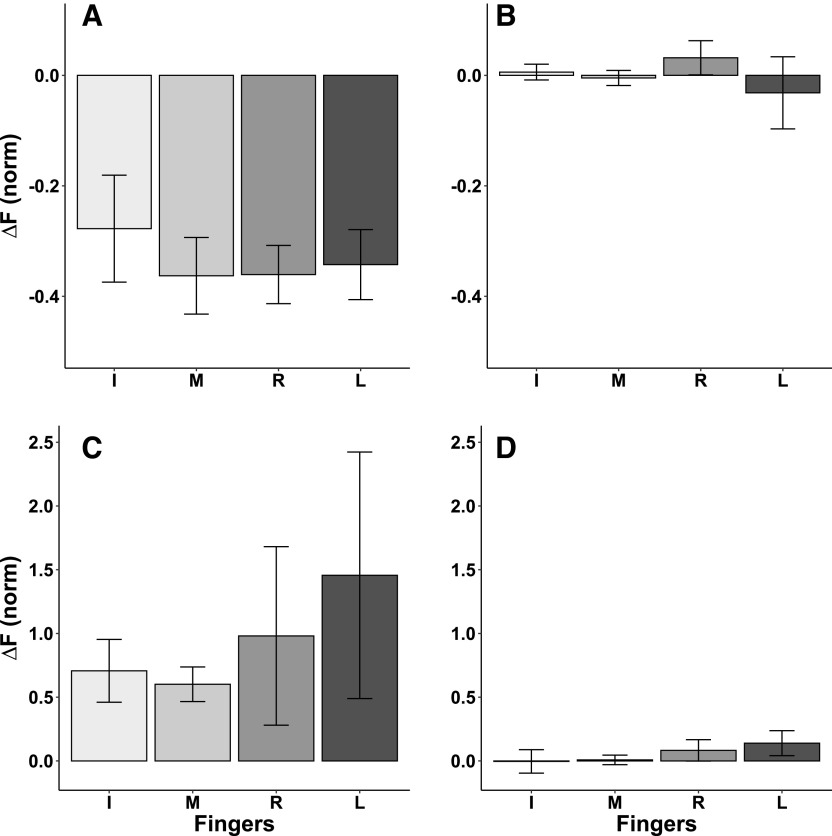
Analysis at the level of individual finger forces confirmed the effects and showed no difference in the force change between the two fingers within each finger pair: effect of Feedback (F1,72 = 86.506; P < 0.001) without other effects. The data for individual finger forces are illustrated in Fig. 4. Note the lack of force drift in fingers that contribute to the force shown on the feedback monitor, namely FMASTER under FMASTER feedback and FSLAVE under FSLAVE feedback (Fig. 4, B and D). In contrast, fingers that contributed to the force not shown on the monitor (FMASTER under FSLAVE feedback and FSLAVE under FMASTER feedback, Fig. 4, A and C) showed consistent force changes similar to those illustrated for the finger pairs in Fig. 3.
Fig. 4.
Normalized individual finger force changes averaged across subjects with standard error bars. A: FMASTER changes when the visual feedback is on FSLAVE. B: FMASTER changes when the visual feedback is on FMASTER. C: FSLAVE changes when the visual feedback is on FMASTER. D: FSLAVE changes when the visual feedback is on FSLAVE. I, Index finger; M, Middle finger; R, Ring finger, L, Little finger.
Moment Drifts
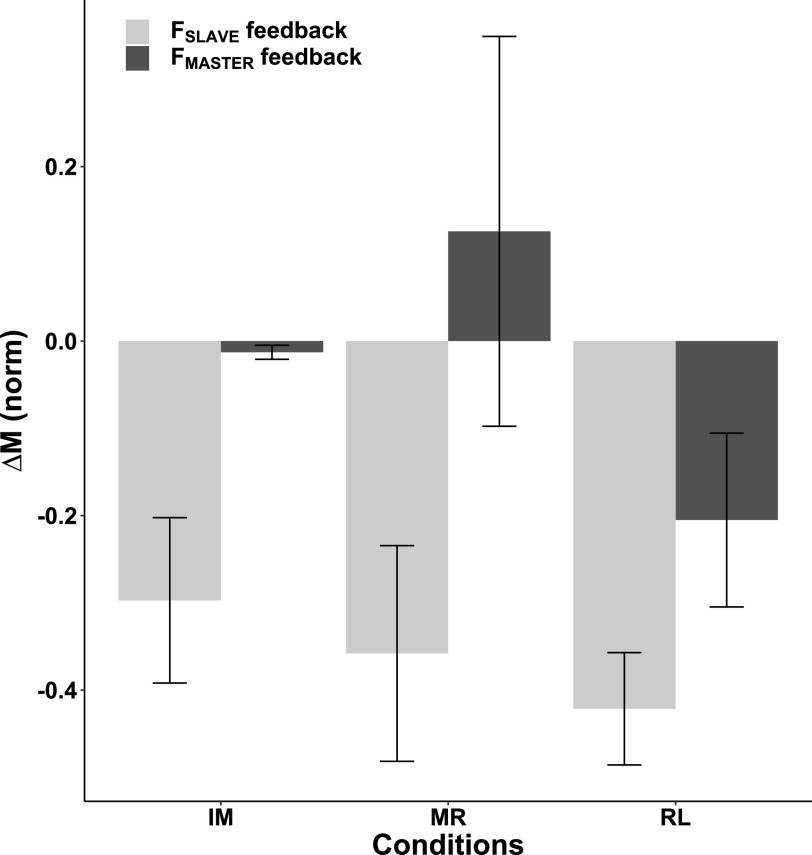
Total moment of force about the longitudinal axis between the M and R fingers (MPS) showed consistent change across the conditions, only when visual feedback on FSLAVE was provided (Fig. 5). The relative drop in the MPS absolute magnitude was ∼35% (F1,36 = 10.978; P = 0.002). In contrast, MPS changes in conditions with feedback on FMASTER were inconsistent and close to zero, on average. There were no statistically significant effects on the index of relative MPS change.
Fig. 5.
The averaged relative moment changes with standard error bars when the visual feedback was on FMASTER (dark gray bars) and on FSLAVE (light gray bars) are shown across subjects for each of the conditions. Positive values of ∆M represent an increase in its absolute magnitude. IM, Index + Middle; MR, Middle + Ring; RL, Ring + Little.
Across-subjects Pearson correlation analysis has shown that the initial MPS magnitude measured within the first time interval (4–4.5 s) was a significant predictor of future force drift magnitude in one condition only, when the instructed finger pair was IM and feedback on FSLAVE was provided (r = 0.925, P = 0.003). In all other conditions, the initial MPS magnitude was not significantly correlated with the force drift magnitude.
Changes in Enslaving
The counter-directional changes in FMASTER and FSLAVE illustrated in Figs. 2 and 3 led to similar drifts in the index of enslaving, E. The index of enslaving computed for the noninstructed finger pairs increased over the trial duration across all three conditions (IM, MR, and RL) and under both feedback conditions (on FMASTER and on FSLAVE). This is illustrated in Fig. 6. On average, the index of enslaving, E, increased from ∼8–10% to ∼12–17% (F1,82 = 15.75; P < 0.001). There were no effects on the relative increase in enslaving, ∆E (it was, on average, 49%) of either Finger-pair or Feedback.
Fig. 6.

Time series of the enslaving index, E, across subjects with standard error shades for the FMASTER feedback (solid line) and FSLAVE feedback (dashed line). IM, Index + Middle; MR, Middle + Ring; RL, Ring + Little.
When quantified for individual enslaved fingers, ∆E for each finger showed consistent increase over the trial duration. The absolute increase in E in the four fingers is illustrated in Fig. 7, which shows the data for each finger averaged across conditions when the finger was enslaved, and feedback was presented on FMASTER. ANOVA showed a significant effect of Finger (F1,36 = 3.057; P = 0.041); pairwise contrasts with Bonferroni corrections confirmed larger ∆E magnitudes in the Middle finger as compared with those in the Little finger (significant effects at P < 0.05 are illustrated in Fig. 7A). When the changes in enslaving were expressed as a percentage of the initial E magnitude, the effects across the fingers became similar (Fig. 7B). No significant effect of Finger was seen.
Fig. 7.
A: changes in the averaged absolute index of enslaving with standard error bars are shown across subjects for each finger. B: averaged relative changes in the index of enslaving with standard error bars are shown across subjects for each finger. I, Index finger, M, Middle finger, R, Ring finger; L, Little finger. *P < 0.05, significant pairwise effect.
DISCUSSION
We reproduced the main findings of the previous study (Hirose et al. In press) using different finger pairs. The observed patterns of unintentional force drifts were consistent across finger pairs: the force of master fingers drifted down when feedback on enslaved finger force was provided [similar to previous studies without visual feedback (Ambike et al. 2015; Vaillancourt and Russell 2002)], and the force of enslaved fingers drifted up under feedback on master finger force. As a result, the experiment falsified the first specific hypothesis. Indeed, unintentional forces drifts during the MR task were similar, both qualitatively and quantitatively, to the drifts observed during the IM and RL tasks.
Two more findings suggest that the counter-directional force drifts were not caused by drifts in control variables (referent coordinates, RC, reviewed by Feldman 2015; Latash 2010) related to the production of the moment of force about the longitudinal hand-forearm axis (MPS). First, the initial magnitude of MPS was not a significant predictor of force drift in all conditions except only one (instructed IM pair, feedback on the enslaved finger force). Second, MPS changes during the force drifts were consistent only under feedback on the enslaved finger force (MPS magnitude decreased under those conditions), but they were inconsistent under feedback on the master finger force. Taken together, these results forced us to reconsider the previous explanation for the counter-directional force drifts offered by Hirose and colleagues (2020).
Our analysis of the changes in enslaving (Zatsiorsky et al. 2000) showed much more consistent behavior across all conditions: The index of enslaving (E) increased by ∼50% over 15 s for all three finger pairs and under visual feedback on both master and enslaved finger force. The invariance of the drift in enslaving suggests that this factor was the origin of other behavioral changes, not their consequence. Further, we elaborate on this idea and its implications for the phenomenon of enslaving, and sketch future studies that could test this hypothesis.
Factors Contributing to Finger Enslaving
Finger nonindependence has been explored in kinematic tasks (Lang and Schieber 2004; Li et al. 2004), force production tasks (Li et al. 1998; Zatsiorsky et al. 2000), and a mixture of both (Kim et al. 2008). It has been discussed as a consequence of both peripheral and central factors (reviewed in Schieber and Santello 2004; van Duinen and Gandevia 2011). Peripheral factors include connective tissue links among fingers (Leijsne et al. 1993 1997) and the presence of extrinsic multitendon finger flexors, flexor digitorum profundus and flexor digitorum superficialis (FDP and FDS). Neural factors include overlapping cortical representations of individual fingers, common neural drive to extrinsic flexor compartments, and diffuse projections of recurrent inhibition and reflex loops (Arpinar-Avsar et al. 2013; Johnston et al. 2004; van Duinen et al. 2010; Winges et al. 2006).
Enslaving has been viewed as a functionally important phenomenon contributing to stability of prehensile tasks (Zatsiorsky et al. 2000; Zatsiorsky and Latash 2008). Its quantitative characteristics have been viewed as robust (cf. Danion et al. 2003a) and used in analysis of stability of multifinger action, as reflected in the structure of intertrial variance in spaces of hypothetical commands to fingers, finger modes (reviewed in Latash 2008, 2019). The possibility of relatively quick changes in characteristics of enslaving (Reschechtko et al. 2014; Wu et al. 2012, 2013), confirmed in our experiments, has to be considered in the design and interpretation of studies that use the notion of finger modes. Indeed, if enslaving can change by ∼50% over 15 s (see Fig. 6), analysis of tasks that take comparable amounts of time has to consider effects of such drifts on estimates of finger mode magnitudes.
Drifts in enslaving over such short time intervals are obviously of a neural origin. We would like to invoke here the concept of “cortical piano” introduced by Schieber (2001). According to this concept, hypothetical neuronal pools at a pre-M1 level generate signals corresponding to intentional involvement of individual fingers, i.e., precursors of the hypothetical finger modes. These signals project on M1 representations of all four fingers, leading to observed patterns of enslaving. These “neuronal chords” are based on the personal lifetime experience and may disintegrate with aging, leading to smaller enslaving and impaired synergies in finger tasks (cf. Kapur et al. 2010; Olafsdottir et al. 2007; Shinohara et al. 2003).
The slow increase in enslaving observed in our study suggests spread of excitation over neighboring M1 neurons (e.g., due to the “Mexican hat” excitability pattern among cortical columns, Kang et al. 2003; Lin et al. 1998; reviewed by Kandel et al. 2012), leading to slowly increasing excitation received by the slave finger representations. Such spread of excitation during steady-state force production may be related to the phenomenon of β-band cortical activity typical of steady states (Engel and Fries 2010; Gilbertson et al. 2005) that shows a tendency to spread over time (Rektor et al. 2006; Tan et al. 2016). As discussed further, this spread of activation could lead to visual feedback-dependent counter-directional force drifts observed in our study.
We explored only relatively low magnitudes of master finger forces, close to 25% of MVC. The documented dependence of enslaving on the magnitude of master finger forces, in particular, within a higher force range, over 50% of MVC (Ejaz et al. 2018; Xu et al. 2017), makes our current conclusions and hypotheses tentative. Exploring higher forces would be highly desirable, although this may not be trivial given possible effects of fatigue.
Factors Contributing to Unintentional Force Drifts
Unintentional force drifts have been studied for ∼20 yr (Slifkin et al. 2000; Vaillancourt and Russell 2002). From the very first studies, it has been clear that fatigue is unlikely to contribute to these phenomena because they are observed consistently at relatively low forces (15–20% of MVC) over relatively short time intervals (10–20 s). Adaptation of peripheral receptors (cf. Iggo and Muir 1969) could be expected to lead to opposite effects and has been invoked to explain unintentional force increase at very low initial force levels (under 5% of MVC; Ambike et al. 2015).
The original studies interpreted force drifts as a reflection of limitations in working memory. This memory hypothesis has been supported by later brain imaging studies (Poon et al. 2012; Vaillancourt et al. 2003) and by observations of larger drifts in patients with Parkinson’s disease known for problems with working memory (Jo et al. 2016; Vaillancourt et al. 2001). On the other hand, a few observations have suggested that the subjects did not forget the initial force level. In particular, when the subjects were asked, in the middle of a trial, to match the force with the contralateral hand, the matching hand produced forces close to the initial force level not the actual, reduced force level (Reschechtko et al. 2018). Similar observations were made during force matching with the same hand after a brief relaxation in the middle of a typical trial with force drift (Solnik et al. 2017).
The phenomena of unintentional force drift have been analyzed within the physical approach to motor control (reviewed by Latash 2016, 2017). According to this approach, voluntary movements are produced by changes in the referent coordinate (RC) for the effector. Their patterns are also defined by the external force field. For example, the same control signals can lead to movement, force production, or both in isotonic, isometric, and mixed-load conditions, respectively. Consider an effector acting along a coordinate X and controlled by two muscle groups, agonists, and antagonists, with RCAG and RCANT, respectively (Fig. 8A). The effector mechanical characteristic (straight thick line) is the algebraic sum of the agonist and antagonist characteristics (dashed lines). In a linear approximation, it can be described with two parameters, intercept (RC) and slope (apparent stiffness, k). Changing RCAG and RCANT in the same direction leads to translation of the effector characteristic in space without a change in its shape, i.e., to a change in RC without a change in k. If RCAG and RCANT change in opposite directions, thus changing the spatial range where both muscle groups are active, k changes without a change in the location of the effector RC. These two basic methods of control have been referred to as changes in the reciprocal and coactivation commands (R- and C-commands), respectively (reviewed in Feldman 2015; Latash 2019).
Fig. 8.
A: an effector acting along a coordinate X is controlled by two muscle groups, agonists and antagonists. Setting their referent coordinates, RCAG and RCANT, results in a F(X) characteristic (straight thick line), which is the algebraic sum of the muscle characteristics (dashed lines). At the level of mechanics, the R- and C-commands define the intercept and slope of F(X). A change in the R-command (∆R) translates the F(X) characteristic. A change in the C-command (∆C) rotates the F(X) characteristic. B: drift of both RCAG and RCANT to the actual coordinate of the effector (X = 0) is expected to lead to a drift in the effector RC toward X = 0 and k toward lower magnitudes, resulting in a drop in the initial force level (compare the black and white circles in Fig. 8B).
Within this framework, an unintentional drift in force in isometric conditions may be caused by a drift in RC and/or k. Indeed, assuming the effector coordinate X = 0, force F = –k•RC. So, a drop in force implies a change of RC to lower absolute magnitudes and/or a drop in k. Such drifts were discussed as consequences of a hypothetical process, RC-back-coupling (cf. Latash et al. 2005; Martin et al. 2009), leading to minimization of the distance between RC for a muscle and the actual length of the muscle (Ambike et al. 2016). This process may be viewed as a tendency of all physical systems to move toward the bottom of the potential field. In Fig. 8B, if both RCAG and RCANT drift to the actual coordinate of the effector (X = 0 in Fig. 8B), this is expected to lead to a drift in the effector RC toward X = 0 and k toward lower magnitudes (compare the black and white circles in Fig. 8B). Both RC drifts and k drifts have been experimentally confirmed (Ambike et al. 2016; Reschechtko and Latash 2017; Reschechtko and Latash 2018).
Enslaving and Control with Referent Coordinates
For simplicity, consider the phenomenon of enslaving between only two finger groups, master fingers and enslaved fingers. Assuming a linear relation between FMASTER and FSLAVE (e.g., Li et al. 1998; Zatsiorsky et al. 2000):
| (2) |
,where ε < 1 is a constant. This simple equation suggests that the typical linear scaling of enslaved force with master finger force may be caused by various couplings at the neural control level. For example, kSLAVE and kMASTER may stay constant, while RCSLAVE scales proportionally to RCMASTER. Alternatively, RC for both finger groups may stay constant while kSLAVE scales proportionally to kMASTER. Given that voluntary force increase is associated with an increase in both activation of the agonist muscles and agonist-antagonist coactivation (Corcos et al. 1990; Ghez and Gordon 1987), changes in both RC and k for the master fingers are likely to take place. Let us consider, for simplicity, that Eq. 2 can be split into two equations:
| (3a) |
| (3b) |
The hypothetical process of RC-back-coupling is likely to happen at the level of control variables for finger forces, not finger modes. This assumption has been supported by both our previous study (Hirose et al. In press) and the results of this study. Indeed, if drifts took place at the level of finger modes (see Eq. 1 in the introduction), providing visual feedback on the master finger force would prevent any drift of that variable (as can be seen in Fig. 5), which means no drift in the modes to those fingers and, consequently, no drifts in the slave finger force. There were, however, large drifts in FSLAVE, suggesting that RC back-coupling led to changes in commands to individual finger pairs (and to individual fingers, since individual finger forces showed patterns similar to those of the respective finger pairs; Fig. 4 and 5).
An increase in FSLAVE under visual feedback on FMASTER implies that off-diagonal entries of matrix E in Eq. 1 increase in magnitude leading to higher enslaved forces. Assuming that keeping FMASTER constant implies both RCMASTER = const. and kMASTER = const. (a strong assumption, cf. Reschechtko and Latash 2017):
| (4a) |
or
| (4b) |
where η(t) is a monotonically increasing time function.
Under visual feedback on FSLAVE, for the initial finger mode vector, m, an increase in the off-diagonal elements of E, as described by Eqs. 4a and 4b, leads to higher visual feedback signal reflecting the actual FSLAVE. Subjects correct the signal deviation by decreasing nonzero entries into m (this is the only method of finger force control allowed by the instruction), which leads to a drop in the master finger forces, which can be due to a drop in the absolute magnitude of RCMASTER and/or kMASTER. Assuming RCSLAVE = const. and kSLAVE = const.:
| (5a) |
or
| (5b) |
Of course, the actual relations between the {RCMASTER; kMASTER} and {RCSLAVE; kSLAVE} pairs may be more complex because numerous such pairs can be used to produce the same finger force magnitude (cf. Ambike et al. 2015, 2016) and because the relation of these variables to force is nonlinear. This simplified scheme, however, allows formulating alternative interpretations for some of the known phenomena and making testable predictions for future studies.
Perception of finger force is rather inaccurate as demonstrated, for example, by the fact that subjects are unaware of rather large changes in force (up to 40% of the initial level) during unintentional force drift under typical conditions (Ambike et al. 2015). When a subject is asked to continue producing the same force level without visual feedback on the force, he or she has to use other sources of information related to the force production. One potential source of this information is sense of “effort”, a subjective measure reflecting primarily efferent processes, which can, however, be modulated by sensory signals (reviewed in Proske and Gandevia 2012; Proske and Allen 2019).
Within the described theoretical framework, sense of effort may be associated with the magnitude of RC. The idea that subjects base perception of force on RC magnitude has been supported by studies of force matching against different spring-like loads (Van Doren 1995, 1998) and by a recent study of the effects of muscle coactivation on force production and perception (Cuadra et al. 2020). In particular, in the last study, the subjects were asked to coactivate arm and hand muscles without changing the initial finger force level. They showed a consistent large increase in force by ∼50% but reported verbally that the force decreased somewhat, consistent with the idea of using RC value to report force.
A number of recent studies have suggested that, during voluntary movements, the corticospinal tract carries signals reflecting RC magnitudes for the effectors (Ilmane et al. 2013; Raptis et al. 2010; Sangani et al. 2011; reviewed by Feldman 2019). It is feasible that, during finger actions, there is central sense of effort associated with the overall output of the motor cortex for all the fingers, RCHAND, even when only a few fingers are explicitly involved. In an earlier subsection, we have suggested that unintentional force drifts observed in our study were consequences of spread of excitation over respective cortical areas, leading to increased E. This is expected to lead to increased RCHAND, perception of increased effort, and lead to corrections, i.e., a drop in the mode signal to master fingers. This prediction is applicable to tasks in the absence of feedback, in particular, to those involving only one finger.
The described mechanism based on hypothetical spread to enslaving may be viewed as complementary to the aforementioned RC-back-coupling. If this mechanism does contribute significantly to the force drift, its quantitative effects are expected to be larger for tasks performed by fingers characterized by higher enslaving indices (e.g., by the Ring finger compared with the Index finger). These effects are expected to be smaller for tasks performed by a larger number of explicitly involved fingers, e.g., in four-finger tasks compared with one-finger or two-finger tasks. In addition, persons with higher enslaving are expected to show larger force drifts (this is true for those with Parkinson’s disease, Jo et al. 2016; Vaillancourt et al. 2001), whereas those with smaller enslaving, such as the healthy elderly (cf. Shinohara et al. 2003) and musicians (cf. Slobounov et al. 2002), are expected to show smaller force drifts. All of these predictions can be checked experimentally.
It is possible that changes at other levels of the neuromotor hierarchy contributed to the increase in enslaving observed in our experiments. In particular, increased synchronization of firing of α-motoneurons innervating different compartments of the extrinsic hand muscles could lead to higher indices of enslaving. Indeed, synchronization of firing of motor units across compartments has been documented for both extrinsic flexors and extensors (Keen and Fuglevand 2004; McIsaac and Fuglevand 2007; Reilly et al. 2004). Although this synchronization is lower than that between motor unit pairs within a compartment (McIsaac and Fuglevand 2007; Reilly and Schieber 2003), it has been considered as a contributor to finger force enslaving (Rearick et al. 2003; Reilly and Schieber 2003). The origin of motor unit synchronization is unclear. It can reflect common descending drive, e.g., from the corticospinal pathways, as well as specific organization of reflex projections from peripheral sensory endings. Possible effects of changes in corticospinal projections have been described earlier in this section. Reflex effects on motor unit synchronization in the human hand muscles are not known well, although such effects have been reported during the tonic vibration reflex (Martin and Park 1997). Whether these effects can change with time during steady-state force production is unknown and, hence, this interpretation remains speculative, although not impossible.
Concluding Comments
We would like to emphasize the most unexpected and robust finding of the invariant drifts in the enslaving index across finger pairs and feedback conditions. This finding is contrasted by the powerful effects of feedback that inverted the direction of force drift. The large and relatively quick changes in enslaving have to be considered in any future studies of finger independence and coordination, in particular, those using the notion of finger modes.
We have to acknowledge the obvious drawbacks of the study, in particular, limiting our experiments to the dominant hand of right-handers only. The well-documented differences in the behavior and control of the dominant and nondominant hands (reviewed by Sainburg 2005) require that the current findings are confirmed across the hands. Testing more subjects would also be desirable, although the main effects that we observe are very strong statistically.
GRANTS
This study received funding from Health and Human Services, National Institutes of Health Grant NS095873.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
V.A. and C.W. conceived and designed research; V.A. and C.W. performed experiments; V.A. analyzed data; V.A. interpreted results of experiments; V.A. prepared figures; V.A. drafted manuscript; C.W. edited and revised manuscript; V.A. and C.W. approved final version of manuscript.
REFERENCES
- Ambike S, Mattos D, Zatsiorsky VM, Latash ML. Unsteady steady-states: central causes of unintentional force drift. Exp Brain Res 234: 3597–3611, 2016. doi: 10.1007/s00221-016-4757-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Zatsiorsky VM, Latash ML. Processes underlying unintentional finger-force changes in the absence of visual feedback. Exp Brain Res 233: 711–721, 2015. doi: 10.1007/s00221-014-4148-x. [DOI] [PubMed] [Google Scholar]
- Arpinar-Avsar P, Park J, Zatsiorsky VM, Latash ML. Effects of muscle vibration on multi-finger interaction and coordination. Exp Brain Res 229: 103–111, 2013. doi: 10.1007/s00221-013-3597-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corcos DM, Agarwal GC, Flaherty BP, Gottlieb GL. Organizing principles for single-joint movements. IV. Implications for isometric contractions. J Neurophysiol 64: 1033–1042, 1990. doi: 10.1152/jn.1990.64.3.1033. [DOI] [PubMed] [Google Scholar]
- Cuadra C, Wojnicz W, Kozinc Z, Latash ML. Perceptual and motor effects of muscle co-activation in a force production task. Neuroscience 437: 34–44, 2020. doi: 10.1016/j.neuroscience.2020.04.023. [DOI] [PubMed] [Google Scholar]
- Danion F, Latash ML, Li S. Finger interactions studied with transcranial magnetic stimulation during multi-finger force production tasks. Clin Neurophysiol 114: 1445–1455, 2003a. doi: 10.1016/S1388-2457(03)00105-6. [DOI] [PubMed] [Google Scholar]
- Danion F, Latash ML, Li Z-M, Zatsiorsky VM. The effect of fatigue on multifinger co-ordination in force production tasks in humans. J Physiol 523: 523–532, 2000. doi: 10.1111/j.1469-7793.2000.00523.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danion F, Latash ML, Li Z-M, Zatsiorsky VM. The effect of a fatiguing exercise by the index finger on single- and multi-finger force production tasks. Exp Brain Res 138: 322–329, 2001. doi: 10.1007/s002210100698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danion F, Schöner G, Latash ML, Li S, Scholz JP, Zatsiorsky VM. A mode hypothesis for finger interaction during multi-finger force-production tasks. Biol Cybern 88: 91–98, 2003b. doi: 10.1007/s00422-002-0336-z. [DOI] [PubMed] [Google Scholar]
- Ejaz N, Xu J, Branscheidt M, Hertler B, Schambra H, Widmer M, Faria AV, Harran MD, Cortes JC, Kim N, Celnik PA, Kitago T, Luft AR, Krakauer JW, Diedrichsen J. Evidence for a subcortical origin of mirror movements after stroke: a longitudinal study. Brain 141: 837–847, 2018. doi: 10.1093/brain/awx384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P. Beta-band oscillations—signalling the status quo? Curr Opin Neurobiol 20: 156–165, 2010. doi: 10.1016/j.conb.2010.02.015. [DOI] [PubMed] [Google Scholar]
- Feldman AG Referent Control of Action and Perception: Challenging Conventional Theories in Behavioral Science. New York: Springer, 2015. [Google Scholar]
- Feldman AG Indirect, referent control of motor actions underlies directional tuning of neurons. J Neurophysiol 121: 823–841, 2019. doi: 10.1152/jn.00575.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghez C, Gordon J. Trajectory control in targeted force impulses. I. Role of opposing muscles. Exp Brain Res 67: 225–240, 1987. doi: 10.1007/BF00248545. [DOI] [PubMed] [Google Scholar]
- Gilbertson T, Lalo E, Doyle L, Di Lazzaro V, Cioni B, Brown P. Existing motor state is favored at the expense of new movement during 13-35 Hz oscillatory synchrony in the human corticospinal system. J Neurosci 25: 7771–7779, 2005. doi: 10.1523/JNEUROSCI.1762-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirose J, Cuadra C, Walter C, Latash ML. Finger interdependence and unintentional force drifts: lessons from manipulations of visual feedback. Hum Move Sci. In press. doi: 10.1016/j.humov.2020.102714. [DOI] [PubMed] [Google Scholar]
- Iggo A, Muir AR. The structure and function of a slowly adapting touch corpuscle in hairy skin. J Physiol 200: 763–796, 1969. doi: 10.1113/jphysiol.1969.sp008721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilmane N, Sangani S, Feldman AG. Corticospinal control strategies underlying voluntary and involuntary wrist movements. Behav Brain Res 236: 350–358, 2013. doi: 10.1016/j.bbr.2012.09.008. [DOI] [PubMed] [Google Scholar]
- Jo HJ, Ambike S, Lewis MM, Huang X, Latash ML. Finger force changes in the absence of visual feedback in patients with Parkinson’s disease. Clin Neurophysiol 127: 684–692, 2016. doi: 10.1016/j.clinph.2015.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston JA, Winges SA, Santello M. Neuromuscular determinants of force coordination during multidigit grasping. Conf Proc IEEE Eng Med Biol Soc 2004: 4645–4648, 2004. doi: 10.1109/IEMBS.2004.1404287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessell TM (Eds.). Principles of Neural Science (5th ed.). New York: McGraw-Hill, 2012. [Google Scholar]
- Kang K, Shelley M, Sompolinsky H. Mexican hats and pinwheels in visual cortex. Proc Natl Acad Sci USA 100: 2848–2853, 2003. doi: 10.1073/pnas.0138051100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapur S, Zatsiorsky VM, Latash ML. Age-related changes in the control of finger force vectors. J Appl Physiol (1985) 109: 1827–1841, 2010. doi: 10.1152/japplphysiol.00430.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keen DA, Fuglevand AJ. Common input to motor neurons innervating the same and different compartments of the human extensor digitorum muscle. J Neurophysiol 91: 57–62, 2004. doi: 10.1152/jn.00650.2003. [DOI] [PubMed] [Google Scholar]
- Kilbreath SL, Gandevia SC. Limited independent flexion of the thumb and fingers in human subjects. J Physiol 479: 487–497, 1994. doi: 10.1113/jphysiol.1994.sp020312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SW, Shim JK, Zatsiorsky VM, Latash ML. Finger inter-dependence: linking the kinetic and kinematic variables. Hum Mov Sci 27: 408–422, 2008. doi: 10.1016/j.humov.2007.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang CE, Schieber MH. Differential impairment of individuated finger movements in humans after damage to the motor cortex or the corticospinal tract. J Neurophysiol 90: 1160–1170, 2003. doi: 10.1152/jn.00130.2003. [DOI] [PubMed] [Google Scholar]
- Lang CE, Schieber MH. Human finger independence: limitations due to passive mechanical coupling versus active neuromuscular control. J Neurophysiol 92: 2802–2810, 2004. doi: 10.1152/jn.00480.2004. [DOI] [PubMed] [Google Scholar]
- Latash ML Synergy. New York: Oxford University Press, 2008. [Google Scholar]
- Latash ML Motor synergies and the equilibrium-point hypothesis. Mot Contr 14: 294–322, 2010. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML Towards physics of neural processes and behavior. Neurosci Biobehav Rev 69: 136–146, 2016. doi: 10.1016/j.neubiorev.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML Biological movement and laws of physics. Mot Contr 21: 327–344, 2017. doi: 10.1123/mc.2016-0016. [DOI] [PubMed] [Google Scholar]
- Latash ML Physics of Biological Action and Perception. New York: Academic Press, 2019. [Google Scholar]
- Latash ML, Huang X. Neural control of movement stability: Lessons from studies of neurological patients. Neuroscience 301: 39–48, 2015. doi: 10.1016/j.neuroscience.2015.05.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Li S, Danion F, Zatsiorsky VM. Central mechanisms of finger interaction during one- and two-hand force production at distal and proximal phalanges. Brain Res 924: 198–208, 2002. doi: 10.1016/S0006-8993(01)03234-6. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multifinger force production tasks. Exp Brain Res 141: 153–165, 2001. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky VM. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern 92: 186–191, 2005. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leijnse JN, Snijders CJ, Bonte JE, Landsmeer JM, Kalker JJ, Van der Meulen JC, Sonneveld GJ, Hovius SE. The hand of the musician: the kinematics of the bidigital finger system with anatomical restrictions. J Biomech 26: 1169–1179, 1993. doi: 10.1016/0021-9290(93)90065-M. [DOI] [PubMed] [Google Scholar]
- Leijnse JN, Walbeehm ET, Sonneveld GJ, Hovius SE, Kauer JM. Connections between the tendons of the musculus flexor digitorum profundus involving the synovial sheaths in the carpal tunnel. Acta Anat (Basel) 160: 112–122, 1997. doi: 10.1159/000148003. [DOI] [PubMed] [Google Scholar]
- Li ZM, Dun S, Harkness DA, Brininger TL. Motion enslaving among multiple fingers of the human hand. Mot Contr 8: 1–15, 2004. doi: 10.1123/mcj.8.1.1. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res 119: 276–286, 1998. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- Lin JK, Pawelzik K, Ernst U, Sejnowski TJ. Irregular synchronous activity in stochastically-coupled networks of integrate-and-fire neurons. Network 9: 333–344, 1998. doi: 10.1088/0954-898X_9_3_004. [DOI] [PubMed] [Google Scholar]
- Martin BJ, Park HS. Analysis of the tonic vibration reflex: influence of vibration variables on motor unit synchronization and fatigue. Eur J Appl Physiol Occup Physiol 75: 504–511, 1997. doi: 10.1007/s004210050196. [DOI] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Comput 21: 1371–1414, 2009. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIsaac TL, Fuglevand AJ. Motor-unit synchrony within and across compartments of the human flexor digitorum superficialis. J Neurophysiol 97: 550–556, 2007. doi: 10.1152/jn.01071.2006. [DOI] [PubMed] [Google Scholar]
- Ohtsuki T Inhibition of individual fingers during grip strength exertion. Ergonomics 24: 21–36, 1981. doi: 10.1080/00140138108924827. [DOI] [PubMed] [Google Scholar]
- Olafsdottir H, Zhang W, Zatsiorsky VM, Latash ML. Age-related changes in multifinger synergies in accurate moment of force production tasks. J Appl Physiol (1985) 102: 1490–1501, 2007. doi: 10.1152/japplphysiol.00966.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Wu Y-H, Lewis MM, Huang X, Latash ML. Changes in multifinger interaction and coordination in Parkinson’s disease. J Neurophysiol 108: 915–924, 2012. doi: 10.1152/jn.00043.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, O’Shea DJ, Zatsiorsky VM, Latash ML. On the nature of unintentional action: a study of force/moment drifts during multifinger tasks. J Neurophysiol 116: 698–708, 2016. doi: 10.1152/jn.00180.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poon C, Chin-Cottongim LG, Coombes SA, Corcos DM, Vaillancourt DE. Spatiotemporal dynamics of brain activity during the transition from visually guided to memory-guided force control. J Neurophysiol 108: 1335–1348, 2012. doi: 10.1152/jn.00972.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proske U, Allen T. The neural basis of the senses of effort, force and heaviness. Exp Brain Res 237: 589–599, 2019. doi: 10.1007/s00221-018-5460-7. [DOI] [PubMed] [Google Scholar]
- Proske U, Gandevia SC. The proprioceptive senses: their roles in signaling body shape, body position and movement, and muscle force. Physiol Rev 92: 1651–1697, 2012. doi: 10.1152/physrev.00048.2011. [DOI] [PubMed] [Google Scholar]
- Raptis H, Burtet L, Forget R, Feldman AG. Control of wrist position and muscle relaxation by shifting spatial frames of reference for motoneuronal recruitment: possible involvement of corticospinal pathways. J Physiol 588: 1551–1570, 2010. doi: 10.1113/jphysiol.2009.186858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rearick MP, Casares A, Santello M. Task-dependent modulation of multi-digit force coordination patterns. J Neurophysiol 89: 1317–1326, 2003. doi: 10.1152/jn.00581.2002. [DOI] [PubMed] [Google Scholar]
- Reilly KT, Nordstrom MA, Schieber MH. Short-term synchronization between motor units in different functional subdivisions of the human flexor digitorum profundus muscle. J Neurophysiol 92: 734–742, 2004. doi: 10.1152/jn.00027.2004. [DOI] [PubMed] [Google Scholar]
- Reilly KT, Schieber MH. Incomplete functional subdivision of the human multitendoned finger muscle flexor digitorum profundus: an electromyographic study. J Neurophysiol 90: 2560–2570, 2003. doi: 10.1152/jn.00287.2003. [DOI] [PubMed] [Google Scholar]
- Rektor I, Sochůrková D, Bocková M. Intracerebral ERD/ERS in voluntary movement and in cognitive visuomotor task. Prog Brain Res 159: 311–330, 2006. doi: 10.1016/S0079-6123(06)59021-1. [DOI] [PubMed] [Google Scholar]
- Reschechtko S, Cuadra C, Latash ML. Force illusions and drifts observed during muscle vibration. J Neurophysiol 119: 326–336, 2018. doi: 10.1152/jn.00563.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Latash ML. Stability of hand force production. I. Hand level control variables and multifinger synergies. J Neurophysiol 118: 3152–3164, 2017. doi: 10.1152/jn.00485.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Latash ML. Stability of hand force production: II. Ascending and descending synergies. J Neurophysiol 120: 1045–1060, 2018. doi: 10.1152/jn.00045.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Zatsiorsky VM, Latash ML. Stability of multifinger action in different state spaces. J Neurophysiol 112: 3209–3218, 2014. doi: 10.1152/jn.00395.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL Handedness: differential specializations for control of trajectory and position. Exerc Sport Sci Rev 33: 206–213, 2005. doi: 10.1097/00003677-200510000-00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sangani SG, Raptis HA, Feldman AG. Subthreshold corticospinal control of anticipatory actions in humans. Behav Brain Res 224: 145–154, 2011. doi: 10.1016/j.bbr.2011.05.041. [DOI] [PubMed] [Google Scholar]
- Schieber MH Constraints on somatotopic organization in the primary motor cortex. J Neurophysiol 86: 2125–2143, 2001. doi: 10.1152/jn.2001.86.5.2125. [DOI] [PubMed] [Google Scholar]
- Schieber MH, Santello M. Hand function: peripheral and central constraints on performance. J Appl Physiol (1985) 96: 2293–2300, 2004. doi: 10.1152/japplphysiol.01063.2003. [DOI] [PubMed] [Google Scholar]
- Shinohara M, Latash ML, Zatsiorsky VM. Age effects on force produced by intrinsic and extrinsic hand muscles and finger interaction during MVC tasks. J Appl Physiol (1985) 95: 1361–1369, 2003. doi: 10.1152/japplphysiol.00070.2003. [DOI] [PubMed] [Google Scholar]
- Slifkin AB, Vaillancourt DE, Newell KM. Intermittency in the control of continuous force production. J Neurophysiol 84: 1708–1718, 2000. doi: 10.1152/jn.2000.84.4.1708. [DOI] [PubMed] [Google Scholar]
- Slobounov S, Chiang H, Johnston J, Ray W. Modulated cortical control of individual fingers in experienced musicians: an EEG study. Electroencephalographic study. Clin Neurophysiol 113: 2013–2024, 2002. doi: 10.1016/S1388-2457(02)00298-5. [DOI] [PubMed] [Google Scholar]
- Solnik S, Qiao M, Latash ML. Effects of visual feedback and memory on unintentional drifts in performance during finger-pressing tasks. Exp Brain Res 235: 1149–1162, 2017. doi: 10.1007/s00221-017-4878-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan H, Wade C, Brown P. Post-movement beta activity in sensorimotor cortex indexes confidence in the estimation from internal models. J Neurosci 36: 1516–1528, 2016. doi: 10.1523/JNEUROSCI.3204-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaillancourt DE, Russell DM. Temporal capacity of short-term visuomotor memory in continuous force production. Exp Brain Res 145: 275–285, 2002. doi: 10.1007/s00221-002-1081-1. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Slifkin AB, Newell KM. Visual control of isometric force in Parkinson’s disease. Neuropsychologia 39: 1410–1418, 2001. doi: 10.1016/S0028-3932(01)00061-6. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Thulborn KR, Corcos DM. Neural basis for the processes that underlie visually guided and internally guided force control in humans. J Neurophysiol 90: 3330–3340, 2003. doi: 10.1152/jn.00394.2003. [DOI] [PubMed] [Google Scholar]
- Van Doren CL Pinch force matching errors predicted by an equilibrium-point model. Exp Brain Res 106: 488–492, 1995. doi: 10.1007/BF00231072. [DOI] [PubMed] [Google Scholar]
- Van Doren CL Differential effects of load stiffness on matching pinch force, finger span, and effort. Exp Brain Res 120: 487–495, 1998. doi: 10.1007/s002210050422. [DOI] [PubMed] [Google Scholar]
- van Duinen H, Gandevia SC. Constraints for control of the human hand. J Physiol 589: 5583–5593, 2011. doi: 10.1113/jphysiol.2011.217810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Duinen H, Gandevia SC, Taylor JL. Voluntary activation of the different compartments of the flexor digitorum profundus. J Neurophysiol 104: 3213–3221, 2010. doi: 10.1152/jn.00470.2010. [DOI] [PubMed] [Google Scholar]
- Winges SA, Johnston JA, Santello M. Muscle-pair specific distribution and grip-type modulation of neural common input to extrinsic digit flexors. J Neurophysiol 96: 1258–1266, 2006. doi: 10.1152/jn.00327.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winges SA, Santello M. Common input to motor units of digit flexors during multi-digit grasping. J Neurophysiol 92: 3210–3220, 2004. doi: 10.1152/jn.00516.2004. [DOI] [PubMed] [Google Scholar]
- Wu Y-H, Pazin N, Zatsiorsky VM, Latash ML. Practicing elements versus practicing coordination: changes in the structure of variance. J Mot Behav 44: 471–478, 2012. doi: 10.1080/00222895.2012.740101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y-H, Pazin N, Zatsiorsky VM, Latash ML. Improving finger coordination in young and elderly persons. Exp Brain Res 226: 273–283, 2013. doi: 10.1007/s00221-013-3433-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Ejaz N, Hertler B, Branscheidt M, Widmer M, Faria AV, Harran MD, Cortes JC, Kim N, Celnik PA, Kitago T, Luft AR, Krakauer JW, Diedrichsen J. Separable systems for recovery of finger strength and control after stroke. J Neurophysiol 118: 1151–1163, 2017. doi: 10.1152/jn.00123.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Multifinger prehension: an overview. J Mot Behav 40: 446–476, 2008. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern 79: 139–150, 1998. doi: 10.1007/s004220050466. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Enslaving effects in multi-finger force production. Exp Brain Res 131: 187–195, 2000. doi: 10.1007/s002219900261. [DOI] [PubMed] [Google Scholar]