Continuous decisions

Abstract

Humans and other animals evolved to make decisions that extend over time with continuous and ever-changing options. Nonetheless, the academic study of decision-making is mostly limited to the simple case of choice between two options. Here, we advocate that the study of choice should expand to include continuous decisions. Continuous decisions, by our definition, involve a continuum of possible responses and take place over an extended period of time during which the response is continuously subject to modification. In most continuous decisions, the range of options can fluctuate and is affected by recent responses, making consideration of reciprocal feedback between choices and the environment essential. The study of continuous decisions raises new questions, such as how abstract processes of valuation and comparison are co-implemented with action planning and execution, how we simulate the large number of possible futures our choices lead to, and how our brains employ hierarchical structure to make choices more efficiently. While microeconomic theory has proven invaluable for discrete decisions, we propose that engineering control theory may serve as a better foundation for continuous ones. And while the concept of value has proven foundational for discrete decisions, goal states and policies may prove more useful for continuous ones.

This article is part of the theme issue ‘Existence and prevalence of economic behaviours among non-human primates’.

1. Introduction

Decisions as studied in the laboratory are typically discrete. Consider a paradigmatic example, the Allais Paradox ([1], figure 1). The Allais Paradox involves a single choice between a pair of categorically distinct fully specified options. It is also prototypical—the vast majority of decisions studied in microeconomics, behavioural economics and neuroeconomics have the same properties [2–4]. In discrete decisions, the decision-maker has, in principle, as long as they want to decide. The result of the choice does not affect what options are made available in the future. The choice itself takes place either instantaneously or irrespective of time, and, once made, is irrevocable. The decision-maker can express their preference verbally, with a button press, or with any other response modality. Finally, the decision-maker's choice is free of context; it is disembodied [5,6].

Figure 1.

The Allais Paradox (left) is a canonical example of what we call a discrete decision. It involves a single choice between two options; the choice is independent of action, context and time. It has no influence on what options are available in the future. A dog moving along a bank preparing to jump and grab a fish (right) is a canonical example of a continuous decision. (Online version in colour.)

Many of the decisions we make in our daily lives are discrete. Examples include selecting an item from a menu in a restaurant and selecting a life insurance plan. However, many other decisions we face in our daily lives are continuous. Consider how a diner selects food bite-by-bite in a large meal, or the daily adjustments to the portfolio of an active stock market investor. Or consider the pursuit behaviour of the window-skimmer dragonfly (Libellula luctuosa). As it pursues its mosquito prey, the dragonfly must continuously monitor the mosquito's position while both prey and predator move rapidly through three-dimensional space [7]. In this situation, the dragonfly is not faced with any obvious discrete decision among fixed options: rather, it must carefully regulate its wings to stabilize its body, track and extrapolate the future position of the prey and plot an intercept course. Actions at each moment come from a large continuum of possibilities, each flowing into the next. Moreover, the mosquito will change its behaviour based on what the dragonfly does, and the dragonfly can exploit its knowledge of that fact to improve its foraging.

While such complex behaviour may be conceptualized as a series of discrete choices—one choice at each moment—this conceptualization is both facile and reductive. It misses some of the most important aspects of continuous decisions, such as the fact that each choice opens many new doors and closes many others. Alternatively, one could view the choice as the selection of an overarching strategy, but this just ignores the important moment-by-moment nature of continuous decisions. It is best to view the decision as encompassing the entire process, from the continuum of motor adjustments to the selection of flight control strategies. Of course, discrete and continuous decisions are not entirely separate categories of decisions. Instead, they represent two extremes of a spectrum of continuousness. Our central message in this manuscript is that the properties of continuous decisions (including the properties of partially continuous ones that are not shared with purely discrete decisions) are deserving of interest.

2. Benefits of studying continuous decisions

The greatest benefit to studying continuous decisions is that they are a type of decision our brains were evolved to make [8–11]. Focusing our research on evolutionarily valid contexts is important because it maximizes our chances of making valid discoveries. If artificial decisions are contrived, then they may, for example, produce preference patterns, including anomalies, that are irrelevant in the natural world.

For example, we and others have argued that the intertemporal choice paradigm, as typically implemented in animals, is quite unnatural and that results from animal intertemporal choice tasks may not paint an accurate picture of natural behaviour [12–17]. Another example comes from the fact that laboratory risk paradigms (including our own) tend to draw possible outcomes from a limited range of possibilities rather than from a continuous probability distribution function [18,19]. Such distributions are mathematically well-behaved, but may be less common than ones with a more continuous and contoured shape. Interestingly, this question of ethological validity applies not just to natural situations but also to markets, which have many properties in common with nature but not with the laboratory (for a compelling discussion of this topic, see [20], figure 2).

Figure 2.

(a) A traditional discrete choice task used to study time preferences is the intertemporal choice task (reviewed in [13]). (b) A patch-leaving task has an ostensibly isomorphic structure, except that the specific options available on the next trial are determined entirely by the choices made on the present trial [12]. This feature has major effects on choice patterns and, although the element of cross-trial dependency is ostensibly more difficult, renders behaviour nearly optimal [21]. (c) The patch-leaving task, but not the intertemporal choice task, is ethologically valid. Here, monkeys at the Cayo Santiago field station travel between their morning foraging site on Large Cay to their afternoon foraging site on Small Cay.

3. Continuous decisions are open-world

We take the term ‘open-world’ from the domain of video games [22]. Open-world games like Grand Theft Auto and Minecraft present players with virtually limitless territory to explore, and terrain filled with a multitude of possible actions. Like the situations in which many real-world decisions occur, they contain more unknowns than knowns, which reward curiosity and search, and a large number of other agents with their own goals [23,24]. Open-world environments pose a significant computational challenge, elided in nearly all laboratory decisions but central to real decisions, of narrowing down a plenitude of possible actions to a small set of ‘live’ options. To meet these challenges, decision-makers must employ cognitive abilities that make these computationally intensive problems tractable, abilities like mental maps, curiosity and heuristics. Note that ‘live’ options have much similarity with afforded options, which have begun to have influence in the neuroscience of decision-making, although the mechanisms by which options activate affordance representations remain poorly understood [18,25–27].

In order to delve into the implications of open-world tasks, we will adopt the language of reinforcement learning (RL) [28,29]. Notably, RL does not need to assume either a model of the world, a fixed set of choices, or even a static set of values. A learner that follows RL can learn online (it does not need to be pre-trained). Moreover, while RL has traditionally been most effective in the tabular setting—the case in which options and contexts are discrete and finite, so that the value of each action can be stored in a lookup table—its formalism is generic enough to extend to continuous decisions. Finally, recent progress in deep RL has opened a new dialogue between machine learning and cognitive neuroscience, producing artificial agents capable of solving challenging continuous tasks like video games while underperforming humans in others like imitation learning (e.g. [30–34]).

(a). States and maps

The first distinction we want to draw between discrete and continuous tasks is in the dimension of what is called the state space. For a given problem, RL always assumes a state, the collection of variables needed to fully define the current context [28,35–38]. For discrete choices, the state space (the set of all possible states) usually consists of a small number of variables—perhaps attribute information for each of the choice options available and some information about current preferences.

For the dragonfly pursuit described above, the current state might include position and velocity information for all joints, estimated position and velocity of both the dragonfly and its prey, and the relative locations of relevant obstacles. The state might also include internal variables of the organisms that might be relevant to predicting behaviour (e.g. hunger, fatigue, etc.). Consequently, the state space in open-world decisions tends to be enormous. In part, the proliferation of these states is related to the mathematical requirements of RL, which assume that the state contains all information on which behaviour at the current time depends. But this explosion of states is also inherent in the complexity of the behaviour itself and the granularity at which it is modelled.

Moreover, it is not just the number of state variables that are increased in continuous decisions, but their ranges. In discrete RL settings, for S state variables with N values each, the size of the state space is N^S. That is, for a decision problem with five yes/no contextual variables (Am I hungry? For sweet or salty snacks? Is there food close by?), there are a total of 2⁵ = 32 possible states. In the case of continuous states, where N becomes infinite, state spaces become infinitely large and tabular approaches must fail. Moreover, in many cases of interest—and not just continuous cases—states are only partially observed, requiring some form of state inference. (For example, in games like poker, opponents' cards are key missing pieces of game state information.)

Fortunately, while practical and algorithmic challenges remain in these cases, they are addressed by existing concepts like models, maps, trajectories and policies that bridge the discrete and continuous cases. The common insight underlying these extensions of tabular RL is that, when states or actions are continuous, we can often make use of a concept of distance, such that ‘nearby’ states are similar and quantities like value can be assumed to change smoothly [28,39,40]. That is, continuous spaces can often, paradoxically, have fewer variables than discrete ones. For instance, if one is given a table of 100 numbers, this data structure has, apparently, 100 free parameters. But if these numbers are samples from a quadratic function at regularly spaced intervals along the x-axis, they are encapsulated by only three parameters. These sorts of geometric and smoothness assumptions often allow one to replace tables with functions and an infinite number of individualized values with a finite number of function parameters, rendering learning feasible once again.

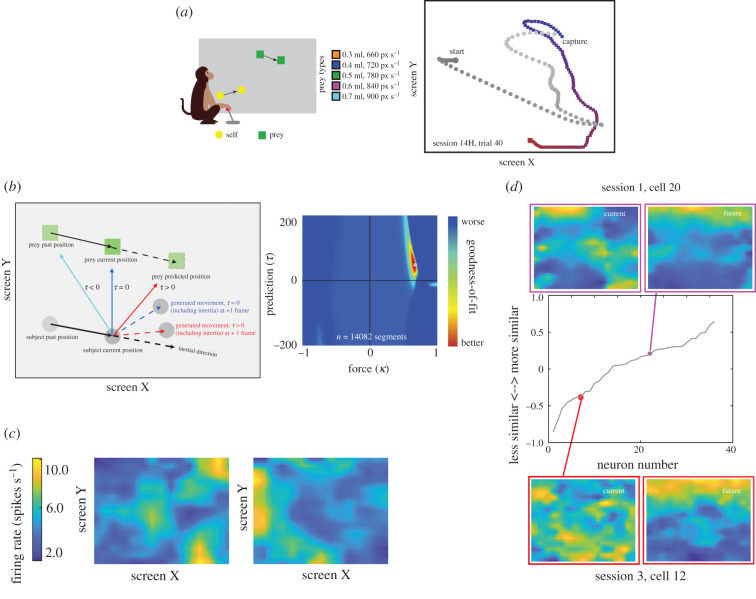
Along related lines, much recent work on RL has focused on the existence and utility of mental models or maps [36,38,41–43]. That work strongly supports the idea that mental maps—originally proposed by Tolman—have a distinct neural reality [44]. To give a specific example, in a simulated pursuit task, we found evidence for such maps in the firing rates of single neurons in the dorsal anterior cingulate cortex (dACC) [45]. Specifically, dACC neurons have complex, non-regular multimodal firing rate place fields, reminiscent of non-grid cells in the medial entorhinal cortex [45]. These maps in dACC (and potentially in other regions as well) likely serve to make possible the kinds of computations necessary for continuous pursuit.

What is important in these cases is that not that such maps are necessary for learning—RL agents who lack them can still eventually learn—but that these maps capture either regularities in state sequences (like random walks on an unseen graph) or structure within the states (like proportions of bird beaks and legs) that facilitate faster learning. In the language of learning theory, they constitute inductive biases that allow learners to make the most of each observation. More importantly, such inductive biases, by making strong assumptions about the possible types of knowledge to be acquired, combat the curse of dimensionality. In the studies above, though numbers of states were large, their dimensionalities remained small. When dimensionality likewise increases, learning becomes an intractable search problem without some form of organizing assumption.

(b). Exploration

Of course, our formulation of continuous, open-world decisions naturally intersects with the question of how open worlds can be mapped. That is, continuous decisions face a much more extreme version of the explore/exploit dilemma than discrete choice paradigms. Thus, curiosity has recently experienced a surge of interest not only in neuroscience, but in RL [23,24,46–49]. This also links to theoretical work on free-energy-inspired models [50,51] that incorporate information seeking, inference and reward into a single framework. However, this rapidly growing body of work is beyond the scope of this review. For our purposes, we are interested in the challenges and opportunities posed by continuous tasks, and focus for the remainder on the necessary integration of action and decision, assuming important quantities like exploratory policy and reward functions as given. More specifically, open-world decisions necessitate exploration, since the world is too big to be known, and that exploration requires strategy because large state spaces cannot be exhaustively visited [48,49]. In short, continuous decision-makers are almost always highly information-starved [23].

(c). Need for heuristics

Finally, it is important to note that the goal of action is not necessarily to find the optimal course of action, but instead to find a course of action that is sufficiently good [52–55]. Heuristic approaches are, of course, valuable even in simple non-continuous decisions. The additional complexity of natural decisions means that satisficing approaches, such as heuristics, are likely to be used in real-world decision-making. In continuous decisions, where the costs of computation are much greater and the time pressures more unrelenting, heuristics are likely to be even more important. Understanding the use of heuristics in continuous decisions, then, represents an important future direction for study (figure 3).

Figure 3.

Task and data from [45]. (a) Left: cartoon of virtual pursuit task. Subject uses a joystick to control an avatar (circle) and pursue prey (square) on a computer screen. Right: avatar and prey trajectories on example trials. Grey: path of avatar; red/blue: path of prey. Colour gradient indicates the time progression through the trial. (b) Left: a generative model explains the trajectory of non-human primates. Right: the model result exhibiting that non-human primates are predicting the future position of the prey. (c) Example filters from neurons that are tuned for the position of the prey within the monitor. (d) Example filters of neurons that are tuned for the future position of the prey.

4. Continuous decisions involve dynamics and feedback

Two more important and closely related features of many continuous decisions are that they are dynamic and involve feedback. Indeed, the importance of both dynamics (sometimes high-dimensional, often nonlinear) and feedback (from both other agents and the environment) is the most obvious distinguishing feature between continuous decisions and their discrete counterparts. The problems imposed by dynamics encompass questions not only of control (e.g. how to move an arm to snatch a passing prey), but also of timing (precisely when to make this move), adding additional complexities often excluded in laboratory decision paradigms. Once again, we believe that RL, particularly its intersection with control theory, offers a conceptual framework for addressing these challenges, even in cases where learning is not the primary dynamic [56,57].

Before stepping further, it is helpful to draw the distinction between modelling a set of actions as sequential decisions and the cognitive experience of the sequential decision-making. For instance, while it is intuitive that the iterated Prisoner's Dilemma involves a sequence of cooperation and defection decisions by each player, it is less intuitive that a short walk down a straight hallway also comprises a series of decisions, one for each step. Yet both can be modelled mathematically as probabilistic sequences of ‘decisions,’ perhaps, in the case of walking, with rewards for staying upright and forward progress. Yet our subjective experience is one of the long periods of automatic behaviour punctuated by changes of mind, phenomena that are only imperfectly captured by the framework of sequential decisions. Instead, we might prefer to mirror mathematically the dissociation between rare goal changes and continuous execution of unconscious behaviours in time.

Help in thinking about these problems comes from control theory, which has a long and fruitful history in motor neuroscience (e.g. [56–59]). In the control framework, a system is endowed with a set of possible controls to apply (forces, torques, electronic commands), a system to which these controls may be applied (typically modelled as a set of differential equations), a goal or set point and a cost for applying control (energy, price, regret). The aim of control theory is to solve for a policy, an algorithm that sets control as a function of the system's state at a given time. The optimal policy is one that best balances control error (how close the system remains to its goal) against control costs. Such a framework automatically addresses two key problems identified above. First, control systems operate in time. Control policies are functions, not discrete actions, and specify how the controller co-evolves with the system. They are thus fundamentally dynamic quantities. Second, control policies do not require the semantics of decisions at all. They are conceptualized as automatic processes that operate adaptively, often deterministically, once a goal has been set. Thus, they have intuitive appeal for a framework that combines sparse, conscious decisions with automatic ongoing processes.

Again, this approach is complementary to the RL perspective reviewed above [28], which likewise attempts to learn a policy that maximizes some set of rewards. In fact, many classic RL problems like cart-pole or learning to walk are control problems [56,60,61]. Such links have often been overlooked in decision neuroscience, where RL actions are most frequently associated with decisions [62], but there is nothing in the formalism to force this view. Before the advent of deep RL, RL methods were often limited to low-dimensional, discrete state and action spaces, but modern applications now routinely feature complex, continuous policies parameterized by deep neural networks [30,63]. Thus, RL likewise offers up the notion of a full policy in place of a discrete action as a building block of continuous decisions.

Just as importantly, while control systems are often assumed to be autonomous, with fixed, pre-specified set points, RL can be extended to the case of hierarchical learning and control [64–70]. That is, the RL framework can easily accommodate the idea of switching between policies or changing goals within the same policy [71,72]. These high-level changes are most often slower (in the case of goals) or sparser (for policy switches) and map neatly onto the experience of rarer deliberative decisions setting in motion automatic behaviours. Moreover, hierarchical formulations of RL allow changes in state to drive high-level actions, facilitating ‘bottom-up’ feedback that renders policies more flexible than purely ‘fire and forget’ processes. And while training such hierarchical RL systems has continued to prove challenging [65–67,73], there is ample evidence that brains have evolved by solving exactly this problem [38].

(a). Example: penalty kick task

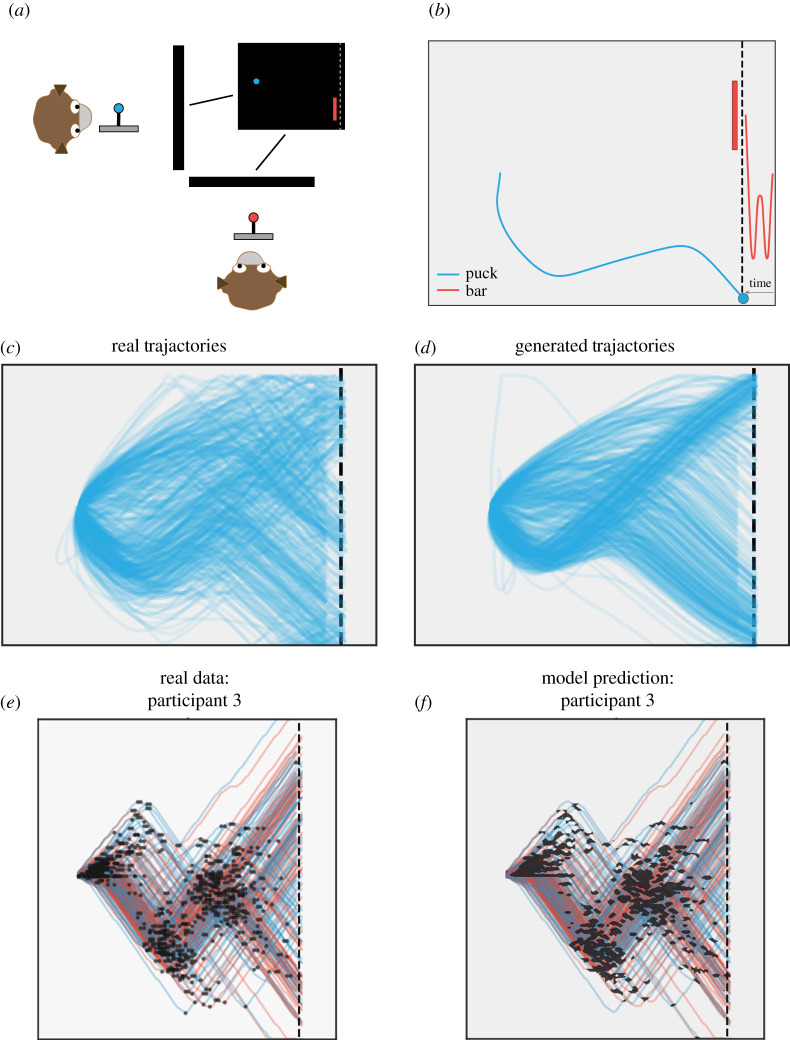
A recent study from our group illustrates this sort of integration of continuous control with sparse strategy changes. In the penalty kick task, monkeys and humans played a competitive video game against conspecifics that required continuous joystick input ([71,72], figure 4). The game is based on the idea of a penalty shot in hockey. One player (the shooter) controlled the motion of a small circle (the puck), while the other player (the goalie) controlled the vertical motion of a bar placed at the opposite side of the screen. Goalies were rewarded for blocking the puck with the bar, while shooters received rewards for reaching a goal line behind the bar. Though the game was highly constrained, players' trajectories proved highly variable, revealing a variety of both individual strategies and inter-player dynamics. Such paradigms as this bear some relation to continuous games such as duels and are closely related to pursuit games in differential game theory, but in the latter, the focus is typically on computing optimal solutions rather than modelling players’ real behaviour [74,75].

Figure 4.

Task from [72]. (a) Pairs of monkeys competed in a zero-sum, real-time game with continuous joystick inputs. One player controlled the position of a blue ball, the other the vertical position of a red bar. The goal of the blue player was to guide the ball past the dotted line at the right of the screen, while the red player attempted to block the ball with the bar. (b) Example of a single pair of player trajectories on a single trial. For display purposes, the trajectory of the bar has been extended in time along the x-axis, though the bar could only move vertically. (c) Continuous control resulted in highly varied trajectories, but these could be captured by a model of players' coevolving goal states that generated realistic trials (d). (e) In a version of the same task in human subjects, players’ trajectories were characterized by sparse changes in trajectory (black dots), and these changepoints could be predicted by modelling players' policies as a function of continuous game state (f). Black patches represent regions of increased probability of direction change. Blue traces indicate trials played against a human bar opponent, red traces those played against a computer. Adapted from [71,72].

These phenomena can be modelled as the result of a control model applied to an evolving value function incorporating each player's trajectory [72,76], while directly modelling players' policies allows for the calculation of a measure of instantaneous coupling between the players [71]. However, in both human and monkey participants, we found that the key strategic variable was not so much shooters’ ability to adjust to their opponents as their ability to advantageously time their final movements on each trial [71]. This work, in other words, provides important information about the specific strategies that human and macaque decision-makers are able to use in such tasks; that information is unavailable in discrete decision-making paradigms.

5. Implications for neuroscience: a preliminary sketch

Traditional ‘box-and-line’ approaches to cognitive neuroscience presume the existence of discrete cognitive functions with intuitive easy-to-name roles. These functions are assumed to be reified in neuroanatomy. For example, if choice consists of evaluation, comparison and selection, then these three conceptually discrete functions ought to correspond to discrete anatomical substrates [77,78]. An alternative viewpoint is distributed; it imagines that choice reflects an emergent process arising from multiple brain regions whose functions may not correspond to nameable processes, and/or that may largely overlap [18,25,79–81].

The greatest debates about modularity concern the prefrontal cortex, which can be readily divided into a few dozen areas based on cytoarchitecture. However, the functions of these areas remain difficult to identify definitively. In fact, this architectural diversity raises the question of why we have so many prefrontal regions to begin with [82]. One possibility is that each region integrates new information from new sources and participates in transforming that information via an untangling process [79]. In this view, each area in sequence provides a partial transformation from one representation format to another [83,84]. Indeed, it is this view, and not that of a modular system, that best accords with recent results in artificial neural networks (e.g. [85–87]). Of course, some cognitive functions are localized at the coarsest levels. Our claim is simply that, once one embraces the framework of continuous decisions, with its tight coupling of action and decision, dynamics and feedback, the tight conceptual link between modularity in space and serial processing in time is no longer as natural as it has traditionally appeared.

To elaborate on this last point, consider choosing between two options. In this simple situation, there is no particular reason (aside from reaction time minimization) for the motor action to begin until comparison and choice of option are complete [18]. In other words, a serial design suffices. And indeed, there is plentiful evidence consistent with the serial model of choice (e.g. [78]). But in continuous decisions, the action is fully interwoven with choice. It is difficult to even think about how choice may occur without consideration of action [18,25].

We explored the idea of how the brain predicts the future in a recent study [45]. In our virtual pursuit project (see above), subjects could gain a strategic advantage over their prey by predicting the prey's future position and moving to it, and a generative model of behaviour allowed us to confirm that subjects indeed moved towards the predicted position of the prey. We then used the mapping algorithm to map the representation of predicted future positions of prey (specifically, one developed in [88]). That is, we computed the average firing rate of each neuron as a function of the position in space of the future position of the avatar. These maps are akin to place cell maps in the hippocampus, but they are for virtual positions (on a computer screen) and for future, rather than present positions. We found that these maps are present in single dACC neurons and that they come from the same cells—multiplexed—as self-position maps.

When decisions are not discrete selections but processes of continuous adjustment made on the fly, action selection can no longer easily be separated from choice. This suggests a link to embodied decision-making arguments forwarded by Shadlen et al. [89], who argue that the responses of single neurons in the lateral intraparietal area (LIP) to visual motion are actually better thought of as an embodied decision variable—the weight of evidence in favour of shifting gaze to a particular location. This theory neatly explains why such signals are found in neurons with response fields, and neatly solves the classic debate about the intentional role of LIP. It is a small move from this theory of perceptual decision-making to economic decisions.

(a). Modularity and continuous decisions

We explored the idea of how the brain predicts the future in a recent study [45]. Predicting the consequences of our actions and using those predictions to guide choice are common to discrete decisions [90,91]. But it is much more difficult in continuous tasks. In our virtual pursuit project (see above), subjects could gain a strategic advantage over their prey by predicting the prey's future position and moving to it—much like the dragonfly discussed above. We then designed a generative model of behaviour and were able to explicitly test the hypothesis that subjects moved towards the predicted position of the prey. We then used the mapping algorithm to map the representation of predicted future positions of prey. We found that these maps are present in single dACC neurons and that they come from the same cells—multiplexed—as self-position maps.

A consequence of this idea is that decision computations ought to be constrained, at least in part, by the motor system. There is plentiful evidence for this idea. For example, we tend to gaze longer at options that we are about to choose. There is evidence that exogenous manipulations that bias our looking times towards one option increase our chances of choosing that option [92]. Another example is the idea from robotics and cognitive science called ‘morphological computation’ [93–95]. The idea is that the shape and material properties of the body can be exploited to make central control processes simpler. It implies that the local computation that is based on certain properties of the body would influence the control process [96]. In this case, if a certain effector is used to implement choice, their biomechanical properties would influence the outcome of the choice. This raises an intriguing possibility—continuous decisions expressed in two modalities may differ owing to different physical properties or biomechanical constraints. Because continuous decisions are more tightly integrated with effector systems than discrete ones are, their underlying computations will be more influenced by the affordances of these systems. That is, we may make the same choice whether the output modality is our eyes, our fingers or our feet, but we may make different decisions when the modality is the same. We may, for example, predict further into the future when using our eyes than our hands.

Further evidence comes from the fact that subjects appear to initiate their action before they have fully decided on an option. That is, they hedge their bets and choose an intermediate path between the two options [97,98]. Then, as their decision process unfolds in their heads, their arm changes its pattern and begins to divert its path towards the chosen option. Critically, the initial hedging path lasts longer if the choice takes more time to unfold. In other words, the beginning of selection takes place before the choice is complete. Taking this idea literally, the choice process occurs simultaneously with the motor action. They are not discrete and the action would provide a feedback signal to the choice, which is opposed to the idea that movement does not influence the choice at all. Ultimately, then, the resolution of the question of modularity requires testing under more naturalistic contexts. That is, natural tasks provide a valuable ‘stress test’ for modular models.

6. Conclusion

Here, we offer a definition for continuous decisions, and, by contrast, a complementary definition for discrete decisions. We argue that the neuroscientific and psychological study of decision-making is impoverished by its near-exclusive focus on discrete decisions, and would be enriched by expanding its scope to include continuous ones.

One practical obstacle is the lack of standardized tasks that can serve as the focus of such research. We propose that simple computerized continuous motion tasks, such as the penalty kick task and pursuit task, can serve that role [45,72]. These two tasks involve a continuum of actions, take place over an extended time, and, because they involve multiple players, exhibit the complex intra-trial feedback relationship for decisions that is characteristic of many naturalistic continuous decisions.

Another practical obstacle to the adoption of continuous decisions is the additional complexity involved in studying continuous tasks. As a result, we propose that the development of new analysis techniques ought to be a major focus moving forward. For example, most traditional analyses in systems neuroscience have relied on averages, both in time and across trials, to reduce the complexity in data and achieve statistical power. But when trial-to-trial behavioural variability is large, these repetitions may no longer be comparable to one another. As a result, single-trial analyses will likely be crucial (e.g. [99,100], also [71,72,76]). And these methods often benefit from denser recording techniques such as calcium imaging [101] and multi-contact multi-electrode recording ([102,103] and [104,105]).

Along a different axis, there is much promise in recent studies that eschew single brain areas in favour of integrative analyses of simple, natural behaviours. Recent technical advances are making such studies possible, and this trend is likely to continue (e.g. [106]). Corresponding analytical tools are being developed too [107,108]. This also requires novel theories about information transformations between areas (e.g. [79,86,109]).

To the degree that some complexity in behaviour is irreducible, the study of continuous decisions is both necessary and inevitable. Not only are these decisions closer to natural behaviour (and so easier to train in model species), they begin to tap the complexity we want to study, offering new puzzles that force us to integrate our knowledge across cognitive levels, brain regions and time scales. If the behaviours we are interested in—our own included—take place in a changing, dynamic world, then our models of that world must grow to embrace these essential features.

Data accessibility

This article has no additional data.

Authors' contributions

All authors worked together to generate this paper.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.