Abstract
Numerous studies have documented changes in the seasonal timing of organisms’ growth and reproduction in response to climate warming. These changes correlate with documented changes in species’ abundance, but mechanisms linking these trends remain elusive. We investigated the joint demographic effects of advanced reproductive phenology and warming on a globally invasive plant (Carduus nutans) in a field experiment, documenting a substantial shift toward completion of the life cycle at younger ages. Demographic modeling projected 71% of warmed individuals flower as annuals, compared to 61% under current conditions. As this species only reproduces once, this represents a major acceleration of the life cycle. We project a 15% increase in this invader’s population growth rate. We show that rising temperatures accelerate this invasive species’ population growth by increasing the average size of reproducing individuals; increasing the proportion of individuals that survive to reproduce; and increasing the fraction that reproduce as annuals. Major increases in population growth in this, and potentially many other, invasive species will threaten food security and require careful planning to avoid significant environmental and economic impacts.
Keywords: climate change, Carduus nutans, demography, integral projection model, invasive species, life cycle, phenology
Introduction
Climate warming has caused changes in many organisms’ phenology (Parmesan and Yohe 2003, Cleland et al. 2007). Changes in phenology may affect demography, but generally the demographic consequences of phenological shifts remain unclear (Miller‐Rushing et al. 2010, but see Ozgul et al. 2010, Iler et al. 2019, Macgregor et al. 2019, Paniw et al. 2019). Although phenology’s effects on individuals’ performance have been documented in numerous cases (Van Dongen et al. 1997, Colautti and Barrett 2013, Scheepens and Stöcklin 2013), linking differences in performance to demographic outcomes is difficult, as changes in traits do not always lead to changes in population dynamics (McLean et al. 2016). Observational work suggests that phenological sensitivity may underlie changes in species’ abundance over time, however. More phenologically sensitive plant and bird species, for example, are less likely to have declined in abundance over time (Møller et al. 2008, Willis et al. 2008). Additionally, high phenological sensitivity may contribute to the growth of invasive populations (Willis et al. 2010). Together, these trends suggest a link between phenology and demography, but mechanisms driving those links remain elusive.
Full understanding of demographic consequences of phenological shifts requires consideration of organisms’ full life cycles. Changes in the timing of plants’ leaf out, for example, may affect duration of growth before flowering, timing of flowering, timing of germination, and thereby the growth and survival of newly produced offspring (Johnson 1993). When organisms’ full life cycles have been considered, the phenology‐mediated impacts of climate warming on demography have been substantial. Ozgul et al. (2010), for example, found earlier spring emergence from hibernation among yellow‐bellied marmots led to earlier births and lengthened the growing season for new offspring, allowing them to reach larger sizes before hibernation, which in turn reduced mortality and led to rapid population growth (Ozgul et al. 2010).
Organisms with flexible life histories may see large changes to their demography as temperatures rise. Short‐lived monocarpic perennial plants, which can grow for one to several years and die after reproducing, may see large effects of warming and phenology on both the number of offspring produced and the time it takes for individuals to produce them. Monocarpic perennials have served as illuminating model systems in which to investigate the evolution of plant life histories (Metcalf et al. 2003), and they make a tractable experimental system in which to investigate climate impacts on life cycles.
Here we report the results of a field experiment in which we independently manipulated temperature and reproductive phenology, specifically, timing of seed release. We focus on musk thistle (Carduus nutans L.), a widespread invasive species that advances flowering in response to warming (Zhang et al. 2012). Musk thistle is a monocarpic perennial with size‐dependent reproduction. Changes in growth are therefore expected to directly affect the musk thistle life cycle and hence its demography. We consider the joint impacts of warming and advanced reproductive phenology across the full life cycle of C. nutans using demographic models, and address the following:
Does temperature affect the size‐dependent vital rates (growth, survival, probability of reproduction, and fecundity) of musk thistle?
Does the timing of seed release affect the size of new recruits, and thereby their probability of reproducing (which only happens once in an individual’s life) as annuals, rather than as biennials or perennials?
How do warming and reproductive phenology interact to influence musk thistle demography?
Methods
Study species
Musk thistle, Carduus nutans L. (Asteraceae), is a weed of Eurasian origin and a pest in pastures and rangelands, where its spiny leaves inhibit grazing, reducing livestock productivity (Desrochers et al. 1988). This thistle has invaded disturbed areas in North America, South Africa, Australia, and New Zealand (Jongejans et al. 2008). It is widespread in North America (USDA NRCS 2012). Musk thistle is a short‐lived monocarpic perennial. Individuals germinate in the fall or spring and can persist for one to several years as rosettes before bolting, flowering, releasing wind‐dispersed seeds, and dying (Desrochers et al. 1988). Musk thistle is a prolific seed producer, with individual plants capable of producing thousands of wind‐dispersed seeds that germinate well immediately following release (Popay et al. 1987).
Field experiment
We conducted a two‐cohort field experiment at the Russell E. Larson Agricultural Research Farm in Rock Springs, Pennsylvania, USA (latitude 40.71° N, longitude 77.94° W). The site was prepared before planting each cohort by applying a miller offset disk two times to kill aboveground vegetation and then applying a roller harrow to level the soil surface. This preparation mimicked the type of disturbance that promotes musk thistle establishment along roadsides and in pastures. Aboveground competition was suppressed by clipping all vegetation other than our focal thistles down to the soil surface weekly to avoid a possible interaction between temperature treatments and vegetative competition. We manipulated temperature using fiberglass cone open top chambers (OTCs) with basal diameter of 1.48 m constructed according to the International Tundra Experiment Manual (Molau and Mølgaard 1996). Throughout the experiment, temperature was monitored in warmed and ambient plots using HOBO pendant temperature loggers (Onset Computer Corporation, Bourne, Massachusetts, USA) installed at the soil surface. Over the course of the experiment, OTCs warmed plots by an average of 0.36°C (95% CI [0.34, 0.37], paired t test, P < 0.001). Prior work at this field site showed no significant effect of OTCs on soil moisture or snow depth (Zhang 2011).
We manipulated the phenology of seed release by planting mature seeds at seven different times throughout the fall growing season (see Appendix S1: Table S1). In each year of the experiment, seeds were collected on a single day in July prior to planting from >50 individual mother plants from a single naturally occurring population of musk thistle to the south of our experimental site in Carlisle, Pennsylvania, USA. Seeds were extracted from flower heads, mixed together, and sifted to retain only ripened seeds. We stored seeds in paper envelopes at room temperature until they were planted. Carduus nutans germination is triggered by suitable microhabitat conditions (Hamrick and Lee 1987) and prior pilot studies in the Shea lab show that similar germination rates are generated by moisture over an extended period. On each planting date, we scattered 100 seeds over an area of 10 × 15 cm and covered them with a dusting of soil that was lightly compressed to hold seeds in place and reduce removal by seed predators. We also marked control plots with no seeds planted to track any background germination of thistles from the seed bank; background contamination was negligible (three seedlings over the whole experiment) and is not discussed further.
The two treatments, temperature and seed release timing, were crossed in a split plot design, with seed release dates splitting temperature treatments. Within each of 6 (cohort 1) and 10 (cohort 2) blocks, we established 2 × 2 m plots for each temperature treatment and randomly divided the eight seed‐release timing treatments (including a control) across them. For the first cohort, each block contained two plots that were randomly assigned to a temperature treatment: one at ambient temperature and one warmed. The seven seed release timing treatments and an unplanted control were randomly allocated to eight areas arranged in a circle in each plot to avoid any effects of chamber edges, which had a slight overhang. For the second cohort, each block contained four plots, two of which were randomly selected to be warmed, leaving the remaining two at ambient temperatures. For this cohort, each plot contained four areas located around the plot center separated by >30 cm, and the seven planting time treatments plus the unplanted control were randomly allocated over the eight warmed and over the eight ambient areas present within the block (now divided over two plots each, see Appendix S1: Fig. S1 for the layout of each cohort).
For both cohorts, germination was observed throughout the summer and fall seasons, and the first three germinating individuals were individually marked. Other seedlings were counted and removed as they appeared. Marked seedlings’ survival, longest leaf length, and number of leaves were monitored throughout the fall. In the spring, one surviving individual from each sub‐plot was randomly selected for continued observation, and the other rosettes within the area were removed to reduce crowding. We harvested bolting individuals as they senesced in late July. We counted the total number of capitula produced by each bolting individual, and we measured capitulum diameter to estimate seed production according to a known, strongly significant relationship (Marchetto et al. 2014). In total, over the course of the experiment (2012–2016 for the first cohort, 2013–2016 for the second cohort), we recorded end‐of‐growing‐season data on 558 rosettes (207 from the first cohort and 351 from the second), 388 of which were thinned out in spring and 170 of which were left to continue growing. Over the course of the experiment we observed 138 bolting plants (51 from the first cohort and 87 from the second).
Vital rate regressions
We fit generalized linear mixed effects models (package lme4 in R v. 3.4.1; Bates et al. 2015, R Core Team 2017) to examine whether musk thistle vital rates including survival, growth, flowering, and fecundity were related to prior plant size in November of the previous year and/or temperature treatment. We used Poisson‐distributed errors for analysis of count data and binomially distributed errors for probabilities. All models included random effects for plot nested in block nested in cohort to reflect the split‐plot design used in this experiment. We found substantial overdispersion in our Poisson regression predicting the expected numbers of seeds, so we modified the model to include an observation‐level random effect (Elston et al. 2001, Harrison 2014). For each vital rate, we first considered models that included fixed effects for individuals’ prior‐year size, temperature treatment, and the interaction between prior size and temperature treatment. We then performed backwards model selection based on AIC. Seed release treatment was not included in any regressions because this treatment strongly influenced plants’ prior size. Seed release treatments in our model determined plants’ prior sizes, not the relationship between size and vital rates.
Integral projection model
To investigate the effects of warming and altered phenology on musk thistle population dynamics and life history patterns, we constructed integral projection models (IPMs; Fig. 1; Easterling et al. 2000, Ellner et al. 2016). We used the natural logarithm of rosettes’ longest leaf length, in centimeters, as our measure of size, the state variable z. This measure is a reliable estimator of individuals’ size, which has been previously shown to be an important predictor of musk thistle vital rates (Shea and Kelly 1998). We used an annual time step from early November to early November, which captures plant size after individuals have stopped growing for the season but before leaves are possibly damaged by repeated frost. Our study had high initial germination, and germination after the first season was rare. Also, our projections are aimed at capturing the potential for newly established populations (with no existing seedbank) to grow in disturbed areas, i.e., the growth rate is intended to capture the initial trajectory rather than the longer term dynamics. In addition, vital rates associated with the musk thistle seed bank have low elasticity (Jongejans et al. 2006). For these reasons, we did not include a seedbank in our model for this study. Generally, including a seed bank decreases the growth rate for rapidly growing populations (Nguyen et al. 2019), so this choice may slightly inflate our projected population growth rates.
Fig. 1.
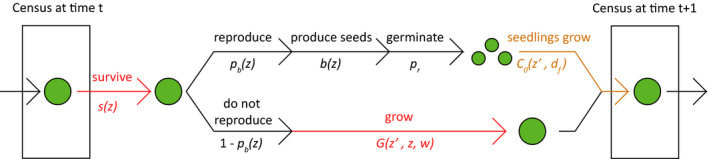
We built our IPM kernel as follows:
| (1) |
where z denotes size at time t, z′ denotes size at time t + 1, w denotes temperature treatment, and d f denotes day of year of first flowering. We included the effects of temperature and phenology in model components wherever statistical analysis indicated they had a significant effect. The kernel K(z′, z, w, d f) describes how the population of individuals with sizes z at time t transitions to a population with sizes z′ at time t + 1, under temperature treatment w and with date of first flowering d f. The first term in the kernel describes year‐to‐year size transitions for individuals that do not reproduce. These individuals survive with probability given by the size‐ and temperature‐dependent survival function s(z,w). They do not reproduce, so this term includes 1 – pb(z), where pb(z) is the size‐dependent probability of reproduction. Non‐flowering individuals grow to a new size given by the size‐ and temperature‐dependent growth kernel G(z′,z,w), which projects the probabilities of all possible annual size transitions from z to z′. The second term in the kernel describes annual transitions for reproducing individuals. Because C. nutans is a monocarp, these individuals all die, but they contribute to the next year’s population by producing offspring. They survive to reproduction with probability s(z, w) and flower with probability pb(z). They produce a number of seeds given by b(z), which germinate and become established with probability pr. Offspring enter the population with size given by c0(z′, d f). This frequency distribution of offspring sizes depends on the day of first flowering as described in the following section. See Appendix S1: Table S2 for fitted model parameters.
We discretized the continuous IPM kernel using 300 mesh points between lower bound L = −1 and upper bound U = 4.5. Note that these bounds are for the log‐transformed longest leaf length in centimeters, and a negative lower bound does not reflect negative leaf sizes. Model predictions were not sensitive to slight increases and decreases in the number of mesh points. We used the mid‐point rule for integration to estimate the numerical solution to the IPM (Easterling et al. 2000). We used this discretized IPM kernel to estimate the stable annual population growth rate λ, the average size at reproduction and the average age at reproduction (Ellner et al. 2016). We estimated 95% confidence intervals for λ and average size and age at reproduction by bootstrapping our original data, stratified by temperature treatment, 2,000 times.
To investigate the life cycle impacts of shifting phenology and altered vital rates, we projected outcomes for cohorts produced by mother plants that flowered on different dates with vital rates corresponding to different temperatures. We projected cohorts through 10 yr and tracked the proportion of individuals that died before flowering and the proportions that flowered as annuals, as biennials, or as longer‐lived perennials.
Estimating new recruit size distribution
To complete our IPM model, here we specify , a probability distribution of z′‐sized offspring produced by a mother plant reaching full flowering on date d f. By the law of total probability
| (2) |
where d r is the date of seed release (). The last equality in Eq. (2) holds, because we assume that the seedlings grow once the seeds are released irrespective of when the mother has flowered, i.e., . We compute Eq. (2) by the following. First, mother plants flower on a given day of the year d f. After flowering, seeds are fertilized, mature, and are released a number of days later, on day of year d r. We estimated the probability of seeds being released on a particular day of year provided that the mother plant flowered on a particular day P(d r|d f) based on data from McCarty (1982), which details seed counts from flower heads collected over time after the first terminal flower head on an individual reached full bloom [McCarty 1982]. Second, after being released, seeds germinate and grow to an end‐of‐season size z′. We estimated the probability of seeds reaching size z′ provided that they were released on a particular day P(z′|d r) using a two‐step process. First we estimated the joint probability P(z′, d r) by two‐dimensional probability density kernel estimation (package KernSmooth in R v. 3.4.1; Ripley 2002) fit to data describing end‐of‐season rosette sizes reached by individuals planted on different dates throughout our field experiment. We selected smoothing parameters for the estimation process that avoided overfitting while still reflecting differences in sizes reached by seeds arriving on different dates. Then, we calculated the conditional probability P(z′|d r) using the Kolmogorov definition of conditional probability
| (3) |
Finally, we summed the product of the two terms P(d r |d f) and P(z′|d r) across all possible seed‐release dates d r to compute c 0(z′, d f), the size distribution of new seedlings, which is equal to .
We modeled the effect of shifts in flowering date on recruit sizes by changing the date of flowering and associated distribution of seed release dates. We assumed that the distribution of seed release probabilities after first flowering was not altered by changing date of first flowering. When modeling seed release occurring earlier than the earliest seed release date in the dataset from our field experiment, we assumed that the size distribution of offspring produced by seeds released at earlier dates was the same as the distribution on our earliest date. This assumption is supported by measurements of rosette sizes in naturally occurring populations of musk thistle, where rosettes larger than those at the upper end of our estimated size distribution are extremely rare (Joseph Keller, personal observation).
Results
Warming significantly increased musk thistle survival and growth across all sizes (Fig. 2, Appendix S1: Table S2). Size‐dependent probability of survival was significantly affected by warming treatment (χ2(1) = 10.05, P = 0.002). Survival was higher for warmed plants, with the estimated probability of survival ranging from 73.2% for small individuals (longest leaf length = 0.5 cm) to 95.8% for large individuals (longest leaf length = 50 cm). For plants grown at ambient temperatures, we estimated small individuals had a 49.9% probability of surviving, while large individuals had an 89.4% probability. Warming also significantly affected growth from year to year (χ2(1) = 16.39, P < 0.001). Across all sizes, warmed plants were expected to have larger next‐year size. For example, under warming, small individuals with longest leaf length 0.5 cm are projected to grow to have longest leaf length 7.4 cm on average at the end of the next year’s growing season, while the same small individuals under ambient temperatures are projected to grow to have longest leaf length of only 4.3 cm on average. We did not observe a significant difference in the number of seeds produced by individuals of a given size when they were subjected to experimental warming (χ2(1) = 2.50, P = 0.11), nor did we observe a significant effect of temperature on size‐dependent probability of flowering (χ2(1) = 0.03, P = 0.858).
Fig. 2.
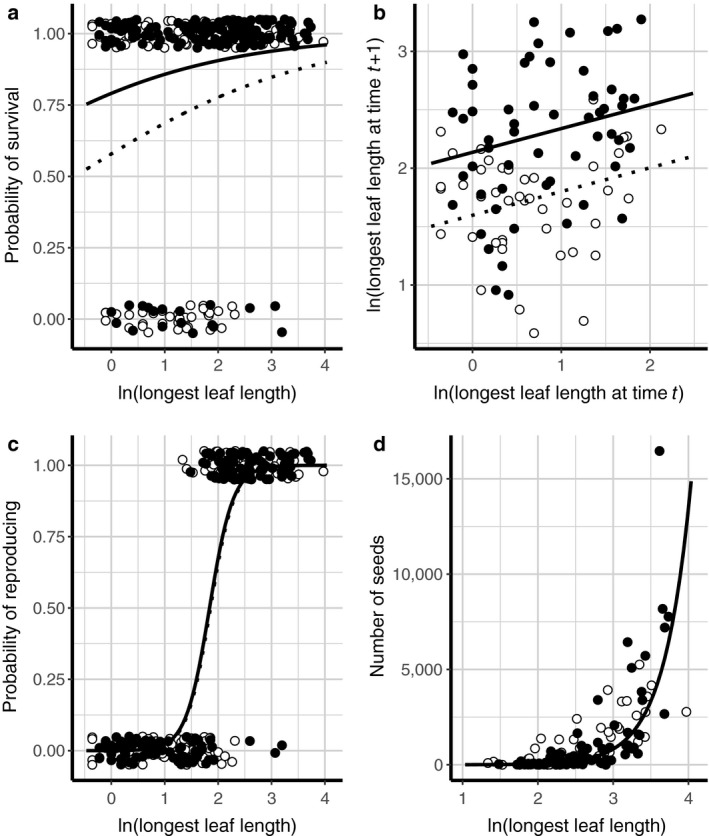
Size‐dependent vital rate regressions for (a) survival, (b) growth, (c) probability of reproducing, and (d) fecundity. Data from warmed individuals is shown with solid points, while data from individuals grown at ambient temperatures are shown with open points. Regression fits for warmed plants are shown with solid lines, and regression fits for ambient plants are shown with dotted lines. Leaf length was measured in cm.
The size distribution of new recruits was strongly related to the date on which seeds were released. Median seedling size trended with date of seed release (Mann‐Kendall trend test, tau = −0.901, P < 0.001, Appendix S1: Fig. S2). Seeds that were released early in the year reached substantially larger rosette sizes than later‐released seeds. Some small individuals (longest leaf length < 2 cm), are projected to occur even with very early seed release phenology, though; 6.0% of seedlings were projected to fall in this size range even for our earliest considered date of full flowering, 13 June.
Demographic modeling integrated changes in vital rates and changes in the size distribution of new seedlings to project a substantial acceleration in the life cycle of musk thistle under warming. Under current conditions (ambient temperatures, first full flowering date 29 June), we project that 60.8% of individuals flower as annuals. Under moderate warming and with the expected corresponding advance in phenology (+0.36°C, first full flowering date 25 June), however, we project that 70.8% of individuals will flower as annuals (mean difference in proportion annuals = 10.0%, 95% CI [9.5%, 10.5%], Fig. 3). The increase in the proportion of individuals flowering as annuals was caused by two factors: larger recruit sizes due to earlier seed release phenology, which increased the proportion of individuals that meet the size requirement for flowering in their first year, and higher survival under warming, which increased the proportion of individuals that survive their first year to reach reproduction. We also project that warming and corresponding phenological shifts are expected to significantly increase the total proportion of individuals that ever successfully reproduce, from 72.6% of individuals under current conditions to 89.5% of individuals under warming (mean difference in proportion that ever reproduce = 16.9%, 95% CI [15.9%, 18.0%]). Here again, improved survival under warming and larger recruit sizes drove this result.
Fig. 3.
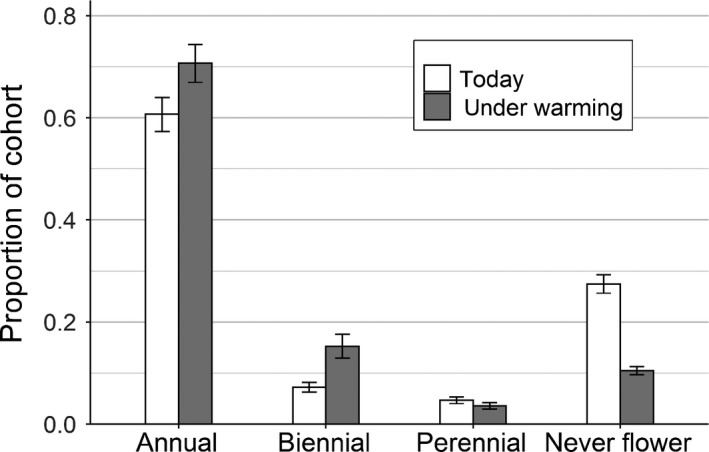
Proportion of individuals projected to flower as annuals, biennials, perennials, and to never flower under two scenarios: current conditions (ambient temperatures, flowering date 29 June) and a projected warming scenario (+0.36°C, flowering date 25 June). Error bars show 95% confidence intervals based on 2,000 bootstrapping iterations.
We did not detect a significant change in the average age at reproduction under warming (mean difference in mean age = −0.048 yr; 95% CI [−0.13, 0.02]). This apparent lack of difference, however, was the result of two opposing trends that both affect mean age at reproduction. Increased new recruit sizes and increased growth caused a greater proportion of individuals to reproduce at younger ages, while increased survival caused more of the individuals that do defer reproduction to successfully survive until they do reproduce, which increased numbers of older individuals reproducing. On balance, these trends result in little change in mean age at reproduction under warming.
The combined effects of earlier reproductive phenology and increased survival and growth under warming increased both the projected mean size at reproduction and the projected annual population growth rate of musk thistle. Under our moderate warming conditions, we project mean longest leaf length in the fall before individuals reproduce will increase by 1.3 cm (95% CI [0.72, 1.80]). Further, we project that the annual population growth rate will significantly increase with warming and advanced flowering phenology (mean difference in λ = 6.08; 95% CI [3.92, 9.48]; current conditions λ = 40.5; future conditions λ = 46.6). This projection represents a 15.0% increase in the annual population growth rate. After just 5 yr of population growth, this change in the population growth rate increases the projected population size by a factor of 2.01, roughly doubling the projected size of a population growing under warming compared to a population under current conditions, regardless of the initial population size.
Discussion
Musk thistle’s life cycle was accelerated by warming and earlier reproductive phenology and, as a result, musk thistle’s projected annual population growth rate increased. Experimentally applied warming significantly increased survival and growth. Our experimental manipulation of the timing of seed release had a strong effect on the sizes that new seedlings reached at the end of the growing season. Improved performance of new recruits had effects that perpetuated throughout the musk thistle life cycle. Earlier seed release resulted in increased annualism and increased size at flowering, both of which contribute to increased population growth rate with earlier seed release.
Phenological responses to warming have been linked to changes in population sizes, but the mechanisms that underlie these correlations remain unknown (Miller‐Rushing et al. 2010). Successful tracking of warming climates has been suggested as a driver of invasive species success (Willis et al. 2010, Wolkovich et al. 2013), while failure to shift phenology has been implicated in the decline in abundance of other species (Willis et al. 2008). Here we focused on a key mechanism by which earlier reproductive phenology may influence demography: increasing the sizes of new recruits and consequently their probability of surviving and reproducing earlier. Similar mechanisms have been observed in studies focused on mammals (Ozgul et al. 2010, Frick et al. 2010), where seasonally earlier reproduction increased offspring survival and reduced age at first reproduction. This pattern, where advancing reproductive phenology allows for increased growth of offspring and subsequent demographic changes may be widely relevant in other systems. Phenological head starts for new recruits may influence population dynamics by increasing the proportion of individuals that are “lucky,” the highly successful individuals that contribute disproportionately high numbers of offspring to populations (Snyder and Ellner 2016).
Our work has implications for which measures are used to infer changes in life history in future climates. Despite the observed increase in the proportion of individuals flowering as annuals (rather than biennials or perennials), we did not detect a significant change in the average age at reproduction under warming. This is because mean age at reproduction is affected by two processes acting in opposite directions. A higher proportion of individuals reproduced at younger ages, but increased survival caused more longer‐lived individuals to successfully survive to reproduction. This work thus provides a caution that considering only the mean age at reproduction may mask important underlying shifts in the life cycle.
The scenario for which we make projections is an important, but specific, case. We focused on a population growing with limited competition, which parallels the agricultural environment in which musk thistle is most economically costly. The λ values we calculated under these conditions are large, as might be expected for the initial population growth rate of an invasive species growing in a newly disturbed without competition or density dependence. Taking a broader view, the impacts of advanced phenology are likely to also depend on the community in which the musk thistle population is situated. Musk thistle’s demography in the future will also be impacted by the relative phenological shifts of interacting mutualists such as pollinators, competitors including native flora and agricultural crops, and consumers including specialist natural enemies that attack rosettes and flowering individuals.
We saw no change in the size threshold for flowering when plants were experimentally warmed. This finding suggests that this trait is insensitive to temperature. Warming increased the average size of flowering individuals, but this was a result of changes in annual growth increments and in the size of new recruits that reproduce as annuals rather than a change in the size threshold for flowering. This threshold is a well‐studied trait (Metcalf et al. 2009, Williams 2009), and prior work shows that thistles trade‐off between the immediate value of reproducing at a given size and the potential to grow larger and produce more offspring in the next growing season, discounted by the probability of dying before being able to realize any future potential reproduction. Because this trait is so closely related to individual plants’ fitness, the threshold size for flowering may be subject to selection (Stearns and Koella 1986, Williams 2009), and as temperature changes occur gradually over time, the size threshold for flowering may shift as well. As natural selection recalibrates this trait to a changing environment, it is possible that future musk thistle populations will outperform our projections.
Accelerated population growth of problematic invasive species will threaten food security (Godfray et al. 2010) and potentially cause significant challenges for managers tasked with controlling them. Managers will need to increase effort, or to consider different or auxiliary management strategies to achieve acceptable intervention outcomes in the future. Building an understanding of how warming and phenological shifts interact to affect species demography in a wide range of species life histories will be an essential component of plans to mitigate the impact of anthropogenic climate change. Here, we have shown that warming is expected to increase the annual population growth rate of a widespread invasive species by 15.0%, threatening the productivity of pastures and rangelands. Similar changes may be observed for many other pest species. A mechanistic understanding of how phenology impacts demography may also shed light on why species that do not shift phenology with warming are more likely to decline in abundance (Willis et al. 2008). Understanding phenology’s role in populations’ growth or decline will be important to guide conservation efforts aimed at preserving species that are negatively impacted by climate change and also efforts to prevent increases in the impacts of invasive species.
Supporting information
Appendix S1
Acknowledgments
We thank C. Hovis, W. Fescemyer, D. Stephan, P. Byrnes, R. J. Chandler, L. Gazda, J. Spivack, K. Porreca, A. Buck, D. Brough, K. McIlroy, C. J. Fisher, C. Mroz, and T. Attia for assistance in the field and in the lab, the late Scott Smiles and other farm managers at the Russell E. Larson Agricultural Research Center for technical support, and O. Bjørnstad for statistical advice. M. Kaye, H. Inamine, and E. Howerton provided helpful feedback on early versions of this manuscript. Financial support came from the Pennsylvania Space Grant Consortium and from National Institute of Food and Agriculture, U.S. Department of Agriculture award number 2016‐67011‐24710. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author and do not necessarily reflect the views of the USDA.
Keller, J. A. , and Shea K..2021. Warming and shifting phenology accelerate an invasive plant life cycle. Ecology. 102(1):e03219 10.1002/ecy.3219
Corresponding Editor: Gordon Fox.
Data Availability Statement
The data generated in this study are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.2bvq83bnm. Code is available on Zenodo: http://doi.org/10.5281/zenodo.4009191.
Literature Cited
- Bates, D. , Maechler M., Bolker B., and Walker S.. 2015. lme4: Linear mixed‐effects models using Eigen and S4. R package version 1.1–15. http://cran.r‐project.org/web/packages/lme4/index.html
- Cleland, E. E. , Chuine I., Menzel A., Mooney H. A., and Schwartz M. D.. 2007. Shifting plant phenology in response to global change. Trends in Ecology & Evolution 22:357–365. [DOI] [PubMed] [Google Scholar]
- Colautti, R. I. , and Barrett S. C.. 2013. Rapid adaptation to climate facilitates range expansion of an invasive plant. Science 342:364–366. [DOI] [PubMed] [Google Scholar]
- Desrochers, A. M. , Bain J. F., and Warwick S. I.. 1988. The biology of Canadian weeds: 89. Carduus nutans L. and Carduus acanthoides L. Canadian Journal of Plant Science 68:1053–1068. [Google Scholar]
- Easterling, M. R. , Ellner S. P., and Dixon P. M.. 2000. Size‐specific sensitivity: applying a new structured population model. Ecology 81:694–708. [Google Scholar]
- Ellner, S. P. , Childs D. Z., and Rees M.. 2016. Data‐driven modelling of structured populations. Springer International Publishing, Cham, Switzerland. [Google Scholar]
- Elston, D. A. , Moss R., Boulinier T., Arrowsmith C., and Lambin X.. 2001. Analysis of aggregation, a worked example: numbers of ticks on red grouse chicks. Parasitology 122:563–569. [DOI] [PubMed] [Google Scholar]
- Frick, W. F. , Reynolds D. S., and Kunz T. H.. 2010. Influence of climate and reproductive timing on demography of little brown myotis Myotis lucifugus . Journal of Animal Ecology 79:128–136. [DOI] [PubMed] [Google Scholar]
- Godfray, H. C. J. , Crute I. R., Haddad L., Lawrence D., Muir J. F., Nisbett N., Pretty J., Robinson S., Toulmin C., and Whiteley R.. 2010. The future of the global food system. Philosophical Transactions of the Royal Society B 365:2769–2777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamrick, J. L. , and Lee J. M.. 1987. Effect of soil surface topography and litter cover on the germination, survival, and growth of musk thistle (Carduus nutans). American Journal of Botany 74:451–457. [Google Scholar]
- Harrison, X. A. 2014. Using observation‐level random effects to model overdispersion in count data in ecology and evolution. PeerJ 2:e616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iler, A. M. , Compagnoni A., Inouye D. W., Williams J. L., CaraDonna P. J., Anderson A., and Miller T. E.. 2019. Reproductive losses due to climate change‐induced earlier flowering are not the primary threat to plant population viability in a perennial herb. Journal of Ecology 107:1931–1943. [Google Scholar]
- Johnson, S. D. 1993. Climatic and phylogenetic determinants of flowering seasonality in the Cape flora. Journal of Ecology 567–572. [Google Scholar]
- Jongejans, E. , Shea K., Skarpaas O., Kelly D., Sheppard A. W., and Woodburn T. L.. 2008. Dispersal and demography contributions to population spread of Carduus nutans in its native and invaded ranges. Journal of Ecology 96:687–697. [Google Scholar]
- Jongejans, E. , Sheppard A. W., and Shea K.. 2006. What controls the population dynamics of the invasive thistle Carduus nutans in its native range? Journal of Applied Ecology 43:877–886. [Google Scholar]
- Macgregor, C. J. et al. 2019. Climate‐induced phenology shifts linked to range expansions in species with multiple reproductive cycles per year. Nature Communications 10:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchetto, K. M. , Shea K., Kelly D., Groenteman R., Sezen Z., and Jongejans E.. 2014. Unrecognized impact of a biocontrol agent on the spread rate of an invasive thistle. Ecological Applications 24:1178–1187. [DOI] [PubMed] [Google Scholar]
- McCarty, M. K. 1982. Musk thistle (Carduus thoermeri) seed production. Weed Science 30:441–445. [Google Scholar]
- McLean, N. , Lawson C. R., Leech D. I., and van de Pol M.. 2016. Predicting when climate‐driven phenotypic change affects population dynamics. Ecology Letters 19:595–608. [DOI] [PubMed] [Google Scholar]
- Metcalf, C. J. E. , Rees M., Buckley Y. M., and Sheppard A. W.. 2009. Seed predators and the evolutionarily stable flowering strategy in the invasive plant, Carduus nutans . Evolutionary Ecology 23:893–906. [Google Scholar]
- Metcalf, J. C. , Rose K. E., and Rees M.. 2003. Evolutionary demography of monocarpic perennials. Trends in Ecology and Evolution 18:471–480. [Google Scholar]
- Miller‐Rushing, A. J. , Høye T. T., Inouye D. W., and Post E.. 2010. The effects of phenological mismatches on demography. Philosophical Transactions of the Royal Society B 365:3177–3186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molau, U. , and Mølgaard P.. 1996. International tundra experiment (ITEX) manual. Danish Polar Center, Copenhagen, Denmark. [Google Scholar]
- Møller, A. P. , Rubolini D., and Lehikoinen E.. 2008. Populations of migratory bird species that did not show a phenological response to climate change are declining. Proceedings of the National Academy of Sciences USA 105:16195–16200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen, V. , Buckley Y. M., Salguero‐Gómez R., and Wardle G. M.. 2019. Consequences of neglecting cryptic life stages from demographic models. Ecological Modelling 408:108723. [Google Scholar]
- Ozgul, A. , Childs D. Z., Oli M. K., Armitage K. B., Blumstein D. T., Olson L. E., Tuljapurkar S., and Coulson T.. 2010. Coupled dynamics of body mass and population growth in response to environmental change. Nature 466:482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paniw, M. , Maag N., Cozzi G., Clutton‐Brock T., and Ozgul A.. 2019. Life history responses of meerkats to seasonal changes in extreme environments. Science 363:631–635. [DOI] [PubMed] [Google Scholar]
- Parmesan, C. , and Yohe G.. 2003. A globally coherent fingerprint of climate change impacts across natural systems. Nature 421:37. [DOI] [PubMed] [Google Scholar]
- Popay, A. I. , Thompson A., Bell D. D., Lemerle D., and Leys A. R.. 1987. Germination and emergence of nodding thistle, Carduus nutans L Pages 175–178 in Proceedings of the Eighth Australian Weeds Conference. 21–25 September, 1987. Weed Society of New South Wales, Sydney, New South Wales, Australia. [Google Scholar]
- R Core Team . 2017. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: https://www.R‐project.org/ [Google Scholar]
- Ripley, B. 2002. The KernSmooth Package. S original by M. Wand, R Port by B. Ripley. R package version 1.11.0. https://CRAN.R‐project.org/package=KernSmooth
- Scheepens, J. F. , and Stöcklin J.. 2013. Flowering phenology and reproductive fitness along a mountain slope: maladaptive responses to transplantation to a warmer climate in Campanula thyrsoides. Oecologia 171:679–691. [DOI] [PubMed] [Google Scholar]
- Shea, K. , and Kelly D.. 1998. Estimating biocontrol agent impact with matrix models: Carduus nutans in New Zealand. Ecological Applications 8:824–832. [Google Scholar]
- Snyder, R. E. , and Ellner S. P.. 2016. We happy few: using structured population models to identify the decisive events in the lives of exceptional individuals. American Naturalist 188:E28–E45. [DOI] [PubMed] [Google Scholar]
- Stearns, S. C. , and Koella J. C.. 1986. The evolution of phenotypic plasticity in life‐history traits: predictions of reaction norms for age and size at maturity. Evolution 40(5):893–913. [DOI] [PubMed] [Google Scholar]
- USDA NRCS . 2012. The PLANTS Database. National Plant Data Team, Greensboro, North Carolina, USA: http://plants.usda.gov [Google Scholar]
- Van Dongen, S. , Backeljau T., Matthysen E., and Dhondt A. A.. 1997. Synchronization of hatching date with budburst of individual host trees (Quercus robur) in the winter moth (Operophtera brumata) and its fitness consequences. Journal of Animal Ecology 66:113–121. [Google Scholar]
- Williams, J. L. 2009. Flowering life‐history strategies differ between the native and introduced ranges of a monocarpic perennial. American Naturalist 174:660–672. [DOI] [PubMed] [Google Scholar]
- Willis, C. G. , Ruhfel B., Primack R. B., Miller‐Rushing A. J., and Davis C. C.. 2008. Phylogenetic patterns of species loss in Thoreau's woods are driven by climate change. Proceedings of the National Academy of Sciences USA 105:17029–17033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willis, C. G. , Ruhfel B. R., Primack R. B., Miller‐Rushing A. J., Losos J. B., and Davis C. C.. 2010. Favorable climate change response explains non‐native species' success in Thoreau's woods. PLoS ONE 5:e8878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolkovich, E. M. , Davies T. J., Schaefer H., Cleland E. E., Cook B. I., Travers S. E., Willis C. G., and Davis C. C.. 2013. Temperature‐dependent shifts in phenology contribute to the success of exotic species with climate change. American Journal of Botany 100:1407–1421. [DOI] [PubMed] [Google Scholar]
- Zhang, R. 2011. Biological invasions in a changing world: responses of two invasive thistles to disturbance and climate change. Dissertation. Retrieved from ProQuest. The Pennsylvania State University, University Park, Pennsylvania, USA. [Google Scholar]
- Zhang, R. , Post E., and Shea K.. 2012. Warming leads to divergent responses but similarly improved performance of two invasive thistles. Population Ecology 54:583–589. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1
Data Availability Statement
The data generated in this study are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.2bvq83bnm. Code is available on Zenodo: http://doi.org/10.5281/zenodo.4009191.


