Validation of presence‐only models for conservation planning and the application to whales in a multiple‐use marine park

Abstract

Identification of species’ Biologically Important Areas (BIAs) is fundamental to conservation planning and species distribution models (SDMs) are a powerful tool commonly used to do this. Presence‐only data are increasingly being used to develop SDMs to aid the conservation decision‐making process. The application of presence‐only SDMs for marine species’ is particularly attractive due to often logistical and economic costs of obtaining systematic species’ distribution data. However, robust model validation is important for conservation management applications that require accurate and reliable species’ occurrence data (e.g., spatially explicit risk assessments). This is commonly done using a random subset of the data and less commonly with fully independent test data. Here, we apply a spatial block cross‐validation (CV) approach to validate a MaxEnt presence‐only model using independent presence/absence survey data for a highly mobile, marine species (humpback whale, Megaptera novaengliae) in the Great Barrier Reef (GBR). A MaxEnt model was developed using opportunistic whale sightings (2003–2007) and then used to identify areas differing in habitat suitability (low, medium, high) to conduct a systematic, line‐transect, aerial survey (2012) and derive a density surface model. A spatial block CV buffering strategy was used to validate the MaxEnt model, using the opportunistic sightings as training data and independent aerial survey sightings data as test data. Moderate performance measures indicate MaxEnt was reliable in identifying the distribution patterns of a mobile whale species on their breeding ground, indicated by areas of high density aligned to areas of high habitat suitability. Furthermore, we demonstrate that MaxEnt models can be useful and cost‐effective for designing a sampling scheme to undertake systematic surveys that significantly reduces sampling effort. In this study, higher quality information on whale reproductive class (calf vs. non‐calf groups) was obtained that the presence‐only data lacked, while sampling only 18% of the GBR World Heritage Area. The validation approach using fully independent data provides greater confidence in the MaxEnt model, which indicates significant overlap with the main breeding ground of humpback whales and the inner shipping route. This is important when evaluating presence‐only models within certain conservation management applications, such as spatial risk assessments.

Introduction

Species distribution models (SDMs) have become increasingly popular for a wide variety of applications, including to support conservation management decision‐making processes in both the terrestrial and marine environment (Elith and Leathwick 2009, Franklin 2010, Robinson et al. 2011, Guisan et al. 2013, Guillera‐Arroita et al. 2015). It is an approach that can be used for understanding patterns in current species distributions, predicting future distribution patterns related to changes in environmental parameters, and assisting in identifying potential conflict with human activities (Elith et al. 2010). SDMs provide spatially explicit predictions of a species occurrence derived from environmental suitability models that combine occurrence data with spatial environmental data (Guisan and Thuiller 2005, Phillips et al. 2006). In the past, the methods for developing SDMs often required presence/absence or abundance data from systematically designed surveys that provide equal coverage probability along environmental gradients (Elith and Leathwick 2009). Due to the widespread availability of presence‐only data (e.g., online databases, citizen science programs), there have been improved modeling capabilities for this type of data and a greater use of these models in conservation management (Elith et al. 2006, Elith and Leathwick 2009). Presence‐only data are often an inexpensive source of data that is particularly common for cryptic (or rare) species (Franklin 2010). Similarly, marine mammals are often “unavailable” to observers due to a large proportion of their time spent underwater. While the application of SDMs to marine species has been considerably less compared to terrestrial species, it has been significantly increasing over the last decade (Robinson et al. 2011, Robinson et al. 2017). In the case of whales, the collection of absence data can often be logistically difficult and expensive given many species are highly mobile and can occupy large spatial scales (e.g., migratory whale species). The application of presence‐only data and predictive habitat modeling is therefore an attractive approach for marine mammals given the logistical and economical costs of collecting distribution data (Bombosch et al. 2014, Derville et al. 2018).

However, there is a trade‐off between the cost of acquiring species distribution data and the quality of the data. Presence‐only data are a relatively inexpensive source of data, although often limited data are associated with sightings (e.g., sampling effort), that might provide information on any underlying sampling scheme. Often the data have potential sampling effort biases and are limited to providing reliable information only on the areas occupied by a species and not unoccupied areas, resulting in a higher probability of commission error (false positive, predicting a species in unoccupied areas; Guillera‐Arroita et al. 2015). Significant effort needs to be made in understanding and addressing any spatial bias in presence‐only data, which is supported by an understanding of the sampling process where possible (Bird et al. 2013). In contrast, presence/absence data are of higher quality due to being obtained from well‐structured sampling designs and a lower probability of omission error (false negative predictions, failure to predict a species in an occupied area), although can be costly to acquire (Franklin 2010). The quality of the data and any inherent errors in estimates of species occurrence can ultimately have an impact on the inference of the model and consequently any associated ecological explanation and management recommendations (Aarts et al. 2011, Soultan and Safi 2017). The model utility of predictive SDMs is dependent on model performance, which is measured by model calibration (ability of the model to correctly predict probability of presence) and discrimination (capacity of the model to differentiate presences from absences or pseudo‐absences) (Pearce and Ferrier 2000, Phillips and Elith 2010). There are a number of different statistical model performance evaluation measures (e.g., AUC, kappa) used to evaluate the discrimination capacity of the model, which often use semi‐independent (e.g., resampling approaches) or preferably independent test data (Araújo et al. 2005, Hirzel et al. 2006, Elith and Leathwick 2009, Franklin 2010, Guisan et al. 2017).

In the absence of external independent data to test the predictive accuracy of SDMs, model performance is often assessed using data resampling, such as cross‐validation (CV) techniques (Guisan et al. 2017). CV partitions a data set into two subsets, one for model training (calibration of data) and the other testing (validation). The training data are used for fitting the model and the test data for evaluating the performance of the trained model (Hastie et al. 2009). Typically, the CV process is undertaken with repeated random selection of the subset data used for testing. In SDMs, nearby sites are often environmentally similar and there can be dependence structures in the data (Roberts et al. 2017). Therefore, a random split of training and test points may not produce training and test sets that can be considered independent because it is possible for data held out for validation to be drawn from these nearby sites. Consequently, using random test and training splits can lead to biased error estimates (Wenger and Olden 2012). This is when spatial block CV should be preferred over random data splits (Renner et al. 2015, Roberts et al. 2017). A spatial block CV can consist of blocking the training and test sets according to different strategies; spatial blocking (i.e., a set of spatially contiguous blocks), spatial buffering (i.e., a circular buffer of specified radius around an observation), and environmental blocking (i.e., sets of similar environmental conditions; Valavi et al. 2018). The data in one block can be considered approximately independent of data in other blocks, because testing is undertaken on more spatially distant records, which effectively decreases spatial dependence (Roberts et al. 2017).

Few studies undertake an evaluation of the reliability of the model using a fully independent data set, to test that each probability is an accurate estimate of the likelihood of detecting the species at a given site (Pearce and Ferrier 2000, Greaves et al. 2006, Hirzel et al. 2006, Rebelo and Jones 2010, Pinto et al. 2016, Fiedler et al. 2018). This is largely due to the expense of obtaining new survey data. While the importance of undertaking this type of validation is likely to depend on the application of the model (Guillera‐Arroita et al. 2015), it should be considered desirable given the potential biases in presence‐only data. It becomes increasingly important in wildlife management when applied to management decisions where accurate and reliable data on species occurrence is necessary (e.g., spatial risk assessments). In studies that have used independent test data, the derived model test statistics from each presence‐only and presence/absence data set have been compared or a measure of difference between the two model outputs has been calculated (Greaves et al. 2006, Hirzel et al. 2006, Shabani et al. 2016, Fiedler et al. 2018). In our study, we validate a presence‐only MaxEnt model with a temporally independent presence/absence aerial survey data set, using a spatial block CV approach. A MaxEnt habitat suitability model was initially developed using opportunistic sightings to determine the distribution of humpback whales in the Great Barrier Reef (GBR; Smith et al. 2012). The MaxEnt model was then used to design and conduct a dedicated, systematic, aerial survey within three areas of the GBR, corresponding to high, medium, and low habitat suitability. We then evaluated the MaxEnt model using a spatial block CV buffering strategy using the presence‐only data as training data and independent aerial survey presence/absence data as testing data using various performance metrics.

Humpback whales are a highly mobile marine species that annually migrate thousands of kilometers from high latitude temperate feeding grounds to low latitude tropical breeding grounds (Dawbin 1966, Rasmussen et al. 2007). The Australian east coast population (breeding stock E1) migrate to the tropical waters of the Great Barrier Reef (GBR) for mating and calving (Simmons and Marsh 1986, Chaloupka and Osmond 1999, Smith et al. 2012, Smith et al. 2020). The Great Barrier Reef Marine Park (GBRMP) is a multiple‐use marine park that utilizes a Zoning Plan to manage the multiple users, e.g., tourism, shipping, and fishing. The Zoning Plan defines what activities can occur in which locations to protect the marine environment and separate potentially conflicting activities, with varying levels of restriction dependent on the Zone, e.g., General Use Zone vs. Preservation Zone. The GBR is a UNESCO World Heritage Area (GBRWHA) that covers approximately 348,000 km² within which the GBRMP comprises 99% of the area. The whale population is currently undergoing a rapid, exponential rate of increase (~11% per annum) following near extinction from commercial whaling (Bejder et al. 2016, Noad et al. 2019). The high rate of population increase ultimately increases interactions with multiple human activities and the potential for anthropogenic impacts (e.g., vessel strikes; Peel et al. 2018), necessitating a need for accurate distribution data at a resolution that can be incorporated into spatial risk assessments.

Methods

MaxEnt presence‐only spatial habitat model

A MaxEnt spatial habitat model was developed (MaxEnt version 3.3.2) to determine the distribution of humpback whales on their breeding ground in the GBRMP. The MaxEnt model was developed using opportunistic presence‐only whale sighting data (2003–2007) and five environmental variables; sea surface temperature (SST), bathymetry, seabed slope, distance from coast, and distance from outer reef. (Appendix S1: Fig. S1, Appendix S1: Fig. S2). Seabed rugosity (a measure of seabed complexity, or roughness) was also investigated, although was excluded from the final model because it was highly correlated with seabed slope based on investigation of multicollinearity among environmental variables and a Pearson product‐moment correlation coefficients test. Detailed information on the MaxEnt model and opportunistic whale sighting data are reported in Smith et al. (2012). The MaxEnt model was trained using 75% of the sightings (N = 80) and tested with 25% of the data (N = 27), which were randomly drawn from the entire data set for 50 bootstrap samples. The MaxEnt model was evaluated using AUC, response curves of the environmental variables and a jack‐knife test to evaluate the relative environmental variable contributions to the model. The opportunistic data consisted of whale sightings collected during an Australian Government Border Protection Command (BPC) aerial surveillance program as part of a broader survey of human vessel use within the GBRMP between 1982 to 2007. Sighting data used in the model consisted of confirmed species identification from the months of peak whale abundance (July, August) between 2003 and 2007, during which time humpback whales are the predominant whale species. No other associated data on sampling effort (due to confidentiality of flight paths), environmental data or identification of calves were provided with the sightings. There was an assumption of unbiased sampling and even coverage in the presence‐only data. This was deemed an adequate assumption due to the BPC aerial surveillance program having initially been established according to a stratified random sampling design (A. N. Pettitt and M. A. Haynes 1994 unpublished manuscript) and no apparent temporal or spatial bias in the whale sighting data (Smith et al. 2012).

Five environmental variables were used in the model; sea surface temperature (sst), bathymetry, seabed slope, distance from coast, and distance from outer reef. The first four variables were selected based on their identified importance in influencing whale distribution from published literature (Ersts and Rosenbaum 2003, Johnston et al. 2007, Rasmussen et al. 2007, Oviedo and Solís 2008, Smith et al. 2012, Lindsay et al. 2016, Trudelle et al. 2016, Derville et al. 2018) and the last was specific to this study site. Bathymetry data were obtained using the 3DGBR high‐resolution digital elevation model (100‐m resolution) for the GBR (Beaman 2010) and seafloor slope was derived from bathymetry data. Sea surface temperature (SST) data were obtained from the AVHRR (Advanced Very High Resolution Radiometer) Pathfinder version 5 data set at 4.8‐km resolution and averaged for the months of July and August across years (SD = 0.24°C). Distance to coast and distance to reef were calculated in ArcGIS 10.6 using shapefile base layers courtesy of the Great Barrier Reef Marine Park Authority. All environmental layers used were raster data at a resolution of 4.8 × 4.8 km (Universal Transverse Mercator [UTM] GDA 1994 Zone 55 projection) that were converted to ASCII files.

Independent aerial survey data and sampling effort

A dedicated, systematic line‐transect aerial survey was undertaken to validate the MaxEnt presence‐only model with an independent presence/absence data set. The MaxEnt model was used to design an aerial survey that sampled the GBRMP within three selected regions representing three different categories of habitat suitability; Region 1, low; Region 2, medium; and Region 3, high (Fig. 1). Three regions were identified based on the calculated maximum, average, and range of habitat suitability values for grid cells across the region. The average of a region approximated 50% of the range and maximum in habitat suitability and the maximum habitat suitability approximated 25% less than the region above (Table 1). Statistics were calculated using the ArcGIS spatial analyst tool, Zonal statistics. The surveyed area of the combined three regions (63,723 km²) represented 18% of the total GBRMP (344,400 km²).

Fig. 1.

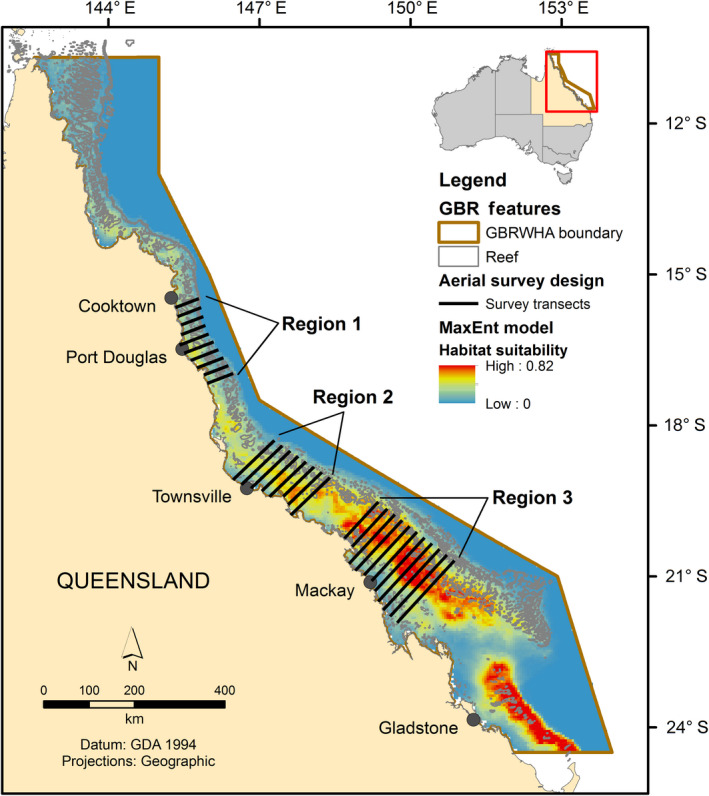
MaxEnt probability of presence model for humpback whales in the Great Barrier Reef World Heritage Area (GBRWHA) and overlay of the aerial survey transects in areas of low (Region 1), medium (Region 2), and high (Region 3) predicted occurrence.

Table 1.

The three regions surveyed during the 2012 aerial survey for humpback whales in the Great Barrier Reef Marine Park (GBRMP), based on habitat suitability (HS) values derived from the MaxEnt model.

Survey region	Habitat suitability class	Area (km2)	HS
			Average	Maximum	Range
1. Port Douglas	low	11,971	0.15	0.42	0–0.42
2. Townsville	medium	17,126	0.29	0.59	0.01–0.59
3. Mackay	high	34,626	0.42	0.79	0.03–0.79

The aerial survey was conducted between 3 and 10 August 2012 using a Partenavia Observer P‐68B six‐seater, twin engine, high‐wing aircraft. The aerial survey was designed to maximize detection of humpback whales as the target species and flown at a ground speed of 100 knots (1 knot = 1.852 km/h) in passing mode at an altitude of 1,000 feet (1 foot = 0.30 m) to improve the ability of identifying calves. Transects were spaced 20 km apart and oriented at an angle from the coastline to survey across the depth gradient. The survey was undertaken to coincide with peak whale abundance within the breeding season (Chittleborough 1965), whereby it is assumed whales are utilizing habitat important to their breeding behavior and not engaging in migratory behavior.

The survey team consisted of four dedicated observers and a survey leader, constituting a double platform observer configuration. The rear observers were acoustically and visually (using curtains) isolated from the front observers to allow perception bias to be calculated (Pollock et al. 2006). Sightings were recorded using aviation headsets on a Zoom H4N handheld digital recorder (Zoom Corporation, China) and environmental conditions (Beaufort sea state, cloud cover, wind speed, turbidity, and glare) were recorded on a handheld GETAC PS236 PDA (Getac Technology Corporation, Shanghai, China). Whale sightings included species identification, declination (using a Suunto PM‐5/360PC clinometer; Suunto, Finland) and horizontal (protractor) angles to the group, total number of animals and calves in a group and sighting cue.

Density Surface Model (DSM) of aerial survey data

Density surface models of the line transect aerial survey data were fitted to calculate spatially explicit estimates of whale density using a two‐stage process in the dsm R package (Miller et al. 2019), as outlined in Smith et al. (2020). The purpose of producing a DSM was to derive aggregated aerial survey segment data, an effective strip area (ESA), and visualize a smoothed density surface of the aerial survey data to visually compare with the MaxEnt model. Predicted whale densities estimated by the DSM were not used in the cross‐validation process because we wanted to validate the MaxEnt model and compare the MaxEnt prediction in areas of low/medium/high habitat suitability to whale count data in the area(s) that the aerial survey was conducted, rather than compare predicted whale occurrence (from MaxEnt) to areas of predicted whale density (from the DSM).

First, the double‐platform data are analyzed using a mark–recapture distance sampling model to develop a detection function model, as described in Laake and Borchers (2004) and Burt et al. (2014) using the MRDS package (Laake et al. 2015) in R (R Development Core Team 2015). To improve detection function fit, sightings were truncated and the best fitting model was selected using AIC.

A detection‐adjusted density surface model is then developed using a generalized additive model (GAM), the detection function model and environmental covariates (Hedley and Buckland 2004) to estimate whale density. Aerial survey track lines (transects) were segmented into pre‐defined lengths of 20 km to capture adequate environmental variability. The number of whale groups and total animals (including the presence and number of calves) were summed for each segment, incorporating the environmental variables and estimating a total effective strip area. The number of whales in each segment is adjusted by the probability of detection of a sighting in that segment given its sighting conditions. This is accomplished via an offset in the model, equivalent to log(effective area) of each segment. A Tweedie distribution was used to account for over‐dispersion in the counts of groups per segment. The DSM incorporated the same spatial variables to those used to create the MaxEnt model; SST, bathymetry, seabed slope, distance from coast, and distance from outer reef. It did not include any spatial covariates (e.g., latitude, longitude), so we could extrapolate beyond the survey area. There was little survey effort in depths > 90 m, so depths > 90 m were set at 90 m to prevent a linear relationship with depth in deeper waters. Predictions of whale densities across the GBR were undertaken at the same resolution as the MaxEnt model (4.8 × 4.8 km) for three whale groups: (1) all whales, (2) groups that contained a calf (hereafter, calf groups), and (3) groups in which a calf was not present (hereafter, non‐calf groups).

Spatial block cross‐validation of MaxEnt model and aerial survey data

To validate the MaxEnt model, we applied a spatial block CV buffering strategy, using BPC occurrence sightings as training data and independent aerial survey data as testing data. The validation process tests whether the MaxEnt presence‐only model is capable of accurately and reliably predicting the occurrence of humpback whales within the GBRMP based on a temporally independent, systematically derived, data set. MaxEnt models were fitted using the R packages dismo (Hijmans et al. 2017) and MaxEnt (version 3.4.1) using default settings except the hinge feature was removed and we retained duplicate presence points (removeDuplicates = False). By not removing duplicates, the resulting fitted model is a Poisson point process model in which presence‐only locations are treated as independent (Renner and Warton 2013). The analysis is based on the number of presence records per unit area rather than probability of presence on a per grid cell basis. The output is a measure of intensity similar to density, defined as the number of presence records per unit area rather than one presence record per grid cell, and is a measure of abundance rather than probability (Renner et al. 2015). By default, MaxEnt fits models with a lasso penalty (Tibshirani 1996), which accounts for potential overfitting of the model to the observed data by shrinking parameter coefficients toward 0. The degree of shrinkage is determined automatically in MaxEnt based on the number of observed points (Phillips and Dudík 2008). Applying a lasso penalty has been shown to improve predictive performance (Elith et al. 2006) and may be part of the reason why MaxEnt remains a popular choice among ecologists.

MaxEnt models were built using BPC presence‐only whale sightings (N = 107, 2003–2007) and five environmental variables (same as used in the initial MaxEnt model and DSM), with a spatial block that created a buffer of specified distance that excluded any BPC sightings around a test point. We used the aerial survey segment data (the midpoint) as test locations, comparing two components of the aerial survey data aggregated in a segment; total number of whales (N count data) and the density of whales standardized for the effective strip area (ESA; density = N/ESA). The number of test locations is determined by the aerial survey transect segment length and this determines the number of MaxEnt models built in the cross‐validation process. For example, a segment length of 20 km results in 165 test locations and a MaxEnt model is built for each of the test locations. For each model, a test point was chosen and a MaxEnt model was built withholding all BPC data within the specified buffer distance around the aerial survey segment test point (e.g., a 20‐km buffer around the midpoint of the test location; Fig. 2). This produced a set of predicted humpback intensities from the BPC data derived by MaxEnt and we used the MaxEnt model prediction at the test location to compare to the aerial survey count and density data using a number of performance metrics.

Fig. 2.

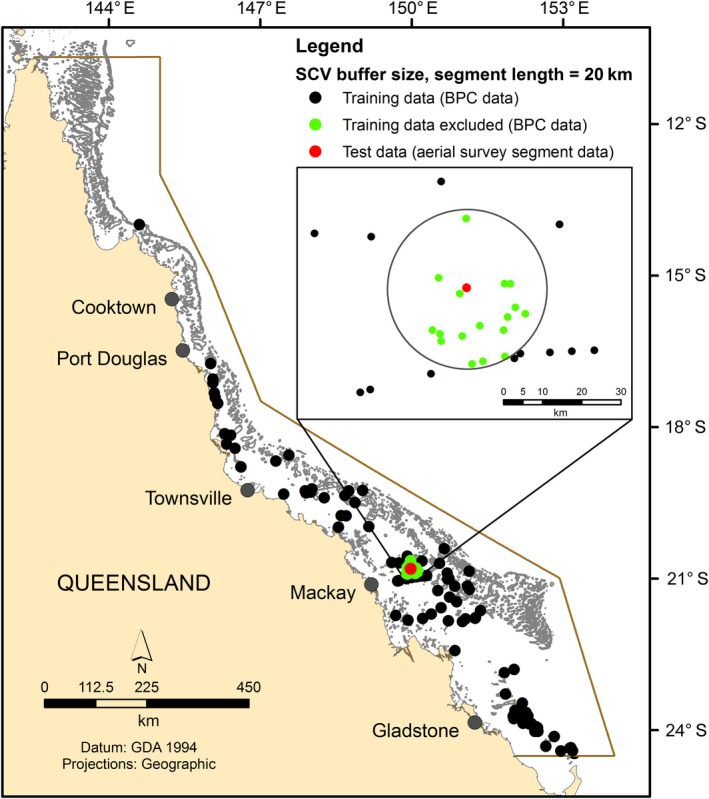
Example of the spatial cross‐validation (SCV) approach, using a buffer size and segment length of 20 km for the Border Protection Command (BPC) presence‐only training data and systematic aerial survey test data.

We explored the effect of buffer size and segment length on the performance measure by assessing different buffer sizes (10, 20 and 40 km) around the test sites and various distances of aerial survey transect segment lengths (5, 10, 20, and 30 km). The choice of these buffer sizes and segment lengths was made with reference to the observed point pattern of the presence‐only sightings, which appeared to exhibit some clustering. A preliminary analysis in spatstat (Baddeley et al. 2015) to investigate spatial autocorrelation was conducted using the same variables as the MaxEnt model, which revealed clustering up to 15 km that was unexplained by the modeled environmental variation. Hence, our choices encompass buffer sizes and segment lengths that allowed us to explore differences in predictive performance over a range of potential spatial autocorrelation.

The spatial block CV evaluated model performance using a number of metrics, including the area under the curve (AUC) of the receiver operating characteristic (ROC), true skill statistic (TSS), and Cohen’s kappa (kappa). The ROC curve is drawn by plotting the true positive rate or sensitivity (i.e., the proportion of verified humpback presences correctly predicted as presences; omission error) against the false positive rate or specificity (i.e., the proportion of verified humpback whale absences falsely predicted as presences; commission error) for various classification thresholds of presence and absence from the fitted MaxEnt intensities. The area under the curve (AUC) can range from 0 to 1, with 0.5 representing an uninformative classifier and values >0.9 considered good, 0.7–0.9 moderate, and <0.7 poor (Fielding and Bell 1997). TSS incorporates sensitivity and specificity, is not sensitive to prevalence and is given by the formula TSS = sensitivity + specificity – 1 (Allouche et al. 2006). TSS provides a value between −1 and + 1, where + 1 indicates perfect agreement and values of ≤0 indicate a performance no better than random. Values >0.6 are considered good, 0.2–0.6 are fair to moderate, and <0.2 are poor. We provide both the maximum and mean true skill statistic over all possible classification thresholds. We also compute Pearson’s correlation coefficient between the fitted MaxEnt intensities and the observed counts of humpback whales and density estimates standardized for effective strip area searched for whales within each segment.

Results

Presence‐only data and MaxEnt model

In total, there were 381 whale sightings collected from 2003 to 2007 by the BPC aerial surveillance program. Of these, 131 (34%) were confirmed humpback whales and 107 occurred during July and August and were used to develop the MaxEnt presence‐only model (Smith et al. 2012). The mean test AUC using the Coastwatch data was 0.86 (range 0.80–0.92 over 50 bootstrap samples), indicating that the model is reliable at predicting presence sites from random background sites (Elith 2002). The environmental variables that contributed the most information to the MaxEnt model were SST and water depth, based on the jack‐knife test of variable importance (Appendix S1: Fig. S3). These two variables had the most useful information as single variables in isolation on training gain (highest gain scores) and the most predictive power (highest AUC) within the model. Response curves indicate a preference for waters within SST ranges of 21°C to 23°C and between 30 and 58 m in water depth (Appendix S1: Fig. S4).

Independent aerial survey data

In total, 343 unique humpback whale groups were sighted during the aerial survey, consisting of 562 individual whales (492 adults, 70 calves; Table 2). Humpback whales were sighted in all three of the regions surveyed, with sightings increasing with latitude: Region 1 (5%), Region 2 (14%), and Region 3 (81%; Fig. 3). Calves were sighted in all three regions among sightings of non‐calf groups, in both inshore and offshore waters (Fig. 3). Region 3 had the highest number of whale sightings although the lowest ratio of calves to adults, whereas Region 1 had the lowest number of whale sightings yet the highest ratio of calves to adults (Table 2). The most common group sizes were single whales (48%) and groups of two (43%), with Region 3 having the greatest variation in group size (range one to six whales).

Table 2.

The number of groups and individuals of humpback whales, mean and range in group size, and ratio of calves to adults sighted in the three survey regions during the 2012 aerial survey.

Survey region	Number of				Calf : adult ratio	Group size
	Groups	Individuals	Adults	Calves		Mean	Range
1. Port Douglas	16	30	24	6	1:4	1.88	1–3
2. Townsville	49	68	56	12	1:4.7	1.39	1–3
3. Mackay	278	464	412	52	1:7.9	1.67	1–6
Total	343	562	492	70

Fig. 3.

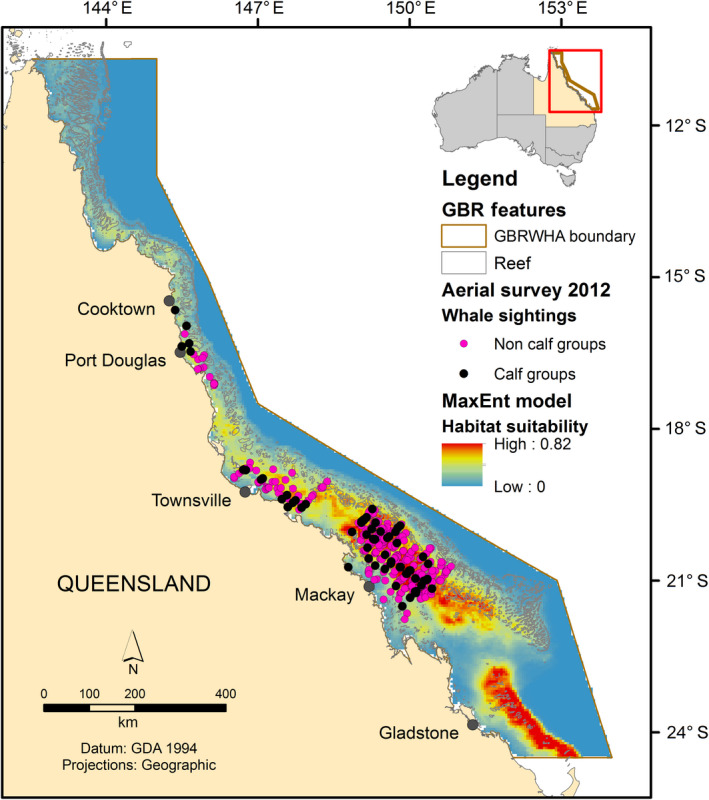
Map of humpback whale sightings from the 2012 dedicated aerial survey overlayed onto the MaxEnt model.

Density Surface Model of aerial survey data

The fitting of a detection function from the aerial survey data was based on 295 observations (268 seen by the front observers and 192 by rear observers; thus 165 were duplicate sightings). To improve the robustness of detection model fitting, aerial sightings data were left truncated at 0.5 km and right truncated at 4.0 km. The double platform model assumed point independence because the full independence model showed a lack‐of‐fit. The best fitting model was a perpendicular distance‐only model for detection and a mark–recapture model that, in addition to distance, included school size and sea state as covariates. Estimated mean group size was 1.54 ± 0.06 (mean ± SE) and the estimated average effective strip half width (uncorrected for g(0); that is, animals on the transect line) was 2.25 km. This model is simply a measure of perception bias and does not take into account the availability of whales at the surface.

The DSM identified sea surface temperature and bathymetry as the top performing covariates from the five habitat variables considered, that contributed the most information in the model explaining the distribution of whales in the GBRWHA. The model identified preferential sea surface temperature between 20° and 22.7°C (peak whale densities between 20.9° and 22.2°C) and favored habitat in water depth between 5 and 80 m (highest densities in depths 47–80 m). Three DSMs for each whale group were developed using the aerial survey data: (1) all whale sightings (Fig. 4), (2) non‐calf groups (Appendix S1: Fig. S5), and (3) calf groups (Appendix S1: Fig. S6).

Fig. 4.

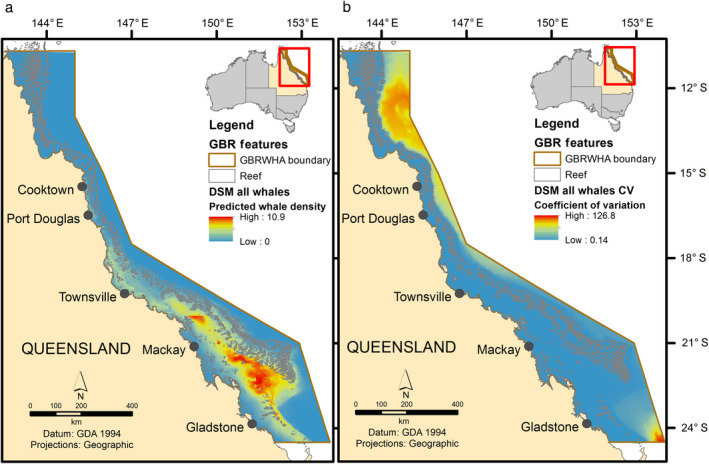
Density surface model (DSM) of the (a) predicted density and distribution of “all whale” humpback whale groups in the Great Barrier Reef Marine Park (GBRMP) based on 2012 line‐transect aerial survey data and (b) corresponding coefficient of variation.

Presence‐only model validation using spatial block cross‐validation

The performance of the MaxEnt models fitted in the spatial block CV and tested with independent aerial survey data was evaluated by a number of metrics. The influence of spatial buffer size around test points and segment length of aerial survey data were tested to determine its effect on model performance (Table 3). Using leave‐one‐out CV, both a 10‐km and 20‐km spatial buffer around the test sites and 20‐km transect segment lengths (165 in total) performed the best in the spatial CV, with similar results. For a spatial buffer and transect segment length of 20 km, there was an AUC of 0.742, a mean and maximum TSS of 0.242 and 0.434, and Pearson correlations between the MaxEnt prediction and the observed counts and densities of whales of 0.383 (Table 3). We chose to highlight a buffer size and segment length of 20 km due to the transects being 20 km apart, which allows for minimal movement of individual whales between transects and reduces the probability of double‐counting whales. We explored other choices of buffer sizes and segment lengths, which produced relatively similar results (Table 3). AUCs ranged from 0.669 to 0.743, mean and maximum TSS ranged between 0.169 to 0.243 and 0.286 to 0.434, respectively, and Pearson correlations between the MaxEnt prediction and the observed counts and densities of whales ranged between 0.265 to 0.466 and 0.254 to 0.449, respectively. The results suggest good congruence between the predicted humpback intensities from MaxEnt and the aerial survey observations, such that areas of high whale density closely reflect areas of predicted high habitat suitability.

Table 3.

Measures of performance of the MaxEnt model using spatial cross‐validation (SCV) evaluated for different segment lengths and buffer sizes around aerial survey data test points.

Segment length (km)	SCV buffer (km)	No. segments	AUC	TSS		Pearson correlation
				Mean	Maximum	Count	Density
5	10	612	0.676	0.176	0.286	0.283	0.272
10	10	314	0.710	0.210	0.336	0.353	0.326
20	10	165	0.743	0.243	0.434	0.390	0.390
30	10	114	0.693	0.193	0.353	0.466	0.449
5	20	612	0.674	0.175	0.288	0.279	0.267
10	20	314	0.712	0.212	0.336	0.347	0.320
20	20	165	0.742	0.242	0.434	0.383	0.383
30	20	114	0.690	0.190	0.327	0.447	0.431
5	40	612	0.669	0.169	0.300	0.265	0.254
10	40	314	0.698	0.198	0.338	0.335	0.311
20	40	165	0.730	0.230	0.413	0.365	0.366
30	40	114	0.679	0.179	0.307	0.443	0.430

Performance measures consist of AUC, True Skill Statistic (TSS) and Pearson correlation.

Discussion

Conservation planning typically requires an understanding of the geographical extent of a given species or landscape to make effective decisions, although accurate information on species distributions is not always available. Errors in estimates of species distributions can reduce the effectiveness (e.g., falsely predicting a species in unoccupied areas) and efficiency (e.g., failing to predict a species in an occupied area) of conservation decisions (Hermoso et al. 2015). Some management frameworks (e.g., spatial risk assessments) may require more spatially accurate data than others (e.g., Biologically Important Areas), and model validation becomes more important within this context. Here, we validated a MaxEnt model of humpback whale distribution in the GBR using a spatial block CV approach to determine its reliability and usefulness in identifying impacts from human activities (e.g., shipping). Moderate performance results from the spatial block CV (Table 3) demonstrates good congruence between the MaxEnt model predicted intensities and aerial survey observations, and visually aligns well with the predicted DSM whale densities (Fig. 4 and Appendix S1: Fig. S1). Areas of higher whale density closely reflect areas of higher habitat suitability, and hence probability of occurrence. In turn, this supports the assumption of unbiased sampling and even coverage in the collection of the BPC opportunistic data (Smith et al. 2012), which is critical for presence‐only data and modeling techniques (Fiedler et al. 2018). Consequently, it suggests the MaxEnt model is reliable in identifying current distribution patterns for this mobile marine species within the GBRMP and highlights conflict with current human activities (e.g., shipping).

The application of SDMs to marine species is not as prolific compared to terrestrial species (Robinson et al. 2011), although their use is increasing due to the logistical and economical costs of collecting systematic distribution data (Redfern et al. 2006, Robinson et al. 2017). This is particularly evident for opportunistic, presence‐only data due to the development of modeling approaches such as MaxEnt, which performs particularly well in its predictive accuracy compared to other modeling methods (Elith et al. 2006). In our study, the performance measures from the spatial block CV show the independent aerial survey presence/absence data support the MaxEnt habitat model. These data suggest the area of highest predicted habitat suitability and density of whales occurs in the southern GBR lagoonal waters (Appendix S1: Figs. S1 and S4). A possible explanation for this is that the distance to offshore reefs decreases as latitude decreases, such that the outer reef structure is considerably closer to the coast in the north (~50 km) compared to the south (~150 km). This is due to the natural structure of the reef, which results in the southern GBR lagoonal waters providing the greatest area of available suitable habitat. Both the DSM and MaxEnt models identified SST (MaxEnt 21°–23°C, DSM 20.9°–22.9°C) and bathymetry (MaxEnt 30–58 m, DSM 47–80 m) as the two top performing environmental covariates that contributed the most in predicting the distribution of whales in the GBRMP.

The performance measures indicated the MaxEnt model performed moderately, although not perfectly, when compared to presence/absence data. This is not surprising given we are comparing two measures of distribution that are static in time for a mobile marine species’. There can be a mismatch in data due to a range of issues including dynamic environmental predictors and inter‐annual variation, sampling biases, various propagated errors throughout the modeling process, and the degree to which species have specific ecological requirements. The marine environment is a highly fluid environment with dynamic environmental parameters (e.g., sea surface temperature, salinity, ocean currents), which can affect the validity of model assumptions and predictive model performance (Robinson et al. 2011). This can be compounded by detectability issues of mobile marine mammals, which can increase the probability of failing to observe a species in an area of identified suitable habitat. Furthermore, it is possible that humpback whales might not have highly restricted ecological requirements on their breeding grounds and consequently environmental features do not completely explain whale distribution. Other factors may be important drivers of whale distribution that are not incorporated into the models, such as social behavior, which may operate at different spatial scales. For example, water temperature may influence whale distribution at a broad scale (hundreds to thousands of kilometers; Rasmussen et al. 2007, Derville et al. 2019), whereas the availability of suitable reproductive habitat (e.g., based on water depth; Rasmussen et al. 2007) and social behavior could influence it at a local scale (tens to hundreds of kilometers; Clapham and Zerbini 2015). Ultimately, the distribution of males and females on the breeding grounds could in part be a consequence of their polygynous mating system (Clapham 2000, Cerchio et al. 2005).

Model validation of SDMs should ideally be undertaken using independent data to increase model reliability (Araújo et al. 2005), although this can be rare due to the expense of acquiring new data. This is particularly important for presence‐only models with potential sampling biases and we suggest is critical for some conservation management applications, e.g., spatial risk assessments. However, in the process of acquiring new data, we demonstrate presence‐only models can be used as a cost‐effective approach to inform the design of systematic surveys for sampling larger areas of interest (Rebelo and Jones 2010). This can reduce the required sampling effort and additionally provide more targeted and detailed species information in BIAs for use in broad‐scale management frameworks. For this to occur though, it is essential that any spatial bias in the presence‐only observations is understood and addressed before any validation process (Fiedler et al. 2018), and an understanding of the sampling process is obtained where possible (Bird et al. 2013). In our study, we designed an aerial survey that targeted three areas in the GBRMP that represented high, medium, and low habitat suitability. This resulted in 18% of the entire Marine Park (344,400 km²) being surveyed across 7° of latitude. Humpback whales were sighted in all three of the regions surveyed, there was an evident decrease in the number of sightings from high to low habitat suitability, and whale sightings closely conformed to suitable areas predicted by the MaxEnt model (Table 2, Fig. 3). The aerial survey presence/absence data enabled the identification of calf and non‐calf groups, which was not available in the presence‐only data, and consequently a better understanding of calving vs. mating areas based on the presence of a calf was achieved. While calf groups occurred among non‐calf groups in all regions, calf groups have a greater predicted range throughout the GBRMP compared to non‐calf groups and higher calf to adult ratio in the northern area of Region 1 (Table 2, Appendix S1: Figs. S5 and S6).

Model error and uncertainty can have a large impact for some management frameworks, for example, spatial risk assessments, where spatially accurate data are necessary for implementing mitigation strategies. Here we demonstrate that comparing a presence‐only model to fully independent data through a robust spatial block CV approach, we can increase confidence in the reliability of the presence‐only model for a risk assessment framework. In the context of this study, the GBRMP is managed as a multiple‐use area and includes a range of commercial and recreational activities such as commercial shipping, marine tourism and recreational boating. The MaxEnt model suggests that the area located offshore of Mackay is a potentially important wintering area for humpback whales during the breeding season (Fig. 3). This area also significantly overlaps with the GBR inner shipping route (Fig. 5). Internationally and within Australia, humpback whales are the most common species involved in ship strikes (Vanderlaan and Taggart 2006, Peel et al. 2018). Given the Australian east coast population is increasing (11% per annum) at close to the maximum plausible biological rate and shipping traffic (commercial and recreational) is increasing in the GBR, impacts from ship strikes and associated ship noise with breeding humpback whales is likely an emerging issue. Validation of the MaxEnt presence‐only model has been critical for providing confidence in the predicted distribution of humpback whales on their breeding ground to be incorporated at an appropriate management scale for a spatial risk assessment of ship strike to humpback whales (Fig. 5). Ultimately, a lack of systematic, dedicated species data should not be an impediment to quantitatively assessing risk from human activities.

Fig. 5.

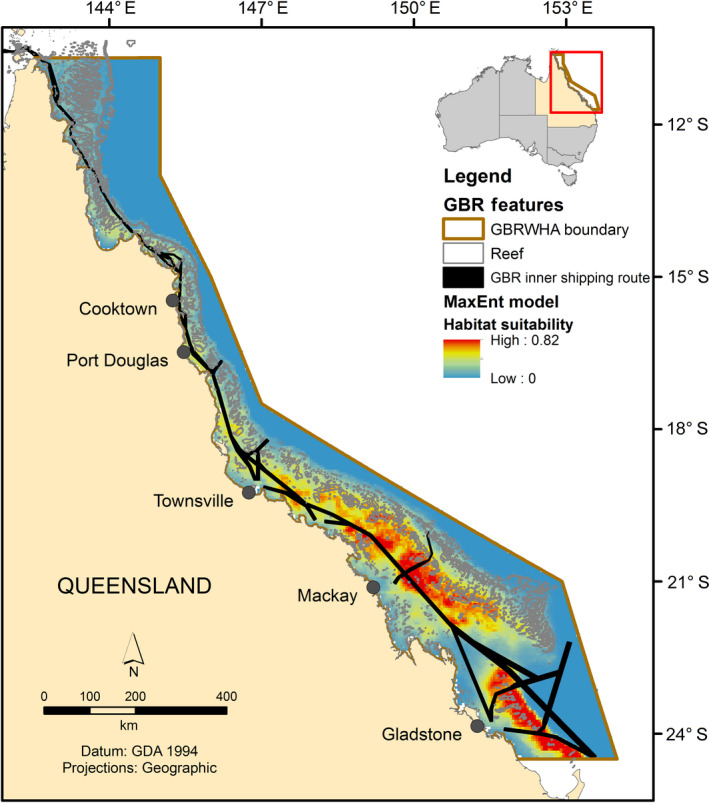
MaxEnt model of habitat suitability for humpback whales in the GBRMP and overlay of the GBR inner shipping route.

Supporting information

Appendix S1

Smith, J. N. , Kelly N., and Renner I. W..2021. Validation of presence‐only models for conservation planning and the application to whales in a multiple‐use marine park. Ecological Applications 31(1):e02214 10.1002/eap.2214

Data Availability Statement

Data are available from the Australian Antarctic Data Centre: https://data.aad.gov.au/metadata/records/AMMC_11‐15_GBR_humpback_aerial_survey