Abstract
We present a mathematical model and a statistical framework to estimate uncertainty in the number of SARS-CoV-2 genome copies deposited in the respiratory tract of a susceptible person, , over time in a well mixed indoor space.
By relating the predicted median for a reference scenario to other locations, a Relative Exposure Index (REI) is established that reduces the need to understand the infection dose probability but is nevertheless a function of space volume, viral emission rate, exposure time, occupant respiratory activity, and room ventilation. A 7 h day in a UK school classroom is used as a reference scenario because its geometry, building services, and occupancy have uniformity and are regulated.
The REI is used to highlight types of indoor space, respiratory activity, ventilation provision and other factors that increase the likelihood of far field ( m) exposure. The classroom reference scenario and an 8 h day in a 20 person office both have an and so are a suitable for comparison with other scenarios. A poorly ventilated classroom (1.2 l s−1 per person) has suggesting that ventilation should be monitored in classrooms to minimise far field aerosol exposure risk. Scenarios involving high aerobic activities or singing have ; a 1 h gym visit has a median , and the Skagit Choir superspreading event has .
Spaces with occupancy activities and exposure times comparable to those of the reference scenario must preserve the reference scenario volume flow rate as a minimum rate to achieve , irrespective of the number of occupants present.
Keywords: Ventilation, Airflow, Infection, School, Classroom
Nomenclature
Filter efficiency
Face covering efficiency
Surface deposition rate ( s−1)
Biological decay rate ( s−1)
Ultraviolet denaturing rate ( s−1)
Filtration removal rate ( s−1)
Mean absorption-adjusted breathing rate for all occupants ( m3 s−1)
Total removal rate ( s−1)
Ventilation removal rate ( s−1)
Respiratory tract absorption removal rate ( s−1)
Floor area (m)
Concentration of droplets in exhaled air ( RNA copies m−3)
Concentration of RNA copies in exhaled droplets ( RNA copies m−3)
Emission rate of RNA copies ( RNA copies s−1)
Emission rate of RNA copies per person (RNA copies s per person)
Fraction of aerosol particles absorbed by respiratory tract
Proportion of droplets containing RNA copies absorbed by respiratory tract of a person
Number of people present
Number of RNA copies in well mixed air (RNA copies)
Number of RNA copies at start of exposure period
Number of infectious people present
Steady state number of RNA copies
Respiratory tract absorption rate ( s−1)
Respiratory rate of a person ( m3 s−1)
Airflow rate through filter ( m3 s−1)
Infected person respiratory rate ( m3 s−1)
Susceptible person respiratory rate ( m3 s−1)
Exposure period (s)
Time (s)
Time interval between the infected person leaving the space and the susceptible person arriving (s)
Infected person departure time (s)
Space volume (m)
Volume of single exhaled droplet (m)
Ratio of the total volume of expelled droplets to the volume of exhaled air then the total emission rate of RNA copies
Number of RNA copies inhaled over exposure period
1. Introduction
Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) is a novel virus that spread rapidly worldwide leading to the global COVID-19 pandemic in 2020. Initially, the primary transmission pathways were thought to be large respiratory droplets generated by coughing and sneezing, and contact with infected surfaces via fomites. Later, the Centers for Disease Controls and Prevention [1] suggested that the fomite pathway is less likely.
The transmission of some infectious diseases via aerosols is established [2], and evidence for the airborne transmission of SARS-CoV-2 contained in aerosols grew as the pandemic progressed. For example, several case studies reported transmission clusters with high attack rates, so called superspreader events, where a single source infects many people in a space. These occurred indoors where aerosol transmission could be an infection pathway [3], [4], [5], [6], [7], [8]. Analysis of these events and evidence of the potential for aerosol airborne transmission of SARS-CoV-2 have been presented by [9], [10], [11], [12], [13] and [14].
Aerosols originate from different parts of the respiratory tract and form during breathing, talking, shouting, singing, coughing, sneezing or laughing [15], [16]. Droplets range in size from 1 m to 100 m, and their size distribution is dependent upon the expiratory activity, but usually follows a log-normal distribution [16], [17], [18], [19]. After their emission, the droplets fall ballistically under gravity in still air. Concurrently, evaporation occurs at a rate dependent upon room temperature and humidity. Evaporation can reduce droplet diameter by 50%–80% [20], [21], decreasing their mass and terminal velocity. Aerosols with an evaporated diameter of 10 m can remain airborne for several hours, buoyed and dispersed by local air currents. Ribonucleic acid (RNA) copies of the SARS-CoV-2 genome have been detected and calculated at a wide range of concentrations, from to RNA copies per ml, in the sputum of people infected with SARS-CoV-2 who may be symptomatic, pre-symptomatic, and asymptomatic [8], [22], [23]. Most of the RNA copies are likely to be remnants of the genome or unviable virions, but a proportion will be virions that are able to infect an individual who has no immunity to SARS-CoV-2, herein referred to as a susceptible person. Laboratory tests demonstrate that SARS-CoV-2 can remain infectious in airborne aerosols for up to 16 h, and have a half-life of over one hour [24], [25]. It is not yet clear what size of respiratory aerosols and droplets carry virus, and how this relates to the viral load in sputum or saliva, however SARS-CoV-2 has been recently sampled from exhaled breath [26] and there is good evidence from exhaled breath studies of influenza and seasonal coronavirus that respiratory viruses are carried in large and small aerosol fractions [27].
The identification of the potential for indoor airborne aerosol exposure led international groups responsible for guidance on building services to recommend that buildings should be ventilated with as much outdoor air as reasonably possible to dilute SARS-CoV-2 laden aerosols [28], [29], [30]. Increasing airflow rates to control diseases is not a new approach. Florence Nightingale’s first canon of nursing was to “keep the air [a person] breathes as pure as the external air, without chilling [them]” [31].
It is difficult to determine an acceptable level of exposure to a novel pathogen, such as SARS-CoV-2, because the probability of infection as a function of the number of RNA copies inhaled, defined as a quantum [32], is unknown. Therefore, it is also difficult to determine the ventilation rate required to reduce the risk to an acceptable level. Consequently, the current advice is to provide as much outdoor air as reasonably possible [29]. Many buildings are already able to increase airflow rates above the minimum rate required for acceptable indoor air quality because the airflow rates required to control indoor temperatures are typically an order of magnitude higher than those required for contaminant dilution.
There are several investigations of the role of aerosol transmission and the efficacy of interventions, such as increased ventilation, face covering use, and activity duration, and tools are publicly available.1 Infection risk is often estimated using the established Wells–Riley model that gives the required quanta emission (emission of infective material) from known outbreaks [8], fitting to the reproductive number, [33], or is calculated from first principles [34]. Mass balance models have also been used to investigate transient effects and the role purging room air during breaks [35]. The impact of varying occupancy has also been considered using the re-breathed fraction of air based on respiratory CO generation and removal [36].
During a pandemic there are no zero-risk situations, and so the aim of this paper is to propose an analytical model to estimate uncertainty in the relative exposure to RNA copies in the air, of which a proportion are viable SARS-CoV-2 virions, for a range of indoor spaces and ventilation and occupancy scenarios. The model considers the probable emission of viable virions by estimating the generation of aerosols, and their subsequent transport and removal via a number of mechanisms, including inhalation. For clarity, the chosen metric is RNA copies inhaled because the proportion of viable virions for SARS-CoV-2 is currently unknown [8], [37] and because this fact does not affect the magnitude of relative exposure. Other factors are also unknown, such as the effect of the lung penetration depth on infectiousness, virion characteristics (viability, emasculating droplet size, age, and half-life in air), and the infection probability for an uninfected person as a function of co-morbidities. Therefore, the Wells–Riley method, which requires an estimate the quanta of infection derived from outbreaks (confounded by rare superspreading events) [32] and a dose–response method are not applied because they cancel when calculating the relative exposure index, which removes an area of significant uncertainty from predictions. However, as information becomes available, the approach can be amended to determine the exposure of individuals to a specific quantity of virus, using a dose–response approach in risk assessments [38], [39].
The approach is novel because it considers relative risks, transient effects (such as purge ventilation rates and its diminishing returns), and uncertainty in the emission of infectious materials. The model is used to consider the factors that affect the inhalation of RNA copies over a time period in a well mixed space. This also allows the relative benefits of interventions to be considered and, in particular, the identification of upper limits of practical interventions, such as ventilation. This will enable sensible engineering judgements to be made about the management and regulation of indoor spaces.
The aim is achieved by meeting a series of objectives that are described in each section. Section 2 introduces the model and its inputs. The classroom reference scenario is discussed in Section 3 and other indoor scenarios are explored in Section 4.
2. Modelling approach
An analytical model is developed to predict the number of viral genome copies with the potential to be viable (RNA copies) inhaled over a time period in an indoor space. The model is implemented to investigate a range of scenarios and spaces using excel spreadsheets and bespoke MATLAB code, contained in a package of Supplementary Materials.2 A statistical modelling framework, following that of [40], [41], [42], is described in the Supplementary Materials and is used to quantify uncertainty in the relative exposure associated with a space.
2.1. Mass-balance model
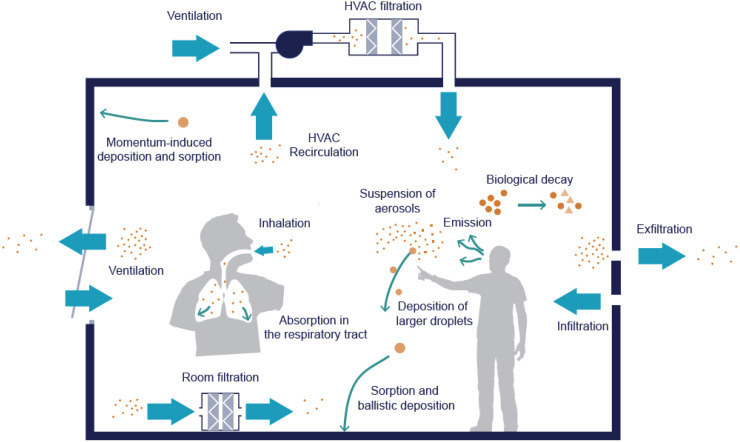
A mass-balance model is used to investigate the number of RNA copies, (RNA copies), contained in aerosols transported to and from an indoor space. This approach is commonly used to model indoor contaminant concentrations in a well mixed airtight space with volume (m) [43]. Therefore, the model assumes that RNA copies are generated at single point at a constant rate, ( RNA copies s−1), and are then mixed rapidly so that the change in the number of RNA copies in the space, (RNA copies), with time, (s), is approximately the same regardless of the sampling point; see Fig. 1. We assume that no RNA copies are transported into the space from outside or connected spaces. The number of RNA copies in the space is diluted by a number of mechanisms that can be normalised by the volume of the space, (m), and combined into a single removal rate, ( s−1), by addition; see Section 2.4.1. The rate of change in the number of RNA copies in the space at time can then be described by a linear differential equation.
| (1) |
Fig. 1.
Single-zone mass-balance model of virus transport via exhaled aerosols.
Image used under a creative commons license1.
Integration over a known time period that starts at , gives the number of RNA copies in the space as a function of time.
| (2) |
Here, is the number of RNA copies at the start of the time period and is the steady state number of RNA copies in the space where
| (3) |
The risk of infection can be estimated from the total number of RNA copies absorbed by the respiratory tract of a susceptible individual, (RNA copies inhaled), over an exposure period (s). It is dependent on the respiratory rate, ( m3 s−1), the space volume, and the ratio of the number of aerosol particles absorbed by the respiratory tract to the total number of aerosol particles that pass through it, .
| (4) |
so that
| (5) |
These equations can be used to consider unique occupancy periods.
2.1.1. Steady state conditions
When an infected person is present in the space for a significant period of time the exponent of Eq. (5) becomes relatively small so that and the number of RNA copies absorbed by a susceptible person is given by
| (6) |
To model the space where the steady state has been reached when a susceptible person enters, , Eq. (6) reduces further to
| (7) |
2.1.2. Step response conditions
When an infected person enters the space where a susceptible person is already present when and , Eq. (5) reduces to
| (8) |
where (s) is the exposure period.
2.1.3. Step response and decay conditions
When an infected person enters an occupied space when and departs at time , a general formula for is found for those remaining in the space. Eq. (8) describes the occupied period and the decay period is represented by substituting Eq. (2) into Eq. (5) and assuming to give
| (9) |
where is the exposure period.
2.1.4. Decay conditions
When a susceptible person enters the space after an infected person has departed, a general formula for is found by assuming during the decay period and when the infected person enters the space.
| (10) |
Here, is the length of time the infected person spent in the space, is the time interval between the infected person leaving the space and the susceptible person arriving, and is the exposure period. Eq. (10) can is simplified by assuming that the infected person is in the space for a long period of time so that .
2.2. Mixing volume,
The volume term in Eq. (5) is an important source of bias because the space volume may include people and objects where viral aerosols cannot mix. Then, the mixing volume and the space volume are not equal; see [44]. When their ratio is , is under-estimated. This is particularly important in areas of high occupancy density.
Space volumes are estimated by their type and are given in Table 1. In this paper we consider situations where space and mixing volumes may be assumed to be identical.
Table 1.
Scenario deterministic inputs.
| Floor area |
Room volume, |
Occupants |
Exposure time, |
Infected occupancy time, |
Conditions | |
|---|---|---|---|---|---|---|
| (m) | (m) | (s) | (s) | |||
| Reference scenario | 55 | 148.5 | 32 | 25200 | 25200 | Step response |
| Class 750 | 55 | 148.5 | 32 | 25200 | 25200 | Step response |
| Class 1000 | 55 | 148.5 | 32 | 25200 | 25200 | Step response |
| Class 2000 | 55 | 148.5 | 32 | 25200 | 25200 | Step response |
| Class 5000 | 55 | 148.5 | 32 | 25200 | 25200 | Step response |
| Office | 220 | 594 | 20 | 28800 | 28800 | Step response |
| Office Low | 220 | 594 | 20 | 28800 | 28800 | Step response |
| Coffee | 110 | 297 | 2 | 1800 | 1800 | Steady state |
| Coffee Low | 110 | 297 | 2 | 1800 | 1800 | Steady state |
| Supermarket | 4645 | 27870 | 160 | 3600 | 3600 | Steady state |
| Gym | 200 | 600 | 20 | 3600 | 3600 | Steady state |
| Guangzhou | 40.5 | 127 | 21 | 4500 | 4500 | Step response |
| Skagit Choir | 180 | 810 | 61 | 9000 | 9000 | Step response |
| German Meeting | 70 | 189 | 13 | 34200 | 34200 | Step response |
2.3. Virus generation rate,
is proportional to the number of people shedding RNA copies in the space, and is also a function of their respiratory rate. This can be given by
| (11) |
where is the number of infectious occupants in the space, and (RNA copies s−1 per person) is the emission rate per person. Then, following Buonanno et al. [34], is calculated by
| (12) |
where ( RNA copies m−3) is the concentration of RNA copies of the SARS-CoV-2 genome in the exhaled droplets, and is assumed to be the same as the concentration in the sputum of the infected individual, is the breathing rate of the infected individual ( m3 s−1), is the concentration of droplets in exhaled air ( RNA copies m−3), (m3) is the volume of a single droplet (m), and is the efficiency of a face covering, herein assumed to be 0. If is the ratio of the total volume of expelled droplets to the volume of exhaled air then the total emission rate of RNA copies is given by
| (13) |
Breathing and respiratory fluid RNA measurements from COVID-19 patients [22], [26] are used to estimate . Following Morawska et al., droplet diameter is assumed to be normally distributed with a mean of m and an arbitrary standard deviation of 10% of the mean. The RNA copies load of the infected individual is also assumed to be normally distributed with a mean of RNA copies per m and a standard deviation of 10% of the mean; see the Supplementary Material for derivations of infector viral loads per ml of respiratory fluid including variation with vocal activities.
Values of and are given by Adams et al. [45], [46], and is derived from Morawska et al. [18] as a function of and droplet diameter. The Supplementary Material discusses these parameters in greater detail. We assume no face coverings are worn in any of the scenarios.
2.4. Removal rate,
The number of RNA copies in the air of the space are diluted by a number of mechanisms, where the total removal rate is given by their sum.
| (14) |
Here, is the removal rate due to ventilation, is the removal rate due to surface deposition, is the removal rate due to biological decay, is the removal rate due to absorption in the respiratory tract, and is the removal rate due to filtration. Re-suspension following surface deposition is not considered. All terms have units of s−1 and are discussed in Sections 2.4.2, 2.4.3, 2.4.4, 2.4.5, respectively.
The system time constant (s) is the reciprocal of , . is a function of the parameters described in Sections 2.4.1, 2.4.2, 2.4.3, 2.4.4, 2.4.5. is also known as the residence time since it indicates the time RNA copies remain in the space after generation and is indicative of the timescale for the system to reach a new steady state.
2.4.1. Air change rate,
The air change rate is a function of the ventilation rate and space volume . Ventilation rates are normally given by standards and guidelines per capita according to the function of the space.
2.4.2. Surface deposition rate,
Surface deposition occurs by two key mechanisms: ballistic deposition, and momentum-induced deposition. However, empirically derived values of do not differentiate between them and so a single term, ( s−1), is used. Thatcher et al. [47] give median measured in a furnished space as a function of droplet diameter and with and without mixing fans. Therefore, we assumed the mixing fans are off where is equally probable between values of 1.17 s−1 and 1.69 s−1; see Table 2.
Table 2.
General inputs.
| Input variable | Assumed PDF | Source |
|---|---|---|
| Biological decay, ( s−1) | LN(,0.43) | [25] |
| Inhaled deposition fraction, | U(0.43,0.65) | [48] |
| RNA concentration in exhaled droplets, (RNA copies m−3) |
N(,) | [8], [21], [22], [26], [49] |
| Surface deposition rate, (s−1) | U(,) | [47] |
| Concentration of aerosols in exhaled air, (m−3) |
[18] |
N, normal; LN, log-normal; U, uniform.
2.4.3. Biological decay rate,
The biological decay rate is a function of the half-life, t (s), and the denaturing rate, ( s−1), where
| (15) |
Van Doremalen et al. [25] report that the half-life of SARS-CoV-2 in aerosols has a median of approximately 1.1–1.2 h and a 95% confidence interval of 0.64 to 2.64 h. This is approximately represented by a log-normal distribution, which when converted to using Eq. (15), has a mean of s−1 and a standard deviation of s−1.
Inactivation from exposure to ultraviolet light (UV-C) is also a biological process. The denaturing rate at a particular airflow rate should be adjusted when a UV-C device is used. Here, RNA copies are not physically removed from a space, but this model assumes they are because they are no longer harmful.
2.4.4. Respiratory tract absorption rate,
The respiratory tract absorption rate is assumed to be proportional to (see Section 2.1) and the number of RNA copies in the air, given by
| (16) |
where is the proportion of droplets containing RNA copies entering the respiratory tract of a person and are absorbed by its surface, assumed to be constant, and ( m3 s−1) is respiratory rate of a person. Then,
| (17) |
where is the total number of occupants within the space, and ( m3 s−1) is the mean absorption-adjusted breathing rate for all of the occupants in the space. The respiratory tract absorption is characterised in by a removal rate, ( s−1), given by
| (18) |
This removal rate is a function of occupancy, and occupant metabolic rate. Therefore, it is unique for each space, and not a general constant.
Darquenne [48] shows that is a function of droplet diameter and tidal volume, the volume of air inhaled per breath. For the droplet diameter given in Table 2, is 0.43–0.65, depending on the tidal volume. In the absence of knowledge, we assume that all values of are equally probable between these limits; see Table 2.
Respiratory rates are given by Adams [46] for male and female occupants sitting and walking, and generally for children sitting. All values are assumed to be normally distributed and to vary with space use; see Table 3.
Table 3.
Scenario probabilistic inputs.
| Input variable | Droplet diameter | Respiratory rates, | Air change rate, | Airflow rate | Respiratory activity |
|---|---|---|---|---|---|
| , , | breathing:talking:vocalisation | ||||
| () | (m h−1) | (h−1) | (l s−1) | (%) | |
| Reference scenario | N(1.840,0.184) | N(0.440,0.044) | 3.9 | 160 | 75:25:0 |
| Class 750 | N(1.840,0.184) | N(0.440,0.044) | 12.2 | 505 | 75:25:0 |
| Class 1000 | N(1.840,0.184) | N(0.440,0.044) | 7.1 | 296 | 75:25:0 |
| Class 2000 | N(1.840,0.184) | N(0.440,0.044) | 2.7 | 110 | 75:25:0 |
| Class 5000 | N(1.840,0.184) | N(0.440,0.044) | 0.9 | 38 | 75:25:0 |
| Office | N(1.840,0.184) | N(0.560,0.056) | 1.2 | 200 | 75:25:0 |
| Office Low | N(1.840,0.184) | N(0.560,0.056) | 0.2 | 40 | 75:25:0 |
| Coffee | N(1.840,0.184) | N(0.560,0.056) | 3.3 | 270 | 75:25:0 |
| Coffee Low | N(1.840,0.184) | N(0.560,0.056) | 0.2 | 16 | 75:25:0 |
| Supermarket | N(1.780,0.178) | N(0.560,0.056) | 1.1 | 8528 | 100:0:0 |
| Gym | N(1.780,0.178) | N(3.510,0.351) | 2.4 | 400 | 100:0:0 |
| Guangzhou | N(1.840,0.184) | N(0.560,0.056) | U(0.2,0.4) | U(7,14) | 75:25:0 |
| Skagit Choir | N(2.50,0.25) | N(0.910,0.091) | U(0.3,0.7) | U(68,158) | 0:0:100 |
| German Meeting | N(1.840,0.184) | N(0.560,0.056) | 0.2 | 105 | 75:25:0 |
N, normal; U, uniform.
Values are converted into SI units before they are applied to the model; see Section 2.1.
2.4.5. Filtration rate,
Mechanical filters actively remove aerosol-borne viruses from the air either when fitted in a mechanical ventilation system or in a stand-alone air purifier. The filtration removal rate is proportional to the volume flow rate of air passing through the filter, ( m3 s−1), sometimes known as a clear air delivery rate, and is given by
| (19) |
where is the filtration efficiency defined as the ratio of the number of RNA copies removed by the filter to the number of RNA copies in the air that is passed through it, and has a value between 0 and 1.
2.5. Indoor spaces
A reference scenario is defined that allows uncertainty in the number RNA copies inhaled to be investigated as a function of space volume, emission and exposure times, occupant activity, and room ventilation. These predictions can then be compared against those for cases within other non-domestic spaces by developing a Relative Exposure Index (REI); see Section 3.2 for its definition. This eliminates the need for an understanding of the dose threshold and RNA copies emission rate by an infector, and highlights types of indoor space and activities that lead to the greatest exposure for the same infector; see Section 1. All scenarios assume a single infected person and the Step response conditions (Section 2.1.2), unless stated otherwise. All model inputs are given in Table 1, Table 2, Table 3.
2.5.1. Reference scenario
A UK school classroom is used as a reference scenario because its geometry and ventilation provision are well described by design guidance documents. Requirements are identified that constitute a worst case scenario. Building Bulletin (BB) 103 [50] requires a minimum floor area of m for a classroom occupied by 30 students and 2 teachers, giving an occupancy density of 1.7 m2 per person. A floor to ceiling height of 2.7 m, gives a reference scenario volume of m. BB101 [51] specifies maximum carbon dioxide (CO) concentrations in learning spaces where natural ventilation is used or when hybrid systems are operating in natural mode, requiring a mean concentration of 1500 ppm averaged over the school day duration, corresponding to an airflow rates of 5 l s−1 per person, and a maximum concentration of 2000 ppm for no more than 20 consecutive minutes, corresponding to an airflow rate of 3.4 l s−1 per person. The mean ventilation rate of 5 l s−1 per person is used unless otherwise stated. These represent air change rates of 3.9 h−1 ( s−1) and 2.7 h−1 ( s−1), respectively for standard classrooms. Many existing UK schools were built when the maximum CO concentration was 5000 ppm, corresponding to an airflow rate of 1.2 l s−1 per person or 0.9 h−1 ( s−1) [52]. Post occupancy assessments of UK naturally ventilated classrooms recorded CO concentrations of over 5000 ppm when ventilation openings were closed [53], [54]. BB101 assumes a school day duration of 7 h, and so we assume all occupants are present throughout, representing a worst case scenario; for example, pupils remaining indoors to shelter from inclement weather.
The ventilation rates given here are generally applicable during the heating season, because higher ventilation rates are required to dissipate heat gains in the summer. They are also less stringent than those required for mechanically ventilated classrooms, where the mean and maximum concentrations are 1000 ppm ( s−1 or 6.2 h−1) and 1500 ppm, respectively [51]. Occupants are assumed to breathe for 75% of the time and talk for 25% of the time. The respiratory activity is used to determine an average number of aerosol droplets and average diameter using data from Morawska et al. [18]; see Supplementary Materials. The breathing rate of susceptible and infected occupants (see Sections 2.1, 2.3 ) is assumed to be m3 s−1, following Adams et al. [46] for children sitting; see Table 3.
2.5.2. Common space scenarios
The occupancy density and ventilation provision of many non-domestic spaces is advised by the Chartered Institution of Building Services Engineers (CIBSE) Guide A [55]. This guidance is used to define three typical spaces where a single infected person is present.
We consider an office with an occupancy density of 11 m per person, a floor to ceiling height of 2.7 m, and a outdoor airflow rate of 10 l s−1 per person ( s−1 or 1.8 h−1). There are 50 occupants who are assumed to be continuously present for 8 h breathing for 75% and talking for 25%.
Small high street shops, such as a coffee shop, generally have an occupancy density of 5 m per person and a recommended ventilation rate of 10 l s−1 per person ( s−1 or 2.7 h−1), representing a high ventilation scenario. However, there may be circumstances where ventilation is not provided and infiltration is the only source of outdoor air. This represents a low ventilation scenario where s−1 or 0.2 h−1 following Buonanno et al. [34]. Occupancy periods are highly variable, and so we model a 30 min visit to a small coffee shop with breathing for 75% of the time and talking for 25%. Here, a shop worker is assumed to be the infected occupant, representing a steady state scenario; see Section 2.1.1.
We model a 1 h visit to a supermarket with a volume of 27,870 m and a ventilation rate of 1.1 h−1 ( s−1) where a store employee is the infected occupant, representing a steady state scenario.
The occupants of gyms have an elevated metabolic and respiratory rate; see Section 2.4.4. We model a 1 h aerobic workout in a small 200 m 600 m3 gym space with a recommended3 maximum occupancy of 20 people and airflow rate of 20 l s−1 per person or 2.4 h−1, where the infected person is an active member of staff, representing a steady state scenario. Deep breathing is likely to generate aerosols with a different number droplets and droplets diameter when compared to breathing at rest and this is reflected by a high respiratory rate; see Supplementary Materials.
2.5.3. High transmission scenarios
The literature reports incidences of high secondary transmission of SARS-CoV-2 in indoor spaces, and so we consider three of them.
A single index case is thought to have transmitted the SARS-CoV-2 virus to nine other patrons of a restaurant in Guangzhou, China, who were sat at adjacent tables; see Li et al. [6]. The space volume is 431 m, but the localisation of the secondary infections and the reported recirculation of air within a zone at the back of the restaurant indicates a mixing volume of 127 m occupied by 21 people. Li et al. report an airflow rate of 0.6 h−1 but the poor mixing suggests that it may be limited to infiltration. Therefore limiting airflow rates of 0.2 h−1 and 0.6 h−1 ( — s−1) are explored with uniform probability. The occupancy time is 1.25 h and we assume 75% of the time is spent breathing and 25% talking.
A single index case is thought to have infected 53 of 61 members of the Skagit Choir over a 2.5 h period in a rehearsal hall [8]. The space volume is 810 m and the ventilation rate is estimated to be between 0.35 h−1 and 1.05 h−1 ( — s−1). The respiratory rate for singing is assumed to be % of that at rest, following Bernardi et al. [56], in the absence of data on aerosols generated by singing we use the vocalisation data of Morawska et al. [18].
During a 9.5 h meeting in a small room in Germany, 11 of 13 participants were infected by a pre-symptomatic index case; see Hijnen et al. [4]. The floor area is 70 m but the space height is unknown and so is assumed to be 2.7 m. The ventilation rate is unknown but personal correspondence with Hijnen revealed that the space was naturally ventilated with all windows closed during the meeting due to cold weather. Therefore, we assume outdoor air is solely provided by infiltration at 0.2 h−1 ( s−1). The room is assumed to be occupied by all participants throughout the meeting.
3. Exposure risk in the reference scenario
3.1. Deterministic estimate
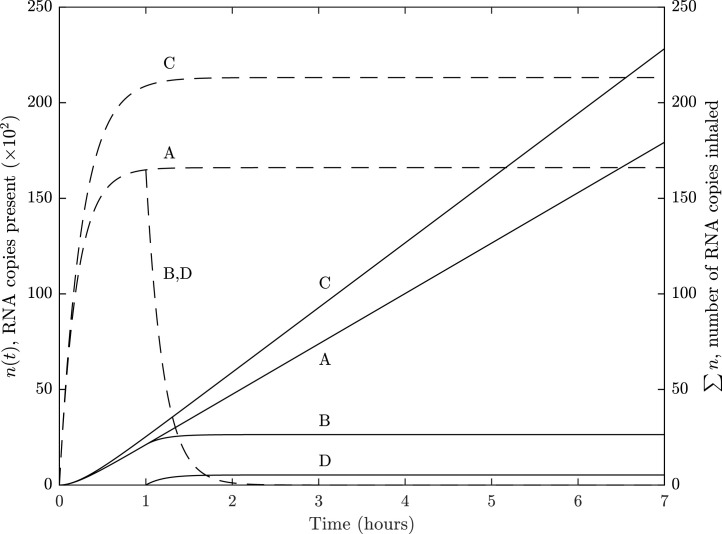
Fig. 2 shows the predicted RNA copies in the volume of the space, , and the number of RNA copies inhaled, , when RNA copies are shed at a concentration of RNA copies per ml of respiratory fluid in the reference scenario when evaluated deterministically for three scenarios; see Sections Section 2.5.1 and the Supplementary Materials. Line A shows that when the RNA emission is over a 7 h period, quickly reaches a steady state of 16,603 RNA copies causing the total number of RNA copies inhaled to be approximately linearly related to the exposure period. After 7 h, an occupant may be expected to inhale 179 RNA copies. The residence time, (see Section 2.4), is 12 min (723 seconds), and the time to reach 95% of the steady state concentration, , is around 35 min, where . The scenario was modelled using Eq. (8) for a novel emission source, but is closely approximated by Eq. (7) for steady state occupancy because is significantly large. Accordingly, Eq. (7) is used to evaluate Fig. 2 and to show how can be minimised in any space. It shows that there are 6 parameters that affect . Those located in the numerator are all linearly related, where a percentage change in their value has a corresponding change in . Not all parameters can be amended immediately to minimise exposure; for example, the number of aerosol particles absorbed by the respiratory tract, (see Section 2.4.4), is a function of physiology and so changes only occur at a population scale in the medium to long term. However, the other parameters can all be addressed in the short term. The respiratory rates of susceptible and infected persons, and (see Section 2.3), are similarly a function of physiology but are also affected by occupant activity. Accordingly, the metabolic rate of occupants should be maintained at as low a rate as possible.
Fig. 2.
Reference scenario: a single infector shedding RNA copies at a concentration of RNA copies per ml of respiratory fluid in a standard school classroom with a volume of 148.5 m3.
—, number of RNA copies inhaled; - - -, RNA copies present.
A, constant emission over a 7 h period; B, infected person leaves space after 1 h and susceptible occupants remain; C, constant emission with removal solely via ventilation where ; D, at hour 1 the infected person leaves the space and is replaced by a susceptible person.
Eq. (13) shows that the emission rate, (see Section 2.3), is linearly related to four parameters, including . We assume a single infected person is in the space for the entire 7 h, but adding another doubles both and . This highlights the need for public health messages to encourage the reporting and isolation of people with SARS-CoV-2 symptoms. The ratio of the total volume of expelled droplets to the volume of exhaled air, , can be reduced by wearing of face coverings that catch droplets before they are allowed to mix in the indoor air. Therefore, it is logical to recommend that all occupants wear face coverings in indoor spaces at all times when it is feasible to do so.
The concentration of RNA copies in exhaled droplets, , is highly variable and may be substantially increased by a so called superspreader, an infected person who transmits the virus to an abnormally large number of other people [57]. Miller et al. [8] report that emission rates for superspreaders are greater than normal infected persons by several orders of magnitude. Then, a corresponding increase in similarly increases and . It should be noted that superspreading events are uncommon, however, it has been estimated that around 80% of infections occur from 10% of people and hence there may be a significant proportion of people who may shed a higher amount of virus [58]. It is possible that superspreading occurs when one of these people is in a scenario with a higher REI. The significant uncertainty in supports the need for a REI because is not a dose risk and so the value of RNA copies inhaled does not itself indicate the probability of infection, which is currently unknown. Utilising values of inhaled RNA copies should not be used to estimate the risk of harm or the probability of secondary transmission in a space. However, any uncertainty in the values used for the RNA copies per ml of respiratory fluid of an infector cancels in a REI allowing scenarios to be compared; see Section 3.2 and the Supplementary Materials.
The final numerator parameter is the exposure time, . In the context of a school day, this value can be reduced by spending as much time outside as possible. Exposure is lowest during the period of transition to the steady state concentration and so it is advantageous to limit occupancy to the time where the rate of change of is greatest. This could be done by allowing frequent outside breaks and purging the indoor air during the changeover. In this example, the value of is relatively short, and it would be advantageous to increase it so that it is comparable to a teaching period.
Line B of Fig. 2 shows the changes to and if the infected person leaves the space after 1 h and all other occupants remain; see Section 2.1.3. Following their departure, decays quickly towards 0 in around an hour and plateaus. is strongly dependent on the length of time the infected person is present in the space with a susceptible person. Line D shows that a susceptible person entering the space as the infected person departs, or afterwards, has a much lower risk; see Section 2.1.4. This is important when the time occupants spend in a space is a variable; for example, there is anecdotal evidence of shop workers who do not wear face coverings even when their customers do. Then, Fig. 2 shows that the greatest risk is to a long-term occupant from a fellow long-term occupant.
Both the steady state concentration and the time to the steady state are inversely proportional to two parameters, the removal rate, , and the volume of the space, , in the denominator of Eq. (7). The easiest parameter to amend in any space is the removal rate, (Eq. (14)), which is dominated by the ventilation rate, (see Section 2.4), which contributes around 80% of the value of ; see Section 2.4. Ventilation is the standard method of diluting pollutants in buildings and as , but with a law of diminishing returns. This is important to note because, in the heating season, there is a near-linear relationship between space heating energy demand and , and care must be taken not to thermally discomfort occupants. Accordingly, there is a trade off between , energy, and thermal comfort that must be considered and will be a function of the dose threshold for infection, which is currently unknown; see Section 1.
In the absence of ventilation and infiltration, a removal rate of around 1.1 h−1 is attributable to other sources. Their importance is shown by line C of Fig. 2, which shows that and both increase when their contribution is ignored and the removal rate is solely attributable to ventilation, where .
The surface deposition rate, (see Section 2.4.2), is a function of aerosol diameter and room airflow velocity. Thatcher et al. [47] suggest that can be increased by around 80% by using ceiling or desk fans to increase the room airflow velocity from 0.02 m/s to 0.19 m/s. Within the model this increases to 5.3 h−1 ( s−1) and decreases the residence time by around 45 seconds, although the change in is negligible. However, in scenarios where is low, such as during the heating season when occupants may close ventilation openings to preserve thermal comfort, becomes an important removal mechanism. Enhancing mixing can increase the number of people exposed to the virus and may increase the overall infection risk [59]. This is particularly relevant in situations where there is very little ventilation, such as in the Guangzo restaurant [6]; see Section 4.2. Care must be taken not to increase the average room velocity beyond 0.21 m s−1 in the heating season [60] to maintain thermal comfort and to ensure that lightweight objects do not blow away. It may be possible to site desk fans to generate areas of high velocity away from occupants balancing the need to increase and maintain occupant comfort. Surface deposition removes infectious particles from the air but it can create contaminated fomites that may lead to contact spread. Surface deposition rates can then give relative information about the likelihood of fomite risk, and inform dose–response models about contact spread and cleaning regimes. It is important to note that, although deposition of large droplets is greatest close to the infector, the deposition of smaller aerosols is on all surfaces in a room, including those that are out of reach.
Finally, the removal rate attributable to mechanical filtration, (see Section 2.4.5), can be implemented quickly and easily using a portable air cleaner that contains a high-efficiency particulate air (HEPA) filter. Eq. (19) shows that the airflow rate through the filter should be considered in proportion to the space volume; for example, to increase by 20%, the required clear air delivery rate through a perfect filter is 1 h−1 or 0.04 m3 s−1. This method of removal could be useful in the heating season, although consideration should be given to noise generated by the system. This model assumes the air in the room is well mixed, and the portable air cleaner will only function as expected if this is the case; stand-alone air cleaners may not be effective at mixing the air throughout a space. Centralised mechanical ventilation systems may also contain HEPA filters, which can be used to filter recirculated air. Here, is the room air recirculation rate and is the fresh air supply rate.
The second parameter in the denominator, the space volume , is an important factor in exposure risk. For the same floor area taller spaces theoretically have a lower exposure risk, however this will depend on the mixing within the space. The airflow rate in many buildings, including UK schools, is specified as a volume flux per capita and so as increases there is a corresponding reduction in . Then, increasing and reducing so that their product is conserved, increases and , which increases the time to and decreases . The steady state concentration of RNA copies in the space () changes slightly, and does not change at all when and are negligible. This would lead to clear changes to the shape of the curves in Fig. 2; for example, the gradient of would decrease and the concavity of the curve would increase when h. Therefore, the risk of exposure is lower in a space with a larger volume where airflow rates are the same.
A further analysis of the reference scenario is in the Supplementary Materials (see footnote 2).
3.2. Probabilistic estimates
There is significant uncertainty in the values used in Section 3.1, and the corresponding uncertainty in predictions of is assessed using the statistical framework described in the Supplementary Materials and the inputs given in Table 1, Table 2, Table 3.
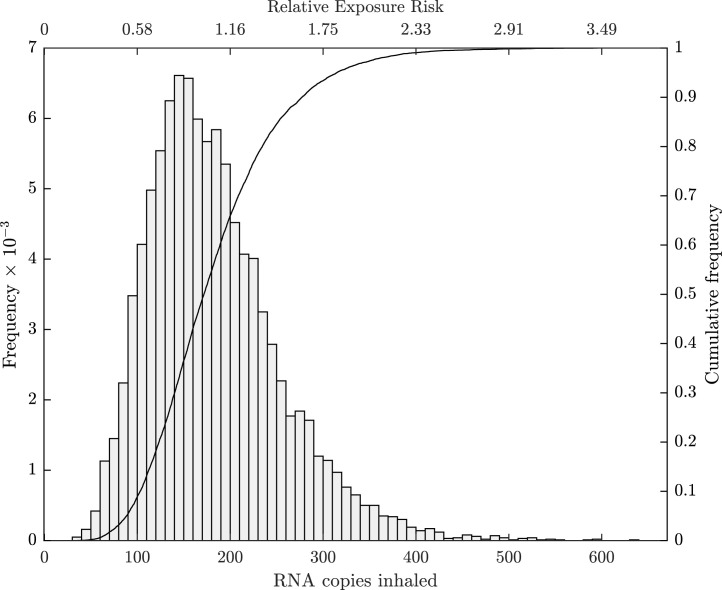
Fig. 3 quantifies uncertainty in using a histogram and cumulative distribution function (CDF), with RNA copies inhaled, with 95% confidence. The distribution of is not normal and so is a more appropriate descriptive statistic for RNA copies inhaled than . The value is approximately equal to that calculated by the deterministic approach (see Section 3.1), and so it can be used for a quick estimate of , although the stochastic approach is required to quantify uncertainty in , to perform a global sensitivity analysis, and to determine effect sizes (see footnote 2) (the magnitude of the differences between the distribution of for the reference space and other spaces) between the reference and other spaces.
Fig. 3.
Reference scenario: uncertainty in RNA copies inhaled when a single infector is shedding RNA copies over a 7 h period in a standard junior school classroom.
The utility of the makes it a suitable choice for a REI where all predicted centiles are given relative to for the reference scenario. Fig. 3 shows the REI on the top -axis for the reference scenario. The 95% REI confidence interval is RNA copies inhaled. This REI is now used in Section 4 to compare exposure risk in other spaces relative to the reference scenario. Clearly, the value of the calculated here is a function of the inputs used, which are uncertain and may change as more evidence becomes available or if the scenario changes; for example, to mitigate against more than one infected person or a reduction in the number of classroom occupants. However, the reference is easily revised using the model.
Any space that wishes to have a REI of unity or less, must at least balance the parameters in Eq. (7). If , , , and are identical to those of the reference scenario, then a ventilation rate of m3 s−1 per infected person (determined by population prevalence) must be preserved as a minimum rate to ensure the REI does not exceed 1, irrespective of the number of occupants present. The total removal rate must be at least m3 s−1 per infected person. It is also important to note that providing a fixed air change rate will lead to when the volume of the space is smaller than that of the reference classroom. Conversely, the REI will increase for a smaller volume. This reinforces the importance of providing a minimum airflow rate with units of m3 s−1 or an equivalent. Per capita and air change rates should only be used with the minimum airflow rate.
The model predictions are dependent on the assumptions made in Section 2.1. Therefore, the sensitivity analysis described in the Supplementary Materials is used to determine the relative importance of stochastic parameters in Eq. (7) (, , , and ) on predicted values of . Parameters and are not tested because they are held constant. All tests indicate that the most sensitive parameters, in order of sensitivity, are: , , , and . All parameters are statistically significant and so their values are important. The test statistics and their p-values are given in the Supplementary Materials (see footnote 2). There is limited evidence for many of the input distributions applied here and so these should be updated in the future as information becomes available.
4. Exposure risk in other indoor spaces
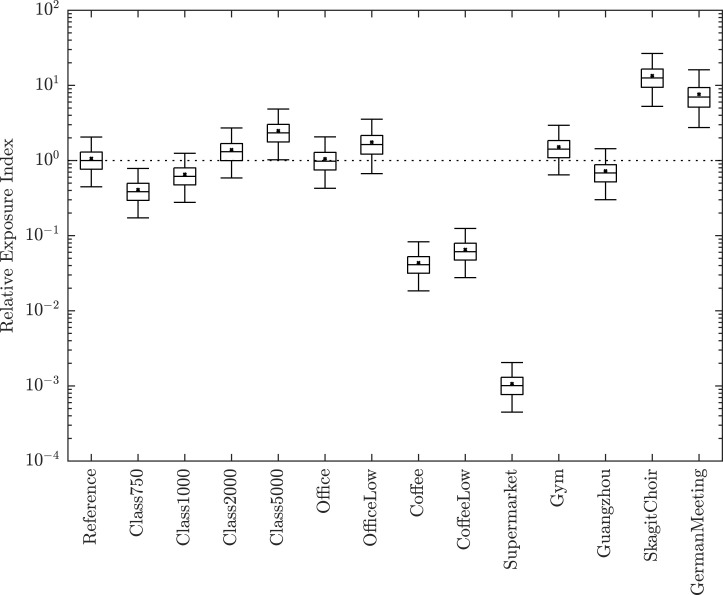
Input parameters for all scenarios are given in Table 1, Table 2, Table 3. Uncertainty in the REI for the common and high transmission spaces (see Section 2.5) is shown in Fig. 4. REIs and effect sizes are given in Table 4.
Fig. 4.
Relative Exposure Index. A comparison of RNA copies inhaled in common and high emitting spaces relative to the Reference Classroom geometry, and its occupants’ activities and exposure time. The lower and upper bars are the 2.5th and 97.5th centiles, the central box bounds the inter-quartile range, the central bar is the median (), and the cross is the sample mean. The reference scenario is the first entry with its used as the REI, indicated by the horizontal dotted line.
Table 4.
Relative exposure index for common spaces and high emission scenarios.
| (%) | Cohen’s d | Effect size | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reference scenario | 0.45 | 0.77 | 1.00 | 1.30 | 2.05 | 1.06 | 0.41 | 39 | ||
| Class 750 | 0.17 | 0.29 | 0.38 | 0.50 | 0.78 | 0.41 | 0.16 | 39 | 2.09 | Very large |
| Class 1000 | 0.28 | 0.47 | 0.62 | 0.80 | 1.25 | 0.66 | 0.25 | 39 | 1.19 | Large |
| Class 2000 | 0.59 | 1.00 | 1.31 | 1.68 | 2.71 | 1.39 | 0.55 | 39 | −0.68 | Medium |
| Class 5000 | 1.02 | 1.77 | 2.33 | 3.02 | 4.84 | 2.49 | 1.00 | 40 | −1.86 | Very large |
| Office | 0.43 | 0.75 | 0.98 | 1.28 | 2.07 | 1.05 | 0.43 | 41 | 0.03 | Negligible |
| Office Low | 0.67 | 1.22 | 1.63 | 2.16 | 3.55 | 1.76 | 0.75 | 43 | −1.14 | Large |
| Coffee | 0.02 | 0.03 | 0.04 | 0.05 | 0.08 | 0.04 | 0.02 | 38 | 3.48 | Very large |
| Coffee Low | 0.03 | 0.05 | 0.06 | 0.08 | 0.12 | 0.07 | 0.03 | 39 | 3.40 | Very large |
| Supermarket () | 0.45 | 0.77 | 1.01 | 1.30 | 2.05 | 1.07 | 0.41 | 39 | 3.63 | Very large |
| Gym | 0.64 | 1.09 | 1.42 | 1.84 | 2.94 | 1.52 | 0.59 | 39 | −0.88 | Large |
| Guangzhou | 0.30 | 0.52 | 0.68 | 0.88 | 1.44 | 0.73 | 0.29 | 40 | 0.95 | Large |
| Skagit Choir | 5.26 | 9.42 | 12.56 | 16.50 | 26.63 | 13.45 | 5.53 | 41 | −3.16 | Very large |
| German Meeting | 2.75 | 5.14 | 7.00 | 9.37 | 16.12 | 7.62 | 3.47 | 46 | −2.65 | Very large |
4.1. Common spaces
Four additional classroom scenarios are explored by varying the per capita ventilation rate between 1.2, 3.4, 9.2, and 15.7 l s−1 per person to achieve maximum mean CO concentrations of 5000, 2000, 1000, and 750 ppm, respectively, as described in Section 2.5.2. Hereon REI values are used for comparison, but confidence intervals are given in Table 4. The poorest ventilated classroom has a REI of 2.33 and a very large effect size (the magnitude of the difference between its distributions and the reference scenario’s), and so adequate ventilation is necessary and important. Increasing has clear advantages, reducing the REI to 0.38 when increased 3-fold. The REI decreases as the ventilation airflow rate in the space increases. The potential benefits of increasing the ventilation rate in a poorly ventilated space are greater than increasing a well ventilated space by the same amount.
The REI of the office is 0.98 and the effect size negligible and so could also be used as a reference scenario. The ventilation rate is greater than that of the reference scenario, but respiratory rates are slightly bigger to reflect adult occupants. In offices with different respiratory activity, such as a call centre where talking predominates breathing, the model should be recalculated with appropriate changes to the volume of respiratory fluid released as aerosols as a function of droplet diameter and volume, . Reducing the airflow rate by 80% to 2 l s−1 per person increases the REI to 1.63.
The REI of the high street coffee shop are 0.04 and 0.06 for the standard and low airflow scenarios, respectively. The effect size for both scenarios is very large. The low values of REI are attributable to the shorter exposure period and highlights the value of avoiding prolonged contact with an infected person. Increasing the exposure time to 8 h results in an REI of 1.07 and 3.37 for the high and low airflow scenarios, respectively, showing that the airflow rate becomes more important for reducing transmission risk as the exposure time increases. This scenario highlights the importance of purpose-provided ventilation provision and the danger of relying on infiltration for virus removal.
The supermarket has the lowest REI of 10−3 and a very large effect size because the airflow rate of 8,528 m3 s−1 is over 50 times that of the reference scenario and the exposure period is 7 times less. Here, the risk of exposure is likely to be dominated by close range transmission rather than aerosols, whereas both pose a risk in the classroom and office.
A 1 h aerobic workout in a gym poses the greatest risk a REIs of 1.42, representing a large effect size. The airflow rate is 2.5 times that of the reference scenario but the magnitude of the REI is highly dependent on the emission rate, which is a function of volume of respiratory fluid released as aerosols during. Further work is required to understand this.
4.2. High transmission spaces
The Skagit Choir and German Meeting superspreader scenarios have REIs of 12 and 7 and very large effect sizes, respectively. These scenarios do not amend suggesting that the increased REI occurs here regardless of the viral load of the infectious case. The choir scenario has a 35-fold increase in the emission rate attributable to an increase in the weighted average droplet size and respiratory rate, which increases the volume of respiratory fluid released as aerosols. The German Meeting has a modest 1.3-fold increase in the emission rate due to speaking, but the exposure period is the longest of any scenario. This indicates that it is possible to generate a very large increase in REI by increasing the exposure period and by increasing the volume of respiratory fluid released as aerosols.
A REI of 0.68 is predicted for the Guangzhou restaurant corresponding to a large effect size. Although the ventilation rate for this space is very low, it is mitigated by the relatively short duration of exposure compared to some of the other scenarios. However, the number of infections that occurred in the space suggest that it is not a safe space and so a would be expected. It could be that we have underestimated and the respiratory activity. More vocalisation increases the geometric mean aerosol droplet volume [18] and, if the volume of conversations was high, it might also increase aerosol generation [61]. Furthermore, air movement generated by a split air conditioning system may have helped to spread the exhaled puff further; see Bourouiba et al. [62].
It is also possible that the infector’s viral load, , is significantly greater than that considered here; see the Supplementary Materials. This suggests that even in a scenario with a low REI, there may be circumstances where the risk may be substantially higher due to the characteristics of the infector.
4.3. Other considerations
The results presented in the scenarios above illustrate how the relationships between the physical environment, activity and time determined the exposure to viral aerosols. However, it is important to acknowledge that this model makes a number of assumptions which need to be considered when applying the model in reality.
The model only considers aerosol transmission in a well mixed scenario. In reality there are important variations in mixing which will change the risk. The most significant is proximity to the infected person. Bourouiba et al. [62] discuss turbulent gas clouds showing greater RNA concentrations closer to source of infection. Then, close contact to exhaled puffs of breath will substantially increase risk because the RNA concentration and therefore virion is higher. This may result in enhanced aerosol exposure, as well as direct exposure to large droplets that can land on the mucous membrane. Several studies have explored this using idealised models, suggesting that the concentration of aerosols at 1.5–2 m from an infectious source is determined by the room ventilation. At a distance of m the concentration is determined by the exhaled plume and may be much higher [62], [63]. This risk should particularly be considered in spaces with a high occupancy density where it is difficult to maintain distance, or where the nature of the activity means that it is essential to have closer contact. Similarly, the model presented here assumes a well-mixed space, which may not be the case in reality [59]. In some circumstances this may be important and this, and the risks of close proximity, should be considered and, if appropriate, investigated with more detailed models, such as computational fluid dynamics, to be able to quantify the transport of RNA copies around the space.
We have not considered any behavioural interventions in the model. Although actions such as hand hygiene will not affect the outcome of this model, the use of face face coverings would have an important effect in reducing both the source emission rate and the exposure; see Eq. (13). These were deliberately excluded as the purpose of the model was to assess the physical environment, but it is important to acknowledge that in some of the cases presented here (the supermarket and coffee shop), face coverings are required, which would reduce the REI further.
The scenarios presented here assume that only one infector is present in the space. This is likely to be a valid assumption where prevalence of the virus is low or the number of people sharing the space is small. However as prevalence or occupancy increases, the probability of more than one infectious source also increases. For large spaces this should be factored into the analysis of the REI using Eq. (13). Similarly the number of occupants, and hence potential number of new cases of infection, is also not explicitly included. The REI essentially gives an individual exposure risk, however this may not give an accurate reflection of risks where there are a higher number of people; a high REI in a space with a very small number of occupants could result in less secondary cases than a space with a lower REI but much a higher occupancy. When considering the influence of a space on community transmission risk, this is an important parameter.
The model only considers exposure and does not estimate the probability of infection. The dose–response for SARS-CoV-2 is not yet known, however information on dose–response behaviour for SARS and coronavirus 229E have been used to estimate transmission by both air and surface contact routes [39]. It is likely that the dose–response for SARS-CoV-2 is similar, following an exponential or beta-Poisson relationship with the exposure. This means that there may be upper or lower thresholds for REI where transmission is more or less likely to occur than that suggested by exposure alone.
Finally, it should be noted that although the probability of secondary transmissions are likely to decrease with a corresponding reduction in the REI, a low REI does not necessarily mean that infections will not occur. A superspreader is likely to be uncommon, but will increase the RNA copy concentration in the air and hence the number inhaled by susceptible occupants. High transmission events are likely to be a combination of high emissions, a long exposure time, and poor ventilation in a confined space. All these are important factors and the REI can assess how different indoor activities can be related to the reference scenario by indicating if mitigation measures are required.
5. Conclusions
A mass-balance model is developed for the number of RNA copies inhaled over a period of time, , by the occupants of a well mixed indoor space comprising six factors that can be moderated to reduce exposure risk. The model is applied to a reference scenario, a standard school classroom with a ventilation rate of 0.16 m3 s−1 (5 l s−1 per person) and a total removal rate of 0.21 m3 s−1 (4.98 h−1), and 32 occupants of which one is infected with SARS-CoV-2, over a 7 h school day. A Monte Carlo approach is used to quantify uncertainty in predictions. It shows that RNA copies inhaled, with 95% confidence. The distribution of data is not normally distributed and so the median () is the most appropriate descriptive statistic, and here RNA copies inhaled.
The for the reference scenario is used as a relative exposure index (REI) by comparing it to predictions for other spaces. This is a measure of the risk of a space relative to the geometry, occupant activities, and exposure times of the reference scenario and so it is not a measure of the probability of infection. It can be used to assess existing and new spaces and to assess the efficacy of mitigation measures. The can be modified in the future as more evidence becomes available or to meet new demands, such as a need to mitigate against more than one infected person.
The is particularly affected by the respiratory rate of a susceptible person, the emission rate of RNA copies, the exposure time, the space volume, and the removal rate. A sensitivity analysis shows that predictions of in the reference scenario are most sensitive to the emission rate of RNA copies. is linearly related to the emission rate and so public health messages to encourage self isolation when exhibiting symptoms of COVID-19 and the wearing of face coverings are important.
If all occupants in a space are undertaking the same activity, the respiratory rate and the emission rate are related. Activities such as exercise and singing increase the REI of a space because the volume of respiratory fluid released as aerosols also increases. This is highlighted by a 1 h workout in a gym where the REI is 1.42 when standard breathing is assumed. This indicates that strenuous activity or singing indoors should be avoided. The REI confidence intervals for an office, a high street coffee shop, and a supermarket are estimated to be , although varying the scenarios for these spaces could lead to different estimations of the REI and will be the subject of further work.
To achieve a REI of unity, and ideally less, a space must at least balance the six parameters that affect . If the occupancy activities and exposure time are identical to those of the reference scenario, then a removal rate of at least 0.21 m3 s−1 per infected occupant must be achieved as a minimum rate (of which ventilation is likely to be a primary component), irrespective of the number of occupants present. Using a fixed air change rate will lead to when its volume is less than that of the reference classroom. Per capita airflow rates will cause the space to exceed unity when there are fewer than 32 occupants present. Therefore, per capita and air change rates should only be used with the minimum airflow rate. Here, using CO sensors that relate pre-determined concentrations to per capita ventilation rates could be problematic if a space is under-occupied.
Ventilation strategies should decrease the residence time, which governs the time taken to reach a steady state number of RNA copies in a space. This can be achieved by increasing the airflow rate and by filtration and denaturing in secondary air systems. The steady state number of RNA copies in a space and are also reduced by increasing the airflow rate, but there is a law of diminishing returns. Maintaining adequate ventilation in the heating season is particularly important because ventilation rates are often lower at this time but risks must be balanced against the thermal comfort of occupants and heating energy demand.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors are grateful to Max Sherman, Robin Wilson, Constanza Molina, Simon Parker and to the members of The Royal Society Rapid Assistance in Modelling the Pandemic (RAMP) Task 7 (Environmental and aerosol transmission) working party, led by Henry Burridge, for their comments on this work.
Footnotes
The MATLAB code and is available under a creative commons license. All materials may be obtained from DOI: 10.13140/RG.2.2.21307.03361.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.buildenv.2021.107617.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
References
- 1.CDC . 2020. How COVID-19 spreads. https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/how-covid-spreads.html. [Google Scholar]
- 2.Jones R.M., Brosseau L.M. Aerosol transmission of infectious disease. J. Occup. Environ. Med. 2015;57(5):501–508. doi: 10.1097/JOM.0000000000000448. [DOI] [PubMed] [Google Scholar]
- 3.Hamner L., Dubbel P., Capron I., Ross A., Jordan A., Lee J., Lynn J., Ball A., Narwal S., Russell S., et al. 2020. High SARS-CoV-2 Attack Rate Following Exposure at a Choir Practice—Skagit County, Washington, March 2020, Vol. 69: MMWR Morb Mortal Wkly Rep; pp. 606–610. [DOI] [PubMed] [Google Scholar]
- 4.Hijnen D., Marzano A., Eyerich K., GeurtsvanKessel C., Giménez-Arnau A., Joly P., Vestergaard C., Sticherling M., Schmidt E. SARS-CoV-2 transmission from presymptomatic meeting attendee, Germany. Emerg. Infect. Dis. 2020;26(8) doi: 10.3201/eid2608.201235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.James A., Eagle L., Phillips C., Hedges D.S., Bodenhamer C., Brown R., Wheeler J.G., Kirking H. High COVID-19 attack rate among attendees at events at a church—Arkansas, March 2020, Vol. 69: MMWR Morb Mortal Wkly Rep. 2020. pp. 632–635. [DOI] [PubMed] [Google Scholar]
- 6.Li Y., Qian H., Hang J., Chen X., Hong L., Liang P., Li J., Xiao S., Wei J., Liu L., et al. Evidence for probable aerosol transmission of SARS-CoV-2 in a poorly ventilated restaurant. medRxiv. 2020 doi: 10.1101/2020.04.16.20067728. [DOI] [Google Scholar]
- 7.Park S.Y., Kim Y.-M., Yi S., Lee S., Na B.-J., Kim C.B., Kim J.-I., Kim H.S., Kim Y.B., Park Y., et al. Coronavirus disease outbreak in call center, South Korea. Emerg. Infect. Diseases. 2020;26(8) doi: 10.3201/eid2608.201274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Miller S.L., Nazaroff W.W., Jimenez J.L., Boerstra A., Dancer S.J., Kurnitski J., Marr L.C., Morawska L., Noakes C. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the skagit valley chorale superspreading event. Indoor Air. 2020 doi: 10.1111/ina.12751. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dietz L., Horve P.F., Coil D.A., Fretz M., Eisen J.A., Van Den Wymelenberg K. 2019 novel coronavirus (COVID-19) pandemic: Built environment considerations to reduce transmission. Msystems. 2020;5(2) doi: 10.1128/msystems.00245-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Allen J.G., Marr L.C. Recognizing and controlling airborne transmission of SARS-CoV-2 in indoor environments. Indoor Air. 2020;30(4):557–558. doi: 10.1111/ina.12697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Prather K.A., Prather K.A., Wang C.C., Schooley R.T. Reducing transmission of SARS-CoV-2. Science. 2020;6197:1–5. doi: 10.1126/science.abc6197. [DOI] [PubMed] [Google Scholar]
- 12.Gao C.X., Li Y., Wei J., Cotton S., Hamilton M., Wang L., Cowling B.J. Multi-route respiratory infection: when a transmission route may dominate. Sci. Total Environ. 2021;752 doi: 10.1016/j.scitotenv.2020.141856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fennelly K.P. Viewpoint particle sizes of infectious aerosols: implications for infection control. Lancet Respir. 2020;2600(20):1–11. doi: 10.1016/S2213-2600(20)30323-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morawska L., Tang J.W., Bahnfleth W., Bluyssen M.P., Boerstra A., Buonano G., Cao J., Dancer S., Floto A., Franchimon F., Haworth C., Hogeling J., Isaxon C., Jimenez J.L., Kurnitski J., Li Y., Loomans M., Marks G., Marr L.C., Mazzarella L., Melikov A.K., Miller S., Milton D.K., Nazaroff W., Neilson P.V., Noakes C., Peccia J., Querel X., Sekhar C., Seppänen O., Tanabe S.-i., Tellier R., Tham K.W., Wargocki P., Wierzbicka A., Yao M. How can airborne transmission of COVID-19 indoors be minimised? Environ. Int. 2020;142(105832) doi: 10.1016/j.envint.2020.105832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009;40(2):122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Duguid J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. J. Hyg. 1946;44(6):471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Loudon R.G., Roberts R.M. Droplet expulsion from the respiratory tract. Am. Rev. Respir. Dis. 1967;95(3):435–442. doi: 10.1164/arrd.1967.95.3.435. [DOI] [PubMed] [Google Scholar]
- 18.Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Chao C.Y., Li Y., Katoshevski D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009;40(3):256–269. doi: 10.1016/j.jaerosci.2008.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vuorinen V., Aarnio M., Alava M., Alopaeus V., Atanasova N., Auvinen M., Balasubramanian N., Bordbar H., Erästö P., Grande R., Hayward N., Hellsten A., Hostikka S., Hokkanen J., Kaario O., Karvinen A., Kivistö I., Korhonen M., Kosonen R., Kuusela J., Lestinen S., Laurila E., Nieminen H., Peltonen P., Pokki J., Puisto A., Råback P., Salmenjoki H., Sironen T., Österberg M. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf. Sci. 2020;130(May) doi: 10.1016/j.ssci.2020.104866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: Emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stadnytskyi V., Bax C.E., Bax A., Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc. Natl. Acad. Sci. USA. 2020:3–5. doi: 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wölfel R., Corman V.M., Guggemos W., Seilmaier M., Zange S., Müller M.A., Niemeyer D., Jones T.C., Vollmar P., Rothe C., Hoelscher M., Bleicker T., Brünink S., Schneider J., Ehmann R., Zwirglmaier K., Drosten C., Wendtner C. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581(March) doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- 23.Hao X., Cheng S., Wu D., Wu T., Lin X., Wang C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature. 2020 doi: 10.1038/s41586-020-2554-8. [DOI] [PubMed] [Google Scholar]
- 24.Fears A.C., Klimstra W.B., Duprex P., Hartman A., Weaver S.C., Plante K.C., Aguilar P.V., Fernández D., Nalca A., Totura A., Dyer D., Kearney B., Johnson R., Garry R.F., Reed D.S., Roy C.J. Comparative dynamic aerosol efficiencies of three emergent coronaviruses and the unusual persistence of SARS-CoV-2 in aerosol suspensions. medRxiv. 2020;pre-print doi: 10.1101/2020.04.13.20063784. [DOI] [Google Scholar]
- 25.van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Tamin A., Harcourt J.L., Thornburg N.J., Gerber S.I., et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. New Engl. J. Med. 2020;382(16):1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ma J., Qi X., Chen H., Li X., Zhang Z., Wang H., Sun L., Zhang L., Guo J., Morawska L., Grinshpun S.A., Biswas P., Flagan R.C., Yao M. COVID-19 patients in earlier stages exhaled millions of SARS-CoV-2 per hour. Clin. Infect. Dis. 2020 doi: 10.1093/cid/ciaa1283. ciaa1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Leung N.H., Chu D.K., Shiu E.Y., Chan K.-H., McDevitt J.J., Hau H.-L.Y., Li Y., Ip D.K., Peiris J.M., Seto W.-H., Leung G.M., Milton D.K., Cowling B.J. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nature Med. 2020;26(April):676–680. doi: 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.RHEVA . REHVA; 2020. REHVA COVID-19 Guidance Document, How to Operate and Use Building Services in Order to Prevent the Spread of the Coronavirus Disease (COVID-19) Virus (SARS-Cov-2) in Workplaces: Tech. rep. [Google Scholar]
- 29.Iddon C., Hathaway A., Fitzgerald S., Mills F., Stevens D., Adams G., Day T., Davies H. CIBSE; 2020. CIBSE covid-19 ventilation guidance; p. 16. [Google Scholar]
- 30.ASHRAE . 2020. ASHRAE issues statement on relationship between COVID-19 and HVAC in buildings. https://www.ashrae.org/about/news/2020/ashrae-issues-statements-on-relationship-between-covid-19-and-hvac-in-buildings. [Google Scholar]
- 31.Nightingale F. Cambridge University Press; Cambridge: 1859. Notes on Nursing (reprint 20) [DOI] [Google Scholar]
- 32.Sze To G.N., Chao C.Y.H. Review and comparison between the Wells–Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dai H., Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Build. Simul. 2020;13:1321–1327. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141(May) doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Melikov A., Ai Z., Markov D. Intermittent occupancy combined with ventilation: An efficient strategy for the reduction of airborne transmission indoors. Sci. Total Environ. 2020;744 doi: 10.1016/j.scitotenv.2020.140908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang S., Ai Z., Lin Z. Occupancy-aided ventilation for both airborne infection risk control and work productivity. Build. Environ. 2021;188 doi: 10.1016/j.buildenv.2020.107506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yan J., Grantham M., Pantelic J., De Mesquita P.J.B., Albert B., Liu F., Ehrman S., Milton D.K. Infectious virus in exhaled breath of symptomatic seasonal influenza cases from a college community. Proc. Natl. Acad. Sci. USA. 2018;115(5):1081–1086. doi: 10.1073/pnas.1716561115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Haas C.N. 2020. Action levels for SARS-CoV-2 in air: A preliminary approach. OSF Preprints. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Watanabe T., Bartrand T.A., Weir M.H., Omura T., Haas C.N. Development of a dose-response model for SARS coronavirus. Risk analysis: an official publication of the society for risk analysis. Risk Anal. 2010;30(7):1129–1138. doi: 10.1111/j.1539-6924.2010.01427.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Das P., Shrubsole C., Jones B., Hamilton I., Chalabi Z., Davies M., Mavrogianni A., Taylor J. Using probabilistic sampling-based sensitivity analyses for indoor air quality modelling. Build. Environ. 2014;78:171–182. [Google Scholar]
- 41.Jones B., Das P., Chalabi Z., Davies M., Hamilton I., Lowe R., Mavrogianni A., Robinson D., Taylor J. Assessing uncertainty in housing stock infiltration rates and associated heat loss: English and UK case studies. Build. Environment. 2015;92:644–656. [Google Scholar]
- 42.O’Leary C., Jones B., Dimitroulopoulou S., Hall I. Setting the standard: The acceptability of kitchen ventilation for the english housing stock. Build. Environ. 2019 doi: 10.1016/j.buildenv.2019.106417. [DOI] [Google Scholar]
- 43.Ott W., Steinemann A.C., Wallace L.A. Boca Raton London : CRC Press; Boca Raton London: 2007. Exposure analysis / edited by Wayne R. Ott, Anne C. Steinemann, Lance A. Wallace. [Google Scholar]
- 44.O’Leary C., de Kluizenaar Y., Jacobs P., Borsboom W., Hall I., Jones B. Investigating measurements of fine particle (PM2.5) emissions from the cooking of meals and mitigating exposure using a cooker hood. Indoor Air. 2019;29(3):423–438. doi: 10.1111/ina.12542. [DOI] [PubMed] [Google Scholar]
- 45.USEPA . U.S. Environmental Protection Agency; Washington DC: 2011. Exposure Factors Handbook 2011 Edition EPA/600/R-09/05F: Tech. Rep. [Google Scholar]
- 46.WC A. California Air Resources Board; Sacramento: 1996. Measurement of Breathing Rate and Volume in Routinely Performed Daily Activities: Final report. contract no. a033-205. [Google Scholar]
- 47.Thatcher T.L., Lai A.C., Moreno-Jackson R., Sextro R.G., Nazaroff W.W. Effects of room furnishings and air speed on particle deposition rates indoors. Atmos. Environ. 2002;36(11):1811–1819. doi: 10.1016/S1352-2310(02)00157-7. [DOI] [Google Scholar]
- 48.Darquenne C. Aerosol deposition in health and disease. J. Aerosol Med. Pulm. Drug Deliv. 2012;25(3):140–147. doi: 10.1089/jamp.2011.0916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chia P.Y., Coleman K.K., Tan Y.K., Wei S., Ong X., Gum M., Lau S.K., Lim X.F., Lim A.S., Sutjipto S., Lee P.H., Son T.T., Young B.E., Milton D.K., Gray G.C., Schuster S., Barkham T., De P.P., Vasoo S., Chan M., Sze B., Ang P. Detection of air and surface contamination by SARS-CoV-2 in hospital rooms of infected patients. Nature Commun. 2020;11(2800) doi: 10.1038/s41467-020-16670-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.DfE . School Building Design and Maintenance: Tech. Rep. Department for education (DfE); 2014. BB103 Area guidelines for mainstream schools; pp. 39–40. [Google Scholar]
- 51.ESFA . Education and Skills Funding Agency; 2018. Building bulletin 101 guidance on ventilation, thermal comfort and indoor air quality in schools. [Google Scholar]
- 52.DfES . Department for education (DfE); 2006. Building Bulletin 101 - Ventilation of School Buildings, Book. [Google Scholar]
- 53.Iddon C., Hudleston N. Indoor Air 2014: The 13th International Conference on Indoor Air Quality and Climate. 2014. Poor indoor air quality measured in UK class rooms, increasing the risk of reduced pupil academic performance and health; p. unknown. [Google Scholar]
- 54.Mumovic D., Palmer J., Davies M., Orme M., Ridley I., Oreszczyn T., Judd C., Critchlow R., Medina H.A., Pilmoor G., Pearson C., Way P. Winter indoor air quality, thermal comfort and acoustic performance of newly built secondary schools in England. Build. Environ. 2009;44(7):1466–1477. doi: 10.1016/j.buildenv.2008.06.014. [DOI] [Google Scholar]
- 55.CIBSE . Chartered Institution of Building Services Engineers; 2016. Environmental Design: CIBSE Guide A. [Google Scholar]
- 56.Bernardi N.F., Snow S., Peretz I., Orozco Perez H.D., Sabet-Kassouf N., Lehmann A. Cardiorespiratory optimization during improvised singing and toning. Sci. Rep. 2017;7(1):1–8. doi: 10.1038/s41598-017-07171-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Galvani A., May R. Dimensions of superspreading. Epidemiology. 2005;438(7066):293–295. doi: 10.1038/438293a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Endo A., Abbott S., Kucharski A., Funk S. Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Wellcome Open Res. 2020;pre-print doi: 10.12688/wellcomeopenres.15842.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Noakes C.J., Sleigh P.A. Mathematical models for assessing the role of airflow on the risk of airborne infection in hospital wards. J. Royal Soc. Interface. 2009;6:S791–S800. doi: 10.1098/rsif.2009.0305.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.BSI . International Standards Organisation; 2005. BS EN 7730. Ergonomics of the Thermal Environment: Report. [Google Scholar]
- 61.Gregson C.J., Watson P.A., Orton A., Haddrell S., McCarthy N., Finnie A., Gent N., Donaldson R., Shah H.A., Calder G., Bzdek C., Costello P., Reid J. Comparing the respirable aerosol concentrations and particle size distributions generated by singing, speaking and breathing. ChemRxiv. 2020 doi: 10.26434/chemrxiv.12789221.v1. [DOI] [Google Scholar]
- 62.Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: Potential implications for reducing transmission of COVID-19. J. Am. Med. Wom. Assoc. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- 63.Abkarian M., Mendez S., Xue N., Yang F., Stone H.A. Speech can produce jet-like transport relevant to asymptomatic spreading of virus. Proc. Natl. Acad. Sci. USA. 2020;117(41):25237–25245. doi: 10.1073/pnas.2012156117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.