Introduction to CAUSES: Description of Weather and Climate Models and Their Near-Surface Temperature Errors in 5 day Hindcasts Near the Southern Great Plains

Abstract

We introduce the Clouds Above the United States and Errors at the Surface (CAUSES) project with its aim of better understanding the physical processes leading to warm screen temperature biases over the American Midwest in many numerical models. In this first of four companion papers, 11 different models, from nine institutes, perform a series of 5 day hindcasts, each initialized from reanalyses. After describing the common experimental protocol and detailing each model configuration, a gridded temperature data set is derived from observations and used to show that all the models have a warm bias over parts of the Midwest. Additionally, a strong diurnal cycle in the screen temperature bias is found in most models. In some models the bias is largest around midday, while in others it is largest during the night. At the Department of Energy Atmospheric Radiation Measurement Southern Great Plains (SGP) site, the model biases are shown to extend several kilometers into the atmosphere. Finally, to provide context for the companion papers, in which observations from the SGP site are used to evaluate the different processes contributing to errors there, it is shown that there are numerous locations across the Midwest where the diurnal cycle of the error is highly correlated with the diurnal cycle of the error at SGP. This suggests that conclusions drawn from detailed evaluation of models using instruments located at SGP will be representative of errors that are prevalent over a larger spatial scale.

1. Introduction

Screen-level or 2 m temperature (T2M) is an important meteorological and climatic variable. Accurate predictions of its evolution on time scales of a few days are important for global and regional weather forecasts, while reliable projections of its change in a future climate are essential for incorporating into adaptation and mitigation plans. A number of climate models have a warm bias in T2M over the midlatitude continents during the warm seasons (Ma, Xie, et al., 2014). This warm bias in T2M is seen over Eurasia and over the American Midwest during summer. By initializing a number of climate models using analyses and running them in weather forecasting mode, Ma, Xie, et al. (2014) showed that, as well as these warm-season T2M biases existing in the models’ climate-mean states, a bias of the same sign was also found in the majority of the same models when running them out to 5 days in forecast mode. This suggests that the causes of the bias are probably errors in the parameterization schemes that represent fast-acting physical processes. Additionally, this means that multiyear simulations are not necessarily required to understand the reasons for the warm bias in the climate models and that following Klein et al. (2006), an understanding of the warm bias can be obtained by running relatively short 5 day simulations with the models initialized from atmospheric analyses.

One region of significant T2M warm bias discussed by Ma, Xie, et al. (2014) is located over the Great Plains of the United States, where the U.S. Department of Energy Atmospheric Radiation Measurement (ARM) Facility has been collecting high-quality observations for many years (Mather & Voyles, 2013). These observations from the Southern Great Plains (SGP) site include the different components of the surface energy balance, radiosondes, and remote sensing observations from radar and lidar. Focusing on SGP allows the T2M error to be studied in the light of supporting information about the profiles of thermodynamic state, cloud cover and condensate amount, and the components of the surface energy balance. As well as observations collected on a routine basis, the ARM program also organizes intense observational campaigns, where those observations are supplemented by additional instruments and soundings. One such campaign, the Midlatitude Continental Convective Cloud Experiment (MC3E, Jensen et al., 2016), took place from 22 April to 6 June 2011, so if models were to be run over the spring of 2011, there would be more observations available than normal with which to evaluate their performance.

Under the auspices of Global Atmospheric System Studies (which is part of Global Energy and Water Exchanges—a project within the World Climate Research Programme), a project has been set up to carry out model simulations over the American Midwest and evaluate them in detail using observations collected at or around the SGP site (Klein et al., 2014). This project is called CAUSES (Clouds Above the United States and Errors at the Surface) and is made up of three experiments focusing on different timescales. Experiment 1 consists of 5 day simulations starting at 00Z on each of the 153 days from 1 April to 31 August 2011. The second experiment, designed to study weekly-to-seasonal timescales, consists of 4 monthlong simulations, starting on the first day of each month of January to August 2011. The third experiment is based on the protocol of the Atmospheric Model Intercomparison Project (Gates et al., 1999) and consists of 10 yearlong climate simulations.

One aim of the CAUSES project is to develop tools for comparing models to observations that highlight the physical parameterization schemes that model developers should focus on. Another is to ensure that these tools are flexible enough to be used to evaluate not just one model, but any model, hence increasing the efficiency of that aspect of model evaluation across the community.

Results of a preliminary study based on CAUSES Experiment 1, involving two global climate models, have been reported by Van Weverberg et al. (2015). They studied the Community Atmosphere Model version 5.1 (CAM5) and the Met Office Unified Model (MetUM) Global Atmosphere 6.0. An additional nine models have since run Experiment 1 to provide simulations which can all be evaluated using similar techniques.

This paper forms an introduction to a series of three companion papers looking at results from the 5 day hindcasts from Experiment 1. As part of this introduction, the first goal of this paper is to give details on the 11 models taking part, including a description of their atmospheric and land parameterization schemes and initialization methods.

The warm bias can be quantified in terms of its magnitude, spatial extent, and depth. It can also vary in time over different timescales: (a) as a function of the month of the year, (b) as a function of lead time into the simulation, and (c) over the course of the diurnal cycle. So the second goal of this paper is to document each of these aspects of the T2M bias in each of the models.

Given the wealth of observations which could be used to understand the processes leading to the creation of a model warm bias near the SGP site, it is reasonable to ask whether those conclusions are likely to help with understanding the reason for the warm bias elsewhere. As a result, the third goal of this paper is to quantify how representative the biases seen in each model at the SGP site are of that model’s behavior over the larger region impacted by the bias. This helps to motivate the detailed analyses of physical processes that are contributing to the bias in each model, which are presented in the companion papers. These include Van Weverberg et al. (2018) who study the short-wave and long-wave surface radiation errors at SGP and quantify the contribution of different cloud regimes to the errors in each of the models and Ma et al. (2018) who presentan analysis of the components of the surface energy budgets over the Midwest. Results from Experiments 2 and 3, looking at the longer timescales, will be presented in future papers. Additionally, in a fourth companion paper, Zhang et al. (2018) study the T2M error over the SGP in the models that took part in the Coupled Model Intercomparison Project Phase 5 (CMIP5) and describe some of the approaches that will be used to analyze the CAUSES 10 yearlong climate runs of Experiment 3 in the future.

Section 2 provides details of the model simulations and describes an observational data set used to evaluate the simulated T2M. Results are presented in section 3 and discussed in section 4. A summary of this paper and its companions is presented in section 5.

2. Method

This section provides details of how the model simulations have been carried out along with a list of the models that has been analyzed. A description of the data set used for evaluating the models is also provided.

2.1. Model Experiments

Following Klein et al. (2006), Ma et al. (2015), and Williams and Brooks (2008) atmospheric analyses are used to initialize each of the participating models. The analyses used are from the European Centre Re-Analyses (ERA-Interim; Dee et al., 2011). Each model is run starting from a global 00Z analysis, and each simulation is allowed to run freely for 5 days. A new simulation is started every 24 h, at 00Z on each day from 1 April to 31 August 2011, thus producing 153 simulations, each 120 h in length. Since the length of each simulation is longer than the frequency with which new simulations are started, the performance of simulations on any given date can be assessed in terms of the length of time into the forecast.

Prior to any of the simulations being run, a list of required output variables was defined. This included the T2M, as well as other two-dimensional fields corresponding to all components of the surface energy balance and top-of-atmosphere short-wave and long-wave radiative fluxes. Each model provided these fields at hourly intervals, over the entirety of the contiguous United States (CONUS), averaged onto a 1°×1° latitude-longitude grid. In addition to the hourly fields provided over the whole of the CONUS, each model also provided, at every model time step, the full profile of all thermodynamics and cloud variables for the model column nearest to the SGP site. To simplify the comparison of model data produced by different models and provided by different institutes, a series of conventions were developed and shared among participants. These included the adoption of standard variable names, units, sign conventions, and the definition of sampling frequencies and time windows for averaging periods.

This paper focusses on the evaluation of the T2M, at hourly intervals from 1 April to 31 August 2011 both as time series for the model grid points nearest to the SGP site and spatially on the 1° × 1° grid over the CONUS. Other variables are evaluated in more detail by Van Weverberg et al. (2018) and Ma et al. (2018).

The 11 models taking part in this study are summarized in Table 1. Details about the dynamical cores, atmospheric, and land surface parameterization schemes used in each of these models are given in Appendix A. The participating models include some global climate models (e.g., CAM5, Taiwan Earth System Model (TaiESM), Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), Canadian Climate Model version 4 (CanCM4), Centre National de Recherches Météorologiques-climate model (CNRM-CM), CAM5-intermediately prognostic higher-order turbulence closure (IPHOC), MetUM), some regional models (Weather Research and Forecasting (WRF)-Noah and WRF-Community Land Model (CLM)), and some global numerical weather prediction models (Integrated Forecast System (IFS), CNRM-numerical weather prediction (NWP) and MetUM).

Table 1.

List of All Participating Models, Giving Abbreviated Model Name, as Used in the Text

Model name	Grid length	Atmospheric model	Land surface model
MetUM	26 km	Walters et al. (2017)	Walters et al. (2017)
CAM5	100 km	Neale et al. (2012)	Lawrence et al. (2011)
IFS	40 km	ECMWF (2015)	ECMWF (2015)
TaiESM	100 km	Wang et al. (2015)	Lawrence et al. (2011)
WRF-Noah	36 km	Ma, Rasch, et al. (2014)	Ek et al. (2003)
WRF-CLM	36 km	Ma, Rasch, et al. (2014)	Lawrence et al. (2011)
LMDZOR	140 km	Hourdin et al. (2013)	Krinner et al. (2005)
CanCM4	310 km	von Salzen et al. (2013)	Verseghy (2000)
CNRM-CM	150 km	Voldoire et al. (2013)	Masson et al. (2013)
CNRM-NWP	20 km	Pailleux et al. (2015)	Noihlan and Planton (1989)
CAM5-IPHOC	100 km	Cheng and Xu (2015)	Lawrence et al. (2011)

Notes. The grid box dimension in the North-South direction is given as a representative value of horizontal grid length. A main reference for the atmospheric and land surface models is given. A full description of each model, with comprehensive references, is given in Appendix A. MetUM = Met Office Unified Model; CAM5 = Community Atmosphere Model version 5.1; IFS = Integrated Forecast System; TaiESM = Taiwan Earth System Model; WRF-Noah = Weather Research and Forecasting-Noah; WRF-CLM = Weather Research and Forecasting-Community Land Model; LMDZOR = Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE; CanCM4 = Canadian Climate Model version 4; CNRM-CM = Centre National de Recherches Météorologiques-climate model; CNRM-NWP = Centre National de Recherches Météorologiques-numerical weather prediction; CAM5-IPHOC = CAM5-intermediately prognostic higher-order turbulence closure.

2.2. Observed Screen Temperature Over the United States

For the region around the SGP site, the best observations of T2M come from the ARM-Best-Estimate (ARM-BE) two-dimensional gridded surface data (Tang & Xie, 2015; Xie et al., 2010). This data set consists of hourly observations of a range of variables such as T2M and surface radiation fields averaged over a region of 3° × 3° surrounding the SGP central facility (36.605°N, 262.515°E). As the ARM-BE is a spatial, rather than point, data set it can be used for evaluating the models by taking data for the column nearest to SGP.

A gridded data set is required to evaluate the models’ simulations of screen-level temperature over the entire CONUS. There are several options available. The first is to use T2M data from the same global ERA-Interim analyses used to initialize the models. The second is to use T2M data from a regional analysis product, such as from the North American Land Data Assimilation System (NLDAS-2; Cosgrove et al., 2003; Mitchell et al., 2004; Xia et al., 2012). Although one should note that the T2M data in NLDAS-2 have actually come from the North American Regional Reanalysis (NARR), with some spatial and temporal interpolation to go from 32 km, 3-hourly to 1/8th degree and hourly.

Figure 1a shows the time series of T2M daily at 00Z from 1 April to 31 August 2011, from ERA-Interim and NARR extracted for the 3° × 3° region around SGP compared to the ARM-BE. Both ERA-Interim and NARR have warm biases compared to ARM-BE, and these are larger in July and August than in the Spring.

Figure 1.

Time series of 2 m temperature (T2M) data averaged over the 3° × 3° region around Southern Great Plains (SGP) for the period 1 April to 31 August 2011: (a) daily values at 00Z, (b) mean diurnal cycle, and (c) hourly value (from National Oceanic and Atmospheric Administration-quality-controlled local climatological data (NOAA-QCLCD) and ARM-Best-Estimate (ARM-BE) only). The inset map in (c) shows the location of the NOAA-QCLCD observational sites used in the reconstruction. NARR = North American Regional Reanalysis; ERA-Interim = European Centre Re-Analyses.

Figure 1b compares the T2M at SGP from these two analysis products to ARM-BE in terms of a mean diurnal cycle (NARR has been interpolated to hourly; ERA-Interim is only available at 00, 06, 12, and 18Z). Averaged over April to August, the mean warm bias at SGP is 1.2 K for ERA-Interim and 4.2 K for NARR (when sampling only at 00Z) and 0.7 K when sampling 6-hourly for ERA-Interim and 2.2 K sampling hourly for NARR. Both ERA-Interim and NARR have their smallest biases around the time of the observed temperature minimum, but while ERA-Interim captures the warming phase of the diurnal cycle well, with a small error at 18Z, NARR warms too quickly, leading to a 3 K warm bias at the warmest point of the day at SGP. Like NARR, ERA-Interim is also too warm at 00Z and 06Z, during the cooling portion of the diurnal cycle.

The T2M variables from both ERA-Interim and NARR are the result of a reanalysis, in which observations are combined with model forecasts in a data assimilation process. However, if the NWP models used in the data assimilation process have a warm bias in T2M near SGP, then that bias may be present in the analysis product and this will impact efforts to quantify the warm bias in any of the models studied here.

Soto complement the ARM-BE data valid at SGP, this study will quantify the T2M error over the wider Midwest by using the U.S. National Oceanic and Atmospheric Administration (NOAA) quality-controlled local climatological data (QCLCD). The NOAA-QCLCD data consist of surface meteorological data including dry-bulb temperature. There are around 1,900 sites recording these observations, which are shown in the inset map in Figure 1c. Depending on the site, the data are available either several times per hour or hourly.

Several steps are required to turn these data into a gridded data set for comparison with model output. First, if more than one temperature value is recorded at a site within a given hour, the multiple values are averaged to produce a mean, which is valid for 60 min leading up to any timestamp hour. The data, which is originally stored in terms of local time, are also converted to Universal Time (Z).

A regular latitude-longitude grid is then defined using 0.2° increments. For each hour from 00Z 1 April to 00Z 1 September 2011, an interpolated value T(ϕ, λ) is calculated as a distance-weighted average using data from the m nearest stations

$$T(\varphi ,\lambda )=\frac{1}{m-1}\sum _{n=1}^m{T}_n\left(\frac{s-r_n}{s}\right)$$ (1)

where T_n is the temperature at observational site n, r_n is the distance between the interpolation location and the observational site n, ϕ and λ are latitude and longitude, and $s={\sum }_{n=1}^m{r}_n$ is the sum of the distance to the m nearest observational sites.

Here m = 4 and for each point on the 0.2° grid the four nearest points are found from the set of sites with a quality-controlled measurement that hour. As a result, if any site has missing data in any given hour, that site is ignored and data from the next nearest neighbor are used instead. The NOAA-QCLCD data consist of observations over land only, so all points over the sea are set to missing data in this reconstruction. The hourly data on the 0.2° grid may be used in a future study for evaluating higher-resolution models; however, for this paper the final step is to coarsen the data using a 5 × 5 average, ready for comparison against the models, that have also provided their output on a 1° × 1° grid.

Although this interpolation technique is simple, it is suitable for deriving a gridded temperature data set over the Great Plains. However, due to the vertical lapse rate of temperature, a screen-level temperature observation at a given site and altitude is unlikely to be representative of the screen-level temperature in its surroundings in regions of steep, or highly variable, topography. Additionally, the topography used in numerical models is smoothed for numerical reasons (e.g., Rutt et al., 2006) and will not capture all the details of the local variations in altitude. This may result in the T2M produced by a model at a given latitude and longitude being in error, simply because of discrepancies in the altitude of the model grid point, which can be of the order of several hundred meters and hence several degrees. This means that the evaluation of model T2M against the temperature reconstruction derived here is unlikely to be reliable in mountainous regions.

To identify these regions, the standard deviation of the subgrid orography (here taken from the MetUM and regridded to 1°×1°) is multiplied by the standard dry-adiabatic lapse rate and any locations where the inferred temperature subgrid variability is more than 1 K are deemed to be where the reconstruction may not be reliable. This test removes data to the west of the eastern edge of the Rockies and over the Appalachians. However, in the Great Plains, which are the focus of this study, this interpolation method is suitable for providing an observation-only data set, with no input from NWP models, for quantifying the biases in each of the models.

To check that this gridded T2M data reconstruction is reasonable, a time series of the mean T2M over the 3°×3° region around SGP has been extracted and is compared to the hourly ARM-BE values from Xie et al. (2004) in Figure 1c. Because ARM-BE is a 60 min average, valid from 30 min before to 30 min after the time stamp, while the NOAA-QCLCD reconstruction, like the model data, has been produced from averages valid for the 60 min before the time stamp, then the NOAA-QCLCD in Figure 1 has been linearly interpolated to produce a value on the hour. The hourly interpolated NOAA-QCLCD reconstruction at SGP follows the ARM-BE well for the period from April to August 2011 (Figure 1c). The mean error is 0.15 K (NOAA-QCLCD is slightly warmer), and the root-mean-square error is 0.64 K. Figure 1b shows the mean diurnal cycle from the NOAA-QCLCD and ARM-BE data sets, highlighting the good agreement and confirming that no error was introduced due to inconsistencies between time stamps and time-averaging window each data set is valid for.

Figure 2 shows the seasonal and monthly mean T2M on a 1° × 1° grid reconstructed from the NOAA-QCLCD data set. Figure 2a shows the multimonth mean from 1 April to 31 August 2011, while Figures 2b–2f show averages for each of those 5 months individually. In each panel, hatching has been overlayed where the standard deviation of the subgrid orography multiplied by the dry-adiabatic lapse rate suggests an altitude-dependent temperature variability of more than 1 K. These data are not used in the model evaluation that follows.

Figure 2.

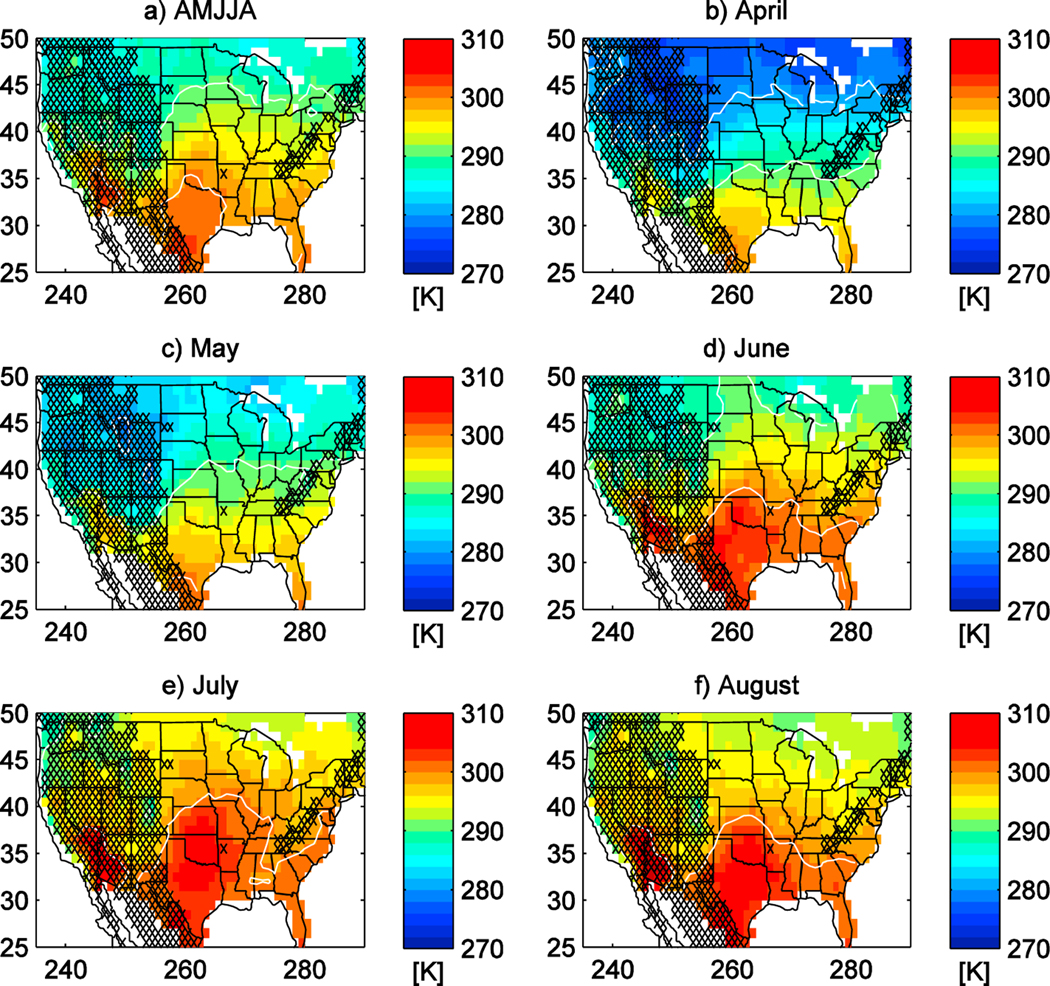
Maps of time mean T2M from the data set produced by interpolating National Oceanic and Atmospheric Administration quality-controlled local climatological data onto a 1° by 1° grid. (a) The 5 month mean for April-August (AMJJA) 2011, (b) April, (c) May, (d) June, (e) July, (f) August. White contours are isotherms every 10 K. Regions where the reconstruction is unreliable due to highly variable topography are hatched.

In northern Oklahoma and southern Kansas, near the SGP site and the region sampled during the MC3E experiment, the temperature averaged over the 5 months is around 298 K (25°C). When looking at the average temperature for each of the 5 months in the period of interest, there is an unsurprising variation, with the continental temperatures increasing as spring turns into summer. This reconstruction of hourly T2M over the CONUS will be used to evaluate the simulations of T2M in the different models.

In section 3, when results are presented as a map, this will have been produced from hourly data on the 1° × 1° grid. When carrying out an evaluation that is not displayed as a map, the results are produced from a 3° × 3° region extracted from both the model and from the observed T2M data. A 3° × 3° region is selected, because it closely matches the size of the domain over which enhanced observations were collected during MC3E and because most of the biases and bias changes seen in the models are of that size at least, allowing multiple similar points to be averaged together. For the two models that did not provide 1° × 1° gridded data (CNRM-NWP and CAM5-IPHOC), the time series are produced using data for the single model grid point nearest to SGP, although these data still represent an average over the spatial size of their model grid box.

Statistical significance tests, performed at the 95% confidence level, are carried out to identify whether any T2M bias at SGP, or anywhere over the CONUS, is significantly different from zero. When comparing daily-averaged temperatures for the same day but at different lead times, a paired t test is used, which is used to identify whether there has been any significant change in the bias with lead time.

3. Results

Eleven different models have simulated the T2M over the CONUS during the warm season of 2011 as part of the CAUSES project. Each of the simulations will be evaluated using common techniques. Unfortunately, not all models taking part in the project were able to provide all the variables with all the time and spatial resolution required for them to be evaluated using all of the methods being developed as part of the project. However, enough data were available from all of the models for at least some of the evaluation to be carried out on all of the models. In the figures in this paper, all available model data are shown. This section outlines the analysis techniques that have been applied to each model, and a more detailed discussion of the results will be presented in section 4.

3.1. Variability of T2M Error at SGP Across Months and Lead Time

Figure 3 shows box and whisker plots of the 5th, 25th, 50th, 75th, and 95th percentiles of the T2M bias for the 3° × 3° region around SGP, for days 1 to 5, for each month from April to August and for each of the models. All of the models have a T2M that is too warm at least half the time in all the months and at all the lead times, apart from CNRM-CM whose median bias is near zero in July, WRF-CLM where it is near zero in June and July and WRF-Noah where the median bias is near zero in all 5 months.

Figure 3.

Box and whisker plots of the 5th, 25th, 50th, 75th, and 95th percentiles of surface temperature error as a function of lead time (five colors) and month at the start of the simulation for each of the models for the 3° × 3° region around Southern Great Plains (SGP): (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4), (j) Centre National de Recherches Météorologiques-numerical weather prediction (CNRM-NWP), and (k) CAM5-intermediately prognostic higher-order turbulence closure (IPHOC).

Typically, the 5th to 95th percentile range increases with lead time and it is larger on day 5 than on days 1 or 2. This is consistent with the models capturing the timing of temperature changes better when closer to the analysis time and with predictability reducing as the hindcasts progress.

Some models show a noticeable warming of the median bias from day 1 to day 5, such as the MetUM in June; CAM5 in April, May, and July; CanCM4 in August; and CNRM-NWP, IFS, and TaiESM in all 5 months. Meanwhile, some models show only a modest change in median bias with lead time during certain months, such as the MetUM and WRF-CLM in April, May, and August or CNRM-CM in July.

3.2. Evolution of T2M Bias Over 5 Days at SGP

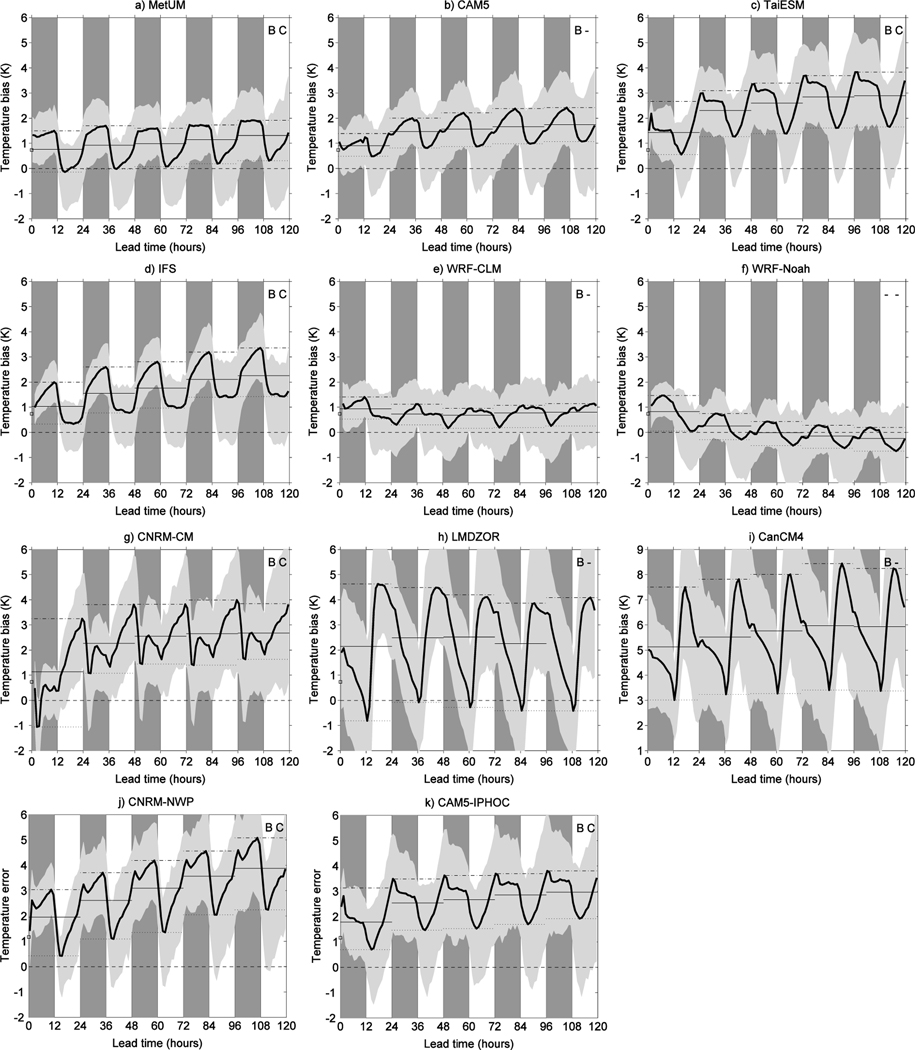
Figure 4 shows the evolution of the T2M error over 120 h for the 3° × 3° region nearest to SGP averaged over the different start days for simulations starting on each day of April to August. Light gray shading indicates the bounds of the 25th and 75th percentiles, to show the variability associated with the 153 start days. Dark gray shading has been added each day from 00Z to 12Z, to indicate the nighttime hours, which corresponds to 19 to 7 Central Daylight Time (CDT).The mean, maximum, and minimum T2M bias in each subsequent 24 h of the simulations is also shown.

Figure 4.

Evolution of 2 m temperature (T2M) error as a function of lead time averaged over the nine grid points within the 3° × 3° region nearest to Southern Great Plains. (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4), (j) Centre National de Recherches Météorologiques-numerical weather prediction (CNRM-NWP), and (k) CAM5-intermediately prognostic higher-order turbulence closure (IPHOC). Note the different y axis in (i) for CanCM4. In each plot, the dark gray and white background show the night and day hours, respectively. The black thick solid curve shows the average over the 153 simulations starting on consecutive days of 1 April to 31 August 2011. The light gray shading shows the 25th and 75th percentiles associated with that variability. For each consecutive 24 h period, the black thin solid line shows the mean, the dashed-dotted line the maximum, and the dotted line the minimum. Zero bias is highlighted with a dashed line.

Although the observed T2M has a diurnal cycle, perhaps the most striking feature of the temperature biases in Figure 4 is that the error is not steady throughout the day but has an oscillation associated with the diurnal cycle. In particular, the maximum-to-minimum range of the T2M biases, of a few Kelvin, is comparable to the magnitude of the mean bias itself. As a result, expressing the bias only in terms of its diurnal mean does not give the full picture.

For the remainder of this study, the data from day 1 of the simulations will be discarded to account for a period of model spin-up. By considering the day 2 to day 5 mean T2M error in each model, and each of the 153 start days, a Student t test is used to identify if there has been a significant bias in the multiday mean at the 95% confidence level. If there is, a “B” for “bias” appears in the top right of the panels in Figure 4. The mean temperature error in the day 5 mean is also compared to the day 2 mean using a paired t test. If there is a significant difference, then a “C” appears in the top right, indicating that there has been a “change.”

All of the models have a statistically significant temperature bias at SGP, apart from WRF-Noah. In addition, the MetUM, TaiESM, IFS, CNRM-CM, CNRM-NWP, and CAM5-IPHOC have a statistically significant change between their day 2 and day 5 temperatures at SGP and this change is always a warming.

3.3. Seasonal and Spatial Coherence

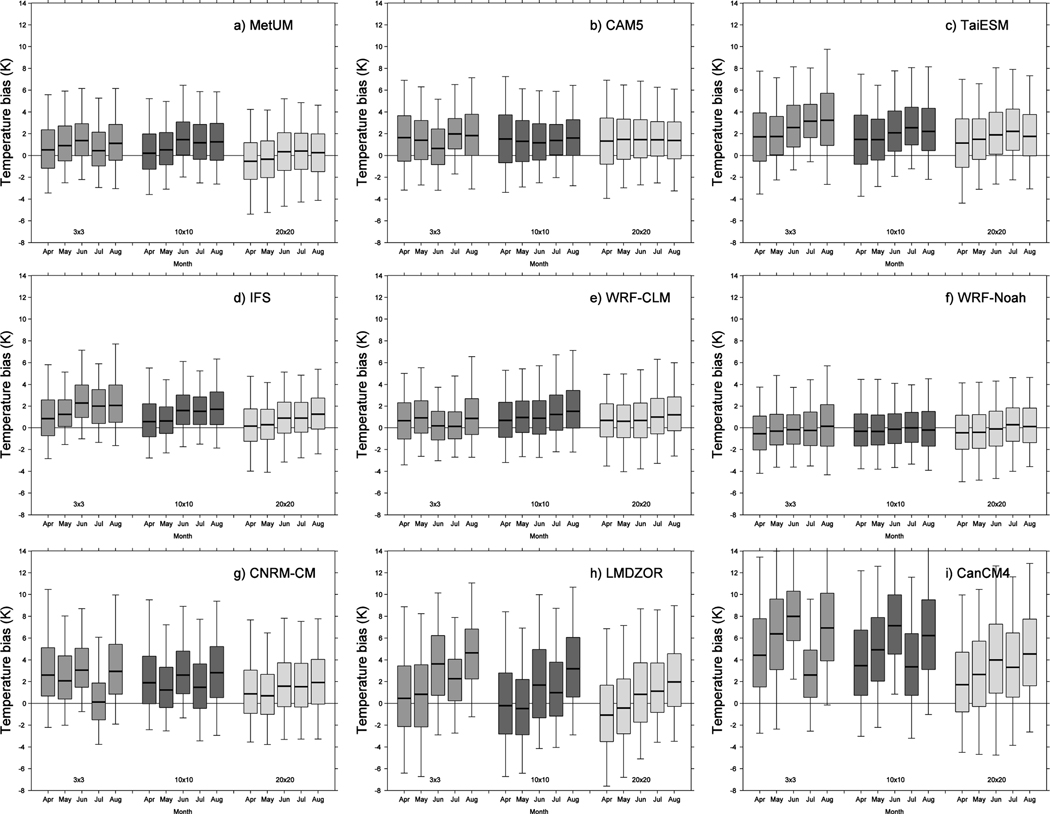
As well as considering a 3° × 3° region around SGP, a 10° × 10° (260–270°E, 32–42°N) region and a 20° × 20° (255–275°E, 30–50°N) region are also used for quantifying the magnitude of the T2M bias during the different months of the simulations. As before, mountainous regions where the NOAA-QCLCD reconstruction is deemed unreliable are excluded from the comparison. Figure 5 shows box and whisker plots of the 5th, 25th, 50th, 75th, and 95th percentiles of the T2M bias for these three different size regions for each month from April to August and for each of the models when considering data from day 2 to day 5. All the models have a median that is too warm during at least one of the months, even over the large 20° × 20° region, although there is significant variability and the 25th to 75th percentiles of the bias across the models span the range from −3 to +10 K.

Figure 5.

Box and whisker plots of the 5th, 25th, 50th, 75th, and 95th percentiles of T2M error as a function of the month at the start of the simulation for each of the models. The data are for day 2 to day 5 and for three different locations: a 3° × 3° region around SGP, a 10° × 10° region spanning (260–270°E, 32–42°N) and a 20° × 20° region covering (255–275°E, 30–50°N). (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), and (i) Canadian Climate Model version 4 (CanCM4).

Comparison between Figures 3 and 5 suggests that the reduced bias at SGP seen in CAM5 in June and in the MetUM in July is a relatively local effect, since those months do not appear noticeably cooler than the others when sampling the 20°×20° region. Conversely, the smaller biases in LMDZOR and CanCM4 in July, compared to June and August, are apparent in all three regions. Most of the models, apart from CAM5 and the two WRF models, tend to have a warm bias that is larger in the summer than in the spring.

3.4. Mean Diurnal Cycles of T2M at SGP

The box and whisker plots in Figures 3 and 5 show that, irrespective of the month or lead time, there is a significant variability in the T2M error. Although some of this will be due to the skill in capturing individual events, some of that variability is due to variations in the size of the T2M bias on the subdaily timescale. Figure 6a shows the mean diurnal cycle of temperature at SGP in both the observations and from each of the models. This is the mean diurnal cycle averaged over the 153 days from April to August, and for the models this is averaged over the second to fifth lead time days of each simulation.

Figure 6.

Mean diurnal cycles of (a) 2 m temperature in the observations and in each of the models (averaged over the second to fifth lead time days). (b) Difference between models and observation. (c) Rate of change of 2 m temperature bias. In panel b, biases which are statistically significant at the 95% confidence level are shown in a bold line and those which are not using a thin line. LT = local time; UTC = Coordinated Universal Time; MetUM = Met Office Unified Model; CAM5 = Community Atmosphere Model version 5.1; IFS = Integrated Forecast System; TaiESM = Taiwan Earth System Model; WRF-Noah = Weather Research and Forecasting-Noah; WRF-CLM = Weather Research and Forecasting-Community Land Model; LMDZ = Laboratoire de Météorologie Dynamique Zoom; CanCM4 = Canadian Climate Model version 4; CNRM-NWP = Centre National de Recherches Météorologiques-numerical weather prediction; CNRM-CM = Centre National de Recherches Météorologiques-climate model; CAM5-IPHOC = Community Atmosphere Model version 5.1-intermediately prognostic higher-order turbulence closure.

On average, the observations have a minimum T2M of around 19.5°C near 11Z (6 CDT), rising to a maximum of around 31°C at 21Z (16 CDT). Figure 6b shows the typical error in the model simulations (thin lines), and a Student t test has been used to identify the errors that are significantly different from zero at the 95% confidence level; these are shown as bold lines overlying the thin lines. All of the models are too warm during the entirety of the day, apart from LMDZOR which has a period of no significant bias during the early morning CDT and WRF-Noah which has the smallest of the T2M biases during the night and no significant bias during the day.

3.5. Maps of Significant T2M Bias

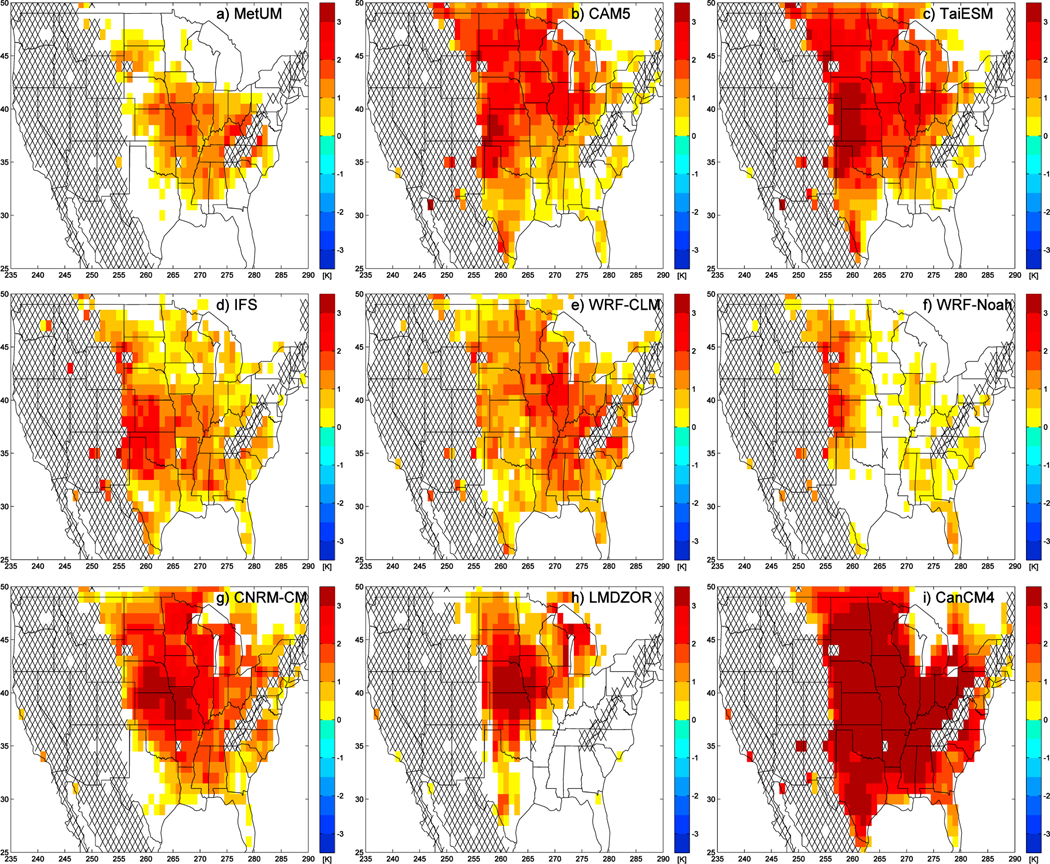
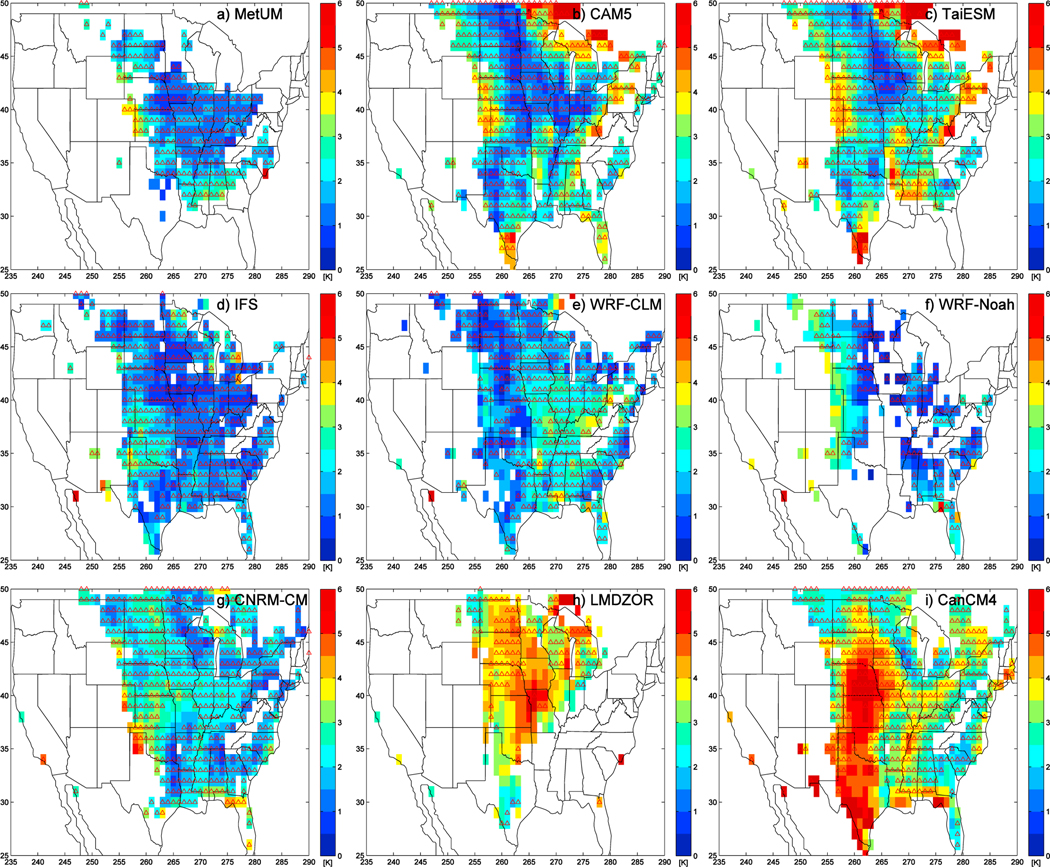
The magnitude and spatial extent of the warm bias is now quantified by calculating the day 2 to day 5 mean T2M bias for each 1°× 1° grid box for the nine models that provided gridded data (Figure 7). Given that there is a 4 day mean associated with each of the simulations starting on each of the days from April to August, a Student t test is then performed on each 1° × 1° grid box to check whether any biases are significantly different from zero, at the 95% confidence level, and insignificant results are masked out by being shown as white regions.

Figure 7.

Maps of April to August and day 2 to day 5 mean 2 m temperature error, where it is significantly different from 0 at the 95% confidence level. (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4).

All the models have a statistically significant warm bias over parts of the American Midwest, and this bias covers the region of north Oklahoma and southern Kansas near the SGP ARM site where additional observations were taken as part of the MC3E campaign. No models have any significant cold bias.

Looking at each model individually, the MetUM has a warm bias covering a number of midwestern states, while CAM5 and TaiESM have a warm bias that extends farther north toward the Canadian Prairies and south to Texas. The bias in IFS is of similar spatial extent but with a smaller magnitude. The bias in WRF-CLM is significant over most of the eastern half of the country, while in WRF-Noah the biases are reduced over the eastern portion of the country and the significant biases are more focussed around western Kansas, Nebraska and the Dakotas. In LMDZOR, the bias is at its largest in Kansas and Nebraska, while in CanCM4 the bias covers most of the eastern half of the United States.

3.6. Maps of Significant Change in T2M bias: Day 2 to Day 5

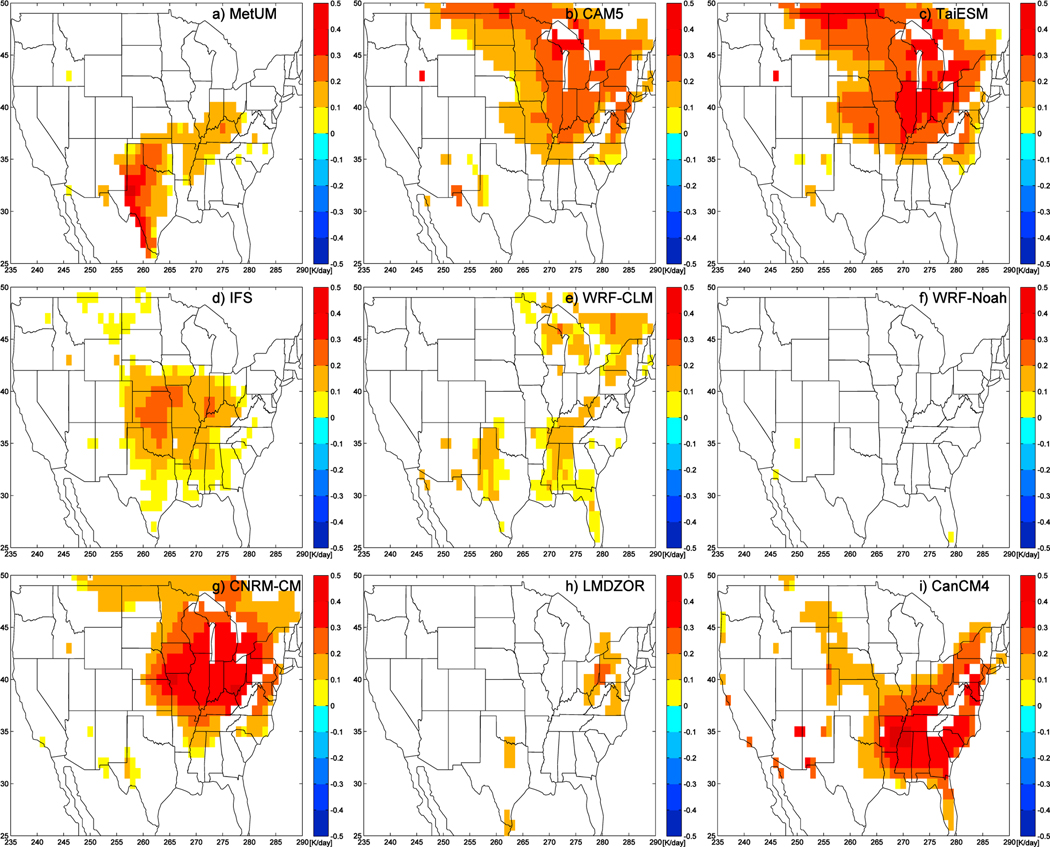
Since all the models have a warm bias over portions of the Midwest, the next step is to assess if that bias is getting warmer as a function of the length of time into the 5 day simulations. At each location, the temperature bias, averaged over the second day of the simulation (hours 25 to 48), is compared to the bias averaged over the fifth day (hours 97 to 120) for the same dates. A paired t testis performed to ignore statistically insignificant results. The statistically significant changes, which happen to always be a warming, are shown in Figure 8.

Figure 8.

Maps of April-to-August mean 2 m temperature error change, from day 2 mean to day 5 mean, expressed as a rate in K d⁻¹ (where there is significant difference between the day 2 and day 5 means, using a paired t test at the 95% confidence level). (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4).

All the models, apart from WRF-Noah, show some warming over some portion of the country. In the MetUM, the largest warming, between 0.2 and 0.4 K d⁻¹, is located in Texas, although there is still some more modest but significant warming of 0.1 to 0.3 K d⁻¹, in the region near SGP. The region of largest bias growth in IFS is located over Kansas and northern Oklahoma, close to the location of the observations near the SGP site.

3.7. Maps of Diurnal Range in T2M Bias

One of the noticeable features of the T2M error seen at SGP is its large-amplitude variations through the diurnal cycle (Figure 4). To see how the amplitude of the T2M bias varies with geographical location, a mean diurnal cycle is produced for each grid point using data from days 2 to 5 and the whole 5 months of the simulations. Figure 9 shows the difference between the maximum T2M error and minimum T2M error, masked so that the diurnal range is only shown where there is a significant bias in the first place.

Figure 9.

Maps of April-to-August mean diurnal range of 2 m temperature error (for those locations with a statistically significant mean error). (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4). Upward pointing red triangles indicate where the diurnal range of 2 m temperature error has increased significantly from day 2 to day 5.

All the models have a bias with a diurnal range of several Kelvin over parts of the Midwest. To see whether the amplitude of the T2M bias changes with lead time, the diurnal range on day 5 is compared to the diurnal range on day 2. If the diurnal range has increased significantly, an upward pointing red triangle is added at that location in Figure 9. There are no locations or models where the range has reduced.

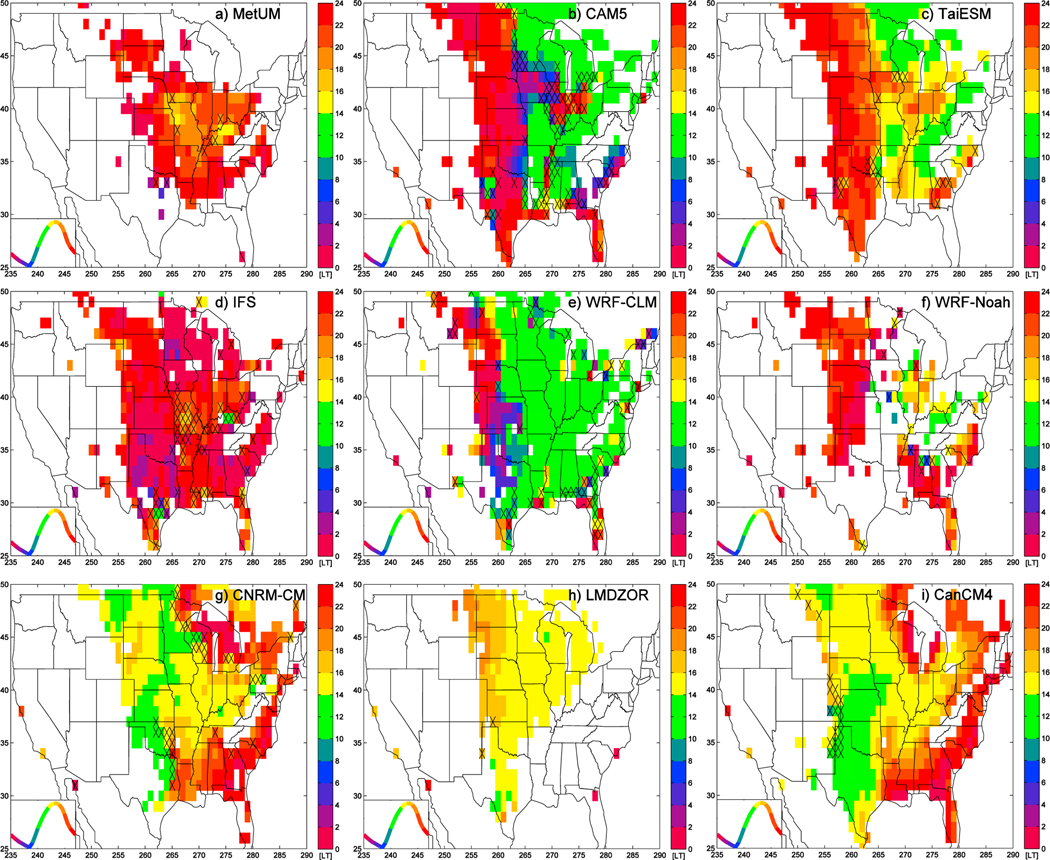
3.8. Maps of Phase of First Harmonic of T2M Bias

Figure 6 showed that at SGP there is a large-amplitude variation in the diurnal cycle of the T2M error and that different models have their largest errors at different times of the day. Fast Fourier Transforms are used to analyze the phase of the first harmonic of the mean diurnal cycle averaged over days 2 to 5 and from April to August. The phase of the first harmonic, which can be interpreted as the time of maximum T2M error, is shown in Figure 10, where the longitude of each point is taken into account to express this in terms of local time (LT). In most locations where there is a warm bias, the first harmonic explains a large part of the diurnal variations; places where it explains less than 50% of the observed variance are hatched. In the bottom left of each panel is the observed mean diurnal cycle at SGP, as a function of local time, which has been color coded to highlight different parts of the diurnal cycle using the same colors as those used in the maps.

Figure 10.

Maps of phase of the diurnal cycle of 2 m temperature error in local time, calculated using fast Fourier transform from the first harmonic of the April-to-August mean diurnal cycle of error at each location. Hatching shows where first harmonic explains less than 50% of the total variance. (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4). The plot in the bottom left of each panel is the April-to-August mean observed 2 m temperature at Southern Great Plains from 00 to 24 LT. The curve is color coded using the same colors as in the main panels, to indicate the different portions of the diurnal cycle.

The feature of a maximum in T2M error occurring during the night, which was seen at SGP in MetUM, CAM5, TaiESM, and IFS, is seen in Figures 10a–10d as a phase of the first harmonic with a value between 22 and 02 LT. This nighttime peak covers large portions of the MetUM and IFS, although it appears confined to roughly 255 to 265°E in CAM5 and TaiESM.

In stark contrast to the other models, LMDZOR has its peak error occurring in the early afternoon (14–16 LT) and this is seen not just over SGP but over an area that extends from there and north-eastward toward the Great Lakes. Meanwhile, in CanCM4 most of the Midwest has a phase indicating an error that peaks around, or shortly after, local noon (12–16 LT). In all the models, the first harmonic explains more than 50% of the variance in the T2M error over large parts of the central and eastern United States.

3.9. Vertical Depth of Bias at SGP

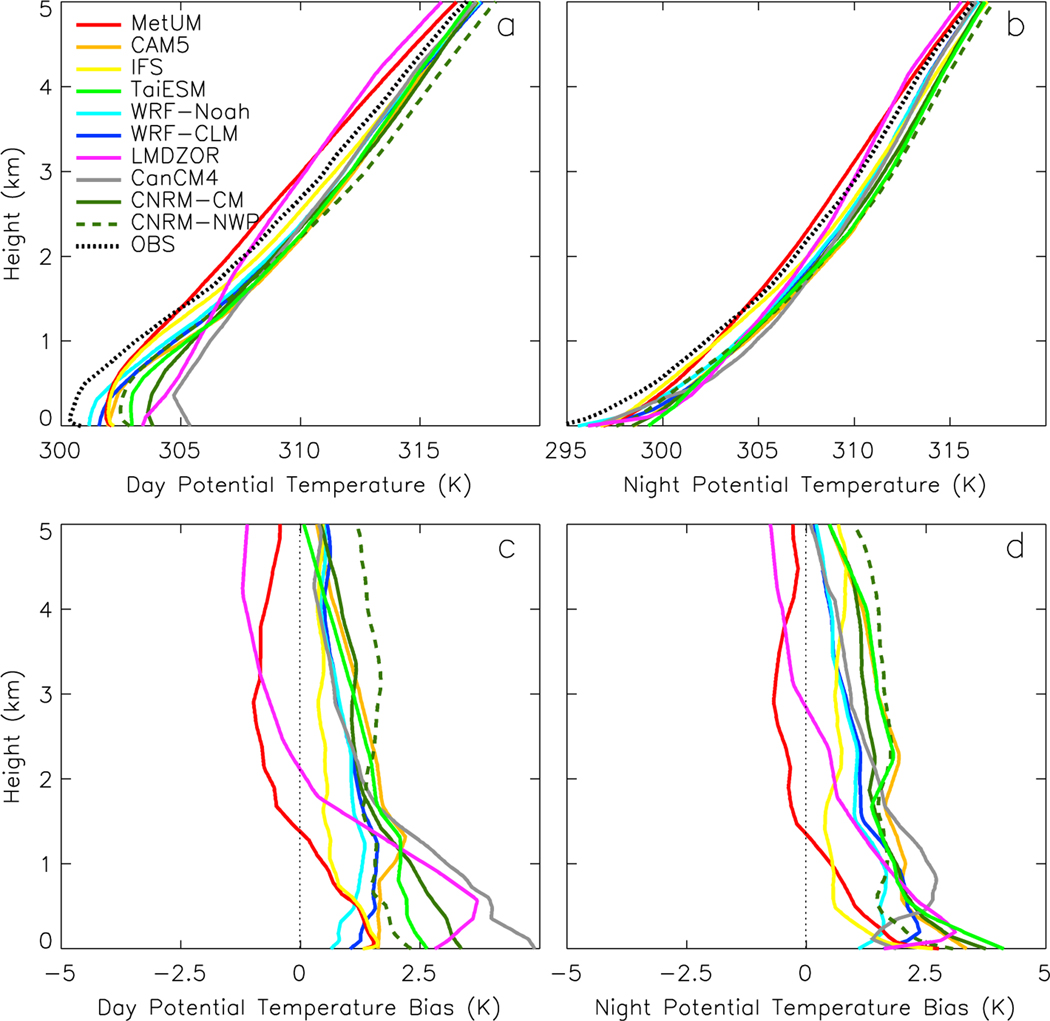
So far the warm bias has been described in terms of its warmth, its horizontal extent, and its evolution in time both as the hindcasts progress and as spring turns into summer. The final dimension which should be documented is its depth. The focus is on SGP, where there are four routine soundings per day from the ARM SGP Central Facility. During the MC3E campaign, the sounding frequency was increased to up to eight soundings per day.

Figure 11 shows profiles of dry potential temperature averaged over the MC3E region from the observations and for each of the models. Since there is a strong variability in T2M error during the diurnal cycle, mean profiles are calculated separately for the daytime and nighttime and these are defined as averages over soundings taken between 0800 and 2000 LT and 2000 and 0800 LT, respectively. All available soundings are used so there are more profiles contributing to the average during the period of the MC3E campaign. Figure 11 shows that the warm bias is not just confined to the surface; in all of the models a warm bias extends over a depth of at least 1 km both day and night, although in many models it extends several kilometers deeper than that.

Figure 11.

Vertical structure of potential temperature from the observations and for each of the models: (a) daytime, (b) nighttime. The biases (model minus observations): (c) daytime, (d) nighttime. All use data from April to August at Southern Great Plains. MetUM = Met Office Unified Model; CAM5 = Community Atmosphere Model version 5.1; IFS = Integrated Forecast System; TaiESM = Taiwan Earth System Model; WRF-Noah = Weather Research and Forecasting-Noah; WRF-CLM = Weather Research and Forecasting-Community Land Model; LMDZOR = Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE; CanCM4 = Canadian Climate Model version 4; CNRM-CM = Centre National de Recherches Météorologiques-climate model; CNRM-NWP = Centre National de Recherches Météorologiques-numerical weather prediction; OBS = observations.

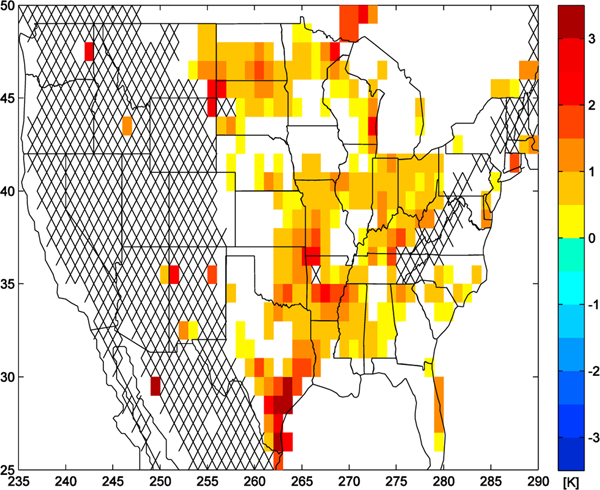
3.10. Biases in Initial Conditions

Since Figure 1 showed that there is a warm bias at SGP in the 00Z ERA-Interim analyses, it is sensible to quantify how extensive those biases are. Figure 12 shows the mean differences between the T2M in the ERA-Interim analyses and the NOAA-QCLCD observations valid at 00Z, averaged over April to August. Statistically insignificant results have been masked out. The 00Z bias in ERA-Interim does not just occur at SGP; biases of 0.5 to 2 K exist over certain parts of the Midwest in the multimonth mean. There are no regions with a cold bias.

Figure 12.

Map of mean 2 m temperature bias in initial conditions (K) calculated from European Centre Re-Analyses minus the National Oceanic and Atmospheric Administration-quality-controlled local climatological data reconstruction both valid at 00Z. The average is for 5 months from April to August 2011. Regions where the National Oceanic and Atmospheric Administration-quality-controlled local climatological data reconstruction is unreliable due to highly variable topography are hatched, and differences not significant at the 95% confidence level are blanked out.

To summarize the different permutations of biases that can be warm, or warming, in locations where the initial conditions were too warm, in Figure 13 regions with a statistically significant warm bias in Figure 7 are shown in red and those with a significant temperature increase in Figure 8 are in yellow. Regions with both a warm bias and a warming trend are shown in orange. In addition, locations from Figure 12 with an average warm bias in ERA-Interim are indicated by a black symbol. However, if the mean 00Z modeled temperature (averaged over the T+24, T+48, T+72, T+96, and T+120 lead times) is significantly warmer than ERA-Interim at the same time, then the symbol is an upward pointing triangle (indicating a warming). If the model is not significantly warmer than the analyses at 00Z, the presence of a warm bias in ERA-Interim is indicated by a cross. No model or location is significantly cooler than ERA-Interim.

Figure 13.

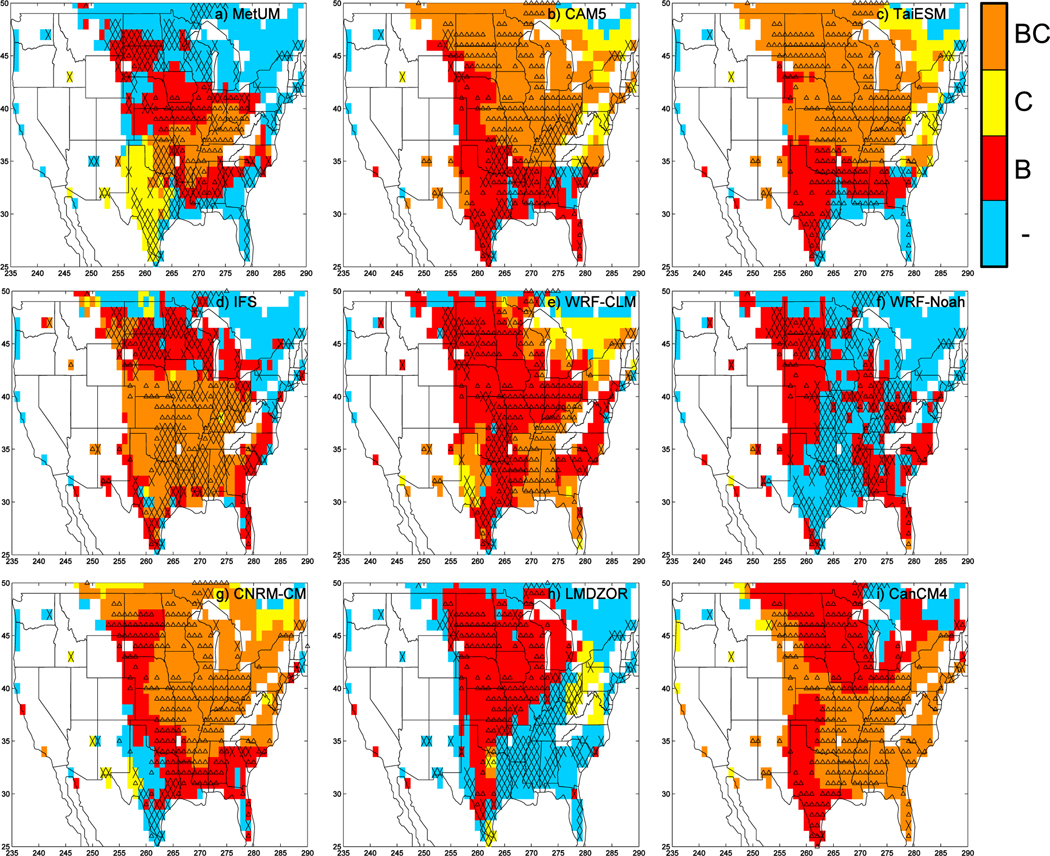
Maps of locations with statistically significant day 2 to day 5 mean bias (red, B on the color scale), with statistically significant change from day 2 mean to day 5 mean (yellow, C on the color scale), and with both (orange, BC on the color scale). Blue regions have no significant mean bias or bias change but a reliable observation of 2 m temperature. White regions are where the temperature reconstruction is unreliable. Black symbols indicate where the European Centre Re-Analyses used to initialize the models is itself biased. If the models are significantly warmer than ERA-Interim at 00Z, the symbol is an upward pointing triangle; if they are not, it is a cross. (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f ) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4). Data are from April to August.

Figure 13 hence provides an at-a-glance summary of the behavior of each of the participating models. All the models have regions with a warm bias of some form. Although many of the models are shown to be warm, or warming, in locations where there was a warm bias in the initial conditions (black symbol), there are still significant portions of the Midwest where the warm bias is warmer than that associated with the analyses (the black symbol is a triangle rather than a cross).

3.11. Representativeness of the Bias at SGP

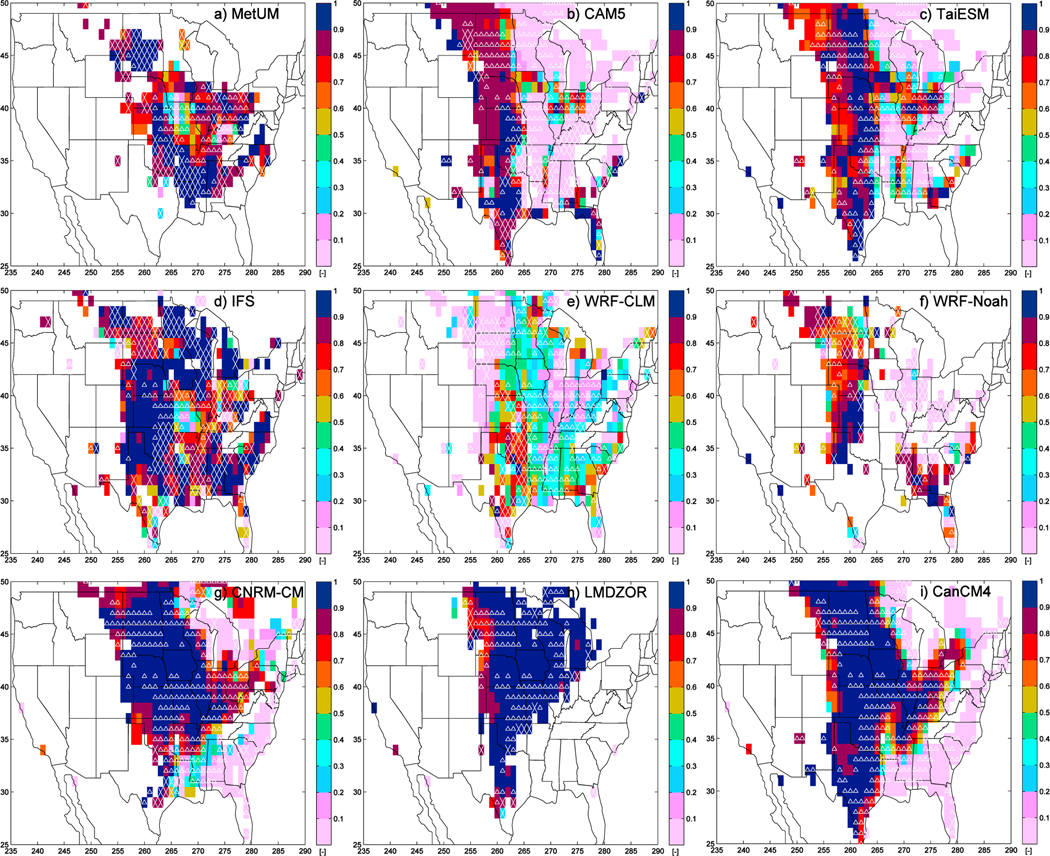
A question remains as to how representative the SGP site is of the warm bias occurring across the Midwest. Indeed, this impacts how useful detailed analyses performed using data from SGP are likely to be in understanding the causes of the bias occurring over a wider region. It is possible to calculate the correlation coefficient between the diurnal cycle of the mean bias at SGP and the diurnal cycle of the bias at all other locations (each of them being expressed in terms of local time). The locations where there is a warm bias in ERA-Interim are again marked with upward pointing triangle and crosses, using the same distinction as in Figure 13 (but white symbols are used for clarity due to the different color scale). As the correlations are only calculated where a significant bias in T2M is found in the first place then Figure 14 shows that in all the models, there are a numerous locations with a warm or warm and warming bias with either no bias in ERA-Interim (no white symbol) or a model bias at 00Z that is larger than it is in the analyses (white triangle). Additionally, within those locations, there are many places where the diurnal cycle of T2M error is highly (> 0.7) correlated with the diurnal cycle of the error at SGP.

Figure 14.

Correlation of April-to-August mean diurnal cycle of 2 m temperature error at any point with diurnal cycle of 2 m temperature error at Southern Great Plains. (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4). White symbols indicate where the European Centre Re-Analyses used to initialize the models is itself biased. If the models are significantly warmer than European Centre Re-Analyses at 00Z, the symbol is an upward pointing triangle, if they are not, it is a cross.

4. Discussion

By running a series of 5 day simulations, initialized from analyses over the spring and summer of 2011, it has been shown that a number of different numerical weather prediction and climate models exhibit a warm screen-level temperature bias over the American Midwest. The magnitude of the bias varies between the models, but there is a tendency for warmer biases in the summer than in the spring. In models exhibiting a warm bias, it is spatially extensive and it is apparent whether considering a wide 20° × 20° region of the Midwest, a smaller 10° × 10° region, or just the 3° × 3° region around the SGP ARM site. At SGP, it is shown that the warm biases are not confined to the surface but extend vertically several thousand meters into the boundary layer and beyond.

Near the SGP site, the observed T2M has a diurnal cycle with a peak-to-peak range of around 11 K. One result from this work is showing that when models have a warm bias, they are not uniformly warm throughout the diurnal cycle. As a result, daily, or monthly mean, temperature errors, such as those often presented when assessing a model’s climate, may not be providing a complete picture and may make some models’ biases look more similar than they really are. Indeed, in some models, the error is at its largest during the daytime, near the time of observed peak temperature, while in other models, the error is at its largest near the time of observed coolest temperature. This suggests a commonality in the physical processes leading to the warm bias in some models and also that the reasons may be quite different in others.

For example, there are only two models whose first harmonic of the diurnal T2M error peaks around midday (CanCM4 and LMDZOR) and these are the ones with the two largest maximum errors (Figure 4). At SGP, both of these models warm up too quickly between dawn and noon and have their quickest rate of error growth around 10 LT (Figure 6c). At SGP, all the other models have their largest T2M bias occurring at night rather than during the day. This behavior is seen over large parts of the country in the MetUM and IFS and over the longitude band of the Great Plains in CAM5 and TaiESM (Figure 10).

Additionally, the MetUM, TaiESM, and CAM5-IPHOC have a relatively steady T2M bias during the night at SGP, which means that although they are too warm, they track the observed gradual cooling of the screen temperature (Figures 6b and 6c). In the hours after the observed T2M minimum, which occurs around 07 LT, the temperature in those models increases more slowly in the morning than observed and the bias is reduced. CAM5, IFS, and CNRM-NWP also show a reduction in the bias shortly after sunrise, due to them not warming up as quickly as the observations; however, their nighttime bias actually increases throughout the night as a result of these models not cooling down quickly enough. WRF-CLM has a fairly steady warm bias throughout the whole day, with little diurnal variation in the magnitude of the bias.

An interesting contrast can be seen between CAM5 and its progeny TaiESM. The locations where a significant bias occurs are very similar in these two models, as are the locations where there is a warming between days 2 and 5. However, in the longitude range 255 to 265°E, CAM5 has the first harmonic of its error peaking at 22–02 LT, while TaiESM, which is based on CAM5, peaks a few hours earlier 18–22 LT (Figure 10). This is most likely due to changes in the triggering of the convection scheme implemented in TaiESM (Wang et al., 2015). It is also worth noting that CAM5, TaiESM, and WRF-CLM all have large portions of the eastern part of the United States where their T2M error peaks with a phase of 10–14 LT; it may be that this results from their common use of the CLM land surface model.

Due to the common ancestry of some of the models, several avenues present themselves for future study. CAM5 and WRF-CLM can be compared to assess the same atmospheric and land surface parameterizations implemented in two different models. WRF-CLM and WRF-Noah can be compared to study the role of the two land surface schemes, while CAM5 and TaiESM can be compared to assess the impact of the different parameterizations used in TaiESM.

Different ways of quantifying the warm bias have been discussed. Some models have a warm bias compared to observations when considering their average temperature over multiple days, while some models show a warming with time over the course of several days. In addition, although the analyses used to initialize the model simulations have a warm bias themselves over parts of the Midwest, it was shown that all the models have locations with warm biases significantly warmer than the warm bias that was there at the initial time.

This paper has shown that in all the participating models there is evidence of the warm bias over the Midwest that the CAUSES project was designed to study. In addition, it has also been shown that in each of the models, there is a large amount of correlation between the diurnal cycle in the T2M error at SGP and the diurnal cycle of the error over a large spatial region. This suggests that whatever combination of physical processes it is that is leading to the diurnal cycle of the T2M error having the shape and phase that it does at SGP, that behavior is likely to also be happening over a much wider area in many of the models. As a result, detailed evaluations of cloud-and-radiation and land surface issues at SGP, such as those presented by Van Weverberg et al. (2018) and Ma et al. (2018), respectively, have the potential to lead to significant reductions in the magnitude and extent of the warm biases which have been presented here.

5. Summary and Conclusions

The key findings of the CAUSES project can be summarized by drawing from this paper and its three companions.

All CMIP5 climate models have a warm bias in their warm-season T2M near the SGP, and this warm bias extends above the surface into the troposphere (Zhang et al., 2018). A similar magnitude warm bias is shown at SGP in this paper when weather forecasting and climate models carry out 5 day hindcasts. At the SGP site this bias also extends several kilometers above the surface. In all hindcast models, the bias is not just confined to SGP but extends over a significant portion of the American Midwest. Throughout the Midwest, the T2M has a strong diurnal cycle; the mean difference between daily maximum and minimum temperatures at SGP is 11 K. The temperature bias in most hindcast models also has a strong diurnal cycle, although some models have their largest bias during the day and others during the night. The observations collected at SGP can help in understanding the reasons for the bias there, and there is a large degree of correlation between the T2M bias over large portions of the Midwest and the bias at SGP. Consequently, conclusions about which physical processes contribute to the creation of the bias, drawn from the detailed studies using data at SGP, are likely to reflect model issues prevalent over a much wider area.

An analysis of the surface energy balance at SGP in the CMIP5 models showed that errors in both the evaporative fraction and the net downward shortwave contributed to the T2M bias there. In the CMIP5 models, an underestimated latent heat flux and overestimated sensible heat flux led to too much energy being used to warm the surface layer rather than being used to evaporate water (Zhang et al., 2018). A similar underestimate of evaporative fraction in the hindcast simulations played an important part in explaining their positive T2M bias (Ma et al., 2018). Errors in the parameterization of the land surface as well as the precipitation input to the surface may contribute to the incorrect partitioning between latent and sensible heat flux. Isolating the relative roles of each was not cleanly possible due to the strong positive land-atmosphere feedbacks present in CMIP5 models and the lack of a more tightly controlled land surface initialization in the hindcast models. However, Ma et al. (2018) provide a theoretical analysis that quantifies the relative roles of evaporative fraction and radiation errors in contributing to the warm bias. Radiation errors explain 0 to 2 K of the warm bias but very much less than evaporative fraction errors. Evaporative fraction errors explain most of the temperature bias in the models with large warm biases, but they compensate for the radiation error in the models with little temperature bias.

In the CMIP5 models studied by Zhang et al. (2018), there is a general underestimate in precipitation in the warm season at SGP. While in the hindcast simulations of Van Weverberg et al. (2018), although the models tend to precipitate too much and too often in the afternoon, most models underestimate the total accumulated precipitation and all underestimate the nocturnal precipitation.

This is consistent with previous studies such as Jiang et al. (2006) who showed that nearly half of summer rainfall in this region is due to nocturnal precipitation events associated with eastward propagating convective systems triggered in the lee of the Rockies, systems which many models have difficulties in representing accurately. Additionally, Klein et al. (2006) and Lin et al. (2017) have emphasized how underestimated precipitation, especially from these missed convective systems, can contribute to the growth of the T2M warm bias in the SGP.

Most CMIP5 models also have excessive net downward SW, and this is linked to clouds having too small a radiative impact and, to a lesser extent, to the surface not being reflective enough (Zhang et al., 2018). A consistent result is seen in the hindcast simulations, with most models having too low an albedo and with clouds having too weak a radiative effect (Van Weverberg et al., 2018). In each model, the total cloud radiative effect is a combination of the radiative effect of each cloud type multiplied by that cloud-type frequency of occurrence and compensating cloud errors that are common. In most hindcast models, the deep convective cloud type is the most significant contributor to the biases in cloud radiative effect. However, the details vary between models, in some cases the frequency of occurrence of this type of cloud is underestimated, while in others it is the radiative effect of those convective clouds that is underestimated. Both types of errors contribute to the excessive net downward SW.

In summary, all the models studied in climate and hindcast mode have a warm bias over parts of the Midwest in the warm season, and from these four CAUSES papers, it is apparent what some of the leading sources of error are in each model.

There are two avenues emerging as worthy of focus for improving the simulations of T2M across the models. These are (a) the partitioning between latent and sensible heat fluxes and the factors that influence it, including the representation of the land surface and the input of precipitation to the surface and (b) convective cloudiness, both in terms of the radiative properties of those clouds and also in terms of the other atmospheric parameterization schemes that impact where, when, and how often convective cloud types occur.

In terms of advice for model developers, it is important to note that in addition to T2M errors, all the models studied have shown biases in various other variables and that these all partly compensate for each other in complex ways. While developing improvements to the schemes which are deemed to be most at fault, one should not forget to assess how those parameterization changes affect other parts of the coupled land-atmosphere system. It is expected that any model changes will get tested using the traditional Atmospheric Model Intercomparison Project-type simulations and assessed in terms of mean climate and variability. In addition, the CAUSES project has developed some common evaluation tools to quantify specific aspects of model performance relating to the Midwest warm bias. The next phase of the CAUSES project will involve using those tools again, to evaluate how proposed new model configurations perform as they get developed in the years to come.

Key Points:

• Eleven models ran 5 day hindcasts, and most models have a warm screen-level temperature bias over the American Midwest

• These biases have large diurnal variations, with some models having their largest error during the day and others at night

• Diurnal cycle of the biases over a wide region is highly correlated with diurnal cycle of the biases at an instrumented site

Appendix A

When carrying out a multi-institute, multimodel comparison, it is sometimes tempting to try to ensure that all models use the same horizontal or vertical resolution or the same time step and so on. This consistency means that individual models can be compared fairly. However, this was not attempted here as it can quickly lead to each center running a configuration that is quite different to what they would normally run as part of their model development. It is then unclear which results are a feature of the original well-studied model and which are a result of the changes enforced by the communal experimental protocol. In this study, each institute performed the simulations using a model configuration they had experience with. This means that it is not necessarily fair to compare some of the models to each other. However, throughout this paper, and its companions, the focus is on comparing models to observations, in order to learn about the behavior of the models. When different models are compared to each other, it is to look for similarities and differences in their behavior rather than to try to determine which model is the best.

In most of the land-atmosphere models run for CAUSES Experiment 1, the soil moisture for the land surface model at the start of each 5 day simulation is taken from a spin-up simulation, started many months earlier, where that land surface model has been run either forced by reanalysis surface fluxes or coupled to the corresponding atmospheric model nudged toward reanalysis atmospheric fields. The soil moisture on any given day will therefore be different for each land surface model. In the case of the IFS, the soil moisture has been taken from the European Centre for Medium-range Weather Forecasts (ECMWF) operational analyses which includes data assimilation of soil moisture (de Rosnay et al., 2013). In the case of the MetUM, although the soil moisture in operational forecasts is initialized via a data assimilation process as described by Dharssi et al. (2011), for the CAUSES simulations the land surface model was initialized by transferring the soil moisture from ERA-Interim. As discussed by Koster et al. (2009), the soil moisture produced by a land surface model is very model dependent and so this transfer of soil moisture from one land surface model to another could lead to some inconsistencies and biases.

Again, we have not attempted to enforce a common approach but have let each participating institute run their hindcasts in the manner which reflects the way they carry out such simulations as part of their normal model development process.

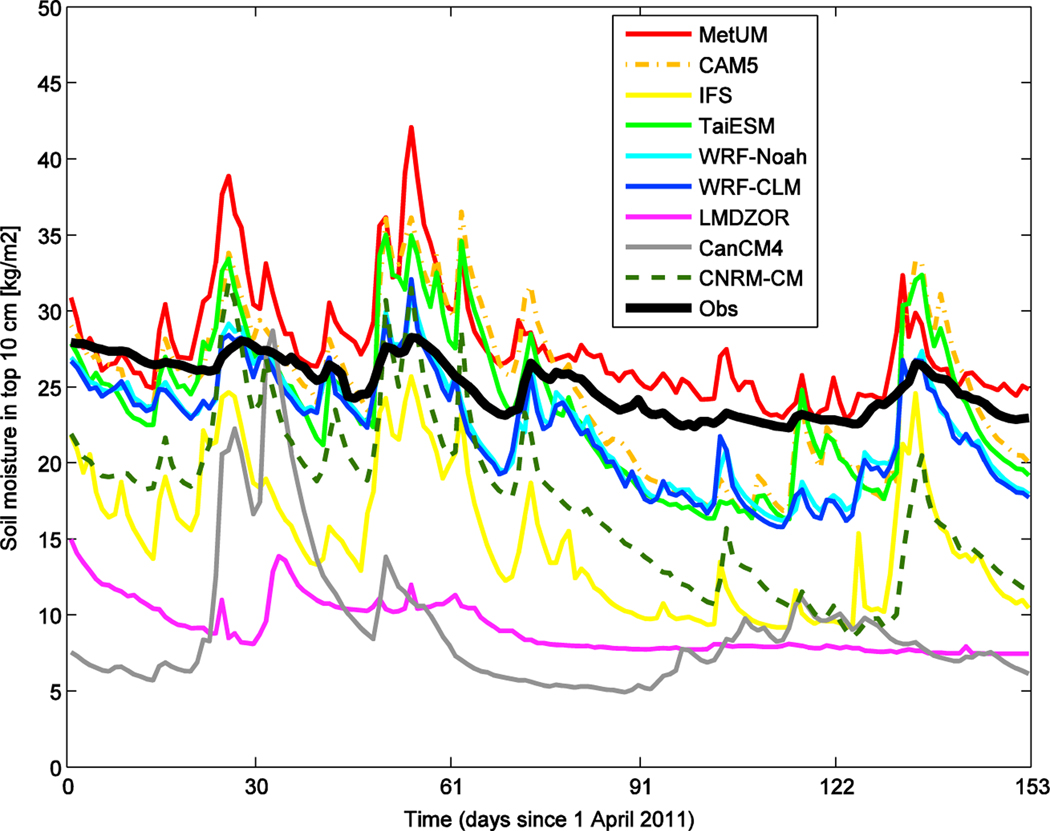
Figure A1 shows the maps of moisture in the top 10 cm of the soil, averaged overall the day 1 forecasts from April to August 2011 for each of the models. Figure A2 shows the time series of moisture in the top 10 cm of the soil from April to August. The observations are from the Soil Water And Temperature System near SGP (Schneider et al., 2003). The model data are averaged over a 3° × 3° region around the SGP site. The model data are catenations from the first 24 h of each forecast.

Each of the models participating in this study is described in turn below.

A1. Met Office: MetUM

The MetUM is a seamless forecasting system (Brown et al., 2012), meaning that the same dynamical core, physical parameterizations, and parameterization settings are used for both global climate simulations and global NWP. The configuration used here is known as Global Atmosphere 6.0 coupled to the Joint UK Land Environment Simulator Global Land 6.0 model (Walters et al., 2017). The land surface model is initialized using the soil state from ERA-Interim, which could lead to some inconsistencies (Koster et al., 2009). The model uses a regular latitude/longitude grid, and a grid size of 0.23° by 0.35° was used in the latitude/longitude directions, respectively.

A2. LLNL: CAM5

The model run at Lawrence Livermore National Laboratory (LLNL) is the U.S. National Science Foundation and Department of Energy’s CAM5. These simulations were done on a latitude/longitude grid with a grid size of 0.9 by 1.25°, respectively. A full description of the representation of the physical parameterizations can be found in Neale et al. (2012). This model uses the CLM (Lawrence et al., 2011). The land initial conditions for CAM5 are obtained from an offline Community Land Model version 4 (CLM4) simulation forced with observed precipitation, winds, and surface fluxes (Ma et al., 2015).

A3. ECMWF: IFS

The model run at the ECMWF is cycle CY41R1 of the IFS which was the operational model version at ECMWF from 12 May 2015 to 8 March 2016 (ECMWF, 2015). The model uses a cloud scheme with five prognostic variables for cloud liquid and ice, rain, snow, and cloud fraction (Forbes & Ahlgrimm, 2014; Tiedtke, 1993).

This enables the model to vary cloud fraction and condensate amount independently and allows a wide range of liquid fractions to be present in mixed-phase clouds for a given temperature. Radiation is calculated using an independent column approximation in combination with the Rapid Radiative Transfer Method (Morcrette et al., 2008). Boundary layer turbulence and clouds are produced through an interaction of the Eddy Diffusivity Mass Flux scheme (Köhler et al., 2011), the shallow convective parameterization (Bechtold et al., 2014), and the cloud scheme. Land surface processes are represented by the Tiled ECMWF Scheme for Surface Exchanges over Land with a revised land surface hydrology (Balsamo et al., 2009). Both the atmosphere and the land surface were initialized using operational ECMWF analyses.

A4. Academia Sinica: TaiESM

The TaiESM is the climate model jointly developed in the Consortium for Climate Change Study and Research Center for Environmental Changes, Academia Sinica, Taiwan. TaiESM is based on the framework of Community Earth System Model V.1.2.2 which includes CAM5.3 (Neale et al., 2012) and CLM4.0 (Lawrence et al., 2011). The land surface model is initialized in the same way as the CAM5 model described earlier. TaiESM includes several new representations of physical processes developed in-house in the Consortium for Climate Change Study. They include (1) a parameterization of radiation effects of three-dimensional topography that accounts for the impact of mountains on surface solar radiation such as shadow and reflection (Lee et al., 2013), (2) improved triggering in the Zhang-Mcfarlane convection scheme (Neale et al., 2008; Wang et al., 2015; Zhang & McFarlane, 1995) that better represents convection initiation due to low tropospheric inhomogeneity, and (3) a probability distribution function (PDF) consistent GFS-TaiESM-Sundqvist macrophysics scheme, (Wang et al. 2016, in prep; Shiu et al. 2016, in prep), which removes several ad hoc assumptions of the CAM5 scheme (Park et al., 2014), such as the critical relative humidity for cloud formation. The TaiESM used in the CAUSES project uses the aerosol package setup of the CAM5.3 (Neale et al., 2012). These simulations were done on a latitude/longitude grid with a grid size of 0.9 by 1.25°. respectively.

A5. Pacific Northwest National Laboratory: WRF-Noah and WRF-CLM

The team at the Pacific Northwest National Laboratory has run simulations using the WRF model v3.6.1 (Skamarock et al., 2012) using the CAM5 physics suite (Neale et al., 2012) ported into WRF as described by Ma, Rasch, et al. (2014). The model was run without atmospheric chemistry, and the horizontal grid length is 36 km. Two WRF configurations have been submitted that use identical atmospheric parameterizations and differ only in the choice of soil model. One set of simulations uses the Unified NCEP/NCAR/AFWA Noah land surface model (Ek et al., 2003) and the other set uses the Community Land Model version 4 (CLM4.0, Lawrence et al. (2011)). Soil moisture and temperature profiles for both WRF configurations are initialized using an offline CLM simulation run with 0.125° grid spacing. The offline soil model simulation was driven by NLDAS-2 data and run to equilibrium by cycling the 1979–2007 period for 36 cycles, that is, 1,008 years (Ke et al., 2012).

A6. LMD/IPSL: LMDZOR

The simulations run at the Laboratoire de Météorologie Dynamique (LMD)/Institut Pierre Simon Laplace (IPSL) use a configuration in between those used for CMIP5 and CMIP6. The horizontal grid is stretchable in both longitude and latitude; hence, the Z in LMDZ stands for this “zoom” capability. The atmospheric physics is based on the configuration used for CMIP5B and described by Hourdin et al. (2013), while the land surface scheme is different to that used for CMIP5.The Land Surface Model is ORCHIDEE (Krinner et al., 2005) but with the soil thermal conductivity and heat capacity parameterized as functions of the moisture profile. When the LMDZ is coupled to ORCHIDEE, the model is known as LMDZOR. The version of ORCHIDEE used for CAUSES has 11 layers, which has been shown to increase the evaporation in summer and reduce the warm bias over Europe (Cheruy et al., 2013). The soil conditions at the start of each 5 day run were taken from a spin-up run where ORCHIDEE was nudged to ERA-Interim (Cheruy et al., 2013; Coindreau et al., 2007). The LMDZOR simulations were done on a latitude/longitude grid with a grid size of 1.26 by 2.5°, respectively.

A7. Canadian Centre for Climate Modelling and Analysis: CanCM4

The CanCM4 run at the Canadian Centre for Climate Modelling and Analysis is documented by Merryfield et al. (2013). It comprises the Canadian Atmospheric Model version 4 (CanAM4), as described by von Salzen et al. (2013), and the Canadian Land Surface Scheme (CLASS), as discussed by Verseghy (2000). The model was run with 128 grid point in longitude and 64 grid points in latitude, hence 2.8° by 2.8°. Deep convection is treated according to Zhang and McFarlane (1995) with a prognostic cloud base closure as in Scinocca and McFarlane (2004) and shallow convection is treated according to von Salzen et al. (2005). Cloud microphysics is prognostic, based on the approach of Lohmann and Roeckner (1996), Rotstayn (1997) and Khairoutdinov and Kogan (2000). The planetary boundary layer is treated as in Abdella and McFarlane (1996) & Abdella and McFarlane (1997), modified as described in von Salzen et al. (2013). Radiation parameterizations include a correlated-k distribution radiative transfer scheme (Li & Barker, 2005) and radiative transfer in the presence of clouds using the Monte Carlo independent column approximation (Barker et al., 2008). CanAM4 uses a prognostic bulk aerosol scheme with a full sulfur cycle, along with organic and black carbon, mineral dust, and sea salt (Croft et al., 2005; Lohmann et al., 1999). CanCM4 hindcasts are initialized from model runs that assimilate 6-hourly atmospheric temperature, winds and specific humidity using a variant of the incremental analysis update method (Merryfield et al., 2013). Initial values of land surface variables for the hindcasts are determined from the response of CLASS in these assimilating model runs without any further data constraints on the land surface.

A8. CNRM: CNRM-CM

Two model configurations were run by the Centre National de Recherches Météorologiques (CNRM). The first set of simulations use CNRM-AM6-DIA, which is very close to the land-atmosphere component of the CNRM-CM5.1 climate model (Voldoire et al., 2013). Compared to the CNRM-CM5.1 land-atmosphere component, the model code was updated to version 6.2.1 for the atmospheric model ARPEGE-Climat and to version 7.3 for the land surface model SURFEX (Masson et al., 2013), while keeping the same physical packages in the two models as those used in the CMIP5 exercise. These physical packages are described in detail in Voldoire et al. (2013). The long-wave radiation scheme is based on the Rapid Radiation Transfer Model (Mlawer et al., 1997) included in the ECMWF IFS model. The shortwave part was originally developed by Fouquartand Bonnel (1980) and now consists of six bands. The convection scheme uses the work of Bougeault (1985), in which convection is triggered when there is moisture convergence in the low layers (resolved and subgrid) and unstable vertical thermodynamical profiles. A Kuo-type closure is used, assuming that moisture convergence is either precipitated or detrained in the environment. The turbulence scheme is based on a diagnostic equation of turbulent kinetic energy (Louis, 1979; Mascart et al., 1995; Mellor, 1977; Mellor & Yamada, 1974, 1982; Ricard & Royer, 1993). The second-order scheme accounts for the effects of liquid water and water vapor. The scheme uses the formulation of Lenderink and Holtslag (2004) for the mixing length, which has a quadratic profile in the boundary layer. Stratiform cloud properties (cover, water, and ice content) are computed following Ricard and Royer (1993) and Bougeault, (1981, 1982), using an asymmetric (decreasing exponential) PDF of the standardized deficit to saturation. Large-scale precipitation is described in Smith (1990) and accounts for evaporation using the formulation of Kessler (1969). Model resolution is T127, which is around 1.4° on the equator. The land initial conditions come from an offline SURFEX model simulation, forced with ERA-Interim surface variables and radiation fluxes and with ERA-Interim precipitation rescaled to the GPCC monthly observed value.

A9. CNRM: CNRM-NWP

The second set of simulations produced by CNRM, referred to as CNRM-NWP, uses the same setup as the operational cycle that was used operationally from 2014 to 2017 (i.e., cy38t1op3 and cy41t1op1). CY41T1 is described by Yessad (2015), while the IFS-ARPEGE system is documented by Pailleux et al. (2015). The radiation scheme for the long wave is based on the Rapid Radiation Transfer Model scheme (Mlawer et al., 1997) and for the short wave on the six band Fouquart-Morcrette scheme (Fouquart & Bonnel, 1980; Morcrette, 1993). The boundary layer parameterization follows (Cuxart et al., 2000) and is based on a prognostic equation for the Turbulent Kinetic Energy. The shallow convection scheme with a CAPE closure is based on Bechtold et al. (2001) and Kain and Fritsch (1990) and is known as the KFB scheme. The boundary layer and KFB schemes are linked, with the thermal production of Turbulent Kinetic Energy computed by the KFB scheme and by a modification of the original mixing length from Bougeault and Lacarrere (1989) by the shallow cloud from KFB (Bazile et al., 2011). The deep convection is represented by an updated version of the mass flux scheme based on a moisture convergence closure Bougeault (1985). The cloud microphysics has four prognostic variables (cloud water, cloud ice, liquid, and solid precipitation) for the resolved precipitation (Bouteloup et al., 2005; Lopez, 2002). The PDF for the statistical cloud scheme comes from Smith (1990). The surface scheme is based on the Interaction between Soil Biosphere and Atmosphere scheme (Noihlan & Planton, 1989), with modifications to the soil freezing parameterization (Bazile, 1999) and to the treatment of snow (Bazile et al., 2002). Unlike the other models, which were initialized from ERA-Interim, the data from CNRM-NWP were produced by the operational model running at the time. Hence, both the atmospheric and soil initial states come from the operational NWP system, which includes soil moisture assimilation (Giard & Bazile, 2000). The model uses a horizontal resolution of T798 with a stretching factor of 2.2. This leads to a horizontal resolution of about 10 km over France, 55 km over Australia, and about 20 km near the SGP ARM site.

A10. National Aeronautics and Space Administration Langley Research Center: CAM5-IPHOC

This model is based on CAM5 (Neale et al., 2012). The simulations were done with a latitude/longitude grid with a grid size of 0.9 by 1.25°.The stratocumulus, cumulus parameterization, and macrophysics parameterizations in the standard CAM5are replaced by IPHOC, which uses a single set of equations to represent boundary layer dry and moist turbulence mixing, shallow convection, and cloud macrophysics. IPHOC assumes a joint double-Gaussian distribution of liquid water potential temperature, total water, and vertical velocity (Cheng & Xu, 2006); and a full description of the physical parameterizations can be found in Cheng and Xu (2015). This model uses the Community Land Model (Lawrence et al., 2011) initialized from a nudged spin-up run using CLM coupled to CAM5.

Figure A1.

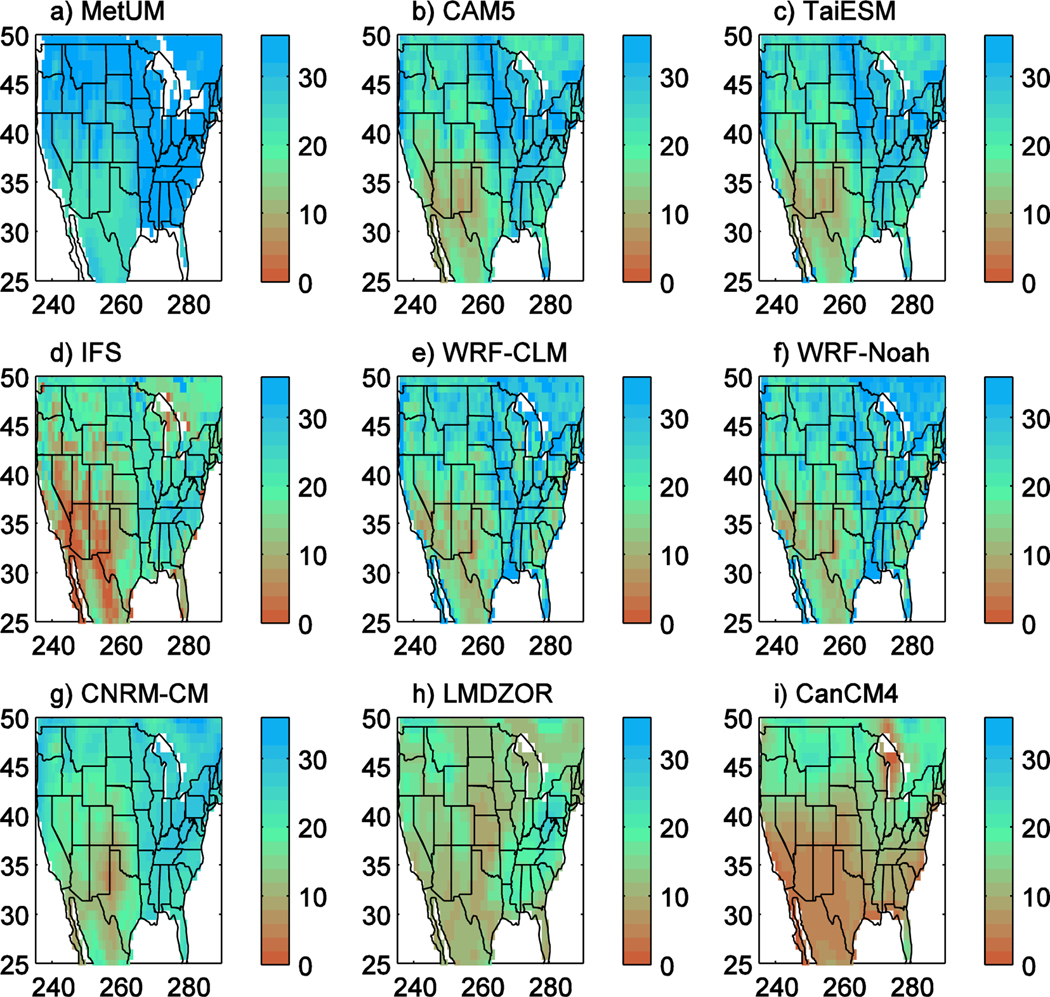
Soil moisture content in top 10 cm of the soil, averaged over all the day 1 forecasts (kg m⁻²). (a) Met Office Unified Model (MetUM), (b) Community Atmosphere Model version 5.1 (CAM5), (c) Taiwan Earth System Model (TaiESM), (d) Integrated Forecast System (IFS), (e) Weather Research and Forecasting-Community Land Model (WRF-CLM), (f ) WRF-Noah, (g) Centre National de Recherches Météorologiques-climate model (CNRM-CM), (h) Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE (LMDZOR), (i) Canadian Climate Model version 4 (CanCM4).

Figure A2.

Time series of day 1 average soil moisture in top 10 cm of the soil in each model from April to August, averaged over a 3° × 3° region around the Southern Great Plains site. Observations are from the Soil Water And Temperature System near Southern Great Plains (Schneider et al., 2003). MetUM = Met Office Unified Model; CAM5 = Community Atmosphere Model version 5.1; IFS = Integrated Forecast System; TaiESM = Taiwan Earth System Model; WRF-Noah = Weather Research and Forecasting-Noah; WRF-CLM = Weather Research and Forecasting-Community Land Model; LMDZOR = Laboratoire de Météorologie Dynamique Zoom coupled to ORCHIDEE; CanCM4 = Canadian Climate Model version 4; CNRM-NWP = Centre National de Recherches Météorologiques-numerical weather prediction; CNRM-CM = Centre National de Recherches Météorologiques-climate model.