Abstract
Ultralight materials present an opportunity to dramatically increase the efficiency of load-bearing aerostructures. To date, however, these ultralight materials have generally been confined to the laboratory bench-top, due to dimensional constraints of the manufacturing processes. We show a programmable material system applied as a large-scale, ultralight, and conformable aeroelastic structure. The use of a modular, lattice-based, ultralight material results in stiffness typical of an elastomer (2.6 MPa) at a mass density typical of an aerogel (5.6 ). This, combined with a building block based manufacturing and configuration strategy, enables the rapid realization of new adaptive structures and mechanisms. The heterogeneous design with programmable anisotropy allows for enhanced elastic and global shape deformation in response to external loading, making it useful for tuned fluid-structure interaction. We demonstrate an example application experiment using two building block types for the primary structure of a 4.27m wingspan aircraft, where we spatially program elastic shape morphing to increase aerodynamic efficiency and improve roll control authority, demonstrated with full-scale wind tunnel testing.
1. Introduction
Across diverse fields, adaptive structures are finding an increasing number of applications due to their ability to respond to changing environments and use-cases. In architectural applications, a building envelope can respond to weather changes [1], whereas, for civil engineering applications, a primary structure can respond to quasi-static and dynamic loading [2].
One of the most promising, and challenging, applications are adaptive aerostructures that respond to changing aerodynamic loading. The need to operate a single aircraft in highly disparate parameter envelopes (i.e., dash/cruise, takeoff/land, maneuver, loiter) throughout a single flight necessarily results in sub-optimal aircraft performance during each portion of the flight [3], which results in lower fuel efficiency and higher direct operating cost.
Flexible mechanical systems, such as morphing wings, have been proposed to adapt wing geometry to changing flight conditions [4], seeking to increase performance at a range of air-speeds [5], reduce vibrations [6], increase maximum lift [7], decrease drag [8], and augment control of the vehicle [9]. However, scalable manufacturing and integration with traditional flight systems remain an open challenge [10]. This work seeks to address these issues with a programmable material system that can be mass produced and implemented as a high performance, conformable aeroelastic system.
Adaptive or shape-morphing aerostructures face a natural conflict between being lightweight and compliant enough to act as a mechanism, while also being able to bear operational loads [11]. Some proposed adaptive aerostructures leverage planar configurations that have much higher stiffness across an orthogonal out-of-plane axis that is oriented to maintain stiffness in one or more dimensions while allowing orthogonal dimensions to retain low stiffness for passive elastic behavior or ease of actuation. Example technologies include specialized honeycombs [8], corrugated designs [12], and custom compliant mechanism designs such as those developed by Kota et al [13]. Planar designs generally choose a single loading plane to achieve airfoil camber morphing, spanwise bending, or span extension.
A truly generalized shape morphing structural strategy might provide for independent parameter control over the entire stiffness matrix. In this direction, higher dimensional tuning of structures and materials, including twist dimensions, have been achieved with elastomeric materials with high strain, energy absorption, and controllable compliance capabilities [14, 15, 16]. These materials accommodate considerable variation in designs and geometric complexity but display lower specific modulus (higher mass density per stiffness) compared to the materials commonly used in large-scale, high-performance aerostructures, such as aluminum or carbon fiber reinforced polymers (CFRP). This presents a significant performance barrier with typical mass critical applications. Recent literature has shown how a Young’s modulus typically associated with elastomers (104 – 109Pa) can be attained at a fraction of the density through architected cellular materials [17, 18]. In addition to novel bulk properties, the ability to decouple and tune mechanical properties within a single material system is a longstanding goal within the mechanical metamaterial community [19]. The approach is to spatially vary microscopic properties, such as cell geometry, density, or material, to achieve programmable macroscopic properties, such as Young’s Modulus, Poisson ratio, or shear/bulk modulus, across a single material system. Architected cellular materials have indeed demonstrated such properties [20], yet scalability remains an open challenge due to inherent limitations of the manufacturing processes.
Many manufacturing scalability limitations of architected materials may be addressed through discrete assembly. High-performance architected materials can be made through the assembly of building block units [17], resulting in a high-performance cellular material that can be mass manufactured at scale and programmed by assembly [21]. The building block approach was successfully applied to a small-scale adaptive aerostructure [22], with components that were highly specific to single aircraft design, and part length scales equal to final system length scales. This limits the ease of manufacturing and extensibility to different designs; a shortcoming shared with the aforementioned adaptive structure designs. Moreover, early examples did not leverage the natural application of programmable matter concepts [23, 24, 25] to building block based cellular solids. Programmable materials provide the structure with a set of instruction on how to react to external loading autonomously through the selective placement of asymmetries, aperiodic structures, or heterogeneous components. This allows the metamaterial to have its mechanical behavior programmed during its construction. This work presents a strategy that seeks to incorporate manufacturing at scale and extensibility across designs and applications.
We combine concepts from assembled architected materials and programmable matter to demonstrate programmable deformation of an air vehicle in response to aerodynamic loading. Using a building block methodology based on the cuboctahedral lattice, we design and build two 4.27m span lattice wing structures, one of which is shown in Figure 1 D. The first baseline homogeneous structure, comprised of just one building block type, served as an experimental control for a second heterogeneous structure, which used two types of building blocks to program aeroelastic structural response for increased aerodynamic efficiency. In addition to passive shape change, we show that the addition of an actuation system can create an active structural mechanism for roll control during flight. The design process built structures, and results from wind tunnel testing are described here.
Figure 1:

A large-scale, ultralight adaptive structural system. A) Modular building block unit, B) 4×4×4 unit cube during mechanical testing, C) Single half-span wing structure composed of 2088 building block units, D) Blended wing body aerostructure with skin, mounted to central load balance in the 14×22 subsonic wind tunnel at NASA Langley Research Center
2. Methodology
For the development of a programmable elastic shape morphing aerostructure, we leveraged the modular nature of the system to facilitate rapid development. In the following sections, we will highlight the tools, methods, and components of the workflow, including the building-block based design, interface and skin blocks, computational design assessment, and finally the experimental set-up.
2.1. Building-block Based Design and Ultra-light Structure
The building block toolkit consists of three-part categories: substructure, interface parts, and skin. In total, there are nine unique structural part types, with quantities summarized in Table B1. In the following sections, we describe the design and integration of each of these categories.
2.1.1. Substructure building blocks
The main substructure building blocks used here are octahedral unit cells (Figure 1 A), which, when connected at their nodes, produce a cuboctahedral lattice structure (Figure 1 B). While the methodology presented in this paper is not geometry specific, the cuboctahedral geometry was chosen here for several reasons. First, it has shown better than quadratic stiffness scaling [17] and therefore provides high specific stiffness performance. Second, it has a lower connectivity than many other high performing geometries, which can simplify unit cell mass manufacturing [21]. In particular, the cuboctahedral geometry was conducive to injection molding, which had a high enough throughput to enable the scale of the structure presented.
Octahedra of two different materials were used: polyetherimide (PEI) with 20% short chopped glass fiber reinforcement and un-reinforced PEI (Ultem 2200 and Ultem 1000, respectively). It is accepted in the cellular solids literature [26] that the resulting structure can be considered as a continuum metamaterial, modeled with standard bulk material mechanics methods. Accordingly, the Ultem 2200 lattice material, which formed the majority of the test samples, displayed absolute stiffness behavior of (8.4MPa) [21], which is comparable to a bulk elastomer material such as silicone, but at roughly 0.5% of the density (5.8 versus ).
2.1.2. Interface building blocks and skin
The interface building block set connects the vertices of the substructure building blocks to the skin components and the root and tip plates. There are several interface types: flat, slope, leading edge, transition, and plate mounting (Figure 2).
Figure 2:

Interface building blocks and plates. A) Top view with color code indicating location and types of interface parts, B–F) Interface parts and descriptions, G) Root and tip plate, H) Top view with color coded skin panel types, I) Sample parts unrolled as flat surfaces ready for cutting.
Flat interface parts mount to the exterior of the substructure in flat regions to provide mounting points for the skin panels shown in Figure 2 B). Slope parts consist of a single skin interface part and two spacing parts, which combine to connect skin and substructure across a 3:1 slope region shown in Figure 2 F). All of these components are made of injection molded RTP 2187 (40% carbon fiber reinforced polyetherimide). The leading edge components, also shown in Figure 2 D), are comprised of 3D printed interface parts to connect to the lattice and a laser-cut engineering plastic section to follow the leading edge geometry. There were a total of 302 interface parts and 35 leading edge assemblies on each half span. Transition components were also needed in the region where multiple slopes intersected near the middle of the wing. These components were also made from 3D printed struts matching the skin hole pattern and a laser-cut engineering plastic core plate shown in 2 E). At the root and tip section, injection molded plate mounting components shown in Figure 2 C) were designed to interface with the aluminum root plate and the carbon fiber tip plate. These components, shown in Figure 2 G), utilized 10–32 screws to interface to those plates. There were a total of 384 for the root plate and 122 for the tip plate. The root plate is a single 6.35mm thick aluminum plate, with holes and features milled and tapped as shown. The tip plate is 1.6mm thick carbon fiber plate; waterjet cut as shown.
The skin is designed to transfer aerodynamic pressure loads directly to the substructure through the interface parts. Panels are not interconnected and thus do not behave as a structural stressed skin. Neighboring panels overlap by 10.2mm to ensure a continuous surface for airflow while still allowing panels to slide past one another during aeroelastic shape change. Prior experiments observed minimal aerodynamic effect of ventilation through such overlapping skin panels at low airspeeds [22]. The primary panel skin design was a 165.1 × 165.1 mm square-shaped patch, with mounting holes that were modified depending on the section of the wing that it attached to (flat, sloped, or transition areas). The parts are 0.254 mm thick PEI (Ultem) film and were cut using a CNC knife machine (Zund). The film had a matte finish to reduce reflectivity and mitigate potential issues with a motion capture system (Vicon). Figure 2 H) shows a map of the top of a half span where we can see that toolbox skin pieces covered about 78% of the total surface area. Custom pieces were only required for complex transition regions and for the areas at the root and tip where the structure attached to the end plates. A single half span has 248 basic skin building blocks and 54 custom parts. A complete list of the parts used is presented in Appendix B.
2.2. Computational Design Assessment
Assuming this base set of the substructure, interface, and skin building blocks, the final design of our aerostructure resulted from an iterative process described here and shown in Figure 3. Our design goals were to maximize the aerodynamic loading of the aerostructure while maintaining the appropriate safety factor for testing. The initial designs in Figure 3 B achieve this by creating a low-speed variation of the early concept of a blended-wing body (BWB) geometry presented by Liebeck [27]. Once we achieved a design with sufficient safety factors under low-speed loading, we began to explore design parameters for stability and controllability. As is common with BWB or flying wings, we used wing sweep to augment pitch stability [28] and dihedral as a means of lateral stability [29].
Figure 3:
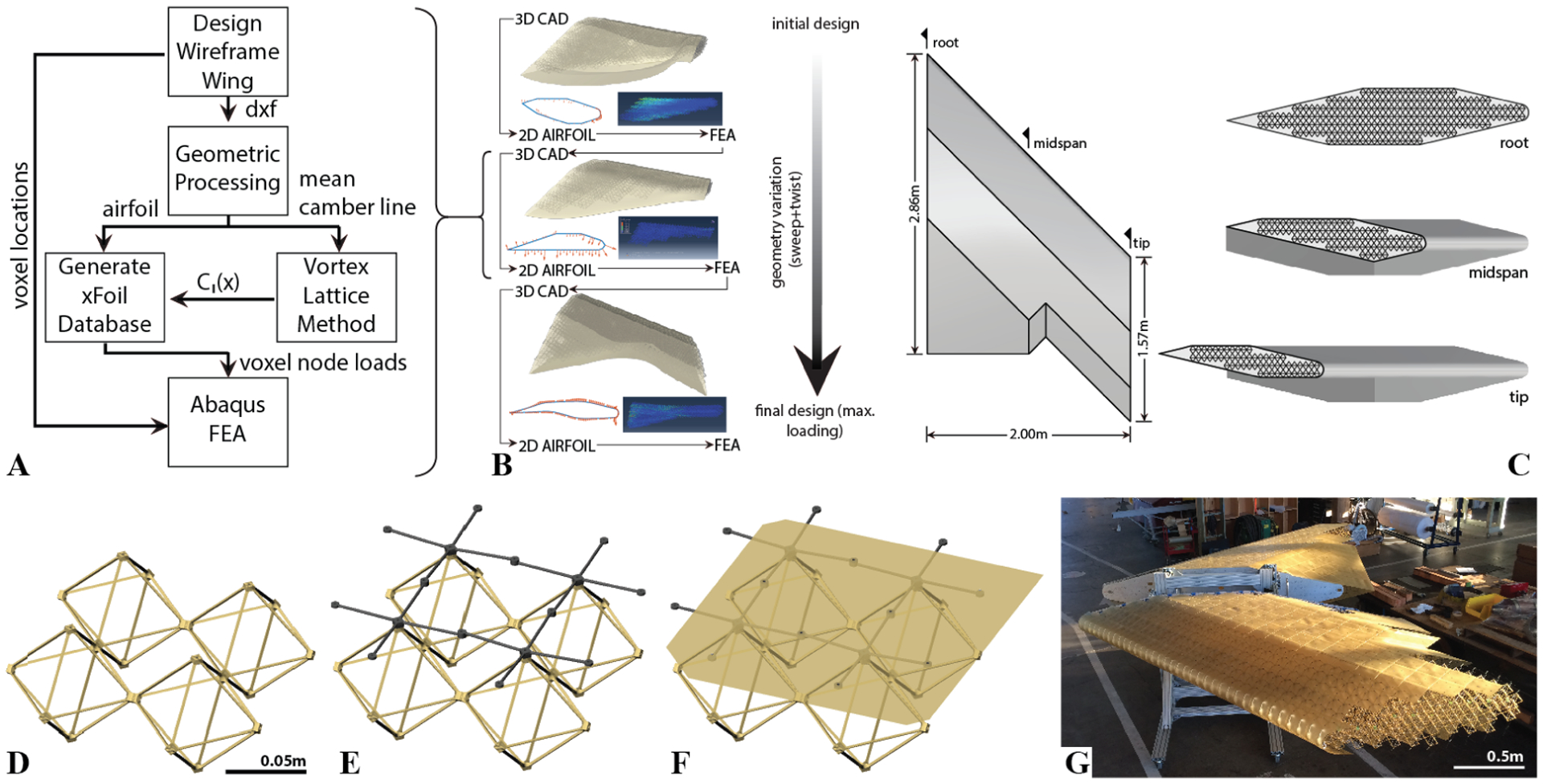
Building block toolkit design work-flow for ultralight aerostructures. A) 2D airfoil section design, 3D lattice material aerostructure, and FEA with aerodynamic loading and elastic deformation. B) The iterative process utilizing software work-flow to arrive at the final design, C) Final Design, D) Substructure building blocks, E) Interface building blocks, F) Skin building block, G) Large scale ultralight aerostructure near completion of manufacturing.
The computational workflow is shown in Figure 3 A) starts with the build-up of the substructure from using the octrahedra building blocks. Once this geometry is generated (using Rhino3D CAD software), the substructure wire-frame was partitioned (using MATLAB) into 77.1mm (3in) span-wise segments from which the true airfoil shape and mean camber line were determined. This airfoil shape was then evaluated for pressure distribution (using XFOIL) at a Reynolds number of 3.5e6, which was determined from the expected experimental conditions, from an angle of attack −35° to 35° by increments of 0.1°. The resulting distribution was used to determine the nodal loads via application of the sectional air pressure loads to the nearest node. The vortex lattice panels were uniformly distributed with 20 chord-wise and 150 span-wise panels on the mean camber line. The local lift coefficient as determined by the vortex lattice method was matched by the pressure distribution results to determine the appropriate loading for structural FEA (ABAQUS). Each strut was represented as four subdivided beam elements (ABAQUS B31) with stiffness of 6.895 GPa (1e6 psi) and density of 1.42×107 kg/m3 (1.329×10−4 lbf s2/in4). These are datasheet properties, and we expect the stiffness values to be conservative due to fiber alignment in the actual struts. The nodes were modeled using a short element (ABAQUS B31) of length 7.62 mm (0.3 in), which matches the actual node length of the building block part. This short beam element was assigned a stiffness of 68.95GPa (1×107psi) to simulate increased stiffness in the nodes. The simulations were run with an assumption of geometric non-linearity (ABAQUS NLGEOM ON) due to expected large displacements within each strut. A time step limit of 1×10−5 was used to help with convergence issues.
When designing heterogeneous models, it was necessary to account for the unique material properties of the different building block materials, which were produced using the same mold tooling. The unfilled PEI parts showed a higher coefficient of thermal expansion that resulted in a fractionally smaller part at final experimental temperatures. The use of slightly different sized parts induces a small amount of residual stress in the structure, which was simulated in our FEA assessment by initializing the full assembled model at mold temperature and evaluating the structural response after a simulated drop to final experimental temperature. Further details of the modeling can be found in [30].
The heterogeneous structure was programmed following these rules and guidelines, with the unfilled PEI considered as secondary voxel groupings:
Rules:
-
i
All second voxel type groupings are limited to linear string shapes
-
ii
No second voxel type strings can be longer than three blocks long
-
iii
Second voxel type strings cannot be placed within two unit spaces of each other
Guidelines:
-
iv
Second voxel type strings placed spanwise will reduce a) bending and b) torsional stiffness
-
v
Second voxel type strings placed chordwise decreases in-plane shape stiffness
-
vi
Second voxel type strings reduce the total length of building block extrusion
The first three rules were created to limit the effect that the residual strain would have on the outer mold line and allow for functional assembly. The last three are guidelines that are used as design mechanisms. Figure 4 shows the programming guidelines general behaviors and how we propose to apply them to our specific application. Guideline (vi) will result in similar behavior to (iv) and (v) when placed in the same configuration though it requires no external loading to achieve the shape change because it is caused by residual stress due to the geometric mismatch.
Figure 4:
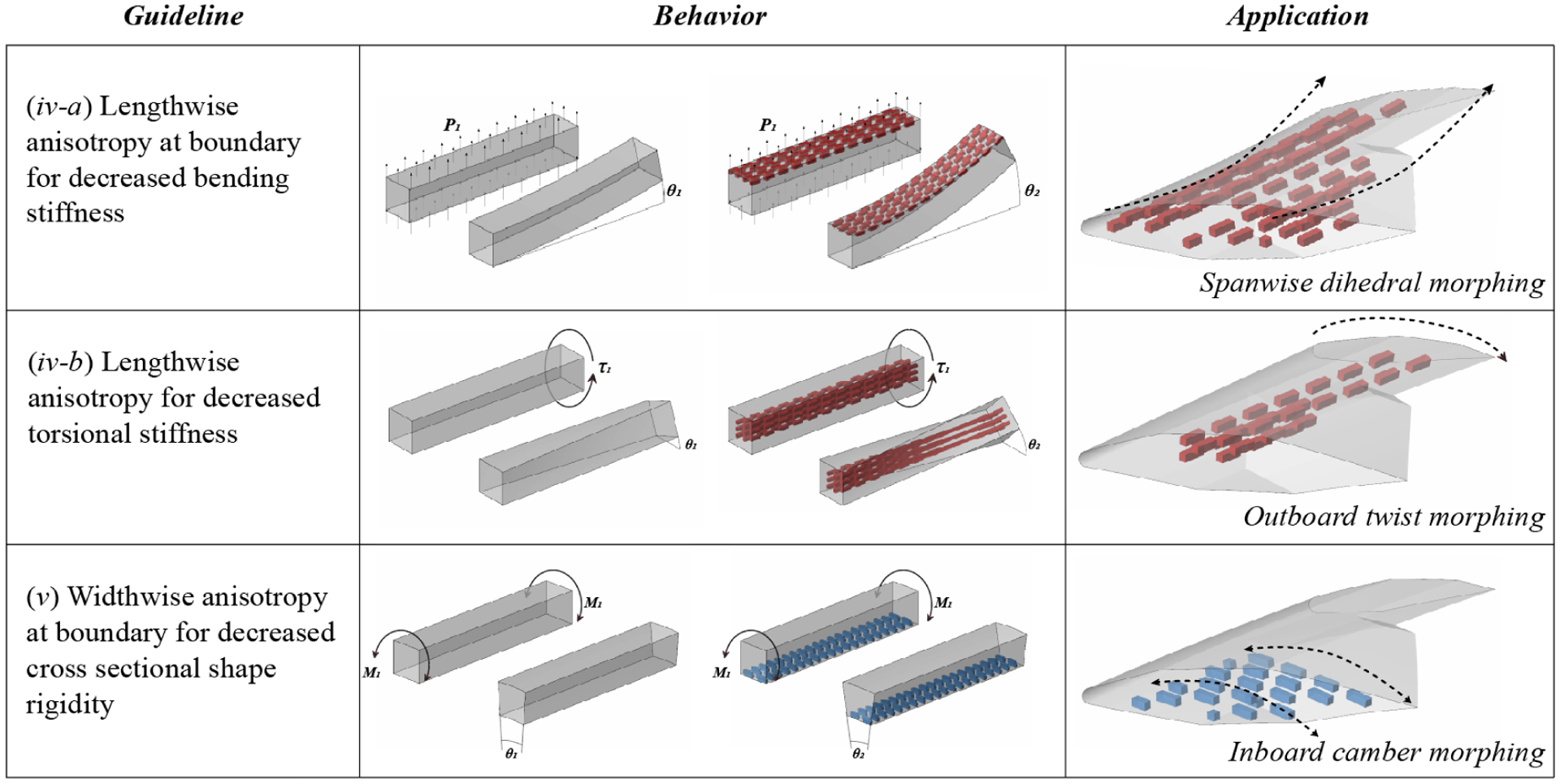
Guidelines, behaviors, and applications of anisotropic spatial programming.
With these rules and principles, the heterogeneous structure was programmed to increase the lift and drag by intelligently inducing twist and increasing camber. A second objective that coincided with the first was to improve the efficacy of the torque rod used as an actuation mechanism. The twist is achieved by placing unfilled PEI chains along the span, but they were biased towards the center of the span to take advantage of (vi) by reducing the center of the outboard wing section and inducing twist. We increased camber by placing chordwise unfilled PEI string on the bottom half of the inboard section effectively reducing the stiffness of that section and encouraging increased camber. The application of these guidelines are shown in the third column of Figure 4.
2.3. Experimental Setup
We performed the experiments in the NASA Langley Research Center 14×22 foot subsonic wind tunnel, as pictured in Figure 5. Unless otherwise noted, the dynamic pressure of the experiments was 95.76Pa (2psf). The angle of attack ranged from −4° – 18° with an accuracy of ±0.05°, measured with a standard inertial measurement unit (Honeywell Q-Flex). Temperature readings were taken with a standard temperature transducer (Edgetech Vigilant) with an accuracy of ±0.36°F. The load measurements were taken with a custom balance (NASA) that was designed to a normal load limit of 2224.1N (500lbs), axial load limit of 667.2N (150lbs), pitch torque limit of 677.9Nm (6,000in - lbs), roll torque limit of 226Nm (2,000in-lbs), yaw torque limit of 226Nm (2,000in - lbs), and sideload limit of 667.2N (150lbs). The full model was fixtured by the load balance near the expected center of mass. The load balance was fixtured to the tunnel via the ≈ 2.79m sting setup as seen in Figure 5. The displacement data was collected through a standard motion capture (VICON) system with four cameras placed in the ceiling of the wind tunnel. Retroflective tape circles of 12.7mm (0.5in) diameter were placed on the model skin surface at every other lattice building block center, 154.2mm (6in) apart from each other, as well as on the leading edge and trailing edge tip. Further details on the processing of the motion capture data results are provided in the online supplementary materials.
Figure 5:

Views of wind tunnel setup. (L) Rear view, (R) Front/side view.
3. Results
Results broadly fall into two categories, the proof of concept simulation design results and the experimental results. The simulation results showed that the work-flow presented above is capable of generating programmable passive shape changes. The experimental demonstrate full-scale performance gains of our novel aerostructure and shape morphing structural mechanism.
3.1. Simulation Results: Programmed Heterogeneous Design and Anisotropic Tuning
We used simple heuristics for a first order exploration of the design space of our set of building blocks in simulation to demonstrate tuning ability and the associated expected performance improvements. The anisotropic tuning simulations were done with the same ABAQUS settings as above. To amplify the effects of heterogeneity for this study, we used two materials with two widely different Young’s moduli- aluminum and PTFE, which were 68.95 GPa (1×107 psi) and 0.6895 GPa (1×105 psi) respectively. Figure 6 shows simulations of three different wing designs, demonstrating our ability to dramatically alter the response of the structure to the same load based on unit cell placement. Figure 6 A) shows the wing with a lower stiffness polymer at the leading edge and a uniform load placed at the bottom of the wing, resulting in the wing tip twisting up. The same load but a different distribution of the building blocks results in no tip twist and a negative tip twist with the same tip displacement in Figures 6 B) and C) respectively. Each of these programmed mechanisms can have advantages depending on the mission criteria; for instance, if the aircraft’s expected operational regime were a long-duration cruise, configuration A) (with the tip twisting up under load) would be better. If the aircraft were going to be performing high angle of attack maneuvers or carrying high loads, then configuration C) would delay stall, and therefore have higher performance than configurations A) or B). This design flexibility extends the application space for a single building block set, the benefits of which will be described further in the Discussion section.
Figure 6:

ABAQUS simulations of various possible anisotropic wing designs using the same building blocks, demonstrating the ability to tune the primary performance metrics through different building block material types and no geometry changes. A) shows through the reduction in the leading edge stiffness the wing would have its tip twist upward under a uniform load, resulting in ”wash in,” which at low angles of attack can result in increased aircraft efficiency. B) shows that through balancing the leading edge and trailing edge stiffness the same deflection of A) can be achieved with no twist, C) is the opposite design to A) which results in ”wash out” which is desirable for enhanced stability and high angle of attack maneuvers.
3.2. Experimental Results and Validation
We present three primary experimental results: 1) Validation of numerical and analytical methods through quasi-static load testing, 2) programmable anisotropy for performance improvement through programmed heterogeneous design, 3) adaptive aeroelastic shape morphing.
3.2.1. Quasi-Static Substructure Validation
With an ultra-light structure, qualification of load-bearing capability is particularly important for safe testing and application. For wings, this is often done with a test that quasi-statically simulates the expected aerodynamic loading. We performed this testing using the whiffletree device shown in Figure 7. The tree linkages were sized and spaced to take a single point load and distribute it to many smaller point loads across the top layer of substructure building blocks. This load profile approximated a worst-case aerodynamic loading pattern determined using the aforementioned numerical methods. This accounted for chord-wise loading distribution per distribution of sample cross sections, and span-wise loading was approximating an elliptical load distribution. Further details on the actual construction of the whiffletree can be found in [31].
Figure 7:
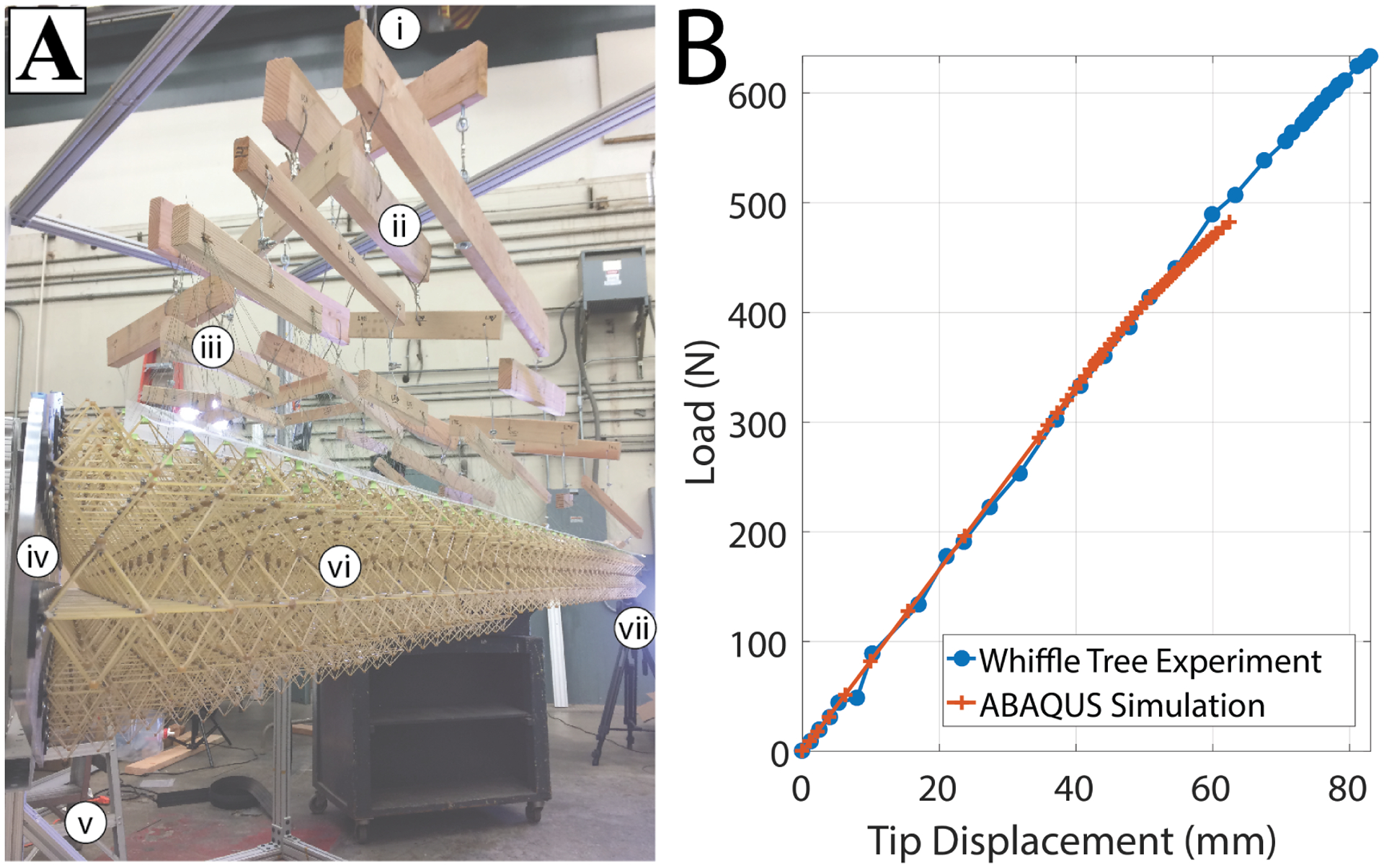
Substructure static load test and simulation. A) the whiffletree test configuration, labeled are the following: i) single point load, ii) whiffle tree load distribution system, iii) cable system for tree to structure load distribution, iv) wing root base plate mounted to test stand, v) fixture weight, vi) building block structure under test load, vii) tip displacement measurement. B) comparison between the whiffletree test and the ABAQUS simulations, showing effecting FEA prediction of structural response behavior.
In this case, whiffletree testing of the substructure provided validation of the simulation and prediction methods, which also demonstrated the robustness of the test structure. A fundamental assumption accepted in the literature on cellular materials is that of continuum behavior, allowing material characterization with traditional coupons to be extended to predicting stress and strain distribution in objects of irregular shape and non-uniform loading [26, 32]. This assumption was also fundamental to our design method, though there is little in the prior literature representing the large-scale application of periodic engineered cellular materials.
Figure 7-B shows that the ABAQUS results accurately predict the load response through the linear region. At the extremes, there are small deviations in the anticipated versus experimental results. The ABAQUS whiffletree simulation used the settings presented above with five beam subdivisions instead of four and incremental static loading. At low loading where there are small jumps in the experimental results, we explain the difference in prediction and experimental results as due to settling in the whiffletree structure, as small manufacturing inconsistencies in the cables, beams, and attachment devices take up the load. The experiments were stopped at the first sign of nonlinearities in the displacement versus loading; the simulations were run up until numeric failure defined as the point when the simulation could not converge for a minimum time step of 1μs. The simulations predict the early onset of nonlinearity due to local buckling. We explain this as numeric softening due to complex interactions between the spatial resolution of the beam subdivisions and nodal attachments. The static load experiments verify three-dimensional engineered cellular solids modeling at an application scale that is much larger than previously published [21].
3.2.2. Aerodynamic Efficiency Gains through Substructure Programmability
The primary goal of wind tunnel testing was to evaluate the ability of the programmed heterogeneous aerostructure to increase aerodynamic efficiency compared with the homogeneous aerostructure. When evaluating commercial flight systems, it is useful to split a typical mission profile into three main phases: take-off, cruise, and landing. The cruise condition is typically assigned as the mode with the maximum lift-to-drag ratio. We will be using this framework as a reference though we are not attempting to get an optimal wing shape for each condition. We are instead trying to increase efficiency over a wide variety of off-nominal conditions. Figure 8 A shows the lift to drag ratio of the baseline homogeneous wing over various angles of attack, and the ”cruise” condition is labeled as L/Dbaseline. This value will serve as the point of comparison to evaluate the efficacy of tuning in the programmed heterogeneous model. Angles of attack above and below that point represent take off and landing regimes respectively.
Figure 8:
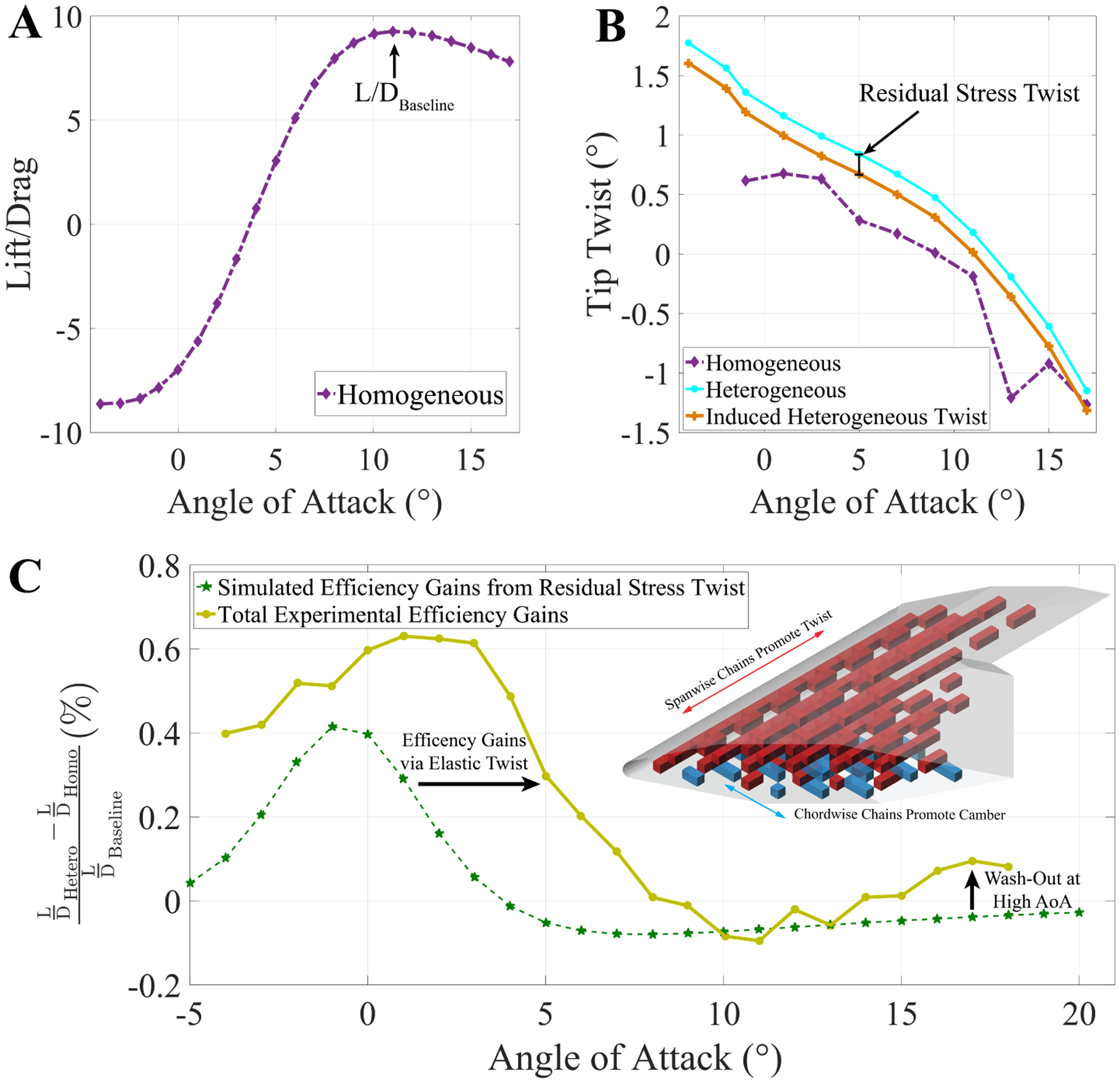
The lift to drag ratio for the baseline homogeneous wing is shown. A) Lift-Drag curve of the homogeneous design and highlighting the defined baseline operation value. B) compares the twist between the baseline homogeneous and programmed heterogeneous models as well as the estimated tip twist of the programmed heterogeneous model due to the change in stiffness. C) compares the total efficiency gains to the gains through the initial residual stress induced shape change, as well as the tuned changes in stiffness due to the programmed heterogeneous building block placement, shown in the right-hand corner of Figure C.
The aerodynamic performance of the programmed heterogeneous model was tuned by several means. Aerodynamic loads induced further tip twist and deformation according to the programmed torsional stiffness of the substructure. We show the tip twist for both the baseline homogeneous and programmed heterogeneous models in Figure 8 B, with a separate curve estimating the tip twist due to aeroelastic tuning alone, by removing the simulated twist due to residual stress. Un-filled PEI parts were also placed orthogonal to the span-wise pattern to add additional camber and inboard lift. This pattern can be seen in the inset of Figure 8 C. While the canonical discretized shape was identical to the baseline homogeneous model, the actual unloaded shape of the programmed heterogeneous model was slightly changed due to residual stress arising from slight dimensional differences between the parts by the constituent material.
Figure 8 C shows the increase in the lift to drag ratio for the programmed heterogeneous structure relative to the baseline homogeneous structure. The green line shows the simulated efficiency gains from the static residual stress twist, and the yellow line shows the total measured efficiency gains. The difference between the two is the efficiency gain from the change in substructure torsional stiffness response. This also shows that the aerodynamic efficiency gains were not solely from initial residual stress induced shape change, but also due to the programmed anisotropic substructure stiffness promoting tip twist under aerodynamic loads. It also demonstrates that the alteration of the stiffness can enhance off-design condition efficiency during flight phases such as take-off, landing, or other maneuvers (angles of attack above and below cruise). Overall, the combined effects of the anisotropic tuning resulted in anisotropic structural response and efficiency gains, which were the primary goals.
Though a relatively small change in the substructure, strategic choice of replacement locations produced significant changes in the normalized aeroelastic stiffness. The programmed heterogeneous aerostructure contained 17% (347 total) building blocks that were more compliant Ultem 1000. The global torsional stiffness decreased by approximately 43% while the bending stiffness was reduced by about 46%. Figure 9 shows the vertical displacement of the tip versus the coefficient of lift in 9 A). Figure 9 B) shows tip twist angle versus pitching moment coefficient. The nonlinear sections of Figure 9 B), suggest an onset of tip stall at the higher loading conditions that support the observations of the mechanisms for increased aerodynamic efficiency made in the previous section. The slope of the linear sections in each figure represents the normalized global aeroelastic bending and torsional stiffness, respectively.
Figure 9:
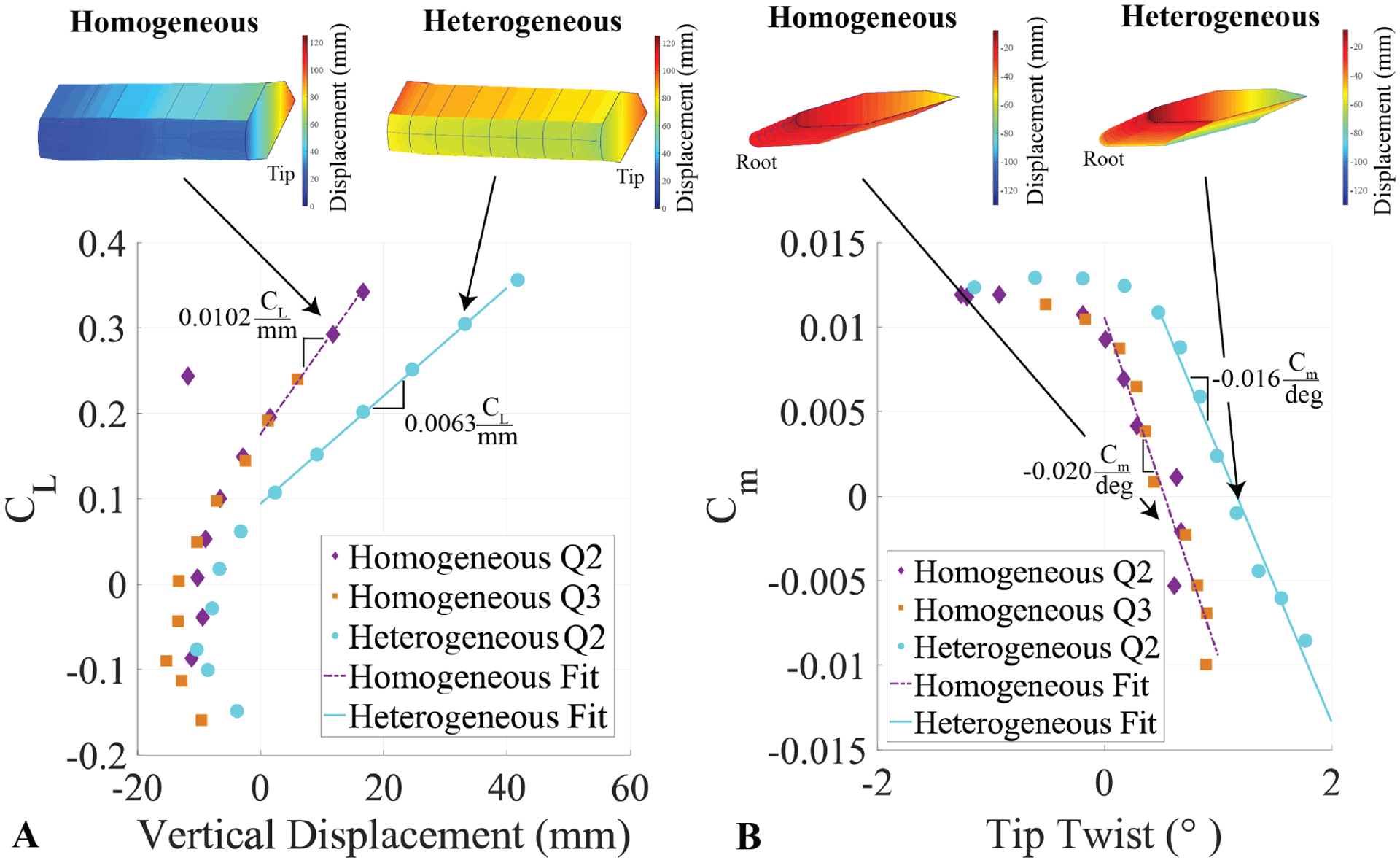
Quasi-static aeroelastic stiffness. A) shows the normalized loading curve of vertical lift displacement and B) shows the normalized pitching moment curve of tip twist, this is the representation of the aeroelastic stiffness of the structure where the stiffness coefficients that are being tuned are the slopes of the linear region.
We also evaluate the wing deformation by reconstructing the geometry based on motion capture data, described in further detail in Appendix A. The charts representing baseline homogeneous and programmed heterogenous experiments in Figure 9 A) and B) show wing deformation at the specified loading condition. The baseline homogeneous span-wise deflection in Figure 9 A) shows that at the high loading conditions in the linear regime, the trailing edge tip has the most significant amount of deflection, whereas for the programmed heterogeneous experiment the most significant amount of deflection is toward the root. The alteration in the maximum deflection location is analogous to alteration of the primary structural mode. The subfigures of Figure 9 B) show the twist variations at low angles of attack, which helps to explain the significant performance increase seen in Figure 8 at low angles of attack, since the trailing edge of the programmed heterogeneous model is lower, resulting in a positive forward twist or ”wash-in” that augments lift.
3.2.3. Adaptive, Shape Morphing Structural Mechanism
The full potential of the structural tuning extends beyond passive aeroelastic response to programmed aeroservo-elastic mechanisms. With a torque rod from the center body section to the wing tip, we demonstrate wing structure behavior as an elastically tuned shape morphing structural mechanism. The torque rod drives the tip twist in the system, and the programmed substructure translates the singular point torque into a global shape deformation. Figure 10 A) shows the actuation mechanism that drives the deformation. The programmed torsional flexibility of the heterogeneous model increased the twist range of the torque rod from ±0.25° to ±0.5°. Figure 10 B) shows the amount of twist for the baseline homogeneous and programmed heterogeneous models over the full angle attack range with the torque rod engaged. Figure 10 B) shows that the baseline homogeneous model has little variation from the commanded tip twist of 0.25°. However, the programmed heterogeneous model in Figure 10 B) shows the tip twist varies quite a bit from its commanded tip twist of 0.5°. Instead of maintaining the commanded value it follows the designed lift enhancing tip twist profile presented in Figure 8 but with a persistent commanded offset of 0.5° which maintains roll control authority. This indicates that quasi-static, passive stiffness tuning can still be implemented during active shape morphing.
Figure 10:
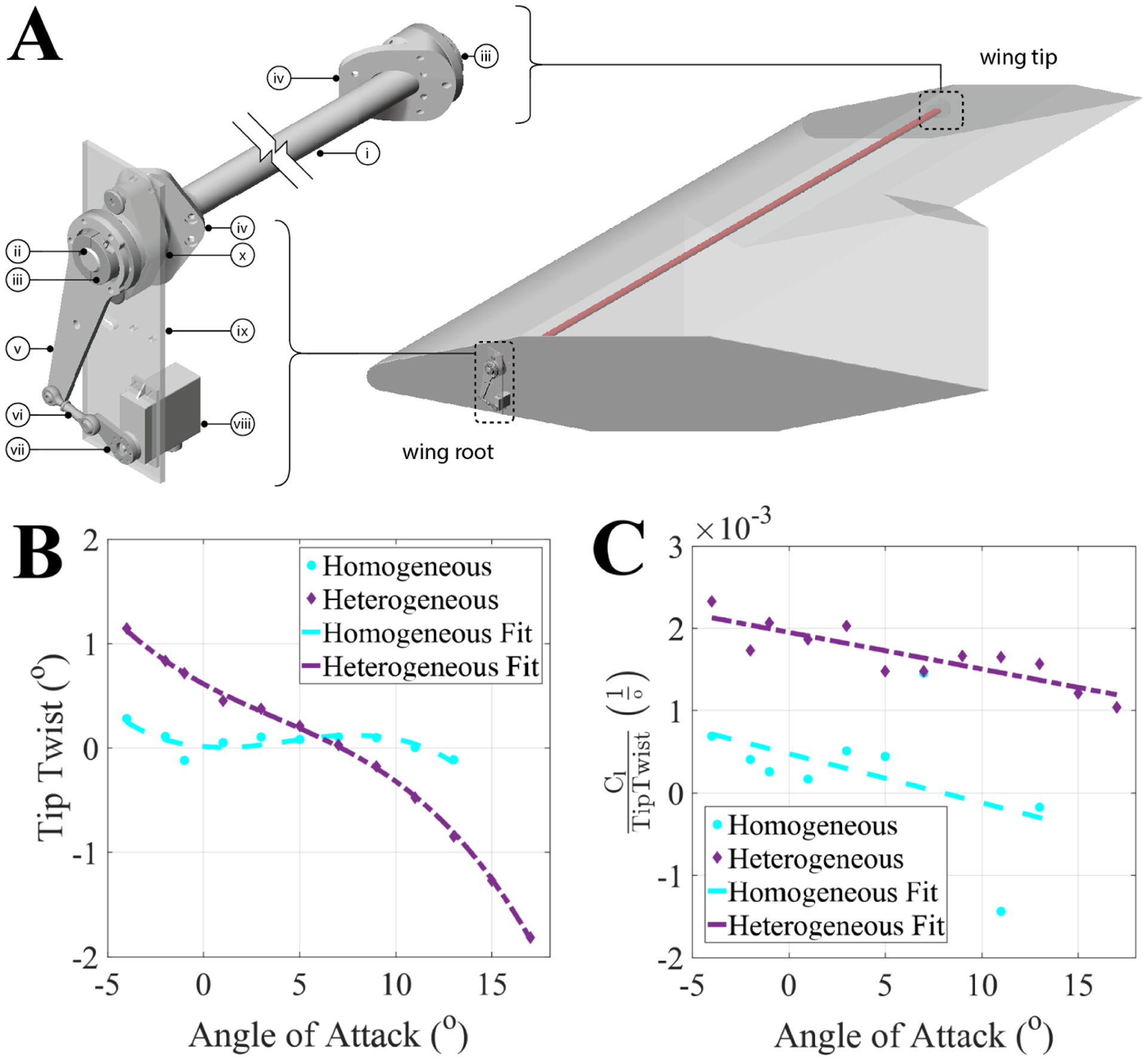
Actuation System and Results. A) A 31.75mm OD, 25.4mm ID carbon fiber tube (i) transfers torque to the wing tip from the actuation source at the root. A 25.4mm OD keyed aluminum shaft (ii) is epoxied to the end of the tube, with 25.4mm extending and clamped by a keyed shaft collar (iii). At the tip, this shaft collar bolts to a milled aluminum fixture (iv) which bolts to the carbon fiber tip plate (not shown). At the root, the shaft collar bolts to a 6mm thick aluminum plate armature (v). This armature connects to a ball-bearing linkage (vi), which connects to a 6mm thick aluminum servo horn armature (vii). This bolts to a high torque servo (viii), which is fixtured to a 6mm aluminum mounting plate (ix). This plate is bolted to a mounted bearing with flanges (x) which bolts to a milled aluminum fixture (iv), which bolts to the root plate on either side. B) shows the tip twist of the aerostructure with the torque rod engaged. The structural tunning allowed for a large amount of tip twist over the range of angles of attack even with the addition of the torque rod. The effect of the increase in flexibility can be seen in C) where the roll authority per tip twist degree was increased for the baseline homogeneous model.
The adaptation of the programmed aerostructure into an adaptive aeroelastic mechanism implements broad elastic structure coupling to a simple actuator, effectively providing a system-wide control gain increase. Figure 10 C shows a comparison of the amount of roll coefficient per amount of tip twist, between the baseline homogeneous and programmed heterogeneous experiments. The programmed heterogeneous model shows a consistent increase over the baseline homogeneous model for the full range of angle of attack with insignificant effects from the change in angle of attack. This steady increase means that the programmed structure is enhancing the control authority of the torque rod mechanism.
We explain the programmed structure’s enhancement of the control authority as a result of the combination of the torsional and inboard camber stiffness alterations. These alterations allow the application of the torque rod point load to translate into active shape morphing, which results in an increase in lift and roll for the actuated wing. Figure 11 A) and B) show the comparison of the displacement of the homogeneous and heterogeneous designs when actuated by the torque rod. The heterogeneous structure shows a consistent displacement across the span. The span-wise displacement can be controlled by the torque rod, as is shown by the application of the torque in Figure 11 B). Figure 11 C) further supports the observation showing that the amount of twist prescribed at the tip by the torque rod is maintained through the outboard span, supporting our theory that the heterogeneous structure helped to translate the point load into shape morphing. The combined results of passive and active shape change show that the building block material system can effectively be used as an adaptive programmable elastic structure.
Figure 11:
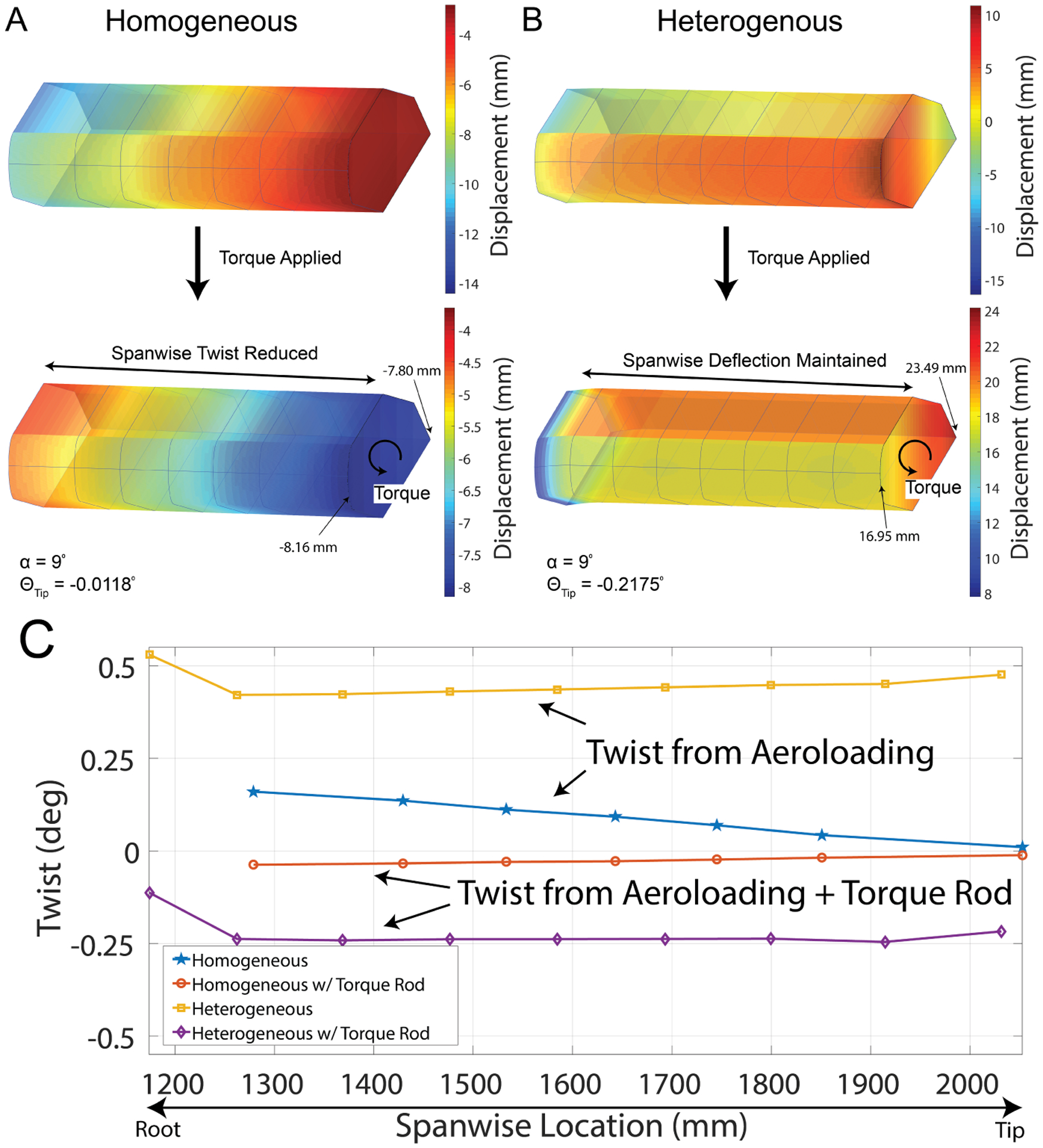
Shape effects of torque rod and heterogeneous configurations. A) and B) show the displacement of the homogeneous and heterogeneous configurations with the impact of the torque rod. C) compares the span-wise twist of each of the configurations and demonstrates that the heterogeneous design results in the nearly flat distribution of twist through the outboard span.
4. Discussion
In this study of an elastic shape morphing air vehicle, we advance the state of the art in cellular material construction by building a large-scale, ultralight adaptive structure. For brevity, we limit the discussion to comparisons of our aerostructure material system to the density of similar aerostructures, the overall manufacturability, and essential design considerations. In this section, we explore some benefits and design considerations of programmed elastic shape morphing material, the scalability of the manufacturing process, and potential future applications. The discrete cellular material approach has several advantages, including mass efficiency, structural programmability, and system modularity.
4.1. Aerostructure Density
The significant potential benefit of cellular lattice structures is high stiffness at ultralight densities. Reduction in weight for transportation and locomotion applications can reduce power requirements, increase fuel efficiency, and decrease costs [33]. Table 1 shows the cumulative weight of the design components and their resulting density. This table also contains various other reference densities, including other aeroelastic wind tunnel test models, such as X-HALE [34], VCCTEF CRM [35], and Vulture CMT [36], as well as a typical commercial aircraft wing for reference. The CRM and the Vulture were designed to match scaled performance parameters rather than to reduce weight and are provided for aeroelastic application reference. The resulting system density, including the substructure, interface, and skin building blocks, is well below 10mg/cm3 (the threshold for classification as ultra-light material). The complete actuated system still displays an overall mass density of 12.7mg/cm3, below the other provided reference densities.
Table 1:
Weights and densities for our ultralight aerostructure and other relevant aerostructures.
| Component | Mass (g) | Density () | Span Length (m) |
|---|---|---|---|
| Building Block Substructure (this work) | 5734 | 5.566 | 4.27 |
| Substructure, Skin, and Actuation (this work) | 13110 | 12.7 | 4.27 |
| X-HALE Wing [34] | - | 16.5 | 6 |
| VCCTEF CRM Core [35] | - | 27 | 4.32 |
| Vulture CMT Model [36] | 21609 | 58.7 | 5.48 |
| Bird Humerous [37] | - | 19 – 22 | 6.5×10−3 – 0.07 |
| Harvard Bee [38] | 0.06 | 50 | 3×10−3 |
| Commercial aircraft wing [39] | 9.15×106 | 746 | 14.75 |
4.2. Manufacturability
To assess the potential of discrete lattice assembly as a manufacturing approach, we consider it in comparison to existing technologies for additive manufacture of lattice materials [18], explicitly looking at throughput.
A single half span wing from this work, containing 2088 substructure building blocks, took approximately 175 person-hours to construct or about 5 minutes per building block. The manual addition of a single octahedral building block to a structure is associated with 3 bolted connections, or 1–2 minutes per connection (time to pick up, place, and tighten the fastening hardware). Common additive manufacturing methods such as selective laser melting (SLM) and polyjet printing display build rate governed by the bounding box of the object, with volumetric throughput ranging from 10–200(cm3/hr). By comparison, our method assembled a bounding volume of roughly 1m3 at a bounding volumetric throughput of about 5000(cm3/hr).
Comparison to 3D printing, automated carbon fiber layup [40], filament winding [41], or anisogrid fabrication [42], shows that automation is extremely important. Development of automated robotic assembly of discrete lattice material systems is in its infancy, on relatively small (< 1m) scale structures, but has already demonstrated a rate of 40 seconds per building block [43], or nearly 40,000(cm3/hr), as shown in Table 2. We see that even mass throughput is on par with current low-cost 3D printers. Volumetric throughput is an order of magnitude greater than current methods, which is a result of the scalability of this manufacturing process - using centimeter scale parts to create meter scale structures.
Table 2:
Comparison of manufacturing methods for high-performance lattice structures.
| Manufacturing Method | Volume Rate () | Mass Rate () | Scale (m) |
|---|---|---|---|
| Selective Laser Melting (SLM) [44] | < 170 | < 195 | < 1 |
| Fused Deposition Modeling (FDM) [45] | < 60 | < 65 | > 1 |
| Polyjet (photopolymer) [46] | < 80 | < 95 | < 1 |
| Discrete lattice material manual assembly (this work) | ≈ 5000 | ≈ 27 | > 1 |
| Discrete lattice material robotic assembly [43] | ≈ 39821 | ≈ 220 | < 1 |
4.3. Design Considerations
While the modulus of the presented lattice structure is elastomeric with a much lower density than elastomers, with near ideal specific strength performance [21], this is expected to display failure strains that are more typical of conventional aerospace materials with similar specific stiffness. Some applications employ elastomers for their hyper-elastic characteristics with an elastic strain of 100% – 500% [47] whereas the presented fiber reinforced polymer lattice structure elongation at failure is at an elastic strain of 1.2% [21]. The presented design takes an approach where we were selectively embedding a softer material in a harder material to meet experimental safety factors. Using the same methodology with higher performance secondary materials might eventually be used to enhance the elastic strain further, while still displaying ultralight properties.
The mechanical behavior of each lattice unit cell is governed by the parameters that govern all cellular solid materials: the relative density, constituent material, and geometry [32]. This means that during the design process the constituent material selection is still a necessary and familiar process. Lastly, the size of the building blocks (and associated resolution when applied) must reflect the geometric characteristics of the expected boundary conditions. For our application, the unit cell is sized to allow manual assembly while also maintaining the desired design flexibility, and ability to support a relatively lightweight skin system, given the spatial variability of expected aerodynamic loading.
5. Conclusions and Future Applications
The ability to rapidly design and fabricate ultralight actuated systems can enable novel applications in the converging fields of transportation and robotics, where the traditionally orthogonal objectives of design flexibility and manufacturability can be aligned. The converging fields may be addressed by our building block based material system, which is targeted towards mass-critical robotic and aerospace applications.
We have shown that it is possible to program our substructure to augment actuation, with the aim of increasing control efficiency, decreasing required actuated inertia, and allowing for increased range, payload, and cost efficiency. Our current approach employs simple servomotors and torque tubes, but the manufacturing strategy may lend itself to ease of implementation of distributed actuation [48]. Similarly, the modularity of the structure provides a potential opportunity for simple integration of a distributed sensing and computation system [49, 50]. The design of these systems can be enhanced from our iterative design approach to include topological optimization like that presented in [51], but due to its modular nature, the substructure is already subdivided, and relatively efficient discrete optimization can be performed on the building block material or relative density.
Lastly, one of the most mass-sensitive applications is robotic exoplanet exploration. Currently, it costs roughly 10,000 USD to launch 1 kg of material to lower earth orbit [52], with ambitious ongoing efforts to reduce this by a factor of two. The cost will remain high enough that mass-efficient and robust hardware technology may continue to be the most significant driver in expanding our exploration capabilities. Modular, ultralight cellular structures can potentially enable new frontiers in aviation, transportation, and space exploration.
Acknowledgments
The authors thank the NASA ARMD Convergent Aeronautics Solutions Program (MADCAT Project), the NASA STMD Game Changing Development Program (ARMADAS Seedling Project), NASA Ames Research Center (ARC), and NASA Langley Research Center (LaRC) for supporting this work. We also thank Mark Croom, Ethan Gasta, Neil Gershenfeld, Steven Hu, Leandre Jones, Otto Lyon, Afsheen Sajjadi, Mircea Teodorescu, Maxwell Woody, and Alden Yellowhorse, the test team at the LaRC 14×22 subsonic wind tunnel, the UCSC DANSER Lab, the MIT Center for Bits and Atoms, and Moog, Inc., for their contributions, research assistance, and critical discussions.
Appendix A. Data Processing
The motion capture (Vicon) data was collected with respect to an arbitrary center point just of the left wing tip. The model is in the global rotation reference frame of the tunnel, and the two need to be matched to be able to compare between baseline homogeneous and tuned heterogeneous models which were calibrated separately and had different reference points. For each angle of attack set point, the average of all the data taken at that set-point for each retro-reflective identifier. A known set of tip identifiers are then used to generate rotation matrices. The tip set is first fit to lines in the y-z and x-y plane and the endpoints of each fit lines are used to calculate the distance between the leading edge and trailing edge identifiers of the set, dx, dy, dz for the x distance, y distance, and z distance respectively. The rotation matrix about the z-axis between the tunnel reference plane and the motion capture system is:
| (A.1) |
where,
| (A.2) |
The distances dx, dy, dz are then rotated into the z-axis global model frame so that the rotated points are
| (A.3) |
The rotated points P can then be used to find the x rotation matrix
| (A.4) |
where θ is the angle of rotation about the global model x-axis and
| (A.5) |
| (A.6) |
where,
| (A.7) |
and
| (A.8) |
The roll rotation matrix can then be found using the roll angle from the wind tunnel QFLEX system.
| (A.9) |
The difference between the known positions of the tip identifier and the balance is the tuple dB. The Vicon data in the global reference, Vrot is then
| (A.10) |
To compare each different angles of attack the wings need to be adjusted so that the balance is in the same relative location. To do that the height of the center of rotation CRh needs to be determined by
| (A.11) |
where Bh is the balance height, α is the angle of attack, T is the distance tuple between the balance and center of rotation and Href is the reference height that all of the different set-points will be compared too. The adjusted Vicon data Vadj which is used for all the results in this paper can be determined by
| (A.12) |
where
| (A.13) |
With the Vicon data for each set-point shares, the same reference plane the sectional twist and displacement can be calculated. We assume that the cross section of the wing does not deform much and stays in the same plane. As a result the coordinates of a reference point i, is related to the deformed point by
| (A.14) |
where
| (A.15) |
| (A.16) |
| (A.17) |
Then the displacement (dispy,dispz) and rotation (θtwist) for that section is solved by minimizing the least squares error between the predicted Pdef of the sectional set and the actual Vicon data vadj. The sectional sets are determined by selecting all the points within a 6-inch span-wise section where retro-reflective identifiers are.
Appendix B. Building Block Parts
Table B1:
Summary of building blocks used per half span
| Part type | Quantity | Material |
|---|---|---|
| Substructure | ||
| 1. Ultem 2000 (homogeneous wing) | 2088 | PEI, 20 % chopped fiber |
| 1a. Ultem 2000 (heterogeneous wing) | 1741 | PEI, 20 % chopped fiber |
| 2. Ultem 1000 (heterogeneous wing) | 347 | PEI |
| Interface | ||
| 3. Flat interface | 414 | RTP |
| 4. Slope interface | 963 | RTP |
| 4a. Slope straight spacer | 318 | RTP |
| 4b. Slope elbow spacer | 309 | RTP |
| 5. Leading edge | 35 | Delrin, 3D print |
| 6. Transition | 2 | Delrin, 3D print |
| 7. Plate mounting | 506 | RTP |
| Skin | ||
| 8. Skin (basic) | 248 | PEI |
| 8a. Skin (custom) | 54 | PEI |
References
- [1].Jun JW, Silverio M, Llubia JA, Markopoulou A, Dubor A et al. 2017
- [2].Senatore G, Duffour P and Winslow P 2018. Engineering Structures 167 608–628 [Google Scholar]
- [3].Joshi S, Tidwell Z, Crossley W and Ramakrishnan S 2004. Comparison of morphing wing stategies based upon aircraft performance impacts 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference p 1722 [Google Scholar]
- [4].Barbarino S, Bilgen O, Ajaj RM, Friswell MI and Inman DJ 2011. Journal of intelligent material systems and structures 22 823–877 [Google Scholar]
- [5].Weisshaar TA. Morphing aircraft technology-new shapes for aircraft design Tech. rep. PURDUE UNIV LAFAYETTE IN. 2006.
- [6].Straub FK, Ngo HT, Anand V and Domzalski DB 2001. Smart materials and structures 10 25 [Google Scholar]
- [7].Monner HP 2001. Aerospace Science and Technology 5 445–455 [Google Scholar]
- [8].Vos R and Barrett R 2011. Smart Materials and Structures 20 094010 [Google Scholar]
- [9].Sanders B, Eastep F and Forster E 2003. Journal of Aircraft 40 94–99 [Google Scholar]
- [10].Kudva JN 2004. Journal of intelligent material systems and structures 15 261–267 [Google Scholar]
- [11].Wagg D, Bond I, Weaver P and Friswell M 2008. Adaptive structures: engineering applications (John Wiley & Sons; ) [Google Scholar]
- [12].Yokozeki T, Takeda S i, Ogasawara T and Ishikawa T 2006. Composites Part A: applied science and manufacturing 37 1578–1586 [Google Scholar]
- [13].Kota S, Hetrick JA, Osborn R, Paul D, Pendleton E, Flick P and Tilmann C 2003. Design and application of compliant mechanisms for morphing aircraft structures Smart Structures and Materials 2003: Industrial and Commercial Applications of Smart Structures Technologies vol 5054 (International Society for Optics and Photonics; ) pp 24–34 [Google Scholar]
- [14].Chen Y, Yin W, Liu Y and Leng J 2011. Smart Materials and Structures 20 085033 [Google Scholar]
- [15].Majji M, Rediniotis O and Junkins J 2007. Design of a morphing wing: modeling and experiments AIAA Atmospheric Flight Mechanics Conference and Exhibit p 6310 [Google Scholar]
- [16].Neal D, Good M, Johnston C, Robertshaw H, Mason W and Inman D 2004. Design and windtunnel analysis of a fully adaptive aircraft configuration 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference p 1727 [Google Scholar]
- [17].Cheung KC and Gershenfeld N 2013. Science 1240889 [DOI] [PubMed]
- [18].Schaedler TA and Carter WB 2016. Annual Review of Materials Research 46 187–210 [Google Scholar]
- [19].Bertoldi K, Vitelli V, Christensen J and van Hecke M 2017. Nature Reviews Materials 2 17066 [Google Scholar]
- [20].Zheng X, Smith W, Jackson J, Moran B, Cui H, Chen D, Ye J, Fang N, Rodriguez N, Weisgraber T et al. 2016. Nature materials 15 1100. [DOI] [PubMed] [Google Scholar]
- [21].Gregg CE, Kim JH and Cheung KC 2018. Advanced Engineering Materials 20 1800213 [Google Scholar]
- [22].Jenett B, Calisch S, Cellucci D, Cramer N, Gershenfeld N, Swei S and Cheung KC 2017. Soft robotics 4 33–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Coulais C, Teomy E, de Reus K, Shokef Y and van Hecke M 2016. Nature 535 529. [DOI] [PubMed] [Google Scholar]
- [24].Florijn B, Coulais C and van Hecke M 2014. Physical review letters 113 175503. [DOI] [PubMed] [Google Scholar]
- [25].Frenzel T, Kadic M and Wegener M 2017. Science 358 1072–1074 [DOI] [PubMed] [Google Scholar]
- [26].Gibson LJ and Ashby MF 1999. Cellular solids: structure and properties (Cambridge university press; ) [Google Scholar]
- [27].Liebeck RH 2004. Journal of aircraft 41 10–25 [Google Scholar]
- [28].Voskuijl M, La Rocca G and Dircken F 2008. Controllability of blended wing body aircraft Proceedings of the 26th International Congress of the Aronautical Sciences, ICAS 2008, including the 8th AIAA Aviation Technology, Integration and Operations (AIO) Conference, Anchorage, Alaska, September 14–19,(2008) (Optimage Ltd.) [Google Scholar]
- [29].Paranjape AA, Chung SJ and Selig MS 2011. Bioinspiration & biomimetics 6 026005. [DOI] [PubMed] [Google Scholar]
- [30].Cramer N, Kim JH, Gregg C, Jenett B, Cheung K and Swei SSM 2019. Modeling of tunable elastic ultralight aircraft (submitted) AIAA Aviation Forum [Google Scholar]
- [31].Jenett B, Cramer NB, Swei SSM and Cheung K 2019. Design approximation and proof test methods for a cellular material structure AIAA Scitech 2019 Forum p 1861 [Google Scholar]
- [32].Ashby M 2006. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 364 15–30 [DOI] [PubMed] [Google Scholar]
- [33].Von Karman T and Gabrielli G 1950. Mechanical Engineering 72 775–781 [Google Scholar]
- [34].Jones J. Development of a Very Flexible Testbed Aircraft for the Validation of Nonlinear Aeroelastic Codes. University of Michigan: 2017. Ph.D. thesis. [Google Scholar]
- [35].Livne E, Precup N and Mor M 2014. Design, construction, and tests of an aeroelastic wind tunnel model of a variable camber continuous trailing edge flap (vcctef) concept wing 32nd AIAA Applied Aerodynamics Conference p 2442 [Google Scholar]
- [36].Britt R, Ortega D, Mc Tigue J and Scott M 2012. Wind tunnel test of a very flexible aircraft wing 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA p 1464 [Google Scholar]
- [37].Dumont ER. Proceedings of the Royal Society of London B: Biological Sciences rspb. 2010. 20100117.
- [38].Wood RJ 2007. Liftoff of a 60mg flapping-wing mav Intelligent robots and systems, 2007. iros 2007. ieee/rsj international conference on (IEEE) pp 1889–1894 [Google Scholar]
- [39].Bai C, Mingqiang L, Zhong S, Zhe W, Yiming M and Lei F 2014. International Journal of Aeronautical and Space Sciences 15 383–395 [Google Scholar]
- [40].August Z, Ostrander G, Michasiow J and Hauber D 2014. SAMPE J 50 30–37 [Google Scholar]
- [41].Vasiliev V, Krikanov A and Razin A 2003. Composite structures 62 449–459 [Google Scholar]
- [42].Vasiliev VV, Barynin VA and Razin AF 2012. Composite structures 94 1117–1127 [Google Scholar]
- [43].Trinh G, Copplestone G, O’Connor M, Hu S, Nowak S, Cheung K, Jenett B and Cellucci D 2017. Robotically assembled aerospace structures: Digital material assembly using a gantry-type assembler Aerospace Conference, 2017 IEEE (IEEE; ) pp 1–7 [Google Scholar]
- [44]. [2018-03-30];Slm spec sheet. https://slm-solutions.com/products/machines/selective-laser-melting-machine-slmr500 accessed:
- [45].Go J, Schiffres SN, Stevens AG and Hart AJ 2017. Additive Manufacturing 16 1–11 [Google Scholar]
- [46].Brajlih T, Valentan B, Balic J and Drstvensek I 2011. Rapid prototyping journal 17 64–75 [Google Scholar]
- [47].Case JC, White EL and Kramer RK 2015. Soft Robotics 2 80–87 [Google Scholar]
- [48].Cramer N, Tebyani M, Stone K, Cellucci D, Cheung KC, Swei S and Teodorescu M 2017. Design and testing of fervor: Flexible and reconfigurable voxel-based robot Intelligent Robots and Systems (IROS), 2017 IEEE/RSJ International Conference on (IEEE; ) pp 2730–2735 [Google Scholar]
- [49].Recht B and D’Andrea R 2004. IEEE Transactions on Automatic Control 49 1446–1452 [Google Scholar]
- [50].Espenschied KS, Quinn RD, Beer RD and Chiel HJ 1996. Robotics and autonomous systems 18 59–64 [Google Scholar]
- [51].Aage N, Andreassen E, Lazarov BS and Sigmund O 2017. Nature 550 84–86 [DOI] [PubMed] [Google Scholar]
- [52].Costs ST. Futron Corporation. 2002.


