Interaction of delaminations and matrix cracks in a CFRP plate, Part II: Simulation using an enriched shell finite element model

Abstract

Numerical simulations are presented of a recently developed test which creates multiple delaminations in a CFRP laminate specimen that grow and interact via transverse matrix cracks [1]. A novel shell element enriched with the Floating Node Method, and a damage algorithm based on the Virtual Crack Closure Technique, were used to successfully simulate the tests. Additionally, a 3D high mesh fidelity model based on cohesive zones and continuum damage mechanics was used to simulate the tests and act as a representative of other similar state-of-the-art high mesh fidelity modeling techniques to compare to the enriched shell element. The enriched shell and high mesh fidelity models had similar levels of accuracy and generally matched the experimental data. With runtimes of 36 minutes for the shell model and 55 hours for the high mesh fidelity model, the shell model is 92 times faster than the high-fidelity simulation.

1. Introduction

The state-of-the-art in aerospace structural design, when using composite materials, is to rely heavily on testing for certification [2, 3, 4]. The ability to simulate progressive damage in composite materials can reduce the need for expensive testing and could thereby reduce the cost of using composite laminate materials in aerospace structures. Reliable and robust numerical damage simulation tools are not available for composite laminates as they are for legacy materials such as aluminum or steel. The damage simulation tools that do exist are generally expensive, often to a prohibitive level, because of the time and expertise required for their use. Furthermore, existing tools cannot always simulate progressive damage problems of the complexity and extent found in real scenarios. If reliable and affordable damage simulation tools were available for composites, certain tests could be replaced with simulations, resulting in cheaper, lighter, and overall more efficient composite structures [5, 6, 7]. Additionally, an efficient simulation tool may allow for better component design early in the design process and prevent costly redesigns.

While there are examples dating back to the 1970s and 1980s [8, 9], numerical simulation of damage in composites did not begin in earnest until computational advances enabled the widespread use of the finite element method. In the 1990s, numerical techniques for damage simulation began to be implemented into finite element models [10, 11, 12]. Since then, progressive damage simulation in laminates has advanced considerably, due partially to advances in computational technology, but also due to advances in numerical simulation methods. The Virtual Crack Closure Technique (VCCT), which is used to predict energy release rate at a crack tip, is one such method. VCCT is computationally efficient and does not suffer from mesh refinement requirements and convergence difficulties associated with cohesive zone (CZ) models [13], a commonly used alternative method. However, predicting damage initiation is not an inherent capability of VCCT, so, unlike CZ models, an initial crack is required.

Simulating a progressive damage process often requires the consideration of interacting transverse matrix cracks and delaminations. Many state-of-the-art models are combinations of several simulation techniques, including continuum damage mechanics (CDM), the eXtended Finite Element Method (XFEM), VCCT, and CZ [14, 15, 16, 17, 18, 19, 20, 21]. These models, usually necessitating a 3D high-fidelity mesh with at least one element per ply in the thickness direction, can be useful and accurate in some cases, but often the complexity of a real damage scenario, which may consist of dozens of delaminations and matrix cracks, exceeds their capabilities. Additionally, the time and user expertise required for these types of simulations often is only available in research or academic settings.

Use of shell element models may offer an alternative. Shell elements have long been used by industry and have proven to be a cost effective analysis tool, albeit, for problems less complex than laminate damage simulation. Use of shell element models for laminate damage simulation, however, introduces a number of challenges, including prediction and representation of transverse matrix cracks and delaminations at multiple interfaces. Previously, use of shell elements for progressive damage simulation has consisted of either a global-local approach [22], where the actual damage simulation takes place in a high mesh fidelity region attached to an otherwise lower mesh fidelity model; or by stacking layers of shell elements to form a laminate [23, 24, 25, 26, 27].

Ideally, in terms of computational efficiency, ease of use, and predictive utility, a thin laminate plate would be modeled as a single layer of shell elements in which delaminations could form and propagate at any location in the layup. This type of approach can be thought of as having adaptive fidelity, in that the model is defined initially in low-fidelity (one shell element thick) and remains in this state everywhere, except where delamination occurs and multiple mesh layers are required. This requirement, dictated by a damage prediction criterion, may change and be updated throughout an analysis solution procedure as damage grows.

Simulation models based on shell elements that use adaptive fidelity have been proposed and studied only recently. Larsson presented a shell element in 2004 [28] which treats delamination as a discontinuity in the displacement field in a shell formulation and uses a CZ to predict growth. Similarly, Brouzoulis et al. [29, 30, 31] have developed a shell element that uses XFEM and CZs to simulate growth of multiple delaminations and transverse matrix cracks in a shell element. Their work is ongoing, but while showing promise, has not yet advanced to the point of being able to simulate a realistic progressive damage problem of the extent and complexity found in real scenarios.

McElroy presented the formulation of an adaptive fidelity shell (AFS) model for use in progressive damage simulation [32, 33]. The model was verified for mixed mode delamination simulation and validated experimentally using a delamination-migration test. The goal of this paper is to present validation of the AFS model for damage scenarios of a higher complexity level than previously considered. A biaxial-bending test will be utilized to this end. The test was presented by McElroy et al. in Part I of this two-part paper series, in which a damage process consisting of multiple delaminations interacting via transverse matrix cracks occurs in a carbon fiber reinforced polymer specimen [1]. In addition to validation of the AFS model, a high mesh fidelity simulation of the same test is performed to provide insight as to the improvement in efficiency of the shell model, compared to a typical existing state-of-the-art technique.

2. Adaptive Fidelity Shell Model

The AFS element is designed to offer a progressive damage simulation tool that is significantly more efficient than existing alternatives. The efficiency is improved because: (1) the runtime is greatly reduced by use of a composite shell element to represent an entire laminate instead of high-fidelity 3D mesh, and (2) the inherent simplicity of the model allows for a faster model definition and verification procedure by the user.

A thorough description of the AFS model formulation can be found in [32, 33]. The model consists of a four-node Mindlin Shell element enriched with the Floating Node Method (FNM) [34] and a damage algorithm based on the Virtual Crack Closure Technique (VCCT) that are coded in user defined element and external database subroutines for use in Abaqus 6.14/Standard [35]. The element enrichment allows for adaptive mesh fidelity, in which a single element splits into subregions only as required locally, to model an evolving damage process. At any location in the model where damage does not occur, the original discretization remains unaffected and a single shell element is used to represent the entire laminate thickness.

The FNM enrichment can be summarized briefly as follows. “Floating nodes” are embedded in an element definition as extra degrees of freedom (DOF) that have predefined connectivity but are associated initially with zero stiffness. If a discontinuity forms (such as a delamination), the floating nodes can be activated and used as needed to define subregions of material, Ω_A and Ω_B, within an element. (See Figure 1). The creation of subregions does not modify the original global nodal definitions or DOF connectivity. In a solution procedure, DOF associated with floating nodes that are not used are condensed out and not included in the numerical solution of the model.

Figure 1:

Floating Node Method [32].

Figure 1 is an illustration of a shell element formulation enriched with the FNM, where a maximum of two subregions, i.e., one delamination, can exist. Two states are shown, with and without the discontinuity. In the case where a delamination does not exist, the floating nodes are not activated and the element stiffness is based on the entire laminate thickness. In the case where a discontinuity does exist, the floating nodes are activated, and the stiffness of each subregion is based on the thickness of that region of laminate. Conceptually, an element can be defined with as many floating nodes as desired, if representation of more than one delamination is needed. When floating nodes are activated, an offset is applied to the stiffness matrix subregions to account for the fact that each subregion of material has a neutral axis that is different than that of the original element definition [32].

VCCT is used with the enriched shell to predict energy release rates after convergence of each increment in an analysis solution procedure (similar to Orifici et al. [36]). Total mixed mode energy release rate, G_T, is calculated at tied nodal locations on a delamination front [33] using equations for shell elements that were determined by Wang et al. [37]. Mixed-mode critical energy release rate, G_c, is determined using the Benzeggagh-Kenane equation [38]. Delamination growth is predicted as part of the multi-step process described below. In instances where growth occurs at a given location, it is captured in the mesh by releasing a nodal tie between opposing subregions of an element, effectively moving the delamination front at that location ahead by one element length [32].

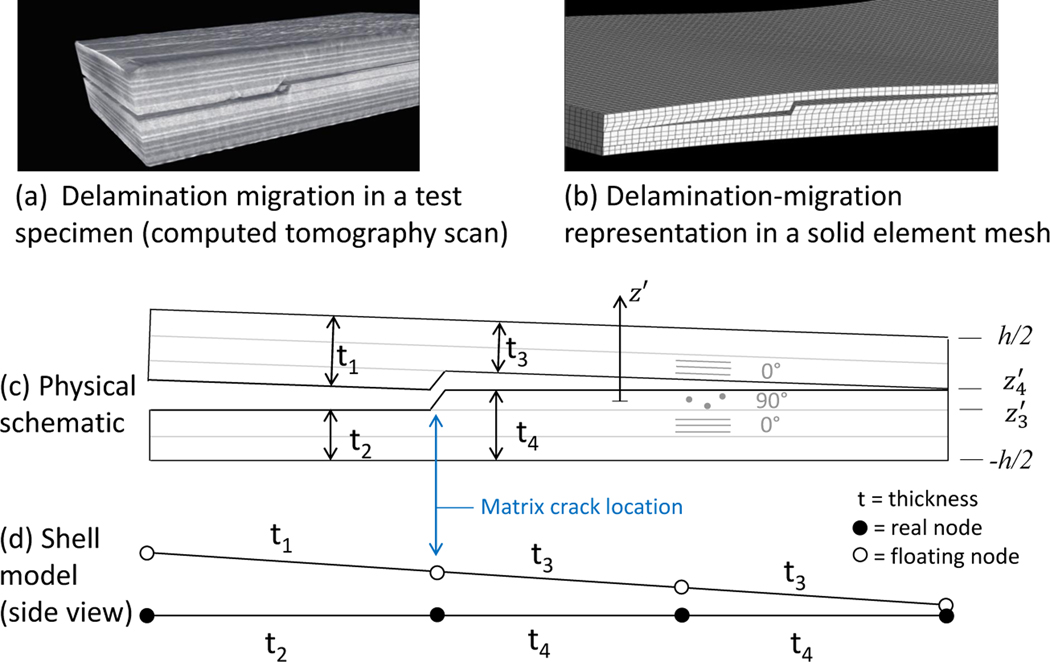
Representation of transverse cracks presents a challenge when using plate or shell elements. Figure 2a shows a computed tomography scan of a composite laminate test specimen in which a delamination, after initial growth at one interface, migrated through a ply, via a transverse matrix crack, to a different interface where it continued to propagate. An example model, shown in Figure 2b, illustrates how this type of damage feature is traditionally represented in a 3D finite element mesh. When using shell elements, a different approach (compared to that shown in Figure 2b) must be taken to represent out-of-plane damage features. The physical schematic in Figure 2c shows a delamination-migration that has occurred in a cross-ply specimen. With the physical schematic as a guide, Figure 2d shows how the transverse crack is represented in the AFS mesh. The transverse matrix crack is not modeled explicitly as a discontinuity in the mesh, but rather the effect of the matrix crack is included in the model as a discontinuity in thickness (i.e., stiffness) between elements.

Figure 2:

Delamination-migration representation in enriched shell model.

Simulations of delamination are usually performed by predefining planes along which damage can evolve. However, the assumption that delaminations remains at a particular plane is not valid in general. The ability to predict whether delamination-migration occurs, or growth continues at the current interface, is necessary for a general predictive model. In between each converged solution increment, a three-step criterion, similar to that used by De Carvalho et al. [39], is used in the AFS model to predict damage growth at each nodal location along a delamination front. In an experiment developed by Ratcliffe et al., the tendency for delamination kinking (i.e., migration) was demonstrated to be related to the sign of the shearing at the delamination front [40, 1]. Figure 3 illustrates how, under alternate +/− shear signs, Mode I microcracks preceding a Mode II delamination would form and be oriented to guide a delamination towards the ply above or below [32].

Figure 3:

Illustration of microcrack orientation as a result of shear sign.

Step I of the damage prediction criterion uses the shear sign at the delamination front to determine the ply (i.e., ply above or ply below), and hence the orientation of fibers, that the delamination has a transverse-growth-tendency towards. Figure 3 illustrates Mode I microcrack orientation resulting from alternate shear signs. In the AFS model, the shear sign is obtained from tie shear forces at nodes along the delamination front. Henceforth, in this report the fibers in the ply that the delamination has a transverse-growth-tendency towards are referred to as “bounding fibers”.

Step II in predicting damage growth consists of an energy-based criterion. A key assumption in how the AFS model handles transverse cracks is that energy dissipated by a such a crack is small compared to energy dissipated by delaminations [1, 41]. It is from this perspective that the following position is taken: it is important to identify the occurrence and location of transverse cracks but it is not necessary to simulate their growth explicitly within a larger delamination-dominated progressive damage process.

In the AFS model, formation of a transverse matrix crack, as in migration, only occurs if that crack is associated with a delamination advance. In Step II of the prediction criterion there are three options within the damage algorithm that may occur at a nodal location under evaluation:

1. no damage growth

   $$G_T<G_c$$ (1)
2. delamination, no migration

   $$G_T>G_c\text{and}{G}_{mig}<G_c^{(tr)}$$ (2)
3. delamination + migration

   $$G_T>G_c\text{and}{G}_{mig}>G_c^{(tr)}$$ (3)

where G_mig and $G_c^{(tr)}$ are the energy release rate and toughness, respectively, that are associated with transverse matrix crack growth. In the AFS model, $G_c^{(tr)}$ is set equal to G_Ic of the matrix material. The quantity, G_mig, is inherently difficult to determine with a shell element model, due to the absence of through thickness mesh discretization. The AFS model includes an assumption that energy release rate associated with shear delamination growth perpendicular to bounding fibers can also be used to predict transverse crack initiation. However, energy release rate is only calculated directly in the AFS model for delamination growth along orthogonal mesh lines. The following methodology, illustrated in Figure 4, uses tie shear forces and VCCT to determine energy release rate at a given nodal location associated with shear delamination growth in a direction defined as perpendicular to bounding fibers.

Figure 4:

Steps to determine energy release rate associated with transverse crack growth, G_mig.

1. VCCT is used to calculate energy release rates, G_IIx and G_IIy, which are associated with shear delamination growth along orthogonal mesh lines parallel to the x and y axes, respectively. Note that in this methodology the mesh is rectangular and aligned with the coordinate system.

2. The vectors Γ_x and Γ_y are defined along the same orthogonal mesh lines and assigned magnitudes equal to the energy release rates associated with delamination growth in their respective orientation (see Figure 4b).

3. The direction of maximum energy release rate, θ, is defined as the direction of the vector sum of the in-plane shear forces, F_x and F_y, at the tied node (see Figure 4a).

4. Energy release rate at the tied node, had it been calculated in the directionin which it is maximum, is assumed to be equal to the magnitude of the vector sum, Γ_T = Γ_x + Γ_y.

5. G_mig is set equal to the magnitude of the component of Γ_T that is perpendicular to the bounding fibers, Γ_mig (see Figure 4c).

This manner of calculating G_mig is not exact and is an attempt at an approximate method for use in a shell element model.

Step III in predicting damage growth is based on recent work where delamination-migration at a given delamination front location was shown to occur under a certain range of the ratio G_II/G_III [42]. Similar observations were made in Part I of this paper [1], in which transverse matrix cracking was seen to occur only under a specific range of relative angles, α, between the shearing direction at a delamination front location and the bounding fibers. The definition of α is illustrated in Figure 5 (see Figure 4c for definition of θ). A critical value, α_c is defined in the AFS model where delamination-migration can only occur if α > α_c.

Figure 5:

Definition of relative angle, α, between the shear force vector at a delamination front location and the bounding fibers.

3. High Mesh Fidelity Model

The high mesh fidelity (HF) model utilizes a previously developed CDM technique [43] combined with a physically-based damage initiation method that is implemented in volumetric elements as a user defined material subroutine (UMAT) in Abaqus 6.14/Standard. Following initiation, progressive damage is captured by introducing a damage variable representing the loss of load carrying area into the constitutive material stress-strain relationship. The HF model was used in this study as an example of a typical state-of-the-art HF approach so that the efficiency offered by the AFS model compared to an existing state-ofthe-art technique could be evaluated.

4. Biaxial-Bending Test Summary

An experiment, inspired by Canturri et al., [44], was designed to create a progressive damage process in a carbon fiber reinforced polymer (CFRP) specimen that consists of 2–3 delaminations growing at different interfaces and interacting with one another via transverse matrix cracks. The specimens, square in shape and containing a quarter circle Polytetrafluoroethylene (PTFE) insert in one corner, were clamped on the two edges opposite the insert. A displacement-controlled quasi-static indentation load normal to the surface was applied to the corner of the specimen containing the pre-existing delamination (i.e., the insert). These loading and boundary conditions result in a biaxial-bending state of deformation in the specimen. The test is illustrated in Figure 6. A thorough description of the test and test results can be found in [1]. Results from quasi-static tests of specimens with two different layups (defined in Figure 6) will be compared to the simulations presented in this paper.

Figure 6:

Test overview and specimen description.

5. Simulation Results

Experimental results from the tests presented previously by McElroy et al. in Part I of this paper [1] are compared to results from the AFS and high mesh fidelity numerical simulations. Each model uses the same geometry, load conditions, and material properties for carbon epoxy system IM7/8552 [1]. The material properties, strength properties, and damage parameters used in the simulations were obtained from Camanho [45] and are shown in Table 1.

Table 1:

Material and strength properties for IM7/8552 [45].

Property	Value	Units	Description
E11	171.4	GPa	elastic modulus
E22 = E33	9.08	GPa	↓
G12 = G13	5.29	GPa
G23	3.9	GPa
ν12 = ν13	0.32	-	Poisson’s ratio
ν23	0.45	-
XT	2326.0	MPa	lamina longitudinal tensile strength
$Y_T^{is}$	129.3	MPa	lamina transverse tensile strength
$S_T^{is}$	112.8	MPa	lamina transverse shear strength
$S_L^{is}$	92.82	MPa	lamina longitudinal shear strength
GIc	0.277	kJ/m2	mode I critical energy release rate*
GIIc	0.787	kJ/m2	mode II critical energy release rate*
ηBK	2.1	-	Benzeggagh-Kenane (BK) law exponent

^*The G_c values were obtained from a 0°/0° interface.

O’Brien et al. investigated an apparent increase in Mode II toughness at the point of onset when a delamination begins from a thin insert representing a pre-existing delamination [46]. This investigation involved testing in which effectively, scaling factors for the Mode II critical energy release rate, G_IIc were determined. O’Brien et al. observed an increase in G_IIc at the boundary of an insert of an average factor of 1.59 in the tests performed. In the AFS model, G_IIc was multiplied by 1.59 in cases where (1) the node is located on the pre-existing delamination boundary and (2) damage initiation consists of delamination that remains at the pre-existing delamination interface. If delamination-migration occurs from a node on the pre-existing delamination boundary, the G_IIc multiplier is not used. This exception is in line with experimental findings by Olsson et al. where Mode II delamination toughness beginning from a thin insert was seen to be lower in cases where delamination-migration occurs than in cases where delamination initiates and remains in-plane [47].

5.1. Adaptive Fidelity Shell Simulation

Figure 7 is an overview of the AFS model. The clamped boundary condition was captured by iteratively adjusting rotational springs on two edges until the slope of the force-displacement curve matched that of the elastic region of the test results. The indentation load was applied via the prescribed displacement of an analytical rigid hemispherical surface that has a radius of 76 mm, matching the indenter tip used in the experiment. Contact between the indenter surface and the shell elements is defined using the built-in Abaqus 6.14/Standard surface-to-surface contact feature. For elements that contain the pre-existing delamination, contact is defined between the upper and lower element subregions using nodal ties enforced in the z-direction (i.e., normal) only. Elsewhere in the model, if an element is split, contact is defined between subregions using the built in Abaqus 6.14/Standard surface-to-surface contact feature between real and floating nodes with a coefficient of friction of 0.74 [48]. The model has 1521 elements and a runtime on a PC using one core and 0.17 GB of RAM of 36 minutes. The parameter α_c was set equal to 55° (see Section 2 and Figure 5). The basis for this value can be found in Part I of this paper where test results showed that transverse matrix cracks form in regions of the specimen where α >55° [1].

Figure 7:

Overview of the AFS model.

Force-displacement results from the AFS model and from the experiment for a Layup 1 (see Figure 6) specimen are shown in Figure 8. As in the experiment, the model undergoes an initial elastic response, followed by nonlinear behavior caused by delamination initiation and growth. There is a good correlation between the AFS model and the experimental force-displacement data, though generally, the forces are under-predicted slightly by the model. An error of 8.9% was observed between the predicted delamination initiation force and the test average. This slight under-prediction was observed previously for the AFS model and may be the result of the manner in which VCCT is applied on the “stepped” or “jagged” delamination front as it is represented in the rectangular mesh [32].

Figure 8:

Force-displacement correlation between tests and the AFS model (Layup 1).

Shown in Figure 9 are ultrasonic test (UT) scans from a representative Layup 1 test specimen and a plot from the AFS simulation showing delamination predictions. Two delaminations grew during the test from the PTFE insert, at the two interfaces identified in Figure 9b. In the region of the PTFE border near the lower edge of the specimen, the delamination migrated immediately down to interface 1 and then continued to grow at that interface, bounded below by 0° fibers. In the region of the PTFE near the right hand edge of the specimen, the delamination grew in the 90° direction and remained at that same interface (interface 0) bounded below by 90° fibers. Both delaminations grew simultaneously along a transverse matrix crack through the 90° plies from interface 0 to interface 1, as shown in Figure 9b. The transverse matrix crack began as the initial migration from the PTFE film.

Figure 9:

Qualitative correlation of delamination size and damage pattern (Layup 1).

There is a good correlation between the AFS Layup 1 model results and the test. Qualitatively, the delaminations and transverse matrix cracks form a damage pattern that matches the experiment. The delamination size predicted by the model is slightly larger than that of the experiment for the same indentation of δ=2.18 mm. This observation supports the previous observation that the model slightly under predicts the strength [32]. A second delamination-migration is predicted by the model to occur from interface 1 to interface 2 that did not initially appear in the tests. To investigate further, a test was performed where the indentation depth was increased to 3.17 mm for one specimen. Shown in Figure 9c is a UT scan of delamination resulting from this extended indentation. The second delamination-migration from interface 1 to interface 2 does in fact occur; the AFS model just tends to predict this event early.

The amount of delaminated area at interface 0 and at interface 1 are shown in Figure 10. Included are data from all of the Laypup 1 tests (6 specimens total) and the prediction from the AFS model. Linear interpolations are curve fit to the experimental and simulation data sets to aid in comparison between the two. Again, the results of the AFS model agree well with the experiments, but predict growth to occur earlier than the test.

Figure 10:

Quantitative correlation of delamination size (Layup 1).

The AFS model was also used to simulate damage observed in the biaxial-bending test in specimens with Layup 2 (see Figure 6). Two parameters were changed in the model formulation for the Layup 2 simulation: the rotational spring stiffness on the boundary conditions was reduced from 95 N·m/rad to 65 N·m/rad and α_c was reduced from 55° to 50°. It was necessary to change these parameters to obtain the closest match possible to the experimentally observed specimen response and damage pattern. The change in rotational spring stiffness indicates that boundary conditions are not well captured in the shell model, but the method used, after calibration, is assumed to be adequate. The modification of α_c is indicative that the delamination-migration criterion is not general and in its current form could be sensitive to layup. The Layup 2 force-displacement correlation is shown in Figure 11. The AFS model results qualitatively have the same behavior as the test, but the predicted force at delamination is 28% lower than that of the test average. Some amount of force under-prediction is to be expected, based on previous verification and validation of the AFS model [32], but the magnitude of error seen in Figure 11 is indicative that there may be an additional mechanism not accounted for in the model (see further discussion in Section 5.2).

Figure 11:

Force-displacement correlation between tests and the AFS model (Layup 2).

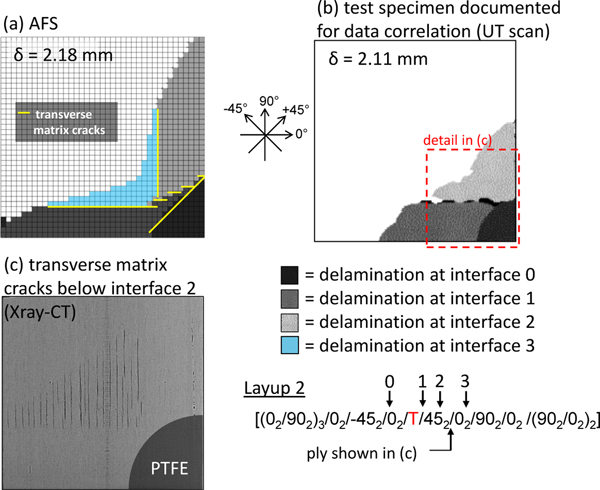
A comparison between delamination patterns predicted by the AFS model and those observed from testing is shown in Figure 12. Delaminations grew during the test from the PTFE insert at interfaces 1 and 2, as shown in in Figure 12. In the region of the specimen near the lower edge, migration occurred through the 45° plies via a transverse matrix crack that was arrested by fibers in the 0° ply. A delamination continued from this location on interface 1. In the region of the specimen near the right hand side of the specimen, “staggered migration” occurred via multiple matrix cracks through two ply blocks of differing fiber orientation. The “staggered migration” here consists of a transverse matrix crack oriented along the 45° fibers, extending down to interface 1. Below this crack are transverse matrix cracks running parallel to the 0° fibers, extending down to interface 2. Delamination growth continued from the staggered migration at interface 2. Connecting the delaminations at interfaces 1 and 2 is a transverse matrix crack.

Figure 12:

Qualitative correlation of delamination size and damage pattern (Layup 2).

It is evident in Figure 12a that the AFS model predicts a delamination to form at interface 3. The delamination at interface 3 was not observed during experimentation; however, upon closer inspection, using the X-ray computed tomography (CT) image in Figure 12 of the ply below interface 2, transverse matrix cracks are seen to have formed in the same region where the AFS model predicts the interface 3 delamination. This shows that the model is predicting the formation of these same matrix cracks correctly; however, the model incorrectly predicts the first instance of the transverse cracks to continue growth and complete the delamination-migration process. Other than this discrepancy, the AFS model qualitatively predicts the same damage pattern that was observed in testing.

5.2. AFS Model Limitations

One goal of the biaxial-bending simulation exercise was to identify and articulate limitations of the AFS formulation in order to guide future research and model improvements. One such limitation has to do with damage initiation. While inclusion of an initial delamination is necessary in the current AFS formulation, future versions of the model could be enhanced to overcome this limitation. Methodologies are currently under development that predict three-dimensional ply level stresses in shell elements for use in a stress-based damage initiation technique [49, 50]. The AFS model could potentially integrate this type of damage initiation technique and use it as a basis for inserting delaminations.

Another limitation has to do with the delamination-migration prediction methodology. Although it is important to know when and where transverse matrix cracks form in a progressive damage process in order to predict delamination-migration, there appears to be an additional mechanism involved during delamination-migration that requires more energy to complete the process, for which the AFS model does not account. According to the Layup 2 UT scan in Figure 12, the AFS model predicts the delamination-migration at and near the PTFE insert correctly; however, the critical force level comparison in Figure 11 shows that the Layup 2 model predicts delamination-migration to occur with a lower amount of force than the test. The force-displacement correlation in Layup 1 may have been a closer match because delamination-migration on the PTFE boundary occurred in one small region near the edge and played less of a role at the initiation of damage compared to Layup 2. The mechanism that the AFS is not capturing may be related to a phenomenon observed in previous work [51], in which transverse crack growth was seen to slow when the crack tip approaches an interface with a stiffer material. In the context of progressive damage in a laminate, a ply of differing fiber orientation behaves as a stiffer material.

Delamination-migration appears to be more complex than simply formation of a transverse matrix crack. In the AFS model, the parameters G_mig and α_c are each central to a two-part prediction criterion for delamination-migration (i.e., Step II and Step III). The parameter α_c, determined based on physical observations, seems well suited for prediction of transverse matrix cracks. However, α_c should be independent of the layup and this could be realized if the method to calculate G_mig were improved to effectively capture, more accurately, the energetic distinction between transverse crack formation and delamination-migration.

5.3. High Fidelity Simulation

Figure 13 is an overview of the HF model. The mesh configuration varies throughout the model. The model is meshed in the thickness direction using one volumetric element per ply in regions away from the PTFE insert and with three volumetric elements per ply in the region near the PTFE. In the finely meshed region near the insert, the CDM UMAT is defined using first-order reduced-integration solid elements (C3D8R) that have a size of approximately 0.2 mm. Elsewhere, a linear elastic material model is defined using reduced integration continuum shell elements (SC8R) that range in size up to 1 mm on the in-plane edges. Cohesive zones are defined on interfaces 0 and 1 (see Figures 6 and 14) throughout the model, using the fracture and strength parameters shown in Table 1. A multiplying factor of 1.59 is applied to a strip of elements 1 mm wide along the PTFE boundary. A coefficient of friction of 0.74 [48] is used between sliding delamination surfaces outside of the PTFE region. The HF model has a total of 187,755 elements and a runtime using one CPU and 0.9 GB of RAM of 55 hours. Details illustrating the mesh, material models, and cohesive zones are presented in Figure 14. Only Layup 1 was considered using the HF model.

Figure 13:

Overview of the HF model.

Figure 14:

Material regions in the HF model.

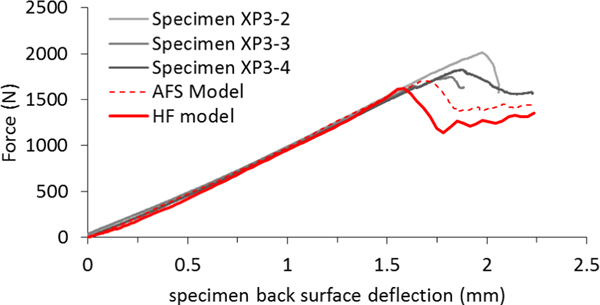
Force-displacement data from the HF model are plotted in Figure 15 (the AFS data are included as well, for reference). Like the AFS model, damage is predicted to initiate slightly before the load seen in the test. The HF model’s predicted delamination initiation force has an error of 13.2% compared to the test average. Predicted delamination plots from the HF model are compared to experimental UT scans in Figures 16a-16c. The transverse matrix crack is shown in Figure 16d, where elements colored red indicate that the stiffness is fully degraded. A correlation of delamination size versus indentation is made in Figure 17 (again the AFS data are included also for reference). Although qualitatively the damage process in the HF model matches that of the experiments, the delaminations in the HF model are shown to initiate late and grow too fast.

Figure 15:

Force-displacement data from the HF model, the AFS model, and the experiments.

Figure 16:

HF model delaminations and matrix crack predictions.

Figure 17:

Delamination area versus indentation from the HF model, the AFS model, and the experiments.

The HF model did successfully simulate the progressive damage process seen in the experiments in a qualitative sense. The accuracy in terms of delamination size and growth rate is similar to that of the AFS model. A stark distinction in computational efficiency is evident between the HF model and AFS model.

The runtime of the HF model was approximately 92 times that of the AFS model. The reasons for the long runtime in the HF model are thought to be a combination of the number of elements, the use of cohesive zones, and the use of a CDM material model. Similarly, the time to prepare the HF model was also much longer than that required for the AFS model; however, this comparison can be somewhat subjective and more difficult to quantify.

6. Conclusion

An enriched shell element model was used to efficiently simulate a progressive damage process in a composite laminate. A high mesh fidelity CDM finite element model was also used to simulate the test and provide an indication of the increase in efficiency offered by the shell model compared to a typical existing method. The numerical results were compared to an experiment which was designed to create 2 to 3 delaminations occurring at different interfaces and interacting via matrix cracks in a laminate.

The enriched shell model, referred to as the adaptive fidelity shell (AFS) model, is based on use of the Floating Node Method and the Virtual Crack Closure Technique. The AFS model proved to be accurate in simulating damage seen in Layup 1. In Layup 2, the AFS model generally captures the damage process in a qualitative sense, but predicts growth to occur early and continue to an interface not seen in the test. This discrepancy may be due to a mechanism that exists in which the growth of a transverse crack tends to slow when the crack tip approaches an interface with a ply of differing fiber orientation. This mechanism is not accounted for in the AFS model. More investigation is needed to understand what enhancements can be made to the shell enrichment to better capture the delamination-migration process.

The high-fidelity (HF) model is based on a continuum damage approach that degrades material stiffness properties after a physically-based failure criterion is met. The HF model, used in this study as representative of an existing typical state-of-the-art simulation tool, was only used to simulate damage in Layup 1. It was successful in a qualitative sense, but was not accurate in terms of the delamination growth rate. The HF model takes approximately 55 hours to run using 1.0 GB of RAM on one core, compared to the AFS model that takes 36 minutes to run on one core with 0.17 GB of RAM. This significant difference in efficiency (two orders of magnitude) indicates that the AFS model, or other similar models, may prove to be a cost effective progressive damage simulation tool.