Atomic-scale spin-polarization maps using functionalized superconducting probes

Functionalized STM tips can map the spin polarization of nanomagnets quantitatively with atomic spatial resolution.

Abstract

A scanning tunneling microscope (STM) with a magnetic tip that has a sufficiently strong spin polarization can be used to map the sample’s spin structure down to the atomic scale but usually lacks the possibility to absolutely determine the value of the sample’s spin polarization. Magnetic impurities in superconducting materials give rise to pairs of perfectly, i.e., 100%, spin-polarized subgap resonances. In this work, we functionalize the apex of a superconducting Nb STM tip with such impurity states by attaching Fe atoms to probe the spin polarization of atom-manipulated Mn nanomagnets on a Nb(110) surface. By comparison with spin-polarized STM measurements of the same nanomagnets using Cr bulk tips, we demonstrate an extraordinary spin sensitivity and the possibility to measure the sample’s spin-polarization values close to the Fermi level quantitatively with our new functionalized probes.

INTRODUCTION

Spin-polarized scanning tunneling microscopy (SP-STM) and spectroscopy (SP-STS) exploit the tunneling magnetoresistance between two spin-polarized electrodes, the sample and the STM tip, separated by a vacuum barrier (1) as shown in Fig. 1A. A bias voltage V is applied, shifting the Fermi energies E_F of the sample and tip by an amount eV. This results in a net current, which is large in the case of parallel alignment (↑↑) of the dominating spin species in the density of states (DOS) of the tip and in the local density of states (LDOS) of the sample, evaluated at the tip apex position ${\overrightarrow{\mathbf{r}}}_{\mathbf{t}}$ in the energy window of tunneling but small for antiparallel alignment (↑↓), realized, e.g., by using an external magnetic field B_z. The resulting asymmetry $A_{\text{SP}}(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ in the measured spin-resolved differential tunneling conductance dI/dV(V) is approximately given by the product of the spin polarizations of tip ${\mathcal{P}}_{\mathrm{t}}(E_{\mathrm{F}})$ and sample ${\mathcal{P}}_{\mathrm{s}}(E_{\mathrm{F}}+\mathrm{eV},{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ (2)

$$\begin{array}{cc}\hfill A_{\text{SP}}(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})& =\frac{\mathrm{d}I/\mathrm{d}V(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}}){\mid {}_{\uparrow \uparrow }-\mathrm{d}I/\mathrm{d}V(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})\mid }_{\uparrow \downarrow }}{\mathrm{d}I/\mathrm{d}V(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}}){\mid {}_{\uparrow \uparrow }+\mathrm{d}I/\mathrm{d}V(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})\mid }_{\uparrow \downarrow }}\hfill \\ & \approx {\mathcal{P}}_{\mathrm{t}}\left(E_{\mathrm{F}}\right)·{\mathcal{P}}_{\mathrm{s}}(E_{\mathrm{F}}+\mathrm{eV},{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})\hfill \end{array}$$ (1)

Fig. 1. Concept of SP-STM and YSR-SP-STM.

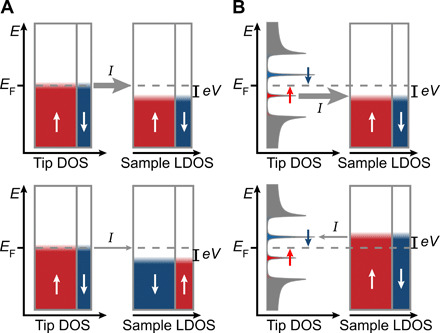
(A) Schematic drawing of the concept of a conventional SP-STM experiment. The spin-resolved tip DOS and sample LDOS are assumed to be energy independent for simplicity. The thickness of the vertical arrows indicate the strength of the main contribution to the tunnel current. Between the top and the bottom panel, the sample magnetization has been reversed, which enables a measurement of the tunneling magnetoresistance effect. (B) Schematic drawing of the concept of a YSR-SP-STM experiment. A single YSR state in the gap of a superconducting tip that is magnetized, e.g., by an external magnetic field, is assumed for simplicity. Between the top and the bottom panel, the bias polarity has been reversed, which enables the measurement of the absolute value of the sample’s spin polarization. Note that there is an intrinsic asymmetry in the intensity of the ↑ YSR state with respect to the ↓ YSR state that is unrelated to magnetism.

This emphasizes the crucial role of a large tip spin polarization. Along these lines, a large number of studies using different tip materials have been performed (1). These include half-metallic ferromagnets (3), bulk 3d transition metals (4, 5), thin films of 3d transition metals (6), or soft magnetic tips periodically magnetized in opposite directions along the tip axis by a small coil (7). For instance, Cr tips feature a low stray field, but the values for their spin polarization are only as large as 10 to 20%, depending on the specific tip apex (1). In addition, because ${\mathcal{P}}_{\mathrm{t}}(E_{\mathrm{F}})$ is usually a priori unknown for most of the common materials, conventional SP-STS cannot be used straightforwardly to measure absolute values of ${\mathcal{P}}_{\mathrm{s}}(E_{\mathrm{F}}+\mathrm{eV},{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$. Tip materials with a well-known spin polarization ${\mathcal{P}}_{\mathrm{t}}(E_{\mathrm{F}})$ can be hard to implement experimentally [such as optically pumped gallium arsenide (GaAs) (8, 9), requiring optical access to the tunneling junction] or require large magnetic fields on the order of a few tesla, thereby considerably perturbing the sample’s magnetic state (10). Last, it is not straightforward to disentangle the magnetoresistive change in tunneling conductance from locally varying electronic contrast of the sample.

Yu-Shiba-Rusinov (YSR) states induced by magnetic impurities in superconductors (11–13) have gained renewed interest in the past years, mainly with the focus to realize topological superconductors and Majorana bound states in one- or two-dimensional arrays of such impurities (14–19). Yet, another interesting feature of these bound states is their perfect, i.e., 100%, spin polarization (20–22), naturally raising the question whether it is possible to use them as a probe for the spin polarization of an unknown sample under investigation.

Along these lines, our idea of a novel “YSR-SP-STM” method is sketched in Fig. 1B: A pair of entirely spin-polarized YSR subgap resonances can appear in the DOS of a superconducting tip, which is experimentally realized by picking up magnetic atoms to the tip apex and magnetizing these atoms with an external magnetic field B_z (23). The energetic position of both peaks is determined by the exchange interaction strength of the impurity spin with the Cooper pairs in the superconductor. Unlike on an ordered surface, the adsorption positions of adatoms on an STM tip can be manifold. It is therefore possible to realize almost arbitrary energetic positions of the tip YSR states. They always appear in pairs at E_F ± ε with a particle-like state (labeled e and ↑ in the following) and a hole-like state (labeled h and ↓). With increasing exchange coupling of the impurity to the host superconductor, the YSR states shift in energy, starting from the superconducting gap edge Δ_tip. They eventually cross at E_F and shift toward −Δ_tip again. At the crossing point, they undergo a quantum phase transition (QPT) (14, 21, 24).

On the other side of the junction, the partially spin-polarized LDOS of the sample is probed. For the case e ∙ V = E_{YSR, ↑} (Fig. 1B, top), tunneling from the ↑ YSR state to the sample is allowed and results in a large tunneling conductance if this state and the spins dominating the sample’s LDOS are aligned (↑↑). With the reversed voltage e ∙ V = E_{YSR, ↓,} tunneling in this setup from the sample to the ↓ YSR state in the tip is less probable because there are fewer spin-down electrons available in the sample’s LDOS. In consequence, the asymmetry $A_{\text{YSR}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ in the intensities a_e and a_h of the two YSR peaks observed in dI/dV measurements will change according to their spin’s relative alignment to the local dominating sample spin direction according to

$$A_{\text{YSR}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})=\frac{a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})-a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})}{a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})+a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})}\approx {\mathcal{P}}_{\mathrm{s}}(E_{\mathrm{F}},{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$$ (2)

In the last equation, we have hypothesized a perfectly spin-polarized pair of YSR states and assumed that the LDOS is largely energy independent in a small energy window around E_F, which is the case for many sample systems of interest. The technique, thus, features several advances compared to traditional SP-STM: Most notably, the perfect spin polarization of the probe gives maximized spin contrast and can allow for a quantitative measurement of spin polarization of the vacuum LDOS above the sample around the Fermi level. It also facilitates the distinction of spin contrast and electronic contrast, as the asymmetry of peaks A_YSR on the micro–electron volt scale is unlikely to be strongly affected by a local change in the nonmagnetic LDOS. Furthermore, it enables the use of superconducting tips providing excellent energy resolution below the Fermi-Dirac limit for spin-polarized measurements. In the following, we experimentally demonstrate that we can realize this technique with a pair of highly spin-polarized YSR states using a Nb-coated W-tip with Fe atoms attached to the apex as a YSR probe and a clean Nb(110) surface with Mn nanomagnets as a sample.

RESULTS

All experiments were performed under ultrahigh-vacuum conditions (p < 2 × 10⁻¹⁰ mbar) in a home-built STM setup at a temperature of T = 300 mK (25). We study a clean Nb(110) surface (26) with Mn and Fe adatoms to characterize the magnetic imaging of our STM tips (see Materials and Methods). Additional information on the preparation of the sample can be found in (27). The Mn and Fe adatoms adsorb on the fourfold coordinated hollow sites of the (110) lattice of surface Nb atoms, as shown in Fig. 2A. Using STM tip–induced single-atom manipulation at typical tunneling resistances of R = 60 kilohms, the Mn atoms can be moved to the desired positions on the Nb(110) surface. In this way, artificial chains with arbitrary interatomic distances and in different crystallographic directions can be constructed. The magnetic ordering in such chains is expected to be strongly affected by these geometric properties, due to the oscillatory behavior of the mediating Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction (28–30). Using the lattice constant of the (110) surface a, we introduce the following nomenclature for referencing to the distance of the nearest neighboring atoms in the three different investigated chains and their orientations (Fig. 2A): 1a − [001], 2a − [001], and $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$. As we will prove in the following experimentally via SP-STS using bulk Cr tips [see (27) for tip preparation procedures], 2a − [001] and $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ chains exhibit an antiferromagnetic spin structure, whereas the 1a − [001] chains are ferromagnetic.

Fig. 2. Conventional SP-STM on chains along different crystallographic directions using a Cr bulk tip.

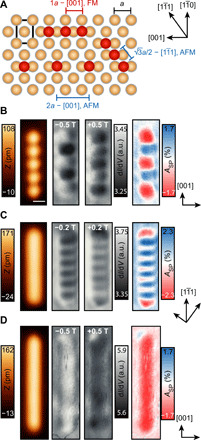
(A) Sketch of the uppermost Nb(110) layer (brown) with Mn adatoms (red) on hollow sites. Using STM tip–based atom manipulation, the adatoms can be arranged with different options for interatomic spacings and crystallographic directions, which strongly affects their magnetic coupling (FM, ferromagnetic; AFM: antiferromagnetic). (B) Constant-current STM image of a 2a − [001] Mn₅ chain, the corresponding dI/dV maps in opposite external magnetic fields B_z, and the calculated A_SP. dI/dV is measured in arbitrary units (a.u.). Scale bar, 500 pm. (C) Constant-current STM image of a $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ Mn₁₃ chain, the corresponding dI/dV maps in opposite external magnetic fields B_z, and the calculated A_SP. (D) Constant-current STM image of a 1a − [001] Mn₁₅ chain, the corresponding dI/dV maps in opposite external magnetic fields B_z, and the calculated A_SP. All images share the same scale. Parameters: V = −5 mV, I = 1 nA, and V_mod = 2 mV for (B) and (C) and V = −6 mV, I = 1 nA, and V_mod = 2 mV for (D).

As a first example, a 2a − [001] Mn₅ chain was constructed (Fig. 2B). Such arrays of weakly RKKY-coupled atoms on metallic surfaces are known to have a very short lifetime of degenerate spin states, and we do not expect any magnetic contrast in zero field (29). Therefore, to stabilize the spin structure of the chains, an external magnetic field of −0.5 T is applied perpendicular to the sample surface in the ↓ direction. Assuming an antiferromagnetic chain consisting of an odd number of atoms, the ↑ ↓ ↑ ↓ ↑ spin configuration is expected to be favored over the ↓ ↑ ↓ ↑ ↓ configuration by Zeeman energy. We find an alternating contrast along the chain when mapping the differential tunneling conductance dI/dV (Fig. 2B). Reversing the magnetic field polarity also inverts the contrast as expected if we have a stable magnetization of the tip while the chain magnetization aligns paramagnetically with the field. This behavior is, thus, consistent with the assumption of a chain of antiferromagnetically RKKY-coupled atoms (29). The total change in magnetic contrast can be seen in the asymmetry map $A_{\text{SP}}(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ on the right side of Fig. 2B. Neighboring atoms clearly exhibit alternating signs in the spin asymmetry, proving antiferromagnetic coupling between the neighboring atoms for this particular chain type. In the same fashion, $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ Mn₁₃ chains (Fig. 2C) and 1a − [001] Mn₁₅ chains (Fig. 2D) have been studied. For the former, we again find an alternating contrast between adjacent atoms, which is inverse when reversing the external magnetic field, clearly indicating a dominant antiferromagnetic nearest neighbor coupling in the chain. The latter exhibits no clear contrast along the chain (Fig. 2D). However, the dI/dV signal changes from bright to dark in B_z = ±0.5 T. This is apparently visible in the corresponding asymmetry map, revealing a ferromagnetic ordering along this chain type.

With this knowledge about the spin structures of the various chains, we can probe similar structures with a tip hosting YSR states in a next step. Superconducting tips were obtained by indenting an electrochemically etched W-tip into the Nb(110) surface for several nanometers. The resulting superconducting cluster of the tip exhibits a much higher critical field B_c than the sample due to its finite size, and it is only weakly affected by the applied magnetic fields of B_z = 0.5 T (see Fig. 3B, gray, and fig. S3), whereas the Nb(110) sample is in the normal conducting state [B_c,2,Nb = 0.4 T (31)]. It is even preferable to keep the sample in the normal conducting state for this experiment because vortices or YSR states in the sample would strongly hamper the interpretation of dI/dV spectra obtained with a YSR tip. Subsequently, magnetic atoms were picked up from the sample surface by lowering the tip close to the atom, applying a voltage pulse of 2 V, and retracting the tip back to normal tunneling conditions. One example can be seen in Fig. 3A, showing a series of images where two Fe atoms are transferred to the tip. The atoms are likely to be located on the tip apex as the imaging quality of the tip is improved, comparing the observed shape of the Mn atom between the right and the left image. As a result, the tip DOS now features two additional in-gap states (Fig. 3B, red). Assuming that the Nb substrate in the normal state features a nearly flat LDOS within a few milli–electron volts around the Fermi level, we can conclude that we measure only the tip DOS in the dI/dV spectroscopy to a good approximation. These states can thus be interpreted as YSR states of the Fe₂ impurity locally perturbing the superconducting tip material. Note that the particle- and hole-like peaks in these spectra measured on the nonmagnetic substrate already have an intrinsic asymmetry in the intensities, which we name $a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})$ and $a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})$, respectively. This is a well-known effect of an additional nonmagnetic scattering term at the impurity (20, 21, 32). The intrinsic asymmetry is quantitatively evaluated by a fit of two Lorentzian distributions to the subgap energy values in the dI/dV spectra (see fig. S2). The resulting peak heights have a ratio of $a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})/a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})=1.82\pm 0.04$.

Fig. 3. Picking up two Fe atoms onto a Nb tip and demonstrating out-of-plane magnetic contrast.

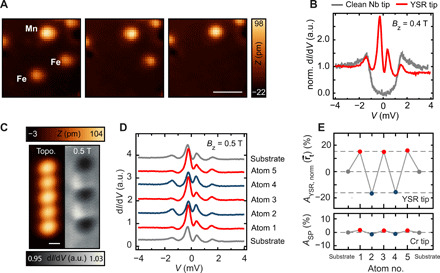
(A) Constant-current STM images before (left two images) and after picking up the two indicated Fe atoms (right image) onto the tip (V = 6 mV and I = 2 nA). Scale bar, 2 nm. (B) dI/dV spectra taken on the normal conducting Nb(110) substrate in an external field of B_z = 0.4 T with (red) and without (gray) Fe atoms attached to the tip (V_stab = −10 mV, I_stab = 2 nA, and V_mod = 100 μV for the YSR tip and V_stab = −6 mV, I_stab = 1 nA, and V_mod = 20 μV for the clean Nb tip). (C) Constant-current STM topography (left) and the corresponding dI/dV map (right) of an antiferromagnetic 2a − [001] Mn₅ chain measured at B_z = 0.5 T and stabilized outside of the superconducting gap (V_stab = −10 mV, I_stab = 2 nA, and V_mod = 3 mV). Scale bar, 0.5 nm. (D) dI/dV spectra taken on the substrate and on the five atoms of the chain (V_stab = −10 mV, I_stab = 2 nA, and V_mod = 100 μV) with the YSR tip in an external field of B_z = 0.5 T. The spectra are vertically offset for clarity. (E) Asymmetry $A_{\text{YSR},\text{norm}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ of the YSR peaks in (D) calculated from Eq. 3 (top) compared to the spin asymmetry $A_{\text{SP}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$ obtained with the Cr tip (bottom) using the data from Fig. 2B and averaging across the atoms and a substrate position. The off-zero dashed gray lines mark the average YSR asymmetry measured on ↑ and ↓ atoms.

With this tip, we were able to assemble various magnetic Mn chains, starting with a structurally identical 2a − [001] chain as it has been presented in Fig. 2B. A dI/dV map at B_z = 0.5 T (Fig. 3C) reproduces the clear alternating antiferromagnetic contrast between neighboring chain atoms, demonstrating a strong out-of-plane magnetic contrast of the tip. The dI/dV spectra of the tip YSR states obtained with this tip stabilized above the five chain atoms (Fig. 3D) reveal a strong change in asymmetry of the peak heights when tunneling between the tip’s YSR states and the Mn atoms along the chain magnetized in opposing directions. This asymmetry can now directly be attributed to spin-polarized tunneling. In the following, we define the YSR asymmetry $A_{\text{YSR},\text{norm}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})$, which has been normalized to account for the intrinsic YSR asymmetry, as

$$A_{\text{YSR},\text{norm}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})=\frac{a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})/a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})-a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})/a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})}{a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})/a_{\mathrm{e}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})+a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}})/a_{\mathrm{h}}({\overrightarrow{\mathbf{r}}}_{\mathbf{t}}=\text{sub})}$$ (3)

From the previous study with the Cr tip, we know that the spin structure of the chain is anti-aligned with the external field and reads ↓ ↑ ↓ ↑ ↓ for positive B_z. The tip apex consists of only two magnetic atoms on a metallic tip material whose spin will probably fully anti-align with a field of strength B_z = ± 0.5 T as well (↓) (33). A plot of A_{YSR, norm} against the spatial position on the chain is shown in Fig. 3E. For parallel alignment of tip and sample magnetization, which is the case for atoms 1, 3, and 5, we find a normalized YSR peak asymmetry of A_{YSR, norm}(1,3,5) = (15.2 ± 0.5)%. For antiparallel alignment on atoms 2 and 4, the asymmetry correspondingly equals A_{YSR, norm}(2,4) = ( − 16.4 ± 0.7)%. Obviously, A_{YSR, norm} resembles the asymmetry map obtained with conventional SP-STM (Fig. 2B), which is plotted in the bottom panel of Fig. 3E for direct comparison. However, we find several striking differences. (i) When comparing the absolute values, we obtain a signal being larger by one order of magnitude using the YSR-SP-STS method with respect to conventional SP-STS. (ii) For the former, we can distinguish between magnetic and nonmagnetic contrast without reversing the magnetic field, while this is not possible for conventional SP-STS. What remains to be proven is the atomic spatial resolution of YSR-SP-STS. The interatomic distance in the 2a − [001] Mn₅ chain studied in Fig. 3 equals 660 pm, which is well above typical lattice constants of investigated single crystals. Therefore, we again built the densely packed $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ Mn₁₅ (Fig. 4A, 285 pm interatomic distance) and 1a − [001] Mn₁₅ chains (Fig. 4B, 330 pm interatomic distance) with the YSR tip to compare the results with those obtained with the bulk Cr tip from Fig. 2 (C and D, respectively). Evaluating A_{YSR, norm} for the two cases, we find an alternating signal on the $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ Mn₁₅ chain (Fig. 4A), indicating antiferromagnetic ordering. Moreover, we find a homogeneous signal strength on the 1a − [001] Mn₁₅ chain, indicating ferromagnetically aligned spins (Fig. 4B). Both results reproduce the magnetic structures found in Fig. 2 (C and D) but yield much larger signal magnitudes, thereby demonstrating that substantial spin contrast can be obtained by the YSR-SP-STS technique even for densely packed structures on the atomic scale.

Fig. 4. Magnetic YSR contrast on densely packed adatom structures.

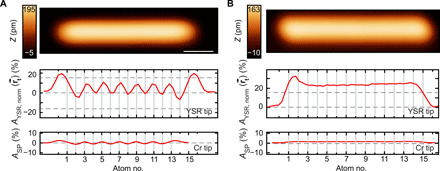
(A) Constant-current STM image of a $\frac{\sqrt{3}a}{2}-[1\overline{1}1]$ Mn₁₅ chain and the YSR asymmetry measured along the chain. The bottom panel shows the contrast obtained with a Cr tip on the similar Mn₁₃ chain of Fig. 2C. Scale bar, 1 nm. (B) Constant-current STM image of a 1a − [001] Mn₁₅ chain and the YSR asymmetry measured along the chain. The bottom panel shows the contrast obtained with a Cr tip on the same Mn₁₅ chain in Fig. 2D. The nonzero dashed gray lines mark the average YSR asymmetry measured on ↑ and ↓ atoms from Fig. 3E. All data were measured with V_stab = −10 mV, I_stab = 2 nA, V_mod = 100 μV, and B_z = 0.5 T.

DISCUSSION

We lastly discuss the proposed possibility to measure the absolute values of the sample’s spin polarization using YSR-SP-STS data (Eq. 2). Assuming that the magnetic field of strength B_z = ± 0.5 T was able to fully saturate the Fe₂ cluster on the tip, the measured spin polarization on the 2a − [001] Mn₅ chain would equal ${\mathcal{P}}_{\mathrm{s}}(E_{\mathrm{F}},{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})=15.8\%$. Considering Eq. 1 and the asymmetry measured by conventional SP-STS on the same chain of $A_{\text{SP}}(V,{\overrightarrow{\mathbf{r}}}_{\mathbf{t}})=1.7\%$, we obtain a spin polarization of 𝒫_t(E_F) = 9.3% for the Cr tip used in Fig. 2 (B and C), which is a reasonable value for bulk Cr tips (1). Similar ratios are found for the examples in Fig. 4. The only reason for a nonperfect spin polarization of the tip states in YSR-SP-STS would be the existence of multiple YSR states that cannot be distinguished due to our energy resolution (25, 34). If the latter states were on different sides of the QPT, they would have opposite spin polarizations, and the net spin polarization in a YSR-SP-STS measurement would be reduced. We have indications that this is the case for the measurements presented here, as it is shown in fig. S4; because different YSR microtips yield even larger signals, we assume that our tip features multiple YSR states. Therefore, further progress can be made in the design of tips featuring only a single pair of YSR states (35) for obtaining even higher spin polarization, e.g., using impurities other than transition metal atoms that typically induce a multiplet of nondegenerate peaks due to their d-orbital magnetism (24, 36, 37).

In summary, our results clearly demonstrate the advantages of using superconducting STM tips functionalized by magnetic impurity bound states to measure atomic-scale spin textures. Because of the inherent perfect spin polarization of YSR states, we can obtain spin contrast with one order of magnitude larger signal intensities compared to conventional Cr bulk tips with the ability to determine absolute values of the sample’s spin polarization at the Fermi level. Thereby, we can access the information of the spin states that are most relevant for the transport properties, e.g., of nanoscale spintronics devices, unconventional superconductors, or systems with topological edge states.

MATERIALS AND METHODS

A clean Nb(110) surface was obtained by flashing the Nb single crystal to T > 2700 K (26). This treatment results in a surface quality as it can be seen in fig. S1A: The Nb(110) surface is about 90% clean, with remaining oxygen contaminations being visible as dark spots in the constant-current STM image. Atomic resolution images of the Nb(110) surface (see fig. S1A) reveal the orientation of the lattice. With this knowledge, magnetic nanostructures can be tailored in a specific crystallographic direction. Single Mn and Fe atoms were deposited successively while keeping the substrate cooled below T = 7 K. This results in a statistical distribution of the adatoms on the surface, as it can be seen in fig. S1B. Fe atoms have an apparent height of about 60 pm compared to about 90 pm for Mn atoms. Cr tips were prepared by electrochemical etching and in situ heating to T = 400°C. Remaining oxide layers were removed by applying voltage pulses to the tips against a Pt(111) surface.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/4/eabd7302/DC1