Plants integrate numerous signals in order to adapt their shape to their environment, modifying their tissues structurally and biochemically so that stems, roots, branches, and leaves have the appropriate shape, orientation, and mechanical properties to track the sun, resist gravity, and harness nutrients. In PNAS, Moulton et al. (1) present a compact mathematical description of the essential components of these tropic responses, providing a framework linking sensing, hormone transport, and growth to three-dimensional form. Their model is expressed as a set of coupled relationships between mathematical functions defined along a curve in space, yielding an elegant field theory that harnesses many of the complexities of plant tropisms.
Many physical “laws” are formulated using fields, that is, smooth mathematical functions that vary in space and time. Although they may be generated by large numbers of discrete processes operating at microscopic scales, fields vary smoothly at macroscopic length scales, allowing their spatiotemporal evolution to be described using the powerful language of vector and tensor calculus, with relationships often expressed with remarkable succinctness. Underpinning many of the triumphs of physical field theories (such as Maxwell’s equations of electromagnetism, or the Navier–Stokes equations of fluid mechanics) is the very large difference between the microscopic length scales at which fields are generated or decay and the macroscopic length scales over which we may seek to describe them, a feature known as “separation of scales.”
What hope might there be to describe biological tissues using a field theory? Cut into the stem or leaf of a plant and its heterogeneity is visible to the naked eye. The underlying cellular structure of plant tissues was clear to the earliest microscopists, and the massive hierarchical complexity of the cell—down to the organization of cellulose microfibrils in the cell wall or microtubules in the underlying cortex—has since been revealed in spectacular detail. When one considers that the bending of a shoot toward the light is driven by reorganization of these and many other molecular components of multiple cells, separation of scales gives way to a bewildering staircase of entwined interactions that operate at numerous levels between molecule and organism. To cut through this complexity, it is necessary to make some bold assumptions, anticipating that the sacrifices made by discarding some details will be compensated by valuable insights.
In this spirit, and building on prior studies (2, 3), Moulton et al. (1) develop a mathematical framework describing the growth and movement of filamentous plants, using shoot tropisms as a model system (although their theory is readily adaptable to other contexts). Their approach is integrative, drawing together current understanding of basic biological processes while respecting essential biophysical and biomechanical constraints. In the spirit of a field theory, the model is formulated at the tissue scale (without resolving individual cells), seeking to describe the evolving shape of the whole shoot in three dimensions. Nevertheless, the model captures processes operating at cellular and subcellular length scales, albeit (presently) in a simplified form. The appeal of a slender shoot as the target for such an exercise is that its shape can be encapsulated compactly by the shape of a curve in three-dimensional space, which can be represented, in turn, by three scalar fields (, , and , in the authors’ notation) collectively describing the stretch, curvature, and torsion of the curve as functions of arclength (distance, ) along it and time . These are the first three fields in the theory, from which a fourth field, the shoot’s centerline location in space , also a function of and , can be constructed using well-established (but awkwardly nonlinear) geometrical relationships.
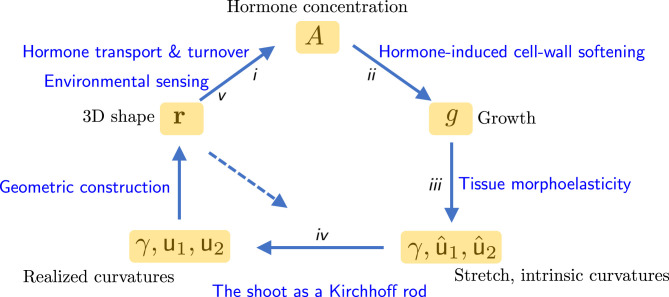
The model is built around a feedback loop (Fig. 1) incorporating processes that pass from the molecular scale to that of the whole organism. Progressing upward in scale, these are the production and transport of a hormone, acting as a morphogen (process i); its impact on cells within tissues to drive growth by cell expansion (process ii); the integration of patterns of growth across the shoot to generate so-called intrinsic curvatures and stretch along the shoot (process iii); the influence of mechanical forces (self-weight, contact, etc.) to determine the overall shape of the shoot (process iv); and the interaction between shoot shape and external signals (light, gravity, touch, etc.) by sensors that drive redistribution of the hormone, closing the cycle (process v). Let us look briefly at each of these components in turn.
Fig. 1.
A schematic showing the interactions between the eight primary fields in the model presented by ref. 1: Hormone concentration and growth vary both along and across the shoot; stretch and intrinsic curvatures , , and , realized curvatures and , and the location of the shoot’s centerline in three-dimensional space vary along the shoot. Interactions between these fields are described in the text as Processes i to v. The dashed arrow represents the mechanical impact of external loads (e.g., self-weight, contact with a rigid surface) in determining the shape of the plant.
Process i: Hormone Transport and Turnover
Distinct hormones can be expected to be involved in different tropisms (4), but the authors (1) use auxin as an exemplar. Its distribution is regulated by active transport from cell to cell in a tissue [for example, by PIN transporters in the gravitropic response (5)], coupled to turnover via sources and sinks. Production may take place near the tropic sensor (in shoot gravitropism) or be more distant (auxin must be transported from the light sensor in the shoot apex to its target site, introducing a delay). Hormone trafficking has been intensively studied in fine molecular detail, but here Moulton et al. take a high-level view (following ref. 6, for example), focusing on the production, transport, and uptake of a concentration field that varies smoothly along and across the shoot.
Process ii: Hormone-Induced Cell Wall Softening
Auxin promotes growth in the shoot, through pathways that have not yet been fully articulated, by promoting enzymatic softening of cell walls (7), leading to irreversible cell expansion. Driven by their internal turgor pressure, individual cells might expand at different rates, yet their tight adherence preserves tissue integrity so that the rate of expansion varies smoothly from cell to cell. This is captured in a growth tensor, a field that smooths out local variations at the cell scale while still capturing variations in growth patterns across tissues. For simple elongation, as in a shoot, growth is represented in ref. 1 by a single scalar field . Variation of along a shoot creates an elongation zone in which there is local stretching. Variation of across a shoot (representing differential cell expansion) allows the shoot to bend and may also generate torsion, allowing movement out of a single plane. In practice, individual tissue elements may not be able to adopt the configuration specified by , and internal mechanical stresses may be generated in order for the tissue to maintain its continuity and integrity.
Process iii: Tissue Morphoelasticity
Just as the growth field integrates (or averages) the expansion of multiple adherent cells in an element of tissue, so itself can be integrated across the cross-section of the shoot to predict the conformation of an element of shoot. This calculation (1) translates hormone-induced differential growth directly into geometrical quantities, namely, the stretch and the intrinsic curvatures and of each segment of the shoot: These capture the shape that a small shoot segment would adopt if it were excised from its surrounding tissue. This calculation is framed using concepts of morphoelasticity (8), which provides a self-consistent description of the mechanics of continuous growing materials.
Process iv: The Shoot as a Kirchhoff Rod
The whole shoot—formed from these individual segments—adopts a shape that is determined by a balance between external forces and torques (weight, loading under wind, contact with neighboring surfaces, etc.) and the internal mechanical forces (the elastic forces arising from deformations of shoot elements relative to their intrinsic configurations). This is captured in ref. 1 by combining the theory of morphoelasticity with Kirchhoff’s theory of elastic rods, yielding a mathematically economical description of growing slender elastic structures (9, 10). Specifically, the mismatch between intrinsic curvatures (, ) and the actual curvatures (, ) realized by a shoot generates elastic stresses that balance environmental loads such as the plant’s own weight. Self-weight is determined by the shape and orientation of the shoot, represented by its centerline location , so nonlinearity intervenes at this point.
Process v: Environmental Sensing
The final component of the model connects the shape of the shoot to environmental signals. Plants deploy a diverse array of sensors at distinct locations. Gravity induces an auxin gradient in shoot tissues via a mechanism mediated by statocytes, cells which exploit settling grains to bias auxin transport (5). Light is sensed at the shoot tip, while physical contact of the shoot with a surface [touch sensing being the least well characterized of the responses (11)] induces a gradient across the shoot. In each case, the relevant sensor influences local production, transport, and uptake of the hormone, translating the shape of the plant with respect to its environment into the concentration field .
Process Integration
To summarize, the eight fields (hormone concentration , growth , stretch , intrinsic curvatures and , realized curvatures and , and shoot shape ) are connected by compact mathematical relationships that encode, parsimoniously, current understanding of primarily biological process with mechanics and geometry . Each relationship involves parameters that, individually, may need significant experimental effort to measure. The theory is used to illustrate gravitropic, phototropic, circumnutational, and thigmotropic responses, and their combination. Despite the substantial simplifications underpinning the model, it retains sufficient complexity in its interactions to challenge intuition; reassuringly, however, the authors (1) show how their model can capture three independent sets of experimental data. Many of the model’s predictions can be rationalized by consideration of the relative size of the timescales of different processes (12), relating, for example, to uptake and transport of hormone, tissue growth, or the environmental forcing. Perhaps the most striking prediction in ref. 1 is that of a shoot finding and wrapping itself around a pole, demonstrating how circumnutation and thigmotropism, collectively mediated by hormone transport, induce a conformational response that enables a slender shoot to exploit a nearby rigid structure and climb toward the light.
The approach taken by Moulton et al. (1) complements other recent studies that have sought to resolve cellular geometry in detail, relying on computational power (13, 14) or spatial averaging (15, 16) to address the separation-of-scales problem. High-resolution treatments can certainly achieve greater fidelity in describing processes i and ii (Fig. 1), but start to become impractical when describing the mechanics of elongating, bending, and coiling structures in three dimensions. With a few exceptions (3, 17), prior models of tropic responses effectively short-circuit elements of the feedback loop in Fig. 1: For example, the classical “sine law” (2, 18) is purely kinematic, in the sense that it bypasses the mechanical processes iii and iv. There is a place, of course, for all of these approaches, particularly in testing and parametrizing the mathematical relationships describing each interaction with greater specificity, and in understanding their competition (19).
With so many processes at play, it is no surprise that tropic responses are complex: The combination of delays (between sensing and response), nonlinearity (particularly in reconstructing three-dimensional shapes from heterogeneous patterns of growth), and the integration of multiple signals together lead to complex outcomes such as oscillations and mechanical inversions (1) (reminiscent of a twist in an old-fashioned telephone cable). Models have revealed important roles for proprioception (20) (sensing of shape and position) and autotropism (1) (the tendency to grow straight), and other regulatory processes that stabilize tropic responses may well emerge. There is significant scope for specializing descriptions of distinct hormone pathways (processes i and ii) by incorporating substantially more molecular and cellular detail, to better understand competition between different tropic signals. These observations emphasize the crucial role for well-grounded theoretical models in the interpretation of experimental observations, as tools for testing hypotheses and the continuing need to improve model accuracy. The mathematical framework provided by ref. 1 will help with the exploration of these ideas, and with the wider challenge of linking molecular level processes to the dramatic shape changes adopted by plants as they adapt to our ever-changing world.
Footnotes
The author declares no competing interest.
See companion article, “Multiscale integration of environmental stimuli in plant tropism produces complex behaviors,” 10.1073/pnas.2016025117.
References
- 1.Moulton D. E., Oliveri H., Goriely A., Multiscale integration of environmental stimuli in plant tropism produces complex behaviors. Proc. Natl. Acad. Sci. U.S.A., 10.1073/pnas.2016025117 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bastien R., Bohr T., Moulia B., Douady S., Unifying model of shoot gravitropism reveals proprioception as a central feature of posture control in plants. Proc. Natl. Acad. Sci. U.S.A. 110, 755–760 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chelakkot R., Mahadevan L., On the growth and form of shoots. J. R. Soc. Interface 14, 20170001 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shkolnik D., Fromm H., The Cholodny-Went theory does not explain hydrotropism. Plant Sci. 252, 400–403 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Moulia B., Fournier M., The power and control of gravitropic movements in plants: A biomechanical and systems biology view. J. Exp. Bot. 60, 461–486 (2009). [DOI] [PubMed] [Google Scholar]
- 6.Band L. R., King J. R., Multiscale modelling of auxin transport in the plant-root elongation zone. J. Math. Biol. 65, 743–785 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Cosgrove D. J., Diffuse growth of plant cell walls. Plant Physiol. 176, 16–27 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goriely A., The Mathematics and Mechanics of Biological Growth (Springer, 2017). [Google Scholar]
- 9.Moulton D., Lessinnes T., Goriely A., Morphoelastic rods. Part 1: A single growing elastic rod. J. Mech. Phys. Solid. 61, 398–427 (2013). [Google Scholar]
- 10.Moulton D., Lessinnes T., Goriely A., Morphoelastic rods III: Differential growth and curvature generation in elastic filaments. J. Mech. Phys. Solid. 142, 104022 (2020). [Google Scholar]
- 11.Reinhold L., Sachs T., Vislovska L., “The role of auxin in thigmotropism” in Plant Growth Substances 1970 (Springer, 1972), pp. 731–737. [Google Scholar]
- 12.Chauvet H., Moulia B., Legué V., Forterre Y., Pouliquen O., Revealing the hierarchy of processes and time-scales that control the tropic response of shoots to gravi-stimulations. J. Exp. Bot. 70, 1955–1967 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Boudon F., et al. , A computational framework for 3D mechanical modeling of plant morphogenesis with cellular resolution. PLoS Comput. Biol. 11, e1003950 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.de Reuille P. B., et al. , MorphoGraphX: A platform for quantifying morphogenesis in 4D. Elife 4, e05864 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dyson R. J., et al. , Mechanical modelling quantifies the functional importance of outer tissue layers during root elongation and bending. New Phytol. 202, 1212–1222 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fozard J. A., Bennett M. J., King J. R., Jensen O. E., Hybrid vertex-midline modelling of elongated plant organs. Interface Focus 6, 20160043 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Agostinelli D., Lucantonio A., Noselli G., DeSimone A., Nutations in growing plant shoots: The role of elastic deformations due to gravity loading. J. Mech. Phys. Solid. 136, 103702 (2020). [Google Scholar]
- 18.Meroz Y., Bastien R., Mahadevan L., Spatio-temporal integration in plant tropisms. J. R. Soc. Interface 16, 20190038 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bastien R., Douady S., Moulia B., A unified model of shoot tropism in plants: Photo-, gravi- and propio-ception. PLoS Comput. Biol. 11, e1004037 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Moulia B., Bastien R., Chauvet-Thiry H., Leblanc-Fournier N., Posture control in land plants: Growth, position sensing, proprioception, balance, and elasticity. J. Exp. Bot. 70, 3467–3494 (2019). [DOI] [PubMed] [Google Scholar]