Pharmacokinetic modeling reveals parameters that govern tumor targeting and delivery by a pH-Low Insertion Peptide (pHLIP)

Significance

Tumors exhibit an acidic extracellular microenvironment that is accentuated at cell surfaces. As a result, they can be targeted by a pH-Low Insertion Peptide (pHLIP), an acid-triggered tumor-targeting peptide that can also serve as a vehicle for drug delivery. In this work, we use a pharmacokinetic modeling approach to deepen our understanding of the mechanisms and factors that influence pHLIP tumor targeting and delivery, and also identify factors that do not. In so doing, we predict pHLIP phenotypes with significantly enhanced capabilities. The model may therefore be useful for guiding the future development of pHLIP variants.

Abstract

A pH-Low Insertion Peptide (pHLIP) is a pH-sensitive peptide that undergoes membrane insertion, resulting in transmembrane helix formation, on exposure to acidity at a tumor cell surface. As a result, pHLIPs preferentially accumulate within tumors and can be used for tumor-targeted imaging and drug delivery. Here we explore the determinants of pHLIP insertion, targeting, and delivery through a computational modeling approach. We generate a simple mathematical model to describe the transmembrane insertion process and then integrate it into a pharmacokinetic model, which predicts the tumor vs. normal tissue biodistribution of the most studied pHLIP, “wild-type pHLIP,” over time after a single intravenous injection. From these models, we gain insight into the various mechanisms behind pHLIP tumor targeting and delivery, as well as the various biological parameters that influence it. Furthermore, we analyze how changing the properties of pHLIP can influence the efficacy of tumor targeting and delivery, and we predict the properties for optimal pHLIP phenotypes that have superior tumor targeting and delivery capabilities compared with wild-type pHLIP.

Tumor cells and associated macrophages acidify their environments via an interrelated combination of metabolic effects, including hypoxia-induced glycolysis, the Warburg effect, and the activity of surface carbonic anhydrases (1). Because of the net outward flux of protons and the influence of the electrochemical potential, the acidity is most pronounced at the cell surfaces. This acidity can serve as a biomarker to distinguish tumors from normal tissue (2). Thus, there is great interest in developing acid-triggered agents, such as pH-Low Insertion Peptides (pHLIPs), which undergo changes in the acidic tumor microenvironment that result in their preferential accumulation within tumors.

A pHLIP is a short, pH-sensitive peptide that docks itself at cell membranes and, when exposed to acidic pH, folds into an alpha helix and inserts to form a transmembrane helix. This behavior is due to multiple acidic residues contained within a pHLIP’s membrane-spanning region and inserting end, which are protonated at acidic pH, thereby neutralizing their charge and increasing the pHLIP’s hydrophobicity, allowing for transmembrane insertion to occur. Imaging agents and therapeutic drugs can be attached to either the noninserting end (the N terminus) or the inserting end (the C terminus) of a pHLIP, resulting in targeted delivery of these agents to tumors (3).

Here we investigated pHLIP tumor targeting and delivery through a pharmacokinetic modeling approach. Pharmacokinetic modeling can be a useful tool for enhancing our understanding of drug mechanisms, establishing optimal dosing protocols, and optimizing or designing new drugs. It can be used to predict tissue concentrations over time, which otherwise may be difficult to measure. In addition, once a robust model for a drug is established, it may be possible to analyze how altering various properties of the drug can affect its ability to reach therapeutic concentrations in target tissues. For a pHLIP, there is the additional advantage that it targets tumors via a well-defined mechanism that is dependent on a measurable tumor property, extracellular pH.

The mechanism for pHLIP targeting has been well studied in liposomes; however, a relationship between the results in liposomes and the behavior of pHLIPs in cells, let alone in animal models, has yet to be established. We addressed this issue by creating a mathematical model of the transmembrane insertion process, and we integrate it into a pharmacokinetic model of a pHLIP’s biodistribution after a single intravenous (i.v.) injection. The model predicts the concentration of pHLIP in the tumor, normal tissue, and the blood over time, as well as the proportion of pHLIP in each of its various states: in free solution (state 1); bound to serum proteins; docked at cell membranes (state 2); and inserted across a cell membrane as a transmembrane helix (state 3). With this model, we can gain a foundational understanding of how various tumor properties and the properties of pHLIPs themselves affect tumor targeting and tumor-specific drug delivery. In addition, we use the model to predict how various properties of pHLIPs should be altered to enhance their efficacy.

Development of a Mathematical Model Describing pHLIP Liposome Insertion and Exit

Several studies have reported pH titration curves for pHLIP transmembrane insertion when incubated over a range of pH values with palmitoyl-oleoyl-phosphatidylcholine (POPC) liposomes (4–13). These results are typically in the form of a tryptophan fluorescence-vs.- pH curve, where a tryptophan fluorescence change from the baseline, pHLIP with liposomes at pH 8, serves as a proxy for the fraction of pHLIP in state 3. The pK_a value of the curve, defined as the pH at the midpoint of the state 2–state 3 transition region, consistently has a reported value of ∼6 for wild-type pHLIP in the literature.

Before developing a pharmacokinetic model to describe pHLIP in animals, we had to first develop a mathematical description of the pHLIP state 2–state 3 transition that is consistent with the published pH titration results in liposomes and can be used to predict the interaction of pHLIP with cells. We assume that the relative amount of pHLIP in state 3 vs. state 2 is the result of the equilibrium between transmembrane insertion and transmembrane exit. The rate of transmembrane insertion is dependent on protonation of all the acidic residues in both the membrane-spanning region and the inserting end of the pHLIP, while the rate of transmembrane exit is dependent on protonation of the acidic residues on only the inserted end, since the residues in the membrane-spanning region should already be protonated when pHLIP is in state 3. Therefore, we generated equations for the rates of transmembrane insertion (k₂₃) and transmembrane exit (k₃₂) at a given external/extracellular pH (pHe) and internal/intracellular pH (pHi). These rates are dependent on the pK_a and cooperativity coefficient (n) for insertion and exit, respectively. The relative proportion of pHLIP in state 3 vs. state 2 at the given pHe and pHi could then be determined from the ratio of the transmembrane insertion and exit rates. A detailed description of this model and how its equations and parameter values were derived is provided in SI Appendix, section 1.

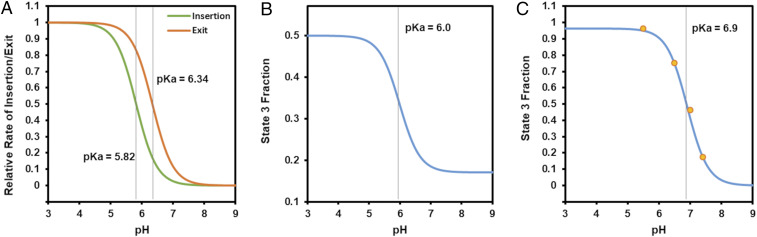
Of note, in our model, if the pK_a and n values for insertion were the same for transmembrane exit, then k₂₃ would equal k₃₂ at all pH values in liposomes (given that pHe = pHi in liposomes). No pH-dependent titration curve for the pHLIP state 2–state 3 equilibrium would be observed if this were the case. Thus, we propose that the pK_a and n for insertion (pK_aIns and n_Ins) and exit (pK_aEx and n_Ex) are actually different. Together, they produce the overall pK_a and n values observed in the published pHLIP titration curves. Previously, NMR spectroscopy was used to determine the pK_a of each aspartate residue of wild-type pHLIP (14), although crowding, mixtures of states, and the low water content of the samples may have influenced the results. As transmembrane insertion is likely dependent on the protonation of all these residues, it follows that the process is limited by the residue with the lowest pK_a. Therefore, we took pK_aIns to be the same as that of the residue that exhibits the lowest pK_a, the D14 residue (pK_a = 5.82). Transmembrane exit likely depends on just the protonation of the C-terminal D31 and D33 residues, and thus we took pK_aEx to be equal to that of the residue with the lower pK_a, the D33 residue (pK_a = 6.34). When we inserted these pK_a values into our model, we obtained a liposome state 2–state 3 equilibrium curve with overall pK_a = 6.0 (Fig. 1 A and B), consistent with the previously reported experimental results (4–13). Interestingly, we also found that when n_Ins and n_Ex are different, various asymmetries may be produced within the shape of the pHLIP titration curve for liposomes, many of which have been observed previously in published experimental results (SI Appendix, section 1 and Fig. S1).

Fig. 1.

Model-predicted pHLIP state 2–state 3 transition rates and equilibrium titration curves. (A) Predicted titration curves for wild-type pHLIP insertion and exit rates into/from lipid membranes were generated using n_Ins = n_Ex = 1.32. (B) These rates in turn were used to produce the titration curve for the equilibrium state 3 fraction in POPC liposomes. (C) When the same model was applied to cells, the titration curve shown was generated. The predicted curve fits published experimental data from ref. (19) (orange dots) well.

Importantly, there are significant differences between POPC liposomes and cells, and assuming that results in one are the same in the other is likely to be erroneous. It has been shown that lipid composition, which differs significantly between vesicles and cells, can alter pHLIP binding and insertion (6, 10, 12); however, relatively little attention has been paid to an arguably far more substantial difference: the fact that intracellular pH is regulated, and hence there is a pH gradient between the intracellular and extracellular environments, whereas no such gradient exists for liposomes. For normal cells, intracellular pH is held constant at ∼7.2, whereas it is often slightly elevated for cancer cells, at around pH 7.3 to 7.4 (15, 16). Therefore, we applied our model to tumor cells by generating pH titration curves in which only pHe was varied; the pHi was held constant at 7.4, and we observed a dramatic shift in the pK_a of the curve to 6.9 (Fig. 1C). This result is encouraging, as tumor cell insertion would likely be very low if the pK_a of the pHLIP state 2-state 3 equilibrium was the same in cells as in liposomes, since the vast majority of tumors have bulk extracellular pH >6.5, although cell surface pH is somewhat lower (17, 18).

It should be noted that in the literature, while the pK_a of the wild-type pHLIP state 2–state 3 equilibrium titration curve in liposomes is consistently found to be ∼6, there is substantial variation in the measured cooperativity coefficient of the curve, with reported values ranging from 0.6 (12) to 2.48 (8), making it difficult to establish appropriate n_Ins and n_Ex values for wild-type pHLIP in our pharmacokinetic model, especially given that the composition of cell membranes is substantially different from that of liposomes. Therefore, we fitted our model to real data from cultured cells, reported previously (19) for the insertion of dansyl by pHLIP at various pH values. We assumed n_Ins ∼ n_Ex, since the state 2–state 3 equilibrium curve is approximately symmetric in most publications, and found that our model produces an excellent fit to the cultured cell data when n_Ins = n_Ex = 1.32 and pK_aIns and pK_aEx are kept at 5.82 and 6.34, respectively (Fig. 1C). This gave us further confidence in the accuracy of these parameter values not just for liposomes, but also for cells.

Development of a Pharmacokinetic Model for the Prediction of pHLIP Concentrations In Vivo

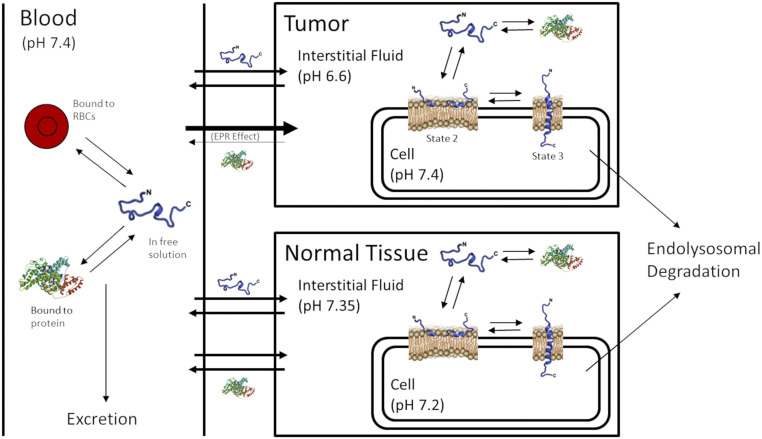
Encouraged by the success of our pHLIP state 2–state 3 transition model, we proceeded to implement it within a compartmental model for the pharmacokinetics of pHLIP when injected into animals (Fig. 2). This pharmacokinetic model predicts the concentration of pHLIP over time in tumor tissue, averaged normal tissue, muscle tissue, and blood, as well as the various states of pHLIP in each of these compartments, after a single i.v. injection. The model takes into account serum protein binding and the enhanced permeability and retention (EPR) effect, which is well known to bias the distribution of nanoparticles and large molecules toward accumulation in tumors. The EPR effect is usually significant for molecules larger than 40 kDa but not for smaller molecules (20, 21); thus, only protein-bound pHLIP is affected by the EPR effect in our model. The code for the model was written in MATLAB (MathWorks) and executed using MATLAB R2018a with the ode15s solver. It is available for access at https://zenodo.org/record/4119903. Details of the model, including all model equations and how the parameter values were derived, are provided in SI Appendix, sections 2 to 4. Of note, the model does not take into account several factors known to influence pHLIP’s biodistribution, such as the presence of a cargo molecule, as well as others (more details in Discussion and Conclusions). As a result, the model’s predictions represent an idealized scenario, and its quantitative accuracy will often be limited when compared with real data.

Fig. 2.

Diagram of compartmental model for pHLIP pharmacokinetics. The model consists of three main compartments: the blood compartment, tumor compartment, and normal tissue compartment. Within each compartment, a pHLIP molecule can exist in one of four states: in free solution, bound to protein, docked at a cell membrane (state 2), or inserted across a cell membrane (state 3). The EPR effect is accounted for and affects protein-bound but not free pHLIP. pHLIP molecules in state 2 or state 3 at the cell membrane are subject to endolysosomal degradation.

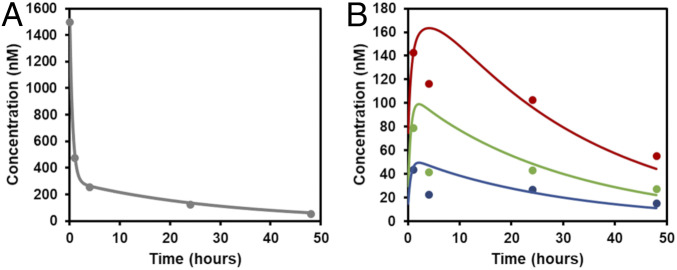
Still, to validate our model, we compared its predictions with data from radiotracer-labeled wild-type pHLIP injected into mice with LNCaP tumors (Fig. 3) (22). We chose these data for our comparison as they contain time points extending to 48 h, they include the relative concentrations over time in various tissues as well as in the blood, and the tumor pH value was known and consistent across multiple studies (pH 6.6) (22, 23). Our model agrees well with the experimental data (Fig. 3). Of note, each of the parameter values in our model was derived from measured or published data, further enhancing our confidence in the model’s predictive strength.

Fig. 3.

Comparison of pharmacokinetic model results to published experimental data. The model-predicted blood concentration of pHLIP over time (A) and the concentrations of pHLIP in tumor (red), averaged normal tissue (green), and muscle over time (blue) (B) were compared with experimental data (points) from ref. (22). The model assumes a single i.v. injection of 3 nmol of pHLIP into a mouse with a 2-mL blood volume. The experimental data were originally in units of % injected dose/g but was converted to nM by setting 100% injected dose = 3 nmol, resulting in the following conversion: 1% injected dose/g = 0.01*(3 nmol)/g × 1.06 g/mL = 31.8 nM.

Nevertheless, we should note that the dataset that we used (from ref. 22), despite being the best available for comparison with our model, has several limitations. In particular, the presence of the radiotracer Cu⁶⁴-DOTA may have influenced wild-type pHLIP’s biodistribution and clearance pathways, and any instability of the Cu⁶⁴-DOTA chelation would have affected the biodistribution measurements. Thus, despite the close agreement of our model with these data, we emphasize that the quantitative values of the model’s predictions may be of limited accuracy and should not be interpreted strictly. Rather, the utility of the model lies chiefly in its ability to make rough comparisons of the relative concentrations of pHLIP in various compartments and to interrogate the relative effects of various parameters on pHLIP’s tumor targeting and delivery capabilities.

Analysis of pHLIP Biodistribution

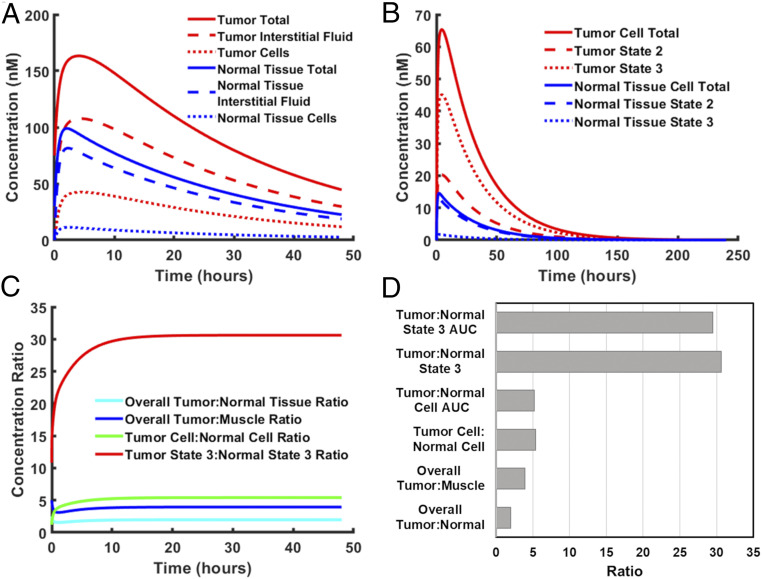
Although previously published biodistribution studies reveal the overall concentration of pHLIP in various tissues over time, they do not tell us the relative concentration of pHLIP in each of its various states (state 1/in solution, state 2, and state 3) within each tissue. Thus, we used our model to gain insight into this. Interestingly, we found that the majority of wild-type pHLIP in tumor or normal tissues lies within the interstitial fluid (state 1) (Fig. 4A). As only a minority of pHLIP molecules are actually bound to cells (state 2 and state 3), the overall tumor:normal tissue contrast ratio observed in imaging experiments might not reflect the ratio for cell-bound pHLIP (the tumor cell:normal cell ratio). Indeed, we find that the overall tumor:normal tissue contrast ratio is significantly less than the cell-bound ratio (Fig. 4 C and D).

Fig. 4.

Analysis of pHLIP biodistribution. Model-predicted concentration profiles were generated for wild-type pHLIP after a single i.v. injection of 3 nmol into a mouse. (A) The total concentration, interstitial fluid concentration, and cell-bound concentration of pHLIP relative to total tumor/normal tissue volume (cells + interstitial fluid). (B) The total cell-bound concentration, state 2 concentration, and state 3 concentration of pHLIP relative to tumor/normal tissue cell volume (which excludes the interstitial fluid). (C) The respective tumor:normal tissue ratios. (D) Quantification of tumor:normal tissue AUC ratios and steady-state concentration ratios.

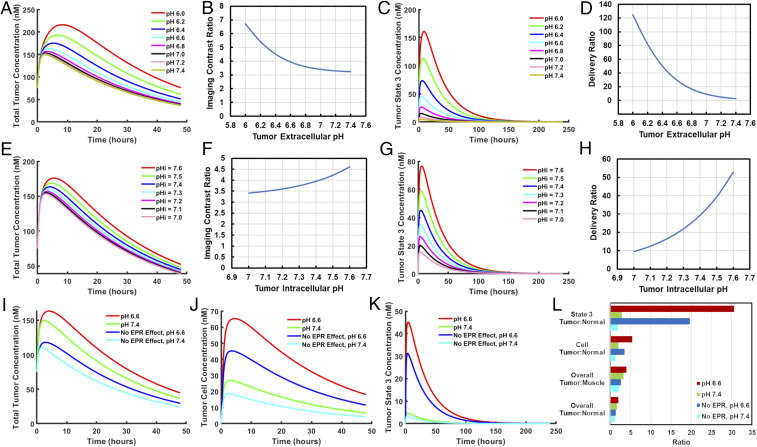
Of note, “normal tissue” in our model refers to the mass fraction-weighted average of nontumor tissues, which includes tissues in which pHLIP accumulates more highly, such as the liver and kidneys. The inclusion of these tissues was necessary, since the model must account for all of the pHLIP inside the mouse at each time point to achieve a mass balance. As a result, the “normal tissue” pHLIP concentration referred to in the model exceeds that of the nondiseased tissue that typically surrounds a tumor, and the “overall tumor:normal tissue ratio” in the model underestimates the contrast ratio seen in actual imaging experiments. Thus, to obtain a useful imaging contrast ratio in our model, we attempted to estimate the pHLIP concentration in muscle tissue, which is the most common reference tissue for contrast ratio in the pHLIP literature. Our analysis of the data in ref. (22) reveals that the pHLIP concentration in the muscle is approximately one-half that of averaged normal tissue at each time point, and thus the overall tumor:muscle contrast ratio is estimated to be twice that of the overall tumor:normal tissue ratio in our model.

Although the overall contrast ratio has clear applications for imaging, the cell-bound ratio is more reflective of pHLIP’s tumor specificity when used as a therapeutic agent. This ratio is particularly useful when the therapeutic cargo that pHLIP is carrying acts at the cell membrane. However, when the site of action for the cargo is intracellular, the ratio of inserted, or state 3, pHLIP is more reflective of the degree of tumor specificity. Therefore, we looked at the relative concentrations of state 2 and state 3 pHLIP within the cell-bound fractions of pHLIP in tumor and averaged normal tissue (Fig. 4B). Here averaged normal tissue is a more appropriate reference than muscle tissue, since we are concerned with drug side effects, which tend to occur in nondiseased tissues with high concentrations of the drug, such as the liver and kidneys. It can be seen that for tumor tissue, the majority of cell-bound pHLIP is in state 3, whereas the opposite is true for normal tissue. Thus, the tumor:normal tissue concentration ratio for state 3 pHLIP is even higher than that for cell-bound pHLIP.

In addition, we measured the area under the concentration vs. time curve (AUC) for both cell-bound pHLIP and state 3 pHLIP. The AUC represents the total drug exposure and hence reflects the effective drug dose to the tumor/normal tissue. The values of the various ratios are shown in Fig. 4 C and D. As can be seen, the ratios for state 3 pHLIP concentration and AUC are far higher than the other ratios. This suggests that while pHLIP has excellent potential as an imaging contrast agent, its optimal use may be as a tumor-targeting delivery agent for drugs with low therapeutic indices. That said, it should be noted that the model’s predicted values assume that the cargo molecule does not affect targeting and delivery. In the majority of cases, this assumption most likely will not hold true, especially with C terminus-linked cargoes, which are known to significantly slow transmembrane insertion (24, 25) and also may affect the pK_a and cooperativity of insertion and exit. In addition, the cargo molecule may affect serum protein and cell binding, as well as the routes of elimination. Thus, actual concentrations may differ significantly when a cargo is present, although the model’s predictions should hold true qualitatively.

In the rest of this paper, we focus on the overall tumor:muscle ratio and the tumor:normal tissue state 3 AUC ratio, which are the most reflective of pHLIP’s use as an imaging agent and as a delivery agent, respectively. Hereinafter, these two ratios are referred to as the “imaging contrast ratio” and the “delivery ratio”, respectively. We also refer to the tumor state 3 AUC as “tumor cell delivery,” as this value reflects the magnitude of tumor cell delivery of a therapeutic agent by pHLIP.

Influence of Tumor Properties on pHLIP Targeting and Delivery

We used our model to investigate how various tumor properties, including extracellular pH, intracellular pH, and the EPR effect, affect pHLIP tumor targeting and delivery. As expected, varying extracellular pH had a substantial influence on tumor targeting and delivery (Fig. 5 A–D). However, while it did produce significant changes in overall tumor concentration, the effect was much more pronounced when the analysis was limited to the state 3 concentration of pHLIP, which is more representative of drug delivery. The imaging contrast ratio increased by ∼2-fold from pH 7.4 to pH 6.0, while the delivery ratio increased by nearly 50-fold, suggesting that the contrast ratio seen in imaging underestimates the tumor specificity of pHLIP-mediated drug delivery.

Fig. 5.

Influence of tumor pH and EPR effect on pHLIP tumor targeting and delivery. The model was run for wild-type pHLIP with tumor extracellular pH ranging from 6.0 to 7.4 while tumor intracellular pH was kept at 7.4 (A–D) or with tumor intracellular pH ranging from 7.0 to 7.6 and tumor extracellular pH kept at 6.6 (E–H). The relationships between tumor extracellular/intracellular pH and total tumor concentration (A and E), the imaging contrast ratio (B and F), tumor state 3 concentration (C and G), and the delivery ratio (D and H) are shown. The model was also run with or without tumor acidity (pH 6.6) and/or the EPR effect, respectively, and the resulting total tumor concentrations (I), tumor cell concentrations (J), tumor state 3 concentrations (K), and tumor:normal tissue contrast ratios were compared (L). Tumor cell and tumor state 3 concentrations are relative to tumor cell volume, which excludes interstitial fluid.

While the importance of extracellular pH for pHLIP targeting has been heavily emphasized in the literature, relatively little attention has been paid to intracellular pH. Intracellular pH is often slightly elevated in cancer cells, and it has been linked to increased cell proliferation, resistance to apoptosis, and promotion of cell invasion (15, 16). As discussed above, the relative amount of state 3 pHLIP is dependent on an equilibrium between transmembrane insertion and exit, and hence intracellular pH, which affects the rate of transmembrane exit, may have a significant effect on tumor targeting and delivery. Therefore, we examined the effects of varying intracellular pH in our model (Fig. 5 E–H). Interestingly, this variation resulted in relatively small changes in total tumor concentration but very large changes in state 3 concentration. Tumor intracellular pH thus seems to have a limited impact on the effectiveness of pHLIP as an imaging agent but can make a substantial difference when pHLIP is used as a delivery agent.

We next examined the impact of the EPR effect on pHLIP tumor targeting and delivery. Our measurements of pHLIP partitioning in the blood show that a substantial fraction of pHLIP binds to serum proteins (SI Appendix, Fig. S2), and thus we wondered whether the EPR effect, which should affect protein-bound pHLIP, could have a significant impact on the biodistribution of pHLIP. Consequently, we ran our model with and without the EPR effect and compared this with the effect of tumor acidity on pHLIP targeting and delivery (Fig. 5 I–L). Interestingly, we found that the EPR effect seems to have a greater impact than pH on total pHLIP tumor concentration. However, the opposite was true for the concentrations of both cell-bound pHLIP and state 3 pHLIP, and this trend was further reflected in the respective contrast ratios. While tumors that lack the EPR effect may exhibit lower contrast ratios when pHLIP is being used as an imaging agent, they may still be viable targets for the pHLIP drug delivery system.

Analysis of Other Biological Parameters on the Biodistribution of pHLIP

Apart from the aforementioned tumor properties, there may be other biological parameters that affect pHLIP tumor targeting and delivery. Therefore, we explored the remaining biological parameter space with a sensitivity analysis, in which we ran our model 1,000 times with randomized biological parameters. With the exception of tumor volume, each parameter was assigned a normal distribution with mean equal to the default parameter value (listed in SI Appendix, section 2). When known, the standard deviation was assigned the appropriate value; when unknown, the standard deviation was assigned a value of 20 to 30% of the mean. Tumor volume was assigned a simple random value from 0 to 2 mL, so that we could explore the full mouse tumor size range with equal propensity. We then analyzed how each parameter influenced the imaging contrast ratio, the delivery ratio, and the magnitude of tumor cell delivery by determining the correlation of each of these values with each varied parameter. The results are shown in SI Appendix, Fig. S5.

The sensitivity analysis produced a number of interesting findings. First, we observed that pHLIP tumor targeting and delivery do not vary with tumor size. However, it should be noted that there is an assumption of constant tumor properties, including extracellular pH. As many tumor properties, including the degrees of hypoxia and necrosis, vary with tumor size (26, 27), tumor pH may vary with size as well, thereby affecting pHLIP targeting and delivery. On another note, we found a strong positive correlation (R² = 0.34) between normal tissue extracellular pH and the pHLIP delivery ratio, but no correlation between the imaging contrast ratio or tumor cell delivery. Thus, when using pHLIP to deliver a drug with low therapeutic index, it may be beneficial to correct any systemic acidosis within the patient before administering the pHLIP-drug conjugate. It may also be possible to improve tumor specificity by purposefully inducing an alkalotic state within the patient, although such a procedure would have to leave the tumor pH unaffected. On a related note, we also found a significant negative correlation (R² = 0.15) between normal tissue intracellular pH and the pHLIP delivery ratio.

As expected, both the EPR permeability factor and the EPR retention factor have strong positive correlations with tumor targeting and delivery. However, the correlations are significantly stronger for the imaging contrast ratio (permeability factor R² = 0.20; retention factor R² = 0.67) than for the delivery ratio (R² = 0.12 and 0.25) or tumor cell delivery (R² = 0.09 and 0.27). This is consistent with our previous results, which suggest that the EPR effect is more important for the use of pHLIP as an imaging contrast agent than for its use as a tumor-specific drug delivery system.

Finally, we observed correlations between the blood-tissue transport rate constants and the magnitude of tumor cell delivery. The correlations between these parameters were either absent or significantly weaker for the imaging contrast ratio and the delivery ratio. Parameters that resulted in increased transport of pHLIP from blood to tissue (k_FBN and k_PBN) were correlated with increased tumor cell delivery, while the opposite was true for the tissue-to-blood transport parameters (k_FNB and k_PNB). Moreover, the rate of free pHLIP elimination from the blood was negatively correlated with tumor cell delivery, but not with imaging contrast ratio or delivery ratio. Taken together, these results suggest that these parameters have a much stronger impact on pHLIP delivery than on tumor targeting.

Effect of Rate of Transmembrane Insertion/Exit on Tumor Delivery

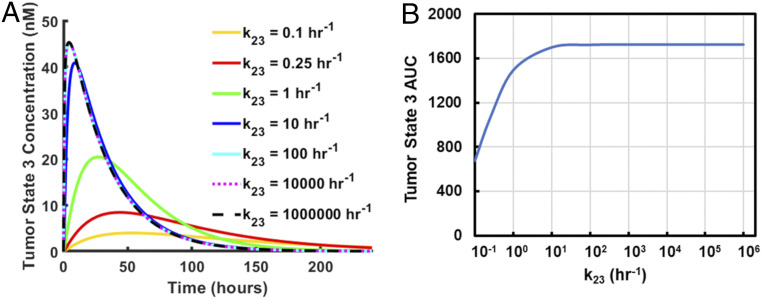
Cargo molecules on the C terminus of pHLIP can result in a dramatic slowing of transmembrane insertion time (24, 25). In addition, many variants of pHLIP have far more rapid transmembrane insertion times than wild-type pHLIP, up to ∼1,000-fold more rapid (28). Thus, we investigated the influence of the insertion/exit rate on tumor delivery (Fig. 6). We found that for maximum rates of ∼100 h⁻¹ and above (a characteristic insertion time of ∼40 s or less), the results are essentially identical. As all pHLIP variants to date, including wild-type pHLIP, have faster or equal base insertion rates (i.e., rates with no cargo on the C terminus) than this, we can conclude that the base insertion time is unlikely to be an important factor in determining the efficacy of a pHLIP variant.

Fig. 6.

Influence of pHLIP transmembrane insertion rate on tumor delivery. The model was run for maximum pHLIP transmembrane insertion/exit rates spanning 0.1 h⁻¹ to 1,000,000 h⁻¹. The resulting tumor state 3 concentrations (relative to cell volume, which excludes interstitial fluid) (A) and the respective tumor state 3 AUCs (B) are shown.

Nevertheless, when the insertion time is slowed to rates below ∼10 h⁻¹, as may be the case when a cargo molecule is attached to the C terminus of pHLIP (24, 25), a significant effect can be observed. The tumor state 3 concentration of pHLIP is significantly reduced throughout early to mid time points for insertion/exit rates on the order of ≤1 h⁻¹. This reduction is accompanied by a reduction in the tumor state 3 AUC, which is indicative of the total drug dose delivered by pHLIP. Depending on the amount of cargo needed for a desired effect, the model suggests that there is a practical limit to the useful cargoes that pHLIP is capable of delivering, in agreement with previous results (25).

Analysis of pHLIP Parameter Values on Tumor Targeting and Delivery

There has been a great deal of interest in producing variants of pHLIP with improved tumor targeting and delivery capabilities (8, 28–31). However, little has been done to elucidate the optimal parameters for such pHLIP variants in terms of insertion/exit pK_a/cooperativity coefficient and partitioning between protein-bound, cell-bound, and free states while in solution, so we performed a sensitivity analysis as we had done previously for the biological parameters in our model, but this time with the pHLIP parameters (SI Appendix, Fig. S6). We excluded pHLIPs with pK_aIns > pK_aEx and n_Ins < n_Ex from this analysis, as such pHLIP phenotypes are unlikely to be found in real life.

As expected, there was no correlation between the rate of transmembrane insertion/exit (randomly sampled from an exponential function to cover the full range of base insertion times) and tumor targeting or delivery, in agreement with our previous results, which suggest this to be an unimportant parameter unless drastically slowed by the presence of a cargo molecule. However, correlations between tumor targeting and/or delivery existed for all other pHLIP parameters. For instance, it can be seen that the imaging contrast ratio and tumor cell delivery, but not the delivery ratio, seem to increase with increasing insertion pK_a and decreasing exit pK_a. This is expected for tumor cell delivery, since shifting these parameters in this way would bias the state 2–state 3 equilibrium toward state 3. In addition, there were strong (R² = 0.43) and moderate (R² = 0.16) positive correlations between tumor delivery ratio and the cooperativity coefficients for insertion and exit, respectively. Higher cooperativity coefficients would narrow the pH range over which the state 2–state 3 transition occurs, thereby increasing the specificity of delivery.

Interestingly, pHLIP partitioning among free, protein-bound, and cell-bound states appears to have a substantial impact on tumor targeting and delivery. There were significant negative correlations between the fraction of free pHLIP and all three indicators of tumor targeting and delivery. On the other hand, the fraction of protein-bound pHLIP was positively correlated with the imaging contrast ratio and the delivery ratio, but not with the magnitude of tumor cell delivery. In contrast, the fraction of cell-bound pHLIP had strong positive correlations with the magnitude of tumor cell delivery and the imaging contrast ratio, but not with the delivery ratio. Taken together, these results suggest that a decreased free fraction of pHLIP is actually advantageous for tumor targeting and delivery. Meanwhile, in applications where the specificity of tumor delivery is most important, increasing the rate of pHLIP protein binding may be beneficial. On the other hand, increasing the rate of pHLIP cell binding is most beneficial for increasing the magnitude of tumor cell delivery. Increasing both rates can be beneficial for enhancing the imaging contrast ratio.

Of note, all the pHLIP parameters that correlated with tumor cell delivery also correlated in the same direction with the imaging contrast ratio. Therefore, we analyzed the relationship between imaging contrast ratio and tumor cell delivery and found a strong correlation between the two (R² = 0.57) (SI Appendix, Fig. S7). This suggests that the imaging contrast ratio might serve as a very rough predictive tool for the magnitude of tumor cell delivery. There was also a significant but much weaker correlation between the imaging contrast ratio and the delivery ratio. There was no correlation between the magnitude of tumor cell delivery and the delivery ratio.

Prediction of Optimal pHLIP Phenotypes

Our sensitivity analysis predicts the possibility of pHLIP variants with superior tumor targeting and delivery compared with wild-type pHLIP. By analyzing the top-performing pHLIP phenotypes, we may gain insight into the characteristics of an optimized pHLIP variant and the degrees of tumor targeting and delivery that can be expected from such a variant. Thus, we screened all the pHLIP phenotypes generated in our sensitivity analysis for the top 5% in each category (i.e., imaging contrast ratio, delivery ratio, and magnitude of tumor cell delivery). This analysis resulted in identification of the key characteristics that would improve tumor targeting and delivery compared with wild-type pHLIP. While wild-type pHLIP has an imaging contrast ratio of ∼4, the top 5% in this category had contrast ratios ranging from ∼10 to ∼29. Likewise, the top 5% in delivery ratio had ratios of ≥114, compared with 29.5 for wild-type pHLIP. However, the most dramatic difference was seen for the magnitude of tumor cell delivery, for which the top 5% exhibited 12-fold to 66-fold greater delivery compared with wild-type pHLIP. Of note, there was a large degree of overlap between categories in these top-performing pHLIP phenotypes (SI Appendix, Fig. S8). One-half of the top performers in tumor cell delivery were also top performers in imaging contrast ratio, consistent with the high correlation between these two categories that we previously observed.

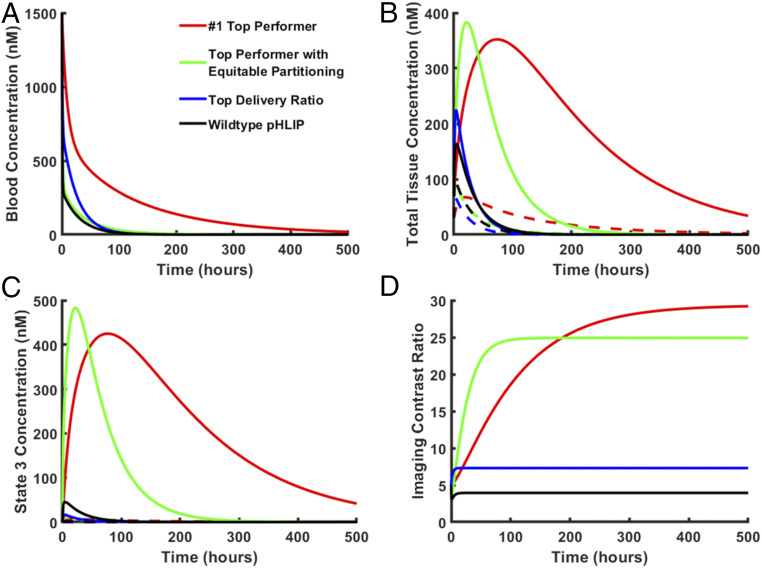
In addition, we found three pHLIP phenotypes that were top performers in all three categories. Of these, one stood out in particular; it was the #1 top performer in both imaging contrast ratio and tumor cell delivery, with an imaging contrast ratio of 29.4 and 66.2-fold greater delivery relative to wild-type pHLIP. It also exhibited a delivery ratio of 114. Of note, this phenotype had an extremely high cell-bound fraction of 92.1% and a free fraction of only 1.2%. We recognize that for a pHLIP variant with such properties, there may be negative consequences not accounted for in our model, such as poor solubility. Thus, we looked for superior top performers with more equitable partitioning fractions. This search yielded a top performer in both the imaging contrast ratio and magnitude of delivery categories, with an imaging contrast ratio of 24.6, a delivery ratio of 79.0, and a magnitude of delivery 22.7-fold greater than that of wild-type pHLIP. We also located the top performer in delivery ratio. While this pHLIP phenotype had an exceptionally high delivery ratio of 497.1, it had a very low magnitude of delivery of approximately one-quarter that of wild type pHLIP. Thus, this phenotype would be ideal for exceptionally potent but low-therapeutic index drugs. The properties of these pHLIP phenotypes and of wild-type pHLIP are summarized in SI Appendix, Table S3. The respective concentration profiles are shown in Fig. 7.

Fig. 7.

Predicted concentration profiles for the top-performing pHLIP phenotypes. The model was run for top-performing pHLIP phenotypes or wild-type pHLIP, respectively. The resulting blood concentration (A), total tissue concentration (B), state 3 concentration (relative to cell volume, which excludes interstitial fluid) (C), and imaging contrast ratio (D) vs. time curves are shown. For total tissue concentration (B) and state 3 concentration (C) curves, solid lines represent tumor concentration, while dashed lines represent normal tissue concentration.

Discussion and Conclusions

We have generated a mathematical model for the pHLIP state 2–state 3 equilibrium and implemented it within a pharmacokinetic model for predicting the biodistribution of pHLIP over time after a single i.v. injection. While the resulting model deepens our understanding of the pHLIP system, it nevertheless exhibits several important limitations. As with every model of a complex biological system, several assumptions had to be made, and a number of factors were unaccounted for. For instance, the partitioning of pHLIP among free, protein-bound, and cell-bound fractions may be influenced by pH. It is possible that the acidic pH of the tumor microenvironment would make pHLIP more hydrophobic, thereby increasing binding to proteins and cells. In addition, endocytosis of state 2 pHLIP also contributes to drug delivery. The significance of this contribution is unclear, and it likely varies substantially among different cell types. However, if significant and comparable between normal cells and tumor cells, it would likely have the effect of reducing the specificity of drug delivery, particularly for pHLIP variants with high cell binding. Furthermore, recent studies suggest that the tumor bulk extracellular pH may underestimate the acidity at the tumor cell surface (17, 18). Although a direct comparison of in vivo tumor cell surface pH to bulk extracellular pH has yet to be performed, the difference is likely around 0.2 pH units (17, 18). Our model suggests that for a bulk tumor extracellular pH of 6.6, this difference would increase total pHLIP tumor concentration somewhat (Fig. 5A) and would slightly improve our model’s agreement with experimental data (Fig. 3B); however, tumor cell delivery and the delivery ratio would be significantly increased. Finally, our model fails to account for certain practical considerations, such as the solubility of a pHLIP construct. pHLIP variants with high cell and protein binding may also exhibit reduced solubility, which could limit their utility. Owing to these and other factors, the quantitative accuracy of the predictions of our model is limited, and the predicted values should be interpreted only as rough estimates under the defined constraints and conditions. Most importantly, it should be emphasized that our model only describes the properties of optimal pHLIP variants in terms of partitioning and insertion/exit pK_a/cooperativity coefficient—it does not describe how to generate a pHLIP variant with such properties.

Nevertheless, our model closely matches the experimental data for wild-type pHLIP, and we have used it to gain further insight into the mechanisms behind pHLIP tumor targeting, as well as the various biological parameters that influence it. For instance, we found that the EPR effect and tumor intracellular pH are also important contributors to pHLIP tumor targeting and delivery, whereas only tumor extracellular pH had previously been emphasized. In addition, the overall tumor:normal tissue contrast ratio obtained in imaging studies significantly underestimates the analogous ratios for cell-bound pHLIP and state 3 pHLIP, respectively. This knowledge suggests to us several avenues for future exploration. For instance, our model supports the use of imaging agents attached to the C terminus that are activated within the cell cytosol. Such a strategy was previously successfully implemented with quenched TAMRA cargoes activated by disulfide reduction in the cell cytosol (32). However, the addition of a cargo to the C terminus can dramatically slow insertion, thereby reducing the amount delivered and thus the overall signal of the imaging agent. Since the tumor:normal tissue ratio of cell-bound (state 2 + state 3) pHLIP is also significantly higher than the overall tumor:normal tissue contrast ratio, it may be beneficial to instead use N terminus-linked imaging agents that are activated at the cell membrane. For example, there exist several fluorophores that exhibit significant increases in brightness when exposed to the lipid environment of the cell membrane, such as indocyanine green. Such a pHLIP imaging agent, while not as tumor-specific as a state 3-activated agent, may produce the best compromise between tumor specificity and overall signal.

Our model also suggests strategies that may aid the search for more effective pHLIP variants. For example, we found that the partitioning of a pHLIP in solution among protein-bound, cell-bound, and free states can have a substantial impact on its tumor targeting and delivery. Thus, we recommend measuring these fractions when screening pHLIP variants before in vivo use. Measurements can be accomplished with methods such as the in vitro blood partitioning assay used in this study (SI Appendix, section 4.1). In addition, we found that the pK_a for the state 2–state 3 equilibrium in liposomes is significantly shifted to higher pH values in cells and is the net result between two different insertion and exit pK_a values. With our state 2–state 3 equilibrium model, we can predict the pK_a shift for cells, and by fitting our model to state 2–state 3 equilibrium titration curve data, we may gain insight into the insertion and exit pK_a values, along with their respective cooperativity coefficients, for a particular pHLIP variant. However, a method for directly measuring these parameters would of course be far more accurate and predictive. Solid-state NMR can be used to obtain the insertion and exit pK_a values (14), but is a difficult and time-consuming process. Thus, the development of a faster and more streamlined method may prove extremely useful for the preclinical screening of pHLIP variants. If methods for determining pK_a, cooperativity coefficient, and partitioning parameters are sufficiently streamlined, it may be possible to use our pharmacokinetic model as an in silico screening tool to predict which pHLIP variants should be advanced to further preclinical, including in vivo, studies.

Finally, our model can be used to predict the properties of optimal pHLIP variants. When we ran our model 1,000 times with randomly generated pHLIP parameters, we found several pHLIP phenotypes with improved properties compared with wild-type pHLIP. Thus, our model might be used to guide the design of better pHLIP variants. An important part of the future path will be to acquire knowledge of how to design or modify a pHLIP peptide to achieve specific insertion/exit pK_a values, cooperativity coefficient values, and partitioning fractions. For example, it is possible that adding hydrophobic groups to a pHLIP peptide will improve its imaging contrast ratio by increasing partitioning to the protein-bound and/or cell-bound states. Therefore, we suggest future studies along these lines. Given the increasing range of clinical applications of the pHLIP technology that appear on the horizon, it is most exciting that there may be even more effective uses possible in the future.

Data Availability.

All study data are included in the article and SI Appendix.