Oral minimal model-based estimates of insulin sensitivity in obese youth depend on oral glucose tolerance test protocol duration

Abstract

Introduction

The Oral Minimal Model (OMM), a differential-equations based mathematical model of glucose-insulin dynamics, utilizes data from a frequently sampled oral glucose tolerance test (OGTT) to quantify insulin sensitivity ($S_I$). OMM-based estimates of $S_I$ can detect differences in insulin resistance (IR) across population groups and quantify effects of clinical or behavioral interventions. These estimates of $S_I$ have been validated in healthy adults using data from OGTTs with durations from 2 to 7 h. However, data demonstrating how protocol duration affects $S_I$ estimates in highly IR populations such as adolescents with obesity are limited.

Methods

A 6-h frequently sampled OGTT was performed in adolescent females with obesity. Two, 3-, and 4- hour implementations of OMM assuming an exponentially-decaying rate of glucose appearance beyond measured glucose concentrations were compared to the 6-h implementation. A 4- hour OMM implementation with truncated data (4h Tr) was also considered.

Results

Data from 68 participants were included (age 15.8 ± 1.2 years, BMI 35.4 ± 5.6 kg/m²). Although $S_I$ values were highly correlated for all implementations, they varied with protocol duration (2h: 2.86 ± 3.31, 3h: 2.55 ± 2.62, 4h: 2.81 ± 2.59, 4h tr: 3.13 ± 3.14, 6h: 3.06 ± 2.85 x 10^-4 dl/kg/min per U/ml). $S_I$ estimates based on 2 or 3 h of data underestimated $S_I$ values, whereas 4-h $S_I$ estimates more closely approximated 6-h $S_I$ values.

Discussion

These results suggest that OGTT protocol duration should be considered when implementing OMM to estimate $S_I$ in adolescents with obesity and other IR populations.

1. Introduction

Measures of insulin sensitivity ($S_I$) quantify the ability of insulin to both suppress endogenous glucose release and promote glucose uptake in response to a glucose challenge. Decreased $S_I$ is a critical component of metabolic syndrome, polycystic ovary syndrome (PCOS), type 2 diabetes mellitus and type 1 diabetes, and it contributes significantly to morbidity and mortality in these populations [[1], [2], [3], [4]]. Decreased $S_I$ is also present in adolescents with obesity [[5], [6], [7]]: adolescents display a puberty related reduction in $S_I$ and greater insulin secretion rates when compared to adults [8,9]; excess weight is known to further decrease the $S_I$ reduction associated with pubertal status; and $S_I$ is markedly lower in teenage girls compared to boys [[10], [11], [12]].

The hyperinsulinemic euglycemic (HE) clamp remains the gold standard for measuring $S_I$ in adults and youth with and without obesity [2,[13], [14], [15], [16], [17]], but it is invasive, labor intensive, and does not represent physiological conditions [[18], [19], [20]]. Similarly, the intravenous glucose tolerance test (IVGTT) is non-physiological due to the IV infusion that bypasses the gut [21]. Several surrogate indices, including HOMA [22], QUICKI [23], and the Matsuda index [24] have been developed to efficiently quantify $S_I$ in the clinical setting [23,[25], [26], [27], [28], [29]]. Alternatively, the Oral Minimal Model (OMM), a mathematical model of glucose-insulin dynamics in the more physiological conditions of an oral glucose tolerance test (OGTT) [[30], [31], [32]], may be used to estimate $S_I$. The OMM describes an individual’s plasma glucose response to a glucose challenge, and model parameters are used to derive a model-based measure of $S_I$ that demonstrates increased sensitivity to group differences compared to fasting and OGTT-based indices of $S_I$ [[33], [34], [35], [36], [37]].

The OMM was developed in healthy adults and validated against the HE clamp using data from a 7-h OGTT, but some implementations of OMM have been applied in adults with type 2 diabetes and adolescent cohorts [30,[38], [39], [40], [41], [42], [43]]. $S_I$ estimates from shorter OGTT/OMM protocols have been validated in adult populations without type 2 diabetes [30,38], lean to obese adolescents [40], and adolescent girls [42,43]. However, insulin resistance (IR) alters the glucose-insulin dynamics represented by OMM, and protocol duration dependence of OMM $S_I$ estimates has not been rigorously assessed in populations expressing diverse metabolic phenotypes.

To address this gap, we compared $S_I$ estimates computed using a 6-h protocol to $S_I$ estimates computed with data from shorter protocols in a cohort of sedentary, highly IR adolescent girls with obesity. In this cohort and other IR populations, glucose may remain elevated for extended periods reflecting dysglycemia [44]. For these individuals, longer OGTT protocols may facilitate a more reliable OMM-based estimation of $S_I$ [41]. However, in IR individuals this constraint may require extending OGTT protocols to durations of 6 or 7 h [30]. Given the extended period of elevated glucose concentrations in our cohort, we hypothesized that estimates of $S_I$ would depend on protocol duration and that at least 4 h of data are required to accurately estimate $S_I$ using OMM.

2. Materials and methods

2.1. Participants

This is a secondary analysis of data collected in the APPLE (Liver and Fat Regulation in Overweight Adolescent Girls; NCT02157974) and PLUM (Post-Prandial Liver Glucose Metabolism in PCOS; NCT03041129) studies performed to explore abnormalities in PCOS. These studies consisted of two visits: 1) consent/screening for eligibility; 2) overnight monitored fast followed by an OGTT for metabolic assessment. Inclusion criteria were female sex, overweight/obese status (BMI ≥ 90th percentile for age and sex), post pubertal status (Tanner Stage 5) and a sedentary lifestyle (<3 h routine exercise per week, validated with both a 3-day activity recall and 7-day accelerometer use). Sixty-eight participants were included in this analysis (18 with normal menses and 50 with PCOS). Participants with PCOS were medication naïve and defined according to the NIH criteria: 1) an irregular menstrual cycle, 2) ≥18 months post-menarche and, 3) clinical and biochemical evidence of hyperandrogenism. Exclusion criteria for the studies included the following: confirmed diagnosis of diabetes, pregnancy, anemia, liver diseases other than non-alcoholic fatty liver disease (NAFLD), an alanine transferase (ALT) level greater than 125 (IU/L) and use of medications known to affect insulin sensitivity or glucose metabolism (including systemic steroids, antipsychotics and treatment with hormonal contraception or metformin) in the last six months. The study was approved by the Colorado Multiple Institutional Review Board. Informed consent was obtained from all participants 18–21 years old, and parental consent and participant assent from all participants between 12 - 18 years old.

2.2. OGTT protocol

Participants refrained from physical activity 3 days prior to the metabolic stay, and consumed an isocaloric diet (65% carbohydrate, 15% protein, 20% fat) the afternoon and evening prior to the OGTT. Following a monitored inpatient 12-h fast, a frequently sampled OGTT was performed. Blood was sampled for glucose and insulin concentrations at the following time points: 0, 10, 20, 30, 45, 60, 75, 90, 105, 120, 135, 150, 180, 210, 240, 300 and 360 min after ingesting 75 g plus an additional 40 mg/kg of glucose and 25 g of fructose. Fructose was included to drive de novo lipogenesis [45] and did not contribute to plasma glucose concentrations [46]. Blood glucose was measured at the bedside with the StatStrip® Hospital Glucose Monitoring System (Novo Biomedical, Waltham, MA, USA). Serum insulin was measured with radioimmunoassay (Millipore, Billerica, MA).

2.3. Oral minimal model

The OMM was used to simulate glucose-insulin dynamics and estimate $S_I$ [30]. The OMM is a one-compartment model represented by the following equations:

$$\{\begin{array}{l}\dot{G}\left(t\right)=-\left[S_G+X\left(t\right)\right]\cdot G\left(t\right)+S_G\cdot G_b+\frac{R{a}_{meal}(\mathit{\alpha },t)}{V}G\left(0\right)=G_b\hfill \\ \dot{X}\left(t\right)=-p_2\cdot X\left(t\right)+p_3\cdot \left[I\left(t\right)-I_b\right]X\left(0\right)=0\hfill \end{array}$$

with

$$R{a}_{meal}\left(\mathit{\alpha },t\right)=\{\begin{array}{l}{\alpha }_{i-1}+\frac{{\alpha }_i-{\alpha }_{i-1}}{t_i-t_{i-1}}\cdot \left(t-t_{i-1}\right)for{t}_{i-1}\le t\le t_i,i=1,\dots ,n\hfill \\ 0otherwise\hfill \end{array}$$

where G(t) is glucose concentration; X(t) is insulin action; I(t) is insulin concentration; G_b and I_b are basal glucose and insulin concentrations, respectively; S_G, p₂ and p₃ are rate constants; and $R{a}_{meal}(\mathit{\alpha },t)$ is a piecewise-linear function describing the rate of appearance of exogenous glucose. The time breakpoints t_i were specified by the sampling times and protocol duration, and parameter $\mathit{\alpha }$ = [${\alpha }_0,{\alpha }_{1,}\dots ,{\alpha }_n$]^T with ${\alpha }_0=0$ are unknown amplitudes [30,31,39]. The breakpoints for the 6-h protocol represent the sampled time points for the full glucose profile, and the breakpoints for the shorter protocols represent truncated subsets of the 6-h breakpoints based on protocol duration (see Supplementary Material for details) [38].

We implemented both “truncated” and “exponential” versions of OMM. For sufficiently long protocols that showed glucose and insulin concentrations returning to baseline values (4- and 6- hours of data), we directly applied the OMM to compute $S_I$ (“truncated models”). For shorter protocols, it has been recommended to assume an exponential decay of $R{a}_{meal}(\mathit{\alpha },t)$ after the last time breakpoint [47]. In our IR population, we explored this approach for 2-, 3- and 4-h OGTT protocols using both fixed and estimated decay time constants (“exponential models,” see Supplementary Material for details). In the exponential models, $S_I$ was estimated directly, and in the other model implementations $S_I$ was defined to be

$$S_I=\frac{p_3}{p_2}\cdot V$$

with units dl/kg/min per $\mu$U/ml [31]. To improve numerical identifiability of OMM, we applied two constraints that have been described previously [30,31]. Details regarding these constraints are included in Supplementary Material.

The OMM was implemented for each participant using 2, 3, 4 and 6 h of data. For exponential models, exponential decay of the rate of appearance of glucose was assumed following the last time point for 2, 3, and 4 h of data. All model equations were implemented in SAAM II (SAAM II software v 2.2, The Epsilon group, Charlottesville, VA, USA).

2.4. Statistical analysis and model comparison

All model comparisons were performed in MATLAB (Mathworks, Natick, MA). Data are reported as the mean ± SD. ANOVA was used to compare $S_I$ values obtained from each method. The 6-h OMM $S_I$ estimates were taken to be the reference estimates because glucose concentrations returned to baseline for all participants by 6 h [30]. Six hour estimates were compared to the $S_I$ estimates from shorter OMM protocol durations using Pearson’s correlation coefficients, linear regressions, and Bland-Altman plots [48] to quantify the differences between estimates obtained using different methods. The Williams correlation test was used for pairwise comparison of the strengths of the correlations [49]. Additionally, the mean squared error (MSE) between 6-h OMM $S_I$ estimates and $S_I$ estimates from protocols of shorter duration were computed, and we compared these errors using paired t-tests. For Bland-Altman plots the bias, the 95% confidence intervals of the bias, and the 95% limits of agreement between the $S_I$ estimates obtained using the two methods are reported.

To investigate the differences in $S_I$ values estimated using the 4-h truncated model and the 4-h exponential model, participants were divided into subgroups based on 4 h glucose concentrations being above, below or within 10 mg/dl of baseline glucose. For each subgroup, the MSE between 4-h $S_I$ estimates associated with the exponential and truncated models and 6-h estimates were calculated. The errors associated with the $S_I$ estimates obtained from 4-h exponential and 4-h truncated models were compared using paired t-tests. Correlations between the $S_I$ estimates from the 6-h OMM and the $S_I$ estimates from the 4-h exponential and 4-h truncated models by subgroup were calculated and compared for each subgroup [50].

The error between the glucose data and simulated 6-h glucose concentrations for each of the four models was computed as the square root of the squared sum of differences between the data and simulated glucose at each sample time. To elucidate how the exponential assumption for $R{a}_{meal}\left(\mathit{\alpha },t\right)$ translates to glucose dynamics across the OGTT, the 2-, 3- and 4-h exponential models were simulated for 6 h. Predicted glucose concentrations associated with each model were plotted with the glucose concentration data and the 6-h model simulations. Model simulations were performed using the MATLAB built-in ode solver ode45. P-values < 0.05 were considered significant; we report p-values greater than 0.001 and otherwise report p-values as <0.001.

3. Results

3.1. Participants

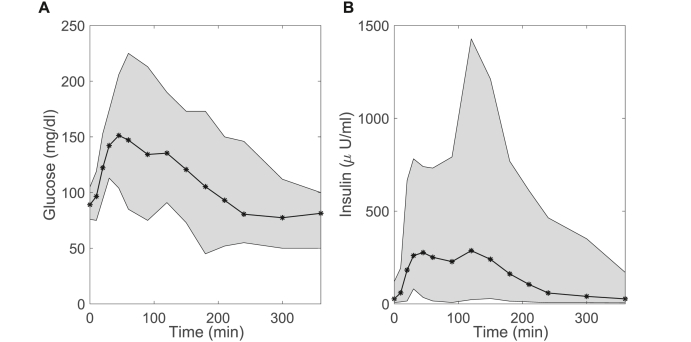
Sixty-eight participants were included in this study. Participant demographics are summarized in Table 1. The mean 2-h glucose is close to the pre-diabetes cut-off of > 140 mg/dl demonstrating that dysglycemia was common in this cohort. The average glucose and insulin concentrations across the OGTT illustrate the moderate variability in glucose and large variability of insulin concentrations for this participant group (Fig. 1).

Table 1.

Participant Characteristics. Data shown are mean ± standard deviation of the mean unless otherwise noted.

Age (years)	15.8 ± 1.2
Race/Ethnicity (N)
Non-Hispanic White	23
Hispanic White	35
Black	8
Asian	2
Age at Menarche (Years)	11.6 ± 1.5
Family history of T2D (%)	76%
Weight (kg)	94.0 ± 16.5
Height (cm)	164 ± 7
BMI (kg/m2)	35.4 ± 5.6
BMI percentile	97.6 ± 2.0
BMI Z-score	2.08 ± 0.34
Waist:Hip Ratio	0.89 ± 0.07
Hemoglobin A1c (%)	5.4 ± 0.3
Fasting glucose (mg/dl)	90 ± 9
2 h glucose (mg/dl)	136 ± 24
Fasting Insulin (mIU/l)	28 ± 16
2 h insulin (mIU/l)	276 ± 200

Fig. 1.

Glucose and insulin concentrations. Glucose (A) and insulin (B) concentration ranges for all study participants (n=68, all female) for 6-h OGTT. Mean glucose and insulin concentrations (black line), ± max/min values (grey shading) indicate range of variability across cohort.

3.2. OMM implementations

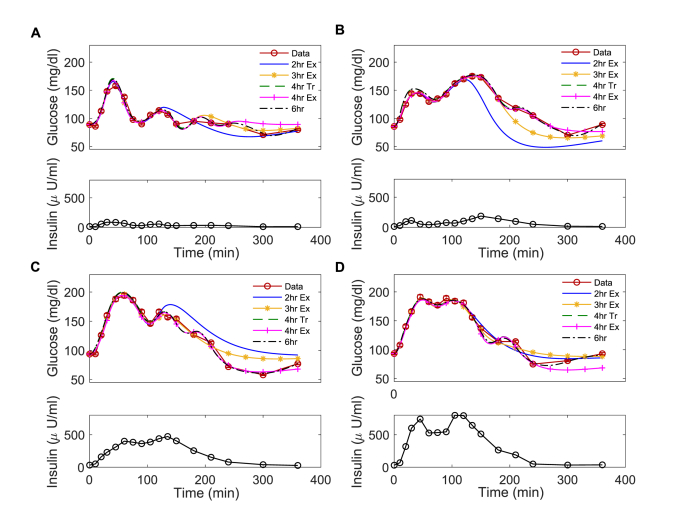
Glucose and insulin data are presented with simulated glucose time traces for each model for four representative participants, ordered from more to less insulin sensitive (Fig. 2). The measured insulin concentration data describe each individual’s insulin response to the OGTT and are used to force the insulin action dynamics in OMM.

Fig. 2.

Simulated glucose dynamics for OMM implementations of different durations. Glucose and insulin (A, B, C, D) profiles for representative participants with high (A, B) or low (C, D) insulin sensitivity as assessed by 6h $S_I$. The simulated glucose dynamics obtained using the 2h Ex, 3h Ex, 4h Tr, 4h Ex, and 6h implementations of OMM are plotted with the glucose data for four participants. For truncated models (4h Tr and 6h), there are no assumptions of glucose dynamics beyond the specified time breakpoints. For the exponential models (2h Ex, 3h Ex and 4h Ex), exponential decay of the rate of appearance of glucose is assumed after 120 min., 180 min., and 240 min., respectively.

All of the models accurately described glucose concentrations over the duration for which data were specified as assessed by least squares error. By contrast with the 6-h and 4-h truncated models, the exponential models predicted glucose concentrations beyond the duration for which data were specified using the assumption of the exponentially decaying $R{a}_{meal}(\mathit{\alpha },t)$. However, in general, exponential assumptions for $R{a}_{meal}\left(\mathit{\alpha },t\right)$ did not accurately reproduce glucose profiles. Error generally decreased with model duration with mean errors of 60.73 ± 36 (mean ± SD), 40.80 ± 23, 29.61 ± 17 and 19.43 ± 6 mg/dl for the 2-, 3- and 4- hour exponential models and the 6-h model, respectively.

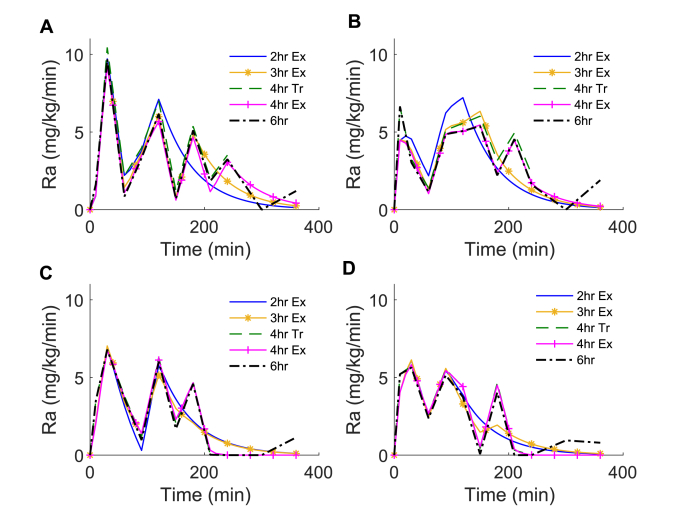
The estimated profiles of $R{a}_{meal}(\mathit{\alpha },t)$ also varied with model duration as seen for the 4 representative participants (Fig. 3). In general, the assumption of exponential decay in the 2-, 3- and 4-h exponential methods resulted in less variability in $R{a}_{meal}(\mathit{\alpha },t)$ compared to the rates predicted in the 6-h OMM implementation.

Fig. 3.

Estimated rate of appearance of drink glucose for OMM implementations of different durations. The rate of appearance of exogenous glucose (Ra) estimated for each model for the 4 representative participants reported in Fig. 2. Onset of exponential decay of 2h Ex, 3h Ex and 4h Ex OMM models is initiated after 120, 180, and 240 min, respectively.

3.3. Model comparisons

To investigate the effect of model duration on estimated $S_I$, we compared $S_I$ values calculated using the 6-h OMM to $S_I$ values calculated from OMM implementations with shorter durations over all participants. For each model, average $S_I$ estimates and average precision of $S_I$ estimates given as the coefficient of variation (CV) were determined (Table 2). Mean $S_I$ values for all participants were not significantly different across methods (ANOVA, p = 0.79). However, the MSE between the 6-h $S_I$ estimates and $S_I$ estimates from shorter OMM implementations decreased with protocol duration with the lowest errors associated with the 4-h truncated model. Specifically, the errors for $S_I$ estimates from the 4-h truncated model were lower compared to the errors for the $S_I$ estimates from other models with the exception of the 2-h exponential model (4-h exponential: p < 0.001; 3-h exponential: p = 0.01; 2-h exponential: p = 0.07). Similarly, the errors for $S_I$ estimates from the 4-h exponential model were lower compared to the errors for $S_I$ estimates from the 3-h exponential model (p = 0.01) and not significantly different from the errors for $S_I$ estimates from the 2-h exponential model (p = 0.78).

Table 2.

Average S_Iestimates, precision of S_Iestimates and MSE.

OMM Implementation	$S_I$, 10-4 dl/kg/min per $\mu$U/ml	Precision, CV %	MSE, 10-9
2-h Ex	2.86 ± 3.31	24.27 ± 5	16.1
3-h Ex	2.55 ± 2.62	19.35 ± 7	10.3
4-h Ex	2.81 ± 2.59	16.25 ± 6	6.79
4-h Tr	3.13 ± 3.14	18.60 ± 6	5.97
6-h	3.06 ± 2.85	12.77 ± 6

Values are mean ± SD. Reported is the average precision of $S_I$ estimates is given as the coefficient of variation (CV %) and the mean squared error (MSE) of $S_I$ estimates from shorter OMM implementations to estimates of $S_I$ from the 6-h.

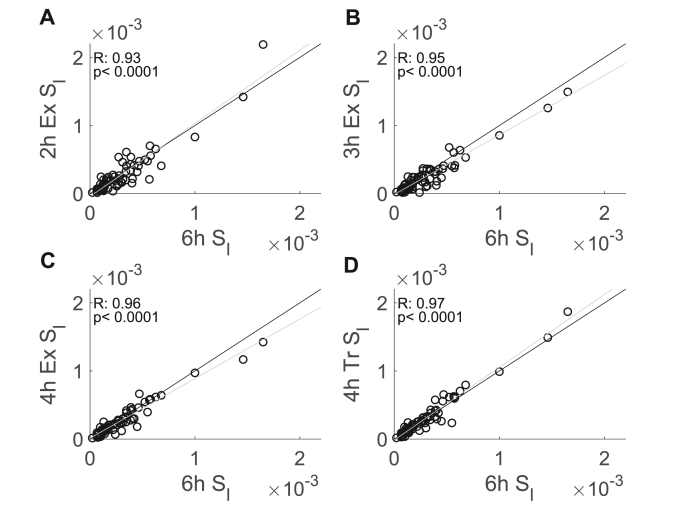
The correlations between the $S_I$ estimates from OMM implementations with shorter durations and the $S_I$ estimates from the 6-h OMM were high and increased monotonically with protocol duration from the 2-h exponential model (R = 0.93) to the 4-h truncated model (R = 0.97) (Fig. 4). Comparisons of correlations showed that the correlations between the 6-h OMM $S_I$ estimates and the 2-h and 3-h exponential $S_I$ estimates, respectively, were generally weaker than the correlations between the 6-h OMM $S_I$ estimates and the 4-h exponential or 4-truncated $S_I$ estimates (2-h exponential v. 4-hour exponential, p = 0.008; 2-h exponential v. 4-hour truncated, p < 0.001; 3-h exponential v. 4-hour truncated, p = 0.02). However, in general, correlations between the 6-h OMM $S_I$ estimates and OMM $S_I$ estimates from OMM exponential implementations were not significantly different (2-h exponential v. 3-hour exponential, p = 0.07; 3-h exponential v. 4-hour exponential, p = 0.29). Moreover, the correlation between the 4-h truncated $S_I$ estimates and the 6-h OMM $S_I$ estimates was not significantly different from the correlation of the 4-h exponential $S_I$ estimates and the 6-h OMM $S_I$ estimates (p = 0.09).

Fig. 4.

Correlations between $S_I$ estimated with the 6-h OMM as a reference and OMM implemented with shorter durations (n = 68, all female). Scatter plots showing the correlations of the 2-h exponential (A), the 3-h exponential (B), the 4-h truncated (C), and the 4-h exponential (D) OMM $S_I$ estimates with the 6-h OMM $S_I$ estimates. The grey line is the least squares fit to the data, and the black line indicates equality of estimates obtained using different models.

To further characterize the correlations between $S_I$ estimates obtained using different OMM implementations, we compared the regression lines associated with $S_I$ estimates from different methods to the identity line. The slopes of the regression lines for the 3- and 4- hour exponential model $S_I$ estimates compared to the 6-h model $S_I$ estimates were 1.03 and 1.05, respectively, and these slopes were not significantly different from 1 (both p < 0.001). The slope of the regression line was 0.79 for the 2-h exponential model $S_I$ estimates and 0.88 for the 3-h exponential model $S_I$ estimates. The intercept for the regression line for the 4-h exponential model $S_I$ estimates was computed as 8.69 x 10^-6, but it was not significantly different from 0 (p < 0.001). All other intercepts were significantly different from 0 (all p < 0.001) with intercepts of 3.03 x 10^-5, 4.24 x 10^-5, and 7.77 x 10^-5 for the $S_I$ estimates associated with the 4-h truncated, 3-h exponential, and 2-h exponential models, respectively.

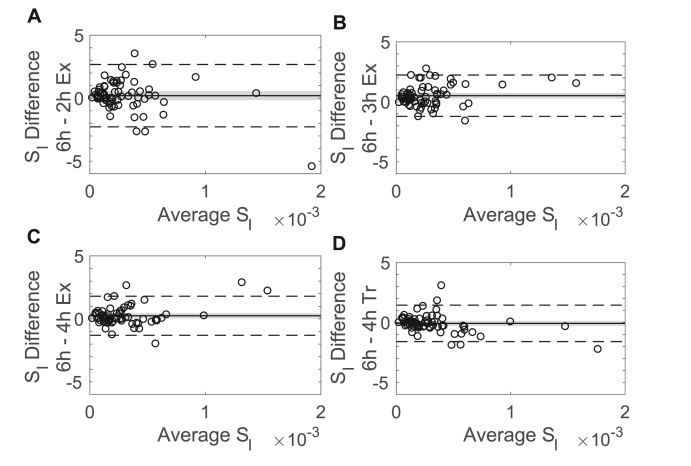
Bland-Altman plots demonstrated the differences in the $S_I$ estimates from shorter OMM implementations compared to the 6-h $S_I$ estimates (Fig. 5). Differences between $S_I$ estimates obtained using different models do not show systematic change with average $S_I$ values, indicating that the variability in the differences is not related to the size of the measurement. The biases for the $S_I$ estimates from the 2-, 3-, and 4-h exponential models were of order 10^-5, positive, and, for the 3- and 4-h exponential models, significantly different from zero, indicating that these models underestimate $S_I$. By contrast, the bias for the 4-h truncated model was an order of magnitude smaller than the bias for the other models, negative, and the CI of the bias contained zero. Similar results were observed when analyzing Bland-Altman plots for the percent differences with the smallest bias in the percent differences occurring for the 4-h truncated model (data not shown).

Fig. 5.

Bland-Altman plot showing the bias of the $S_I$ estimates computed with the 6-h OMM and with OMM implementations of shorter durations (n=68, all female). The bias (solid line), the confidence interval of the bias (shaded region), and the 95% limits of agreement (dashed line) are reported. The 2-h exponential model (A), 3-h exponential model (B), and 4-h exponential model (C), all showed a small positive bias indicating that these models underestimate $S_I$. The 4-h truncated model (D) had a small negative bias indicating this model overestimated $S_I$.

3.4. Baseline glucose affects variability in S_I estimates

To better understand the effects of delayed return to baseline and reactive hypoglycemia on the 4-h OMM implementations, we considered glucose concentrations 4 h after drink ingestion relative to return to baseline glucose for each participant. After dividing participants into subgroups based on whether they were above, below, or within 10 mg/dl of their baseline glucose concentrations at 4 h we compared 4-h $S_I$ estimates from both the exponential and truncated models for each subgroup. Approximately 54% (n = 37) of participants had 4-h glucose concentrations at least 10 mg/dl below their baseline glucose levels; 10% (n = 7) of participants had 4-h glucose concentrations at least 10 mg/dl above their baseline glucose levels; and the remaining participants (n = 24) had 4-h glucose concentrations within 10 mg/dl of their baseline glucose levels.

We compared $S_I$ estimates from the 4-h exponential and 4-h truncated models relative to the 6-h $S_I$ estimates using MSE. The MSE of the 4-h exponential $S_I$ estimates was 1.07 x 10^-8, 1.27 x 10^-8, and 2.21 x 10^-9 for subgroups with 4-h glucose concentrations that were 10 mg/dl above, within, or below baseline glucose concentrations, respectively. The MSE of the 4-h truncated $S_I$ estimates was 3.50 x 10^-9, 9.98 x 10^-9, and 3.50 x 10^-9 for the above, within, and below 10 mg/dL subgroups, respectively. For each subgroup, the errors in $S_I$ estimates from the 4-h exponential and 4-h truncated models were significantly different: errors in $S_I$ estimates associated with the 4-h exponential model were lower for the 10 mg/dl below baseline subgroup (p = 0.003), and errors in $S_I$ estimates from the 4-h truncated model were lower for the 10 mg/dl above (p = 0.002) and within (p = 0.03) subgroups.

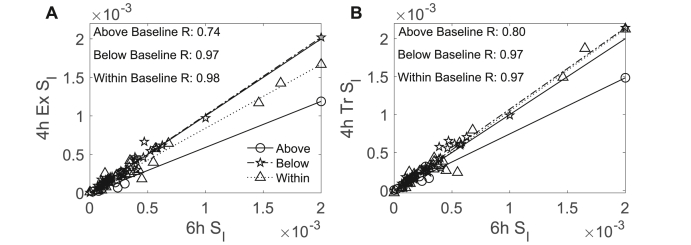
We also compared the correlations for $S_I$ estimates from both 4-h models to $S_I$ estimates from the 6-h model by subgroup. We did not detect differences in correlations of $S_I$ estimates based on the 4-h model used; however, we did observe differences by subgroup. Specifically, we found that for the 4-h exponential model, the correlation in $S_I$ estimates for the 10 mg/dl above baseline subgroup (R = 0.74) was weaker compared to the correlations for other subgroups (all R ≥ 0.97; within: p = 0.02; below: p = 0.02) (Fig. 6). Similarly, for the 4-h truncated model, the correlation in $S_I$ estimates for the 10 mg/dl above baseline subgroup (R = 0.80) was weaker compared to the correlation for the 10 mg/dl within baseline subgroup (R = 0.97; p = 0.05) and marginally weaker compared to the correlation for the 10 mg/dl below baseline subgroup (R = 0.97; p = 0.06). There were no differences in the correlations of $S_I$ estimates from either 4-h model for the 10 mg/dl below or within subgroups (4-h exponential: p = 0.92, 4-h truncated: p = 0.73). These results indicate that the $S_I$ values estimated using either 4-h model were less reliable for the 10 mg/dl above baseline subgroup compared to the other subgroups.

Fig. 6.

Strength of correlation of $S_I$ estimates using 4- and 6-h OMM protocols varies for subgroups specified by participants’ 4-h glucose concentrations relative to their baseline glucose concentrations. $S_I$ estimates calculated with the 4-h exponential OMM were strongly correlated with 6-h OMM $S_I$ estimates for participants who were 10 mg/dl within (n=24, all female, p < 0.001) and below (n=37, all female, p < 0.001) their baseline glucose concentrations after the first 4 h of the OGTT protocol but not for participants who were 10 mg/dl above (n=7, all female, p=0.06) (A). $S_I$ estimates calculated with the 4-h truncated OMM were correlated with 6-h OMM $S_I$ estimates for participants who were 10 mg/dl above (n=7, all female, p=0.03), within (n=24, all female, p < 0.001), and below (n=37, all female, p < 0.001) their baseline glucose concentrations after the first 4 h of the OGTT protocol (B).

4. Discussion

We investigated differences in $S_I$ estimates obtained from 2-, 3- and 4-h implementations of OMM as compared to a 6-h OMM implementation to describe OGTT glucose concentration data in adolescent girls with obesity. Insulin sensitivity is reduced in adolescents compared to adults [9,51], and the estimates of $S_I$ in our cohort of adolescent girls with obesity are consistent with reduced insulin sensitivity as reported in previous studies [52]. However, our results established that, in this cohort, OMM-based $S_I$ estimates depend on the duration of the data considered and generally improve with inclusion of more data up to 6 h. OMM-based estimates of $S_I$ utilize the full dynamics of glucose and insulin during the course of an OGTT to describe $S_I$ [53]. In the current analysis, we took the $S_I$ estimates from a 6-h OMM to represent the reference estimate against which other $S_I$ estimates are compared because the 6-h protocol was sufficiently long that glucose concentrations returned to baseline levels for all participants, a feature associated with optimal numerical identifiability of OMM. Furthermore, longer protocol durations enabled the inclusion of the full glucose profile, so more features of the data were represented in these estimates of $S_I$.

Of the shorter implementations, the 4-h truncated OMM provided the most reliable estimates of $S_I$ compared to $S_I$ estimates from other OMM implementations. For the majority of participants, glucose concentrations return to baseline after 4 h, and, therefore, 4- and 6-h $S_I$ estimates reflect similar data features. Estimates of $S_I$ using implementations of OMM for shorter durations of data were highly correlated with the 6-h OMM $S_I$ estimates consistent with results in healthy adult populations [38]. However, in our IR cohort, $S_I$ estimates from 2-, 3-, and 4-h exponential OMM implementations showed significant bias indicating that these methods may underestimate $S_I$ compared to 6-h OMM $S_I$ estimates, thereby potentially misrepresenting the degree of metabolic disease experienced by a particular individual or patient population. These results suggest that, in a cohort of adolescent girls with obesity, reliable estimates of $S_I$ using OMM require OMM implementations based on OGTT data of at least 4 h. These findings are consistent with results suggesting that glucose and insulin concentrations at the 240 min time point may help estimate $S_I$ in adults with severe type 2 diabetes [41].

By contrast with our results, previous studies that investigated the effect of protocol duration on OMM-based estimates of $S_I$ did not find that $S_I$ was sensitive to protocol duration [38]. However, these studies focused on healthy adult populations or small populations of adolescents [40]. The protocol duration-dependence we observed may arise from assumptions in the model that do not apply to our cohort of adolescent girls with obesity. For example, we observed more variability in the rate of appearance of glucose ($R{a}_{meal}\left(\mathit{\alpha },t\right)$) in our cohort compared to published estimates from adults [31]. This difference reflected the increased variability in glucose trajectories following drink ingestion, longer durations of elevated glucose, and frequent incidence of reactive hypoglycemia (in which glucose concentrations fall below baseline levels during the recovery from the glucose challenge) in our cohort compared to the glucose profiles of healthy adults [9]. To account for these features of the glucose profiles in our cohort, we included more breakpoints in our linear approximation of $R{a}_{meal}\left(\mathit{\alpha },t\right)$. This approach produced robust simulated glucose profiles, however, it may have contributed to overfitting of $R{a}_{meal}\left(\mathit{\alpha },t\right)$ in our participants. More work is needed to establish optimal breakpoints for the representation of $R{a}_{meal}\left(\mathit{\alpha },t\right)$ in populations, such as adolescent girls with obesity, with atypical glucose trajectories following drink ingestion.

Relatedly, we found that the glucose-insulin dynamics in our cohort were not well described by implementations of OMM that assumed exponential decay of $R{a}_{meal}\left(\mathit{\alpha },t\right)$ after 2, 3, or 4 h in contrast to results for other populations [31]. Specifically, previous work describing implementations of OMM with 2- or 3- hour OGTT protocols has imposed an exponential decay in $R{a}_{meal}\left(\mathit{\alpha },t\right)$ to account for the time course of glucose absorption in 2- or 3-h OGTT protocols when glucose concentrations have not returned to baseline levels by the 120 min or 180 min time point, respectively. This method was developed in relatively healthy adults and successfully described glucose dynamics in these participants [30]. However, this assumption did not represent the glucose dynamics observed in most participants in this study even when time constants of decay were estimated as a parameter of the model. This mismatch was particularly pronounced in the glucose profiles of participants with the lowest $S_I$ estimates whose glucose concentrations tended to remain high beyond 120 min. Furthermore, the assumption of exponential decay in the 4-h exponential model adversely affected reliability of $S_I$ estimates, although this effect was minimized for participants with 4-h glucose concentrations near or below baseline glucose levels where this assumption minimally affected glucose dynamics. These results highlight the challenges of applying OMM in populations with diverse metabolic phenotypes such as adolescents with increased insulin secretion rates, women and girls with PCOS, and individuals with other metabolic diseases.

Our results demonstrating that estimates of $S_I$ may depend on protocol duration suggest that preliminary assessment of the typical features of the glucose-insulin dynamics of the study population is necessary to select a protocol duration that is sufficiently long to obtain a reliable estimate of $S_I$. Specifically, shorter OGTT protocols may be sufficient for OMM-based estimates of $S_I$ when the return to baseline of glucose concentrations following peak glucose is rapid, but they may not be sufficient for populations with atypical glucose-insulin dynamics. Thus, the requirements for the precision of $S_I$ estimates should be considered when designing OGTT protocols for OMM-based measures of $S_I$ in IR populations. Furthermore, care should be taken when comparing $S_I$ values estimated using OMM implementations with different protocol durations. Future work using data assimilation techniques may allow for more robust identification of optimal protocol durations for assessing $S_I$ using the OMM in patient populations with diverse metabolic phenotypes.

CRediT authorship contribution statement

Kai Bartlette: Formal analysis, Methodology, Software, Visualization, Writing - original draft, preparation, Review & Editing. Anne-Marie Carreau: Methodology, Software, Writing – review & editing. Danielle Xie: Software, Writing - review & editing. Yesenia Garcia-Reyes: Data curation, Investigation, Resources, Writing - review & editing. Haseeb Rahat: Data curation, Investigation, Resources, Writing - review & editing. Laura Pyle: Formal analysis, Writing - review & editing. Kristen J. Nadeau: Conceptualization, Funding acquisition, Project administration, Supervision, Resources, Writing - review & editing. Melanie Cree-Green: Conceptualization, Funding acquisition, Project administration, Supervision, Resources, Writing - review & editing. Cecilia Diniz Behn: Formal analysis, Methodology, Software, Visualization, Funding acquisition, Writing - original draft, preparation, Review & Editing.

Author contribution

K.B. researched data, performed modeling and statistical analysis, and wrote the manuscript; A.M.C. researched data, performed modeling and co-wrote the manuscript; D.X. performed calculations and edited the manuscript; Y.G.R. researched data and edited the manuscript; H.R. researched data and edited the manuscript; LP contributed to statistical analysis and edited the manuscript; M.C.G. and K.J.N. designed the study, researched data, contributed to discussion and edited the manuscript; C.D.B. contributed to study design, performed modeling and statistical analysis, and wrote the manuscript.

Declaration of competing interest

The authors declare no competing financial interests.

Funding sources

M.C.G.: BIRCWH K12HD057022, NIDDK K23DK107871, Doris Duke 2015212.

D.X.: Bryn Mawr College LILIAC internship program, Endocrine Society Fellowship.

A.M.C. Diabetes Canada Fellowship Award.

C.D.B and K.B.: NSF DMS 1853511. This research was also supported by NCATS Colorado CTSA Grant Number UL1TR002535.

Appendix A. Supplementary data

The following is the Supplementary data to this article: