Abstract
Generating numbers has become an almost inevitable task associated with studies of the morphology of the nervous system. Numbers serve a desire for clarity and objectivity in the presentation of results and are a prerequisite for the statistical evaluation of experimental outcomes. Clarity, objectivity, and statistics make demands on the quality of the numbers that are not met by many methods. This review provides a refresher of problems associated with generating numbers that describe the nervous system in terms of the volumes, surfaces, lengths, and numbers of its components. An important aim is to provide comprehensible descriptions of the methods that address these problems. Collectively known as design‐based stereology, these methods share two features critical to their application. First, they are firmly based in mathematics and its proofs. Second and critically underemphasized, an understanding of their mathematical background is not necessary for their informed and productive application. Understanding and applying estimators of volume, surface, length or number does not require more of an organizational mastermind than an immunohistochemical protocol. And when it comes to calculations, square roots are the gravest challenges to overcome. Sampling strategies that are combined with stereological probes are efficient and allow a rational assessment if the numbers that have been generated are “good enough.” Much may be unfamiliar, but very little is difficult. These methods can no longer be scapegoats for discrepant results but faithfully produce numbers on the material that is assessed. They also faithfully reflect problems that associated with the histological material and the anatomically informed decisions needed to generate numbers that are not only valid in theory. It is within reach to generate practically useful numbers that must integrate with qualitative knowledge to understand the function of neural systems.
Keywords: quantitative morphology, design‐based stereology, number, length, surface, volume
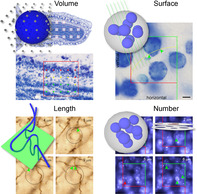
Design‐based stereological methods allow the estimation of basic morphological parameters in representative samples of the sectioned central nervous system. Point probes can be used to estimate volume (illustrated for the Area Fraction Fractionator), line probes can be used to estimate surface area (illustrated for a vertical sections design), area probes can be used to estimate length (illustrated for the Spaceball probe), and volume probes must be used to estimate number (illustrated for the Disector). This review provides an introduction to how these methods solve problems associated with other quantitative approaches, how they are applied to histological material, how a sampling scheme can be designed and evaluated, and which practical problems need to be solved to generate the numbers that we will need to come to an understanding of central nervous system function.
1. INTRODUCTION
Quantitative morphology in the neurosciences is, in the context of this review, defined as studies that provide information about the basic structural organization of the nervous system in terms of—to mention but a few parameters—volumes of brain regions, the numbers of cells or synapses within them, the length of capillaries supplying them, or of membrane areas that are available for substance exchange or synaptic contacts. Like many other specialties within the neurosciences, quantitative morphology is the principal focus of comparatively few research groups. Unlike other specialties and as a consequence of a general striving toward objectivity in the presentation and evaluation of data, quantitative morphology has also been imposed on those whose primary interests are elsewhere. A specialist in a neurodegenerative disease model showing unequivocal qualitative evidence of cell loss will almost inevitably be asked for the provision of data that provide an objective measure—implicitly meaning “numbers”—of how many cells are lost. The next demand will be statistical testing—requiring numbers—that sets diseased apart from healthy. Trying to comply with the demand for numbers, one may check who has previously generated the numbers needed, how they were generated and where the outcome was published. A judgment of quality concerning the “who” and “where” and a judgment of effort concerning the “how” is likely to follow. Unfortunately, quantitative morphology only reached methodological maturity after the onset of the quest for numbers. The bulk of the quantitative morphological methods that together constitute what was called the new or unbiased stereology and what today is commonly referred to as design‐based stereology was introduced in the 1980s and 1990s (for early reviews, see Gundersen, 1986; Gundersen, Bagger, et al., 1988; Gundersen, Bendtsen, et al., 1988; Royet, 1991). Prior to that, studies of respected researchers published in respected journals had hardly an alternative but to resort to methods that, for a large part, were fraught with possible sources of error. A following of studies that use these precedences and that themselves function as precedences must be expected in the course of a methodological paradigm shift. However, one would hope for their numbers to dwindle quickly and for the transition to be brief and uncontroversial.
Subsequent to the introduction of design‐based stereological methods, some journals, for example, The Journal of Comparative Neurology (Coggeshall & Lekan, 1996; Saper, 1996), Neurobiology of Aging (West & Coleman, 1996), or The Journal of Chemical Neuroanatomy (Kordower, 2000) strongly promoted the use of these methods, precipitating a vigorous discussion—in part about the freedom of choice of methods (Guillery & Herrup, 1997). This freedom should, of course, not be challenged. Data collected by any quantitative morphological method in a replicable manner are true by definition of the method. Problems first arise with the interpretation of the data. Do the data provide sound evidence, for example, for a loss of cells following an experimental intervention? Or should they elicit the death knell of a manuscript under review because “the data provided do not support the conclusions being drawn”? In dealing with numbers, the freedom of interpretation of the data is far more restricted than the freedom of choice of methods. If, for example, the method of choice only allows the presentation of a density, that is, a ratio of something (numerator; e.g., cell number or capillary length) per something else (denominator; e.g., tissue volume or cells), it is simply not possible from the ratio alone to make conclusive statements about changes in the total of the numerator or denominator. Figure 1 provides an example for which the idea that differences in densities reflect differences in number would be almost intuitively rejected. Instead, one has to argue why a density, under the particular circumstances of the experiment, may provide good evidence for such a change. Although this may be possible, it would appear more fruitful to either save the time and energy required by the argument or to expend them on discussing what the biological significance of the change would be (Cruz‐Orive, 1994).
FIGURE 1.
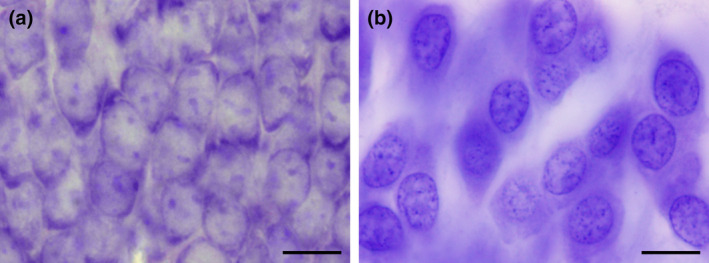
C57 mouse and human hippocampal dentate granule cells. Despite the much higher packing density (a) of ~550,000 granule cells in C57 mice (Ben Abdallah, Slomianka, Vyssotski, & Lipp, 2010), they are by far outnumbered by ~15,000,000 granule cells (West & Gundersen, 1990) in the human hippocampus (b). It is a change in the denominator of density—the total volume of the granule cell layer—that is responsible for the discrepancy between appearance and numbers. Scale bars in a and b: 10 μm [Color figure can be viewed at wileyonlinelibrary.com]
What is puzzling is that, decades after the introduction and vigorous discussion of a new methodology, a shift to more powerful and rather simple methods is, if at all, proceeding at a snail's pace. The reasons are manifold. The very strength of the methods, that is, a mathematical proof can be and often is included in their original description, renders much of the primary methodological literature next to impossible to read for many biologists. Popularizations of the methods may try to restrict themselves to a basic vocabulary, but often fail to realize that the audience simply may not (want to) speak a language of mathematics or statistics (Fawcett & Higginson, 2019). Also, when quantitative morphological methods were prominent tools in neuroscience, many of their users were keenly aware of their problems. This awareness has faded with time and the vast expansion of the neuroscience toolbox.
Yet another reason is the effort required to obtain the measures. Design‐based stereology prided itself to have cut the workload substantially through rational study design (e.g., Gundersen & Østerby, 1981). However, the methods are still, at best, semiautomatic. They require user intervention and hours of work to return a measure. While other methods were equally or even more time consuming in the past, increased computing power has allowed the development of image analysis methods that return data within minutes. Without an understanding why the extra effort provides more reliable data than those quickly generated, the extra effort seems hard to justify—in particular if the additional effort does not seem necessary to publish well. It is a vicious circle that is difficult to break.
The intention of this review is to refresh memories on the problems inherent to quantitative morphology of the sectioned CNS, to provide comprehensible explanations how design‐based stereological methods address these problems and to provide sufficient detail on the application of the methods to allow the design, execution, and evaluation of the outcome of a quantitative morphological study. For more formal introductions, the texts of Russ and Dehoff (2000), Howard and Reed (2010) or West (2012a; serialized in Cold Spring Harbor Protocols) are recommended. Brief introductions have been published by, for example, Schmitz and Hof (2005) or Boyce, Dorph‐Petersen, Lyck, and Gundersen (2010).
Most brain regions contain so many objects—neurons, glia, synapses, and so forth—that workload would make it prohibitive to count them all. The few cases in which “everything” was counted, usually based on serial reconstructions, were primarily concerned with the validation of other approaches that reduce workload (e.g., Baquet, Williams, Brody, & Smeyne, 2009; Delaloye, Kraftsik, Kuntzer, & Barakat‐Walter, 2009; Pover & Coggeshall, 1991). Alternative approaches will always consist of a two‐step process. The first step reduces the workload by sampling only a small fraction of a region of interest. The second step consists of probing the sample in a way that makes the final estimate free from probing related artifacts (see Section 2). Although many of the design‐based stereological methods have been presented as bundled sampling‐probing combinations (e.g., West & Gundersen, 1990; West, Slomianka, & Gundersen, 1991), the two steps are not inextricably linked and can individually be subject to modifications and improvements. Therefore, they will be treated separately in Section 3, which is concerned with sampling, and Sections 4, 7, which are concerned with probes. Once an estimate has been generated, the inevitable question is if it is good enough. Section 8 will help in approaching the answer to this question. Section 9 tries to point out and address some of the problems that arise when theory hits the less than mathematically perfect life in the laboratory.
An argument that occasionally is being put forward against the use of design‐based methods is the cost associated with the software and hardware tools that may be needed to apply them. First, this cost may only be small compared to that of other equipment commonly used. It may not even amount to the operational expenses associated with a single project. Most importantly, the purchase of specialized software and hardware is a purchase of convenience and speed but not one of ability. These tools were not around when many of the methods were developed—sometimes in the form of first applications. Almost all methods that will be presented here can, in principle, be used without special resources. Some simple ways that have been devised to facilitate the work will be presented in conjunction with the sections on sampling and the introduction of specific probes.
2. A PROBLEM
Although the paradigm shift that one could have expected is barely proceeding, the introduction and discussion of new methods have sensitized some experimenters to problems associated with generating quantitative morphological data. One of these problems relates to answering the question “How many are there?” that is, to estimating number. Some responses to the problem, which unfortunately fall short of solving it, and the current best solution will be described here.
2.1. Easy ways to fail
When tissue is cut into sections, some of the objects, for example, cells, contained within the tissue will inevitably be cut too. Fragments of cells that have been cut will be present in two sections. In two‐dimensional representations of the sections, for example, images that have been acquired, the fragments are seen as profiles. If cell profiles would be counted in all sections, the number of profiles would be higher than the number of cells. Now we have the problem: A profile count represents an overcount of actual cell number. The following, very slightly paraphrased responses to the problem of overcounting have been published in descriptions of methodology: “… to avoid double counting of the same cell, sections used to count were a minimum of 100 μm apart. …” or “… we then took every fourth section, so the distance between sections that were counted was 80 μm. Given that the typical cell diameter is smaller than 30 μm, this ensures that the same cell was not counted twice.” There are further variations on this theme.
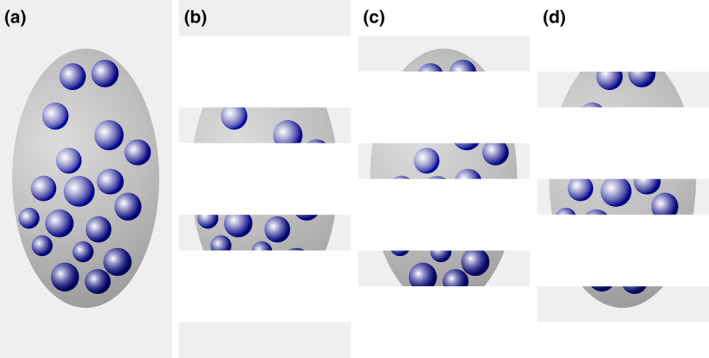
The simplicity of this solution is appealing. It was used in Figure 2 to generate an example of three series of sections fulfilling the criterion that the spacing of the sections is larger than the size of the cells (blue objects) contained in the region of interest (dark gray). The example also has the advantage that the number of cells prior to cutting is known. There are 18 (Figure 2a). Every third section was “collected” in each of the series represented in Figure 2b–d: Figure 2b, sections 1, 4, 7, and 10; Figure 2c, sections 2, 5, and 8; and Figure 2d, sections 3, 6, and 9. None of the individual cells can be double counted in any one of the series. Each series represents, on average, one‐third of the entire region of interest. An estimate of total cell number would, according to the simple solution, be the number of cells counted in any one of the series multiplied by three. The average of the estimates of the three series should correspond to the number of cells contained in the structure—18. Does it?
FIGURE 2.

Profile counts cannot be extrapolated to total cell number. (a) A region (dark gray) containing 18 cells (blue objects) is cut into three series of sections (b–d). In each series, the profiles of cells visible in the sections are counted. Eight cell profiles are counted in the two sections of the region contained in series (b). The three sections in series (c) contain10 cell profiles. The three sections in series (d) contain nine cell profiles. Extrapolating the mean profile count, 9, to total cell number by multiplying with 3 generates an estimate of 27 cells instead of the true value of 18 cells [Color figure can be viewed at wileyonlinelibrary.com]
Unfortunately, it does not; 8, 10, and 9 cell profiles are counted (Figure 2b–d), resulting in estimates of 24, 30, and 27 cells. The average of the three estimates, 27, is 150% of the true number. The possibility that a specific cell is counted twice cannot be the reason for the overestimate. Instead, the problem is caused by assigning a count of “1” to cell fragments that represent less than one entire cell (Billingsley & Ranson, 1918). As long as cells can be fragmented during the sectioning this error will occur, and the size of the error will depend on the likelihood of a cell being cut. The latter depends on the average cell height in relation to the thickness of the sections. If this relation was known, the error could be corrected, which is the basis of Abercrombie's cell counting method (1946; see Section 6.7). Without correction, the true total cell number cannot be obtained using the simple solution. Ironically, this error will not increase even if the sections are spaced close enough together for a specific cell to be present and counted in two sections. If we count in all sections, we see 27 fragments—the same number that we obtained by estimating from every third section. The extrapolation of profile counts to total number will provide us with an estimate of fragment number and not cell number.
Correct total cell numbers are, however, not always the primary aim of a study. When control groups are compared with experimental groups, group differences may be more important than correct total numbers. This has led some investigators to state that “… because the absolute, unbiased number of neurons was not needed to address the questions posed in this study, a profile‐sampling method was used,” or that “… unbiased stereological methods were not used as the data of interest is relative difference and not absolute value,” or that “… no corrections were made for overcounting because we were interested in relative rather than absolute differences in the number of neurons.” The point appears valid at a first glance, if one could be certain that at least the group differences were correct. Figure 3 reexamines the region illustrated in Figure 2. Figures 2 and 3 now may represent members of a control group (Figure 2) and an experimental group (Figure 3).
FIGURE 3.
Dependence of profile counts on object size. (a) A region (dark gray) containing 18 cells (blue objects) is cut into three series of sections (b–d). In each series, the profiles of cells visible in the sections are counted. In series (b), (c), and (d), 10, 13, and 11 profiles are counted. The average of the 3 possible estimates, 30, 39, and 33, is 34. The increase in the size of the cells relative to those in Figure 2 results in an estimate of 34 instead of 27 cells. The true cell number is 18 [Color figure can be viewed at wileyonlinelibrary.com]
Then, 10, 13, and 11 cells are counted (Figure 3), resulting in estimates of 30, 39, and 33 cells. The average of the three estimates, 34, is ~126% of the control value (27 cells estimated from Figure 2). This increase is observed even though the number of cells in the region of interest did not change. There are, again, 18 cells. What did change is the size of the cells. Because their height increased, the likelihood of producing fragments increased and, consequently, the profile count increased. The observed difference in cell number estimates between control (Figure 2) and experimental (Figure 3) individuals is an artifact generated by the increase in size of the cells.
That changes in number occur without changes in size is the central but often unspoken or unrealized assumption that must be true for a faulty method to generate similarly sized errors in controls and experimentals. It is not only counterintuitive—cells do not instantaneously pop in and out of existence—but changes in size of neurons as a reaction to stimuli have been known almost since it became possible to stain neurons (Nissl, 1892). A little more recently, neurons in the entorhinal cortex were found to decrease in size by ~30% following the destruction of hippocampal granule cells (Goldschmidt & Steward, 1992). The age‐related dopaminergic cell death in the substantia nigra is accompanied by an increase in the volume of the remaining cells (Rudow et al., 2008). The age‐related loss of phrenic motor neurons is accompanied by a decrease in the size of the remaining cells (Fogarty, Omar, Zhan, Mantilla, & Sieck, 2018). There are age‐related changes in the volumes of the perikaryon and nucleus of human neocortical neurons (Barger, Sheley, & Schumann, 2015; Stark et al., 2007). Also, an increase in the size of both dentate mossy cells (40%) and interneurons (58%) that survive pilocarpine‐induced seizures has been described (Zhang et al., 2009; Zhang, Thamattoor, LeRoy, & Buckmaster, 2015). A survey of age‐related changes in cell sizes based on earlier methods can be found in Flood and Coleman (1988).
Figures 2 and 3 used spheres to represent cells. If cells are not spherical, the number of profiles counted in a section will not only depend on the size of the cells. It will also depend on their orientation, which may change because of experimental interference or, quite simply, because of a change in the direction in which the tissue is cut. For the sake of brevity, the regions of interest in Figure 4, which illustrates the effect of orientation on profile counts, were not split up into samples of sections. Recall that the number of profiles that can be counted in all sections would correspond to the faulty number of cells (in reality cell fragments) that we would estimate from a series.
FIGURE 4.
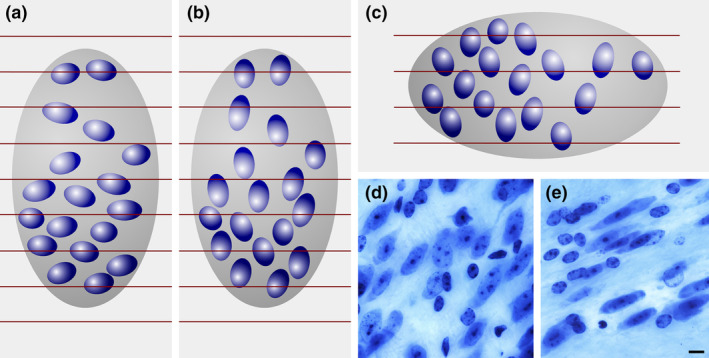
Influence of orientation on a profile count. Red lines represent borders between adjacent sections. The ellipsoid cells in (a) result in a count, across all sections, of 27 profiles. The same cells, unchanged in size but oriented differently in (b), result in a count of 33. Changing the direction of the cutting from, for example, coronal in (a) to sagittal in (c), the profile count increases from 27 to 32. (a) and (c) could also be two brain regions that are cut in the same direction. A laboratory may, for example, claim that the ratio of neurons in (a) to those in (c) is 27/32 = 0.84, while another laboratory using a different cutting direction may claim this ratio to be 32/27 = 1.19—a 40% discrepancy between two results that are both wrong. There are again 18 cells in each structure, and the ratio is 1. One does not have to search long to find neuronal nuclei that are even more elongated than the ones in (a–c): (d) bed nucleus of the stria terminalis, (e) zona incerta, C57 mouse, hematoxylin stain, minimum density projections. Scale bar: 5 μm [Color figure can be viewed at wileyonlinelibrary.com]
If an error can be present because of changes in factors other than number, does an error have to be present? No. The problem is that we do not know. Without further evidence, it is impossible to judge the presence, size, or direction of an error. Also, if significant differences exist between groups, something must have happened. However, without further knowledge about the size, shape, or orientation of the cells, the data generated do not provide unequivocal evidence about the parameter of interest—the number of cells.
Even if we could guess at the approximate size of the error, trying to define a value for an acceptable error does not make sense. First, the outcomes of statistical testing depend not only on the difference between the group means but also on the variability of the groups and the number of individuals in each group. However small a difference may be, it can generate a positive statistical outcome provided the number of individuals is large enough or the variability is small enough. It is not just the perhaps small danger of finding a completely artificial difference, but also the increase in the risks of false‐positive and false‐negative findings that make even small errors treacherous. The definition of an acceptable error would require an argument, and most likely a very contentious one, that relates errors to group variability, group size, and the biological relevance of effect sizes. If reaching a common ground on these issues is possible at all, it is tedious considering that the problem can be avoided without too much effort.
2.2. An almost as easy solution
The problem described in the preceding section is caused by the counting of “something” (profiles) that is not unique for the objects of interest, but that can occur more than once for each object in a series of sections. If the section thickness remains unchanged, selecting a smaller structure to count—the nucleus instead of the cell, or the nucleolus instead of the nucleus—does reduce the error because the chance that it is sectioned decreases. However, even if the error in thick light microscopic sections may not be detectable, this may not be the case if section thickness is reduced dramatically, for example, when only one confocal plane is used or when tissue sections are prepared for electron microscopy. The error depends on a parameter, that is, section thickness, which is chosen during the preparation of the tissue. This also adds to the complexity of comparing results of different studies.
An error‐free estimate can only be obtained if a “something” is identified that only occurs once for each object of interest in a series of sections. Thompson (1932) may have been the first to state that the first time an object is recognized in a series of sections is such a unique feature. Regardless of how big an object is and how many profiles it may produce when the tissue is sectioned; it will only once be seen for the first (or last) time. His idea went sadly unnoticed until Sterio (1984) rediscovered and extended it in the form of the disector. In its conceptually simplest form, the disector is based on the examination of two (di‐) sections (‐sector). One of the sections, the sample section, is used to count cells. The other section, called the look‐up section, is used to decide which of the cells visible in the sample section are to be counted and which ones are not. The rules that determine what to count are rather simple.
If a cell is visible for the first time in the sample section, i.e., it is not present in the look‐up section, it should be counted.
If a cell is visible in the sample section but was already visible in the look‐up section, it should NOT be counted.
There should be no anxiety that the disector must be used in this form, that is, as a tedious‐at‐best comparison of two real sections (physical sections and, hence, physical disector) in which cellular features need to be identified in both sections. Nor should it be necessary to compare an entire section, which may contain thousands of cells, with another entire section. How the disector has improved technically will be described in detail in Section 6. However, the physical disector remains the easiest way to explain the counting rules and why they return the correct number. They are illustrated in Figures 5 and 6, in which the region already illustrated in Figures 2 and 3 is evaluated using the disector.
FIGURE 5.
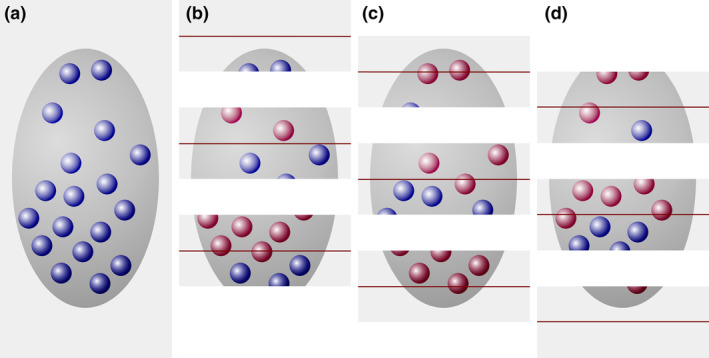
The disector generates an estimate of true object number. (a) A region (dark gray), containing 18 cells (blue objects), is cut into three series of sections. For each of the three series that may be used to count, the sections of the previous series are used as look‐up sections (b–d). According to the counting rules of the disector, cells that are present in the look‐up section (red objects in b–d) are NOT counted. The three sections of the structure in series (b) contain eight cell profiles that were not present in the adjacent look‐up sections. The three sections in series (c) and (d) both contain five cell profiles that can be counted [Color figure can be viewed at wileyonlinelibrary.com]
FIGURE 6.
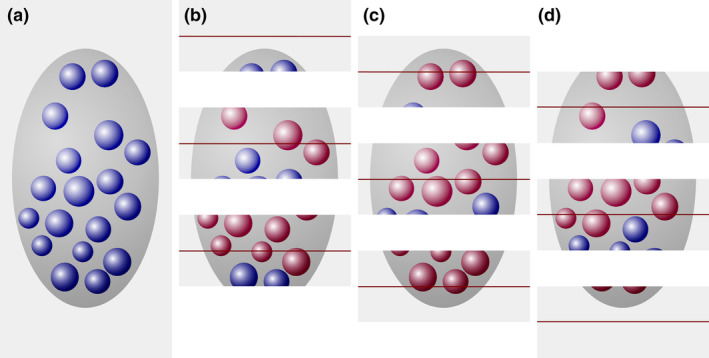
A number estimate obtained by the disector is independent of object size. (a) A region (dark gray), containing 18 cells (blue objects), is cut into three series of sections. For each of the three series that can be used to count, the sections of the previous series are used as look‐up sections (b–d). In series (b), eight cells are counted in the sample sections (blue objects) that were not present in the look‐up sections (red objects). In series (c) and (d), four and six cells are counted. The average count is six cells in one‐third of the sections, which multiplied by three provides the true number of 18 cells [Color figure can be viewed at wileyonlinelibrary.com]
Every third section is used as a sample section. In the three possible sets of sample and look‐up sections, eight, five, and five cell profiles are countable according to disector counting rules. In that each series represents one‐third of the total, we multiply by three and obtain estimates of 24, 15, and 15 cells. The average of the three estimates, 18 cells, corresponds to the true number of cells in the region of interest.
In that cells, regardless of their size along the z‐axis, only once can appear for the first time in a section, the disector should also return the correct cell number for the member of the experimental group that was used for the profile counts in Figure 3. Figure 6 illustrates that it does. Once again, we count an average of six cells in each of the three possible sets of sample and look‐up sections, providing the true number of 18 cells contained within the region of interest.
The disector would, of course, also return the correct estimate for the change in orientation or for a change in the direction of the sectioning illustrated in Figure 4.
Examples similar to those in this section could be constructed for the estimation of most of the morphological parameters that we may want to quantify. Here, the disector has been used as a representative of the design‐based stereological probes that share in returning the correct value for one parameter of interest (number, length, surface, volume) in the region of interest regardless of changes in one or more of the other parameters.
3. SAMPLING
Subsequent statistical testing of group differences is one of the main motivations of quantitative morphological descriptions. One prerequisite for meaningful statistical testing is representative (for the many interpretations of this word, see Kruskal & Mosteller, 1979) sampling. If the sample is not statistically representative for the region of interest, statistical outcomes may not apply to the region either. Key to representative sampling is that each part of the region must have the same chance to contribute to the sample as any other part of the region. Opinion polls are sometimes used to illustrate principles of good (and bad) sampling. If we are interested in the opinion of a population, everyone in the population should have a chance of being asked. Sampling in an opinion poll means deciding on whom one should ask. Sampling in quantitative morphology means deciding on where one should make a measurement. Two ways in which representative samples can be obtained are described in Sections 3.2 and 3.3.
3.1. The representative section
It is common that quantitative methods are employed in a (small set of) representative section(s). Most often “representative” means sections in which the region of interest has its typical anatomical looks, and it is assumed that typical looks will result in typical quantitative measures. The only way to ascertain if this is true is beforehand knowledge of the entire region of interest. If an experiment is performed, this extends to beforehand knowledge about changes in the entire region of interest. However, if this is already known, why would one perform these measurements at all? Kruskal and Mosteller (1979) harshly translate this type of “representative” sampling to “My sample will not lead you astray; take my word for it even though I give you no evidence.” It is at least unfortunate that the credibility of statistical outcomes should rest solely on the credibility of the investigator (but see Section 9.6). In a formal comparison, effects of prenatal low‐dose irradiation of the hippocampus and cerebellum shown in a statistically representative sample could not be observed in “representative” sections (Schmitz et al., 2005).
Independent of the credibility of sample selection, a critical problem of restricting the sample to this type of representative sections is that number, length, or surface estimates will have to be presented as densities—either raw, as estimate (numerator) per section (denominator), or standardized to some reference also obtained from the section, for example, as estimate (numerator) per unit area or unit volume (denominator). Densities alone do not allow statements about changes in the numerator without knowledge of the total size of the denominator for the region of interest (Gundersen, 1986). The problem was already illustrated in Figure 1. Additional examples from the literature emphasize the importance of the problem. Cell density increased in the hippocampal CA3 pyramidal cell layer 30 days after contusion injury relative to shorter survival times even though cell number remained constant (Baldwin et al., 1997). Significant and similar differences in both hippocampal granule cell number and granule cell layer volume, but no differences in cell density, were found between superior and inferior learners among aged Wistar rat (Syková et al., 2002). Decreases in both hippocampal CA1 pyramidal cell number and pyramidal cell layer volume were also observed in monkeys after simian‐immunodeficiency virus infection (Curtis et al., 2014). Unchanged cell numbers but decreased cell densities were found in adult human medullary nuclei when compared to infant ones (Porzionato, Macchi, Parenti, & de Caro, 2009). Hippocampal granule cell density was found to be highest in C57 mice when compared to DBA and NZB mice although total granule cell number in the three strains was the lowest in C57 mice (Abusaad et al., 1999). GFAP‐positive cell numbers increase in all hippocampal division in Bassoon‐mutant mice, but their densities remain unchanged (Heyden et al., 2011). In the same mutant, hilar cell numbers also increase, but density decreases. An increase in the density of cholinergic fibers and expansion of the width of the commissural‐associational zone in the hippocampal dentate molecular layer after entorhinal cortex lesions were long interpreted as examples of reactive plasticity, but later found to be secondary to molecular layer shrinkage (Phinney, Calhoun, Woods, Deller, & Jucker, 2004; Shamy, Buckmaster, Amaral, Calhoun, & Rapp, 2007). Both primary visual cortex volume and the neuron number in schizophrenics were found to be lower than in controls, but cell density did not differ (Dorph‐Petersen, Pierri, Wu, Sampson, & Lewis, 2007). While vascular density increases in the cerebellum of Lurcher mice, total vascular length actually decreases (Kolinko, Cendelin, Kralickova, & Tonar, 2016). Even large increases in cell number can go hand in hand with decreases in cell density in the canary song system following androgen treatments (Yamamura, Barker, Balthazart, & Ball, 2011). An age‐related loss of hippocampal granule cells in APP/PS1KI mice was accompanied by an age‐related increase in volume (Cotel, Bayer, & Wirths, 2008; Cotel, Jawhar, Christensen, Bayer, & Wirths, 2012), which would lead to a larger decline in density than in number. Further examples from research on the morphological basis of neuropsychiatric disorders can be found in Dorph‐Petersen and Lewis (2011). In each of these cases, conclusions drawn based on the numerator of a density obtained from representative sections would have been misleading because of changes in the denominator. Unknown changes in the denominator of a density have also been named the “reference trap” (Brændgaard & Gundersen, 1986). Changes in density indicate changes in the functional relations between the structures that provide numbers for the numerator and the denominator. Changes in density may be worthwhile discussing in this context, and they must have a cause. However, there are always two numbers that can change a density, and we do not know if it is the one of our primary interest (for similar arguments and examples see, for example, Mayhew, 1996). Note that all the examples come from stereological studies, which incidentally looked at both solid number and density estimates. If it was possible to get more bewildered than by attempts to find a consistent relation between density and number, adding biases due to the orientation or size of objects would sure do the trick.
3.2. A representative sample of sections
One way to draw a representative sample from a series of sections of a brain region would be akin to drawing lottery tickets. Each lottery ticket has the same (a uniform) chance (random) of being drawn, and the chance that a ticket is being drawn is independent of the chance that another ticket is being drawn. This type of sampling is therefore referred to as uniform random independent sampling. Sections that are selected in this manner would constitute a statistically representative sample of the region that has been cut. This approach is hardly ever used in quantitative morphological studies. First, it is actually more tedious to draw a random sample than one may expect. Just fishing with a brush for a section in an Eppendorf tube is not good enough—large sections may be more likely to stick to the brush than small ones (or the other way round—who knows?). Some formal randomization procedure would have to be used. The frequently used phrase “randomly selected” is hardly ever accompanied by a description how randomness was achieved. Second, it is counterintuitive and may be disruptive to other procedures. Randomization would mean that a sample from one animal actually may not contain any of those cherished anatomically typical sections, while the sections sampled in the next animal may contain all those cherished sections. Also, there is an intuitive resistance to the large variability of the estimates that one correctly may expect across this type of samples.
Another way of representative sampling is much closer to procedures already in place in many laboratories—uniform random systematic sampling. We rarely collect and process all sections of larger brain regions to look at one particular parameter. Instead, series of sections are collected, in which the distance between sections is determined by the needs of anatomical coverage (the series ought to contain examples of the typical appearance of the region of interest) and the number of ways in which the sections will be processed. If, for example, four antibodies will be used, we may need four series. To that, we may add an additional series to try out antibody concentrations. Another one or two series may be added in case something should go wrong or in case a different type of assessment is considered useful later in the course of the study. The four antibodies, trial sections, and backup section require, in this example, a total of seven series to be cut. The seven series may then be collected into Eppendorf tubes or well plates, each tube or plate containing every seventh section that was cut. Each series is a systematic sample (every seventh) of the region of interest. To make these systematic samples statistically representative only one small additional step is required. Each section must have the same (uniform) chance (random) to give its opinion with regard to, for example, the antibody used as any other section. We cannot always use series one (containing sections 1, 8, 15 …) for antibody A and always use series two (containing sections 2, 9, 16 …) for antibody B. If we did, sections 1, 8, 15 … would never be allowed to give their opinion on antibody B and sections 2, 9, 16 … would never be allowed to give their opinion on antibody A. Instead, we must pick one of our seven series at random when we assign them to a particular stain. This is the only step required to turn a traditional series of histological sections into a statistically representative uniform random systematic sample of sections.
In Section 9, the number of series to be cut (any number is good, but some numbers give more options than others) and ways to deal with missing sections will be discussed.
3.3. Representative sites within sections
Similar to the sampling of sections, sampling within sections must be statistically representative. Again, one has to resort to either uniform random independent sampling or to uniform random systematic sampling. Similar to the sampling of sections, uniformly and randomly sampling the area of the section in a systematic way requires us to randomly select a starting point and proceed from the starting point at regular intervals along the two dimensions of the area of the section. In the most common cases of square or rectangular grids of sampling locations, the distances between sampling locations are often referred to as the x‐ and y‐step sizes.
Both uniform random independent sampling and uniform random systematic sampling are illustrated in Figure 7. The distribution of dots in the circular region of interest may resemble the distribution of ganglion cells in the retina—they are spaced closer to each other in the region of the center of the visual field than in its periphery. Figure 7a illustrates three of the infinitely many possible patterns of uniform random independent samples; Figure 7b three of the infinitely many possible patterns of uniform random systematic samples.
FIGURE 7.
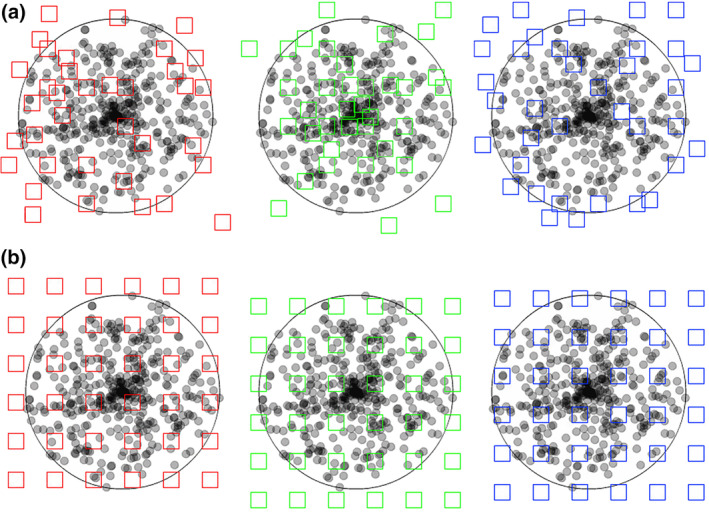
Uniform random independent sampling and uniform random systematic sampling. The area of a section containing unevenly distributed objects is probed in (a) with three uniform random independent samples of the area (red, green, and blue squares) and in (b) with three uniform random systematic samples of the area. Both types of sampling are statistically representative. However, note that the systematic samples, unlike the blue independent sample, never completely miss the central part of the section, in which the objects of interest are spaced closely together. Also, they never, like the green independent sample, contain an unduly large number of samples in the central part of the section [Color figure can be viewed at wileyonlinelibrary.com]
Figure 7 illustrates a strength of systematic sampling. If the objects of interest are unevenly distributed within the region of interest, a systematic sample is more likely to capture this heterogeneity than an independent sample. Just from the visual impression of the distribution of the sampling locations in the section, the red independent sample appears to probe areas of different density “just about right.” The green independent sample seems to have “too many” sampling locations within the dense part of the section, whereas the blue independent sample seems to miss the dense part of the section almost completely. As long as these three possibilities are equally likely to occur, it does not matter. Across the sampling of several sections (or across several individuals), the differences between sections will average out to a correct group mean. In contrast to the independent samples, the systematic samples do not show a visually apparent overemphasis on parts of the region either densely or sparsely populated by the objects. The systematic placement of the sampling locations together with the distance between the sampling locations makes it impossible to happen. As a consequence, the variability of estimates obtained from a systematic sample may be lower than the variability obtained from an independent sample. Less variability between the samples typically also means less variability between subjects in a group and a greater chance to detect statistical differences between groups. In biological regions of interest, gradual changes in the density of the objects of interest are common, and the efficiency of systematic sampling can be expressed in simple mathematical terms. Variability between estimates decreases typically with a factor of when independent samples are used, whereas it may decrease with a factor of 1/number of sampling locations when systematic samples are used (Gundersen & Jensen, 1987; Roberts et al., 1993). That means that if a certain precision can be obtained looking at 10,000 (or 400 or 100) sampling locations that were collected in a uniform random independent manner, the same degree of precision may be obtained from only 100 (or 20 or 10) sampling locations that were placed in a uniform random systematic manner. Importantly, it also means that it will typically require much less work to generate a precise outcome using a uniform random systematic sample.
Of course, Figure 7 has been drawn to make a point and may considered “unfair” to uniform random independent sampling with regard to the differences between the three samples. However, it is far from exaggerating what might happen when independent samples are used. That all samples fall outside the region of interest and return a count of zero is statistically just as likely as all samples hitting the central part of the section returning a count of very, very many. Any combination of sampling locations is just as likely to occur as any sequence of numbers in a lottery. Another example of the difference in the efficiency between independent and systematic samples is provided in Section 5.2.
The efficiency of systematic sampling, which was illustrated for the sampling within sections in Figure 7, applies to all levels of the sampling scheme. If the area of a region of interest shows gradual changes in size from section to section, using a systematic sample of sections will not only be more conform to routine laboratory procedures but also more efficient than using an independent sample. Depending on the demands of the study, the sampling scheme may be extended to additional levels—like a sample of brain slabs (Dorph‐Petersen et al., 2009) from which a sample of blocks are prepared, which are then sectioned and, again, sampled (Lyck et al., 2009).
There are two special cases in which systematic samples do not compare favorably with independent samples. If the region of interest shows truly random fluctuations in size from section to section or if the objects of interest are distributed at random within the region of interest, the variability of estimates obtained from systematic or independent samples will be the same. The variability of estimates obtained from a systematic sample may be larger than that obtained from an independent sample if there are periodic changes in the size of the region of interest and a match of such periodic changes with the intervals with which sections are collected. The same is true for a match between the distances between sampling locations within a section and a regular periodic distribution of objects within the sections. The case of periodic anatomical change will be discussed in more detail in Section 8.10.
3.4. Fractionator sampling
The fractionator (Gundersen, 1986) allows to calculate totals of number, length, surface or volume based on counts obtained from a sample of a region without any further knowledge about quantitative parameters of the region in which the counts were made. A uniform random systematic sample is taken at regular intervals, which allows calculating the fraction of the region of interest that is included in the sample. If a series of every third section of the region was collected, the sample contains only one‐third of the entire region and one‐third of the objects that one may want to measure. The section sampling fraction, ssf, is one‐third. If only part of the area of the section is investigated, for example, one‐tenth, only one‐tenth of the objects of interest in the section will be contained in this sample of the area. The area sampling fraction, asf, is one‐tenth. If one looks at the areas that were selected at high magnification, one may not look at every possible location along the thickness (z‐axis) of the section but restrict analysis to, for example, half of the thickness of the section. Again, only one‐half of the objects of interest that are located beneath the area will be contained in the sample. The thickness sampling fraction, tsf, is one‐half.
Whatever we measure and however we perform measurements in the sample, we know how much of all‐that‐there‐is we have looked at—one‐half of the thickness of one‐tenth of the area in one‐third of the sections, that is, one‐sixtieth (1/2 × 1/10 × 1/3) of all‐that‐there‐is. If what we measure is one‐sixtieth of all‐that‐there‐is, all‐that‐there‐is in the entire structure must be 60 times what we measured. Uniform random systematic sampling and fractionator sampling are two sides of the same coin. Uniform random systematic sampling becomes fractionator sampling if we use the information about the sample to calculate the fraction of the region that we analyzed, and if we use this fraction to calculate the amount of all‐that‐there‐is in the region.
The number of fractions that are included in a fractionator sampling scheme can be extended according to the practical demands of a study. If, for example, the human neocortex is the region of interest, it may be divided in a number of smaller blocks that can be cut and stained following standard protocols (Lyck et al., 2009). Not all blocks need to be processed as long as the fraction of blocks that have been processed is known. Although not yet very useful in the neurosciences, the sections that are being used do not need to be parallel, equally thick or evenly spaced (Baddeley, Dorph‐Petersen, & Vedel Jensen, 2006; Gundersen, 1986) as long as each section has the same chance to contribute to the sample as any other section and as long as it is known which fraction of all sections was sampled. Using a uniform random independent sample that represents a known fraction of all sections would also be a fractionator sample. The same applies to the other levels at which one may want to sample.
Sampling schemes like the smooth fractionator (Andersen, Fabricius, Gundersen, Jelsing, & Stark, 2004; Gardi, Nyengaard, & Gundersen, 2006; Gundersen, 2002a) and the proportionator (Gardi, Nyengaard, & Gundersen, 2008) have been developed that can take into account regional differences in the distribution of the region that we may want to know something about. Briefly, the smooth fractionator adjusts the distribution of the region of interest across sections to efficient fractionator sampling. The proportionator instead adjusts sampling intensity within sections to the local distribution of the objects of interest. When the appearance of a region of interest in different sections is very heterogeneous or when objects are distributed very heterogeneously within the sections, these approaches have the potential to generate more precise estimates per unit of work invested than even uniform random systematic samples.
3.5. No sampling
Correct sampling is important, but it is only a means to reduce workload and not an inevitable part of design‐based stereology. Workload may not be prohibitive to the assessment of everything, or at least everything at one or more levels of the sampling scheme. If one can assess all sections but not all objects within them, one only needs to sample within sections. If there are too many sections but only few objects in each section, one only has to sample sections but not within sections. At each step at which sampling can be avoided, a source of variability can be avoided. An example of no sampling is the study of ganglion cell distribution in retinal whole‐mounts by Coimbra, Collin, and Hart (2014). Instead of sectioning the eye (e.g., Fileta et al., 2008), the retina is prepared as a whole‐mount, and the sampling of sections is not necessary. The section sampling fraction is one. The depth of the entire retinal ganglion cell layer can be assessed with high magnification lenses, and it is technically not necessary to restrict sampling to part of the depth of the tissue. The thickness sampling fraction can therefore also be one. If workload is not a prohibitive factor to intensive or even exhaustive sampling at one or more levels of the sampling scheme, the question remains if the work is sensibly spent (Gundersen & Østerby, 1981). This question will be addressed in Section 8.
4. A BRIEF INTRODUCTION TO PROBES
Probes are the tools with which the amount of objects, length, surface, or volume can be estimated. While sampling determines the place at which a measurement is being made, the probe that is selected determines how a measurement will be made. Stereological probes resemble other probes commonly used to investigate tissues. First, there is a similarity of the type of probe and the thing that is probed for. Proteins, in the form of antibodies, can be used to immunocytochemically probe for the proteins in tissues. In situ hybridization uses RNA probes to detect RNA in tissues. Not surprisingly, numbers of point probes, lengths of line probes, areas of surface probes and volume probes are used to probe for volume, area, length, and number. Traditional and stereological probes share another feature—complementarity or the lock‐and‐key principle. Antibodies need to be matched to their antigens and RNA probes need to be complementary to the sequence that they are supposed to detect. There is a similar requirement relating stereological probes to the morphological parameter that they measure. If one is interested in the quantitative morphology of three‐dimensional structures, the dimension of the probe and the dimension of the parameter that is being measured must sum up to at least three. A point (zero‐dimensional) can be used to estimate volumes (three‐dimensional; 0 + 3 = 3); a line (one‐dimensional) can be used to estimate areas (two‐dimensional; 1 + 2 = 3); an area (two‐dimensional) can be used to estimate length (one‐dimensional; 2 + 1 = 3), and a volume (three‐dimensional) must be used to estimate numbers (zero‐dimensional; 3 + 0 = 3). No method has been found that will work if the sum is smaller than three, and a proof presented by Gual‐Arnau, Cruz‐Orive, and Nuño‐Ballesteros (2010) suggests that none can be found.
If the dimensions of probe and parameter do not fulfill this requirement, the probe will start cross‐reacting with other parameters. This is akin to an antibody of insufficient specificity that cross‐reacts with a protein different from the one it was intended to react with. The example in Section 2 illustrated what happens if this requirement is not fulfilled. Not only do we generate the wrong number if we estimate number (zero‐dimensional) with a count in an area (two‐dimensional; 0 + 2 = 2), but the wrong number depends on the size or orientation of the objects that are being counted. A probe that we aimed at the number of objects cross‐reacts with the size or orientation of the objects.
The advantage of the dimensions of the probe and the parameter to add up to precisely three is that one can simply count the interactions between a probe and an object—the number of times that point probes fall within its volume, that a line probe pierces its surface, that an area probe intersects with its length and that objects are contained within a volume probe (Figure 8). The counts and the size of the probes enter into, yet again, very simple equations that allow the calculation of densities. These equations are referred to as relationship equations.
FIGURE 8.

Probes for volume, surface, length, and number. Probes for volume, surface, and length are depicted how they would look like applied to the three dimensional tissue and how they would look like in sections that have been prepared from the tissue. For number, two sections and the distance (h) between them define the volume probe of the disector. The two sections have also been superimposed on each other in the last view presented. For each probe, one of the places in which probes and feature interact has been marked by an arrowhead in the sections. The total number of probe feature interactions in the examples are nine (volume), ten (surface), five (length), and two (number) [Color figure can be viewed at wileyonlinelibrary.com]
The relationship equations are: for volume density
(Glagolev, 1933, 1955), for surface density
(Saltykov, 1946 as cited by Saltykov, 1974; Smith & Guttman, 1953), for length density
(Saltykov, 1946 as cited by Saltykov, 1974; Smith & Guttman, 1953), and for number density
(Sterio, 1984).
Q refers to “Querschnitt,” the German word for profile or cross section. The superscript minus in number density refers to the “seen in one section but not the other.” Reviews of the historical development of the relationship equations were presented by Hykšová, Kalousová, and Saxl (2012) or, with an emphasis on mathematical theory, by Cruz‐Orive (1997, 2017).
Next, densities can be converted to estimates of total number, length, area, or volume using equally simple equations. The conversion of densities to totals will be addressed in the sections on specific probes.
In Figure 8, the probes for surface and length were placed in the plane of the section. This is how the probes would be intuitively applied, by defining an area of the section or by placing lines on the section and count intersections. However, a requirement for all probes is that the number of the interactions of probes with volume, surface, length or number must only depend on the amount of volume, surface, length, or number. Section 2 showed how the disector accomplished this for a number estimate. Section 7 will briefly describe why orientation (of the sections or probes) may impact on estimates of surface and length and how tissue preparation or special shapes of test areas or lines rid these estimates from the influence of orientation. For estimating volume or number, there are no further theoretical requirements, but a number of practical constraints that are discussed together with the probes in the following sections.
The dimensions of the probe and of the parameter can sum up to more than three, and such probe/parameter combinations are part of some stereological methods. However, to obtain an estimate of the parameter does now require measurements instead of counts. If a surface area is, for example, estimated by area probes, the length of the lines of intersection of surface and area probe need to be measured to obtain an estimate of the area. One popular method that uses line probes (one‐dimensional) to estimate volume (three‐dimensional; 1 + 3 = 4) is the nucleator (Gundersen, 1988).
Finally, we may be interested in systems, which are not three‐dimensional. Cells can be grown in a “two‐dimensional” monolayer cell culture in a Petri dish. As the number of dimensions in our world of interest has changed to two, the sum of probe and feature only needs to be two ("Petri‐metrics" in Howard & Reed, 2010). A test area (two‐dimensional) is sufficient to count cell number (zero‐dimensional; 2 + 0 = 2) and lines (one‐dimensional) may be sufficient to estimate the length of their processes (one‐dimensional; 1 + 1 = 2). Some of the sampling strategies mentioned in the preceding section, or the counting frame described in Section 6.2 will still be useful tools. As soon as we become interested in something three‐dimensional, for example, the volume of the cells in the monolayer, we are back at a sum‐of‐three rule and the methods described in this review.
5. PROBING VOLUME: THE CAVALIERI ESTIMATOR
Volume estimates of brain compartments may serve different purposes. It is relatively easy to generate precise volume estimates. If changes in the numbers of neurons or synapses or dendrites or vessels are reflected in changes of the gross volume of the region that contain them, the volume change may be easier to detect than the underlying more specific changes. Volume estimates may therefore be an efficient first means to assess the likelihood of morphologically more specific structural changes (e.g., de Groot et al., 2005). If biological variability is low, differences as small as ~5% have been detected statistically in moderately sized groups (Slomianka & West, 1987). Also, volume estimates may be necessary if fractionator sampling (see Section 3) is not possible or desirable. In this case, estimates can be generated from density estimates and reference volumes (Pakkenberg & Gundersen, 1997; West & Gundersen, 1990). Finally, area estimates, which are part of the generation of volume estimates, are helpful in the design of sampling schemes that aim at other parameters than volume (see Section 8.11).
5.1. Calculating volume from area estimates
Following Cavalieri's theorem (translated by Evans, 1917), the volume of a region is equal to the sum of the areas of the region in parallel sections that pass through it, multiplied by the distance between the subsequent sections, or
We do know the distance between subsequent sections of our histological series. Note that the distance between areas is the distance between the same surfaces of the sections used in the series. If all sections are used there is no gap or distance between the sections, but there still is a distance, corresponding to section thickness, between the top surfaces of two adjacent sections. In addition to distance, the only thing needed to calculate volumes are estimates of the areas that a region of interest occupies in the sections. What comes to mind immediately is to outline the region in some graphics application and have the application calculate the area. As will be discussed in Section 5.4, this may not be the most convenient way to estimate an area, and it is prone to errors. Instead, we can use point counts to estimate the area of the region of interest in the sections.
5.2. A point probe to estimate an area
Imagine a region (blue circle in Figure 9) that occupies an unknown area within a reference area (all of the square and blue circle in Figure 9). If a point is placed many times at a random position within the reference area, the number of times that the point will fall onto the region depends on how much of the reference area is occupied by the region. If the region would occupy all of the reference area, a point would fall onto the region each time a point is placed in the reference area. In this case, the probability of the point to fall onto the region is 1. If the region would only occupy half of the reference area, a point would fall onto the region in about half of the trials, that is, the probability is about 0.5.
FIGURE 9.

Using points to estimate an area. The reference area (entire gray and blue areas of this figure) is probed with 25 randomly placed points to estimate the area of the blue circle within it. Twelve of the twenty‐five points fall onto the circle. The area of the circle can therefore be estimated to 12/25th of the reference area. In that we can arbitrarily choose the size of the reference area, we can calculate an estimate of the size of the circle [Color figure can be viewed at wileyonlinelibrary.com]
Usually it is the other way around. We do not know the area of the region, and we use the probability of points to fall onto it to estimate the area. The more trials are made, the better is the estimate of the area. The probability that we observe is equal to the proportion of the reference area occupied by the region—that is, if we observe a probability of 0.48 (12 points out of 25 that hit the structure in Figure 9), about 48% of the reference area is occupied by the region.
The area occupied by the region can now be calculated by multiplying the probability with the size of the reference area. We can arbitrarily decide on the size of the reference area before we start this little experiment.
In Figures 8 and 9, the points are represented by a small crosshair (a dimensionless mathematical point would be invisible), which is also the most common representation of point probes in illustrations and in stereology software packages. Unfortunately, a crosshair does not always allow it to decide if a point hit the area of interest or not. First, it is not the entire cross that needs to fall onto the area of interest for the cross to be counted. Even the intersection of the bars of the cross does not always allow us to see if this point is located inside or outside the structure (Figure 10a).
FIGURE 10.
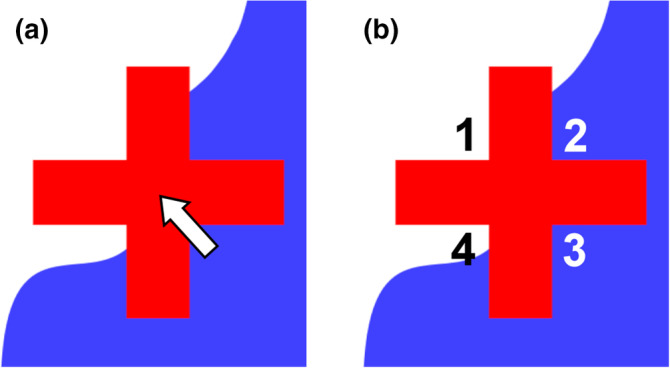
Representing a point probe. The representation of a point probe, a crosshair, falls onto the boundary of a blue region. In (a), the boundary is hidden by the crosshair, and it is not possible to decide if the intersection of the arms (arrow) falls onto the region or not. Using any one of the four corners of the crosshair in (b) allows an unequivocal decision. Corners 1 and 4 are falling outside the structure, while Corners 2 and 3 fall inside [Color figure can be viewed at wileyonlinelibrary.com]
The corners of the crosshair provide better probes (Glagolev, 1955). In Figure 10b, two of the corners are located inside the structure, while the two other corners are located outside the structure. Note that it is the very point at which the arms of the crosshair meet that is used as a probe. Any one of the four corners can be used as a probe, but which one should be decided upon before the probe is applied to the section. In the survey of probes (Figure 8), the lower left corner was selected and generated a count of nine. The upper right corner would have generated a count of eleven.
5.3. A point‐grid as an area probe
Using points that are placed completely at random within the reference area, like in Figure 9, would represent a uniform random independent sample of sites. Following the uniform random systematic way of sampling, the area of interest can also be probed by placing a grid of regularly spaced points over the reference area (Figure 11). Nine of twenty‐five points hit the area of interest, and an estimate of this area would be 9/25th of the reference area.
FIGURE 11.
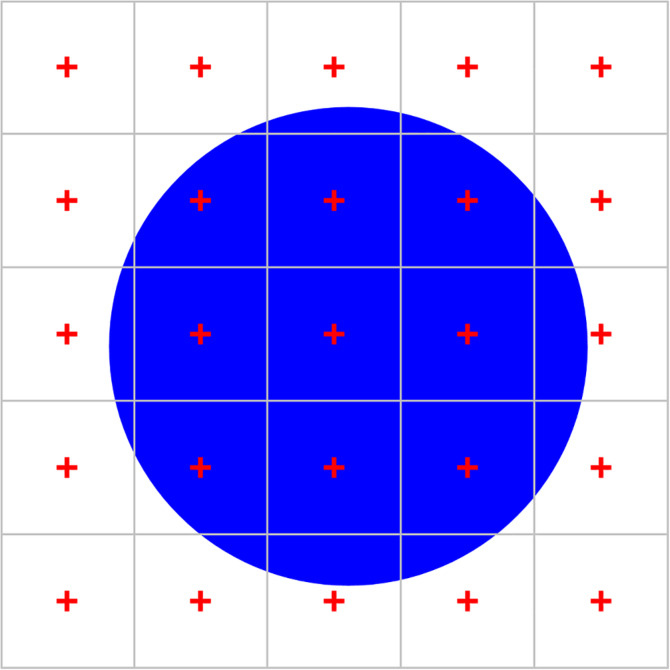
Using a point grid to estimate area. When the reference area is probed with a grid containing 25 points, 9 points fall onto the blue circle. We estimate the area of the blue circle to 9/25th of the reference area. Alternatively, we can look at this sample as 25 smaller areas, each with 1/25th of the full area, that are each probed with one point. The area estimate of the blue circle would correspond to nine times the smaller area, that is, we do not need to know the reference area but only the area associated with each point [Color figure can be viewed at wileyonlinelibrary.com]
Now, let us get rid of the need to know the total number of points applied or the size of the reference area. Each point of the grid is not only a probe within the reference area, but also for a smaller area associated with each point. If the points are, for example, spaced 1 cm apart from each other, this new, smaller “reference area” is 1 cm2.
Within each small square, the probability to hit the structure with the point will either be 1 (the point hit the region) or 0 (the point did not hit the region). In Figure 11, we obtain nine trials of the smaller areas in which the probability of the point to fall onto the structure was observed to be 1 (1 hit/1 trial) and 16 trials in which this probability was 0 (0 hits/1 trial). An estimate of the area would be 9 × 1 × 1 cm2 + 16 × 0 × 1 cm2 = 9 cm2. Changing the size of the reference area (keeping the area per point constant) would only change the number of probes that return a zero probability. The only things that matter are the points that hit and the area associated with them. The area of the structure is directly proportional to the number of points that hit it, 9. This number multiplied by the area associated with each point (1 cm2) is an estimate of the area occupied by the structure in the section (9 cm2). We do no longer need to know the size of the entire reference area covered by the point grid or the number of points in the grid.
5.4. The precision of an area estimate
As already mentioned, the estimate of area would be more precise, if we repeated the random placement of the points many times. Instead of adding more points by repeating the estimate, we can use more points for each estimate, that is, place the points closer together in the grid that we apply to the structure.
In Figure 12, points counted in the green squares return an exact estimate of the area that is associated with these points. A hit is seen, the observed probability is 1, and the area is indeed one time the area associated with each point. The estimate of the red area is less precise. Using the coarse point grid in Figure 12a, four hits are seen in the 16 squares that contain some red area. For those four points, we add the entire area associated with the point to our estimate even though the red area occupied less than that. Statistically, adding too much for the four points that hit will be balanced by adding nothing for the remaining 12 squares, which also contain a little bit of red area even though their points are not counted. Increasing point density fourfold in Figure 12b, the green area, for which we obtain an exact area estimate, increases. At the same time, the red area decreases. Not only does it decrease, it is also probed 26 times (each little square that contains a little red) instead of 16 times, which should provide a more precise estimate.
FIGURE 12.
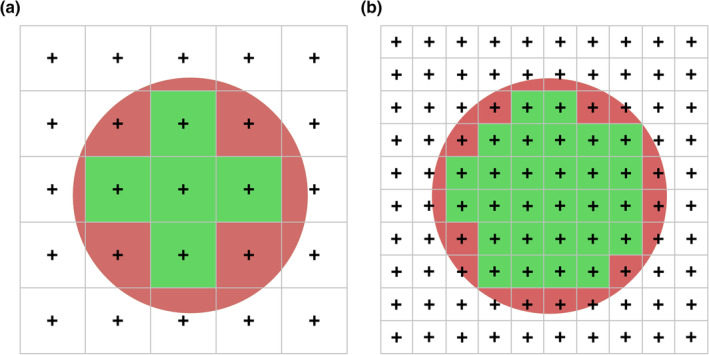
Increasing the density of a point grid increases precision. Point grids of different densities are placed over the round profile of a region. If point density increases, the area that is estimated less precisely (red) is found in 26 squares (b) instead of 16 squares (a). The red area also decreases relative to green areas that are estimated exactly by a point count. With more trials available to estimate the size of a relatively smaller area, the precision of the estimate of the area of the round region increases with increasing point density [Color figure can be viewed at wileyonlinelibrary.com]
Note that it is at least possible for all points to fall outside the structure or for all points to fall inside the structure if they are placed in the random independent manner that was used in Figure 9. This cannot happen for the grids (uniform random systematic samples) of points used in Figures 11 and 12. That means that when estimates are repeated, we would see fewer extreme values if we use a uniform random systematic sample. If we apply the point grids to different animals, we are therefore also likely to see fewer extreme values that are caused by the placement of the points. The standard deviation that we see in groups of animals would therefore also be smaller, and we would have a better chance to observe a difference between two groups. For the same number of points used, a grid (uniform random systematic samples) is more efficient than randomly placed points to generate estimates that can be used to document changes that may occur between groups.
How large is the region of interest illustrated in Figures 9, 11, and 12? By now we have three estimates—48% (12/25th) of the reference area from the independent sample in Figure 9, and 36% (9/25th) and 40% (10/25th = 40/100th) from the two systematic samples in Figures 11 and 12. The region of interest in the figures actually occupies 40.5% of the reference area. Aside from efficiency, systematic samples do have another advantage over independent samples. We can estimate the margin of error based on the number of points that have hit the region of interest. For the 36% estimate the margin of error is ~11% of the estimate and, for the 40% estimate, it is ~3% of the estimate. How this margin of error is estimated will be described in Section 8.4. Note that the margin of error indeed decreased to less than a third by increasing sampling density by a factor of 4, that is, by counting 40 instead of 9 hits. To obtain the same increase in precision using a uniform independent sample of points, sampling density would have to be increased by about a factor 16.
5.5. An example of a volume estimate
A full example of a Cavalieri estimate is useful to illustrate how much time it takes to generate an estimate once the material has been prepared, to provide a small dataset that can be used in the following sections of this review and to show how the observer impacts on the estimate.
Figure 13 provides images of a hamster olfactory bulb taken in a horizontal series of every 24th 20 μm thick, plastic‐embedded and Nissl‐stained section. The first section is placed at random in the first sampling interval (here the 12th sections, or 240 μm after the first appearance of the olfactory bulb). We therefore have a uniform random systematic sample of sections. A counting grid, in which the points are 350 μm apart along the x‐ and y‐axes, is superimposed onto each of the images. The grid was positioned at random onto each section, and the sections are therefore probed at a uniform random systematic set of sampling sites. Note that the grid was not just shifted at random along the x‐ and y‐axis. It was also rotated at random. If a longish structure of interest maintains its orientation from section to section, a row of points may miss the structure in some sections while hitting the structure in other sections. Rotating the grid eliminates the chance that this will happen often. Rotating or not rotating the grid will not affect the mean of repeated estimates, but it can reduce their variability.
FIGURE 13.

Cavalieri estimator applied to the hamster olfactory bulb. A 20 μm thick plastic sections (methacrylate) were Nissl‐stained (Giemsa). The region of interest is highlighted in the lower right image: granule cell layer—green, internal plexiform layer—yellow and mitral cell layer—red. Their combined volume is estimated. Any point falling on any one of them is counted. Sections are 480 μm apart from each other. Distances between the points in the grids are 350 μm along the x‐ and y‐axes [Color figure can be viewed at wileyonlinelibrary.com]
The region of interest has been selected to be the combined granule cell, internal plexiform, and mitral cell layers (schematic in Figure 13, lower right). They are treated here as one structure, and any point falling onto anyone of these three layers should be counted. We do not need to keep track of which layer the counts came from because we are only interested in their combined volume. To obtain the area estimates needed to estimate the volume, a point count is performed for each image. The upper right corners of the crosses were selected to represent the points, but any of the corners will do. To calculate a volume estimate, only the total number of points counted across all sections is needed. Counts are nevertheless recorded per section because they are needed to estimate the precision of the volume estimate (in Section 8). Recording counts per section is also necessary when the anatomical distribution of the volume (or number, length, or surface) has a scientific interest (e.g., Amrein et al., 2015; Buckmaster & Dudek, 1997; Chen & Buckmaster, 2005; Slomianka & West, 1987)
Along the dorsoventral axis (from 240 μm to 3140 μm), the following sequence of counts was obtained: 3, 16, 13, 11, 12, 9, and 2. The total number of points counted is 66. The area associated with each point is 350 × 350 μm = 122,500 μm2. The total area is therefore 66 × 122,500 μm2 = 8,085,000 μm2. The sections are 480 μm apart. Using Cavalieri's theorem, we obtain a volume estimate of 8,085,000 μm2 × 480 μm = 3,880,800,000 μm3 ≈ 3.9 mm3.
The counts quoted above and those of other observers are likely to vary a little even though the same images and points are used. This may be because of the use of a different corner. It may also be because the schematic is used differently to define the region of interest in the other sections. It may also be because criteria to count a point differ. How does the tissue in the corner of the cross need to look like to be counted? The Cavalieri estimator cannot generate a bias in its own right, but the data that it is fed with may vary with the interpretation of the material by the observer, that is, with observer bias. Observer bias cannot be avoided by any method involving an observer. It even cannot be avoided by many methods that do not involve an observer, for example, an automated, image analysis‐based assessment. The use of automated methods only transfers the observer bias to the person that at some time in the past calibrated the automated assessment or trained a learning algorithm. Hmm, at least someone else could be blamed for mistakes.
5.6. Outlines or point counts?
Areas are often measured by outlining a structure and the subsequent automated calculation of the area of the structure based on the outline. How well the calculated area corresponds to the actual area does, of course, depend on how well the outline is done. The complexity of the shapes and, therefore, the effort to define precise outlines may vary with the region of interest. In Figure 13, the region of interest was chosen to be the combined granule cell, internal plexiform and mitral cell layers because the border is rather clearly defined, which suits an exercise. It also makes outlining rather easy. For the two thinner layers, the internal plexiform layer and the mitral cell layer, outlining becomes tedious work. An error that has only a small effect on the combined volume of the three layers will have a much larger effect on the volumes of the thinner layers. One may have to go to higher magnification to generate better outlines for the thinner layers—only to realize that borders which look well defined a low magnifications often present increasingly complex outlines at higher magnifications. At one point, it becomes the observer's decision to accept possible errors because a precise border simply cannot be seen or because the outline needs to be approximated because the border is too complex to be traced precisely with a reasonable effort. Point counting does not have this problem. The only decision that has to be made is whether the point falls onto the region of interest or not. The number of times that this decision will have to be made depends on the point density and the area of the region, but it does not depend on the complexity of the outline of the region of interest. Using outlines, an additional source of error may be associated with the calculation of areas based on the points that have been placed to define the outline. The area may, for example, be calculated for the polygon that is defined by the points of the outline (Figure 14a) or based on smooth lines that are approximated to the points (splines; Figure 14b,c). How well the area is estimated depends on how well the area fulfills the underlying assumptions of being a polygon or an area with smooth outlines. Although the resulting bias may become small with an increase in the number of points used to define the outline, it will always be there, and it may become significant (Bonilha, Kobayashi, Cendes, & Li, 2003).
FIGURE 14.
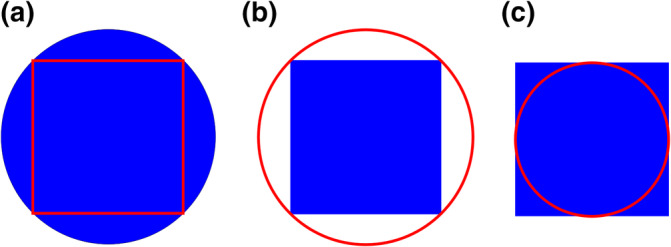
Polygonal‐ and spline‐based approximations of an area to boundary points. (a) If a region is not polygonal, an area estimate (red) based on outlines will underestimate the actual area (blue) if the calculation is based on the area of a polygon. (b,c) If the area is estimated using smooth curves approximated to the points (splines), the area is, depending on the placement of points, overestimated (b) or underestimated (c) if the region is polygonal. The direction and size of the error depend on the number of points used to define the outline and the shape of the region outlined [Color figure can be viewed at wileyonlinelibrary.com]
5.7. A caveat: Overprojection
Cavalieri's principle is valid if the area estimate is made in planes passing through the structure, which would correspond to infinitely thin sections. This requirement is impossible to fulfill. To estimate area, we have to treat sections as two‐dimensional representations of the region of interest. However, tissue sections do have a thickness, that is, they are three‐dimensional structures. As soon as the sum‐of‐three rule is violated, cross‐reactivity sneaks in. In this case, the volume estimate will be influenced by the three‐dimensional shape of the region of interest (Gundersen, 1986). The conflict of theory with practical constraints will result in an overestimate of volume—regardless if we are using point counts or outlines. Figure 15 illustrates the problem. In practice (see below), it may be of little importance.
FIGURE 15.
The overprojection error of volume estimates. (a) If a section that is thick when compared to the region—in a worst case in which it is actually thicker than the region—the volume of the region is overestimated. The area of the region will look like a circle, which, when multiplied with the thickness of the section, will give us a volume estimate of a cylinder rather of the sphere that the region actually looks like. Looking at sections of the sphere from the side (b), the error (red) decreases as sections become thinner and thinner. The errors made in each section will sum up to the volume of the largest of the sections [Color figure can be viewed at wileyonlinelibrary.com]
For sections of a convex structure (e.g., a sphere), the error amounts to volume of the largest section (Gundersen, 1986), and this volume could be subtracted from the estimate of the total volume of the structure. If the shape has dents or contains hollows, the size of the error will be larger.
The error occurs when the border of the region that we see in a section is sharp and unequivocal even at low magnification—essentially like it would appear when a structure is opaque, like the sphere in Figure 15. In histological sections, this will rarely be the case. The whole purpose of sectioning, at least in neuroscience, is to make a region transparent so that we can examine its internal structure—to see the cells, their processes, vessels, and so forth. Because of that, one is rarely faced with the problem of sharp boundaries, but rather with the problem of finding boundaries in the first place. The size of the error will also depend on how many sections can be cut from the region of interest. If hundreds of sections can be cut from a region, even the largest section may only represent a percent fraction of the total volume. If only very few sections can be cut, one may decide to perform a point count at high magnifications. Because the thickness of the focal plane is usually much thinner than the thickness of the section (about 0.5 μm for an oil‐immersion objective), the size of the error would diminish to the volume contained in the largest focal plane.
In an analysis of MRI scans, a dependence of volume estimates on slice thickness has been noted that shows overprojection effects (Bonilha et al., 2003).
5.8. Area fraction fractionator
A volume estimate may require high magnification to identify the border of the region(s) of interest and/or to minimize overprojection. A region of interest may also be embedded in another, larger region of interest. One approach would be a count at low magnification using a coarse grid for the large region and a subsequent count with a much finer grid for the regions that require high magnification. The latter count may become prohibitively laborious if we need to assess a small region that is distributed over a large area. It can be avoided by using an approach based on Delesse's principle proposed by Howard and Reed (2010). It is now commonly referred to as the area fraction fractionator. Only a small fraction of the entire area needs to be assessed, but this small fraction can be sampled with a high density of points.
The approach is illustrated for a section of the olfactory bulb in Figure 16. It can be used to estimate the volumes of the mitral and inner plexiform layers (Figure 13). These two layers would have required higher magnifications and a much denser grid than the grid used in Figure 13 to obtain a precise volume estimate. The areas that are sampled in one of the sections of the olfactory bulb are shown in Figure 16a. One of the small areas that comprise the sampled area is illustrated in Figure 16b. The sum of the points counted for each layer at each sampling site in all sections is used to estimate the fraction of the entire volume that is occupied by the layers. Once the fraction is known, it can be used to estimate layer volume. If one would examine all 24 sites in Figure 16, 48 point would be counted for the mitral cell layer, 27 for the inner plexiform layer and 360 for the granule cell layer. The sum of all points in all layers is 435. The mitral, inner plexiform and granule cell layers account for 0.11 (48/435), 0.06 (27/435), and 0.83 (360/435) of the total volume in this section. We should, of course, look at all sections. However, if these relations hold for all of sections, the volumes of the layers could be estimated by multiplying their area fractions with the estimate of their combined volume, which was 3.9 mm3. We would obtain 0.11 × 3.9 mm3 = 0.43 mm3 for the mitral cell layer, 0.06 × 3.9 mm3 = 0.23 mm3 for the inner plexiform layer and 0.83 × 3.9 mm3 = 3.24 mm3 for the granule cell layer.
FIGURE 16.
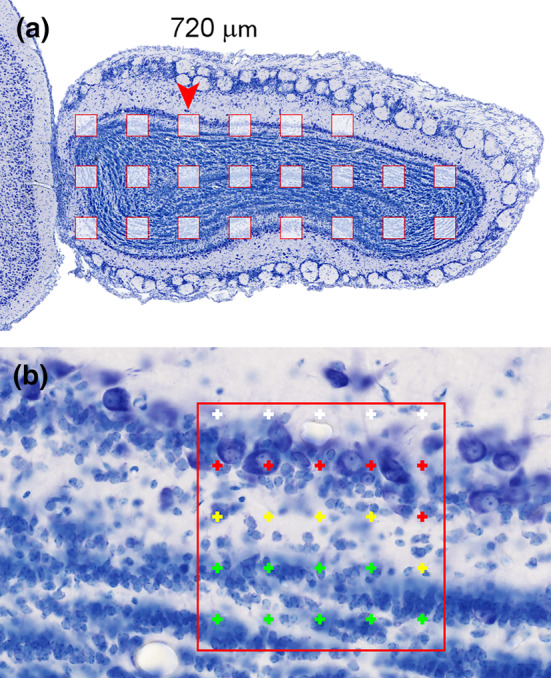
Area fraction fractionator. (a) Areas that are sampled in this section. The sampling sites are 350 μm apart along the x‐ and y‐axes. The arrowhead marks the sampling site illustrated in (b). At each sampling site, a small area (150 × 150 μm) is probed with a grid of points that are 30 μm apart along the x‐ and y‐axes. At this sampling site, six points are counted in the mitral cell layer (red), five points in the inner plexiform layer (yellow), and nine points in the granule cells layer. Five points (white) fall outside the region of interest [Color figure can be viewed at wileyonlinelibrary.com]
A common application of the area fraction fractionator is the estimation of cortical amyloid plaque load (e.g., Heggland, Storkaas, Soligard, Kobro‐Flatmoen, & Witter, 2015; Riudavets et al., 2007). Other applications have, for example, been concerned with cortical vascularization (e.g., Wälchli et al., 2015) or with olfactory bulb structure (Schoenfeld & Knott, 2004).
5.9. Simple Cavalieri estimator implementation
The Cavalieri estimator is probably the method easiest and least expensive to implement. Several plug‐ins that generate point grids are available for ImageJ. Point grids can be prepared using any graphics software that allows a placement of the test points with reasonably consistent point‐to‐point distances. Even recreational graphics software often contains a useable function, one of which was used to generate Figure 13. The point grids can next be placed over images of the region of interest—either digitally or, copied onto transparency sheets, onto prints or onto a screen. The point grid can be calibrated with images of an object micrometer taken under the same conditions as the tissue. If a region is too large to be imaged on the screen or on a print, simple tools allow regions to be probed across several fields of view of the microscope (Adiguzel, Duzcan, Akdogan, & Tufan, 2003; Kaplan, Canan, Aslan, Ünal, & Sahín, 2001; Melvin, Poda, & Sutherland, 2007). In a nutshell, two (or more) points that are separated by a known distance along the x‐ and y‐axes are marked on the screen. Once a field of view has been examined, a feature visible close to one of the points is moved in the x‐ or y‐direction to the next point.
6. PROBING NUMBER: THE DISECTOR
We have already probed for number using the disector in Section 2.2. The example used in Figure 5 and 6 were based on the comparison of two real, physical sections. The variation of the disector using this approach is referred to as physical disector. Using this approach and the statistical demand that each object of interest, for example, cells, must have a chance to contribute to the sample requires that it must be possible to decide for every cell if it is present in the counting section, look‐up section or both. Although image analysis features of stereological software packages may facilitate the process, both the generation of material of a quality that permits the analysis and the analysis itself remain demanding. Consequently, few studies have been published that used the physical disector (e.g., Korbo et al., 1990; Miki, Harris, Wilce, Takeuchi, & Bedi, 2003, 2004; West, Coleman, & Flood, 1988). Today, the physical disector is used almost only if it is not possible to use the optical disector, for example, in electron microscopic quantitative morphological studies (see Section 9). If the physical disector is used, the two sections need to be assessed independently from each other (Hedreen, 1998a), that is, the structures of interest are identified in look‐up and sample sections, and it is only examined afterward which object appeared for the first time in the sample section.
Two conceptual/technical advances, beyond the way in which the disector was introduced in Section 2, have allowed its routine application in a large number of studies. The first, the unbiased counting frame (Gundersen, 1977), allows restricting the sample to a small fraction of the area of the sections. The second, the optical sectioning of thick tissue sections (Gundersen, 1986; West et al., 1991) has made it unnecessary to compare two physical sections.
6.1. Which object should be counted?
If the object of interest is easy to recognize, nothing prevents us from just counting them. If recognition becomes difficult, we may have to look for a proxy. Could we count a neuron when we, for the first time, recognize one of its dendrites? If not impossible, it seems at least very impractical. Even the soma may require closer scrutiny. Is it actually two small somata we count, or are they the trunks of two primary dendrites that merge into a larger soma outside the optical plane we are looking at? One suitable unit to count would be the nucleus, which typically has an easily recognizable and fairly simple shape. Note that “simple shape” is not a requirement to estimate the true number, but it simply makes it more convenient to estimate the true number. What is more important than convenience is that the nucleus also has a fixed numerical relationship to the objects that we are actually interested in. There is one nucleus in every cell. The frequencies of binucleate neurons or glia in the scarce CNS studies that report them (e.g., Ackman, Siddiqi, Walikonis, & LoTurco, 2006; Rezze, 1966) are so low that they can be safely ignored in the vast majority of studies, but this may be different for the PNS (Forsman, Lindh, Elfvin, & Hallman, 1989; Ribeiro, 2006). Another convenient unit may be the nucleolus, which in some (but not all) cell populations of some species has a 1:1 relation to the nucleus/cell. The key to the suitability of any structure to serve as a proxy for the objects that we are interested in is a known numerical relationship between the structure we can count and the objects we want to count. This relation does not need to be 1:1, but it needs to be known. Most humans could be counted by counting hands (2:1) or fingers (10:1) but not by counting hairs.
6.2. The unbiased counting frame
Even a single section may contain too many of the objects of interest to count them all. A smaller sample needs to be drawn in a way that provides each object with the same chance to contribute to the sample. The counting frame devised by Gundersen (1977) allows just that (Figure 17). The counting rule of the disector allows the unique identification of an object along the z‐axis. In essence, the unbiased counting frame applies the same rules to the x‐ and y‐axis of the section. Imagine that the section is recut first parallel to the x‐ and then parallel to the y‐axis (Figure 17b,c). The first cuts (parallel to the y‐axis) divide the section in a series of strips (Figure 17b). Applying the rules for the z‐axis to the strips from left to right, we are allowed to count what is seen in a strip if it was not visible in the previous strip. The next cuts (parallel to the x‐axis) further divide the strips into small squares (Figure 17c). Applying the counting rules now from bottom to top, we are allowed to count what is seen in a square if it was not visible in the previous square. Two sides of the square end up becoming exclusion lines. If an object crosses these lines, it will have been counted in an adjacent square. The borders of the squares that an object may cross and still be counted are referred to as the inclusion lines. These rules are not quite sufficient yet. One object (labeled ? in Figure 17c) crosses the inclusion lines of two squares that touch each other with their corners. This object would be double counted if we would look at all frames. Analog to the example in Section 2, spacing the frames far enough apart to avoid double counting does not solve the problem. Instead, the exclusion lines are extended to avoid this from happening. If their length is at least as great as the largest diameter of the objects that are to be counted, no object has a chance to be double counted (Figure 17d).
FIGURE 17.
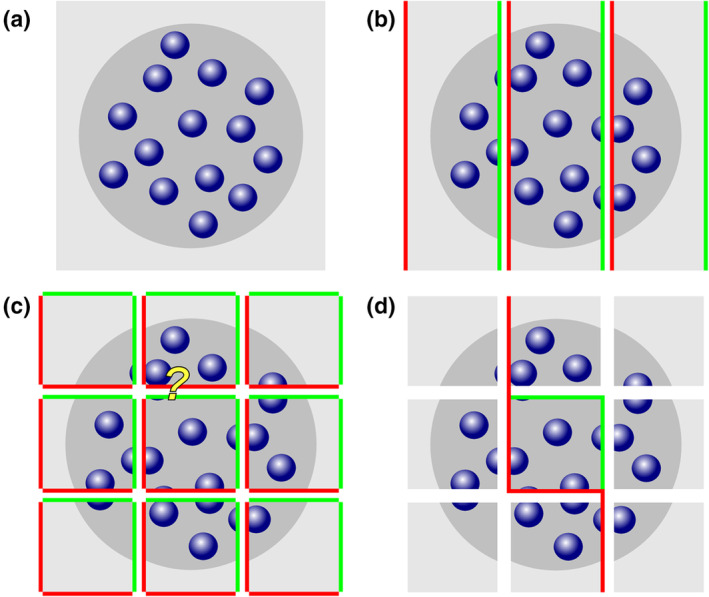
The unbiased counting frame. A section containing 14 objects (a) is successively divided first parallel to the y‐axis (b) and then parallel to the x‐axis (c). Along the dividing lines, the same counting rules that have been established along the z‐axis are now applied along the x‐ (b) and then x‐ and y‐axes (d). Fifteen objects instead of 14 are detected if all objects fully contained within the squares and all object fragments touching a green inclusion line are counted in (c). The overcount is due to the double count of the cell labeled with the question mark. The double count is avoided by the extension of the red exclusion lines in (d) [Color figure can be viewed at wileyonlinelibrary.com]
Figure 17d represents the traditional, square counting frame with exclusion lines extending along the y‐axis of the section plane. The counting frame may also be rectangular, and the exclusion lines may just as well extend along the x‐axis as along the y‐axis. As long as a complete tessellation, that is, a complete covering by nonoverlapping tiles of the surface of the section is possible (Figure 18), counting frames/exclusion lines may take on complex shapes (Gundersen, 1977). In practice, squares or rectangles are almost exclusively used.
FIGURE 18.
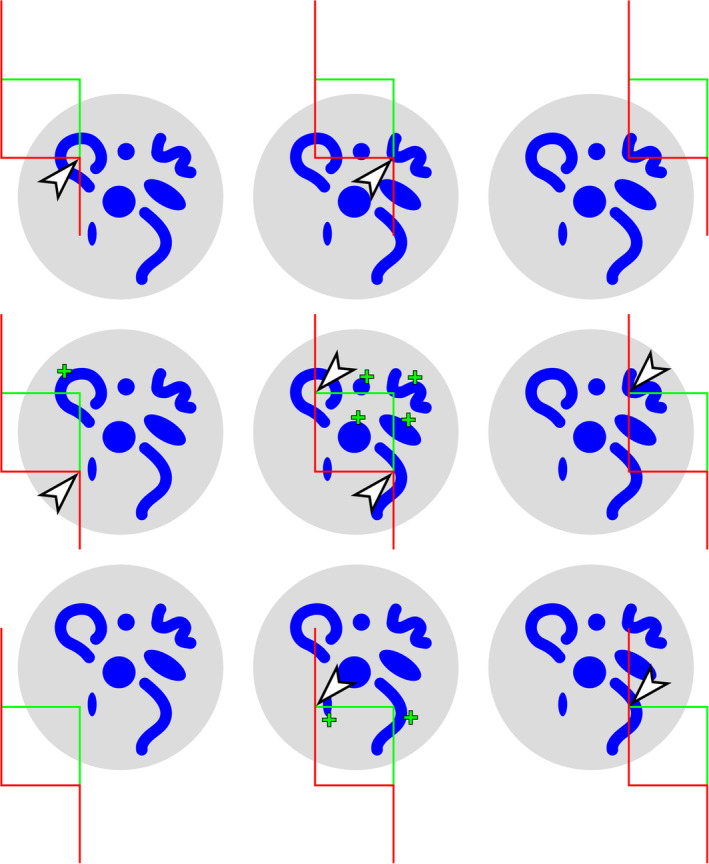
A complete tessellation of a region containing objects of varying size and shape. If the counting rules are applied, each object is counted at least once and never more than once independent of its size, shape, or orientation. The objects are marked with a plus sign in the image of the frame in which they are counted. Sometimes one also needs to know how many counting frames have been applied to a region of interest (see Section 6.5). Any selection of the corners of a counting frame, in this case the top‐left and bottom‐right corner, can be used to estimate the number of entire counting frames that fell on the structure. Eight of the selected corners (arrowheads) fall inside the gray region of interest. Objects were therefore counted in an area estimated to that of 8/2 = 4 counting frames [Color figure can be viewed at wileyonlinelibrary.com]
In the above description, “to cross” an exclusion or inclusion line was used as counting criterion. One may equally well use “to touch” as the criterion for inclusion or exclusion. Critical is the use of the same criterion for both the inclusion and exclusion lines of the counting frame. In the complete tessellation shown in Figure 18, each object will be counted once independent of its size, shape, or orientation.
6.3. Optically sectioning a section
The acceptance that the disector has found relates to the fact that its second incarnation, the optical disector, is practically far less demanding than the physical disector. Instead of comparing two physical sections, we count in optical sections, that is, within a part of a physical section. The top and bottom of the optical disector are defined by two focal planes of the microscope placed at different positions along the z‐axis of the physical section. The counting criterion of the physical disector, “not present in the look‐up section but present in the sample section,” is simply exchanged by the corresponding optical criterion (Figure 19).
FIGURE 19.

Independence of optical disector counts from object recognition criteria. Two observers are looking at the same sample of cells. One of them (early) recognizes the object rather early and one of them (late) recognizes them rather late. Differences in the first recognition (arrows) of objects between observers cancel each other across the top and bottom focal planes that define the height of the optical disector. Regardless how objects are recognized, both observers will count two objects (green arrows) in this example. (Adapted from West et al. (1991), figure 7) [Color figure can be viewed at wileyonlinelibrary.com]
An object is counted if it is not recognized in the top focal plane of the optical section, but first recognized as we gradually move, within the section, to the bottom focal plane of the optical section.
The distance between the top and bottom focal planes, h, defines the height of the optical disector in which we perform the count.
Typically, one would first recognize an object when the object appears in focus for the first time. Unfortunately, the perception of “in focus” may vary from observer to observer. One of the strengths of the optical disector is that it is not crucial to agree on a specific focal plane as long as each observer can recognize each object at least once. This is because we use two focal planes to decide if objects should be counted or not. An observer (early recognizer in Figure 19) may decide that, according to her or his criteria, the top‐most object is in focus in the top focal plane of the optical disector. Therefore, it cannot be counted. An object placed similarly in relation to the bottom focal plane will be counted. Another observer (late recognizer in Figure 19) may only recognize the object when the focal plane is moving slightly further into the section. The top‐most object that was not counted by the early recognizer is counted by the late recognizer. If this personal perception of “focus” is applied consistently to the top and bottom planes, the late recognizer will not count the object crossing the bottom focal plane of the optical disector. Differences in counts due to different perceptions of focus cancel each other over the top and bottom focal planes of the disector. This will not happen in each and every disector, but across all sampling sites, all positions of cells should occur with the same likelihood. As far as the optical disector is concerned, the focus of a student is likely to be as good as the focus of a professor. Attempts to introduce some morphological criteria to define “recognition”, for example, “… were counted when the nucleus was widest,” are not necessary and will reintroduce the possibility of bias.
Critical aspects of the application of the optical disector are the ability to measure the distance between the top and bottom focal planes and to decide if an object can be recognized or not as we move the focal plane from top to bottom. Both demands are satisfied by the use of high magnification oil‐immersion lenses with large numerical apertures (NAs) in conjunction with a microcator, which is a device that measures the distance that the section moves along the z‐axis as we focus through the section.
It is important to know that the distance that we move the section along the z‐axis with the focus knob of the microscope does not necessarily correspond to the distance that the focal plane moves within the section (Galbraith, 1955; Majlof & Forsgren, 1993). This is only the case if the refractive index of the embedded tissue corresponds to the refractive index of the medium between section and microscope lens. For most embedding media this will be the case if oil‐immersion lenses are used. If air or water‐immersion lenses are used instead, the physical movement of the section along the z‐axis will typically no longer correspond to the distance moved by the focal plane. If this situation cannot be avoided, conversion factors need to be applied—a task that can be automated by stereology software packages.
Figure 20 illustrates two optical disector samples—both are fluorescence stacks of mouse hippocampal CA1 pyramidal cell nuclei recorded using either traditional epifluorescence illumination or structured illumination (Karadaglić & Wilson, 2008; Mertz, 2011; Neil, Juskaitis, & Wilson, 1997). The latter is visually similar to a confocal stack. Although the visual appearance of the stacks is strikingly different, nuclei can be counted reliably in both of them. It appears that individual nuclei cannot be recognized in as many optical planes in the traditional stack when compared to the confocal‐like stack. It does not matter, as long as they can be recognized at least once. It also appears that they need to be a little larger before they are recognized in the traditional stack. It does not matter either, because the position at which a structure is recognized does not matter as long as it is similar at the top and bottom planes of the stack.
FIGURE 20.
Examples of optical disector probes. Image stacks representing two optical disector probes that are 7 μm deep in a DAPI‐stained mouse hippocampal CA1 pyramidal cell layer. The upper stack was recorded using structured illumination, which generates confocal‐like images with little out‐of‐focus light. The lower stack represents normal epifluorescence images. In both stacks, nuclei marked with green arrow can be counted according to disector counting rules, that is, they are not present in the top focal plane of the disector (0 μm), they do not cross the red lines at the depth at which they are first recognized (nuclei marked with red arrows), and they are contained within the counting frame or cross the green lines at the depth at which they are first recognized. The personal criterion for the recognition of a nucleus was a nice, crisp outline. The counting frame measures 30 × 30 μm. The white arrow at a depth of 5 μm in the first stack most likely represents a capillary endothelial cell nucleus that is not being counted [Color figure can be viewed at wileyonlinelibrary.com]
6.4. Guard zones
The term “guard zone” (Figure 19) is used for the parts of the physical section located above and below an optical disector. Their use is recommended for two reasons. First, the surfaces of the sections may be “disturbed” by the cutting, meaning that objects that are cut or even just close to the surface of the sections may become distorted or damaged (see Helander, 1983 for an illustration of disturbances in paraffin and plastic sections). If the disturbance is great, one may not be able to recognize the objects that are affected (Andersen & Gundersen, 1999). If they cannot be recognized, they cannot be counted. This violates the one firm requirement of design‐based stereology—namely that each object must be able to contribute to the sample. How far an optical disector sample should stay away from the surfaces of the section depends on the depth of the disturbance and the sensitivity of the object to it
Formally, it is best determined by a small pilot study in which disector samples spanning the entire thickness of the section are used. While counting, the position of objects along the z‐axis is recorded. Next, the numbers of objects located in intervals along the z‐axis is plotted (Figure 21). One would not expect that the number of objects varies along the z‐axis of the section, and the graph should ideally look like a rectangle. If objects at or close to the surfaces of the sections cannot be recognized, the numbers in the intervals at or close to the section surfaces will be smaller than in intervals located in the middle of the section. The disector samples should only span the part along the z‐axis in which the plot is close to horizontal. The remainder of the depth of the section should become part of the guard zones.
FIGURE 21.
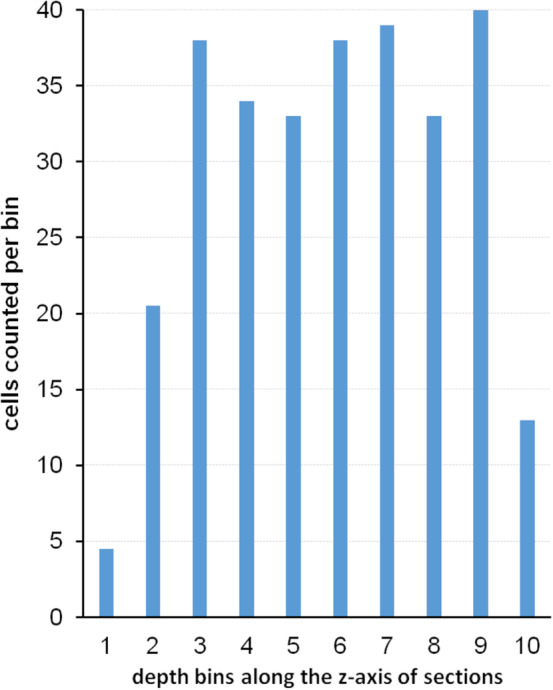
Z‐axis plot of cells. Hippocampal CA3 pyramidal cells are observed throughout the depth of methacrylate sections. The depth of their first recognition is recorded. Cells already visible in the top focal plane of the section are omitted. If cells distribute evenly throughout the thickness of the sections, similar numbers should appear in each bin. In this example, cells distribute evenly from Bin 3 to Bin 9. Low numbers in Bins 1 and 2 were due to low counts in the top 2 μm of the sections. Low numbers in Bin 10 were due to low cell numbers in the bottommost 1 μm of the sections [Color figure can be viewed at wileyonlinelibrary.com]
The formal assessment of the distribution of cells along the z‐axis presented in Figure 21 may be useful for another reason. It allows detecting if, for example, an antibody used to stain the objects of interest has evenly penetrated the section. If that is not the case, one may observe a distribution along the z‐axis that shows a depression in the middle of the section (Torres, Meldrum, Kirik, & Dunnett, 2006). This issue, and others that relate more to practical aspects of the bench work than to the principles of the method, will be discussed again in Section 9.2.
The second reason why a guard zone may be useful is the shape of the objects that are to be counted. Some shapes may not allow to decide if an object recognized in the last focal plane of a disector should be counted or not (Figure 22). If that is the case, the part below the last focal plane needs to be examined to make the decision. This part, the lower guard zone, should be large enough to allow deciding if a profile should be counted or not.
FIGURE 22.
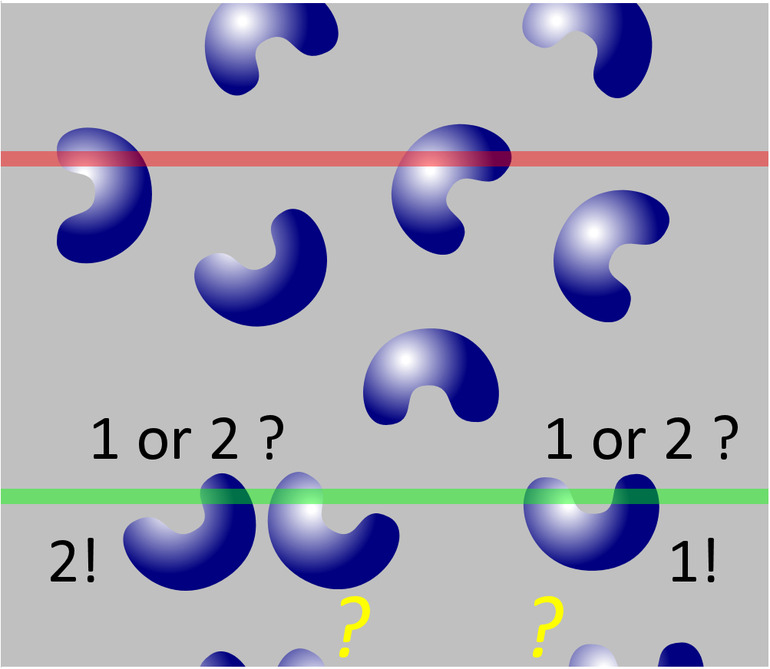
Guard zone and object shape. A deep guard zone may allow the correct identification of profiles if the shape of the objects is complex. In this example, the part of the section below the disector needs to be examined to determine if object profiles visible in the lowest focal plane (green line) should be counted as one or two objects. This decision is not possible if the disector is extended to the bottom of the physical section [Color figure can be viewed at wileyonlinelibrary.com]
Finally, the guard zone below the disector provides the space that may be necessary for objects to be counted using individually variable criteria for the recognition of objects (Figure 19).
6.5. From disector counts to total number: Fractionator and NV × VRef
Ironically, given my complaints about the use of density changes as evidence for changes in number, all that the disector probes initially deliver is a number density estimate, NV, that is, the number of objects counted in the volume of all the disector probes that were used to count. One could, of course, also calculate the average number per volume of one disector probe or a number per “unit of choice” of volume. There are two ways to convert the counts to estimates of total number—the optical Fractionator and the N V × V Ref method.
The optical fractionator (West et al., 1991) — If uniform random systematic sampling was used throughout, we can safely ignore the volume information provided by the disector. Uniform random systematic sampling also means fractionator sampling (see Section 3.4). It is therefore known which fraction of the volume of the region of interest has been included in the sample. Total number can be calculated by multiplying the number of objects, for example, cells, counted with the disector probes with the inverse of the sampling fractions that have been used to sample.
If, for example, the height, h, of the disector probes spanned 10 μm along the z‐axis and section thickness, t, is 20 μm, the thickness sampling fraction (tsf) would be 0.5. The inverse of the thickness sampling fraction is 2. Note that section thickness here refers to the actual thickness of the stained and mounted section on the slide and not the value that has been set on the microtome. Thickness will have to be measured (see Section 9.3).
If the distances between the disector probes along the x‐ and y‐axes are 200 μm, one disector probe is placed in an area of 200 × 200 μm2 = 40000 μm2. If the disector probes measures 10 by 10 μm along the x‐ and y‐axes, that is, 100 μm2, the probes will include only 100/40,000th = 1/400th of the total area of the section. The area sampling fraction (asf) is 1/400, and the inverse of this fraction is 400.
If the series contained only every 10th section, the section sampling fraction (ssf) is 1/10th, and the inverse of this fraction is 10.
If we counted ∑Q — = 200 cells in all the disector probes, we know that this is ½ × 1/400 × 1/10 = 1/8,000th of all the cells that there are. If we multiply the 200 cells with the inverse of the sampling fraction, that is, 8,000, we obtain an estimate of total cell number—1.6 million.
The number or volume of all the disector probes that were used to generate the sample actually never enter into the equation. If the objects that are counted can be recognized directly, for example, serotonin immunoreactive cells of the raphe or hippocampal CA3 pyramidal cells, the border of the area that we counted in does not matter. The sampled area could be extended by vast numbers of disector probes beyond the raphe or beyond CA3 to encompass the entire country of residence of the investigator. The vast majority of probes would return counts of 0 and not alter the number estimate. It is therefore not necessary to outline the area to be sampled very precisely.
It is different if the objects of interest cannot be recognized directly. A cortical layer III pyramidal cell in V1 may be difficult to tell from a layer III pyramidal cell in V2 in the small field of view available at high magnifications. In such cases, an outline needs to be defined that allows the identification of the objects of interest. The outline may be defined based on regional cytoarchitecture at low magnification or based on other stains in parallel series that allow its definition (e.g., Gritti et al., 2006; Morgan, Barger, Amaral, & Schumann, 2014). In these and similar circumstances, the area that is sampled needs to be defined as good as possible along the parts of the border that have the potential to add to the counts. For example, a cortical area would need to be delimited as good as possible from neighboring areas but not necessarily against the surface/pia mater or white matter. If one is interested in cortical oligodendrocytes, one would, of course, also need a precise outline toward the white matter. Correct outlines may be needed to allow the correct identification of the objects, but, again, the area of the outline or the numbers of probes placed within it do not enter into any calculation.
N V × VRef — Another approach to obtain an estimate of total numbers needs both the volume contained in the disector probes and the volume of the region of interest. If 200 cells were counted in 100 disector probes that measure, as in the example above, 10 × 10 × 10 μm or 1000 μm3, an estimate of number density, N V, could be 200/(100 × 1,000 μm3) or 2/1,000 μm3. If number density is multiplied by a reference volume, V Ref, that is, the volume of the same region of interest used in the fractionator example above, an estimate of total number is obtained. If the volume of the region of interest is estimated to be, for example, 0.35 mm3 or 355,000,000 μm3 we obtain an estimate of total number of 710,000 cells.
If it is indeed the same region of interest used in fractionator example, something really does not work here! Using the fractionator estimate, we obtain an estimate of 1.6 million cells, but using the volume of our region of interest and the N V × V Ref approach, we obtain only 710,000 cells. The discrepant estimates can be caused by the fact that some disector probes may not be contained completely within the region of interest but instead fall on the border of the region of interest (this just must happen sometimes—see below). The parts of the disector probes that lie outside the border cannot contribute to the counts, while their volume still contributes to the estimate of number density. How this can be accounted for has already been illustrated in Figure 18. While counting, we can keep track of how much of each probe is inside the region of interest. An easy way to do so is to keep track of the number of corners of the counting frame that fall within the region of interest. Depending on the degree of precision that is desired, one may choose one, two or more corners to represent the counting frame. In Figure 18, two corners (top left and bottom right) were selected. Although nine counting frames are applied to the region of interest, only 8 of the 18 possible corners fall into the region of interest. As two corners represent one counting frame, the nine frames applied to the region of interest yield only four full frames, that is, only 4/9 of the volume of all the probes applied was contained within the region of interest. If this was also the case for the region in this example, we can use a factor of 4/9 to correct and obtain an estimate of 1,597,500 cells is obtained.
Note that within each disector, regardless of the disector itself being counted as 1, ½, or 0, we count all objects that are located within the region of interest and that comply with the counting rules of the disector probe.
Small differences that may remain between fractionator and N V × V Ref estimates (here 2,500 cells) originate from chance—small differences in the volume estimates due to the random placement of the point grid or small differences in the estimate of the number of probes that were used. Across estimates in a number of individuals, the means of fractionator and N V × V Ref estimates should be close to identical.
As pointed out above, counting frames that fall onto the border of the region of interest cannot be avoided. If we decided to only include disectors that are completely contained within the region of interest, objects contained within the region do no longer have equal chances to contribute to the count. The problem is illustrated in Figure 23. Objects close to the border of the region of interest would only rarely or even never be included in the count, whereas objects that lie farther away from the border have a chance to be counted in many differently positioned counting frames. We can only provide the objects with equal probabilities to be counted if we permit counting frames that overlap the border of the region of interest. This is a requirement for both the optical fractionator and the N V × V Ref method.
FIGURE 23.
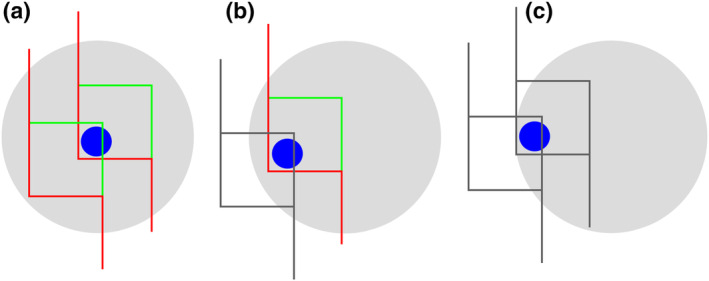
Counting frames that are not fully contained in the region of interest must be used. An object located fairly centrally in the region of interest (a) can be contained in many differently positioned counting frames (only two examples are drawn). If only counting frames that are fully located in the region of interest are used (colored frames), while partial frames (gray frames) are excluded, the number of frames that could contain a more peripheral object decreases (b) until the object cannot be contained in any frame placed on the region (c). Number would consequently be underestimated [Color figure can be viewed at wileyonlinelibrary.com]
There is one more thing that needs to be paid attention to when the N V × V Ref approach is used—a form of the reference trap. If errors sneak into the calculation of the reference volume, they will generate errors in the estimate of total number. For example, sections may be cut at 40 μm thickness but shrink to 20 μm after mounting, drying and coverslipping. During shrinkage, the objects come closer together, and the N V estimate may double. The reference volume needs to be calculated based on the section thickness at the time of counting, that is, based on 20 μm and not on 40 μm. There may be many steps between reference volume estimation and counting. The reference volume may have been estimated by in vivo MRI imaging. The cells are then counted after maybe dehydration of the brain, embedding, cutting of sections, rehydration, staining, dehydration, clearing, and mounting. Changes of the reference volume that can affect N V or V Ref estimates need to be monitored (see Section 9.5) and adjusted for.
6.6. Simple disector implementation
Possibilities to move along the x‐ and y‐ axis have already been described in Section 5.7. A slightly more advanced solution to repeated movements at high magnification was presented by Kaplan et al. (2005). For z‐axis measurements of section thickness or disector height, a microcator can be attached to the microscope. A costly microcator will return measurements of z‐axis movements of the microscope stage with a precision within small μm fractions. Simpler solutions allow readings to within one micrometer (Howard & Reed, 2010, appendix A). Microscopes with motorized z‐axis movement may offer a read‐out of the z‐axis movement that is sufficiently precise to omit a microcator. Finally, even the z‐drive knobs of fully manual microscopes may be calibrated to permit z‐axis movements of a defined size (Korkmaz & Tümkaya, 1997; Xavier‐Vidal, 2010). When using the optical fractionator, this size does not need to be in μm. If the disectors are two‐tick‐marks‐movement of the focusing wheel thick and the sections are on average four‐tick‐marks‐movement thick, the thickness sampling fraction is one‐half, which is all we need to know.
If a simple imaging setup is available, ImageJ extensions that generate counting frames are available to analyze image stacks. To count live, a calibrated counting frame can be drawn onto a transparency and taped to a display. Microscope eyepiece reticules that show grids useable as counting frames are available for live counting.
6.7. A comment on Abercrombie's methods
As pointed out in Section 2, a profile count obtained from sections could be converted into an estimate of cell number using Abercrombie's method (1946), if it was known how likely, for example, cells are to be cut during sectioning. The likelihood to be cut depends on the height of the cells in relation to the thickness of the section. It is therefore necessary to measure cell height. Abercrombie was well aware of sources of error of the measurement and underlying assumptions, but accepted them for the sake of feasibility and because the error seemed much smaller than the errors possibly associated with earlier methods. Height measurements of a number‐weighed, that is, disector‐sampled, selection of cells would allow such measurements but, as discussed in detail by Hedreen (1998b), this would require all the steps that are needed to generate a disector‐based number estimate and render the measurement of cell height for an Abercrombie estimate redundant. Height measurements in the plane of the section, which have commonly been substituted for measurements along the z‐axis, will introduce a possibility of bias that cannot be overcome by any correction.
Prior to the introduction of the disector, Abercrombie's method was the method of choice to obtain cell numbers. Sadly, the issue of Abercrombie versus disector dominated many early methodological discussions. At a critical time, the championship fight between incumbent and contending methods unfortunately diverted energy and attention from addressing the fact that many approaches that pretend to generate information about object number are far, far worse than either of the combatants claimed the other to be.
Interestingly, Abercrombie also describes a method to estimate cell numbers that is based on counts in sections of different thicknesses (Abercrombie, 1946). A count obtained in a thin section is subtracted from the count obtain in a thick section. The difference between the counts is an unbiased estimate of cell number in a section of a thickness equal to the thickness difference of the thick and thin sections. The disector is a special case of this method, in which the thin section would have a thickness of zero. It corresponds to subtracting the count in the top plane of an optical disector, from a count of all objects, including those in the top plane, in the disector probe. This is the same as excluding objects in the top plane from the count. Although the method has been reintroduced several times (Collan, 1998; Ebbeson & Tang, 1965), I am not aware of recent applications in the neurosciences.
7. LENGTH AND SURFACE ESTIMATORS
7.1. Orientation sensitivity of probe‐feature interactions
Critical for the understanding of length and surface estimators is the orientation sensitivity of probe‐object interactions when length and surface are estimated by area and line probes (Figure 24). If we probe for the length of, for example, axons (blue in Figure 24a) running more or less parallel in a fiber tract, an area probe (green in Figure 24a) that is parallel to the axons will never be intersected by the axons, that is, there are no probe–object interactions that can be counted. The number of area‐axon intersections will increase as the angle between the probe and the axons increases (Figure 24b) until we obtain the maximum amount of probe‐axon interactions/area when the area probe is perpendicular to the axons (Figure 24c). The number of interactions per unit area is dependent on orientation and the length of the axons instead of just the length of the axons. It is only when we sample the axons with all possible orientations of the area probe that the number of interactions between area and axons is directly proportional to the length of the axons. The roles of probe and object in Figure 24 can also be exchanged. We could use line probes (blue) to probe for, for example, cortical surface (green), and we face the same problem of orientation dependence of line–surface interactions.
FIGURE 24.
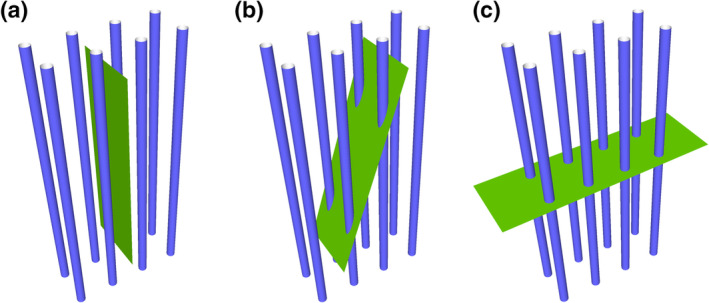
Orientation effects on interactions between a length and an area. The number of interactions between area and length is sensitive to orientation. Even though the blue length and green area are identical in all three images, 0 interactions are observed in (a), 4 in (b), and 8 in (c). This orientation sensitivity applies to estimates of length using area probes and to estimates of area using line probes [Color figure can be viewed at wileyonlinelibrary.com]
The situation in Figure 24 is, of course, an extreme case. Locally, the orientations of neuronal processes may appear more or less random, but they usually are not (Figure 25a), and randomness, when suspected, would be difficult to verify. If orientations are completely random, they are also called isotropic orientations. The very names that are applied to many structures, for example, cortical columns and barrels, or bi‐tufted (Figure 25b), chandelier or pyramidal cells imply some sort of spatial organization of the cells and their processes. Rather than the randomness of isotropy, we should expect some orderliness, that is, anisotropy, in the brain.
FIGURE 25.
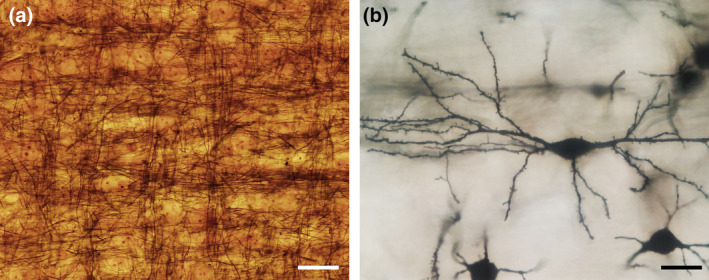
Isotropy and the structure of the brain. Randomness and the structure of the brain do not go well together. (a) Many axons in the deep layers of the somatosensory cortex of the bank vole (Myodes glareolus) travel roughly perpendicular to each other between the neurons. Nauta stain. (b) Oriented dendrites of a sparsely spinous bi‐tufted interneuron (perhaps a Martinotti interneuron) of the Sprague–Dawley rat somatosensory cortex. Golgi stain, montage of several focal planes. Scale bars: 25 μm [Color figure can be viewed at wileyonlinelibrary.com]
Probing the nervous tissue for length and surface requires isotropy, yet we have to expect anisotropy. The problem can be solved by randomizing either the orientation of the objects of interest during tissue preparation or by randomizing the orientation of the probe. Randomizing the orientation of objects in the sections would require that the orientation in which the tissue is cut is randomized. At a first glance, this is really not a very attractive prospect. However, it is very easy to count probe‐object interactions in randomly oriented sections. Approaches to estimate length and area in sections of (partly) random orientation are therefore described in Section 7.4. Randomizing the orientation of probes within sections has become the preferred approach, because it retains the free choice of the orientation of the section. Thick sections are required because sufficient space is needed within the sections to allow the placement of line or area probes in any orientation, that is, also along the z‐axis, which typically limits the size of the probes that can be applied.
Two slightly different approaches have been developed to place randomly oriented area probes within sections. The use of isotropic virtual planes (Larsen, Gundersen, & Nielsen, 1998) refers to changing orientations of probe planes at different sampling locations. This method is computationally demanding and the counting rules are not simple. Subsequently, a method was developed that places a spherical area probe at each sampling location (Mouton, Gokhale, Ward, & West, 2002). The probe has become known as a spaceball and is, together with its use, described in the following section. Well documented applications have been published by, for example, Calhoun, Mao, Roberts, and Rapp (2004), Shamy et al. (2007), Gondré‐Lewis, Darius, Wang, and Allard (2016) or Nykjær Nikolajsen, Kotynski, Jensen, and West (2017),
7.2. Using spaceballs to probe for length
A spherical probe or spaceball fulfills the requirement of equal probabilities of all possible orientations, or isotropy, because the surface of a sphere presents all possible orientations of a surface in space. A representation of the surface of a spaceball can be generated by a computer interfaced to a microscope as the focal plane is moved through the depth of the section (Figure 26). Probe‐object interactions occur each time the objects of interest touch or cross the circles that represent the surface of the spaceball.
FIGURE 26.
Interactions of a length with a spherical probe. (a) A spaceball, that is, a spherical probe, interacts with two tubular structures. (b,c) Two views of the sectioned spaceball, corresponding to the movement of the focal plane (gray) in a thick histological section. The tubular structures intersect the surface of the spaceball twice in each of the two section planes. The black outlines of the spaceball surfaces in (a,c) would appear as circles as the focal plane is moved through the depth of a histological section (see Figure 27) [Color figure can be viewed at wileyonlinelibrary.com]
Each orientation in space is not only represented once, but twice on the surface of a spaceball—once each at opposing sides of the spaceball. That means that the application of a hemisphere is sufficient to probe the tissue. In practice, this has the nice effect that a larger probe area can be used at each sampling location. If 20 μm thick sections are probed, the largest sphere that can fit inside the section has a radius of 10 μm and a surface area of 1257 μm2 (Asphere = 4πr2). Instead, we can place a hemisphere with a radius of 20 μm and a surface area of 2,513 μm2 at the same sampling site. In principle, a hemisphere could even be partitioned into multiple slices at each sampling site (Mouton et al., 2002). While this would allow for a further increase in the available probe area, it would also complicate the counting (see below).
A hemisphere was used as a spaceball in Figure 27 to count intersections of tyrosine hydroxylase (TH) immunoreactive axons with the spaceball surface. Small circles appear close to the top of the hemisphere that, at first, quickly increase in size as the focus is moved downward (Figure 27, 0–3 μm). Close to the equator of the hemisphere, the size of the circles increases very little (Figure 27, 8–10 μm). In contrast to the counting frame, touch and cross are not equivalent interactions but may be differently influenced by the thickness of the structure of interest (see below). In Figure 27, to cross the surface, that is, to cross the circle in the 2D representation that we see, was used as a counting criterion. The rapidly changing diameter of the circles close to the top of the spaceball may make it difficult to observe the actual crossing of the object of interest with the circle. If it was seen once on the outside and once on the inside, it must have crossed in the meantime and an intersection should be counted (e.g., Figure 27 at 1 and 2 μm).
FIGURE 27.
Estimating length using a spaceball as probe. A hemispherical spaceball (black circles) with a radius 10 μm inside a 10 μm deep image stack of neocortex containing tyrosine hydroxylase (TH) immunoreactive axons. Intersections of the axons with the surface of the spaceball are marked with arrows. At 0 μm, the spaceball only touches the image and is not yet visible as a cross section. The green circle was added to help identify axons that are in focus at 0 μm and, at 1 μm, inside the spaceball. Such axons would intersect the surface of the spaceball and should be counted (no such cases are observed here). At 9 μm, an axon briefly enters the spaceball to immediately leave it again. It must therefore intersect the surface twice (see object C in Figure 28). The two intersections observed at 10 μm (yellow arrows) would also be visible in the very first plane of the hemisphere completing the spaceball to a sphere. They would therefore be counted in two hemispheres. To avoid overcounting, these intersections are therefore only counted as 0.5. A total of six axon‐spaceball intersections (five green, 2 × 0.5 yellow) are observed [Color figure can be viewed at wileyonlinelibrary.com]
Note also that an intersection observed in the very last focal plane that contains the spaceball would also be counted in the very first focal plane of the hemisphere that continues the spaceball. Intersections in the last focal plane should therefore only be counted as 0.5 to avoid overcounting. Alternatively, one could declare one‐half of the last circle an “exclusion semicircle.” If the spaceball was sliced further to increase the available probe area, any probe‐feature interactions occurring at the edges of the slices would also have to be counted as 0.5. Using the intersections of the object of interest with the surface of the spaceball is rather straightforward if the objects are thin. The decision if an intersection is present or not may not always be unequivocal if the objects get thicker (Figure 28). In this case, it is helpful to use the imagined center, or spine, of the object to judge if one or more intersections took place (Gundersen, 2002b; Mouton et al., 2002).
FIGURE 28.
Identifying interactions of lengths with an area probe. Sometimes it is easy to decide how many interactions need to be counted based on the appearance of the objects of interest alone (Objects A and D in (a)). Other objects are more doubtful (B, C, and E in (a)). If one does not want to count touches as interactions between the spaceball and the length that is to be estimated, imagining the spines (white broken lines in (b)) may be helpful. Even though object C touches the circle only once, the spine of this object crosses the spaceball twice. We need to count two interactions. Instead, object B touches the spaceball twice, but its spine does not intersect the surface of the spaceball. No interactions are counted. Even though object E interacts only once with the surface of the spaceball, its spine crosses twice and two interactions need to be counted [Color figure can be viewed at wileyonlinelibrary.com]
In Figure 27, we count six interactions of axons with a hemisphere that has a radius of 10 μm and a surface area of (4 × π × 102)/2 = 628 μm2. Following the relationship equation for length using an area probe, we obtain a length density estimate, LV.
in which Q is the number of intersections counted with the spaceballs, and A is the surface area of the spaceball that was used to probe the tissue.
Usually, there should be more than six interactions, and, of course, we should probe our region of interest with more than a single spaceball. Similar to the calculation of the NV × Vref estimate of number, we may need to keep track of how many of the spaceballs actually were located inside the reference volume. One or more arbitrarily placed points can be included with the spaceball—often the corners of a square drawn around the spaceball. The number of points would tell us how many spaceballs were contained within the reference volume. If we had counted 84 intersections using 53 spaceballs located inside the reference volume, Lv would be (2 × 84)/(53 × 628 μm2).
The length density estimate can be converted to the total length by multiplying LV with the volume of the region that contained the objects of interest.
Note that of the μm2 in the denominator of LV and the μm3 as the unit of Vref only a unit of length, μm, remains.
Alternatively, a fractionator approach can be used to calculate total length. Getting at the formula, which is simple enough, is a little more convoluted than was the case for a fractionator cell count. When LV is multiplied with Vref, we nicely get rid of the area in the denominator of LV and conveniently end up with a length. Multiplying by the dimension‐less inverse of the sampling fraction does not help us to get rid of the area to end up with length. LV needs to be converted to a length before we can multiply it with the inverse of the sampling fraction. We can convert LV to a length by multiplying LV with the volume of arbitrarily sized boxes that we place around the spaceballs. The most conveniently sized box contains the volume, Vbox, of the tissue that is probed with each spaceball. In the plane of the section, this box has an area of Astep. The depth of the box would be section thickness, h. There is one box per spaceball, and the number of boxes that we looked at corresponds to the number of sampling sites, nsampling sites. So, the volume of all the boxes would be nsampling sites × Vbox. This is the volume we use to multiply with LV.
The dimensions of this box are also used to calculate the area and thickness sampling fractions. The chosen size of the box is convenient because its area equals Astep and its height equals h. Area and thickness sampling fractions are 1 and can be ignored. Only the section sampling fraction, ssf, is needed. Length can now be estimated from parameters that we know and the counts.
Note that, the number of probes or the total volume probed do no longer appear in the final equation. As long as probe‐object interactions are only counted within the region of interest, it does not matter if much of the volume associated with each sampling location would be outside the region of interest when the probe itself is inside the region and vice versa. Note also that the most complicated mathematical operations required are simple divisions and multiplications, and not even many of them.
Figure 28 shows that it sometimes may be difficult to decide if an object intersects the probe area or not. This is because biological structures are not infinitely thin mathematical lines but have a thickness, and it would really not make things easier if they were invisibly thin. That there is a thickness of an axon or a vessel may result in a bias if we use “touching the probe area” instead of the preferred “intersecting the probe area” as the counting criterion (Gundersen, 2002b). For example, object B in Figure 28b touches twice but does not intersect. This will bias estimates of length, and the size of the bias depends on the thickness of the structures in relation to the diameter of the spaceball. The size of the bias can be defined for simple shapes in the form of a factor 1 + 0.25(d2/t2) (factor for hemispheres; Mouton et al., 2002), in which d is the diameter of the structure of interest and t the radius of the spaceball. If, for example, the length of 2 μm thick axons or 6 μm thick capillaries are estimated with spaceballs of a radius of 20 μm, the factors would be 1.01 and 1.09. We see 1.01 times (1%) more touches than there are actual intersections of the axon with the area of the spaceball and 1.09 times (9%) more touches of capillaries than there are actual intersections. Even though the bias is not large, it may be avoided by using “intersect” instead of “touch” as counting criterion.
7.3. Probing surface: Isotropic line estimators
Conceptually the roles of probe and objects of interest introduced for length estimators are exchanged when surfaces are probed, while the problem of orientation sensitivity remains (Figure 24). The solution is, again, a randomization of the orientation of line probes if we want to remain free to choose the orientation of the tissue sections that we like best. Two methods using a randomization of line orientations have been presented. Similar to the randomly oriented isotropic virtual planes (Larsen et al., 1998) that can be used for length estimates, the isotropic fakir (Kubínová & Janácek, 1998) uses randomly oriented sets of straight lines. Similar to the spaceballs (Mouton et al., 2002), virtual cycloids (Gokhale, Evans, Mackes, & Mouton, 2004) use test lines that each incorporate multiple orientations. Both the isotropic fakir and virtual cycloids are applied as virtual probes to thick tissue sections.
The easiest way to generate a line with a random orientation is to decide on a point of origin and, thereafter, randomly select two angles that would correspond to the longitude and latitude used to specify positions on the surface of the earth (Figure 29a). Surface density estimates require that the number of interactions between the line probes and a surface is directly proportional to the length of the lines and surface area and nothing else. Unfortunately, the simple selection of two angles does not quite yet fulfill this requirement. In Figure 29a, areas that are associated with a degree of longitude and a degree of latitude are much smaller close to the poles than they are close to the equator. Because of this, countries far up north or down south look—bolstering national self‐esteem—much larger in some maps than they are in reality. Also, a unit of surface close to the poles would interact more often with randomly oriented line probes than a unit of surface close to the equator (Figure 29b), and we would erroneously confirm that some countries are much larger than they are. This can be compensated for by sine weighting the angle for the latitude of the probe lines. Instead of picking a random angle, a random sine value (between zero and one) is selected, and the corresponding angle is calculated and used (Figure 29c). Using sine weighted angles, line probe‐surface interactions distribute evenly over the globe.
FIGURE 29.
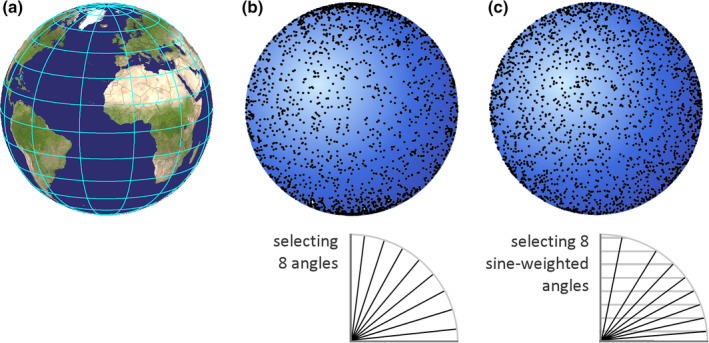
Interactions of randomly oriented lines with a surface. (a) Using the common latitude and longitude coordinate system, the areas associated with a degree of latitude and a degree of longitude are much smaller close to the poles than close to the equator. (b) Random latitude and longitudes are selected for lines originating from the center of a sphere. They interact more frequently with the surface of the sphere close to the poles than with the surface close to the equator. (c) Randomly selected longitudes are combined with randomly selected sine weighted latitudes. The interactions between the lines and the surface of the sphere are now evenly distributed over the surface. Angles for latitudes below (b) and (c) show eight uniform random systematic angles in (b) and eight uniform random systematic sine‐weighted angles in (c). (Globe in (a) generated using satglobe4 (Kleder, 2005)) [Color figure can be viewed at wileyonlinelibrary.com]
A sphere and an origin of the lines from the center of the sphere were chosen to illustrate the problem and its solution. The solution also works when the shape is not a sphere and when the origin of the lines lies outside the object of interest.
While sine weighting does allow the placement of randomly oriented lines, it still requires the placement of many differently oriented lines at the sampling sites. In the same way in which a spaceball, used to estimate length, contains all orientations of a surface in space, some convenience can be gained by using a line which contains all orientations in a sine weighted manner. Such a line is called a cycloid. A cycloid would be formed by the movement of a point on a rolling circle (Figure 30). A cycloid's steep initial segment is rather short (corresponding to fewer lines going to the polar region) compared to the longer, shallow‐angled approach to its' peak value (corresponding to more lines going to the equatorial region).
FIGURE 30.
Cycloids. (a) The curved shape that is formed by attaching eight sine weighted lines (Figure 29c) of equal length to each other resembles a cycloid. If increasingly more and shorter lines were used, the shape would be indistinguishable from the cycloid in (b), which is the curve formed by a point (red) on the perimeter of a rolling circle (gray) [Color figure can be viewed at wileyonlinelibrary.com]
As a virtual probe, the cycloid will be represented by a point that moves as the focal plane is moved up or down through the section (Gokhale et al., 2004). Note that at different sampling sites, the point must move in different directions because randomly selected longitudes, that is, random directions in the plane of the section, must be used at each sampling site. A probe‐object interaction is counted each time the point moves across/intersects a surface (Figure 31).
FIGURE 31.
Estimating surface using virtual cycloids. The image stack was acquired using structured illumination of mouse DAPI stained hippocampal pyramidal cell nuclei. In each image, the intersections between the image plane and two 7 μm high virtual cycloids (passing from the center of the image to the lower left and upper right) are marked by red dots. The parameter estimated is nuclear surface area. The yellow tails of the dots are helpful in this illustration to mark the path that the dots traveled since the last image of the stack. They would not be needed during the live application of the probe, when the dots move smoothly and can actually be seen crossing nuclear boundaries. The dots pass five times across the nuclear boundaries. Both cycloids pass from outside of a nucleus to the inside of a nucleus between 0 and 1 μm generating one probe‐object interaction for each cycloid (green arrowheads); they are leaving the nucleus again at 3 and 4 μm, again generating one probe‐object interaction for each cycloid. The last interaction is generated as one of the cycloid passes inside a nucleus at 7 μm. The length of a cycloid is twice its height, that is, 14 μm. Two cycloids are used and the total probe length is 28 μm. Scale bar: 10 μm [Color figure can be viewed at wileyonlinelibrary.com]
The number of interactions between cycloids and a surface can now be used in the relationship equation for surface density, SV.
in which I is the number of intersections counted.
The length of a cycloid is twice its height, that is, 14 μm for each of the cycloids in the 7 μm high stack in Figure 31.
For the one sampling site using two cycloids illustrated in Figure 31, SV is 10/28 μm. The calculation of total surface is analogous to the calculation of total length. We can obtain an estimate by multiplying with a reference volume, S = SV × Vref. For example, the volume represented by the stack in Figure 31 is 50 μm × 50 μm × 7 μm, that is, 17,500 μm3. An estimate of the nuclear surface contained in this volume is (10/28 μm) × 17,500 μm3 = 6250 μm2.
For a fractionator estimate, SV needs to be first converted to a surface in the same way in which it was done for length in Section 7.2. In addition to the actual counts, only the sampling parameters and section thickness need to be known to calculate an estimate of total surface.
A problem of virtual isotropic line estimators is the recognition of line‐surface interactions in thick tissue sections, which can be difficult if the surface is tangential to the plane of the section. While the surface of a spaceball is represented by a quickly moving but otherwise distinct line close to the top of the spaceball, this is most likely not the case for, for example, neuronal membranes or vascular surfaces. If recognizing probe‐object interactions is judged to be too uncertain, surface estimators that are described in the following section could be used.
7.4. Length and surface estimates in isotropic and vertical sections
When isotropic surface or line estimators are used in thick tissue sections, the orientation of the section in which they are applied does not matter. The probes guarantee that interactions between probe and object are independent of the orientation of the section. The freedom to choose the plane of the section comes at a price. The sections need to be relatively thick, shrinkage along the z‐axis ought to be minimized (see Section 9.5), and it may occasionally be difficult to judge if the probe and object interact. Although simple and inexpensive ways to implement probes can be devised, their implementation is not as straight forward as one might wish. Some of these difficulties can be overcome by giving up the freedom to cut the tissue in a desired direction. Before the advent of virtual probes in thick sections, this was part of earlier approaches that guaranteed isotropic probe‐object interactions.
7.4.1. The isector
The most radical approach to guarantee isotropic probe–object interactions is to prepare isotropic sections, that is, sections in which the direction of cutting has been completely randomized. The approach is called the isector (Nyengaard & Gundersen, 1992). Using the isector, samples of the tissue are embedded in random orientations and cut (Figure 32). The sections that are generated are also called isotropic uniform random (IUR) sections. Using the isector may appear almost ludicrous in the central nervous system, in which the orientation of the section may even determine if the region of interest can be recognized or not. However, it is less so than it appears at a first glance. A practical approach for the preparation of isector samples was outlined by Løkkegaard, Nyengaard, and West (2001) in a study that estimated capillary length in the subdivision of the human hippocampus. In this study, sections of varying thicknesses were cut from larger blocks and used for different stains. Samples for the isector were prepared by microdissecting samples from thick sections that were stained free floating prior to embedding to allow the identification of regions. The isector does not demand that the entire structure is cut at random. Sections can be cut and stained in the usual manner provided that tissue blocks for subsequent embedding/recutting can be obtained from these or adjacent sections. By now, it should not be necessary to say that the blocks should be a uniform random independent or systematic sample.
FIGURE 32.
Isotropic section prepared using the isector. In the form the isector was originally proposed, tissue blocks are embedded in a spherical mold. The sphere containing the tissue (left) was thereafter randomly rotated, reembedded and cut to generate an isotropic section through the tissue blocks (right) [Color figure can be viewed at wileyonlinelibrary.com]
Because the sections are isotropic, estimates of surface can be obtained by applying line probes of any orientation to the sections to count line–surface intersections. For length estimates, the plane of the section represents the available probe area. Estimates of length can be obtained by counting intersections of objects with the plane of the section. For both length and surface estimates, the estimation procedure can be restricted to a sample of the area of the section using the unbiased counting frame (Section 6.2; Figure 33). The resulting surface or length density estimates can be converted to total length or surface using either the fractionator or the N V × V Ref approach (for example, Jørgensen, Marner, & Pakkenberg, 2008; Tang & Nyengaard, 1997).
FIGURE 33.
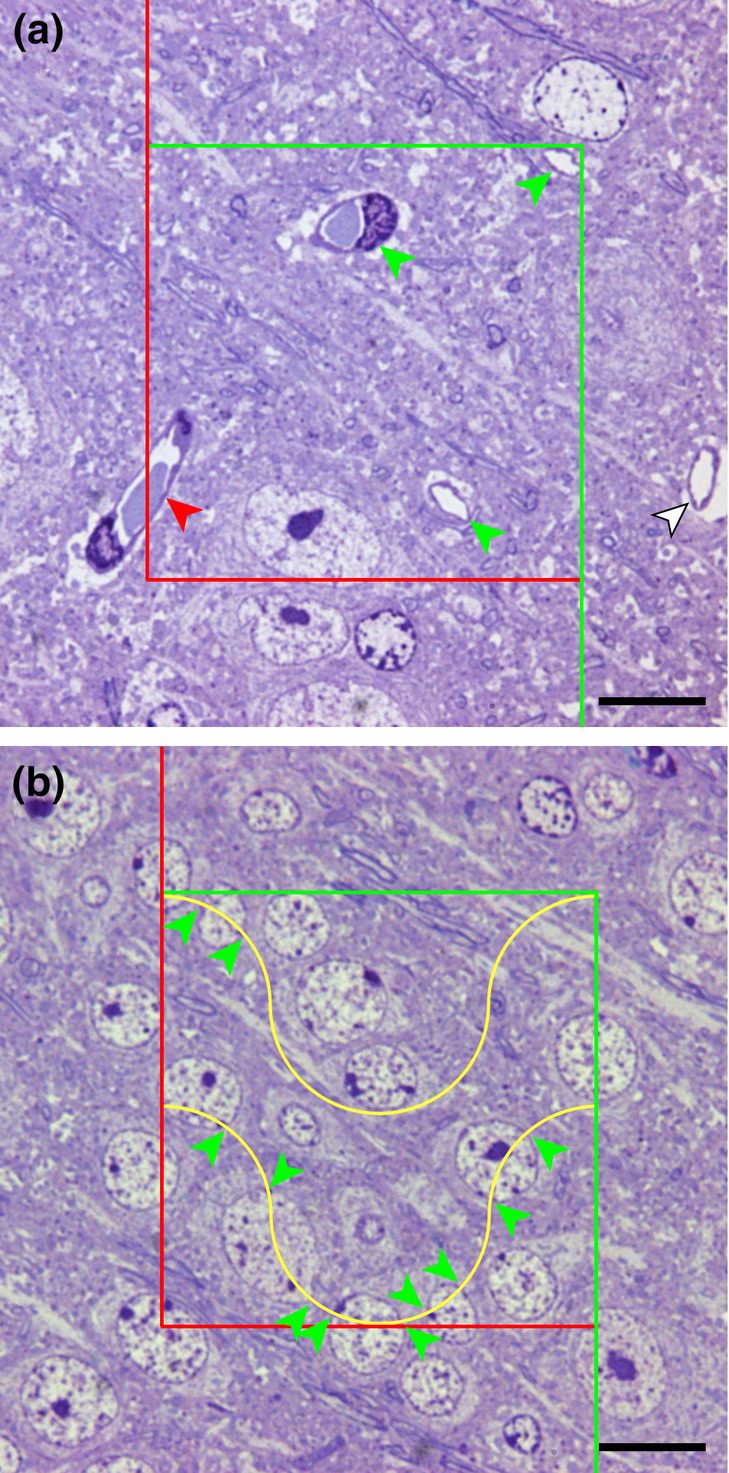
Probing for length and surface in isotropic 0.2 μm semithin sections of Epon‐embedded, toluidine blue stained mouse neocortex. (a) A counting frame used to define a sample of the area and to count intersections of capillaries with the plane of the section in this area. The three capillaries labeled with green arrows can be counted. The capillary marked with the red arrow crosses the exclusion line of the counting frame and is not counted. An additional capillary is labeled with a white arrow. (b) Merz test lines are used to count intersections of the lines with the surface of cortical nuclei. The area to which the lines are applied is again defined by a counting frame. Straight lines could also be used, but the hemicircles composing the Merz lines may be more efficient if the surfaces to be estimated have a preferred orientation in the section (Merz, 1967). Eleven intersections of the lines and the boundaries of nuclei are counted (green arrows). Scale bars: 10 μm [Color figure can be viewed at wileyonlinelibrary.com]
In the example for length (Figure 33a), three intersections of vessels are counted within 40 × 40 μm = 1600 μm2 area defined by the counting frame. An estimate of LV based on just this one probe would therefore be 2 × 3/1600 μm2. The volume associated with the probe equals the area of the frame × section thickness, that is, 1600 μm2 × 0.2 μm = 320 μm3. An estimate of the length, L, of vessels in the volume associated with this one probe would be (2 × 3/1600 μm2) × 320 μm3 = 1.2 μm.
In the example for surface (Figure 33b), the length of the test lines (two circles with a radius of 10 μm) is about 126 μm. The sizes of the counting frame area and section thickness are identical to those in the example for length. An estimate of the surface, S, of nuclei in the volume associated with this one probe would be (2 × 11/126 μm) × 320 μm3 = 55 μm2.
7.4.2. Vertical sections
Vertical sections as a means to guarantee isotropic probe‐object interactions were first introduced for surface estimators by Baddeley, Gundersen, and Cruz‐Orive (1986) and subsequently also for length estimators (Gokhale, 1990). Vertical sections do not require the complete randomization of the cutting direction. Essentially, half of the randomization is generated during the cutting of the tissue, while the other half of the randomization relies on the application of the probes to the sections. These two randomizations work similar to the randomization of the orientations of test lines already introduced in Section 7.3. A random angle for the longitude is chosen to rotate the region of interest or slabs of the region prior to cutting (Figure 34). Note that the horizontal, that is, the plane in which we rotate the tissue, can still be chosen freely. The horizontal would correspond to a plane passing through the equator in Figure 29.
FIGURE 34.
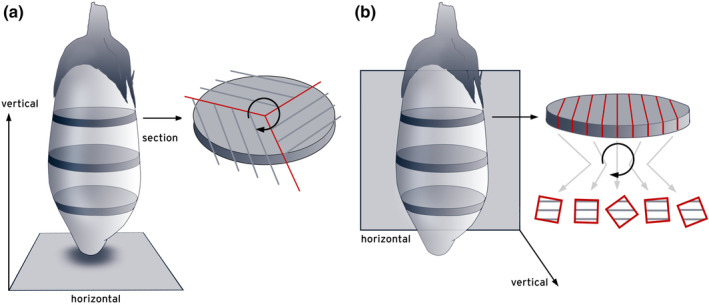
Two‐ways to prepare vertical sections from a region of interest. A plane parallel to the equator, the horizontal, can be chosen freely. The choice of the horizontal does not necessarily impact on the way in which sections are prepared. Slabs of the region of interest can prepared in the same way in (a) and (b) despite the choice of different horizontals. The choice of horizontal does impact on the way the slabs must be rotated prior to sectioning to generate the random angles that are necessary to ensure isotropy. Slabs or parts of them must be rotated around the vertical, an axis perpendicular to the horizontal [Color figure can be viewed at wileyonlinelibrary.com]
Next, the rotated tissue is cut into sections perpendicular/vertical (hence, vertical sections) to the horizontal. The sections generated in this way would pass through a randomly selected longitude. They are called vertical uniform random (VUR) sections. The randomization of the angle that would specify the latitude is achieved during the application of the line or area probes. The major gain, in comparison to sections prepared with the isector, is that it is possible to at least decide where we place the horizontal. From an anatomist's point of view, vertical sections are suited to parts of the brain that have a natural horizontal. If we rotate neocortex (as a flat‐mount or a cortex block; Dorph‐Petersen et al., 2009) in a horizontal that is parallel to its surface and cut it vertical to the surface, we will always see the typical six layered organization of the cortex. The same will be true for any part of the CNS that has a tiered organization in one plane or can be prepared to have one. Other structures may have a natural vertical. Rotating, for example, the olfactory bulbs around their central axis will provide sections looking fairly similar to sections cut either sagittally or horizontally. Similar to the practical approaches that have been used with the isector, it is not necessary to sacrifice the entire region of interest to vertical sectioning (Hosseini‐Sharifabad & Nyengaard, 2007). Also, if a region of interest has no natural vertical or horizontal, sections taken from tissue slabs prepared in a convenient anatomical orientation can be used to map the location of regions in vertical sections prepared from adjacent slabs (Dorph‐Petersen, 1999).
Line probes applied to vertical sections face the same problem that was already discussed for virtual isotropic lines. Choosing random angles for their application will result in too many lines passing into the direction of the poles. The solution to this problem is, again, a sine weighted selection of the angles, that is, picking a random value between zero and one, calculating which angle would have this value as its sine, and using this angle to apply a line to the section. Again, efficiency can be gained by using a line that is a cycloid, that is, a line representing all orientations in a sine weighted manner (Figure 35a). Intersections between the lines and the surfaces are counted. In contrast to the use of isotropic virtual lines, sections can be thin, because the cycloid is now placed in the plane of the section instead of perpendicular to it. Probe‐object interactions may be easier to recognize in thin sections. Also, in the critical zone along the long axis of the cycloid, we are looking for probe‐feature interactions “from the side” instead of “from the top,” which should make it easier to define probe‐object interactions when the surface and the line probe are running close to parallel through the tissue. Total surface is calculated using fractionator or SV × Vref approaches.
FIGURE 35.
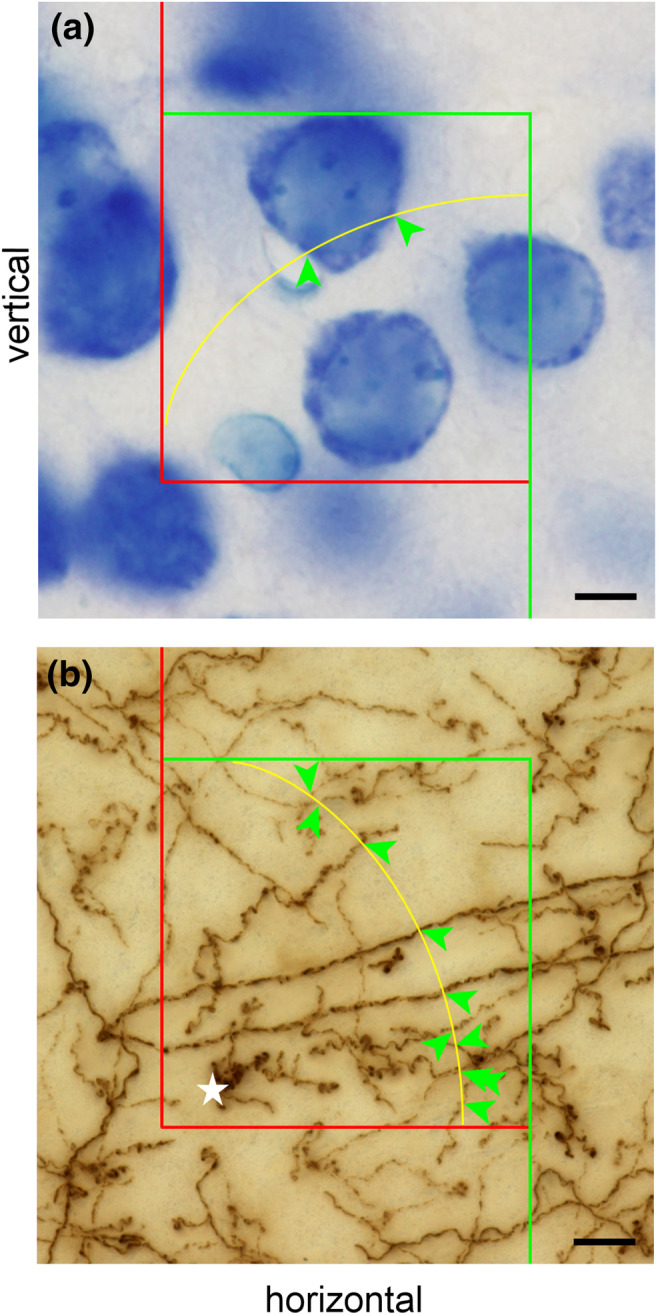
Surface and length estimates in vertical sections. (a) A cycloid line probe interacts twice with the surface of a neuron. Scale bar: 5 μm. (b) A cycloid area probe interacts 10 times with tyrosine hydroxylase immunoreactive axons in a minimum density projection of an image stack spanning a 40 μm thick section. Image planes were spaced 0.2 μm apart. To resolve interactions between an area probe and axons in dense axon clusters (asterisk), the image stack would have to be examined image by image. Scale bar: 10 μm [Color figure can be viewed at wileyonlinelibrary.com]
In contrast to length estimates using spaceballs, length estimates in vertical sections face the same problem as surface estimates. We therefore again have to apply a weighting to area probes applied to the sections. However, the roles of probe and feature have been exchanged. Instead of a line probe that will estimate an area, we use an area probe to estimate a length. To compensate for the fact that lengths pointing into the direction of the poles of the vertical section would interact more often with a spherical surface probe than lengths pointing toward the equator, we need to compensate by providing more area close to the equator. This can be achieved by cosine weighting the area probes—either by randomly selecting cosine‐weighted directions of flat probe areas or by using an area probe that bends into a (surprise!) cycloid shape. While the long‐axis needed to be parallel to the horizontal to estimate surface, this cycloid will have its long axis parallel to the vertical (Gokhale, 1990). The area that we apply would be a projection of a line, whether straight or in the form of a cycloid, through the depth of the section, that is, the length of the line multiplied by the thickness of the section (Figure 35b). In practice, the focal plane is moved through the depth of the section and intersections of the line (representing the probe area) and objects of interest are counted. If we see an interaction between the length and the area probe in the top focal plane, we do not count it, because it would be counted in the bottom focal plane of another probe. Once again, total length can be calculated using fractionator or LV × Vref approaches. Well documented applications of length estimators in vertical sections can be found in, for example, Artacho‐Pérula, Roldán‐Villalobos, and Cruz‐Orive (1999), Chen et al. (2017), or Kubíková, Kochová, Tomášek, Witter, and Tonar (2017). Vertical sections are also easily applied to macroscopic in vivo imaging data sets, in which the plane in which a structure is visualized can be chosen freely (Acer et al., 2010; Cruz‐Orive, Gelšvartas, & Roberts, 2014).
7.5. Simple implementation of virtual length and surface probes
For the selection of sampling sites and the spacing of stack images along the z‐axis, some of the simple and inexpensive ways already introduced in the preceding sections may be useful.
If image stacks of sampling sites are available, circles that represent a spaceball can be drawn onto the individual images of the stack. If, for example, 10 μm along the z‐axis of the stack contain 21 images (one image at zero μm and 20 images at increments of 0.5 μm) that need to be probed with a spaceball (hemisphere) that has a radius of 10 μm, the sine is divided into 21 equally spaced values separated by increments of 0.05 (0, 0.05, 0.10, 0.15 … 0.95, 1) and the angles corresponding to the values are calculated (0, 2.9, 5.7, 8.6 … 71.8, 90). The radius of the circles that need to be drawn onto individual images will be the cosine of these angles multiplied by the radius of the spaceball (10, 9.99, 9.95, 9.89 … 3.12, and 0 μm). If the graphics software permits the recording of image manipulations in form of an executable script (even recreational graphics software may allow this), the script can be applied to the remaining stacks of the sample. Figure 27 was prepared in this manner. It is advisable to keep an unmodified backup of the stacks.
Even isotropic line probes may be implemented without the aid of advanced software. A point could be moved from image to image of a stack by the distances that correspond to the displacement of the point along the x‐axis of a cycloid for y‐axis increments of the cycloid. The y‐axis increments would correspond to the distances between the images in the stack. The x values will be . h is the height of the entire cycloid/image stack and y the height (in the stack) of the image that the x value needs to be calculated for. The length of the cycloid probe is 2h. Note, that the displacement of the point in the plane of the section should take place in all possible directions. The x‐positions for different height in the stack could be marked on a ruler that is applied to the screen as a physical or digital overlay. Working live with the microscope one would at least need a precise readout of z‐axis movement of the stage.
Length and surface estimators in IUR and VUR sections are back into the realm of very simple implementations. A counting frame that samples the area of an IUR section for intersections of the objects of interest with the plane of the section can be placed on a section by way of an eyepiece reticule, transparencies, or as a digital overlay on recorded images. Images of cycloids for length and surface estimates in VUR sections are difficult to draw freehand, but suitably scaled ones may be generated with MATLAB and placed over images or taped to displays. Also, a cycloid grid plug‐in is available for ImageJ.
8. GOOD ENOUGH?—ESTIMATE PRECISION
A recurrent question pertaining to estimates of number, length, surface, or volume is whether they are “good enough.” If the tissue has been sampled and probed correctly, statistically valid estimates are obtained. Unfortunately, statistically valid does not necessarily mean useful. It is the precision of estimates that determines how good, that is, useful, the estimates can be. In purely descriptive quantitative studies, the precision indicates how close the reported mean of the estimates is likely to be to the true mean of the sample. In experimental studies, estimate precision in part determines how likely it is that differences between control and experimental groups can be detected statistically. To answer the question if the estimate is “good enough,” we need to generate a number that we can use to assess precision in the context of the study. Considering that “not good enough” usually means “useless” even if the sampling and probing were done correctly in a statistical sense, an understanding of the preceding sections is equally useless if we cannot at least get close to an answer of the “Good enough?” question. Consequently, some space will be spent on estimating and judging precision. There will be quite a few new concepts, and it may be a good idea to take a break before setting out.
8.1. What is a CE?
A parameter that is useful to describe the precision of an estimate is the Coefficient of Error or, short, the CE. To understand what the CE is, we again need to take a look at why and how an estimate is generated. Typically, estimates are generated because it is not feasible to determine the precise values of the parameters that one is interested in. There are, for example, simply too many cells in too many sections to count them all. To generate a valid estimate, a statistically representative sample needs to be drawn from each individual, that is, the mean of the estimates obtained from all possible samples will be the true value of the parameter of interest in that individual.
Let us estimate the volume of a brain region. If we use the Cavalieri Estimator to estimate the area of a brain region in all sections that can be cut and, next, plot the point counts obtained in each section along the axis in which the brain was cut, we obtain a graph like Figure 36a. This is what we often cannot do because it would require too much work. Instead, we draw a sample of the sections. Because the size of the brain region differs slightly from section to section, each sample will return a slightly different point count. The resulting estimates differ even though we sample the same structure each time.
FIGURE 36.
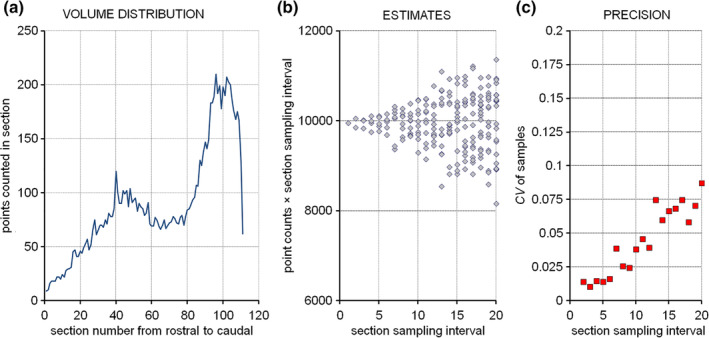
Sampling a volume and the precision of volume estimates. (a) Volume distribution of the hippocampal dentate gyrus granule cell layer in an exhaustive series of 20 μm thick coronal sections (data from Basler, Gerdes, Wolfer, & Slomianka, 2017). (b) If subsamples are drawn with increasingly larger distances between the sections, the volume estimates (point counts from the sections scaled by the sampling interval) start to diverge. (c) The standard deviation of the estimates generated by a particular sampling divided by the mean, that is, the coefficient of variation, is a measure of the precision that can be obtained with the sampling scheme. If, for example, every 10th section is analyzed, the variability of the estimates generated with this sampling scheme amounts to less than 0.05, that is, less than 5% of the mean [Color figure can be viewed at wileyonlinelibrary.com]
Figure 36b illustrates the estimates obtained from all samples that used sampling intervals of every 2nd, 3rd, 4th … 12th, … or 20th section. As one may expect, the estimates tend to vary more if fewer and fewer sections are used. If data of this type is available, the coefficient of variation or, short, CV, of the samples that belong to a particular sampling interval can be calculated. The CV is the standard deviation of all estimates of a particular sampling interval divided by their mean. The CV provides a measure of how much the estimates vary relative to the mean (Gundersen & Jensen, 1987). Figure 36c is a plot of the CVs that were obtained from the variability of the estimates in Figure 36b.
CE estimators provide an estimate of the CV that is calculated from repeated estimates in the manner described above. Notably, one does not need to count in all sections to be able to draw the subsamples that belong to a particular sampling interval. Instead, several approaches have been developed that allow a CE estimate to be calculated from a single sample. While the ability to calculate the CE from a single sample saves a significant amount of work, it does come at a price. CE estimators do not provide more than their name promises: an estimate of the CE. In the same way in which any one estimate of, for example, cell number may deviate from the mean of the group of animals, any one CE estimate may not be close to the true precision that is associated with a sampling scheme (Schmitz & Hof, 2000). In neither case is it likely that the final assessment of the data will be based on a single observation, that is, an n of 1.
8.2. Why is a CE important?
Let us assume that we sample a brain region that in all individuals of a control group is totally and utterly completely identical in size and shape (black circle in Figure 37). The true value of whatever we are interested in is 100. If the regions are completely alike, sampling the different individuals of the control group would correspond to the repeated sampling of one region illustrated in Figure 36. Because we sample, we will not obtain the same value from each individual but slightly different ones. Instead of seeing identical values for all individuals in the control group, they are now represented by the green circles in Figure 37.
FIGURE 37.
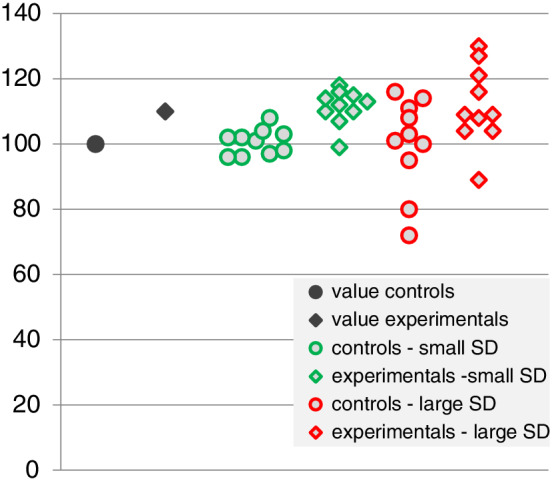
The impact of sampling generated variance on group variance. Sampling generates variability in a data set. Identical values (dark circle and diamond) may turn into a variable set of values with low (green) or high (red) variances depending on how much work we invest into sampling. If instead the green values reflect the true values of a parameter that has a natural variability indicated by the scatter of the point (circles and diamonds statistically different), adding variance by the sampling may turn them into the red data points (circles and diamonds statistically not different). Knowing the amount of variability that we add by sampling tells us if additional work could reduce the scatter in the red data points. It also tells us if we can expect a statistically significant outcome for the comparison between groups if we invest more work [Color figure can be viewed at wileyonlinelibrary.com]
Let us now add an experimental group, in which the size and shape of the region are, again, identical in each individual. In our experimental group, the region is slightly larger (black diamond in Figure 37) than that of our control group. In the experimental group, the true value of whatever we are interested in is 110. Once again, because we sample we will see slightly different values for each individual instead of identical ones. We now obtain the green diamonds in Figure 37 for our experimental group.
We were lucky. The difference between the green control sample and the green experimental sample is highly significant using a two‐tailed t test (p = .00008). Had we been lazier and sampled less, the estimates would be less precise and the variability of the estimates would be larger. Control and experimental values may now look like the red circles and red diamonds in Figure 37. More variability in the groups means a smaller chance to detect a group difference. Luck has left us. The p value for the group comparison is now 0.065. The variability around the mean that we generated because we sampled obscures a difference that we know exists. We sampled too little and the CEs are not “good enough.”
CEs are important because their size has direct influence on statistical outcomes
Drawing samples generates variability that adds to the natural variability present in the group. This relation is often expressed in the following simple formula.
Individuals in groups are, most likely, never absolutely identical. The true values may look like the green markers in Figure 37 reflecting biological variance (Varbiology), and the variability added by the sampling (Varsampling) may turn them into the red markers in Figure 37. Group variance (Vargroup) is given to us by standard statistics. A useful estimate of how much variability we added, that is, the CE, would allow us to figure out if working harder on the sampling would allow us to obtain a statistically significant outcome. If not, we need more individuals in our groups, that is, a larger n. Not only that—if the statistical outcome of a group comparison has shown a significant effect, a useful CE estimate would also allow us to figure out how much less work in terms of sampling or fewer individuals we may be able to afford without jeopardizing our chances to see the effect.
8.3. Estimating the CE based on a single sample
Several ways have been proposed to calculate the variance that originates from the sampling of sections. A prerequisite for their use is that the sections form a uniform random systematic sample, that is, that they form a series of sections of the type typically cut in a laboratory.
The key to understanding why the variability that originates from the sampling of sections can be calculated based on a single sample is to realize that counts obtained from one section will always be able to forecast—more or less well—the counts that are likely to be obtained from nearby sections. The shape of brain structures was not generated by a random number table. If the cortex is large in section 10 and in section 20 of a series, there is a good chance that it will be large in section 15 too (Gundersen & Jensen, 1987). Counts obtained from sections in a series co‐vary with each other, and we should be able to calculate how much they do so. The variance that is not explained by covariance between sections can be approximated mathematically using the formula proposed by Gundersen and Jensen (1987) based on the work of Matheron (1965, 1971). For a volume estimate using counts of points in sections, Pi, the formula would be
in which
A is the sum, across all sections of the sample, of the counts in each individual section, that is, P i, squared
B is the sum, across all section of the sample, of P i multiplied by the counts in the following section of the sample, that is, P i + 1, and
C is the sum, across all sections of the sample, of P i multiplied by the counts obtained in the next to the following section, that is, P i + 2
Note that the region, hopefully, was not present in the section that would be following the last section that was collected using the sampling scheme. The counts obtained from sections following the sample are zero (see Table 1), that is, the last number to be summed up for B and the last two numbers to be summed up for C will be zero because P i is multiplied by zero.
TABLE 1.
An example of a CE calculation. The example is based on the olfactory bulb point counts from Figure 13. Even though, there are only seven sections in the sample in which only 66 counts were obtained, the CE generated by the sampling of the sections amounts to only 0.06 or 6% of the mean. The olfactory bulb was no longer present in sections 8 and 9. The counts are therefore 0, and the last entries in the two columns to the right will also be 0
| Section i | P i | P i× P i | P i× P i + 1 | P i× P i + 2 | |
|---|---|---|---|---|---|
| 1 | 3 | 3 × 3 = 9 | 3 × 16 = 48 | 3 × 13 = 39 | |
| 2 | 16 | 16 × 16 = 256 | 16 × 13 = 208 | 16 × 11 = 176 | |
| 3 | 13 | 13 × 13 = 169 | 13 × 11 = 143 | 13 × 12 = 156 | |
| 4 | 11 | 11 × 11 = 121 | 11 × 12 = 132 | 11 × 9 = 99 | |
| 5 | 12 | 12 × 12 = 144 | 12 × 9 = 108 | 12 × 2 = 24 | |
| 6 | 9 | 9 × 9 = 81 | 9 × 2 = 18 | 9 × 0 = 0 | |
| 7 | 2 | 2 × 2 = 4 | 2 × 0 = 0 | 2 × 0 = 0 | |
| 8 |
0 no olfactory bulb present |
||||
| 9 |
0 no olfactory bulb present |
||||
| ∑P i = 66 | A = 784 | B = 657 | C = 494 | ||
|
| |||||
A variance estimate is nice, but what it is more informative to know how variable the counts are relative to the mean. We therefore calculate how large the variance is in relation to the counts. The calculation is similar to that of the CV, in which we divide the square root of the variance, that is, the standard deviation, by the mean. To obtain the CE, we divide the square root of the variance originating from the sampling of sections by the count.
Table 1 provides a brief example of the calculations using the small dataset generated in Section 5.3. The point count used in the example could be exchanged for any other count of probe–object interactions.
In this form, the Gundersen–Jensen CE estimator was used in, for example, the paper that introduced the optical fractionator (West et al., 1991). Several improvements have been made since then (Gundersen, Jensen, Kieu, & Nielsen, 1999) and will be introduced in the following sections.
Variability in the data is generated each time a region is sampled. Typically, we sample a region twice. A sample of sections is used and, within the sections, we apply the probe to a sample of sites in the sections. The variance that originates from sampling of the sections is accounted for by the Gundersen–Jensen CE estimator in its original form. Variance originating from the sampling within the sections can now also be accounted for. The way in which this component of the variance is estimated depends on the type of probe that is being applied. Fortunately, there are currently only two ways—one for the point probes used within sections to obtain a Cavalieri estimate of volume and one for probes of area, length and number that return counts of probe–object interactions, for example, isotropic lines, spaceballs, and disectors (Section 8.4).
A second area of improvement pertains to the smoothness factor of the structure that is being investigated. The ability of counts in one section to forecast counts in adjacent sections may differ between structures. Sections of a structure with a smooth surface (e.g., an almond) are more likely to resemble each other than sections of a structure with a crumpled surface (e.g., a walnut). How well counts from sections can forecast counts from adjacent sections does, of course, also depend on the distance between the sections in the sample. The smoothness factor allows the adjustment of CE estimators to the quantitative morphological peculiarities of the region that we assess (Section 8.5).
8.4. Variance originating from the sampling within sections
The variance originating from the sampling within sections has unfortunately been referred to by a variety of names, for example, local error, noise or nugget (referring to an irregular shape) variance. Here, it is called it S 2, which is short and the expression used in many equations in the literature.
Variance originating from point counts within sections — As already illustrated in Figure 11, the precision of an area estimate based on a point count in a section depends on the density of points used. Obviously, the point count will have to be used. Another factor that influences the precision of the estimate is the shape of the area. The counts that a very “thin” area will return when a point grid is applied to estimate area will be more variable than the counts that a very “thick” area may return. (Figure 38). Consequently, a second factor that we will need to use is a number describing the shape of the area to which we apply the points. The relation between the variance that is generated by the estimate, point counts, and shape was described by Matérn (1985) and brought into an applicable form by Gundersen and Jensen (1987) by way of the following equation.
FIGURE 38.

Shape and the precision of point‐count area estimates. Using this point grid, a circle with the smallest possible shape factor of 3.54 will, depending on how the grid was placed, return a count between 7 and 9. The second shape, composed of two hemicircles (shape factor 5.8) with the same area of the circle, will return counts between 6 and 10. The top right corner of the crosshairs was used to count [Color figure can be viewed at wileyonlinelibrary.com]
The point count obtained enters in the form of ∑Pi, that is, the total number of points counted in all sections. Shape enters the formula in the form of the shape factor , that is, the boundary length, b, of the structure divided by the square root of the area of the structure, a. This factor grows when the region becomes thinner. n refers to the number of sections in which the counts were made.
Boundary length and area need to be known to calculate the shape factor. While one obtains at least an estimate of the area from the point count itself, this is not so for the boundary length. It is fairly easy to estimate (Buffon, 1777, translated by Hey, Neugebauer, & Pasca, 2010; Cruz‐Orive, 1997; Howard & Reed, 2010), but one may decide not to bother. Points come very cheap in terms of the time needed to count them. If only 200 points are counted in 10 sections, the relative variability of the mean for areas in the shape of a circle (the smallest possible shape factor of 3.54) would amount to only about 1.7% of the area estimate.
Very, very “thin” areas rarely exceed a shape factor of 30, and the variability would still amount to less than 5%. Software packages allow thousands of points to be counted with ease, and 1,000 points would limit the CE to 0.5 and 1.5% for shape factors of 3.54 and 30, respectively. Aside from this, software packages may provide a rough approximation of the shape factor based on the boundary length of the area associated with the marked points. The shape factor could also be approximated using the nomogram provided by Gundersen and Jensen (1987). Point counting within sections will likely be a negligible source of variance if the number of points is as large as it easily can be. The section‐to‐section variability of the shape of a region and, therefore, the sampling of sections will likely be the dominant source of variance.
For the olfactory bulb data in Table 1 and a conservative guess at the shape factor of 5 (the region in Figure 13 does not look like a circle, but definitely not like two half circles either),
or relative variability of the mean of or 4%—not bad for counting a total of only 66 points in seven sections.
Variance originating from other estimators within sections — While an understanding of the variance generated by point counts is rather intuitive (many points ≈ lots of precision, crumpled shape ≈ less precision) this is not so for the variance originating from other probe–object interactions in sections. Currently, there is no statistical well‐founded approach to estimate it. Instead, one has to resort to a nonintuitive approximation that, at least, has the advantage of extremely easy calculation.
If 100 cells are being counted in disector probes, S2 for the number estimate would be 100. If we observe 214 interactions of capillaries with the surface of spaceballs, S2 of the length estimate would be 214.
The assumption that allows this easy calculation is that the numbers of interactions that we count each time we place a probe are Poisson distributed (Cruz‐Orive & Geiser, 2004). The usefulness of the assumption has been verified in models (Schmitz, 1998) and real object populations (Chia, 2002; Cruz‐Orive & Geiser, 2004). A convenient mathematical property of a Poisson distribution is that the sum of two Poisson distributions is a Poisson distribution and that the variance of a Poisson distribution is equal to its mean. If the counts coming from each probe originate from a Poisson process, than their sum will do so too and the variance is equal to the sum – S2 = ∑ interactions.
Probe‐feature interactions for number, length, or surface are harder to come by than point counts for volume. Routinely, one is first outlining the structure of interest, which takes a nontrivial amount of time even if done roughly. Subsequent work with high magnification oil lenses requires time to change lens, oil or clean the section and step across the tissue, and we of course need to look for the probe–object interactions. Counting in excess of 200 interactions quickly becomes tedious work. And 200 interactions could still generate a S 2amounting to 7%.
In contrast to point counts, variance originating from sampling within sections with probes for number, length, or surface may contribute a large part to the total variance that we introduce with the sampling.
8.5. The smoothness factor
As mentioned above, the ability to predict counts in sections based on the counts in close‐by sections depends on both the shape of the region that is being assessed and the distance between the sections. If the distribution of the object of interest changes very gradually from section to section, even sections that are spaced far apart may provide a good forecast. If the structure is shaped very irregularly, even closely spaced section may have a poor ability to provide a good prediction of what is happening in adjacent sections. The quality of the prediction that can be expected from a sample of sections enters the calculations of the CE by way of the smoothness, m. Smoothness refers here to the appearance of the plot that is formed when the data points obtained from the sample are plotted in order.
Once again, we need a number that can enter into the calculation of estimate precision. The smoothness of the plot can itself be estimated (Cruz‐Orive, 1999, 2006; Gundersen et al., 1999; Kiêu, 1997), and stereology software packages may include an estimate of smoothness in their output. Estimators of smoothness are however not robust when based on the small datasets that are available from typical quantitative studies (Cruz‐Orive, 1999; García‐Fiñana & Cruz‐Orive, 2004; Gundersen et al., 1999), that is, individual estimates may be far off the true value. Also, estimates of smoothness must be converted into the smoothness factor, α(m) or just α, before it can enter into the equation that will provide the estimate of the CE. This conversion is not trivial and may still require the use of interpolation tables (Cruz‐Orive, 2006). The bottom line is that smoothness is currently judged rather than calculated—perhaps also because estimating something to enter into an estimator of something related to the variability of an estimate of something is exhausting the trust in the number that is finally generated.
Typically only two values of m are considered—zero or one. m can be set to one if all jumps in the plot can be “predicted” by the preceding or succeeding points (Figure 39a). m can be set to zero if the distribution contains jumps that are not “predicted” by the preceding or succeeding points (Figure 39b). If one is conservative and/or uncomfortable with making this judgment, one may decide on m being zero independent of the appearance of the distribution. Estimates of the precision are unlikely to be worse than the ones obtained for an m of zero (Cruz‐Orive, 1999, 2004).
FIGURE 39.
The smoothness of volume distributions. The graphs show samples of 12 sections (red dots) of the (a) entire mouse dentate gyrus and (b) rat hippocampal CA1 pyramidal cell layer in coronal series of sections. Dark lines show the volume distribution based on all sections. Sample values in (a) appear reasonably predictable by the surrounding values and m = 1 seems suitable for this sample, which also has been verified empirically (Basler et al., 2017). Sample values in (b) do show sudden jumps (arrows) that do not appear to be predicted by the preceding or following sample values. The appearance of the data plot and empirical results (Slomianka & West, 2005) suggest that m = 0 would be the most suitable choice [Color figure can be viewed at wileyonlinelibrary.com]
Note that while selecting m does impact on the quality of the CE estimate, an m of zero does not generate CEs that necessarily must be much larger than those predicted by an m of one. Samples comprised of twelve sections will generate CEs between only two and three percent for both structures illustrated in Figure 39 (Basler et al., 2017; Slomianka & West, 2005), even though they are best predicted by a different m. That one may expect small CEs from both samples is also suggested by the good fit between the lines connecting the data points of the sections belonging to the samples and the underlying volume distributions.
For the two cases of m, we can finally obtain smoothness factors to enter into the CE calculations.
For m = 0, the smoothness factor, a, is 1/12; for m = 1, α is 1/240.
The value to be used for m = 0 did already appear in the equation introduced in Section 8.3. We now have the opportunity to change it according to our perception of the smoothness of the count distribution that we obtained from a sample.
With the improvement of the CE estimator, it was suggested that an m = 1 would be a more satisfying approximation than an m = 0 (Gundersen et al., 1999). Software packages may provide CE estimates for m of both zero and one. These values may be taken as the upper and lower bounds (e.g., Filice, Vörckel, Sungur, Wöhr, & Schwaller, 2016), which, independent of the spacing of the sections, are rarely exceeded (Basler et al., 2017; Cruz‐Orive, 2004; Slomianka & West, 2005).
8.6. Putting it together: The current Gundersen–Jensen CE estimator
In the original form, the Gundersen–Jensen estimator did not account for the fact that the counts obtained from the sections are themselves only estimates. The count that is used for a section may not be small because the section is small but because, by chance, there were few probe–object interactions. Because we only have estimates for the values of the sections, we underestimate the ability of the sections to predict counts in nearby sections. We therefore overestimate the variance that is generated by the sampling of sections. In Section 8.4, estimates of the variance, S 2, originating from the probe–object interactions in sections were calculated. S 2 is subtracted in the term that defines the variance originating from the sampling of sections, because it led us to overestimate the error produced by the sampling of sections. On the other hand, we actually generate this variance during the sampling within sections. S 2 is therefore added to the total variance as an independent component.
Together with the possibility to adjust for the smoothness that we perceive, we now have the Gundersen–Jensen CE estimator in a generalized form that is in use today.
in which
S 2 is the variance originating from the sampling within sections calculated according to Section 8.4.
f is the value of our measurement function—a term that covers any type of counts obtained in a section using the estimators presented in this review. ∑f is the sum of the counts of whatever across all sections.
A CE landscape that could be generated from a very large dataset (all sections, >10,000 disector probes) of the hippocampal CA1 pyramidal cell layer (Figure 40a) was reasonably well approximated by Gundersen–Jensen CE estimates (Figure 40b).
FIGURE 40.
Empirical CE estimates and CE estimators. In (a), CEs of a number estimate were estimated empirically by collecting a very large data set from hippocampal CA1 pyramidal cells (Slomianka & West, 2005). From this data set subsamples were drawn and the CEs were estimated (CV of the mean of all subsamples for each combination of subsampling intervals). The Gundersen–Jensen (GJ) estimator (b) and Curz–Orive's split sample estimator (c) provide useful approximations of the variance generated by the sampling. The estimator of Schmitz (1998) (d) considers only the variance component generate by sampling within sections and provides a simple to calculate, rough‐and‐ready estimate if the sampling of sections contributes very little variance to estimates [Color figure can be viewed at wileyonlinelibrary.com]
The CE of the olfactory bulb data set (Table 1) can now be recalculated, for the last time, using the current Gundersen–Jensen estimator. A CE estimate of ~0.07 is obtained for m = 0 and an estimate of ~0.04 for m = 1. It is an almost certain win to bet that it is somewhere between the two values.
Although trying to convey an intuitive understanding of how this estimator works fills some space, and although the formula looks fairly impressive to nonmathematicians, the most complicated mathematical operation that has to be performed is drawing a square root. A CE estimator is easily implemented in a spreadsheet, in which one only would have to enter the counts obtained from the sample of sections in their correct anatomical order to obtain a CE estimate. I have even seen CEs being calculated using mobile phones.
What we gain from either the small effort that is required to generate a CE estimate or from “just” understanding the estimates provided by software packages is a way to judge if the estimates that were performed are not only statistically valid—they always will be, provided that the sampling was representative—but, finally, also if they are “good enough” in the context of the study in which the estimates are used.
8.7. Finally: Good enough or not?
We have now two of the variables that formed the equation presented in Section 8.2.
The relative group variance, that is, the standard deviation squared divided by the mean, can be calculated from the mean and standard deviation provided by routine statistics—whether they are part of a pocket or desktop calculator, a spreadsheet or more or less advanced statistics packages. It would be difficult to avoid seeing them somewhere even if one tried. And the last couple of pages have been about estimating the CEs. Note that the mean CE 2 is calculated as
and not by first calculating a mean CE and subsequently squaring it.
Well, when is a CE good enough? It is good enough if it is not the weakest link of our quantitative procedures. If something needs to be improved, the proper place to invest work would be the weakest link. The ratio between the mean of the CE 2s and the relative group variance will provide a guess at where the weakest link is located (Gundersen & Østerby, 1981).
If this ratio is smaller than 0.5, the variability introduced by the sampling contributes less than half of the total variability that is seen between animals. Natural differences between animals contribute more to the variability seen in the group than the sampling that we used. If we wanted to improve the reliability of the means presented in a descriptive quantitative study or if we wanted to improve the chance of statistically detecting a group difference, the proper place to invest work would be the source of most of the variance. If the main source is natural differences between subjects, increasing the number of subjects would be more efficient than increasing the amount of work that we invest into each subject. The CEs are good enough; if necessary, we ought to increase n. If the ratio is larger than 0.5, the reverse applies. Sampling is a larger source of variance than natural differences between animals. Improving the data by investing more work into the subjects at hand would be more efficient than increasing the number of subjects. Strictly speaking, the CEs are not good enough.
How does one handle CEs that are not good enough? It depends on the outcomes of statistical testing, the workload associated with increasing n or improving CEs, but, first, a look at available data. In, for example, Amrein, Slomianka, and Lipp (2004), we reported a ratio of 1.44 for one of the species in which dentate granule cells were counted. The estimate of the sampling‐induced variability by far exceeded the variability that was observed in the group. This ought to be impossible—if we introduce variability by estimating, we ought to see it in the group. The ratio between what we introduce and what we see should never be larger than 1. Yet it is possible because we talk statistics. It is possible because both the estimates of the CE and the observed group variance are just that—statistical estimates based on samples. We may, by chance, have drawn samples that generate CE estimates that are larger than the real CE. We also may, by chance, have generated estimates that by statistical accident are very similar to each other. In this particular case, the CEs for the granule cell counts were less than 0.1—the value that we also aimed for. The group CV for the granule cell counts was however as low as ~2%. We would still be counting today if we had attempted to decrease CEs to a value that would return a ratio below 0.5. Despite the large ratio, we considered the CEs to be good enough.
Statistical outcomes by themselves may, for the time being, justify a poor CE2/CV2 ratio. Sampling may be the weakest link, but if one actually has detected a significant group difference, sampling was apparently not sloppy enough to hide a significant effect. If the effect is real, it also means that a smaller n, which is more responsible with regard to animal experimentation ethics, would be sufficient to detect the difference if the sampling is improved.
If assessments of the data and/or statistical outcomes do not provide a loophole for poor ratios, it is time to think. A ratio below 0.5 is advice toward more subjects. Above 0.5, the advice is more sampling. Whether one follows the advice depends on the workload and feasibility associated with increasing n or decreasing the CE. Variance may need to be just a little better to generate an outcome; additional subjects may not be available, but additional sections may still be available from the subjects that we have already, or we could count more in the sections we already have. In this case, it may be worthwhile trying to improve estimates even though it would not be the most efficient way to obtain an outcome. A fully calculated example that can provide a clue if it is even worth trying can be found in West (2012c).
What CE value would be good enough for a descriptive study? In that the size of the CE has no immediate impact on further calculations, the decision is somewhat arbitrary. One may aim for a CE that, because of its relatively small size, implies some quality. A value typically aimed for is a CE of 0.1 or 10%. A more rational way is to adjust the desired CE to the variability that is expected in the group (e.g., West & Gundersen, 1990). One may also aim for a CE that in subsequent experimental studies involving statistical testing would allow the detection of group differences of a specified size for the least amount of work (Gundersen & Østerby, 1981). In case of the quantitatively nasty subventricular zone of mice (Azim et al., 2012), we found that decreasing the CE from 20 to 10% would require an increase in workload of 300% and allow the detection of a 20% effect in group sizes of five. Retaining a CE of 20% would require group sizes of eight, that is, an increase in workload of “only” 60%, to detect a 20% effect. In this case, we decided that it would not be sensible to increase precision in a descriptive study because later experimental studies would more efficiently address their questions by a slight increase in n instead of aiming for a lower CE. A similar rationale for choice of a sampling scheme that balances the power to detect differences against the effort of analysis was also presented by Kim et al. (2015).
8.8. Other CE estimators
While the Gundersen–Jensen estimator is the most commonly used one, several other CE estimators are available. The split‐sample estimator introduced by Cruz‐Orive (Cruz‐Orive, 1990; Cruz‐Orive & Geiser, 2004) is particularly attractive. While it is based on the mathematical ideas also at the root of the Gundersen–Jensen estimator, the split‐sample estimator is intuitively easier to understand. We can split our data in half. If the two estimates based on only half the data are very similar to each other and therefore also to the estimate based on all data, than the estimate based on all data must be pretty robust. If doing less would not have made the estimate much less reliable, doing more probably would not make it much more reliable. Of course, a CE can be calculated.
in which τ is the thickness sampling fraction (tsf) multiplied by the section sampling fractions (ssf), and and are the counts obtained from the odd and even sections of the sample.
Similar to the Gundersen–Jensen estimator, the split‐sample estimator returns CE values that correspond well to values observed empirically (Slomianka & West, 2005) but without a need to find a smoothness factor or to calculate S2. Finally, CE estimates returned by this estimator do not increase smoothly but show regional valleys and peaks that are very similar to the CE landscape observed in the empirical data (Figure 40c).
Using computer simulations, both Glaser and Wilson (1998) and Schmitz (1998) found that closely approximated the empirically observed CE in their models. Note that this approximation is identical to an estimate based on S2 alone. Notably, section‐to‐section variability was minimal in these models. They therefore confirm the validity of S2 and that the CE will be dominated by S2 if regions are very smooth. If a region is very smooth, one may use a CE based on S2 alone as a rough‐and‐ready CE preview (Figure 40d).
8.9. Estimate precision and the orientation of the sections
Estimate precision depends on how well a sample captures changes in the distribution of the regions and objects of interest along the axis of sectioning. Changing the orientation in which the sections are prepared often changes the appearance of the region that contains the objects of interest. If it does, it may also change the distribution along the axis of sectioning. If the distributions differ in their smoothness there will also be differences in the efficiency of the sampling (Gundersen et al., 1999). One of the three directions in which the central nervous system is usually cut may return a much higher precision for a given amount of sampling than the other two directions. If workload is the most critical factor, cutting directions may be evaluated for efficiency before a final decision on how to cut the tissue is made.
Figure 41 illustrates the effect of sectioning direction on the efficiency of sampling for the dentate gyrus granule cell layer in the mouse hippocampus. First, the cell layer requires about 110 sections (20 μm thick) to be cut when the brain is sectioned coronally (Figure 36) or sagittally but close to 140 horizontal sections. The workload for the collection and processing of section can be cut by ~20% by deciding in favor of coronal or sagittal sections. Coronal sections return a CE consistently below 5% for the sampling intervals up to 12 and well below 10% for all tested sampling intervals up to 20 (Figure 41). Sagittal sections are only slightly less efficient, but precision is less reliably predicted (Figure 41; see Section 8.10). Horizontal sections do not only require more sections to cut, but precision decreases more rapidly with increasing sampling intervals. The CE for larger sampling intervals exceeds that of coronal or sagittal section by almost a factor 2 (Figure 41). The largest tested interval, that is, every 20th section or five to six section per granule cell layer (110/20), returns a CE of 8% from coronal sections. To obtain the same precision in horizontal sections, every 12th section or ~12 sections (140/12) have to be examined. In terms of the sections that need to be prepared and analyzed, coronal sections actually require half the work to obtain a precision of 8%. Savings of 20% while cutting and 50% while preparing and analyzing sections are well worth considering in large‐scale projects. Similar differences in sampling efficiency between sections of different orientation were also observed for the hippocampal pyramidal cell layer (Slomianka & West, 2005).
FIGURE 41.
Sectioning and estimate precision. Graphs show the empirically derived CVs (red) and Gundersen–Jensen CE estimates (triangles for m = 0 and circles for m = 1) for the mouse dentate gyrus granule cell layer (data from Basler et al., 2017). CV estimates are based on exhaustive series of 20 μm thick methacrylate sections. The graphs represent the CVs and CEs for coronal, sagittal, and horizontal series of sections. With larger intervals between sampled section, CEs increase slower when the coronal and sagittal series are sampled than when the horizontal series is sampled. With the exception of sampling intervals between 12 and 15 (see Section 8.10), empirical CVs are estimated reasonably well by CE estimates using an m of 0 [Color figure can be viewed at wileyonlinelibrary.com]
Alas, our laboratory often uses horizontal section for this region of the brain because the surrounding cortical areas are much easier to assess using this orientation. We can look at all the things we are interested in the same series. Overall efficiency is better, even though we have to work a bit harder when going for some numbers.
8.10. Estimates, CEs, and systematic variations in morphology
What happens if there are systematic changes in the anatomy of the region of interest? For many regions of the brain we know that they are composed of repetitive units with distinct anatomical appearances that represent functional entities—cortical columns or barrels, thalamic barreloids or cerebellar aldolase stripes to mention but a few. If the distance between the samples matches the distance between the anatomical units, not every part of the unit will have a chance to be included in the sample, because the sample will hit the same spot in each unit. Consequently, sampling as outlined in Section 3.4 would not be representative, and the estimate generated and the assessment of sampling precision would be fatally flawed. This supposition is as easily dismissed as it is to step into the actual traps that anatomy has lain.
The supposition may turn out to be true if there is a near perfect match of sampling intervals and the size of the anatomical unit across the entire section and if very few sections are used and if there are very few animals per group. As soon as the intervals do not match perfectly, the units will, sooner or later, again be hit in different places. For example, cortical curvature alone will change the spatial relation between cortical columns and a rectangular sampling grid. The section or the sampling grid may also be rotated to minimize the chances that intervals stay synchronized—an option that is part of stereology software packages. If multiple sections are used and a random starting point is used in each section, the units will be hit in different places in different sections even in the unlikely event that this does not occur in each section. In the very unlikely event that units are hit in the same place in each section, there is still the chance that they are hit in different places in different animals. If we consistently, against all statistical odds, hit the same spots, the estimate obtained would still be statistically valid, because it is the outcome, however unlikely, of sampling that should be (and in the long run will be) representative. The estimate at hand would, of course, be practically useless. Notably, the chance of this happening is only smaller but still present if random independent samples are used. Suffice is to say that sampling intervals should avoid known anatomical regularities to keep the good odds as good as possible. Problems of periodicity when sampling in sections could be avoided by the unaligned sampling (e.g., Figure 6 in Cruz‐Orive & Weibel, 1981), in which the sampling locations still sample a systematic set of areas defined by the x‐ and y‐steps, but they are placed at a random location in these areas. However, unaligned sampling has not been implemented in the major stereology software packages.
Rather than the functional units of the brain, it is the unexpected quirks of anatomy that may play tricks with our ability to obtain precise estimates and/or to formally assess precision. In Figure 41, the empirical estimate of the CEs obtained from sagittal sections do, around sampling intervals 13 and 14, exceed any of the estimates that are provided by the Gundersen–Jensen CE estimator and an m of zero. Looking at the volume distribution of the sagittally sectioned series in Figure 42, we see two sharp peaks that are separated by a distance of 13–14 sections. With these sampling intervals, either both peaks are contained within the samples of sections or both peaks are missing from the samples, which generates either very large or very small estimates.
FIGURE 42.
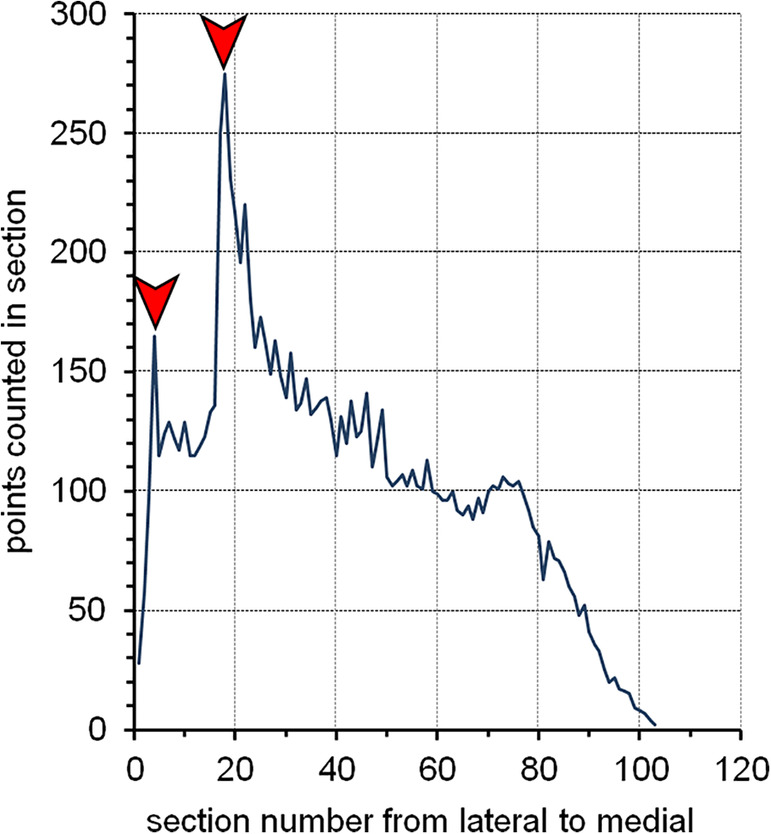
Periodicity in a volume distribution. In sagittal sections, large parts of the mouse dentate granule cell layer will twice run almost parallel to the plane of the sections. The large areas of the layer in these sections will result in large point counts (red arrows). If a sample of sections includes or misses both peaks (section sampling intervals of 13 or 14) the resulting volume estimates will be very large or very small generating the large CVs for these intervals in sagittal sections shown in Figure 41 (data from Basler et al., 2017) [Color figure can be viewed at wileyonlinelibrary.com]
The variance generated by the sampling is not detected by the Gundersen–Jensen CE estimators (Figure 41), which may underestimate actual sampling related variance for these section sampling intervals by a factor 2. It is the folding of the cell layer in relation to the plane of the section that plays a trick on the CE estimates. Sagittal sections will twice pass through a large part of the cell layer, and two peaks are sufficient to generate a period. That does not make CE estimators useless. It does however mean that having a good feeling for how anatomy may impact on the precision of estimators is helpful when evaluating estimates of precision. Once again, sampling intervals close to such periods should be avoided.
8.11. Designing a useful sampling scheme
For the sampling scheme, we need to select parameters for the selection of the sections, for the selection of sampling locations within each section and for the size of the probes that will be applied at each sampling location.
Selection of the sections — Selecting sections means deciding on the spacing of the sections, that is, the section sampling fraction, in the series that will be used for an estimate. The number of the sections that are needed will depend on the shape of the region of interest and the distribution of the objects of interest within the region. Shape and distribution define how much signal there is in each section. If a region appears large in a section, we can expect to see many of the objects if they are more or less evenly distributed in the region. If the objects are distributed unevenly, the amount of signal depends on both the size of the region in the section and the local density of the objects. Key to the selection of a useful section sampling fraction is not to miss the parts of the region which contain most of the signal that we are interested in. Looking at the volume distributions of hippocampal divisions and cell layers in Figure 36 or Figure 39, I would not want to miss the large peaks. This means looking at the width of the peaks, and deciding on section sampling fractions that place two or three sections within the peaks. If the signal is distributed rather evenly, the use of about 10 or even fewer sections has been suggested (Gundersen et al., 1999). A rather even distribution of the signal would mean a smoothness factor close to 1 and, using this number of sections, only a small contribution of section‐to‐section variability to the total variability of the estimate. It would, of course, be nice to have actual sections or distributions to look at. If that is not the case, a careful evaluation of an atlas may help. Where does a region begin and where does it end? And how does its shape change from one level to another? Looking at the respective coordinates may provide a clue to the appropriate spacing of sections. The final decision on the section sampling fraction must rest with the person most experienced with the distribution of the signal in a region—more likely the principal investigator rather than a stereologist knowing not much more about a region than its name.
Selection of sampling locations — In Section 3.3, it was shown that any unevenness in the distribution of the structures of interest will be captured better and better the more sampling sites are placed in a region. A typical recommendation would be a total, across all sections, of 100–200 sampling sites (Gundersen et al., 1999). Next, the distances between sampling sites along the x‐ and y‐axes of the sections need to be estimated. This requires an estimate of the area of the region of interest that is available in the sections selected for analysis
In Section 5.3, point counts were used to estimate the area of combined granule cell, internal plexiform and mitral cell layers in the hamster olfactory bulb. The total number of points counted was 66 and the area associated with each point was 125,000 μm2. The total area in the sections is therefore 66 × 125,000 μm2 = 8,250,000 μm2. If the region is to be hit by 100 probes, it needs to be hit once for each 1/100th of its area, that is, once for each 8,250,000 μm2/100 = 82,500 μm2. The step size along the x‐ and y‐axes would therefore be the square root of 82,500 μm2 or ~287 μm. If the estimate was made in one series and the decision is made afterward to rather pool two series for actual quantification, about twice the area will be available. Step sizes of ~406 μm would return ~100 sampling sites.
The area sampled for each step along the x‐ and y‐axis does not need to be a square. Depending on the looks of the region in a typical section, a rectangle may be more suitable. For example, if a region forms a more or less vertical, long, and narrow band, one may select smaller x‐steps and larger y‐steps (West & Gundersen, 1990). This increases the chances to occasionally hit the region in each section instead of hitting it very often in some sections and very rarely in others. The variability of the estimates from section to section and, thereby, the variability of the final estimate, will decrease.
Also, 100 sampling sites should be amended with “of which a satisfying fraction returns some signal.” Objects of interest may be heavily clustered within the sections, for example, all the structures of interest may be focused within one spot about the size of 1/100th of the total area. Of the 100 samples applied, there would be 99 empty samples and only one which contains signal. It also means that the cluster may be completely missed in some animals while being hit twice in other animals. This would massively increase estimate variability. If there are many clusters within each animal the danger of hitting very few or very many decreases. Depending on the perceived heterogeneity of the signal distribution, step sizes may be adjusted to increase the number of samples that return a signal.
Selection of the probe size — If a site of the section is sampled that contains objects of interest, the probe should be sized to also return a signal from this sampling site. This is just a matter of efficiency. Some data should be returned by the probe to pay for the effort of generating it. We should, on average, observe one or more probe‐feature interactions. A disector should, on average, return a count of one or more cells, or a spaceball should, on average, intersect one or more axons. There will always be some variability that depends on the distribution of the objects of interest within the region, and some probes may well return a count of zero. Without beforehand knowledge, selecting the probe size is a trial‐and‐error process. One or more sections are selected and a probe is tried out in a few sampling locations chosen more or less at random. If there are much more than two counts from each probe and no or very few probes that do not return a count, the size of the probe could be decreased. If there are many probes that do not return a count and few that return a count of one or two, probe size should be increased. Instead of using probes that consistently return high counts, it would make more sense to use a smaller probe and more sampling sites. First, more sampling sites would allow a better coverage of any unevenness in the distribution of the objects of interest. Second, it may be visually more comfortable to count few interactions with each probe. While illustrative of many cases related to counting rules, most of the figures of probes in this review show more probe‐feature interactions than one would hope to see in an average probe actually used to count.
With about 100 sampling sites and probes that return between one to two counts on average, the final count will be in the range of 100–200. Note that because of S2, the CE obtained with the Gundersen–Jensen estimator cannot be smaller than the square root of the count divided by the count. For a count of 100 that would be 10/100 or 0.1 or 10%. Improving this number would demand significant amounts of additional work. To decrease the CE to 5% we would have to obtain a count of 400. An overall CE of 10% is often aimed for (e.g., Mills Schumann & Amaral, 2005) because it can be achieved with a reasonable amount of work and, maybe more importantly, because in many cases a CE of this size accounts for little of the group variance (Gundersen & Østerby, 1981). Group variance is therefore more efficiently improved by adding animals instead of counting more within each animal.
The high magnifications required to count probe‐feature interactions limit the field of view that is accessible to us. If there are very few of the objects of interest, many fields may not contain any, and many probes will not be able to return a count. We may just have to accept that. It does not impact on the ability to generate a valid estimate (West, Oestergaard, Andreassen, & Finsen, 1996). At least, empty probes do not take that much time to count. At one point or another, it may become more efficient to just look at the entire section (asf = 1) or to resort to more advanced area sampling schemes (Boyce & Gundersen, 2018; Gardi et al., 2008; Keller et al., 2013).
Better be safe than sorry — When a sampling scheme is designed, one may add a little to everything—maybe a few more sections than one expects to need, some extra sampling sites and a slightly larger probe. There are two reasons to do so.
First, it is not known if the animal that was used to design the sampling scheme is close to the group average. If the animal would return large counts compared to others in the group, a sampling scheme that keeps to minimum requirements will return few and maybe too few counts in the other animals. The sample that we drew from this animal may not be close to the average of this animal either. The series of sections may have contained a larger section than other series. The area estimate may have been on the large side of the average, and the probe may accidentally have returned a few more cells from the sites at which it was tried than it would do on average. Cutting it close may result in subsequent estimates to return less signal than it was hoped for. At this point, for example, the step size that has been calculated may be rounded down to a number that is both easy to remember and to report. Instead of the 287 μm that were calculated above, one may use 270 μm, which should increase the number of sampling sites by about 13% (2872/2702 ≈ 1.13).
Second, nothing is more frustrating than having to do the same animal twice. Being generous with parameters at the first trial does not only mean that there are solid data to adjust the sampling scheme. It also means that one is definitely done with the animal.
Assessing the sampling scheme — Once the first complete estimate has been generated, the sampling scheme should be revisited. Was the desired number of sampling sites obtained using the selected step sizes? Did the probes generate the number of counts that was aimed for? Which CE was obtained using the sampling scheme? According to the answers to these questions, the step or probe sizes or the number of sections used can be increased or decreased.
9. QUANTITATIVE MORPHOLOGY AT THE BENCH
The beauty of design‐based stereological methods lies in their very strong mathematical foundations. If these methods are applied correctly, we will obtain a correct number associated with the objects that we have probed in our samples of the tissue. Another fact that hardly needs discussion is that whenever a beautiful theory is faced with everyday life there will be problems, and when design‐based stereological methods are faced with the lab bench, there will be problems too. Reread the second sentence of this section—“the objects that we have probed in our samples of the tissue” is a strong qualifier of “correct number.” It leaves plenty of room for questioning the numbers. Are all objects that we should be interested in visible in the sections? How does tissue processing—before we ever have a chance to look at a sample—influence the parameter that we are interested in? And are the representative samples that we draw as representative as they ought to be? Some of the problems that need to be solved to answer these questions positively are addressed in the following sections.
Note that these are purely practical problems that have no bearing on the theoretical validity of stereological methods. More importantly, note that any quantitative morphological approach is likely to be faced with one or more or all of the very same problems. We may fail in addressing these problems. However, if we do so, we will fail least miserable if the methods that we use are not fraught with intrinsic problems and, at least in theory, must provide the right result.
9.1. Brightfield, fluorescence, confocal, or electron microscopy
The principles of sampling and probing do not change with the type of microscopy that is being used. However, workload and technical requirements may differ dramatically. If objects of interest can be resolved reliably using traditional brightfield microscopy, there is no reason to use more advanced techniques. Single‐label immunofluorescence microscopy means working in the dark with expensive, fading, sometimes less than brilliant dyes without offering clear methodological advances over brightfield immunohistochemistry. For multiple‐label studies one may have to resort to fluorescence, and multiple labels are a means of efficiency (Amrein et al., 2015; Filice et al., 2016; Kreutz & Barger, 2018), although there would be alternatives (Hsu & Soban, 1982; McMenamin, 1999; Osman, Oijordsbakken, Costea, & Johannessen, 2013). Not all traditional epifluorescence images are as blurry as advertisements for confocal microscopes would suggest, and they are suited to count the interactions of objects like nuclei, nucleoli, or axons with probes (e.g., Figure 20). Confocal microscopy must be resorted to if the increase in resolution is needed. Stack acquisition times may be very fast, but analysis of the stacks is not. Confocal microscopy is likely to require the intermittent storage of large numbers of high‐resolution stacks for offline analysis. Further practical points that need attention when confocal microscopy becomes part of quantitative morphology have been discussed by Peterson (2014) and Kubínová and Janáček (2015). Confidence and routine are important ingredients to the generation of high quality material necessary for quantitative assessment, and they may well outweigh other considerations when a method of light microscopy is chosen.
The generation of a sufficient number of sampling sites has been a critical factor in many electron microscopic applications. Often each site to be sampled is equal to one tissue block that needs to be processed (e.g., Cardoso et al., 2008; Geinisman, Gundersen, van der Zee, & West, 1996; West, Bach, Søderman, & Ledet Jensen, 2009), limiting the sampling sites assessed to numbers that would be considered very low in other contexts. A detailed workflow for electron microscopic study can be found in West et al. (2009). Advances in the control of the stage and image acquisition techniques in electron microscopy have made it possible to collect multiple samples from large sections (Reichmann et al., 2015). Ion beam milling (Knott, Marchman, Wall, & Lich, 2008) may facilitate sample acquisition further. Because of the large depth of field of traditional transmission electron microscopy, there is no equivalent to the optical application of probes in light microscopy. Physical sections need to be compared for number estimates, and isotropic probe‐feature interactions for length and surface estimates need to be guaranteed by randomizing the orientation of the tissue using the Isector or vertical sections. Using electron tomography, it has been possible to apply probes for volume and number to the equivalent of extremely thin (2–5 nm) optical sections (Vanhecke, Studer, & Ochs, 2007).
9.2. Cutting, staining, and coverslipping
Both the placement of optical probes within tissue section and the measurement of section thickness (see Section 9.3) ask for thick sections. This request is sometimes in conflict with our abilities to cut or embed sections and, importantly, to adequately stain the sections.
Before these problems are addressed, we will quickly look at the number of series that are to be cut. Unless only one or two series are cut, prime numbers of series should be avoided. If, for example, five series are cut, the only options are either counting in one series, that is, at every 5th section, or in every section by pooling all series. There are no choices in‐between that would allow the pooling of series and maintaining uniform distances between the sections that have been pooled. If, instead, six series are cut, all series could be pooled to count in every section, every second series (Series 1, 3, and 5, or Series 2, 4, and 6) could be pooled to look at every second section, every third series (Series 1 and 4, Series 2 and 5, or Series 3 and 6) could be pooled to look at every third section, or just one series could be used to count in every sixth section. If it is not clear from the outset if one of the six series is sufficient to obtain a count that is “good enough,” other series may be reserved. One may try to obtain a good estimate using Series 1 and reserve Series 4 just in case it turns out that more sections are needed.
Cutting — Cutting presents the least problem when fixed tissue is being processed. From our own experience, it does become difficult to cut cryostat sections much thicker than 50 μm without the sections developing cracks that may interfere with subsequent processing or with the assessment under the microscope. Thicker sections of excellent quality can be cut in the form of frozen sections (Figure 43), that is, a frozen tissue block is cut with a room‐temperature knife. The sections melt in the form of ugly little sausages onto the knife, but unfold beautifully without rolling once they are picked up with a brush and placed into a liquid medium (cryoprotectant, buffer, etc., Figure 43c,d). Depending on the speed of the movement of the knife (thicker sections—slower movement), we have cut sections up to 200 μm thick and not reached the limit of what would be feasible. Sliding microtomes are easily modified to cut frozen sections (Figure 43a). Paraffin embedding and cutting techniques have also been adjusted to allow the preparation of sections up to 100 μm thick (Feldengut, Del Tredici, & Braak, 2013). If the sections do not require staining because the structures are intrinsically visible, for example, because of pigmentation, autofluorescence or the induced expression of fluorescent proteins, only the working distance of the microscope objective limits the thickness of the sections that can be assessed.
FIGURE 43.
Preparing frozen sections on a modified sliding microtome. (a) A custom‐made freezing attachment filled with dry ice (and a few ml of alcohol to facilitate the cooling) cools the mounted tissue. (b) A well plate to collect sections of a reference series in correct anatomical order and lockable tubes to collect nine additional series for storage prior to further processing. (c) Disconcerting appearance of a freshly cut 40 μm thick section being collected off the knife, and (d) beautiful unfolding of the actual section illustrated in (c) when placed into buffer [Color figure can be viewed at wileyonlinelibrary.com]
The calculation of the CEs requires the counts from individual sections to be in the correct anatomical order. If multiple sections are stained free floating in one well or if they are collected in, for example, an Eppendorf tube for efficient storage, it is advisable to collect a reference series in anatomical order (Figure 43b). This series may be used as a reference to correctly order the sections of other series once they have been processed.
Staining — Staining is not critical using many classical histological stains that are based on low molecular weight dyes that easily penetrate the tissue, such as counterstains applied to immunohistochemically stained sections or as stand‐alone Nissl stains. Using high molecular weight compounds during, for example, immunohistochemical staining, penetration of the compounds into the tissue rapidly becomes the factor that limits the thickness of the sections that can be processed (e.g., Lyck et al., 2006; Nomura et al., 1997). While decreasing aldehyde concentration in the fixative may increase penetration, increasing incubation time or membrane permeabilization may improve penetration less than one would expect (Torres et al., 2006). The use of zinc‐based fixatives (Beckstead, 1994) instead of aldehyde‐based ones has been reported to increase penetration for some surface antigens to 100 μm (Nykjær Nikolajsen, Jensen, & West, 2016). Critical to the suitability of the material is the presence of stained structures in the center of the section. Ideally, the stained structures are evenly distributed throughout the section, which can be formally assessed by looking at the z‐axis distribution of probe–object interactions (Figure 21, see also Section 9.5).
Did every object that we are interested in stain? Even classical Nissl counterstains have been reported to poorly stain some neurons that are rendered clearly visible immunohistochemically (Whitney, Kemper, Rosene, Bauman, & Blatt, 2008) or to return significantly lower number estimates than those obtained from immunohistochemically stained sections (Zhu, Liu, Zou, & Torbey, 2015). In turn, markers like NeuN, which are thought to be expressed by most neurons (Mullen, Buck, & Smith, 1992, who already defined some exceptions), may generate much lower neuron counts than classical stains (Lyck et al., 2009). The selective loss of NeuN from neurons (McPhail, McBride, McGraw, Steeves, & Tetzlaff, 2004; Portiansky, Barbeito, Gimeno, Zuccolilli, & Goya, 2006; Ünal‐Cevik, Kilinc, Gürsoy‐Özdemir, Gurer, & Dalkara, 2004; Wu et al., 2010) is maybe not that surprising if one considers that it is a gene splicing factor (Rbfox‐3; Dent, Segura‐Anaya, Alva‐Medina, & Aranda‐Anzaldo, 2010; Kim, Adelstein, & Kawamoto, 2009; Kim, Kim, Adelstein, & Kawamoto, 2011) with phosphorylation‐dependent antigenicity (Lind, Franken, Kappler, Jankowski, & Schilling, 2005). It has been suggested that functional states of neurons may influence NeuN expression or that NeuN may even be suitable to investigate functional state (Duan et al., 2016; Maxeiner, Glassmann, Kao, & Schilling, 2014). The loss of marker expression rather than a loss of the cells that expressed the marker has been observed in other instances (e.g., Filice et al., 2016; Stanley & Shetty, 2004). Using a single marker, it would be difficult to answer if all objects of interest stained with absolute certainty. Both the loss of marker expression from otherwise persisting structures and the loss of the structures themselves may be viable and equally interesting interpretations of the data.
Coverslipping — Another way to “gain” section thickness is to avoid losing section thickness during the final steps of tissue processing. Most of the decrease in section thickness is due to the drying and dehydration of the sections prior to coverslipping. A section cut at 40–60 μm in the cryostat may only be 12–15 μm thick once it has been processed and is coverslipped (Bonthius et al., 2004; Carlo & Stevens, 2011). An efficient way to conserve section thickness is the coverslipping with aqueous mounting media that avoid the drying and dehydration steps (Bonthius et al., 2004). Although commercial preparations are quite expensive in comparison to solvent‐based media, the expense may be small in comparison to the remainder of a project. Also, it is possible to prepare rather inexpensive aqueous media like Moviol or Apathy's mounting medium. Using aqueous coverslipping media, section thicknesses close to the value set during cutting can be obtained. Yet another possibility is the coverslipping of sections by epoxy resin embedding, which also conserved most of the section thickness (Miettinen, Kalesnykas, & Koivisto, 2002). In addition to providing thick sections that minimize errors of section thickness estimates and that have ample room for the placement of optical probes, the wider spacing of structures along the z‐axis also makes it easier to identify probe–object interactions. For example, densely packed cells are easier to count in a disector if they retain their size along the z‐axis instead of shrinking into a stack of pancakes.
Missing sections — The loss of sections during the cutting of the tissue is usually obvious. The number of the series concerned and the position of the missing section should be noted. The loss of sections or parts thereof during later stages of, in particular, free‐floating tissue processing may be less obvious. Sections may inadvertently stick to sieves or tube caps, become entangled in brushes or be siphoned into oblivion during the pipetting of solutions. The loss of sections can and should be a rare event. It is a very rare event in many labs, and it is recommended to consult one of these for advice or training if the loss of material is considered a problem. A problem that needs to be solved when dealing with sections lost unknowingly during tissue processing is to find out if sections are actually missing. The easiest way would be noting down how many sections have been cut and collected in each series. The reference series already mentioned may also allow determining the (at least approximate) position of the lost section in the series by comparing the appearance of the sections that are present with each other and with the appearance of the sections in the reference series.
How are missing sections dealt with? If sections or parts of sections are lost in some animals of a group but not in all of them, the estimates obtained from the animals in which material is lost will turn out smaller than the estimates in the animals in which all material was available. The group mean will decrease and the group variance will increase. If the amount of lost material in control and experimental groups is similar and if the position of the lost material is random, one may decide not to do anything and just accept increased group variances. Increased variances will decrease chances of detecting group differences, but, again, provided that losses are comparable in controls and experimental, differences in the means should be preserved. If the position of the missing section can be determined, it is valid to interpolate a value for the missing section from the adjacent sections. Some stereology software packages do contain the necessary routines.
If the purpose of the study is descriptive, that is, the actual mean and not a difference between two means carry the important information, interpolation will be necessary. If the lost section carries a significant amount of signal or if multiple sections have been lost, it may be advisable to discard the series from further analysis. There are no firm rules when this needs to be done.
9.3. Measuring section thickness
Optical fractionator estimates typically require measurements of section thickness. Also, a volume estimate may require a measurement of section thickness if the estimate is used as a reference volume for estimators that themselves only return density estimates. Currently there are no methods to generate an unbiased estimate of section thickness. In contrast to disector probes, in which errors at the top and bottom faces of the probe cancel out, errors in measuring section thickness are likely to be additive (Figure 44; West et al., 1991). A measurement of section thickness requires the definition of the top and bottom of a section to determine the distance between them. This in turn requires decisions about when features at the top and bottom appear in the focal plane of the objective lens. The focal plane actually has a thickness—the “depth of field.” Features at the very top and bottom of the sections will appear in focus at all possible locations within the depth of field (Figure 44), and an observer may choose any of these positions depending on the perception of focus.
FIGURE 44.
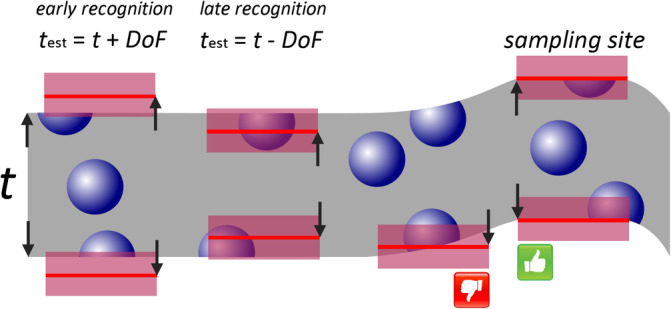
Measuring section thickness. Section thickness, t, can only be measured with a precision to within twice the depth of field (DoF, red boxes) of the objective that is used to make the measurement. Depending on the perception of focus, it may be overestimated (early recognition) or underestimated (late recognition) by the depth of field of the focal plane. Variations in top and bottom focal plane positions within the field of view but outside the actual sampling site require top and bottom focal plane positions to be found at the sampling site [Color figure can be viewed at wileyonlinelibrary.com]
For oil immersion lenses with a NA (usually present on the objective lens collar) in the range of 1.2–1.4, the depth of field would be around 0.5 μm. For fluorescence microscopy, this value varies with the wavelength of the light that is used. It becomes smaller toward the blue end of the spectrum and may reach about 0.8 μm toward the red end of the spectrum for a NA 1.2 objective lens. Using 0.5 μm thickness for the focal plane in the middle of the visible spectrum, it will only be possible to measure section thickness to within 1 μm of its true value. Note that the error is independent of section thickness, that is, the thicker the section is, the smaller will the relative error become. One μm of a five μm thick section amounts to a possible error of 20%—the same measurement error will amount to only 2% if the sections are 50 μm thick. There are no firm rules for the size of the error that would be acceptable, but a thickness of the sections close to 20 μm or more after processing is often aimed for (e.g., Wirenfeldt, Dalmau, & Finsen, 2003), that is, a possible error of 5% for oil immersion objective lenses with NAs around 1.3.
So far, top and bottom surfaces of the section have been taken for flat planes. They may not be. Depending on the embedding and sectioning, the surfaces will appear more or less uneven (Carlo & Stevens, 2011; Helander, 1983). The least unevenness will be present in sections from tissues embedded in hard media (Hasselholt, Lykkesfeldt, & Overgaard Larsen, 2015; Helander, 1983) cut with very sharp knives, while vibratome‐cut fresh tissue may exhibit massive surface irregularities. When we approach the irregular section surface with the focal plane, not all parts of the field of view will appear in focus at the same time. Deciding at which time to start the measurement is a second source of error. Ideally, section thickness should be measured within the areas of the section, in which we will place the probes (Figure 44). For example, if disectors are used, it is best to measure somewhere within the counting frame that represents the disector. Alas, this generates yet another problem. At the location of the probe, there may not be anything stained present at the top or bottom of the section if the stained structures occupy only little of the tissue. Fortunately, even unstained tissue is not invisible or impossible to focus. Background staining and/or light diffraction of different tissue components will give the tissue a fine texture when in focus (Figure 45). Also, small dust particles that have settled on the section during processing should be contained in the depth of field together with focused tissue at the top of the section (Figure 45).
FIGURE 45.
Finding the top focal plane of a section. The three images of Giemsa stained methacrylate embedded rat cortex were acquired with 0.6 μm steps along the z‐axis. Image (a) is clearly out of focus. Some cellular features appear sharp and the background becomes finely structured in Image (b), which may represent the early recognition of the top focal plane in Figure 44. While sharpness further increases in the Image (c), a fine grain of dust resting on the surface of the section (arrowheads) is now out of focus. The depth of field should be able to contain both dust and tissue at the very top of the section. Image (c) may represent the late recognition of the top focal plane in Figure 44. Scale bar: 10 μm [Color figure can be viewed at wileyonlinelibrary.com]
Measuring thickness is not trivial, and a single measurement may consume more time than assessing a sampling site for probe–object interactions. To limit the effort, section thickness does not need to be measured at each sampling location. In the same ways in which we can select representative samples of the tissue to assess with probes, we may select a representative sample of thickness measurements, that is, we can decide to measure thickness at, for example, every 2nd, 5th or 10th sampling location. Also, as will be discussed in Section 9.5, it may not make sense to measure thickness at all at locations at which we do not obtain counts with the probes. Thickness measurements at these locations may therefore be skipped.
9.4. Using the entire thickness of the section
Guard zones have been included in the optical disector on technical or observational rather than mathematical grounds (Andersen & Gundersen, 1999). The technical reason of the loss of objects close to the section surfaces can be investigated. Although sections prepared using different cutting techniques do exhibit different degrees of surface artifacts, these artifacts may not interfere with the probing of the tissue. In contrast to observations in vibratome sections (Andersen & Gundersen, 1999), Carlo and Stevens (2011) found that although cryostat sections do show a surface roughness, the surface can be considered smooth when nuclei are counted. Because surface irregularities were on a much smaller scale than the size of the nucleus, they would be unlikely to result in the loss of counts. If there is no loss, there is no technical reason to include a guard zone. Sections of methacrylate embedded tissue were also found to be smooth when nuclei or nucleoli were used as the counting units (Hasselholt et al., 2015).
There are two observational reasons that may require guard zones. First, as already mentioned in Section 6.4, the correct identification of counting units that have a complex shape may require a deep guard zone. At least with regard to the appearance of nuclei or nucleoli in the nervous system, we are lucky. Light microscopically, their correct identification is not a problem. Complexly shaped structures, like vascular branch points, are more demanding and at least their valence, that is, whether a vessel divides into two, three or more smaller vessel, is likely to require a deep guard zone if we want to count branch points of a specific valence.
The second observational reason for the inclusion of guard zones is the lost caps problem that already haunted Abercrombie's method (Konigsmark, 1970). Lost caps refer to parts of the counting unit that are too small to be recognized in a section, like the topmost cap of a nucleus just included in the section at its lower surface. If this cap is not recognized, that is, lost from the count, an underestimate will result. This will occasionally be the case if we include the lower surface of the section in the disector probe. After the cap was lost in one section, the remainder of the counting unit will be located in the following section. Would the nucleus (or any other counting unit) be immediately recognized when we look at the top of this section or not? If we do, the unit is indeed lost. If we do not, the nucleus would be counted in the following section. As pointed out by West (2012b), the theoretical chance that the exact point is hit at which the unit is not recognized in one section but recognized in the next one is negligible. Practically, this is not the case. What is recognized in the topmost focal plane of a section will be influenced by what is seen out of focus behind it—a phenomenon also known from the physical disector (Tang, Nyengaard, de Groot, & Gundersen, 2001). There is no way of telling how much of the underestimate will remain. Empirical evidence suggests that counts that are obtained with minimal guard zones may not differ from those with larger ones (Schmitz et al., 2000). We would like to obtain the best possible numbers. We therefore need to judge if errors associated with maximizing and measuring section thickness are likely to be smaller or larger than those associated with the omission of guard zones. This call can only be made by an assessment of the material at hand.
9.5. Shrinkage
The measurement of section thickness is required because of shrinkage along the z‐axis during processing. Shrinkage is the antagonist of all quantitative morphological methods. Beyond section thickness, shrinkage may or may not influence the counts that are returned by the probes that are applied to the tissue.
Volume — Implicit in the term shrinkage is a change in the volume of the tissue that is investigated. Dorph‐Petersen et al. (2005) provide a detailed description how gross volume changes can be monitored prior to sectioning. If shrinkage is known, pre‐shrinkage estimates may be calculated to facilitate the comparison of data from different laboratories. Note that different regions of the brain and different compartments of each region may shrink differently (discussed in Dorph‐Petersen & Lewis, 2011).
Number — Estimates of number, which is a dimensionless parameter, are sometimes presented as the only estimates that are not affected by tissue shrinkage. Raisins in dough are the example that has often been used to illustrate why this should be so. The dough may rise or collapse/shrink, but the numbers of raisins in the dough will stay the same. Raisin density, of course, will change. That number estimates are not affected by shrinkage is at least true for physical fractionator designs. They do not require measurements along any of the tissue axes, and they assess the entire thickness of the sections. Other number estimators require a measurement along the z‐axis to obtain section thickness. The thickness of the fully processed section may, for example, depend on the number of objects found at the location of the probe. This is akin to dough that collapses and that now has bumps in the places in which there were many raisins. We see a differential shrinkage; section thickness is dependent on the local number of objects that one is interested in. This type of differential shrinkage can be accounted for. The thickness sampling fraction needs to be corrected by calculating a number‐weighted section thickness (Dorph‐Petersen, Nyengaard, & Gundersen, 2001). If one cell is counted at a sampling site at which thickness is measured to 14 μm and five cells are counted at a site at which thickness is measured to 20 μm, number weighted mean section thickness would be (1 × 14 μm + 5 × 20 μm)/(1 + 5) = 19 μm. A full example of the calculations has been provided by Dorph‐Petersen et al. (2001). If there is no differential shrinkage, estimates based on number weighted mean section thickness will not differ from estimates based on mean thickness alone. Estimates based on number weighted thickness can therefore be a default choice even if there is no suspicion of differential shrinkage. Stereology software packages may provide estimates based on both the mean and number weighted mean thickness.
The attentive reader may have noticed that sampling was discussed with regard to sections, the selection of sampling sites within sections, but not with regard to the placement of probes along the thickness of the section. It is again the guard zones that prevent using the entire thickness of the sections. Because parts of the section are excluded from probing, no practical approach to sample the depth of the sections was developed for the optical disector (Andersen & Gundersen, 1999; Hasselholt et al., 2015). This has raised concerns about the z‐axis representativeness of the sampling sites. If, for example, a 10 μm deep disector probe is always placed below a two μm thick guard zone, all samples come from a depth of the section between 2 and 12 μm. Other depths of the tissue do not contribute to the sample, and the sample is no longer guaranteed to be representative of the tissue. If the section is affected by shrinkage in its most unpleasant form—nonhomogeneous shrinkage (Dorph‐Petersen et al., 2001)—it may not be representative. Nonhomogeneous shrinkage refers to shrinkage that has different effects at different depth of the section. Tissue close to the surface may shrink more than tissue in the center of the section. If all samples come from one depth range, a bias is generated that amounts to the difference of the counts at this specific depth and the counts that would have been obtained if depth had been sampled representatively. Depending on the material, object density differences along the depth of the section may be substantial. All preparation techniques may be affected (Baryshnikova, von Bohlen und Halbach, Kaplan, & von Bartheld, 2006; Gardella, Hatton, Rind, Rosen, & von Bartheld, 2003), including plastic sections (Hatton & von Bartheld, 1999), and the effect may well differ from laboratory to laboratory (compare Figure 21 with data in Hatton and von Bartheld (1999)). The z‐axis distribution of objects (Figure 21), which is also used to decide on the size of the guard zones, can show if the problem is present. Without it, the presence and severity of the problem is difficult to judge, and a formalized solution to this problem has not been proposed yet. However, it is rare that one has to decide where the probes should be placed in sections that are substantially thicker than required. Usually, it is more problematic to obtain sections thick enough to place a decently sized probe within the tissue. Probes often cover much of the tissue depth and thereby include much of the variation in local densities if it should be present. Omitting guard zones and assessing the entire depth of the section is an option already discussed in Section 9.4.
Surface and length — The situation becomes more complicated for surface and length estimates. As two‐ and one‐dimensional measures, they do not occupy a volume. Therefore, length and area estimates may change, but they do not have to change when the tissue shrinks. For example, cell membranes can crumple instead of decreasing in size, and axons or capillaries can take a more tortuous course rather than shorten. If shrinkage is accompanied by any changes and, if so, how large they are is impossible to determine retrospectively. The bottom line is that shrinkage should be avoided if it is important that surface or length estimates are close to the in vivo value of the parameter. If z‐axis shrinkage is present and if it does effect surface or length, spaceballs or virtual cycloids may be more sensitive to its effects than line probes placed on thin VUR or IUR sections.
9.6. Estimate presentation
Sometimes it is unintentionally funny to see how quantitative methodology is presented. Cells were counted “according to the principles of unbiased stereology” or “following StereoInvestigator” (the name of a stereology software package). This may mean no more than something being counted somehow in a series of sections and multiplied afterward by the section sampling fraction. Alas, the systematic and maybe even representative sampling of sections is at least a start. However, one wonders if “according to the principles of good immunocytochemistry” or “following Bond‐III” (an automatic staining machine) would have passed review just as easily. The specific methods must of course be mentioned, and credit should be given to the researchers that went through the trouble of devising them. Beyond that, everything that is needed to replicate a study is needed in the presentation of an estimate, and information useful to evaluate the quality of the outcomes would at least be helpful. Recommendations made here overlap to a large degree with those made by others (Dorph‐Petersen & Lewis, 2011; Schmitz & Hof, 2005; West, 2012a)
Definitions — Even perfect sampling and probing are no guarantee for similar estimates across different laboratories. The definition of the region of interest provides ample opportunity for estimates to diverge. This is because of the requirement to assess the entire region and not just some “representative” sections. It is in the parts of the region in which its anatomical appearance starts to diverge from the typical in which differences in definitions may create differences in the estimates. Divergent estimates may all be methodologically valid, but only for the definitions that have been used. It may appear that the demands of the methods that have been introduced here negate anatomical expertise (Section 3.1). They do, in fact, require anatomical expertise because of the need to define the region of interest when it is not looking foolproof. Definitions will impact on the outcomes, and outcomes should be replicable. Definitions should therefore be part of the presentation of the estimates. In quantitative studies, comprehensive definitions have been provided for, for example, the hippocampus in mouse (West, Danscher, & Gydesen, 1978) and human (West & Gundersen, 1990), the rat striatum (Oorschot, 1996), the rat and primate amygdala (Carlo, Stefanacci, Semendeferi, & Stevens, 2010; Chareyron, Banta Lavenex, Amaral, & Lavenex, 2011; Mills Schumann & Amaral, 2005) or the rat and human entorhinal cortex (Mulders, West, & Slomianka, 1997; West & Slomianka, 1998). Outside the quantitative realm, the amply illustrated literature produced during the heydays of descriptive morphology in the 1950s to 1980s may be helpful in defining regions beyond their typical appearance in today's often single and stamp‐sized images. If definitions at a sufficient level of detail have been published, they can, of course, be referred to.
Sampling parameters and estimate precision — Sampling parameters are essential to replicate the outcomes of a study. For each stage at which a sample was drawn, the associated parameters should be provided: the frequency at which sections were sampled, the distance between sampling sites within sections and the size of the probes (e.g., the dimensions of the disector or the radius of the spaceballs). Collectively, the parameters represent the amount of probe that was used to obtain the quantitative signal. Conceptually, these parameters are similar to the dilutions of an antibody or of an RNA‐probe used to obtain an immunocytochemical or hybridization signal.
In immunocytochemical or in situ hybridization studies, images are used to illustrate the strength and quality of the signal that was obtained. In quantitative studies, the strength of the signal corresponds to the number of probe‐feature interactions that were counted. By themselves, these numbers do not provide any information on the quality of the quantitative signal, but they do allow a judgment of the workload associated with a particular sampling scheme. It is not the strength of the signal per se that determines its quality, but the signal‐to‐noise ratio. An immunohistochemically stained cell that looks almost black may be showing strong signal, but it is not very helpful if the background is almost as dark. The CE is a measure of the noise that sampling will generate in a quantitative morphological study. The critical CE 2/CV 2 can be calculated if the standard deviations, means and CEs are reported. It may be sufficient to comment on the overall size (>0.5 or <0.5) of this ratio to document that the estimation procedures are likely to be “good enough.” While other parameters, such as the number of sections or sampling sites, are informative, an anatomically informed reader/reviewer can at least guess at them quite well based on the sampling parameters.
Exemplary descriptions of methodology can be found in, for example, Woodruff‐Pak (2006), Carlo et al. (2010), Stranahan, Jiam, Stocker, and Gallagher (2012), or Filice et al. (2016). If manuscript space is at a high premium, shortcuts to the inclusion of parameters related to quantitative procedures are possible if they have been documented before and if they are referenced.
10. PERSPECTIVES IN QUANTITATIVE MORPHOLOGY
Design‐based stereological methods are the only ones that currently provide statistically valid estimates about quantitative morphological features in tissue sections when the actual determination (e.g., counting all cells) is not practically feasible. Methods to probe for the basic parameters volume, surface, length, and number are mature and may not improve significantly. Improvements are to be expected primarily with regard to sampling efficiency (e.g., Boyce & Gundersen, 2018; Witgen, Grady, Nyengaard, & Gundersen, 2006), the estimation of the precision of estimates (e.g., Hall & Ziegel, 2011; Mattfeldt, 2006, 2011; Ziegel, Baddeley, Dorph‐Petersen, & Vedel Jensen, 2010) and the automation of probing (e.g., Ahmady Phoulady, Goldgof, Hall, Nash, & Mouton, 2019; Hansen, Nyengaard, Andersen, & Jensen, 2011). There are also efforts to automate section thickness measurements (Elozory et al., 2012).
Tissue sectioning will always be an impediment to the three‐dimensional visualization and understanding of brain structure. If it is not necessary to section the tissue and if it is practically feasible to determine instead of estimate a parameter, design‐based stereology will become obsolete. Not surprisingly, there is a vigorous proliferation of methods that allow the morphological assessment of a brain in one piece, for example, BABB (Dodt et al., 2007), Scale and ScaleS (Hama et al., 2011; Hama et al., 2015), 3DISCO (Ertürk et al., 2012), ClearT (Kuwajima et al., 2013), CLARITY (Bastrup & Larsen, 2017; Chung et al., 2013), PACT/RIMS/PARS (Yang et al., 2014), 3D BrainCV (J. Wu et al., 2014), SWITCH (Murray et al., 2015), CUBIC (Murakami et al., 2018), or FOCM (Zhu et al., 2019). It will be interesting to see how far these approaches can be pushed in terms of the size of tissue that can be processed (there is life beyond C57), the range of the traditional probes (antibodies, RNA probes, etc.) that can be applied to them and the accessibility to a wide community of scientists. Only processing power limits the automated analysis of image stacks of the entire brain, and the first quantitative data have been presented for the mouse on Purkinje cell number (Silvestri et al., 2015), c‐Fos+ cells in a large number of regions (Renier et al., 2016), regional cell numbers in an experimental context (Seiriki et al., 2017) or total regionalized brain cell numbers (Murakami et al., 2018). If there is not sufficient power for a determination and in the course of validation (see next paragraph), statistically representative probes will have to be efficiently drawn and analyzed (e.g., Kim et al., 2015). In these contexts, the probing and sampling aspects of the methods introduced here will be retained.
As far as the estimation of number is concerned, several approaches for the automated detection of objects in three dimensions have been proposed (e.g., Bjornsson et al., 2008; Chinta & Wasser, 2012; Dumitriu et al., 2012; Fish, Sweet, Deo, & Lewis, 2008). Approaches that have been tested for their detection of cells did however not return robust values when compared to a human observer. Depending on the setting, true positive detection rates ranged between 33 and 99%, and false negative detections ranged between 3.6 and 82% for the best approach tested (Schmitz et al., 2014). Ahmady Phoulady, Goldgof, Hall, and Mouton (2019) reported false positive/negative rates of 10 to 20% for the better of two markers that were tested using yet another automatic analysis approach. While the generation of algorithms that produce accurate numbers under a defined set of condition seems possible, little efficiency is gained if they time and again need to be calibrated to different stains or experimental conditions. There is an awareness that algorithms need to be resistant to morphological variability, object densities and variations in staining intensity. It is an active research area, and new algorithms try to address these issues (e.g., Ruszczycki et al., 2019; Shuvaev et al., 2017).
Anyone interested in quantitative morphology must be keenly looking forward to the solution of problems of automated quantitative morphological assessments. Unfortunately, solutions are not just around the corner, and quantitative morphology as introduced here will still be with us for some time to come. Also, much of the brain is still quantitatively uncharted territory. A basic parameter like the number of neurons in a volume unit of the somatosensory cortex had to be estimated for a not that old study that aimed at a simulation of cortical function (Markram et al., 2015). Even well‐done descriptive quantitative studies now rarely appear in the highest impact‐factor publications. However, their scientific impact may well outlast many studies that do, because, sooner or later, qualitative and quantitative parameters will have to integrate to provide an understanding of function of neural systems.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
ACKNOWLEDGMENTS
The author has always been very lucky with kind, fair, and fostering teachers. The author remembers Frau Schloo, Lothar Schwetlik, Herbert Blaffert, and Jürgen Captuller with particular regard. The author is grateful for the friendship and support of Mark J. West. The author sincerely thanks for the contributions in the form of time, encouragement, comments, criticism, numbers, or images by Irmgard Amrein, Gery Barmettler, Stanley E. Lazic, Heinz Sonderegger, R. Maarten van Dijk, and David P. Wolfer. The author is particularly grateful for the comments and criticism provided by Luis M. Cruz‐Orive. All mistakes are, of course, the author's.
Slomianka L. Basic quantitative morphological methods applied to the central nervous system. J Comp Neurol. 2021;529:694–756. 10.1002/cne.24976
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
REFERENCES
- Abercrombie, M. (1946). Estimation of nuclear population from microtome sections. The Anatomical Record, 94, 239–247. 10.1002/ar.1090940210 [DOI] [PubMed] [Google Scholar]
- Abusaad, I. , MacKay, D. , Zhao, J. , Stanford, P. , Collier, D. A. , & Everall, I. P. (1999). Stereological estimation of the total number of neurons in the murine hippocampus using the optical disector. The Journal of Comparative Neurology, 408, 560–566. https://doi.org/10.1002/(SICI)1096-9861(19990614)408:4<560::AID-CNE9>3.0.CO;2-P [DOI] [PubMed] [Google Scholar]
- Acer, N. , Çankaya, M. N. , İşçi, Ö. , Baş, O. , Çamurdanoğlu, M. , & Turgut, M. (2010). Estimation of cerebral surface area using vertical sectioning and magnetic resonance imaging: A stereological study. Brain Research, 1310, 29–36. 10.1016/j.brainres.2009.11.017 [DOI] [PubMed] [Google Scholar]
- Ackman, J. B. , Siddiqi, F. , Walikonis, R. S. , & LoTurco, J. J. (2006). Fusion of microglia with pyramidal neurons after retroviral infection. The Journal of Neuroscience, 26, 11413–11422. 10.1523/JNEUROSCI.3340-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adiguzel, E. , Duzcan, S. E. , Akdogan, I. , & Tufan, A. C. (2003). A simple low‐cost method for two dimensional microscopic measuring and stepping on the microscopic plate. Neuroanatomy, 2, 6–8. [Google Scholar]
- Ahmady Phoulady, H. , Goldgof, D. , Hall, L. O. , & Mouton, P. R. (2019). Automatic ground truth for deep learning stereology of immunostained neurons and microglia in mouse neocortex. Journal of Chemical Neuroanatomy, 98, 1–7. 10.1016/j.jchemneu.2019.02.006 [DOI] [PubMed] [Google Scholar]
- Ahmady Phoulady, H. , Goldgof, D. , Hall, L. O. , Nash, K. R. , & Mouton, P. R. (2019). Automatic stereology of mean nuclear size of neurons using an active contour framework. Journal of Chemical Neuroanatomy, 96, 110–115. 10.1016/j.jchemneu.2018.12.012 [DOI] [PubMed] [Google Scholar]
- Amrein, I. , Nosswitz, M. , Slomianka, L. , van Dijk, R. M. , Engler, S. , Klaus, F. , … Azim, K. (2015). Septo‐temporal distribution and lineage progression of hippocampal neurogenesis in a primate (Callithrix jacchus) in comparison to mice. Frontiers in Neuroanatomy, 9, 85 10.3389/fnana.2015.00085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amrein, I. , Slomianka, L. , & Lipp, H.‐P. (2004). Granule cell number, cell death and cell proliferation in the dentate gyrus of wild‐living rodents. European Journal of Neuroscience, 20, 3342–3350. 10.1111/j.1460-9568.2004.03795.x [DOI] [PubMed] [Google Scholar]
- Andersen, B. B. , Fabricius, K. , Gundersen, H. J. G. , Jelsing, J. , & Stark, A. K. (2004). No change in neuron numbers in the dentate nucleus of patients with schizophrenia estimated with a new stereological method—the smooth fractionator. Journal of Anatomy, 205, 313–321. 10.1111/j.0021-8782.2004.00337.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen, B. B. , & Gundersen, H. J. G. (1999). Pronounced loss of cell nuclei and anisotropic deformation of thick sections. Journal of Microscopy, 196, 69–73. 10.1046/j.1365-2818.1999.00555.x [DOI] [PubMed] [Google Scholar]
- Artacho‐Pérula, E. , Roldán‐Villalobos, R. , & Cruz‐Orive, L. M. (1999). Application of the fractionator and vertical slices to estimate total capillary length in skeletal muscle. Journal of Anatomy, 195, 429–437. 10.1046/j.1469-7580.1999.19530429.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azim, K. , Fiorelli, R. , Zweifel, S. , Hurtado‐Chong, A. , Yoshikawa, K. , Slomianka, L. , & Raineteau, O. (2012). three‐dimensional examination of the adult mouse subventricular zone reveals lineage‐specific microdomains. PLoS One, 7, e49087 10.1371/journal.pone.0049087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley, A. , Dorph‐Petersen, K.‐A. , & Vedel Jensen, E. B. (2006). A note on the stereological implications of irregular spacing of sections. Journal of Microscopy, 222, 177–181. 10.1111/j.1365-2818.2006.01585.x [DOI] [PubMed] [Google Scholar]
- Baddeley, A. J. , Gundersen, H. J. G. , & Cruz‐Orive, L. M. (1986). Estimation of surface area from vertical sections. Journal of Microscopy, 142, 259–276. 10.1111/j.1365-2818.1986.tb04282.x [DOI] [PubMed] [Google Scholar]
- Baldwin, S. A. , Gibson, T. , Callihan, C. T. , Sullivan, P. G. , Palmer, E. , & Scheff, S. W. (1997). Neuronal cell loss in the CA3 subfield of the hippocampus following cortical contusion utilizing the optical disector method for cell counting. Journal of Neurotrauma, 14, 385–398. 10.1089/neu.1997.14.385 [DOI] [PubMed] [Google Scholar]
- Baquet, Z. C. , Williams, D. , Brody, J. , & Smeyne, R. J. (2009). A comparison of model‐based (2D) and design‐based (3D) stereological methods for estimating cell number in the substantia nigra pars compacta (SNpc) of the C57BL/gJ mouse. Neuroscience, 161, 1082–1090. 10.1016/j.neuroscience.2009.04.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barger, N. , Sheley, M. F. , & Schumann, C. M. (2015). Stereological study of pyramidal neurons in the human superior temporal gyrus from childhood to adulthood. The Journal of Comparative Neurology, 523, 1054–1072. 10.1002/cne.23707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baryshnikova, L. M. , von Bohlen und Halbach, O. , Kaplan, S. , & von Bartheld, C. S. (2006). Two distinct events, section compression and loss of particles ("lost caps"), contribute to z‐axis distortion and bias in optical disector counting. Microscopy Research and Technique, 69, 738–756. 10.1002/jemt.20345 [DOI] [PubMed] [Google Scholar]
- Basler, L. , Gerdes, S. , Wolfer, D. P. , & Slomianka, L. (2017). Sampling the mouse hippocampal dentate gyrus. Frontiers in Neuroanatomy, 11, 123 10.3389/fnana.2017.00123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastrup, J. , & Larsen, P. H. (2017). Optimized CLARITY technique detects reduced parvalbumin density in a genetic model of schizophrenia. The Journal of Neuroscience Methods, 283, 23–32. 10.1016/j.jneumeth.2017.03.011 [DOI] [PubMed] [Google Scholar]
- Beckstead, J. H. (1994). A simple technique for preservation of fixation‐sensitive antigens in paraffin‐embedded tissues. Journal of Histochemistry and Cytochemistry, 42, 1127–1134. 10.1177/42.8.8027531 [DOI] [PubMed] [Google Scholar]
- Ben Abdallah, N. M.‐B. , Slomianka, L. , Vyssotski, A. L. , & Lipp, H. P. (2010). Early age‐related changes in adult hippocampal neurogenesis in C57 mice. Neurobiology of Aging, 31, 151–161. 10.1016/j.neurobiolaging.2008.03.002 [DOI] [PubMed] [Google Scholar]
- Billingsley, P. R. , & Ranson, S. W. (1918). On the number of nerve cells in the ganglion cervicale superius and of nerve fibers in the cephalic end of the truncus sympathicus in the cat and on the numerical relations of preganglionic and postganglionic neurones. The Journal of Comparative Neurology, 29, 359–366. 10.1002/cne.900290404 [DOI] [Google Scholar]
- Bjornsson, C. S. , Lin, G. , Al‐Kofahi, Y. , Narayanaswamy, A. , Smith, K. L. , Shain, W. , & Roysam, B. (2008). Associative image analysis: A method for automated quantification of 3D multi‐parameter images of brain tissue. Journal of Neuroscience Methods, 170, 165–178. 10.1016/j.jneumeth.2007.12.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonilha, L. , Kobayashi, E. , Cendes, F. , & Li, L. M. (2003). Effects of method and MRI slice thickness on entorhinal cortex volumetry. Neuroreport, 14, 1291–1295. 10.1097/01.wnr.0000077545.91466.73 [DOI] [PubMed] [Google Scholar]
- Bonthius, D. J. , McKim, R. , Koele, L. , Harb, H. , Karacay, B. , Mahoney, J. , & Pantazis, N. J. (2004). Use of frozen sections to determine neuronal number in the murine hippocampus and neocortex using the optical disector and optical fractionator. Brain Research Protocols, 14, 45–57. 10.1016/j.brainresprot.2004.09.003 [DOI] [PubMed] [Google Scholar]
- Boyce, R. W. , Dorph‐Petersen, K.‐A. , Lyck, L. , & Gundersen, H. J. G. (2010). Design‐based stereology: Introduction to basic concepts and practical approaches for estimation of cell number. Toxicologic Pathology, 38, 1011–1025. 10.1177/0192623310385140 [DOI] [PubMed] [Google Scholar]
- Boyce, R. W. , & Gundersen, H. J. G. (2018). The automatic proportionator estimator is highly efficient for estimation of total number of sparse cell populations. Frontiers in Neuroanatomy, 12, 19 10.3389/fnana.2018.00019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brændgaard, H. , & Gundersen, H. J. G. (1986). The impact of recent stereological advances on quantitative studies of the nervous system. Journal of Neuroscience Methods, 18, 39–78. 10.1016/0165-0270(86)90112-3 [DOI] [PubMed] [Google Scholar]
- Buckmaster, P. S. , & Dudek, F. E. (1997). Neuron loss, granule cell axon reorganization, and functional changes in the dentate gyrus of epileptic kainate‐treated rats. The Journal of Comparative Neurology, 385, 385–404. https://doi.org/10.1002/(SICI)1096-9861(19970901)385:3<385::AID-CNE4>3.0.CO;2-# [PubMed] [Google Scholar]
- Buffon, G.‐L. L. (1777). Essais d'srithmetique morale L'histoire naturelle, générale et particulière, avec la description du Cabinet du Roi, suppléments IV (pp. 46–109). Paris: L'Imprimerie Royale. [Google Scholar]
- Calhoun, M. E. , Mao, Y. , Roberts, J. A. , & Rapp, P. R. (2004). Reduction in hippocampal cholineric innervation is unrelated to recognition memory impairment in aged rhesus monkey. The Journal of Comparative Neurology, 475, 238–246. 10.1002/cne.20181 [DOI] [PubMed] [Google Scholar]
- Cardoso, A. , Assuncão, M. , Andrade, J. P. , Pereira, P. A. , Madeira, M. D. , Paula‐Barbosa, M. M. , & Lukoyanov, N. V. (2008). Loss of synapses in the entorhinal‐dentate gyrus pathway following repeated induction of electroshock seizures in the rat. Journal of Neuroscience Research, 86, 71–83. 10.1002/jnr.21474 [DOI] [PubMed] [Google Scholar]
- Carlo, C. N. , Stefanacci, L. , Semendeferi, K. , & Stevens, C. F. (2010). Comparative analyses of the neuron numbers and volumes of the amygdaloid complex in old and new world primates. The Journal of Comparative Neurology, 518, 1176–1198. 10.1002/cne.22264 [DOI] [PubMed] [Google Scholar]
- Carlo, C. N. , & Stevens, C. F. (2011). Analysis of differential shrinkage in frozen brain sections and its implications for the use of guard zones in stereology. The Journal of Comparative Neurology, 519, 2803–2810. 10.1002/cne.22652 [DOI] [PubMed] [Google Scholar]
- Chareyron, L. J. , Banta Lavenex, P. , Amaral, D. G. , & Lavenex, P. (2011). Stereological analysis of the rat and monkey amygdala. The Journal of Comparative Neurology, 519, 3218–3239. 10.1002/cne.22677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, L. , Zhou, C. , Tan, C. , Wang, F. , Gao, Y. , Huang, C. , … Tang, Y. (2017). Stereological study on the positive effect of running exercise on the capillaries in the hippocampus in a depression model. Frontiers in Neuroanatomy, 11, 93 10.3389/fnana.2017.00093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, S. , & Buckmaster, P. S. (2005). Stereological analysis of forebrain regions in kainate‐treated epileptic rats. Brain Research, 1057, 141–152. 10.1016/j.brainres.2005.07.058 [DOI] [PubMed] [Google Scholar]
- Chia, J. L. C. (2002). Data models and estimation accuracy in stereology. (PhD), University of Western Australia, Perth.
- Chinta, R. , & Wasser, M. (2012). Three‐dimensional segmentation of nuclei and mitotic chromosomes for the study of cell divisions in live Drosophila embryos. Cytometry, 81, 52–64. 10.1002/cyto.a.21164 [DOI] [PubMed] [Google Scholar]
- Chung, K. , Wallace, J. , Kim, S.‐Y. , Kalyanasundaram, S. , Andalman, A. S. , Davidson, T. J. , … Deisseroth, K. (2013). Structural and molecular interrogation of intact biological systems. Nature, 497, 332–337. 10.1038/nature12107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coggeshall, R. E. , & Lekan, H. A. (1996). Methods for determining numbers of cells and synapses: A case for more uniform standards of review. The Journal of Comparative Neurology, 364, 6–15. https://doi.org/10.1002/(SICI)1096-9861(19960101)364:1<6::AID-CNE2>3.0.CO;2-9 [DOI] [PubMed] [Google Scholar]
- Coimbra, J. P. , Collin, S. P. , & Hart, N. S. (2014). Topographic specializations in the retinal ganglion cell layer of Australian passerines. The Journal of Comparative Neurology, 522, 3609–3628. 10.1002/cne.23624 [DOI] [PubMed] [Google Scholar]
- Collan, Y. (1998). Alternatives for morphometric and stereologic analysis in toxicopathology. Toxicology Letters, 102‐103, 393–397. 10.1016/S0378-4274(98)00239-2 [DOI] [PubMed] [Google Scholar]
- Cotel, M.‐C. , Bayer, T. A. , & Wirths, O. (2008). Age‐dependent loss of dentate gyrus granule cells in APP/PS1KI mice. Brain Research, 1222, 207–213. 10.1016/j.brainres.2008.05.052 [DOI] [PubMed] [Google Scholar]
- Cotel, M.‐C. , Jawhar, S. , Christensen, D. Z. , Bayer, T. A. , & Wirths, O. (2012). Environmental enrichment fails to rescue working memory deficits, neuron loss, and neurogenesis in APP/PS1KI mice. Neurobiology of Aging, 33, 96–107. 10.1016/j.neurobiolaging.2010.02.012 [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. (1990). On the empirical variance of a fractionator estimate. Journal of Microscopy, 160, 89–95. 10.1111/j.1365-2818.1990.tb03050.x [DOI] [Google Scholar]
- Cruz‐Orive, L. M. (1994). Toward a more objective biology. Neurobiology of Aging, 15, 377–388. 10.1016/0197-4580(94)90039-6 [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. (1997). Stereology of single objects. Journal of Microscopy, 186, 93–107. 10.1046/j.1365-2818.1997.1380695.x [DOI] [Google Scholar]
- Cruz‐Orive, L. M. (1999). Precision of Cavalieri sections and slices with local errors. Journal of Microscopy, 193, 182–198. 10.1046/j.1365-2818.1999.00460.x [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. (2004). Precision of the fractionator from Cavalieri designs. Journal of Microscopy, 213, 205–211. 10.1111/j.1365-2818.2004.01291.x [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. (2006). A general variance predictor for Cavalieri slices. Journal of Microscopy, 222, 158–165. 10.1111/j.1365-2818.2006.01535.x [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. (2017). Stereology: A historical survey. Image Analysis & Stereology, 36, 153–177. 10.5566/ias.1767 [DOI] [Google Scholar]
- Cruz‐Orive, L. M. , & Geiser, M. (2004). Estimation of particle number by stereology: An update. Journal of Aerosol Medicine, 17, 197–212. 10.1089/jam.2004.17.197 [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. , Gelšvartas, J. , & Roberts, N. (2014). Sampling theory and automated simulations for vertical sections, applied to human brain. Journal of Microscopy, 253, 119–150. 10.1111/jmi.12103 [DOI] [PubMed] [Google Scholar]
- Cruz‐Orive, L. M. , & Weibel, E. R. (1981). Sampling designs for stereology. Journal of Microscopy, 122, 235–257. 10.1111/j.1365-2818.1981.tb01265.x [DOI] [PubMed] [Google Scholar]
- Curtis, K. , Rollins, M. , Carryl, H. , Kimberley, B. , van Rompay, K. K. , Abel, K. , & Burke, M. W. (2014). Reduction of pyramidal and immature hippocampal neurons in pediatric simian immunodeficiency virus infection. Neuroreport, 25, 973–978. 10.1097/WNR.0000000000000148 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Groot, D. M. G. , Hartgring, S. , van de Horst, L. , Moerkens, M. , Otto, M. , Bos‐Kuijpers, M. H. M. , … Gundersen, H. J. G. (2005). 2D and 3D assessment of neuropathology in rat brain after prenatal exposure to methylazoxymethanol, a model for developmental neurotoxicty. Reproductive Toxicology, 20, 417–432. 10.1016/j.reprotox.2005.04.006 [DOI] [PubMed] [Google Scholar]
- Delaloye, S. , Kraftsik, R. , Kuntzer, T. , & Barakat‐Walter, I. (2009). Does the physical disector method provide an accurate estimation of sensory neuron number in rat dorsal root ganglia? Journal of Neuroscience Methods, 176, 290–297. 10.1016/j.jneumeth.2008.09.004 [DOI] [PubMed] [Google Scholar]
- Dent, M. A. , Segura‐Anaya, E. , Alva‐Medina, J. , & Aranda‐Anzaldo, A. (2010). NeuN/Fox‐3 is an intrinsic component of the neuronal nuclear matrix. FEBS Letters, 584, 2767–2771. 10.1016/j.febslet.2010.04.073 [DOI] [PubMed] [Google Scholar]
- Dodt, H. U. , Leischner, U. , Schierloh, A. N. J. , Mauch, C. P. , Deininger, K. , … Becker, K. (2007). Ultramicroscopy: Three‐dimensional visualization of neuronal networks in the whole mouse brain. Nature Methods, 4, 331–336. 10.1038/nmeth1036 [DOI] [PubMed] [Google Scholar]
- Dorph‐Petersen, K. A. (1999). Stereological estimation using vertical sections in a complex tissue. Journal of Microscopy, 195, 79–86. 10.1046/j.1365-2818.1999.00471.x [DOI] [PubMed] [Google Scholar]
- Dorph‐Petersen, K.‐A. , Delevich, K. M. , Marcsisin, M. J. , Zhang, W. , Sampson, A. R. , Gundersen, H. J. G. , … Sweet, R. A. (2009). Pyramidal neuron number in layer 3 of primary auditory cortex of subjects with schizophrenia. Brain Research, 1285, 42–57. 10.1016/j.brainres.2009.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorph‐Petersen, K. A. , & Lewis, D. A. (2011). Stereological approaches to identifying neuropathology in psychosis. Biological Psychiatry, 69, 113–126. 10.1016/j.biopsych.2010.04.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorph‐Petersen, K.‐A. , Nyengaard, J. R. , & Gundersen, H. J. G. (2001). Tissue shrinkage and unbiased stereological estimation of particle number and size. Journal of Microscopy, 204, 232–246. 10.1046/j.1365-2818.2001.00958.x [DOI] [PubMed] [Google Scholar]
- Dorph‐Petersen, K.‐A. , Pierri, J. N. , Perel, J. M. , Sun, Z. , Sampson, A. R. , & Lewis, D. A. (2005). The influence of chronic exposure to antipsychotic medications on brain size before and after tissue fixation: A comparison of haloperidol and olanzapine in macaque monkeys. Neuropsychopharmacology, 30, 1649–1661. 10.1038/sj.npp.1300710 [DOI] [PubMed] [Google Scholar]
- Dorph‐Petersen, K.‐A. , Pierri, J. N. , Wu, Q. , Sampson, A. R. , & Lewis, D. A. (2007). Primary visual cortex volume and total neuron number are reduced in schizophrenia. The Journal of Comparative Neurology, 501, 290–301. 10.1002/cne.21243 [DOI] [PubMed] [Google Scholar]
- Duan, W. , Zhang, Y. P. , Hou, Z. , Huang, C. , Zhu, H. , Zhang, C.‐Q. , & Yin, Q. (2016). Novel insights into NeuN: From neuronal marker to splicing regulator. Molecular Neurobiology, 53, 1637–1647. 10.1007/s12035-015-9122-5 [DOI] [PubMed] [Google Scholar]
- Dumitriu, D. , Berger, S. I. , Hamo, C. , Hara, Y. , Bailey, M. , Hamo, A. , … Morrison, J. H. (2012). Vamping: Stereology‐based automated quantification of fluorescent puncta size and density. Journal of Neuroscience Methods, 209, 97–105. 10.1016/j.jneumeth.2012.05.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebbeson, S. O. E. , & Tang, D. (1965). A method for estimating the number of cells in histological sections. Journal of Microscopy, 84, 449–464. 10.1111/j.1365-2818.1965.tb02146.x [DOI] [PubMed] [Google Scholar]
- Elozory, D. T. , Kramer, K. A. , Chaudhuri, B. P. B. O. , Goldgof, D. B. , Hall, L. O. , & Mouton, P. R. (2012). Automatic section thickness determination using an absolute gradient focus function. Journal of Microscopy, 248, 145–259. 10.1111/j.1365-2818.2012.03669.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ertürk, A. , Becker, K. , Jährling, N. , Mauch, C. P. , Hojer, C. D. , Egen, J. G. , … Dodt, H. U. (2012). Three‐dimensional imaging of solvent‐cleared organs using 3DISCO. Nature Protocols, 7, 1983–1995. 10.1038/nprot.2012.119 [DOI] [PubMed] [Google Scholar]
- Evans, G. W. (1917). Cavalieri's theorem in his own words. American Mathematical Monthly, 24, 447–451. 10.2307/2973769 [DOI] [Google Scholar]
- Fawcett, T. W. , & Higginson, A. D. (2019). Heavy use of equations impedes communication among biologists. Proceedings of the National Academy of Sciences of the United States of America, 109, 11735–11739. 10.1073/pnas.1205259109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldengut, S. , del Tredici, K. , & Braak, H. (2013). Paraffin sections of 70–100 μm: A novel technique and its benefits for studying the nervous system. Journal of Neuroscience Methods, 215, 241–244. 10.1016/j.jneumeth.2013.03.010 [DOI] [PubMed] [Google Scholar]
- Fileta, J. B. , Huang, W. , Kwon, G. P. , Filippopoulos, T. , Ben, Y. , Dobberfuhl, A. , & Grosskreutz, C. L. (2008). Efficient estimation of retinal ganglion cell number: A stereological approach. Journal of Neuroscience Methods, 170, 1–8. 10.1016/j.jneumeth.2007.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filice, F. , Vörckel, K. J. , Sungur, A. Ö. , Wöhr, M. , & Schwaller, B. (2016). Reduction in parvalbumin expression not loss of the parvalbumin‐expressing GABA interneuron subpopulation in genetic parvalbumin and shank mouse models of autism. Molecular Brain, 9, 10 10.1186/s13041-016-0192-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fish, K. N. , Sweet, R. A. , Deo, A. J. , & Lewis, D. A. (2008). An automated segmentation methodology for quantifying immunoreactive puncta number and fluorescence intensity in tissue sections. Brain Research, 1240, 62–72. 10.1016/j.brainres.2008.08.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flood, D. G. , & Coleman, A. E. (1988). Neuron numbers and sizes in aging brain: Comparisons of human, monkey, and rodent data. Neurobiology of Aging, 9, 453–463. 10.1016/S0197-4580(88)80098-8 [DOI] [PubMed] [Google Scholar]
- Fogarty, M. J. , Omar, T. S. , Zhan, W. Z. , Mantilla, C. B. , & Sieck, G. C. (2018). Phrenic motor neuron loss in aged rats. Journal of Neurophysiology, 119, 1852–1862. 10.1152/jn.00868.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forsman, C. A. , Lindh, B. , Elfvin, L. G. , & Hallman, H. (1989). Measurements of the DNA amount in mono‐ and binucleate cells in the celiac superior mesenteric ganglion of the guinea pig. Anatomy and Embryology, 179, 587–590. 10.1007/BF00315700 [DOI] [PubMed] [Google Scholar]
- Galbraith, W. (1955). The optical measurement of depth. Quarterly Journal of Microscopical science, 96, 285–288. [Google Scholar]
- García‐Fiñana, M. , & Cruz‐Orive, L. M. (2004). Improved variance prediction for systematic sampling on R. Statistics, 38, 243–272. 10.1080/0233188032000158826 [DOI] [Google Scholar]
- Gardella, D. , Hatton, W. J. , Rind, H. B. , Rosen, G. D. , & von Bartheld, S. (2003). Differential tissue shrinkage and compression in the z‐axis: Implications for optical disector counting in vibratome‐, plastic and cryosections. Journal of Neuroscience Methods, 124, 45–59. 10.1016/S0165-0270(02)00363-1 [DOI] [PubMed] [Google Scholar]
- Gardi, J. E. , Nyengaard, J. R. , & Gundersen, H. J. G. (2006). Using biased image analysis for improving unbiased stereological number estimation—A pilot simulation study of the smooth fractionator. Journal of Microscopy, 222, 242–250. 10.1111/j.1365-2818.2006.01552.x [DOI] [PubMed] [Google Scholar]
- Gardi, J. E. , Nyengaard, J. R. , & Gundersen, H. J. G. (2008). Automatic sampling for unbiased and efficient stereological estimation using the proportionator in biological studies. Journal of Microscopy, 230, 108–120. 10.1111/j.1365-2818.2008.01963.x [DOI] [PubMed] [Google Scholar]
- Geinisman, Y. , Gundersen, H. J. G. , van der Zee, E. , & West, M. J. (1996). Unbiased stereological estimation of the total number of synapses in a brain region. Journal of Neurocytology, 25, 805–819. 10.1007/BF02284843 [DOI] [PubMed] [Google Scholar]
- Glagolev, A. A. (1933). On geometrical methods of quantitative mineralogical analysis of rocks [in Russian (Vol. 59, pp. 1–47). Moscow: Transactions of the Institute of Economic Mineralogy. [Google Scholar]
- Glagolev, A. A. (1955). On geometrical methods of quantitative mineralogical analysis of rocks (translated from Russian by J.B. Sykes) (Vol. 567). Harwell, England: Atomic Energy Research Establishment. [Google Scholar]
- Glaser, E. M. , & Wilson, P. D. (1998). The coefficient of error of optical fractionator population size estimates: A computer simulation comparing three estimators. Journal of Microscopy, 192, 163–171. 10.1046/j.1365-2818.1998.00417.x [DOI] [PubMed] [Google Scholar]
- Gokhale, A. M. (1990). Unbiased estimation of curve length in 3‐D using vertical slices. Journal of Microscopy, 159, 133–141. 10.1111/j.1365-2818.1990.tb04771.x [DOI] [Google Scholar]
- Gokhale, A. M. , Evans, R. A. , Mackes, J. L. , & Mouton, P. R. (2004). Design‐based estimation of surface area in thick tissue sections of arbitrary orientation using virtual cycloids. Journal of Microscopy, 216, 25–31. 10.1111/j.0022-2720.2004.01392.x [DOI] [PubMed] [Google Scholar]
- Goldschmidt, R. B. , & Steward, O. (1992). Retrograde regulation of neuronal size in the entorhinal cortex: Consequences of the destruction of dentate granule cells with colchicine. Restorative Neurology and Neuroscience, 3, 335–343. 10.3233/RNN-1992-3606 [DOI] [PubMed] [Google Scholar]
- Gondré‐Lewis, M. C. , Darius, P. J. , Wang, H. , & Allard, J. S. (2016). Stereological analyses of reward system nuclei in maternally deprived/separated alcohol drinking rats. Journal of Chemical Neuroanatomy, 76, 122–132. 10.1016/j.jchemneu.2016.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gritti, I. , Henny, P. , Galloni, F. , Mainville, L. , Mariotti, M. , & Jones, B. E. (2006). Stereological estimates of the basal forebrain cell population in the rat, including neurons containing choline acetyltransferase, glutamic acid decarboxylase or phosphate‐activated glutaminase and colocalizing vesicular glutamate transporter. Neuroscience, 143, 1051–1064. 10.1016/j.neuroscience.2006.09.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gual‐Arnau, X. , Cruz‐Orive, L. M. , & Nuño‐Ballesteros, J. J. (2010). A new rotational integral formula for intrinsic volumes in space forms. Advances in Applied Mathematics, 44, 198–308. 10.1016/j.aam.2009.09.003 [DOI] [Google Scholar]
- Guillery, R. W. , & Herrup, K. (1997). Quantification without pontification: Choosing a method for counting objects in sectioned tissues. The Journal of Comparative Neurology, 386, 2–7. https://doi.org/10.1002/(SICI)1096-9861(19970915)386:1<1::AID-CNE1>3.0.CO;2-6 [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. (1977). Notes on the estimation of the numerical density of arbitrary profiles: The edge effect. Journal of Microscopy, 147, 219–223. 10.1111/j.1365-2818.1977.tb00062.x [DOI] [Google Scholar]
- Gundersen, H. J. G. (1986). Stereology of arbitrary particles. Journal of Microscopy, 143, 3–45. 10.1111/j.1365-2818.1986.tb02764.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. (1988). The nucleator. Journal of Microscopy, 151, 3–21. 10.1111/j.1365-2818.1988.tb04609.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. (2002a). The smooth fractionator. Journal of Microscopy, 207, 191–210. 10.1046/j.1365-2818.2002.01054.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. (2002b). Stereological estimation of tubular length. Journal of Microscopy, 207, 155–160. 10.1046/j.1365-2818.2002.01047.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. , Bagger, P. , Bendtsen, T. F. , Evans, S. M. , Korbo, L. , Marcussen, N. , … West, M. J. (1988). The new stereological tools: Disector, fractionator, nucleator and point sampled intercepts and their use in pathological research and diagnosis. APMIS, 96, 857–881. 10.1111/j.1699-0463.1988.tb00954.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. , Bendtsen, T. F. , Korbo, L. , Marcussen, N. , Møller, A. , Nielsen, K. , … West, M. J. (1988). Some new, simple and efficient stereological methods and their use in pathological research and diagnosis. APMIS, 96, 379–394. 10.1111/j.1699-0463.1988.tb05320.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. , & Jensen, E. B. (1987). The efficiency of systematic sampling in stereology and its prediction. Journal of Microscopy, 147, 229–263. 10.1111/j.1365-2818.1987.tb02837.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. , Jensen, E. B. V. , Kieu, K. , & Nielsen, J. (1999). The efficiency of systematic sampling in stereology—Reconsidered. Journal of Microscopy, 193, 199–211. 10.1046/j.1365-2818.1999.00457.x [DOI] [PubMed] [Google Scholar]
- Gundersen, H. J. G. , & Østerby, R. (1981). Optimizing sampling efficiency of stereological studies in biology: Or "Do more less well!". Journal of Microscopy, 121, 65–73. 10.1111/j.1365-2818.1981.tb01199.x [DOI] [PubMed] [Google Scholar]
- Hall, P. , & Ziegel, J. (2011). Distribution estimators and confidence intervals for stereological volumes. Biometrika, 98, 417–431. 10.1093/biomet/asr012 [DOI] [Google Scholar]
- Hama, H. , Hioki, H. , Namiki, K. , Hoshida, T. , Kurokawa, H. , Ishidate, F. , … Miyawaki, A. (2015). ScaleS: An optical clearing palette for biological imaging. Nature Neuroscience, 18, 1518–1529. 10.1038/nn.4107 [DOI] [PubMed] [Google Scholar]
- Hama, H. , Kurokawa, H. , Kawano, H. , Ando, R. , Shimogori, T. , Noda, H. , … Miyawaki, A. (2011). Scale: A chemical approach for fluorescence imaging and reconstruction of transparent mouse brain. Nature Neuroscience, 14, 1481–1488. 10.1038/nn.2928 [DOI] [PubMed] [Google Scholar]
- Hansen, L. V. , Nyengaard, J. R. , Andersen, J. B. , & Jensen, E. B. V. (2011). The semi‐automatic nucleator. Journal of Microscopy, 242, 206–215. 10.1111/j.1365-2818.2010.03460.x [DOI] [PubMed] [Google Scholar]
- Hasselholt, S. , Lykkesfeldt, J. , & Overgaard Larsen, J. (2015). Thick methacrylate sections devoid of lost caps simplify stereological quantifications based on the optical fractionator design. The Anatomical Record, 298, 2141–2150. 10.1002/ar.23266 [DOI] [PubMed] [Google Scholar]
- Hatton, W. J. , & von Bartheld, C. S. (1999). Analysis of cell death in the trochlear nucleus of the chick embryo: Calibration of the optical disector counting method reveals systematic bias. The Journal of Comparative Neurology, 409, 169–186. https://doi.org/10.1002/(SICI)1096-9861(19990628)409:2<169::AID-CNE1>3.0.CO;2-O [PubMed] [Google Scholar]
- Hedreen, J. C. (1998a). Lost caps in histological counting methods. The Anatomical Record, 250, 366–372. https://doi.org/10.1002/(SICI)1097-0185(199803)250:3<366::AID-AR11>3.0.CO;2-M [DOI] [PubMed] [Google Scholar]
- Hedreen, J. C. (1998b). What was wrong with the Abercrombie and empirical cell counting methods? A review. The Anatomical Record, 250, 373–380. https://doi.org/10.1002/(SICI)1097-0185(199803)250:3<373::AID-AR12>3.0.CO;2-L [DOI] [PubMed] [Google Scholar]
- Heggland, I. , Storkaas, I. S. , Soligard, H. T. , Kobro‐Flatmoen, A. , & Witter, M. P. (2015). Stereological estimation of neuron number and plaque load in the hippocampal region of a transgenic rat model of Alzheimer's disease. European Journal of Neuroscience, 41, 1245–1262. 10.1111/ejn.12876 [DOI] [PubMed] [Google Scholar]
- Helander, K. G. (1983). Thickness variations within individual paraffin and glycol methacrylate sections. Journal of Microscopy, 132, 223–227. 10.1111/j.1365-2818.1983.tb04276.x [DOI] [PubMed] [Google Scholar]
- Hey, J. D. , Neugebauer, T. M. , & Pasca, C. M. (2010). Georges‐Louis Leclerc de Buffon's ‘Essays on Moral Arithmetic’ In Ockenfels A. & Sadrieh A. (Eds.), The Selten school of behavioral economics. A collection of essays in honor of Reinhard Selten (pp. 245–282). Berlin, Germany: Springer. [Google Scholar]
- Heyden, A. , Ionescu, M.‐C. S. S. R. , Kracht, B. , Ghiglieri, V. , Calabresi, P. , … Gundelfinger, E. D. (2011). Hippocampal enlargement in Bassoon‐mutant mice is associated with enhanced neurogenesis, reduced apoptosis, and abnormal BDNF levels. Cell and Tissue Research, 346, 11–26. 10.1007/s00441-011-1233-3 [DOI] [PubMed] [Google Scholar]
- Hosseini‐Sharifabad, M. , & Nyengaard, J. R. (2007). Design‐based estimation of neuronal number and individual neuronal volume in the rat hippocampus. Journal of Neuroscience Methods, 162, 206–214. 10.1016/j.jneumeth.2007.01.009 [DOI] [PubMed] [Google Scholar]
- Howard, C. V. , & Reed, M. G. (2010). Unbiased stereology. Three‐dimensional measurements in microscopy (2nd ed.). Liverpool, England: QTP Publications. [Google Scholar]
- Hsu, S. M. , & Soban, E. (1982). Color modification of diaminobenzidine (DAB) precipitation by metallic ions and its application for double immunohistochemistry. Journal of Histochemistry and Cytochemistry, 30, 1079–1082. 10.1177/30.10.6182185 [DOI] [PubMed] [Google Scholar]
- Hykšová, M. , Kalousová, A. , & Saxl, I. (2012). Early history of geometric probability and stereology. Image Analysis & Stereology, 31, 1–16. 10.5566/ias.v31.p1-16 [DOI] [Google Scholar]
- Jørgensen, A.‐M. B. , Marner, L. , & Pakkenberg, B. (2008). No change in total length of white matter fibers in Alzheimer's disease. Neuroscience, 157, 878–883. 10.1016/j.neuroscience.2008.06.075 [DOI] [PubMed] [Google Scholar]
- Kaplan, S. , Canan, S. , Aslan, H. , Ünal, B. , & Sahín, B. (2001). A simple technique to measure the movements of the microscope stage along the x and y axes for stereological methods. Journal of Microscopy, 203, 321–325. 10.1046/j.1365-2818.2001.00931.x [DOI] [PubMed] [Google Scholar]
- Kaplan, S. , Gökyar, A. , Ünal, B. , Tunc, A. T. , Bahadir, A. , & Aslan, H. (2005). A simple technique for localizing consecutive fields for disector pairs in light microscopy: Application to neuron counting in rabbit spinal cord following spinal cord injury. Journal of Neuroscience Methods, 145, 277–284. 10.1016/j.jneumeth.2005.02.012 [DOI] [PubMed] [Google Scholar]
- Karadaglić, D. , & Wilson, T. (2008). Image formation in structured illumination wide‐field fluorescence microscopy. Micron, 39, 808–818. 10.1016/j.micron.2008.01.017 [DOI] [PubMed] [Google Scholar]
- Keller, K. K. , Andersen, I. T. , Andersen, J. B. , Hahn, U. , Stengaard‐Pedersen, K. , Hauge, E. M. , & Nyengaard, J. R. (2013). Improving efficiency in stereology: A study applying the proportionator and the autodisector on virtual slides. Journal of Microscopy, 251, 68–76. 10.1111/jmi.12044 [DOI] [PubMed] [Google Scholar]
- Kiêu, K. (1997). Three lectures on systematic geometric sampling (Vol. 13). Aarhus, Denmark: Department of Theoretical Statistics, Institute of Mathematics, University of Aarhus. [Google Scholar]
- Kim, K. K. , Adelstein, R. S. , & Kawamoto, S. (2009). Identification of neuronal nuclei (NeuN) as Fox‐3, a new member of the Fox‐1 gene family of splicing factors. Journal of Biological Chemistry, 284, 31052–31061. 10.1074/jbc.M109.052969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, K. K. , Kim, Y. C. , Adelstein, R. S. , & Kawamoto, S. (2011). Fox‐3 and PSF interact to activate neural cell‐specific alternative splicing. Nucleic Acids Research, 39, 3064–3078. 10.1093/nar/gkq1221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, Y. , Venkataraju, K. U. , Pradhan, K. , Mende, C. , Taranda, J. , Turaga, S. C. , … Osten, P. (2015). Mapping social behavior‐induced brain activation at cellular resolution in the mouse. Cell Reports, 10, 292–305. 10.1016/j.celrep.2014.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleder, M. (2005). WGS84 ellipsoidal earth plotted at 4 pixels per degree. Retrieved from http://www.mathworks.com/matlabcentral/fileexchange/8590-wgs84-ellipsoidal-earth-plotted-at-4-pixels-per-degree/all_files
- Knott, G. , Marchman, H. , Wall, D. , & Lich, D. (2008). Serial section scanning electron microscopy of adult brain tissue using focused ion beam milling. The Journal of Neuroscience, 28, 2959–2964. 10.1523/JNEUROSCI.3189-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinko, Y. , Cendelin, J. , Kralickova, M. , & Tonar, Z. (2016). Smaller absolute quantities but greater relative densities of microvessels are associated with cerebellar degeneration in Lurcher mice. Frontiers in Neuroanatomy, 10, 35 10.3389/fnana.2016.00035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konigsmark, B. W. (1970). Methods for the counting of neurons In Nauta W. J. H. & Ebbeson S. O. E. (Eds.), Contemporary research methods in neuroanatomy (pp. 315–340). Berlin: Springer. [Google Scholar]
- Korbo, L. , Pakkenberg, B. , Ladefoged, O. , Gundersen, H. J. G. , Arlien‐Søborg, P. , & Pakkenberg, H. (1990). An efficient method for estimating the total number of neurons in rat brain cortex. Journal of Neuroscience Methods, 31, 93–100. 10.1016/0165-0270(90)90153-7 [DOI] [PubMed] [Google Scholar]
- Kordower, J. H. (2000). Making the counts count: The stereology revolution. Journal of Chemical Neuroanatomy, 20, 1–2. 10.1016/S0891-0618(00)00079-X [DOI] [PubMed] [Google Scholar]
- Korkmaz, M. , & Tümkaya, L. (1997). Estimation of the section thickness and optical disector height with a simple calibration method. Journal of Microscopy, 187, 104–109. 10.1046/j.1365-2818.1997.2180777.x [DOI] [Google Scholar]
- Kreutz, A. , & Barger, N. (2018). Maximizing explanatory power in stereological data collection: A protocol for reliably integrating optical fractionator and multiple immunofluorescence techniques. Frontiers in Neuroanatomy, 12, 73 10.3389/fnana.2018.00073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruskal, W. , & Mosteller, F. (1979). Representative sampling, II: Scientific literature, excluding statistics. International Statistical Review, 47, 111–127. 10.2307/1402564 [DOI] [Google Scholar]
- Kubíková, T. , Kochová, P. , Tomášek, P. , Witter, K. , & Tonar, Z. (2017). Numerical and length densities of microvessels in the human brain: Correlation with preferential orientation of microvessels in the cerebral cortex, subcortical grey matter and white matter, pons and cerebellum. Journal of Chemical Neuroanatomy, 88, 22–32. 10.1016/j.jchemneu.2017.11.005 [DOI] [PubMed] [Google Scholar]
- Kubínová, L. , & Janácek, J. (1998). Estimating surface area by the isotropic fakir method from thick slices cut in an arbitrary direction. Journal of Microscopy, 191, 201–211. 10.1046/j.1365-2818.1998.00356.x [DOI] [PubMed] [Google Scholar]
- Kubínová, L. , & Janáček, J. (2015). Confocal stereology: An efficient tool for measurement of microscopic structures. Cell and Tissue Research, 360, 13–28. 10.1007/s00441-015-2138-3 [DOI] [PubMed] [Google Scholar]
- Kuwajima, T. , Sitko, A. A. , Bhansali, P. , Jurgens, C. , Guido, W. , & Mason, C. (2013). ClearT: A detergent‐ and solvent‐free clearing method for neuronal and non‐neuronal tissue. Development, 140, 1364–1368. 10.1242/dev.091844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen, J. O. , Gundersen, H. J. G. , & Nielsen, J. (1998). Global spatial sampling with isotropic virtual planes: Estimators of length density and total length in thick, arbitrarily oriented sections. Journal of Microscopy, 191, 238–248. 10.1046/j.1365-2818.1998.00365.x [DOI] [PubMed] [Google Scholar]
- Lind, D. , Franken, S. , Kappler, J. , Jankowski, J. , & Schilling, K. (2005). Characterization of the neuronal marker NeuN as a multiply phosphorylated antigen with discrete subcellular localization. The Journal of Neuroscience, 79, 295–302. 10.1002/jnr.20354 [DOI] [PubMed] [Google Scholar]
- Løkkegaard, A. , Nyengaard, J. R. , & West, M. J. (2001). Stereological estimates of number and length of capillaries in subdivisions of the human hippocampal region. Hippocampus, 11, 726–740. 10.1002/hipo.1088 [DOI] [PubMed] [Google Scholar]
- Lyck, L. , Dalmau Santamaria, I. , Pakkenberg, B. , Chemnitz, J. , Schrøder, H. D. , Finsen, B. , & Gundersen, H. J. G. (2009). An empirical analysis of the precision of estimating the numbers of neurons and glia in human neocortex using a fractionator‐design with sub‐sampling. Journal of Neuroscience Methods, 182, 143–156. 10.1016/j.jneumeth.2009.06.003 [DOI] [PubMed] [Google Scholar]
- Lyck, L. , Ljelsing, J. , Søndergaard Jensen, P. , Lambertsen, K. L. , Pakkenberg, B. , & Finsen, B. (2006). Immunohistochemical visualization of neurons and specific glial cells for stereological application in the porcine neocortex. Journal of Neuroscience Methods, 152, 229–242. 10.1016/j.jneumeth.2005.09.009 [DOI] [PubMed] [Google Scholar]
- Majlof, L. , & Forsgren, P.‐O. (1993). Confocal microscopy: Important considerations for accurate imaging. Methods in Cell Biology, 70, 149–164. 10.1016/S0091-679X(02)70005-8 [DOI] [PubMed] [Google Scholar]
- Markram, H. , Muller, E. , Ramaswamy, S. , Reimann, M. W. , Abdellah, M. , Sanchez, C. A. , … Schürmann, F. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell, 163, 456–492. 10.1016/j.cell.2015.09.029 [DOI] [PubMed] [Google Scholar]
- Matérn, B. (1985). Estimating area by dot counts In Lanke J. & Lindgren G. (Eds.), Contributions to probability and statistics in honour of Gunnar Blom (pp. 243–257). Lund, Sweden: Department of Mathematical Statistics, Lund University. [Google Scholar]
- Matheron, G. (1965). Les variables régionalisées et leur estimation. Paris: Masson et Cie. [Google Scholar]
- Matheron, G. (1971). The theory of regionalized variables and its applications. Paris: École National Supérieure des Mines de Paris. [Google Scholar]
- Mattfeldt, T. (2006). Prediction of the variance of stereological volume estimates from systematic sections using computer‐intensive methods. Journal of Microscopy, 222, 166–176. 10.1111/j.1365-2818.2006.01584.x [DOI] [PubMed] [Google Scholar]
- Mattfeldt, T. (2011). A brief introduction to computer‐intensive methods, with a view towards applications in spatial statistics and stereology. Journal of Microscopy, 242, 1–9. 10.1111/j.1365-2818.2010.03452.x [DOI] [PubMed] [Google Scholar]
- Maxeiner, S. , Glassmann, A. , Kao, H. T. , & Schilling, K. (2014). The molecular basis of the specificity and cross‐reactivity of the NeuN epitope of the neuron‐specific splicing regulator, Rbfox3. Histochemistry and Cell Biology, 141, 43–55. 10.1007/s00418-013-1159-9 [DOI] [PubMed] [Google Scholar]
- Mayhew, T. M. (1996). How to count synapses unbiasedly and efficiently at the ultrastructural level: Proposal for a standard sampling and counting protocol. Journal of Neurocytology, 25, 793–804. 10.1007/BF02284842 [DOI] [PubMed] [Google Scholar]
- McMenamin, P. G. (1999). Distribution and phenotype of dendritic cells and resident tissue macrophages in the dura mater, leptomeninges, and choroid plexus of the rat brain as demonstrated in wholemount preparations. The Journal of Comparative Neurology, 405, 553–562. https://doi.org/10.1002/(SICI)1096-9861(19990322)405:4<553::AID-CNE8>3.0.CO;2-6 [PubMed] [Google Scholar]
- McPhail, L. T. , McBride, C. B. , McGraw, J. , Steeves, J. D. , & Tetzlaff, W. (2004). Axotomy abolishes NeuN expression in facial but not rubrospinal neurons. Experimental Neurology, 185, 182–190. 10.1016/j.expneurol.2003.10.001 [DOI] [PubMed] [Google Scholar]
- Melvin, N. , Poda, D. , & Sutherland, R. J. (2007). A simple and efficient alternative to implementing systematic random sampling in stereological designs without a motorized microscope stage. Journal of Microscopy, 228, 103–106. 10.1111/j.1365-2818.2007.01828.x [DOI] [PubMed] [Google Scholar]
- Mertz, J. (2011). Optical sectioning microscopy with planar or structured illumination. Nature Methods, 8, 811–819. 10.1038/nmeth.1709 [DOI] [PubMed] [Google Scholar]
- Merz, W. A. (1967). Die Streckenmessung an gerichteten Strukturen im Mikroskop und ihre Anwendung zur Bestimmung von Oberflächen‐Volumen‐Relationen im Knochengewebe. Mikroskopie, 22, 132–142. [PubMed] [Google Scholar]
- Miettinen, R. A. , Kalesnykas, G. , & Koivisto, E. H. (2002). Estimation of the total number of cholinergic neurons containing estrogen receptor‐alpha in the rat basal forebrain. Journal of Histochemistry and Cytochemistry, 50, 891–902. 10.1177/002215540205000703 [DOI] [PubMed] [Google Scholar]
- Miki, T. , Harris, S. J. , Wilce, P. A. , Takeuchi, Y. , & Bedi, K. S. (2003). Effects of alcohol exposure during early life on neuron numbers in the rat hippocampus. I. Hilus neurons and granule cells. Hippocampus, 13, 388–398. 10.1002/hipo.10072 [DOI] [PubMed] [Google Scholar]
- Miki, T. , Harris, S. J. , Wilce, P. A. , Takeuchi, Y. , & Bedi, K. S. (2004). Effects of age and alcohol exposure during early life on pyramidal cell numbers in the CA1‐CA3 region of the rat hippocampus. Hippocampus, 14, 124–134. 10.1002/hipo.10155 [DOI] [PubMed] [Google Scholar]
- Mills Schumann, C. , & Amaral, D. G. (2005). Stereological estimation of the number of neurons in the human amygdaloid complex. The Journal of Comparative Neurology, 491, 320–329. 10.1002/cne.20704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan, J. T. , Barger, N. , Amaral, D. G. , & Schumann, C. M. (2014). Stereological study of amygdala glial populations in adolescents and adults with autism spectrum disorder. PLoS One, 9, e110356 10.1371/journal.pone.0110356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouton, P. R. , Gokhale, A. M. , Ward, N. L. , & West, M. J. (2002). Stereological length estimation using spherical probes. Journal of Microscopy, 206, 54–64. 10.1046/j.1365-2818.2002.01006.x [DOI] [PubMed] [Google Scholar]
- Mulders, W. H. A. M. , West, M. J. , & Slomianka, L. (1997). The numbers of neurons in the presubiculum, parasubiculum and entorhinal area of the rat. The Journal of Comparative Neurology, 385, 83–94. https://doi.org/10.1002/(SICI)1096-9861(19970818)385:1<83::AID-CNE5>3.0.CO;2-8 [PubMed] [Google Scholar]
- Mullen, R. J. , Buck, C. R. , & Smith, A. M. (1992). NeuN, a neuronal specific nuclear protein in vertebrates. Development, 116, 201–211. [DOI] [PubMed] [Google Scholar]
- Murakami, T. C. , Mano, T. , Saikawa, S. , Horiguchi, S. A. , Shigeta, D. , Baba, K. , … Ueda, H. R. (2018). A three‐dimensional single‐cell‐resolution whole‐brain atlas using CUBIC‐X expansion microscopy and tissue clearing. Nature Neuroscience, 21, 625–637. 10.1038/s41593-018-0109-1 [DOI] [PubMed] [Google Scholar]
- Murray, E. , Cho, J. H. , Goodwin, D. , Ku, T. , Swaney, J. , Kim, S. Y. , … Chung, K. (2015). Simple, scalable proteomic imaging for high‐dimensional profiling of intact systems. Cell, 163, 1500–1514. 10.1016/j.cell.2015.11.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neil, M. , Juskaitis, R. , & Wilson, T. (1997). Method of obtaining optical sectioning by using structured light in a conventional microscope. Optics Letter, 22, 1905–1907. 10.1364/OL.22.001905 [DOI] [PubMed] [Google Scholar]
- Nissl, F. (1892). Ueber die veränderungen der ganglienzellen am facialiskern des kanninchens nach ausreissung der nerven. Allgemeine Zeitschrift für Psychiatrie, 48, 197–198. [Google Scholar]
- Nomura, T. , Fukuda, T. , Aika, Y. , Heizmann, C. W. , Emson, P. C. , Kobayashi, T. , & Kosaka, T. (1997). Distribution of nonprincipal neurons in the rat hippocampus, with special reference to their dorsoventral difference. Brain Research, 751, 64–80. 10.1016/S0006-8993(96)01395-9 [DOI] [PubMed] [Google Scholar]
- Nyengaard, J. R. , & Gundersen, H. J. G. (1992). The isector: A simple and direct method for generating isotropic, uniform random sections from small specimens. Journal of Microscopy, 165, 427–431. 10.1111/j.1365-2818.1992.tb01497.x [DOI] [Google Scholar]
- Nykjær Nikolajsen, G. , Jensen, M. S. , & West, M. J. (2016). A zinc fixative for 3D visualization of cerebral capillaries and pericytes. Journal of Neuroscience Methods, 257, 1–6. 10.1016/j.jneumeth.2015.09.016 [DOI] [PubMed] [Google Scholar]
- Nykjær Nikolajsen, G. , Kotynski, K. A. , Jensen, M. S. , & West, M. J. (2017). Quantitative analysis of the capillary network of aged APPswe/PS1dE9 transgenic mice. Neurobiology of Aging, 36, 2954–2962. 10.1016/j.neurobiolaging.2015.08.004 [DOI] [PubMed] [Google Scholar]
- Oorschot, D. E. (1996). Total number of neurons in the neostriatal, pallidal, subthalamic, and substantia nigral nuclei of the rat basal ganglia: A stereological study using the cavalieri and optical disector methods. The Journal of Comparative Neurology, 366, 580–599. https://doi.org/10.1002/(SICI)1096-9861(19960318)366:4<580::AID-CNE3>3.0.CO;2-0 [DOI] [PubMed] [Google Scholar]
- Osman, T. A. , Oijordsbakken, G. , Costea, D. E. , & Johannessen, A. C. (2013). Successful triple immuno‐enzymatic method employing primary antibodies from same species and same immunoglobulin subclass. European Journal of Histochemistry, 57, e22 10.4081/ejh.2013.e22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pakkenberg, B. , & Gundersen, H. J. G. (1997). Neocortical neuron number in humans: Effect of sex and age. The Journal of Comparative Neurology, 384, 312–320. https://doi.org/10.1002/(SICI)1096-9861(19970728)384:2<312::AID-CNE10>3.0.CO;2-K [PubMed] [Google Scholar]
- Peterson, D. A. (2014). High‐resolution estimation of multiple cell populations in tissue using confocal stereology In Cornea A. & Conn P. M. (Eds.), Fluorescence microscopy. Super‐resolution and other novel techniques (pp. 171–184). London, England: Academic Press. [Google Scholar]
- Phinney, A. L. , Calhoun, M. E. , Woods, A. G. , Deller, T. , & Jucker, M. (2004). Stereological analysis of the reorganization of the dentate gyrus following entorhinal cortex lesions in mice. European Journal of Neuroscience, 19, 1731–1740. 10.1111/j.1460-9568.2004.03280.x [DOI] [PubMed] [Google Scholar]
- Portiansky, E. L. , Barbeito, C. G. , Gimeno, E. J. , Zuccolilli, G. O. , & Goya, R. G. (2006). Loss of NeuN immunoreactivity in rat spinal cord neurons during aging. Experimental Neurology, 202, 519–521. 10.1016/j.expneurol.2006.07.014 [DOI] [PubMed] [Google Scholar]
- Porzionato, A. , Macchi, V. , Parenti, A. , & de Caro, R. (2009). Morphometric analysis of infant and adult medullary nuclei through optical disector method. The Anatomical Record, 292, 1619–1629. 10.1002/ar.20957 [DOI] [PubMed] [Google Scholar]
- Pover, C. M. , & Coggeshall, R. E. (1991). Verification of the disector method for counting neurons, with comments on the empirical method. The Anatomical Record, 231, 573–578. 10.1002/ar.1092310419 [DOI] [PubMed] [Google Scholar]
- Reichmann, F. , Painsipp, E. , Holzer, P. , Kummer, D. , Bock, E. , & Leitinger, G. (2015). A novel unbiased counting method for the quantification of synapses in the mouse brain. Journal of Neuroscience Methods, 240, 13–21. 10.1016/j.jneumeth.2014.10.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renier, N. , Adams, E. L. , Kirst, C. , Wu, Z. , Azevedo, R. , Kohl, J. , … Tessier‐Lavigne, M. (2016). Mapping of brain activity by automated volume analysis of immediate early genes. Cell, 2016, 1789–1802. 10.1016/j.cell.2016.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rezze, C. J. (1966). Células binucleadas no núcleo do nervo hipoglosso humano através dos grupos etários. Arquivos de Neuro‐Psiquiatria, 24, 247–256. 10.1590/S0004-282X1966000400002 [DOI] [Google Scholar]
- Ribeiro, A. A. C. M. (2006). Size and number of binucleate and mononucleate superior cervical ganglion neurons in young capybaras. Anatomy and Embryology, 211, 607–617. 10.1007/s00429-006-0113-1 [DOI] [PubMed] [Google Scholar]
- Riudavets, M. A. , Iacono, D. , Resnick, S. M. , O'Brien, R. B. Z. A. , Martin, L. J. , … Troncoso, J. C. (2007). Resistance to Alzheimer's pathology is associated with nuclear hypertrophy in neurons. Neurobiology of Aging, 28, 1484–1492. 10.1016/j.neurobiolaging.2007.05.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts, N. , Cruz‐Orive, L. M. , Reid, N. M. K. , Brodie, D. A. , Bourne, M. , & Edwards, R. H. T. (1993). Unbiased estimation of human body composition by the Cavalieri method using magnetic resonance imaging. Journal of Microscopy, 171, 239–253. 10.1111/j.1365-2818.1993.tb03381.x [DOI] [PubMed] [Google Scholar]
- Royet, J. P. (1991). Stereology: A method for analyzing images. Progress in Neurobiology, 37, 433–474. 10.1016/0301-0082(91)90009-P [DOI] [PubMed] [Google Scholar]
- Rudow, G. , O'Brien, R. , Savonenko, A. V. , Resnick, S. M. , Zonderman, A. B. , Pletnikova, O. , … Troncoso, J. C. (2008). Morphometry of the human substantia nigra in ageing and Parkinson's disease. Acta Neuropathologica, 115, 461–470. 10.1007/s00401-008-0352-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russ, J. C. , & Dehoff, R. T. (2000). Practical stereology (2nded. ed.). New York, NY: Plenum Press. [Google Scholar]
- Ruszczycki, B. , Karolina Pels, K. K. , Walczak, A. , Zamłyńska, K. , Such, M. , Szczepankiewicz, A. A. , … Wilczyński, G. M. (2019). Three‐dimensional segmentation and reconstruction of neuronal nuclei in confocal microscopic images. Frontiers in Neuroanatomy, 13, 81 10.3389/fnana.2019.00081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saltykov, S. A. (1946). The method of intersections in metallography (in Russian). Zavodskaja Laboratorija, 12, 816–825. [Google Scholar]
- Saltykov, S. A. (1974). Stereometrische metallographie (3rd ed.). Leipzig, Germany: VEB Deutscher Verlag für Grundstoffindustrie. [Google Scholar]
- Saper, C. B. (1996). Any way you cut it: A new journal policy for the use of unbiased counting methods. The Journal of Comparative Neurology, 364, 5. https://doi.org/10.1002/(SICI)1096-9861(19960101)364:1<5::AID-CNE1>3.0.CO;2-9 [DOI] [PubMed] [Google Scholar]
- Schmitz, C. (1998). Variation of fractionator estimates and its prediction. Anatomy and Embryology, 198, 371–397. 10.1007/s004290050191 [DOI] [PubMed] [Google Scholar]
- Schmitz, C. , Born, M. , Dolezel, P. , Rutten, B. P. F. , de Saint‐Georges, L. , Hof, P. R. , & Korr, H. (2005). Prenatal protracted irradiation at very low dose rate induces severe neuronal loss in rat hippocampus and cerebellum. Neuroscience, 130, 935–948. 10.1016/j.neuroscience.2004.08.034 [DOI] [PubMed] [Google Scholar]
- Schmitz, C. , Dafotakis, M. , Heinsen, H. , Mugrauer, K. , Niesel, A. , Popken, G. J. , … Korr, H. (2000). Use of cryostat sections from snap‐frozen nervous tissue for combining stereological estimates with histological, cellular, or molecular analyses on adjacent sections. Journal of Chemical Neuroanatomy, 20, 21–29. 10.1016/S0891-0618(00)00075-2 [DOI] [PubMed] [Google Scholar]
- Schmitz, C. , Eastwood, B. S. , Tappan, S. J. , Glaser, J. R. , Peterson, D. A. , & Hof, P. R. (2014). Current automated 3D cell detection methods are not a suitable replacement for manual stereologic cell counting. Frontiers in Neuroanatomy, 8, 27 10.3389/fnana.2014.00027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitz, C. , & Hof, P. R. (2000). Recommendations for straightforward and rigorous methods of counting neurons based on a computer simulation approach. Journal of Chemical Neuroanatomy, 20, 93–114. 10.1016/S0891-0618(00)00066-1 [DOI] [PubMed] [Google Scholar]
- Schmitz, C. , & Hof, P. R. (2005). Design‐based stereology in neuroscience. Neuroscience, 130, 813–831. 10.1016/j.neuroscience.2004.08.050 [DOI] [PubMed] [Google Scholar]
- Schoenfeld, T. A. , & Knott, T. K. (2004). Evidence for the disproportionate mapping of olfactory airspace onto the main olfactory bulb of the hamster. The Journal of Comparative Neurology, 476, 186–201. 10.1002/cne.20218 [DOI] [PubMed] [Google Scholar]
- Seiriki, K. , Kasai, A. , Hashimoto, T. , Schulze, W. , Niu, M. , Yamaguchi, S. , … Hashimoto, H. (2017). High‐speed and scalable whole‐brain imaging in rodents and primates. Neuron, 94, 1085–1100.e1086. 10.1016/j.neuron.2017.05.017 [DOI] [PubMed] [Google Scholar]
- Shamy, J. L. , Buckmaster, P. S. , Amaral, D. G. , Calhoun, M. E. , & Rapp, P. R. (2007). Reactive plasticity in the dentate gyrus following bilateral entorhinal cortex lesions in cynomolgus monkeys. The Journal of Comparative Neurology, 502, 192–201. 10.1002/cne.21313 [DOI] [PubMed] [Google Scholar]
- Shuvaev, S. A. , Lazutkin, A. A. , Kedrov, A. V. , Anokhin, K. V. , Enikolopov, G. N. , & Koulakov, A. A. (2017). DALMATIAN: An algorithm for automatic cell detection and counting in 3D. Frontiers in Neuroanatomy, 11, 117 10.3389/fnana.2017.00117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvestri, L. , Paciscopi, M. , Soda, P. , Biamonte, F. , Iannello, G. , Frasconi, P. , & Pavone, F. S. (2015). Quantitative neuroanatomy of all Purkinje cells with light sheet microscopy and high‐throughput image analysis. Frontiers in Neuroanatomy, 9, 68 10.3389/fnana.2015.00068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slomianka, L. , & West, M. J. (1987). Asymmetry in the hippocampal region specific for one of two closely related species of wild mice. Brain Research, 436, 69–75. 10.1016/0006-8993(87)91557-5 [DOI] [PubMed] [Google Scholar]
- Slomianka, L. , & West, M. J. (2005). Estimators of the precision of stereological estimates: An example based on the CA1 pyramidal cell layer of rats. Neuroscience, 136, 757–767. 10.1016/j.neuroscience.2005.06.086 [DOI] [PubMed] [Google Scholar]
- Smith, C. S. , & Guttman, L. (1953). Measurement of internal boundaries in three‐dimensional structures by random sectioning. Transactions of the AIME, 197, 81–87. 10.1007/BF03397456 [DOI] [Google Scholar]
- Stanley, D. P. , & Shetty, A. K. (2004). Aging in the rat hippocampus is associated with widespread reductions in the number of glutamate decarboxylase‐67 positive interneurons but not interneuron degeneration. Journal of Neurochemistry, 89, 204–216. 10.1111/j.1471-4159.2004.02318.x [DOI] [PubMed] [Google Scholar]
- Stark, A. K. , Toft, M. H. , Pakkenberg, H. , Fabricius, K. , Eriksen, N. , Pelvig, D. P. , … Pakkenberg, B. (2007). The effect of age and gender on the volume and size distribution of neocortical neurons. Neuroscience, 150, 121–130. 10.1016/j.neuroscience.2007.06.062 [DOI] [PubMed] [Google Scholar]
- Sterio, D. C. (1984). The unbiased estimation of number and sizes of arbitrary particles using the disector. Journal of Microscopy, 134, 127–136. 10.1111/j.1365-2818.1984.tb02501.x [DOI] [PubMed] [Google Scholar]
- Stranahan, A. M. , Jiam, N. T. , Stocker, A. M. , & Gallagher, M. (2012). Aging reduces total neuron number in the dorsal component of the rodent prefrontal cortex. The Journal of Comparative Neurology, 520, 1318–1326. 10.1002/cne.22790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syková, E. , Mazel, T. , Hasenöhrl, R. U. , Harvey, A. R. , Simonová, Z. , Mulders, W. H. A. M. , & Huston, J. P. (2002). Learning deficits in aged rats related to decrease in extracellular volume and loss of diffusion anisotropy in hippocampus. Hippocampus, 12, 269–279. 10.1002/hipo.1101 [DOI] [PubMed] [Google Scholar]
- Tang, Y. , & Nyengaard, J. R. (1997). A stereological method for estimating to total length and size of myelin fibers in human brain white matter. Journal of Neuroscience Methods, 73, 193–200. 10.1016/S0165-0270(97)02228-0 [DOI] [PubMed] [Google Scholar]
- Tang, Y. , Nyengaard, J. R. , de Groot, D. M. G. , & Gundersen, H. J. G. (2001). Total regional and global number of synapses in the human brain neocortex. Synapse, 41, 258–273. 10.1002/syn.1083 [DOI] [PubMed] [Google Scholar]
- Thompson, W. R. (1932). The geometric properties of microscopic configurations. I. general aspects of projectometry. Biometrika, 24, 21–26. 10.1093/biomet/24.1-2.21 [DOI] [Google Scholar]
- Torres, E. M. , Meldrum, A. , Kirik, D. , & Dunnett, S. B. (2006). An investigation of the problem of two‐layered immunohistochemical staining in paraformaldehyde fixed sections. Journal of Neuroscience Methods, 158, 64–74. 10.1016/j.jneumeth.2006.05.016 [DOI] [PubMed] [Google Scholar]
- Ünal‐Cevik, I. , Kilinc, M. , Gürsoy‐Özdemir, Y. , Gurer, G. , & Dalkara, T. (2004). Loss of NeuN immunoreactivity after cerebral ischemia does not indicate neuronal cell loss: A cautionary note. Brain Research, 1015, 169–174. 10.1016/j.brainres.2004.04.032 [DOI] [PubMed] [Google Scholar]
- Vanhecke, D. , Studer, D. , & Ochs, M. (2007). Stereology meets electron tomography: Towards quantitative 3D electron microscopy. Journal of Structural Biology, 159, 443–450. 10.1016/j.jsb.2007.05.003 [DOI] [PubMed] [Google Scholar]
- Wälchli, T. , Mateos, J. M. , Weinman, O. , Babic, D. , Regli, L. , Hoerstrup, S. P. , … Vogel, J. (2015). Quantitative assessment of angiogenesis, perfused blood vessels and endothelial tip cells in the postnatal mouse brain. Nature Protocols, 10, 53–74. 10.1038/nprot.2015.002 [DOI] [PubMed] [Google Scholar]
- West, M. J. (2012a). Basic stereology for biologists and neuroscientists. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. [Google Scholar]
- West, M. J. (2012b). Estimating object number in biological structures. Cold Spring Harbor Protocols, 2012, 1049–1066. 10.1101/pdb.top071423 [DOI] [PubMed] [Google Scholar]
- West, M. J. (2012c). The precision of estimates in stereological analyses. Cold Spring Harbor Protocols, 2012, 937–949. 10.1101/pdb.top071050 [DOI] [PubMed] [Google Scholar]
- West, M. J. , Bach, G. , Søderman, A. , & Ledet Jensen, J. (2009). Synaptic contact number and size in stratum radiatum CA1 of APP/PS1E9 transgenic mice. Neurobiology of Aging, 30, 1756–1776. 10.1016/j.neurobiolaging.2008.01.009 [DOI] [PubMed] [Google Scholar]
- West, M. J. , & Coleman, P. D. (1996). How to count. Neurobiology of Aging, 17, 503 10.1016/0197-4580(96)00061-9 [DOI] [Google Scholar]
- West, M. J. , Coleman, P. D. , & Flood, D. G. (1988). Estimating the number of granule cells in the dentate gyrus with the disector. Brain Research, 448, 167–172. 10.1016/0006-8993(88)91114-6 [DOI] [PubMed] [Google Scholar]
- West, M. J. , Danscher, G. , & Gydesen, H. (1978). A determination of the volumes of the layers of the rat hippocampal region. Cell and Tissue Research, 188, 345–359. 10.1007/BF00219777 [DOI] [PubMed] [Google Scholar]
- West, M. J. , & Gundersen, H. J. G. (1990). Unbiased stereological estimation of the number of neurons in the human hippocampus. The Journal of Comparative Neurology, 296, 1–22. 10.1002/cne.902960102 [DOI] [PubMed] [Google Scholar]
- West, M. J. , Oestergaard, K. , Andreassen, O. A. , & Finsen, B. (1996). Estimation of the number of somatostatin neurons in the striatum: An in situ hybridization study using the optical fractionator method. The Journal of Comparative Neurology, 370, 11–22. https://doi.org/10.1002/(SICI)1096-9861(19960617)370:1<11::AID-CNE2>3.0.CO;2-O [DOI] [PubMed] [Google Scholar]
- West, M. J. , & Slomianka, L. (1998). Total number of neurons in the layers of the human entorhinal cortex. Hippocampus, 8, 69–82. https://doi.org/10.1002/(SICI)1098-1063(1998)8:1<69::AID-HIPO7>3.0.CO;2-2 [DOI] [PubMed] [Google Scholar]
- West, M. J. , Slomianka, L. , & Gundersen, H. J. G. (1991). Unbiased stereological estimation of the total number of neurons in the subdivisions of rat hippocampus using the optical fractionator. The Anatomical Record, 231, 482–497. 10.1002/ar.1092310411 [DOI] [PubMed] [Google Scholar]
- Whitney, E. R. , Kemper, T. L. , Rosene, D. L. , Bauman, M. L. , & Blatt, G. J. (2008). Calbindin‐D28k is a more reliable marker of human Purkinje cells than standard Nissl stains: A stereological experiment. Journal of Neuroscience Methods, 168, 42–47. 10.1016/j.jneumeth.2007.09.009 [DOI] [PubMed] [Google Scholar]
- Wirenfeldt, M. , Dalmau, I. , & Finsen, B. (2003). Estimation of absolute microglial cell numbers in mouse fascia dentata using unbiased and efficient stereological cell counting principles. Glia, 44, 129–139. 10.1002/glia.10277 [DOI] [PubMed] [Google Scholar]
- Witgen, B. M. , Grady, M. S. , Nyengaard, J. R. , & Gundersen, H. J. G. (2006). A new fractionator principle with varying sampling fractions: Exemplified by estimation of synapse number using electron microscopy. Journal of Microscopy, 222, 251–255. 10.1111/j.1365-2818.2006.01563.x [DOI] [PubMed] [Google Scholar]
- Woodruff‐Pak, D. S. (2006). Stereological estimation of Purkinje neuron number in C57BL/6 mice and its relation to associative learning. Neuroscience, 141, 233–243. 10.1016/j.neuroscience.2006.03.070 [DOI] [PubMed] [Google Scholar]
- Wu, J. , He, Y. , Yang, Z. , Guo, C. , Luo, Q. , Zhou, W. , … Gong, H. (2014). 3D BrainCV: Simultaneous visualization and analysis of cells and capillaries in a whole mouse brain with one‐micron voxel resolution. Neuroimage, 87, 199–208. 10.1016/j.neuroimage.2013 [DOI] [PubMed] [Google Scholar]
- Wu, K.‐L. , Li, Y.‐Q. , Tabassum, A. , Lu, W.‐Y. , Aubert, I. , & Wong, C. S. (2010). Loss of neuronal protein expression in mouse hippocampus after irradiation. Journal of Neuropathology & Experimental Neurology, 69, 272–280. 10.1097/NEN.0b013e3181d1afe4 [DOI] [PubMed] [Google Scholar]
- Xavier‐Vidal, R. (2010). Disector Z‐axis mechanical method for stereology. Anais da Academia Brasileira de Ciências, 82, 539–544. 10.1590/S0001-37652010000200028 [DOI] [Google Scholar]
- Yamamura, T. , Barker, J. M. , Balthazart, J. , & Ball, G. F. (2011). Androgens and estrogens synergistically regulate the expression of doublecortin and enhance neuronal recruitment in the song system of adult female canaries. The Journal of Neuroscience, 31, 9649–9657. 10.1523/JNEUROSCI.0088-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, B. , Treweek, J. B. , Kulkarni, R. P. , Deverman, B. E. , Chen, C. K. , Lubeck, E. , … Gradinaru, V. (2014). Single‐cell phenotyping within transparent intact tissue through whole‐body clearing. Cell, 158, 945–958. 10.1016/j.cell.2014.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, W. , Thamattoor, A. K. , LeRoy, C. , & Buckmaster, P. S. (2015). Surviving mossy cells enlarge and receive more excitatory synaptic input in a mouse model of temporal lobe epilepsy. Hippocampus, 25, 594–604. 10.1002/hipo.22396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, W. , Yamawaki, R. , Wen, X. , Uhl, J. , Diaz, J. , Prince, D. A. , & Buckmaster, P. S. (2009). Surviving hilar somatostatin interneurons enlarge, sprout axons, and form new synapses with granule cells in a mouse model of temporal lobe epilepsy. The Journal of Neuroscience, 29, 14247–14256. 10.1523/JNEUROSCI.3842-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, X. , Huang, L. , Zheng, Y. , Song, Y. , Xu, Q. , Wang, J. , … Gong, W. (2019). Ultrafast optical clearing method for three‐dimensional imaging with cellular resolution. Proceedings of the National Academy of Sciences of the United States of America, 116, 11480–11489. 10.1073/pnas.1819583116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, Y. , Liu, F. , Zou, X. , & Torbey, M. (2015). Comparison of unbiased estimation of neuronal number in the rat hippocampus with different staining methods. Journal of Neuroscience Methods, 254, 73–79. 10.1016/j.jneumeth.2015.07.022 [DOI] [PubMed] [Google Scholar]
- Ziegel, J. , Baddeley, A. , Dorph‐Petersen, K.‐A. , & Vedel Jensen, E. B. (2010). Systematic sampling with errors in sample locations. Biometrika, 97, 1–13. 10.1093/biomet/asp067 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.


