Abstract
Protein–ligand docking programs are indispensable tools for predicting the binding pose of a ligand to the receptor protein. In this paper, we introduce an efficient flexible docking method, gwovina, which is a variant of the Vina implementation using the grey wolf optimizer (GWO) and random walk for the global search, and the Dunbrack rotamer library for side‐chain sampling. The new method was validated for rigid and flexible‐receptor docking using four independent datasets. In rigid docking, gwovina showed comparable docking performance to Vina in terms of ligand pose RMSD, success rate, and affinity prediction. In flexible‐receptor docking, gwovina has improved success rate compared to Vina and AutoDockFR. It ran 2 to 7 times faster than Vina and 40 to 100 times faster than AutoDockFR. Therefore, gwovina can play a role in solving the complex flexible‐receptor docking cases and is suitable for virtual screening of compound libraries. gwovina is freely available at https://cbbio.cis.um.edu.mo/software/gwovina for testing.
Keywords: autodock vina, gwovina, nature‐inspired algorithm, protein–ligand docking, side‐chain flexibility, structure‐based drug design, swarm intelligence
Developed a first grey wolf optimizer based on autodock vina implementation (gwovina) for rigid and flexible‐receptor docking. Enhanced with random walk and rotamer library for side‐chain flexibility. Achieved significant speedup of 2‐ to 7‐fold compared to Vina, and 40‐ to 100‐fold compared to AutoDockFR. GWO has potential usefulness for robust searches in molecular conformational space
1. INTRODUCTION
Predicting the correct interaction between a small molecule and the target biomolecule is fundamental in drug discovery (Jorgensen, 2004; Taft, Da Silva, & Da Silva, 2008). Protein–ligand docking is a computational approach to calculate the three‐dimensional structure of a protein–ligand complex and measure the docking pose affinity. A number of protein–ligand docking programs have been developed in the past two decades (Chen, Liu, Huang, Hwang, & Ho, 2007; Jones, Willett, Glen, Leach, & Taylor, 1997; Korb, Stützle, & Exner, 2009; Liu et al., 2013; Morris et al., 1998; Ng, Fong, & Siu, 2015; Tai, Jusoh, & Siu, 2018; Tai, Lin, & Siu, 2016; Uehara, Fujimoto, & Tanaka, 2015). The design of these docking programs only considered ligand flexibility but was able to achieve certain degree of success in their results. Other studies (Bonvin, 2006; Carlson, 2002; Kokh & Wenzel, 2008; Lexa & Carlson, 2012; Teague, 2003; Yuriev, Holien, & Ramsland, 2015) took into account receptor flexibility and allowed adjustment of the protein conformation to accommodate more ligand motions at the binding site. However, modeling the receptor as flexible during docking increases the degree of freedom exponentially, which challenges the search ability of docking programs. Existing flexible‐receptor protein–ligand docking programs can be grouped into three categories: (a) soft‐docking methods that modify the potential energy function to allow a closer approach between ligand and receptor such that small side‐chain conformational changes is mimicked (Mizutani, Takamatsu, Ichinose, Nakamura, & Itai, 2006; Sherman, Day, Jacobson, Friesner, & Farid, 2006); (b) ensemble docking methods (Cavasotto, Kovacs, & Abagyan, 2005; Kazemi, Krüger, Sirockin, & Gohlke, 2009; Leis & Zacharias, 2011; Österberg, Morris, Sanner, Olson, & Goodsell, 2002; Wong, Kua, Zhang, Straatsma, & McCammon, 2005) that generate a set of receptor conformations as receptor candidates to simulate the protein conformational changes caused by binding the ligand into the pocket; and (c) induced‐fit docking methods (Davis & Baker, 2009; Meiler & Baker, 2006; Morris, Huey, et al., 2009; Ravindranath, Forli, Goodsell, Olson, & Sanner, 2015; Shin & Seok, 2012; Trott & Olson, 2010b; Verdonk, Cole, Hartshorn, Murray, & Taylor, 2003; Zavodszky, 2005; Zhao & Sanner, 2007), where both receptor and ligand conformations are dynamic during the docking process. The first category is similar to rigid docking but uses a softer potential function, thereby limiting the magnitude of the range of binding motions. The advantage of ensemble docking is that there is no requirement to modify the existing docking program. However, the main constraint of this approach is the capacity of the ensemble to represent conformational changes, which directly affects the success rate. The set of receptor conformations can be generated by using molecular dynamics (MD) (Wong et al., 2005), or normal‐mode analysis (NMA; Cavasotto et al., 2005), or by experimentation. Methods using consensus grid (Österberg et al., 2002) or other potential grids (Kazemi et al., 2009; Leis & Zacharias, 2011) to represent various conformations of receptor are also developed. Induced‐fit methods differ from these approaches, in that they consider both receptor and ligand flexibility simultaneously during docking. Considering a receptor to be fully flexible is extremely expensive (Davis & Baker, 2009); therefore, treating the receptor as partially flexible is a viable alternative (Meiler & Baker, 2006; Morris, Huey, et al., 2009; Ravindranath et al., 2015; Shin & Seok, 2012; Trott & Olson, 2010b; Verdonk et al., 2003; Zavodszky, 2005; Zhao & Sanner, 2007). These methods predefine some specific receptor side chains as flexible, allowing the conformation to change during the docking process. Although only parts of a receptor are flexible, the approach still faces two challenges: it is hard to reach the global energy minimum, and the number of false‐positive cases is increased. May and Zacharias (May & Zacharias, 2008) mentioned that the use of an approximate scoring function in current docking programs and the increase in the number of potential solutions for flexible‐receptor protein–ligand docking are the main cause for more false‐positive solutions. To overcome these difficulties, autodock4 (Morris, Ruth, et al., 2009) applied a genetic algorithm (GA), and autodockfr (Ravindranath et al., 2015) further improved the effectiveness of the GA and used a customized scoring function for flexible‐receptor protein–ligand docking. autodock vina (Trott & Olson, 2010a) used a Monte Carlo (MC) algorithm to improve the runtime performance and a new scoring function which differed from the AutoDock4 scoring function to improve pose prediction accuracy. Conformational space annealing (CSA) (Lee, Scheraga, & Rackovsky, 1997) was also implemented in GalaxyDock (Shin & Seok, 2012) as the global optimization method.
In this paper, we introduce a docking program called gwovina, which improves the search algorithm based on autodock vina to deal with docking problems involving higher molecular flexibility, such as flexible‐receptor protein–ligand docking. Like autodock vina, gwovina accepts a set of specific receptor side chains, which will be defined as flexible during docking. An improved Grey Wolf Optimizer (GWO) (Mirjalili, Mirjalili, & Lewis, 2014) was implemented as the global search algorithm replacing MC used in autodock vina. The powerful GWO search algorithm has shown that it is comparable to current popular metaheuristic algorithms such as particle swarm optimization (PSO), genetic algorithm (GA), and differential evolution (DE) because it maintains a good balance between convergence and divergence. The SCWRL4 backbone‐dependent rotamer library (Shapovalov & Dunbrack, 2011) is used to initialize the conformations of side chains before the search begins. We validated our program by testing the ability of rigid docking in comparison with autodock vina and three other open‐source docking programs: ledock (Zhang & Zhao, 2016), plant (Korb et al., 2009), and smina (Koes, Baumgartner, & Camacho, 2013). In addition, the flexible docking of gwovina was compared to autodock vina and AutoDockFR.
2. METHODS
2.1. Grey Wolf Optimizer (GWO)
GWO is a population‐based metaheuristic optimization technique that simulates the leadership hierarchy and hunting behavior of grey wolves in nature. Previous studies (Mirjalili et al., 2014; Lal, Barisal & Tripathy, 2016) showed that GWO can provide very competitive results in both speed and accuracy when compared to other well‐known optimization algorithms such as PSO and DE in various engineering problems. In this section, the mathematical model of the hierarchy and hunting behavior of a wolf pack is introduced.
2.2. Hierarchy
The hierarchy of a wolf pack from high to low can be described as having four levels, namely, alpha, beta, delta, and omega. The alpha wolf is the leader of the wolf pack that takes all the decisions based on the information passed on by the betas and deltas. The beta wolves are the helpers or subordinates of the alpha, and are the best candidates to be the next leader in the pack. The delta wolves are the lowest level of dominant wolves in the wolf pack. They help the alpha and beta wolves to collect the information found by the omegas. The omega wolves are the workers and scapegoats of a wolf pack; they undertake the hard work and suffer all the dangers to the wolf pack.
In GWO, the wolf pack is simulated as a list of search agents. Each search agent is a vector representing a position in the search space. The search problem is to find the global optimum solution, either a maximum or a minimum, depending on the domain problem. The search agent with the best fitness is considered as the leader (α). The top two fittest search agents following the best one are designated as the beta (β) and delta (δ), and the remaining populations are the omegas (ω).
2.3. Hunting behavior
In nature, the hunting behavior of a wolf pack consists sequentially of locating, encircling, and finally hunting down the prey. In the GWO algorithm, the position of each search agent is updated according to the position of the prey (assuming that we know it) and its own position at the current iteration:
| (1) |
| (2) |
where all vectors appearing in the formulas have the same number of dimensions as the search agent. is the position of the search agent i, and is the position of the promising solution, which will be discussed below. and are coefficient vectors calculated as follows:
| (3) |
| (4) |
where are random vectors; each of them contains a list of random values in [0, 1]. The elements in the coefficient vector are linearly decreased from 2.0 to 0.0 during the search process.
Based on Equations (1) to (4), the hunting behavior of the wolf pack is simulated by a population of randomly initialized search agents in space. The next position of a search agent is generated within the hypercubic volume in which the centroid of the hypercube is the position of the prey. Here, the trajectory of a search agent imitates the encircling action of a wolf. For example, in the two‐dimensional case, the next position of a search agent will be computed as a location in the square in which the centroid is the prey . The size of the square is defined by , as well as the coefficient vectors A and C that vary over time with some randomness. The larger the values of A and C, the bigger is the square. The value of A decides the moving direction of the search agent. When > 1, the agent leaves the prey and searches for another prey; otherwise, it moves toward the prey. As a linearly decreases over iterations, the population of search agents exhibit divergent movement from the prey at the beginning of the search, which is called exploration in optimization algorithms. After half of the search process (based on the initial value of a) is over, all search agents move toward the prey emulating the attack action, known as exploitation. A balance between these two search processes in the algorithm controls the divergence and convergence of the search.
As the actual position of the prey in (1) is not known in real problems, it has to be guessed. A reasonable guess would be to assume that the best wolves—alpha, beta and delta—know the approximate position of the prey, in which case the estimated prey positions are computed accordingly:
| (5) |
| (6) |
where , , and are the estimated prey positions based on the three best wolves, respectively. Finally, the next position of a wolf is taken as the average position of the three estimated prey positions.
| (7) |
2.4. Random search mechanism
In nature, a wolf may not receive information from the wolf pack due to some reasons such as getting lost. In this case, the wolf may have no idea where it should go. To emulate this behavior, we added a random search mechanism to the standard GWO algorithm. Here, a wolf has a small probability that it will perform a random walk instead of doing the normal position update of GWO:
| (8) |
where is a position vector same to and is a coefficient vector having values in the range of [0, 0.2]; so represents a small step of a random walk of the wolf.
In addition, the wolf should only accept the new move if it is safe to do so. To this end, a greedy strategy is included in the search; that is, the wolf accepts the move if and only if the next position is better than the current position.
2.5. gwovina
gwovina is a metaheuristic molecular docking program based on the implementation of autodock vina (named Vina here) (Trott & Olson, 2010b). In Vina, the search process includes global and local optimization, and scoring of the ligand–protein interaction, where MC is the global optimizer and the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is the local optimizer. The scoring function calculates the binding affinity of the predicted complex by summing up contributions from a number of distance‐dependent energetic terms. In order to improve the search ability, in gwovina, the more efficient search algorithm GWO and a random search were combined to replace the original global optimizer, while keeping the local search and scoring function unchanged. Thus, the original Vina scoring function was used as the fitness function in the GWO search and as the objective function in the random search. The search is run until a defined maximum number of iterations are reached. However, early stopping is appropriate when the search comes to a stagnant condition, for example, when an optimal solution is found. Here, an exponential increment of the step is applied based on the number of stagnant conditions that the search has experienced. When an improvement of the position is found, the step is incremented by 1. If the position found in this iteration is not better than the previous one, then the next increment will be doubled; the increment is reset to 1 after any improvements are found. Figure 1 shows the pseudocode of the gwovina global search algorithm.
Figure 1.

Pseudocode of the gwovina global search algorithm
2.6. Grey wolf representation in GWOVina
In Vina, the structure of an input protein receptor can be treated as either rigid or flexible during the docking process. To allow flexible side‐chain docking in GWOVina, a grey wolf was represented as a vector containing all modifiable variables defining the conformations of the ligand and receptor side chains. Figure 2 shows the vector representation of a wolf in GWOVina. The ligand part includes the translation in three dimensions, rotation in the quaternion form, and all rotatable torsion angles. The receptor part contains all rotatable χ angles of user‐defined flexible side chains. During the GWOVina docking process, both ligand and receptor conformational variables are evolved iteratively accordingly to the GWO algorithm (Equations (3), (4), (5), (6), (7)). Then, the three‐dimensional structures of the ligand and receptor are generated based on the updated values of the conformational variables. Finally, the docking score of the receptor–ligand structure is computed to measure the fitness of the generated pose.
Figure 2.

Vector representation of a grey wolf in gwovina
2.7. Parameters in gwovina
In the case not mentioned, the following parameters were used in a gwovina docking—the population size of the wolf pack was 12 and the maximum exponential increment of the step size was 100,000. Parameter analysis for the population size was carried out to determine this optimal value as will be discussed below.
2.8. Rotamer library
Rotamers of an amino acid are the different conformations of its side chain. GWOVina allows users to input a rotamer list for the side chain of a protein residue selected to be treated flexibly. It uses this list to generate the initial side‐chain conformation based on a Gaussian distribution of defined mean and standard deviation. In our experiments, we used the backbone‐dependent rotamer library developed by Shapovalov & Dunbrack (2011) called SCWRL4. SCWRL4 library provides a list of rotamers according to the backbone dihedral angles phi and psi of each amino acid. A probability is assigned to each rotamer representing how frequently that side‐chain conformation appears in their collected set of protein structures. Each χ angle in a rotamer is the mean value of the collection, and the deviation is also provided.
2.9. Dataset
Four datasets were used to evaluate the docking performance of GWOVina: Astex, CASF‐2013, SEQ17, and CDK2. The first two sets were used to measure the performance of the docking algorithm for rigid receptor protein–ligand docking and the last two sets for flexible side‐chain docking. Astex (Hartshorn et al., 2007) is a high‐quality and diverse dataset widely used to validate docking methods. Astex contains 85 well‐curated protein–ligand complexes with a resolution better than 2.5 Å. These complexes were selected from clusters of structures that are relevant to drug discovery; therefore, complexes containing non‐drug‐like ligands were excluded. PDBbind is a database of protein–ligand complexes containing their structural information and binding affinity. We used the core set of PDBbind version 2013 that is also named CASF‐2013, the benchmark for assessing scoring functions (Li et al., 2014). It contains 195 diverse protein–ligand complexes chosen from the clusters of around 13,000 complexes; the set includes strong, medium, and weak binders based on the binding affinity values. SEQ17 is a cross‐docking dataset containing 17 apo–holo pairs, used to test the previously developed flexible docking program AutoDockFR (Ravindranath et al., 2015). These pairs of complexes were special in that at least one side chain in the apo receptor has to be rotated away to allow correct docking of the ligand into its pocket as compared to the holo receptor counterpart. There should be no clashes involving the backbone atoms, and all cases should be successfully re‐docked using autodock vina (Ravindranath et al., 2015). The CDK2 dataset is a cross‐docking dataset built using the structures of cyclin‐dependent kinase 2. The dataset contains one high‐resolution apo structure (4EK3) and 52 holo structures with different ligands. The number of ligand‐interacting side chains of the superimposed apo structure to the 52 bound ligands in the holo structures ranges from 0 to 12.
All datasets were prepared according to the procedure described in our previous study (Tai et al., 2018), except for the Astex diverse set that was obtained from the study of rDock (Ruiz‐Carmona et al., 2014). The structures in the CASF‐2013 set were converted into PDBQT format using the python script prepare_protein4.py and prepare_ligand4.py provided in MGLTools (Morris, Huey, et al., 2009). Missing hydrogens were added (except for non‐polar hydrogens), which were merged to the neighboring carbon based on the united‐atom model scheme. Moreover, the input ligands of Astex and CASF‐2013 were randomized using the randomize_only function of autodock vina to prevent any biases toward the initial conformation in the search algorithm (Trott & Olson, 2010a)(Ravindranath et al., 2015). Both SEQ17 and CDK2 datasets were prepared by the authors of AutoDockFR (Ravindranath et al., 2015). The docking box was centered on the bound ligand for Astex, SEQ17, and CDK2 while the center of the docking box for CASF‐2013 structure was calculated from the residues given in the pocket of each complex. The box size of Astex is 22.5 Å in each side. For CASF‐2013, the box lengths are the largest distance between atoms in X‐, Y‐, and Z‐dimensions in the pocket. Both SEQ17 and CDK2 datasets used a larger box with a side length of 26.6 Å to accommodate movement of flexible side chains.
2.9.1. Docking performance analysis
In this study, performance of a docking program is mainly measured by the accuracy of the predicted ligand binding pose, which is based on the root‐mean‐square deviation (RMSD). RMSD computes the spatial difference between the predicted ligand pose and the respective experimental pose. For rigid receptor–ligand docking, an RMSD of <2 Å is considered successful docking, as conventionally used. In our experiments, 10 docking repeats were performed for each receptor–ligand pair. The average RMSD and success rate of the top‐1 poses collected from all docking repeats were reported. Furthermore, the best‐scoring pose, that is, the top‐1 pose that has the highest affinity among all docking repeats, whose RMSD and success rate were also reported. GWOVina uses the scoring function of Vina, and thus, its scoring performance should be similar to Vina. To confirm this, we extracted the docking scores of the best‐scoring poses by GWOVina and compared them with those predicted by Vina using the Pearson's correlation coefficient. With the CASF‐2013 dataset, we can evaluate the ranking power of a scoring function. It has two levels of measurement. The “high‐level” ranking power measures the number of cases where the three ligands of the same target are correctly ranked according to their binding affinities. The “low‐level” ranking power measures the number of cases where the highest binding ligand is ranked above the two lower‐affinity ligands.
For the flexible‐receptor cross‐docking experiments, the reference ligand of the apo structure was generated by superimposition of the apo structure onto the holo structure. As the position of the reference ligand was only approximate, the RMSD cutoff value was relaxed to 2.5 Å. Again, 10 docking repeats were performed and the best‐scoring pose among these runs was reported. Experiments were performed on a Dell XPS 8700 desktop with an Intel i7 Quad‐Core 3.6 GHz processor and 24 GB of memory running CentOS 6.2.
We compared gwovina to autodock vina and three other open‐source docking programs: ledock (Zhang & Zhao, 2016), plant (Korb et al., 2009), and smina (Koes et al., 2013). ledock is based on simulated annealing and evolutionary optimization. To dock with ledock, the ligand structure files in PDB were converted into mol2; then, the docking was run using standard parameters. plant uses ant colony optimization as the global search algorithm and Nelder–Mead simplex as the local search algorithm. To use plant, both protein and ligand structures were converted into mol2. We took the recommended parameters from the program manual, that is, scoring_function = chemplp, cluster_structures = 10, cluster_rmsd = 2.0; both search_speed values of 1 and 4 were tested. Finally, smina is a version of autodock vina with a modified scoring function to improve the sampling of low RMSD ligand poses. For running smina, the same docking parameters as those in autodock vina were used. In all cases, the same or similar docking box co‐ordinates as those used in GWOVina were configured to ensure fair comparison.
3. RESULTS
3.1. Parameter analysis
To validate the implementation of GWOVina, we performed ligand re‐docking of the Astex and CASF‐2013 datasets, in which the co‐crystallized ligand of a protein–ligand complex was firstly randomized for its position and conformation, and then re‐docked to the receptor; ten docking repeats were carried out. In order to understand how different numbers of wolves affect the docking performance, we tested the population of the wolf pack range from 4 to 40. Figure 3 shows the average score and RMSD of top‐1 poses from the docking repeats as a function of the number of wolves. Obviously, as the number of wolves increases, the average score of top‐1 poses reduces, which indicates that the higher affinity ligand pose could be found through extensive search with more wolves. Using 12–20 wolves, GWOVina can obtain an average score similar to Vina. The further increase of wolves to 30 and 40 enabled GWOVina to predict even higher affinity poses that were not predicted by Vina. However, due to the approximate scoring function, the higher affinity pose is not necessarily the closest to the native pose, as demonstrated in the RMSD plot. The running time of GWOVina is proportional to the number of wolves in the wolf pack. With 12 wolves, GWOVina ran using only half of the time of Vina; with 20 wolves, the average runtime values of GWOVina and Vina are the same.
Figure 3.
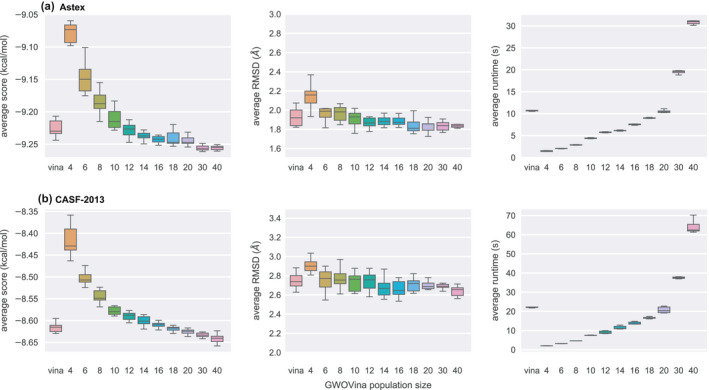
Population size effect on the average docking performance of gwovina in top‐1 pose
Figure 4 shows the docking performance of GWOVina based on the best‐scoring pose. As shown in the figure, the docking score, RMSD, and success rate varied within a narrow range. It turns out that the highest success rate was achieved using 12, 16, and 20 wolves for Astex and 12, 20 wolves for CASF‐2013. Interestingly, high success rate can also be obtained using 4 wolves; however, the accuracy of solutions obtained from different docking instances varies greatly, rendering them unreliable.
Figure 4.
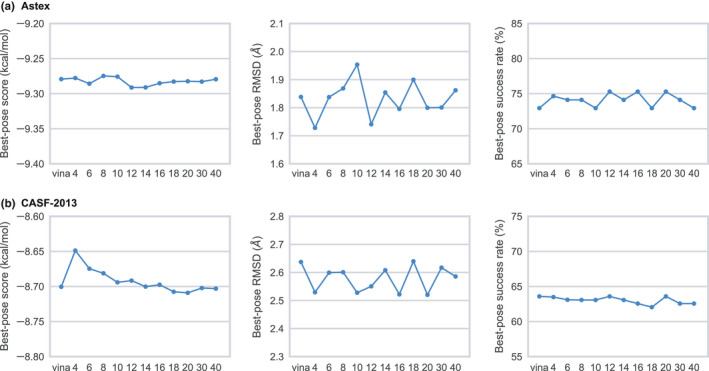
Population size effect of docking performance of gwovina in best‐scoring pose
3.2. Rigid docking
The docking performance of GWOVina using 12 wolves was compared with autodock vina and three other docking programs, ledock, plant, and smina in terms of their best‐scoring pose success rate, average success rate, and runtime. As shown in Table 1 for Astex dataset, plant (78%) has the highest best‐scoring pose success rate, followed by GWOVina (75%), smina (74%), Vina (73%), and ledock (61%). For CASF‐2013 in Table 2, the highest best‐scoring pose success rate was achieved by GWOVina and Vina (64%), and closely followed by smina and plant (62%), and finally ledock (36%). It is noteworthy that all Vina variants (GWOVina, Vina, and smina) have high average success rates indicating that they generate similarly high‐quality solutions between different docking instances, whereas plant and ledock generate more suboptimal solutions in different docking runs. Figure 5 shows the cumulative distribution of the best‐scoring pose RMSD for Astex and CASF‐2013. Except ledock, the docking performance of the three Vina variants and plant are close. At higher RMSD values (>4 Å), only there some differences between them can be seen. GWOVina is slightly better than vina and smina while plant is behind.
Table 1.
Rigid protein–ligand docking performance of autodock vina, gwovina, ledock, plant, and smina on the Astex dataset (85 complexes)
| Best‐scoring pose RMSD (Å) | Average RMSD (Å) | Best‐scoring pose success rate | Average success rate | Pearson's correlation coefficient, R | Runtime (s) | |
|---|---|---|---|---|---|---|
| autodock vina | 1.84 | 1.93 | 72.94 | 71.65 | 0.51 | 10.67 |
| smina | 1.84 | 1.93 | 74.12 | 72.24 | 0.51 | 12.81 |
| ledock | 2.74 | 2.77 | 61.18 | 55.65 | 0.28 | 7.53 |
| plant | 2.10 | 4.25 | 77.65 | 51.76 | 0.29 | 14.21 |
| GWOVina (this study) | 1.74 | 1.87 | 75.29 | 72.94 | 0.51 | 5.76 |
The best results are printed in bold.
Table 2.
Rigid protein–ligand docking performance of autodock vina, gwovina, ledock, plant, and smina on the CASF‐2013 dataset (195 complexes)
| Best‐scoring pose RMSD (Å) | Average RMSD (Å) | Best‐scoring pose success rate | Average success rate | Pearson's correlation coefficient, R | Runtime (s) | |
|---|---|---|---|---|---|---|
| autodock vina | 2.64 | 2.75 | 63.59 | 61.08 | 0.61 | 22.52 |
| smina | 2.66 | 2.73 | 62.05 | 61.08 | 0.59 | 29.67 |
| ledock | 4.07 | 4.37 | 36.41 | 29.44 | 0.32 | 10.45 |
| plant | 3.16 | 6.92 | 61.66 | 36.22 | 0.31 | 39.81 |
| gwovina (this study) | 2.55 | 2.73 | 63.59 | 62.10 | 0.60 | 9.05 |
The best results are printed in bold.
Figure 5.
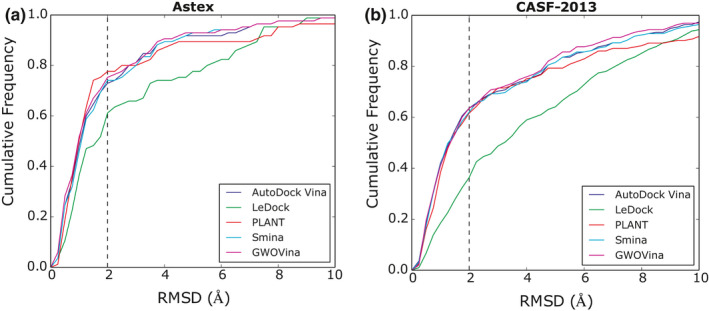
Cumulative distribution of the best‐scoring pose RMSD for Astex and CASF‐2013
We evaluated the scoring and ranking power of the five programs. The predicted binding affinities of best‐scoring pose by the Vina variants have correlation coefficients of 0.5 in Astex and 0.6 in CASF‐2013, which are significantly better than plant and ledock that are about 0.3 only. In consistent to the higher scoring power of Vina and GWOVina, the ranking power of them also showed superiority. In the CASF‐2013 benchmark, the high‐level/low‐level success rates of Vina are 49%/64% and GWOVina is 49%/63%, while ledock is 8%/21% and plant was 48%/62%. Therefore, results of the scoring and ranking power evaluation of GWOVina, in comparison with Vina and other docking programs, confirm that GWOVina has maintained the scoring ability of Vina.
Regarding time efficiency, GWOVina is the fastest among the five programs. It completed one protein–ligand docking with an average of 6 – 9 s, whereas it was 8 – 10 s for ledock, 11 – 23 s for Vina, and 13 – 30 s for smina. The slowest running program is plant which took 14 – 40 s to complete a docking. In short, the docking efficiency of the five programs follows this order: GWOVina > ledock > Vina > smina > plant.
3.3. Flexible‐receptor docking
For cross‐docking experiments, autodock vina, autodockfr, and gwovina were compared. The autodockfr program used in our experiments was provided in the mgltools 2.1.0 (available from website: http://adfr.scripps.edu/AutoDockFR/downloads.html). The parameter setting of autodockfr was used default (50 GAs, 20,000 evals) with random seed value 1 (option ‐S 1). For gwovina and vina, the same parameters were used as those in the rigid docking experiment. A docking solution was considered correct if the best‐RMSD pose that was returned in the list of docking solutions is 2.5 Å or below.
3.3.1. SEQ17
In this cross‐docking experiment, ligands from the holo structures were docked to the respective apo structures. The predicted docking pose of a ligand was compared with the crystallographic pose of the holo. As shown in Table 3, out of the 17 cases, gwovina predicted 12 cases successfully (71%), leading among three programs. autodock vina predicted 6 cases successful (35%), and autodockfr predicted 7 cases (41%). Interestingly, our results obtained for autodockfr, although using the same run parameters as stated in the study of Ravindranath et al. (Ravindranath et al., 2015), are different from what was reported in the literature, where they showed that autodockfr docked 12 cases successfully. Regarding time efficiency, gwovina ran faster than both autodock vina and autodockfr. gwovina used 21 min to complete the prediction of the whole dataset while autodock vina used 140 min and autodockfr used 657 min (note that 3PTE is not included here, as it failed to run).
Table 3.
Cross‐docking with flexible side chains for SEQ17 dataset
| Holo | Apo | Num. of Rot. bonds | Rank of lowest RMSD pose with RMSD < 2.5 Å | Runtime (min) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lig | Rec | Tot | vina | autodockfr | gwo vina | vina | autodockfr | gwo vina | ||
| 1IT8 | 1IQ8 | 1 | 11 | 12 | 1 | 1 | 1 | 0.47 | 11.14 | 0.13 |
| 1K4H | 1PUD | 5 | 19 | 24 | 1 | 1 | 1 | 2.29 | 35.62 | 0.47 |
| 1GX9 | 1BSQ | 5 | 27 | 32 | 10 (–) | 1 | 1 | 4.86 | 38.38 | 0.90 |
| 2H8H | 1FMK | 4 | 16 | 20 | – | 4 (1) | 12 | 3.01 | 35.09 | 0.79 |
| 3JRX | 2HJW | 6 | 30 | 36 | 1 | –(1) | 1 | 12.93 | 49.42 | 1.74 |
| 1Z6P | 2GPN | 7 | 24 | 31 | – | –(2) | 5 | 6.95 | 41.96 | 1.31 |
| 1AQ1 | 1HCL | 2 | 22 | 24 | – | 7 (2) | – | 4.01 | 36.85 | 0.59 |
| 1QKJ | 2BGT | 8 | 24 | 32 | – | –(3) | 4 | 4.63 | 34.45 | 0.79 |
| 1LNM | 1KXO | 3 | 27 | 30 | 3 (4) | 3 | 2 | 14.82 | 51.54 | 1.74 |
| 1IKG | 3PTE | 13 | 28 | 41 | 1 | – (14) | 1 | 17.75 | Fail to run | 2.29 |
| 1C1H | 1DOZ | 8 | 31 | 39 | – | – (14) | 12 | 19.91 | 43.39 | 2.72 |
| 3ERK | 1ERK | 4 | 20 | 24 | – | 4 (14) | 21 | 2.48 | 40.30 | 0.47 |
| 1RBP | 1BRQ | 6 | 18 | 24 | – (6) | – | 3 | 1.75 | 17.82 | 0.36 |
| 1BR5 | 1RTC | 7 | 16 | 23 | – | – | – | 2.48 | 37.30 | 0.36 |
| 1YXT | 1XQZ | 6 | 27 | 33 | – | – | – | 7.65 | 49.28 | 1.64 |
| 1ZG3 | 1ZHF | 4 | 18 | 22 | – | – | – | 2.04 | 39.72 | 0.42 |
| 2A9K | 2A78 | 16 | 36 | 52 | – | – | – | 31.98 | 94.62 | 4.22 |
| Total | 6 (6) | 7 (12) | 12 | 140.12 | 656.88 | 20.94 | ||||
| Percentage | 35% (35%) | 41% (71%) | 71% | |||||||
The docking that did not produce any poses with RMSD <= 2.5 Å is indicated by the symbol “–“.
The docking result reported in (Ravindranath et al., 2015) that is different from our own experimental result is given in brackets.
We see that the rank of the best‐RMSD pose is independent of the number of ligand or receptor rotatable bonds (see Figure S1). However, as shown in Figure 6, the docking runtime correlates to the number of rotatable bonds in all three programs. This is reasonable as the conformational space is proportional to the degree of freedom pertaining to the ligand and protein flexibility. The high failing rate in Vina to find correct poses in flexible‐receptor docking suggests that its search capability is insufficient. Here, we see that GWOVina has improved the search power of Vina by modifying its pose sampling strategy. As the same scoring function as Vina is used in GWOVina, the improvement of flexible docking can be attributed to the effectiveness of the search method.
Figure 6.
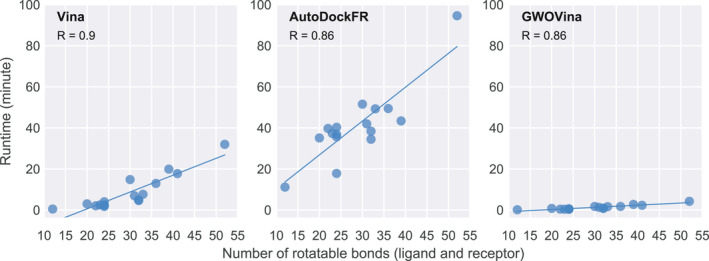
Correlation of runtime and the number of rotatable bonds
There were 4 cases (1RTC, 1XQZ, 1ZHF, 2A78) that could not be docked successfully by any programs, so we performed the holo structure re‐docking using autodock vina to check whether the unsuccessful cases were due to inaccuracies in scoring or failure in searching. Table 4 shows our rigid re‐docking result of holo structure in the SEQ17 dataset by autodock vina. In our result, all predicted poses scored better than their experimental poses. Only in two cases, 1GX9 and 1ZG3, the best‐scoring pose was not the lowest RMSD pose to the crystal structure. The first predicted pose with RMSD < 2.0 Å of these was ranked as the 3rd and 5th, respectively. These indicated that the scoring of autodock vina is reasonably good in docking pose ranking in majority of the cases.
Table 4.
Holo structure rigid re‐docking result of SEQ17 dataset by vina
| Holo | Apo | Score of crystal pose in holo (kcal/mol) | Score of best‐scoring pose in re‐docking (kcal/mol) | RMSD of best‐scoring pose | Rank of lowest RMSD pose with RMSD < 2.0 |
|---|---|---|---|---|---|
| 1IT8 | 1IQ8 | −8.02 | −8.6 | 0.30 | 1 |
| 1K4H | 1PUD | −6.50 | −8.0 | 1.06 | 1 |
| 1GX9 | 1BSQ | −7.00 | −8.7 | 3.36 | 3 |
| 2H8H | 1FMK | −10.05 | −11.3 | 1.36 | 1 |
| 3JRX | 2HJW | −12.96 | −13.1 | 0.89 | 1 |
| 1Z6P | 2GPN | −8.56 | −10.5 | 0.59 | 1 |
| 1AQ1 | 1HCL | −13.26 | −13.4 | 0.31 | 1 |
| 1QKJ | 2BGT | −8.03 | −9.0 | 0.89 | 1 |
| 1LNM | 1KXO | −12.48 | −13 | 0.41 | 1 |
| 1IKG | 3PTE | −7.20 | −8.1 | 0.96 | 1 |
| 1C1H | 1DOZ | −12.81 | −13.6 | 0.60 | 1 |
| 3ERK | 1ERK | −8.04 | −8.4 | 1.41 | 1 |
| 1RBP | 1BRQ | −8.84 | −9.8 | 0.69 | 1 |
| 1BR5 | 1RTC | −6.23 | −7.7 | 1.62 | 1 |
| 1YXT | 1XQZ | −2.94 | −9.1 | 1.27 | 1 |
| 1ZG3 | 1ZHF | −6.06 | −7.2 | 5.56 | 5 |
| 2A9K | 2A78 | −9.80 | −11.2 | 1.02 | 1 |
| Total | 17 (100%) |
To figure out the reason why there is a large docking score difference of 6 kcal/mol between the holo co‐crystallized ligand of 1YXT (−2.94 kcal/mol) and the re‐docked ligand (−9.1 kcal/mol), we examined their 3D structures after superimposition. As shown in Figure 7a, we found that there exists a close interaction of 1.6 Å between the oxygen atom of ASP186 and the oxygen atom of the ligand in the holo complex. This unusual short‐distance interaction is considered as a clash in the wwPDB X‐ray Structure Validation report. Therefore, the Vina scoring function yielded a high‐energy value for this ligand pose, and in the cross‐docking experiment of the apo structure 1XQZ, the pose with this interaction was not accepted, resulting in unsuccessful prediction. The failure of cross‐docking the ligand into 1RTC and 2A78 (Figure 7b) was caused by the backbone difference between the apo and holo structures. The TYR80 of 1RTC lies on the pocket where it clashes with the ligand in the holo structure. The Phi and Psi angles of TYR80 in the apo structure are −89° and 150°, while the two dihedral angles in the holo structure are −65° and 137°, respectively. These large differences in the backbone conformation prevent the side chain of TYR80 in the apo from reverting to the holo position as backbone flexibility was not accommodated by the docking programs. Same situation was also found in the holo–apo pair 2A9K and 2A78 (Figure 7c). In this case, the Phi and Psi angle of the residue PHE183 in 2A9K were (−87°, −11°) whereas in 2A78 they were (−106°, −30°).
Figure 7.
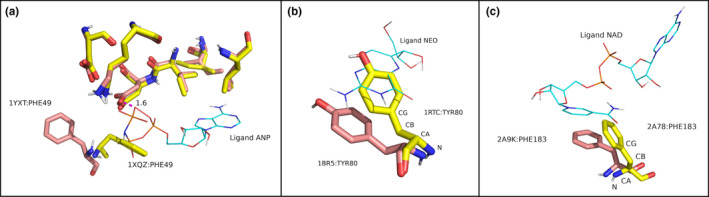
Failure cases in flexible‐receptor docking. The holo structure is represented as sticks and colored pink, the apo yellow, and the co‐crystallized ligand of the holo is drawn as lines. (a) The co‐crystallized ligand of the holo complex (1YXT) has too short distance to the pocket atoms of the protein resulting in bad interaction energy. (b) Shifted backbone positions between holo (1BR5) and apo (1RTC), and C) holo (2A9K) and apo (2A78)
3.3.2. CDK2
Figure 8 shows the CDK2 docking success rates of the best‐scoring pose and top 10 best poses as a function of the level of receptor flexibility; the complete result can be found in Table S1. The number of flexible side chains considered in the docking (in the figure from left to right) was 0, 4, 10, and 12, corresponding to 0, 10, 22, and 27 flexible χ angles, respectively. The results show that for the docking experiment with 0 and 4 flexible side chains, autodockfr predicted with the highest success rates in both the best‐scoring (42.3%) and top‐10 (76.9%) poses prediction. Remarkably, gwovina outperforms autodockfr when more side chains were treated as flexible in the docking. It achieved the best‐scoring success rate of 42.3% with 10 flexible side chains and the top‐10 success rate of 82.7% with both 10 and 12 flexible side chains. The higher success rate of autodockfr than GWOVina when fewer number of flexible side chains were allowed suggests that the scoring function of autodockfr might be able to accommodate finer conformational changes of the ligands, so that near‐native poses can still be found in the binding site with more restricted protein side‐chain movement. Notably, all docking programs are effective in finding the correct ligand pose when more side chains are treated with flexibility. This suggests that the level of flexibility in this experiment, that is, 12 side chains or 27 flexible χ angles, is tractable by current docking programs.
Figure 8.
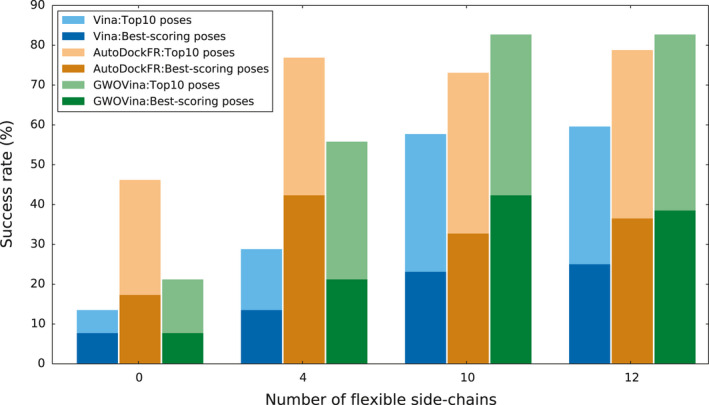
CDK2 cross‐docking success rate of the best‐scoring pose and top 10 best poses as a function of the level of receptor flexibility
Figure 9 shows the total runtime of the CDK2 cross‐docking experiment by the three programs; the complete result can be found in Table S2. All programs required longer runtime to complete the search when the number of flexible side chains is increased. Among the three programs, GWOVina has the least runtime. Specifically, GWOVina costs 3–58 min to complete the docking of the whole dataset, depending on the number of flexible side chain selected. It is about 2 to 6 times faster than autodock vina and 40 to 100 times faster than autodockfr.
Figure 9.
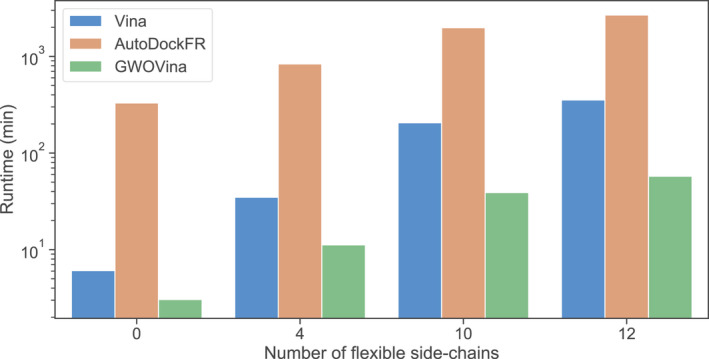
Runtime of CDK2 cross‐docking as a function of the number of flexible side chains
4. CONCLUSIONS
In this paper, we present a new swarm intelligence docking method, GWOVina, which is based on the preying behavior of grey wolves (Mirjalili et al., 2014). Using autodock vina as the basis, we designed and implemented the GWO algorithm with random walk, in place of the MC global optimizer used in vina. We tested GWOVina with four independent datasets and compared their performances to vina, ledock, plants, and smina in rigid receptor docking and to vina and autodockfr in flexible‐receptor docking. The results showed that our method improves the exploration capability of the docking algorithm leading to significant speedup. In the rigid docking experiments, gwovina achieved 2‐fold improved speed with comparable docking accuracy to vina. By adjusting the population size parameter of gwovina, the ligand conformational search becomes more comprehensive, so the chance of hitting the highest affinity pose is also increased.
In the flexible docking experiments, compared with vina, the docking performance of gwovina has been greatly improved. Instead of randomly rotating the flexible side chains, we used a rotamer library to help generate promising side‐chain conformations according to the background frequency from known experimental structures. As a consequence, GWOVina has twice the success rate of Vina in flexible‐receptor docking as demonstrated in the SEQ17 cross‐docking experiment, and 1.2 to 2 times in the CDK2 experiment. Comparing with the flexible docking tool autodockfr, gwovina also showed advantages. Not only did it achieve the same level of success rate in the best‐scoring pose prediction of SEQ17 and CDK2, but it also outperforms in the top‐10 poses prediction, yielding the highest success rate of 83% with 12 flexible side chains. As in rigid docking, the most remarkable improvement of gwovina is its shortened running time. Docking with flexible side chains is notoriously slow; however, the effective search strategy in GWOVina has successfully accelerated the docking speed. Compared with vina, the speed is increased by 2 to 7 times, and compared to autodockfr, the speed is increased by 40 to 100 times. Overall, gwovina can be instrumental in solving more complex flexible‐receptor docking cases in drug discovery projects, or as a virtual screening tool to complete the screening task in short time with good accuracy.
Despite many years of effort, flexible‐receptor docking is still challenging. The limitations of existing docking programs are their inability to handle conformational search in high‐dimensional space and the approximate scoring function used. In this work, we put our focus in the search algorithm improvement and treatment of side‐chain flexibility, and have showed some successes. Nevertheless, the ultimate goal of flexible docking is full protein flexibility which includes both the side chain and backbone movements. Our analysis of the flexible docking failures in SEQ17 shows that in some cases, a small degree of background flexibility may be required to solve the docking problem.
CONFLICT OF INTEREST
None.
AUTHOR CONTRIBUTIONS
Shirley W.I. Siu involved in conceptualization, methodology, validation, writing—review and editing, and funding acquisition. Kin Meng Wong involved in methodology, software, investigation, validation, and writing—original draft preparation. Hio Kuan Tai: involved in methodology, investigation, and validation.
Supporting information
Supplementary Material
ACKNOWLEDGMENTS
This work is supported by University of Macau [grant no. MYRG2017‐00146‐FST]. The authors thank the support of the Faculty of Science and Technology and the Information and Communication Technology Office of University of Macau for the computing facilities.
Wong KM, Tai HK, Siu SWI. GWOVina: A grey wolf optimization approach to rigid and flexible receptor docking. Chem Biol Drug Des. 2021;97:97–110. 10.1111/cbdd.13764
DATA AVAILABILITY STATEMENT
The source code of GWOVina is available at https://cbbio.cis.um.edu.mo/software/gwovina for public use. The docking datasets that support the findings of this study are available in PDBbind at http://www.pdbbind.org.cn/ and PDB database at https://www.rcsb.org/; flexible docking datasets are available in autodockfr at http://adfr.scripps.edu/AutoDockFR/adfr.html.
REFERENCES
- Bonvin, A. M. (2006). Flexible protein‐protein docking. Current Opinion in Structural Biology, 16(2), 194–200. 10.1016/j.sbi.2006.02.002 [DOI] [PubMed] [Google Scholar]
- Carlson, H. A. (2002). Protein flexibility and drug design: How to hit a moving target. Current Opinion in Chemical Biology, 6(4), 447–452. 10.1016/S1367-5931(02)00341-1 [DOI] [PubMed] [Google Scholar]
- Cavasotto, C. N. , Kovacs, J. A. , & Abagyan, R. A. (2005). Representing receptor flexibility in ligand docking through relevant normal modes. Journal of the American Chemical Society, 127(26), 9632–9640. 10.1021/ja042260c [DOI] [PubMed] [Google Scholar]
- Chen, H. M. , Liu, B. F. , Huang, H. L. , Hwang, S. F. , & Ho, S. Y. (2007). SODOCK: Swarm optimization for highly flexible protein‐ligand docking. Journal of Computational Chemistry, 28(2), 612–623. 10.1002/jcc.20542 [DOI] [PubMed] [Google Scholar]
- Davis, I. W. , & Baker, D. (2009). RosettaLigand docking with full ligand and receptor flexibility. Journal of Molecular Biology, 385(2), 381–392. 10.1016/j.jmb.2008.11.010 [DOI] [PubMed] [Google Scholar]
- Hartshorn, M. J. , Verdonk, M. L. , Chessari, G. , Brewerton, S. C. , Mooij, W. T. M. , Mortenson, P. N. , & Murray, C. W. (2007). Diverse, high‐quality test set for the validation of protein‐ligand docking performance. Journal of Medicinal Chemistry, 50(4), 726–741. 10.1021/jm061277y [DOI] [PubMed] [Google Scholar]
- Jones, G. , Willett, P. , Glen, R. C. , Leach, A. R. , & Taylor, R. (1997). Development and validation of a genetic algorithm for flexible docking. Journal of Molecular Biology, 267(3), 727–748. 10.1006/jmbi.1996.0897 [DOI] [PubMed] [Google Scholar]
- Jorgensen, W. L. (2004). The many roles of computation in drug discovery. Science, 303(5665), 1813–1818. 10.1126/science.1096361 [DOI] [PubMed] [Google Scholar]
- Kazemi, S. , Krüger, D. M. , Sirockin, F. , & Gohlke, H. (2009). Elastic potential grids: Accurate and efficient representation of intermolecular interactions for fully flexible docking. ChemMedChem, 4(8), 1264–1268. 10.1002/cmdc.200900146 [DOI] [PubMed] [Google Scholar]
- Koes, D. R. , Baumgartner, M. P. , & Camacho, C. J. (2013). Lessons learned in empirical scoring with Smina from the CSAR 2011 benchmarking exercise. Journal of Chemical Information and Modeling, 53(8), 1893–1904. 10.1021/ci300604z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kokh, D. B. , & Wenzel, W. (2008). Flexible side chain models improve enrichment rates in in silico screening. Journal of Medicinal Chemistry, 51(19), 5919–5931. 10.1021/jm800217k [DOI] [PubMed] [Google Scholar]
- Korb, O. , Stützle, T. , & Exner, T. E. (2009). Empirical scoring functions for advanced Protein‐Ligand docking with PLANTS. Journal of Chemical Information and Modeling, 49(1), 84–96. 10.1021/ci800298z [DOI] [PubMed] [Google Scholar]
- Lal, D. K. , Barisal, A. K. , & Tripathy, M. (2016). Grey Wolf optimizer algorithm based fuzzy PID controller for AGC of multi‐area power system with TCPS. Procedia Computer Science, 92, 99–105. 10.1016/j.procs.2016.07.329 [DOI] [Google Scholar]
- Lee, J. , Scheraga, H. A. , & Rackovsky, S. (1997). New optimization method for conformational energy calculations on polypeptides: Conformational space annealing. Journal of Computational Chemistry, 18(9), 1222–1232. [DOI] [Google Scholar]
- Leis, S. , & Zacharias, M. (2011). Efficient inclusion of receptor flexibility in grid‐based protein‐ligand docking. Journal of Computational Chemistry, 32(16), 3433–3439. 10.1002/jcc.21923 [DOI] [PubMed] [Google Scholar]
- Lexa, K. W. , & Carlson, H. A. (2012). Protein flexibility in docking and surface mapping. Quarterly Reviews of Biophysics, 45(3), 301–343. 10.1017/S0033583512000066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, Y. , Liu, Z. , Li, J. , Han, L. , Liu, J. , Zhao, Z. , & Wang, R. (2014). Comparative assessment of scoring functions on an updated benchmark: 1. compilation of the test set. Journal of Chemical Information and Modeling, 54(6), 1700–1716. 10.1021/ci500080q [DOI] [PubMed] [Google Scholar]
- Liu, Y. , Zhao, L. , Li, W. , Zhao, D. , Song, M. , & Yang, Y. (2013). FIPSDock: A new molecular docking technique driven by fully informed swarm optimization algorithm. Journal of Computational Chemistry, 34(1), 67–75. 10.1002/jcc.23108 [DOI] [PubMed] [Google Scholar]
- May, A. , & Zacharias, M. (2008). Protein‐ligand docking accounting for receptor side chain and global flexibility in normal modes: Evaluation on kinase inhibitor cross docking. Journal of Medicinal Chemistry, 51(12), 3499–3506. 10.1021/jm800071v [DOI] [PubMed] [Google Scholar]
- Meiler, J. , & Baker, D. (2006). ROSETTALIGAND: Protein‐small molecule docking with full side‐chain flexibility. Proteins: Structure, Function and Genetics, 65(3), 538–548. 10.1002/prot.21086 [DOI] [PubMed] [Google Scholar]
- Mirjalili, S. , Mirjalili, S. M. , & Lewis, A. (2014). Grey Wolf optimizer. Advances in Engineering Software, 69, 46–61. 10.1016/j.advengsoft.2013.12.007 [DOI] [Google Scholar]
- Mizutani, M. Y. , Takamatsu, Y. , Ichinose, T. , Nakamura, K. , & Itai, A. (2006). Effective handling of induced‐fit motion in flexible docking. Proteins: Structure, Function and Genetics, 63(4), 878–891. 10.1002/prot.20931 [DOI] [PubMed] [Google Scholar]
- Morris, G. M. , Goodsell, D. S. , Halliday, R. S. , Huey, R. , Hart, W. E. , Belew, R. K. , & Olson, A. J. (1998). Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. Journal of Computational Chemistry, 19(14), 1639–1662. [DOI] [Google Scholar]
- Morris, G. M. , Huey, R. , Lindstrom, W. , Sanner, M. F. , Belew, R. K. , Goodsell, D. S. , & Olson, A. J. (2009). AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. Journal of Computational Chemistry, 30(16), 2785–2791. 10.1002/jcc.21256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris, G. M. , Ruth, H. , Lindstrom, W. , Sanner, M. F. , Belew, R. K. , Goodsell, D. S. , & Olson, A. J. (2009). AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. Journal of Computational Chemistry, 30(16), 2785–2791. 10.1002/jcc.21256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng, M. C. K. , Fong, S. , & Siu, S. W. I. (2015). PSOVina: The hybrid particle swarm optimization algorithm for protein‐ligand docking. Journal of Bioinformatics and Computational Biology, 13(3), 1541007 10.1142/S0219720015410073 [DOI] [PubMed] [Google Scholar]
- Österberg, F. , Morris, G. M. , Sanner, M. F. , Olson, A. J. , & Goodsell, D. S. (2002). Automated docking to multiple target structures: Incorporation of protein mobility and structural water heterogeneity in autodock. Proteins: Structure, Function and Genetics, 46(1), 34–40. 10.1002/prot.10028 [DOI] [PubMed] [Google Scholar]
- Ravindranath, P. A. , Forli, S. , Goodsell, D. S. , Olson, A. J. , & Sanner, M. F. (2015). AutoDockFR: Advances in Protein‐Ligand Docking with Explicitly Specified Binding Site Flexibility. PLoS Computational Biology, 11(12), e1004586 10.1371/journal.pcbi.1004586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruiz‐Carmona, S. , Alvarez‐Garcia, D. , Foloppe, N. , Garmendia‐Doval, A. B. , Juhos, S. , Schmidtke, P. , … Morley, S. D. (2014). rDock: A Fast, Versatile and Open Source Program for Docking Ligands to Proteins and Nucleic Acids. PLoS Computational Biology, 10(4), e1003571 10.1371/journal.pcbi.1003571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapovalov, M. V. , & Dunbrack, R. L. (2011). A smoothed backbone‐dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure, 19(6), 844–858. 10.1016/j.str.2011.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman, W. , Day, T. , Jacobson, M. P. , Friesner, R. A. , & Farid, R. (2006). Novel procedure for modeling ligand/receptor induced fit effects. Journal of Medicinal Chemistry, 49(2), 534–553. 10.1021/jm050540c [DOI] [PubMed] [Google Scholar]
- Shin, W. H. , & Seok, C. (2012). GalaxyDock: Protein‐ligand docking with flexible protein side‐chains. Journal of Chemical Information and Modeling, 52(12), 3225–3232. 10.1021/ci300342z [DOI] [PubMed] [Google Scholar]
- Taft, C. A. , Da Silva, V. B. , & Da Silva, C. H. T. D. P. (2008). Current topics in computer‐aided drug design. Journal of Pharmaceutical Sciences, 97(3), 1089–1098. 10.1002/jps.21293 [DOI] [PubMed] [Google Scholar]
- Tai, H. K. , Jusoh, S. A. , & Siu, S. W. I. (2018). Chaos‐embedded particle swarm optimization approach for protein‐ligand docking and virtual screening. Journal of Cheminformatics, 10(1), 1–13. 10.1186/s13321-018-0320-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tai, H. K. , Lin, H. , & Siu, S. W. I. (2016). Improving the efficiency of PSOVina for protein‐ligand docking by two‐stage local search. 2016 IEEE Congress on Evolutionary Computation. CEC, 2016, 770–777. 10.1109/CEC.2016.7743869 [DOI] [Google Scholar]
- Teague, S. J. (2003). Implications of protein flexibility for drug discovery. Nature Reviews Drug Discovery, 2(7), 527–541. 10.1038/nrd1129 [DOI] [PubMed] [Google Scholar]
- Trott, O. , & Olson, A. J. (2010a). AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. Journal of Computational Chemistry, 31(2), 455–461. 10.1002/jcc.21334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trott, O. , & Olson, A. J. (2010b). Software news and update AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. Journal of Computational Chemistry, 31, 455–461. 10.1002/jcc.21334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uehara, S. , Fujimoto, K. J. , & Tanaka, S. (2015). Protein‐ligand docking using fitness learning‐based artificial bee colony with proximity stimuli. Physical Chemistry Chemical Physics, 17(25), 16412–16417. 10.1039/c5cp01394a [DOI] [PubMed] [Google Scholar]
- Verdonk, M. L. , Cole, J. C. , Hartshorn, M. J. , Murray, C. W. , & Taylor, R. D. (2003). Improved protein‐ligand docking using GOLD. Proteins: Structure, Function and Genetics, 52(4), 609–623. 10.1002/prot.10465 [DOI] [PubMed] [Google Scholar]
- Wong, C. F. , Kua, J. , Zhang, Y. , Straatsma, T. P. , & McCammon, J. A. (2005). Molecular docking of balanol to dynamics snapshots of protein kinase A. Proteins: Structure, Function and Genetics, 61(4), 850–858. 10.1002/prot.20688 [DOI] [PubMed] [Google Scholar]
- Yuriev, E. , Holien, J. , & Ramsland, P. A. (2015). Improvements, trends, and new ideas in molecular docking: 2012–2013 in review. Journal of Molecular Recognition, 28(10), 581–604. 10.1002/jmr.2471 [DOI] [PubMed] [Google Scholar]
- Zavodszky, M. I. (2005). Side‐chain flexibility in protein‐ligand binding: The minimal rotation hypothesis. Protein Science, 14(4), 1104–1114. 10.1110/ps.041153605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, N. , & Zhao, H. (2016). Enriching screening libraries with bioactive fragment space. Bioorganic & Medicinal Chemistry Letters, 26(15), 3594–3597. 10.1016/j.bmcl.2016.06.013 [DOI] [PubMed] [Google Scholar]
- Zhao, Y. , & Sanner, M. F. (2007). FLIPDock: Docking flexible ligands into flexible receptors. Proteins: Structure, Function and Genetics, 68(3), 726–737. 10.1002/prot.21423 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
The source code of GWOVina is available at https://cbbio.cis.um.edu.mo/software/gwovina for public use. The docking datasets that support the findings of this study are available in PDBbind at http://www.pdbbind.org.cn/ and PDB database at https://www.rcsb.org/; flexible docking datasets are available in autodockfr at http://adfr.scripps.edu/AutoDockFR/adfr.html.


