Assessment of Planetary Boundary Layer parametrizations and urban heat island comparison: Impacts and implications for tracer transport

Abstract

Accurate simulation of planetary boundary layer height (PBLH) is key to greenhouse gas emission estimation, air quality prediction and weather forecasting. This manuscript describes an extensive performance assessment of several Weather Research and Forecasting (WRF) model configurations where novel observations from ceilometers, surface stations and a flux tower were used to study their ability to reproduce planetary boundary layer heights (PBLH) and the impact that the urban heat island (UHI) has on the modeled PBLHs in the greater Washington, D.C. area. In addition, CO₂ measurements at two urban towers were compared to tracer transport simulations. The ensemble of models used 4 PBL parameterizations, 2 sources of initial and boundary conditions and 1 configuration including the building energy parameterization (BEP) urban canopy model. Results have shown low biases over the whole domain and period for wind speed, wind direction and temperature with no drastic differences between meteorological drivers. We find that PBLH errors are mostly positively correlated with sensible heat flux errors, and that modeled positive UHI intensities are associated with deeper modeled PBLs over the urban areas. In addition, we find that modeled PBLHs are typically biased low during nighttime for most of the configurations with the exception of those using the MYNN parametrization and that these biases directly translate to tracer biases. Overall, the configurations using MYNN scheme performed the best, reproducing the PBLH and CO₂ molar fractions reasonably well during all hours, thus opening the door to future nighttime inverse modeling.

1. Introduction

Turbulent mixing drives the transport of mass, heat and momentum in the planetary boundary layer (PBL) (Stull (1988)) and, therefore, numerical weather prediction (NWP) models need to include PBL parametrizations to ensure that this phenomenon is properly represented. In addition, atmospheric transport models rely strongly on the proper representation of the PBL by the NWP model driving them to properly account for the mixing of pollutants. These transport models are fundamental tools for air quality prediction as well as for the inference of trace gas (pollutant or greenhouse gas) sources using top-down approaches (Nisbet and Weiss (2010)).

Many different PBL schemes are available; they differ from each other by the vertical mixing formulation (local vs. non-local) and the closure order. Local schemes only consider adjacent vertical levels in the fluxes computations, while nonlocal schemes take into account multiple levels, often from the surface up to the estimated PBL height, in representing the fluxes through the PBL. In addition, PBL schemes are coupled to the surface layer parametrizations, that generally are not interchangeable, and strongly influence the near surface variables and PBL mean properties, (Shin and Hong (2011)).

Recent studies have looked at different PBL schemes with the focus of atmospheric transport modeling in mind. For example, Angevine et al. (2012) and Feng et al. (2016) studied the performance of different PBL schemes in the Weather Research and Forecasting (WRF) model along with other physics options for the CalNex-2010 campaign (late spring, 2010). Kretschmer et al. (2012, 2014) compared the impact of two PBL schemes on CO₂ transport over Europe and evaluated them with radiosondes during late summer. Sarmiento et al. (2017) studied the behavior of PBL schemes and their interactions with Land Surface models and the land use representation over Indianapolis (Indiana, USA) for a month in late winter and a month in summer. Lian et al. (2018) studied WRF PBL schemes and their impacts on CO₂ transport for a month in winter over Paris (France) area. Díaz-Isaac et al. (2018) did a comparison of multiple WRF physics schemes for a summer month in the Midwest of the United states. Over the Washington DC - Baltimore (Maryland, USA) area, WRF PBL schemes were also evaluated as part of the DISCOVER-AQ campaign (Hegarty et al. (2018)) during July 2011. These studies demonstrate that there is much interest in finding the best performing configuration for WRF so that the errors introduced in trace gas transport are minimized. However, the results obtained are somewhat dependent on the region and period studied, the observations used for verification, the methods applied to derive PBLH and the WRF version.

PBLH observations are not very common. Their availability is sparse, in space and time, and rely strongly on operational radiosondes that sample the PBL only twice a day. This lack of measurement data limits understanding of PBL dynamics and validation studies, and therefore parameterization development. The introduction of new measurement techniques for mixing height, such as those based on ceilometers and particle Lidars, has the potential to be a game changer for model validation due to the greater temporal coverage and resolution that they provide. In the last few years, Lidar observations and ceilometers have been used to evaluate WRF simulations (Ware et al. (2016); Feng et al. (2016); Hegarty et al. (2018)).

Impervious urban surfaces are characterized by lower albedo, lower specific heat capacity, higher thermal conductivity and much smaller rainfall retention than rural surfaces (Oke (1982)). These properties cause higher Bowen ratios (larger sensible heat fluxes and lower latent heat fluxes) and surface temperatures in the urban landscape and, therefore, induce perturbations in the wind, air temperature, water vapor content as well as in the boundary layer height, (Angevine et al. (2003); Zhang et al. (2009, 2011)). Understanding how the meteorological models reproduce this feature is also essential for atmospheric transport.

The WRF model undergoes continuous development with two releases per year as new measurements and techniques become available, therefore new comparisons and testing are needed. In addition, it is clear from previous studies that there is no single configuration that works best under all circumstances and validation for specific areas and periods are required.

In this work, we intend to better understand the performance of eight configurations of WRF over the Washington DC/Baltimore area during winter, to uncover similarities and differences in PBL parametrizations regarding PBLH and urban heat island related variables and the impacts on tracer transport with the aim of identifying the best performing configuration for the purpose of greenhouse gas (GHG) inverse modeling in the North East Corridor - Baltimore / Washington DC test bed (Lopez-Coto et al. (2017a)). In Section 2, the eight model configurations as well as the surface stations, CO₂ measurements,flux tower and ceilometers used for comparison are described. In Section 3, the model performance is presented as well as an analysis between the heat island produced by each configurations and how it impacts on PBLH. In Section 4, implications of our findings on tracer transport and inverse modeling are discussed. Last, in Section 5, the main conclusions obtained are highlighted.

2. Methods

a. Observational data

1). Surface stations

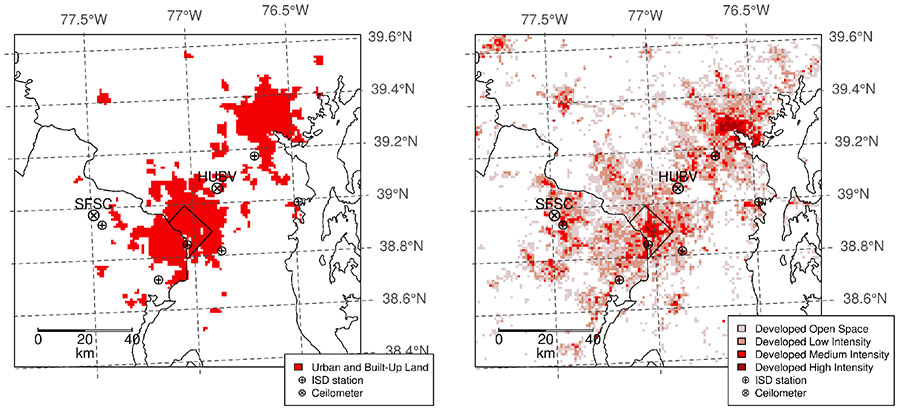
The Integrated Surface Database (ISD) consists of global hourly and synoptic observations from more than 100 original data sources that collectively archived hundreds of meteorological variables. It is compiled by the NOAAs National Climatic Data Center (NCDC) and accessible through the web (https://www.ncdc.noaa.gov/isd). The primary data sources include the Automated Surface Observing System (ASOS), Automated Weather Observing System (AWOS), Synoptic, Airways, METAR, Coastal Marine (CMAN), Buoy, and various others, from both military and civilian stations including both automated and manual observations (Smith et al. (2011)). More than 14,000 active stations worldwide are updated daily in the database. As described in Smith et al. (2011), ISD contains 54 quality control (QC) algorithms, which serve to process each data observation through a series of validity checks, extreme value checks, internal (within observation) consistency checks, and external (versus another observation for the same station) continuity checks. For the month of February 2016 and the domain of interest, six ISD surface stations had data with the highest level of quality control flag, Figure 1.

Fig. 1.

Innermost computational domain (1 km) showing the urban land use categories employed in the model: left, USGS and right, NLCD for the area of interest (Washington DC / Baltimore region) along with the location of the ISD surface stations and two ceilometers used for verification.

2). CO₂ measurements

Three towers equipped with Cavity Ring Down Spectrometers are used to measure CO₂. The sites, NDC, HAL and BUC are located near Washington, D.C., Baltimore, M.D., and a more background area in the Delmarva peninsula about 100 km away from the urban centers respectively. Further details about the stations, calibration and quality control can be found in Karion et al. (2020).

CO₂ enhancements were computed subtracting from each hourly observation, the measurements at the background tower (BUC) similarly to other work in urban areas (Lauvaux et al. (2016).)

3). Ceilometers and Planetary Boundary Layer Height (PBLH) retrieval

Two Vaisala ceilometers were used to derive PBLHs during the period of interest: the CL-31 at the National Weather Service (NWS) Sterling Field Support Center (SFSC) in Sterling, VA and the CL-51 at Beltsville, MD (HUBV) (Figure 1)

Both ceilometers use an InGaAs laser diode with a 910 nm wavelength. They use a single lens optics system where the inner part of the lens is employed for transmitting and the outer part for receiving light. This system provides a good overlap of the transmitter and the receiver field-of-view over the whole measuring range, conferring an improved near-range performance compared to two lens systems and allows reliable detection of very low nocturnal stable layers below 200 m. The latest model, the CL-51, is equipped with a larger lens and a more powerful laser transmitter module. These improvements increase the reporting range and signal-to-noise ratio.

Thirty-minute averaged two-way attenuated backscatter profiles with a vertical resolution of 20 m from the surface are processed to derive PBL heights using the Wavelet Covariance Transform (WCT; Davis et al. (2000); Compton et al. (2013)) method for unstable/neutral conditions and the Hybrid-Lowest for stable conditions (Hicks et al. (2015)). The stability was determined in base to the averaged low-altitude Bulk Richardson values (below 0.2 km); values lower than −0.01 were considered unstable, near neutral if between or equal to −0.01 and 0.01, and stable if greater than 0.01. The Hybrid-Lowest method is a combination of the WCT method and the Error Function-ideal profile (ERF; Steyn et al. (1999)) method. They are combined such that the WCT method detects the significant gradient layers and the ERF method determines which of the layers correspond to PBL height below significant elevated aerosol layers. We note that the Hybrid-Lowest algorithm expects there to be a residual layer at night and attempts to locate the PBL height beneath it. In addition, a height constraint based on the lifting condensation level (LCL) is applied for both techniques. Details of the methods can be found in Hicks et al. (2015, 2019).

The PBLHs derived from the ceilometers, as described above, were manually filtered after visual inspection by removing those corresponding to rain events and other apparent artifacts on the backscatter signals such as a dirty lens or malfunctioning hardware leading to an acceptance rate of 77.4 % (N=1100) for SFSC and 73.4 % (N=1043) for HUBV.

In Hicks et al. (2015, 2019) the consistency rate (Co) parameter was defined as the percentage of the ceilometer PBLH observations that measured within ± 300 m when compared to radiosondes. The consistency rate reported in these previous works for the PBLH retrieval methods employed was 65 % for unstable conditions and 74 % for stable conditions. These comparisons were performed in the context of the NWS CL31 Planetary Boundary Layer project, (Atkinson et al. (2017)). Here we use the consistency rate (Co) parameter to compare the simulated PBLH to the ceilometer observations.

4). Flux tower

At HUBV, a micrometeorological tower has been collecting micrometeorological parameters since 2006. The campus is located in a complex suburban/rural/industrial landscape, however, the campus itself has minimal urban development, and it is principally covered by a mix of deciduous (maple and mixed oak) and coniferous (mainly Virginia Pine) trees. At the tower, fast response instruments measure variables such as wind speed, temperature (CSAT, Campbell Scientific), water vapor, and CO₂ concentrations (LI7500, LICOR Inc) at 31.5 m above ground level (~ 15 m above the canopy). Before the eddy covariance technique (Stull (1988)) is used to estimate turbulent fluxes, a flow rotation to the wind field is applied (McMillen (1988)). Also, scalar fluxes are corrected due to density fluctuations (Webb et al. (1980)).

b. Model configurations

1). Meteorological model

Simulations for the month of February 2016 were conducted with the Weather Research and Forecasting (WRF) model. February was selected because is a representative month of winter in the study area. In addition, inverse modeling studies are carried out mostly during winters so that biogenic activity is small and cause little influence on CO₂ estimated fluxes. The Advanced Research WRF (ARW) core uses fully compressible, non-hydrostatic Eulerian equations on an Arakawa C-staggered grid with conservation of mass, momentum, entropy, and scalars (Skamarock et al. (2008)).

Two datasets were tested as initial and boundary conditions: North America Regional Reanalysis (NARR) three hourly data (Mesinger et al. (2006)) and High Resolution Rapid Refresh (HRRR) model hourly analyses (Benjamin et al. (2016)) following Blaylock et al. (2017), both provided by the National Center for Environmental Prediction (NCEP). As in Lopez-Coto et al. (2017b), the model was configured with 3 nested domains (with feedback) of 9, 3 and 1 km horizontal resolution respectively. However, for the case of HRRR, only two domains were used being 3 and 1 km horizontal resolution. 60 vertical levels with monotonically increasing thickness from the surface resulted in 34 levels below 3 km for better boundary layer representation. Adaptive time step was selected with a Courant-Friedrichs-Lewy (CFL) criterion of 1. The RRTMG radiation scheme, (Mlawer et al. (1997)), Thompson microphysics scheme, (Thompson et al. (2004, 2008)), Noah land surface model, (Chen and Dudhia (2001)) and the Kain-Fritsch cumulus scheme, for the 9 km domain only, (Kain (2004)) were used and kept constant across configurations.

Four PBL schemes were compared, three local schemes and one non-local scheme: 1) YSU is a nonlocal, first order closure scheme. It includes a countergradient correction term in the down-gradient diffusion and represents the entrainment explicitly (Hong et al. (2006)). Later on, Hong (2010) removed the counter-gradient flux terms and included other changes for stable boundary layers. The PBL height in the YSU scheme is determined from the Rib method calculated from the surface to the top of the PBL. A threshold value of zero is used for stable cases, while 0.25 is used for unstable conditions. 2) QNSE is a local, 1.5-order local closure, scheme (Sukoriansky et al. (2005)). It is intended to account for wave phenomena within stable boundary layers. The QNSE theory is valid for stable stratification and weakly unstable conditions. The PBLH is diagnosed based on a TKE threshold. 3) BouLac is also a local, 1.5-order local closure scheme including a prognostic equation for TKE, (Bougeault and Lacarrere (1989)). It is designed for use with the BEP (Building Environment Parametrization) multi-layer, urban canopy model (Martilli et al. (2002); Salamanca et al. (2011a,b)). BouLac diagnoses PBL height as the height where the virtual potential temperature exceeds the surface virtual potential temperature by 0.5 K. Here we use this scheme with and without the BEP parametrization. 4) MYNN is a local scheme (Nakanishi and Niino (2004, 2006)). In particular, we tested the 1.5-order closure scheme (MYNN2). The expressions of stability and mixing length are based on the results of large eddy simulations rather than on observations. In recent years, MYNN has undergone extensive development, including the addition of BouLac mixing length in the free atmosphere, changing the turbulent mixing length to be integrated from the surface to the top of the boundary layer plus a transition layer depth, the addition of a scale-aware mixing length following Ito et al. (2015) and the addition of an eddy mass-flux option (Angevine et al. (2018); Olson et al. (2019)) that confers to this scheme some non-local characteristics as well. For the PBL height diagnosis, a hybrid method is used, which blends a theta-v-based definition in neutral/convective boundary layer and a TKE-based definition in stable conditions. We tested here MYNN with and without the eddy mass-flux option.

The land-use classification plays a role in the model since it determines the values for the surface properties as the roughness length, albedo and heat capacity which are important for the surface energy balance and heat and momentum fluxes to the atmosphere. Here we tested two datasets available in WRF: The USGS dataset and the more up to date NLCD 2011. The main difference between these datasets, as concerns this work, is the representation of the urban land use; in the USGS, only one urban category is defined while in the NLCD, four categories exist going from developed open space to developed high intensity (Figure 1). For the configuration using the Building Energy Parameterization (BEP) multilayer Urban Canopy Model (UCM) a modified version of USGS was used that included 3 urban categories taken from the NLCD dataset where the developed open space and low intensity categories were added together. In addition, the BEP specific parameters for Washington, DC, and Baltimore, MD, cities were taken from the NUDAPT dataset already included in the WRF data distribution.

All the options described above total to eight different configurations that were tested here (Table 1).

Table 1.

WRF model configurations

Label	Version	PBL scheme	Surface Layer	IC/BC	Land use	Urban canopy model
YSU	3.8	YSU	MOST	HRRR	USGS	—
YSU+NARR	3.8	YSU	MOST	NARR	USGS	—
MYNN	3.8	MYNN	MYNN	HRRR	USGS	—
MYNNe	3.9.1.1	MYNN+edmf	MYNN	NARR	USGS	—
MYNNe+nlcd	3.9.1.1	MYNN+edmf	MYNN	NARR	NLCD	—
BOUL	3.8	BouLac	MOST	HRRR	USGS	—
BOUL+UCM	3.8	BouLac	MOST	HRRR	USGS33	BEP
QNSE	3.8	QNSE	QNSE	HRRR	USGS	—

Model-data comparison was performed similarly for each data source. Hourly (or half-hourly) measurements for each station were compared to model predictions extracted at the location and time of each observation. Then, daily cycles, bias (model - observations), standard deviation of the differences and percentiles were computed for all stations together. In the case of the ceilometers, metrics for each ceilometer are provided as well as both combined.

2). Tracer transport model

The CO₂ transport was simulated similarly to Lopez-Coto et al. (2017a). We used the Stochastic Time-Inverted Lagrangian Transport model (STILT; Lin (2003); Nehrkorn et al. (2010)), driven by meteorological fields generated by four of the configurations described above (MYNN, YSU, QNSE, BOUL+UCM). Five-hundred particles were released from both urban sites (NDC and HAL) hourly, and were tracked as they moved backwards in time for 24 h. The footprint was calculated from the particle density and residence time in the layer that sees surface emissions, defined as 0.5 PBLH (Gerbig et al. (2003)) and then convolved with CO₂ fluxes provided by ACES inventory (Gately and Hutyra (2017)).

3. Results

a. Surface variables

Overall, over the month of February, the temperature bias ranged from −0.92 K for MYNNe+nlcd to 1.96 K for BOUL+UCM while standard deviation ranged from 1.60 K for YSU to 2.04 K for MYNNe and YSU+NARR. Wind speed bias was negative for all but BOUL, ranging from −1.12 m/s for MYNNe+nlcd to 0.69 m/s for BOUL. The standard deviation ranged from 1.70 m/s for YSU and QNSE to 2.16 m/s for BOUL+UCM. Wind direction bias ranged from −5.03° for QNSE to 6.43° for BOUL+UCM while standard deviations did from 36.62° for BOUL to 47.12° for MYNN (Table 2). It is interesting that by looking at YSU and YSU+NARR, it seems that the HRRR driver provided better results; however, by looking at MYNN and MYNNe, the conclusions would be the opposite. It is worth noting that due to the circular nature of the wind direction, differences larger (lower) than 180° (−180°) were measured in the opposite direction, for example, if the model had a wind direction of 175 while the observations were at −160, the difference is equal to −25, not 335. This step removes the fat tails of the distribution and makes them much more Gaussian and hence gains significance for the mean and standard deviation calculated here.

Table 2.

ISD statistics mean bias (model - observations), standard deviation (SD) and the interquartile range (IQR) of the differences. February 2016.

		YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
	Bias	0.09	−0.63	−0.56	−0.55	−0.92	1.26	1.96	−0.71
T (K)	SD	1.60	2.04	1.76	2.04	2.00	1.92	2.02	1.62
	IQR	1.63	2.16	1.84	2.16	2.33	2.03	2.30	1.68
	Bias	−0.45	−0.53	−0.88	−0.60	−1.12	0.69	−0.70	−0.91
ws (m/s)	SD	1.70	1.81	1.96	1.73	1.72	2.00	2.16	1.70
	IQR	2.03	2.17	2.37	2.02	2.12	2.31	2.40	1.99
	Bias	1.04	0.99	−1.42	−0.07	−3.27	5.79	6.43	−5.03
wd (°)	SD	36.64	42.11	47.12	41.63	43.99	36.62	37.53	40.03
	IQR	27.91	36.42	34.76	37.26	42.84	27.49	28.80	29.73

In the overall statistics, the urban canopy model decreased the performance of the BouLac parametrization for the 3 surface variables analyzed here making it too warm and more variable regarding wind speeds and direction errors. In addition, the MYNN scheme showed the largest wind direction error variability, especially when it was driven by HRRR. On the other hand, including the eddy mass flux option in MYNN had a positive impact on wind speed and direction but using the NLCD dataset caused the model to be colder and reduced the wind speeds.

The daily cycle of the temperature differences (Fig 2a) reflects that BOUL was too warm during nights while during the day the median bias was close to zero. The addition of the UCM did however increase the bias during the day as well. QNSE was colder during nighttime while for MYNN and MYNNe the median temperature bias was similar during day and night. The inclusion of NLCD caused the temperatures to decrease during day time. The wind speed errors had a clear daily cycle for BouLac, with winds being too strong during night time (Fig 2b). The UCM corrected this bias at the cost of increasing the (negative) bias during daytime. For the rest of configurations, the bias was slightly more negative during daytime but not as marked as for BOUL. No significant cycle was observed for the wind direction errors for any configuration (Fig 2c).

Fig. 2.

Median daily cycle of the differences for (a) temperature, (b) wind speed, (c) wind direction, (d) planetary boundary layer heights, (e) sensible heat flux and (f) latent heat flux. Grey lines correspond to the rest of configurations not present in the legend. February 2016.

b. Planetary Boundary Layer Heights

1). Observed Planetary Boundary Layer Heights

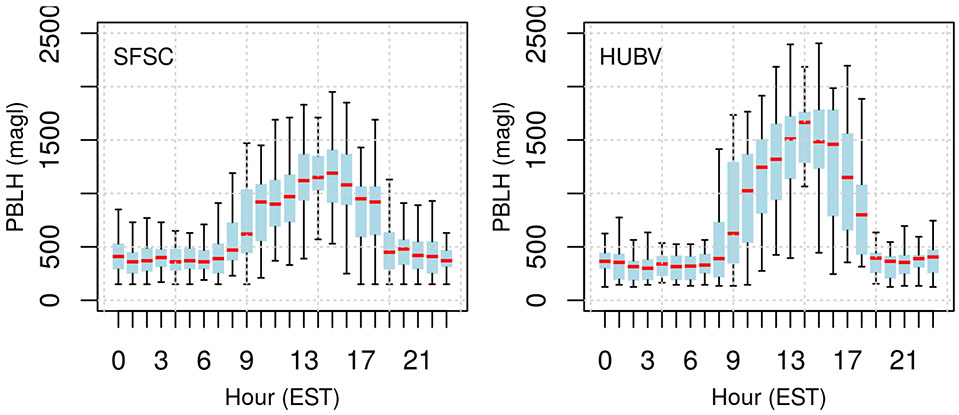
Figure 3 shows the daily cycle observed at the two ceilometer locations for the month of February 2016. The observed PBLHs are in good agreement with previous climatological results (Seidel et al. (2012)), and more specifically with the results published for the area under study by Hegarty et al. (2018).

Fig. 3.

Daily cycle for the observed Planetary Boundary Layer Heights (PBLH) at the two ceilometer locations for the month of February 2016. Red line is the median, blue bar represents the first and third quantile and the whisker bars are limited to 1.5 times the IQR. February 2016.

Beltsville (HUBV) shows typically higher PBL depths during the day as well as sharper transitions during the morning and especially during the evening as compared to Sterling (SFSC). This is likely due to the more urban surroundings for that location and the typical westerly flows dominant over the region that likely transport air masses with deeper PBL from the denser Washington DC metro area adjacent to this location (Angevine et al. (2003); Zhang et al. (2009, 2011)). However, we also note that the differences between ceilometers between both locations might have played a role as well on the observed differences.

2). Performance of Model Configurations

Table 3 shows the overall statistics for the PBLH differences for the eight tested configurations using both ceilometers together and for each ceilometer independently. For both ceilometers, the consistency rate ranged from 52 % for QNSE and BOUL to 60 % for MYNN. The mean values were higher than the median values indicating the differences were skewed to higher values. In the extreme case, QNSE provided the largest values for all the statistics estimators but the lowest consistency parameter. For each ceilometer, the results resemble the global values, showing slightly better model performance for Beltsville (HUBV) than for Sterling (SFSC). Reasons for that are not clear but it is possible that the Vaisala CL-51 ceilometer at HUBV, which has a better signal-to-noise ratio than the CL31 at SFSC, might have achieved a higher quality PBLH retrieval. Overall, the three variants of MYNN provided the best consistency rate and the lowest standard deviation followed closely by YSU.

Table 3.

Global statistics for the PBLH errors (model minus observed). February 2016.

BOTH	YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
Co (%)	56	55	60	57	59	52	55	52
Mean (m)	−38	−73	−57	−32	15	−50	50	152
SD (m)	494	496	462	496	480	519	513	542
Median (m)	−93	−119	−72	−89	−47	−126	−25	77
IQR (m)	484	502	460	462	479	516	571	630
SFSC	YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
Co (%)	50	51	58	51	56	46	48	47
Mean (m)	−17	−41	−27	−11	43	−15	53	163
SD (m)	497	509	459	528	479	535	523	545
Median (m)	−94	−121	−69	−110	−37	−116	−46	96
IQR (m)	579	541	469	530	519	623	655	692
HUBV	YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
Co (%)	63	60	62	63	61	58	61	56
Mean (m)	−61	−107	−88	−55	−15	−86	48	139
SD (m)	491	480	463	460	480	499	503	539
Median (m)	−91	−114	−77	−80	−56	−133	−9	59
IQR (m)	396	459	440	416	433	411	481	554

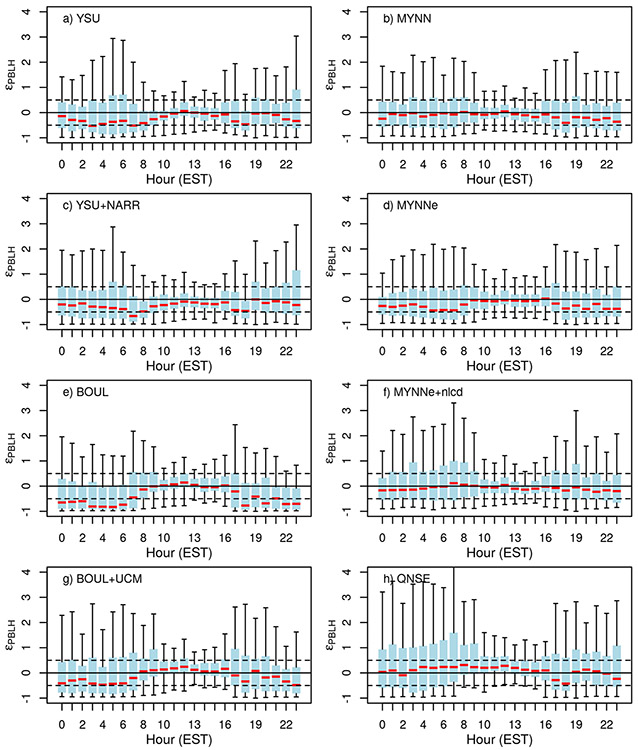
To better understand the performance of each model configuration, we analyzed both the daily cycle of the differences (Fig. 2d) and the daily cycle of the relative differences, Figure 4. Nocturnal PBLH bias is typically smaller than daytime values. Although in relative terms, they are comparable, or larger at night due to the typically low measured nocturnal PBLH values.

Fig. 4.

Daily cycle of the relative differences for the PBLH, including both ceilometers, for the eight configurations tested. Red line is the median, blue bar represents the first and third quantile and the whisker bars are limited to 1.5 times the IQR. February 2016.

BOUL provided the lowest nocturnal PBLH values, reaching median bias between −50 % and −60 % of the observed values, followed by YSU (− 50%). During daytime, both BOUL and YSU performed much better providing median relative bias close to zero. The inclusion of the urban canopy parameterization increased PBLH values, slightly improving the BouLac schemes nocturnal performance but at the cost of an increased daytime bias. The QNSE configuration gave the largest PBLH values during the day, followed by BOUL+UCM. QNSE performed better during nighttime but still over-predicted the PBLH. It also showed the largest IQR. On the other hand, MYNN performed well during most hours, slightly under-predicting PBLH during the evening. The usage of NARR driver data did however decrease the MYNN performance during the night causing a slight underestimation of the PBLH during these hours. This configuration had also the eddy mass flux option activated, however, the decreased nighttime performance cannot be attributed to it because this option only gets triggered during convective situations. The inclusion of the NLCD dataset had a positive impact on the prediction, causing MYNNe+nlcd to be nearly unbiased for all hours. Interestingly, most of the configurations showed a noticeable PBLH drop at 18 EST probably coinciding with the evening transition. It is not clear however whether this result is caused by a too quick evening transition in the models or a problem on the retrieved PBLH in this complex situation. Overall, MYNN produced the best predictions of the PBLH for all hours.

c. Surface fluxes

Table 4 shows the sensible and latent heat flux errors at Beltsville (HUBV). Sensible heat flux bias ranged from −23 W m⁻² for MYNN to 12 W m⁻² for MYNNe+nlcd while the standard deviation ranged from 86 W m⁻² for YSU+NARR to 97 W m⁻² for BOUL+UCM. For the latent heat flux, the bias ranged from −11 W m⁻² for MYNNe+nlcd to 21 W m⁻² for QNSE. The standard deviation ranged from 57 W m⁻² for BOUL+UCM to 65 for W m⁻².

Table 4.

Global statistics for the sensible (HFX) and latent (LE) heat fluxes errors (model - observed) at Beltsville (HUBV) (units: W m⁻²). February 2016.

HFX	YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
Mean	−13	−15	−23	−16	12	−19	8	−20
SD	90	86	96	89	96	94	97	92
Median	−2	−2	−9	−5	16	−7	3	−10
IQR	46	48	56	51	65	57	61	61
LE	YSU	YSU+NARR	MYNN	MYNNe	MYNNe+nlcd	BOUL	BOUL+UCM	QNSE
Mean	8	9	11	13	−11	13	0.5	21
SD	58	59	61	61	58	58	57	65
Median	5	6	9	8	0.2	11	0.6	12
IQR	23	27	26	30	22	29	16	39

The daily cycle of the sensible heat flux differences (Fig 2e) shows that all the configurations are nearly unbiased from 17 EST to 7 EST with the exception of MYNNe+nlcd, which shows a slight positive bias during those hours. During daytime, the model performance is more variable: YSU, YSU+NARR, MYNNe, BOUL and QNSE are nearly unbiased during the morning while showing negative bias during the afternoon; MYNN shows negative bias during all daytime hours, being the largest in the afternoon; BOUL+UCM presents positive bias during all daytime, being the largest during the late morning and MYNNe+nlcd is nearly unbiased during these hours.

The daily cycle of the latent heat flux differences (Fig 2f) shows a similar behavior during non-daylight hours (17 - 7 EST) as in the previous case with very little to no bias for all the schemes. However, in this case MYNNe+nlcd and BOUL+UCM are the best performing configurations with almost zero bias while the rest show a slightly positive bias. During daytime hours, all the configurations show a positive bias that is the largest close to noon, with the exception of MYNNe+nlcd which has a negative bias.

Figure 5 presents a scatter plot of the mean daily cycle of PBLH differences vs. the sensible heat flux differences. As expected, all configurations show a positive correlation between the two, with the exception of BOUL+UCM. However, both the magnitude of the dependence, as measured by the slope of a linear model, and the intensity of the correlation, as measured by the Pearson correlation coefficient, differs between configurations. BOUL and YSU exhibit the largest slope of them all, followed by MYNNe, QNSE, YSU+NARR, MYNN, MYNNe+nlcd and BOUL+UCM, which is the only one with negative slope. The correlations are between 0.66 and 0.8 for MYNN, YSU+NARR, MYNNe, YSU, QNSE and BOUL, but below 0.35 for MYNNe+nlcd and BOUL+UCM. This analysis shows that when the model underestimates the sensible heat flux, the PBLH tends to be underestimated as well. This is true for all the configurations but BOUL+UCM and to a lesser extent for MYNNe+nlcd.

Fig. 5.

Scatter plot of the mean daily cycle of PBLH differences vs the sensible heat flux differences at Beltsville (HUBV). February 2016.

d. Urban Heat Island Effect

The Urban Heat Island (UHI), computed here as the difference between the area-averaged surface skin temperature (TSK) for the urban area and the non-urban area, is reproduced similarly by all configurations being about 2 - 3 K during nights with a peak during early evening (Fig 6a). During the daytime, the median values are close to zero for all configurations but BOUL+UCM which showed UHI intensities over 2 K for these hours.As shown by Basara et al. (2008), and by comparison to the rest of the models, the values shown by BOUL+UCM are rather large. Overall, all models reproduced the larger sensible heat fluxes in the urban areas as expected (Wood et al. (2013)). However, QNSE and BOUL+UCM showed the largest contrast between urban and non-urban sensible heat fluxes (ΔHFX) of all configurations being the largest for the latter (Fig 6c). In addition, the peak was at least three hours earlier than for the rest of configurations. The usage of NARR driver data in MYNN caused the sensible heat flux differences between urban and non-urban areas to increase while the addition of the NLCD land cover dataset had the opposite effect.

Fig. 6.

Median daily cycle for the (a) urban heat island (UHI), (b) the area averaged Bowen ratio for urban areas over Bowen ratio for non-urban areas (β_ua/β_nua), (c) the area averaged sensible heat flux difference between urban and non-urban areas (ΔHFX) and (d) the area averaged latent heat flux difference between urban and non-urban areas (ΔLE). Grey lines correspond to the rest of configurations not present in the legend. Note that in (b) the black horizontal dashed line marks the value 1. February 2016.

On the other hand, BOUL+UCM had the smallest difference between urban and non-urban latent heat fluxes (ΔLE) while QNSE had the largest (Fig 6d). The median Bowen ratio over urban areas during daytime was between 5 to 15 times larger than those for the non urban areas for most of the models, with MYNNe+nlcd being the smallest and QNSE the largest (Fig 6b). These values are within the range of observed values but on the large side of the typical ones (Oke (1982)). However, BOUL+UCM showed two peaks, at 8 a.m. and 4 p.m. (EST), with values of up to 20 times those of the non urban areas. This feature is not seen in any other configuration and can be attributed to the UCM since the BOUL configuration without UCM behaved similarly to the rest of configurations.

QNSE and BOUL+UCM had consistently the largest PBLH difference between the urban and non-urban areas (ΔPBLH) while MYNNe+nlcd had the lowest (Figure 7). QNSE and BOUL+UCM also had positive ΔPBLH during daytime while the rest of configurations had a median value close to zero during these hours. As with the UHI, the maximum differences were simulated during the early evening, about 17 - 18 EST depending on the configuration. The usage of NARR driver data as well as the inclusion of the eddy mass flux option in MYNN caused the median PBLH differences to decrease. For YSU, ΔPBLH was the most different of all configurations having a median value near zero during nighttime but with the distribution skewed to negative values indicating that in many occasions the PBL was deeper in the non-urban areas than in the urban areas. Attending to the results published by Godowitch et al. (1985) and Angevine et al. (2003) and by comparison with the rest of models, this result is not expected and seems odd. The reasons for this are not clear because neither the UHI nor the ΔHFX showed a cycle that could suggest this type of behavior.

Fig. 7.

Daily cycle for the area averaged PBLH difference between urban and non-urban areas (ΔPBLH). Red line is the median, blue bar represents the first and third quantile and the whisker bars are limited to 1.5 times the IQR. February 2016.

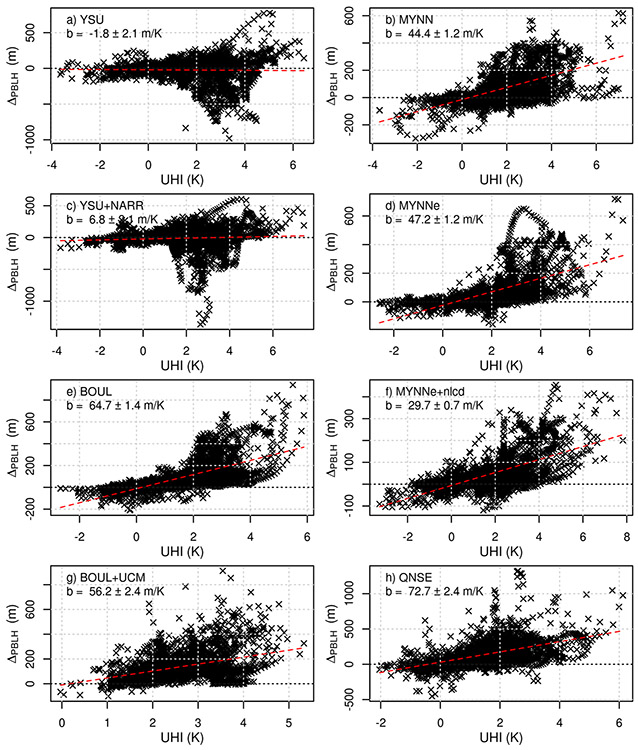
To understand the relationship between the PBLH differences between the urban and non-urban areas and the Urban Heat Island (UHI) intensity, Figure 8 shows a scatter-plot for all simulated values for the month of February along with the slope of a linear model between the two variables for each model configuration. Overall, negative UHI intensities resulted in deeper PBLs over the non-urban areas while positive UHI intensities were associated with deeper PBLs over the urban areas, as expected, (Godowitch et al. (1985); Angevine et al. (2003)). This relationship shows a somewhat linear trend where larger UHI values resulted in larger PBLH differences between urban and non-urban areas for all configurations but YSU. Slopes ranged from −1.8 ± 2.1 m/K for YSU to 72.7 ± 2.4 m/K for QNSE. BOUL and BOUL+UCM had higher slopes than MYNN while the inclusion of the NLCD dataset reduced the slope considerably from 47.2 to 29.7 m/K. Correlation coefficients ranged from 0.02 and 0.06 for YSU and YSU+NARR respectively to 0.65 and 0.64 for BOUL and MYNNe+nlcd respectively. The rest of the configurations also had correlation coefficients larger than 0.5, except for BOUL + UCM, which had a correlation of 0.4.

Fig. 8.

Scatter plot and linear model fit of the relationship between the UHI and the ΔPBLH. February 2016.

The near zero correlation coefficient and slope showed by YSU and YSU+NARR is caused by the large hysteresis shown in the median cycle of these two variables for both configurations (Figure 9). During night and until late morning, the median UHI intensity decreases while the PBLH difference between urban and non-urban areas slightly increases. This behavior is the opposite to the rest of configurations and previously published works (Spangler and Dirks (1974); Godowitch et al. (1985); Dupont (1999); Angevine et al. (2003)) where decreasing the UHI intensity results in a reduced PBLH difference between urban and non-urban areas.

Fig. 9.

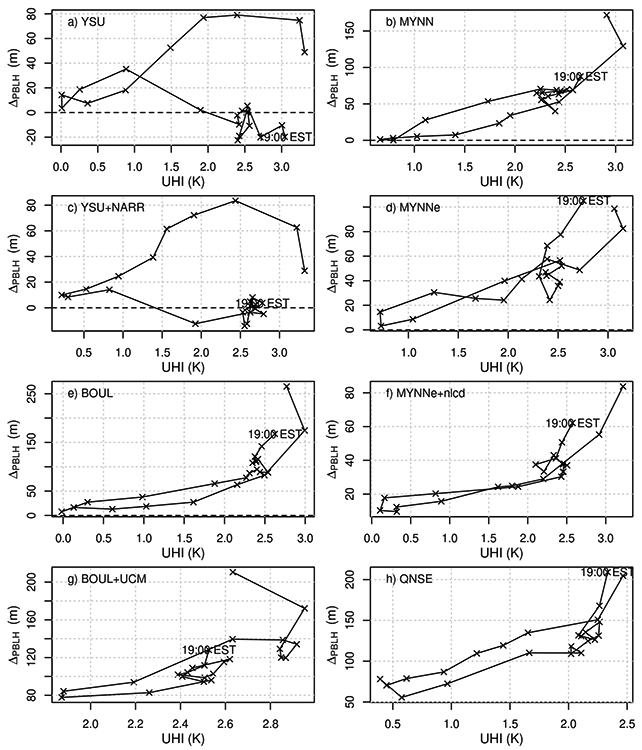
Median daily cycle of the UHI and the PBLH difference between urban and non-urban areas (ΔPBLH). The marked point represents the time 19 EST while the line connects the points as the time increases, thus ending at 18 EST. February 2016.

4. Implications for tracer transport and inverse modeling

As expected, the different performance of each configuration is reflected in the tracer transport. The daily cycle of the integrated footprint from the STILT model (Figure 10 (a) ) reflects large differences between configurations. The strongest daily cycle (largest amplitude) is the one for BOUL+UCM while the weakest is for MYNN. During the night BOULC+UCM and YSU behave similarly while QNSE and MYNN behave similarly to each other as well. On the other hand, during the day the similarities are changed and YSU and MYNN show similar response while QNSE resembles the BOUL+UCM values. Indeed, the differences with respect to MYNN (Figure 10 (b) ) are between 10 to 50 % for YSU and BOUL+UCM during nighttime and about −30 % for QNSE and BOUL+UCM during daytime. These differences are reflected in the CO ₂ mole fraction and thus in the bias as well. Figure 10 (c) shows that mean daily cycle for MYNN is the least biased for all hours. During nighttime, MYNN shows a positive bias between 1 to 2 ppm while the rest show much stronger biases with up to 6 ppm for BOUL+UCM. During daytime, YSU still shows a positive bias about 1 to 2 ppm while MYNN fluctuates around 0 ppm. On the other hand, BOUL+UCM and QNSE show negative biases between −1 and −4 ppm depending on the hour.

Fig. 10.

Daily cycle of the a) Integrated footprint (ppm), b) relative difference to MYNN (%),c) CO ₂ mean bias (ppm) and, d) CO ₂ median bias (ppm) for the two towers and 4 configurations. February 2016.

In general, strong underestimation of PBLH during nights as shown by the configurations tested in this work with the exception of MYNN, results in large accumulation of pollutants emitted from local sources and thus strong nighttime positive bias. During daytime, the situation is different as most models show a small relative PBLH bias. Nevertheless, the CO₂ daytime bias is non-zero and different in direction depending on the configuration. The smaller daytime bias in most models supports the typical practice in inverse modeling of only using afternoon hours. However, the results shown here imply that MYNN has the potential of extending the inversion analysis to nighttime as well due to the much smaller biases (and comparable to daytime) during this time of the day.

The fact that positive UHI intensities are associated with deeper modeled PBLs over the urban areas and that positive UHI are generally simulated by all models during nights implies that the pollutant mixing during these hours in the urban areas is more active than in the rural counterpart. In addition, it could also favor the development of urban centripetal circulations, as described in Oke (1995), further impacting the pollutant advection. However, the fact that YSU is reproducing in many occasions deeper nocturnal PBLHs over the non-urban areas would imply a more active mixing outside of the city and the inhibition of the urban centripetal circulation.

In addition, inverse modeling based on the concept of footprints (observations’ sensitivity to surface fluxes) relies on Lagrangian Particle Dispersion Models (LPDMs) driven by meteorological fields as those generated in this work. The footprints depend mostly on the advection of the particles (driven by the wind field), the turbulent mixing (driven by the turbulent velocity variances) and the planetary boundary layer height (PBLH). Deeper modeled PBLHs than observed would result in artificial dilution of the footprints and, therefore, source term overestimation. In addition, some Lagrangian models parametrize the turbulent velocities as a function of the heat flux at the surface. The fact that PBLH errors are mostly positively correlated with sensible heat flux errors implies that an overestimation of the heat flux will cause an overestimation of the turbulent mixing as well as PBLH, having a non-linear impact on the overall strength of the footprints.

5. Conclusions

We show that using ceilometers we were able to analyze the daily cycles of the PBLH and found that most PBL schemes largely underestimate PBLH during nights. We also show that with these measurements, correlations between PBLH errors and heat fluxes errors can be calculated and serve to identify models that do not follow the proper trend. These results could not be obtained using operational radiosondes as they are very limited in time (only twice a day).

We find the BEP urban canopy model did not improve the model performances in general and it had an adverse impact on PBLH and sensible heat flux as compared to measurements. The UCM partially corrected the Boulac nocturnal positive wind speed bias and negative PBLH bias at the cost of increasing the negative bias as well as increasing the positive PBLH bias during daytime. In addition, the UHI and ratio urban-rural of Bowen ratio did not compare well with the rest of configurations or previously published results.

We find that modeled PBLHs are typically biased low during nighttime for most of the configurations with the exception of those using the MYNN parametrization. In addition, we find that PBLH errors are mostly positively correlated with sensible heat flux errors, and that modeled positive UHI intensities were associated with deeper modeled PBLs over the urban areas. Overall, the configurations using MYNN scheme performed the best, reproducing the PBLH reasonably well during all hours.

We show that strong underestimation of PBLH during nights results in large accumulation of pollutants emitted from local sources and thus strong nighttime positive CO₂ bias. However, MYNN results suggest that, given the low night-time biases for this model, which are similar in magnitude to the daytime biases, an inversion analysis may be extended into nighttime hours.

Last, we find that while most of the configurations performed as expected on reproducing the urban heat island effect, noticeable differences remain that may have an impact on weather and tracer dispersion simulations in urban and regional studies. Further research is needed and experimental intensive campaigns must be carried out to address these issues and differences as well as to better understand the differences between PBL schemes during other seasons for the Washington, DC, / Baltimore, MD, area.