Abstract
Internal states shape stimulus responses and decision-making, but we lack methods to identify them. To address this gap, we developed an unsupervised method to identify internal states from behavioral data and applied it to a dynamic social interaction. During courtship, Drosophila melanogaster males pattern their songs using feedback cues from their partner. Our model uncovers three latent states underlying this behavior and is able to predict moment-to-moment variation in song-patterning decisions. These states correspond to different sensorimotor strategies, each of which is characterized by different mappings from feedback cues to song modes. We show that a pair of neurons previously thought to be command neurons for song production are sufficient to drive switching between states. Our results reveal how animals compose behavior from previously unidentified internal states, which is a necessary step for quantitative descriptions of animal behavior that link environmental cues, internal needs, neuronal activity and motor outputs.
Internal states can have a profound effect on behavioral decisions. For example, we are more likely to make correct choices when attending versus when distracted, and will consume food when hungry but suppress eating when sated. A number of studies in animals highlight that the nervous system encodes these context-dependent effects by remodeling sensorimotor activity at every level, from sensory processing to decision-making, all the way to motor activity1–4. For instance, recordings from rodent cortical neurons revealed that neural activity is more strongly correlated with the state of body motion versus the statistics of sensory stimuli during sensory-driven tasks5,6. Across model systems, locomotion can also change the gain of sensory neurons, causing them to be more or less responsive and leading to the production of distinct behavioral outputs when these neurons are activated7–10. It is not simply action that modulates neural activity but also internal goals and needs. For example, circuits involved in driving courtship or aggression behaviors in rodents and flies show different patterns of activity as the motivation to court or fight, respectively, changes11–13. Neurons can be modulated via multiple mechanisms to promote these goals. For example, during hunger states, chemosensory neurons that detect desirable stimuli are facilitated and enhance their response to these cues14,15. Downstream from sensory neurons, the needs of an animal can cause the same neurons to produce different behaviors—foraging instead of eating, for instance—when ensembles of neurons are excited or inhibited by neuromodulators that relay information about state16–18.
Despite evidence to indicate that internal states affect both behavior and sensory processing, we lack methods to identify the changing internal states of an animal over time. While some states, such as nutritional status or walking speed, can be controlled for or measured externally, animals are also able to switch between internal states that are difficult to identify, measure or control. One approach to solving this problem is to identify states in a manner that is agnostic to the sensory environment of an animal. These approaches attempt to identify whether the behavior an animal produces can be explained by some underlying state, for example, with a hidden Markov Model (HMM)19–22. However, in many cases, the repertoire of behaviors produced by an animal may stay the same, while what changes is either the way in which sensory information patterns these behaviors or patterns the transitions between behaviors. Studies that dynamically predict behavior using past sensory experiences have provided important insight into sensorimotor processing, but typically assume that an animal is in a single state23–26. These techniques make use of regression methods such as generalized linear models (GLMs) that identify a ‘filter’ that describes how a given sensory cue is integrated over time to best predict future behavior. Here, we take a novel approach to understanding behavior by using a combination of hidden state models (that is, HMMs) and sensorimotor models (that is, GLMs) to investigate the acoustic behaviors of the vinegar fly D. melanogaster.
Acoustic behaviors are particularly well suited for testing models of state-dependent behavior. During courtship, males generate time-varying songs27, the structure of which can in part be predicted by dynamic changes in feedback cues over timescales of tens to hundreds of milliseconds24,28,29. Receptive females respond to attractive songs by reducing locomotor speed and eventually mating with suitable males30,31. Previous GLMs of male song structure did not predict song decisions across the entire courtship time24. We do so here and found that by inferring hidden states, we captured 84.6% of all remaining information about song patterning and 53% of all remaining information about transitions between song modes, both relative to a ‘Chance’ model that only knows about the distribution of song modes. This represents an increase of 70% for all song and 110% for song transitions compared with a GLM. The hidden states of the HMM rely on sensorimotor transformations, represented as GLMs, that govern not only the choice between song outputs during each state but also the probability of transitioning between states. Using GLM filters from the wrong state worsened predictive performance. We then used this model to identify neurons that induce state switching and found that the neuron pIP10, which was previously identified as a part of the song motor pathway32, additionally changes how the male uses feedback to modulate song choice. Our study highlights how unsupervised models that identify internal states can provide insight into nervous system function and the precise control of behavior.
Results
A combined GLM and HMM effectively captures the variation in song production behavior.
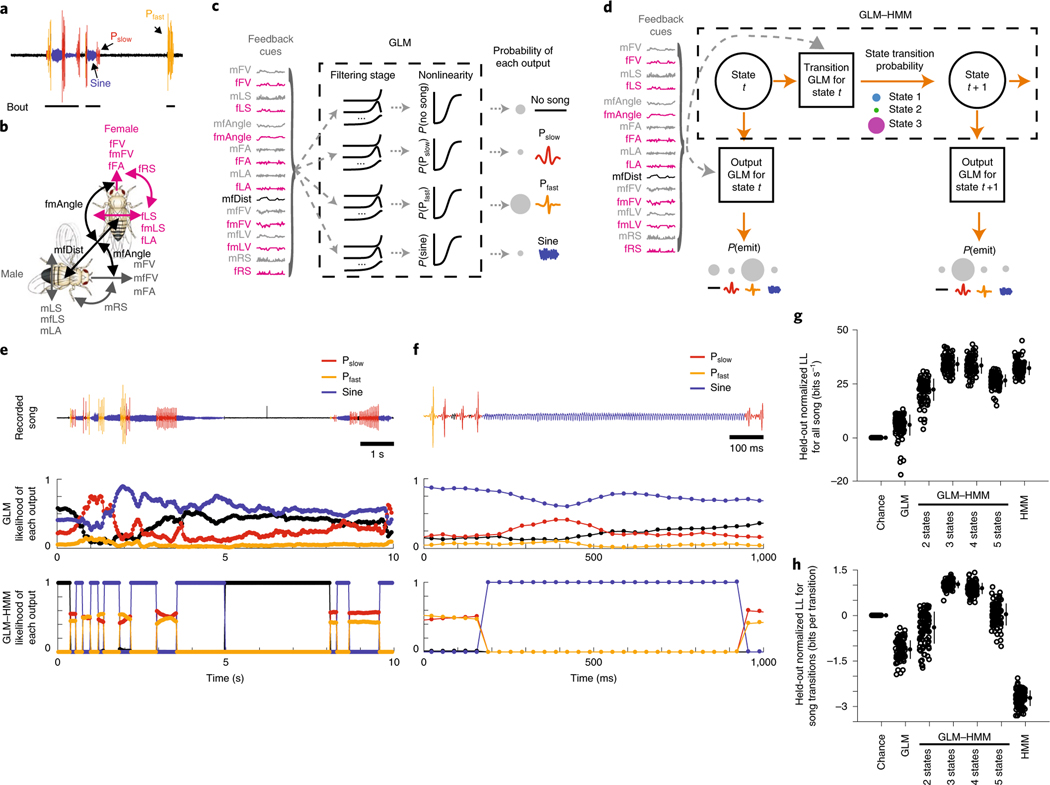
During courtship, Drosophila males sing to females in bouts composed of the following three distinct modes (Fig. 1a): a sine song and two types of pulse song29. Previous studies have used GLMs to predict song-patterning choices (about whether and when to produce each song mode) from the feedback available to male flies during courtship24,28. Inputs to the models were male and female movements in addition to his changing distance and orientation to the female (Fig. 1b). This led to the discovery that males use fast-changing feedback from the female to shape their song patterns over time. Moreover, these models identified the time course of cues derived from male and female trajectories that were predictive of song decisions. While these models accurately predicted up to of 60% of song-patterning choices, they still left a large proportion of variability unexplained when averaged across the data24.
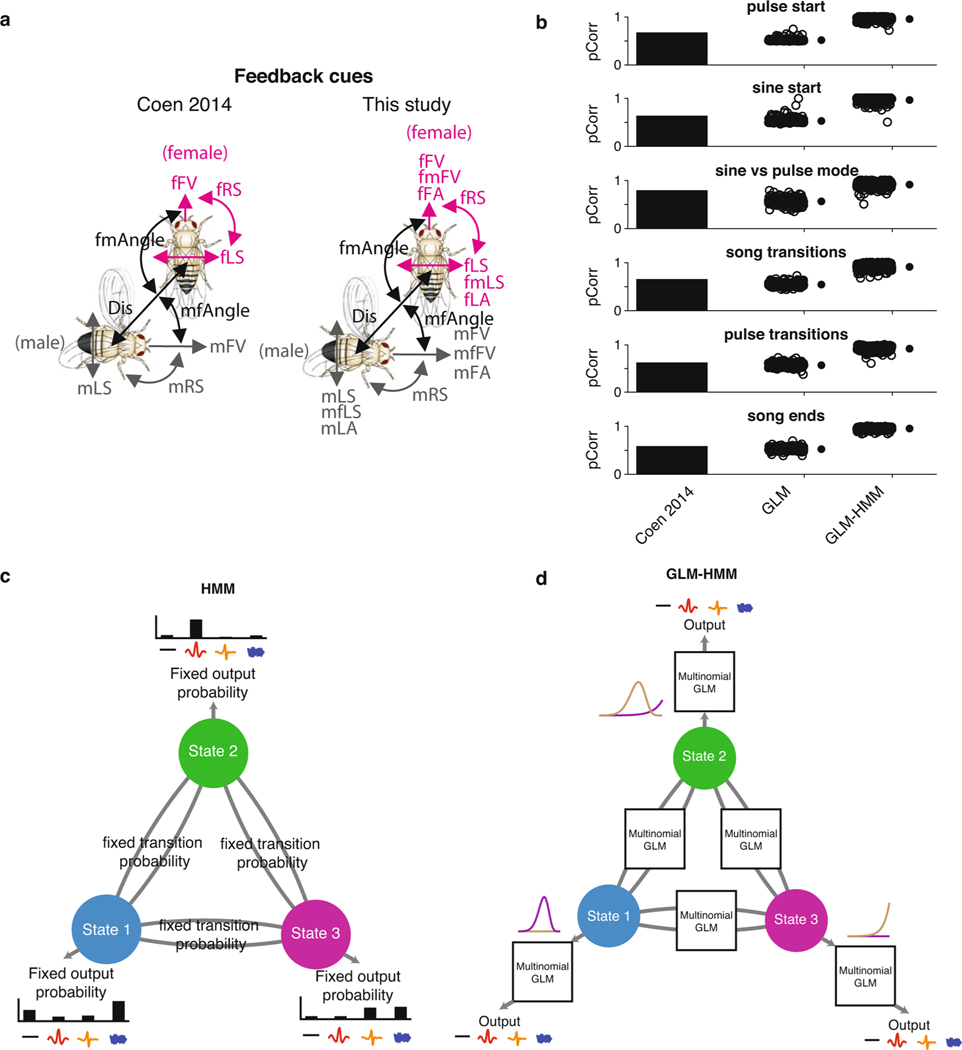
Fig. 1 |. A model with hidden states effectively predicts song patterning.
a, The fly song modes analyzed: no song (black), Pfast (orange), Pslow (red) and sine (blue). Song is organized into trains of a particular type of song in a sequence (multiple pulses in a row constitute a pulse train) as well as bouts (multiple trains followed by no song, represented here by a black line). b, The fly feedback cues analyzed: mFV and female forward velocity (fFV); male lateral speed (mLS), fLS, male rotational speed (mRS) and female rotational speed (fRS); male forward lateral accelerations (mFA), female forward accelerations (fFA), male lateral accelerations (mLA) and female lateral accelerations (fLA); the component of male forward and lateral velocity in the direction of the female (mfFV and mfLS) and the component of the female forward and lateral velocity in the direction of the male (fmFV and fmLS); the distance between the animals (mfDist) and the absolute angle from female/male heading to male/female center (mfAngle and fmAngle). c, Schematic illustrating the multinomial GLM, which takes feedback cues as input and passes these cues through a linear filtering stage. There is a separate set of linear filters for each possible song mode. These filters are passed through a nonlinearity step, and the relative probability of observing each output (no song, Pfast, Pslow, sine song) gives the overall likelihood of song production. d, Schematic illustrating the GLM–HMM. At each time point t, the model is in a discrete hidden state. Each hidden state has a distinct set of multinomial GLMs that predict the type of song that is emitted, as well as the probability of transitioning to a new state. e, Top: 10 s of natural courtship song consisting of no song (black), Pfast, Pslow and sine. Middle: the conditional probability of each output type for this stretch of song under the standard GLM. Bottom: the conditional probability of the same song data under the three-state GLM–HMM; predictions are made one step forward at a time using past feedback cues and song mode history (see Methods). f, Top: 100 ms of natural song. Middle and bottom: conditional probability of each song mode under GLM (middle) and GLM–HMM (bottom), as in e. g, Normalized log-likelihood (LL) on test data (in bits s−1; see methods). The GLM outperforms the chance model (P = 2.9 × 10−29), but the three-state GLM–HMM produces the best performance (each open circle represents predictions from one courtship pair (only 100 of the 276 pairs shown for visual clarity); filled circles represent the mean ± s.d.). The three-state model outperformed a two-state GLM–HMM (P = 2.2 × 10−33) and a five-state GLM–HMM (P = 4.1 × 10−30), but was not significantly different from a four-state model (P = 0.16). On the basis of this same metric, the three-state GLM–HMM slightly outperformed a Hmm (1 bit s−1 improvement, P = 1.8 × 10−5). All P values from Mann–Whitney U-tests. h, Normalized test log-likelihood during transitions between song modes (for example, transition from sine to Pslow). The three-state GLM–HMM outperformed the GLM (P ≤ 2.55 × 10−34) and the two-state GLM–HMM (P = 2.3 × 10−34), and substantially outperformed the Hmm (P ≤ 2.55 × 10−34). Filled circles represent the mean ± s.d., 100 of the 276 pairs shown. All P values from Mann–Whitney U-tests.
Leveraging a previously collected dataset of 2,765 min of courtship interactions from 276 wild-type pairs24, we trained a multinomial GLM (Fig. 1c) to predict song behavior over the entire courtship time (we predicted the following four song modes: sine, fast pulses (Pfast), slow pulses (Pslow) and no song) (Fig. 1a) from the time histories of 17 potential feedback cues defined by male and female movements and interactions (Fig. 1b)—what we will refer to as ‘feedback cues’. The overall prediction of this model (Fig. 1e–h, GLM) was similar to prior work24, which used a smaller set of both feedback cues and song modes and a different modeling framework (Extended Data Fig. 1a,b, compare ‘Coen 2014’ with ‘This study’ and ‘GLM’). We compared this model to one in which we examined only the mean probability of observing each song mode across the entire courtship (Chance).
We next created a model that incorporated hidden states (also known as latent states) when predicting song from feedback cues; this model is derived from the family of input–output HMMs that we term the GLM–HMM33 (Fig. 1d). A standard HMM has fixed probabilities of transitioning from one state to another, and fixed probabilities of emitting different actions in each state. The GLM–HMM allows each state to have an associated multinomial GLM to describe the mapping from feedback cues to the probability of emitting a particular action (one of the three types of song or no song). Each state also has a multinomial GLM that produces a mapping from feedback cues to the transition probabilities from the current state to the next state (Extended Data Fig. 1c,d). This allows the probabilities to change from moment to moment in a manner that depends on the feedback that the male receives and allows us to determine which feedback cues affect the probabilities at each moment. This model was inspired by previous work that modeled neural activity33, but we use multinomial categorical outputs to account for the discrete nature of male singing behavior. One major difference between this GLM–HMM and other models that predict behavior20,34 is that our model allows each state to predict behavioral outputs with a different set of regression weights.
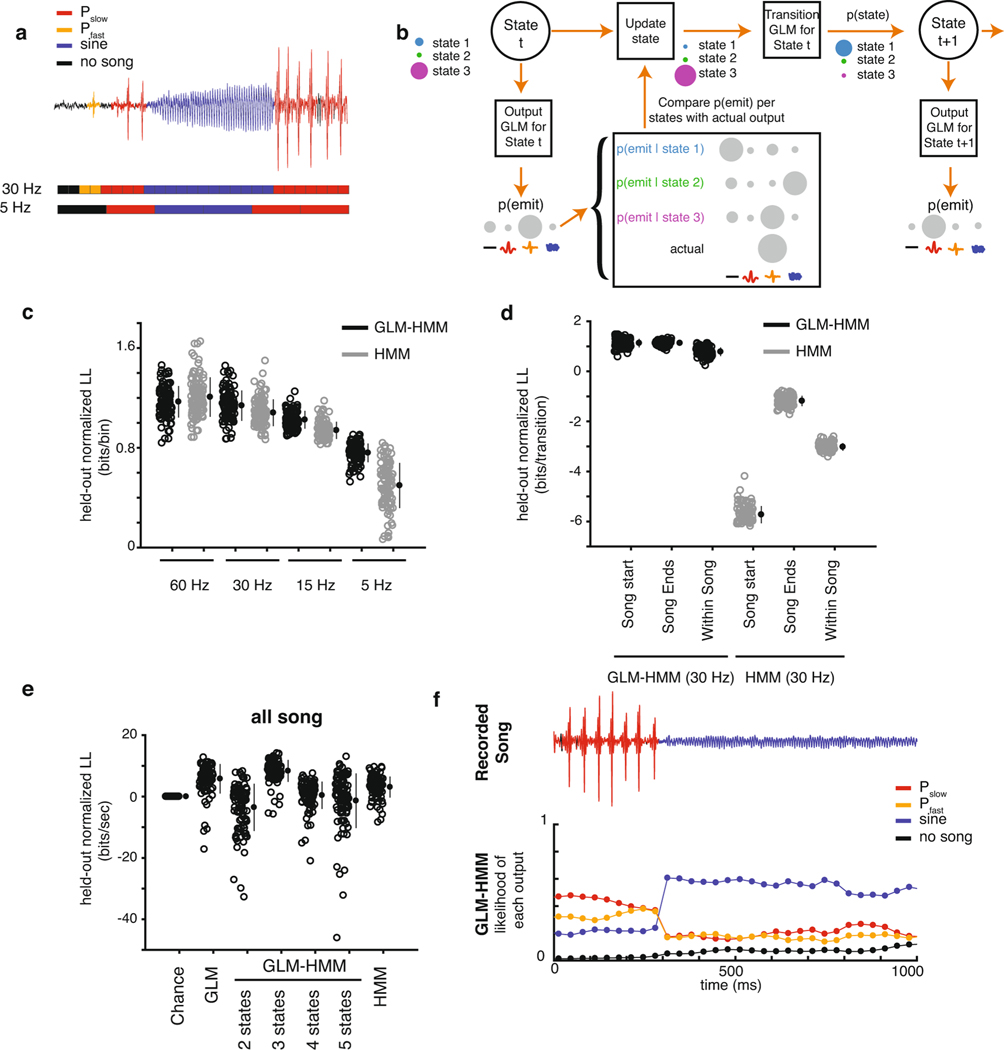
We used the GLM–HMM to predict song behavior (Extended Data Fig. 2a,b) and compared its predictive performance on held-out data to a Chance model, which only captures the marginal distribution over song modes (for example, males produce no song 68% of the time). We quantified model performance using the difference between the log-likelihood of the model and the log-likelihood of the Chance model (see Methods). For all models with a HMM, we used the feedback cue and song mode history to estimate the probability of being in each state. We then predicted the song mode in the next time bin using this probability distribution over states (see Methods). For predicting all song, or every bin across the held-out data, a three-state GLM–HMM outperformed the GLM (Fig. 1e,f, compare middle and lower rows). We found an improvement of 32 bits s−1 relative to the Chance model for the three-state GLM–HMM (versus 6 bits s−1 for the GLM). Given the song-binning rate (30 bins s−1) and knowledge of the mean song probability, a performance of 40.3 bits s−1 would indicate that our model has the information to predict every bin with 100% accuracy. Therefore, the three-state GLM–HMM captured 84.6% of the remaining information as opposed to only 14.6% with a GLM (Fig. 1g). The three-state GLM–HMM also offered a significant improvement even when only the history of feedback cues (not song mode history) was used for predictions (Extended Data Fig. 2e,f; see Methods); however, fitting models with additional states did not significantly improve performance and tended to decrease the predictive power, which was likely due to overfitting (Fig. 1g).
Nevertheless, a HMM was nearly as good at predicting all song, because the HMM largely predicts in the next time bin what occurred in the previous time bin (see Methods), and song consists of runs of each song mode (Fig. 1g; Extended Data Fig. 2c). A stronger test then is to examine song transitions (for example, times at which the male transitions from sine to Pfast)—in other words, predicting when the male changes what he sings. The three-state GLM–HMM offers 1.02 bits per transition over a Chance model (capturing 53% of the remaining information about song transitions, an increase of 110% compared to the GLM), while the HMM was significantly worse than the Chance model at −2.7 bits per transition (Fig. 1h; Extended Data Fig. 2d). Such events were rare and therefore not well captured when examining the performance across all song. Moreover, the three-state GLM–HMM outperformed previous models24, even considering that those models were fitted to subsets of courtship data (for example, only times when the male was close to and oriented toward the female) (Extended Data Fig. 1b). Thus, the GLM–HMM can account for much of the moment-to-moment variation in song patterning by allowing for three distinct sensorimotor strategies or states. We next investigated what these states correspond to and how they affect behavior.
Three distinct sensorimotor strategies during song production.
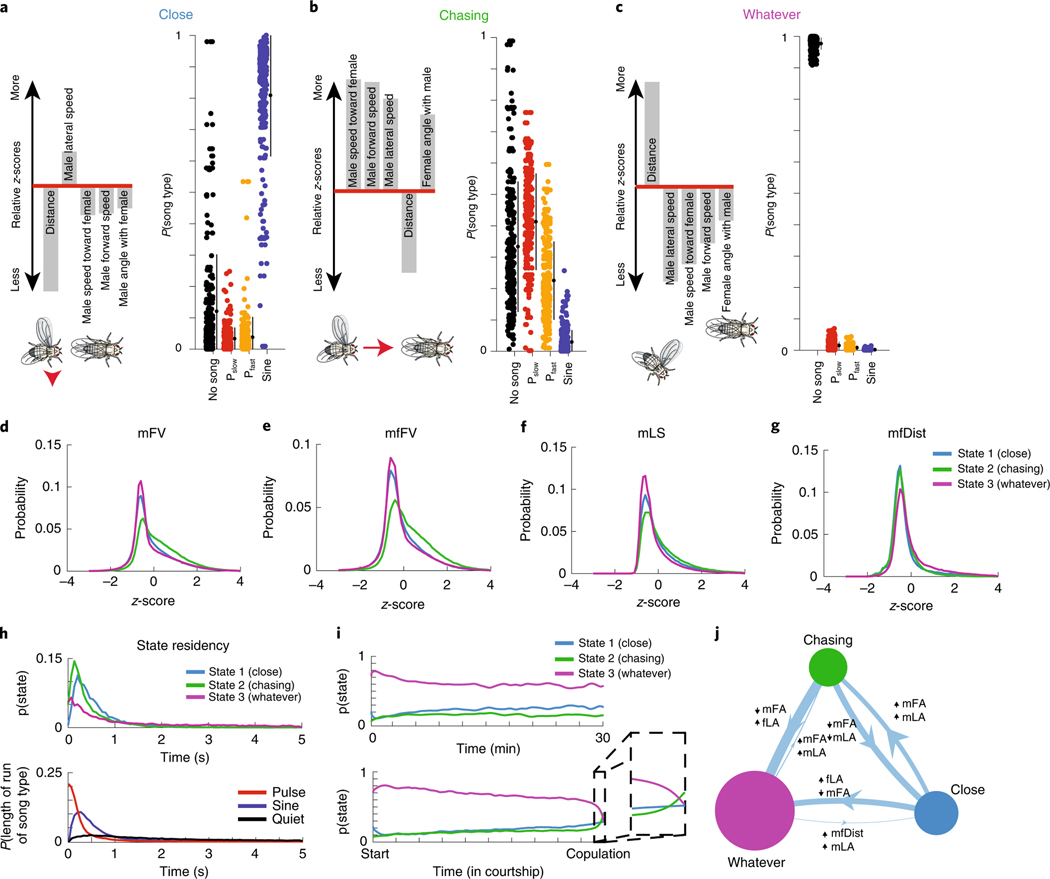
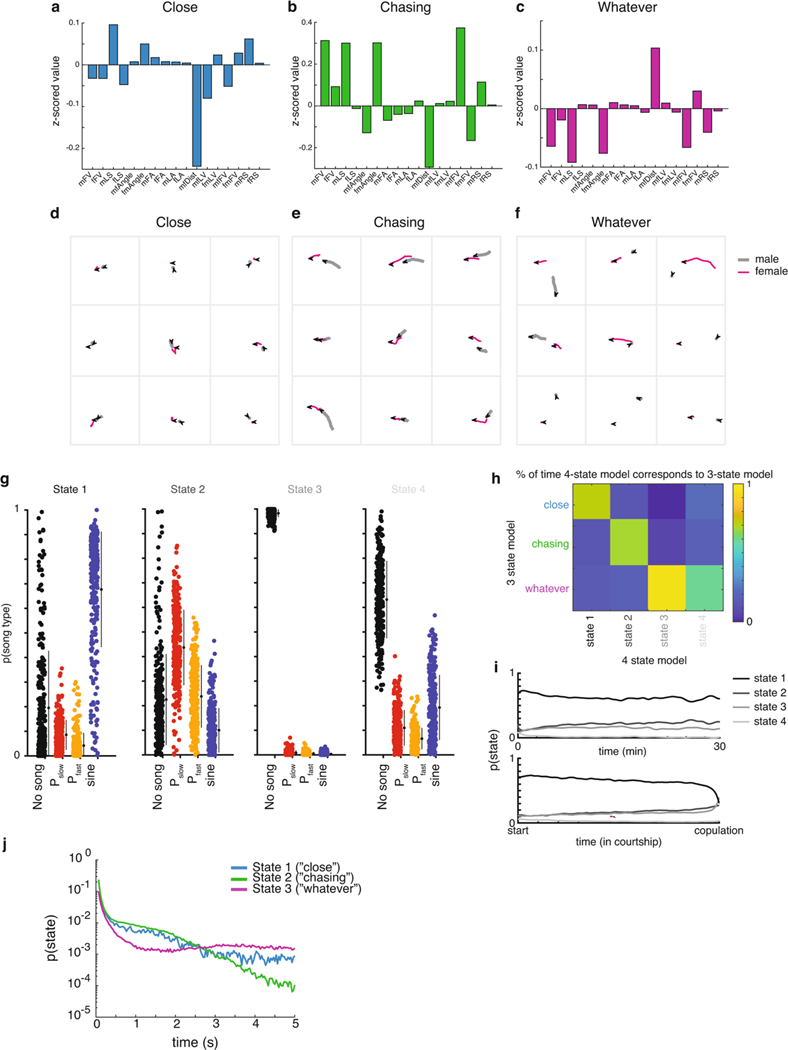
We next determined how the 17 feedback cues and 4 song modes differed across the 3 states of the GLM–HMM. We examined mean feedback cues (Fig. 1b) during each state. We found that in the first state, the male, on average, is closer to the female and moving slowly in her direction; we therefore termed this state the ‘Close’ state (Fig. 2a; Extended Data Fig. 3a,d). In the second state, the male is, on average, moving toward the female at higher speed while still close, and so we called this the ‘Chasing’ state (Fig. 2b; Extended Data Fig. 3b,e). In the third state, the male is, on average, farther from the female, moving slowly and oriented away from her, and so we called this the ‘Whatever’ state (Fig. 2c; Extended Data Fig. 3c,f). However, there was also substantial overlap in the distribution of feedback cues that describe each state (Fig. 2d–g), which indicates that the distinction between each state is more than just these descriptors. Another major difference between the states is the song output that dominates—the Close state mostly generates sine song, while the Chasing state mostly generates pulse song and the Whatever state mostly no song (Fig. 2a–c). However, we note that there is not a simple one-to-one mapping between states and song outputs. All four outputs (no song, Pfast,Pslow and sine) were emitted in all three states, and the probability of observing each output depended on the feedback cues that the animal received at that moment. We compared this model to a GLM–HMM with four states, and it performed nearly as well as the three-state GLM–HMM (Fig. 1g,h). We found that three out of the four states corresponded closely to the three-state model, while the fourth state was rarely entered and best matched the Whatever state (Extended Data Fig. 3g–i). We conclude that the three-state model is the most parsimonious description of Drosophila song-patterning behavior.
Fig. 2 |. Three sensorimotor strategies.
a–c, Left: the five feedback cues that are most different from the mean when the animal is in the Close (a), Chasing (b) or Whatever (c) state (see Methods for details on z-scoring). Illustration of flies is a representation of each state according to these feedback cues. Right: the probability of observing each type of song when the animal is in that state. Filled circles represent individual animals (n = 276 animals, small black circles with lines are the mean ± s.d.). d–g, Distributions of values (z-scored, see Methods) for four of the feedback cues (see Fig. 1b) and for each state. Although a state may have features that are larger or smaller than average, the distributions are highly overlapping (the key in g also applies to d–f). h, Top: the dwell times of the Close, Chasing and Whatever states across all of the data (including both training and validation sets). Bottom: the dwell times of sine trains, pulse trains and stretches of no song (see Fig. 1a for definition of song modes; Pfast and Pslow are grouped together here) across all of the data are dissimilar from the dwell times of the states with which they are most associated. Data from all 276 animals. i, Top: the mean probability across flies of being in each state fluctuated only slightly over time when aligned to absolute time (bottom) or the time of copulation (bottom). Immediately before copulation, there was a slight increased probability of being in the Chasing state (bottom, zoomed-in area). Data are from all 276 animals. j, Areas of circles represent the mean probability of being in each state and the width of each line represents the fixed probability of transitioning from one state to another. The filters that best predicted transitioning between states (and modify the transition probabilities) label each line, with the up arrow representing feedback cues that increase the probability and the down arrow representing feedback cues that decrease the probability.
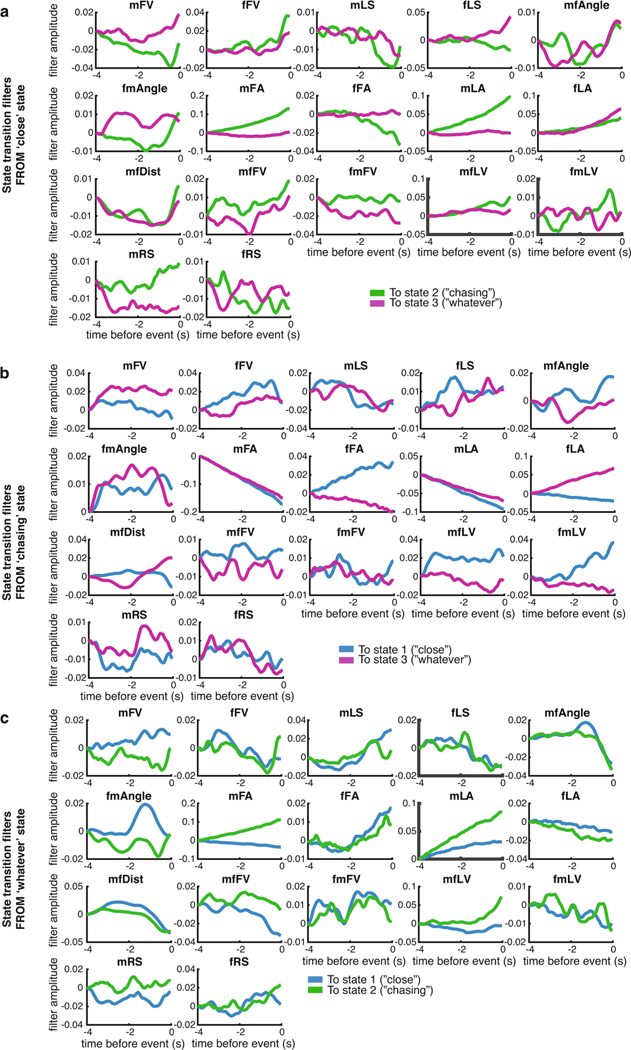
HMMs are memoryless and thus exhibit dwell times that follow exponential distributions. However, natural behavior exhibits very different distributions20,34,35. In our model, which is no longer stationary (memoryless), we found that the dwell times in each state followed a nonexponential distribution (Fig. 2h, upper; Extended Data Fig. 3j). Moreover, the majority of dwell times were on the order of hundreds of milliseconds to a few seconds, which indicates that males switch between states even within song bouts (Fig. 2h, middle). In addition, we found that the mean probability of being in each of the three states was either steady throughout courtship (Fig. 2i, upper) or aligned to successful copulation (Fig. 2i, lower). The only exception was that just before copulation, males were more likely to sing. Accordingly, the probability of the Chasing state increases while the probability of the Whatever state decreases (Fig. 2i, inset) when males stay close to females (Fig. 2g). We next examined which feedback cues (Fig. 1b) predicted the transitions between states (Fig. 2j; Extended Data Fig. 4a–c). These were different from the feedback cues that had the largest magnitude mean value in each state (Fig. 2a–c), which suggests that the dynamics of what drives an animal out of a state is different from the dynamics that are ongoing during the production of a state.
Feedback cues possess different relationships to song behavior in each state.
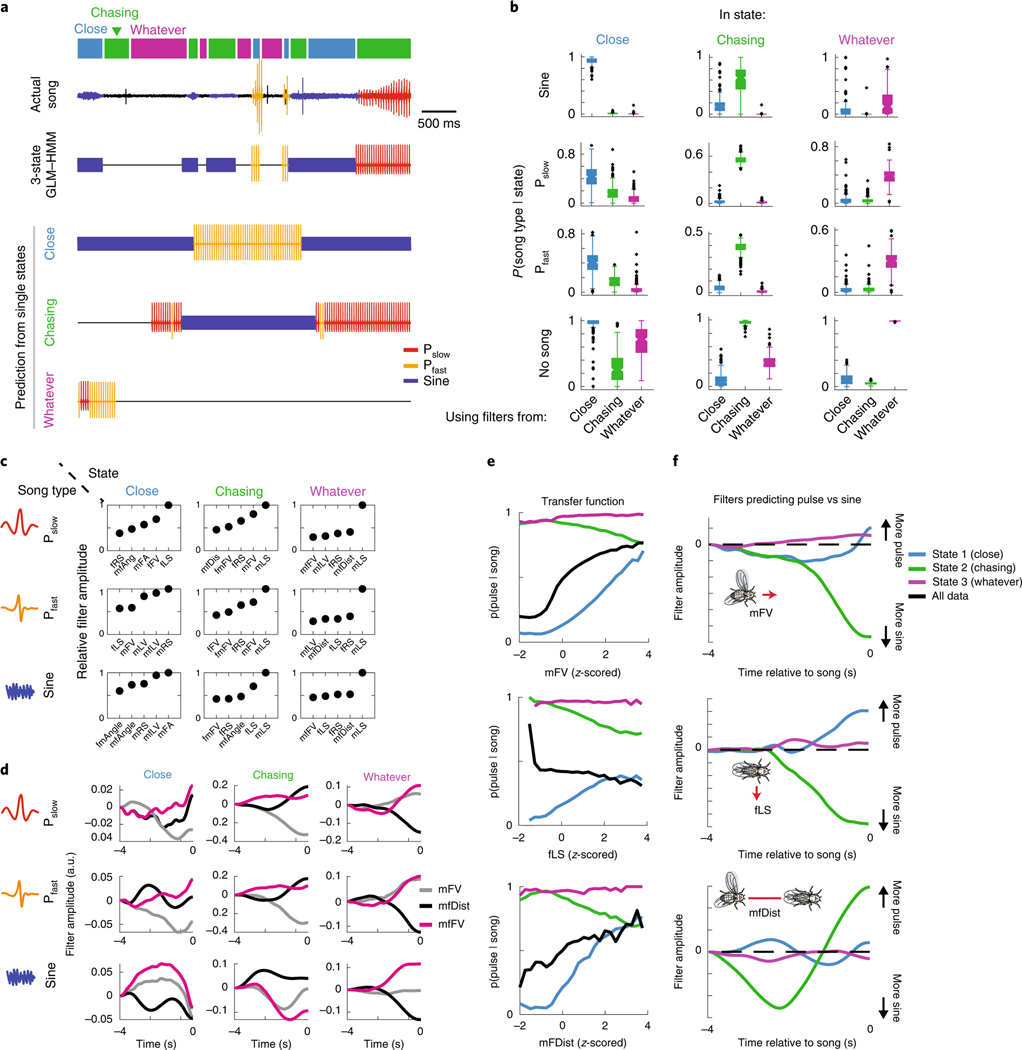
The fact that each song mode is produced in each state of the three-state GLM–HMM (Fig. 2a–c) suggests that the difference between each state is not the type of song that is produced but is the GLM filters that predict the output of each state (which we will refer to as the ‘output filters’). To test this hypothesis, we generated song based on either the full GLM–HMM model or used output filters from only one of the three states (Fig. 3a). This confirmed two features of the model. First, that each set of output filters can predict all possible song outputs depending on the input. Second, the song prediction from any one state is insufficient for capturing the overall moment-to-moment changes in song patterning. To quantify this, we performed a similar analysis over 926 min of courtship data. In this way, we determined what the conditional probability was of observing that song either using only the output filters of that state or only using the output filters of one of the other states (Fig. 3b). We found that the predictions were highly state-specific and that performance degraded dramatically when using filters from the wrong state. For example, even though the Close state was mostly associated with the production of sine song (Fig. 2a), the production of both types of pulse song and no song during the Close state was best predicted using the output filters from the Close state. The same was true for the Chasing and Whatever states, whereby the dynamic patterning by feedback cues showed that the distinction between states was not merely based on the different types of song. Taken together, the highly divergent predictions by state (Fig. 3a) and the lack of explanatory power from other output filters of the states (Fig. 3b) suggest that Close, Chasing and Whatever are in fact distinct states.
Fig. 3 |. Internal states are defined by distinct mappings between feedback cues and song behavior.
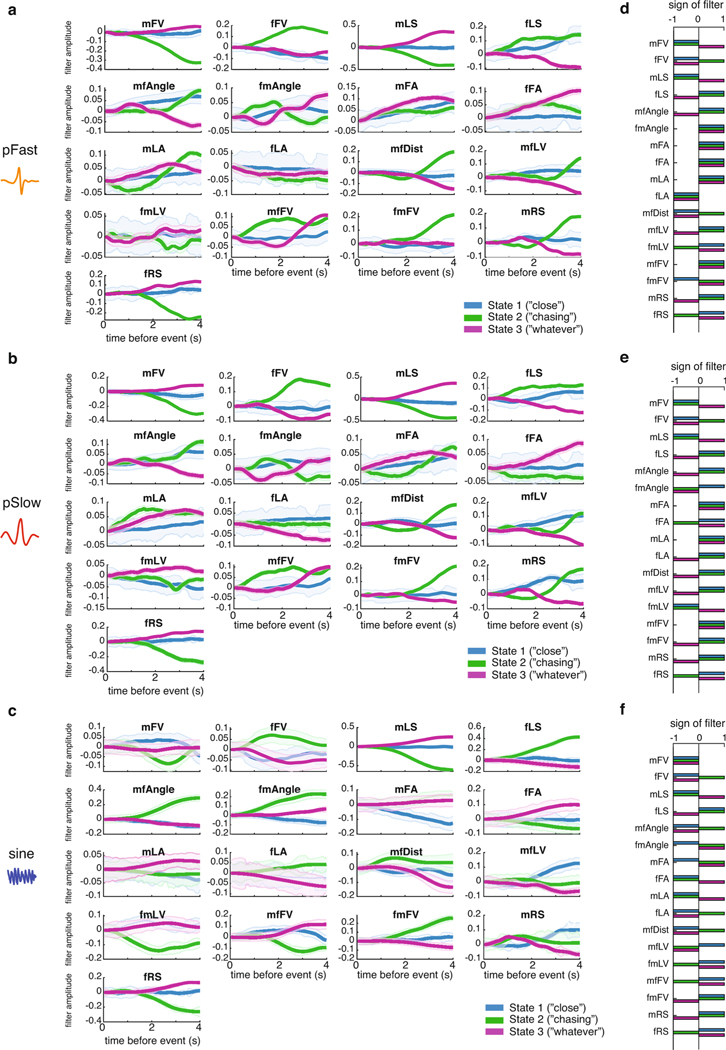
a, A stretch of 500 ms of song production from the natural courtship dataset, with the prediction of states indicated above in colored squares. The prediction of the full GLM–HMM model (third row) is very different from the prediction if we assume that the animal is always in the Close state, Chasing state or Whatever state. The output using the song prediction filters from only that state is illustrated in the lower three rows. b, The conditional probability (across all data, n = 276 animals, error bars represent the s.e.m.) of observing a song mode in each state (predicted by the full three-state GLM–HMM), but using output filters from only one of the states. Conditional probability of the appropriate state is larger than the conditional probability of the out-of-state prediction (largest P = 6.7 × 10−6 across all comparisons, mann–Whitney U-test). Song-mode predictions were highest when using output filters from the correct state. Center lines of box plots represent the median, the bottom and top edges represent the 25th and 75th percentiles, respectively. Whiskers extend to ±2.7 times the standard deviation. c, The five most predictive output filters for each state and for prediction of each of the three of the types of song. Filters for types of song are relative to no-song filters, which are set to a constant term (see Methods). d, Example output filters for each state revealed that even for the same feedback cues, the GLM–HMM shows distinct patterns of integration. Plotted here are the mFV, mfDist and the mfFV; filters can change sign and shape between states. e, Transfer functions (the conditional probability of observing song choice (y axis) as a function of the magnitude of each feedback cue (x axis)) for producing pulse (both Pslow and Pfast) versus sine have distinct patterns based on state. For mFV (upper), fLS (middle) and mfDist (lower), the average relationship or transfer function between song choice and the movement cue (black line) differs with transfer functions separated by state (blue, green and purple). f, Output filters that predict pulse versus sine song for each of the following three feedback cues: mFV (upper), fLS (middle) and mfDist (lower).
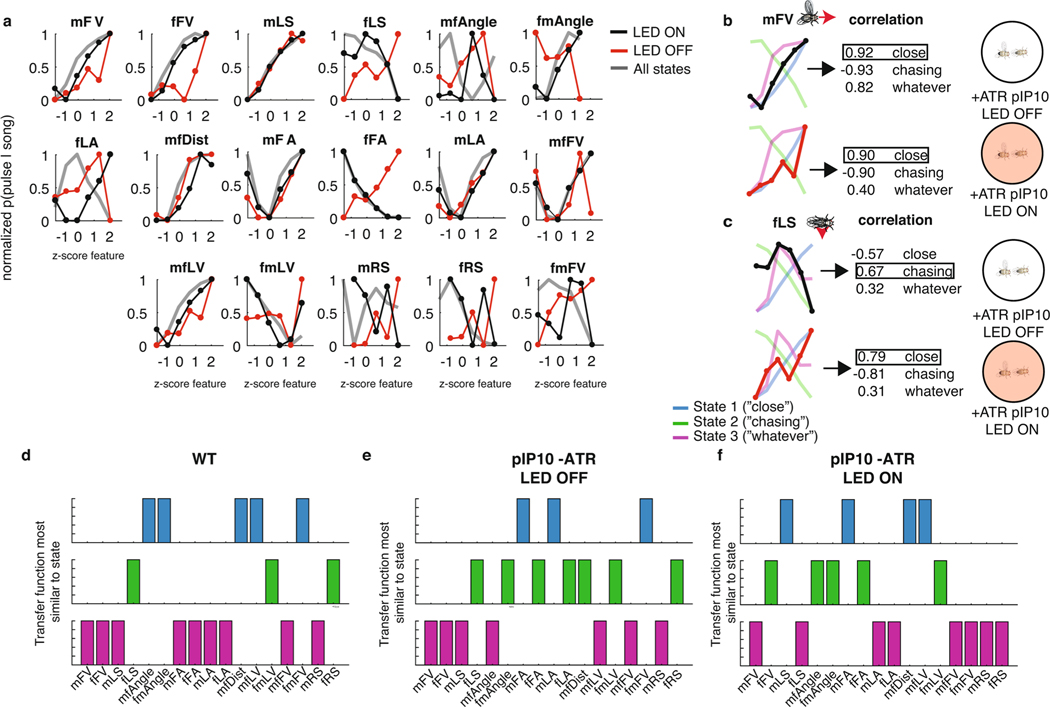
Which feedback cues (Fig. 1b) are most predictive of song decisions in each state? We examined all feedback cues of each song type in each state in rank order (Extended Data Fig. 5; Fig. 3c plots the top five most predictive feedback cues per state and per song type). This revealed that the most predictive feedback cues were strongly reweighted by state; for instance, male lateral velocity (mLV) was the largest predictor of both Pfast and Pslow in the Chasing and Whatever states, but was not one of the top five predictors in the Close state. By comparing the output filters of the same feedback cues for different states, we observed that both the temporal dynamics (Fig. 3d; Extended Data Fig. 6a–c) and the sign of the output filters changed according to state (Fig. 3d; Extended Data Fig. 6d,f). Taken together, these observations suggest that state switching occurs due to both the reweighting of which feedback cues are important and the reshaping of the output filters themselves.
We next determined whether the state-specific sensorimotor transformations uncovered relationships between feedback cues (Fig. 1b) and song behaviors that were previously hidden. Previous work on song patterning identified male forward velocity (mFV), female lateral speed (fLS) and male–female distance (mfDist) as important predictors of song structure24, with, for example, increases in mFV and mLS predicting pulse song, while decreases predicted sine song. By contrast, our model revealed that while, on average, the amount of pulse song increased with male velocity (Fig. 3e, upper, black), this was only true for the Close state, and the relationship (or transfer function) was actually inverted in the Chasing state (Fig. 3e, upper, green and blue). Increased fLS was previously shown to increase the probability of switching from pulse to sine song24; however, when we examined the fLS by state, we found that this feature was positively correlated with the production of pulse song in the Close state (Fig. 3e, middle, blue), but negatively correlated with the production of pulse song in the Chasing state (Fig. 3e, middle, green). Finally, the mfDist was previously shown to predict the choice to sing pulse (at greater distances) over sine (at shorter distances), whereby the relatively quieter sine song is produced when males and females are in close proximity29. Again, we found this to be true only when the animals were in the Close state (Fig. 3e, lower), but the relationship between distance and song type (pulse versus sine) was inverted in the Chasing state. Interestingly, when we examined the feedback cue filters (Fig. 3f), we found that while mFV and fLS were cumulatively summed to predict song type, the distance filter was a long-timescale differentiator across different timescales in each state, as opposed to the short-timescale integrator as previously found24. Our GLM–HMM therefore reveals unique relationships between input and output that were not uncovered when data are aggregated across states.
Activation of pIP10 neurons biases males toward the Close state.
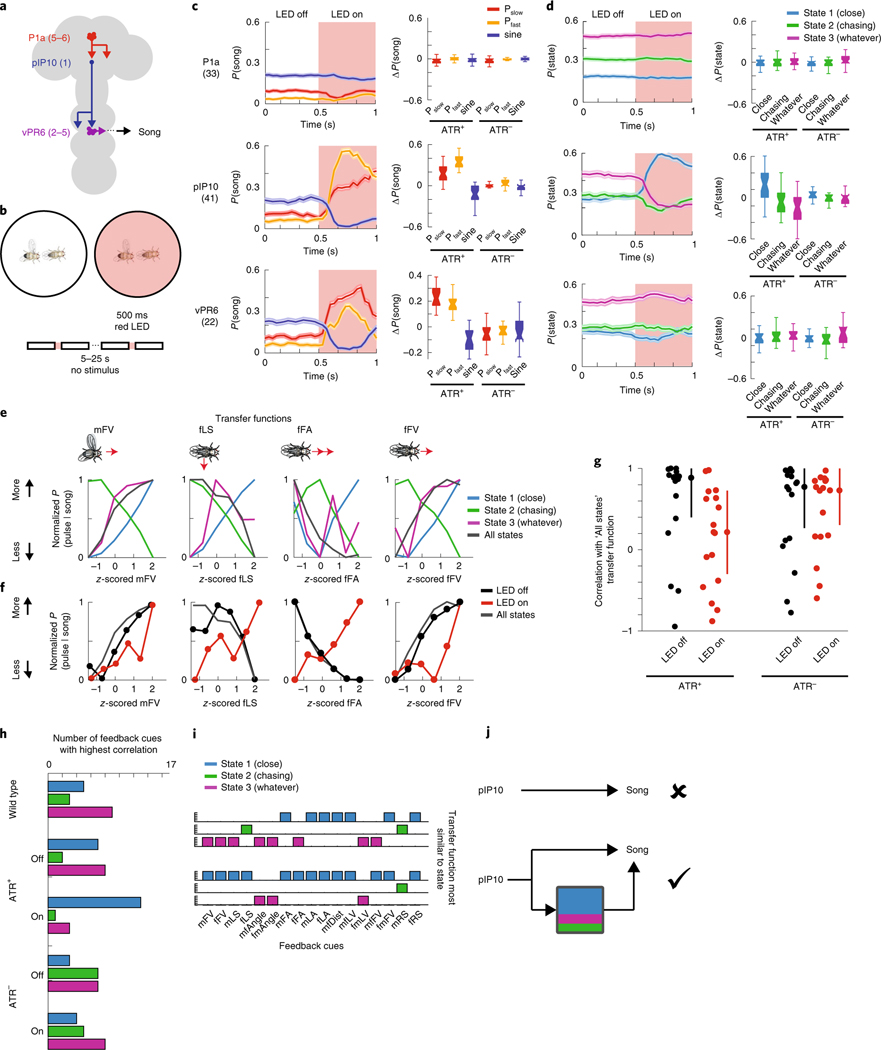
Having uncovered three distinct sensorimotor-patterning strategies via the GLM–HMM, we next used the model to identify neurons that modulate state switching. To do this, we optogenetically activated candidate neurons that might be involved in driving changes in state specifically during acoustic communication; we reasoned that such a neuron might have already been identified as part of the song motor pathway13,32. The goal was to perturb the circuitry underlying state switching, thereby changing the mapping between feedback cues and song modes. We focused on the following three classes of neurons that, when activated, produce song in solitary males: P1a, a cluster of neurons in the central brain; pIP10, a pair of descending neurons; and vPR6, a cluster of ventral nerve cord premotor neurons (Fig. 4a). Across a range of optogenetic stimulus intensities, P1a and pIP10 activation in solitary males induces the production of all three (Pfast, Pslow and sine) types of song, whereas vPR6 activation induces only pulse song (Pfast and Pslow)29. We hypothesized that activation of these neurons produces changes in song either through directly activating motor pathways or through changing the transformation between sensory information and motor output. Previous work has demonstrated that visual information related to estimating the distance between animals is likely relayed to the song pathway between pIP10 neurons and ventral nerve cord song premotor neurons28. pIP10 neurons could therefore influence how sensory information modulates the song premotor network, and consequently affect the mapping between feedback cues and song modes.
Fig. 4 |. Optogenetic activation of song pathway neurons and state switching.
a, Schematic of the three classes of neurons in the Drosophila song-production pathway. b, Protocol for optogenetically activating song-pathway neurons using csChrimson targeted to each of the neuron types in a. c, Left: the observed probability of each song mode aligned to the onset of the optogenetic stimulus. Right: the difference between the mean during LED on from the mean during LED off before stimulation. The numbers of flies tested are indicated in parentheses; error bars represent the s.e.m. Control males are of the same genotype but have not been fed ATR, the required co-factor for csChrimson. Center lines of box plots represent the median, the bottom and top edges represent the 25th and 75th percentiles, respectively. Whiskers extend to ±2.7 times the standard deviation. d, Left: the posterior probability of each state given the feedback cues and observed song (under the three-state GLM–HMM trained on wild-type data), aligned to the onset of optogenetic stimulation; error bars are the s.e.m. Right: activation of pIP10 neurons biases males to the close state and away from the Chasing and Whatever states. The difference between the mean during LED on from the mean during LED off before stimulation is shown on the right. The numbers of flies are listed in parentheses in c. Center lines of box plots represent the median, while the bottom and top edges represent the 25th and 75th percentiles, respectively. Whiskers extend to ±2.7 times the standard deviation. e, Comparison of transfer functions (the conditional probability of observing song choice (y axis) as a function of the magnitude of each feedback cue (x axis; see also Fig. 3e). Shown here are transfer functions for four feedback cues (mFV, fLS, fFA and fFV). Average across all states (dark gray) represents the transfer function from all data without regard to the state assigned by the model. Transfer functions are calculated from all data. f, Transfer functions for the same four feedback cues shown in e, but in animals expressing csChrimson in pIP10 while the LED is off (black) or on (red); transfer functions for data from wild-type animals across all states (dark gray) reproduced from e. g, For all 17 feedback cues, median Pearson’s correlation between transfer functions between all states and the four conditions (pIP10 and ATR+ (LED off or on) or ATR− (LED off or on). Error bars represent the median absolute deviation. h, The number of feedback cues with the highest correlation between the wild-type transfer functions (separated by state) and the transfer functions for each of the conditions (pIP10 and ATR+ (LED off or on) and pIP10 and ATR− (LED off or on). Blue represents transfer functions most similar to the Close state, green to the Chasing state, and purple to the Whatever state. i, Unpacking the data in h for the ATR+ condition. j, Top: schematic of the previous view of pIP10 neuron function. Bottom: pIP10 activation both drives song production and state switching; this revised view of pIP10 neuron function would not have been possible without the computational model.
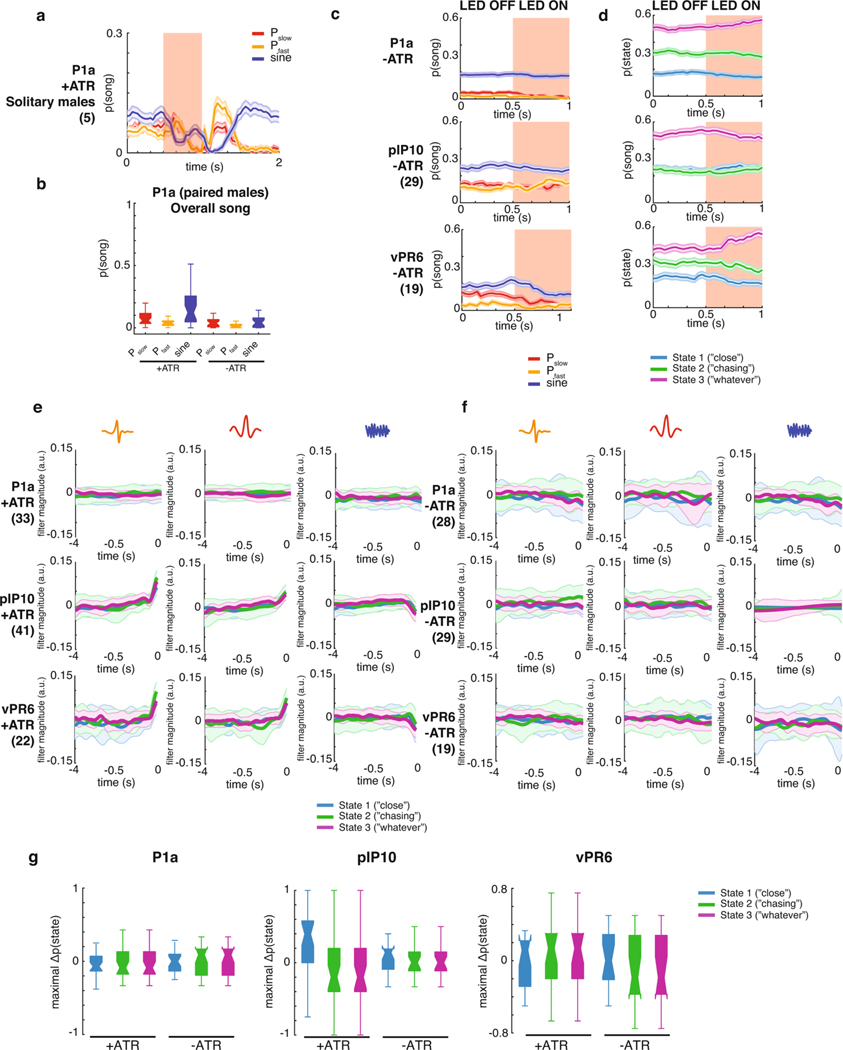
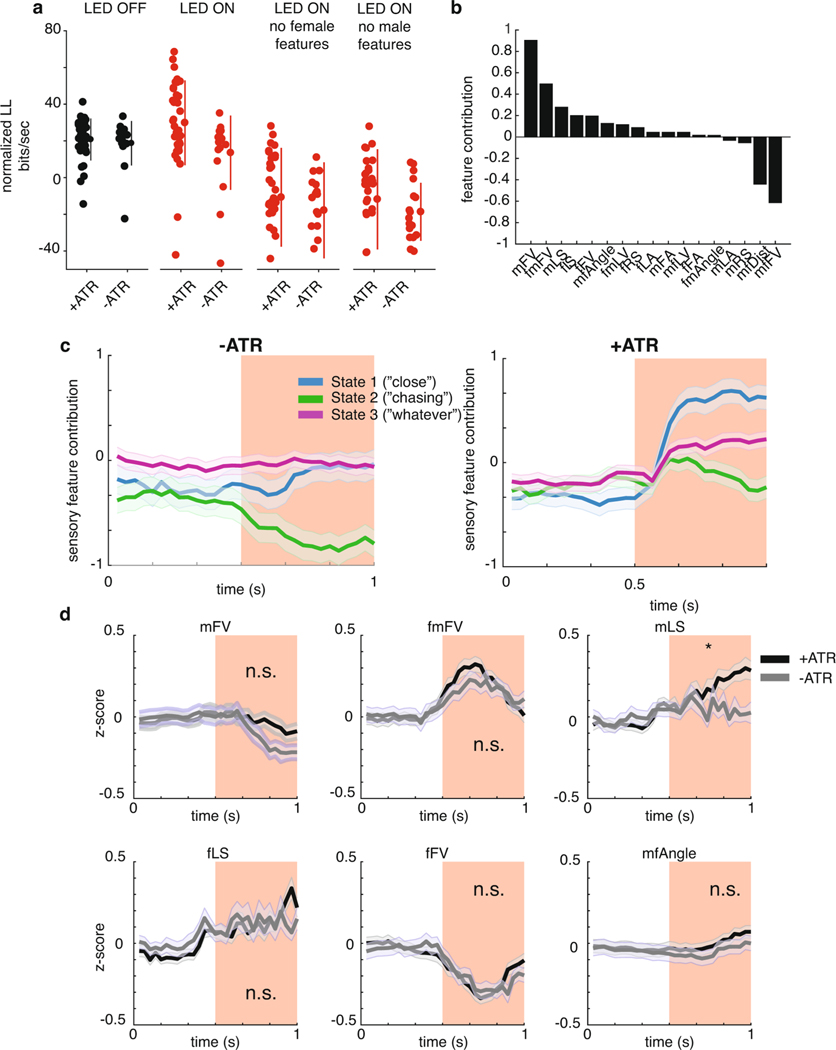
We expressed the light-sensitive opsin csChrimson using driver lines targeting P1a, vPR6 and pIP10 (see Methods), and chose a light intensity level, duration and inter-stimulus interval that reliably produces song in solitary males for these genotypes29. Here, we activated neurons in the presence of a female, with varying pauses between stimuli to induce a change in state without completely overriding the role of feedback cues (Fig. 4b). We recorded song via an array of microphones tiling the floor of the chamber and wrote new software, called DeepFlyTrack, for tracking the centroids of flies on such difficult image backgrounds (see Methods). Using this stimulation protocol, P1a activation drove a general increase in song during courtship (Extended Data Fig. 7a–c), while pIP10 and vPR6 activation reliably drove song production during the optogenetic stimulus (Fig. 4c; Extended Data Fig. 7c). The activation of P1a during courtship is different from previous findings in solitary males, which showed stimulus-locked changes in song production29 (Extended Data Fig. 7b), while the type and quantity of song production from pIP10 and vPR6 activation were more similar29. To determine whether optogenetic activation affected state switching, we fitted our GLM–HMM to recordings from males of all three genotypes (including both experimental animals and controls not fed the csChrimson channel co-factor all trans-retinal (ATR− animals; see Methods).
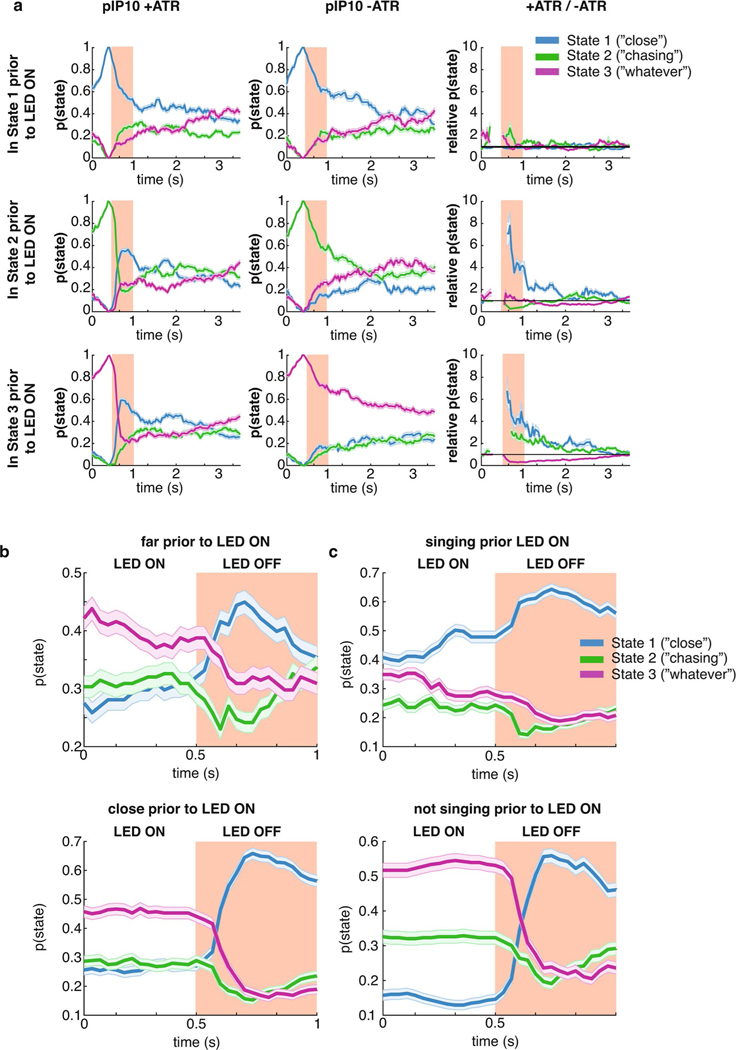
To account for the possibility that activating these neurons directly drives song production, we supplemented the GLM–HMM model (Fig. 1) with a filter encoding the presence or absence of the optogenetic light-emitting diode (LED) stimulus. This filter (termed the ‘opto filter’) was fitted separately for each genotype (Supplementary Table 1) and accounted for the change in probability of producing song that was unrelated to sensory information. The opto filters for each output type were similar across all states in ATR-fed flies (Extended Data Fig. 7e,f), which indicates that any differences we found between states could be attributable to other aspects of the model (not the presence or absence of the LED light). As expected, flies not fed ATR had opto filters that showed no influence of the LED stimulus on song (Extended Data Fig. 7f). We found that there was a large increase in the probability of entering the Close state when pIP10 neurons were activated, but little effect on state when P1a or vPR6 neurons were activated (Fig. 4d; Extended Data Fig. 7d,g). We found a consistent effect when we tested another line that labeled pIP1036 (data not shown). The Close state was typically associated with an abundance of sine song, although it also produced all other song modes during natural behavior (Fig. 2a); nonetheless, in this case, pIP10 activation was associated with increased pulse song (Fig. 4c; Extended Data Fig. 7e). Even though the male mostly sang pulse song during optogenetic activation of pIP10, the dynamics of the feedback cues that predict song were better matched to the output filters of the Close state of the GLM–HMM. Activation of pIP10 neurons always increased the probability that the animal would transition into the Close state, independent of which state the animal was in previously; however, if the male was already in the Close state, there was no significant change in state (Extended Data Fig. 8a) whether the animal was close to or far away from the female (Extended Data Fig. 8b) or singing or not singing (Extended Data Fig. 8c).
We next explored the possibility that the effect was somehow due to nuances of model fitting. Because vPR6 activation resulted in changes in song that were similar in aggregate to pIP10 activation (Fig. 4c) without a change in state (Fig. 4d), we concluded that changing state is not synonymous with changing song production. We removed male and female feedback cues from the GLM–HMM by zeroing out their values (see Methods) and found that a model without feedback cues poorly predicted song choice, which suggests that the prediction of the Close state relies on the moment-to-moment variation in these features (Extended Data Fig. 9a). In addition, we examined individual feedback cues and found that the vast majority were more like the Close state (Extended Data Fig. 9b,c). We finally tested whether activation of pIP10 neurons puts the animal in a different behavioral context with respect to the female (for example, driving him closer to the female). By looking at the six feedback cues that were the strongest predictors of being in the Close state, we found that the dynamics were indistinguishable from ATR− controls and could not explain the observed difference in state (Extended Data Fig. 9d). Instead, our data point to the fact that pIP10 neurons affect the way in which feedback cues (Fig. 1b) modulate song choice.
We next tested whether we could observe, following pIP10 activation, a change in song strategy independent of the GLM–HMM model. As in Fig. 3e, we examined the choice by males to produce pulse versus sine song. Because pIP10 directly drove an overall increase in pulse song (Fig. 4c), we normalized the data to the highest and lowest pulse rate to more easily visualize the transfer function (the relationship between feedback cues and song choice) used by the male (Fig. 4e). The relationship between feedback cues and the probability of producing pulse song was reversed between the Close and the Chasing state. We examined the correlation between these transfer functions from wild-type males and males with pIP10 activation during LED on or LED off (see Methods). We found that these transfer functions were similar to wild type (combining across all three states) for pIP10-activated flies during LED off, but were highly dissimilar when the LED is on, which suggests that song patterning changed during these times (Fig. 4f,g; Extended Data Fig. 10a). We then tested whether these transfer functions are shifted in a particular direction, such as toward the functions from the Close state in the wild-type data (Extended Data Fig. 10b, blue lines). During periods when the LED is off, the transfer function resembled a mix of states (Fig. 4h). However, transfer functions during LED on shifted toward Close state transfer functions (Fig. 4). This was true across 13 out of 17 feedback cues (Fig. 4i; Extended Data Fig. 10d–f). This analysis, independent of the GLM–HMM, confirms that pIP10 activation biases the nervous system toward the Close state set of sensorimotor transformations that shape song output. pIP10 neurons therefore play a dual role in the acoustic communication circuit during courtship (Fig. 4j) in that they both directly drive pulse song production (Fig. 4c) and bias males toward the Close state (Fig. 4i). These results highlight the value of the GLM–HMM for identifying the neurons that influence dynamically changing internal states and are critical for shaping behavior.
Discussion
Here, we developed a model (the GLM–HMM) that allows experimenters to identify, in an unsupervised manner, dynamically changing internal states that influence decision-making and, ultimately, behavior. Using this model, we found that during courtship, Drosophila males utilize three distinct sensorimotor strategies (the three states of the model). Each strategy corresponded to a different relationship between inputs (17 feedback cues that affect male singing behavior) and outputs (three types of song and no song). While previous work had revealed that fly feedback cues predict song-patterning decisions24,29, the discovery of distinct state-dependent sensorimotor strategies was only possible with the GLM–HMM. This represents an increase in information captured of 70% for all song and 110% for song transitions compared to a GLM. While we have accounted for much of the variability in song patterning, we speculate that the remaining variability is due to either noise in our segmentation of song37 or the fact that we did not measure some male behaviors that are known to be part of the courtship interaction, including tapping of the female via the forelegs and proboscis extension38. The use of new methods that estimate the full pose of each fly39 combined with acoustic recordings should address this possibility.
Several recent studies have used latent state models to describe with incredible accuracy what an animal is doing over time19–21,34,40. These models take continuous variables (for example, the angles between the joints of an animal) and discretize them into a set of outputs or behavioral actions. This generates maps of behavioral actions (such as grooming, fast walking and rearing) and the likelihood of transitions between actions. In this study, the behavior we focused on can also be considered as a continuous variable: the song waveform of the male, which is generated by the vibration of his wing. This variable can be discretized into three separate types of song in addition to no song. We show here that it is crucial to sort these actions according to how feedback cues bias choices between behavioral outputs. In other words, we demonstrated the importance of considering how changes in feedback cues affected the choice of behavioral outputs and the transitions between these choices. Animals do not typically switch between behaviors at random, and the GLM of our GLM–HMM provides a solution for determining how feedback cues modulate the choice of behavioral outputs over time. This will be useful not only for the study of natural behaviors, as we illustrate here, but also for identifying when animals switch strategies during task-based behavior16,41. The broader framework presented here can also flexibly incorporate continuous internal states with state-dependent dynamics42. Alternatively, states themselves may operate along multiple timescales that necessitate hierarchical models in which higher-order internal states modulate lower-order internal states, which in turn modulate the actions of the animal43.
In our study, differences in internal state corresponded to differences in how feedback cues pattern song. This is analogous to moving toward someone and engaging in conversation when in a social mood and avoiding eye contact or turning away when not. In both cases, the feedback cues remain the same (the approaching presence of another individual), but what changes is the mapping from sensory input to behavior. Previous studies of internal state have focused mostly on states that can either be controlled by an experimenter (for example, hunger and satiety) or easily observed (for example, locomotor status). By using an unsupervised approach to identify states, we expand these studies to states that animals themselves control and are difficult to measure externally. This opens the door to finding the neural basis of these states. We provide an example of this approach by investigating how the activation of neurons previously identified to drive song production in Drosophila affect the state predictions from the GLM–HMM. We found that activation of a pair of neurons known as pIP10 not only robustly drove the male to produce two types of song (Pfast and Pslow), as shown previously29, but also drove males into the Close state, a state that is mostly associated with the production of sine, not pulse, song in wild-type flies. pIP10 neurons are hypothesized to be postsynaptic to P1 neurons that control the courtship drive of male flies12,32,44. Previous work28 found that dynamic modulation of pulse song amplitude likely occurred downstream of pIP10 neurons, in agreement with what we have found here. In other words, activation of pIP10 neurons both directly drives pulse song production (likely via vPR6; see Fig. 4) and affects the way feedback cues modulate song choice. While we do not yet know how this is accomplished, our work suggests that pIP10 neurons affect the routing of sensory information into downstream song premotor circuits in a manner analogous to that of amygdala neurons, which gate sensory information and suppress or promote particular behaviors17,45.
What insight does our model provide to studies of Drosophila courtship more broadly? We expect that internal state also affects the production of other behaviors produced during courtship, such as tapping, licking, orienting and mounting. This includes not only states such as hunger15,46, sexual satiety47, or circadian time48, but also states that change on much faster timescales, as we have observed for acoustic signal generation. Identifying these states will require the monitoring of feedback cues that animals have access to during all behaviors produced during courtship. The feedback cues governing these behaviors may extend beyond the ones described here and may include direct contact between the male and the female or the dynamics of pheromonal experience. The existence of these states may indicate that traditional ethograms detailing the relative transitions between behaviors exhibit additional complexity or that there are potentially overlapping ‘state’ ethograms.
Why does the male fly possess the three states that we identified? What is striking about the three states is that feedback cues in one state have a completely different relationship with song outputs versus in another state. For example, increases in mFV correlated with increased pulse song in the Close state, but increased sine song in the Chasing state. These changes in relationship may be due to changing female preferences over time (that is, the female may prefer different types of song at different times depending on changes in her state), changing goals of the male (potentially to signal the female to slow down when she is moving quickly or to prime her for copulation if she is already moving slow) or changes in energetic demands (that is, the male balancing conserving energy with producing the right song for the female). The existence of different states may also generate more variable song over time, which may be more attractive to the female31, a behavior that is consistent with work in birds49. Future studies that investigate the impact of state switching on male courtship success and mating decisions may address some of these hypotheses.
In conclusion, in comparison to classical descriptions of behavior as fixed action patterns50, even instinctive behaviors such as courtship displays are continuously modulated by feedback signals. We also show here that the relationship between feedback signals and behavior is not fixed, but varies continuously as animals switch between strategies. Instead, just as feedback signals vary over time, so too do the algorithms that convert these feedback cues into behavior outputs. Our computational models provide a method for estimating these changing strategies and serve as essential tools for understanding the origins of variability in behavior.
Methods
Flies.
For all experiments, we used 3–7-day-old virgin flies collected from density-controlled bottles seeded with 8 males and 8 females. Fly bottles were kept at 25 °C and 60% relative humidity. Male virgined flies were then housed individually across all experiments, while female virgined flies were group-housed in wild-type experiments and individually housed in the transgenic experiments (Fig. 4), and kept in behavioral incubators under a 12–12 h light–dark cycle. Before recording with a female, males were painted with a small spot of opaque ultraviolet-cured glue (Norland Optical and Electronic Adhesives) on the dorsal mesothorax to facilitate identification during tracking. All wild-type data were collected in a previous study24 and consisted of either a random subset of 100 flies not used for model training (Fig. 1g,h; Extended Data Fig. 2c–g) or all wild-type flies in the dataset. In Fig. 4, we collected additional data using transgenic flies. Asterisks indicate previously published data24.
Behavioral chambers.
Behavioral chambers were constructed as previously described24,28,29. For optogenetic activation experiments, we used a modified chamber in which the floor was lined with white plastic mesh and equipped with 16 recording microphones and video recorded at 60 Hz. To prevent the LED from interfering with the video recording and tracking, we used a short-pass filter (ThorLabs FESH0550, cut-off wavelength of 550 nm). Flies were introduced gently into the chamber using an aspirator. Recordings were timed to be within 150 min of the behavioral incubator lights switching on to catch the morning activity peak. Recordings were stopped after 30 min or after copulation, whichever was sooner. If males did not sing during the first 5 min of the recording, the experiment was discarded. In Fig. 4, all ATR+ animals (flies fed ATR) that did not vibrate their wings when tested under red LED light the day before the experiment were excluded from analysis. The dataset of wild-type flies (Figs. 1–3) came from a previous study24; for that study, data from flies that moved 1.5 mm min−1 or sang at low amplitudes relative to other flies of the same strain were excluded on the basis of possible poor health (this criterion applied to 25 out of 679 males).
Optogenetic activation.
Flies were maintained for at least 5 days before the experiment on either regular fly flood or fly food supplemented with retinal (1 ml ATR solution (100 mM in 95% ethanol) per 100 ml of food). CsChrimson51 was activated using a 627-nm LED (Luxeon Star) at an intensity of 0.46 mW mm−2 for pIP10 neuron activation. Light stimuli were delivered for 500 ms of constant LED illumination, randomized to occur every 5–25 s. Sound recording and video were synchronized by positioning a red LED that turned on and off with a predetermined temporal pattern in the field of view of the camera and whose driving voltage was recorded on the same device as the song recording.
Data collection and analyses were not performed blinded to the conditions of the experiments, but all analyses of song and tracking of flies was automated using custom-written software. No statistical methods were used to predetermine sample sizes, but our sample sizes were similar to those reported in previous publications24,28,29. Animals were randomly assigned to the ATR+ or ATR− groups following collection.
Statistical methods.
Data were checked for normality using the Lilliefors test and found to be non-normal. As such, all pairwise comparisons were made using the Mann–Whitney U-test. All reported correlations were calculated using Pearson’s correlation.
Fly tracking via DeepFlyTrack.
Data from a previous study24 were previously tracked.
For new data, tracking was performed using a custom neural network tracker we call DeepFlyTrack. The tracker has the following three components: identifying fly centroids, orienting flies and tracking fly identity across frames. Frames were first annotated to indicate the position of a blinking LED, which was then used for synchronization with the acoustic signal and to indicate the portion of the video frame containing the fly arena.
We designed a neural network trained on 200 frames containing fly bodies annotated with the centroid, the head and the tail. These annotations were convolved with a two-dimensional Gaussian with a standard deviation of five. The network was trained to reconstruct this annotated data from grayscale video frames using a categorical cross entropy loss function. The neural network contained five 4 × 4 convolutional layers. The first four layers passed through a ReLu activation function and the final layer passed through a sigmoidal nonlinearity. The network was trained using Keras with the input frames being a 192 × 192 × 3 patch containing 0, 1 or 2 flies. After training, the network predicted entire video frames. These were thresholded, and points were fit with k-means, where k = 2. To keep track of fly identity, we used the Hungarian algorithm to minimize the distance between flies identified in subsequent frames. The points were fit to an ellipse to extract putative body center and orientation. We used this ellipse for the centroid and an angle of ±180°. To fully orient flies, we assumed that the fly typically moves forward and rarely turns more than 90° per frame. In 1,000 frame chunks, we found the 360° orientation that best fit these criteria. Position and orientation were smoothed every two frames to downsample from 60 Hz to the 30 Hz used in previous work24. Fly identity and orientation were then manually fixed (average 4.5 identity flips per 30 min).
Song segmentation.
Song data from a previous study24 was resegmented to separate Pfast and Pslow according to another previous study29. New song data (Fig. 4) were also segmented using this new pipeline.
Chance model.
The probability of observing each of the four song modes (no song, Pfast, Pslow and sine) in a given frame was calculated from a random sample of 40 wild-type flies, which we denote as pChance(song type). We used two Chance models: one drawn from song statistics averaged across all of the courtship and one drawn from song only at transitions between output types. Thus, the probability of observing a particular song mode was determined as follows:
| (1) |
where Ni is the number of time bins during the courtship with song mode i, and N is the total number of time bins, either during the entire courtship or only at the time of song transitions, averaged across all 40 flies. The likelihood of observed song sequences under the Chance models (Fig. 1g,h) was computed using 100 additional flies that were sampled from the wild-type dataset.
Cross-validation.
All hyperparameters were inferred by cross-validation from held-out data not used for fitting. Across all analyses, models were fitted using one dataset consisting of 40 flies, and performance was validated on data from individual flies that were not used in the fitting or the hyperparameter fitting. Because performance was cross-validated on test data, increasing the number of parameters did not necessarily give higher performance values. See, for instance, Fig. 1g, whereby the five-state model achieved lower performance than the three- or four-state model despite more free parameters.
Feedback cues.
Data from tracked fly trajectories were transformed into a set of 17 feedback cues that were considered as inputs to the model for male singing behavior. For each cue, we extracted 4 s of data before the current frame, sampled at 30 Hz (120 time samples for each cue), which results in a feature vector of length of 17 × 120 = 2,040. We augmented this vector with a ‘1’ to incorporate an offset or bias, yielding a vector of length 2,041 as input to the model in each time bin.
For model fitting, we formed a design matrix of size T × 2,041, where T is the number of time bins in the dataset from a single fly after discarding the initial 4 s. We concatenated these design matrices across flies so that a single GLM–HMM could be fitted to the data from an entire population.
Multinomial GLM.
Previous work24 used a Bernoulli GLM (also known as a logistic regression model) to predict song from a subset of the feedback cues that we consider here. That model sought to predict which of two types of song (pulse or sine) a fly would sing at the start of a song bout during certain time windows (for example, times when the two flies were less than 8-mm apart, and the male had an orientation <60° from the centroid of the female).
Here, we instead use a multinomial GLM (also known as multinomial logistic regression) to predict which of four types of song (no song, Pfast, Pslow and sine) a fly will sing at an arbitrary moment in time. The model was parameterized by a set of four filters {Fi}, i ∈ {1, 2, 3, 4}, which map the vector of feedback cues to the non-normalized log-probability of each song mode.
The probability of each song mode given under the model given feedback cue vector st can be written as follows:
| (2) |
Note that we can set the first filter to all-zeros without loss of generality, since probabilities must sum to 1. We fit the model via numerical optimization of the log-likelihood function to find its maximum and used a penalty on the sum of squared differences between adjacent coefficients to impose smoothness. See the description of the GLM–HMM below for more details (this is a one-state GLM–HMM).
GLM–HMM.
The simplest form of a HMM has discrete hidden states that change according to a set of fixed transition probabilities. At each discrete time step, the model is in one of the hidden states and has a fixed probability of transitioning to another state or staying in the same state. If the outputs are discrete, the HMM has a fixed matrix of emission probabilities, which specifies the probability over the set of possible observations for each hidden state.
The GLM–HMM we introduce in this paper differs from a standard HMM in two ways. First, the probability over observations is parameterized by a GLM, with a distinct GLM for each latent state. This allows for a dynamic modulation of output probabilities based on an input vector, st, at each time bin. Second, transition probabilities are also parameterized by GLMs, one for the vector of transitions out of each state. Thus, the probability of transitioning from the current state to another state also depends dynamically on a vector of external inputs (feedback cues) that vary over time.
A similar GLM–HMM has been previously described33, although that model used Poisson GLMs to describe probability distributions over spike train outputs. Here, we considered a GLM–HMM with multinomial GLM outputs that provides a probability over the four song modes (as described above).
Fitting.
To fit the GLM–HMM to data, we used the expectation–maximization (EM) algorithm33 to compute maximum-likelihood estimates of the model parameters. EM is an iterative algorithm that converges to a local optimum of the log-likelihood. The log-likelihood (which may also be referred to as the log-marginal likelihood) is given by
| (3) |
where Y = y1,...,yT are the observations at each time point and Z = z1,...,zT are the hidden states that the model enters at each time point. The joint probability distribution over data and latents, known as the complete-data log-likelihood, can be written as follows:
| (4) |
where θ1 is a parameter vector specifying the probability over the initial latent state z1, θtr denotes the transition model parameters and θ0 denotes the observation model parameters. We abbreviate as follows:
| (5) |
| (6) |
| (7) |
P(z1|θ1) is initialized to be uniformly distributed across states and then fit on successive E-steps.
E-step.
The E-step of the EM algorithm involves computing the posterior distribution P(Z|Y, θ) over the hidden variables given the data and model parameters. We use the adapted version of the Baum–Welch algorithm as previously described33. The Baum–Welch algorithm has two components: a forward step and a backward step. The forward step identifies the probability am(t) = P(Y1 = y1,...,Yt = yt, Zt = m|θ) of observing Y = y1, y2,...,yt and, assuming there are N total states, of being in state m at time t by iteratively computing as follows:
| (8) |
where ai(1) = πi. The backward step does the reverse in that it identifies the conditional probability of future observations given the latent state, as follows:
| (9) |
where bi(T) = 1. These allow us to compute the marginal posterior distribution over the latent state at every time step, which we denote γ(Zt) = P(Zt|Y, θ), and over pairs of adjacent latent states, denoted ξ(Z t, Zt+1) = P(Zt, Zt+1|Y, θ), which are given by
| (10) |
| (11) |
| (12) |
In practice, for larger datasets, it is common to run into underflow errors due to the repeated multiplication of small probabilities in the equations above. Thus, it is typical to compute {am(t)} and {bm(t)} in scaled form. See ref. 52 for details.
M-step.
The M-step of the EM algorithm involves maximizing the expected complete-data log-likelihood for the model parameters, whereby the expectation is with respect to the distribution over the latents computed during the E-step, as follows:
| (13) |
As noted above, our model describes transition and emission probabilities with multinomial GLMs, each of which is parameterized by a set of filters. Because these GLMs contribute independently to the α, η and π terms above, we can optimize the filters for each model separately. Maximizing the π term is equivalent to finding πi = P(Z1 = i|Y, θ). We maximize the α term as previously described33 (in appendix B of that publication) with the addition of a regularization parameter. The transition probability from state i to state j at time t is defined as
| (14) |
where we define all filters from one state to itself Fi, i to be 0 without loss of generality.
Additionally, we added regularization penalties into the model to avoid overfitting. We used both Tikhonov regularization and difference smoothing and found difference smoothing to provide both better out-of-sample performance and filters that were less noisy. Difference smoothing adds a penalty for large differences in adjacent bins in each filter. However, because each filter was applied across U features of length L, we did not apply a penalty between bins across features. For some regularization coefficient r, the model that we fit became
| (15) |
In the previous study33, both the gradient and Hessian for fitting the transition filters during the M-step were provided. In our hands, we found that computing the Hessian was computationally more expensive for the large datasets that we are working with and did not speed up the fitting procedure. We computed the inverse Hessian at the end of each stage of fitting to provide an estimate of the standard error of the fit.
The previously described GLM–HMM33 was formulated for neural data, in which the outputs at each time were Poisson or Bernoulli random variables (binned spike counts). As noted above, we modified the model to use categorical outputs to predict the discrete behaviors that the animal was performing. Similar to the transition filters, for emission filters, one filter may be chosen to be the ‘baseline’ filter set to 0. We used a multinomial model that assumes coefficients F = PF1,…,Fn, where the filter F1 is assumed to be the baseline filter equal to 0. The probability of observing some output yt (out of O possible outputs) is governed by the equation
| (16) |
We then maximize the following:
| (17) |
To avoid overfitting, we increased the smoothness between bins by penalizing differences between subsequent bins for each feature using the difference operator D multiplied by the regularization coefficient r as described for the transition filter. No smoothing penalty was applied at the boundary between features. The objective function to optimize becomes
| (18) |
which has the gradient
| (18) |
After the M-step was completed, we ran the E-step to find the new posterior given the parameters found in the M-step, and continued alternating E and M steps until the log-likelihood increased by less than a given threshold amount.
We used the minfunc function in Matlab to minimize the negative expected complete-data log-likelihood in the M-step, and used cross-validation to select the regularization penalty r over a grid of values. The selected penalty for the three-state model was r = .0 05. Because the EM algorithm is not guaranteed to find the local maximum, we performed the fit many times with different parameter initializations. We used the model with the best cross-validated log-likelihood (see the section “Testing” below).
Testing.
We assessed model performance by calculating the log-likelihood of data held-out from training. In particular, we assessed how well the model predicted the next output given knowledge of all the data up to the present moment. This allowed for an accurate estimate of the state up to time t and then evaluated how well the transition and output filters explain what happens at time t + 1. We can write this as logP(Yt+1|Y1 = y1,...,Yt = yt, θ), which can be calculated in the same manner as the forward pass of the E-step described in the previous section. The prediction for t + 1 is then
| (20) |
Note that this equivalent to the scaling factor was used when fitting the forward step of the model in the preceding section. The mean forward log-likelihood that we report is then
| (21) |
To report the log-likelihood in more interpretable units, we normalized by subtracting the log-likelihood under the Chance model (described above; Fig. 1g; Extended Data Fig. 2c,e), as follows:
| (22) |
The Chance model was either drawn from the entirety of the courtship (Fig. 1g) or only at transitions between outputs (Fig. 1h) (see the static Chance model above). To place these in appropriate units, we present either as bits s−1 (dividing Lnorm(model) by the number of seconds of courtship) or as bits bin−1 (dividing Lnorm(model) by the number of bins). While this provides a bound on the level of uncertainty of each model, we do not have a way of estimating the intrinsic variability in the song-patterning system of the male fly (to do so, would require presenting the identical feedback cue history twice in a row, with the animal in the same set of states).
An alternative metric that we report is the log-likelihood of the model where we did not use the past song output to estimate the current state. In other words, logP(Yt+1|θ). This alternative required us to use only the feedback cues st to predict the current state and its output. Recall from the previous section that P(zt|zt−1, st, θtr) is the probability of transitioning using only the transition model. Then we can compute the probability of being in each state at time t without conditioning on past output observations, as follows:
| (23) |
and the log-likelihood of the output is
| (24) |
Giving a normalized log-likelihood measure similar to before as follows:
| (25) |
The normalized log-likelihood of the forward model reports improvements over the Chance model for predicting the song mode given knowledge of the song history to improve the prediction of the current state. The normalized log-likelihood using only the feedback cues reports improvements over the Chance model for predicting song mode, without accurately estimating the state of the animal; in other words, model performance that comes only from dynamics of the feedback cues.
Binning of song.
We discretized the acoustic recording data to fit the GLM–HMM. Song was recorded at a sampling rate of 10 kHz, segmented into 4 song modes (sine, Pfast, Pslow and no song) and then discretized into time bins of uniform width (33 ms), which corresponds to roughly the inter-event interval between pulse events. We used the modal type of song in each bin to define the song mode in that bin. Because some song pulses have an inter-event interval of >33 ms, we artificially introduced no-song bins within trains of pulses. To correct this error, we identified the start and end of a run of song as either a transition between types of song (sine, Pfast or Pslow) or as the transition between a song type and no song if the quiet period lasted for >80 ms. We then corrected no-song bins that occurred within runs of each song type. To up-sample and down-sample song (Extended Data Fig. 2a,c), we use the modal song per interpolated bin.
Applying filters from only one state.
The likelihood of observing song is typically calculated by applying the filters for each state and multiplying that by the probability of being in each of those states P(state|data)P(emission,state). To calculate the probability of being in a given state, we used the Viterbi algorithm used in HMMs to find the most likely state. We then applied the filter for state i when the most likely state at time t is j to find the mean likelihood of observing an emission k (Fig. 3a,b), as follows:
| (26) |
Predictions of pulse versus sine.
When fitting multinomial GLM filters, one set of filters is set to 0 and is used as a reference point for other filters (since it is always possible to scale all filters together). In our model, the no-song output was the filter set to 0. To visualize the filter that represented the probability of observing pulse versus sine, we took the average of the Pfast and Pslow filters and subtracted that from the sine filter.
We then computed the raw data by taking the histogram of z-scored feedback cues that occur just before pulse and divided it by the histogram of z-scored feedback cues that occur immediately before both pulse and sine. This gave us the probability of observing pulse versus sine at each feature value (Fig. 3e).
Fit of GLM–HMM to optogenetic activation.
Optogenetic activation (driven by a LED stimulus) of previously identified song pathway neurons can, as expected, directly drive song production. To account for this, we add in an additional offset term (because each genotype produces different distributions of types of song) and an extra filter for the LED (that is, the LED stimulus pattern is another input to the model, similar to the 17 feedback cues) and then refit the GLM–HMM. The offset term and the additional LED filter were fit using expectation maximization (see above); no other filters (for the 17 feedback cues) were refit from the original GLM–HMM (Fig. 4).
Normalization of pulse/sine ratio.
Optogenetic activation of courtship neurons dramatically changes the fixed probability of observing pulse song. To visualize the song output during this activation in spite of the decreased dynamic range, we normalized the output by subtracting the minimal probability of observing pulse versus sine song and dividing by the maximum. This maintained the shape and relationship of the pulse versus sine data to be constant but compressed it to be between 0 and 1 (Fig. 4).
Comparison of GLM–HMM to previous data.
pCorr values were taken from a previous study24. To generate a fair comparison, we took equivalent song events in our data (for example, ‘pulse start’ compared times at which the male was close to and oriented toward the female and either started a song bout in pulse mode or did not start a song bout) and found (with either the multinomial GLM or the three-state GLM–HMM) the song mode (pulse, sine or no song) that generated the maximum-likelihood value. Similarly to the previous study24, we adjusted the sampling of song events to calculate pCorr. Pfast and Pslow events were both counted as pulse. The pCorr values reported for the multinomial GLM and three-state GLM–HMM are the percentage of time that the highest likelihood value corresponded to the actual song event (Extended Data Fig. 1b).
Zeroing out filters.
To assess the performance of the model without key features (male feedback cues or female feedback cues), the filters were set to 0. This removes the ability of the model to perform any prediction with this feature. We then inferred the likelihood of the data using this new model (Fig. 4).
Reporting Summary.
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Data are available at http://arks.princeton.edu/ark:/88435/dsp01rv042w888.
Code availability
The code for tracking flies (DeepFlyTrack) is available at https://github.com/murthylab/DeepFlyTrack. The code for running the GLM–HMM algorithm is available at https://github.com/murthylab/GLMHMM.
Extended Data
Extended Data Fig. 1 |. Comparison of GLMs and GLM-HMM.
a, Fly feedback cues used for prediction in (Coen et al. 2014) (left) or the current study (right). b, Comparison of model performance using probability correct (‘pCorr’) (see Methods) for predictions from (Coen et al. 2014) (reproduced from that paper) for the single-state GLM (See Fig. 1c) and 3-state GLM-HMM (see Fig. 1d). Each open circle represents predictions from one courtship pair. The same pairs were used when calculating the pCorr value for each condition (GLM and 3-state GLM-HMM); filled circles represent mean +/− SD; 100 shown for visualization purposes. c, Schematic of standard HMM, which has fixed transition and emission probabilities. d, Schematic of GLM-HMM in the same format, with static probabilities replaced by dynamic ones. Example filters from the GLM are indicated with the purple and light brown lines.
Extended Data Fig. 2 |. Assessing model predictions.
a, Illustration of how song is binned for model predictions. Song traces (top) are discretized by identifying the most common type of song in between two moments in time, allowing for either fine (middle) or coarse (bottom) binning - see Methods. b, Illustration of how model performance is estimated, using one step forward predictions (see Methods). c, 3-state GLM-HMM performance at predicting each bin (measured in bits/bin) when song is discretized or binned at different frequencies (60 Hz, 30 Hz, 15 Hz, 5 Hz) and compared to a static HMM - all values normalized to a ‘chance’ model (see Methods). Each open circle represents predictions from one courtship pair. Note that the performance at 30Hz represents a re-scaled version of the performance shown in Fig. 1g. Filled circles represent mean +/− SD, n=100. d, Comparison of the 3-state GLM-HMM with a static HMM for specific types of transitions when song is sampled at 30 Hz (in bits/transition, equivalent to bits/bin; compare with panel (c)) - all values normalized to a ‘Chance’ model (see Methods). The HMM is worse than the ‘Chance’ model at predicting transitions. Filled circles represent mean +/− SD, n=100. e, Performance of models when the underlying states used for prediction are estimated ignoring past song mode history (see b) and only using the the GLM filters - all values normalized to a ‘Chance’ model (see Methods). The 3-state GLM-HMM significantly improves prediction over ‘Chance’ (p = 6.8 e-32, Mann-Whitney U-test) and outperforms all other models. Filled circles represent mean +/− SD, n=100. f, Example output of GLM-HMM model when the underlying states are generated purely from feedback cues (e).
Extended Data Fig. 3 |. Evaluating the states of the GLM-HMM.
a-c. The mean value for each feedback cue in the (a) ‘close’, (b) ‘chasing’, or (c) ‘whatever’ state (see Methods for details on z-scoring). d-f. Representative traces of male and female movement trajectories in each state. Male trajectories are in gray and female trajectories in magenta. Arrows indicate fly orientation at the end of 660 ms. g. In the 4-state GLM-HMM model, the probability of observing each type of song when the animal is in that state. Filled circles represent individual animals (n=276 animals, small black circles with lines are mean +/− SD). h. The correspondence between the 3-state GLM-HMM and the 4-state GLM-HMM. Shown is the conditional probability of the 3-state model being in the ‘close’, ‘chasing’, or ‘whatever’ states given the state of the 4-state model. i. The mean probability across flies of being in each state of the 4-state model when aligned to absolute time (top) or the time of copulation (bottom). j. Probability of state dwell times generated from feedback cues. These show non-exponential dwell times on a y-log plot.
Extended Data Fig. 4 |. State transition filters.
a-c, State-transition filters that predict transitions from one state to another for each feedback cue (see Fig. 1B for list of all 17 feedback cues used in this study).
Extended Data Fig. 5 |. Amplitude of output filters.
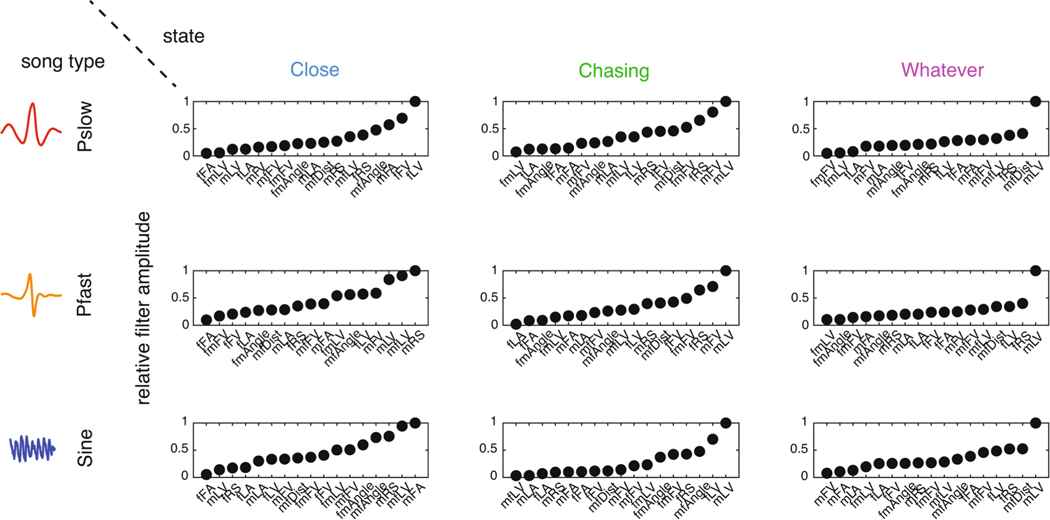
The amplitude of output filters (see Methods) for each state/output pair. Output filter amplitudes were normalized between 0 (smallest filter amplitude) and 1 (largest filter amplitude).
Extended Data Fig. 6 |. Output filters.
a-c, Output filters for each feedback cue (see Fig. 1b) that predict the emission of each song type for a given state. ‘No song’ filters are not shown as these are fixed to be constant, and song type filters are in relation to these values (see Methods). Heavy line represents mean, shading represents Sem. d-e, Sign of filter for each emission filter shows the same feature can be excitatory or inhibitory depending on the state.
Extended Data Fig. 7 |. Activation of song pathway neurons.
a, Solitary ATR-fed P1a males produce song when exposed to the same LED stimulus used in Figure 4. In solitary males, song production is both long-lasting and time-locked to the LED stimulus. Number of animals in parentheses (n=5), heavy line represents mean, shading represents SEM. b, ATR-fed P1a males courting a female produce significantly more Pfast (p = 1e-4), Pslow (p = 1e-3), and significantly-different amounts of sine song (p = 0.009). All p-values from Mann-Whitney U-test. Animals from (a) (n=5), center lines of box plots represent median, the bottom and top edges represent the 25th and 75th percentiles (respectively). Whiskers extend to +/− 2.7 times the standard deviation. c, The probability of observing each song mode aligned to the opto stimulus shows that LED activation of flies not fed ATR does not increase song production. Number of animals in parentheses, heavy line represents mean, shading represents SEM. d, The probability of the model being in each state aligned to the opto stimulus shows that LED activation of flies not fed ATR does not change state residence. Error bars represent Sem. Number of animals in parentheses, heavy line represents mean, shading represents SEM. e-f, ‘Opto’ filters represent the contribution of the LED to the production of each type of song for (e) ATR+ and (f) ATR− flies. Number of animals in parentheses, heavy line represents mean, shading represents SEM. The filters for each strain and song type are not significantly different between states. g, Measuring the maximal change in state probability between LED ON and LED OFF shows that only pIP10 activation produces a significant difference between ATR+ and ATR− flies (two-tailed t test). Number of animals in parentheses in (e-f), center lines of box plots represent median, the bottom and top edges represent the 25th and 75th percentiles (respectively). Whiskers extend to +/− 2.7 times the standard deviation. All p-values from two-tailed t test.
Extended Data Fig. 8 |. Activating piP10 biases males toward the close state.
a, Conditioning on which state the animal is in prior to the light being on (left, ATR-fed pIP10 flies, n=41; middle ATR-free pIP10 flies, n=28; right, ratio of ATR-fed to ATR-free state dwell time), activation of pIP10 results in an increase in the probability of being in the close state unless the animal was already in the close state. Shaded area is SRM. b, When the male was both close (<5mm) and far (> 8mm), pIP10 activation increases the probability that the animal will enter the close state. Shaded area is SRM. c. When the male was already either singing or not singing, pIP10 activation increases the probability that the animal will enter the close state. Shaded area is SRM.
Extended Data Fig. 9 |. Bias toward close state is due to the altered use of feedback cues.
a, Predictive performance is not significantly different between light ON and light OFF conditions for both ATR-fed (n=41, p=0.08) and ATR-free animals (n=28, p=0.46). Performance suffers without male (+ATR p=4e-12, −ATR p=1e-9) or female feedback cues (+ATR p=1e-10, −ATR p=1e-9), suggesting these state-specific features are needed to predict animal behavior. Dots represent individual flies, center line is mean and lines are +/− SD. All statistical tests are Mann-Whitney U-test. b, The similarity between each feedback cue and the filters for the ‘close’ state are subtracted by the similarity of that feedback cue to the filters for the ‘chasing’ state during LED activation of ATR-fed pIP10 flies. This reveals song patterning is more similar to the ‘close’ state than the ‘chasing’ state for most feedback cues. c, Animals that were not fed ATR (n=28) do not show a change in the contribution of the feedback cues to being in a given state, while animals that are fed ATR (n=41) do show a change in feedback cue contribution. Shaded area is SRM. d, Most aspects of the animal trajectory do not differ in response to red light when males are either fed (black, n=41) or not fed (gray, n=28) ATR food. Plotted are the six strongest contributors from (b). p-values are p=0.056 for mFV, p=0.11 for fmFV, 9.7e-5 for mLS, p=0.64 for fLS, p=0.67 for fFV, p=0.009 for mfAngle Mann-Whitney U-test, significance at p = 0.05 corrected to p = 0.0083 by Bonferroni. * represents p < 0.0083, n.s. p > 0.008. Shaded area is SEM.
Extended Data Fig. 10 |. The relationship between feedback cues and song patterns changes when LED is ON in piP10 +ATR flies.
a, The transfer functions of each feedback cue when the LED is OFF (black) and when the LED is ON (red) compared to the wild-type average (dark gray). b-c, Illustration of Pearson’s correlation between transfer functions of two feedback cues (mFV (g) and fLS (h)) when the LED is off (top, black) and on (bottom, red) and the transfer function in each state (not the average as in Fig. 4f). The feature is considered most similar to the state with which it has the highest Pearson’s correlation. All ATR-fed pIP10 animals were used (n=41). d, The state transfer function that is closest to the wild-type average for each feedback cue. For instance, the mFV average is closest to the ‘whatever’ state and the fLS average is closest to the ‘chasing’ state. e-f, Same as (d), but for pIP10 – ATR flies when the LED is off (e) or on (f).
Supplementary Material
Acknowledgements
The authors thank M. Choi, F. Roemschied, R. Fathy and D. Deutsch for assistance with establishing triggered LED stimulation (for optogenetics) in the acoustic behavioral assay chamber. They thank P. Andolfatto, V. Jayaraman, G. Rubin and B. Dickson for flies.
They also thank G. Guan for excellent technical assistance and the entire Murthy Lab for feedback on this manuscript. This work was funded by the Simons Foundation SCGB (AWD494712, AWD1004351 and AWD543027 to A.J.C. & J.W.P.), NIH BRAIN R01 (NS104899 to M.M. and J.W.P.) and the Howard Hughes Medical Institute (to M.M.).
Footnotes
Competing interests
The authors declare no competing interests.
Additional information
Extended data is available for this paper at https://doi.org/10.1038/s41593-019-0533-x.
Supplementary information is available for this paper at https://doi.org/10.1038/s41593-019-0533-x.
Peer review information Nature Neuroscience thanks Benjamin de Bivort, Sarah Woolley, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41593-019-0533-x.
References
- 1.Berman GJ Measuring behavior across scales. BMC Biol. 16, 23 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Calhoun AJ & Murthy M. Quantifying behavior to solve sensorimotor transformations: advances from worms and flies. Curr. Opin. Neurobiol 46, 90–98 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Egnor SER & Branson K. Computational analysis of behavior. Annu. Rev. Neurosci 39, 217–236 (2016). [DOI] [PubMed] [Google Scholar]
- 4.Anderson DJ Circuit modules linking internal states and social behaviour in flies and mice. Nat. Rev. Neurosci 17, 692–704 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Stringer C. et al. Spontaneous behaviors drive multidimensional, brain-wide activity. Science 364, eaav7893 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Musall S, Kaufman MT, Gluf S. & Churchland AA Single-trial neural dynamics are dominated by richly varied movements. Nature Neurosci. 22, 1677–1686 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Saleem AB, Ayaz A, Jeffery KJ, Harris KD & Carandini M. Integration of visual motion and locomotion in mouse visual cortex. Nat. Neurosci 16, 1864–1869 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Suver MP, Mamiya A. & Dickinson MH Octopamine neurons mediate flight-induced modulation of visual processing in Drosophila. Curr. Biol 22, 2294–2302 (2012). [DOI] [PubMed] [Google Scholar]
- 9.Liu M, & Sharma AK, Shaevitz JW. & Leifer AM. Temporal processing and context dependency in Caenorhabditis elegans response to mechanosensation. eLife 7, e36419 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.vanBreugel F, Huda A. & Dickinson MH Distinct activity-gated pathways mediate attraction and aversion to CO2 in Drosophila. Nature 564, 420–424 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Remedios R. et al. Social behaviour shapes hypothalamic neural ensemble representations of conspecific sex. Nature 550, 388–392 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang SX, Miner LE, Boutros CL, Rogulja D. & Crickmore MA Motivation, perception, and chance converge to make a binary decision. Neuron 99, 376–388 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hoopfer ED, Jung Y, Inagaki HK, Rubin GM & Anderson DJ P1 interneurons promote a persistent internal state that enhances inter-male aggression in Drosophila. eLife 4, e11346 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leinwand SG & Chalasani SH Neuropeptide signaling remodels chemosensory circuit composition in Caenorhabditis elegans. Nat. Neurosci 16, 1461–1467 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Root CM et al. A presynaptic gain control mechanism fine-tunes olfactory behavior. Neuron 59, 311–321 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Iigaya K, Fonseca MS, Murakami M, Mainen ZF & Dayan P. An effect of serotonergic stimulation on learning rates for rewards apparent after long intertrial intervals. Nat. Commun 9, 2477 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gründemann J. et al. Amygdala ensembles dynamically encode behavioral states. Science 364, eaav8736 (2019). [DOI] [PubMed] [Google Scholar]
- 18.Dietrich MO, Zimmer MR, Bober J. & Horvath TL Hypothalamic agrp neurons drive stereotypic behaviors beyond feeding. Cell 160, 1222–1232 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berman GJ, Choi DM, Bialek W. & Shaevitz JW Mapping the stereotyped behaviour of freely moving fruit flies. J. R. Soc. Interface 11, 99 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wiltschko AB et al. Mapping sub-second structure in mouse behavior. Neuron 88, 1121–1135 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eyjolfsdottir E, Branson K, Yue Y. & Perona P. Learning recurrent representations for hierarchical behavior modeling. Preprint at arXiv https://arxiv.org/abs/1611.00094 (2016). [Google Scholar]
- 22.Katsov AY, Freifeld L, Horowitz M, Kuehn S. & Clandinin TR Dynamic structure of locomotor behavior in walking fruit flies. eLife 6, e26410 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Corrado GS, Sugrue LP, Seung HS & Newsome WT Linearnonlinear-Poisson models of primate choice dynamics. J. Exp. Anal. Behav 84, 581–617 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Coen P. et al. Dynamic sensory cues shape song structure in Drosophila. Nature 507, 233–237 (2014). [DOI] [PubMed] [Google Scholar]
- 25.Calhoun AJ et al. Neural mechanisms for evaluating environmental variability in caenorhabditis elegans. Neuron 86, 428–441 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tai L-H, Lee AM, Benavidez N, Bonci A. & Wilbrecht L. Transient stimulation of distinct subpopulations of striatal neurons mimics changes in action value. Nat. Neurosci 15, 1281–1289 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bennet-Clark HC & Ewing AW Stimuli provided by courtship of male Drosophila melanogaster. Nature 215, 669–671 (1967). [Google Scholar]
- 28.Coen P, Xie M, Clemens J. & Murthy M. Sensorimotor transformations underlying variability in song intensity during Drosophila courtship. Neuron 89, 629–644 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Clemens J. et al. Discovery of a new song mode in Drosophila reveals hidden structure in the sensory and neural drivers of behavior. Curr. Biol 28, 2400–2412 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bussell JJ, Yapici N, Zhang SX, Dickson BJ & Vosshall LB Abdominal-B neurons control Drosophila virgin female receptivity. Curr. Biol 24, 1584–1595 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Clemens J. et al. Connecting neural codes with behavior in the auditory system of Drosophila. Neuron 87, 1332–1343 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.von Philipsborn AC et al. Neuronal control of Drosophila courtship song. Neuron 69, 509–522 (2011). [DOI] [PubMed] [Google Scholar]
- 33.Escola S, Fontanini A, Katz D. & Paninski L. Hidden Markov models for the stimulus-response relationships of multistate neural systems. Neural Comput. 23, 1071–1132 (2011). [DOI] [PubMed] [Google Scholar]
- 34.Sharma A, Johnson R, Engert F. & Linderman S. Point process latent variable models of larval zebrafish behavior in Proc. Neural Information Processing Systems 31 (eds Bengio S. et al. ) 10942–10953 (Curran Associates, 2018). [Google Scholar]
- 35.Berman GJ, Bialek W. & Shaevitz JW Predictability and hierarchy in Drosophila behavior. Proc. Natl Acad. Sci. USA 113, 11943–11948 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ding Y. et al. Neural evolution of context-dependent fly song. Curr. Biol 29, 1089–1099 (2019). [DOI] [PubMed] [Google Scholar]
- 37.Arthur BJ, Sunayama-Morita T, Coen P, Murthy M. & Stern DL Multi-channel acoustic recording and automated analysis of Drosophila courtship songs. BMC Biol. 11, 11 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McKellar CE et al. Threshold-based ordering of sequential actions during Drosophila courtship. Curr. Biol 29, 426–434 (2019). [DOI] [PubMed] [Google Scholar]
- 39.Pereira TD et al. Fast animal pose estimation using deep neural networks. Nat. Methods 16, 117–125 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vidaurre D, Myers NE, Stokes M, Nobre AC & Woolrich MW Temporally unconstrained decoding reveals consistent but time-varying stages of stimulus processing. Cerebral Cortex 29, 863–874 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mante V, Sussillo D, Shenoy KV & Newsome WT Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Linderman S. et al. Bayesian learning and inference in recurrent switching linear dynamical systems. PMLR 54, 914–922 (2017). [Google Scholar]
- 43.Tao L, Ozarkar S, Beck JM & Bhandawat V. Statistical structure of locomotion and its modulation by odors. eLife 8, e41235 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yu JY, Kanai MI, Demir E, Jefferis GSXE & Dickson BJ Cellular organization of the neural circuit that drives Drosophila courtship behavior. Curr. Biol 20, 1602–1614 (2010). [DOI] [PubMed] [Google Scholar]
- 45.Burgos-Robles A. et al. Amygdala inputs to prefrontal cortex guide behavior amid conflicting cues of reward and punishment. Nat. Neurosci 20, 824–835 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Farooqi IS et al. Leptin regulates striatal regions and human eating behavior. Science 317, 1355 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhang SX, Rogulja D. & Crickmore MA Dopaminergic circuitry underlying mating drive. Neuron 91, 168–181 (2016). [DOI] [PubMed] [Google Scholar]
- 48.Sakai T. & Ishida N. Circadian rhythms of female mating activity governed by clock genes in Drosophila. Proc. Natl Acad. Sci. USA 98, 9221–9225 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nowicki S. & Searcy WA Song function and the evolution of female preferences: why birds sing, why brains matter. Ann. NY Acad. Sci 1016, 704–723 (2004). [DOI] [PubMed] [Google Scholar]
- 50.Tinbergen N. Social releasers and the experimental method required for their study. Wilson Bull. 60, 6–51 (1948). [Google Scholar]
References
- 51.Klapoetke NC et al. Independent optical excitation of distinct neural populations. Nat. Methods 11, 338–346 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rabiner LR A tutorial on hidden markov models and selected applications in speech recognition. Proc. IEEE 77, 257–286 (1989). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are available at http://arks.princeton.edu/ark:/88435/dsp01rv042w888.