Membrane-Mediated Ligand Unbinding of the PK-11195 Ligand from TSPO

Abstract

The translocator protein (TSPO), previously known as the peripheral benzodiazepine receptor, is of longstanding medical interest as both a biomarker for neuroinjury and a potential drug target for neuroinflammation and other disorders. Recently, it was shown that ligand residence time is a key factor determining steroidogenic efficacy of TSPO-binding compounds. This spurs interest in simulations of (un)binding pathways of TSPO ligands, which could reveal the molecular interactions governing ligand residence time. In this study, we use a weighted ensemble algorithm to determine the unbinding pathway for different poses of PK-11195, a TSPO ligand used in neuroimaging. In contrast with previous studies, our results show that PK-11195 does not dissociate directly into the solvent but instead dissociates via the lipid membrane by going between the transmembrane helices. We analyze this path ensemble in detail, constructing descriptors that can facilitate a general understanding of membrane-mediated ligand binding. We construct a set of Markov state models augmented with additional straightforward simulations to determine pose-specific ligand residence times. Together, we combine over 40 μs of trajectory data to form a coherent picture of the ligand binding landscape. We find that multiple starting poses yield residence times that roughly agree with the experimental quantity. The ligand binding transition states predicted by these Markov state models occur when PK-11195 is already in the membrane and involves only minimal ligand-protein interactions. This has implications for the design of new long-residence-time TSPO ligands.

Significance

Kinetics-oriented drug design is an emerging objective in drug discovery. However, whereas ligand binding affinity (or the binding free energy) is purely a function of the bound and unbound states, the binding kinetics depends on the nature of the paths by which the (un)binding occurs. This underscores the importance of approaches that can reveal information about the ensemble of (un)binding paths. Here, we used advanced molecular dynamics approaches to study the unbinding of PK-11195 from translocator protein (TSPO) and find it dissociates from the protein by dissolving into the membrane and that the transition state occurs after the PK-11195 molecule has largely separated from TSPO. These results motivate the design of future long-residence-time TSPO ligands that destabilize the membrane-solvated transition states.

Introduction

The binding affinity of a ligand to its protein target has long been viewed as the key parameter determining its efficacy. However, recent studies have shown that in some protein-ligand systems, residence time correlates more strongly with efficacy than binding affinity (1). But, unlike the binding affinity, residence time is not a state function; it depends on the height of the free energy barrier separating the bound and unbound states. To rationally design ligands for longer residence times, we need to understand the (un)binding mechanism and what molecular interactions occur along the ligand (un)binding pathway.

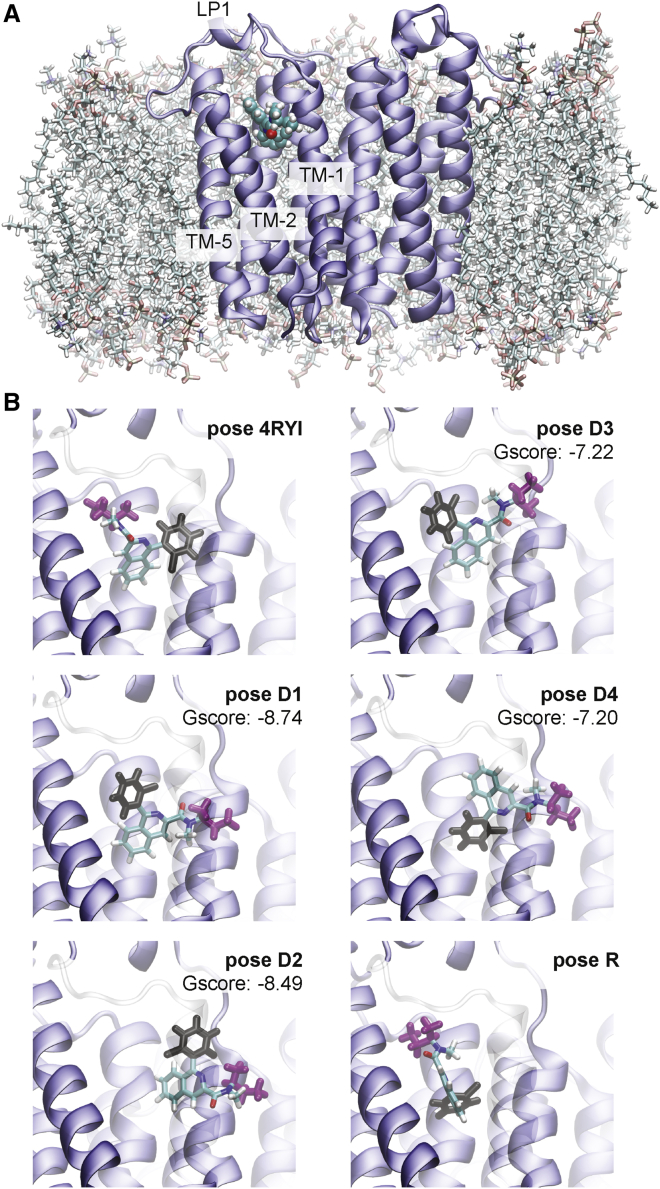
Previous studies have shown that the translocator protein 18 kDa (TSPO) is one such protein for which residence time is important for predicting efficacy (2). TSPO is a well-conserved membrane protein, being present in all kingdoms, including prokaryotes, as well as in the outer mitochondrial membrane of eukaryotes (3). TSPO has five transmembrane α-helices (TM1–5) along with a small helical region in a 20-residue loop (hereafter denoted as the LP1 region) connecting TM1 and TM2 on the cytosolic side (Fig. 1 A). When in the membrane, TSPO is largely found in a dimeric state (4). To date, four different structures have been solved for TSPO for both bacterial (4,5) and mammalian (6,7) organisms: the former by x-ray crystallography, the latter by NMR.

Figure 1.

TSPO-PK-11195 system. (A) Front view of the TSPO dimer in the membrane with PK bound is shown. (B) All six starting poses are shown from the side view along the interdimer axis. To compare poses, two moieties of PK are colored in black (o-chlorophenyl) and magenta (1-methylpropyl), with the rest of the molecule colored according to atom name. TM-2 is shown as transparent for clarity. Poses D1-D4 were obtained by docking with Schrödinger Glide (8) and their corresponding Gscore values are shown. To see this figure in color, go online.

Although the structure of TSPO has been solved, its function remains unknown. In humans, TSPO is highly expressed in steroidogenic tissues, consistent with the hypothesis that it is involved in the regulation of cholesterol transport across the mitochondrial membrane. Indeed, TSPO has been shown to have a high binding affinity for cholesterol (9). There are other studies linking it to apoptosis (10,11) and cellular stress regulation in TSPO knockout mice (12,13), although evidence for this is mixed (14,15). Increased TSPO expression has also been observed in cases of neurodegenerative diseases such as Alzheimer’s and Parkinson’s diseases (16). Relatedly, because of its high expression in areas of inflammation, TSPO serves as a biomarker for neurodegenerative disease and brain trauma, and radiolabeled ligands such as (H3)-PK-11195 are commonly used in positron emission tomography scans (17). PK-11195 (hereafter denoted “PK”) is an isoquinoline carboxamide with no known therapeutic effect (15) and a residence time of 34 min in the human TSPO sequence (2,18).

Molecular dynamics (MD) simulations have been previously performed using a bound TSPO-PK complex. Researchers recently determined the unbinding pathway of PK from a rat TSPO model generated from the Protein Data Bank, PDB: 2MGY structure (19). To generate unbinding paths, they used a combination of random accelerated MD (RAMD) (20) and steered MD (21) and determined that PK unbinds into the cytosol through the largely disordered LP1 region (Fig. 1 A). Unfortunately, this starting structure, determined by NMR, was significantly destabilized by the detergent used in the purification (22,23). Also, the methods used to determine the unbinding pathway, RAMD, have the potential to impart bias on the predicted (un)binding path. Another group performed an induced-fit docking of PK using Glide (24) with a homology model to resemble the mammalian (mouse) TSPO structure using the PDB: 4UC1 Rhodobacter sphaeroides structure. They simulated the TSPO-PK complex for 700 ns and did not observe significant ligand displacement, which is expected because of the extremely long residence time of the TSPO-PK complex.

Here, we study the unbinding mechanism for the TSPO-PK complex, using PDB: 4UC1 as the TSPO starting structure (4) and using a weighted ensemble algorithm, resampling of ensembles by variation optimization (REVO), to generate continuous unbinding pathways without perturbing the underlying dynamics (25). REVO has been previously applied to study ligand unbinding on a series of host-guest systems (26) and the trypsin-benzamidine system (25). In the next section, we discuss the methodology used for the simulations: the REVO resampling algorithm, the clustering algorithm used for the construction of Markov state models (MSMs) and the conformation space network (CSN) representation, and rate calculations. In the Results, we analyze pathways found for dissociation of PK from TSPO, residues that bound strongly to PK along the observed pathways, and we compare residence times between different starting poses. We then summarize our findings and discuss how they relate to existing research.

Materials and Methods

Protein preparation

The initial TSPO dimer structure is composed of chains A and B from PDB: 4UC1 (4). This x-ray crystal structure comes from R. sphaeroides with an A139T mutation to resemble human TSPO. The CHARMM-GUI membrane generator (27) was used to place the TSPO complex into a membrane composed of 174 phospholipids consisting of 53.4% phosphatidylcholine, 28.2% phosphatidylethanolamine, and 18.4% phosphatidylinositol lipids. 10,268 TIP3 water molecules were inserted up to a cutoff of 10 Å from the complex, and 121 potassium ions and 27 chloride ions were added to reach a salt concentration of 150 mM and to neutralize the system. The system was placed into a rectangular box with dimensions 96.4 Å × 96.4 Å × 91.8 Å. The protein was simulated using the CHARMM36 force field (28), and parameters for the PK ligand were obtained with CGenFF (29,30).

Docking

Six different PK poses were used in the simulations. Docking was carried out with extra precision (XP) by using Schrödinger Glide (8). The center of mass (COM) of PK was placed at the COM of the bound protoporphyrin IX in the chain A monomer of TSPO protein from PDB 4UC1 without any constraints. The XP docking yielded four poses (D1–D4), and the XP Gscores for the resultant poses can be seen in Fig. 1 B. A homology model of PK-bound TSPO (pose R) was generated by Xia et al. as a Rosetta comparative model of the mouse TSPO structure constructed using TSPO structures from Mus musculus (PDB: 2MGY (6)), R. sphaeroides (PDB: 4UC1 (4)), and Bacillus cereus (PDB: 4RYI (5)); more details can be found in (31). The TSPO monomer bound to PK from this model was then aligned to chain A of the 4UC1 structure using PyMol 1.7.2.1 (32), and the ligand coordinates from the D1 pose were changed to reflect the new pose. The 4RYI pose was generated by x-ray crystallography, and the coordinates of the PK ligand were added to the 4UC1 structure in the same way as pose R. The system’s energy was minimized using a series of constraints with scripts provided by CHARMM-GUI for all poses. The molecular structure for each pose is shown in Fig. 1 B, and pose view diagrams are shown in Fig. S1.

MD

All MD simulations were performed using OpenMM (33) v7.1.1. The timestep for every simulation was 2 fs. To enforce constant temperature and pressure, a Langevin heat bath was used with a set temperature of 300 K, a friction coefficient of 1 ps⁻¹ was coupled to a Monte Carlo barostat set to 1 atm, and volume moves were attempted every 50 time steps. The nonbonded forces were computed using the CutoffPeriodic function in OpenMM with a cutoff of 10 Å. The atomic positions and velocities are saved every 15,000 time steps or every 30 ps of simulation time, which is the resampling period (τ) used here.

REVO resampling

To observe long-timescale unbinding of PK, we used a variant of the weighted ensemble algorithm: REVO (25). In this algorithm, we perform unbiased MD simulation on 48 separate trajectories in a parallel fashion. Each of these trajectories (called “walkers”) has a statistical weight (w) that governs the probability with which it contributes to statistical observables. With periodicity τ, a resampling procedure is performed, in which similar walkers are merged together and unique walkers are cloned, as defined by a distance metric. During cloning, weights are split, and during merging, weights are added to ensure conservation of probability.

Below, we briefly describe the REVO method, focusing on the details of its application in this work. More information on the algorithm can be found in previous work (25). In REVO, merging and cloning is done to maximize a variation function: V = $\sum _i{V}_i=\sum _i\sum _j{\left(\frac{d_{ij}}{d_0}\right)}^{\alpha }{\varphi }_i{\varphi }_j$, where d_ij is the distance between walker i and walker j determined using a distance metric of choice. For these simulations, the distance metric used was the root mean-square deviation of the PK atoms between each walker, after alignment to a selection of binding site atoms in TSPO. The exponent α is used to modulate the influence of the distances in the variation calculation and was set to 4 for all simulations. d₀ = 0.148 nm is a characteristic distance used to make V dimensionless and to normalize the variance for comparison between different distance metrics. ϕ is a novelty and here is defined as ϕ_i = log(w_i) − log$\left(\left(p_{\text{min}}/100\right)\right)$. The minimal weight, p_min, allowed during the simulation was 10⁻¹². The walker that is selected for cloning is the one that has the highest V_i, and the resultant weight of the clones is larger than p_min. The two walkers selected for merging are at most 2 Å away, have a combined weight lower than the maximal allowed weight p_max = 0.1, and are the walker pair j, k that minimizes $\left(V_j{w}_k+V_k{w}_j/w_j+w_k\right)$. Once the walkers (i, j, k) are selected, the new variation is calculated: if it increases, then these operations are performed, and another (i, j, k) is proposed; if it decreases, then resampling for that cycle is terminated, and a new cycle of MD is performed. Three simulations were run for each docked pose using 48 walkers and 1200 cycles, for 1.728 μs of simulation time per simulation. In total, each pose was simulated for 5.184 μs.

Boundary conditions

The overall goal of the simulations was to determine the pathways along which PK can transition from the initial starting poses to an unbound state. During the simulations, we defined PK as being unbound when the minimal distance between the ligand and TSPO was at least 10 Å. When the ligand crossed this boundary, the weight was recorded, and the walker was “warped” back to the initial conformation. The structure recorded before warping is known as an exit point. When the walker warps back, the atomic positions and velocities are reset to their initial values before the simulation began. The walker weight does not change as a result of warping.

Clustering and network layout

The trajectory frames of all 18 REVO runs were clustered together using the MSMBuilder 3.8.0 Python library. The frames were featurized using a vector of atomic distances between TSPO and PK atoms initially within 8 Å of each other from the 4RYI starting pose for a total of 7527 distances. A k-centers clustering algorithm was used to generate 2000 clusters using the featurized space, and each frame was assigned to a cluster. The clustering was done using the Canberra distance metric. A count matrix describing the cluster-cluster transitions was calculated for a lag time of 30 ps.

We then construct a CSN from the count matrix, which is a graphical representation of the transition matrix. Each node, representing each row of the transition, and the edges, representing nonzero off diagonal elements of the transition matrix, were determined using the CSNAnalysis package (34). Gephi 0.9.2 (35) was used to visualize the CSN. The size of each node is proportional to the statistical population of the cluster. For visualization, the smallest node was set to be 20 times smaller than the largest node. The layout of the network was determined using a force minimization algorithm, Force Atlas, included in Gephi. The algorithm repulses nodes that are not connected and attracts nodes that are connected via an edge. The strength of the attractive force is proportional to the weight of the edges. The directed edge weights were values between 0.1 and 100 as determined by w_ij = 100p_ij, where p_ij is the transition probability of cluster i transitioning to cluster j. Unidirectional edge weights were then determined using the average between the two directed edge weights. Force Atlas was applied twice. The first minimization was done without adjusting for node sizes, allowing the nodes to overlap. The second minimization adjusted for the node size and prevented overlap. For visualization, all edges are shown with a uniform line weight.

Quantifying unbinding pathways

Upon analysis of the simulation results, the only unbinding pathways observed in our simulations were PK dissociating through pairs of transmembrane helices. We therefore introduce the coordinate Q_ij, which measures the minimal x-y distance from the COM of PK to the line formed by the COMs of helices i and j to measure the dissociation progress of PK into the membrane. Negative values indicate the COM of the ligand is closer to the center of the helical bundle, and positive values indicate the COM is closer to being fully dispersed in the membrane. All six poses had trajectories along which PK traveled between transmembrane helices 1 and 2, and only pose R had trajectories along which PK went between transmembrane helices 2 and 5. For pose R analysis, we separate the conformations according to which value (Q₁₂ or Q₂₅) is largest. Projections onto a given Q-value will only use conformations for which that Q-value is the largest.

Calculating nonbonded energies

We calculated the nonbonded interaction energies by E_int = V_LJ + V_ES, where V_LJ is the Lennard-Jones potential energy and V_ES is the potential energy from electrostatic interactions. The Lennard-Jones interactions were determined using a 12-6 potential given as V_LJ = 4ɛ$\left[{\left(\frac{\sigma }{(r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$, where r is the atomic distance between atoms, σ is the interatomic distance at which the potential is 0, and ɛ is the depth of the potential well. To calculate σ and ɛ, we used the Lorentz-Berthelot combining rule. There was a hard cutoff distance of 10 Å when calculating the Lennard-Jones potential. The electrostatic energy was calculated using V_ES = $\left(1/4\pi {\epsilon }_0\right)\left(Q_i{Q}_j/r_{ij}\right)$, where Q_a is the charge of atom a, r_ij is the interatomic distance between atoms i and j, and ɛ₀ = 8.854 × 10⁻¹² F/m is the permittivity of free space in farads per meter. The specific σ, ɛ, and Q for each atom type was provided by CHARMM-36 parameter files obtained through CHARMM-GUI. Two sets of nonbonded energies were calculated: between PK and TSPO and between PK and lipids in the membrane.

Calculating off rates and mean first-passage times using Hill relation

The rates are calculated using the flux of trajectories into the unbound basin, also known as the Hill relation (36, 37, 38), defined as k_off = $\left({\sum }_i{w}_i/T\right)$, where w_i is the weight of the walker entering the unbound basin and T is the total simulation time. During the simulations, the unbound basin was defined by the 10 Å boundary condition. However, although many walkers had dissociated into the membrane, no walkers made it to the boundary. Therefore, to obtain estimates of unbinding rates, after the simulations were completed, the unbound basin was redefined using a minimal distance of 5 Å, as we found negligible interaction energy between PK and TSPO at this distance (Fig. S2). In our simulations, we observed a total of 2285 instances of trajectory crossings into the five-unbound basin. This is broken down by starting pose as follows: 4RYI (47), D1 (4), D2 (1804), D3 (278), D4 (152), and R (0). In our analysis, once a walker entered the unbound basin, we ignored all future trajectories associated with that walker. This was done to prevent double counting of unbinding transitions. The mean first-passage time (MFPT), synonymous with the residence time, was calculated as MFPT = $\left(1/k_{off}\right)$. The uncertainty of off rates and MFPT for each pose is the standard error across each set of simulations.

Calculating MFPTs using Markov state models

We create transition matrices, T(τ), for various lag times (τ) using the cluster identities from the CSN and tracking walkers through merging and cloning operations in the REVO resampler. We alter these matrices to include a probability sink for states that are unbound, defined as when PK is at least 5 Å away from the TSPO dimer. We run a Markov chain simulation for a given starting pose and lag time by initializing a probability vector, P, where all of the probability starts at the state of a given starting pose. To progress the simulation, we use the following: P_k = P₀T(τ)^k, where P₀ is the initial probability vector and P_k is the probability vector after k time steps. We continue the simulations until all the probability accumulates in the unbound basin. We then calculate the MFPT using the following formula: MFPT = Σ_k(p_k − p_{k − 1})$\left(t_k+t_{k-1}/2\right)$, where p_k is the probability of being unbound at timestep k and t_k is the time associated with time step k. We repeat this for all initial poses and lag times to determine MFPT as a function of lag time.

Selecting poses for straightforward MD simulations

To strengthen the accuracy of our MSMs, we run straightforward simulations at weak points in the network. To determine these weak points, we randomly multiplied the elements of a row on the transition matrix with numbers drawn from a Gaussian distribution with a mean (μ) at 1 with a standard deviation (σ) of 0.2, and we renormalized the row after perturbation. We rerun the Markov chain simulations to calculate the MFPT. To get a sense of how consistently the cluster alters the MFPT, we randomly perturb the transition matrix 10 times independently. Weak points in the network are determined by the clusters whose perturbations affect the MFPT the most, using the following formula: δ_MFPT/$\overline{\text{MFPT}}$, where δ_MFPT and $\overline{\text{MFPT}}$ are the standard deviation and average of the perturbed MFPT values, respectively. For two poses, this ratio was greater than 0.2; we identified these clusters as weak points and reran straightforward MD simulations from the highest-weighted structure in that cluster. From each weak point, we launched 144 independent straightforward MD simulations for a length of 500 cycles (15 ns). In addition, we launched trajectories from high-LASA (lipid-accessible surface area) clusters in the central unbound region and each of the high-LASA states originating from pose R. In total, we ran 10.8 μs of supplemental trajectories to bolster our MSMs.

Results

PK-11195 unbinding pathway

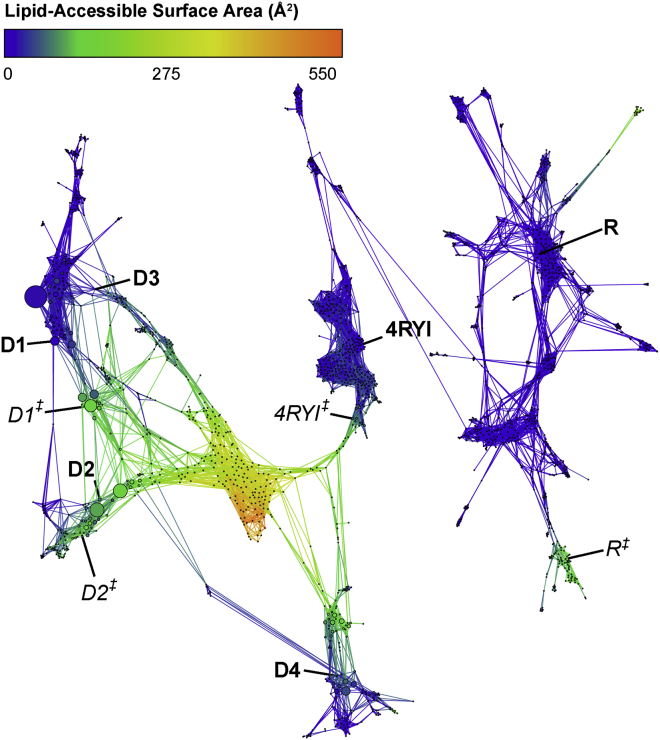
We comprehensively studied the TSPO-PK interaction landscape using a set of REVO simulations initialized at six different starting poses (Fig. 1 B), simulating 5.184 μs per pose. After the simulations were completed, all frames were clustered together into a CSN shown in Fig. 2, in which each node represents a PK pose and the edges reveal which poses interconvert in our simulations within a 30 ps lag time. All of the starting poses form a connected network, though pose R is only connected via two low probability edges to the pose 4RYI ensemble (Fig. S3). The 4RYI pose is similarly connected to pose D4 but is also connected to the other docked poses via the high-LASA clusters. It is worth noting that both pose 4RYI and pose R were the only poses that were not designed for this specific protein structure and were instead inserted from other protein structures after alignment. Consistent with this fact, both of these regions in the CSN do not show accumulation of probability into one or more high-probability states. Instead, we observe a broader distribution among many low probability states, indicating a lack of a local funneling in the energy landscape. Interestingly, all of the docked poses (D1–D4) show at least one high-probability state, although this is not necessarily at the initial docked pose itself, indicating that some relaxation is required from the docked poses to reach the true local minima.

Figure 2.

Combined CSN of all REVO simulations from each starting pose. Each node in the network represents a cluster of ligand poses and is sized according to the cluster weight. Nodes are connected by edges if the ligand poses are observed to interconvert in the REVO trajectory segments. Nodes are colored according to the LASA. Starting poses are marked in bold, and transition state poses shown in Fig. 3D are marked in italics. To see this figure in color, go online.

Contrary to what was observed in previous work (19), PK did not dissociate into the solvent via the LP1 region; instead, it dissociates into the membrane. The CSN shows that all the poses, besides pose R, connect directly to the unbound states, shown in yellow and orange, in which PK is fully dissolved into the lipid membrane. In all of these pathways, PK exits between TM1 and TM2. The pose R trajectories show two different pathways that have a moderate LASA—one between TM1 and TM2 and another between TM2 and TM5—for which PK forms direct interactions with membrane lipids.

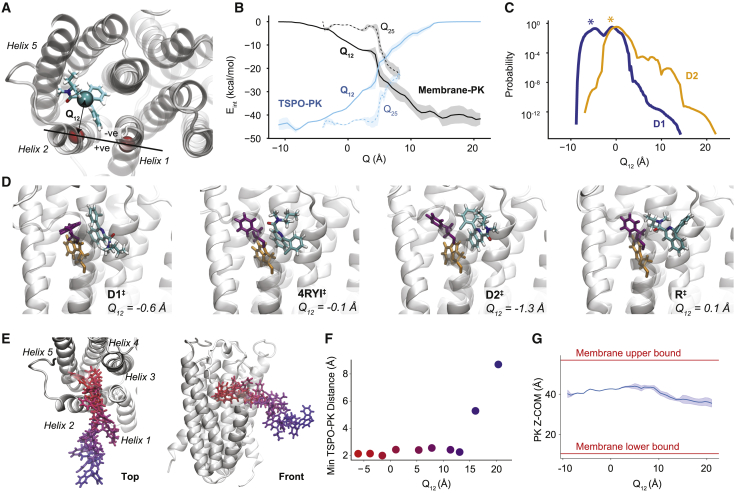
We introduce the coordinate Q_ij, which measures the minimal x-y distance from the COM of the ligand to the line connecting the centers of mass of helix i and helix j (Fig. 3 A). Negative Q-values indicate the ligand is within the helical bundle, and positive values indicate the ligand is outside the bundle. This provides a basis to compare between different pathways and a means of obtaining general information about membrane-mediated ligand unbinding pathways. Fig. 3 B compares the TSPO-PK interaction energy (E_int) with membrane-PK interaction energy. In the Q₁₂ pathway (solid lines), PK interacts more closely with the lipid membrane than TSPO after ∼5 Å. For the Q₂₅ pathway (dashed lines), this crossover occurs at 7.5 Å. The difference is due to differences in the orientation of PK along the two pathways. Fig. 3 D shows the transition states labeled in Fig. 2 in which the Q-values are approximately equal to zero along each dissociation pathway. We see that each structure is still heavily informed by its starting pose, with very different PK orientations. Fig. 3 C shows probability distributions projected onto Q₁₂ for starting poses D1 and D2. This shows that although D1 started further backward on the unbinding pathway, the simulations discovered another high-probability basin around Q₁₂ = 0, which can also be seen by the high-probability states around D1^‡. A representative Q₁₂ dissociation pathway is shown and analyzed in Fig. 3, E and F. Note that although the Q₁₂-value increases steadily along the pathway, the minimal distance between TSPO and PK (used to define the unbound state) rises rapidly only as PK reaches a Q₁₂ of ∼15 Å. Additionally, we track the PK COM as a function of Q₁₂ (Fig. 3 G). Once it gets fully dissociated into the membrane, PK does not travel closer toward the solvent in either direction. Rather, it interacts strongly with the hydrophobic tails and remains at approximately the membrane midpoint over the course of our simulations.

Figure 3.

Analysis of membrane-mediated exit paths. (A) The coordinate Q_ij is defined as the x-y distance between the COM of PK, shown as sticks and colored by atom type, and the line that connects the centers of mass of helix i and helix j. LP1 is not shown here for clarity. (B) The expectation values of the interaction energy between PK and TSPO (blue) and between PK and the membrane (black) are shown as a function of Q. In each case, the solid line shows Q₁₂, and the dashed line shows Q₂₅. The shaded region indicates the standard error over the ensemble of measurements at each Q-value. (C) Probability curves projected onto Q₁₂ for simulations initialized in Pose D1 (blue) and D2 (orange) are shown. Q₁₂-values of the starting structures are marked with asterisks. (D) Poses from transition pathways with Q ≈ 0 are shown. These poses are also labeled in the CSN of Fig. 2. Phe46 is shown in purple, and Trp50 is shown in orange. (E) A set of poses along the Q₁₂ pathway colored from bound (red) to unbound (blue) is given. Top view is shown on the left, and a front view is shown on the right. (F) The minimal PK-TSPO distance and the Q₁₂-value are shown for each pose in (E). (G) The z COM position is shown as a function of Q₁₂. The red lines indicate the upper and lower bounds of the membrane as defined by the maximal and minimal z coordinate of the lipid membrane. To see this figure in color, go online.

We also measure interaction energies between PK and individual residues for all residues on TM1, TM2, TM5, and LP1 (Figs. S4–S7). Early in both the Q₁₂ and Q₂₅ pathways, PK strongly interacts with aromatic residues Phe46 and Trp50, forming π-π interactions. These aromatic residues with long side chains follow PK along the unbinding pathway, which is observed by plotting the Q-value of individual residues as a function of Q-PK (Figs. S8 and S9). Interestingly, this phenomenon occurs for smaller amino acid side chains as well; Gly22 and Pro47 both change Q-value significantly over the Q₁₂ pathway, indicating significant distention of the helices during unbinding.

Finally, we investigated the similarity of the PK conformations within each cluster with respect to the dihedral angles along four different rotatable bonds (see Figs. S10–S12). The standard deviation for all the angles is generally low (below 85°); however, there are clusters in high-LASA regions on the network that have a higher standard deviation. This indicates that PK has more rotational flexibility when it is within the membrane. However, when looking at the overall angle range for the network clusters, there are several clusters with a high overall range, indicating that different ligand conformations are occasionally being clustered together. In particular, rotatable bond 1 has a range of 90° or higher for most states, and rotatable bond 2 has a range over 150° in the D1–D3, D4, and R basins as well as in the states in which PK has dissociated into the membrane. Therefore, it is likely that the distance metric, defined as a set of atomic distances from PK to the TSPO binding site, is good at distinguishing the PK location but not necessarily good at defining the internal coordinates of PK. It is thus possible that the clustering procedure introduced some unphysical connections, and the network should be seen as representing an upper bound of the connectivity between the bound states.

PK-11195 rates and residence times

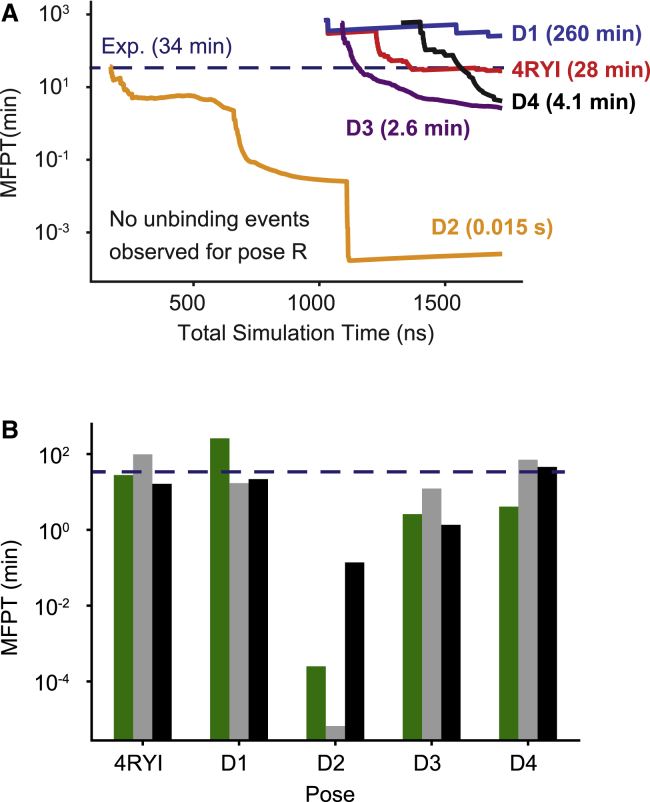
We directly estimate the unbinding rates (k_off) by summing the weights of the unbinding trajectories, and we calculate the MFPT by inverting the unbinding rate for each starting pose (Fig. 4 A). Pose D2 had a high unbinding flux and a predicted MFPT of less than 0.02 s, indicating a clear lack of stability with respect to the other poses. Poses D3 and D4 had predicted MFPTs of 2.6 and 4.1 min, respectively, still lower than the experimental measurements; these estimates are likely to continue to decrease with further simulation time. Poses 4RYI and D1 had MFPT estimates near or above the experimental MFPT (28 and 260 min, respectively). No unbinding events were observed for pose R, implying an even longer MFPT than 260 min.

Figure 4.

(A) Mean first-passage time (MFPT) estimates using unbinding fluxes observed over the course of REVO simulations. (B) A bar graph of the final MFPTs comparing the Hill relation (green) and MSM simulations before (gray) and after (black) the addition of new straightforward MD simulations is given. Pose-specific MFPTs were computed from MSMs that were built using only trajectories generated from that starting pose. Simulations starting from pose R never entered the unbound basin, and thus, MFPTs could not be determined by either method. The experimental MFPT of 34 min is shown as a dashed blue line in each panel. To see this figure in color, go online.

One of the issues with performing simulations via weighted ensemble is ensuring the simulations converge. A lack of convergence introduces additional uncertainty into k_off and MFPT calculations. To address this issue, we launch a set of Markov chain simulations using the transition matrix that constructed the CSN. Because of the unphysical connections between various clusters, we constructed pose-specific networks by only including states that were visited by trajectories that were generated from a given starting pose. We again find that the D2 pose has a low MFPT, though two orders of magnitude less than that calculated by the Hill relation. Calculating the MFPT using the MSM showed that all poses besides D2 were on the same order of magnitude as the experimental residence time and were within an order of magnitude of that determined by the Hill relation. Because there were no trajectories starting from pose R that entered the unbound basin, a MFPT could not be computed for this starting pose without additional simulations.

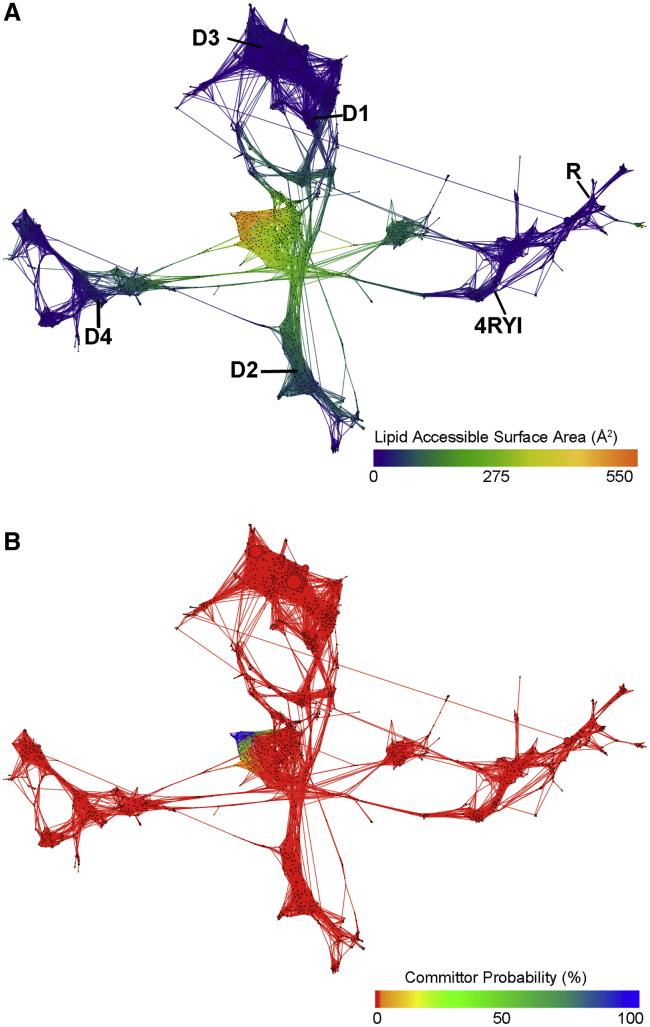
The accuracy of the MFPT calculations, however, assumes that the transition matrix determined from the simulations has converged. To test for convergence, we run additional straightforward simulations at the bottlenecks of the network and rerun the MFPT calculations by combining the old and new trajectory data. Two such bottlenecks were identified: the connections between pose R and pose 4RYI, as well as between poses D2 and D4. To better sample the unbound state, we also ran straightforward MD simulations from high-LASA poses in the Q₁₂ and Q₂₅ pathways that were seen by pose R, as well as the most probable state in the unbound basin. We then reclustered and remade the CSN network to include the new frames (Fig. 5). Several connections were formed between pose 4RYI and pose R, which also gained connections to the other poses after reclustering. Additionally, the most probable region in the network was once again the D1–D3 basin, as determined by the steady state probabilities of each state.

Figure 5.

Combined CSN of all REVO simulations from each starting pose with the addition of frames from straightforward MD simulations, colored by (A) LASA and (B) committor probability. Starting poses are marked in bold in (A). To see this figure in color, go online.

With the addition of the straightforward simulations, we recalculated the pose-specific MFPTs from each starting pose. The new simulations did not show pose R progress enough along the unbinding pathway to enter the unbound basin, and therefore, we again could not compute a residence time for this pose. The MFPT for pose D2 increased by five orders of magnitude in the new D2 MSM, but it is still the pose with the fastest unbinding pathway. This is likely a result of reclustering after the addition of the new trajectories. Accordingly, when we recalculate a new MSM that uses the new clusters but excludes the new trajectories from the transition matrix, we find only an additional slight increase of the D2 MFPT from 0.13 to 0.16 min.

Poses 4RYI, D1, and D4 all had MFPTs on the same order of magnitude as the original MSM simulations, and D3 had an MFPT that was lower by a factor of ∼10. The lack of change between the MFPT calculations for slow unbinding events indicates that the original MSM had converged enough to produce a reliable estimation for those poses. In terms of stability, D2 consistently has the fastest unbinding events and is consistently the most unstable pose we simulated. Poses 4RYI, D1, D3, and D4 all have similar levels of stability, as can be seen by their similar residence times. Because of the lack of unbinding events for pose R, we cannot measure how stable it is in comparison to the other starting poses, but we can say that starting in the pose R basin is more stable than the other poses we simulated.

PK-11195 transition state

Our final goal was to determine the location of the transition state along the unbinding pathway. Fig. 5 B shows the committor probability of each state in the final network. The vast majority of the states have a near-zero committor to the unbound state. Only once PK is dissociated into the membrane does the committor probability begin to significantly increase. We built an ensemble of transition states using the centroid structures for the two nodes with committor probabilities between 0.4 and 0.6. In this way, we estimate that the transition state—in which the committor equals 0.5—occurs when PK has begun dissociating into the membrane and has reached a Q₁₂ of ∼10 Å. For these states, we find that the nonbonded interaction energy between TSPO and PK is roughly −5 kcal/mol (compared to −45 kcal/mol in the bound state), whereas the interaction energy between PK and the lipid membrane has increased to −40 kcal/mol at this Q₁₂ (Fig. 3 B).

To ensure that this result is not affected by any unphysical connections between bound poses, we also calculated the committor probability for each state in the pose-specific networks (Figs. S13–S17). We determined pose-specific transition states for each of the initial poses that had unbinding events (i.e., all except pose R) and found that they were all located in the membrane after PK had dissociated from TSPO. This confirms the results from the committor probability analysis of the full network. Further, these transition states all demonstrated a mix of direct PK-TSPO interactions and PK-lipid interactions. Together, these results suggest that the membrane presents a physical barrier that acts to trap PK near TSPO and forms the rate-limiting step of PK dissociation into the membrane.

Discussion

The results of our simulation show that from all six initial PK poses using the R. sphaeroides TSPO structure, the ligand dissociates into the membrane through the transmembrane helices. We found a pathway between TM1 and TM2 and a lower-probability pathway between TM2 and TM5. These pathways identify residues with which PK has high interaction energy. Among them are aromatic residues Phe46 and Trp50, which form π-π interactions with the ligand. The interactions with the Trp50 rings are also found in different bound states. We note that the Trp50 residue happens to be highly conserved across organisms of several species and kingdoms. These stabilizing interactions could lower the barrier to entry for other TSPO ligands such as protoporphyrin IX and heme, which are also largely aromatic.

Previous results (19) using a different starting pose and TSPO structure showed PK dissociating into the cytosol through the LP1 loop region. The TSPO structure used in the previous study was built from a homology model based on the mouse NMR TSPO structure and used the rat sequence, whereas our structure was determined from x-ray crystallography from R. sphaeroides TSPO. As mentioned in the Introduction, this NMR structure was destabilized by the detergent used in the purification (22,23), which likely affected the homology model structure as well. This, in addition to the differences in sequence, results in several key structural differences between the mouse (PDB: 2MGY (6)) and R. sphaeroides (PDB: 4UC1 (4)) structures. TM1 in the mouse structure is significantly longer, and the top portion of the helix is at a drastically different angle than the helix in the structure we used in our simulations. Although the LP1 region is present in both structures, the R. sphaeroides sequence has a small α-helix that in the mouse structure is incorporated into TM1. Finally, the LP1 region in R. sphaeroides has several stabilizing interactions (4) between nonbonded residues such as between Trp30-Met97, Asp32-Arg43, and Trp39-Gly141 that are not present in the mouse structure. This stabilization limits the freedom of motion of the LP1 loop, sterically hindering PK from leaving via the LP1 pathway. In addition to TSPO structural differences, previous results were obtained using a 2:1 POPC/cholesterol lipid bilayer, whereas our results used an ∼2.9:1.6:1 mixture of POPC/POPE/POPI lipids. Cholesterol is known to bind to TSPO, although known binding sites are not close to the TM1-TM2 pathway found here. Differences in lipid composition could also affect membrane fluidity, which could impact the relative probabilities of the LP1 and TM1-TM2 pathways. It will be an important goal of future work to parse the relative impact of these differences (protein sequence, protein structure, and membrane composition) in determining ligand dissociation pathways.

There is interest in designing new TSPO ligands with longer residence times (2,18). The ligand binding transition state is the rate-limiting step of ligand binding and release, which can also be identified in simulations by a committor probability of 0.5 between the bound and unbound basins. Here, we find that the ligand binding transition state occurs when the ligand has only minimal direct contact with TSPO, with a Q₁₂ of ∼10 Å. In addition to details of the bound state, this implies that TSPO ligand residence time is primarily affected by properties related to membrane permittivity and diffusivity, such as hydrophobicity. These results lead to the hypothesis that the membrane composition could have a direct impact on ligand binding kinetics of PK.

This work also raises questions about membrane insertion and removal along ligand binding paths. Additional REVO simulations with only PK and the lipid membrane could reveal the membrane diffusion coefficient of PK as well as rate constants for insertion and removal to form holistic models of membrane-mediated binding that stretch from solvent to binding site. A larger question is how the presence of other proteins known to interact with TSPO, such as voltage-dependent ion channel (10) and cytochrome P450s (39), affect the unbinding and binding and insertion and removal pathways. Cholesterol could also affect the binding pathways of PK, either by binding to TSPO and affecting a conformational change or through membrane fluidity, which could affect the (un)binding rate of PK as it interacts with the membrane (40).

Although it is exciting that our predicted residence times come so close to experimental quantities, some caution should be exercised in making this comparison. First, it has been previously shown that some simulations using traditional MD force fields do not produce reliable estimations for residence time (41). However, we note that this result was mainly due to a lack of polarizability in the force field and errors in parameters that overestimate the electrostatic interactions. In our system, PK is uncharged, and we do not expect these errors from the force field to dramatically influence our estimates of kinetics. Another thing to note is the experimental MFPT reported by Costa (2,18) was determined using human TSPO, whereas our simulations used the structure from R. sphaeroides containing an A139T mutation. Although the mutation was designed to mimic the human TSPO structure (4), the human and R. sphaeroides sequences have low homology (30%), which could potentially result in different transition paths, transition states, and unbinding rates. Furthermore, these results emphasize that we should take care to ensure consistency of the “unbound” state from simulation and experiment. In radioligand displacement assays, any ligand pose that is not sterically blocking entry of the radiolabeled competitor ligand would be considered “unbound” (42). However, in surface plasmon resonance, a ligand would still be considered bound until it dissociated from the detergent that is bound to the chip along with TSPO. Our simulations show how differences in the definition of the unbound state can lead to significant differences in residence time and could help rationalize differences between experimental residence times obtained with different methods.

Author Contributions

T.D., S.F.-M., and A.D. designed the project. T.D. and A.U. prepared and conducted the simulations. T.D. analyzed the data. T.D. and A.D. wrote the manuscript, which was edited by all the authors.

Editor: Chris Chipot.