Distinguishing pedigree relationships via multi-way identity by descent sharing and sex-specific genetic maps

Summary

The proportion of samples with one or more close relatives in a genetic dataset increases rapidly with sample size, necessitating relatedness modeling and enabling pedigree-based analyses. Despite this, relatives are generally unreported and current inference methods typically detect only the degree of relatedness of sample pairs and not pedigree relationships. We developed CREST, an accurate and fast method that identifies the pedigree relationships of close relatives. CREST utilizes identity by descent (IBD) segments shared between a pair of samples and their mutual relatives, leveraging the fact that sharing rates among these individuals differ across pedigree configurations. Furthermore, CREST exploits the profound differences in sex-specific genetic maps to classify pairs as maternally or paternally related—e.g., paternal half-siblings—using the locations of autosomal IBD segments shared between the pair. In simulated data, CREST correctly classifies 91.5%–100% of grandparent-grandchild (GP) pairs, 80.0%–97.5% of avuncular (AV) pairs, and 75.5%–98.5% of half-siblings (HS) pairs compared to PADRE’s rates of 38.5%–76.0% of GP, 60.5%–92.0% of AV, 73.0%–95.0% of HS pairs. Turning to the real 20,032 sample Generation Scotland (GS) dataset, CREST identified seven pedigrees with incorrect relationship types or maternal/paternal parent sexes, five of which we confirmed as mistakes, and two with uncertain relationships. After correcting these, CREST correctly determines relationship types for 93.5% of GP, 97.7% of AV, and 92.2% of HS pairs that have sufficient mutual relative data; the parent sex in 100% of HS and 99.6% of GP pairs; and it completes this analysis in 2.8 h including IBD detection in eight threads.

Introduction

Modern scale genetic datasets contain tens to hundreds of thousands of individuals, sample sizes within which numerous close relatives exist.^1,2 Characterizing relatives within such datasets is essential to avoid spurious signals and to improve power in genetic association studies,3, 4, 5 but standard models consider only kinship estimates and ignore the potential for different relationship types to vary in their shared environmental effects and therefore their heritabilities.^6,7 Moreover, while population genetic studies typically filter close relatives to avoid modeling violations,⁸ such an approach will dramatically reduce sample sizes in large datasets.^1,2 One way to enable analyses of more study samples is to directly model the transmission of shared haplotypes—i.e., identitity by descent (IBD) segments⁹—using the pedigree structure of each set of relatives, but this requires accurate determination of those pedigrees. And although several approaches exist for inferring pedigrees from genetic data,10, 11, 12 ambiguities in the samples’ true pedigree relationships limit the utility of these methods.

Identifying pedigree relationships is simple for first degree relatives¹³—parent-child (PC) and full sibling pairs—yet distinguishing relatives only one degree more distant, including grandparent-grandchild (GP), avuncular (AV), and half-sibling (HS) pairs, remains a challenge. Most methods infer only the degree of relatedness of a pair using either the number and length of pairwise IBD segments^14,15 or the proportion of their genome a pair shares identical by descent.^13,16 However, an existing method that leverages these pairwise signals provides limited ability to discriminate among second-degree relationships.¹⁷ Still, IBD segment number distributions overlap little between GP and AV types,¹⁵ and it may be possible to leverage segment position to infer relationship types using only pairwise IBD segments.¹⁸ Turning to multi-way IBD approaches, a recent method detects aunts/uncles of siblings,¹⁹ but it requires at least two siblings to work and can only identify their aunts/uncles.

We developed CREST (classification of relationship types), a two-part approach for inferring sex-specific pedigree relationships that leverages multi-way IBD sharing and sex-specific genetic maps. In the first part, CREST utilizes multi-way IBD sharing to differentiate relationship types, relying on the fact that a pair of close relatives is expected to share IBD regions with their mutual relatives at different rates depending on the pair’s relationship. For example, consider a mutual relative that is the parent of the genetically older member of a second-degree relative pair. Because each meiosis leads to the transmission of half a parent’s DNA, a grandchild will, in expectation, inherit 1/4 of the regions shared IBD between the grandparent and the mutual relative—i.e., the parent of that grandparent. In the case of AV pairs, since two full siblings have equal IBD sharing with their parent, the child of one sibling—the niece/nephew of the other—is expected to share 1/2 as many sites IBD with her/his grandparent as the aunt/uncle does. Lastly, two half-siblings have equal IBD sharing with their common parent. These same sharing rates—the genetically younger sample in GP, AV, and HS pairs sharing fractions of 1/4, 1/2, and 1 compared to the older sample, respectively—arise for many other types of mutual relatives, enabling the classification of relationship types. Thus, we derived IBD sharing quantities based on this idea and trained kernel density estimation models (KDEs) to classify these three types of second-degree relatives in CREST.

This approach of leveraging IBD sharing with mutual relatives not only determines the pedigree relationship types of second-degree relatives, it also identifies the directionality of the relationship—that is, which sample is genetically older (e.g., which is the grandparent or aunt/uncle). In particular, the sample with higher levels of IBD sharing with mutual relatives is most likely to be from an earlier generation. (Other pedigree inference methods similarly identify this information using kinship coefficients.^10,11) CREST applies this logic to GP and AV pairs and to PC relatives to detect which sample is the parent. When available, age information unambiguously implies the genetically older sample for direct descendants (PC and GP relationships) but can fail for AV pairs since a niece/nephew may be (temporally) older than an aunt/uncle.

The second part of CREST uses a model to infer the sex of ungenotyped parents that connect second-degree relatives to each other, further refining CREST’s inferred pedigree relationships. More specifically, CREST infers the sex of the shared parent of HS pairs or of the intermediate parent in GP pairs. While the mean amount of DNA shared between HS and GP pairs is unaffected by the sex of this parent, we leverage the substantial differences in male and female genetic maps²⁰ to distinguish between the two possibilities. The signature of male and female recombinations on IBD segments is strikingly different, to such an extent that we use autosomal IBD segments alone to perform inference. This application of sex-specific maps liberates CREST from requiring sex chromosome or mitochondrial data for inference, which may be less precise than recombination-based inference and would impose additional restrictions on the sample pairs to which it can be applied (i.e., in terms of their sexes).

We used a combination of simulated and real pedigree data to evaluate CREST, the latter from the Generation Scotland^21,22 (GS) cohort. The GS data consist of 20,032 samples recruited as part of families and include 848 GP, 6,599 AV, and 381 HS pairs. We also compared CREST’s results in simulated data to those of PADRE,²³ a composite likelihood method that infers pedigree structures for two sets of close relatives when members of the sets are also related to each other. PADRE makes use of the relationship between the two sets to choose the PRIMUS pedigree that maximizes its composite likelihood and, in the process, implicitly infers the pedigree relationship of the second-degree pairs.

In addition to classifying second-degree relatives, the CREST approach may be extended to infer more distant relationship types. For example, when using simulated pedigrees that include a pair of third-degree relatives and two first cousins of the genetically older sample, CREST can also distinguish third-degree relatives with high accuracy, thus highlighting the potential for expanding CREST’s target relationships as datasets further grow in size.

Material and Methods

CREST takes inferred IBD segments from a set of samples as input and applies a multi-way IBD sharing analysis to classify pedigree relationships among pairs; it also uses the locations of IBD segments in HS and GP pairs to infer whether they are maternally or paternally related. The multi-way IBD segment analysis calculates ratios from the IBD regions that a target pair of close relatives and their mutual relatives share, as described below. The algorithm then uses KDEs we trained on ratios from simulated relative sets to infer the pair’s relationship type. CREST is open source and freely available (Web Resources).

We used IBIS,²⁴ an approach that operates on unphased genotype data, to infer both IBD segments and degrees of relatedness. While CREST can use good-quality IBD segments inferred by any method, IBIS produces IBD segments that are largely free of internal gaps,²⁴ with the trade-off that by default it identifies ≥7 cM segments. Gap-free segments are necessary for the second part of CREST, as false gaps between IBD segments inflate the observed crossover count and induce bias in the sex inference. Furthermore, our experimental results indicate that use of these long segments suffices for discriminating between second-degree relationship types. Still, the use of shorter, gap-free IBD segments has the potential to increase the quality of CREST’s inference further.

Throughout, we refer to IBD regions that two or more samples share on only one haplotype copy as IBD1 segments, and those the individuals share identical by descent on both chromosomes as IBD2 regions. Correspondingly, IBD0 regions are those where the given samples do not share an IBD segment.

Multi-way identity by descent sharing ratios

CREST utilizes the IBD regions shared between a pair of close relatives x₁ and x₂ and one or more of their mutual relatives to distinguish their relationship. The expected IBD rates we adopt are based on the assumption that each mutual relative y is related to both x₁ and x₂ only through the most recent common ancestor(s) (MRCA(s)) of x₁ and x₂. CREST further assumes that there is only one lineage from the MRCA(s) to both x₁ and x₂, thus excluding cases of close inbreeding. Under these assumptions, all IBD segments shared between y and one or both of x₁ and x₂ must have been transmitted by this/these MRCA(s) through one lineage. For example, if x₁ is the grandparent of x₂, we take their MRCA to be x₁ itself, and if y is the half-sibling of x₁, y is related to both x₁ and x₂ only through x₁ (via the common parent of x₁ and y), so the assumptions hold. However, if y is the half-sibling of the grandchild x₂, y is related to x₂ through their common parent, and not only through x₁, in conflict with the assumption. In fact, mutual relatives that are descendants of either x₁ or x₂ violate the assumption in many cases. To exclude direct descendants of x₁ and x₂, we analyze only mutual relatives that are third degree (e.g., a first cousin) or more distant relatives of both x₁ and x₂. Because most genetic datasets span only two or three generations, this strategy should generally prevent analyses involving descendant mutual relatives.

The intuition behind the approach CREST uses is that x₁ and x₂ will have different relative amounts of IBD sharing with a given mutual relative y depending on their relationship. We use two ratios to quantify the IBD sharing rates:

$$R_i=\frac{length\left(IBD\left(x_1,x_2,y\right)\right)}{length\left(IBD\left(x_i,y\right)\right)},i\in \left\{\mathrm{1,2}\right\}.$$

Here $IBD\left(s_1,s_2,\dots ,s_n\right)$ denotes the set of IBD regions that all samples $s_1,s_2,\dots ,s_n$ share, i.e., the intersection of the IBD segments each of the $\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)$ pairs share. The length function sums the genetic length (i.e., Morgan [M] length) of a set of IBD segments, accounting for the diploid status of each segment. That is, for a given set of IBD segments I,

$$length\left(I\right)=\sum _{i\in I}\{\begin{array}{ll}\frac{1}{2}\ell \left(i\right)\hfill & \text{if }i\text{ is IBD}1\hfill \\ \ell \left(i\right)\hfill & \text{if }i\text{ is IBD}2,\hfill \end{array}$$

where $\ell \left(i\right)$ denotes the (M) genetic length of an IBD segment i, here from a sex averaged genetic map. The numerators are the same in both ratios and give the genetic length of IBD regions shared jointly by all three samples. The denominators are the length of IBD segments shared by x₁ and y in R₁, and by x₂ and y in R₂.

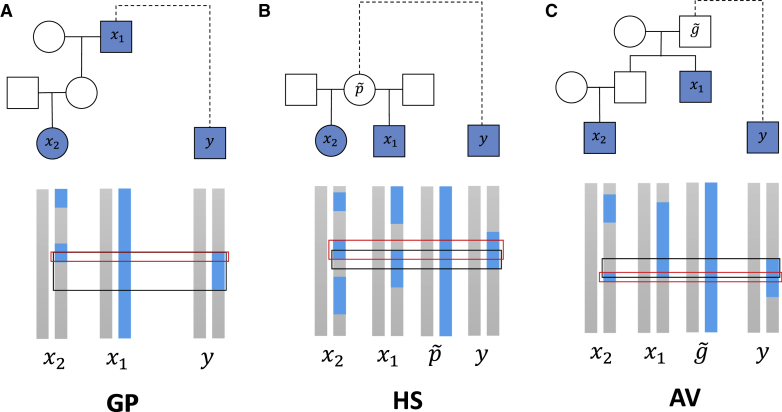
These ratios differ according to the relationship type of the second-degree relatives. Specifically, for a GP pair, if x₁ is the grandparent of x₂, the numerator $length\left(IBD\left(x_1,x_2,y\right)\right)=length\left(IBD\left(x_2,y\right)\right)$ since x₂ will inherit a subset of the IBD segments x₁ shares with y (Figure 1A). Additionally, $E\left[length\left(IBD\left(x_2,y\right)\right)\right]=\frac{1}{4}\cdot length\left(IBD\left(x_1,y\right)\right)$ since x₂ is two meioses away from x₁ and each meiosis leads to the transmission of an average of one-half of the IBD segment length any pair of relatives shares. Thus, $E\left[R_1\right]=\frac{1}{4}$ and $E\left[R_2\right]=1$. Similarly, each member of a HS pair independently inherits one-half of the genome of their common parent $\tilde{p}$, so the probability that they both inherit a given IBD region that $\tilde{p}$ and y share is ${\left(\frac{1}{2}\right)}^2$ (Figure 1B). Therefore the expected numerator is $\frac{1}{4}\cdot length\left(IBD\left(\tilde{p},y\right)\right)$, and the expected denominator is $\frac{1}{2}\cdot length\left(IBD\left(\tilde{p},y\right)\right)$ for both R₁ and R₂, so $E\left[R_1\right]=E\left[R_2\right]=\frac{1}{2}$. In the case of an AV pair, the aunt/uncle inherits half the genome of her/his parent $\tilde{g}$—the grandparent of the niece/nephew—that is related to y. And, as in the GP case, the niece/nephew is expected to inherit one-quarter of the genome of $\tilde{g}$ (Figure 1C). Therefore the expected numerator is $\frac{1}{2}\cdot \frac{1}{4}\cdot length\left(IBD\left(\tilde{g},y\right)\right)$, the expected denominator of R₁ is $\frac{1}{2}\cdot length\left(IBD\left(\tilde{g},y\right)\right)$, and that of R₂ is $\frac{1}{4}\cdot length\left(IBD\left(\tilde{g},y\right)\right)$, resulting in $E\left[R_1\right]=\frac{1}{4}$ and $E\left[R_2\right]=\frac{1}{2}$.

Figure 1.

Example IBD sharing between the three types of second-degree relatives and one of their mutual relatives

Samples with filled shapes are those for which data are available and include the close relative pair x₁ and x₂ and their mutual relative y. The dashed line connecting an MRCA of x₁ and x₂ to y indicates that the pedigree structure between that MRCA and y need not be known. Sexes here are arbitrary and the pedigree relationship type inference works identically for all sample sexes. Haplotypes for the genotyped individuals appear below each pedigree plot as blue or gray vertical bars, with haplotypes for ungenotyped common ancestors of the HS and AV pairs that are related to y also shown. The blue regions are either one haplotype of an MRCA of x₁ and x₂ or IBD segments other individuals share with this haplotype. (Grey portions of the vertical bars are not identical by descent with the blue haplotype in the MRCA and do not enter the analysis.) The black boxes outline the regions shared identical by descent between x₁ and y, and the red boxes outline the regions x₂ and y share identical by descent.

In practice, the above ratios vary around their expectations. This variability arises from three sources: errors in IBD segment detection, the variance in IBD sharing between the close relative pair (i.e., depending on the outcome of the small number of meioses that separate them), and the variance in the meioses that separate y from the MRCA(s) of x₁ and x₂. This latter variance increases for greater meiotic distance. More specifically, mutual relatives y with a large meiotic separation share on average a comparatively small fraction of their genome identical by descent with the MRCA(s) of x₁ and x₂, and they have a higher coefficient of variation for this sharing rate than closer relatives,²⁵ leading to higher variance in the ratios. Therefore, the more closely related y is to the MRCA(s) of x₁ and x₂, the more precise the ratios will be.

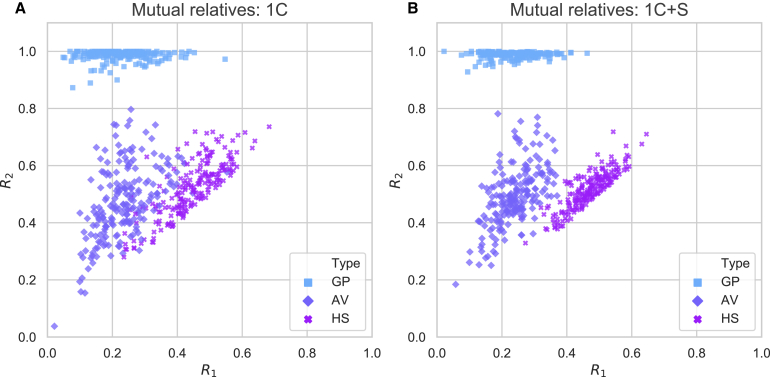
In large samples, data for multiple mutual relatives can be common, and considering only a single y will typically provide less information than combining data from multiple samples. In particular, combining IBD regions from multiple mutual relatives will often capture a larger fraction of the IBD regions that the MRCA(s) of x₁ and x₂ transmitted to the pair. Our approach to incorporating multiple mutual relatives into the ratios is to take the union over these samples of their three- and two-way IBD sharing regions. This effectively reconstructs the IBD sharing pattern of one or more ungenotyped sample¹⁹ that is more closely related to x₁ and x₂ than any single y, thereby reducing the variance of the calculated ratios (Figure 2). The ratios are:

$$R_i=\frac{length\left({\cup }_{y_j}IBD\left(x_1,x_2,y_j\right)\right)}{length\left({\cup }_{y_j}IBD\left(x_i,y_j\right)\right)},i\in \left\{\mathrm{1,2}\right\},$$

where y_j ranges over the mutual relatives that are available in the dataset and satisfy CREST’s assumptions.

Figure 2.

The R₁ and R₂ ratios cluster more tightly when using multiple mutual relatives

Ratios R₁ and R₂ from 200 simulated pairs of each relationship type, calculated using (A) one first cousin (1C) of the genetically older sample and (B) combining one first cousin and his/her sibling (1C+S). Here we swap labels if needed so that R₁ ≤ R₂.

Ideally, the union operation in the above would be defined on two possible haplotypes of each x_i such that, if different relatives y_m and y_n share IBD segments to a given x_i on different haplotypes and in the same region, the segments would be merged into an IBD2 segment. For example, as shown in Figure S1, a grandparent can share overlapping IBD regions with a maternal relative and a paternal relative on different haplotypes. Merging these into a single IBD1 segment would yield biased ratios—reducing the grandparent’s IBD sharing length by 1/2 at this location. A challenge in addressing this is that IBIS and some other IBD detectors do not report which haplotype a segment resides on. Thus we extended CREST to determine when a set of shared IBD regions belong to the same or different haplotypes. This procedure utilizes the fact that if either sample x_i has overlapping IBD regions on the same haplotype with any two relatives y_m and y_n, these regions should also be identical by descent between y_m and y_n. That is, regions x_i shares IBD1 to these relatives should have three-way IBD sharing such that $IBD\left(x_i,y_m\right)\cap IBD\left(x_i,y_n\right)\subseteq IBD\left(y_m,y_n\right)$. On the other hand, if y_m and y_n share IBD segments to the same region on different haplotypes of x_i, the corresponding haplotypes of y_m and y_n will not, in general, be identical by descent in that region. Thus, in regions where y_m and y_n are IBD0, CREST treats x_i as being IBD2 to the set of mutual relatives (which is equivalent to the $IB{D}^{\left(011\right)}$ concept implemented in DRUID¹⁹). Note that this approach does not detect all instances of IBD2 sharing: it is possible for y_m and y_n to be IBD1 to each other on one of their haplotypes while sharing their other haplotypes to each of x_i’s two haplotypes. Therefore, this method is an approximation that does not consider this latter case since we lack information to distinguish which haplotypes the samples share.

Classifying relationship types using kernel density estimation models

CREST adopts KDEs to classify the three second-degree relationship types using the ratios R₁ and R₂ as features. To train and evaluate the KDEs, for each such relationship type, we first simulated genotype data for a range of pedigree structures that include various mutual relatives, and we derived R₁ and R₂ ratios from the IBD segments that IBIS²⁴ detects in the simulated genotypes (see simulations section for details). Because the R₁ and R₂ values are ordered, and since we seek to classify only the relationship types (with directionality considered separately), CREST exchanges the order of the two ratios if needed such that R₁ ≤ R₂. This shrinks the space the features range over, increasing precision. We then trained separate KDEs for each relationship type and used 5-fold cross validation to select both their optimal bandwidth (from 10⁻² to 10^−1/2) and kernel function from among the Gaussian, Linear, and Exponential forms.

As noted earlier, the closer the mutual relatives are to the target pair, the less variance the ratios will tend to have, yielding more reliable classification. Therefore, to build models that account for this, we incorporate another feature that is associated with the variance: what we term the genome coverage rate, C, of the pair for a given set of mutual relatives. We define this as $C=\text{max}\left(\frac{1}{L}length\left({\cup }_{y_j}IBD\left(x_1,y_j\right)\right),\frac{1}{L}length\left({\cup }_{y_j}IBD\left(x_2,y_j\right)\right)\right),$ where L is the total (M) genetic length of the genome. Thus, C is the larger of either the IBD sharing rate between x₁ and the mutual relatives or that of x₂. This genome coverage rate is anti-correlated with the variance in the ratios (Figure S2) since it is related to how much of the genome of x₁ and x₂’s MRCA(s) is/are covered by IBD segments in the mutual relatives.

To incorporate genome coverage into our models, we built KDEs stratified by C, one for each of several bins. When C < 0.2, the bins span intervals of size 0.025, and we use only one bin for C ≥ 0.2 because the variances of R₁ and R₂ appear more constant above this threshold (Figure S2). CREST does not attempt to classify pairs with a C < 0.025 since distinguishing relationships is difficult with such a low signal. For a given genome coverage bin, we trained KDEs using 5-fold cross validation as noted above for each bin separately.

To classify a pair’s relationship type, CREST calculates the posterior probability of each type. It outputs these probabilities, calculated as $\text{Pr}\left(T|R_1,R_2,C\right)=\text{Pr}\left(R_1,R_2|T,C\right)\cdot \text{Pr}\left(T\right)/\left(\sum _{T^{\prime }}\text{Pr}\left(R_1,R_2|T^{\prime },C\right)\cdot \text{Pr}\left(T^{\prime }\right)\right)$, where $T\in \left\{\text{GP},\text{AV},\text{HS}\right\}$ is the type, and $\text{Pr}\left(T\right)$ is the prior probability of the given type, which defaults to $\frac{1}{3}$ for all T, but can be specified by the user. $\text{Pr}\left(R_1,R_2|T,C\right)$ is the likelihood of R₁ and R₂ for a given relationship T from the KDE applicable to the given genome coverage value C. As CREST reports all these probabilities, users can choose to use the maximum a posteriori relationship type or to incorporate the probabilities into downstream analyses. In results, we use the maximum a posteriori type unless otherwise specified. When C < 0.025 (including when no mutual relatives are available) or R₁ = R₂ = 0 (i.e., $length\left({\cup }_{y_j}IBD\left(x_1,x_2,y_j\right)\right)=0$, so there is no detected multi-way IBD sharing to the mutual relatives), CREST does not infer the relationship but outputs the prior probabilities.

Inferring the directionality of the relationship

CREST leverages the ratios R₁ and R₂ to determine the directionality of the relationships. More specifically, CREST identifies which sample is the grandparent, aunt/uncle, and parent in GP, AV, and PC pairs, respectively, by comparing these ratios. In principle, the genetically older sample in the pair should inherit more DNA from the MRCA(s) than the younger sample. Thus, the union of pairwise IBD sharing over mutual relatives for the genetically older sample is expected to be greater than that of the younger sample. This pairwise IBD sharing quantity is in the denominator of the ratios, so CREST uses $D={\text{log}}_2\frac{R_2}{R_1}={\text{log}}_2\frac{length\left({\cup }_{y_j}IBD\left(x_1,y_j\right)\right)}{length\left({\cup }_{y_j}IBD\left(x_2,y_j\right)\right)}$ to determine the directionality. For instance, if x₁ is genetically older, then D is more likely to be positive. We trained KDE models with D values from simulated GP, AV, and PC pairs and CREST uses these to calculate the probability of the relationship directionality.

Inferring the sexes of ungenotyped relatives

CREST provides information beyond the relationship type of HS and GP pairs by inferring the sex of ungenotyped relatives: the common parent of an HS pair and the intermediate parent of a GP pair. This inference is possible due to distinct features of male and female genetic maps that lead to different patterns in the IBD segments maternal and paternal pairs of these types share. It is common practice to use a sex-averaged genetic map when analyzing relatives,^14,17,19 but to do so overlooks the substantial differences between the sex-specific maps. In general, the female map has a greater genetic length than the male map (1.6× on the autosomes), but the male map is locally longer near the telomeres.²⁰ The autosomal length difference between the maps affects the number of crossovers—and thus the number of IBD segments—transmitted through male or female meioses.²⁶ Accordingly, the distributions of IBD segment numbers differ meaningfully between maternal and paternal HS and GP relatives (Figure S3) to such an extent that classification is possible using segment number alone. Consistent with this, a recent study demonstrated that observed segment number differences are sufficient to distinguish 80%–90% of maternal and paternal HS pairs in an endogamous population.²⁷ Even so, exploiting the meaningful differences between male and female recombination rates at given physical positions has the potential to improve classification beyond what segment number alone can provide. To best utilize all the information in sex-specific maps, CREST therefore leverages the IBD segment positions and lengths to compute the probability that the observed segments were transmitted through male or female meioses.

HS and GP pairs represent special cases of relationship types that lend themselves well to this analysis. In HS pairs, all IBD segments shared between the half-siblings necessarily coalesce in the common parent. Thus exactly two meioses in that parent are responsible for the crossovers that determine the IBD segment locations (Figure S4).

By contrast, for GP pairs, the IBD segments coalesce in the grandparent—the grandchild having inherited the segments after two rounds of meiosis. The first meiosis, grandparent to parent, transmits a haplotype consisting of switches from one grandparental haplotype to the other. The second, parent to grandchild, introduces crossovers between the parent’s two haplotypes, only one of which derives from the focal grandparent. CREST is designed to operate on unphased IBD segments such as those provided by IBIS. Unphased segments between the grandparent and grandchild will span the crossovers in the grandparent-to-parent meiosis, but will break at the crossovers in the parent-to-grandchild meiosis (Figure S4). In other words, the grandparent-to-parent meiosis will not introduce observable crossovers, so the only detectable meiosis for GP pairs is parent-grandchild. As such we model GP pairs as undergoing only a single IBD-affecting meiosis. (It is straightforward to adapt CREST to handle high-quality phased IBD segments from GP pairs. In this case, the segments would include breaks due to crossovers from the grandparent-to-parent meiosis, and CREST could merge adjacent segments broken by these crossovers to recreate the forms of the unphased segments it considers.)

The above implies that the observed IBD segments in both HS and GP pairs were shaped by crossovers in a single individual, and thus they can be modeled as the result of a meiotic process of a single sex. This is not the case for AV pairs: their IBD segments descend from two grandparents, one male and one female. This results in segments that were generated from a mixture of the male and female crossover processes, and, with no prior information about which grandparent each IBD segment coalesces in, the ability to determine the sex of the parent of the niece/nephew is limited. More distant relatives pose similar challenges, and at present we subject neither AV pairs nor relatives of other relationship types to sex inference.

CREST models crossover events as following a Poisson process for mathematical convenience, although we acknowledge this neglects the phenomenon of crossover interference. Recent work provides the means to model interference within arbitrary numbers of meioses from a given genetic map,²⁶ but to our knowledge there is no corresponding analytical model capable of handling interference from combinations of both male and female meioses.

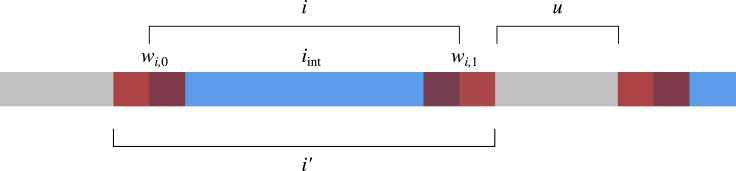
By definition, an IBD segment i consists of a region of sequence shared between two or more individuals that is flanked by a pair of crossovers or by the start or end of the chromosome. However, in practice the inferred boundaries of segments will not correspond exactly to the locations of any crossovers.^24,28 We therefore model the flanking crossovers as falling within windows of fixed physical length denoted $w_{i,0}$, $w_{i,1}$, where 0 and 1 correspond to an earlier and later physical position, respectively. These windows are of equal length and are centered symmetrically on the ends of the reported IBD segments. The window length is a parameter but must be small relative to the minimum length of the detected IBD segments. Put broadly, the window length imposes an upper bound on the distance between the actual and inferred segment boundaries: the more accurately the IBD segments have been called, the smaller the window can be. Tuning the window length to match the inferred IBD segments will increase the precision of the inference (up to the limit of the genetic maps’ resolution). We have chosen a window length of 500 kb for all our analyses.

For each HS and GP pair, our model partitions the genome into disjoint sets of the IBD segments, I and the remaining non-IBD regions, U. Importantly, the segments in I and non-IBD regions in U do not correspond exactly to those found by the IBD detection software because of the crossover-containing windows $w_{i,0}$ and $w_{i,1}$. In the case of a segment bordering the start or end of a chromosome, we give the window that would fall at that location zero length. Thus, every reported segment i is modeled as the union of three non-overlapping windows: $w_{0,i}$, $w_{1,i}$, and the remainder of the segment interior $i_{\text{int}}$ (Figure 3). These three windows form a segment $i^{\prime }$ that is an approximation of a detected IBD segment i, and I contains these extended segments. The IBD0 regions $u\in U$ span from the right-hand window of one $i^{\prime }$ to the left-hand window of the next, except in cases where u reaches a chromosome end and so does not border a window on that side. Therefore, our segments in I and IBD0 intervals in U approximate (slightly over- and underestimate, respectively) the inferred IBD segments and IBD0 regions.

Figure 3.

Modeling IBD segments as non-overlapping intervals

An IBD segment i, in blue, is a region of sequence shared between two or more individuals. The segment i must necessarily be flanked by a pair of crossovers (or by one or both chromosome ends). To account for imprecision in the detected IBD segment bounds, we model the flanking crossovers as falling within windows $w_{i,0}$ and $w_{i,1}$, in translucent red, centered at the IBD start and end points. The interior of the segment that is not overlapped by those windows is an interval itself, which we label $i_{\text{int}}$. Taken together, $w_{i,0}$, $i_{\text{int}}$, and $w_{i,1}$ form $i^{\prime }$, which approximates i. The IBD0 regions in gray that remain surrounding the approximations $i^{\prime }$ are labeled u, and all $i^{\prime }$ and u cover the genome.

Given the earlier considerations of unphased IBD segments in HS and GP pairs, we designate all interior intervals $i_{\text{int}}$ as containing zero crossovers and the segment-bounding windows $w_{i,0}$ and $w_{i,1}$ not located at a chromosome start or end as containing exactly one crossover. A further consideration is that the focal parent transmits one of two haplotypes to each half-sibling or to the grandchild. This means that, where a HS pair is IBD0, a crossover will switch the affected sibling’s haplotype to match that of the other half-sibling, thus initiating an IBD1 segment. Likewise in GP pairs, the parent will transmit a haplotype descended from either the focal grandparent (IBD1) or from the other grandparent (IBD0), and a crossover induces a switch (Figure S4). Given this, we model IBD0 regions u as containing 0 crossovers.

The genetic length of a region in Morgans is the number of crossovers expected to occur in that span of sequence during a single meiosis, i.e., the Poisson rate of crossing over. We define ${\ell }_S\left(r\right)$ to be the genetic length of a region r measured on the genetic map of sex $S\in \left\{\text{F},\text{M}\right\}$, F for female, M for male. The probability of k crossovers occurring within this interval over n meioses is given by the Poisson mass function with rate $n{\ell }_S\left(r\right)$, i.e., $\text{Pr}\left(k|n,r,S\right)=f\left(k;n{\ell }_S\left(r\right)\right)$, because the rate of the sum of independent Poisson processes is equal to the sum of their rates.

The probability of finding one crossover in the flanking windows and none in the interior window of an IBD segment is:

$$\text{Pr}(i^{\prime }|n,S)=\text{Pr}(k=1|n,w_{0,i},S)\cdot \text{Pr}(k=0|n,i_{\text{int}},S)\cdot \text{Pr}(k=1|n,w_{1,i},S).$$

In the same manner, the probability of finding no crossovers in a non- IBD interval u is given by $\text{Pr}(u|n,S)=\text{Pr}(k=0|n,u,S)$.

To calculate the likelihood of all IBD-approximating segments $i^{\prime }\in I$ and non-IBD regions $u\in U$, we assume that each segment forms independently, which follows from the Poisson model, so $\text{Pr}\left(I,U|n,S\right)=\prod _{i^{\prime }\in I}\text{Pr}\left(i^{\text{′}}|n,S\right)\cdot \prod _{u\in U}\text{Pr}\left(u|n,S\right)$. This equation gives the probability of observing all IBD segments and non-IBD intervals given some number of meioses n. As remarked, all crossover-generating meioses in the special case of HS and GP pairs occur in a single individual of sex S, and n = 2 for HS pairs and n = 1 for GP pairs. Given this restriction, for an n appropriate to the relationship type, CREST can use the two likelihoods $\text{Pr}\left(I,U|n,\text{F}\right)$ and $\text{Pr}\left(I,U|n,\text{M}\right)$ to calculate a logarithm of odds (LOD) score

$$LOD={\text{log}}_{10}(\text{Pr}(I,U|n,\text{F}))-{\text{log}}_{10}(\text{Pr}(I,U|n,\text{M})),$$

which we use to classify pairs. Here, negative-scoring pairs likely derive from a male parent, and positive-scoring pairs from a female.

Simulations

To train and test CREST’s relationship type inference, we used Ped-sim²⁶ to simulate a range of pedigree structures that include one GP, AV, or HS pair and one or more of their mutual relatives (Figure S5). In all cases we used sex-specific genetic maps²⁰ and crossover interference²⁹ modeling in these simulations, and a collection of European descent samples³⁰ as the input phased data (EGA:EGAD00000000120). (The latter were previously phased using Beagle³¹ and filtered so that no pair is more closely related than fifth degree.¹⁹)

The simulated data we used for training include mutual relatives that vary from first cousins to second cousins of the genetically older sample in the second-degree pair. We simulated enough samples to obtain 1,000 pedigrees within each KDE genome coverage bin. As the coverage rate varies for a given pedigree structure, we simulated 1,000 pedigrees for each relationship type and pedigree structure class in five batches of 200 pedigrees each. We then mapped these to the corresponding genome coverage bin based on the IBD segments IBIS inferred, and we randomly downsampled to obtain 1,000 pedigrees per bin. The pedigrees include nine different combinations of mutual relatives that have the following relationships to the genetically older sample: one first cousin; one first cousin and his/her sibling; two first cousins that also are first cousins to each other (i.e., non-sibling first cousins); three first cousins that are first cousins to each other; one first cousin and his/her niece/nephew; one first cousin once removed and his/her sibling; one first cousin once removed and his/her niece/nephew; one second cousin; one second cousin and his/her sibling. Thus, we include third-degree relatives (first cousins) and as far as seventh-degree relatives (second cousins twice removed of a grandchild) for training.

To compare CREST with PADRE,²³ we also simulated seven different pedigree structures that include the second-degree pair and mutual relatives consisting of (again with respect to genetically older sample): one first cousin and his/her sibling (1C+S); one first cousin and his/her child (1C+C); one first cousin and his/her niece/nephew (1C+N); one first cousin once removed and his/her sibling (1C1R+S); one first cousin once removed and his/her child (1C1R+C); one first cousin once removed and his/her niece/nephew (1C1R+N); and one second cousin and his/her sibling (2C+S). We tested both methods using 200 replicate pedigrees of each structure for all three types of second-degree relatives.

We further evaluated CREST’s inference sensitivity and specificity across genome coverage bins. For this analysis, we simulated 200 copies for each relationship type of the same nine pedigree structures we used for training (above). We then mapped these to genome coverage bins and randomly downsampled to obtain 200 copies per bin. To generate calibration curves, we performed another five batches of simulations of the same nine pedigree structures and analyzed 1,000 pairs for each bin following random downsampling.

To test CREST’s ability to perform sex inference of the ungenotyped parent linking HS and GP pairs, we simulated 1,800 HS and GP pedigrees. We used a feature of Ped-sim to constrain the sexes in each pedigree, such that it generated 900 each of maternal and paternal HS pairs and 900 maternal and paternal GP families, the latter including data for the relevant grandmother and grandfather. To obtain GP pairs, we chose at random only one of the two grandparents generated per family, ensuring analysis of only one pair per family so that the results for every pair were independent. To increase the sample size, we performed five replicates of these simulations, for a total of 9,000 HS and GP pairs, split evenly into 4,500 maternal and paternal pairs.

Parameters used to run each method

To collect IBD segments for both the relationship type and sex inference parts of CREST, we first ran IBIS v.1.19.1 with default parameters on the simulated data. Since PADRE requires results from ERSA¹⁴ and PRIMUS¹⁰ as inputs, we ran them separately on the simulated data. To run PRIMUS (v.1.9.0), we first used the --no_IMUS and --no_PR options, which corresponds to only running PLINK³² (v.1.90b2k) to calculate relatedness estimates. We then filtered the output file from PLINK to only include pairs from the same pedigree. Next we ran PRIMUS on this file to reconstruct pedigrees, allowing it to search for up to second-degree relatives using the --degree_rel_cutoff 2 option (all simulated pedigrees it applies to include only first- and second-degree relatives). Meanwhile, ERSA needs inferred IBD segments from GERMLINE³³ as input, while GERMLINE works on phased data, so we ran Eagle³⁴ v.2.4 to phase the simulated unphased genotypes.

Each of the Ped-sim simulation runs for the PADRE comparison generated data for 200 pedigrees for all three relationship types, and each pedigree includes data from four samples, for a total of 2,400 samples output by one Ped-sim run. After running Eagle on these 2,400 samples separately for all seven of the pedigree structure types used to compare CREST and PADRE, we ran GERMLINE v.1.5.1 with the options -err_het 2 -err_hom 1 -min_m 1 -bits 64 as specified in the ERSA paper. Then we ran ERSA v.2.1 with default settings on the GERMLINE output for each dataset.

After all these steps, we ran PADRE v.1.0. We found that PADRE initially crashed in some tests, with the source of the crashes being some of the pedigrees PRIMUS inferred, so we removed the pedigrees that cause the crashes from consideration by PADRE (as in another PADRE analysis¹⁹). This avoids calling these tests as PADRE failures, thereby improving its performance.

In a separate test, to exclude the possible effects of phasing quality on PADRE’s results, we simulated replicates of the same pedigree structures and used the true haplotypes produced by the Ped-sim --keep_phase option, keeping the subsequent analysis steps the same as described above.

Runtimes on the simulated data are from the same server configuration as in the real data tests (below).

Real data processing

To test CREST’s relationship type inference on the GS dataset, we ran IBIS v.1.20 using -maxDist 0.116131 and otherwise with default parameters. The -maxDist option sets the maximum genetic distance between SNPs and can reduce false positive segment calls.²⁴ Following this, we used CREST to analyze the second-degree relatives that IBIS inferred and excluded potential double cousins or other pairs that may violate CREST’s assumptions by requiring the IBD2 sharing fraction between these pairs to be less than 0.02 (a default CREST option). We also restricted CREST’s analysis to mutual relatives that are third- to sixth-degree relatives of both members of the target pairs since IBIS has been validated on relatives up to sixth degree.²⁴ (Note that we used all mutual relatives for the analyses of simulated data.)

Some GS samples are part of multiple target pairs—for example, one grandparent can have several grandchildren resulting in several GP pairs—and we averaged the classification results across those pairs for each relationship type. The reason for this is that each sample shares the same IBD segments with his/her relatives regardless of which pair CREST analyzes it in, so the ratios of pairs with overlapping members are correlated. Thus we averaged the sensitivity and specificity of all pairs that have the same genetically older sample in GP and AV pairs, and also averaged the results for HS pairs with the same common parent (Figure S6). For instance, for a grandparent with four grandchildren, each pair contributes a count of 1/4 toward the sensitivity and specificity metrics. We calculated the averages within relationship types, so a given sample can be both a grandchild and a half-sibling, with results from the two types considered independently.

For sex inference, we analyzed all HS pairs and a set of independent GP pairs. Two grandparents related to a grandchild through the same parent—i.e., a grandparental couple—have entirely non-independent unphased IBD segments shared with their grandchild. Specifically, under theoretically optimal IBD detection, the segments of the two GP pairs would be the inverse of one another (an IBD region in one grandparent would be IBD0 in the other grandparent and vice versa). So, as in the simulations, in cases where the GS have both GP pairs in this configuration represented in the data, we select one at random to keep for analysis and discard the other. This removed 148 GP pairs from the results.

To perform X chromosome analysis of selected paternal half-sisters, we ran PLINK --genome on the X chromosome genotype data to get the number of sites where the pairs share no alleles—i.e., have opposite homozygous genotypes.

The runtimes we report are from servers with four Xeon E5 4620 2.20 GHz processors, and we ran IBIS with eight threads on the real data. (CREST is not multithreaded.)

Results

To evaluate CREST’s ability to distinguish among second-degree relationship types, we first compared its performance with that of PADRE using simulated pedigrees. We also used simulated data to characterize CREST’s performance across variable genome coverage rates; its ability to infer directionality for PC, AV, and GP pairs; and its potential to classify third-degree relationship types. Furthermore, we assessed the sex-specific relationship type inference model implemented in CREST, initially in simulated data. As we are unaware of another tool to perform sex-specific relationship type inference using autosomal genotypes, we report only CREST’s inference rates for this latter analysis.

To validate CREST in real samples, we ran it on the GS dataset and compared its inferred second-degree relationship types and parental sex inferences with those of the reported relationships.

Classifying second-degree relationship types via CREST and PADRE

We tested CREST and PADRE using simulated data from seven different types of pedigrees. These pedigrees include the target second-degree pair and two of their mutual relatives, and we define them by the relationship of the mutual relatives to the genetically older target sample: 1C+S, 1C+C, 1C+N, 1C1R+S, 1C1R+C, 1C1R+N, and 2C+S (material and methods). PADRE was designed to infer degrees of relatedness but can be used to classify relationship types of close relatives when given data from their more distant relatives.¹⁹ In fact, its accuracies for inferring second-degree relationship types are higher than those previously reported for RELPAIR,¹⁷ a close relationship type classifier. More specifically, PADRE assigns the degrees of relatedness that maximize the composite likelihood between two sets of close relatives, this likelihood being the product of (1) the PRIMUS-inferred pedigree likelihoods²³ for each close relative set and (2) the pairwise relatedness likelihoods¹⁴ between members of different sets. We read off the second-degree relationship type of the target pair from the corresponding maximum composite likelihood PRIMUS pedigree. PRIMUS pedigrees must contain at least two closely related samples to work, and PADRE analyzes a pair of related PRIMUS pedigrees. Thus, all the simulated pedigrees we used to compare PADRE and CREST include the target second-degree pair and two mutual relatives that are first- or second-degree relatives of each other. However, we note that CREST works even with only one mutual relative of the target pair.

We ran both CREST and PADRE on 200 replicates of each of the pedigree structures. As noted in material and methods, PADRE crashed for some tests, and we applied a previously used fix¹⁹ that enabled it to analyze most of these cases, but it continued to crash for 2.10% of the pedigree structures. In turn, for 0.830% of pedigrees, CREST did not infer a type due to IBIS not inferring the target pair as second-degree relatives, C < 0.025, or R₁ = R₂ = 0 (material and methods). To account for the effects of these pairs, we show classification results both with and without the unclassified pairs.

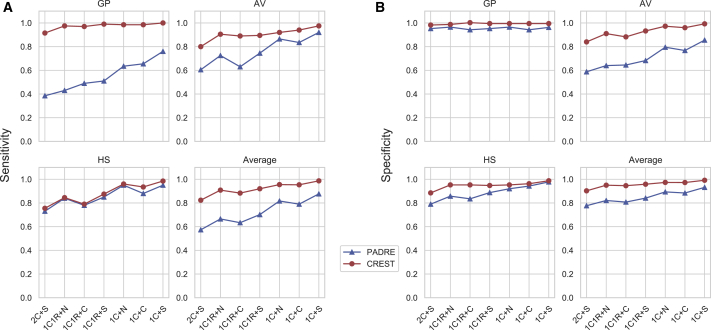
Figure 4 plots the sensitivity and specificity from all 200 pedigrees for the seven types of pedigree structures. (If a tool did not classify a target pair, we scored it as having a sensitivity of 0 and a specificity of 0.) CREST’s overall sensitivity (Figure 4A) ranges from 0.915 to 1.00 for GP, 0.800 to 0.975 in AV, and 0.755 to 0.985 in HS pairs across the seven types of mutual relatives. In contrast, PADRE’s overall sensitivity is 0.385 to 0.760 for GP, 0.605 to 0.920 in AV, and 0.730 to 0.950 in HS pairs. This corresponds to an increase in sensitivity of 0.110 to 0.250 in CREST across all mutual relative types, averaged over the three target relationships (Figure 4A). Turning to specificity (Figure 4B), CREST’s performance rates are 0.978–0.995 in GP, 0.885–0.993 in AV, and 0.903–0.988 in HS, while PADRE’s rates are 0.943–0.965 in GP, 0.589–0.855 in AV, and 0.790–0.978 in HS. Averaged over the three relationship types, CREST’s specificity is 0.060–0.130 higher (Figure 4B). When only considering the subset of pairs that both PADRE and CREST classify (97.1% of pairs), PADRE’s average sensitivity and specificity over all relationship and pedigree types increase, respectively, by 0.016 and 0.019 (Figure S7). CREST’s comparative performance remains similar, as its sensitivity and specificity are 0.101–0.250 and 0.051–0.125 higher on average, respectively.

Figure 4.

Performance of CREST and PADRE for second-degree relationship type classification

The sensitivity (A) and specificity (B) of CREST and PADRE for inferring GP, AV, and HS relationship types in simulated data, along with the average of these rates across the three relationships. The x axis indicates the mutual relative types included in the analysis (abbreviations in material and methods), with each target relationship type and mutual relative combination including data from 200 target pairs.

To determine whether phasing quality adversely impacts PADRE’s results, we compared CREST and PADRE on another 200 replicates of the same pedigree structures but used perfectly phased haplotypes output by the simulator. This step should not affect CREST’s performance since IBIS ignores phase information. Use of these optimal haplotypes improves PADRE’s sensitivity by 0.039 on average, and most especially improves its sensitivity for GP pairs, by a range of 0.105–0.330 (Figures S8 and S9). Nevertheless, CREST’s average sensitivity is still 0.107–0.203 higher in these data, and its specificity is 0.059–0.116 greater, averaged over the three relationship types.

In general, for the types of mutual relatives we tested, both CREST and PADRE perform well at classifying HS pairs, while CREST has higher sensitivity for AV and GP pairs. PADRE’s high performance in HS pairs may be because the mutual relatives are equally close to the target samples for this relationship type. Alternatively, previous work indicated that PADRE may be biased against GP relationship classification and in favor of HS.¹⁹ Along these lines, the confusion matrices show that PADRE misclassified more GP pairs as AV when given more distant mutual relatives (Figures S10 and S11). In turn, CREST tends to mix HS and AV classifications and is better at identifying GP pairs.

Considering the runtime of these analyses, the IBD detector IBIS ran on the 2,400 samples simulated for each of the seven types of mutual relative classes in an average of 11.2 CPU minutes (single threaded), and CREST completed its classification in another 1.75 min on average. On the other hand, the pre-processing steps for running PADRE require that the samples be phased, have IBD segments detected (with GERMLINE), and be analyzed using both PRIMUS and ERSA. Phasing using Eagle and ERSA together take more than two CPU days to finish processing data from one of the mutual relative type simulations.

The performance of CREST under variable genome coverage rates

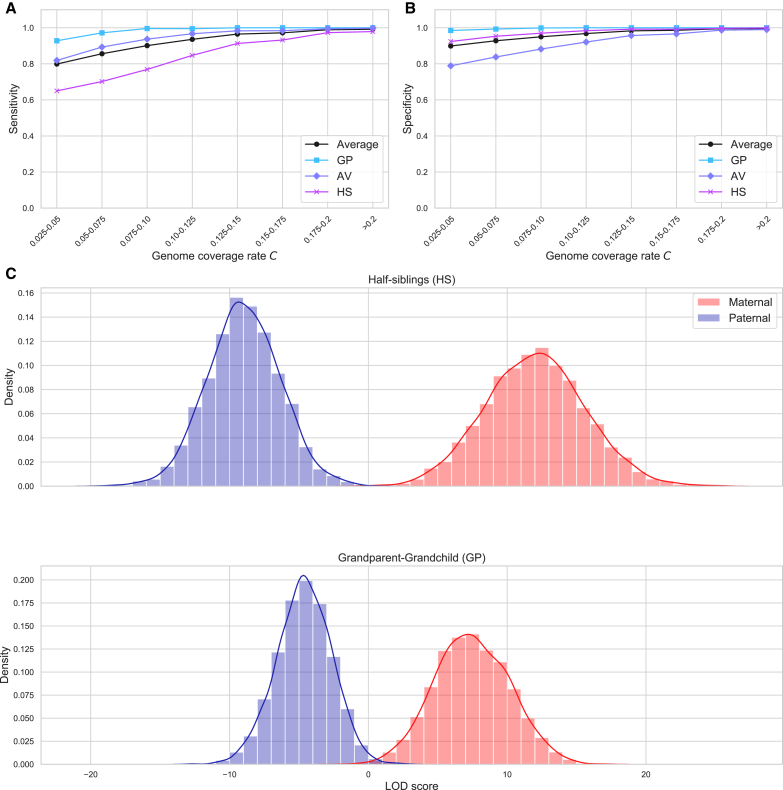
As discussed in material and methods and depicted in Figure 4, classification using close mutual relatives has better performance than using more distant relatives. To ensure that CREST’s KDE distributions more accurately represent the true relationship probabilities for a given target pair and their mutual relatives, we trained stratified KDEs based on the genome coverage rate C of a set of mutual relatives (material and methods).

Figures 5A and 5B show the sensitivity and specificity of CREST in simulated data across the same bins of genome coverage rates on which we trained separate KDEs. As expected, the sensitivity and specificity both increase as the coverage grows. For coverage rates between 0.125 and 0.15, or roughly that expected when using one first cousin, CREST’s sensitivity and specificity are both 1.00 for GP, 0.983 and 0.957 for AV, and 0.913 and 0.992 in HS pairs, respectively. Even when C is in the lowest bin of 0.025–0.05, CREST still achieves sensitivities and specificities, respectively, of 0.928 and 0.985 for GP, 0.819 and 0.789 in AV, and 0.650 and 0.924 in HS pairs. Notably, the inference of GP pairs generally has quite high sensitivity and specificity regardless of the genome coverage rate. This is likely because, if x_i is the grandchild, in theory R₁ = 1, with no variance from the meioses that separate x_i from the grandparent, but only due to false positive and/or false negative IBD segments.

Figure 5.

CREST performance on simulated relatives

(A and B) The sensitivity (A) and specificity (B) within genome coverage rate (C) bins for GP, AV, and HS pairs, and the average across these three types.

(C) Histograms showing the distributions of LOD scores for the inferred parental sex of HS (top) and GP (bottom) pairs. Blue samples represent scores for pairs where the true sex is male, and likewise red for female.

The results above consider only the highest posterior probability relationship as the type that CREST infers, but this probability is informative about CREST’s confidence and can be used in applications of the method. Figure S12 depicts calibration curves for each relationship type in each genome coverage bin. In general, CREST gives reasonably well-calibrated probabilities across bins, though there are some biases evident for HS and AV pairs for lower coverage values. GP probabilities are well calibrated regardless of the coverage, while the probabilities for AV and HS are well calibrated for coverage rates larger than 0.125. For lower coverage rates, the probabilities are still informative, especially for values near 0 or 1.

Detecting the directionality of relationships

To test CREST’s ability to detect the directionality of relationships, we used the same simulated pedigree structures as in the above genome coverage analysis, but instead of analyzing HS pairs, we took their common parent and one of the half-siblings to serve as PC pairs. We applied the KDE classifier to infer which sample is the grandparent, aunt/uncle, or parent in 200 pairs for each genome coverage bin. As shown in Figure S13, averaged over all pairs with C > 0.025, or roughly using one fifth degree or more closely related mutual relative, CREST achieved sensitivity of 1.00 in determining the directionality of GP pairs, 0.99 for AV, and 1.00 for PC pairs. Moreover, the probabilities from this test are nearly perfectly calibrated (Figure S14).

CREST has the potential to infer third-degree relationship types

In principle, the CREST approach need not be limited to second-degree relationships, as a similar logic applies to more distant relatives. To analyze the potential for CREST to distinguish third-degree relatives, we tested its ability to classify four third-degree relationship types: great-grandparent (GGP), grand-avuncular (GAV), half-avuncular (HAV), and first cousin (1C). Assuming that x₁ is the genetically older sample, for a GGP pair, $E\left[R_1\right]=\frac{1}{8}$ and $E\left[R_2\right]=1$; for a GAV pair, $E\left[R_1\right]=\frac{1}{8}$ and $E\left[R_2\right]=\frac{1}{2}$; for a HAV pair, $E\left[R_1\right]=\frac{1}{4}$ and $E\left[R_2\right]=\frac{1}{2}$; and for a 1C pair, $E\left[R_1\right]=E\left[R_2\right]=\frac{1}{4}$.

To train and test this extension of CREST, we simulated 1,000 pedigrees for each of the third-degree relative types, with each pedigree including two first cousins of the genetically older sample as mutual relatives. After calculating R₁ and R₂, we trained KDEs using 800 pairs and 5-fold cross validation for each type. We then tested on the remaining 200 pairs and found that the inference accuracy is high, with sensitivities of 0.990 for GGP, 0.940 for GAV, 0.925 for HAV, and 0.975 for 1C pairs (Figure S15). Furthermore, the classification probabilities are well calibrated (Figure S16). Thus, CREST has potential utility to distinguish relationship types even for third-degree pairs given sufficient mutual relative data.

Sex-specific classification

To evaluate CREST’s sex-specific classification, we used Ped-sim to generate 4,500 maternal and 4,500 paternal pairs for each of the HS and GP relationship types (material and methods). Figure 5C plots the resulting LOD scores, which are positive for pairs CREST infers as maternally related and negative for paternal, with a greater magnitude of LOD corresponding to greater confidence in the call.

For the HS pairs, CREST correctly infers the sex of the parent in 99.9% (4,499) of maternal pairs and 99.9% (4,499) of paternal pairs. In turn, for GP pairs, CREST infers 99.8% (4,491) of maternal pairs and 99.1% (4,461) of paternal pairs correctly. We used the LOD scores to generate receiver operating characteristics (ROCs) for these relationship types, as shown in Figure S17. The area under the curve (AUC) of these ROCs are high, with values for HS and GP pairs of >0.999, consistent with the classification results highlighted here.

Validation in Generation Scotland data

In order to test our model in real data, we used CREST to classify second-degree relationships in the GS samples, which are enriched in close relatives and include reported pedigree structures. Analyzing these data required 2.8 h to run IBIS using eight threads, 2.7 CPU minutes to infer relationship types, and 2.5 CPU minutes to perform sex inference. We considered those pairs that IBIS detects as second-degree relatives and who have at least one sufficiently related mutual relative for performing relationship type inference (material and methods). For sex-specific classification, since this part of CREST does not require information from mutual relatives, we used all pairs IBIS infers as second-degree relatives and that were reported as HS or GP pairs.

When analyzing CREST’s performance for inferring relationship types, we found a few relative pairs it confidently infers as having a conflicting type, so we inspected the pairs using sample ages and IBD sharing to other relatives. For two pairs, CREST shows strong evidence that they are AV instead of HS and GP as reported (inferred probability of 1.00 with C = 0.162 and C = 0.121, respectively). For the pair labeled as GP, we found that the (ungenotyped) intermediate parent is listed as five years younger than his labeled father, indicating that this pair cannot be GP and supportive of the AV type. The other pair was labeled as paternal HS, but, denoting the individuals as A and B, we found that individual A has IBD sharing with B’s maternal relatives (A is a fourth-degree relative of B’s maternal first cousin), and, in turn, B does not share IBD segments with A’s maternal aunt. This indicates that they cannot be either paternal or maternal HS. In addition, B is 24 years older than A, supporting CREST’s prediction of an AV relationship. A third case concerns a set of labeled maternal HS pairs, where we found that purported paternal first cousins of some of these samples are in fact their niece and nephew. We confirmed this by calculating an $IB{D}^{\left(011\right)}$ rate of 129 cM; this is a signal DRUID uses to detect aunts and uncles of two or more siblings, with a threshold of 50 cM reliably discriminating aunts and uncles.¹⁹ However, after correcting this part of the pedigree, we noticed other inconsistent degrees of relatedness among the relatives, and the true relationship of the labeled HS pairs is difficult to determine. We therefore excluded this entire pedigree (which contains only one reported HS pair after averaging) from our analysis. After relabeling the HS and GP pairs as AV and removing the noted pedigree, the relationship type analysis includes 233 GP, 2,616 AV, and 344 HS pairs.

For the sex-specific classification analysis, after excluding the two pairs and pedigree identified above, we noticed that an additional four pairs, three HS and one GP, had anomalous scores that warranted inspection (Figure S18). Returning to the GS pedigree data, we were able to conclude that two of the HS pairs—which are called as HS by CREST—were initially labeled with the incorrect parental sex. One is a reported maternal HS pair with a LOD $\approx$ −12.1, and in fact had been reported as paternal HS in the original pedigree data but was mis-transcribed in one file. The other is a reported pair of paternal half-sisters, with a LOD $\approx$ 7.9. Paternal half-sisters are expected to share at least one allele at every site on the X chromosome, and the average percentage of opposite homozygous X sites across all 18 reported paternal half-sister pairs in the GS data is only 0.41% (including the noted pair). By contrast, the pair in question exhibited opposite homozygous genotypes at 2.5% of X chromosome sites, contradicting their reported relationship (p < 2.2 × 10⁻¹⁶, one-sided binomial test).

For the other HS pair and the GP pair, CREST lacked the necessary mutual relatives to return relationship type predictions. This HS pair also consists of reportedly paternal half-sisters but has LOD $\approx$ 5.7. Nevertheless, the pair have opposing homozygous genotypes at 4.6% of X chromosome sites, disproving the reported paternal HS type (p < 2.2 × 10⁻¹⁶, one-sided binomial test). Although this might suggest a truly maternal pairing, a single mitochondrial marker mismatch discounts a shared maternal parent, and we concluded that the pair may not be HS and so excluded it from the rest of the analysis. The remaining misclassified maternal GP pair has a LOD $\approx$ −5.1 and includes a grandmother who should transmit her mitochondrial DNA to maternal grandchildren. Even so, the grandchild differs at six mitchondrial markers from her grandmother, while the grandmother shares these markers identically with other maternal relatives in the pedigree. This is strong evidence against the pair being maternal, and, with an age difference of 45 years, we reclassified this as a paternal GP pair. Following these changes and filtering to independent GP pairs (material and methods), 371 HS and 692 GP pairs remained for the sex classification analysis.

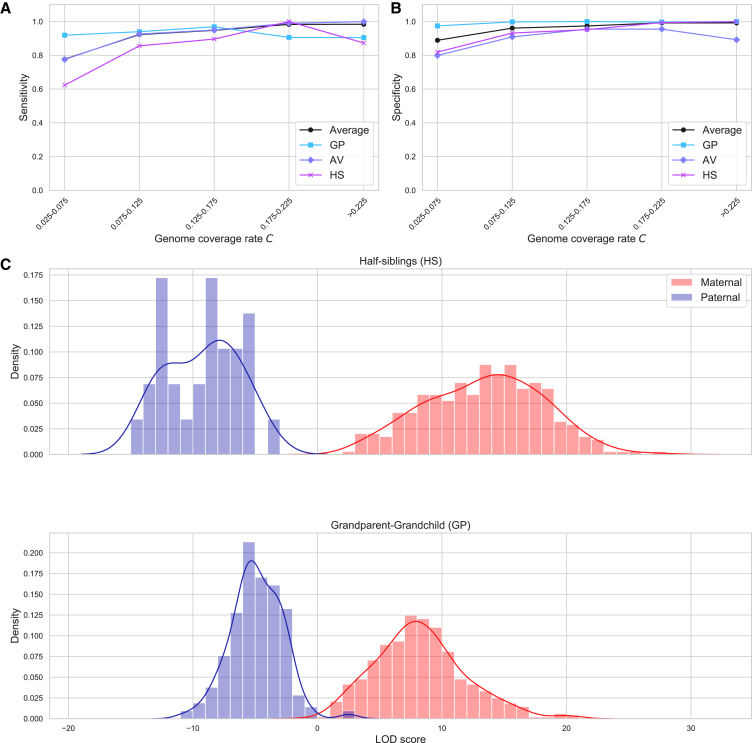
Figures 6A and 6B plot CREST’s relationship type inference sensitivity and specificity in the GS data across different genome coverage rates C. As expected, both the sensitivity and specificity tend to increase with C. Overall, for C > 0.125, CREST’s sensitivity is relatively high at 0.935 for GP, 0.977 for AV, and 0.922 for HS pairs. Similarly, the specificity is high in this coverage range, with values of 0.999 for GP, 0.937 for AV, and 0.979 for HS pairs. However, relative to the next lower coverage bin, the sensitivity of GP pairs drops when C > 0.175, and that of HS pairs drops for the C > 0.225 bin. For the GP pairs, these last two bins include only 1.5 and 2 misclassified pairs (after averaging), and for HS pairs, the last bin has 1.75 misclassified pairs. These misclassifications are due to CREST using mutual relatives that either (1) include another grandchild of the grandparent that IBIS infers as a third-degree relative of the grandparent or (2) violate CREST’s MRCA assumptions but only occur with three or more generations of sample collection (e.g., a great-grandchild or descendants of a HS member’s full sibling). We note that GS’s recruitment provides more of the latter category of relatives than is typical for population-based studies,¹ so fewer assumption violations may occur in population samples. Still, extending CREST to detect mutual relatives that violate its MRCA assumptions is the subject of future work.

Figure 6.

CREST performance on the Generation Scotland data

(A and B) The sensitivity (A) and specificity (B) of relationship type classification for GP, AV, and HS pairs, and the average across these three types in the GS dataset. These plots use a genome coverage rate (C) bin size of 0.05 because several bins have a small number of HS and GP pairs with a bin size of 0.025 (minimum of 7 for HS and 7 for GP using 0.025 versus 14 and 16 here).

(C) Histograms showing the distributions of LOD scores for the inferred parental sex of HS (top) and GP (bottom) pairs. Blue samples represent scores for pairs where the reported sex is male, and likewise red for female.

Within these GS pedigrees, CREST’s sex inference LOD scores nearly always correspond to the reported relationship types (Figure 6C). In particular, CREST correctly infers 100% (342) of maternal HS pairs, 100% (29) of paternal HS pairs, 99.8% (480 of 481) of maternal GP pairs, and 99.1% (209 of 211) of paternal GP pairs. Genotype data are available for the intermediate parent in the three misclassified GP pairs (one maternal with a LOD $\approx$ −0.6 and two paternal with LOD $\approx$ 2.4 and 2.7). Accordingly, IBIS detects IBD1 segments at nearly all sites in the grandparent-parent and parent-grandchild pairs, consistent with PC relationships that validate the reported relationships. The ROCs for the GS data demonstrate the effectiveness of the classifier, yielding AUCs of 1.00 for the HS pairs and 0.999 for the GP pairs (Figure S19).

Discussion

Pedigrees have wide ranging utility throughout genetics, with the modeling of transmitted haplotypes among relatives and/or the use of their IBD sharing fractions being central to both linkage analysis and recent heritability estimation procedures.^6,7 Family data are also needed to identify de novo recombinations^20,29,35 and mutations^36,37 and to enable family-based phasing and imputation, the gold-standard means of addressing these problems.³⁸

Given these applications, several methods exist for pedigree reconstruction and for confirming or disproving reported pedigree relationships.10, 11, 12^,17,23,39 However, differentiating among the relationships that map to a given degree of relatedness has remained challenging. Pairwise relatedness measures, the standard signal for detecting relatives until recently,¹⁶ have limited information to enable the classification of relationship types.¹⁷

We developed CREST, an approach that infers both pedigree relationships and whether HS and GP pairs are maternally or paternally connected. This latter inference relies on male and female genetic maps,²⁰ whose genome-wide rate differences were observed in early human genetic analyses.⁴⁰ Sex-specific maps also differ markedly in their local crossover rates, and these differences form a key basis to the signals CREST uses for its inference. For example, IBD segment counts, a quantity affected by genome-wide crossover rates, overlap meaningfully in maternal and paternal GP pairs (Figure S3), whereas CREST’s LOD scores in GP pairs are well separated (Figures 5C and 6C).

CREST’s relationship type inference assumes that mutual relatives connect to both members of a target pair only through one or more MRCA(s) of the target pair. To enforce this assumption, which is most readily violated by descendants of the MRCA(s), CREST does not analyze first- and second-degree relatives of the target pair. However, such close relatives carry IBD segments that span a large fraction of a target sample’s genome—i.e., they have high coverage rates—and so have the potential to be very informative for relationship type inference. On the other hand, in the GS dataset, some relatives that violate the MRCA assumption are more distantly related than first or second degree, and CREST’s use of these samples lowered its performance in the high coverage rate bins (Figures 6A and 6B). We view the proper utilization of such samples as a subject of interest for future work.

At present, CREST does not require age information even though the difference in age of the target pair is also informative for distinguishing among relationship types. However, the age difference distribution in the GS data reveals large overlapping ranges between HS and AV pairs and between AV and GP pairs (Figure S20). Still, straightforward extensions of CREST may benefit from use of ages when they are available.

Here we applied CREST to simulated and real relatives using IBD segments detected with IBIS. In both forms of data, so long as the mutual relatives do not violate CREST’s assumptions, the method appears relatively insensitive to errors in the IBD segments. Nevertheless, the quality of IBIS and other IBD detectors depend on several factors, including SNP density. Therefore, users must be careful to ensure that the detected IBD segment quality does not adversely impact CREST’s results. One way to accomplish this is to simulate relatives with properties such as marker density and population membership similar to the target samples and tune the IBD detector’s parameters accordingly to ensure that CREST’s performance matches the user’s goals.

While this paper was under review, PONDEROSA²⁷—a method for pedigree reconstruction and second-degree relationship type inference in endogamous populations—was released. PONDERSA uses highly reliable phased IBD segments to make inference, leveraging both segment numbers and whether the segments reside on only one haplotype in order to distinguish among types. These signals are distinct from those that CREST uses, and PONDEROSA is therefore complementary to CREST. Indeed, depending on haplotype phase quality and the availability of mutual relatives, one approach may shed light on a pairs’ type when the other method falls short.

As direct-to-consumer genetic testing companies provide customers with estimated relationships among samples, CREST has several uses. Most apparently, it can enable these companies to report specific relationship types, including which parent an individual is related through for some relationships. Additionally, while the mutual relatives of a target pair inform the pedigree structure between the pair, providing this pedigree structure to the method DRUID can enable more exact detection of the distance between those close relatives and their more distant mutual relatives.¹⁹ Thus, an iterative procedure is possible, with mutual relatives of unknown relationship to a set of close relatives enabling the detection of the latter pairs’ relationship types, and the resulting pedigrees enabling more precise characterization of their distance to the mutual relatives.

Lastly, a key factor influencing CREST’s performance is the genome coverage rate of the available mutual relatives. In general, more closely related pairs will have a higher genome coverage. Consequently, with ever increasing sample sizes—and therefore datasets with greater numbers of relatives, including close relatives—CREST’s inference of relationship types will have greater reliability going forward.

Data and code availability

The code generated during this study is available at https://github.com/williamslab/crest.

Genotype data for Generation Scotland subjects are available through an application from https://www.ed.ac.uk/generation-scotland/for-researchers.

The simulated genotype data supporting the current study have not been deposited in a public repository but can be reproduced using Ped-sim and the European descent data, which is available by application from the European Genome-Phenome Archive (EGAD00000000120).

Declaration of interests

A.L.W. is the owner of HAPI-DNA LLC. All other authors declare no competing interests.

Published: December 23, 2020

Web resources

• CREST, https://github.com/williamslab/crest