Abstract
A major challenge in the development of antibody biotherapeutics is their tendency to aggregate. One root cause for aggregation is exposure of hydrophobic surface regions to the solvent. Many current techniques predict the relative aggregation propensity of antibodies via precalculated scales for the hydrophobicity or aggregation propensity of single amino acids. However, those scales cannot describe the nonadditive effects of a residue’s surrounding on its hydrophobicity. Therefore, they are inherently limited in their ability to describe the impact of subtle differences in molecular structure on the overall hydrophobicity. Here, we introduce a physics-based approach to describe hydrophobicity in terms of the hydration free energy using grid inhomogeneous solvation theory (GIST). We apply this method to assess the effects of starting structures, conformational sampling, and protonation states on the hydrophobicity of antibodies. Our results reveal that high-quality starting structures, i.e., crystal structures, are crucial for the prediction of hydrophobicity and that conformational sampling can compensate errors introduced by the starting structure. On the other hand, sampling of protonation states only leads to good results when combined with high-quality structures, whereas it can even be detrimental otherwise. We conclude by pointing out that a single static homology model may not be adequate for predicting hydrophobicity.
Significance
Hydrophobicity is an important concept in the development of novel antibody-based therapeutics. Computational methods to evaluate hydrophobicity are typically based on hydrophobicity scales and either ignore the effects of the surroundings or model them through a sum of contributions of nearby residues. Here, we present a method based on molecular dynamics that does not include any per residue or per atom parameters except for the underlying force field and therefore automatically takes nonlinear effects into account in a physically meaningful way. We show that the method performs well at identifying hydrophobic antibodies if reliable structures are available and conclude that physics-based descriptors might lead to substantial improvements in computational assessment of hydrophobicity.
Introduction
In the past few decades, biopharmaceuticals have emerged as one of the largest areas of interest in the pharmaceutical industry. As of 2018, there were over 300 biopharmaceutical products licensed in the US, with the largest group of active agents being monoclonal antibodies (mAbs) (1, 2, 3, 4). Though large improvements have been made in the discovery of mAbs binding to a certain target (5), problems may arise regarding the stability, solubility, or pharmacokinetics while developing an active mAb into a drug. Those properties are generally referred to by the term developability (6).
A major problem in the development process is the inherent tendency of some concentrated protein solutions to form aggregates. This problem may be influenced by various factors such as temperature, mechanical stress, and pH (7, 8, 9). Aggregation can be reversible or irreversible and covalent or noncovalent, and the resulting aggregates may be soluble or insoluble (8). Furthermore, multiple mechanisms of antibody aggregation have been discussed in literature (7,10), indicating that various factors contribute to antibody aggregation. Structural instability may lead to aggregation at both hot and cold temperatures (11,12), and hydrophobic surface patches have repeatedly been discussed to be involved (13,14) especially in the formation of reversible aggregates (8). Furthermore, aggregation of antibodies should not be confused with amyloid aggregation, in which peptides or proteins form macroscopic, β-rich fibers or aggregates (15).
Hydrophobic patches on the surface of an antibody have been repeatedly discussed as one of the main contributions to aggregation propensity (8,16). Furthermore, hydrophobic patches can lead to high viscosity (17), though electrostatic properties are usually more predictive in this regard (17, 18, 19). Therefore, there is a strong interest in methods that can quantify the hydrophobicity of a biomolecule.
However, different definitions of hydrophobicity have been used in literature. The hydrophobicity of small molecules is usually quantified in terms of log p-values, which describe the ratio of the molecule’s solubility in octanol and in water (20). In the field of secondary structure prediction, hydrophobicity scales are used to differentiate between amino acids in an aqueous environment and those in more hydrophobic regions such as membranes or in the protein’s interior (21). The probability of a single amino acid to be buried in the hydrophobic core has been related to its free energy of solvation, ΔGsolv (22). Similarly, theoretical descriptions of hydrophobic interactions have focused on calculating ΔGsolv or related quantities (23).
The aim of this work is to explore whether hydrophobic molecules as identified by hydrophobic interaction chromatography (HIC) can also be distinguished from more hydrophilic ones via their free energy of solvation.
Experimental reference data
Several experimental methods have been devised to screen antibodies for their aggregation propensity during the early development stages. For instance, size-exclusion chromatography (24) is commonly used to determine the amount and the mass distribution of soluble aggregated species (25,26). Self-interaction chromatography (27) and cross-interaction chromatography (CIC) (28) measure the interactions of a protein with identical or similar protein molecules, respectively. Standup monolayer adsorption chromatography (SMAC) (29) measures the interaction of a protein with various side chains that resemble the polarity of protein surfaces. Affinity-capture self-interaction nanoparticle spectroscopy (AC-SINS) or salt-gradient AC-SINS quantify the interaction between antibodies bound to the surface of gold nanoparticles by measuring the phonon wavelength (30).
Hydrophobicity of antibodies is often quantified using HIC. This method measures the retention time of molecules in a hydrophobic column, whereas elution is achieved by gradually decreasing the salt concentration (31). There is a clear correlation between HIC retention times and phonon wavelengths from salt-gradient AC-SINS at comparable salt concentrations, which indicates that protein-protein interactions at such salt concentrations are dominated by the same forces as the interactions with a hydrophobic column (30). Furthermore, high HIC retention times of antibodies have been shown to correlate with increased nonspecific interactions with size-exclusion chromatography columns (31).
Throughout this study, we compare our computational results to a data set by Jain et al. (32). This data set contains 137 antibodies, for each of which 11 experimental assays have been performed. Because we attempt to quantify hydrophobicity rather than aggregation, we primarily focus on the hydrophobic HIC data. Furthermore, we use SMAC and CIC assay data. The main difference between those assays is that HIC quantifies interactions with a hydrophobic column, whereas SMAC uses a wide range of functional groups and CIC measures interactions with other (different) antibodies.
Computational estimation of hydrophobicity
The importance of hydrophobicity in antibody research is also highlighted by the number of tools that are aimed at aggregation prediction using hydrophobicity as a main parameter of their input data. For example, the spatial aggregation propensity (16) method is based on the hydrophobicity scale by Black and Mould (33). The therapeutic antibody profiler aims to detect antibodies with abnormal hydrophobic and electrostatic properties or loop lengths compared with clinical-stage antibodies (6). The AggScore algorithm uses descriptors for hydrophobic and electrostatic patches to detect aggregation-prone regions in antibodies (14).
Previous methods in the field of biomolecular research generally apply a residue-wise attribution of hydrophobicity or aggregation propensity based on predefined scales (34,35). Even though some methods contain contributions based on the three-dimensional protein structure, those contributions are generally not physics based. For instance, the spatial aggregation propensity algorithm applies an average of amino-acid-specific hydrophobicity values of nearby solvent-exposed residues (16), and the AggScore algorithm applies a Fermi-type function to weight the contribution of residues in the vicinity (14).
However, the strength of hydrophobic interactions in molecular systems is inherently nonadditive (36, 37, 38). Acharya et al. show a sigmoidal relationship between the perturbations in the hydration shell and the size of a hydrophobic patch (23). Furthermore, roughness can strengthen the effect of hydrophobic as well as hydrophilic surfaces (38). Therefore, we expect that any method based on a linear combination of hydrophobic contributions will not be able to fully describe the conformation dependence of protein hydrophobicity.
Many computational studies have been conducted that investigate the nature of hydrophobic interactions in detail. The interactions between water and a perfectly hydrophobic (i.e., noninteracting) particle can be physically described using the probability of randomly finding a cavity of the appropriate shape in bulk water (39,40). Other methods quantify hydrophobic interactions by simulating a mixture of water and multiple hydrophobic solutes and investigating the solute-solute radial distribution function (40). Those methods have proven effective in describing the hydration free energy of hydrophobic solutes of various sizes and at different temperatures. However, such studies have mostly been limited to simple systems such as noninteracting spheres (39), fully nonpolar molecules (39), or hydrophobic surfaces (23).
Here, we present an approach to describe the hydrophobicity of antibodies in terms of their hydration free energy, based on the GIST (grid inhomogeneous solvation theory) algorithm introduced by Nguyen et al. (41, 42, 43, 44).
We have recently shown that GIST can directly estimate local hydrophobicity on the surface of a given protein based on its interactions with water molecules (45). We further introduced an enhanced GPU implementation of the GIST approach, in which we demonstrate a substantial increase of calculation speed. Thus, it is now possible to calculate hydration free energies, i.e., surface hydrophobicity, for large biomolecular systems such as serine proteases (45) or antibody fragments (this work) with high accuracy at manageable computational cost.
Sampling of conformations and protonation states
An additional challenge in predicting surface properties such as hydrophobicity lies in the inherently dynamic nature of antibodies. It has been well established that proteins constantly fluctuate between a multitude of conformational states (46,47). With these structural rearrangements, the local environment also changes, which can affect surface properties. Recent studies highlight their inherent flexibility of antibodies and its impact on physicochemical properties such as binding promiscuity or aggregation propensity (10,48, 49, 50, 51, 52, 53). Molecular dynamics simulations offer the unique opportunity to capture this flexibility at atomic resolution (54). Current advances in the field, such as enhanced sampling techniques and Markov state modeling, allow for an efficient profiling of highly diverse structural ensembles (50, 51, 52).
In the interplay with conformational dynamics, there are several further environmental aspects contributing to surface hydrophobicity. As previously mentioned, one major determinant for the aggregation behavior of antibodies is the pH value. Small changes in pH can be enough to prevent or promote aggregation (8). The macroscopic change in pH is microscopically reflected by changes in the protein’s protonation states. How and at which pH this reaction occurs is determined by the pKa value of each titratable residue. However, the pKa strongly depends on the local environment of a residue. Consequently, the pronation can change upon structural rearrangements, and variation of the protonation can further translate into altered local hydrophobicity.
However, a reliable prediction of protonation states is rather challenging. Multiple theoretical techniques have emerged to predict the pKa values of a protein, either focusing on a static structure (e.g., PROPKA (55) or H++ (56)) or coupling the prediction with dynamics (family of constant pH methods (57,58)). It has been shown that constant pH molecular dynamics (CpHMD) simulations can closely reproduce experimental pKa values while at the same time capturing pH-dependent structural changes of biomolecules (59).
Aim of this work
Here, we assess whether antibodies that exhibit high hydrophobicity in HIC experiments can be identified via their free energy of hydration as calculated from GIST. We combine state-of-the-art simulation techniques to investigate the distribution of hydrophobic regions on the surface of 126 Fv structures and compare the results with available experimental data from the literature (32). We employ Gaussian accelerated MD simulations (60) to capture diverse conformational ensembles. Furthermore, we incorporate the Monte-Carlo-based CpHMD framework to obtain protonation state ensembles. With the aid of our recent GPU-based implementation of the GIST algorithm (45), we are able to describe the hydrophobicity of antibodies while taking changes in structure and protonation into account.
Methods
GIST
The hydrophobicity of a molecule is reflected by its interaction with water molecules. GIST (41, 42, 43, 44,61) translates information on locations and orientations of water molecules into localized thermodynamic properties of water on a grid. This allows for an in-depth analysis of solvation around a solute, such as a protein in aqueous solution.
The GIST method provides information on the solvation free energy ΔGsolv(qu) of a single solute conformation. In the case of a flexible solute, multiple GIST calculations of different solute conformations qu must be performed. The overall ΔGsolv is then
| (1) |
where kB is Boltzmann’s constant, T is the system temperature, and p(qu) is the probability of solute conformation qu. A derivation of this equation is shown in the Supporting Materials and Methods. The following equations refer to a single conformation, but the parameter qu will be omitted.
To calculate the individual ΔGsolv(qu), the spatial integrals from the Inhomogeneous Solvation Theory (IST) are replaced by a discrete sum over voxels in a grid.
The localized, density-weighted free energy is split into energetic and entropic contributions (Eq. 2). The energy is again split into solvent-solvent and solute-solvent contributions (Eq. 3).
| (2) |
| (3) |
Here, G denotes the free energy, E the energetic contribution, T the temperature, and S the entropy; rk are the coordinates of voxel k, u denotes the solute, and v denotes the solvent.
The entropy is approximated by the two-body solute-solvent entropy contribution, neglecting all higher order contributions. A comparison of the ΔG-, ΔE-, and ΔS-values to results from thermodynamic integration can be found in Loeffler et al. (62). They report good correlations between GIST and thermodynamic integration for the enthalpy and the free energy, whereas the entropy approximation is less accurate.
The solute-solvent term is further split into two different expressions for orientational and translational entropy (Eq. 4).
| (4) |
Both the translational (ΔStrans) and orientational (ΔSorient) contributions to entropy are calculated using a nearest neighbor algorithm (Eqs. 5 and 6). Alternatively, both contributions can be computed together, approximating the six-dimensional integral over the rotational and orientational degrees of freedom (44).
| (5) |
| (6) |
| (7) |
Here, R is the ideal gas constant, Nk is the total number of water molecules in voxel k, Nf is the total number of frames, γ is Euler’s constant that corrects for an asymptotic bias, dtrans,i is the cartesian distance between the solvent molecule i and its nearest neighbor, Δωi is the angular distance between solvent molecule i and its rotationally nearest neighbor in the same voxel, and ρ0 is the number density of bulk solvent.
The interaction energy can readily be computed using the force field energy. Subsequent binning of the water molecules yields the solvent-solvent interaction energy Evv, as well as the solute-solvent interaction energy Euv in each voxel.
Starting structures
This work makes use of an experimental data set by Jain et al. (32). Two different subsets were defined: one set of 49 antibodies for which structures were available in the Protein Data Bank (PDB) (63), which will be called the “PDB set” hereafter. The accession codes we used can be found in Table S1.
Furthermore, a nonoverlapping set of 77 antibodies, for which no crystal structures were available, was investigated starting from homology models. The Rosetta antibody modeling protocol was used. To reduce the calculation time, the modeling was run partly on the ROSIE online server (64, 65, 66, 67, 68) and partly on the HPC infrastructure of the University of Innsbruck (LEO). For the local homology modeling calculations, we used Rosetta 2017.52 (68). We employed the kinematic loop closure (NGK) algorithm (69) to produce 1024 H3 loop models starting from the top grafted model, as well as 224 H3 loop models starting from the nine other (non-top-grafted) models, analogous to the ROSIE server. From each homology modeling run, the top-scored model was used as a starting structure. This set will be called the “homology models.”
MD simulations
All simulations were performed using Amber18 (70). The ff14SB force field (71) was used for all simulations, together with the TIP3P (72) water model. Periodic boundary conditions were applied after solvating the systems in a cubic box with a minimal wall distance of 12 Å.
Simulations were performed using the PME algorithm (73) for long-range electrostatic interactions and a cutoff of 8.0 Å for the short-range interactions. A 2 fs time step was employed while constraining the length of all bonds involving hydrogen atoms using SHAKE (74). All simulations were performed in an NpT ensemble using the Langevin thermostat (75) at a temperature of 300 K and a collision frequency of 2 ps−1, as well as a pressure of 1 bar. The Monte Carlo barostat (76) was employed with a volume change attempt every 100 steps for all simulations except the GIST calculations, for which a Berendsen barostat (77) was used with a pressure relaxation time of 1 ps.
Before starting production simulations, all starting structures were equilibrated following a protocol previously developed in our group (78).
Gaussian accelerated molecular dynamics (GaMD) simulations (60) were run applying a dual boost. The threshold energy was set to its upper limit. The number of simulation steps to update the potential energy statistics was set to four times the number of atoms in the system, according to the recommendation in the Amber manual (79), and rounded up to a multiple of 500. With a typical system size of 37,000 atoms and a 2 fs time step, this corresponds to ∼300 ps. The closest multiple of this time to 2 ns was used as equilibration time, using conventional molecular dynamics. Similarly, the closest multiple of the averaging time to 6 ns was used to update the GaMD acceleration parameters. Subsequently, production simulations of 200 ns were performed using the final set of acceleration parameters.
CpHMD simulations were run in explicit solvent at a pH of 7.0 with a salt concentration of 0.1 mol/L (59). Protonation state changes were attempted every 200 steps, followed by 200 steps of solvent relaxation after a successful attempt. The production runs were 100 ns long.
Clustering and GIST analysis
GIST calculations were started for representative structures from a clustering of the respective simulations. Clustering was performed using the k-means algorithm (80) implemented in cpptraj (79) and in the case of GaMD simulations, cluster populations were reweighted using cumulant expansion to the second order (81). Five clusters were produced from each of the GaMD and CpHMD simulations. For each cluster representative, 20 ns of simulation were performed using a restraint weight of 1000 kcal mol−1Å−2 on all protein heavy atoms. 10,000 frames were collected. The center of mass of all Cα atoms was set to the origin. The GIST grid was also centered at the origin and sized in such a way that each atom is at least 7 Å away from the walls and that the number of voxels is a multiple of 10 in each direction, resulting in ∼2 × 106 grid voxels. All analyses were performed using our recently published GPU implementation of the GIST algorithm (45).
Postprocessing
All postprocessing was performed using a set of in-house tools written in Python (81, 82, 83).
The protein structures were aligned to a reference using the ABangle core set as a selection mask (84). As reference, we used the Fv region of the PDB: 1N8Z structure, rotated in such a way that the x, y, and z axes correspond to the eigenvectors of the inertia matrix. The CDR loops point in the +z direction and the heavy chain in the +x direction. The coordinates of the GIST grids were transformed accordingly.
For all analyses, a reference value of −9.540 kcal/mol was subtracted from the normalized water-water interaction energy Evv. This value was determined from a GIST calculation obtained from 100 ns cMD of a cubic water box containing 11,452 water molecules. 10,000 frames were used for the GIST analysis. The localized hydration free energy was calculated by summing up the water-water interaction energy, the solute-water interaction energy Euv, and the entropy contribution calculated from a sixth-order integral −TΔSsix.
For further postprocessing, we first projected the free-energy contributions onto a set of predefined points on a unit sphere. To do so, we generated a set of 998 points using the method described by Deserno (85). We then selected all voxels within 5 Å of the protein, calculated their angular coordinates, and assigned each voxel to the closest sphere point based on the angular distance. We then summed the values of all voxels assigned to the same sphere point. We note that this procedure preserves the total hydration free energy, i.e., the sum over all sphere points is exactly the sum over all grid voxels.
The total ΔGsolv was calculated by summing the contributions of sphere points with z > 0, after applying a Gaussian blur with a sigma of 0.3 radians. By excluding points with z below 0, we omit the “lower” half of the Fv region, i.e., the one pointing toward the CH2 domain. This is advantageous because the CDR loops, as well as their surroundings, are completely included, but the region that contacts the CH2 domain is omitted. The latter would be problematic because omitting the CH2 domain in the simulation can lead to artificial hydrophobic surfaces. Furthermore, we note that the Gaussian blur only alters the summed ΔG in the vicinity of the cutoff, effectively leading to a smooth cutoff in the z direction.
The spherical representation allows us to introduce a new metric, called ΔGunfavorable. For this metric, we apply a cutoff function that is zero below a cutoff ΔG0 and linear above this cutoff (Eq. 8).
| (8) |
The constant ΔG0 determines where the switching function transitions from zero to a linear function. Throughout this study, −0.2 was used. In contrast to the free energy of solvation, ΔGunfavorable ignores the hydrophilic regions of an antibody while preserving all information about the most hydrophobic regions. Again, a total ΔGunfavorable was calculated by summing all sphere points with z > 0. The performance of our method as a function of ΔG0 is shown in Fig. 1 and the Supporting Materials and Methods.
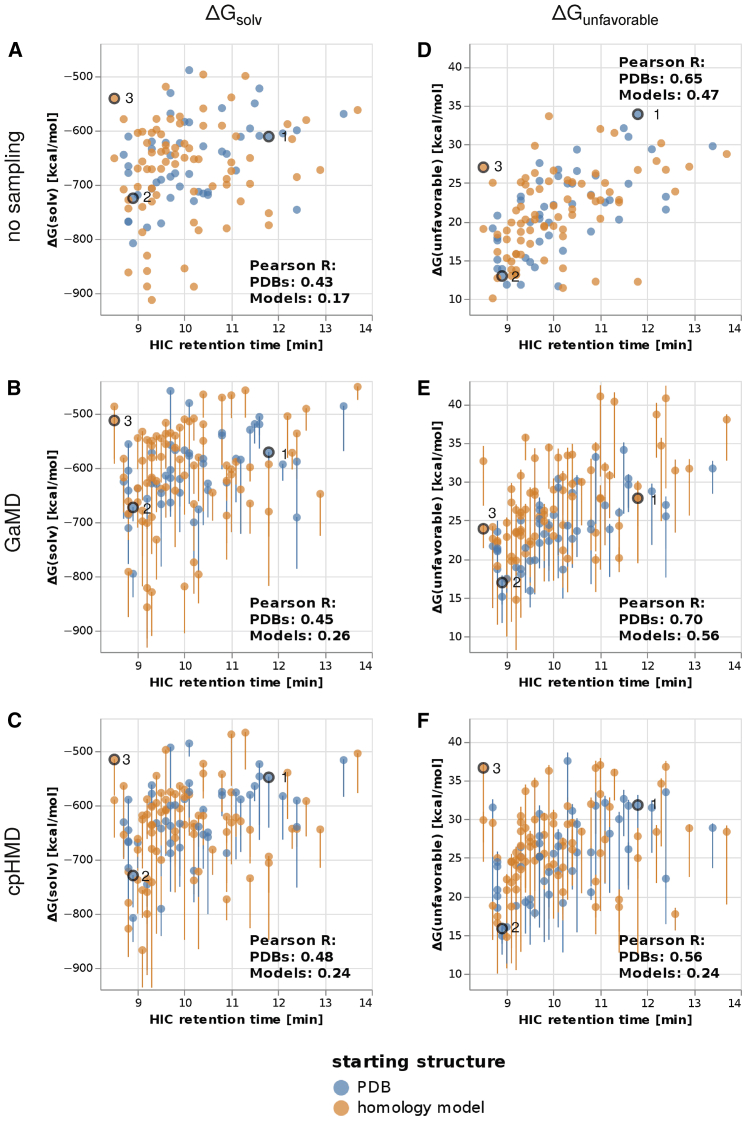
Figure 1.
Total ΔGsolv (A–C) and ΔGunfavorable (D–F), using different amounts of sampling. (A and D) No sampling. (B and E) 200 ns GaMD simulations. (C and F) 100 ns CpHMD. In the second and third row, each point represents the weighted average according to Eq. 1 of five GIST calculations started from different cluster representatives, and the error bars represent the minimum and maximum of the five individual values. Bevacizumab, muromonab, and dacetuzumab are labeled with 1, 2, and 3, respectively. To see this figure in color, go online.
Based on the spherical representation of ΔGunfavorable, we applied the uniform manifold approximation and projection (UMAP) (86) algorithm to project our GIST calculations onto a two-dimensional representation. UMAP is a dimension-reduction algorithm that is based on the assumption that the data are uniformly distributed on the Riemannian manifold and that tries to find a low-dimensional projection that preserves the local topological structure of the high-dimensional input data.
We applied a Gaussian blur to the spherical representation of our hydrophobicity data, using a standard deviation of 0.3 radians. We then apply UMAP using 30 points as the local neighborhood and a Euclidean distance metric. All parameters were kept at their default values.
For visualization purposes, we calculated the average contribution to the hydration free energy per water molecule in a shell of 5 Å around each atom and colored the protein surface according to those values for visualization purposes. The visualizations were done using PyMOL (87).
Reference data
We compare our computed ΔGsolv- and ΔGunfavorable-values to an experimental data set by Jain et al. (32). In this work, the results of 11 assays are presented for a set of 137 antibodies, all of which were either approved as drugs or undergoing clinical trials at the time of publication.
In our study, we primarily use the HIC retention time as a reference value for experimental hydrophobicity. Furthermore, we investigate the ability of our method to distinguish antibodies that strongly bind HIC, SMAC, or CIC columns from those that bind weakly to the same column.
A short summary of the experimental conditions that Jain et al. used for those assays (32) is given in the Supporting Materials and Methods.
Results
Hydrophobicity computed from crystal structures and homology models
Following the procedure described in the Methods, we calculated solvation free energies ΔGsolv, as well as ΔGunfavorable, for 49 PDB structures and 77 homology models and compared the results to the experimental HIC retention times, as shown in Fig. 1, A and D. As explained in the Methods, we limit all our analyses to the upper half of the spherical projection, corresponding to the part of the antibody that is farthest away from the CH1-CL region and that contains the CDR loops.
The Pearson correlation between ΔGsolv and the HIC retention time is 0.43 for the PDB set and 0.17 for the homology models. The correlation between ΔGunfavorable and the HIC retention time is 0.65 for the PDBs and 0.47 for the homology models. Using either metric, the results are significantly better using crystal structures than using homology models. Furthermore, the correlations using ΔGunfavorable are significantly improved compared with those using ΔGsolv, which implies that HIC retention times are dominated by the most hydrophobic regions of an antibody.
Enhanced sampling using GaMD
To investigate the effect of conformational sampling on the accuracy of our method, we performed 200 ns GaMD simulations to obtain a structural ensemble. We used k-means clustering to obtain five representative structures of each trajectory and calculated ΔGsolv and ΔGunfavorable as a weighted average using Eq. 1, as shown in Fig. 1, B and E. The error bars show the minimum and maximum of the values per cluster representative.
Using this approach, we obtain Pearson correlations of 0.45 and 0.26 between ΔGsolv and the HIC retention time for the PDB set and the homology models, respectively. The correlation between ΔGunfavorable and the HIC retention time is 0.70 for the PDB set and 0.56 for the homology models.
As with the direct calculations, ΔGunfavorable correlates significantly better with the HIC retention time than ΔGsolv. However, the conformational sampling only leads to a small improvement compared to the direct calculation. This is equally true for the PDB set and for the homology models, indicating that the sampling provided by GaMD is often insufficient to correct the errors introduced by the modeling. We note, however, that for some homology models that are predicted significantly too hydrophilic in Fig. 1 D, the conformational sampling provided by GaMD leads to significant improvements in the calculated ΔGunfavorable.
Protonation state sampling using CpHMD
Furthermore, we performed 100 ns CpHMD simulations to incorporate sampling of protonation states and calculated ΔGsolv and ΔGunfavorable analogously, as shown in Fig. 1, C and F. We obtain Pearson correlations between ΔGsolv and the HIC retention time of 0.48 for the PDB set and of 0.24 for the homology models. The correlation between ΔGunfavorable and the HIC retention time is 0.56 for the PDB set and 0.24 for the homology models.
Again, we find that ΔGunfavorable performs significantly better than ΔGsolv. Furthermore, as with the structural sampling, there is no large improvement compared to the direct GIST calculations. Interestingly, the correlation between ΔGunfavorable and the HIC retention is even worse than without the protonation state sampling. This is less pronounced when (more reliable) PDB structures are used.
Combining conformational and protonation state sampling
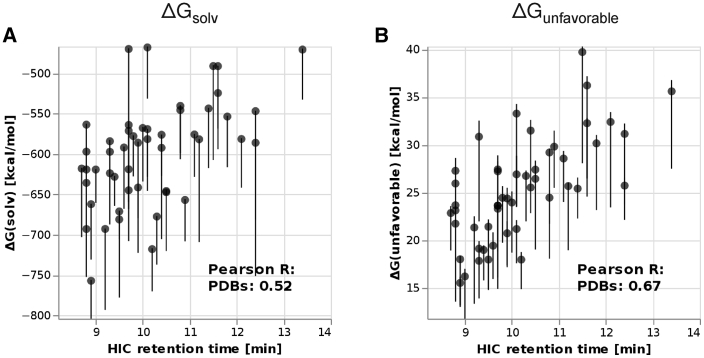
To investigate the combined effect of structural sampling and protonation state sampling, we ran 10 ns CpHMD simulations starting from each of the cluster representatives of the GaMD simulations. We then fixed the protonation state of each amino acid to the most prominent state of the CpHMD and performed GIST calculations of those structures.
Fig. 2 shows the comparison of the calculated hydration free energies with the experimental HIC retention times. We find Pearson correlations of 0.52 and 0.67 using ΔGsolv and ΔGunfavorable, respectively. This is comparable to the results based directly on the representatives of the GaMD simulations, indicating that protonation states only play a minor role for hydrophobicity of antibodies.
Figure 2.
Total ΔGsolv (A) and ΔGunfavorable (B) of the antibodies in the PDB set, using the combined structural and protonation sampling approach. Each point represents the weighted average according to Eq. 1 of five GIST calculations started from different cluster representatives, and the error bars represent the minimum and maximum of the same five values.
Visualization of hydrophobicity
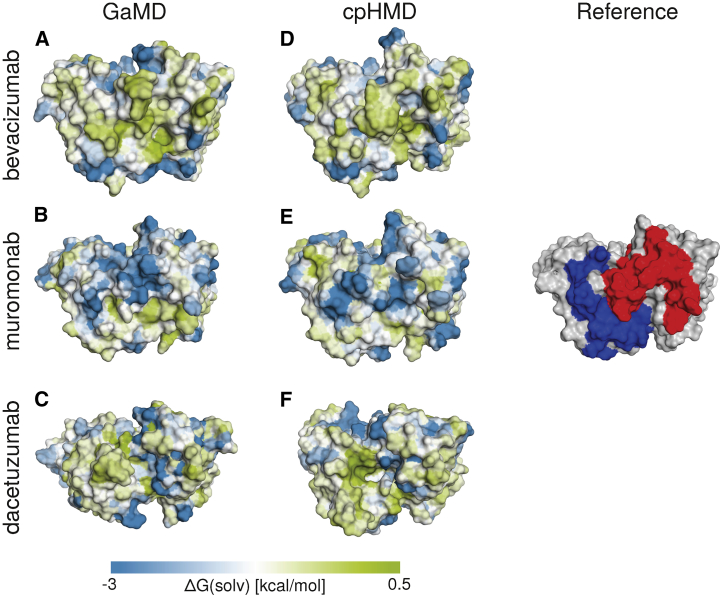
To set the obtained hydrophobicity estimates in a structural context, we projected the hydration free energy onto the protein surface. As an example, we show visualizations of three antibodies in Fig. 3. Bevacizumab and muromonab were chosen as hydrophobic and hydrophilic examples, respectively. Crystal structures of the Fab fragments are available in both cases. Furthermore, dacetuzumab was chosen as an example for which the hydrophobicity of the starting structure is overestimated based on a homology model but for which structural sampling leads to an improvement. The left column (Fig. 3, A–C) depicts the localized hydrophobicity of the three systems started from the most highly populated cluster of the ensemble captured with GaMD. It is clearly visible that there is a large hydrophobic region at the CDRs of bevacizumab, whereas muromonab is predicted to be significantly more hydrophilic. This is in line with experimental results, as reflected by the lower HIC retention time of muromonab (8.9 min) compared to bevacizumab (11.8 min).
Figure 3.
Averaged hydration free energy of the highest populated cluster representative mapped onto its surface representation using six different simulations. (A and D) Fv fragments of bevacizumab, (B and E) muromonab, and (C and F) dacetuzumab. (A–C) Cluster representatives from GaMD simulations. (D and E) Cluster representatives taken from CpHMD simulations. For reference, the surface of muromonab is also shown with the heavy chain CDR loops colored in red and the light chain CDR loops colored in blue, in the same orientation. To see this figure in color, go online.
When looking at the CpHMD representative of dacetuzumab, we find that there is a large cavity between the CDR-H3 and CRD-L3 loops. This leads to an increased surface hydrophobicity because residues of the hydrophobic core become solvent exposed. In the GaMD representative, this cavity has been closed, leading to a more realistic representation of dacetuzumab’s hydrophobicity in solution.
Although the localized hydrophobicity in Fig. 3 facilitates visual comparison of different antibodies, this representation is not well suited for automated postprocessing workflows. We therefore seek to reduce the surface hydrophobicity data to a fixed number of points per antibody. To do so, we project ΔGsolv to points on the surface of a sphere, as described in the Methods. This projection is visualized in Fig. 4. In contrast to the depictions in Fig. 3, this representation is more suitable for postprocessing and might be used as input for machine learning or pattern recognition algorithms in future works.
Figure 4.
Spherical projections of the highest populated cluster representative of six different simulations. All spheres were generated after rotating the GIST grids according to the reference orientation shown in Fig. 3. (A and D) Fv fragments of bevacizumab, (B and E) muromonab, and (C and F) dacetuzumab. (A–C) Cluster representatives taken from GaMD simulations. (D–F) Cluster representatives taken from CpHMD simulations. The orientation of the spheres matches the surfaces in Fig. 3. To see this figure in color, go online.
Binary classification, receiver operating characteristic
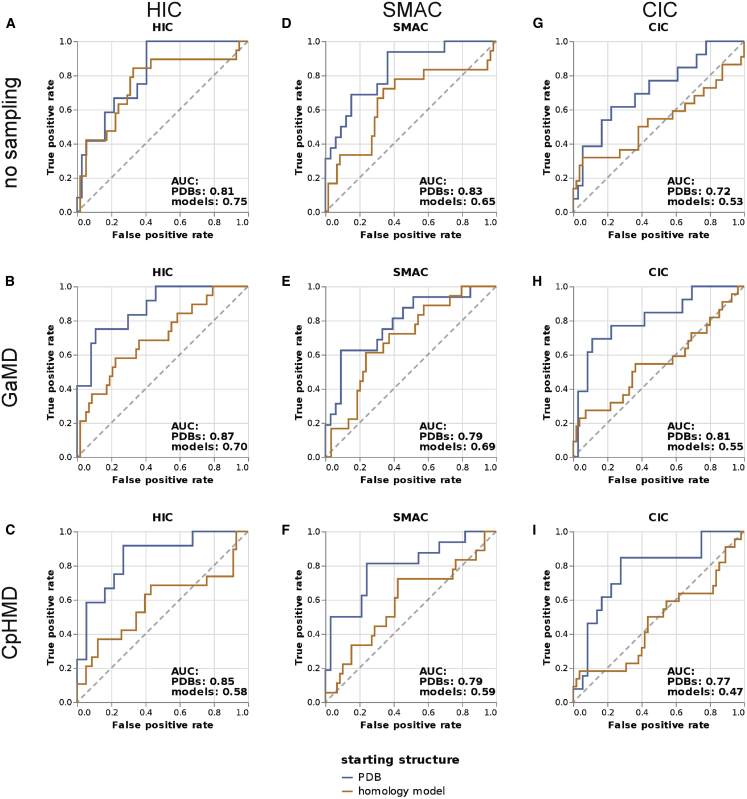
To assess the capability of our method to detect antibodies that show increased hydrophobicity or other signs for nonspecific interactions, we separated the data set into delayed (retention time above the third quartile) and nondelayed (retention time ≤the third quartile) antibodies based on the HIC, SMAC, and CIC assays and plotted the receiver operating characteristic in Fig. 5, A–C, respectively. We generally find slightly better predictivity for HIC than for SMAC and CIC, with an AUC of 0.87 for the PDB set combined with GaMD sampling. In accordance with the Pearson correlations shown in Fig. 1, the area under the curve (AUC) is significantly higher when starting from PDB structures as compared to homology models. An explanation could be that in both SMAC and CIC, interactions other than hydrophobic interactions, e.g., hydrogen bonding, may contribute to column retention.
Figure 5.
Receiver operating characteristic plots showing the ability of ΔGunfavorable to separate between antibodies showing delayed (>3rd quartile) and normal (≤3rd quartile) elution based on the (A–C) HIC retention times, (D–F) SMAC retention times, and (G–I) CIC retention times. (A), (D), and (G) represent data collected without sampling, (B), (E), and (H) represent data from 200 ns GaMD simulation, and (C), (F), and (I) represent data from 100 ns CpHMD simulation. To see this figure in color, go online.
Explorative data analysis using the UMAP algorithm
Because there is still a significant amount of unexplained variance when comparing the total hydration free energy to the experimental HIC data, we used the UMAP algorithm to create two-dimensional representations of our PDB and homology model sets. This algorithm aims at creating a low-dimensional representation of a data set while retaining the high-dimensional distance between similar points (86).
We compare the three different types of sampling (GaMD, CpHMD, or both) and the total ΔGsolv and ΔGunfavorable. The resulting plots are shown in Fig. 6.
Figure 6.
UMAP projections of the ΔGunfavorable compared with the experimental HIC retention times. The five GIST simulations for each antibody are treated as individual data points. (A–C) PDB set. (D and E) Homology models. (A and D) Results using 200 ns of GaMD for sampling. (B and E) Results using 100 ns CpHMD. (C) Combined structural and protonation state sampling approach. To see this figure in color, go online.
Discussion
In our study, we characterize the hydrophobicity of antibodies using GIST and investigate the impact of conformational diversity and pH on the predicted surface hydrophobicity. We compare our results with experimental HIC retention times from the literature. HIC has been shown to correlate with the aggregation behavior of antibodies (31), as well as with their aromatic amino acid content (88).
We investigate the impact of environmental effects like the pH or conformational diversity, which have been discussed in the literature as major contributors to surface hydrophobicity and aggregation propensity (89). It has been shown that the ability of an antibody to adopt various distinct conformations strongly influences its biophysical properties and function and thus dramatically increases the size of the antibody repertoire (90, 91, 92, 93, 94). This intrinsically flexible nature of antibodies and the crucial role of protonation render the prediction of surface properties difficult.
Various studies have shown that crystal packing effects can result in strong distortions of the CDR loops (53,95,96). These findings further emphasize that conformational sampling is vital to identify dominant structures in solution.
Our method is computationally slower than methods that rely on precalculated hydrophobicity scales, with several hundreds of nanoseconds of simulation time per antibody (with a typical system size around 37,000 atoms, we achieve simulation speeds around 200 ns/day on a GeForce GTX 2080 GPU; NVIDIA, Santa Clara, CA). However, the recent improvements to the GIST algorithm make it applicable to medium-sized data sets with around a hundred candidates. On the other hand, a big advantage of our method is that it does not make any prior assumptions on the relation between conformation and hydrophobicity and is thus well suited to investigate the impact of conformations or protonation states.
Effects of the starting structure on hydrophobicity
Starting from a set of 49 crystal structures obtained from the PDB, as well as a set of 77 homology models of different antibodies, we perform GIST calculations to obtain the free energy of solvation ΔGsolv, as well as the free energy of hydrophobic regions ΔGunfavorable as defined in Eq. 8. We compare our results with experimental HIC retention times and find significantly stronger correlations when using crystal structures than when using homology models. This shows that errors in the homology modeling procedure can have a large impact on the calculated surface hydrophobicity of antibodies.
Those findings emphasize the decisive role of reliable structures in the prediction of surface properties such as hydrophobicity. However, in the early stages of biopharmaceutical development, it is often not feasible to obtain crystal structures for each considered antibody. Therefore, substantial scientific efforts have been dedicated in recent years to improve structure prediction tools for antibodies (66, 67, 68,97).
The β-sheet framework of antibodies is structurally highly conserved and its structure prediction thus rather straightforward. However, accurate modeling of the CDR is less apparent. The CDR consists of six hypervariable loops known to strongly influence function and properties of an antibody (98). Five of these six CDR loops, except for the CDR-H3 loop, have been classified to a limited set of main-chain conformations, so-called canonical structures, according to their length and sequence (99, 100, 101). Therefore, their structure can be correctly predicted in many cases. However, structure prediction of the CDR-H3 loop remains challenging (97,101).
Our results show that potential shortcomings of the structure prediction strongly affect structure-based hydrophobicity predictions. This might be one reason for the continued popularity of sequence-based hydrophobicity prediction methods (13,102,103) because it implies that structure-based methods, which should, in principle, outperform their sequence-based counterparts, are significantly limited by the quality of their input structures.
Furthermore, we find that the distribution of ΔGsolv and ΔGunfavorable is slightly different between PDB structures and homology models. On the one hand, some homology models have unusually low ΔGsolv-values, which can be seen most clearly in Fig. 1 A. Upon visual inspection, we found that many of those examples contain an accumulation of negatively charged residues. For instance, the L1 loop of lampalizumab contains four aspartate residues. It has been reported (104) that negatively charged residues have very negative hydration free energies in GIST calculations. Thus, we surmise that the conformation of such negatively charged residues strongly impacts the free energy of solvation ΔGsolv.
On the other hand, some homology models show an unusually high ΔGunfavorable, which can be seen best in Fig. 1 E. This metric focuses mainly on the most hydrophobic regions of an antibody while ignoring all details of the hydrophilic regions. Therefore, this implies that homology models are also not always optimal at burying hydrophobic side chains.
Effects of structural sampling on hydrophobicity
We performed GaMD simulations, which have been designed to capture an extended conformational space (60), on all of the 49 crystal structures and 77 homology models, and performed GIST calculations on five cluster representatives each.
Generally, we find that our simulations only lead to small improvements in the Pearson correlation between ΔGunfavorable and experimental HIC retention times. This is true both for the crystal structures and for the homology models. For instance, we find a correlation of 0.65 when doing calculations on the PDB set without any sampling, which improves to 0.70 through the GaMD simulations. However, the considerable magnitude of the depicted error bars shows that there is strong variability of the surface hydrophobicity during the simulation. Together with the comparison between homology models and crystal structures, these findings show that protein conformation strongly impacts the hydrophobicity but that very long simulations might be necessary to correct mistakes introduced during the homology modeling (50, 51, 52).
On the other hand, there are some cases of antibodies for which our simulations lead to significant improvements. Using ΔGunfavorable, there are some cases in which homology models are predicted significantly too hydrophilic without sampling (Fig. 1 D) and in which structural sampling using GaMD can improve the prediction (Fig. 1 E).
Furthermore, there are also examples where GaMD can correct an overprediction of hydrophobicity. For example, the experimentally hydrophilic antibody dacetuzumab displays high surface hydrophobicity both when using the homology model directly and when performing protonation state sampling with CpHMD, but not when using GaMD to cover a larger conformational space. This can be seen from the ΔGunfavorable-values in Fig. 1, D–F. Fig. 3, C and F visualize the localized free energy of solvation ΔGsolv of dacetuzumab in conformations from the CpHMD and GaMD ensembles, respectively. In the CpHMD structure, nonoptimal packing of side chains leads to exposure of hydrophobic residues from the VH-VL interface and therefore to an artificial hydrophobic patch on the surface. In the GaMD ensemble, however, this cavity is closed and the respective side chains are buried, leading to a more realistic estimation of the surface hydrophobicity.
Effects of protonation state sampling on hydrophobicity
Another factor of interest when calculating hydrophobicity and aggregation, besides the conformational ensemble, is the pH. Gentiluomo et al. have shown that even small changes in the pH can substantially shift the aggregation propensity (8). In contrast, our results show that protonation state sampling using CpHMD does not improve the prediction of HIC retention times and may even deteriorate the results when no reliable starting structures are available. This may be seen by comparing Fig. 1, C and F to Fig. 1, A and D.
Combining the protonation state sampling from CpHMD with starting structures from the PDB and the structural ensemble from GaMD, we again find better correlations to the HIC retention time, which are comparable with the results using GaMD only.
Taken together, these findings indicate that protonation states are not the primary source of error in our hydrophobicity calculations. On the other hand, the abovementioned study by Gentiluomo et al. (8) found a strong influence of the pH on aggregation. However, we note that hydrophobicity and aggregation propensity are different properties. It is plausible that interactions of a protein with a hydrophobic column are less charge dependent than protein-protein interactions.
Total ΔG vs. ΔG of hydrophobic regions
In Fig. 1, we compare both the total hydration free energy ΔGsolv and the hydrophobic free energy ΔGunfavorable to experimental HIC retention times and find significantly better Pearson correlations using ΔGunfavorable. The difference between those metrics is that ΔGunfavorable only takes the most hydrophobic surface regions into account, whereas ΔGsolv describes the solvent-water interaction of the whole molecule. This indicates that the interaction between antibodies and HIC columns is dominated by the most hydrophobic regions of the antibody surface. Similar ideas have been proposed in the literature (105). Furthermore, our result is consistent with the common practice to base hydrophobicity predictions on quantities like the areas of hydrophobic patches (105), which also disregards the more hydrophilic surface regions.
UMAP
To show how our spherical projection might be used as input for further data analysis, we project our data set to a two-dimensional subspace using the UMAP method. The results are shown in Fig. 6. Consistent with our previous analyses, we find a clearly better separation of high and low HIC retention times in the PDB set than in the homology models, which further indicates that characterization of surface hydrophobicity strongly depends on the initial structure. Furthermore, we observe that protonation state sampling using CpHMD leads to very poor separation when applied to homology models, whereas the results are quite good when crystal structures or, even better, a combination of crystal structures and conformational sampling is available as the structural basis for the CpHMD. Hence, as discussed above, the impact of conformational sampling clearly outweighs solely optimizing the protonation states.
A main difference between the UMAP results depicted in Fig. 6 and the preceding analysis is that the latter show ensemble averages. In the UMAP projections, on the other hand, each of the five cluster representatives per antibody is depicted individually. The UMAP algorithm can clearly identify cluster representatives that belong to the same antibody, whereas a simple summation of ΔGsolv or ΔGunfavorable leads to very high noise because of conformational differences.
Our hypothesis is that the summed ΔG-values suffer more from the noise that is introduced by taking a limited set of structures from the conformational ensemble. Because solvation is conformation dependent, antibodies can have different ΔGsolv and ΔGunfavorable even in regions that are identical in their sequence, because of the limited sampling of conformations. In the UMAP calculations, a Euclidean distance metric is used that automatically places higher weights on strongly different regions, thus favoring real structural differences over random deviations from the limited sampling. The good separation in Fig. 6 C indicates that this is a better use of the available information and that this translates to reduced two-dimensional space. However, further work will need to be done to see how this can be used to improve hydrophobicity predictions.
Binary classification and receiver operating characteristic
We test the performance of our method in performing a binary classification, i.e., in detecting the most hydrophobic antibodies of our data set. We find an AUC of 0.87 for the detection of delayed elution in a HIC column and an AUC of 0.79 when comparing to a SMAC column (using the GaMD results). This shows that our method can be useful in filtering the strongest-binding antibodies from a data set, even though not all antibodies are predicted correctly. However, we again observe that the predictivity of our method substantially deteriorates when using homology models instead of PDB structures, indicating that high-quality structures are necessary to detect hydrophobic antibodies based on protein-water interactions.
Conclusions
We have developed a purely physics-based method to predict the hydrophobic behavior of antibodies based on a localized description of the free energy of hydration. Our method does not contain any residue-specific hydrophobicity parameters but performs well at predicting the relative aggregation propensity in a set of antibodies, especially when reliable structural information is available. Furthermore, our method allows a visualization of the hydrophobicity on the antibody surface, which might be a valuable tool for rational design of less aggregation-prone antibody variants.
Our analyses show that high a quality structure is crucial for the correct prediction of surface hydrophobicity using physics-based methods. The correlation between our metrics and experimental hydrophobicity is significantly better when using crystal structures than when using homology models as starting structure. Furthermore, we highlight that conformational sampling, i.e., describing hydrophobicity as an ensemble property, can reduce inaccuracies resulting from the uncertainties of structure prediction tools. However, we also show that structural inaccuracies can be long lived in molecular dynamics simulations, which represents a major challenge for structure-based hydrophobicity prediction, especially when large data sets are investigated.
Our results show that hydrophobicity is strongly dependent on the protein conformation. Ensembles generated from homology models may overestimate hydrophobicity, indicating that those structures are unable to sufficiently bury their hydrophobic side chains. We also investigate the effect of protonation state sampling on hydrophobicity and find that it only performs well when combined with enhanced sampling techniques because the protonation states are themselves conformation dependent.
Furthermore, we show that localized data on the hydration free energy can be used as input for the UMAP dimensionality reduction method. We presume that the localized information that our method provides will enable substantial improvements to our prediction quality once we gain a deeper understanding of the postprocessing methodology.
Author Contributions
F.W. performed research and wrote most of the manuscript. M.L.F.-Q. performed research. A.S.K. analyzed data. J.K. assisted with the GIST calculations. F.H. assisted with the CpHMD simulations. H.K. helped supervising the research. G.G. helped supervise the research. K.R.L. supervised the research. All authors contributed to writing the manuscript.
Acknowledgments
The computational results presented her have been achieved (in part) using the LEO HPC infrastructure of the University of Innsbruck.
This work was supported by the Austrian Science Fund via the grants P30565, P30737, and P30402, as well as DOC 30. H.K. and G.G. are Roche employees. Roche has an interest in developing antibody-based therapeutics.
Editor: Chris Chipot.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.11.010.
Supporting Material
References
- 1.Walsh G. Biopharmaceutical benchmarks 2018. Nat. Biotechnol. 2018;36:1136–1145. doi: 10.1038/nbt.4305. [DOI] [PubMed] [Google Scholar]
- 2.Kaplon H., Reichert J.M. Antibodies to watch in 2018. MAbs. 2018;10:183–203. doi: 10.1080/19420862.2018.1415671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kaplon H., Muralidharan M., Reichert J.M. Antibodies to watch in 2020. MAbs. 2020;12:1703531. doi: 10.1080/19420862.2019.1703531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kaplon H., Reichert J.M. Antibodies to watch in 2019. MAbs. 2019;11:219–238. doi: 10.1080/19420862.2018.1556465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mould D.R., Meibohm B. Drug development of therapeutic monoclonal antibodies. BioDrugs. 2016;30:275–293. doi: 10.1007/s40259-016-0181-6. [DOI] [PubMed] [Google Scholar]
- 6.Raybould M.I.J., Marks C., Deane C.M. Five computational developability guidelines for therapeutic antibody profiling. Proc. Natl. Acad. Sci. USA. 2019;116:4025–4030. doi: 10.1073/pnas.1810576116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mahler H.C., Friess W., Kiese S. Protein aggregation: pathways, induction factors and analysis. J. Pharm. Sci. 2009;98:2909–2934. doi: 10.1002/jps.21566. [DOI] [PubMed] [Google Scholar]
- 8.Gentiluomo L., Roessner D., Frieß W. Characterization of native reversible self-association of a monoclonal antibody mediated by Fab-Fab interaction. J. Pharm. Sci. 2020;109:443–451. doi: 10.1016/j.xphs.2019.09.021. [DOI] [PubMed] [Google Scholar]
- 9.Hauptmann A., Hoelzl G., Loerting T. Distribution of protein content and number of aggregates in monoclonal antibody formulation after large-scale freezing. AAPS PharmSciTech. 2019;20:72. doi: 10.1208/s12249-018-1281-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Codina N., Hilton D., Dalby P.A. An expanded conformation of an antibody Fab region by X-ray scattering, molecular dynamics, and smFRET identifies an aggregation mechanism. J. Mol. Biol. 2019;431:1409–1425. doi: 10.1016/j.jmb.2019.02.009. [DOI] [PubMed] [Google Scholar]
- 11.Lazar K.L., Patapoff T.W., Sharma V.K. Cold denaturation of monoclonal antibodies. MAbs. 2010;2:42–52. doi: 10.4161/mabs.2.1.10787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.King A.C., Woods M., Krebs M.R.H. High-throughput measurement, correlation analysis, and machine-learning predictions for pH and thermal stabilities of Pfizer-generated antibodies. Protein Sci. 2011;20:1546–1557. doi: 10.1002/pro.680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Conchillo-Solé O., de Groot N.S., Ventura S. AGGRESCAN: a server for the prediction and evaluation of “hot spots” of aggregation in polypeptides. BMC Bioinformatics. 2007;8:65. doi: 10.1186/1471-2105-8-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sankar K., Krystek S.R., Jr., Maier J.K.X. AggScore: prediction of aggregation-prone regions in proteins based on the distribution of surface patches. Proteins. 2018;86:1147–1156. doi: 10.1002/prot.25594. [DOI] [PubMed] [Google Scholar]
- 15.Rousseau F., Schymkowitz J., Serrano L. Protein aggregation and amyloidosis: confusion of the kinds? Curr. Opin. Struct. Biol. 2006;16:118–126. doi: 10.1016/j.sbi.2006.01.011. [DOI] [PubMed] [Google Scholar]
- 16.Voynov V., Chennamsetty N., Trout B.L. Predictive tools for stabilization of therapeutic proteins. MAbs. 2009;1:580–582. doi: 10.4161/mabs.1.6.9773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nichols P., Li L., Allen M.J. Rational design of viscosity reducing mutants of a monoclonal antibody: hydrophobic versus electrostatic inter-molecular interactions. MAbs. 2015;7:212–230. doi: 10.4161/19420862.2014.985504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Agrawal N.J., Helk B., Trout B.L. Computational tool for the early screening of monoclonal antibodies for their viscosities. MAbs. 2016;8:43–48. doi: 10.1080/19420862.2015.1099773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tomar D.S., Li L., Kumar S. In-silico prediction of concentration-dependent viscosity curves for monoclonal antibody solutions. MAbs. 2017;9:476–489. doi: 10.1080/19420862.2017.1285479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Low Y.W., Blasco F., Vachaspati P. Optimised method to estimate octanol water distribution coefficient (logD) in a high throughput format. Eur. J. Pharm. Sci. 2016;92:110–116. doi: 10.1016/j.ejps.2016.06.024. [DOI] [PubMed] [Google Scholar]
- 21.Simm S., Einloft J., Schleiff E. 50 years of amino acid hydrophobicity scales: revisiting the capacity for peptide classification. Biol. Res. 2016;49:31. doi: 10.1186/s40659-016-0092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chothia C. The nature of the accessible and buried surfaces in proteins. J. Mol. Biol. 1976;105:1–12. doi: 10.1016/0022-2836(76)90191-1. [DOI] [PubMed] [Google Scholar]
- 23.Acharya H., Vembanur S., Garde S. Mapping hydrophobicity at the nanoscale: applications to heterogeneous surfaces and proteins. Faraday Discuss. 2010;146:353–365. doi: 10.1039/b927019a. discussion 367–393, 395–401. [DOI] [PubMed] [Google Scholar]
- 24.Brusotti G., Calleri E., Temporini C. Advances on size exclusion chromatography and applications on the analysis of protein biopharmaceuticals and protein aggregates: a mini review. Chromatographia. 2018;81:3–23. [Google Scholar]
- 25.Goyon A., D’Atri V., Guillarme D. Characterization of 30 therapeutic antibodies and related products by size exclusion chromatography: feasibility assessment for future mass spectrometry hyphenation. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci. 2017;1065–1066:35–43. doi: 10.1016/j.jchromb.2017.09.027. [DOI] [PubMed] [Google Scholar]
- 26.Fekete S., Beck A., Guillarme D. Theory and practice of size exclusion chromatography for the analysis of protein aggregates. J. Pharm. Biomed. Anal. 2014;101:161–173. doi: 10.1016/j.jpba.2014.04.011. [DOI] [PubMed] [Google Scholar]
- 27.Tessier P.M., Lenhoff A.M., Sandler S.I. Rapid measurement of protein osmotic second virial coefficients by self-interaction chromatography. Biophys. J. 2002;82:1620–1631. doi: 10.1016/S0006-3495(02)75513-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jacobs S.A., Wu S.J., O’Neil K.T. Cross-interaction chromatography: a rapid method to identify highly soluble monoclonal antibody candidates. Pharm. Res. 2010;27:65–71. doi: 10.1007/s11095-009-0007-z. [DOI] [PubMed] [Google Scholar]
- 29.Kohli N., Jain N., Lugovskoy A.A. A novel screening method to assess developability of antibody-like molecules. MAbs. 2015;7:752–758. doi: 10.1080/19420862.2015.1048410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Estep P., Caffry I., Xu Y. An alternative assay to hydrophobic interaction chromatography for high-throughput characterization of monoclonal antibodies. MAbs. 2015;7:553–561. doi: 10.1080/19420862.2015.1016694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Haverick M., Mengisen S., Ambrogelly A. Separation of mAbs molecular variants by analytical hydrophobic interaction chromatography HPLC: overview and applications. MAbs. 2014;6:852–858. doi: 10.4161/mabs.28693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jain T., Sun T., Wittrup K.D. Biophysical properties of the clinical-stage antibody landscape. Proc. Natl. Acad. Sci. USA. 2017;114:944–949. doi: 10.1073/pnas.1616408114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Black S.D., Mould D.R. Development of hydrophobicity parameters to analyze proteins which bear post- or cotranslational modifications. Anal. Biochem. 1991;193:72–82. doi: 10.1016/0003-2697(91)90045-u. [DOI] [PubMed] [Google Scholar]
- 34.Eisenberg D., Schwarz E., Wall R. Analysis of membrane and surface protein sequences with the hydrophobic moment plot. J. Mol. Biol. 1984;179:125–142. doi: 10.1016/0022-2836(84)90309-7. [DOI] [PubMed] [Google Scholar]
- 35.Zamora W.J., Campanera J.M., Luque F.J. Development of a structure-based, pH-dependent lipophilicity scale of amino acids from continuum solvation calculations. J. Phys. Chem. Lett. 2019;10:883–889. doi: 10.1021/acs.jpclett.9b00028. [DOI] [PubMed] [Google Scholar]
- 36.Bruge F., Fornili S.L., Palma M.U. Solvent-induced forces on a molecular scale: non-additivity, modulation and causal relation to hydration. Chem. Phys. Lett. 1996;254:283–291. [Google Scholar]
- 37.Wang L., Friesner R.A., Berne B.J. Hydrophobic interactions in model enclosures from small to large length scales: non-additivity in explicit and implicit solvent models. Faraday Discuss. 2010;146:247–262. doi: 10.1039/b925521b. discussion 283–298, 395–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jamadagni S.N., Godawat R., Garde S. Hydrophobicity of proteins and interfaces: insights from density fluctuations. Annu. Rev. Chem. Biomol. Eng. 2011;2:147–171. doi: 10.1146/annurev-chembioeng-061010-114156. [DOI] [PubMed] [Google Scholar]
- 39.Hummer G., Garde S., Pratt L.R. An information theory model of hydrophobic interactions. Proc. Natl. Acad. Sci. USA. 1996;93:8951–8955. doi: 10.1073/pnas.93.17.8951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pratt L.R., Chaudhari M.I., Rempe S.B. Statistical analyses of hydrophobic interactions: a mini-review. J. Phys. Chem. B. 2016;120:6455–6460. doi: 10.1021/acs.jpcb.6b04082. [DOI] [PubMed] [Google Scholar]
- 41.Nguyen C., Gilson M.K., Young T.K. Structure and thermodynamics of molecular hydration via grid inhomogeneous solvation theory. arXiv. 2011 doi: 10.1063/1.4733951. http://arxiv.org/abs/1108.4876v1 arXiv:1108.4876v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nguyen C.N., Young T.K., Gilson M.K. Grid inhomogeneous solvation theory: hydration structure and thermodynamics of the miniature receptor cucurbit[7]uril. J. Chem. Phys. 2012;137:044101. doi: 10.1063/1.4733951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nguyen C.N., Cruz A., Kurtzman T. Thermodynamics of water in an enzyme active site: grid-based hydration analysis of coagulation factor Xa. J. Chem. Theory Comput. 2014;10:2769–2780. doi: 10.1021/ct401110x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ramsey S., Nguyen C., Kurtzman T. Solvation thermodynamic mapping of molecular surfaces in AmberTools: GIST. J. Comput. Chem. 2016;37:2029–2037. doi: 10.1002/jcc.24417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kraml J., Kamenik A.S., Liedl K.R. Solvation free energy as a measure of hydrophobicity: application to serine protease binding interfaces. J. Chem. Theory Comput. 2019;15:5872–5882. doi: 10.1021/acs.jctc.9b00742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Henzler-Wildman K., Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 47.Boehr D.D., Nussinov R., Wright P.E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jay J.W., Bray B., Ren G. IgG antibody 3D structures and dynamics. Antibodies (Basel) 2018;7:18. doi: 10.3390/antib7020018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Blech M., Hörer S., Garidel P. Structure of a therapeutic full-length anti-NPRA IgG4 antibody: dissecting conformational diversity. Biophys. J. 2019;116:1637–1649. doi: 10.1016/j.bpj.2019.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fernández-Quintero M.L., Kraml J., Liedl K.R. CDR-H3 loop ensemble in solution - conformational selection upon antibody binding. MAbs. 2019;11:1077–1088. doi: 10.1080/19420862.2019.1618676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fernández-Quintero M.L., Loeffler J.R., Liedl K.R. Characterizing the diversity of the CDR-H3 loop conformational ensembles in relationship to antibody binding properties. Front. Immunol. 2019;9:3065. doi: 10.3389/fimmu.2018.03065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Fernández-Quintero M.L., Math B.A., Liedl K.R. Transitions of CDR-L3 loop canonical cluster conformations on the micro-to-millisecond timescale. Front. Immunol. 2019;10:2652. doi: 10.3389/fimmu.2019.02652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fernández-Quintero M.L., Heiss M.C., Liedl K.R. Antibody CDR loops as ensembles in solution vs. canonical clusters from X-ray structures. MAbs. 2020;12:1744328. doi: 10.1080/19420862.2020.1744328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Henderson R., Watts B.E., Alam S.M. Selection of immunoglobulin elbow region mutations impacts interdomain conformational flexibility in HIV-1 broadly neutralizing antibodies. Nat. Commun. 2019;10:654. doi: 10.1038/s41467-019-08415-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Søndergaard C.R., Olsson M.H.M., Jensen J.H. Improved treatment of ligands and coupling effects in empirical calculation and rationalization of pKa values. J. Chem. Theory Comput. 2011;7:2284–2295. doi: 10.1021/ct200133y. [DOI] [PubMed] [Google Scholar]
- 56.Bashford D., Karplus M. pKa’s of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 57.Alexov E., Mehler E.L., Word J.M. Progress in the prediction of pKa values in proteins. Proteins. 2011;79:3260–3275. doi: 10.1002/prot.23189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chen W., Morrow B.H., Shen J.K. Recent development and application of constant pH molecular dynamics. Mol. Simul. 2014;40:830–838. doi: 10.1080/08927022.2014.907492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Swails J.M., York D.M., Roitberg A.E. Constant pH replica exchange molecular dynamics in explicit solvent using discrete protonation states: implementation, testing, and validation. J. Chem. Theory Comput. 2014;10:1341–1352. doi: 10.1021/ct401042b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Miao Y., Feher V.A., McCammon J.A. Gaussian accelerated molecular dynamics: unconstrained enhanced sampling and free energy calculation. J. Chem. Theory Comput. 2015;11:3584–3595. doi: 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lazaridis T. Inhomogeneous fluid approach to solvation thermodynamics. 1. Theory. J. Phys. Chem. B. 1998;102:3531–3541. [Google Scholar]
- 62.Loeffler J.R., Schauperl M., Liedl K.R. Hydration of aromatic heterocycles as an adversary of π-stacking. J. Chem. Inf. Model. 2019;59:4209–4219. doi: 10.1021/acs.jcim.9b00395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Berman H.M., Westbrook J., Bourne P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lyskov S., Chou F.C., Das R. Serverification of molecular modeling applications: the rosetta online server that includes everyone (ROSIE) PLoS One. 2013;8:e63906. doi: 10.1371/journal.pone.0063906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Marze N.A., Lyskov S., Gray J.J. Improved prediction of antibody VL-VH orientation. Protein Eng. Des. Sel. 2016;29:409–418. doi: 10.1093/protein/gzw013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sivasubramanian A., Sircar A., Gray J.J. Toward high-resolution homology modeling of antibody Fv regions and application to antibody-antigen docking. Proteins. 2009;74:497–514. doi: 10.1002/prot.22309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Weitzner B.D., Gray J.J. Accurate structure prediction of CDR H3 loops enabled by a novel structure-based C-terminal constraint. J. Immunol. 2017;198:505–515. doi: 10.4049/jimmunol.1601137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Weitzner B.D., Jeliazkov J.R., Gray J.J. Modeling and docking of antibody structures with Rosetta. Nat. Protoc. 2017;12:401–416. doi: 10.1038/nprot.2016.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Stein A., Kortemme T. Improvements to robotics-inspired conformational sampling in rosetta. PLoS One. 2013;8:e63090. doi: 10.1371/journal.pone.0063090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Case D.A., Ben-Shalom I.Y., Kollman P.A. University of California; San Francisco, CA: 2019. AMBER 2019. [Google Scholar]
- 71.Maier J.A., Martinez C., Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015;11:3696–3713. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 73.Darden T., York D., Pedersen L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 74.Ryckaert J.-P., Ciccotti G., Berendsen H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 75.Adelman S.A., Doll J.D. Generalized Langevin equation approach for atom-solid-surface scattering - general formulation for classical scattering off harmonic solids. J. Chem. Phys. 1976;64:2375–2388. [Google Scholar]
- 76.Åqvist J., Wennerström P., Brandsdal B.O. Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chem. Phys. Lett. 2004;384:288–294. [Google Scholar]
- 77.Berendsen H.J.C., Postma J.P.M., Haak J.R. Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 78.Wallnoefer H.G., Handschuh S., Fox T. Stabilizing of a globular protein by a highly complex water network: a molecular dynamics simulation study on factor Xa. J. Phys. Chem. B. 2010;114:7405–7412. doi: 10.1021/jp101654g. [DOI] [PubMed] [Google Scholar]
- 79.Case D.A., Ben-Shalom I.Y., Kollman P.A. University of California; San Francisco, CA: 2018. AMBER 2018. [Google Scholar]
- 80.Shao J., Tanner S.W., Cheatham T.E. Clustering molecular dynamics trajectories: 1. Characterizing the performance of different clustering algorithms. J. Chem. Theory Comput. 2007;3:2312–2334. doi: 10.1021/ct700119m. [DOI] [PubMed] [Google Scholar]
- 81.Miao Y., Sinko W., McCammon J.A. Improved reweighting of accelerated molecular dynamics simulations for free energy calculation. J. Chem. Theory Comput. 2014;10:2677–2689. doi: 10.1021/ct500090q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Python Software Foundation Python language reference, version 3.7. http://www.python.org
- 83.Virtanen P., Gommers R., van Mulbregt P., SciPy 1.0 Contributors SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods. 2020;17:261–272. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Dunbar J., Fuchs A., Deane C.M. ABangle: characterising the VH-VL orientation in antibodies. Protein Eng. Des. Sel. 2013;26:611–620. doi: 10.1093/protein/gzt020. [DOI] [PubMed] [Google Scholar]
- 85.Deserno M. 2004. How to generate equidistributed points on the surface of a sphere.https://www.cmu.edu/biolphys/deserno/pdf/sphere_equi.pdf [Google Scholar]
- 86.McInnes L., Healy J., Melville J. UMAP: uniform manifold approximation and projection for dimension reduction. arXiv. 2018 https://arxiv.org/abs/1802.03426 arXiv:1802.03426. [Google Scholar]
- 87.Schrodinger, LLC . 2015. The PyMOL molecular graphics system, version 1.8. [Google Scholar]
- 88.Hebditch M., Roche A., Warwicker J. Models for antibody behavior in hydrophobic interaction chromatography and in self-association. J. Pharm. Sci. 2019;108:1434–1441. doi: 10.1016/j.xphs.2018.11.035. [DOI] [PubMed] [Google Scholar]
- 89.van der Kant R., Karow-Zwick A.R., Rousseau F. Prediction and reduction of the aggregation of monoclonal antibodies. J. Mol. Biol. 2017;429:1244–1261. doi: 10.1016/j.jmb.2017.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Foote J., Milstein C. Conformational isomerism and the diversity of antibodies. Proc. Natl. Acad. Sci. USA. 1994;91:10370–10374. doi: 10.1073/pnas.91.22.10370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.James L.C., Roversi P., Tawfik D.S. Antibody multispecificity mediated by conformational diversity. Science. 2003;299:1362–1367. doi: 10.1126/science.1079731. [DOI] [PubMed] [Google Scholar]
- 92.Landsteiner K. Dover Publications; New York: 1962. The Specificity of Serological Reactions. [Google Scholar]
- 93.Wedemayer G.J., Patten P.A., Stevens R.C. Structural insights into the evolution of an antibody combining site. Science. 1997;276:1665–1669. doi: 10.1126/science.276.5319.1665. [DOI] [PubMed] [Google Scholar]
- 94.Pauling L. A theory of the structure and process of formation of antibodies. J. Am. Chem. Soc. 1940;62:2643–2657. [Google Scholar]
- 95.Kossiakoff A.A., Randal M., Eigenbrot C. Variability of conformations at crystal contacts in BPTI represent true low-energy structures: correspondence among lattice packing and molecular dynamics structures. Proteins. 1992;14:65–74. doi: 10.1002/prot.340140108. [DOI] [PubMed] [Google Scholar]
- 96.Rapp C.S., Pollack R.M. Crystal packing effects on protein loops. Proteins. 2005;60:103–109. doi: 10.1002/prot.20492. [DOI] [PubMed] [Google Scholar]
- 97.Almagro J.C., Teplyakov A., Gilliland G.L. Second antibody modeling assessment (AMA-II) Proteins. 2014;82:1553–1562. doi: 10.1002/prot.24567. [DOI] [PubMed] [Google Scholar]
- 98.Schroeder H.W., Jr., Cavacini L. Structure and function of immunoglobulins. J. Allergy Clin. Immunol. 2010;125:S41–S52. doi: 10.1016/j.jaci.2009.09.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Chothia C., Lesk A.M. Canonical structures for the hypervariable regions of immunoglobulins. J. Mol. Biol. 1987;196:901–917. doi: 10.1016/0022-2836(87)90412-8. [DOI] [PubMed] [Google Scholar]
- 100.Morea V., Tramontano A., Lesk A.M. Antibody structure, prediction and redesign. Biophys. Chem. 1997;68:9–16. doi: 10.1016/s0301-4622(96)02266-1. [DOI] [PubMed] [Google Scholar]
- 101.Regep C., Georges G., Deane C.M. The H3 loop of antibodies shows unique structural characteristics. Proteins. 2017;85:1311–1318. doi: 10.1002/prot.25291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Walsh I., Seno F., Trovato A. PASTA 2.0: an improved server for protein aggregation prediction. Nucleic Acids Res. 2014;42:W301–W307. doi: 10.1093/nar/gku399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Sormanni P., Aprile F.A., Vendruscolo M. The CamSol method of rational design of protein mutants with enhanced solubility. J. Mol. Biol. 2015;427:478–490. doi: 10.1016/j.jmb.2014.09.026. [DOI] [PubMed] [Google Scholar]
- 104.Schauperl M., Podewitz M., Liedl K.R. Enthalpic and entropic contributions to hydrophobicity. J. Chem. Theory Comput. 2016;12:4600–4610. doi: 10.1021/acs.jctc.6b00422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Lauer T.M., Agrawal N.J., Trout B.L. Developability index: a rapid in silico tool for the screening of antibody aggregation propensity. J. Pharm. Sci. 2012;101:102–115. doi: 10.1002/jps.22758. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.