Targeting Telomeres: Molecular Dynamics and Free Energy Simulation of Gold-Carbene Binding to DNA

Abstract

DNA sequences in regulatory regions and in telomers at the ends of chromosomes frequently contain tandem repeats of guanine nucleotides that can form stacked structures stabilized by Hoogsten pairing and centrally bound monovalent cations. The replication and elongation of telomeres requires the disruption of these G-quadruplex structures. Hence, drug molecules such as gold (Au)-carbene that stabilize G-quadruplexes may also interfere with the elongation of telomeres and, in turn, could be used to control cell replication and growth. To better understand the molecular mechanism of Au-carbene binding to G-quadruplexes, we employed molecular dynamics simulations and free energy simulations. Whereas very restricted mobility of two Au-carbene ligands was found upon binding as a doublet to one side of the G-quadruplex, much larger translational and orientational mobility was observed for a single Au-carbene binding at the second G-quadruplex surface. Comparative simulations on duplex DNA in the presence of Au-carbene ligands indicates a preference for the minor groove and weaker unspecific and more salt-dependent binding than to the G-quadruplex surface. Analysis of energetic contributions reveals a dominance of nonpolar and van der Waals interactions to drive binding. The simulations can also be helpful for proposing possible modifications that could improve Au-carbene affinity and specificity for G-quadruplex binding.

Significance

Gold-carbenes bind specifically to G-quadruplexes and can interfere with telomerase activity that is essential for cancer growth. Molecular dynamics and free energy simulations have been used to investigate the binding of gold-carbenes to G-quadruplexes and regular B-DNA in molecular detail. Large differences in ligand mobility at different quadruplex binding sites that influence binding affinity and specificity were observed. Much weaker affinity and a larger salt dependence for binding to B-DNA was found. The study gives new, to our knowledge, insights into the mechanism of ligand binding to G-quadruplexes and could be helpful for designing modifications for improved affinity and specificity.

Introduction

Telomeres at the ends of chromosomes are repetitive noncoding DNA sequences that contain tandem repeats of guanine (G) nucleotides, which can form G-quadruplexes (1, 2, 3). These quadruplexes represent guanine-rich nucleic structures in which the guanines form a square plane with several possible levels. The structural motifs consist of stacked guanines and are stabilized through Hoogsten hydrogen bonds and monovalent cations bound at a central cavity. Recently, the stabilization of G-quadruplexes has gained increased attention in the field of drug design because it may interfere with the growth of cancer cells (4, 5, 6, 7, 8, 9). The rationalization behind this promise is that drug-induced stabilization of DNA quadruplexes prevents elongation of telomeres. Telomere elongation is carried out by a reverse transcriptase as part of the telomerase complex (10), which requires unfolding of the DNA quadruplex structures before elongation (11,12). Consequently, stabilization of the DNA quadruplex structures may inhibit telomerase binding and thus telomere maintenance. Shortening of the telomeres, in turn, can induce cell apoptosis that is suppressed in cancer cells because of telomerase overexpression, which mediates telomere maintenance. Thus, downregulation of telomerase fidelity through quadruplex stabilization may represent a promising anticancer strategy (13, 14, 15).

In this regard, gold (Au)-carbene complexes have a potential in cancer treatment because carbon-gold bonds significantly reduce the risk of unselected damage in noncancer cells as a consequence of their regulated redox properties (16, 17, 18). Bertrand and co-workers have successfully synthesized a class of Au-carbene complexes that allow for efficient uptake by cells and show strong antiproliferative activity against cancer cells. In the past, crystal structures formed by DNA quadruplexes and Au-carbenes have been solved (19). Binding of up to three Au-carbenes to a DNA quadruplex was observed in the crystal structure and in solution studies (illustrated in Fig. 1). Binding of Au-carbenes results also in an increased DNA quadruplex melting temperature and selective inhibition of telomerase (16, 17, 18, 19, 20, 21).

Figure 1.

(A) Structure of the Au-carbene (Au(9-methylcaffein-8-ylidene)₂+, ball and stick model with a central Au atom in yellow). (B) Crystal structure of the Au-carbene in complex with the telomer G-quadruplex (PDB: 5CCW) viewed from the side is shown with the first bound Au-carbene (singlet state or mode I). The binding position is off center with respect to the central axis of the G-quadruplex. (C) View from the opposite site as in (B) is given with two additional bound Au-carbenes (doublet state). Note that in the crystal structure, the Au-carbene molecules are sandwiched between G-quadruplex structures. Mode I denotes the Au-carbene on one side (termed top side), whereas modes II and III are referring to the left and right Au-carbene placements, respectively, on the other side of the quadruplex. To see this figure in color, go online.

Further improvement of the affinity and specificity of Au-carbene binding to quadruplexes requires an understanding of the binding mechanism in molecular detail. Force-field-based molecular dynamics (MD) techniques have already been used frequently to study the dynamics of G-quadruplexes (reviewed in (22, 23, 24)), the specificity of ion binding (25), and ligand binding (8,26). In this study, we employ molecular dynamics free energy simulations to investigate the interaction and mobility of Au-carbene associated with three binding sites on a telomeric G-quadruplex. The simulations indicate dramatic differences in the mobilities of the ligand at the three sites. In addition to binding at the G-quadruplex, we also study nonspecific binding of Au-carbenes to the minor groove of B-DNA. Free energy simulations indicate a considerably lower affinity and also much stronger salt dependence of Au-carbene binding to B-DNA compared with G-quadruplexes. Based on our simulations, we discuss effects that stabilize binding to double-stranded DNA (dsDNA) and eventually propose design principles pursuing increased quadruplex over duplex selectivity.

Materials and Methods

Molecular dynamics simulations

For all simulations, the Amber16 MD Package (27), in combination with the DNA.bsc1 force field (28) for nucleic acids, was applied (for force field parameterization of the ligand, see below). The starting structure (Protein Data Bank, PDB: 5CCW) was solvated in explicit water (TIP3P) (29) with rectangular boxes and a 10 Å minimal distance between complex and box boundary. Additional sodium counterions were added to neutralize the system. After energy minimization (10,000 steps), the system were heated up to 300 K within three stages (each 0.5 ns) and with a restraint (force constant: 2.388 kcal/(mol ⋅ Ų)) to the starting positions (on all nonhydrogen atoms). Subsequently, the positional restraining was reduced to 0.6 kcal/(mol ⋅ Ų), followed by a short equilibration without restraints (1 ns) under constant pressure of 1 bar. After this equilibration step, the data-gathering MD simulations were carried out with the pmemd.cuda module at a temperature of 300 K and in NVT ensemble for up to 2 μs.

Force field parameterization of Au-carbene

Derivation of the force field parameters for the Au(9-methylcaffein-8-ylidene)₂+ molecule (Fig. 1 C) was performed with the MCPB.py module of Amber16 (27) in combination with the Gaussian09 package (30,31). This includes geometry optimization, frequency calculation, and Merz-Kollmann population analysis on the B3LYP/6-31G^∗ level of theory (32). For the gold atom, we used the LANL2DZ basis set (33). Partial charges were assigned with the resp module of Amber16, whereby we constrained identical atoms in the symmetric carbene dimer to have the same charge. Bond and angle parameters were obtained with the Seminario method, which excludes dihedral parameters around the gold atom (Fig. S1; Tables S1–S3; (34)). A Lennard-Jones radius of 1.6465 Å and depth of 0.0390 was assigned to the gold atom.

Calculation of the absolute binding free energy

To quantitatively compare Au-carbene binding to the quadruplex structure and to DNA, the binding free energy is calculated for both systems. To improve convergence, the advanced sampling method developed by Woo and Roux is used (35), which includes additional restraining of relevant degrees of freedom orthogonal to the reaction coordinate, i.e., axial, orientational, and conformational degrees of freedom. The restraints are defined between three virtual sites (abbreviated as VS) in the DNA or quadruplex structure (VS 1–3) and three virtual sites in the Au-carbene molecule (VS 4–6) (see Fig. 2). The resulting restraint binding free energy ΔG_bind,0,restr needs to be corrected to obtain a physically meaningful standard binding free energy ΔG_bind,0 (see Fig. 5 A); in a first step, the introduction of axial and orientational restraints is corrected for via free energy perturbation at the binding site (ΔG_a,site, ΔG_o,site) and numeric calculation in the bulk (ΔG_o,bulk). Note that ΔG_a,bulk is corrected for implicitly in the context of ΔG_bind,0,restr (35). In a subsequent step, the free energy associated with the conformational dihedral restraint ζ_Dih, which prevents internal Au-carbene ring rotation, is obtained by Boltzmann-weighted integration of a PMF calculated along ζ_Dih (ΔG_conf,site, ΔG_conf,bulk).

Figure 5.

Schematic illustration of the contributions to absolute binding free energy calculations. In addition to the PMF along the separation coordinate, the free energies associated with the release of axial and orientational as well as conformational restraints both in the bound state and the unbound state need to be included for calculating the binding free energy ΔG_bind,0,restr (see Materials and Methods for details). To see this figure in color, go online.

The resulting ΔG_bind,0 amounts to

$$\Delta G_{\text{bind},0}=\Delta G_{\text{bind},0,\text{restr}}+\Delta \left(\text{Δ}{G}_{\text{o},\text{bulk}}+\Delta G_{\text{c},\text{bulk}}\right)-\left(\Delta G_{\text{a},\text{site}}+\Delta G_{\text{o},\text{site}}+\Delta G_{\text{c},\text{site}}\right).$$ (1)

The restraint potential of mean force (PMF) along the center-of-mass distance coordinate d is calculated via umbrella sampling by pulling the Au-carbene molecule out of an instantaneous binding position from the G-quadruplex or the B-DNA binding site. The simulations cover a distance range from 4.0 to 12.8 Å, with a window spacing of 0.4 Å in the case of Au-carbene-quadruplex binding, and a distance range from 9.1 to 17.6 Å, with a window spacing of 0.5 Å in the case of Au-carbene-B-DNA binding. Each umbrella window is simulated for 10 ns with a distance-restraint force constant of 10 kcal/(mol ⋅ Ų) and a force constant of 240 kcal/(mol ⋅ rad²) for axial and orientational restraints, as well as for the dihedral restraint within Au-carbene. For histogram overlap in the case of the Au-carbene-quadruplex complex, additional umbrella windows are inserted at positions 5.6, 6.0, 6.1, 6.2, 6.3, and 6.4 Å, with a stronger distance-restraint force constant of 40 kcal/(mol ⋅ Ų). The PMF is calculated using the weighted histogram analysis method (36).

Starting from an entirely restraint conformation of the first umbrella window, the correction terms ΔG_a,site and ΔG_o,site are calculated via free energy perturbation and the Zwanzig equation (37), with the axial and orientational restraint force constants gradually reduced from 240 to 0 kcal/(mol ⋅ rad²) in 10 steps and each window simulated for 10 ns. Because of bulk isotropy, the corresponding correction terms in the unbound state can be calculated numerically (for equations, see (35)).

For obtaining ΔG_conf,site in the binding site, conformational PMFs are calculated along the dihedral restraint coordinate ζ_Dih, starting from a planar Au-carbene conformation with ζ_Dih = 0.0 rad. Via umbrella sampling, internal Au-carbene rotation is enforced by pulling ζ_Dih in both directions to ±3.14 rad in steps of 0.31 rad with 10 ns simulation length per window and a dihedral restraint force constant of 100 kcal/(mol ⋅ rad²). Configurational contributions in the bulk, ΔG_conf,bulk, have been obtained from Boltzmann inversion of a 200-ns-long unrestrained simulation of the Au-carbene exposed to explicit solvent. Thereby, we calculated the probability along the dihedral angle ζ_Dih in 15° bins. The corresponding free energy profile is then given by F = −k_BT × ln(p(ζ)).

Molecular mechanics Poisson-Boltzmann binding energy calculation

For calculation of mean interaction energies, the MMPBSA (molecular mechanics Poisson-Boltzmann/surface area) method was employed (38, 39, 40, 41, 42) using the mmpbsa module of Amber16. In the MMPBSA approach, a trajectory generated in explicit solvent is re-evaluated with the same force field but the solvent replaced by a dielectric continuum (with a dielectric constant, ɛ = 80 for solvent and ɛ = 1 for the solute). The electrostatic reaction field is calculated using the finite difference Poisson-Boltzmann approach (as implemented in Amber 16), and nonpolar solvation contributions are obtained from the solvent accessible surface area (surface tension of 0.0052 kcal/mol ⋅ Ų) (42). For most calculations, a salt concentration of 150 mM was used. The internal K+ ions of the quadruplex were included explicitly in the calculations. For the application of Au-carbene binding to the G-quadruplex, the average over 4000 regularly spaced simulation snapshots were taken from 2 μs simulations.

Results and Discussion

Molecular dynamics simulations of Au-carbene bound to G-quadruplex

The crystal structure (PDB: 5CCW) of a G-quadruplex with a human telomeric DNA sequence (23 nucleotides with sequence 5′-TAGGGTTAGGGTTAGGGTTAGGG) in complex with Au(9-methylcaffein-8-ylidene)₂ (Au-carbene) ligands formed the basis of our MD simulations. The structure includes three Au-carbene molecules that bind noncovalently to the two planar surfaces on opposite sides of the G-quadruplex (see Fig. 1). One side (the “top”) of the G-quadruplex accommodates one single Au-carbene (singlet state), whereas on the other side (the “bottom”), two Au-carbenes are bound. In the crystal structure, the single Au-carbene prefers an off-center location because of stronger stacking overlap with guanines, which also allows a thymine of a loop to bind to the top surface. In addition, the G-quadruplex DNA formation is stabilized by two potassium ions at the center between the planes formed by four guanines (Fig. 1).

The MD simulation systems included the quadruplex without ligands (apo), with a single Au-carbene (the singlet state), and the quadruplex interacting with all three Au-carbenes on both planar surfaces. The root mean-square deviation (RMSD) of the DNA with respect to the crystal start structure increased at the beginning significantly to reach ∼5–7 Å (Fig. 2). However, the RMSD of the guanine nucleotides that form the quadruplex remained close to the start structure (2–3 Å) in all cases, indicating that the rearrangement of the connecting loops and terminal nucleotides is responsible for the increased total RMSD. Hence, the loop segments relax from a packed structured stabilized by the crystal lattice. The presence of the Au-carbene ligands leads to a slight reduction in RMSD (especially with three ligands) and also to a reduced conformational fluctuation (RMSF) of the connecting loops.

Figure 2.

(A) Root mean-square deviation (RMSD) of all nonhydrogen DNA atoms with respect to the start structure versus simulation time for MD simulations (300 K) of only the G-quadruplex (dark red), G-quadruplex with one stacked Au-carbene (dark blue), and G-quadruplex with three Au-carbenes as observed in the crystal structure (dark green). The RMSD was also computed only for the guanosine nucleotides involved in the quadruplex (without connecting loops and terminal nucleotides) in corresponding light colors. (B) RMSFs of the respective MD simulations versus nucleotide are shown (same color scheme as in A). The RMSFs represent averages over all nonhydrogen atoms of each nucleotide. To see this figure in color, go online.

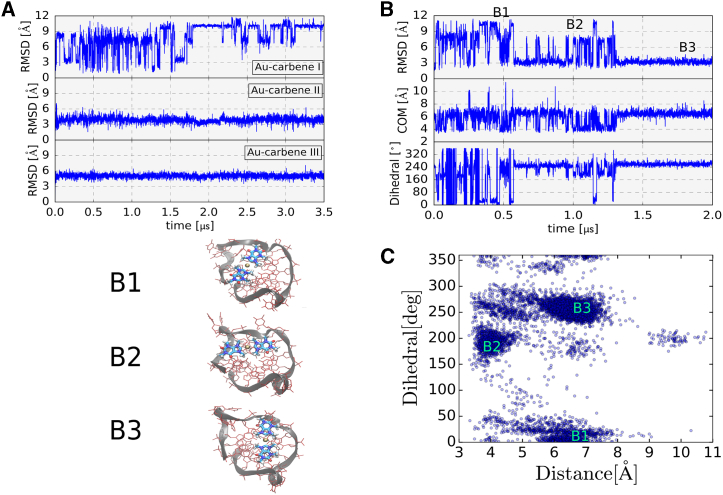
Interestingly, the Au-carbene bound as singlet on the top surface undergoes significant motions with an RMSD (after best superposition of the G-quadruplex) that fluctuates between 2 and 10 Å (Fig. 3). This behavior is seen in both the simulations with one bound Au-carbene and the simulation with three Au-carbenes. In contrast, the two Au-carbenes on the bottom side plane are much less mobile with an RMSD of less than 4 Å with respect to the start structure. The large mobility of the singlet bound Au-carbene is mostly due to an overall rotation coupled to significant shifts of the center of mass (Fig. 3 B). The simulations indicate a variety of placements of the single Au-carbene on the top surface of the G-quadruplex that are accessible and three main arrangements (B1–B3) can be distinguished. No such overall rotation is observed for the ligands on the other (bottom) quadruplex side.

Figure 3.

(A) RMSD versus simulation time (300 K) of the Au-carbene ligands after best superposition of the G-quadruplex on the starting structure. (B) RMSD of the Au-carbene (after best superposition of the G-quadruplex on the start structure) is shown for the simulation of the G-quadruplex with a single bound Au-carbene. In addition, the center-of-mass (COM) distance between ligand (Au atom) and G-quadruplex and the dihedral angle describing the orientation of the Au-carbene relative to the G-quadruplex versus simulation time is also shown. The dihedral angle is defined by the each of the two carbenes and two top-planed neighboring nucleotides. (C) Sampled distribution of Au-carbene on the side with a single bound ligand during simulations in terms of COM distance and angular orientation is shown. Snapshots for (B) and (C), respectively of the most sampled states are indicated. To see this figure in color, go online.

To qualitatively investigate the stability of the G-quadruplex-Au-carbene complex, we also performed simulations at elevated temperatures of 350 K. Also, at this temperature and on the timescale of the simulations, no dissociation of the ligands and a similar pattern of RMSD versus simulation time and RMSF versus nucleotide sequence are observed (Figs. S3 and S4). This agrees qualitatively with the experimental result of a stable complex at elevated temperatures (16).

Binding of Au-carbene to B-DNA minor groove

In addition to Au-carbene binding to a G-quadruplex, we also perform simulations of duplex B-DNA in the presence of several randomly placed Au-carbene ligands. The MD simulations indicate rapid binding in the DNA minor groove presumably caused by electrostatic attraction between the positively charged Au-carbene and the negative charge density in the DNA minor groove. The most long-lived complex was formed within a few nanoseconds and remained bound for the entire simulation. The binding mode is also stabilized by hydrogen bonds between an oxygen of the drug and a hydrogen atom of guanine’s amino group (Fig. 4 A). It was also used for subsequent comparative binding free energy simulations.

Figure 4.

(A) Simulated binding complex between Au-carbene drug and dsDNA. Besides electrostatic attraction, binding into DNA’s minor groove is stabilized by a hydrogen bond between an Au-carbene-oxygen and a hydrogen atom of guanine’s amino group. (B) RMSD of dsDNA and Au-carbene molecule with respect to final predicted structure is shown. To see this figure in color, go online.

Absolute binding free energy calculation

The MD simulations of Au-carbene binding to the G-quadruplex and the B-DNA minor groove give qualitative insights into the stability of the complexes. We used a restrained umbrella sampling approach to calculate the standard binding free energy ΔG_bind,0 according to a scheme by Woo and Roux (35). The method allows a rigorous calculation of absolute binding free energies including, in principle, all energetic and entropic contributions. Solvent is included explicitly; hence, solvent entropic and energetic contributions are also considered. It allows for a quantitative comparison of Au-carbene binding to the quadruplex structure versus binding in the B-DNA minor groove. It is, however, still limited by possible force field inaccuracies. The approach employs geometrical and conformational restraints during calculation of a PMF along a distance coordinate to separate the binding partners. The inclusion of restraints allows for rapid convergence of the calculated free energy along the separation coordinate. The contributions to binding because of the release of restraints on axial rotation and orientation between quadruplex/B-DNA and Au-carbene, as well as relaxation of Au-carbene conformational restraints, can be calculated separately at the end points (bound and fully separate states) (see Fig. 5 and Materials and Methods).

In the case of quadruplex binding, the calculated absolute binding free energy ΔG_bind,0 amounts to −10.4 ± 1.0 kcal/mol, which corresponds to a twice as high binding affinity compared with −5.2 ± 1.2 kcal/mol for binding to B-DNA (see Tables 1 and 2). For G-quadruplex binding, an affinity in the nanomolar regime was found experimentally (19), which agrees qualitatively with our result (−10.4 kcal/mol corresponds to a K_d = 0.03 μM). The main difference between quadruplex and B-DNA binding results from the restrained PMF upon dissociation, which yields a free energy difference between binding site and bulk of −14.9 ± 0.7 kcal/mol for quadruplex and −10.9 ± 0.9 kcal/mol for dsDNA binding (see Fig. 6, A and B). This free energy difference is obtained between the bound state and the converged PMF plateau for large distances. However, in the case of quadruplex binding, the PMF shows a significant local minimum at around 7.6 Å. This can be explained by a strong increase in the number of water molecules in the first hydration layer around the Au-carbene upon dissociation (see Fig. S5). The orientational free energy contribution ΔG_o,bulk of Au-carbene in bulk amounts to around 6.4 kcal/mol in both cases because of bulk isotropy and the independence of the receptor surface.

Table 1.

Calculated Absolute Binding Free Energy for Au-Carbene-G-Quadruplex Binding

Contribution	Result [kcal/mol]	Standard Error [kcal/mol]
ΔGbind,restr	−14.9	±0.7
ΔGo,bulk	6.4	N/A
ΔGconf,bulk	3.6	±0.1
−ΔGa,site	−0.6	±0.2
−ΔGo,site	−3.1	±0.6
−ΔGconf,site	−1.8	±0.1
ΔGbind,0	−10.4	±1.0

N/A, not applicable.

Table 2.

Calculated Absolute Binding Free Energy for Au-Carbene-dsDNA Minor Groove Binding

Contribution	Result [kcal/mol]	Standard Error [kcal/mol]
ΔGbind,restr	−10.9	±0.9
ΔGo,bulk	6.4	N/A
ΔGconf,bulk	3.7	±0.1
−ΔGa,site	−0.3	±0.1
−ΔGo,site	−1.5	±0.7
−ΔGconf,site	−2.6	±0.1
ΔGbind,0	−5.2	±1.2

N/A, not applicable

Figure 6.

Calculated free energy change (PMF) along the Au-carbene-DNA separation distance (d). (A) PMF for Au-carbene separation from the singlet binding site on the quadruplex structure is shown. The uncertainty of the PMF ɛ_SI is estimated by splitting the data set into subintervals of 1 ns, respectively (dotted curves and blue shadow). (B) PMF for Au-carbene dissociation and association with respect to the minor groove binding site on the duplex DNA structure is shown. To see this figure in color, go online.

The Au-carbene-inherent conformational flexibility is parametrized by a dihedral coordinate ζ_Dih describing the relative orientation of the Au-carbene rings. For unbound Au-carbene, the PMF along ζ_Dih results in a free energy contribution ΔG_conf,bulk of 3.7 ± 0.1 kcal/mol (see Table 1). The PMF along ζ_Dih in the bound state shows a more rugged energy landscape, with slightly tilted Au-carbene rings being most favorable. In contrast to unbound Au-carbene, the perpendicular ring conformation is considerably less favorable in the bound state, which can be explained by the loss of ring stacking interactions with DNA and especially the quadruplex surface, the latter leading to a reduced conformational flexibility and hence a smaller value of ΔG_conf,site = 1.8 ± 0.1 kcal/mol compared with 2.6 ± 0.1 kcal/mol in the case of B-DNA binding. In addition, the large orientational mobility of the Au-carbene in mode I binding results in a significant stabilization of the quadruplex bound state (ΔG_o,site) compared with B-DNA minor groove binding (Tables 1 and 2).

MMPBSA interaction energy calculations

To investigate the energetic contributions to Au-carbene-DNA binding, we employed the MMPBSA method to reanalyze the MD trajectories based on a continuum solvent model (see Materials and Methods). It also allows us to estimate the interaction energy of Au-carbenes at the bottom side relative to the top side of the G-quadruplex. It should be emphasized that the method (in contrast to the absolute binding free energy method used in the previous paragraph) does not provide a free energy of binding, but rather provides a mean interaction energy between receptor and ligand (39). It also does not include the effect of conformational changes upon binding and employs an implicit solvent description. Nevertheless, the methodology can give useful hints on the relative interaction energies between the Au-carbene ligands and the DNA and the energetic contributions to the interaction. The total MMPBSA interaction energies of the Au-carbene molecule binding in mode I amount to −17.3 kcal/mol for G-quadruplex DNA and −38.7 kcal/mol for dsDNA at a physiological salt concentration of 150 mM (Table 3). It is important to note that the calculated interaction energy does not account for the reorganization of the DNA (and ligand) upon association and also does not account for conformational entropy contributions in the underlying MMPBSA calculations. Hence, it is not comparable with the calculated binding free energies of the previous paragraph. The calculated mean interaction energies of the two Au-carbenes binding to the opposite side, however, yield −30.5 and −38.4 kcal/mol for placements II and III, respectively, which indicates strong interactions of both Au-carbenes (and reduced mobility). When considering both Au-carbenes II and III as one unit, the mean interaction energy with the G-quadruplex turns out to be −64.4 kcal/mol. This is less than the sum of the binding energies of II and III, which is −68.9 kcal/mol. Hence, there is a mean attraction between both ligands at the bottom side, further stabilizing the complex. Indeed, experiments indicate a positive cooperation for Au-carbene binding to quadruplexes (16). The calculated mean Coulomb contribution of the Au-carbene interaction with the B-DNA is 66% higher compared to the Au-carbene interaction with the G-quadruplex. However, the unfavorable polar solvation or reaction field energy is always higher than the Coulomb attraction energy. The total electrostatic contribution of mode I binding amounts to 29.5 kcal/mol and for modes II and III, respectively, to 32.0 and 24.8 kcal/mol. Binding to B-DNA, on the other hand, gives only 18.3 kcal/mol of total electrostatic repulsion. According to the MMPBSA analysis, the main driving force for binding is due to van der Waals interactions and nonpolar solvation contributions in all cases.

Table 3.

MMPBSA Interaction Energy Contributions for Au-Carbene-DNA Binding in kcal/mol

Binding Mode	<Ebind>	<EvdW>	<ECoulomb>	<Epol-solv>	<Enonpol>	$\frac{\Delta \langle E_{bind}\rangle }{\Delta ln\left(I\right)}$
Quadruplex I	−17.3 ± 4.0	−43.7 ± 3.6	−453.2 ± 12.3	482.7 ± 13.2	−2.9 ± 0.2	−0.14
Quadruplex II	−30.5 ± 4.7	−58.8 ± 3.2	−446.7 ± 10.8	478.7 ± 12.1	−3.7 ± 0.1	−0.02
Quadruplex III	−38.4 ± 4.2	−59.0 ± 3.9	−459.5 ± 11.3	484.3 ± 12.8	−4.2 ± 0.2	−0.05
Quadruplex II + III	−64.4 ± 5.7	−110.7 ± 4.7	−956.8 ± 17.0	1010 ± 18.0	−6.9 ± 0.2	N/A
dsDNA	−38.7 ± 4.4	−53.2 ± 5.2	−750.5 ± 18.2	768.8 ± 20.5	−3.9 ± 0.3	−1.81

N/A, not applicable.

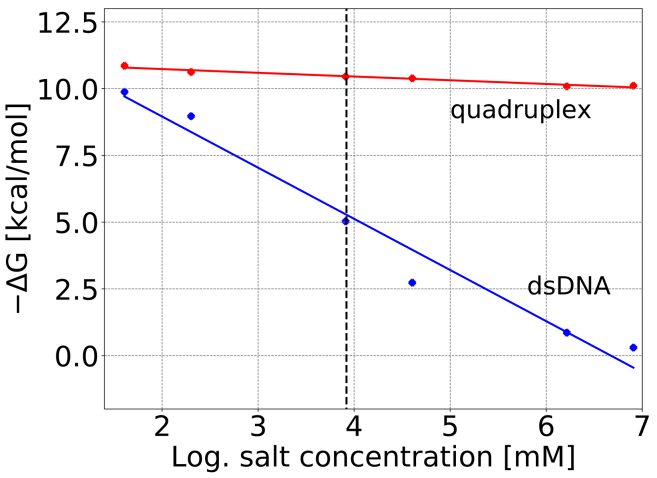
Salt concentration dependence of the binding energy

The MMPBSA method can be used to predict the change in binding affinity with increasing salt concentration. Only a very modest salt dependence of binding was found for the Au-carbene in complex with the G-quadruplex compared with a significant binding affinity reduction for the binding to B-DNA (Fig. 7; Table 3). At around 150 mM (approximately physiological salt concentration), the Au-carbene binding free energy to B-DNA is reduced to ∼−3 kcal/mol (K_d = 6.7 mM), and to the G-quadruplex binding mode I, it is still ∼−10 kcal/mol (K_d = 0.03 μM). It agrees qualitatively with the experimental results that demonstrate specific binding of Au-carbenes to the G-quadruplex under physiological conditions and no significant competition of binding due to 15-fold excess of B-DNA (16). Unfortunately, precise experimental binding data on the Au-carbene binding to G-quadruplexes are not available.

Figure 7.

Calculated relative binding free energy of Au-carbene-DNA binding versus salt concentration based on MMPBSA calculations at different salt concentrations. Increased salt concentrations significantly reduce the binding strength of Au-carbene to dsDNA but have little effect on binding to the G-quadruplex (mode I binding). The vertical dashed line represents approximately the salt concentration used in the binding free energy calculations. To see this figure in color, go online.

Conclusion

Gold-carbenes are a new class of ligands binding and stabilizing G-quadruplex structures that can form in telomere sequences at chromosome termini. Keeping the termini of chromosomes intact is essential for chromosome replication (6,15). Small drug-like molecules that are able to bind and block telomerases generally manifest significant anticancer properties, and G-quadruplex binding properties correlate well with antitelomerase activity (43). Hence, the stabilization of G-quadruplexes by specific drug molecules such as Au-carbenes and inhibition of telomerase is a possible route to interfere with the rapid growth of cancer cells (5,21). Understanding the molecular details of the Au-carbene interaction with G-quadruplexes and possible competing interactions with B-DNA is a prerequisite for the design of Au-carbenes with improved affinity and specificity. These free energy simulations confirm the experimental observation of specific Au-carbene binding to G-quadruplexes compared with nonspecific binding in the B-DNA minor groove, especially at increased salt concentration (19). It was also found that Au-carbene interaction with the bottom side of the G-quadruplexes is much stronger compared to the top side with a single bound Au-carbene. Both Au-carbenes indicate similar binding energies to the bottom side. Hence, the design of a covalent linkage between the two Au-carbenes could be a route for strongly increased binding affinity. A remarkable and unexpected result is the observed much higher mobility of the Au-carbene in mode I binding, which allows large translation of the ligand by several angstroms and complete rotation on the top surface of the G-quadruplex. The large residual mobility contributes favorably to the Au-carbene binding on the G-quadruplex surface. Typically, strong binding ligands form fairly rigid complexes (e.g., filling cavities in the case of proteins or associating with the narrow DNA minor groove in the case of DNA) with little residual mobility of the ligand relative to the receptor. The unusually large mobility of the mode I binding also demonstrates accessible sterical space that could be filled by chemical groups attached to the carbene compounds and could increase nonpolar interactions with the G-quadruplex. Design of slightly larger Au-carbenes could also reduce the binding to the narrow B-DNA minor groove and further reduce competing nonspecific binding to duplex DNA. However, for the application as drugs, one should keep in mind that not only the specificity and affinity of Au-carbenes are of critical importance but also possible side effects and the toxicity of metal-containing complexes (44,45).

Author Contributions

A.N. performed research, analyzed data, and contributed to writing of the article. K.L. analyzed data and contributed to writing the article. C.V.F. performed research and contributed analytic tools. M.Z. designed the research and wrote the article. All authors reviewed the manuscript.

Editor: Wilma Olson.