The effect of a constraint on the maximum number of controls matched to each treated subject on the performance of full matching on the propensity score when estimating risk differences

Abstract

Many observational studies estimate causal effects using methods based on matching on the propensity score. Full matching on the propensity score is an effective and flexible method for utilizing all available data and for creating well‐balanced treatment and control groups. An important component of the full matching algorithm is the decision about whether to impose a restriction on the maximum ratio of controls matched to each treated subject. Despite the possible effect of this restriction on subsequent inferences, this issue has not been examined. We used a series of Monte Carlo simulations to evaluate the effect of imposing a restriction on the maximum ratio of controls matched to each treated subject when estimating risk differences. We considered full matching both with and without a caliper restriction. When using full matching with a caliper restriction, the imposition of a subsequent constraint on the maximum ratio of the number of controls matched to each treated subject had no effect on the quality of inferences. However, when using full matching without a caliper restriction, the imposition of a constraint on the maximum ratio of the number of controls matched to each treated subject tended to result in an increase in bias in the estimated risk difference. However, this increase in bias tended to be accompanied by a corresponding decrease in the sampling variability of the estimated risk difference. We illustrate the consequences of these restrictions using observational data to estimate the effect of medication prescribing on survival following hospitalization for a heart attack.

1. INTRODUCTION

Matching‐based methods are popular when using observational data to estimate the effects of treatments, exposures, and interventions. Many matching‐based methods use the propensity score, which is defined as the probability of receiving the active treatment conditional on observed baseline covariates. ¹ The most common implementation of propensity score matching is pair‐matching, in which pairs of treated and control subjects are formed who share a similar value of the propensity score. Methods for forming matched pairs include nearest neighbor matching, with or without a caliper, and optimal matching. ² Alternatives to pair‐matching include many‐to‐one matching, and variable ratio matching. ³ , ⁴

An alternative matching method is full matching, which constructs strata or matched sets consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. ⁵ , ⁶ Subsequent analyses can incorporate weights that are derived from the stratification imposed by the matched sets. There are at least two attractive features of full matching compared to other matching approaches. First, it retains all subjects in the analytic sample. This contrasts with conventional matching methods in which some subjects are excluded from the final matched sample. Because of this, it avoids bias due to incomplete matching, which can occur when some treated subjects are excluded from the matched sample. ⁷ Second, full matching permits estimation of either the average treatment effect (ATE) or the average treatment effect in the treated (ATT), whereas conventional pair‐matching only allows for estimation of the ATT.

Recent studies have explored methodological issues related to the use of full matching. These include evaluating its performance for estimating the effect of treatments on binary outcome and extending it for use with survival or time‐to‐event outcomes. ⁸ , ⁹ Furthermore, the sensitivity to full matching to mis‐specification of the propensity score model was assessed. ¹⁰ However, one important issue related to the implementation of full matching remains to be determined. As described above, full matching constructs matched sets consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. In the conventional implementation of full matching there is no constraint on the size of the matched sets. For example, in Hansen's application of full matching to estimate the effect of coaching on the SAT, the composition of the matched sets ranged from six exposed subjects matched to one control subject to 161 control subjects matched to one exposed subject. ⁶ Hansen suggests that there are two potential drawbacks to placing no restrictions on the size of the matched sets. First, the estimated treatment effect may be strongly dependent on the specification of the propensity score. Second, it can result in estimated treatment effects with decreased precision compared to what would be observed with smaller matched sets, essentially leading to a few subjects being particularly influential in subsequent analyses. The second drawback is echoed by Stuart and Green, who suggest that not constraining the size of the matched sets can result in an inflation of the standard error (SE) of the estimated treatment effect. ¹¹

Accordingly, the objective of the current paper is to examine the impact of constraining the size of the matched sets when using full matching to estimate risk differences. The paper is structured as follows: in Section 2, we briefly describe propensity scores, full matching, and statistical methods for estimating the effect of treatment on binary outcomes when using full matching. In Section 3, we describe a series of Monte Carlo simulations to examine the effect of restricting the size of matched sets on the performance of full matching when estimating risk differences. Section 4 reports the results of these simulations. In Section 5, we provide a case study in which we illustrate the use of full matching for estimating the effect of discharge prescribing of medication in patients who were discharged from hospital following admission for a heart attack. Finally, in Section 6, we summarize our findings and place them in the context of the existing literature.

2. STATISTICAL METHODS

We provide a brief review of: (i) the propensity score; (ii) full matching; (iii) full matching with constraints; (iv) using full matching to estimate risk differences.

2.1. The propensity score

In an observational study of the effect of treatment on outcomes, the propensity score is the probability of receiving the treatment of interest conditional on measured baseline covariates: e = Pr(Z = 1| X), where X denotes the vector of measured baseline covariates and Z denotes treatment status (Z = 1 for treated and Z = 0 for control). ¹ There are four ways in which the propensity score is typically used for estimating the effects of treatments or interventions: matching, stratification, weighting, and covariate adjustment. ¹ , ¹² , ¹³ The use of propensity score methods rests upon the assumption of strongly ignorable treatment assignment. ¹ This assumption has two components. The first, known as the assumption of “no unmeasured confounders” states that treatment assignment is independent of the potential outcomes conditional on the measured baseline covariates. In other words, the observed covariates include all prognostically important covariates that are related to treatment assignment. The second, known as the assumption of “positivity,” states that all subjects have a non‐zero probability of receiving either treatment.

2.2. Full matching

Full matching forms strata or matched sets consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. ⁵ An optimal full match is a full match that minimizes the mean within matched‐set differences in the propensity score between treated and control subjects. For the remainder of the paper, we will use the term full matching to refer to optimal full matching. A refinement of optimal full matching is optimal full matching with a caliper restriction, in which treated and control subjects can only be included in the same matched set if their propensity scores differ by less than a pre‐specified distance. ¹⁴

To estimate effects using the full matching structure weights can be derived from the stratification imposed by the full matching. One set of weights permits estimation of the ATE, while a second set of weights permits estimation of the ATT. Weights that permit estimation of the ATT are constructed as follows: treated subjects are assigned a weight of one, while each control subject has a weight proportional to the number of treated subjects in its matched set divided by the number of controls in the matched set. ¹⁵ , ¹⁶ The control group weights are scaled such that the sum of the control weights across all the matched sets is equal to the number of uniquely matched control subjects. As the current paper focuses on estimation of the ATT, we refer the reader elsewhere for a description of ATE weights for use with full matching. ¹⁷

2.3. Full matching with constraints on the maximum ratio of control subjects to treated subjects

As noted above, full matching forms matched sets consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject (with or without a caliper restriction). However, in the conventional full matching algorithm there is no constraint on the size of the individual matched sets. The full matching algorithm can be modified to impose a constraint on the maximum ratio of control subjects to treated subjects within each matched set. ⁶ While full matching with no constraint will result in the inclusion of all subjects in the resultant full matching stratification the imposition of a constraint (either a constraint on the number of control subjects matched to each treated subject or a caliper restraint) can result in the exclusion of some subjects from the resultant full matching stratification.

2.4. Using full matching to estimate treatment risk differences

Full matching on the propensity score can be used to estimate the effect of treatment on binary outcomes. ⁸ This approach involves computing the marginal probabilities of the occurrence of the outcome. Using the weights induced by full matching, one can estimate the probability of the occurrence of the outcome in treated subjects and in control subjects, separately. These denote the marginal probabilities of the occurrence of the outcome, reflecting the probability of the outcome in the treated population (if using the ATT weights) if all these subjects were treated and if all these subjects received the control condition. Formally, define $P_1=E[Y(1)=1]=\frac{1}{N_1}{\sum }_{i=1}^N{w}_i{Y}_i{Z}_i$ and $P_0=E[Y(0)=1]=\frac{1}{N_0}{\sum }_{i=1}^N{w}_i{Y}_i(1-Z_i)$, where N ₁ and N ₀ denote the number of treated and control subjects, respectively, and w _i denotes the weight induced by full matching. The full matching estimator of the risk difference is P₁ − P₀.

3. MONTE CARLO SIMULATIONS TO EXAMINE THE EFFECT OF CONSTRAINTS ON THE SIZE OF MATCHED SETS ON THE PERFORMANCE OF FULL MATCHING

We conducted a series of Monte Carlo simulations to examine the effect of constraining the ratio of the number of controls to treated subjects in each matched set on estimation of the marginal risk difference when the target estimand is the ATT. We considered a range of scenarios that varied in terms of the extent of confounding and the prevalence of treatment. The performance of estimation of the risk difference was assessed using the following criteria: (i) bias in estimating the true treatment effect; (ii) the standard deviation (SD) of the estimated risk differences across simulation replicates; and (iii) the mean squared error (MSE) of the estimated treatment effect. These simulations were similar in design to those used in a previous study that compared the performance of full matching with pair‐matching on the propensity score and inverse probability of treatment weighting (IPTW) using the propensity score. ⁸

3.1. Simulating baseline covariates

We simulated data for a super‐population of 1 000 000 subjects. For each subject, we simulated 10 baseline covariates (X ₁, …, X ₁₀) from independent standard normal distributions.

3.2. Simulating treatment status

For each subject in the super‐population we randomly generated a treatment status (Z = 1 treated vs Z = 0 control) using the logistic model described in formula (1).

$$\begin{array}{ll}& \text{logit}(\mathrm{Pr}(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+\\ & {\beta }_8{X}_8+{\beta }_9{X}_9+{\beta }_{10}{X}_{10}\end{array}$$ (1)

The intercept, β ₀, in the treatment‐selection model was chosen using a bisection approach so that the prevalence of treatment was equal to the desired value (this will be one of the factors allowed to vary in the simulations). The regression coefficients in the treatment‐selection model, β ₁ through β ₁₀ were set equal to log(k × 1.05), log(k × 1.10), log(k × 1.20), log(k × 1.25), log(k × 1.50), log(k × 1.75), log(k × 2.00), log(k × 1.50), log(k × 1.25), and log(k × 1.10) respectively. The parameter k affects the strength of the treatment‐selection model (this will be one of the factors allowed to vary in the simulations). As k increases, the strength of the treatment‐selection process increases.

3.3. Simulating binary outcomes

A binary outcome Y was simulated for each subject in the super‐population using the logistic model described in formula (2).

$$\begin{array}{ll}& \text{logit}(\mathrm{Pr}(Y=1))={\alpha }_0+{\alpha }_{\text{treat}}Z+{\alpha }_1{X}_1+{\alpha }_2{X}_2+{\alpha }_3{X}_3+{\alpha }_4{X}_4+{\alpha }_5{X}_5+{\alpha }_6{X}_6+{\alpha }_7{X}_7+\\ & {\alpha }_8{X}_8+{\alpha }_9{X}_9+{\alpha }_{10}{X}_{10}\end{array}$$ (2)

The regression coefficients, α ₁ through α ₁₀ were set equal to 2, 1.75, 1.50, 1.25, 1.10, 1.05, 1.50, 1.75, 2, and 1.25, respectively. The intercept, α ₀, was selected using a bisection approach so that the marginal probability of the outcome if all subjects were untreated was 0.20. We used a bisection approach to select α_treat so that the marginal population risk difference in treated subjects was −0.02 (ie, the ATT was the target estimand).

3.4. Factors in the design of the Monte Carlo simulations

Our Monte Carlo simulations used a full factorial design in which two factors were varied. The first factor was the magnitude of the effect of covariates on treatment‐selection. To do so, we allowed the scalar k (defined above in the coefficients for the treatment‐selection model) to range from one to four in increments of one. The second factor was the prevalence of treatment, which took on the following six values: 0.10 to 0.60 in increments of 0.10. We thus examined 24 (4 × 6) different scenarios. For each of the 24 scenarios, we drew 1000 random datasets, each consisting of 1000 subjects, sampled without replacement from the super‐population.

In the primary set of simulations described above, the true risk difference was −0.02 and we conducted full matching in samples of size 1000. We considered three secondary sets of simulations. In the first two of these sets of secondary simulations, we set the true risk difference to 0 and −0.04, while keeping the size of the samples at 1000. We thus examined a null effect (0), a moderate effect (−0.02), and a strong effect (−0.04). These are equivalent to relative risk reductions of 0%, 10%, and 20%. In the third set of secondary simulations, we set the size of the samples to 500 while keeping the true risk difference at −0.02.

3.5. Statistical analyses in sampled datasets

In each of the sampled datasets, we estimated the propensity score using a logistic regression model to regress treatment assignment on the 10 variables X ₁ through X ₁₀. In each of the sampled datasets, we created 40 matched samples using full matching. First, 19 matched samples were created using optimal full matching using the estimated propensity score. We allowed the constraint on the maximum number of controls per treated subject to range from 2 to 20, increments of 1. Thus, in the first matched sample, we constrained the matched sets to contain at most two controls per treated subject, while in the 19th matched sample, we constrained the matched sets to contain at most 20 controls per treated subject. We then repeated the above process using full matching with a caliper restriction. Subjects were matched on the logit of the propensity score with the restriction that matched treated and control subjects could not have a difference in the logit of the propensity score of more than 0.2 of the SD of the logit of the propensity score. As with the first set of matched samples, we created 19 matched samples using the different constraints on the maximum number of controls per treated subject in each of the matched sets. Individuals who were not included in a matched set due to this restriction were dropped from the analysis. For comparative purposes we created two additional matched samples in which no constraints were placed on the maximum number of matched controls per treated subject (one created without a caliper restraint and one created with a caliper restraint). Thus, using each sampled dataset, we constructed a total of 40 matched samples using full matching.

In each of the 1000 sampled datasets for a given scenario, we assessed balance in each of the 10 measured baseline covariates before matching and after matching in each of the 40 matched samples (balance was assessed separately in each of the 40 matched samples constructed using full matching). We estimated the absolute standardized difference for each of the 10 baseline covariates. ¹⁸ For each covariate we then determined the mean absolute standardized difference across the 1000 sampled datasets, both before and after matching.

Let θ denote the true treatment risk difference that was built into the data‐generating process, and let ${\widehat{\theta }}_i$ denote the estimated risk difference in the ith simulated sample (i = 1, …,1000). The mean estimated risk difference was estimated as $\bar{\theta }=\frac{1}{1,000}{\sum }_{i=1}^{1,000}{\widehat{\theta }}_i$, while the relative bias was computed as $100\times \frac{\bar{\theta }-\theta }{\theta }$. The MSE was estimated as $\frac{1}{1,000}{\sum }_{i=1}^{1,000}{({\widehat{\theta }}_i-\theta )}^2$. We also computed the SD of the estimated risk differences across the 1000 sampled datasets.

All analyses were conducted in the R statistical programming language (version 3.5.0). Full matching was implemented using the matchit function from the MatchIt package (version 3.0.2). ¹⁵ , ¹⁶ Full matching with a caliper restriction was implemented using the fullmatch function in the optmatch package (version 0.9‐10).

3.6. Bootstrapping for estimating the SE of estimated risk differences

We conducted a limited set of Monte Carlo simulations to examine the performance of the bootstrap for estimating the SE of the estimated risk difference. ¹⁹ These simulations are an extension of those that we reported previously. ⁸ We restricted the current simulations to two of the settings described above with a true risk difference of −0.02 and sample sizes of 500 and 1000. Furthermore, we only used full matching without a caliper restriction and with no constraint on the maximum number of controls matched to each treated subject. In the previous examination of bootstrapping with full matching, we restricted our simulations to scenarios with k = 1 in the treatment‐selection process. ⁸ In the current simulations, we considered all four values of k, as well as the two different sample sizes. From each simulated sample drawn from the super‐population, we drew 200 bootstrap samples. In each bootstrap sample we estimated the propensity score and then used full matching to estimate the risk difference. The SE of the estimated risk difference in the simulated sample was estimated as the SD of the estimated risk difference across the 200 bootstrap samples. A confidence interval for the estimated risk difference was constructed using standard normal theory methods using the estimated SE.

Two analyses were conducted across the 1000 simulation replicates. First, we computed the ratio of the mean estimated SE across the 1000 simulation replicates to the SD of the estimated risk difference across the 1000 simulation replicates. If the bootstrap is performing as anticipated, this ratio should be close to one. Second, we determined the proportion of estimated confidence intervals that contained the true risk difference. Given our use of 1000 simulation replicates, empirical coverage rates lower than 0.9365 or greater than 0.9635 are statistically significantly different from the nominal rate of 0.95 based on a standard normal theory test.

4. MONTE CARLO SIMULATIONS: RESULTS

4.1. Construction of the full matching stratification

In each stratification induced by full matching we computed: (i) the size of the resultant sample; (ii) the maximum weighted induced by the stratification; (iii) the largest number of control subjects matched to one treated subject. We determined the mean of these quantities across the 1000 simulation replicates for each scenario. Results regarding the mean size of the resultant sample are summarized in Figures A1 (no caliper restriction) and A2 (caliper restriction) in the supplemental online appendix. There is one panel for each of the four different strengths of the treatment‐selection model. We have superimposed horizontal lines denoting the mean sample size when full matching with no constraint was imposed on the maximum number of controls per treated subject (note that the maximum size of the matched samples was 1000). When matching without a caliper, imposing a constraint on the maximum number of controls matched to each treated subject resulted in the exclusion of subjects from the resultant matched sample when the prevalence of treatment was less than or equal to 30%. When no such constraint was imposed, all subjects were included in the matched sample. When a caliper restriction was also imposed, then imposing a constraint on the maximum number of controls matched to each treated subject resulted in a reduction in the size of the matched sample, with the magnitude of the reduction in sample size being inversely proportional to the prevalence of treatment.

The mean maximum weight across the 1000 simulation replicates are reported in Figures A3 (no caliper restriction) and A4 (with a caliper restriction) in the supplemental online appendix. In both settings, imposing a constraint on the maximum number of controls matched to each treated subject resulted in a decrease in the maximum weight, as expected.

The maximum number of control subjects matched to each treated subject are reported in Figures A5 (no caliper restriction) and A6 (with a caliper restriction) in the supplemental online appendix. With or without a caliper restriction, the imposition of a constraint on the maximum number of control subjects matched to each treated subject resulted in a substantially smaller maximum number than if no such constraint is imposed. In examining this number when no constraint is imposed, we observe that there are matched sets containing more than 100 control subjects, regardless of the strength of the treatment‐selection process.

4.2. Balance of baseline covariates

The mean absolute standardized differences for each of the 10 baseline covariates across the 1000 original unmatched samples are described in Figure A7 in the supplemental online appendix. There is one panel for each of the six prevalences of treatment. On each panel we have superimposed a horizontal line denoting a standardized difference of 0.1, as some authors have suggested that standardized differences that exceed this threshold may be indicative of meaningful imbalance. ²⁰ The intent of this figure is to inform the reader about the initial imbalance in the 10 baseline covariates between the treated and control groups in the original sample. In each of the 24 scenarios there was substantial imbalance in the 10 baseline covariates between the treated and control groups.

Due to the large number of matched sets formed (19 with a constraint on the maximum ratio of controls to treated subjects and no caliper restriction; 19 with a constraint on the maximum ratio of controls to treated subjects and a caliper restriction; 1 with no constraint on the maximum ratio of controls to treated subjects and no caliper restriction; 1 with no constraint on the maximum ratio of controls to treated subjects and with a caliper restriction), we computed the maximum mean absolute standardized difference across the 10 baseline covariates. The maximum mean absolute standardized differences are reported in Figures A8 (no caliper restriction) and A9 (with caliper restriction) in the supplemental online appendix. In each figure there is one panel for each of the strengths of the treatment‐selection process (as indexed by the parameter k). We have plotted the maximum mean absolute standardized difference against the maximum ratio of controls to treated subjects in the matched sets (ranging from 2 to 20), with one line for each of the six prevalences of treatment. We have also added horizontal dashed lines denoting covariate balance when full matching with no constraint on the maximum number of controls per treated subject in each matched set.

When using full matching with no caliper restriction (Figure A8), imposing a constraint on the ratio of controls per treated subject tended to result in greater residual covariate imbalance compared to when no such constraint was imposed. Furthermore, the degree of residual imbalance increased with the strength of the treatment‐selection model. When the prevalence of treatment was 10%, 20%, or 30%, the greatest residual imbalance was observed when the maximum ratio of controls per treated subject in the matched sets was approximately equal to the ratio of control subjects to treated subjects in the overall sample. When using full matching with a caliper restriction (Figure A9), the residual imbalance tended to be the same regardless of the constraint on the maximum number of controls per treated subject. As above, the degree of residual imbalance tended to increase with the strength of the treatment‐selection model.

4.3. Relative bias in estimating marginal risk differences

Under the primary set of simulations (N = 1000 and risk difference = −0.02), the relative bias in estimating the marginal risk difference is reported in Figures 1 (no caliper restriction) and 2 (with a caliper restriction). There is one panel for each of the four different strengths of the treatment‐selection model. We have superimposed horizontal lines denoting the relative bias when full matching with no constraint was imposed on the maximum number of controls per treated subject. When no caliper restriction was imposed (Figure 1), relative bias tended to be lowest when no constraint was imposed on the maximum number of controls per treated subject. There were some values for the maximum number of controls per treated subject that resulted in a very large relative bias. These large relative biases tended to be observed when the maximum ratio of controls to treated subjects in the matched sets was approximately equal to the ratio of controls to treated subjects in the overall sample. When a caliper restriction was imposed (Figure 2), imposing a constraint on the maximum number of controls per treated subject tended to have no effect on relative bias compared to when no such constraint was imposed. Furthermore, the relative bias did not vary according to the magnitude of this constraint on the maximum number of controls per treated subject.

FIGURE 1.

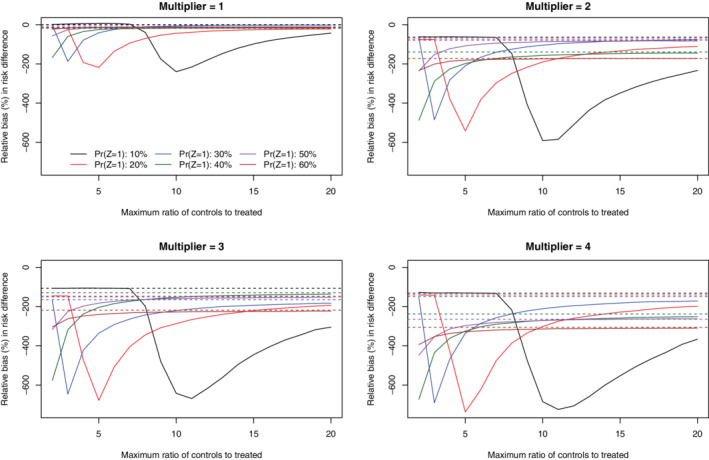
Relative bias (%) in estimated risk difference (no calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2.

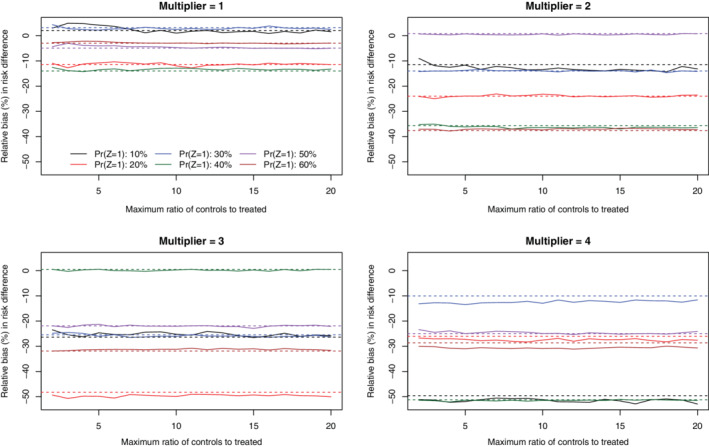
Relative bias (%) in estimated risk difference (with calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

The corresponding results for the secondary sets of simulations are reported in Figures A10 and A11 (N = 1000 and risk difference = 0), Figures A16 and A17 (N = 1000 and risk difference = −0.04), and Figures A22 and A23 (N = 500 and risk difference = −0.02) in the supplemental online appendix. Note that when the risk difference is equal to zero, we report bias, rather than the relative bias. Qualitatively similar results were observed in each of these settings as in the primary set of simulations.

We hypothesize that the observed bias that arises from the imposition of a constraint on the number of controls matched to each treated subject has two potential sources. First, imposing a constraint on the maximum number of controls matched to a treated subject can induce residual bias because the quality of the matches is not as good as if a truly optimal match without such constraints was used. Second, we saw increasing bias with increasing strength of the treatment‐selection process. This increasing bias may reflect a greater dissimilarity between treated and control subjects. Full matching without a caliper constraint forces the inclusion of all subjects, regardless of their dissimilarity, which can allow for the residual bias to persist.

The large biases that we observed when the maximum ratio of controls to treated subjects in the matched sets was approximately equal to the ratio of controls to treated subjects in the overall sample was a surprising observation. We hypothesize that this may occur because there may be less capacity for full matching to generate well‐balanced groups when the ratio in the matched sample is the same as in the original data. It is possible that not much reordering can happen in either direction (with treated or control subjects). An analogy may be what occurs with pair matching when there are an equal number of treated and control subjects in the overall sample.

4.4. SD of the estimated risk differences across simulation replicates

Under the primary set of simulations (N = 1000 and risk difference = −0.02), the SD of the estimated risk differences across the 1000 simulation replicates is reported in Figures 3 (no caliper restriction) and 4 (with a caliper restriction). When no caliper restriction was imposed (Figure 3), the sampling variability of the estimated risk difference when a constraint was imposed on the maximum number of controls per treated subject tended to be no larger than when no such constraint was imposed. When there was a moderate to strong treatment‐selection process (k = 2, 3, or 4), the SD of the risk difference tended to be minimized when the number of controls to treated subjects was constrained to approximately equal the ratio of controls to treated subjects in the overall sample. Thus, in these settings, selecting a maximal number of controls matched to treated subjects equal to that observed in the overall sample resulted in a substantial reduction in the variability of the estimated treatment effect compared to when no such constraint was imposed. When a caliper restriction was imposed (Figure 4), imposing a constraint on the maximum number of controls per treated subject tended to have no effect on the variability of the sampling distribution of the estimated risk difference compared to when no such constraint was imposed. Furthermore, the sampling variability of the estimated risk difference did not vary according to the magnitude of this constraint on the maximum number of controls per treated subject.

FIGURE 3.

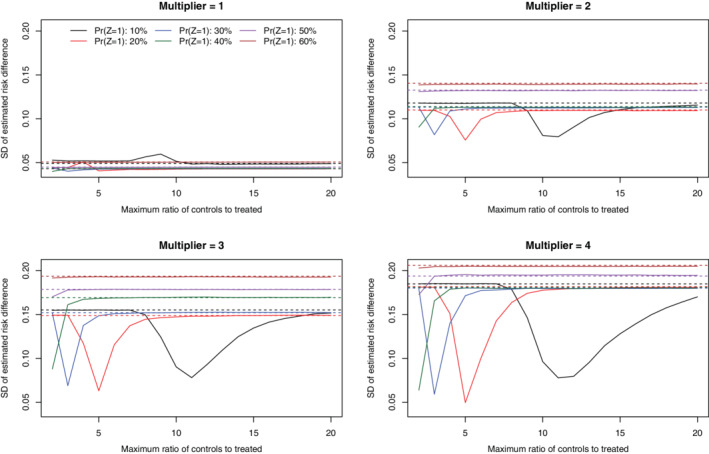
SD of estimated risk difference (no calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4.

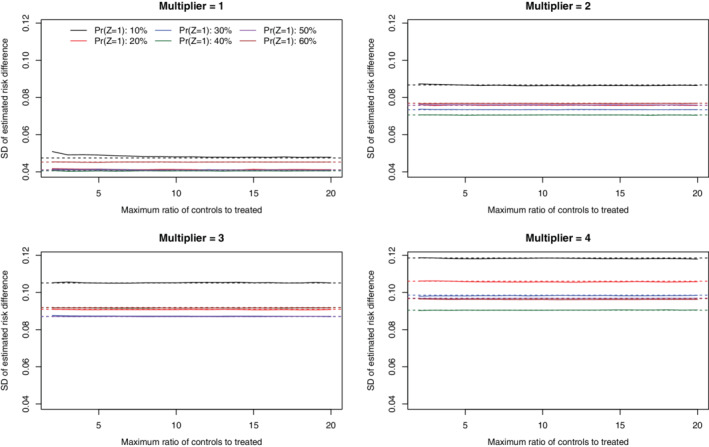
SD of estimated risk difference (with calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

The corresponding results for the secondary sets of simulations are reported in Figures A12 and A13 (N = 1000 and risk difference = 0), Figures A18 and A19 (N = 1000 and risk difference = −0.04), and Figures A24 and A25 (N = 500 and risk difference = −0.02) in the supplemental online appendix. Qualitatively similar results were observed in each of these settings as in the primary set of simulations.

4.5. MSE of estimated risk differences

Under the primary set of simulations (N = 1000 and risk difference = −0.02), the MSE of the estimated risk differences across the 1000 simulation replicates is reported in Figures 5 (no caliper restriction) and 6 (with a caliper restriction). In general, when no caliper restriction was imposed (Figure 5), imposing a constraint on the maximum number of controls per treated subject tended to result in an MSE that was equal to or greater than that obtained when no such constraint was imposed. There were a few exceptions to this generalization, particularly when there was a very strong treatment‐selection process and the prevalence of treatment was modest. In those settings, using a constraint that was approximately equal to the ratio of controls to treated subjects in the overall sample tended to minimize MSE. When a caliper restriction was imposed (Figure 6), imposing a constraint on the maximum number of controls per treated subject tended to have no effect MSE of the estimate risk difference compared to when no such constraint was imposed. Furthermore, the MSE of the estimated risk difference did not vary according to the magnitude of this constraint on the maximum number of controls per treated subject.

FIGURE 5.

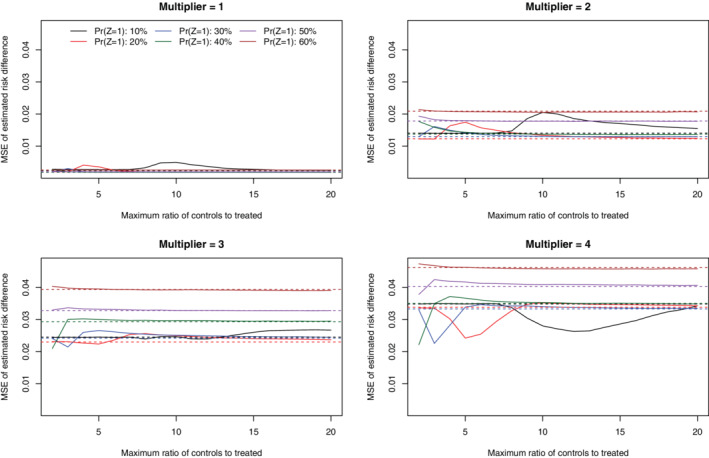
MSE of estimated risk difference (no calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 6.

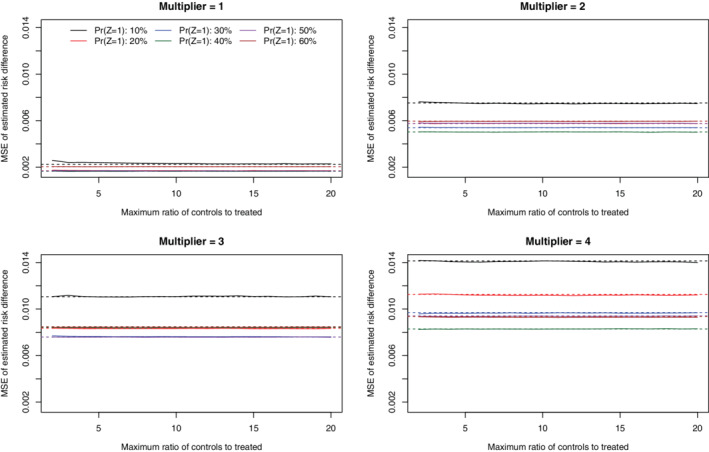
MSE of estimated risk difference (with calipers) (N = 1000 & RD = −0.02) [Colour figure can be viewed at wileyonlinelibrary.com]

The corresponding results for the secondary sets of simulations are reported in Figures A14 and A15 (N = 1000 and risk difference = 0), Figures A20 and A21 (N = 1000 and risk difference = −0.04), and Figures A26 and A27 (N = 500 and risk difference = −0.02) in the supplemental online appendix. In general, qualitatively similar results were observed in each of these settings as in the primary set of simulations.

4.6. Bootstrapping for estimation of SEs

Results of the simulations to examine the performance of the bootstrap for estimating the SE of the estimated risk difference and empirical coverage rates of bootstrap‐based confidence intervals are reported in Table 1. In general, the bootstrap estimate of the SE approximated the SD of the sampling distribution of the risk difference when the strength of the treatment‐selection process was weak to moderate (k = 1) and when the prevalence of treatment was between 0.3 and 0.6. The ratio was less than one when k > 1, indicating that the bootstrap estimate of the SE under‐estimated the SD of the sampling distribution of the risk difference in the presence of a strong treatment‐selection process. Furthermore, the magnitude of under‐estimation increased as the strength of the treatment‐selection process increased. When k = 1, the empirical coverage rates of estimated 95% confidence intervals tended to be either conservative or approximately equal to the advertised rate. When k ≥ 2, empirical coverages rates were lower than the advertised rate. For both estimation of the SE and empirical coverage rates of 95% confidence intervals, there were no meaningful differences between when samples were of size 500 compared to when samples were of size 1000.

TABLE 1.

Estimation of SEs and 95% confidence intervals using bootstrapping

Ratio of SE to SD		Empirical coverage rate
Prevalence of treatment	Treatment‐strength multiplier (k)	N = 500	N = 1000	N = 500	N = 1000
0.1	1	1.12	1.16	0.979	0.979
0.1	2	0.97	0.92	0.917	0.890
0.1	3	0.87	0.88	0.854	0.852
0.1	4	0.89	0.80	0.799	0.809
0.2	1	1.12	1.10	0.962	0.969
0.2	2	0.92	0.88	0.869	0.860
0.2	3	0.81	0.79	0.765	0.756
0.2	4	0.82	0.74	0.774	0.747
0.3	1	1.03	1.04	0.959	0.956
0.3	2	0.87	0.84	0.823	0.822
0.3	3	0.79	0.78	0.752	0.726
0.3	4	0.77	0.75	0.739	0.723
0.4	1	1.01	1.03	0.944	0.951
0.4	2	0.85	0.86	0.799	0.800
0.4	3	0.73	0.74	0.695	0.731
0.4	4	0.73	0.71	0.661	0.665
0.5	1	1.01	1.02	0.939	0.950
0.5	2	0.81	0.77	0.775	0.769
0.5	3	0.74	0.71	0.691	0.682
0.5	4	0.70	0.67	0.605	0.605
0.6	1	1.02	0.96	0.942	0.940
0.6	2	0.76	0.76	0.707	0.710
0.6	3	0.67	0.65	0.578	0.599
0.6	4	0.66	0.63	0.571	0.566

5. CASE STUDY

5.1. Methods

The case study used data on patients hospitalized with acute myocardial infarction (or heart attack) who survived to hospital discharge. We considered two different treatments: (i) receipt of a prescription for a statin lipid lowering medication at hospital discharge; (ii) receipt of an angiotensin converting enzyme (ACE) inhibitor medication at hospital discharge (each treatment was considered independently of the other treatment). These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, an initiative intended to improve the quality of care for patients with cardiovascular disease in Ontario. ²¹ For the purposes of these analyses, subjects with missing data on any of the variables listed below that were used to estimate the propensity score were excluded from the case study. While methods for imputing missing data when using the propensity score have been described, ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ we chose to conduct a simple complete case analysis as our objective was simply to illustrate the choice of the maximum number of controls matched to each treated subject using a convenience sample. Furthermore, we would also note that these studies that examined the use of imputation when using propensity score methods focused on conventional matching on the propensity score, stratification on the propensity score, and inverse probability of treatment weighting using the propensity score. Research on the use of multiple imputation with optimal full matching merits investigation in future research.

For the current study, the dichotomous outcome was survival to 3 years after hospital discharge. The study sample for the case study consisted of 6978 subjects, of whom 2505 (35.9%) received a statin prescription at discharge and 4100 (58.8%) received an ACE inhibitor prescription at discharge. Of the study sample, 1554 (22.3%) patients died within 3 years of hospital discharge.

For each of the two treatments, the propensity score was estimated using 36 baseline covariates: demographic characteristics (age and sex); presenting signs and symptoms (acute cardiogenic shock, pulmonary edema); vital signs on admission (systolic blood pressure, diastolic blood pressure, heart rate, respiratory rate); classic cardiac risk factors (diabetes, hyperlipidemia, hypertension, family history of coronary artery disease, and current smoker); comorbid conditions and vascular history (stroke and/or transient ischemic attack, angina, cancer, dementia, peptic ulcer disease, previous myocardial infarction, asthma, depression, peripheral arterial disease, previous coronary revascularization, chronic congestive heart failure, hyperthyroidism, aortic stenosis); laboratory tests (glucose, white blood count, hemoglobin, sodium, potassium, creatinine, and urea); cardiac measures (raised cardiac enzymes); results of echocardiogram (presence of ST segment depression); and in‐hospital cardiac procedures during the initial hospitalization (whether the patient underwent a percutaneous coronary intervention). The propensity score was estimated using a logistic regression model in which treatment status was regressed on these 36 baseline variables.

Full matching on the estimated propensity score was used to create a stratification of the study sample. We constructed 40 matched samples using full matching: 19 with a constraint on the maximum ratio of controls to treated subjects (ranging from 2 to 20 in increments of 1) and no caliper restriction; 19 with a constraint on the maximum ratio of controls to treated subjects (ranging from 2 to 20 in increments of 1) and a caliper restriction; 1 with no constraint on the maximum ratio of controls to treated subjects and no caliper restriction; 1 with no constraint on the maximum ratio of controls to treated subjects and with a caliper restriction.

Within each matched sample we computed absolute standardized differences of the mean for each of the 36 covariates using the weights induced by the full matching. We also estimated the risk difference for the outcome comparing each of the two treatments in each of the 40 matched samples.

All analyses were conducted in the R statistical programming language (version 3.5.0). Full matching was implemented using the fullmatch function in the optmatch package (version 0.9‐10).

5.2. Results

Covariate balance and estimated risk differences are reported in Figure 7. The top two panels report results for statin treatment, while the lower two panels report results for ACE inhibitor treatment. For covariate balance we report the maximum absolute standardized difference across the 36 baseline covariates. Each panel reports the relationship between either balance (maximum absolute standardized difference) or the estimated risk difference and the maximum ratio of treated to control subjects within each matched set. We have superimposed on each panel a horizontal line denoting either the maximum absolute standardized difference or the estimated risk difference when no constraint on the maximum ratio of controls to treated subjects within each matched sample.

FIGURE 7.

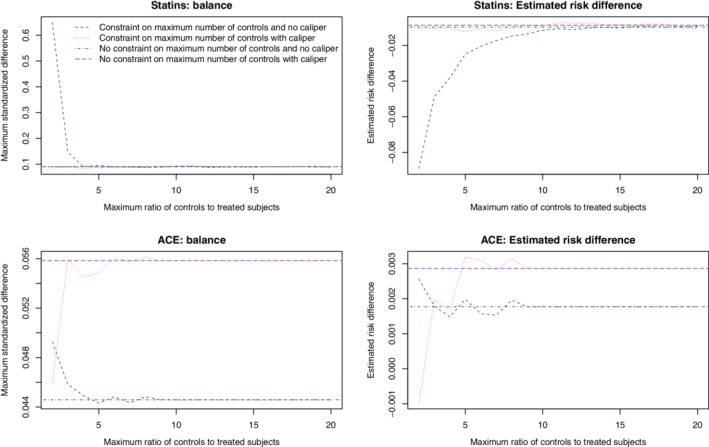
Covariate balance and estimated risk differences in case study [Colour figure can be viewed at wileyonlinelibrary.com]

When considering statin treatment (vs no statin treatment), excellent covariate balance (all standardized differences less than 0.1) was observed when using caliper matching (with or without a restriction on the maximum ratio of controls to treated subjects in the matched sets) or when using matching without calipers and without a restriction on the maximum ratio of controls to treated subjects in the matched sets. In contrast to this, when using matching without calipers, there was moderate residual covariate imbalance when the ratio of controls to treated subjects in the matched sets was restricted to be three or less. When estimating the risk difference for statin treatment, estimates obtained using caliper matching were essentially unchanged regardless of whether or not a restriction was placed on the maximum ratio of controls to treated subjects in the matched sets. When using matching without calipers, the estimated risk difference was substantially larger in magnitude when the maximum ratio of controls to treated subjects in the matched sets was four or smaller.

When considering ACE inhibitor treatment (vs no ACE inhibitor treatment), the choice of constraint on the maximum ratio of controls to treated subjects in the matched sets had at most a negligible impact on balance of baseline covariates (note the scale of this panel is different from that of the corresponding panel for statin treatment). Similarly, absolute differences in the estimated risk difference were negligible across the different matching methods, regardless of the constraint that was imposed.

6. DISCUSSION

We examined the impact of imposing a constraint on the maximum number of controls matched to each treated subject on estimation of risk differences when using full matching. We found that, in general, bias was minimized when no such constraint was imposed. In certain settings with a very strong treatment‐selection process and a low prevalence of treatment (≤30%), constraining the maximum number of controls matched to each treated subject to the ratio of controls to treated subjects in the overall sample tended to result in estimated risk differences that had lower variability and lower MSE compared to when no such constraint was imposed. Thus, in some settings (characterized by a moderate to strong treatment selection process combined with a low prevalence of treatment), the decision to impose a constraint on the number of control subjects matched to each treated subject reflects the classic bias‐variance trade‐off. Bias was increased when such a constraint was imposed, while the variability of the estimated treatment effect decreased. When full matching with a caliper constraint was used, then imposing an additional constraint on the maximum number of controls matched to each treated subject had no effect on estimation of risk differences.

The effect of constraining the maximum number of controls matched to each treated subject has received little attention in the literature. In an application of full matching to estimate the effect of adolescent marijuana smoking on adult outcomes, Stuart and Green imposed such a restriction and used the ratio of control subjects to treated subjects in the overall sample to inform the magnitude of this constraint. ¹¹ Their rationale for imposing such as restriction was that it could improve the precision of the estimated treatment effect. Similarly, in an empirical application of full matching, Hansen observed that imposing such a constraint resulted in estimates with improved precision. ⁶ In our Monte Carlo simulations, we observed that improved precision was indeed achieved by such a constraint. However, it came at the cost of a substantial increase in bias in the estimated risk difference. MSE was minimized by imposing such a constraint only when there was a very strong treatment‐selection process and the overall prevalence of treatment was low to moderate (≤30%).

As noted elsewhere, full matching has many attractive features. ⁶ , ⁸ , ⁹ , ²⁹ In particular, unlike conventional pair‐matching, it allows for the inclusion of all subjects in the matched sample. Many analyses that use full matching incorporate weights that are induced by the stratification. The occurrence of extreme weights may be rarer than occurs with inverse probability of treatment weights that are frequently used when using weighting to estimate causal treatment effects. The current study addressed a void in the literature on full matching. By examining the impact of constraining the number of control subjects matched to each treated subject, we have provided applied analysts with guidance on the implementation of full matching so as to improve inferences of risk differences.

Our Monte Carlo simulations on the performance of the bootstrap with full matching extend those we reported previously. ⁸ In the previous simulations, which were limited to scenarios with a weak to moderate treatment‐selection process, we found that the bootstrap had relatively good performance. In the current extension to these simulations, we found that in the presence of a strong treatment‐selection process, the bootstrap resulted in poor estimates of the SE of the risk difference and confidence intervals with sub‐optimal coverage rates. We also found that sample size had no meaningful impact on the performance of the bootstrap. The sub‐optimal performance of the bootstrap highlights a limitation of using full matching when outcomes are binary: the lack of a formal variance estimator for the estimated risk difference. However, the settings in which the bootstrap performed well (ie, those in which the odds ratios for treatment selection were between 1.05 and 2) may represent scenarios that are common in applied research. These results complement earlier findings on the use of the bootstrap with propensity‐score matching. Previously, it had been shown that the bootstrap should not be used with pair‐matching when matching with replacement, ³⁰ while the bootstrap performed well when using pair‐matching without replacement. ³¹ Methods for estimating the variance of the estimated risk difference and to improve the performance of the bootstrap with full matching merit further investigation.

Optimal full matching may be seen by some as an alternative to IPTW. To the best of our knowledge, only four studies have formally compared the performance of full matching with that of IPTW. ⁸ , ⁹ , ¹⁰ , ³² The first focused on the use of full matching with time‐to‐event or survival outcomes. ⁹ In the presence of strong confounding, both methods resulted in essentially unbiased estimation of the true hazard ratio, when the ATT was the target estimand. In the presence of moderate confounding, the use of full matching resulted in minor bias (<5%) when the prevalence of treatment was low. However, full matching resulted in estimates that displayed less variability than did IPTW in the presence of moderate confounding. Furthermore, the MSE of the estimated log‐hazard ratio was comparable between the two approaches. The second study focused on settings with binary outcomes and when the ATT was the target estimand. ⁸ Full matching tended to result in estimates of the risk difference with less bias than did IPTW. The relative performance of the two methods when assessed using MSE was inconsistent, with the results depending on the prevalence of treatment. The third study examined scenarios with time‐to‐event outcomes when the propensity‐score model was mis‐specified and when the ATE was the target estimand. ¹⁰ In this study, it was observed that IPTW tended to result in more subjects with extreme weights than did full matching. The fourth study compared the performance of a variety of propensity score methods and methods for estimating the propensity score when outcomes are rare. ³² Extreme weights were found to affect both IPTW and full matching. A final point of comparison is the nature of weights generated from each approach. IPTW allows for the estimation of unique weights for each subject. Full matching, in contrast, will result in the same weights for all controls matched to the same treated subject (and all treated subjects matched to the same control subject). It is possible that unique weights for each subject may lead to too much coarseness, and if the model is wrong, then the weights may be more variable than they should be. Full matching gives some smoothing to these values and may lead to less reliance on individual values (which may have been inaccurately estimated).

The current study is subject to certain limitations. The primary limitation was our reliance on Monte Carlo simulations to assess the effect of constraints on the matching algorithm on estimation of the risk difference. Due to computational limitations, we restricted our attention to a limited number of scenarios. However, these scenarios included a wide range of treatment prevalences, a range of strengths of the treatment‐selection process, a range of risk differences, and different sample sizes. Thus, the included scenarios reflect a range of scenarios that are encountered in applied research. Furthermore, analytic calculations in this context are not feasible. A second limitation was that, while we examined the variability of the estimated risk differences across simulation replicates, we did not conduct an extensive formal assessment of the estimation of SEs of the risk difference. As discussed in a previous paper, formal estimators of the SE of the risk difference when using full matching have not been developed. ⁸ However, we conducted a limited assessment of the performance of the bootstrap for estimating the SE of the estimated risk difference. We found that this approach performed well when the prevalence of treatment was moderate and the strength of the treatment‐selection process was weak to moderate. A third limitation was that we restricted our attention to settings in which the propensity score model was correctly specified. In previous research, we examined the effect of mis‐specification of the propensity score model on full matching and inverse probability of treatment weighting. ¹⁰ An examination of the effect of model mis‐specification in conjunction with a constraint on the number of control subjects matched to each treated subject is beyond the scope of the current study. A fourth limitation is that we have focused on the ATT as the target estimand. While full matching can also be used to estimate the ATE, our impression is that it is typically used to estimate the ATT (possibly because matchit provides the ATT weights and not the ATE weights). The impact of constraints on the number of controls matched to each treated subject on estimation of the ATE is beyond the scope of the current study. We speculate that comparable results would be observed when estimating the ATE. A final limitation was that we focused our attention on estimation of risk differences for binary outcomes. Binary outcomes are common in biomedical research. ³³ However, examination of estimation of differences in means for continuous outcomes and differences in survival for time‐to‐event outcomes merits examination in future research.

In conclusion, when using full matching with a caliper restriction, imposing a second restriction on the maximum ratio of the number of control subjects matched to each treated subject had no effect on the quality of inferences about the risk difference. When no caliper restraint was imposed, the imposition of a constraint on the maximal ratio of the number of controls matched to each treated subject tended to result in an increase in bias in the estimated relative risk. However, this could be accompanied by a decrease in the sampling variability of the estimated risk. Thus, the choice of whether or not to impose such a constraint reflects the traditional variance‐bias tradeoff.

Supporting information

Appendix S1 Supporting information

Austin PC, Stuart EA. The effect of a constraint on the maximum number of controls matched to each treated subject on the performance of full matching on the propensity score when estimating risk differences. Statistics in Medicine. 2021;40:101–118. 10.1002/sim.8764

DATA AVAILABILITY STATEMENT

The data sets used for this study were held securely in a linked, de‐identified form and analysed at ICES. While data sharing agreements prohibit ICES from making the data set publicly available, access may be granted to those who meet pre‐specified criteria for confidential access, available at www.ices.on.ca/DAS.