Ancient life and moving fluids

ABSTRACT

Over 3.7 billion years of Earth history, life has evolved complex adaptations to help navigate and interact with the fluid environment. Consequently, fluid dynamics has become a powerful tool for studying ancient fossils, providing insights into the palaeobiology and palaeoecology of extinct organisms from across the tree of life. In recent years, this approach has been extended to the Ediacara biota, an enigmatic assemblage of Neoproterozoic soft‐bodied organisms that represent the first major radiation of macroscopic eukaryotes. Reconstructing the ways in which Ediacaran organisms interacted with the fluids provides new insights into how these organisms fed, moved, and interacted within communities. Here, we provide an in‐depth review of fluid physics aimed at palaeobiologists, in which we dispel misconceptions related to the Reynolds number and associated flow conditions, and specify the governing equations of fluid dynamics. We then review recent advances in Ediacaran palaeobiology resulting from the application of computational fluid dynamics (CFD). We provide a worked example and account of best practice in CFD analyses of fossils, including the first large eddy simulation (LES) experiment performed on extinct organisms. Lastly, we identify key questions, barriers, and emerging techniques in fluid dynamics, which will not only allow us to understand the earliest animal ecosystems better, but will also help to develop new palaeobiological tools for studying ancient life.

I. INTRODUCTION

Since the beginning of life on Earth, organisms have evolved in environments characterized by moving fluids. Fluids have therefore been fundamental constraints throughout many key step‐changes in the history of life, including the emergence of coordinated behaviour (Drescher et al., 2011), the acquisition of multicellularity (Goldstein, 2015), and the evolution of locomotion in macroscopic aquatic organisms (Gazzola, Argentina, & Mahadevan, 2014). In modern oceans, eukaryotes have evolved morphologies and behaviours that take advantage of fluid motion to aid feeding, locomotion, inter‐ and intra‐specific community interactions, etc. (Rubenstein & Koehl, 1977; Chia, Buckland‐Nicks, & Young, 1984; Arkema, 2009; Full, 1997). Moreover, the fossil record preserves a large number of bizarre and unusual forms, which are hypothesized to have evolved as a means to mitigate, or take advantage of, the effects of fluid flow (Furbish & Arnold, 1997). Thus, understanding the ways in which organisms interacted with moving fluids can provide a fundamental window into evolutionary processes, but requires a knowledge base of the underlying fluid physics.

In recent years, this approach has become particularly important for reconstructing the palaeobiology and palaeoecology of the latest Neoproterozoic Ediacara biota [~571–539 million years ago (Ma)], which is an enigmatic group of soft‐bodied multicellular organisms that represents the first radiation of complex, eukaryotic macroscopic life (Xiao & Laflamme, 2009; Liu, Kenchington, & Mitchell, 2015; Darroch, Laflamme, & Wagner, 2018a). These organisms first appear in late Ediacaran sediments (~571–566 Ma) preserved around Mistaken Point, Newfoundland (Liu et al., 2015; Pu et al., 2016), become more diverse and widespread in younger and shallower‐water sediments (~558–550 Ma) from South Australia and the White Sea area of Russia (Martin et al., 2000; Droser et al., 2019), and persist right up until the Cambrian boundary ~539 Ma in both Namibia (Grotzinger et al., 1995; Narbonne, Saylor, & Grotzinger, 1997; Darroch et al., 2015; Linnemann et al., 2019) and southwestern USA (Smith et al., 2016, 2017). Following nearly 30 million years as the dominant component of benthic ecosystems, the Ediacara biota disappear at the base of the Cambrian in what some have suggested represents the first mass extinction of complex life (Amthor et al., 2003; Laflamme et al., 2013; Darroch et al., 2015, 2018a, 2018b; Muscente et al., 2018; Zhang et al., 2018). Reconstructing the palaeobiology, palaeoecology, and biological affinities of the Ediacara biota is thus key to understanding the origins of the modern marine biosphere (Darroch et al., 2018b ).

While some of the Ediacara biota likely represent metazoans (Fedonkin, Simonetta, & Ivantsov, 2007; Gold et al., 2015; Dunn, Liu, & Donoghue, 2017; Bobrovskiy et al., 2018), many members do not appear to share synapomorphies with extant metazoan clades (Budd & Jensen, 2000; Xiao & Laflamme, 2009; Darroch et al., 2018a ), and are characterized by bizarre body plans that hamper our ability to understand their relationships to extant eukaryotic groups (see Fig. 1). Despite these challenges, fluid physics studies have shed new light on the Ediacara biota, enabling rigorous tests of hypotheses for how these organisms moved and fed. These studies rely on physics‐based approaches using fluid mechanics (Schopf & Baumiller, 1998; Singer, Plotnick, & Laflamme, 2012), and increasingly employ complex numerical algorithms such as computational fluid dynamics (CFD) (Ghisalberti et al., 2014; Rahman et al., 2015a ; Darroch et al., 2017; Gibson et al., 2019a).

Fig 1.

Enigmatic fossils from the late Ediacaran: (A) Dickinsonia costata (N4853; White Sea area, Russia); (B) Tribrachidium heraldicum (N3993/5056; White Sea area, Russia); (C) Charniodiscus sp. (Mistaken Point, Canada); (D) Bradgatia sp. (Mistaken Point, Canada); (E) Kimberella quadrata (N4853/57; White Sea area, Russia); (F) Ernietta plateauensis (Karas Region, southern Namibia); (G) Archaeichnium (Karas Region, southern Namibia). All scale bars are 1 cm.

Here, we discuss important aspects of fluid physics that are fundamental to designing, conducting, and interpreting flume and CFD studies of fossil organisms. We provide an overview of fluid physics theory and address several misconceptions in the palaeontological and biological literature. We review advances in Ediacaran palaeobiology stemming from fluid mechanics approaches and present a case study of CFD applied to the sack‐like Ediacaran organism Ernietta plateauensis, outlining a rigorous experimental design that has not yet been adopted in palaeontological studies. Lastly, we discuss future directions in palaeobiological fluid mechanics studies focused on the Ediacaran, and identify tractable research questions that will help discern the role of these enigmatic organisms in the proliferation of animal ecosystems.

II. EDIACARAN PALAEOBIOLOGY AND PALAEOECOLOGY

Historically, the latest Ediacaran has been characterized as consisting of ecologically simple communities with a relatively low number of feeding modes and few mobile taxa (see ‘the Garden of Ediacara’; McMenamin, 1986), but more recent studies highlight increased behavioural and ecological complexity during this time. Behaviours, particularly feeding and movement, are crucial facets of Ediacaran ecosystems because they provide critical information on the grade of biological organization, the complexity of ecological interactions, levels of ecosystem engineering, and patterns of nutrient cycling. For example, the feeding traces left by Kimberella informed its reconstruction as a lophotrochozoan (Fedonkin & Waggoner, 1997; Butterfield, 2006). Other studies have demonstrated that some modern feeding ecologies were likely co‐opted from Proterozoic ones (Rothman, Hayes, & Summons, 2003; Sperling, Pisani, & Peterson, 2007; Sperling & Vinther, 2010), emphasizing that the roots of many Phanerozoic behaviours lie in the Precambrian (Peterson, McPeek, & Evans, 2005; Sperling & Vinther, 2010).

(1). Ediacaran feeding modes

The soft‐bodied Ediacara biota are characterized by a range of non‐analogue body plans, many of which have no parallels amongst extant animal groups (Erwin et al., 2011). Regardless of their phylogenetic affinities, the discovery of many fossilized Ediacaran organisms preserved in deep‐water sediments (in particular in Newfoundland and NW Canada; Wood et al., 2003; Narbonne et al., 2014; Liu et al., 2015) deposited far below the presumed photic zone, implies they were unlikely to have been photoautotrophic (or to have possessed photosynthetic symbionts; Clapham & Narbonne, 2002; Laflamme, Xiao, & Kowalewski, 2009). Few feeding appendages or internal digestive structures have been recognized in Ediacaran organisms (e.g. Fedonkin et al., 2007; Schiffbauer et al., 2020), although this may be in part due to taphonomic biases (see Wade, 1968; Norris, 1989; Liu et al., 2011; Gibson, Schiffbauer, & Darroch, 2018). Consequently, the mechanisms by which many Ediacaran groups fed remain unclear.

Until recently, the number of feeding modes inferred for members of the Ediacara biota was limited compared to the Cambrian, and was typically based on either morphological evidence, or the presence of trace and trace‐maker interactions. For example, Dickinsonia and Yorgia are thought to have fed via external digestion of microbial mats using their ventral sole (i.e. quasi‐saprophytically; see Sperling & Vinther, 2010), an inference supported by the discovery of fossils at the end of long chains of ‘resting traces’, which presumably mark previous sites of feeding (Ivantsov & Malakhovskaya, 2002; Gehling, Droser, & Runnegar, 2005; Ivantsov, 2011; Evans, Gehling, & Droser, 2019a). The frequent association between Kimberella and radially arranged scratch marks (‘Kimberichnus’) indicates that this taxon fed via grazing of microbial mats (Fedonkin et al., 2007; Gehling, Runnegar, & Droser, 2014; Ivantsov, Nagovitsyn, & Zakrevskaya, 2019). Likewise, a spatial association between the bilaterian trace fossil Helminthoidichnites and putative carcasses has been taken as evidence for scavenging (Gehling & Droser, 2018). Lastly, osmotrophy was originally suggested for rangeomorph taxa (on the basis of their ‘fractal’ architecture, which maximized surface area‐to‐volume ratios; Laflamme & Narbonne, 2008). Other feeding modes, such as chemoautotrophy (McMenamin & McMenamin, 1990; Dufour & McIlroy, 2017) and suspension feeding (Clapham, Narbonne, & Gehling, 2003; Wood & Curtis, 2014) have been suggested, but direct fossil evidence for these behaviours is lacking.

(2). Ediacaran mobility

Ediacaran mobility has traditionally been inferred based on the trace fossil record, from either sediment traces or preserved microbial mat disturbances (Seilacher, 1989; Fedonkin & Waggoner, 1997; Ivantsov & Malakhovskaya, 2002; Jensen, 2003; Gehling et al., 2005). While originally regarded as overwhelmingly sessile (McMenamin, 1986), Ediacaran benthic ecosystems are now thought to have been more dynamic than stated previously (Gehling & Droser, 2009; Darroch et al., 2017; Droser, Tarhan, & Gehling, 2017; Evans et al., 2018; Tarhan et al., 2018; Droser et al., 2019). Evidence for Ediacaran locomotion has been reported as far back as the Avalonian biota from Mistaken Point (Liu, Mcilroy, & Brasier, 2010), with abundant evidence of resting, movement, and grazing traces in younger White Sea material from Russia and South Australia. Iconic Dickinsonia (Fig. 1A) and Yorgia resting and movement traces are common, with some slabs preserving both trace and body fossils (see Ivantsov & Malakhovskaya, 2002; Gehling et al., 2005; Ivantsov, 2011; Evans et al., 2019a ). Ichnological and body fossil evidence, including some body fossils with associated trace fossils, strongly suggests that Kimberella was capable of movement (Fedonkin et al., 2007; Gehling et al., 2014; Ivantsov et al., 2019). In South Australia, abundant Parvancorina specimens are preserved on bedding surfaces in a common orientation, which is unlikely to be the result of passive current alignment, indicating that these organisms possessed the ability to reorient themselves with respect to flow (Paterson et al., 2017). Most recently, the trilobate bilaterian Yilingia was reported from China, with body fossils described in direct association with traces (Chen et al., 2019). While the trace fossil record has allowed us to show definitively that at least six Ediacara taxa were mobile, the Ediacaran fossil record is still characterized by the unusual nature of the Ediacaran substrate (i.e. widespread and thick microbial mats) and unusual body fossil taphonomy (Sappenfield, Droser, & Gehling, 2011). This has led to reinterpretations of several Ediacaran body and trace fossils (Droser, Gehling, & Jensen, 2005; Jensen, Droser, & Gehling, 2006). In this context, alternative methods for determining potential mobility will be useful.

Direct evidence of Ediacaran feeding and mobility are preserved in the fossil record (Fedonkin et al., 2007; Gehling et al., 2014; Chen et al., 2019), but new approaches to address Ediacaran behaviour and associated biomechanics could provide additional insights. The fidelity of preservation in these deposits enables us to understand key biomechanical controls on behaviours like locomotion, such as tissue rigidity (see e.g. Evans, Droser, & Gehling, 2015; Evans et al., 2019b ). Taking these approaches one step further, we can use physics‐based models to fill in information gaps in the fossil record. Fluid mechanics and other modelling techniques provide unique opportunities for understanding how organisms lived and behaved in their environments, beyond what can be observed from the fossil record alone.

III. COMPUTATIONAL FLUID DYNAMICS AS A METHOD

Palaeontologists interested in extinct organisms and fluid flows frequently look to Vogel (1996), which has been foundational in our understanding of fluid–life interactions. While Vogel's simplified approach to fluid problems laid the foundation for tackling (palaeo)biological fluid experiments, fluid motions and interactions with life are far more complicated than what is offered there and elsewhere. To investigate questions of interest rigorously using tools like CFD, we recognize that we cannot simply take a plug‐and‐play approach with fluid modelling software due to the risk of obtaining unrealistic and incorrect results, analogous to conducting statistical analyses without understanding the probabilistic basis of statistics. For this reason, we provide an overview of key physical and mathematical concepts used to describe fluid motions. Our intent is to offer a sense of the complexities of fluid flow systems that are valuable for palaeontological CFD studies, and to correct misunderstandings presented in the literature. However, we emphasize that this section does not provide a sufficient background for conducting CFD analyses, and those lacking a formal training in fluid mechanics will benefit from close collaboration with experts in fluid mechanics. We also recognize that some readers may benefit from practical examples before returning to the underlying theory. It is therefore entirely reasonable either to read this section or Section IV first, while recognizing that the fundamentals of the key turbulence discussions presented in Section IV are provided here.

(1). Basic elements

We normally consider ordinary fluids, including water, to be continuous substances. However, when viewed at the molecular scale, fluids are comprised of discrete particles (molecules). Following Furbish (1997; and references therein), at ordinary pressures and temperatures, there are about 3 × 10²² molecules in 1 cm³ of water. The mean free path λ of liquid water molecules is on the order of 10⁻¹⁰ m. Average molecular speeds between collisions are on the order of hundreds of meters per second. Let L denote a characteristic length scale, which is defined by the resolution scale at which we observe the fluid, the size of a flow domain (e.g. the size of a particle within the fluid or the diameter of a flow conduit), or the size of a computational grid cell. We then define the Knudsen number (Knudsen, 1909) as Kn = λ/L. When Kn << 1, it is permissible to define ‘local’ thermodynamic quantities such as the fluid mass density ρ, the temperature T, and the pressure p. Kinetic theory also yields the dynamic viscosity μ, and we may additionally define the local fluid velocity – effectively the average molecular velocity at the characteristic length scale L. We can view these quantities as smoothly varying functions of space and time, and in so doing the fluid is considered a continuum, which permits us to use differential calculus in describing these quantities and the fluid continuum behaviour without focusing on individual fluid particles. Under continuum conditions, fluid velocities are zero at solid boundaries, providing the ‘no‐slip’ condition. However, for Kn ≥ 0.01, the continuum assumption is not necessarily satisfied. Slip conditions can occur at solid boundaries and describing the behaviour of the fluid therefore requires kinetic theory or methods of statistical mechanics.

When fluid viscous (frictional) forces are large relative to other forces, fluid motion is laminar, meaning the streamlines are quasi‐parallel as they converge and diverge in the vicinity of an irregular object (e.g. an organism) within the flow. When inertial forces (see Section III.2.a) are large relative to viscous forces, the flow becomes unstable, leading to the onset of turbulent motions, with streamlines unsteady and complex across spatial and temporal scales (Fig. 2). In this context, it is useful to describe flows in terms of the dimensionless Reynolds number Re (Reynolds, 1883), conventionally defined as

$$\mathit{Re}=\frac{\mathit{\rho UL}}{\mu }=\frac{\mathit{UL}}{\nu },$$ (1)

where U is a characteristic fluid velocity, L is a characteristic length, μ is the dynamic viscosity of the fluid, and ν = μ/ρ is the kinematic viscosity (a molecular momentum diffusivity; see below). The Reynolds number can be interpreted in several ways. Often, it is described as the ratio of inertial to viscous forces, although this importantly does not imply that this ratio is fixed at all locations within a flow. Rather, under this description the Reynolds number represents a characteristic ratio of these forces in defining the dynamic similarity, or dissimilarity, of flow systems (see below). Here, it is important to distinguish between a systems‐scale Reynolds number Re _s and a particle Reynolds number Re _p. For example, for flow through a conduit (Fig. 3), U is normally selected to be the magnitude of the average velocity and L the conduit diameter, yielding a system‐scale value of Re _s. With flow around a particle (Fig. 4), U is the magnitude of the relative velocity between the particle and surrounding fluid outside the boundary layer (i.e. the far‐field velocity) and L is the radius or diameter of the particle, yielding a particle Reynolds number Re _p. Moreover, for a specified flow system, there is no prescribed value of Re indicating the onset of turbulence, which can vary within an individual system depending on initial and boundary conditions, and varies between geometrically dissimilar systems. Expanding on the latter point, objects are geometrically similar if they are scaled versions of each other. Steady fluid motions around spheres of different sizes are geometrically similar if the streamlines are geometrically similar. The same holds for cubes, which additionally require that the orientation relative to the mean motion is identical. Two flows are dynamically similar if the Reynolds number is the same for geometrically similar systems. Importantly, this means that the Reynolds numbers for geometrically dissimilar objects are not comparable; identical Reynolds numbers in dissimilar systems does not imply the systems behave the same mechanically. Thus, the meaning and significance of Re = 1 for flow around a brachiopod has little to do with Re = 1 for flow around a crinoid. Similarly, a given Reynolds number for two identical objects, one within a free stream and one next to a solid boundary, does not involve dynamic similitude and therefore does not imply that the systems behave the same mechanically.

Fig 2.

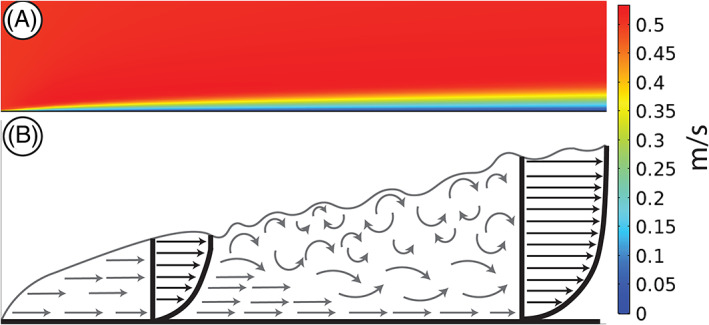
Development of the turbulent boundary layer. (A) Direct numerical simulation (DNS) solution. (B) Theoretical development modified from COMSOL.com and Furbish (1997). Grey arrows represent instantaneous velocities of the boundary layer. Black arrows and profiles represent time‐averaged velocities. Boundary layer is initially fully laminar until it separates into the viscous sublayer (straight grey arrows) and the turbulent boundary layer (curved grey arrows).

Fig 3.

Stationary analytical solution of laminar flow through a conduit from left to right with an inlet velocity of 0.05 m/s. Black line represents velocity profile and arrows indicate flow direction.

Fig 4.

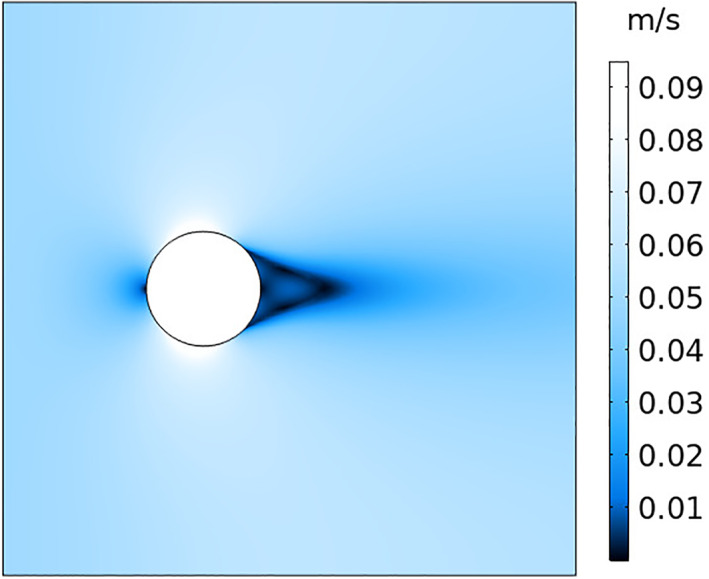
k−ω Reynolds‐averaged Navier–Stokes (RANS) simulation of flow around a sphere from left to right with an inlet velocity of 0.5 m/s.

Of particular interest is the drag force F _D that fluid motion exerts on an organism. This drag force is equal to the integral of the pressure and the viscous stress acting on the surface of the object, measured in a direction parallel to the mean relative motion. As described by Newton's first law, the object exerts a force on the fluid that is equal in magnitude to the drag force. Dimensional analysis leads to the conclusion that the drag force can be expressed in terms of a dimensionless coefficient of drag (see e.g. Schlichting & Gersten, 2000), defined as

$$C_D=\frac{F_D}{\frac{1}{2}\rho U^{2}A}.$$ (2)

Here, U is a characteristic flow velocity, normally defined by the relative velocity between the object and surrounding far‐field velocity, or by a well‐defined approach velocity for an object attached to a solid boundary. The quantity A is a characteristic area such as the frontal area (silhouette) of the object normal to the mean fluid flow or, more simply, an area defined by the square of the characteristic length of the object. The quantity (1/2)ρU ² defines a characteristic dynamic pressure acting on the object.

Theory and experiments [see e.g. Furbish, 1997 and references therein] indicate that for laminar flows at small Reynolds number, the coefficient C _D varies inversely with Re, as C _D = C/Re for geometrically similar objects (where the constant C varies with object shape). Following a transition over intermediate Reynolds numbers, the coefficient of drag becomes approximately constant at large Re with fully developed turbulence, although this represents an average value (C _D fluctuates with turbulence). Moreover, like the Reynolds number, the coefficients of drag for two identical objects, one within the free stream and one next to a solid boundary, are not the same.

Organisms suspended within a fluid may move passively with the fluid motion or, if sufficiently massive, detach inertially from the fluid motion during acceleration of the fluid. The fluid–particle coupling can be characterized by the dimensionless Stokes number (Stokes, 1851), defined as

$$\mathit{St}=\frac{\mathit{U\tau }}{L},$$ (3)

where U is the fluid velocity surrounding the particle (organism), L is the characteristic length (e.g. diameter) of the particle, and τ is the relaxation time of the particle due to drag. If flow surrounding the particle is laminar (small Re), then the relaxation time is τ = ρ _p L ² /Cμ, where ρ _p is the density of the particle and C is a constant (equal to 18 for spherical particles). For St >> 1, particles behave as passive tracers, closely following streamlines. For St ≪ 1, particles detach inertially from the fluid motion during fluid accelerations and tend to continue their initial trajectories. The relaxation time τ must be modified when the particle Reynolds number is large.

Of interest is the relative contribution of advection and diffusion to the transport of a dissolved substance, notably in relation to delivery of nutrients to an organism or removal of waste products released by an organism. Starting with the advection–diffusion equation, dimensional analysis leads to the conclusion that this relative contribution can be characterized by the dimensionless compositional Péclet number Pe (e.g. Batchelor, 1973), defined as

$$\mathit{Pe}=\frac{\mathit{UL}}{\kappa },$$ (4)

where κ is the molecular diffusivity of the substance within the fluid. As with the Reynolds number, U is a characteristic relative velocity. The characteristic length L is the thickness of the compositional boundary layer, normally approximated by the characteristic particle size. A suspended particle passively moving with the fluid (St ≪ 1) does not ‘see’ advection toward or away from it so that Pe ≪ 1. Conversely, the small diffusivities of common ions in water mean that small relative velocities U yield large Pe. Advective transport is far more effective than diffusive transport in delivering dissolved nutrients or removing waste products.

Returning to the Reynolds number Re given in Equation (1), note that the kinematic viscosity is in fact a diffusivity (see e.g. Furbish, 1997). Thus, the Reynolds number is also a momentum Péclet number. It can be interpreted as the rate of advection of momentum at the macroscopic (continuum) scale to diffusion of momentum at the molecular scale. While there are numerous other quantities and dimensionless numbers frequently cited in the fluid mechanics literature, the quantities described above will be of greatest relevance for most palaeontologists and evolutionary biologists.

(2). Equations of motion

(a). Navier–Stokes equations

Newton's second law for the motion of ordinary Newtonian fluids is expressed by the Navier–Stokes equations (e.g. Batchelor, 1973), also referred to as the momentum equations. Letting u = i u ₁ + j u ₂ + k u ₃ denote the local (continuum) fluid velocity, with components u ₁, u ₂ and u ₃ parallel to the Cartesian x ₁, x ₂ and x ₃ coordinate axes (Fig. 5), then using Einstein notation and neglecting the gravitational force for simplicity, the Navier–Stokes equations for an incompressible flow are

$$u_j\frac{\partial u_i}{\partial x_j}+\frac{\partial u_i}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\upsilon \frac{\partial }{\partial x_j}\left(\frac{\partial u_i}{\partial x_j}\right),$$ (5)

where t denotes time, p is pressure, and ν = μ/ρ is the kinematic viscosity of the fluid, where μ is the dynamic viscosity and ρ is the fluid density. In this compact form, Equation (5) represents three component equations with four unknowns (u ₁, u ₂, u ₃ and p). These are therefore supplemented with the continuity equation for an incompressible flow, namely,

$$\frac{\partial u_i}{\partial x_i}=0.$$ (6)

If thermal or compositional buoyancy effects are involved, then Equation (5) and Equation (6) must be further supplemented with the thermal energy equation, the compositional advection–diffusion equation, or both.

Fig 5.

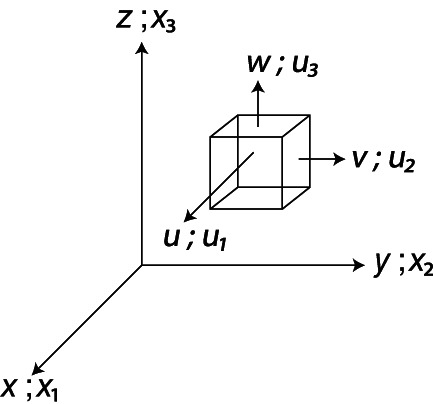
Three‐dimensional coordinate system with box showing directions of movement for individual velocity components, where u, v and w are u ₁, u ₂ and u ₃, respectively, for movement in the directions of x, y, and z, respectively.

The three terms represented by ∂u _i /∂t are referred to as local accelerations. The nine terms represented by u _j ∂u _i /∂x _j are convective accelerations. These non‐linear terms are the source of the instabilities in fluid motions that give rise to turbulence (see e.g. Batchelor, 1973; Furbish, 1997). The three terms involving p are pressure stems that induce flow together with the unwritten gravitational terms. The nine terms involving ν are the viscous terms. These linear terms represent viscous friction, which tends to stabilize fluid motions. At sufficiently low Reynolds number Re, the viscous terms are much larger than the convective terms, and Equation (5) reduces to a diffusion equation with a source term due to pressure.

For simple, often idealized, flow configurations, simplified versions of Equation (5) and Equation (6) can be solved analytically (see e.g. Blazek, 2001). For realistic flow configurations, notably involving flow around objects or over irregular surfaces, numerical treatments of these equations are required. As described below, all fluid simulations involve solving Equation (5) and Equation (6) or modified forms of these equations for specified initial and boundary conditions. Because solving these equations at each numerical grid point in the flow field at all times is computationally challenging, different numerical schemes are used. These include finite element method (FEM) and finite volume method (FVM) procedures, for which an in‐depth treatment is beyond the scope of this review. Historically, FVM procedures have been favoured for integrating these equations across the flow field. Blazek (2001) and Jeong & Seong (2014) provide a comprehensive treatment of FEM and FVM.

(b). Reynolds‐averaged Navier–Stokes equations

Osborne Reynolds provided two of the most important contributions to the field of fluid mechanics in his systematic description of turbulent flows leading to what is now referred to as the Reynolds number (Reynolds, 1883), Equation (1) (see above), and in formulating a scheme for averaging the Navier–Stokes equations (e.g. Reynolds, 1895). His descriptions came from experiments in which he introduced small jets of dyed water into the centre of a large, glass conduit of flowing water. At low flow velocities, the dye remained visible as a coherent streak for the entire length of the conduit, but at higher velocities the dye became mixed throughout the cross section of the conduit. This represented a transition from laminar to turbulent flow. He spent approximately 20 years developing and publishing the framework for understanding fluctuating motions of turbulence at large Reynolds numbers, which is presented below.

Letting x = (x ₁,x ₂,x ₃), we start by writing the three velocity components and the pressure as.

$$u_i\left(\mathbf{x},t\right)=\overline{u_i}\left(\mathbf{x}\right)+u_i^{\prime }\left(\mathbf{x},t\right)\text{and}p\left(\mathbf{x},t\right)=\overline{p}\left(\mathbf{x}\right)+p^{\prime }\left(\mathbf{x},t\right),$$ (7)

where the overline represents an average and the prime denotes a fluctuation about the average. Moreover, we assume that the averages can vary with position x but not time t, that is, the velocity signal is stationary. By definition, the averages of the fluctuations are zero, namely, $\overline{u_i^{\prime }}=0$ and $\overline{p^{\prime }}=0$. The averages in Equation (7) are formally ensemble averages as defined by Gibbs (1902). Namely, we are to imagine a great number (an ensemble) of nominally identical but independent systems, each evolving in time according to the laws of physics. An ensemble average at any geometrically similar position x within the member systems is then taken as the average over the ensemble of systems at any instant. If behaviour is strictly ergodic, then the ensemble average is identical to a time average defined as

$$\overline{u_i}\left(\mathbf{x}\right)=\underset{T_s\to \infty }{\lim }\frac{1}{T_s}{\int }_{t_0}^{t_0+T_s}{u}_i\left(\mathbf{x},t\right)\mathrm{d}t,$$ (8)

for arbitrary starting time t ₀. In practice, the sampling interval T _s is finite and we assume that the average is satisfactorily estimated as

$$\overline{u_i}\left(\mathbf{x}\right)=\frac{1}{T_s}{\int }_{t_0}^{t_0+T_s}{u}_i\left(\mathbf{x},t\right)\mathrm{d}t,$$ (9)

for a sufficiently large interval T _s. If the continuous time series u _i(x,t) is discretely sampled, then Equation (9) is replaced with the ordinary arithmetic average. Other similar averaging, including spatial averaging, can be applied to certain flow conditions, including nominally homogeneous turbulence and slowly varying (non‐stationary) conditions.

Upon taking averages of Equations (5) and Equation (6), the continuity equation becomes

$$\frac{\partial \overline{u_i}}{\partial x_i}=0,$$ (10)

yielding the additional result that ∂u' _i /∂x _i = 0 with $\overline{u_i^{\prime }}=0$ by the definition of averaging. In turn, and again neglecting gravity, the Reynolds‐averaged Navier–Stokes equations (e.g. Batchelor, 1973) are

$$\rho \left(\overline{u_j}\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_i}}{\partial t}\right)=-\frac{\partial \overline{p}}{\partial x_j}+\frac{\partial }{\partial x_j}\left(\mu \frac{\partial \overline{u_i}}{\partial x_j}-\rho \overline{u_i^{\prime }{u}_j^{\prime }}\right).$$ (11)

This has the same form as Equation (5), but with the addition of the nine terms defined by $\mathrm{\rho }\overline{u_i^{\prime }{u}_j^{\prime .}}$,

which are the Reynolds stresses. Specifically, these define the Reynolds stress tensor (Reynolds,

$${\tau }_{\mathit{ij}}^R=-\rho \overline{u_i^{\prime }{u}_j^{\prime }}=-\rho \left[\begin{array}{ccc}\overline{u_1^{\prime 2}}& \overline{u_1^{\prime }{u}_2^{\prime }}& \overline{u_1^{\prime }{u}_3^{\prime }}\\ \overline{u_2^{\prime }{u}_1^{\prime }}& \overline{u_2^{\prime 2}}& \overline{u_2^{\prime }{u}_3^{\prime }}\\ \overline{u_3^{\prime }{u}_1^{\prime }}& \overline{u_3^{\prime }{u}_2^{\prime }}& \overline{u_3^{\prime 2}}\end{array}\right].$$ (12)

Each element $\mathrm{\rho }\overline{u_i^{\prime }{u}_j^{\prime }}$ in Equation (12) represents a momentum flux associated with fluctuating motions. For example, the product $\rho u_1^{\prime }{u}_3^{\prime }$ may be interpreted as an instantaneous flux of momentum $\rho u_1^{\prime }$ per unit volume associated with the x ₁ direction at the rate $u_3^{\prime }$ in the transverse direction x ₃. Then $\mathrm{\rho }\overline{u_1^{\prime }{u}_3^{\prime }}$ is the averaged momentum flux, and the negative sign in Equation (12) makes this a stress resisting the mean motion parallel to x ₁. These stresses dominate the resistance to motion in fully turbulent flows, except within the viscous sublayer next to a solid boundary (Prandtl, 1905).

(c). Turbulence closures

Solving the Reynolds‐averaged equations requires expressing the elements of the Reynolds stress tensor in terms of other averaged quantities (Reynolds, 1895). A particularly important early effort on this closure problem was that of Boussinesq (1877, 1896), who assumed that momentum transfers associated with turbulence fluctuations are dominated by mixing of the largest eddies. In analogy with Stokes's theorem for the viscous stresses in laminar flows, he further assumed that the Reynolds stresses can be expressed in terms of the mean rate of strain. The Boussinesq hypothesis (1877) is thus expressed as

$${\tau }_{\mathit{ij}}^R=-\rho \overline{u_i^{\prime }{u}_j^{\prime }}=\rho {\nu }_t\left(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i}\right)-\frac{2}{3}\mathit{\rho k}{\delta }_{\mathit{ij}}.$$ (13)

Here, ν _t denotes an eddy viscosity that is a function of local flow conditions and position rather than being a characteristic of the fluid (as is the molecular viscosity), δ _ij denotes the Kronecker delta function, and k denotes the turbulence kinetic energy formed from the sum of the covariances in the principal diagonal of Equation (12), namely,

$$k=\frac{1}{2}\overline{u_i^{\prime }{u}_i^{\prime }}=\frac{1}{2}\left[\overline{u_1^{\prime 2}}+\overline{u_2^{\prime 2}}+\overline{u_3^{\prime 2}}\right].$$ (14)

This closure means that the momentum equations must be supplemented with the mechanical energy equations to obtain the kinetic energy k. Note also that Equation (13) sometimes is written more compactly as

$${\tau }_{\mathit{ij}}^R=-\rho \overline{u_i^{\prime }{u}_j^{\prime }}=\rho {\nu }_t\overline{S_{\mathit{ij}}}-\frac{2}{3}\mathit{\rho k}{\delta }_{\mathit{ij}}.$$ (15)

Here, S _ij denotes the Reynolds‐averaged strain‐rate tensor, the elements of which are represented by the parenthetical part of Equation (12). This turbulence closure remains relevant in numerical modelling for Reynolds‐averaged Navier–Stokes models (Reynolds, 1895), such as k − ε and k − ω (see Section III.3).

For the specific situation of a uniform, turbulent boundary‐layer shear flow that is steady in the mean, a particularly important turbulence closure is provided by Prandtl's mixing length hypothesis (Prandtl, 1905). In analogy with kinetic theory, Prandtl assumed that boundary‐normal motions of fluid parcels (eddying motions) momentarily retain their streamwise momentum during transverse motions, thus inducing the velocity fluctuations in the boundary‐parallel Reynolds stress. With vertical axis x ₃ = z normal to the streamwise velocity u ₁ = u in the x ₁ = x direction, he proposed that the eddy viscosity (or eddy diffusivity) can be approximated as

$${\mathrm{\nu }}_t=l^2\left|\frac{\mathrm{d}\overline{u}}{\mathrm{d}z}\right|,$$ (16)

where l denotes the mixing length, a measure of the transverse distance of eddying motion, which Prandtl assumed to increase linearly above the boundary. Prandtl's (1905) development (1905) leads to the well‐known logarithmic velocity law (or ‘law of the wall’) describing the averaged streamwise velocity $\overline{u}\left(z\right)$ above the solid boundary, namely,

$$\overline{u}\left(z\right)=\frac{u_{*}}{\mathrm{\kappa }}\ln \left(\frac{z}{z_0}\right).$$ (17)

Here, u_* = $\sqrt{{\tau }_0/\rho }$ is the friction (or shear) velocity where τ ₀ is the fluid stress at the boundary, κ ≈ 0.41 is the von Kármán constant, and z ₀ is the roughness length at which u goes to zero. For hydrodynamically smooth conditions, the length z ₀ is on the order of the thickness of the viscous sublayer and scales with ν/ u_*. For hydrodynamically rough conditions, this length scales with the height of the roughness (e.g. sand grains). The logarithmic velocity law, Equation (17), stands as one of the most important results in the field of fluid mechanics. As described below, this result is an important if not essential benchmark for numerical simulations of flow next to a solid boundary.

Before turning to the topic of numerical modelling, we end this section with an important point. Consider a flow field for which solutions of the Reynolds‐averaged velocity field $\overline{u_i}\left(\mathbf{x},t\right)$ and the pressure field $\overline{p}(\mathbf{x}$,t) are obtained either analytically or numerically. Recall that these formally involve ensemble averaging, or, assuming ergodic behaviour, that time averaging suffices. For illustration, let us then recall Prandtl's mixing‐length hypothesis concerning fluctuating motions (Prandtl, 1905), leading to the logarithmic velocity law for uniform flow that is steady in the mean. At this juncture, we have replaced the continuum description of fluid motion with a new scheme, in which the velocity field described by the logarithmic law does not exist in a physical sense at any instant anywhere in the flow. It is a mathematical abstraction – a continuously differentiable function describing the ensemble expected (average) velocity state. Although this law emerges from a description of fluctuating motions, it contains by itself no information regarding fluctuating motions. More generally, the Reynolds‐averaged Navier–Stokes equations describe an imaginary fluid‐like motion in which the velocity field represents statistically expected conditions, not actual conditions occurring in the continuum prototype. This point is an important guide for choosing the correct numerical modelling approach. Specifically, we may choose to use such a time‐averaged approach when addressing a problem for which we only need to understand a system's basic flow patterns, or more specifically situations where we are less interested in details such as localized fluxes or force fluctuations.

(3). Numerical Reynolds‐averaged Navier–Stokes (RANS) models

While there are several turbulence models, we focus on a subset that are most widely used in and applicable to palaeontological studies. Unlike the previous section, we do not discuss in depth the underlying closures for these models, but we urge the reader to consult relevant literature (such as Blazek, 2001). For a more detailed comparison of turbulence models and their underlying mechanics, Bardina, Huang, & Coakley (1997) is an excellent resource.

In Equation (15), ν _t denotes the eddy viscosity, which is a function of local flow conditions and not a physical characteristic of the fluid (which the molecular dynamic viscosity is). Importantly, ν _t retains memory in that it is affected by the local history of flow. Once we know ν _t, the Navier–Stokes equations can be used to address fluid flow questions using averaged flow variables. Implementing the eddy‐viscosity approach, the dynamic viscosity μ in the viscous stress tensor embedded within the Navier–Stokes equations is replaced with individual components for laminar and turbulent flows, such that μ = μ _L + ν _t. Once the eddy viscosity ν _t is calculated, we can add it to the laminar viscosity and incorporate it into the averaged flow variables from before to simulate turbulent flow.

(a). k–ε model

The k–ε family of models (Jones & Launder, 1972; Launder & Sharma, 1974) is widely used in engineering and palaeontological CFD studies. These two‐equation eddy viscosity models rely on the turbulent kinetic energy k described previously and the turbulent dissipation rate ε. Because many of these models often require a dampening function to calculate correctly through the viscous sublayer, those with this function are frequently referred to as low Reynolds number models. Often these models have turbulence equations with stiff source terms requiring high grid resolution near walls to model the viscous sublayer accurately. To make this process more computationally feasible, many programs employ time‐stepping schemes. Initialization of these models can require significant effort, but two possible approaches are to: (i) use freestream values for k and ε, or (ii) prescribe profiles for these values near the walls. Depending on the implementation, some software suites may discretize the domain without an increased mesh resolution near the walls, as they do not resolve these cells analytically (e.g. OpenFOAM; p. U‐40).

(b). k–ω model

The k–ω model (Wilcox, 1988, 1993) works by solving for the turbulent kinetic energy k and the dissipation per unit turbulent kinetic energy ω (i.e. a rate). It was developed because many of the convergence issues with k–ε models were due to the modelling of the turbulent dissipation rate ε. Particularly near walls, the ε equation is less accurate and difficult to solve due to local extrema.

(c). SST model

The k–ω shear stress transport turbulence (SST) model (Menter, 1994; Menter & Rumsey, 1994) combines a high Reynolds number version of the k–ε model with a k–ω model (Wilcox, 1988, 1993), providing the benefits of both models. Under the SST model, the k–ω model is applied to sublayers near any walls because it does not require a dampening function. Further up in the logarithmic velocity profile near the walls, the k–ω model is also exploited to avoid the numerical issues associated with the k– ε model that result from adverse pressure flows. The k–ε model is then heavily relied upon in the downstream turbulent wakes, where the k–ω model is often too sensitive to the freestream ω values. The SST turbulence model also has a modified turbulent eddy‐viscosity function to improve performance in flows characterized by strong pressure gradients or pressure‐induced boundary separation.

(4). Numerical turbulence models

(a). Direct numerical simulations

Direct numerical simulations (DNS) are numerically complex models that compute the entire range of turbulent length scales at all locations, potentially down to the Komolgorov microscales where turbulent kinetic energy is dissipated into heat; these approaches can therefore overcome the limitations of RANS simulations by solving all the governing equations without using simplified, averaged quantities (Orszag, 1970). However, they are extremely computationally intensive and have never been used in palaeontological studies to date. While such accuracy is desirable, even with cluster computing the computational requirements often limit the applicability of these models for most experiments.

(b). Large eddy simulations

Between the two end‐members of RANS and DNS, another family of models exists that solves turbulent scales above the Komolgorov scale. Large eddy simulation (LES) models (Smagorinsky, 1963) employ a time and/or spatial convolution

$$\overline{\mathrm{\varphi }\left(x,t\right)}={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\mathrm{\varphi }\left(r,t\right)G\left(x-r,t-\mathrm{\tau }\right)\mathrm{d\tau }\mathrm{d}r,$$ (18)

where $\overline{\varphi \left(\mathrm{x},t\right)}$ is the filtered field, G is the convolution kernel that has associated length and time cutoff scales, and r and τ are length and time quantities, respectively. When applied to the incompressible flow Navier–Stokes equations, the LES governing equations become the filtered incompressible continuity equation

$$\frac{\partial \overline{u_i}}{\partial x_i}=0$$ (19)

and the filtered Navier–Stokes equations

$$\frac{\partial \overline{u_i}}{\partial t}+\frac{\partial }{\partial x_j}\left(\overline{u_i{u}_j}\right)=-\frac{1}{\mathrm{\rho }}\frac{\partial \overline{p}}{\partial x_i}+\mathrm{\nu }\frac{\partial }{\partial x_j}\left(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i}\right)=-\frac{1}{\mathrm{\rho }}\frac{\partial \overline{p}}{\partial x_i}+2\mathrm{\nu }\frac{\partial }{\partial x_j}{S}_{\mathit{ij}}.$$ (20)

Through the use of substitution and some algebra, the governing LES equations then become

$$\frac{\partial \overline{u_i}}{\partial t}+\overline{u_j}\frac{\partial \overline{u_i}}{\partial x_j}=-\frac{1}{\mathrm{\rho }}\frac{\partial \overline{p}}{\partial x_i}+\mathrm{\nu }\frac{{\partial }^2\overline{u_i}}{\partial x_j\partial x_j}-\frac{\partial {\mathrm{\tau }}_{\mathit{ij}}}{\partial x_j}.$$ (21)

In these equations, the overbars no longer represent time or ensemble averages, but instead represent spatially filtered quantities. While LES resolves vector fields to much finer scales than RANS, there are still unresolved scales that can be broken into resolved sub‐filter scales and sub‐grid scales. The resolved sub‐filter scales are those with wave numbers above a specified cutoff k _c, which are thus dampened by the filter. Sub‐grid scales are all the scales smaller than the cutoff spatial filter of width ∆. These are solved for using a variety of methods each specific to the individual LES model that is being used, such as the eddy‐viscosity models, the Smagorinsky classic model (Smagorinsky, 1963), or the Germano dynamic models (Germano et al., 1991). While RANS are the most widely used turbulence models in palaeontological studies thus far, LES represents an excellent opportunity for more accurate modelling of the turbulent flows in which many organisms typically live, and can be used to examine fluctuations and force impulses that the fluid imparts on a structure or organism (Furbish & Parker, 1992). LESs were originally exploited for meteorological studies in the 1960s (Smagorinsky, 1963), but have been increasingly adapted for a range of fluid flow studies (Wu et al., 1998; Cook, 1999). In engineering, they are often employed when RANS solutions are unacceptable due to solution failure, or in cases where the mean flow frequencies are of the same order of magnitude as their associated fluctuations. The greatest obstacle to these studies has been the required computational capabilities. These arise for several reasons. LES models are time‐dependent three‐dimensional (3D) solutions to the governing Navier–Stokes equations, and they thus require high‐resolution grids in both the streamwise and cross‐sectional directions of flow. While the increased computational requirements have been a drawback, the increased accuracy in modelling turbulence over a range of spatial scales sets this method apart from RANS models. Furthermore, improvements in workstation capabilities and easier access to cluster computing has made these approaches more feasible. See Piomelli (1998b ) for a current overview of LESs, while Ferziger (1998), Piomelli (1998a ), and Mossi (1999) provide in‐depth treatments of these models.

IV. FLUID DYNAMICS AND THE EDIACARA BIOTA

(1). Case studies

(a). Physical experiments

The earliest studies of the hydrodynamics of Ediacaran organisms were conducted using physical flume tanks. Schopf & Baumiller (1998) used recirculating flow tanks to analyse the effects of tissue density on the stability of Dickinsonia. Their results provided the first quantitative constraints on the plausible range of tissue densities required to permit Dickinsonia to remain stable on the seafloor. Singer et al. (2012) used a similar approach to test between hypothesized methods for feeding in frondose taxa, in particular how the leaf‐like morphology and hypothesized tissue rigidity affected macroscopic flow around the organism, and how fine‐scale flow over the frond surface differed between two species of Charniodiscus. The authors demonstrated that more textured frond surfaces lowered drag while increasing entrainment, and also that models oscillated in flow – potentially increasing gas and/or nutrient exchange in the living organisms. Although they tackled very different questions, these two studies illustrate the beginnings of a new research avenue in Ediacaran palaeobiology focused on mechanics and functional morphology, using the characteristics of fluid flow as a means for hypothesis testing. It is also worth noting that the three aspects of fluid and organism mechanics investigated in these studies – drag force calculations, tissue properties (i.e. rigidity and density), and fluid flow patterns around organisms – have been repeatedly targeted in subsequent studies, and thus have had a disproportionate influence on the field. Other properties such as the individual velocity components (u, v, w), turbulent kinetic energy magnitude k, viscous stresses, and spatial distribution of pressure magnitudes may be equally or more important for a given question.

(b). Computational fluid dynamics

While the bizarre body plans of Ediacaran organisms have proved contentious among palaeontologists, fluid mechanics offers an opportunity to obtain palaeobiological information about individual organisms while remaining agnostic about their phylogenetic position. This information can then be used in a careful, targeted fashion to inform understanding of evolutionary history (see Rahman et al., 2015b ). Laflamme & Narbonne (2008) and Laflamme et al. (2009) proposed that some Ediacaran groups could have used their high surface area‐to‐volume (SA/V) ratios to feed via direct osmosis (osmotrophy). Among modern organisms, only a small number of forms rely solely on osmotrophy for obtaining nutrients (e.g. megasulfur bacteria; Schulz et al., 1999); however, in the absence of any preserved feeding appendages, guts, or orifices, coupled with their occurrence below the photic zone, there remain few alternative feeding modes. One prediction of osmotrophy that can be tested using CFD is the distribution of flow; macroscopic osmotrophs would be expected to adopt a morphology and/or position in the water column that distributes flow over their entire absorptive surface (see for example, the distribution of water flow over Charniodiscus fronds in Singer et al., 2012), thus maximizing the potential for nutrient absorption. By contrast, sessile organisms adopting an alternative mechanism such as suspension feeding adopt life positions whereby feeding structures are repositioned in flow [such as crinoid fans – see Baumiller (1997) and Byrne & Fontaine (1981], or they develop morphologies that redirect flow to sites of feeding, such as in thecosomatous pteropods (Gilmer, 1990), upside‐down jellyfish (Santhanakrishnan et al., 2012), and black fly larvae (Chance & Craig, 1986; Lacoursière & Craig, 1993). However, while these flow patterns can be used to infer locations of nutrient acquisition in Ediacaran organisms, they provide little information about actual mechanisms for moving nutrients across body tissues (Liu et al., 2015).

Amongst Ediacaran organisms, this logic structure was applied to the enigmatic fossil Tribrachidium (Fig. 1B) by Rahman et al. (2015a ). Tribrachidium is a small (2–4 cm diameter) and approximately hemispherical organism with triradial symmetry produced by three raised primary ‘arms’, which spiral anti‐clockwise outward from the apex towards the margin. It also possesses three equally spaced circular depressions near the apex, termed ‘apical pits’. Field studies reveal that Tribrachidium is commonly preserved in a variety of shallow‐water facies, alongside sedimentological evidence for currents (Gehling & Droser, 2013; Hall et al., 2015), thus suggesting that Tribrachidium, like many taxa in present‐day nearshore environments, was likely adapted to life in variable water flows. Using CFD simulations, Rahman et al. (2015a ) demonstrated that Tribrachidium's three primary arms redirected flow toward the organism's centre, where slow‐velocity recirculation developed inside the apical pits. This pattern of flow was interpreted as characteristic of suspension feeding, rather than osmotrophy, and implied a strategy whereby larger food particles would fall out of suspension under the influence of gravity, which is thought to be an important mechanism of food acquisition in some extant bivalves and zooanthids (Koehl, 1977; Vogel, 1996). Crucially, CFD simulations showed that these flow patterns were consistent regardless of the organism's orientation with respect to the current, potentially revealing that the shape of Tribrachidium represents an adaptation to environments where current directions were variable. These results establish Tribrachidium as potentially one of the oldest macroscopic suspension feeders known from the fossil record.

Similarly, Darroch et al. (2017) tested between hypothesized feeding modes in the enigmatic Ediacaran organism Parvancorina, which is a small, bilaterally symmetrical fossil with a shield‐like base and a dorsal anchor‐shaped ridge, principally known from shallow‐marine sediments in Australia and Russia (Naimark & Ivantsov, 2009; Gehling & Droser, 2013). CFD analysis of Parvancorina illustrated consistent redirection of fluid to specific regions of the organism (again refuting a solely osmotrophic feeding model), but in contrast to Tribrachidium, these flow patterns were highly dependent on orientation with respect to the current direction (Fig. 6D–F). In addition, drag forces varied widely according to orientation, suggesting that Parvancorina may have re‐oriented itself with respect to the current direction to reduce drag (Darroch et al., 2017; Coutts et al., 2018). Interestingly, Paterson et al. (2017) independently described evidence for mobility in Parvancorina on the basis of rheotactic behaviour evident in preserved fossil surfaces from South Australia.

Fig 6.

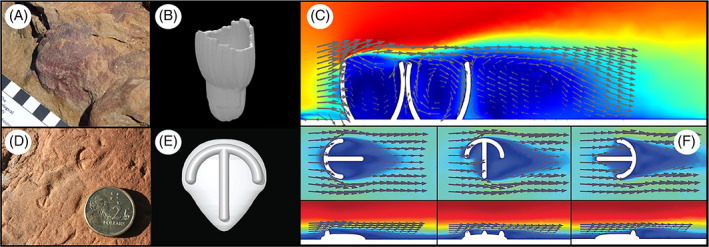
Computational fluid dynamics (CFD) analyses of the Ediacaran organisms Ernietta (A–C) and Parvancorina (D–F). (A) Fossil specimen of Ernietta. Scale bar, 1 cm. (B) Digital model of Ernietta. (C) Results from CFD simulation of turbulent flow around Ernietta. A–C from Gibson et al. (2019a). (D) Fossil Parvancorina. Coin diameter is 2 cm. Photograph by Phoebe Cohen, distributed under a CC‐BY 2.0 license. (E) Digital model of Parvancorina. (F) Results from CFD simulations of turbulent flow around Parvancorina models at different orientations to the inlet. D–F from Darroch et al. (2017). In C and F flow is from left to right; arrows indicate the direction of flow.

Most recently, CFD has been used to shed light on the functioning of ecological populations of the late Ediacaran taxon Ernietta (Gibson et al., 2019a). Like many Ediacaran fossils, Ernietta possesses no unambiguous metazoan synapomorphies (being a broadly bag‐shaped organism constructed from repeated tube‐shaped modules, lacking a mouth, gut, or any discernible feeding structures), and so occupies an uncertain position on the eukaryotic tree of life (Seilacher, 1992; Crimes & Fedonkin, 1996; Dzik, 1999; Elliott et al., 2016; Ivantsov et al., 2016). Furthermore, field investigations reveal that individual Ernietta are typically found in aggregated patches, and when found in life position are shown to have lived at least partially buried in the sediment, with open cavities facing upwards into the water column (Ivantsov et al., 2016). These observations prompted two questions: (i) how was Ernietta feeding, and (ii) why were these organisms living gregariously? Addressing the first question, Gibson et al. (2019a) used CFD simulations to demonstrate the consistent generation of fluid recirculation within cavities of the organism (Fig. 6A–C), which is suggestive of suspension feeding and reminiscent of flow patterns seen within (for example) brachiopods (Shiino, Kowazuru, & Yoshikawa, 2009; Shiino & Kuwazuru, 2010). On the basis of these results, the authors hypothesized that this low‐velocity recirculation would have allowed food particles as well as transported sediment to fall out of suspension and settle within the cavities (further providing an explanation for the laminated sediment found inside Ernietta cavities by Ivantsov et al., 2016). CFD also offers a means for addressing the second question; when multiple Ernietta models were placed together in simulations, enhanced recirculation was observed in downstream individuals (Fig. 6). Furthermore, visualizing simulations in terms of turbulent kinetic energy k instead of velocity magnitude revealed a thickening of the turbulent mixing layer above the aggregated populations of Ernietta. These results illustrate that living gregariously likely provided a mechanism for enhancing nutrient delivery (and availability) to the broader community, while also reducing waste water being funneled into downstream neighbours. These hydrodynamic patterns have been well described in modern benthic invertebrates that live in aggregated patches, where they are understood to form an important commensal behaviour. For example, early flume studies conducted by Bertness, Gaines, & Yeh, 1998) demonstrated that Semibalanus balanoides mussel hummocks redistribute food supply by manipulating boundary layer flow. They note that with increasing free stream velocity, momentum fluxes increase towards hummocks living along a bed, which actively redistributes food supply towards the individuals within the hummock. Comparing the flow patterns from these modern hummocks to the Ernietta populations, Gibson et al. (2019a) suggest that Ernietta gregariousness was likely advantageous for suspension feeding.

Similarly, two‐dimensional (2D) fluid flow studies have assessed how the distribution of flow impacted multi‐species community structures. Making use of an osmotrophic feeding assumption, Ghisalberti et al. (2014) used the maximum cross‐sectional areas of Avalon‐aged frondose taxa from Mistaken Point to reconstruct flow through idealized 2D communities using a canopy flow model, which they then coupled with a nutrient partitioning model. Such models are ideal for flows where dense 2D vertical structures generate bed topography that affects the time‐averaged velocity profile (e.g. law of the wall velocity profile). Their results demonstrate that at low temperatures there is a thinning in the diffusive boundary layer, which allowed for greater transport of nutrients from the bed to tiered fronds, supporting an interpretation whereby vertical tiering developed as a consequence of biotic competition (see also Clapham et al., 2003). While the setup of this experiment was geometrically simplified, it provides a strong foundation for more sophisticated and realistic community‐scale CFD experiments.

It should be noted that the fractal architecture of many Ediacaran organisms also lends itself to increased oxygen uptake (Laflamme et al., 2009; Dufour & McIlroy, 2017). While many studies have argued that such architecture is conducive for an osmotrophic feeding ecology, this argument is easily extended to increasing the potential for gas exchange (Weibel, 1991). For example, fractal anatomical regions of modern organisms are frequently used for increasing oxygen uptake efficiency (e.g. fish gills; Saunders, 1962). Some literature regarding oxygen constraints for Ediacaran life exists for non‐fractal organisms (Runnegar, 1982; Sperling et al., 2007; Sperling, Knoll, & Girguis, 2015; Evans et al., 2018), and metabolic studies are now being explored rigorously (Boag et al., 2018). Future CFD analyses coupled with metabolic and oxygen diffusion models may help elucidate the role of fractal geometries for these apparently competing drivers.

In summary, early experiments in Ediacaran fluid mechanics provided first‐order tissue density values for Ediacaran tissues. More recent studies have affirmed feeding ecologies that were only previously speculated, and demonstrated mobility for taxa that otherwise lacked physical traces of this behaviour. They have also demonstrated complex behavioural interactions not yet documented within the Ediacaran, but which are known to have existed throughout the Phanerozoic marine biosphere. Each of these examples demonstrates the value of this approach, and emphasizes that careful model and hypothesis construction is crucial for shedding new light on ancient fossils. Next, we provide an example experiment where we document two approaches for simulating fluid flow over an Ediacaran organism.

(2). Example analysis: Ernietta feeding

(a). Introduction

Fluid dynamics experiments have provided rich insights into the character of fluid–organism interactions in the palaeontological record; the applications of these techniques are continuing to grow, and this necessitates in‐depth examples that include specifics of experimental design and interpretation. Whereas Rahman (2017) and Hebdon, Ritterbush, & Choi (2020) present pragmatic approaches to conducting CFD experiments (and review a breadth of palaeontological CFD studies), here we present a more theory‐based approach to CFD focused on the underlying physics. Moreover, we provide an alternative, more robust application of CFD for future palaeontology studies. The specifics of any CFD simulation will vary with the question at hand, and we stress that there is no standard ‘pipeline’ that can be used in all instances. Instead, we emphasize a few steps that occur in a relatively consistent order, but which often require multiple iterations as an analysis progresses. Figure 7 shows a general outline for our case study.

Fig 7.

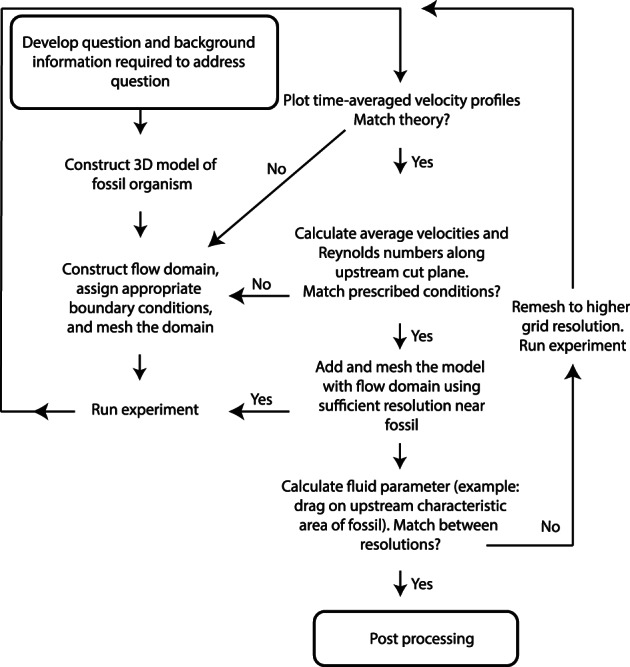
Flow chart of computational fluid dynamics (CFD) experimental setup used for the Ernietta case study.

Gibson et al. (2019a) tested whether Ernietta fed via osmotrophy or suspension feeding using the logic structure outlined in Section IV.1.b. Further examination of their results demonstrates an unexpected high‐velocity jet near the no‐slip boundary condition (Fig. 8A), which incorrectly does not approximate the logarithmic law of the wall in a time‐averaged sense. Here, we perform a set of experiments detailing this phenomenon while simultaneously providing a more sophisticated and accurate experimental design for future palaeontology CFD studies.

Fig 8.

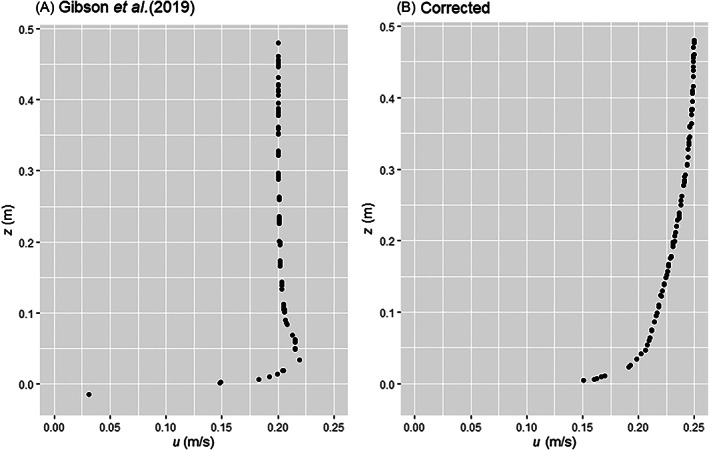
Streamwise u velocity profiles along vertical distance from wall z of the fluid domain around Ernietta. (A) The result from Gibson et al. (2019a), characterized by an anomalous high‐velocity jet near the no‐slip condition. (B) The result from the present study, with the characteristic logarithmic law of the wall profile.

Following Gibson et al. (2019a) as an example, we conduct a series of CFD experiments to test between two plausible feeding ecologies for Ernietta: osmotrophy and suspension feeding. If fluid flow is evenly dispersed over exposed tissue surfaces, this would suggest that Ernietta was primarily osmotrophic. Alternatively, if fluid flow is redirected to specific anatomical regions, this would imply that Ernietta was more likely a suspension feeder. Because SA/V ratios do not rely on CFD, we will a priori assume that Ernietta exhibits lower SA/V ratios than those required for osmotrophy (see Gibson et al., 2019a), and instead focus on CFD as a means for hypothesis testing.

(b). Methods

On the basis of field evidence, Ernietta is interpreted as a semi‐infaunal, sack‐like organism that lived in shallow marine environments (Elliott et al., 2016; Ivantsov et al., 2016). To represent this lifestyle, we set the sediment–water interface halfway below the midline of the digital model (provided from Gibson et al., 2019b). Coupling grain‐size fluid flow experiments (Paphitis, 2001) with sedimentological descriptions of Ediacaran deposits in which Ernietta fossils are found (Ivantsov et al., 2016; Maloney et al., 2020), we reconstruct palaeoenvironmental flow velocity ranges of 0.01–0.5 m/s, noting that these fall within the typical velocity ranges measured in modern shallow marine environments (Valle‐Levinson & Matsuno, 2003). For reasons related to the geometrical similitude of systems discussed above (Section III.1), we choose to use a 3D hexahedron that is scaled larger than our fossil model as the flow domain. Our domain is sufficiently long that the flow field is capable of fully developing the boundary layer. We use an arbitrary but sufficient starting point for the dimensions of the hexahedron of ~10× the width, ~20× the depth, and ~6× the height of the digital Ernietta model. The flow domain size is then increased if flow does not match theory, or decreased to reduce computational resources while still ensuring it correctly reflects theory. After these sensitivity tests, our final setup is ~5× the width, ~40× the depth, and ~3× the exposed model height; this allows the use of multiple turbulence closures (see below), and is required for geometric similitude (Fig. 9).

Fig 9.

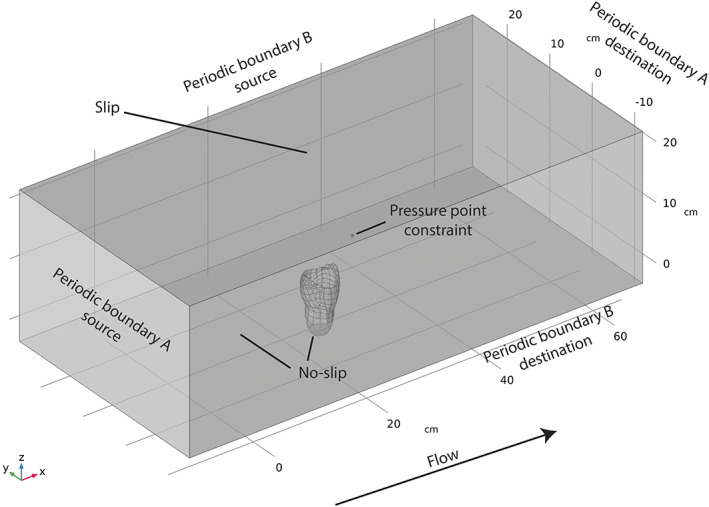
Large eddy simulation (LES) experimental setup (prior to meshing). Periodic boundary A has a pressure differential of 0.05 Pa, which yields a depth‐averaged velocity of 0.05 m/s.

We briefly note that in the past, alternative (although strictly theoretical) models for the construction of Ernietta have been proposed, specifically those whereby the modules making up the main body of the organism were hollow and open to the surrounding water (see e.g. Laflamme et al., 2009). If tubes making up erniettomorph body walls were indeed open, then this would conceivably have implications for the design of digital models, patterns of fluid flow, and interpretation of feeding mode (for example, favouring osmotrophy). However, Laflamme et al. (2009) concluded that modules were likely not empty (instead filled with non‐biologically active fluids), and subsequent work by Elliott et al., (2016) and Ivantsov et al. (2016) has both favoured a closed, lapped‐like termination. On the basis of this recent work, we opt for this better supported model for Ernietta construction, involving closed modules not open to circulating fluid.

Making use of Equation (1), we calculate a systems Re _S = 4988.46 based on our domain height (depth) of 0.25 m and using a maximum fluid velocity of 0.05 m/s, which falls within the range of velocities reconstructed from the field. This Re _S represents our maximum systems Reynolds number Re _S, and can be used to inform on whether a laminar or turbulent flow regime is likely. Given such a low systems Reynolds number (i.e. Re < ~20,000), our system could feasibly be modelled with a simplified turbulence or laminar model, but for the illustrative purposes mentioned above, we instead use SST RANS (as in Gibson et al., 2019a) and LES turbulence closures to demonstrate an example methodology compatible with a greater number of experimental questions and to compare the fidelity of data between them. For fully turbulent flow, we advocate using a turbulence model from the LES family, which allows us to observe turbulent structures that would typically be smoothed over in RANS studies. While LES has thus far not been applied to palaeontological questions, it promises great fidelity in pushing the field forward. LES allows us to construct temporal averages that reduce in essence to RANS results. Finally, we also conduct particle‐imaging velocimetry (PIV) analyses for comparison between physical experiments and CFD.

For our CFD analyses, we prescribe the boundary conditions outlined in Fig. 9. Due to Ernietta's semi‐infaunal lifestyle, the base of the hexahedron must accurately approximate the solid boundary of the seafloor and is therefore prescribed a no‐slip condition. We also apply a no‐slip condition to the exhumed portion of the Ernietta model where fluid may not pass through the ‘tissues’ of the organism, and apply a slip condition to the top surface of our hexahedron, whereby velocity will not approach 0 m/s due to decreased fluid momentum. In Gibson et al. (2019a), the authors applied slip conditions to the two opposing walls of the hexahedron that ran parallel with flow. They then prescribed inlet and outlet conditions to the remaining two walls. In their study, the inlet face has a uniform velocity profile initiating from the seafloor to the top slip condition. In the ocean, the seafloor does not experience uniform velocity profiles, but instead follows the logarithmic law of the wall in a time‐averaged sense. Due to conservation of mass (Equation 6) and the placement of these slip conditions, the velocity profiles from Gibson et al. (2019a) (Fig. 8A) actually do not approximate the logarithmic law of the wall, but instead develop an acceleration near the fluid–seafloor intersection (i.e. a ‘jet’; Fig. 8A). To resolve this issue, we can take either of two approaches: (i) prescribe that our inlet velocity is ‘fully developed’ flow or at least non‐uniform in profile (i.e. a priori prescribe the correct time‐averaged velocity profile at inlet); or (ii) use periodic boundary conditions where fluid that is sourced from the outlet is immediately delivered back to the inlet, which in essence creates a recirculating flow but requires a specified pressure to drive flow. Using either of these approaches circumvents inconsistencies regarding conservation of mass/volume (Equation 6) that led to the flow anomalies observed in Gibson et al. (2019a) (Fig. 8A). To demonstrate this, we use the first approach for our SST RANS experiment and the second approach for our LES experiment.

For our SST RANS experiment, we use the same general setup as Gibson et al. (2019a), with opposing inlet/outlet faces, a no‐slip seafloor, and slip walls on the remaining faces. Our inlet is provided a fully developed flow (e.g. not ‘uniform velocity’), and our outlet suppresses backflow pressure. We then vary this setup for our LES setup. For the hexahedron walls that correspond to Gibson et al.’s (2019a) slip walls and inlet/outlet, we use opposing periodic boundary conditions. The walls parallel to our desired flow direction (e.g. the long axis) have a periodic condition with no additional pressure differential ∆p, which permits turbulent flow to approach the model laterally as we might expect in a realistic seafloor environment. We prescribe a pressure difference ∆p between the periodic conditions for upstream and downstream to drive the flow at a desired velocity, namely,

$$\mathrm{\Delta }p=u_{*}^2\mathrm{\rho }\frac{B}{A},$$ (22)

where ρ is the density of the fluid, B is the surface area of the floor in the flow domain, A is the cross‐sectional area of the outflow face, and u _* is the shear velocity. In turn, we estimate the shear velocity from the specified desired depth‐averaged flow velocity. From a pragmatic view, this pressure differential is often first estimated, and subsequently determined, through trial and error. RANS experiments, such as SST models, can also make use of Equation (22) and may additionally incorporate a surface roughness at no‐slip conditions which will change boundary layer development [see also Appendix, Section VIII.2, which expands on this). We use a pressure differential of 0.05 Pa that corresponds to an average velocity of ∼0.05 m/s. Important to note is that for this approach to satisfy the logarithmic law of the wall in a time‐averaged sense, the flow domain length parallel to flow must be sufficiently long that free‐stream velocity perturbations caused by the pressure of the model dissipate before they reach the upstream face of the model. Depending on which turbulence model is being used (e.g. LES), we must also provide a pressure point constraint on a no‐slip condition to inform the software of a known absolute pressure. Importantly, this should not be a point along periodic boundaries, so we instead choose an arbitrary point along the no‐slip ‘seafloor’ that is far from both our organism and any slip/periodic boundary conditions. This minimizes programmatic or ‘ill‐posed problem’ issues. For a summary of the boundary conditions that we prescribed, see Fig. 9.

We mesh the flow domain to provide a discretized field for which the fluid equations will be solved. In practice, we iteratively solve and re‐mesh at higher grid resolution (i.e. increasing number of mesh elements) to assess the dependence of our solutions on the grid resolution. Smaller grid cells, or finer resolutions, yield more resolved flow fields, but come at the cost of increased computational time and resources. For our experiment, we use COMSOL's unstructured meshing routines using free‐tetrahedral elements and structured boundary layer elements, the latter of which are necessary to compute the velocity gradient accurately from the no‐slip boundary conditions to fully turbulent flow in an approximate logarithmic law of the wall profile from a time‐averaged sense. To verify this, we plot time‐averaged velocity profiles of streamwise velocity magnitude at several free‐stream locations within our flow domain (for example, see Fig. 8B). We further compare the time‐averaged drag coefficients on the upstream face of our Ernietta model to see when these values converge (i.e. no significant difference in computed values as mesh resolution changes), which informs us of the dependence of our solutions on grid resolution.

We ran the same experiment using both the LES residual‐based variational multiscale model and SST RANS turbulence model. To ensure that results from these two experiments are directly comparable, we calculated the Reynolds number of a cut plane on the same slice upstream from the digital model in both experiments (Fig. 10). LES experiments were time‐dependent simulations run for 60 s, with data recorded at 0.01 s intervals. Time averages were always calculated using data from the final 40 s to ensure proper formation of the boundary layer had occurred. SST experiments were allowed to reach a stationary relaxation state.

Fig 10.

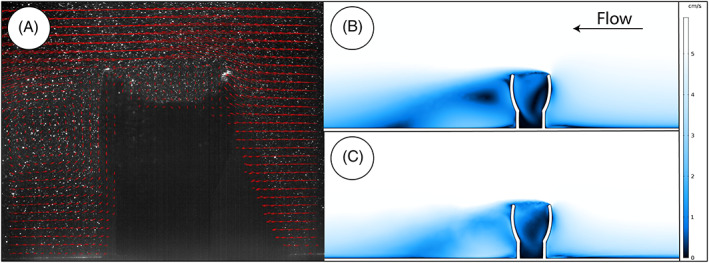
(A) Particle imaging velocimetry (PIV) of a three‐dimensional printed model of Ernietta. Arrows are averaged over ∼30 s and scaled to velocity magnitude. (B) Shear surface transport Reynolds averaged Navier–Stokes (SST RANS) stationary solution. (C) Temporally averaged large eddy simulation (LES) over final 40 s of simulation. In all cases, flow is from right to left.

Lastly, we also conducted particle‐imaging velocimetry (PIV) to observe fine‐scale flow features that may be too small to be captured by our grid resolution. We 3D printed our model using a Lulzbot TAZ6 with 3 mm ABS filament. While this is likely not an optimal proxy for Ernietta dermal lability because erniettomorph tissues were probably more pliable, they were also unlikely to deform radically due to the flow velocities being simulated (Meyer et al., 2014; Gibson et al., 2019a). The model was then attached to the flume floor using double‐sided tape. We used irregularly shaped microplastic particles (~8 μm) as tracers in the flow. A 1.5 W, 1.4 nm laser was directed incident from above to allow the camera to pick up these particles. We used a Redlake MotionPro PCI capturing at 200 fps and shutter speed of 1/800 s with combined Nikon Nikkor 85 mm 1:1.4 244914 lens and additional Canon 72 mm close‐up 500 D running at 2.8 f‐stop. The camera was positioned ~90° from flow at organism level. To capture the images, we used RedLake MIDAS Software. We collected PIV data at the position of the model as well as downstream to acquire the reattachment of flow and mixing. We then calculated pressure and velocity fields using OpenPIV (Taylor et al., 2010).

(c). Results and discussion

In all experiments (PIV and CFD), the viscous sublayer (e.g. see Fig. 2) developed and transitioned to fully turbulent flow above the no‐slip seafloor (Fig. 10). Time‐averaged velocity profiles confirm that the jet near the no‐slip boundary from Gibson et al.’s (2019a) data did not develop in either SST or LES experiments, and the velocity profiles of our time‐averaged results match the logarithmic law of the wall (Fig. 8B). All three experiments exhibit a decrease in average velocity along the upstream face of the model, and develop recirculation within the cavity of the Ernietta model. Pressure magnitude maps show the upstream face of the model creates a region of backflow pressure that accelerates flow over and around the model organism, which is to be expected from analytical solutions such as flow around a sphere.

In the PIV and CFD experiments, small eddies are shed from the top upstream face of the Ernietta model in the form of Kármán vortex streets. In the SST RANS experiment, this is observed as a zig‐zagged trail of almost 0 m/s flow; however, the time‐averaged LES experiment resolved this eddy trail with more detail exhibiting the classic pattern of swirling vortices. We also note that in all physical and digital experiments, there is consistent recirculation, with fluid flow downstream of the model redirected towards the backwards face of the model (Fig. 10). Not so easily captured in the time‐averaged PIV and CFD results, there is an ephemeral recirculation vortex on the upstream face of the model near the no‐slip seafloor (see online Supporting Information, ESM Movies S1 and S2). Consistently observable in all the results is the flow separation initiating at the upstream face of the model, with reattachment several model lengths downstream. Lastly, all three experiments demonstrated varying patterns of recirculation within the cavity of the Ernietta model. This recirculation region in the PIV as well as both CFD results develops repeated turbulent mixing, but stagnation zones are also apparent in the SST with some stagnation less apparent in the LES results. This is likely a result of the turbulence closure and its reliance on turbulent kinetic energy k. The LES and PIV time‐dependent solutions (ESM Movies S1 and S2) both demonstrate that these zones of low‐magnitude velocity fluid are not permanent features within the flow. Instead, the time‐averaged low‐magnitude velocity reflects areas that on average receive slower velocity flow than other locations. Interestingly, the PIV and LES results were broadly comparable in terms of the quality of information. Perhaps the greatest advantage to PIV data over LES is the ability to observe even higher resolution details in flow features, such as with the Kármán vortex streets, but the necessity of such detail will obviously be question specific. In our case, both provided benefits over stationary SST by resolving smaller eddy scales, showing time‐dependent and time‐averaged behaviours, and not over‐estimating the effects of low‐velocity regions.

These results represent the first LES CFD analysis performed in palaeontology, and they confirm the fidelity of CFD in comparison to PIV experiments. While both LES and SST RANS turbulence closures show the consistent recirculation within the cavity of Ernietta also noted by Gibson et al. (2019a), more detail is observed in the time‐averaged results of the LES than the SST experiment. Furthermore, the development of flow patterns through time (ESM Movie S1) demonstrate that regions of stagnant flow in the SST model are ephemeral. Taken together, these results emphasize the importance and prevalence of recirculation within the cavity, but also provide additional information informing us that stagnation zones are over‐represented in the SST stationary solution. These ephemeral, low‐magnitude velocities recirculating within the cavity are likely responsible for depositing the laminated sediments described in fossil material (Ivantsov et al., 2016). Furthermore, fine‐scale features such as the Kármán vortex streets were better resolved in LES using the same mesh resolution as the SST experiment. While not as important for the specific question of Ernietta feeding, these results do emphasize the importance of resolving higher resolution patterns when focusing on smaller anatomical regions for other questions or smaller spatial scales. Our SST RANS simulations are unlikely to resolve such patterns without increased mesh resolution.

Using the same logic structure as outlined in other studies, i.e. that regions receiving consistent redirection of fluid are likely locations of feeding (Rahman et al., 2015a ), our results support the interpretation of Gibson et al. (2019a) that Ernietta central cavities were likely the location of nutrient acquisition, which in turn suggests that Ernietta was more likely to be a suspension feeder than an osmotroph [although we note that some organisms supplement suspension feeding with osmotrophy, for example in corals (de Goeij & van Duyl, 2007) and mussels (Baines, Fisher, & Cole, 2005)]. This interpretation of suspension feeding is further supported by the SA/V ratios calculated in Gibson et al. (2019a), which are orders of magnitude lower than those of extant organisms using osmotrophy as their primary feeding mode.

(3). Future directions

(a). Techniques

CFD is increasingly being used in palaeontological studies (Rigby & Tabor, 2006; Shiino et al., 2009, 2012; Shiino & Kuwazuru, 2010; Rahman et al., 2015b ; Dynowski et al., 2016), but there are opportunities for more sophisticated and detailed experiments. With advances in computational resources, palaeontologists may now take advantage of more complex and accurate turbulence models, such as the LES example presented above. LES and DNS experiments permit the description of turbulent structures at finer resolutions than previously possible, and provide the ability to make time‐averaged comparisons to the currently widely used RANS stationary experiments. Using LES/DNS and time‐dependent analyses, we may address time‐dependent and turbulence‐dependent behaviours which we were unable to address previously. Better still, averaging LES solutions allows us to observe both the instantaneous flow structures (LES solution), as well as persistent emergent flow phenomena (averaged LES) associated with fluid flow around organisms.

Another advantage of recent increases in computing power is the ability to conduct fully coupled multiphysics analyses more easily. Structural mechanics is a powerful tool that can be used in conjunction with CFD to assess how fluid flow deforms the bodies of organisms (e.g. Sponaugle & LaBarbera, 1991). Using fluid–structure interaction (FSI) CFD studies, we can assess the role of tissue rigidity on flow patterns (Fig. 11; Gibson et al., 2019a), or gain insight into spatial competition among organisms such as rangeomorphs and arboreomorphs (e.g. a multi‐model approach to Fig. 11). FSI experiments are not meant to constrain accurately the exact tissue rigidity of ancient Ediacaran organisms, but they permit limits on labilities and possible behaviours. Coupled with moving meshes, FSI CFD studies may allow us to begin to test tiering and spatial competition models such as for Ediacaran fronds [e.g. compare Clapham et al., 2003 with Mitchell & Kenchington, 2018]. Importantly, such coupled experiments require careful treatment of turbulence model choice and boundary conditions, otherwise there is the very real possibility of solving nonsensical problems, such as incorrectly using averaged turbulence quantities to assess time‐specific turbulence‐induced phenomena.

Fig 11.

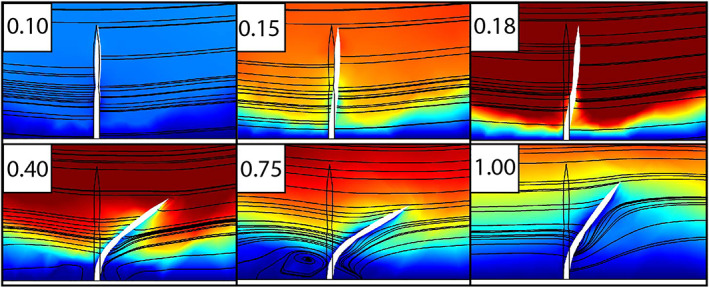
Example fluid–structure interaction (FSI) simulation of a simple three‐dimensional model of a rangeomorph oriented with the largest surface area perpendicular to flow. Numbers represent timesteps normalized to the final timestep, and velocity increases from blue to red with inflow on the left face. Flow is from left to right.

Ediacaran and palaeontological CFD studies have used streamlines and arrows to infer movement of nutrient particles via fluid parcels, but we also have the ability to use individual particle tracing with CFD to simulate nutrient particle capture via one‐way or fully coupled mass‐balanced experiments. Such techniques could be used to inform gamete dispersal experiments for individual Ediacaran organisms, or could be used to quantify sediment mixing and migration in the vicinity of organisms like Ernietta. Similar to the FSI CFD experiments, these types of experiments are not meant to replicate Ediacaran reproduction exactly, but instead would be aimed at providing limits on individual reproductive behaviour.

Furthermore, we are nearing the point where we may combine several of these approaches such as particle tracing, FSI, and time‐dependent LES to assess methods for gamete release and dispersal from individual fronds, or mechanisms for waste export from any number of taxa. It is also worth noting that while advances in computing have opened these doors, such experiments are still limited to cluster computing, particularly when performed using complex 3D geometries. Furthermore, with increasing complexity, we must explicitly understand and make transparent any assumptions that are inherently built into our experiments. We stress that all of these techniques do not accurately reflect real flow, but are instead ideal techniques for testing specifically tailored hypotheses for well‐defined questions.

With access to advanced workstations and cluster‐computing capabilities, comprehensive models are now possible. While recent analyses have focused on individuals or small idealized populations of individuals, it will soon be computationally feasible to run experiments on entire bedding surfaces of benthic organisms. These studies will be highly informative for understanding aspects such as gamete dispersal, larval recruitment, and spatial competition in Ediacaran organisms. However, with the inclusion of additional individuals, we must think carefully about research questions and hypotheses, and experimental designs (including meshing). We reiterate that the information CFD provides is dependent on the turbulence closure implemented. RANS provides a description of an idealized fluid that is informative for emergent phenomena like consistent locations of recirculation. LES approximates a real fluid more accurately, but must rely on approximations at small mesh scales. As such, no CFD result provides an exact reconstruction of Ediacaran organisms in flow, but instead indirectly provides details that can then inform us about individual taxa or Ediacaran ecosystems.

Lastly, much like other methodologies used in digital palaeontology [e.g. microcomputed tomography (μCT)], there is currently no accepted protocol to make such data available. As with any data analysis, CFD code and files should be reposited where others can access them and reproduce the experiments. Fortunately, these data sets are typically smaller than other digital data sets allowing us to share data more easily. While file sizes are smaller, there is no currently accepted protocol for which data to make available for future palaeontological CFD studies. We propose that any μCT scan or organism model, all simulation codes or files, and even vector field exports of pressure and velocity magnitudes (if using proprietary software) should be reposited. With increasing model complexity and the addition of multiphysics approaches, more data exports will need to be made available. While the application of this and related techniques is still fairly young within the field, we recommend erring on the side of repositing too much rather than too few data and descriptions of methods.

(b). Research questions

There are numerous opportunities for using fluid mechanics studies to target key questions surrounding the Ediacaran–Cambrian transition. For example, shallow marine microbial mats were ubiquitous during the Ediacaran (Gehling et al., 2005; Gehling & Droser, 2009), but their effects on vertical velocity profiles have not been formally described. Low‐tiered organisms on the scale of the viscous sublayer and turbulent transition layer would be particularly affected by flow differences due to textured organic surfaces, as these flow patterns dictate nutrient particle delivery. At the larger community scale, it is currently unknown how Ediacaran tiering from White Sea and Nama intervals may have been affected by patterns of canopy flow (see e.g. Ghisalberti et al., 2014), and how this interaction evolved with the changing structure of Ediacaran communities through time. Additionally, in the context of ecological escalation during the latest Ediacaran, the proliferation of benthic suspension feeding is thought to have been particularly crucial (Wood & Curtis, 2014); suspension feeding has several important geobiological impacts, including influencing the structure of food webs, filtering and oxygenating the water column, creating unique habitats, and delivering waste organics to the substrate, thus providing a direct link between pelagic and benthic ecosystems (Hentschel & Shimeta, 2008; Erwin & Tweedt, 2012; Wood & Curtis, 2014; Schiffbauer et al., 2016). CFD has the potential to examine how many Ediacaran taxa were suspension feeders, and how their unusual morphologies may represent sophisticated adaptations to interact with moving fluids in a way that aids particle capture.

On a broader scale, the application of fluid physics studies may contribute to debates surrounding end‐Ediacaran extinction, and the character of the Ediacaran–Cambrian transition. After ~30 million years as the dominant components of benthic ecosystems, the Ediacara biota disappeared, broadly coincident with the beginning of the Cambrian. Recent analyses (Darroch et al., 2018b ; Muscente et al., 2019) reveal that this apparent extinction event occurred in two pulses – one at the White Sea–Nama boundary ~548 Ma, and a second at the Ediacaran–Cambrian boundary (~539 Ma) itself. An open question surrounding these two extinction pulses is the extent to which these extinction pulses were selective. Patterns of selectivity in extinction can offer clues as to what the proximal extinction drivers were in any given event (see e.g. Knoll et al., 1996). As detailed above, studies using CFD have begun to establish feeding modes among a variety of Ediacaran taxa. By expanding these experiments to include additional taxa, we can ascertain if individual Ediacaran extinction pulses targeted specific ecological groups. As a specific example, one hypothesis surrounding the end‐Ediacaran extinction explains the loss of osmotrophs at the expense of suspension feeders as a result of changes in the character of dissolved and particulate organic material (Dornbos et al., 2012). By applying CFD more widely to successive ‘assemblages’ of Ediacaran fossils, the feeding ecologies of many more Ediacaran taxa (and patterns of selectivity in their extinction) may eventually offer a test of this hypothesis, and thus shed valuable new light on a critical interval in Earth history.

V. CONCLUSIONS

(1) Studies in experimental biology have shown that organisms in aquatic environments have evolved a spectacular array of adaptations to aid life in moving fluids (Denny, 1988; Vogel, 1996). As well as shedding light on the processes of evolution and adaptation in extant organisms, this observation offers a valuable window into reconstructing the palaeobiology and palaeoecology of ancient and enigmatic fossils, allowing us to pose the question: how might the unusual morphologies seen in extinct organisms have aided feeding, movement, or reproduction in the fluid environment?

(2) The number of palaeobiological studies employing fluid physics, and specifically CFD, is increasing rapidly. This is particularly true for the Ediacara biota, where studies using CFD demonstrate that Neoproterozoic ecosystems were surprisingly dynamic and ecologically complex, with a larger diversity of feeding modes and inter−/intraspecific ecological interactions than previously suspected.

(3) CFD offers an innovative new means for addressing broader questions in Ediacaran palaeobiology, including those surrounding the evolution of new community structures, the appearance of new behaviours, and (potentially) the drivers of Ediacaran–Cambrian biotic turnover.

(4) We describe the underlying theory on which CFD studies are based, and dispel common misunderstandings frequently observed in the literature. We provide a sophisticated and robust worked example for performing CFD analysis of fossil organisms, involving (for the first time) large eddy simulations, as well as a combined CFD/PIV approach to examining flow patterns.

(5) Lastly, we attempt to establish a starting set of guidelines for data reproducibility and transparency in CFD and related studies. This field will inevitably continue to evolve and expand, and as it does so, it is important that we continue to evaluate best practices for data storage and methods reporting (as is happening in many other palaeobiological fields; see, for example, Parham et al., 2012). We emphasize, however, that experiments in fluid physics represent an exciting frontier in palaeontology and evolutionary biology, and one which promises to shed new light on key intervals in the history of life.

VII. DATA REPOSITED

COMSOL simulation files are available at Dryad (doi: 10.5061/dryad.gmsbcc2jv).

Appendix

(1) Derivation of Equation ( 22 )

To calculate the pressure difference for a laminar flow, we start by choosing our desired Reynolds number. Then, we calculate our associated velocity using Equation (1), which in this case would be our depth‐averaged velocity U for a parabolic velocity profile as

$$U=\frac{h^2}{3\mathrm{\mu }}\frac{\mathrm{\Delta }p}{L},$$ (23)

where h is the height from the seafloor to the maximum height of the hexahedron flow domain, μ is the dynamic viscosity, L is the characteristic length (depth) of the flow domain parallel to flow, and ∆p is the change in pressure. Rearranging this we get,

$$\mathrm{\Delta }p=U\mathrm{L}\frac{3\mathrm{\mu }}{h^2},$$ (24)

which provides the pressure differential for our periodic boundary conditions to drive laminar flow. Alternatively, not every problem can be treated with laminar flow, such that we must derive Equation (24) for a transitional or fully turbulent flow following the logarithmic law of the wall. We begin with the time averaged velocity $\overline{u_t}$ defined as

$${\overline{u}}_t\left(z\right)=\frac{u_{*}}{\mathrm{\kappa }}\ln \frac{z}{z_0},$$ (25)

where u _* is the shear velocity, κ is the von Kármán constant equal to 0.41, z is the height of the surface, and z ₀ is the roughness height of the seafloor. To get the depth‐averaged velocity, we solve

$$U=\frac{1}{h-z_0}{\int }_{z_0}^h\overline{u_t}\mathrm{d}t,$$ (26)

where we can substitute Equation (25) into Equation (26) as

$$U=\frac{1}{h-z_0}{\int }_{z_0}^h\overline{u_t}\mathrm{d}z=\frac{1}{h-z_0}\frac{u_{*}}{\kappa }\left|z\ln \frac{z}{z_0}-z\left|\genfrac{}{}{0pt}{}{h}{z_0}\right.=\frac{1}{h-z_0}\right.\frac{u_{*}}{\kappa }h\ln \frac{h}{z_0}-\frac{1}{h-z_0}h\frac{u_{*}}{\kappa }+\frac{z_0}{h-z_0}\frac{u_{*}}{\kappa },$$ (27)

which due to scaling (e.g. the disparity in variable magnitudes) can reduce to

$$U\approx \frac{u_{*}}{\mathrm{\kappa }}\ln \frac{h}{z_0}-\frac{u_{*}}{\kappa }.$$ (28)

With some rearranging and solving for u_* we see,

$$u_{*}=\frac{U\mathrm{\kappa }}{\ln \frac{h}{z_0}-1}.$$ (29)

Using the definition $u_{*}=\sqrt{\frac{{\mathrm{\tau }}_0}{\mathrm{\rho }}}$, we may substitute and rearrange as

$${\mathrm{\tau }}_0=u_{*}^2\mathrm{\rho },$$ (30)

and input this into Equation (24) as

$$\mathrm{\Delta }p=\frac{{\mathrm{\tau }}_{0}B}{A},$$ (31)

where A is the cross‐sectional area of the periodic boundary and B is the area of the digital seafloor. Of note is that this will lead to the pressure difference for our flow domain if there is no fossil organism in the domain. The actual pressure difference will be lower when the fossil is incorporated because the organism will extract momentum from the flow through drag. Through substitution this leads to

$$\mathrm{\Delta }p={\left(\frac{\mathit{U\kappa }}{\ln \left(h/z_0\right)-1}\right)}^2\mathrm{\rho }\frac{B}{A}.$$ (32)

(2) Surface roughness u_s

This can be calculated as

$$u_{*}\approx \frac{U\mathrm{\kappa }}{\ln \frac{0.37h}{z_0}},$$ (33)

where h is the height of the flow domain, z ₀ is an effective height that incorporates an experimentally determined surface roughness of the substrate k _s and a coefficient k ₁ which is 1/30th the diameter of the grain size for a sand grain, and κ is the von Kármán constant, typically 0.41. Fortunately, in many CFD software suites (i.e. see fvOptions in OpenFOAM), this calculation is not necessary as there are under‐the‐hood algorithms that will assert this differential based off the depth‐averaged velocity that we prescribe.

Supporting information

Movie S1. Computational Fluid Dynamics Large Eddy Simulation (CFD LES) of flow around an Ernietta.

Movie S2. Particle Imaging Velocimetry (PIV) of flow over plastic Ernietta.