uKIN combines new and prior information with guided network propagation to accurately identify disease genes

Summary

Protein interaction networks provide a powerful framework for identifying genes causal for complex genetic diseases. Here we introduce a general framework, uKIN, that uses prior knowledge of disease associated genes to guide, within known protein-protein interaction networks, random walks that are initiated from newly-identified candidate genes. In large-scale testing across 24 cancer types, we demonstrate that our network propagation approach for integrating both prior and new information not only better identifies cancer driver genes than using either source of information alone but also readily outperforms other state-of-the-art network-based approaches. We also apply our approach to genome-wide association data to identify genes functionally relevant for several complex diseases. Overall, our work suggests that guided network propagation approaches that utilize both prior and new data are a powerful means to identify disease genes. uKIN is freely available for download at: https://github.com/Singh-Lab/uKIN.

In Brief

We develop a guided network propagation approach to identify disease genes that combines prior knowledge of disease-associated genes with newly identified candidate genes. We demonstrate the effectiveness of our approach by applying it to somatic mutations observed across tumors to discover genes causal for cancer, as well as to genome-wide association data to discover genes causal for complex diseases.

Graphical Abstract

Introduction

Large-scale efforts such as the 1000 Genomes Project (1000 Genomes Project Consortium and others, 2015), The Cancer Genome Atlas (TCGA) (TCGA Research Network, n.d.), and the Genome Aggregation Database (Karczewski et al., 2019), among others, have catalogued millions of variants occurring in tens of thousands of healthy and disease genomes. Despite this abundance of genomic data, however, understanding the genetic basis underlying complex human diseases remains challenging (Kim and Przytycka, 2013). In contrast to simple Mendelian diseases, for which a small set of commonly shared genetic variants are responsible for disease phenotypes, complex heterogeneous diseases are driven by a myriad of combinations of different alterations. Individuals exhibiting the same phenotypic outcome—a particular disease—may share very few, if any, genetic variants, thereby making it difficult to discover which of numerous variants are associated with heterogeneous diseases, even when focusing just on changes that occur within genes.

Biological networks provide a powerful, unifying framework for identifying disease genes (Barabási et al., 2011; Cowen et al., 2017; Goh et al., 2007; Ozturk et al., 2018). Genes relevant for a given disease typically target a relatively small number of biological pathways, and since genes that take part in the same pathway or process tend to be close to each other in networks (Hartwell et al., 1999; Spirin and Mirny, 2003), disease genes cluster within networks (Gandhi et al., 2006; Oti and Brunner, 2007). Consequently, if genes known to be causal for a particular disease are mapped onto a network, other disease-relevant genes are likely to be found in their vicinity (Krauthammer et al., 2004). Thus, the signal from known disease genes can be “propagated” across a network to prioritize either all genes within the network or just candidate genes within a genomic locus where single nucleotide polymorphisms have been correlated with an increased susceptibility to disease (Chen et al., 2009; Erten et al., 2011; Köhler et al., 2008; Lundby et al., 2014; Navlakha and Kingsford, 2010; Smedley et al., 2014; Vanunu et al., 2010).

While initial network approaches to identify disease genes focused on propagating knowledge from a set of known “gold standard” disease genes, with the widespread availability of cancer sequencing data and genome-wide association studies (GWAS), the source of where information is propagated from has shifted to genes that are newly identified as perhaps playing a role in disease (Babaei et al., 2013; Carlin et al., 2019; Cerami et al., 2010; Jia and Zhao, 2014; Lee et al., 2011; Leiserson et al., 2015; Vandin et al., 2011). For example, in the cancer context, diffusing a signal from genes that are somatically mutated across tumors is highly effective for identifying cancer-relevant genes and pathways (Leiserson et al., 2015; Vandin et al., 2011); notably, while frequency-based approaches identify genes that “drive” cancer by searching for those that are recurrently mutated across tumor samples beyond some background rate (Lawrence et al., 2013), such a network propagation approach can even pinpoint rarely mutated driver genes if they are within subnetworks whose component genes, when considered together, are frequently mutated.

Thus there are two dominant network propagation paradigms for uncovering disease genes: spreading signal either from well-established, annotated disease genes or from genes that have some new evidence of being disease-relevant. While both have been successful independently, we argue that both sources of information should be utilized together, and that existing knowledge of disease genes should inform the way new data is examined within networks. That is, while our prior knowledge of causal genes for a given disease may be incomplete, it nevertheless is a valuable source of information about the biological processes underlying the disease; furthermore, in many cases, there is substantial prior knowledge and there is no reason disease gene discovery should proceed de novo from newly observed alterations.

In this paper, we introduce a guided network propagation framework to uncover disease genes, where signal is propagated from new data so as to tend to move towards genes that are closer to known disease genes. Our core method of propagating information within a network is via either diffusion (Qi et al., 2008) or random walks with restarts (RWRs) (Köhler et al., 2008), as these are mathematically sound, well-established approaches, where numerical solutions are easily obtained. In particular, our approach first diffuses a signal from known disease genes, and then performs either guided random walks or guided diffusion from the new data so as to preferentially move towards genes that have received higher amounts of signal from the initial set of known disease genes. In contrast, previous network propagation methods for disease gene discovery have performed diffusion or random walks uniformly from each node (i.e., in an “unguided” manner, as in e.g., (Jia and Zhao, 2014; Vandin et al., 2011)), or where the diffusion is scaled by weights on network edges that reflect their estimated reliabilities (e.g., (Babaei et al., 2013)). Alternatively, several approaches have attempted to uncover disease genes by explicitly connecting in the network genes that have genetic alterations with genes that have expression changes (Bashashati et al., 2012; Kim et al., 2011; Paull et al., 2013; Ruffalo et al., 2015; Shi et al., 2016; Shrestha et al., 2014); while well-suited for finding genes causal for observed expression changes, such approaches are less appropriate as a means to link prior and new information, and our approach instead uses prior knowledge to simply influence information propagation within the network.

We demonstrate the efficacy of our method uKIN—using Knowledge In Networks—by first applying it to discover genes causal for cancer. Here, new information consists of genes that are found to be somatically mutated in tumors—only a small number of which are thought to play a functional role in cancer—and prior information is comprised of subsets of “driver” genes known to be cancer-relevant (Futreal et al., 2004). In rigorous large-scale, cross-validation style testing across 24 cancer types, we demonstrate that propagating signal by integrating both these sources of information performs substantially better in uncovering known cancer genes than propagating signal from either source alone. Notably, even using just a small number of known cancer genes (5–20) to guide the network propagation from the set of mutated genes results in substantial improvements over the unguided approach. Next, we compare uKIN to four state-of-the-art network-based methods that use somatic mutation data for cancer gene discovery and find that uKIN readily outperforms them, thereby demonstrating the advantage of additionally incorporating prior knowledge. We also show that by using cancer-type specific prior knowledge, uKIN can better uncover causal genes for specific cancer types. Finally, to showcase uKIN’s versatility, we show its effectiveness in identifying causal genes for three other complex diseases, where the genes known to be associated with the disease come from the Online Mendelian Inheritance in Man (OMIM) (Online Mendelian Inheritance in Man, OMIM®, 2000) and genes comprising the new information arise from genome-wide association studies (GWAS).

Results

Algorithm Overview

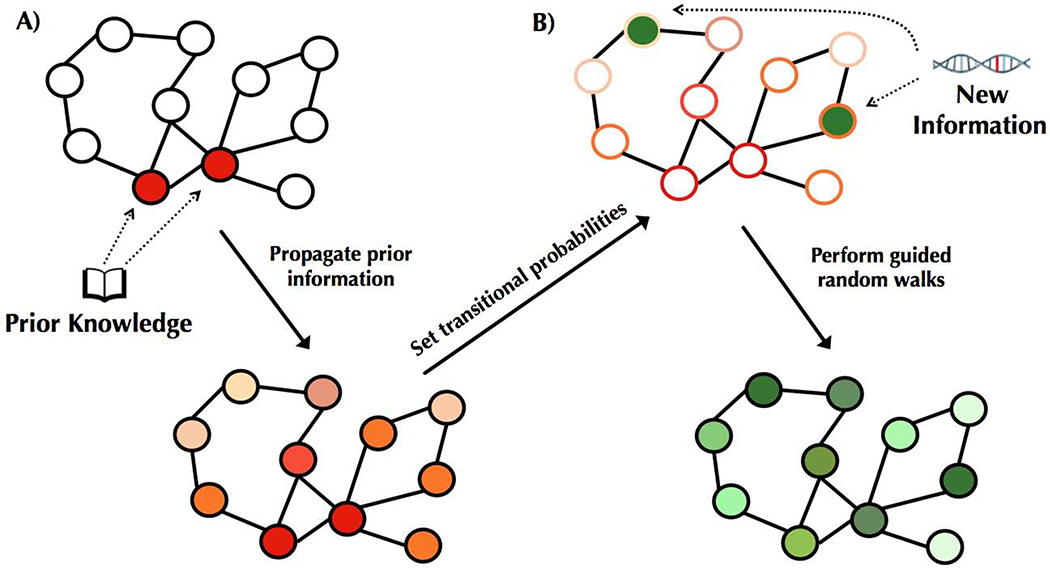
At a high level, our approach propagates new information across a network, while using prior information to guide this propagation (Figure 2). While our approach is generally applicable, here we focus on the case of propagating information across biological networks in order to find disease genes. We assume that prior knowledge about a disease is given by a set of genes already implicated as causal for that disease, and new information consists of genes that are potentially disease-relevant. In the scenario of uncovering cancer genes, prior information comes from the set of known cancer genes, and new information corresponds to those genes that are found to be somatically mutated across patient tumors. For other complex diseases, new information may arise from (say) genes weakly associated with a disease via GWAS studies or found to have de novo or rare mutations in a patient population of interest.

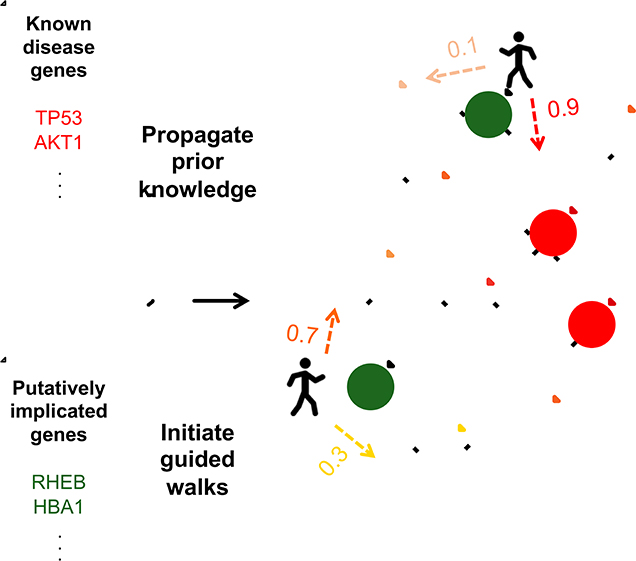
Figure 2. Overview of our approach.

(A) Known disease-relevant genes (prior knowledge) are mapped onto an interaction network (shown in red, top). Signal from this prior knowledge is propagated through the network via a diffusion approach (Qi et al., 2008), resulting in each gene in the network being associated with a score such that higher scores (visualized in darker shades of red, bottom) correspond to genes closer to the set of known disease genes. These scores are used to set transition probabilities between genes such that a neighboring gene that is closer to the set of prior knowledge genes is more likely to be chosen. (B) Genes putatively associated with the disease—corresponding to the new information—are mapped onto the network (shown in green, top). To integrate both sources of information, RWRs are initiated from the set of putatively associated genes, and at each step, the walk either restarts or moves to a neighboring gene according to the transition probabilities (i.e., walks tend to move towards genes outlined in darker shades of red). These prior-knowledge “guided” RWRs have a stationary distribution corresponding to how frequently each gene is visited, and this distribution is used to order the genes. Higher scores correspond to more frequently visited genes (depicted in darker greens, bottom).

The first step of our approach is to compute for each gene a measure that captures how close it is in the network to the prior knowledge set of genes $\mathcal{K}$ (Figure 2A). To accomplish this, we spread the signal from the genes in $\mathcal{K}$ using a diffusion kernel (Qi et al., 2008). Next, we consider new information consisting of genes $\mathcal{M}$ that have been identified as potentially being associated with the disease. As we expect those that are actually disease-relevant to be proximal to each other and to the previously known set of disease genes, we spread the signal from these newly implicated genes $\mathcal{M}$, biasing the signal to move towards genes that are closer to the known disease genes $\mathcal{K}$ (Figure 2B). We accomplish this by performing random walks with restarts, where with probability α, the walk jumps back to one of the genes in $\mathcal{M}$. That is, α controls the extent to which we use new versus prior information, where higher values of α weigh the new information more heavily. With probability 1- α, the walk moves to a neighboring node, but instead of moving from one gene to one of its neighbors uniformly at random as is typically done, the probability instead is higher for neighbors that are closer to the prior knowledge set of genes $\mathcal{K}$. Genes that are visited more frequently in these random walks are more likely to be relevant for the disease because they are more likely to be part of important pathways around $\mathcal{K}$ that are also close to $\mathcal{M}$. We thus numerically compute the probability with which each gene is visited in these random walks, and then use these probabilities to rank the genes. See Methods for details.

We apply our method uKIN to uncover cancer genes as well as genes associated with three rare heterogeneous disorders. Unless stated otherwise, uKIN integrates prior and new information using α = 0.5; further, prior knowledge is spread using the diffusion kernel with its sole parameter γ set to 1, as in (Qi et al., 2008). To uncover cancer genes, we use somatic point mutation data from 24 different TCGA cancer types. Genes that have missense and nonsense somatic mutations comprise the new information, and random walks start from these genes with probability proportional to their mutation rates. We use the curated list of 499 cancer census genes (CGCs) available from COSMIC (Futreal et al., 2004) to derive both our prior knowledge $\mathcal{K}$ of cancer driver genes as well as the hidden set of true positives which we will use for evaluation. We test our approach for all 24 cancer types, but showcase results for glioblastoma multiforme (GBM). To uncover genes associated with each of the three rare diseases, we obtain our prior knowledge from the Online Mendelian Inheritance in Man (OMIM), and genes that have been implicated via GWAS studies provide our new information. All results in the main paper use the HPRD protein-protein interaction network (Prasad et al., 2009), with results shown for BioGrid (Stark et al., 2006) in the Supplement.

uKIN successfully integrates prior knowledge and new information

We compare uKIN’s performance when using both prior and new knowledge (RWRs with α = 0.5), to versions of uKIN using either only new information (α = 1) or only prior information (α = 0). Briefly, we use 20 randomly drawn CGCs to represent the prior knowledge $\mathcal{K}$ and another 400 randomly drawn CGCs to be the hidden set $\mathcal{H}$ of unknown cancer-relevant genes that we aim to uncover (see Performance evaluation for details). We repeat this process 100 times, each time spreading signal using the diffusion approach (Qi et al., 2008) before performing RWRs from the genes observed to be somatically mutated. For each run, we analyze the ranked list of genes output by uKIN as we consider an increasing number of output genes, and average across runs the fraction that are members of the hidden set $\mathcal{H}$ consisting of cancer driver genes.

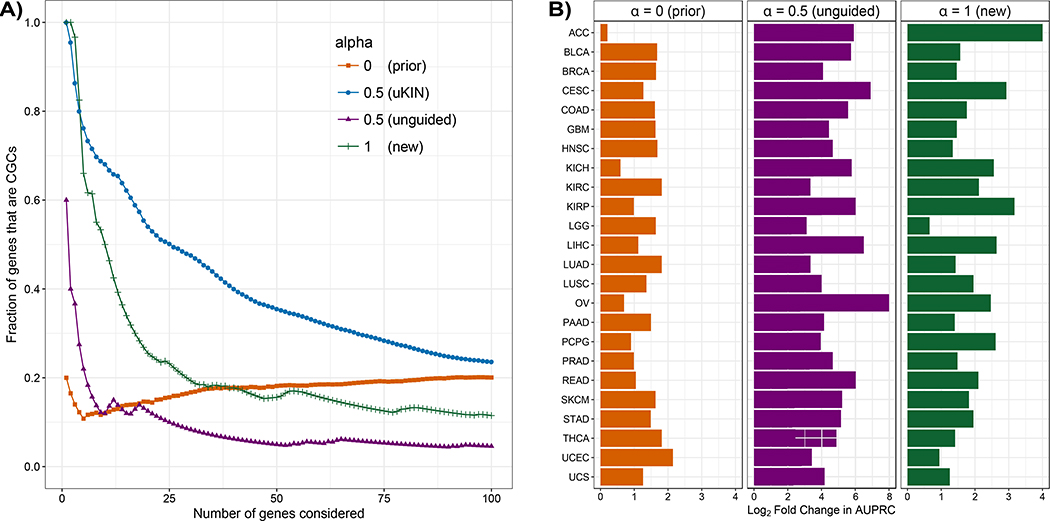
For α = 0.5, we observe that a large fraction of the top predicted genes using the GBM dataset are part of the hidden set of known cancer genes (Figure 3A). At α = 1, our method completely ignores both the network and the prior information $\mathcal{K}$ and is equivalent to ordering the genes by their mutational frequencies. The very top of the list output by uKIN when α = 1 consists of the most frequently mutated genes (in the case of GBM, this includes TP53 and PTEN). As we consider an increasing number of genes, ordering them by mutational frequency is clearly outperformed by uKIN with α = 0.5. At the other extreme with α = 0, the starting locations and their mutational frequencies are ignored as the random walk is memoryless and the stationary distribution depends only upon the propagated prior information. As expected, performance is considerably worse than when running uKIN with α = 0.5. Nevertheless, we observe that several CCGs are found for α = 0; this is due to the fact that known cancer genes tend to cluster together in the network (Cerami et al., 2010) and our propagation technique ranks highly the genes close to the genes in $\mathcal{K}$.

Figure 3. uKIN successfully integrates new information and prior knowledge.

(A) We illustrate the effectiveness of our approach uKIN on the GBM data set and the HPRD protein-protein interaction network using 20 randomly drawn CGCs to represent the prior knowledge. We combine prior and new knowledge using a restart probability of α = 0.5 (blue line). As we consider an increasing number of high scoring genes, we plot the fraction of these that are part of the hidden set of CGCs. As baseline comparisons, we also consider versions of our approach where we use only the new information (α = 1) and order genes by their mutational frequency (green line); where we use new information to perform unguided random walks with α = 0.5 and order genes by their probabilities in the stationary distribution of the walk (which uses new information but not prior information, purple line); and where we use only prior information (α = 0) and order genes based on information propagated from the set of genes comprising our prior knowledge (orange line). Integrating both prior and new sources of information results in better performance. (B) The performance of uKIN when integrating information at α = 0.5 is compared to the three baseline cases where either only prior information is used (α = 0, left) or when only new information is used (α = 1, right and unguided RWRs with α = 0.5, middle). In all three panels, for each cancer type, we plot the log₂ ratio of the AUPRC of uKIN with guided RWRs with α = 0.5 to the AUPRC of the other approach. Across all 24 cancer types, using both sources of information outperforms using just one source of information.

We also consider uKIN’s performance as compared to an unguided walk with the same restart probability α = 0.5. In this case, the walk selects a neighboring node to move to uniformly at random. The stationary distribution that the walk converges to depends upon the starting locations and the network topology but is independent of the prior information. Such a walk provides a good baseline to judge the impact the propagated prior information has on the performance of our algorithm, and is an approach that has been widely applied (Köhler et al., 2008). As evident in Figure 3A, an unguided walk (purple line) performs considerably worse than uKIN with α = 0.5, highlighting the importance of prior information in guiding the walk.

Notably, the trends we observe on GBM hold across all 24 cancers (Figure 3B). For each cancer type, we consider the log₂ ratio of the AUPRC of the version of uKIN that uses both prior and new information with α = 0.5 to the AUPRC for each of the other variants. For all cancer 24 cancers, when uKIN uses both prior and new information with α = 0.5, it outperforms the cases when using only prior information (Figure 3B, left) or using only new information (Figure 3B, middle and right).

uKIN is effective in uncovering cancer-relevant genes

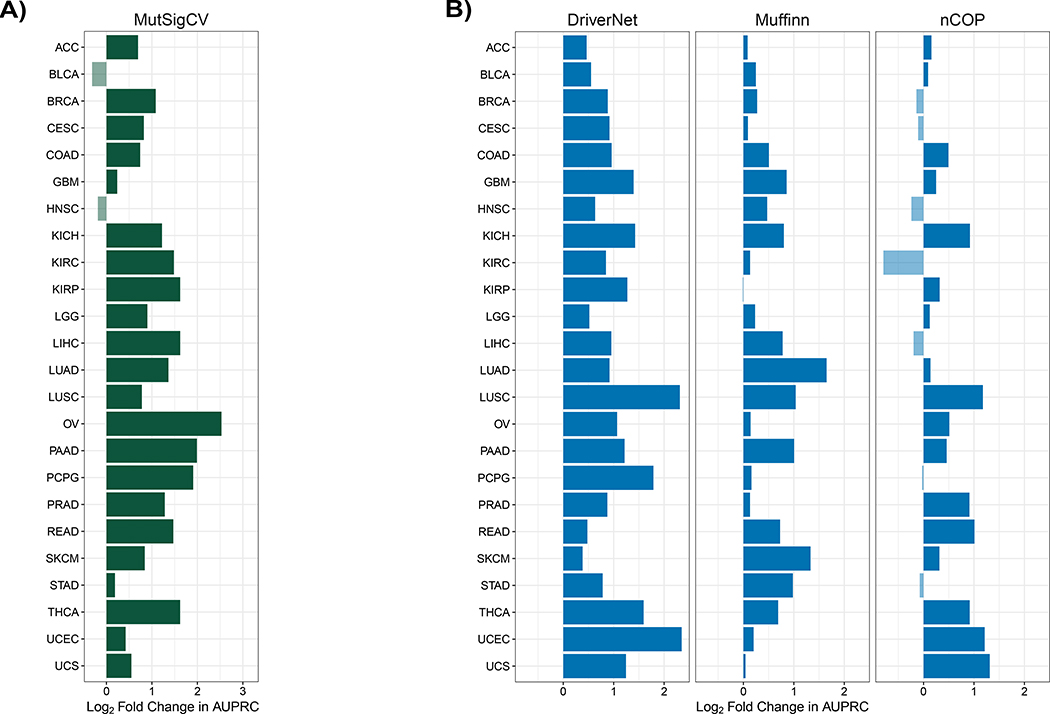
We next evaluate uKIN’s performance in uncovering cancer-relevant genes as compared to several previous methods. These methods do not use any prior knowledge of cancer genes, and any performance differences between uKIN and them may be due either to the use of this important additional source of information or to specific algorithmic differences between the methods. Nevertheless, such comparisons are necessary to get an idea of how well uKIN performs as compared to the current state-of-the-art. All methods are run and AUPRCs computed as described in Methods. First, we compare uKIN with α = 0.5 to MutSigCV 2.0 (Lawrence et al., 2013), perhaps the most widely used frequency-based approach to identify cancer driver genes. We find that uKIN outperforms MutSigCV 2.0 on 22 of 24 cancer types (Figure 4A). Next, we compare uKIN to three network-based approaches (Figure 4B): Muffinn (Cho et al., 2016), which considers mutations found in interacting genes; DriverNet (Bashashati et al., 2012), which finds driver genes by uncovering sets of somatically mutated genes that are linked to dysregulated genes; and nCOP (Hristov and Singh, 2017), which examines the per-individual mutational profiles of cancer patients in a biological network. uKIN exhibits superior performance across all cancer types when compared to DriverNet, and outperforms Muffinn in 23 out of 24 cancer types and nCOP in 17 of the 24 cancer types. In several cancers, the performance improvements of uKIN are substantial. For example, uKIN has a four-fold improvement over MutSigCV 2.0 in predicting cancer genes for ovarian cancer (OV) and pancreas adenocarcinoma (PAAD), and a four-fold improvement over DriverNet for uterine corpus endometrial carcinoma (UCEC) and lung squamous cell carcinoma (LUSC). The limited number of patient samples available for uterine carcinosarcoma (UCS) limits nCOP’s perfomance (Hristov and Singh, 2017) whereas uKIN is able to leverage the prior knowledge available, resulting in uKIN’s two fold improvement over nCOP; this highlights the benefits from incorporating existing knowledge of disease-relevant genes, especially when the new data is sparse. We also compare to Hotnet2 (Leiserson et al., 2015), whose core algorithmic component is diffusion (Qi et al., 2008), and as such uKIN is more similar to it than other methods. Hotnet2 does not output a ranked list of genes, so we instead examine the list of genes highlighted by both methods. We find that uKIN exhibits higher precision and recall than Hotnet2 for all cancer types (Suppl. Figure S1); since both uKIN and Hotnet2 are network propagation approaches, these performance improvements illustrate the benefit of using prior information in identifying cancer-relevant genes.

Figure 4. uKIN is more effective than other methods in identifying known cancer genes.

For each method, for each cancer type, we plot the log₂ ratio of uKIN’s AUPRC to its AUPRC. (A) Comparison of uKIN to MutSigCV 2.0, a state-of-the-art frequency-based approach. uKIN outperforms MutSigCV 2.0 on 22 of the 24 cancer types. (B) Comparison of uKIN to DriverNet (left), Muffinn (middle), and nCOP (right). Our approach uKIN outperforms DriverNet on all cancer types, Muffinn on all but one cancer type and nCOP on 17 out of 24 cancer types.

Robustness tests

The overall results shown hold when we use different lists of known cancer genes as a gold standard (Suppl. Figure S2A), different numbers of predictions considered when computing AUPRCs (Suppl. Figure S2B), and different networks (Suppl. Figure S2C). Further, we confirm the importance of network structure to uKIN, by running uKIN on two types of randomized networks, degree-preserving and label shuffling, and show that, as expected, overall performance deteriorates across the cancer types (Suppl. Figure S2D); we note that while network structure is destroyed by these randomizations, per-gene mutational information is preserved, and thus highly mutated genes are still output.

We also determine the effect of using different values of α (Suppl. Figure S3), and find that running uKIN with α ∈ [0.1, 0.9] is superior to running it using only prior (α = 0) or new (α = 1) information; that is, the integration of prior and new information is helpful even when the precise value of α is not carefully tuned. Further, we determine the effect of the amount of prior knowledge used by uKIN, and find that while performance increases with larger numbers of genes comprising our prior knowledge, even as few as five prior knowledge genes leads to a ~4-fold improvement over ranking genes by mutational frequency (Suppl. Figure S4A). Finally, we investigate the effect of some incorrect prior knowledge, and find that while uKIN’s performance decreases with more incorrect knowledge, uKIN with α = 0.5 performs reasonably with < 20% incorrect annotations (Suppl. Figure S5B).

Alternate formulations

We also tested guided diffusion from the somatically mutated genes instead of RWRs (see Methods). We empirically find that, for α = 0.5, diffusion with γ = 1 yields nearly identical per-gene scores on the cancer datasets we tested (GBM and kidney renal cell carcinoma). Similarly, for other α, we were able to find values of γ such that the RWRs and diffusion have highly similar results. On the other hand, replacing the initial diffusion from the prior knowledge with a RWR (with α = 0.5) results in somewhat worse performance (e.g., ~10% drop in AUPRC for GBM).

uKIN highlights infrequently mutated cancer-relevant genes

A major advantage of network-based methods is that they are able to identify cancer-relevant genes that are not necessarily mutated in large numbers of patients (Leiserson et al., 2015). We next analyze the mutation frequency of genes output by uKIN with α = 0.5. In particular, for each cancer type, for each gene, we obtain a final score by averaging scores across the 100 runs of uKIN; to prevent “leakage” from the prior knowledge set, if a gene is in the set of prior knowledge genes $\mathcal{K}$ for a run, this run is not used when determining its final score. We confirm that, for all cancer types, the top scoring genes exhibit diverse mutational rates, and include both frequently and infrequently mutated genes (Suppl. Figure S5).

We next highlight some infrequently mutated genes in GBM that are given high final scores by uKIN (i.e., are predicted as cancer-relevant). For example, LAD1 and SMAD4 are two well known cancer players that are highly ranked by uKIN, and that have mutational rates in GBM that are in the bottom 70% of all genes and are therefore hard to detect with frequency-based approaches. Of uKIN’s top 100 scoring genes, 23 are are in the bottom half with respect to mutational rates, and 5 of these are CGCs (p < 10⁻², hypergeometric test). When considering the top scoring 100 genes by uKIN for each cancer type, those that have mutational ranks in the bottom half of all genes are each found to have a statistically significant enrichments of CGC genes. Thus, uKIN provides a means for pulling out cancer genes from the “long tail” (Garraway and Lander, 2013) of infrequently mutated genes.

In addition to highlighting known cancer genes, uKIN also ranks highly several non-CGC genes that may or may not play a functional role in cancer, as our knowledge of cancer-related genes is incomplete. Among these predictions for GBM are ATXN1, SMURF1, and CCR3, all of which have been recently suggested to play a role in cancers (Kang et al., 2017; Lee et al., 2016; Li et al., 2017) and are each mutated in less than 5% of the samples. ATXN1 is a chromatin-binding factor that plays a critical role in the development of spinocerebellar ataxia, a neurodegenerative disorder (Rousseaux et al., 2018), and mutants of ATXN1 have been found to stimulate the proliferation of cerebellar stem cells in mice (Edamakanti et al., 2018). This is a promising gene for further investigation because glioblastoma is a cancer that usually starts in the cerebrum and the potential role of ATXN1 in tumorigenesis has only recently been suggested (Kang et al., 2017). SMURF1 and its highly ranked by uKIN network-interactor SMAD1 have already been implicated in the development of several cancers (Yang et al., 2017). SMURF1 also interacts with the nuclear receptor TLX whose inhibitory role in glioblastoma has been revealed (Johansson et al., 2016). Overall, we also find that the top scoring genes by uKIN for GBM are enriched in many KEGG pathways and GO terms relevant for cancer, including microRNAs in cancer, cell proliferation, choline metabolism in cancer and apoptosis (Bonferroni-corrected p < 0.001, hypergeometric test).

Cancer-type specific prior knowledge yields better performance

In several cases, CGC genes are annotated with the specific cancers they play driver roles in. We next test how uKIN’s performance changes when using such highly specific prior knowledge. We consider four cancer types, GBM, breast invasive carcinoma (BRCA), skin cutaneous carcinoma (SKCM), and thyroid carcinoma (THCA), with 33, 32, 42 and 29 CGC genes annotated to them, respectively. We repeatedly split each of these sets of genes in half, and use half as the set $\mathcal{K}$ of prior knowledge, and the other half as the set $\mathcal{H}$ to test performance.

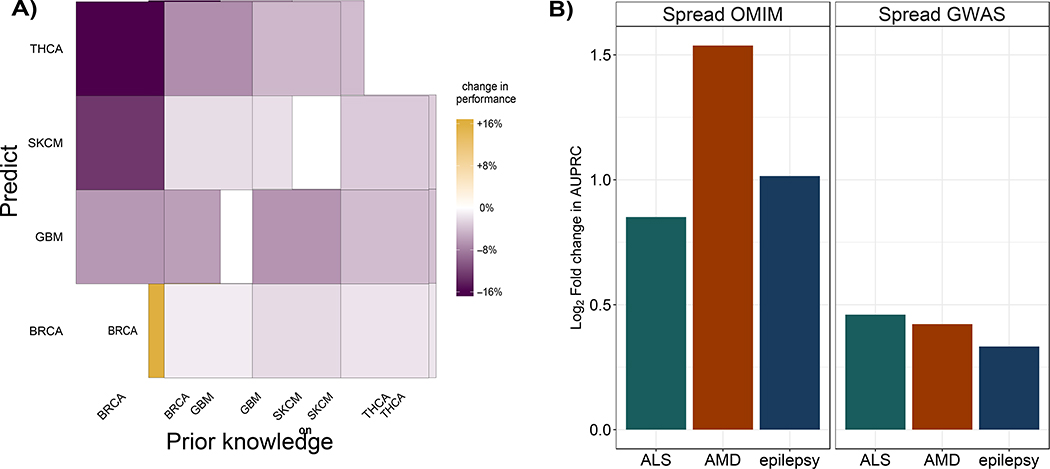
We first use knowledge consisting of genes specific to a cancer type of interest together with the TCGA data for that cancer to uncover that cancer’s specific drivers. Given the small number of genes annotated to each cancer, we assess performance by, for each of these genes, computing the rank of its score by uKIN over the splits where these genes are in $\mathcal{H}$. Next, for the same cancer type, we use a set $\mathcal{K}$ corresponding to a different cancer type as prior knowledge (excluding any genes that are annotated to the original cancer type) while still trying to uncover the genes in the original cancer of interest (i.e., using TCGA mutational data and $\mathcal{H}$ belonging to the original cancer type). That is, we are testing the performance of uKIN when using knowledge corresponding to a different cancer type. For all four cancer types, we find that performance is best when uKIN uses prior knowledge for the same cancer cancer type (Figure 5A), as genes in $\mathcal{H}$ appear higher in the list of genes output by uKIN. This suggests that uKIN can utilize cancer-type specific knowledge and highlights the benefits of having accurate prior information.

Figure 5.

(A) Use of cancer-type specific knowledge improves performance. For four cancer types, BRCA, GBM, SKCM, and THCA, we consider the performance of uKIN with α = 0.5 when using TCGA mutational data for that cancer type with prior knowledge consisting of genes known to be driver in that cancer type, as compared to performance when the prior knowledge set consists of genes that are annotated as driver only for one of the other three cancer types. For each cancer, performance is measured by the average ranking by uKIN of genes known to be driver for that cancer. For all combinations of possible prior knowledge sets (x-axis) and specific cancer gene sets that we wish to recover (y-axis), using prior knowledge from another cancer (off diagonal entries) leads to a decrease in performance as compared to the corresponding pairs (diagonal entries), as measured by the increase in uKIN’s average ranking of genes we aimed to uncover. (B) uKIN is effective in identifying complex disease genes. We demonstrate the versatility of the uKIN framework by integrating OMIM and GWAS data for three complex diseases, ALS, AMD, and epilepsy. For each disease, we compare uKIN’s performance when using OMIM annotated genes as prior information and GWAS hits as new information with α = 0.5, to baseline versions that propagate only information via diffusion from OMIM (left) or GWAS studies (right). In each panel, for each disease, we plot the log₂ ratio of the AUPRC obtained by uKIN to that obtained by the baseline method; in all cases, we observe that these values are positive, thereby demonstrating that uKIN outperforms the baseline methods by successfully integrating prior and new information.

Application to identify disease genes for complex inherited disorders

A major advantage of our method is that it can be easily applied in diverse settings. As proof of concept, we apply uKIN to detect disease genes for three complex diseases: Amyotrophic lateral sclerosis (ALS), age-related macular degeneration (AMD), and epilepsy. For each disease, we randomly split in half the OMIM database’s (Online Mendelian Inheritance in Man, OMIM®, 2000) list of genes associated with the disease 100 times to form the set of prior knowledge $\mathcal{K}$ and the hidden set $\mathcal{H}$. We use the GWAS catalogue list of genes with their corresponding p-values to form the set $\mathcal{M}$. For all three diseases, uKIN combining both GWAS and OMIM sources of information (α = 0.5) performs better than diffusing the signal with γ - 1 using only knowledge from OMIM (Figure 5B, left panel). For each of these diseases, there is virtually no overlap between the GWAS hits $\mathcal{M}$ and a set of OMIM genes $\mathcal{H}$; simply sorting genes by their significance in GWAS studies (i.e., uKIN with α = 1) results in AUPRC of 0. Instead, we spread information from the set of GWAS genes $\mathcal{M}$ in the same fashion as from OMIM and observe again that using this single source of information alone does not work as well as uKIN’s using both GWAS and OMIM information together (Figure 5B, right panel).

Discussion

In this paper, we have shown that uKIN, a network propagation method that incorporates both existing knowledge as well as new information, is a highly effective and versatile approach for uncovering disease genes. Our method is based upon the intuition that prior knowledge of disease-relevant genes can be used to guide the way information from new data is spread and interpreted in the context of biological networks. Because uKIN uses prior knowledge, it has higher precision than other state-of-the-art methods in detecting known cancer genes. Further, it excels at highlighting infrequently mutated genes that are nevertheless relevant for cancer. Additionally, we have shown that uKIN can be applied to discover genes relevant for other complex diseases as well.

The extent to which uKIN uses prior and new knowledge is balanced by a single parameter, α. While performance clearly varies with different values of this parameter, all tested values of α that combine both prior and new information result in performance improvements as compared to using either source of information alone (Suppl. Figures S3); this suggests that careful calibration of α is not necessary as long as both prior and new data are used. Nevertheless, the amount of prior knowledge available can guide selection of α. In particular, when substantial prior knowledge is available, uKIN can leverage it better when a smaller α is employed (Suppl. Figure S4). On the other hand, when knowledge is sparse or unreliable, a larger α allows uKIN to focus on the new information, as the walks restart more frequently and hover around the newly implicated genes.

The framework presented here can be extended in a number of natural ways. First, in addition to positive knowledge of known disease genes, we may also have “negative” knowledge of genes that are not involved in the development of a given disease. These genes can propagate their “negative” information, thereby biasing the random walk to move away from their respective modules and perhaps further enhancing the performance of our method. Second, uKIN is likely to benefit from incorporating edge weights that reflect the reliability of interactions between proteins; these weights will have an impact on both the propagation of prior knowledge as well as the guided random walks. Third, since a recent study (Przytycki and Singh, 2017) has shown that contrasting cancer mutation data with natural germline variation data helps boost the true disease signal by downgrading genes that vary frequently in nature, uKIN’s performance may benefit from scaling the starting probabilities of the new putatively implicated genes to account for their variation in healthy populations. Fourth, while here we have demonstrated how uKIN can use cancer-type specific knowledge, cancers of the same type can often be grouped into distinct subtypes, and such highly-detailed knowledge may improve uKIN’s performance even further. Finally, we note that network propagation approaches have been applied to other settings as well, including biological process prediction (Nabieva et al., 2005; Wang and Marcotte, 2011) and drug target identification (Picart-Armada et al., 2019). We conjecture that our guided network propagation approach will have wide applicability in computational biology, including where new data (e.g., arising from functional genomics screens) need to be interpreted in the context of what is already known about a biological process of interest.

In conclusion, uKIN is a flexible and effective method that handles diverse types of new information. As our knowledge of disease-associated genes continues to grow and be refined, and as new experimental data becomes more abundant, we expect that the power of uKIN for accurately prioritizing disease genes will continue to increase.

STAR Methods

Resource availability

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mona Singh (mona@cs.princeton.edu).

Materials Availability

This study did not generate new materials.

Data and Code Availability

All original code is freely available for download at https://github.com/Singh-Lab/uKIN.

Method details

Background and notation

The biological network is modeled, as usual, as an undirected graph G = (V, E) where each vertex represents a gene, and there is an edge between two vertices if an interaction has been found between the corresponding protein products. We require G to be connected, restricting ourselves to the largest connected component if necessary. We explain our formulation with respect to cancer, but note that it is applicable in other settings (both disease and otherwise). The set of genes already known to be cancer associated is denoted by $\mathcal{K}=\left\{k_1,k_2,\dots ,k_l\right\}$. The set of genes that have been found to be somatically mutated in a cohort of individuals with cancer is denoted by $\mathcal{M}=\left\{m_1,m_2,\dots ,m_p\right\}$, with $\mathcal{F}=\left\{f_{m_1},f_{m_2},\dots ,f_{m_p}\right\}$ corresponding to the rate with which each of these genes is mutated. We refer to $\mathcal{K}$ as the prior knowledge and $\mathcal{M}$ as the new information. We assume that $\mathcal{K}\subset V$ and $\mathcal{M}\subset V$; in practice, we remove genes not present in the network. The genes within $\mathcal{K}$ and $\mathcal{M}$ may overlap (i.e., it is not required that $\mathcal{K}\cap M=\varnothing$).

Guided RWR Algorithm

For each gene i ∈ V, assume that we have a measure q_i that represents how close i is to the set of genes $\mathcal{K}$. We will use the nonnegative vector q, which we describe in the next section, to guide a random walk starting at the nodes in $\mathcal{M}$ and walking towards the nodes in $\mathcal{K}$. Each walk starts from a gene i in $\mathcal{M}$, chosen with probability proportional to its mutational rate f_i. At each step, with probability α the walk can restart from a gene in $\mathcal{M}$, and with probability 1 — α the walk moves to a neighboring gene picked probabilistically based upon q. Specifically, if $\mathcal{N}(i)$ are the neighbors of node i, the walk goes from node i to node $j\in \mathcal{N}(i)$ with probability proportional to $q_j/{\sum }_{k\in \mathcal{N}(i)}{q}_k$. That is, if at time t the walk is at node i, the probability that it transitions to node j at time t + 1 is

$$p_{ij}=(1-\alpha ){\delta }_{ij}\cdot \frac{q_j}{{\sum }_{k\in N(i)}{q}_k}+\alpha \cdot \frac{f_j}{{\sum }_{k\in \mathcal{M}}{f}_k}$$

where δ_ij = 1 if $j\in \mathcal{N}(i)$ and 0 otherwise. Hence, the guided random walk is fully described by a stochastic transition matrix P with entries p_ij. By the Perron-Frobenius theorem, the corresponding random walk has a stationary distribution π (a left eigenvector of P associated with the eigenvalue 1). If the graph G is connected, then the back edges to $\mathcal{M}$ easily ensure that π is unique. Therefore, πP^t = π and we can compute the stationary distribution π that the guided random walk converges to. For each gene i, its score is given by the ith element of π. The genes whose nodes have high scores are most frequently visited and, therefore, are more likely relevant to cancer as they are close to both the mutated starting nodes as well as to known cancer genes. For the results presented in the main manuscript, α is set to 0.5.

Incorporating prior knowledge

For each gene in the network, we wish to compute how close it is to the set of cancer-associated genes $\mathcal{K}$. While many approaches have been proposed to compute “distances” in networks, we use a network flow/diffusion technique where each node $k\in \mathcal{K}$ introduces a continuous unitary flow which diffuses uniformly across the edges of the graph and is lost from each node v ∈ V in the graph at a constant first-order rate γ (Qi et al., 2008). Briefly, let A = (a_ij) denote the adjacency matrix of G (i.e., a_ij = 1 if (i, j) ∈ E and 0 otherwise) and let S be the diagonal matrix where s_ii is the degree of node i ∈ V. Then, the Laplacian of the graph G shifted by γ is defined as L = S + γI — A. The equilibrium distribution of fluid density on the graph is computed as q = L⁻¹ b (Qi et al., 2008), where b is the vector with 1 for the nodes introducing the flow and 0 for the rest (i.e., b_i = 1 if v_i ∈ K and b_i = 0 if v_i ∉ K for ∀v_i ∈ V). Note that L is diagonally dominant, hence nonsingular, for any γ ≥ 0. When spreading information from the set of prior knowledge genes, we set γ = 1, as recommended in (Qi et al., 2008). The vector q can be efficiently computed numerically. Thus, at equilibrium, each node i in the graph is associated with a score q_i which reflects how close it is to the nodes already marked as causal for cancer.

Guided diffusion

Instead of performing RWRs to propagate knowledge in a guided manner, it is also possible to adapt the diffusion approach just outlined by letting A = (a_ij) be defined such that $a_{ij}=q_j/{\sum }_{k\in \mathcal{N}(i)}{q}_k$, and using A to compute L and the equilibrium density as above.

Quantification and statistical analysis

Data sources and pre-processing

We test uKIN on two protein-protein interaction networks: HPRD (Release 9_041310) (Prasad et al., 2009) and BioGrid (Release 3.2.99, physical interactions only) (Stark et al., 2006). Biological networks often contain spurious interactions as well as proteins with many interactions. Since both can be problematic for network analysis, we pre-process the networks as described in (Hristov and Singh, 2017). Briefly, we remove all proteins with an unusually high number of interactions (> 900 interactions and more than 10 standard deviations away from the mean number of interactions). For BioGrid, this removes UBC, APP, ELAVL1, SUMO2 and CUL3. For HPRD, this removes no proteins. To further handle the connectivity arising within networks due to proteins with many interactions, we filter interactions using the diffusion state distance (DSD) metric introduced in (Cao et al., 2013); the DSD metric captures the intuition that interactions between proteins that also share interactions with low degree proteins are more likely to be functional than interactions that do not (and thus are assigned closer distances). For each interaction, the DSD scores (as computed by the software of (Cao et al., 2013)) between the corresponding proteins are Z-score normalized, and proteins with Z-scores > 0.3 are removed. This process leaves us with 9,379 proteins and 36,638 interactions for HPRD and 14,326 proteins and 102,552 interactions for BioGrid.

We use level 3 cancer somatic mutation data from TCGA (TCGA Research Network, n.d.) for 24 cancer types (Supplemental Table 1). For each cancer type, we process the data as previously described and exclude samples that are obvious outliers with respect to their total number of mutated genes (Hristov and Singh, 2017). Our set of prior knowledge is constructed from the 719 CGC genes that are labeled by COSMIC (version August 2018) as being causally implicated in cancer (Futreal et al., 2004). For each cancer type, our new information consists of genes that have somatic missense or nonsense mutations, and we compute the mutational frequency of a gene as the number of observed somatic missense and nonsense mutations across tumors, divided by the number of amino acids in the encoded protein.

We obtain 24, 28, and 63 genes associated with three complex diseases, age-related macular degeneration (AMD), Amyotrophic lateral sclerosis (ALS) and epilepsy, respectively, from OMIM (Online Mendelian Inheritance in Man, OMIM®, 2000). These genes are used to construct the set of prior knowledge. For each disease, we form the set M by querying from the GWAS database (Buniello et al., 2018) the genes implicated for the disease; we note that the genes reported by a given GWAS study are usually, but not always, those closest to the identified SNPs. We use the corresponding p-values for these genes to compute the starting frequencies f. Specifically, for each disease, for each GWAS study i, if a gene j’s p-value is p_i,j, we set its frequency to $\log \left(p_{i,j}\right)/{\sum }_k\log \left(p_{i,k}\right)$ and then for each gene average these frequencies over the studies.

Performance evaluation

To evaluate our method in the context of cancer, we subdivide the CGC genes that appear in our network into two subsets. We randomly draw from the CGCs 400 genes to form a set $\mathcal{H}$ of positives that we aim to uncover. From the remaining 199 CGCs present in the network, we randomly draw a fixed number l to represent the prior knowledge $\mathcal{K}$ and run our framework. Unless otherwise stated, we use l = 20 for all reported results. As we consider an increasing number of most highly ranked genes, we compute the fraction that are in the set $\mathcal{H}$ of positives. All CGC genes not in $\mathcal{H}$ are ignored in these calculations. Importantly, the genes in $\mathcal{K}$ which are used to guide the network propagation are never used to evaluate the performance of uKIN. Note that this testing set up, which measures performance on $\mathcal{H}$, allows us to compare performance of uKIN when choosing prior knowledge sets of different size l from the CGC genes not in $\mathcal{H}$.

We also compute area under the precision-recall curves (AUPRCs). In this case, all CGC genes in $\mathcal{H}$ are considered positives, all CGC genes not in $\mathcal{H}$ are neutral (ignored), and all other genes are negatives. Though we expect that there are genes other than those already in the CGC that play a role in cancer, this is a standard approach to judge performance (e.g., see (Jia and Zhao, 2014)) as cancer genes should be highly ranked. To focus on performance with respect to the top predictions, we compute AUPRCs using the top 100 predicted genes. To better estimate AUPRCs and account for the randomness in sampling, we repeatedly draw (10 times) the set $\mathcal{H}$ and for each draw we sample the genes comprising the prior knowledge $\mathcal{K}$ 10 times. The final AUPRC results from averaging the AUPRCs across all 100 runs.

We compare uKIN on the cancer datasets to the frequency-based method MutSigCV 2.0 (Lawrence et al., 2013) and four network-based methods, DriverNet (Bashashati et al., 2012), Muffinn (Cho et al., 2016), nCOP(Hristov and Singh, 2017) and HotNet2 (Leiserson et al., 2015). All methods are run on each of the 24 cancer types with their default parameters. Muffinn, nCOP and HotNet2 are run on the same network as uKIN, whereas MutSigCV does not use a network and DriverNet instead uses an influence (i.e., functional interaction) graph and transcriptomic data (we use their default influence graph and provide as input TCGA normalized expression data). Since uKIN uses a subset of CGCs as prior knowledge, we ensure that all methods are evaluated with respect to the hidden sets $\mathcal{H}$ (i.e., of CGCs not used by uKIN). Though we could just consider performance with respect to one hidden set, considering multiple sets enables a better estimate of overall performance. For these comparisons, uKIN with α = 0.5 is run 100 times, as described above, with 20 randomly sampled genes comprising the prior knowledge, and evaluation is performed with respect to the genes in the hidden sets. All methods’ AUPRCs are computed using the same randomly sampled test sets $\mathcal{H}$ and averaged at the end. Since HotNet2 outputs a set of predicted cancer-relevant genes and does not rank them, we cannot compute AUPRCs for it; instead we compute precision and recall for its output with respect to the test sets $\mathcal{H}$ and compare to uKIN’s when considering the same number of top scoring genes. Note that all methods use all TCGA data for a cancer type for each run.

To evaluate our method in the context of the three complex diseases, we subdivide evenly the set of OMIM genes associated with each disease into the prior knowledge set $\mathcal{K}$ and the set of positives $\mathcal{H}$. As with the cancer data, we do this repeatedly (100 times) and average AUPRCs at the end.

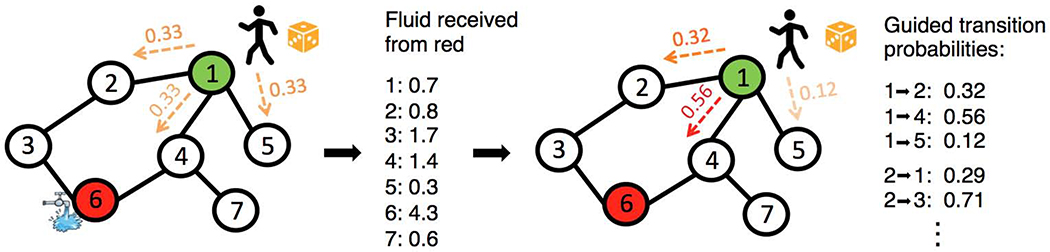
Figure 1. Illustration of guided random walks.

A schematic of a network with seven genes is shown, with node 1 as a putatively implicated disease gene (in green) and node 6 as a known disease gene (in red). Our approach performs guided random walks with restarts from putatively implicated genes. (Left) In a traditional random walk procedure, a walker at node 1 is equally likely to move to one of the neighboring nodes. In our procedure, before random walks are initiated from putative disease genes, fluid is injected at known disease genes and diffused along the edges of the network. (Center) Nodes closer to the source of the fluid receive larger amounts of fluid. (Right) Instead of performing a random walk with uniform transition probabilities to any neighboring node, the walker uses the amount of fluid at each node to update the transition probabilities; these transition probabilities guide the walk so as to tend to move the walker closer to known disease genes.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
DriverNet	Bashashati et al., (2012)	https://www.bioconductor.org/packages/release/bioc/html/DriverNet.html
DSD	Cao et al. (2013)	http://dsd.cs.tufts.edu/server/
Hotnet2	Leiserson et al. (2015)	https://github.com/raphael-group/hotnet2
Muffinn	Cho et al. (2016)	http://www.inetbio.org/muffinn/
MutSigCV	Lawrence et al. (2013)	http://archive.broadinstitute.org/cancer/cga/mutsig
nCOP	Hristov and Singh (2017)	https://github.com/Singh-Lab/nCOP
uKIN	This paper	https://github.com/Singh-Lab/uKIN
Other
Biogrid	Stark et al. (2006)	https://thebiogrid.org/
GWAS	Buniello et al., (2019)	https://www.ebi.ac.uk/gwas/
HPRD	Prasad et al. (2009)	http://www.hprd.org/
OMIM	Online Mendelian Inheritance in Man	https://omim.org/
TCGA	TCGA Research Network	https://cancergenome.nih.gov/

Primer.

Biological networks provide a powerful framework for discovering disease genes. Genes relevant for a given disease typically target a relatively small number of biological pathways, and since genes that take part in the same pathway or process tend to be close to each other in networks, disease genes cluster within networks. It is well established that if genes known to be causal for a particular disease are mapped onto a network, other disease-relevant genes are likely to be found in their vicinity. The simplest methods to predict disease genes using interaction networks rely on finding those that directly interact with a known disease gene, or that are a short number of “hops” on the network to at least one known disease gene.

More sophisticated methods aim to uncover genes that are close not just to a single disease gene but that are close, as a whole, to all disease genes. The concept of random walks on graphs (or networks) underlies many approaches to measure these distances within biological networks. In its simplest version, we imagine a “walker” at a particular protein (or node) at a specific time, and at every time point, the walker moves to one of its neighbors at random. We consider a variant where at the start of the process, the walker is at each node with some probability, and at each subsequent time point, the walker can either restart with probability α or otherwise walk to one its neighbors. When we constrain these walks by having the walker only start at a set of known disease genes, then the walker will tend to “hover” around this set of genes. Mathematically, it is possible to compute the fraction of time the walker is at each node over very long random walks, and this so-called stationary distribution can be used to prioritize disease genes, as those genes that are closer to the initial set of disease genes will tend to have higher values. An alternative but closely related formalism relies on the idea of diffusion, where fluid is pumped into an initial set of genes and spreads through the graph over the edges with fluid “leaking” out at some rate at each node; again, in the limit, genes closer to the initial set of genes will have more fluid, and this can be computed mathematically.

Random walk and diffusion-based methods can each be used to identify disease genes, by spreading signal either from well-established, annotated disease genes or from genes that have some new evidence of being disease-relevant (e.g., genes somatically mutated in cancers or identified via genome-wide association studies). Here we introduce a framework that uses both sources of biological information, as existing knowledge of disease genes should inform the way new mutational data is examined within networks (Figure 1). We propose a guided random walk approach to uncover disease genes, where walks initiate from the new data and when choosing which nodes to walk to, the walks are biased so as to tend to move towards genes which have been determined via a diffusion process to be closer to known disease genes. We apply our approach to somatic mutations observed across tumors to discover genes causal for cancer, as well as to genome-wide association data to discover genes causal for complex diseases. We demonstrate that propagating signal by integrating both known disease genes as well as new putative disease genes performs substantially better than propagating signal from either source alone.

Highlights.

• Guided network propagation method for discovery of disease-relevant genes

• Uses known disease genes to guide random walks initiated at newly implicated genes

• The guided walks allow for network-based integration of prior and new data

• Effectiveness of method shown on cancer genomics and genome-wide association data