Approximations of the power functions for Wald, likelihood ratio, and score tests and their applications to linear and logistic regressions

Summary.

Traditionally, asymptotic tests are studied and applied under local alternative (Aivazian, et al., 1985). There exists a widespread opinion that the Wald, likelihood ratio, and score tests are asymptotically equivalent. We dispel this myth by showing that These tests have different statistical power in the presence of nuisance parameters. The local properties of the tests are described in terms of the first and second derivative evaluated at the null hypothesis. The comparison of the tests are illustrated with two popular regression models: linear regression with random predictor and logistic regression with binary covariate. We study the aberrant behavior of the tests when the distance between the null and alternative does not vanish with the sample size. We demonstrate that these tests have different asymptotic power. In particular, the score test is generally asymptotically biased but slightly superior for linear regression in a close neighborhood of the null. The power approximations are confirmed through simulations.

1. Introduction

Uniformly most powerful tests exist only in rare statistical models - usually they exist for linear model with fixed/nonrandom predictors and normal distribution (Aivazian et al. 1985; Lehmann and Romano, 2005). On the other hand, asymptotic tests, such as the Wald, likelihood ratio, and score tests can be applied to a much wider variety of statistical distributions and models when the sample size, n, increases to infinity. For a short review of these test we refer the reader to a recent book by the author [9].There exists a widespread opinion that the three tests are asymptotically optimal and equivalent for large n, as stated by Rayner (1997), Young and Smith (2005), among many others. Because of this opinion, not much preference is given to what test to use to determine the desired sample size.

Usually, the treatment of asymptotic tests is reduced to the analysis with local alternatives, or in the terminology of Cox and Hinkley (1974), contiguous alternatives, based on the concept of contiguity (Lehmann and Romano, 2005). It is a textbook result that the Wald and likelihood ratio tests are equivalent for alternatives at the distance of O(n^−1/2) from the null value. The following warning on page 156 from a book by Robert Serfling (1980) is the impetus to the present work: “Therefore, under appropriate regularity conditions, the statistics λ_n, W_n and V_n are asymptotically equivalent in distribution, both under the null hypothesis and under local alternatives converging sufficiently fast. However, at fixed alternatives these equivalences are not anticipated to hold.” (Here, λ_n, W_n and V_n are likelihood ratio, Wald and score statistics, respectively.) Moreover, we argue that the study with contiguous alternatives is not appealing from the practical point of view. For example, it’s not applicable to the sample size determination where the alternative is fixed.

The goal of the present work is to analyze the two-sided tests in the presence of nuisance parameters using the power function with the emphasis on the global (or fixed) alternatives. Respectively, the local properties are expressed in terms of the first and second derivative evaluated at the null value of the parameter. The tests are then illustrated with linear regression and normally distributed predictor when the variance is unknown and logistic regression with Bernoulli covariate for which the asymptotic power function is derived in closed form.

It is natural to expect that the rate of rejecting the null hypothesis increases as the alternative gets farther from the null. However, Hauck and Donner (1977) and Væth (1985) showed that the Wald test may be aberrant in this respect - we investigate the aberrant behavior of the likelihood ratio and score tests as well.

Much of the effort, with some controversy, has been made on the comparison of the tests using the method of contiguous alternatives. In particular, several claims have been made that the Rao’s score test is superior to Wald and likelihood ratio test (Chandra and Joshi, 1983; Chandra and Mukerjee, 1984). We confirm this claim for a linear model with random predictors in a close proximity to the null. Otherwise, these tests are different and it is impossible to claim an overall champion. Moreover, the score test is usually biased.

The organization of the paper is as follows. After introducing notation and definitions, we derive the power function for the Wald, likelihood ratio, and score tests in each of the following sections and illustrate it with linear and logistic regression models. The three tests are compared in terms of power.

2. Notation and definitions

Throuthout the paper, we deal with iid observations {z_i, i = 1, …, n} having common density f = f(z; θ) dependent on a vector parameter θ =(β, γ); formally, θ₁ = β. The first component, β, is treated as the parameter of interest and γ is treated as a p-dimensional vector of nuisance parameters (Pawitan, 2001). The null hypothesis is composite, H₀ : β = β₀ with the two-sided alternative, H_A : β ≠ β₀. For expository purposes, we shall assume that β₀ = 0, so that the null hypothesis takes the form

$$H_0:\beta =0.$$ (1)

If T = T(z₁, …, z_n) is a test statistic such that the null is rejected when T > c, the power function for (1) can be expressed as a function of the alternative,

$$P(\beta ;\gamma )=\text{Pr}(T>c\mid \theta ).$$ (2)

Here, P(0; γ) = α is the the significance level or the size of the test (typically, α = 0.05) and |θ means that the probability (2) is computed under the assumption that the true parameter is θ. We vary β but fix γ, so we treat (2) as a function of β. In this paper, the power function (2) is computed, or more precisely, approximated, for large n. This, fortunately, implies that P(0) does not depend on nuisance parameters. We assume that the necessary regularity conditions for asymptotic maximum likelihood estimation and hypothesis testing are fulfilled, such as the support of f does not depend on the parameter, differentiation under the expectation is valid and the power function is twice differentiable (Casella and Berger, 1990; Schervish, 1995; Bickel and Doksum, 2001).

The log-likelihood function is

$$l(\beta ,\gamma )=\sum _{i=1}^n\text{ln}f\left(z_i;\beta ,\gamma \right).$$ (3)

The maximum likelihood estimator (MLE), (${\widehat{\beta }}_{ML}$, ${\widehat{\gamma }}_{ML}$), is the solution of 1 + p score equations

$$\frac{\partial l(\beta ,\gamma )}{\partial \beta }=0,\frac{\partial l(\beta ,\gamma )}{\partial \gamma }=0.$$ (4)

The Fisher expected information matrix is defined as

$$\left[\begin{array}{cc}{I}_{11}& I_{12}^{\prime }\\ I_{12}& I_{22}\end{array}\right]=-E\left[\begin{array}{cc}\frac{{\partial }^2\text{ln}f}{\partial {\beta }^2}& \frac{{\partial }^2\text{ln}f}{\partial \beta \partial \gamma }\\ \frac{{\partial }^2\text{ln}f}{\partial \gamma \partial \beta }& \frac{{\partial }^2\text{ln}f}{\partial {\gamma }^2}\end{array}\right].$$ (5)

(As a part of regularity conditions we assume that the information matrix is nonsingular.) Asymptotically, the variance of ${\widehat{\beta }}_{ML}$ can be derived from the (1, 1)th element of the inverse matrix,

$$var\left({\widehat{\beta }}_{ML}\right)=\frac{1}{n}V(\beta ),$$ (6)

where

$$V(\beta )=\frac{1}{I_{11}-I_{12}^{\prime }{I}_{22}^{-1}{I}_{12}}$$ (7)

is the variance function evaluated at the alternative, β. In this formula, V is evaluated at the true value of the nuisance parameter, γ. When studying the likelihood ratio and score tests, we shall evaluate V at other values which will be indicated as V (β|γ₀). Sometimes, it is more convenient (especially for the Wald test) to deal with the standard deviation (SD) function, ${\sigma }_{\beta }=\sqrt{V(\beta )}$.

Now we describe the local properties of the tests in terms of the first and second derivatives of the power function evaluated at the null, β = 0; see Rao (1973, p. 454). First, since we require the tests to have size α we assume

$${P(\beta )|}_{\beta =0}=\alpha .$$ (8)

Second, we want the test to be asymptotically (locally) unbiased, which means that the first derivative at the null is zero,

$$P^{\prime }(0)={\frac{dP}{d\beta }|}_{\beta =0}=0.$$ (9)

Third, the local power for an unbiased test is determined by the second derivative,

$$P^{\prime \prime }(0)={\frac{d^{2}P}{d{\beta }^2}|}_{\beta =0}.$$ (10)

The higher the value of the second derivative, the more powerful the test is for local alternatives. In fact, we can approximate the power as $P(\beta )=\alpha +\frac{1}{2}{P}^{\prime \prime }(0){\beta }^2$ in the neighborhood of the null. Finally, the test is consistent if lim_n→∞ P (β) = 1 for all β ≠ 0.

Now we derive the power functions for the three tests and illustrate them with popular statistical models: linear and logistic regressions.

3. Wald test

The Wald test is based on the fact that under the null and large n, the ratio of the MLE to its standard error, sometimes called the Z-score, is normally distributed,

$$\frac{{\widehat{\beta }}_{ML}}{SE\left({\widehat{\beta }}_{ML}\right)}~\mathcal{N}(0,1)$$

for large n. The test statistic is the absolute value of the Z-score with c = Z_1−α/2, the (1 − α/2) quantile of the standard normal distribution, namely, Z_1−α/2 = Φ(1 − α/2). The power function of the Wald test in large sample can be approximated as follows

$$P_W(\beta )\simeq \Phi \left(-Z_{1-\alpha /2}+\frac{\beta }{{\sigma }_{\beta }}\sqrt{n}\right)+\Phi \left(-Z_{1-\alpha /2}-\frac{\beta }{{\sigma }_{\beta }}\sqrt{n}\right),$$ (11)

where sign ≃ means the approximation for large n. The validity of the approximations follows from Slutsky’s theorem and uniform convergence follows from continuity of derivatives (see details in Bickel and Doksum, 2001; Demidenko, 2004, p. 644). Apparently, the larger the n the better approximation.

Property (8) holds for the Wald power. It is easy to see that Wald power is symmetric about the null, β = 0. Consequently, the Wald power is asymptotically unbiased, which can be verified directly by evaluating the derivative at zero,

$${\frac{d{P}_W}{d\beta }|}_{\beta =0}=\left[\varphi \left(-Z_{1-\alpha /2}\right)\frac{\sqrt{n}}{{\sigma }_0}-\varphi \left(-Z_{1-\alpha /2}\right)\frac{\sqrt{n}}{{\sigma }_0}\right]\times {\frac{dV}{d\beta }|}_{\beta =0}=0,$$

where ϕ = Φ′, the standard normal density. The test is consistent (or better to say asymptotically consistent) because lim_n→∞ P_W(β) = 1 if β ≠ 0.

The second derivative of the power function (11) at the null takes the form

$${\frac{d^{2}P}{d{\beta }^2}|}_{\beta =0}=\frac{2n}{V(0)}\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2},$$ (12)

so approximately in the neighbourhood of zero P_W(β) ≃ α + nϕ + (Z_1−α/2) Z_1−α/2β²/V (0).

As follows from (11), the Wald power simplifies under z-parametrization,

$$P_W(z)=\Phi \left(-Z_{1-\alpha /2}+z\sqrt{n}\right)+\Phi \left(-Z_{1-\alpha /2}-z\sqrt{n}\right),$$ (13)

where

$$z=\frac{\beta }{{\sigma }_{\beta }}$$ (14)

can be treated as a theoretical counterpart of the Z-score statistic. We refer to (14) as the z-ratio at the alternative, β. In applications, the z-ratio is called the effect size (Cohen, 1994). It is easy to show that the Wald power is an increasing function for β > 0 and a decreasing function of z for β < 0. In other words, the larger the absolute value of the z-function, the greater the power. The z-parametrization reappears in the power functions of the likelihood ratio and score tests for a linear model.

3.1. Linear regression

We illustrate the calculation of the Wald power with linear regression under normal distribution. Note that typically, the power analysis is conducted for the case when predictor x is fixed/nonrandom. We however, develop the power analysis for a more complicated model when x is random, or more precisely, normally distributed. Thus, vector z has a multivariate normal distribution; the first component is the dependent variable, y; the second component is the variable of interest, x; the rest are covariates combined in vector u. We test the significance of the coefficient, β, at the variable of interest, x. Without loss of generality, we can assume that the means of all regression variables are zero and the marginal variances and covariances are known:

$$\left[\begin{array}{l}x\hfill \\ u\hfill \end{array}\right]~\mathcal{N}\left(\left[\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right],\left[\begin{array}{cc}{\sigma }_x^2& {\sigma }_{xu}^{\prime }\\ {\sigma }_{xu}& {\Sigma }_u\end{array}\right]\right).$$

The linear regression is specified through conditional mean as

$$E(y\mid x,u)=\beta x+{\mathit{\tau }}^{\prime }u,$$ (15)

where var(y|x, u) = σ². The conditional (error) variance, σ², is unknown and subject to estimation along with the vector of regression coefficients. Linear regression is used as an example of hypothesis testing in many texts, but σ² is assumed known (Cox and Hinkley, 1974). A more realistic set up with unknown variance brings up several surprises, as we shall see later.

Since the distribution is normal and marginal variance-covariance parameters are known, the log density of z, up to a constant, is given by

$$\text{ln}f(z;\beta ,\gamma )=-\frac{1}{2{\sigma }^2}{\left(y-\beta x-{\mathit{\tau }}^{\prime }u\right)}^2-\frac{1}{2}\text{ln}{\sigma }^2,$$ (16)

where γ =(τ, σ²). The information matrix takes the form

$$\frac{1}{{\sigma }^2}\left[\begin{array}{ccc}{\sigma }_x^2& {\sigma }_{xu}^{\prime }& 0\\ {\sigma }_{xu}& {\Sigma }_u& 0\\ 0& 0& \frac{1}{2}{\sigma }^{-2}\end{array}\right],$$

so that the Wald power is given by (11) with

$${\sigma }_{\beta }=\frac{\sigma }{\sqrt{{\sigma }_x^2-{\sigma }_{xu}^{\prime }{\Sigma }_u^{-1}{\sigma }_{xu}}}.$$ (17)

The Wald power function has a familiar V-shape, and it monotonically increases with |β| and approaches 1 - no surprises so far.

3.2. Logistic regression with binary covariate

In general regression problems, the distribution of z is defined through conditional distribution as f(z; θ) = f(y|x; θ) f(x; θ), where y is treated as the dependent variable and x as the vector of covariates. As in the previous example, statistical hypothesis is concerned with testing of the slope coefficient, β.

Here, we illustrate the Wald test with logistic regression and binary covariate. This means that both y and x are binary. The probability of the dependent variable is defined through conditional probability as

$$\text{pr}(y=1\mid x)=\frac{e^{\gamma +\beta x}}{1+e^{\gamma +\beta x}}.$$

The marginal probability of x is specified as Pr(x = 1) = p_x, which can be assumed known without loss of generality. Logistic regression is a member of the family of generalized linear models (GLM, Bickel and Doksum, 2001). After elementary calculations, the information matrix takes the form

$$\left[\begin{array}{cc}\frac{GB{p}_x}{{(1+GB)}^2}+\frac{G\left(1-p_x\right)}{{(1+G)}^2}& \frac{GB{p}_x}{{(1+GB)}^2}\\ \frac{GB{p}_x}{{(1+GB)}^2}& \frac{GB{p}_x}{{(1+GB)}^2}\end{array}\right],$$

where to shorten the notation, we let G = e^γ and B = e^β. Applying formula (7), we derive the variance function:

$$V(\beta )=\frac{p_x{(1+G)}^{2}B+\left(1-p_x\right){(1+GB)}^2}{p_x\left(1-p_x\right)GB}.$$ (18)

For a small alternative, the Wald power can be approximated quadratically as

$$P_W(\beta )\simeq \alpha +\frac{p_x\left(1-p_x\right)G}{{(1+G)}^2}n\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}{\beta }^2.$$ (19)

As follows from this formula, maximum power for small alternatives occurs for a symmetrically distributed covariate, p_x = 1/2. Using elementary calculus, one can show that symmetric distribution of the dependent variable leads to maximum power, G = 1 and P(y = 1) = 1/2. Combining these facts, we obtain an upper bound for the Wald power, P_W(β) ≤ α+(n/16)ϕ (Z_1−α/2) Z_1−α/2β². With a popular choice, α = 0.05, we have P_W(β) ≤ 0.05 + 0.0036nβ². For example, to detect β = 1 with power 0.8, one needs at least n = 208 observations.

The trouble with Wald power (11) begins when it is computed for large alternatives, because as follows from (18), the z-ratio (14) vanishes at infinity, lim_β→±∞ z = 0. The fact that the Wald power for logistic regression may fall for large alternative was noticed by Hauck and Donner (1977); they termed it aberrant behavior. This negative property of the Wald test was later studied in a broader context of a family of exponential distributions by Væth (1985), and for a linear model by Fears et al. (1996). For large alternatives the Wald power decreases to the size of the test—see Figure 1 for a geometrical illustration. The power function is computed for α = 5% and Pr(y = 1|β = 0) = G/(1 + G) = 0.25, and p_x = Pr(x = 1) = 0.2 with n = 100. The quadratic approximation (19) is valid in a close neighborhood of the origin. The Wald power falls at β = −2.4 and beyond this point decreases back to α when β → −∞. We show four simulation results for alternatives β = −3, −2, 1/2, and 1 (the number of experiments equals 5,000). For large negative values of β, the power approximation (11) is not valid because n = 100 is too small. To account for change in the variance function at the alternative versus the variance at the null, we introduce the effective sample size,

$$n_e=\frac{V(0)}{V(\beta )}n.$$ (20)

The effective sample size can be interpreted as the sample size modification for detection of a large alternative versus a local alternative due to the change of variance. For example, the effective sample size to detect alternative β = −2 with n = 100, as follows from (18), is

$$n_e=\frac{B{(1+G)}^2}{p_x{(1+G)}^{2}B+\left(1-p_x\right){(1+GB)}^2}n=32.$$

The effective sample size, one third the size of the original, explains why simulations at β = −2 in Figure 1 do not quite match the power: n_e = 32 is simply not large enough for the Central Limit Theorem to give a good approximation.

Figure 1.

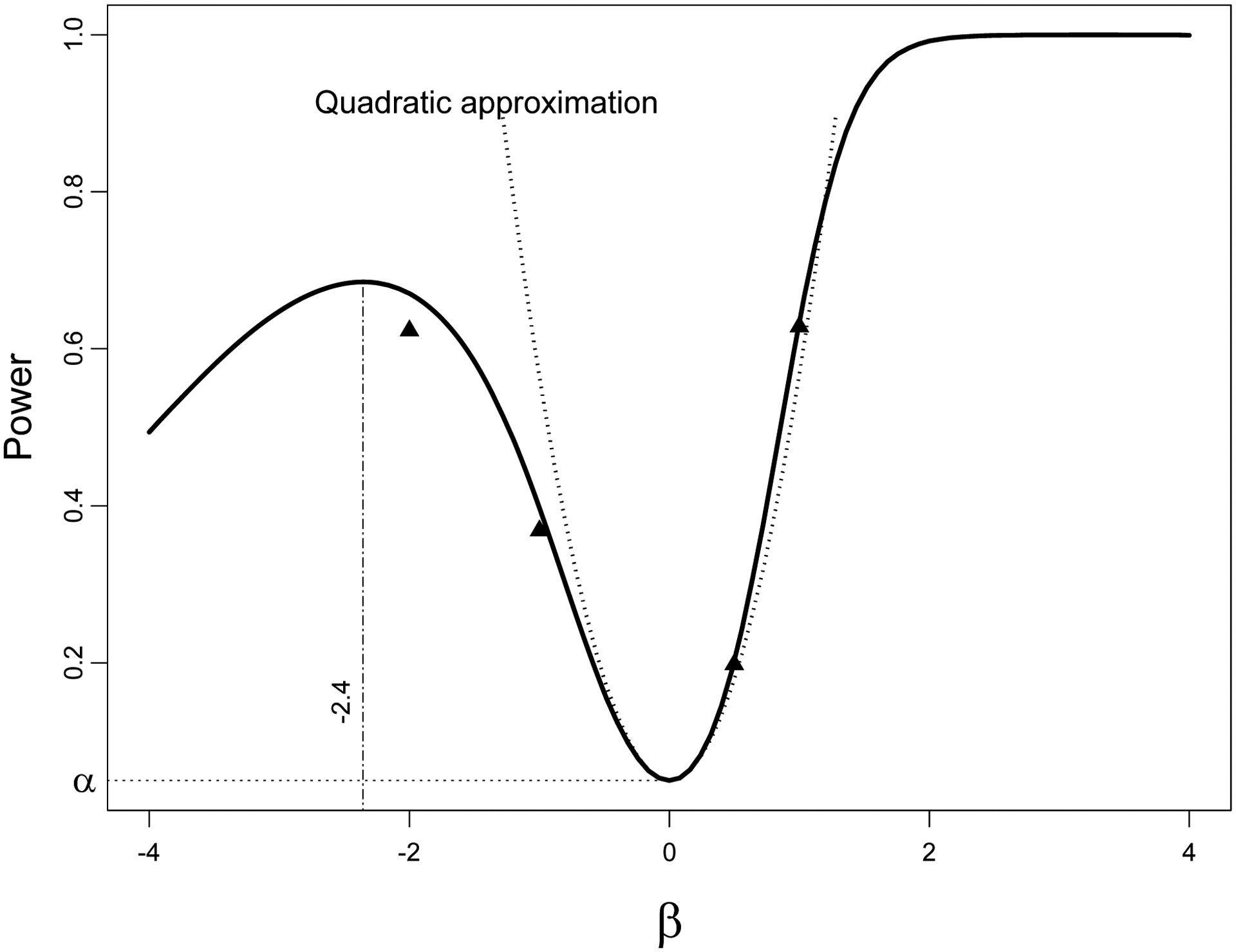
The Wald power and its quadratic approximation for logistic regression with a binary covariate, α = 0.05, Pr(y = 1|β = 0) = 0.25, Pr(x = 1) = 0.2, and n = 100. The Wald power falls at β = −2.4. Simulations (▲) are good match of the power approximation especially for positive alternatives (N_exp=5,000).

As follows from z-parametrization (13), the value of the alternative where the monotonicity of the Wald power falls satisfies the equation

$$\beta \frac{d\text{ln}{\sigma }_{\beta }}{d\beta }=1,$$ (21)

which will be referred to as the Wald break-down equation. In Figure 2, we show the region within which the Wald power behaves well, meaning that it increases for β > 0 and decreases for β < 0. The boundary of the shaded region is where its derivative turns zero as defined by equation (21). Roughly, one could say that the Wald power for logistic regression is well-behaved for alternatives in the interval (−2, 2).

Figure 2.

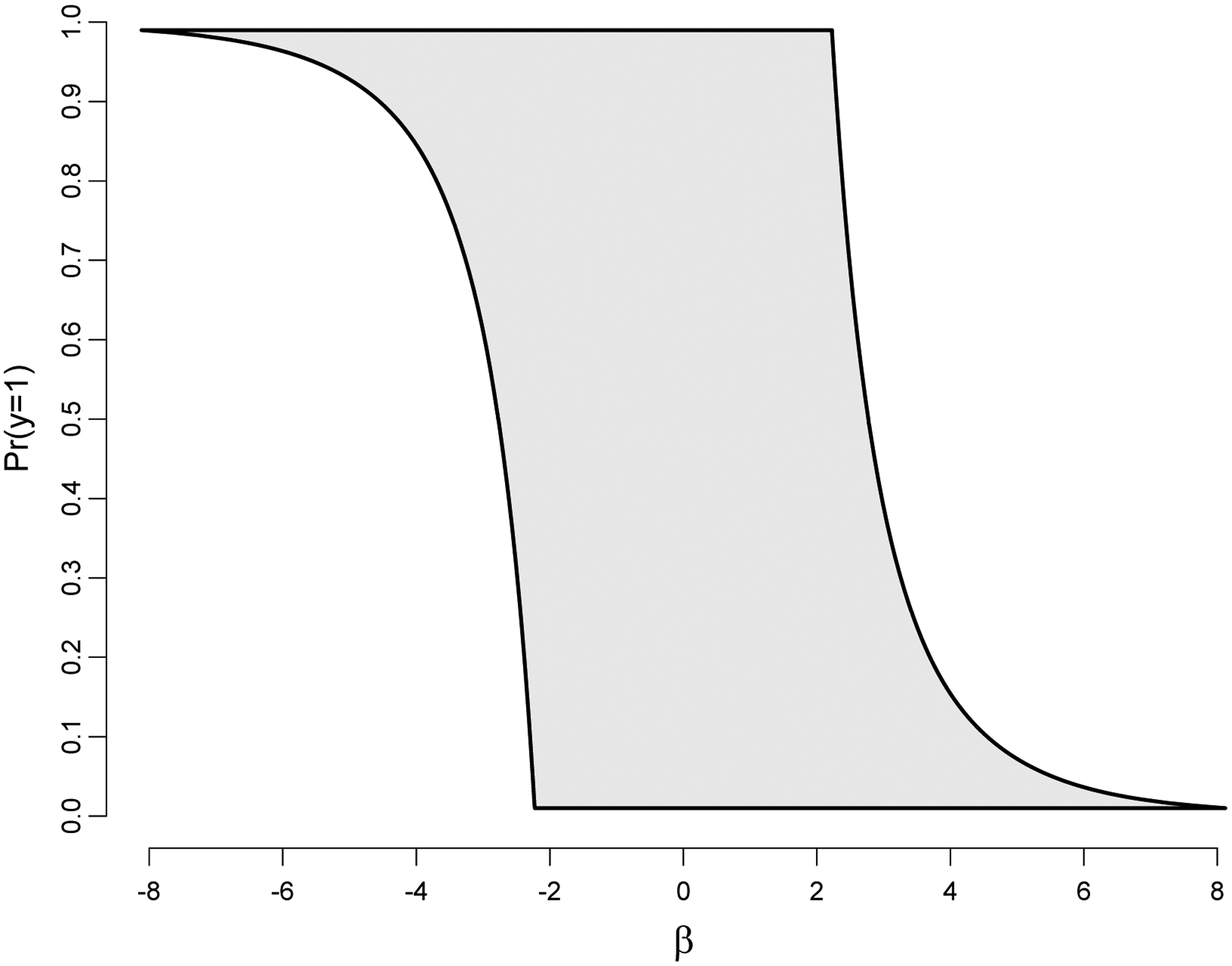
The power function is increasing for positive alternative and decreasing for negative alternative for (β, p_x) within the gray region. Approximately, the Wald power is an increasing function of the distance from the null if |β| ≤ 2.

4. Likelihood ratio test

The test statistic of the likelihood ratio (LR) test is

$$T=2\left[\underset{\beta ,\gamma }{\text{max}}l(\beta ,\gamma )-\underset{\gamma }{\text{max}}l(0,\gamma )\right],$$

which under the null has χ²-distribution with one degree of freedom, χ²(1). Hence, according to the likelihood ratio test, we reject the null if T > q_1−α, where q_1−α is the (1 − α)th quantile. Under the alternative, the maximizer of l(0, γ), which is referred to as a profile nuisance parameter, ${\widehat{\gamma }}_0$, yields a biased estimator of γ. To derive the power function, we represent the rejection probability in the following way (Self et al., 1992),

$$\begin{gathered} \text{pr}\left(T>q_{1-\alpha }\right) \\ =\text{pr}\left\{2\left[\left(\underset{\beta ,\gamma }{\text{max}}l(\beta ,\gamma )-l(\beta ,\gamma )\right)+\left(l(\beta ,\gamma )-\underset{\gamma }{\text{max}}l(0,\gamma )\right)\right]>q_{1-\alpha }\right\}. \end{gathered}$$

Using the biased estimation equation theory, one can prove that the maximizer of l(0, γ) converges to γ₀ = γ₀(β, γ), which is the solution to the equation

$$E_{(\beta ,\gamma )}\left(\frac{\partial \text{ln}f\left(z;0,{\gamma }_0\right)}{\partial {\gamma }_0}\right)=0,$$ (22)

which will be referred to the limit profile nuisance parameter. Since

$$\underset{n\to \infty }{\text{lim}}\frac{1}{n}(l(\beta ,\gamma )-\underset{\gamma }{\text{max}}l(0,\gamma )=E_{(\beta ,\gamma )}\left(\text{ln}f(z;\beta ,\gamma )-\text{ln}f\left(z;0,{\gamma }_0\right)\right)$$

with probability 1, the distribution of T under the alternative is χ²(1) with the noncentrality parameter 2nη(β), where

$$\eta (\beta )=E_{(\beta ,\gamma )}\left(\text{ln}f(z;\beta ,\gamma )-\text{ln}f\left(z;0,{\gamma }_0\right)\right)$$ (23)

will be referred to as the η-function. Note that the η-function is nonnegative, specifically, η(β) > 0 for all γ ≠ γ₀. Notice that for a local alternative (β → 0), we have γ₀ → γ and η(β) → 0. The noncentrality parameter depends on β and γ, but we fix the latter and consider η only as a function of β.

Finally, the power function of the LR test can be expressed via Φ as

$$P_{LR}(\beta )=\Phi \left(-Z_{1-\alpha /2}+\sqrt{2n\eta (\beta )}\right)+\Phi \left(-Z_{1-\alpha /2}-\sqrt{2n\eta (\beta )}\right).$$ (24)

An advantage of expressing the power in terms of Φ, is that one can apply it for a signed LR test, which is useful for one-sided hypotheses (Severeni, 2000). Note that the power is completely specified by function η.

The local equivalence of the Wald and LR tests has been established using the method of local alternatives, β = O(0), Serfling (1980). We prove this by showing that the second derivatives of the power functions evaluated at β = 0 are the same.

Theorem 1.

The Wald and LR tests are asymptotically unbiased (the first derivative of the power function vanishes at the null) and locally equivalent,

$${\frac{d^2{P}_W}{d{\beta }^2}|}_{\beta =0}={\frac{d^2{P}_{LR}}{d{\beta }^2}|}_{\beta =0}.$$

The proof is found in the Appendix.

Note that if the η-function (23) is an increasing function of β then the likelihood ratio power increases with distance from the null. Now we derive the power function for the two regressions, as we did for the Wald power.

4.1. Linear regression

We derive the likelihood ratio power for linear regression from Section 3.1. The regression is specified by equation (15) with the log density (16). First, we find the limit profile nuisance parameter, γ₀ = γ₀(β, γ) as the solution to (22), which for linear regression is equivalent to the pair of equations, $E\left[\left(y-{\tau }_{*}^{\prime }u\right)u\right]=0$ and ${\sigma }_{*}^2=E{\left(y-{\tau }_{*}^{\prime }u\right)}^2$. In this section, we omit the subscript (β, γ) on the expectation for brevity. Using some algebra, we obtain

$$\begin{gathered} E\left[\left(y-{\mathit{\tau }}_{*}^{\prime }u\right)u\right]=E\left[\left(y-\beta x-{\tau }^{\prime }u+\beta x-{\left({\tau }_{*}-\tau \right)}^{\prime }u\right)u\right] \\ =E\left[\left(\epsilon +\beta x-{\left({\tau }_{*}-\tau \right)}^{\prime }u\right)u\right]=\beta {\sigma }_{xu}-{\Sigma }_u\left({\tau }_{*}-\tau \right), \end{gathered}$$

which yields the solution

$${\tau }_{*}=\tau +\beta {\Sigma }_u^{-1}{\sigma }_{xu},$$ (25)

$${\sigma }_{*}^2={\sigma }^2+{\beta }^2\left({\sigma }_x^2-{\sigma }_{xu}^{\prime }{\Sigma }_u^{-1}{\sigma }_{xu}\right).$$ (26)

Now we find the noncentrality parameter. Specifically, we want to express function (23) through unknown parameters β, τ, and σ². From (16) we obtain

$$\eta (\beta )=-\frac{1}{2}+\frac{1}{2{\sigma }_{*}^2}E{\left(y-{\tau }_{*}^{\prime }u\right)}^2+\frac{1}{2}\text{ln}\frac{{\sigma }_{*}^2}{{\sigma }^2}=\frac{1}{2}\text{ln}\left(1+\frac{{\beta }^2}{{\sigma }_{\beta }^2}\right),$$

where σ_β is given by (17). Finally, the power function of the LR test on the z-scale (14) can be approximated as

$$P_{LR}(z)=\Phi \left(-Z_{1-\alpha /2}+\sqrt{n}\sqrt{\text{ln}\left(1+z^2\right)}\right)+\Phi \left(-Z_{1-\alpha /2}-\sqrt{n}\sqrt{\text{ln}\left(1+z^2\right)}\right).$$ (27)

Clearly, the Wald and LR power are different for linear regression contrary to the case when σ² is known. Further test comparisons are found in Section 6.

4.2. Logistic regression with binary covariate

Now we apply the LR test to the logistic regression with a binary covariate from Section 3.2. For this statistical model, we have

$$\text{ln}f(y,x;\beta ,\gamma )=y\gamma +\beta (xy)-\text{ln}\left(1+e^{\gamma +\beta x}\right).$$ (28)

To calculate the noncentrality parameter, we need the expectation:

$$\begin{gathered} E[\text{ln}f(y,x;\beta ,\gamma )] \\ =\gamma \text{pr}(y=1)+\beta \text{pr}(y=1,x=1)-p_x\text{ln}(1+GB)-\left(1-p_x\right)\text{ln}(1+G) \\ =\gamma \left[\frac{GB}{1+GB}{p}_x+\frac{G}{1+G}\left(1-p_x\right)\right]+\beta \frac{GB}{1+GB}{p}_x-p_x\text{ln}(1+GB)-\left(1-p_x\right)\text{ln}(1+G). \end{gathered}$$

To find γ₀, we take the derivative of (28) at γ = γ₀ and β = 0,

$$\frac{d\text{ln}f\left(y,x;0,{\gamma }_0\right)}{d\gamma }=y-\frac{e^{{\gamma }_0}}{1+e^{{\gamma }_0}}.$$

We find the limit profile nuisance parameter, γ₀, as the solution to the equation

$$E_{(\gamma ,\beta )}\left(\frac{d\text{ln}f\left(y,x;0,{\gamma }_0\right)}{d\gamma }\right)=E_{(\gamma ,\beta )}(y)-\frac{e^{{\gamma }_0}}{1+e^{{\gamma }_0}}=0$$

or equivalently

$$\frac{GB}{1+GB}{p}_x+\frac{G}{1+G}\left(1-p_x\right)=\frac{G_0}{1+G_0},$$

where following our convention $G_0=e^{{\gamma }_0}$. After some simplification, we express G₀ as a function of true β and γ as

$$G_0=G_0(\gamma ,\beta )=G\frac{1+GB+(B-1)p_x}{1+GB-(B-1)G{p}_x}.$$ (29)

Finally, the η-function takes the form

$$\begin{gathered} \eta (\beta )=\left(\gamma -{\gamma }_{\text{0}}\right)\left[\frac{GB}{1+GB}{p}_x+\frac{G}{1+G}\left(1-p_x\right)\right] \\ +\beta \frac{GB}{1+GB}{p}_x-p_x\text{ln}(1+GB)-\left(1-p_x\right)\text{ln}(1+G)+\text{ln}\left(1+G_0\right). \end{gathered}$$

From elementary calculus, it is easy to show that the η-function has finite limits when β →∞ or β →−∞, meaning that the power does not approach 1 when the alternative goes to infinity. However, for mild values of γ and p_x, those limits are very close to 1 when n is fairly large. More details are found in Section 6.

5. The score test

The score test was originally developed by Rao (1948). This test is especially simple when the null hypothesis is simple. However, in the presence of nuisance parameters we need to derive the MLE for γ under the restrictive model β = 0 (see Pawitan (2001) for more detail). The idea of the score test is easy: if the null hypothesis is true then the derivative of the log-likelihood function evaluated at null should be close to zero. Specifically, let ${\widehat{\gamma }}_0$ return the maximum of the log-likelihood function under β = 0. In other words, ${\widehat{\gamma }}_0$ is the MLE of the profile likelihood. It is proven that the distribution of the normalized derivative,

$$S=\sqrt{\frac{V\left(0\mid {\widehat{\gamma }}_0\right)}{n}}\frac{\partial l\left(0,{\widehat{\gamma }}_0\right)}{\partial \beta }$$ (30)

is asymptotically normal with zero mean and unit variance, where $V\left(0\mid {\widehat{\gamma }}_0\right)$ is the asymptotic variance (7) evaluated at β = 0 and $\gamma ={\widehat{\gamma }}_0$.

The derivation of the power function of the score test is similar to the derivation of the likelihood ratio test, mainly because both use the concept of the profile likelihood. Let γ₀ = γ₀(β, γ) be the solution to (22). Then the power function of the score test is derived from the following approximations somewhat similar to what we used for the Wald test:

$$\begin{gathered} P_S(\beta )=\text{pr}\left(\left|S\right|>Z_{1-\alpha /2}\right) \\ =\text{pr}\left\{\sqrt{\frac{V\left(0\mid {\widehat{\gamma }}_0\right)}{n}}\left|\frac{\partial l(\beta ,\gamma )}{\partial \beta }+\left(\frac{\partial l\left(0,{\widehat{\gamma }}_0\right)}{\partial \beta }-\frac{\partial l(\beta ,\gamma )}{\partial \beta }\right)\right|>Z_{1-\alpha /2}\right\} \\ \simeq \text{pr}\left\{\left|\sqrt{\frac{V\left(0\mid {\widehat{\gamma }}_0\right)}{V(\beta )}}Z+\sqrt{n}\sqrt{V\left(0\mid {\widehat{\gamma }}_0\right)}\frac{1}{n}\left(\frac{\partial l\left(0,{\widehat{\gamma }}_0\right)}{\partial \beta }-\frac{\partial l(\beta ,\gamma )}{\partial \beta }\right)\right|>Z_{1-\alpha /2}\right\}, \end{gathered}$$

Where $Z~\mathcal{N}(0,1)$. In terms of Φ, the power function can be approximated as

$$P_S(\beta )=\Phi \left(-r(\beta ,\gamma )Z_{1-\alpha /2}-\sqrt{n}\sqrt{V(\beta )}\delta (\beta )\right)+\Phi \left(-r(\beta ,\gamma )Z_{1-\alpha /2}+\sqrt{n}\sqrt{V(\beta )}\delta (\beta )\right),$$ (31)

Where $r(\beta ,\gamma )=\sqrt{V(\beta )/V\left(0\mid {\gamma }_0\right)}$, and

$$\delta (\beta )=E_{(\beta ,\gamma )}\left(\frac{d\text{ln}f\left(z;0,{\gamma }_0\right)}{d\beta }\right)$$ (32)

will be referred to as the delta-function. When β → 0, we have V (0|γ₀) → V(0) and δ(β) → 0, implying that P_S(β) → 2Φ(−Z_1−α/2) = α, the power of the score test at the null equals the size of the test (8). Regarding the unbiasedeness of the score test, it is easy to see that

$${\frac{d{P}_S}{d\beta }|}_{\beta =0}=-\frac{\varphi \left(-Z_{1-\alpha /2}\right)Z_{1-\alpha /2}}{\sqrt{V(\beta )V\left(0\mid {\gamma }_0\right)}}\times {\frac{dV}{d\beta }|}_{\beta =0},$$ (33)

so that it is unbiased if and only if the derivative of the variance is zero. For linear regression V does not depend on β and therefore the score test is unbiased. However in general the score test is asymptotically biased. We shall find out in Section 6 that this test is not equivalent to the Wald or likelihood ratio test even in the neighborhood of the null.

5.1. Linear regression

We illustrate the score power with linear regression as we did earlier for the Wald and likelihood ratio tests. The needed ${\tau }_{*}$ and ${\sigma }_{*}^2$ are defined by (25) and (26). Now we express function (32) through parameters β, τ and σ². Assuming that the expectation is taken under the true parameters (β, τ, σ²), we obtain $\delta (\beta )=-\beta /\left({\sigma }_{\beta }^2+{\beta }^2\right)$ implying that on the z-scale the power takes the form

$$P_S(z)=\Phi \left(-\frac{Z_{1-\alpha /2}}{\sqrt{1+z^2}}-\frac{z}{1+z^2}\sqrt{n}\right)+\Phi \left(-\frac{Z_{1-\alpha /2}}{\sqrt{1+z^2}}+\frac{z}{1+z^2}\sqrt{n}\right).$$ (34)

It is easy to see that P_S(0) = α, and condition (8) holds. After some algebra, one may check that the score test is asymptotically unbiased—condition (9) holds. We shall compare this power approximation to that of the other two tests in Section 6.

5.2. Logistic regression

As in Section 4.2, the limit profile nuisance parameter G₀ is found as the solution to equation (22) provided by expression (29). Thus, to find the power, it suffices to find the delta-function (32). After some algebra and using (28), we obtain

$$\delta (\beta )=E_{(\gamma ,\beta )}\frac{\text{ln}f\left(y,x;0,{\gamma }_0\right)}{\partial \beta }=\frac{GB}{1+GB}-\frac{G_0}{1+G_0}{p}_x.$$ (35)

The variance function, V was derived earlier and is given by (18); the variance at null is

$$V\left(0\mid {\gamma }_0\right)=\frac{{\left(1+G_0\right)}^2}{p_x\left(1-p_x\right)G_0}.$$

Unlike for linear regression, the score test is asymptotically biased for logistic regression. Namely, the first derivative at β = 0 given by (33) is not zero. We shall compare this test to the other two tests in Section 6.

6. Tests comparison

In this section, we compare the Wald, LR, and score tests using two regression models as examples: linear regression with an unknown σ² under normal distribution and logistic regression with binary covariate.

We start our analysis with linear regression. It is convenient to compare the tests on the z-scale using representations (13), (27) and (34). From (14), it is easy to see that for each test the second derivatives on the original β-scale and the z-scale are related through a coefficient, which is the reciprocal of the variance at the null,

$${\frac{d^{2}P}{d{\beta }^2}|}_{\beta =0}={\frac{1}{V(0)}\frac{d^{2}P}{d{z}^2}|}_{z=0}.$$

Theorem 2.

All three tests are asymptotically unbiased for linear regression under a normal distribution with an unknown σ² (the first derivative of the power function evaluated at the null vanishes). The power function of the Wald test is uniformly greater than that of the LR test (β ≠ 0). The second derivatives of the three tests at the null are as follows:

$${\frac{d^2{P}_W}{d{z}^2}|}_{z=0}={\frac{d^2{P}_{LR}}{d{z}^2}|}_{z=0}=2\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}n,$$ (36)

$${\frac{d^2{P}_S}{d{z}^2}|}_{z=0}=2\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}(n+1).$$ (37)

Thus, the score test is slightly superior in a close neighborhood of the null.

Proof.

The asymptotic unbiasedeness of the tests (the first derivatives vanish at zero) have been noted previously. The superiority of the Wald over the LR test follows from an elementary inequality $\sqrt{\text{ln}\left(1+z^2\right)}<|z|$ for all z ≠ 0. The second derivative of the Wald test at β = 0 has been derived earlier (12). The second derivative of the LR test follows from (34). The evaluation of the second derivative of the score test (37) is somewhat tedious but straightforward. A slight superiority of the score test in the neighborhood of the null follows from the fact that the difference of the derivatives is 2ϕ(Z_1−α/2)Z_1−α/2 although this difference rapidly diminishes on the relative scale as n →∞.■

We illustrate the power approximation of the three tests in Figure 3 with linear regression y = βx + τu + ε where all random variables have normal distributions with zero mean, $var(x)={\sigma }_x^2$, $var(u)={\sigma }_u^2$, var(ε) = σ² The power functions of the Wald, LR, and score tests are plotted as functions of the z-ratio (14) with n = 100, σ_x = σ = 1, ρ_xu = 0.9 and τ = 1, assuming that the significance level |z| = 5%. Notice that the power functions are very close in the interval |z| < 0.2 with the maximum difference around z = 0.5.

Figure 3.

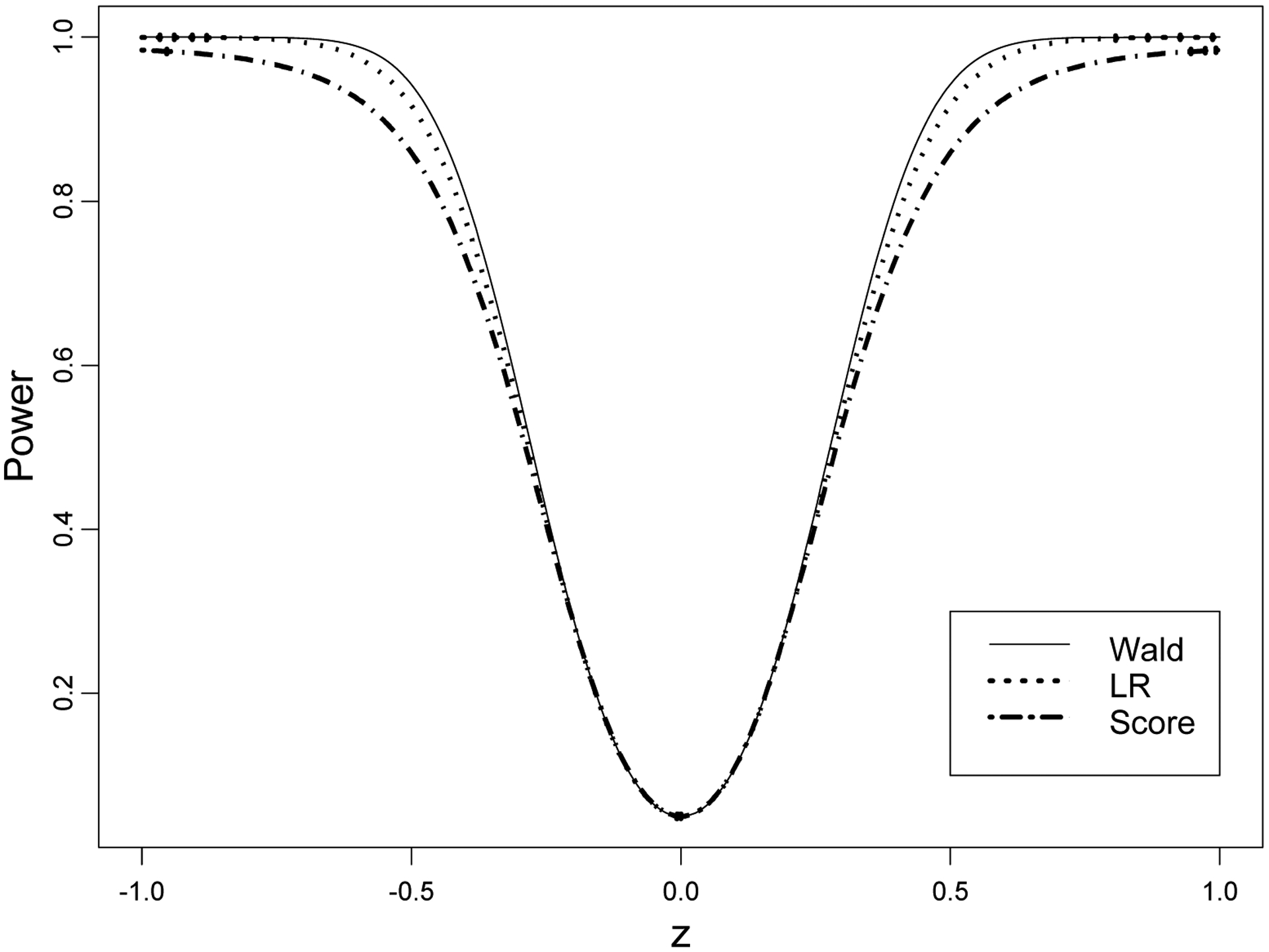
Power of three tests for linear regression with unknown σ² on the z-scale (n = 100, σ_x = σ = 1, ρ_xu = 0.9, τ = 1 with α = 0.05). All three tests have the same size (α) and the first derivative vanishes at β = 0. The Wald and likelihood ratio tests have the same second derivatives at the null, but the second derivative of the score test is higher (actually invisible). However, globally, the Wald test is superior.

Now we compare the three tests for logistic regression with a binary covariate. See Figure 4 as an example with α = 0.05, p_x = Pr(x = 1) = 0.2, Pr(y = 1|x = 0) = 0.1 (G = 1/9), and n = 500. We intentionally use a rare parameter set up (p_x = 0.2) because at symmetry (p_x = 0.5 and G = 1) the power functions are practically identical. Recall the Wald and LR power functions have zero derivatives and the same second derivative at β = 0. However, the first derivative of the score test is positive at β = 0 meaning that the power of the score test is slightly less in the neighborhood to the left of the null. Recall that the Wald power falls to α when β →−∞ or β →∞ which is not true for the LR and score tests. Although the LR power does not approach 1 when β →−∞ the limit is very close to 1. In order to test the power approximations, we conducted simulations for β = −1 and β = 0.5 (the number of experiments is 5,000)–simulations and power approximations are in good agreement.

Figure 4.

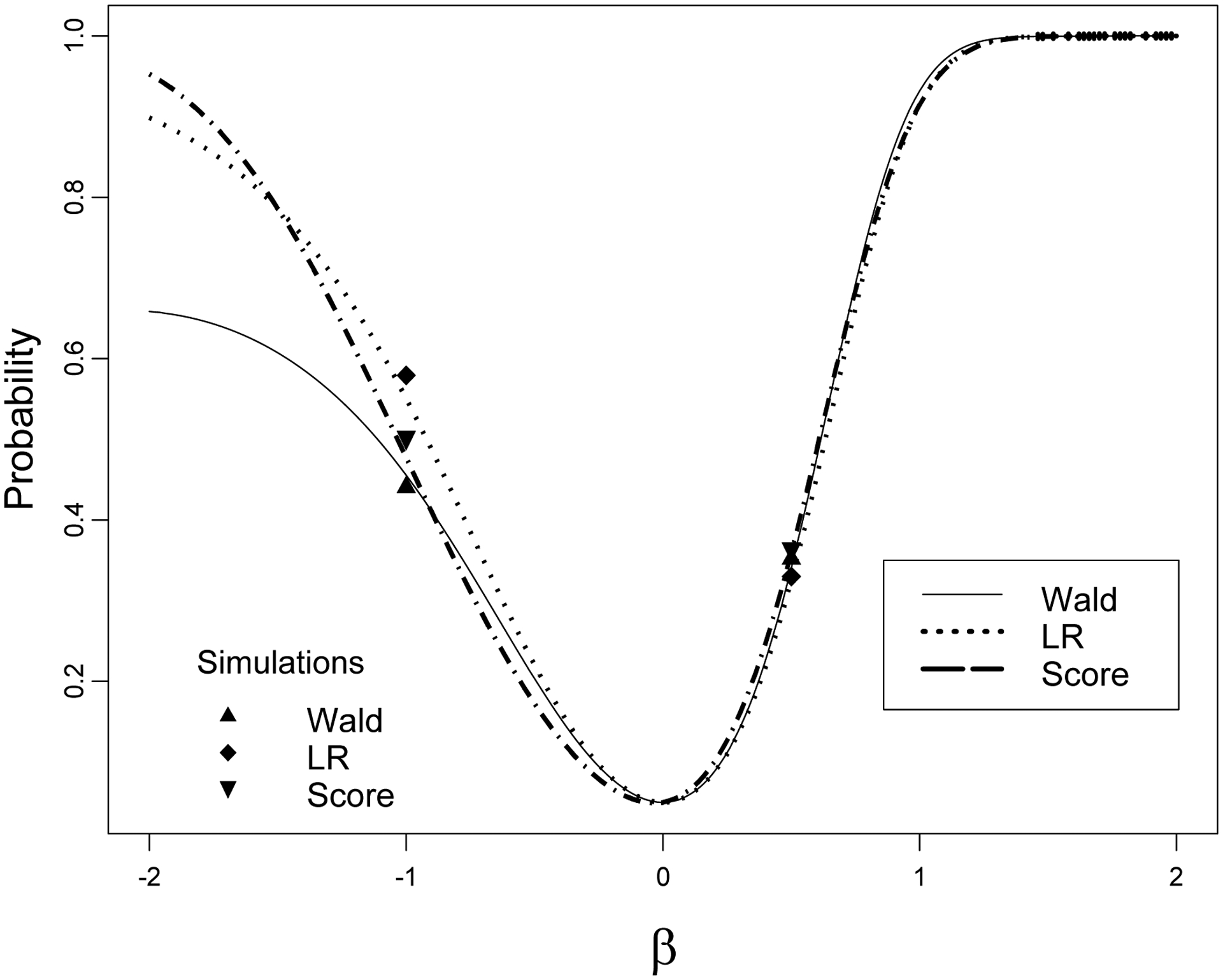
Three power functions for logistic regression with a binary covariate, p_x = 0.2, G = 1/9, n = 500 with α = 5%. The first derivative of the Wald and likelihood ratio tests vanishes, but the derivative of the score test power is positive at β = 0. Simulations for β = −1 and 0.5 are in good agreement with the power approximations.

7. Discussion and summary points

Asymptotic tests are at the heart of statistical inference. Early authors studied which test is superior. For example, Madansky (1989) raised this question, and in early edition of Rao’s book it was conjectured that the score test is locally more powerful than the other two. (There is no such conjecture in the latest, 1973 edition of the book!) Yes, as follows from Theorem 2, there exists a slight superiority of the score test for linear regression in a close proximity to the null. However, for other statistical models this superiority disappears-moreover, the score test is generally biased (the first derivative is not zero) which means that for a double-sided test the score power will be less on one side of the null.

The main points of the paper are as follows:

• The Wald test may exhibit aberrant behavior for some statistical models, namely, the power increases and then drops to the size of the test as the alternative approaches negative infinity. For logistic regression with a binary covariate, the Wald test behaves well for alternatives in the interval (−2, 2). The chance that the likelihood ratio or score test have aberrant behavior is smaller, but still exists.

• The Wald and LR tests are asymptotically unbiased (the first derivative of their power function vanishes at the null), but the score test is generally biased. The Wald and LR tests are locally equivalent (the second derivatives are the same at the null), but the score test is not.

• It is well known that all three tests are the same for a linear model under the normal distribution when the error variance, σ² is known. However, when σ² is unknown (nuisance parameter) the tests are different. The power of the Wald test is higher than that of the LR test for all alternatives, but locally the tests are equivalent. The score test for this model is also asymptotically unbiased and has slightly higher power in close proximity to the null.

• The behavior of the tests changes from distribution to distribution and from one statistical model to another. Even members of the same family of generalized linear model (linear and logistic) have quite different test properties. Especially drastic are the differences for low probability and/or larger true values of nuisance parameters.

• Simulations show a good agreement with power approximations especially for moderate parameter values.

• No test is superior over another in the whole range of statistical models and distributions. For example, tests are close for moderate parameter values, particularly when p_x is around 1/2. However, tests may be very different with extreme parameter values, such as for rare events in logistic regression (p_x ≃ 0). Thus, different tests may be optimal for different statistical models, moreover for different ranges of the alternative.

Besides theoretical interest, the power analysis has an important application for study design, particularly in epidemiology and clinical trials. Usually, one wants to determine the sample size required to achieve a specified power or minimum detectable difference (the alternative beta value). Several commercial and noncommercial software packages are available on the market. However, there is no consensus on what test to use as the basis for the sample size determination–some authors use the Wald test (Whittemore, 1981), some the likelihood ratio test (Self et al., 1992 and Shieh, 2000) and some the score test (Self and Mautitzen, 1988) mainly because of the popular opinion that asymptotic tests are all the same. True, when alternatives are close to null and nuisance parameters do not take extreme values, the powers look alike. However, in some cases, we plan studies for large alternatives such as in epidemiologic studies with gene—gene or gene—environment interaction or observational studies of rare diseases (cancer), see Duchateau (1998) and Gauderman (2002) for examples. In such studies, the choice of the test becomes crucial. The test used for the sample size determination should be the same as the test in future significance testing (Demidenko 2007, 2008).

Much additional work is to be done in the following areas: (1) Extend our power analysis to one-sided tests and the multivariate null hypothesis; (2) identify what asymptotic tests are optimal for specific statistical models, such as members of generalized linear model family, and (3) improve power approximations for extreme values of alternative and nuisance parameters, particularly when the effective sample size is small.

Finally, the study of the tests in this paper, as well as in many others, relies on standard conditions on the density function, such as independence of the density support on the parameter. In my private conversation with S.A. Aivazian, he told me that one of the problems he considered in his doctoral dissertation, was studying superefficient estimation and the respective statistical inference when the support of the distribution dependens on the unknown parameter, like in the uniform distribution with unknown upper limit.

8. Appendix.

Proof of Theorem 1

The fact that the first derivative of the Wald power vanishes at β = 0 was proven in Section 3. For the LR power, we have

$$\frac{d{P}_{LR}}{d\beta }=\sqrt{\frac{n}{2}}\left[\varphi \left(-Z_{1-\alpha /2}+\sqrt{2n\eta (\beta )}\right)-\varphi \left(Z_{1-\alpha /2}+\sqrt{2n\eta (\beta )}\right)\right]\frac{d\eta /d\beta }{\sqrt{\eta (\beta )}}.$$

This implies that the LR test is asymptotically unbiased (9) because η(0) = 0 (we show below that $d\eta /d\beta /\sqrt{\eta (\beta )}$ is a finite number at zero).

Now we evaluate the second derivative of the power function at zero. Using the property that dϕ/dx = −xϕ(x), we obtain

$${\frac{d^2{P}_{LR}}{d{\beta }^2}|}_{\beta =0}={n\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}\frac{{(d\eta /d\beta )}^2}{\eta (\beta )}|}_{\beta =0}.$$ (38)

Since the numerator and denominator with the η-function are both zero we need to consider the limit. From L’Hopital’s rule

$$\underset{\beta \to 0}{\text{lim}}\frac{{(d\eta /d\beta )}^2}{\eta (\beta )}=2\underset{\beta \to 0}{\text{lim}}\frac{(d\eta /d\beta )\left(d^2\eta /d{\beta }^2\right)}{d\eta /d\beta }={2\frac{d^2\eta }{d{\beta }^2}|}_{\beta =0},$$

so that (38) is rewritten as

$${\frac{d^2{P}_{LR}}{d{\beta }^2}|}_{\beta =0}={2n\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}\frac{d^2\eta }{d{\beta }^2}|}_{\beta =0}.$$

Thus, the evaluation of the second derivative of the power reduces to the evaluation of the second derivative of the η-function. We aim to find the second derivative of η at zero. Interchanging expectation and differentiation from (23), we obtain $\frac{d}{d\beta }{E}_{(\beta ,\gamma )}$. This implies

$$\frac{d\eta }{d\beta }=-\frac{d}{d\beta }{E}_{(\beta ,\gamma )}\left(\text{ln}f\left(z;0,{\gamma }_0\right)\right)=-{\left(\frac{\partial }{\partial {\gamma }_0}{E}_{(\beta ,\gamma )}\left(\text{ln}f\left(z;0,{\gamma }_0\right)\right)\right)}^{\prime }\left(\frac{d{\gamma }_0}{d\beta }\right).$$

From differentiation of an implicit function, we have

$$\frac{d{\gamma }_0}{d\beta }=-{\left[\frac{\partial }{\partial \gamma }{E}_{(\beta ,\gamma )}\left(\frac{\partial \text{ln}f(z;0,\gamma )}{\partial \gamma }\right)\right]}^{-1}\left[\frac{d}{d\beta }{E}_{(\beta ,\gamma )}\left(\frac{\partial \text{ln}f(z;0,\gamma )}{\partial \gamma }\right)\right],$$

but

$$\frac{d}{d\beta }{E}_{(\beta ,\gamma )}\left(\frac{\partial \text{ln}f(z;0,\gamma )}{\partial \gamma }\right)=I_{12},\frac{\partial }{\partial \gamma }{E}_{(\beta ,\gamma )}\left(\frac{\partial \text{ln}f(z;0,\gamma )}{\partial \gamma }\right)=I_{22},$$

which results in $d{\gamma }_0/d\beta =-I_{22}^{-1}{I}_{12}$. Finally, the second derivative of the η-function at zero is

$$\begin{gathered} \frac{d^2}{d{\beta }^2}{E}_{(\beta ,\gamma )}(\text{ln}f(z;\beta ,\gamma ))-{\left(\frac{d{\gamma }_0}{d\beta }\right)}^{\prime }\left(\frac{{\partial }^2}{\partial {\gamma }_0}{E}_{(\beta ,\gamma )}\left(\text{ln}f\left(z;0,{\gamma }_0\right)\right)\right)\left({\frac{d{\gamma }_0}{d\beta }|}_{\beta =0}\right) \\ =I_{11}-I_{12}^{\prime }{I}_{22}^{-1}{I}_{22}{I}_{22}^{-1}{I}_{12}=I_{11}-I_{12}^{\prime }{I}_{22}^{-1}{I}_{12}. \end{gathered}$$

Combining the results, we arrive at the second derivative at the null

$${\frac{d^2{P}_{LR}}{d{\beta }^2}|}_{\beta =0}=2n\varphi \left(Z_{1-\alpha /2}\right)Z_{1-\alpha /2}\left(I_{11}-I_{12}^{\prime }{I}_{22}^{-1}{I}_{12}\right),$$

which coincides with the second derivative of the Wald test (12). This means that the Wald and LR tests are locally equivalent.