Abstract
Laboratory-based animal research has revealed a number of exposures with multigenerational effects—ones that affect the children and grandchildren of those directly exposed. An important task for epidemiology is to investigate these relationships in human populations. Without the relative control achieved in laboratory settings, however, population-based studies of multigenerational associations have had to use a broader range of study designs. Current strategies to obtain multigenerational data include exploiting birth registries and existing cohort studies, ascertaining exposures within them, and measuring outcomes across multiple generations. In this paper, we describe the methodological challenges inherent to multigenerational studies in human populations. After outlining standard taxonomy to facilitate discussion of study designs and target exposure associations, we highlight the methodological issues, focusing on the interplay between study design, analysis strategy, and the fact that outcomes may be related to family size. In a simulation study, we show that different multigenerational designs lead to estimates of different exposure associations with distinct scientific interpretations. Nevertheless, target associations can be recovered by incorporating (possibly) auxiliary information, and we provide insights into choosing an appropriate target association. Finally, we identify areas requiring further methodological development.
Keywords: clustered data, endocrine disruptors, environmental exposure, epidemiologic methods, maternal exposure, multigenerational associations, study design
Abbreviations
- ADHD
attention-deficit/hyperactivity disorder
- CPP
Collaborative Perinatal Project
- DES
diethylstilbestrol
- GEE
generalized estimating equations
- IEE
independence estimating equations
- WEE
weighted estimating equations
Epidemiologists have recently shown interest in studying multigenerational associations—where exposures are related to not only persons directly exposed but also their progeny (1–29). Despite a rich body of epidemiologic methods, however, multigenerational studies exhibit a number of distinct features that require special methodological consideration.
One hypothesized mechanism by which multigenerational effects arise is through modifications of the epigenome of germline cells, such as methylation patterns, which are inherited by subsequent generations (7, 30). Much of the evidence for this has been gathered via laboratory-based animal studies (1, 7, 31–41). Given the degree of control that laboratories provide, these studies have typically been conducted by exposing members of an initial generation (and leaving some unexposed) and prospectively ascertaining outcomes among future generations of the exposed and unexposed groups (1, 7, 8, 31–34, 37).
Whether interest lies in the epigenetic action of environmental pollutants (3–7) or in the downstream consequences of social determinants of health (19–28), the practical and ethical limitations of population-based multigenerational studies seldom allow for the straightforward study designs of animal studies or randomized controlled trials. Instead, researchers have exploited birth registries and existing cohort studies, ascertaining exposures within them (sometimes retrospectively) and measuring outcomes across multiple generations (2–6, 9–15, 30). Typically, however, such registries/cohorts have not been constructed specifically for investigation of multigenerational associations, and the data structure available has varied substantially, raising a number of methodological issues unique to population-based studies of multigenerational associations. In Nurses’ Health Study II (NHS II), for example, children’s outcomes were not just cluster-correlated within families but also varied by family size (6). In addition, with multiple generations of people on which to make observations, selecting a study design and analysis strategy that permits estimation of the association of interest is an important task. These issues—and their interrelationships—warrant careful consideration even in studies tailored to investigating multigenerational associations.
In this paper, we illustrate these methodological issues in detail. We first introduce 2 motivating cohorts and, with these as a guide, outline key terms for describing multigenerational study designs and associations. We then explore via simulation how the interplay between study design, variation in cluster sizes, and the approach to analysis affects the scope of scientific inquiry.
MOTIVATING EXAMPLES
Studies of multigenerational associations require measurements across multiple generations. One such example of a study that has been used to investigate multigenerational associations is the Collaborative Perinatal Project (CPP) (16–18, 42), which recruited 48,197 pregnant women between 1959 and 1964. In addition to outcomes pertaining to the pregnancy at recruitment, the CPP ascertained outcomes retrospectively for prior pregnancies and prospectively for subsequent pregnancies in the same mothers. Using these data, Huang et al. (14) investigated the association between mother’s prepregnancy obesity and the neurodevelopment of her children, while Nelson and Ellenberg (15) studied the association between mother’s smoking history and febrile seizures in her children. In 1992–1994, a follow-up study called CPP Pathways to Adulthood investigated the health, cognitive development, and educational achievement of the grandchildren of mothers at the Baltimore, Maryland, CPP site (12, 13, 27).
As a second example, NHS II incorporated both retrospective and prospective observations to capture information about 3 successive generations. The NHS II investigators recruited 116,686 female nurses aged 25–42 years in 1989, who responded to multiple questionnaires over several years of follow-up, reporting health outcomes and exposures about not only themselves but also their families (43, 44). In 1993, for example, nurses retrospectively reported whether their mothers had taken any hormones while pregnant with them; in 2005, nurses reported neurodevelopmental outcomes among their children. In this way, Kioumourtzoglou et al. (6) were able to investigate the association between in-utero maternal diethylstilbestrol (DES) exposure and third-generation diagnosis of attention-deficit/hyperactivity disorder (ADHD).
While these examples highlight different study designs, many variations exist. Some other examples of multigenerational studies include the Dutch Famine Birth Cohort Study (9, 10, 45), the National Longitudinal Study of Adolescent to Adult Health (19, 29), and studies of birth cohorts from northern Finland (26), Sweden (23, 24), and Hong Kong (28).
KEY TERMS
Investigating multigenerational associations requires at least 2 successive generations. By convention, we label the first generation, the one that is directly exposed, the F0 generation (1, 7, 31–33, 46). In the CPP, the F0’s consisted of the pregnant women recruited into the study. In contrast, the F0’s in NHS II consisted of the mothers of the nurses/individuals who were recruited. Subsequent generations are indexed sequentially: The children of the F0’s belong to the F1 generation; the grandchildren of the F0’s belong to the F2 generation (12, 13).
Many different study designs may be employed to estimate multigenerational associations, as shown in Figure 1. Ideally, we would prospectively obtain data on the full population of F0’s and all associated F1’s (Figure 1A), but this is often infeasible. Researchers have instead implemented a range of subsampling strategies, which vary according to 1) the primary sampling generation—the generation to which the individuals recruited into the study belong—and 2) the completeness of the family structure—whether all or some offspring are observed. For example, investigators may recruit F0’s and then obtain information on all of their F1 children (Figure 1B) or on a single F1 child (e.g., the child from the current pregnancy; Figure 1C). Alternatively, researchers may initially recruit F1’s and obtain exposure information on the corresponding F0’s (Figure 1D). We explore the implications of these design considerations below.
Figure 1.
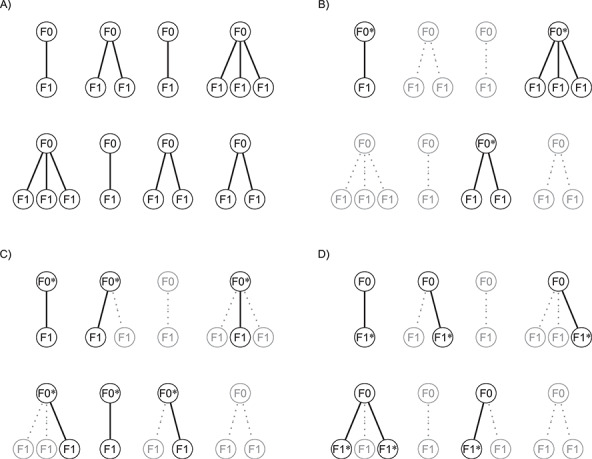
Example data structures for multigenerational studies. A) Full population; B) design I: sampling entire F0 families; C) design II: sampling single F1’s within F0 families; D) design III: sampling F1’s directly. Gray circles indicate people not observed in the sample. Asterisks (*) indicate the primary sampling units in designs I–III.
SIMULATION STUDY
Here we present a simulation study exploring the interplay between sampling designs and analysis considerations, specifically in terms of what exposure associations are estimable from the resulting data. We consider a hypothetical study spanning 2 generations, where the goal is to estimate the risk ratio characterizing the association between a binary F0-level exposure, 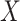 , and a binary F1-level outcome,
, and a binary F1-level outcome, 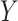 . We anchor select details of the simulated populations, specifically the distribution of family sizes and the outcome prevalence, to the study of DES exposure and ADHD reported by Kioumourtzoglou et al. (6) (see also McGee et al. (47)). The question we aim to answer is, Does each design estimate the same risk ratio?
. We anchor select details of the simulated populations, specifically the distribution of family sizes and the outcome prevalence, to the study of DES exposure and ADHD reported by Kioumourtzoglou et al. (6) (see also McGee et al. (47)). The question we aim to answer is, Does each design estimate the same risk ratio?
Generating full cohorts
We generated R = 1,000 full cohorts, each consisting of K = 40,000 families (i.e., a single member from the F0 generation and their F1 children). Within each family, 25% of the F0’s (mothers) were “exposed” 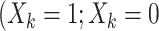
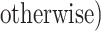 . A major consideration in multigenerational studies is the interplay between F0 exposure, family size, and F1 outcomes; as such, we simulate the F1 generation via a joint model for family size and F1 child outcomes (47, 48). Technical details are given in the Web Appendix (available at https://academic.oup.com/aje). Briefly, in our simulation study, both family size
. A major consideration in multigenerational studies is the interplay between F0 exposure, family size, and F1 outcomes; as such, we simulate the F1 generation via a joint model for family size and F1 child outcomes (47, 48). Technical details are given in the Web Appendix (available at https://academic.oup.com/aje). Briefly, in our simulation study, both family size 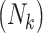 and F1 outcomes
and F1 outcomes 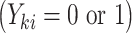 depended on the exposure status of the F0 mother as well as a shared (unobserved) random effect. Each family had at least 1 child in the F1 generation; we discuss the implications of families with no children below.
depended on the exposure status of the F0 mother as well as a shared (unobserved) random effect. Each family had at least 1 child in the F1 generation; we discuss the implications of families with no children below.
Under this data-generating mechanism, family sizes varied around the mode of 2 children, with 15% of the families having singletons 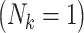 and 6% having 5 or more children (Table 1). Average family size among the unexposed F0’s was 2.6, while that among the exposed F0’s was 2.3. Overall, the outcome was rare (1.5%) and more common among children of exposed mothers than children of unexposed mothers (2.5% vs. 1.3%). Moreover, outcomes were related to family size, with higher incidence in smaller families, ranging from 4.7% among single-child families to 0.2% in families of 5 or more (Table 1).
and 6% having 5 or more children (Table 1). Average family size among the unexposed F0’s was 2.6, while that among the exposed F0’s was 2.3. Overall, the outcome was rare (1.5%) and more common among children of exposed mothers than children of unexposed mothers (2.5% vs. 1.3%). Moreover, outcomes were related to family size, with higher incidence in smaller families, ranging from 4.7% among single-child families to 0.2% in families of 5 or more (Table 1).
Table 1.
Characteristics (%) of a Simulated Full Population by Family Size (Number of F1’s), Computed on the Basis of a Single Population of Size K = 1,000,000a
| All F0’s | Unexposed F0’s (X 1k = 0) | Exposed F0’s (X 1k = 1) | |||||
|---|---|---|---|---|---|---|---|
| No. of F1’s | Proportion of F0’s | Exposure Prevalence | Outcome Prevalence | Proportion of F0’s | Outcome Prevalence | Proportion of F0’s | Outcome Prevalence |
| 1 | 14.7 | 30.2 | 4.7 | 13.7 | 4.5 | 17.7 | 5.0 |
| 2 | 47.2 | 27.9 | 2.4 | 45.4 | 2.1 | 52.6 | 3.1 |
| 3 | 16.4 | 23.8 | 1.1 | 16.7 | 0.9 | 15.6 | 1.8 |
| 4 | 15.7 | 18.7 | 0.6 | 17.0 | 0.4 | 11.7 | 1.2 |
| ≥5 | 6.0 | 9.8 | 0.2 | 7.2 | 0.1 | 2.3 | 0.6 |
a K, number of clusters; X1k, exposure for the kth cluster.
Analyses of the full cohorts
To estimate the risk ratio for the association between 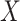 and
and 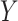 , we assume the following working (marginal) model:
, we assume the following working (marginal) model:
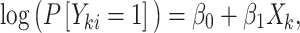 |
where 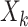 is the exposure of the mother in the kth family and
is the exposure of the mother in the kth family and 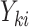 is the outcome of the ith child in the kth family. In a standard cluster-correlated data setting, one can estimate
is the outcome of the ith child in the kth family. In a standard cluster-correlated data setting, one can estimate 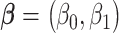 using generalized estimating equations (GEE), for which the analyst specifies a working covariance structure (49). Typically, even if this structure is incorrectly specified, the resulting estimate of β is consistent for the true value, and valid inference can be obtained by using the robust sandwich form of the variance. Here, however, the choice has important consequences because the family (or cluster) size is informative; that is, the outcomes among the individuals in the F1 generation are conditionally associated with the size of the family (i.e., associated not only though exposure/covariates) (48, 50, 51). This might occur if, say, some unaccounted-for factor such as toxicity or a shared genetic frailty affected both fertility and the offspring’s health outcomes.
using generalized estimating equations (GEE), for which the analyst specifies a working covariance structure (49). Typically, even if this structure is incorrectly specified, the resulting estimate of β is consistent for the true value, and valid inference can be obtained by using the robust sandwich form of the variance. Here, however, the choice has important consequences because the family (or cluster) size is informative; that is, the outcomes among the individuals in the F1 generation are conditionally associated with the size of the family (i.e., associated not only though exposure/covariates) (48, 50, 51). This might occur if, say, some unaccounted-for factor such as toxicity or a shared genetic frailty affected both fertility and the offspring’s health outcomes.
A number of statistical methods have been proposed to acknowledge informative cluster sizes (48). Prominent among these is the use of working independence GEE coupled with either no further weighting (referred to as independence estimating equations (IEE)) or inverse cluster-size weights, 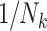 (weighted estimating equations (WEE)) (51). Applying these to the simulated cohorts, the average estimated log risk ratio from IEE is log(1.9), while that from WEE is log(1.6) (Table 2). Rather than one estimator’s being biased for an unambiguous true value of the risk ratio, this difference is instead analogous to the role that noncollapsibility has in changing the “true” value of the odds ratio in logistic regression (52). The choice of weighting scheme thus has implications for the parameter being estimated when cluster size is informative. We elaborate on this below. In the remainder of this section, we consider the interplay between study design and analysis and their impact on the parameter being estimated.
(weighted estimating equations (WEE)) (51). Applying these to the simulated cohorts, the average estimated log risk ratio from IEE is log(1.9), while that from WEE is log(1.6) (Table 2). Rather than one estimator’s being biased for an unambiguous true value of the risk ratio, this difference is instead analogous to the role that noncollapsibility has in changing the “true” value of the odds ratio in logistic regression (52). The choice of weighting scheme thus has implications for the parameter being estimated when cluster size is informative. We elaborate on this below. In the remainder of this section, we consider the interplay between study design and analysis and their impact on the parameter being estimated.
Table 2.
Mean Log Risk Ratio Estimates of the Exposure-Outcome Association for Various Study Design–Analysis Pairs Across 1,000 Simulated Data Sets, Exponentiated to the Risk Ratio Scale (Simulation Results)a
| Data Structure | Weighting Scheme (Analysis) | ||
|---|---|---|---|
| 1 (IEE) |
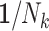 (WEE) (WEE)
|
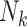
|
|
| Full population | 1.9 | 1.6 | |
| Design I | 1.9 | 1.6 | |
| Design II | 1.6 | 1.9 | |
| Design III | 1.9 | 1.6 | |
Abbreviations: IEE, independence estimating equations; WEE, weighted estimating equations.
a Nk, size of the kth cluster.
THE ROLE OF THE SAMPLING SCHEME
Motivated by the CPP and NHS II, described above, suppose it is not possible to observe the full cohorts. We consider 3 subsampling designs that vary according to the primary sampling generation and the completeness of the family structure. For each of the R = 1,000 simulated full cohorts, we obtained subsamples based on each design.
Design I: sampling F0 families
A natural subsample could be generated by recruiting F0’s and then obtaining information on all of their F1’s. The observed data would consist of a random sample of complete families (Figure 1B).
To implement this design, we randomly selected 8,000 F0’s (20%) and their families in each of the 1,000 full cohorts. Because of the variation in family sizes, 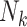 , the number of F1’s included in the rth subsample—denoted
, the number of F1’s included in the rth subsample—denoted 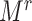 —varied across data sets. (
—varied across data sets. (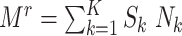 , where
, where 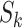 is 1 if the kth F0 is selected in the design I sample and 0 otherwise, and
is 1 if the kth F0 is selected in the design I sample and 0 otherwise, and 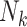 is the kth F0’s number of children).
is the kth F0’s number of children).
Design II: sampling F1’s within F0-indexed families
Suppose again that we collect a random sample of F0’s (the primary sampling generation) but resources are only available for ascertaining outcomes on a single birth (Figure 1C). Regardless of the ultimate size of the family, 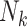 , the family structure is incomplete, with observed data in the form of parent-child dyads. With only 1 child per family, methods such as GEE would likely be seen as “unnecessary,” so one might naturally proceed by means of a standard regression analysis without robust variance estimation. Note that the resulting estimator is the same as the IEE estimator.
, the family structure is incomplete, with observed data in the form of parent-child dyads. With only 1 child per family, methods such as GEE would likely be seen as “unnecessary,” so one might naturally proceed by means of a standard regression analysis without robust variance estimation. Note that the resulting estimator is the same as the IEE estimator.
To implement this, we randomly selected 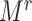 individuals in the F0 generation in the rth cohort, and we then randomly drew 1 F1 per selected F0.
individuals in the F0 generation in the rth cohort, and we then randomly drew 1 F1 per selected F0.
Design III: sampling F1’s directly
Taking the F0 generation as the primary sampling generation, as done by designs I and II, may not always be feasible. Emanuel et al. (2), for example, studied birth weight in a sample of babies born between March 3 and 9, 1958, in the United Kingdom, with a range of exposures measured retrospectively on their parents. Thus, the primary sampling generation was the F1 generation. NHS II similarly sampled F1’s directly (43). Depending on the time frame and mode of recruiting, one may or may not observe siblings within families (Figure 1D). Either way, family structures are generally incomplete. As a consequence, analysis may or may not require consideration of within-cluster correlation.
To implement design III, we randomly selected 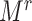 individuals in the F1 generation in the rth cohort.
individuals in the F1 generation in the rth cohort.
Simulation results
We applied IEE (weights of 1) and WEE (inverse cluster size weights, 1/Nk) to each subsample and report average log risk ratios across the 1,000 simulated cohorts in Table 2. Perhaps not surprisingly, design I behaved like the full cohort analyses: IEE and WEE yielded average log risk ratios of log(1.9) and log(1.6), respectively. By contrast, IEE applied to design II yielded log(1.6), whereas WEE recovered neither of the full-cohort risk ratio estimates. Interestingly, however, weighting by cluster size—that is, 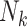 , as opposed to the inverse cluster size weights of WEE—yielded log(1.9). Design III performed similarly to design I: IEE and WEE recovered the full-cohort risk ratio estimates of log(1.9) and log(1.6).
, as opposed to the inverse cluster size weights of WEE—yielded log(1.9). Design III performed similarly to design I: IEE and WEE recovered the full-cohort risk ratio estimates of log(1.9) and log(1.6).
A key takeaway is that each design was able to recover the full-cohort IEE and WEE risk ratios with appropriate weighting schemes. In practice, however, the weighted analyses rely on knowledge of the full cluster size, which may not be readily available in design II or III. We emphasize that auxiliary information on full cluster sizes may be necessary to recover the full-cohort IEE and WEE estimates.
TOWARD A MORE PRECISE SCIENTIFIC QUESTION
The simulation study suggested that when cluster size is informative, analyses based on different weighting schemes estimate different parameters. It is thus tempting to conclude that one is biased, but this is not so. Consider the mean value and the median value: While the two have different interpretations, both summarize the center of a distribution. In certain settings, they are numerically equal (i.e., symmetrical distributions), despite having different interpretations. Elsewhere they differ—yet neither represents the “correct” measure of the center of a distribution.
Table 2 shows an analogous phenomenon: 1.6 and 1.9 correspond to different parameters that offer distinct representations of the relationship between exposure and outcome; each carries a distinct interpretation and thus answers a subtly different scientific question (48, 51). As with the mean and median, the key to deciding which to pursue rests with careful consideration of how to interpret the 2 parameters—and pairing an interpretation to the scientific question of interest.
Toward this, consider 2 hypothetical randomized trials. In the first, we obtain a random sample of individuals from the F0 generation and randomly assign them to treatment or control status. Outcomes are then prospectively ascertained on all of their children, and we compare the outcomes of all children with mothers in the treatment arm to those of all children with mothers in the control arm. Thus, the comparison corresponds to the exposure association among all F1’s across all F0’s. We refer to this as the all F1 association.
In the second trial, we again obtain a random sample of individuals from the F0 generation and assign them to treatment or control status. At this point, however, the outcomes from 1 randomly selected child from each family are ascertained and form the basis of the comparison. In this sense, the contrast is not among all F1’s but rather corresponds to the exposure association for a typical F1 from a typical F0. We refer to this as the typical F1 association.
The all F1 association captures the exposure-outcome relationship in a way that acknowledges and, as such, varies with the outcome–cluster size relationship. Figure 2 illustrates this: Repeating the simulations described above with different outcome–cluster size relationships (within exposure groups), the all F1 association increases as cluster sizes and outcomes become more negatively correlated. As suggested by the first hypothetical trial, the all F1 association reflects what might occur in an entire population of F1’s; in this way, it balances the contributions of all existing F1’s. Put differently, it answers the question, What are the downstream consequences for the next generation if we introduce an exposure to a population? This implicitly incorporates the outcome-size association, which may or may not reflect some underlying biological mechanism—for example, if the burden of raising children with health issues leads to having fewer children. Consider investigating DES and ADHD: If the goal is to characterize the impact on public health that would result from exposing a population to DES—for example, to assess the overall burden it induces, or for planning purposes—the all F1 association may be an appropriate target of inference.
Figure 2.

Comparison of “all F1” effects and “typical F1” effects for multigenerational studies, by informativeness. The y-axis shows the mean estimate of the log odds ratio (OR) for the exposure effect, fitted via independence estimating equations (all F1 effect) and weighted estimating equations WEE (typical F1 effect), in R = 1,000 simulated populations. The x-axis shows the strength of the association between outcome risk and cluster size, conditional on exposure—intuitively, the informative cluster size relationship—quantified by the risk difference comparing exposed families with 3 children to exposed families with 1 child, computed in 1 population of K = 1,000,000 F0’s. Note that at x = 0, outcome risk is still related to cluster size, but only through the exposure (i.e., cluster size is noninformative). See the Web Appendix for details on the data-generating mechanism.
In contrast, the typical F1 association isolates the exposure-outcome relationship in that it remains constant under different outcome-size associations (Figure 2). It, too, averages over a population, albeit a hypothetical one that is free of the outcome–cluster size relationship; in this way, it balances the contributions of all existing F0’s. As such, the typical F1 association may be viewed as speaking less to some impact on public health writ large and more to studies of risk factors for diseases or of specific biological relationships. Returning to the DES-ADHD example, the fact that ADHD is more common in smaller families may, for example, be irrelevant to the goal of understanding the role of maternal DES exposure in brain development. In such a case, the typical F1 association may be a suitable target of inference.
Notably, if cluster size is noninformative—that is, related to outcomes only through the exposure/covariates—then the all F1 and typical F1 associations coincide numerically (Figure 2; x = 0). Their precise interpretations in this case may not be crucial, and analysts can proceed with the usual population-averaged interpretation that accompanies results from a GEE analysis.
OTHER METHODOLOGICAL CONSIDERATIONS
Above, we explored the interplay between study design, analysis, and the parameter being estimated in multigenerational studies. Here we briefly outline other methodological considerations, highlight recent developments, and indicate where new methods are needed.
Empty clusters
In multigenerational studies, the exposure is directly applied to members of the F0 generation, while outcomes are measured in their progeny. With this in mind, we have so far assumed that each individual in the F0 generation has at least 1 child, which may not be the case. That is, the observed F1 outcome data for an individual in the F0 generation may constitute an empty cluster. This presents unique challenges, both conceptually and analytically. If whether or not a woman bears children is unrelated to their potential health outcomes (given covariates), we say that clusters are noninformatively empty and no adjustments are needed; otherwise, clusters are informatively empty and the analysis requires more care (47).
Informative emptiness is a natural extension of informative cluster size. Recall that the all F1 association can be viewed through the lens of having balanced the contributions across the individuals in the F1 population. Since nonexistent F1’s play no role in this population, estimates of the all F1 association remain valid under informative emptiness. By contrast, the typical F1 association can be viewed as balancing the contributions of all F0’s. As such, F0’s with no children—as all F0’s—should contribute equally; and yet such empty clusters, containing no outcomes to report, are excluded from standard analyses. To resolve this, in settings where the full cohort is available or data are available through design I described above (sampling F0 families) and information is available on the empty clusters, one can adopt a joint marginalized model of outcomes and cluster sizes, a parametric analysis that can directly incorporate empty clusters into a likelihood framework (47, 48).
More generally, the interplay between design and informative emptiness needs to be characterized. Retrospective approaches like design III (sampling F1’s directly) are probably susceptible to selection bias, since they may never register information on empty clusters. Further research is needed to determine how—and whether—both exposure associations described here could be recovered from different designs under informative emptiness.
Misclassification
Given the practical limitations of following a population over the course of multiple generations, exposure data may only be available retrospectively, making them vulnerable to misclassification and recall bias (53–55). The circumstances of data collection may exacerbate the problem even more—for example, in NHS II, F1’s reported whether or not they had been exposed to DES in utero (6).
While misclassification and measurement error are commonplace in epidemiology (53, 54), multigenerational studies present new challenges. Take DES, for example, an exposure related to both family size and neurodevelopmental outcomes in NHS II. McGee et al. (56) showed that misclassification in such an exposure actually induces informative cluster size when cluster size would otherwise be noninformative. Moreover, the extent of misclassification itself varied by cluster size, with larger families exhibiting more severe misclassification (56). In particular, misclassification that depends on informative cluster size induces differential misclassification, leading to complex bias structures (56). Researchers might incorporate bias analyses to assess the impact of different misclassification patterns.
Volume-outcome studies (family size as a covariate)
We have thus far assumed that the goal of analysis is to estimate an exposure-outcome association and that the outcome–family size association is a nuisance. When the outcome–family size relationship is itself of interest, family size (or some function of it) can be incorporated into the model as a covariate (48). This intuitively “adjusts away” the outcome–family size relationship, such that cluster size would no longer be informative. As such, this represents an alternative method for handling informative cluster size, although it changes the scientific interpretation of the exposure association. It remains population-averaged, but it compares populations only of families of the same size. This is often inadvisable—for example, when cluster size is a mediator (see Seaman et al. (48) for a discussion).
DISCUSSION
As multigenerational cohorts mature and proliferate, so do opportunities to answer new epidemiologic questions. We have identified a number of methodological challenges inherent to these studies and summarized existing methods for analysis. Importantly, we have summarized when to consider informative cluster size, how this might affect design decisions, how the choice of analysis intersects with the design to determine what is being estimated, and how to differentiate the 2 target associations. Yet new challenges will surely emerge. For instance, we considered only 2 generations, which will generally be insufficient to isolate transgenerational associations—a subset of multigenerational associations that manifest through pathways distinct from the one through which direct exposure influences outcomes, for example, via epigenetic inheritance. Typically F2 outcomes are needed to identify an association as transgenerational, but F3 outcomes may even be necessary if F0 women pregnant with a female fetus are exposed (see Skinner et al. (46)). A next step is therefore to explore how the same basic building blocks as those summarized in Table 3—primary sampling generations, family completeness, cluster correlation, informative cluster size, empty clusters, weighting schemes—interact in studies spanning 3 or more generations. Nevertheless, the issues discussed here apply broadly to F0-F1 settings, including many studies of maternal exposures and child development (57–61).
Table 3.
Select Methodological Considerations Relevant to Population-Based F0-F1 Studies of Multigenerational Effectsa
| Notation | Significance |
|---|---|
| Cluster correlation | Health outcomes are often correlated within families (clusters). |
| Empty clusters | Unlike many cluster-correlated settings, clusters may be of size zero (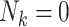 ) since F0’s may have no children. ) since F0’s may have no children. |
| Informative cluster size | If some latent factor is related to outcomes and number of children (i.e., cluster size), the typical F1 effect differs from the all F1 effect. |
| Informatively empty clusters | Informative emptiness occurs when an informative cluster-size mechanism causes clusters of size zero (i.e., some F0’s with no children). Empty clusters must be incorporated into the analysis to recover the typical F1 effect. Informatively empty clusters may interact with study designs (e.g., cause selection bias). |
| Primary sampling generation | The generation initially recruited (e.g., F0 or F1) is a key component of multigenerational study designs that affects the interpretation of exposure effects estimated from an unweighted analysis.  may be unobservable if F1 is the primary sampling generation. may be unobservable if F1 is the primary sampling generation. |
| Family completeness | Whether all children or a random subset of children are sampled for each recruited F0 is another component of study designs that affects the interpretation of exposure effects estimated from an unweighted analysis. Family size 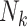 may be unobservable when families are incomplete. may be unobservable when families are incomplete. |
| Weighting schemes | Unweighted analyses (GEE with working independence) recover an exposure effect implied by the study design. Weighting by cluster size (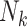 ) or its inverse ( ) or its inverse (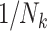 ) can recover the alternative effect. Both require that the design permit complete family size to be observed. ) can recover the alternative effect. Both require that the design permit complete family size to be observed. |
| Misclassification | Retrospective multigenerational designs are particularly susceptible to exposure misclassification. Misclassification bias manifests in complex ways when the degree of misclassification is related to number of children. |
Abbreviation: GEE, generalized estimating equations.
a 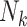 , number of children born to the kth F0 (family size).
, number of children born to the kth F0 (family size).
When a population exhibits informative cluster size, subsamples inherit its limitations on the scope of scientific inquiry—even when they do not exhibit cluster correlation (see “Simulation study: designs II and III”). By default, they estimate either an “all F1” association or the “typical F1” association. (While the simulation study produced results for risk ratios, we observe analogous results on the odds ratio and risk difference scales; see Tables 4 and 5). These differ in subtle ways, and choosing between them is a difficult task, requiring investigators to make explicit their scientific aims beyond simply estimating an exposure-outcome association. By analogy to 2 hypothetical clinical trials, we highlighted their differences and argued that the “all F1” association better suits studies assessing overall impacts on public health, while the “typical F1” association better suits studies of risk factors for disease and underlying biological relationships. Nevertheless, the two can often be estimated in the same sample, and one might ultimately report both.
Table 4.
Mean Log Odds Ratio Estimates of the Exposure-Outcome Association for Various Study Design–Analysis Pairs Across 1,000 Simulated Data Sets, Exponentiated to the Odds Ratio Scale (Simulation Results)a
| Data Structure | Weighting Scheme (Analysis) | ||
|---|---|---|---|
| 1 (IEE) |
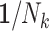 (WEE) (WEE)
|
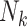
|
|
| Full population | 2.0 | 1.6 | |
| Design I | 2.0 | 1.6 | |
| Design II | 1.6 | 2.0 | |
| Design III | 2.0 | 1.6 | |
Abbreviations: IEE, independence estimating equations; WEE, weighted estimating equations.
a 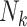 , size of the kth cluster.
, size of the kth cluster.
Table 5.
Mean Risk Difference Estimates (%) of the Exposure-Outcome Association for Various Study Design–Analysis Pairs Across 1,000 Simulated Data Sets (Simulation Results)a
| Data Structure | Weighting Scheme (Analysis) | ||
|---|---|---|---|
| 1 (IEE) |
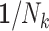 (WEE) (WEE)
|
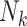
|
|
| Full population | 1.2 | 1.1 | |
| Design I | 1.2 | 1.1 | |
| Design II | 1.1 | 1.2 | |
| Design III | 1.2 | 1.1 | |
Abbreviations: IEE, independence estimating equations; WEE, weighted estimating equations.
a 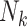 , size of the kth cluster.
, size of the kth cluster.
Designing multigenerational studies requires careful consideration. For example, one may need to collect auxiliary information—such as cluster size in design II or III or empty clusters—to recover an association of interest. Moreover, practical constraints on prospective studies spanning multiple generations motivate adapting outcome-dependent designs to this setting (62–68). These and other design challenges will likely play an important role in future research.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, Massachusetts (Glen McGee, Brent A. Coull, Sebastien Haneuse); Epidemiology Branch, Division of Intramural Population Health Research, Eunice Kennedy Shriver National Institute of Child Health and Human Development, Bethesda, Maryland (Neil J. Perkins, Sunni L. Mumford, Enrique F. Schisterman); Department of Environmental Health Sciences, Mailman School of Public Health, Columbia University, New York, New York (Marianthi-Anna Kioumourtzoglou); Department of Environmental Health, Harvard T.H. Chan School of Public Health, Boston, Massachusetts (Marc G. Weisskopf); and Department of Biostatistics, School of Medicine, Vanderbilt University, Nashville, Tennessee (Jonathan S. Schildcrout).
This work was funded in part by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, as well as by National Institutes of Health grants ES026555, ES000002, and P30-ES009089 from the National Institute of Environmental Health Sciences and R01-HL094786 from the National Heart, Lung, and Blood Institute.
Conflict of interest: none declared.
REFERENCES
- 1. Skinner MK, Anway MD, Savenkova MI, et al. Transgenerational epigenetic programming of the brain transcriptome and anxiety behavior. PLoS One. 2008;3(11):e3745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Emanuel I, Filakti H, Alberman E, et al. Intergenerational studies of human birthweight from the 1958 birth cohort. 1. Evidence for a multigenerational effect. Br J Obstet Gynaecol. 1992;99(1):67–74. [DOI] [PubMed] [Google Scholar]
- 3. Eubanks AA, Nobles CJ, Hill MJ, et al. Intergenerational effects of maternal lifestyle behaviors on the AMH of adult female offspring. Fertil Steril. 2018;110(4 suppl):e53. [Google Scholar]
- 4. Titus-Ernstoff L, Troisi R, Hatch EE, et al. Birth defects in the sons and daughters of women who were exposed in utero to diethylstilbestrol (DES). Int J Androl. 2010;33(2):377–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Titus-Ernstoff L, Troisi R, Hatch EE, et al. Offspring of women exposed in utero to diethylstilbestrol (DES): a preliminary report of benign and malignant pathology in the third generation. Epidemiology. 2008;19(2):251–257. [DOI] [PubMed] [Google Scholar]
- 6. Kioumourtzoglou M-A, Coull BA, O’Reilly ÉJ, et al. Association of exposure to diethylstilbestrol during pregnancy with multigenerational neurodevelopmental deficits. JAMA Pediatr. 2018;172(7):670–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Skinner MK, Manikkam M, Guerrero-Bosagna C. Epigenetic transgenerational actions of endocrine disruptors. Reprod Toxicol. 2011;31(3):337–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Heijmans BT, Tobi EW, Stein AD, et al. Persistent epigenetic differences associated with prenatal exposure to famine in humans. Proc Natl Acad Sci. 2008;105(44):17046–17049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Painter RC, Osmond C, Gluckman P, et al. Transgenerational effects of prenatal exposure to the Dutch famine on neonatal adiposity and health in later life. BJOG. 2008;115(10):1243–1249. [DOI] [PubMed] [Google Scholar]
- 10. Veenendaal MV, Painter RC, Rooij SR, et al. Transgenerational effects of prenatal exposure to the 1944–45 Dutch famine. BJOG. 2013;120(5):548–553. [DOI] [PubMed] [Google Scholar]
- 11. Qian M, Chou SY, Gimenez L, et al. The intergenerational transmission of low birth weight and intrauterine growth restriction: a large cross-generational cohort study in Taiwan. Matern Child Health J. 2017;21(7):1512–1521. [DOI] [PubMed] [Google Scholar]
- 12. Misra D, Astone N, Lynch C. Maternal smoking and birth weight: interaction with parity and mother’s own in utero exposure to smoking. Epidemiology. 2005;16(3):288–293. [DOI] [PubMed] [Google Scholar]
- 13. Hardy JB, Shapiro S. Pathways to Adulthood: A Three-Generation Urban Study, 1960–1994: [Baltimore, Maryland]. Ann Arbor, MI: Inter-University Consortium for Political and Social Research; 2019. 10.3886/ICPSR02420.v2. Accessed June 13, 2019. [DOI] [Google Scholar]
- 14. Huang L, Yu X, Keim S, et al. Maternal prepregnancy obesity and child neurodevelopment in the Collaborative Perinatal Project. Int J Epidemiol. 2014;43(3):783–792. [DOI] [PubMed] [Google Scholar]
- 15. Nelson KB, Ellenberg JH. Prenatal and perinatal antecedents of febrile seizures. Ann Neurol. 1990;27(2):127–131. [DOI] [PubMed] [Google Scholar]
- 16. Klebanoff MA. The Collaborative Perinatal Project: a 50-year retrospective. Paediatr Perinat Epidemiol. 2009;23(1):2–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hardy JB, Drage JS, Jackson EC. The First Year of Life. The Collaborative Perinatal Project of the National Institute of Neurological and Communicative Disorders and Stroke. Baltimore, MD: The Johns Hopkins University Press; 1979. [Google Scholar]
- 18. Niswander KR, Gordon MJ. The Women and Their Pregnancies: The Collaborative Perinatal Study of the National Institute of Neurological Diseases and Stroke. Bethesda, MD: National Institutes of Health; 1972. [Google Scholar]
- 19. Huang JY, Gavin AR, Richardson TS, et al. Are early-life socioeconomic conditions directly related to birth outcomes? Grandmaternal education, grandchild birth weight, and associated bias analyses. Am J Epidemiol. 2015;182(7):568–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Cohen AK, Lê-Scherban F. Invited commentary: multigenerational social determinants of health—opportunities and challenges. Am J Epidemiol. 2015;182(7):579–582. [DOI] [PubMed] [Google Scholar]
- 21. Foster HW, Wu L, Bracken MB, et al. Intergenerational effects of high socioeconomic status on low birthweight and preterm birth in African Americans. J Natl Med Assoc. 2000;92(5):213–221. [PMC free article] [PubMed] [Google Scholar]
- 22. Goodman A, Heshmati A, Koupil I. Family history of education predicts eating disorders across multiple generations among 2 million Swedish males and females. PLoS One. 2014;9(8):e106475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Ahrén-Moonga J, Silverwood R, Klinteberg BA, et al. Association of higher parental and grandparental education and higher school grades with risk of hospitalization for eating disorders in females: the Uppsala Birth Cohort Multigenerational Study. Am J Epidemiol. 2009;170(5):566–575. [DOI] [PubMed] [Google Scholar]
- 24. Chaparro MP, Koupil I. The impact of parental educational trajectories on their adult offspring’s overweight/obesity status: a study of three generations of Swedish men and women. Soc Sci Med. 2014;120:199–207. [DOI] [PubMed] [Google Scholar]
- 25. Lê-Scherban F, Diez Roux AV, Li Y, et al. Associations of grandparental schooling with adult grandchildren’s health status, smoking, and obesity. Am J Epidemiol. 2014;180(5):469–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Härkönen J, Kaymakçalan H, Mäki P, et al. Prenatal health, educational attainment, and intergenerational inequality: the Northern Finland Birth Cohort 1966 Study. Demography. 2012;49(2):525–552. [DOI] [PubMed] [Google Scholar]
- 27. Astone NM, Misra D, Lynch C. The effect of maternal socio-economic status throughout the lifespan on infant birthweight. Paediatr Perinat Epidemiol. 2007;21(4):310–318. [DOI] [PubMed] [Google Scholar]
- 28. Kwok MK, Leung GM, Lam TH, et al. Grandparental education, parental education and child height: evidence from Hong Kong’s “Children of 1997” birth cohort. Ann Epidemiol. 2013;23(8):475–484. [DOI] [PubMed] [Google Scholar]
- 29. Gavin AR, Thompson E, Rue T, et al. Maternal early life risk factors for offspring birth weight: findings from the Add Health Study. Prev Sci. 2012;13(2):162–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Hanson MA, Gluckman PD. Developmental origins of health and disease: new insights. Basic Clin Pharmacol Toxicol. 2008;102(2):90–93. [DOI] [PubMed] [Google Scholar]
- 31. Anway MD, Cupp AS, Uzumcu M, et al. Epigenetic transgenerational actions of endocrine disruptors and male fertility. Science. 2005;308(5727):1466–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Anway MD, Leathers C, Skinner MK. Endocrine disruptor vinclozolin induced epigenetic transgenerational adult-onset disease. Endocrinology. 2006;147(12):5515–5523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Anway MD, Skinner MK. Epigenetic transgenerational actions of endocrine disruptors. Endocrinology. 2006;147(suppl 6):s43–s49. [DOI] [PubMed] [Google Scholar]
- 34. Schoevers EJ, Santos RR, Colenbrander B, et al. Transgenerational toxicity of zearalenone in pigs. Reprod Toxicol. 2012;34(1):110–119. [DOI] [PubMed] [Google Scholar]
- 35. Kimberly DA, Salice CJ. If you could turn back time: understanding transgenerational latent effects of developmental exposure to contaminants. Environ Pollut. 2014;184:419–425. [DOI] [PubMed] [Google Scholar]
- 36. Kimberly DA, Salice CJ. Multigenerational contaminant exposures produce non-monotonic, transgenerational responses in Daphnia magna. Environ Pollut. 2015;207:176–182. [DOI] [PubMed] [Google Scholar]
- 37. Lombó M, Fernández-Díez C, González-Rojo S, et al. Transgenerational inheritance of heart disorders caused by paternal bisphenol A exposure. Environ Pollut. 2015;206:667–678. [DOI] [PubMed] [Google Scholar]
- 38. Minguez L, Ballandonne C, Rakotomalala C, et al. Transgenerational effects of two antidepressants (sertraline and venlafaxine) on Daphnia magna life history traits. Environ Sci Technol. 2015;49(2):1148–1155. [DOI] [PubMed] [Google Scholar]
- 39. Jeong TY, Yuk MS, Jeon J, et al. Multigenerational effect of perfluorooctane sulfonate (PFOS) on the individual fitness and population growth of Daphnia magna. Sci Total Environ. 2016;569:1553–1560. [DOI] [PubMed] [Google Scholar]
- 40. Prud’homme SM, Chaumot A, Cassar E, et al. Impact of micropollutants on the life-history traits of the mosquito Aedes aegypti: on the relevance of transgenerational studies. Environ Pollut. 2017;220(A):242–254. [DOI] [PubMed] [Google Scholar]
- 41. Cheng H, Yan W, Wu Q, et al. Parental exposure to microcystin-LR induced thyroid endocrine disruption in zebrafish offspring, a transgenerational toxicity. Environ Pollut. 2017;230:981–988. [DOI] [PubMed] [Google Scholar]
- 42. Louis GB, Dukic V, Heagerty PJ, et al. Analysis of repeated pregnancy outcomes. Stat Methods Med Res. 2006;15(2):103–126. [DOI] [PubMed] [Google Scholar]
- 43. Bao Y, Bertoia ML, Lenart EB, et al. Origin, methods, and evolution of the three Nurses’ Health studies. Am J Public Health. 2016;106(9):1573–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Colditz GA, Philpott SE, Hankinson SE. The impact of the Nurses’ Health Study on population health: prevention, translation, and control. Am J Public Health. 2016;106(9):1540–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Painter RC, Roseboom TJ, Bleker OP. Prenatal exposure to the Dutch famine and disease in later life: an overview. Reprod Toxicol. 2005;20(3):345–352. [DOI] [PubMed] [Google Scholar]
- 46. Skinner MK. What is an epigenetic transgenerational phenotype?: F3 or F2. Reprod Toxicol. 2008;25(1):2–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. McGee G, Weisskopf MG, Kioumourtzoglou MA, et al. Informatively empty clusters with application to multigenerational studies [published online ahead of print April 8, 2019] Biostatistics. (doi: 10.1093/biostatistics/kxz005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Seaman S, Pavlou M, Copas A. Review of methods for handling confounding by cluster and informative cluster size in clustered data. Stat Med. 2014;33(30):5371–5387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc.; 2012. [Google Scholar]
- 50. Hoffman EB, Sen PK, Weinberg CR. Within-cluster resampling. Biometrika. 2001;88(4):1121–1134. [Google Scholar]
- 51. Williamson JM, Datta S, Satten GA. Marginal analyses of clustered data when cluster size is informative. Biometrics. 2003;59(1):36–42. [DOI] [PubMed] [Google Scholar]
- 52. Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Stat Sci. 1999;14(1):29–46. [Google Scholar]
- 53. Carroll RJ, Ruppert D, Stefanski LA, et al. Measurement Error in Nonlinear Models: A Modern Perspective. Boca Raton, FL: Chapman & Hall/CRC Press; 2006. [Google Scholar]
- 54. Buonaccorsi JP. Measurement Error: Models, Methods, and Applications. Boca Raton, FL: Chapman & Hall/CRC Press; 2010. [Google Scholar]
- 55. Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 56. McGee G, Kioumourtzoglou MA, Weisskopf MG, et al. On the interplay between exposure misclassification and informative cluster size [published online ahead of print July 26, 2020] J R Stat Soc Ser C Appl Stat. (doi: 10.1111/rssc.12430). [DOI] [Google Scholar]
- 57. Whyatt RM, Liu X, Rauh VA, et al. Maternal prenatal urinary phthalate metabolite concentrations and child mental, psychomotor, and behavioral development at 3 years of age. Environ Health Perspect. 2012;120(2):290–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Roberts AL, Lyall K, Rich-Edwards JW, et al. Association of maternal exposure to childhood abuse with elevated risk for autism in offspring. JAMA Psychiatry. 2013;70(5):508–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Raz R, Roberts AL, Lyall K, et al. Autism spectrum disorder and particulate matter air pollution before, during, and after pregnancy: a nested case-control analysis within the Nurses’ Health Study II cohort. Environ Health Perspect. 2015;123(3):264–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Eskenazi B, Chevrier J, Rauch SA, et al. In utero and childhood polybrominated diphenyl ether (PBDE) exposures and neurodevelopment in the CHAMACOS Study. Environ Health Perspect. 2013;121(2):257–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Rundle A, Hoepner L, Hassoun A, et al. Association of childhood obesity with maternal exposure to ambient air polycyclic aromatic hydrocarbons during pregnancy. Am J Epidemiol. 2012;175(11):1163–1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Anderson JA. Separate sample logistic discrimination. Biometrika. 1972;59(1):19–35. [Google Scholar]
- 63. Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66(3):403–411. [Google Scholar]
- 64. Neuhaus J, Scott AJ, Wild CJ. The analysis of retrospective family studies. Biometrika. 2002;89(1):23–37. [Google Scholar]
- 65. Cai J, Qaqish B, Zhou H. Marginal analysis for cluster-based case-control studies. Sankhyā Ser B. 2001;63(3):326–337. [Google Scholar]
- 66. Schildcrout JS, Rathouz PJ. Longitudinal studies of binary response data following case-control and stratified case-control sampling: design and analysis. Biometrics. 2010;66(2):365–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Park E, Kim Y. Analysis of longitudinal data in case-control studies. Biometrika. 2004;91(2):321–330. [Google Scholar]
- 68. Schildcrout JS, Mumford SL, Chen Z, et al. Outcome-dependent sampling for longitudinal binary response data based on a time-varying auxiliary variable. Stat Med. 2012;31(22):2441–2456. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


