Stabilization of a brain-computer interface via the alignment of low-dimensional spaces of neural activity

Abstract

The instability of neural recordings can render clinical brain-computer interfaces (BCIs) uncontrollable. Here, we show that the alignment of low-dimensional neural manifolds (low-dimensional spaces that describe specific correlation patterns between neurons) can be used to stabilize neural activity, thereby maintaining BCI performance in the presence of recording instabilities. We evaluated the stabilizer with non-human primates during online cursor control via intracortical BCIs in the presence of severe and abrupt recording instabilities. The stabilized BCIs recovered proficient control under different instability conditions and across multiple days. The stabilizer does not require knowledge of user intent and can outperform supervised recalibration. It stabilized BCIs even when neural activity contained little information about the direction of cursor movement. The stabilizer may be applicable to other neural interfaces and may improve the clinical viability of BCIs.

Brain-computer interfaces (BCIs) allow individuals with paralysis to control assistive devices using movement commands extracted from the brain. Recent clinical BCIs have enabled functional restoration of movement, including intracortical control of robotic arms^1,2, paralysed limbs^3,4 and computer interfaces^5,6. A critical barrier to the clinical adoption of BCI technology is that neural activity recorded by implanted cortical electrodes can vary over time⁷. This is due to small movements of the electrodes relative to the surrounding brain tissue, as well as cell loss and scar tissue build-up^8–11. Left unmitigated, these neural recording instabilities can lead the BCI to become uncontrollable, often within hours¹².

BCI systems commonly use a fixed relationship between neural activity and movements to translate recorded neural signals into assistive device commands. This relationship—referred to as a decoder—is determined in a calibration session where neural activity is recorded while the movement intent of the user is known. When recording instabilities occur, they make previously calibrated decoders no longer appropriate, resulting in a decline in BCI performance. Such instabilities are particularly problematic for clinical BCIs using intracortical recordings^13,14, which have provided the highest BCI performance demonstrations to date but can be prone to severe recording instabilities. To restore control, it is common to stop using the BCI to re-estimate decoding parameters by performing another calibration session. Such recalibration procedures are burdensome for the user, as they are time consuming and often require the intervention of a technician. In response to this need, BCI decoders have been developed that attempt to provide stable BCI performance in the presence of neural instabilities by recalibrating the BCI during ongoing BCI control^13,15–19. Nearly all of these self-recalibrating decoders attempt to form estimates of the user’s movement intent on the fly so that decoder parameters can be updated without an explicit recalibration procedure. Although these approaches have worked well in controlled environments, their ability to recover BCI performance depends critically on the level of user engagement.

To obviate the need to re-estimate decoding parameters, here we developed a neural signal stabilizer to provide stabilized input into the BCI. Our approach leverages the scientific finding that neural population activity tends to lie within a low-dimensional space, termed the neural manifold^20–23. The neural manifold (also known as the intrinsic manifold) describes the population activity patterns that are readily expressed by a population of neurons, and is believed to reflect constraints imposed by the underlying neural circuitry^24,25. Here, we exploit the existence of this low-dimensional space to improve the clinical viability of BCIs for individuals with paralysis.

We hypothesized that even though the specific neurons being recorded may change over time, the recorded population activity reflects a stable underlying representation of movement intent that lies within the neural manifold. We developed a manifold-based stabilizer to align estimates of the manifold obtained from possibly unstable neural recordings at different points in time. Using the manifold-stabilized neural activity, a decoder with a fixed set of parameters can then be used to accurately estimate intended BCI movements. In this manner, our stabilized BCI can compensate for neural recording instabilities such as tuning changes, drop-outs or baseline shifts without knowledge of the user’s intended BCI movements. These categories of instabilities cover a wide range of those that could impact intracortical BCI use. Neural manifolds can be estimated using just minutes of neural activity, enabling the rapid restoration of control even in the presence of severe recording instabilities. Furthermore, our approach represents a general framework for achieving stable BCI control that can be applied to different neural recording modalities and decoding algorithms.

We assessed the performance of the manifold-based stabilizer during BCI cursor control in two rhesus monkeys, each of which was implanted with an intracortical microelectrode array in the primary motor cortex. We show that the manifold-based stabilizer was able to compensate for a wide range of neural recording instabilities, including those resulting in severe control impairment. In addition, the stabilizer was able to overcome instabilities applied over multiple days. Finally, we show that our stabilized BCI outperformed self-recalibrating techniques that rely on estimating the intent of the user, particularly during periods when the amount of movement-related information in the neural activity was low. Preliminary versions of this work have been previously reported^26–28.

Manifold-based stabilization of neural population activity

To overcome neural recording instabilities, we designed a stabilized BCI that first extracts a stable low-dimensional representation of neural activity (also referred to as the latent state) and then passes this stable representation to a fixed decoder to produce BCI movements. Specifically, we used a two-stage approach consisting of: (1) a manifold-based stabilizer based on factor analysis^20,29; and (2) a BCI decoder, which in this case was a velocity Kalman filter³⁰ that produces a continuous-valued estimate of cursor velocity in real time (Fig. 1). Whereas parameters of the stabilizer are updated automatically across time to account for neural recording instabilities, the parameters of the BCI decoder are held fixed.

Fig. 1 |. Stabilized BCI framework.

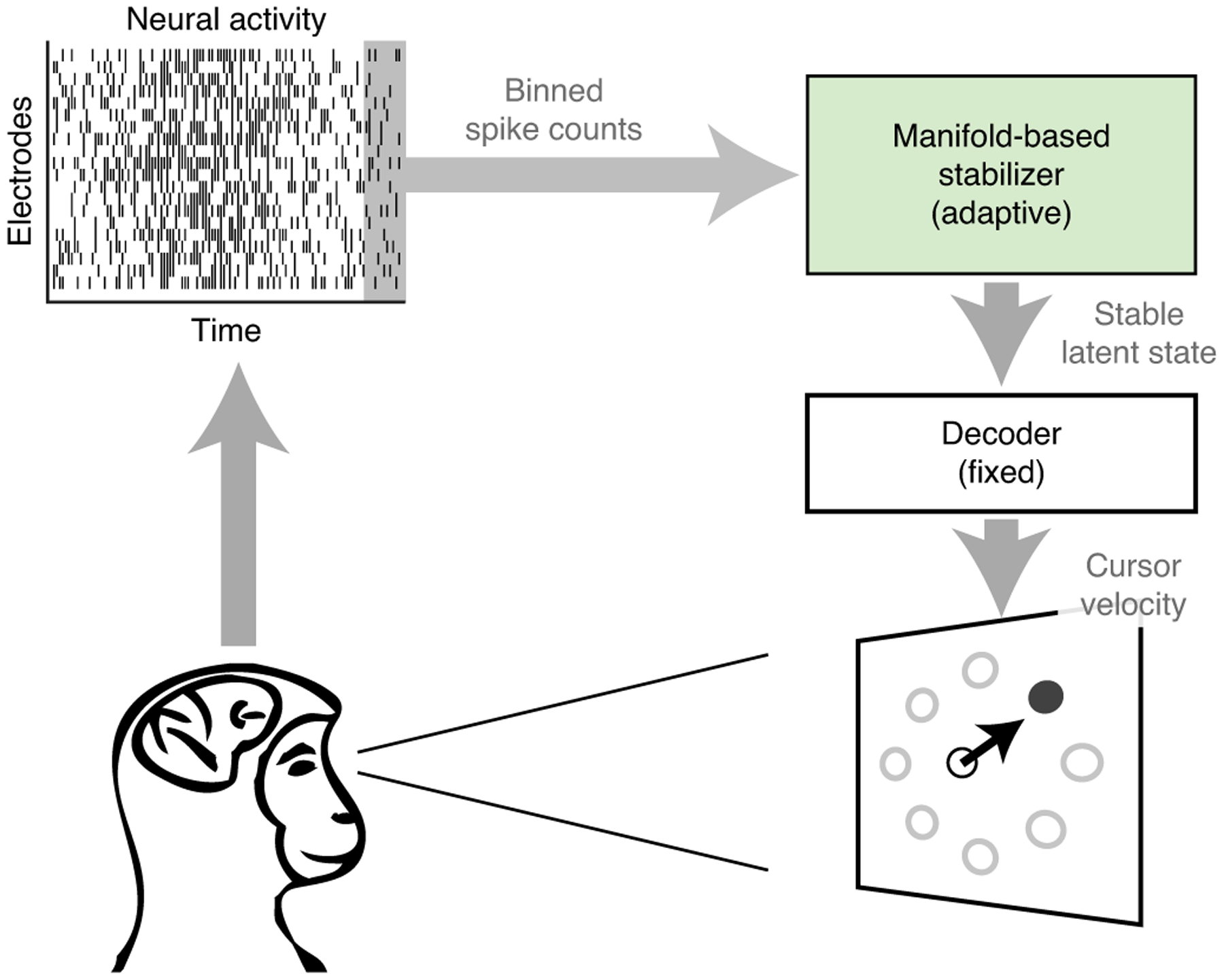
Schematic of the stabilized BCI framework. Neural activity recorded from multiple electrodes, shown here in the form of a spike raster plot, is binned and passed to the manifold-based stabilizer. The stabilizer extracts a stable latent state, which is passed to the decoder to estimate the velocity of a BCI cursor. Whereas the stabilizer dynamically adjusts for neural recording instabilities, the parameters of the decoder are held fixed over time.

To understand how the manifold-based stabilizer works, consider the scenario where the identity of some of the recorded neurons changes across days (Fig. 2a). In this example, electrodes 1 and 2 are stable across days 1 and 2, whereas electrode 3 is unstable in that it is recording the activity of a different neuron on day 2. This in turn results in changes in the patterns of recorded neural population activity, which can lead to a degradation in performance when using fixed decoding parameters (Fig. 2b). One possible solution is to simply turn off electrode 3 on day 2, but this approach would lead to the number of usable electrodes decreasing rapidly over time¹⁴, leading to irrevocably degraded BCI performance.

Fig. 2 |. Manifold-based stabilization intuition and design.

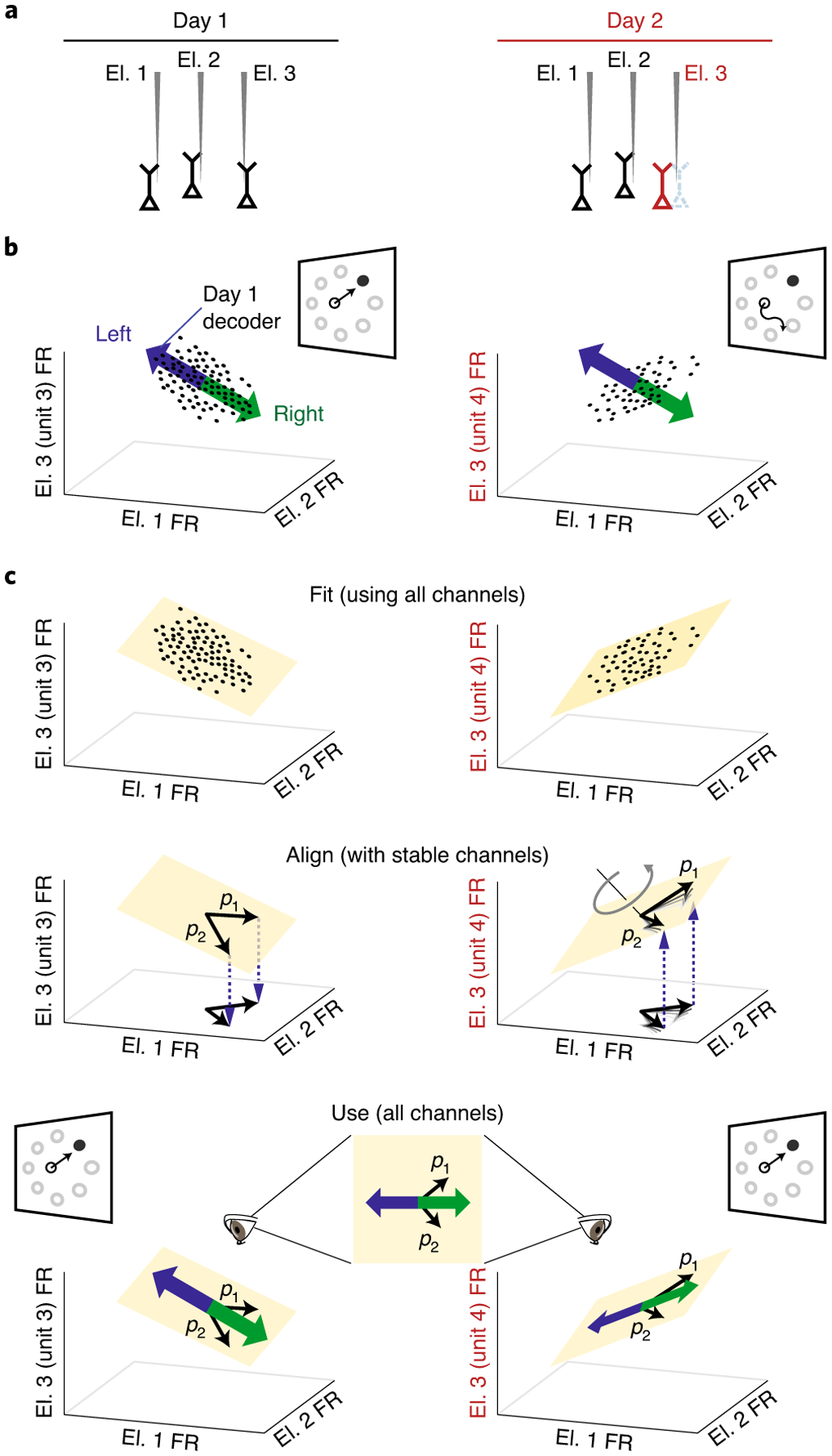
a, Neural recording instabilities, such as a change in a neuron being recorded by a particular electrode (for example, electrode 3 (El. 3); red), result in changes in the recorded neural population activity across days. b, With a fixed BCI decoder alone, neural instabilities can result in the day 1 decoder (blue/green arrows, shown as a one-dimensional vector for simplicity) becoming inconsistent with neural activity recorded on day 2 (right; black dots). This leads to poor BCI performance. Cursor velocities are obtained by projecting the neural activity (black dots) onto the decoder axis. c, Combining stabilization with a fixed decoder allows the BCI performance to remain high across days. To extract a stable representation of neural population activity across days, low-dimensional neural manifolds are first fit to the neural population activity recorded on each day. The coordinate system for the neural manifold on day 2 is aligned so that neurons that are stable across days (electrodes 1 and 2) are defined in a consistent manner with respect to the coordinate systems for both days (denoted by the axes labelled p₁ and p₂). The thick black lines depict the final aligned coordinate system. Alignment ensures that unstable neural population activity is mapped to the same stable low-dimensional manifold across days, providing a stabilized latent state that can be used for decoding across days. FR, firing rate.

Instead, to solve this problem, we draw on the observation that neural population activity tends to lie within a low-dimensional neural manifold that captures the movement intent of the user^23,25. If we are able to recover a stable representation of this manifold over time, we can continue to use all of the available electrodes without needing to turn off those that are unstable. Consider estimating a manifold from the recorded population activity at different times, where the neural recordings are unstable (Fig. 2c, top). To align the manifolds across time, we first identify the electrodes with stable recordings (see Methods). Then, we specify that the coordinate axes (p₁ and p₂) for the different estimates of the manifold are defined in the same way with respect to the stable electrodes (Fig. 2c, middle). This involves transforming the coordinate axes within the neural manifold on day 2 until they achieve the same relationship with the stable electrodes as on day 1 (see Methods). Stabilized neural activity in the aligned manifold (that is, neural activity expressed in terms of the coordinate axes (p₁ and p₂) is then passed to the decoder to control the BCI (Fig. 2c, bottom).

Stabilization overcomes severe and abrupt recording instabilities

We evaluated the manifold-based stabilizer in two rhesus macaques (Macaca mulatta) as they performed a centre-out BCI cursor control task. The monkeys were each implanted with a 96-electrode array in the primary motor cortex (M1). To systematically test the performance of the stabilizer, we applied instabilities to the neural activity used for BCI control. These instabilities were designed to mimic the naturally occurring instabilities seen in clinical BCIs. We focused on instabilities resulting in severe degradation of BCI control to test the performance of the stabilizer more extensively than would be possible with natural instabilities alone.

Instabilities observed in intracortical electrode recordings (Fig. 3a) typically involve a combination of: (1) baseline shifts, where there is a change in the baseline firing rate of an electrode; (2) unit drop-out, where a neuron dies or moves away from the electrode tip; and (3) tuning changes, where there is a change in the functional relationship between the neural activity and the intended cursor movement due to a change in the neurons in the electrode’s recording sphere. To generate these types of instabilities, we modified in real time the recorded activity used for BCI control (Fig. 3b). Baseline shifts were generated by applying a different random constant to the spike counts recorded on each electrode. Unit drop-out instabilities were generated by setting the activity of a subset of electrodes to 0. Instabilities resulting in tuning changes were generated by replacing the activity of a subset of electrodes with that of a held-out set of electrodes. Additionally, we generated combination instabilities, which consisted of simultaneously applied baseline shifts, unit drop-out and tuning changes (see Methods).

Fig. 3 |. Examples of neural recording instabilities.

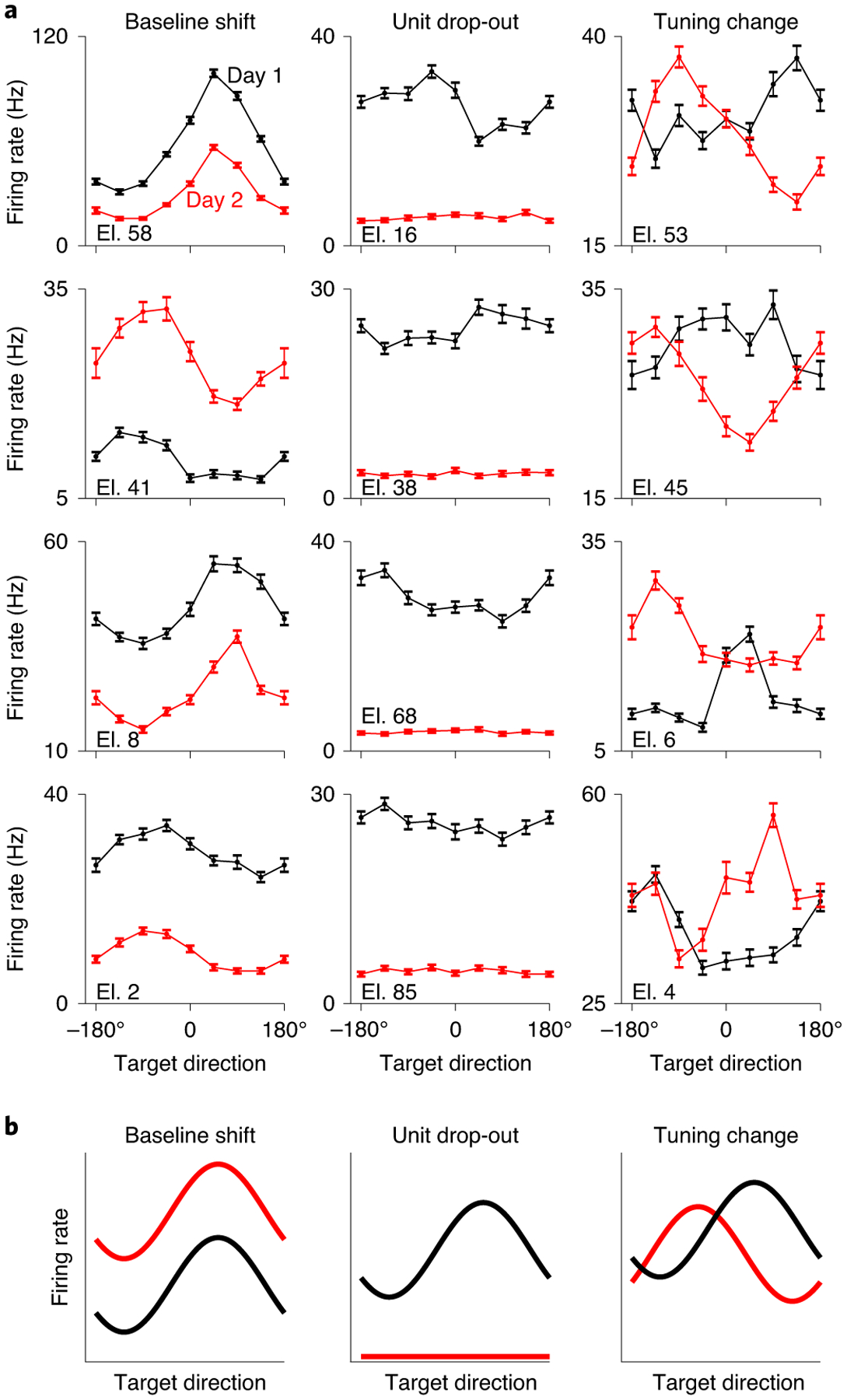
a, Examples of differences in tuning curves during an eight-target centre-out arm-reaching task across days for monkey N. Each panel shows the average firing rate as a function of reaching direction for a single electrode on two different days (black and red curves). Firing rates were estimated over a 500-ms window beginning 100 ms before the onset of each reach. Individual examples may come from separate days. Error bars represent s.e. for each target direction. Tuning curves were calculated based on 500 trials per day randomly distributed across target directions (range: 50–81 trials per target direction). b, Schematic of the three types of applied neural instabilities used to evaluate the performance of the stabilized BCI.

We assessed the ability of the stabilizer to overcome these imposed instabilities (Fig. 4a). Each day’s experiment began with a supervised calibration session (144 trials) where the initial parameters of the stabilizer and the fixed parameters of the decoder were determined. Following this, the monkey performed 128 trials of BCI control using the calibrated decoder in the absence of instabilities. Performance during these trials was typically high (average success rate: 99.9%; average target acquisition time: 0.6 s; Fig. 4b, blue region), with cursor trajectories consistently straight to the target (Fig. 4c, first panel). We then introduced a recording instability and began updating the parameters of the stabilizer every 16 trials while the animal continued to use the BCI (the stabilizer block; Fig. 4b, grey region). Performance decreased following introduction of the recording instability, with cursor trajectories severely impacted (Fig. 4c, second panel). Updates of the stabilizer rapidly improved performance; cursor trajectories became straighter and more consistent with subsequent updates (Fig. 4c, third and fourth panels).

Fig. 4 |. Representative experimental session.

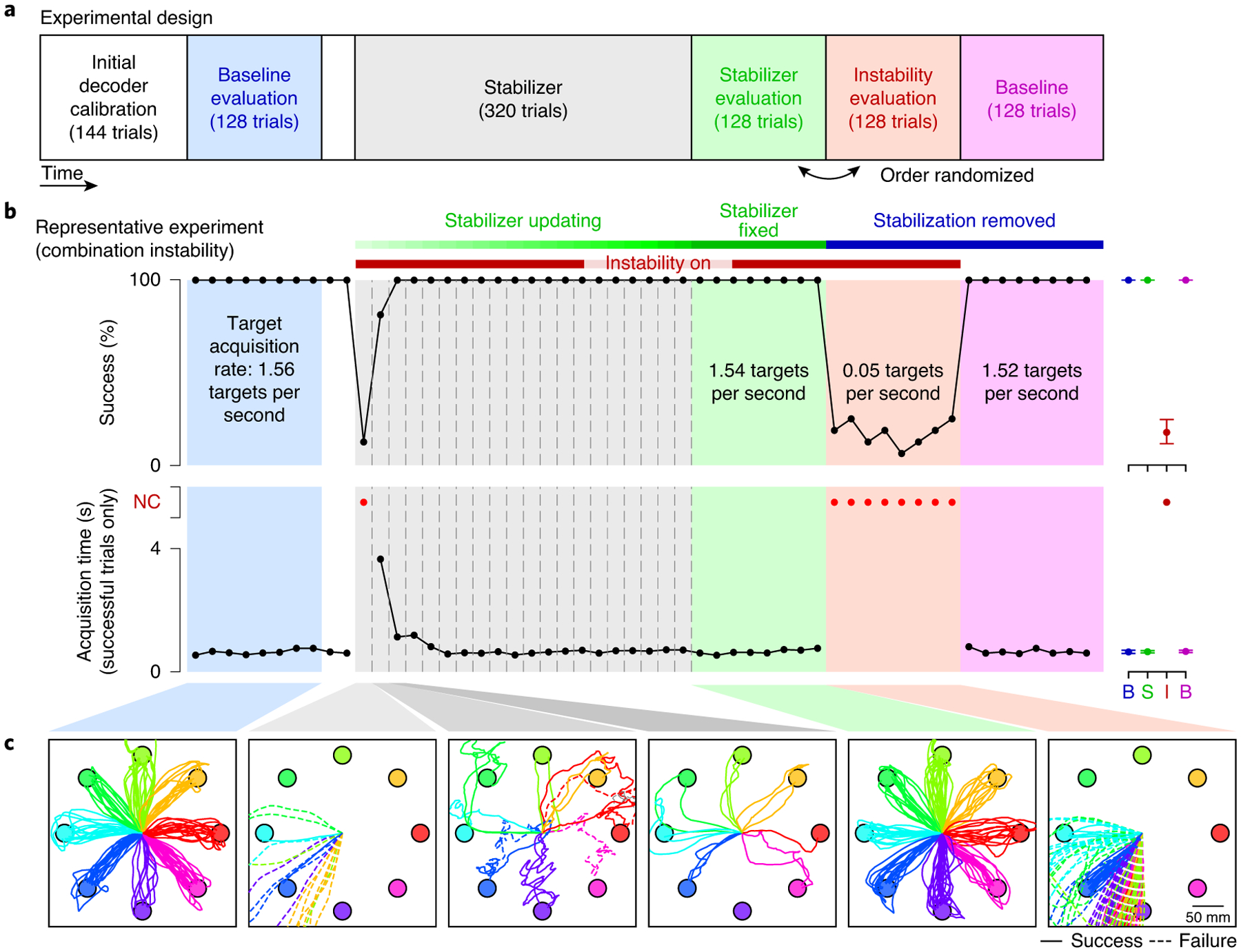
a, Experimental sessions began with calibration of the initial BCI decoder, followed by a baseline evaluation trial block (blue). An instability was then applied to the neural activity and the stabilizer was turned on and allowed to run for approximately 320 trials. The stabilizer updates were then turned off, and the performance of the stabilized BCI was evaluated (green). To assess performance in the presence of the instability alone, the animals also performed a block of trials with the non-stabilized BCI decoder in the presence of the instability (red). A final baseline block with the non-stabilized BCI decoder and no instability was performed at the end of each experimental session (magenta). This was done to determine whether there were any transient changes in baseline performance (that is, after-effects) following stabilization that may be indicative of learning by the animal. b, Cursor control success rate and acquisition times for a representative experiment (L20160325). Vertical dashed lines represent stabilizer updates. Black dots represent success rate and acquisition time averaged over non-overlapping sets of 16 trials for all blocks except the stabilizer block. For this block, black dots represent success rate and average acquisition time calculated using all trials between stabilizer updates, which occurred nominally every 16 trials. Acquisition times for blocks with success rates of <50% were not quantified and are instead represented as red dots. For visual clarity, average success rates and acquisition times for the evaluation blocks are shown to the right of each trace. B (blue), baseline evaluation; B (magenta), post-stabilization baseline; I, instability evaluation; NC, not computed; S, stabilizer evaluation. Error bars represent the 95% confidence interval of the mean. c, Cursor trajectories during selected blocks for experiment L20160325. Successful trials are shown by solid lines, and failed trials by dashed lines.

After 320 trials, stabilizer updates were then stopped and two blocks of trials were performed in the presence of the recording instability: one with the final set of stabilizer parameters (the stabilizer evaluation block) and another with stabilization removed (the instability evaluation block). Cursor control during the stabilizer evaluation block was comparable to that of the baseline evaluation block (Fig. 4b (green region) and Fig. 4c (fifth panel)), indicating that the stabilizer was able to restore high-performance BCI control. In contrast, cursor control during the instability evaluation block (Fig. 4b (red region) and Fig. 4c (last panel)) was comparable to that immediately following introduction of the instability, indicating that the animal was not able to overcome the instability without the aid of the stabilizer. Neural activity in the latent space was found to be similar during the baseline and stabilizer evaluation blocks, indicating that the stabilizer was able to extract a stable representation (see Supplementary Fig. 1).

Across 42 single-day experiments, we observed similar trends in both success rate (Fig. 5a) and target acquisition time (Fig. 5b) to those shown in Fig. 4, with stabilization rapidly improving BCI performance following the introduction of instabilities. Average success rates during the stabilizer evaluation block (98.3 ± 0.4% (mean ± s.e.)) were comparable to those during the baseline evaluation block (99.9 ± 0.6%), with average target acquisition times slightly longer following stabilization (baseline evaluation: 0.61 ± 0.02 s; stabilizer evaluation: 0.73 ± 0.02 s). To quantify BCI performance using a single metric, we used target acquisition rate (TAR; the number of targets the animal was capable of successfully acquiring divided by the time the cursor was under brain control) (Fig. 5c). Across all of the experiments, the results were consistent with the example session shown in Fig. 4. That is, introducing the recording instability resulted in a significant decrease in performance (P < 10⁻⁷, Wilcoxon signed-rank test). The stabilizer restored performance (as measured by the TAR) with an exponential time constant of 0.92 ± 0.15 updates (mean ± s.e.) during the stabilizer block, corresponding to 88.9 ± 7.9 s (mean ± s.e.) of control time.

Fig. 5 |. Summary of the single-day experimental sessions.

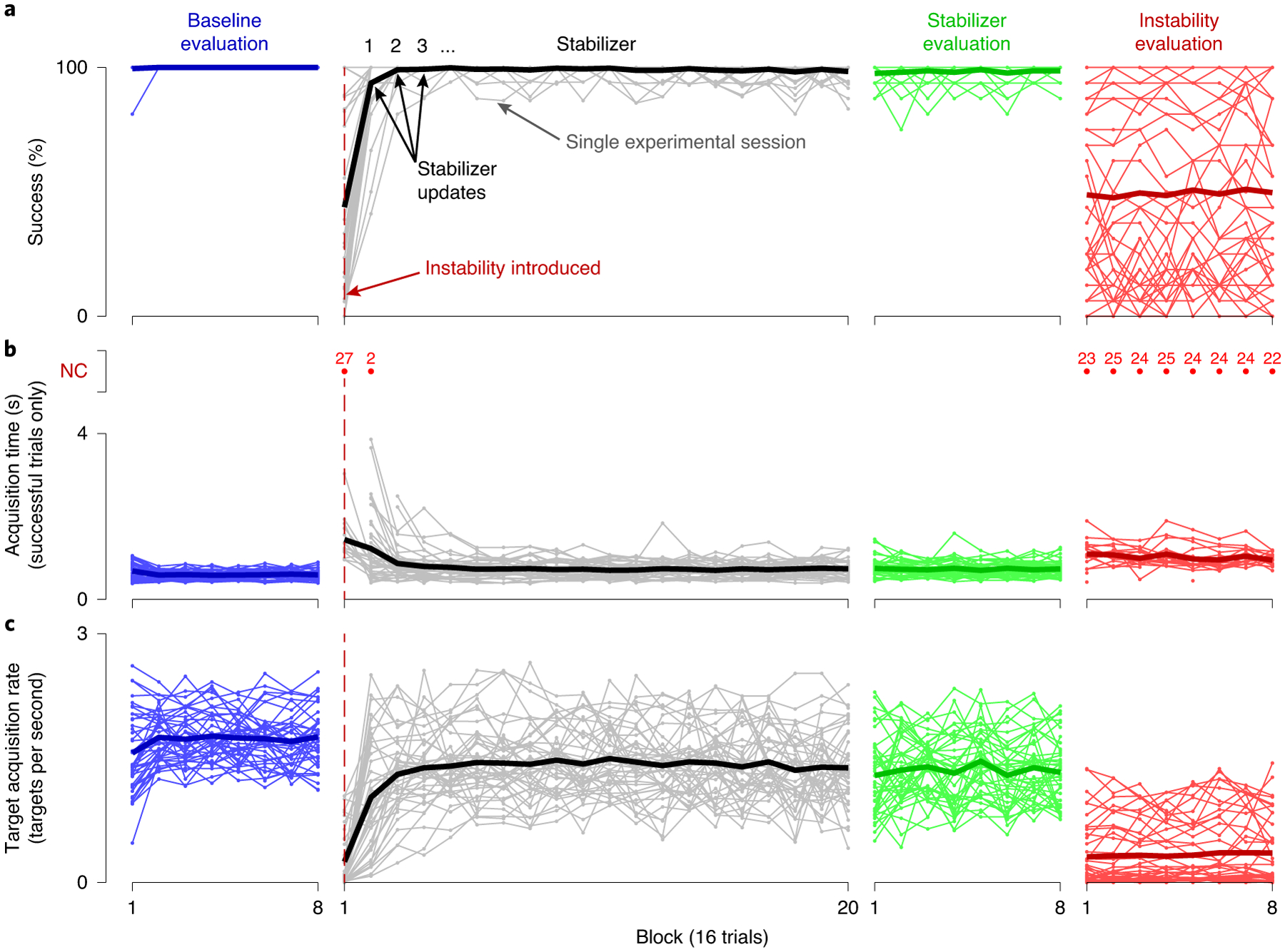
a–c, Success rate (a), mean acquisition time (b) and TAR (c), calculated over 16-trial blocks, are shown for all single-day experimental sessions for both monkeys. Blue lines indicate performance metrics calculated for the baseline evaluation block immediately following calibration of the BCI decoder. Grey lines indicate performance metrics calculated while stabilizer updates were occurring. Green lines indicate performance metrics calculated during the stabilizer evaluation block, when the stabilizer was held fixed. Red lines indicate performance metrics calculated during the instability evaluation block, when BCI control was performed using the non-stabilized decoder. Thin lines indicate the results for individual experiments, whereas thick lines indicate the mean across experiments. Acquisition times for blocks with success rates of <50% are plotted as red dots, with the number of experiments for which the acquisition time could not be computed for a given block shown above each red dot. Acquisition times for these blocks are not included in the average across experiments. As in Fig. 4, performance metrics for the stabilizer block were calculated for all trials between stabilizer updates, which occurred nominally every 16 trials.

To summarize these results, we compared TARs between the stabilized and non-stabilized BCIs for all of the experiments. We first examined whether there was a difference between the stabilizer and instability evaluation blocks (Fig. 6a), and found that TARs were significantly higher when the stabilizer was used (P < 10⁻⁷, Wilcoxon signed-rank test). Next, we asked whether, on an experiment-by-experiment basis, the stabilizer improved performance in the presence of the applied instabilities (Fig. 6b). We found that the stabilizer improved performance in 38 out of 42 experiments (P < 0.05, permutation test), and was able to recover stabilizer parameters that were appropriate for the instability applied (see Supplementary Fig. 2). Furthermore, stabilization never significantly decreased performance in the presence of the instabilities. We observed that performance during the stabilizer and instability evaluation blocks was similar for some experiments (Fig. 6b, points near the dashed line). However, the impact of the applied instabilities on BCI performance was relatively small for these experiments (Fig. 6b, colour of symbols). In other words, improvements in performance were greater for those instabilities resulting in larger initial decreases in performance (increase in TAR due to stabilization versus decrease in TAR due to instability; R² = 0.75; P < 10⁻¹²), consistent with the notion that the stabilizer restored performance to a level at or near the baseline. This indicated that performance gains from the stabilizer were most evident when the instability had a large impact on performance.

Fig. 6 |. Manifold-based stabilization restores performance in the presence of instabilities.

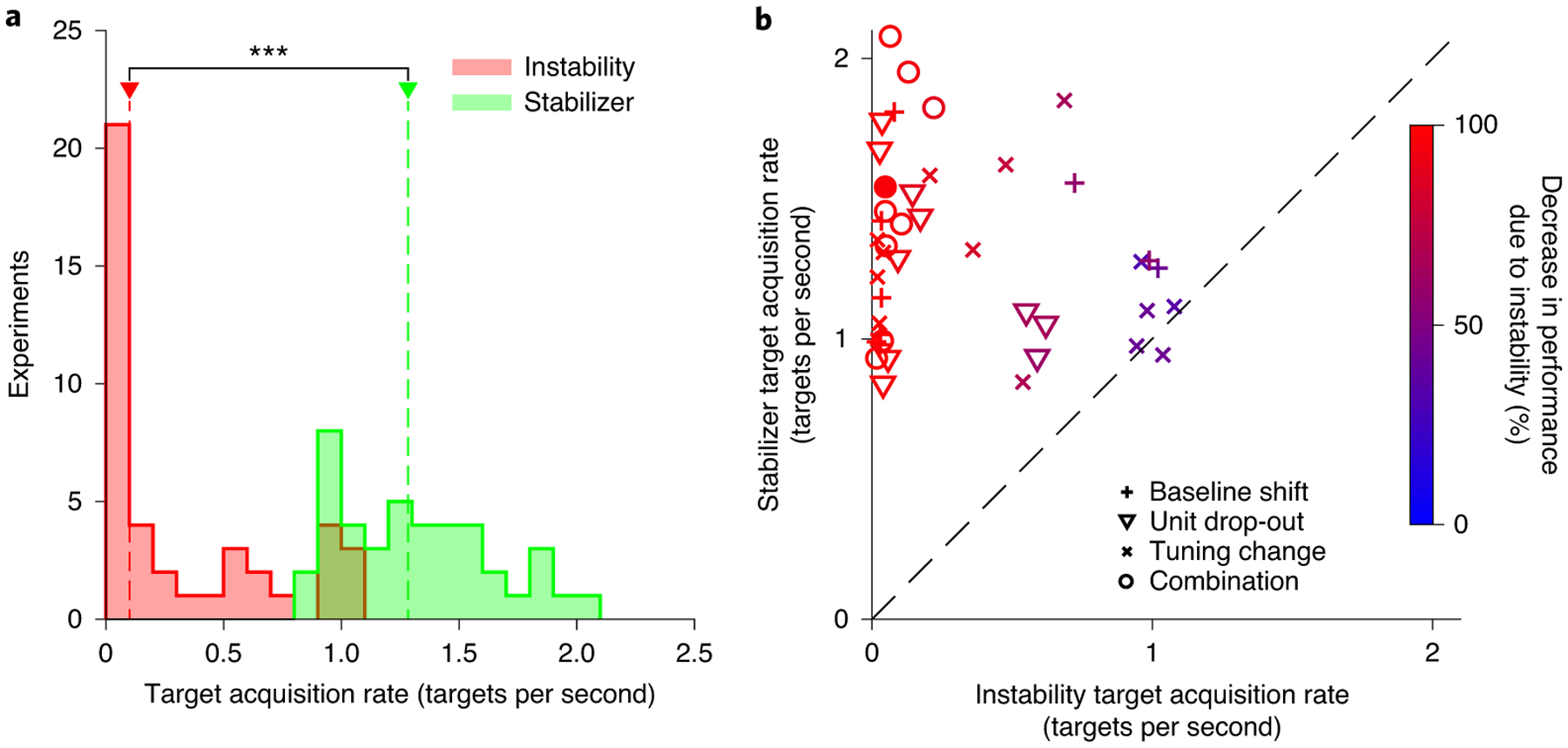
a, Histograms of the TAR for instability (red) and stabilizer (green) evaluation blocks. Red and green arrows indicate the median TAR across the experiments for the instability and stabilizer blocks, respectively; ***P < 10⁻³ (two-sided Wilcoxon rank-sum test). b, TAR for the stabilizer evaluation block versus the TAR during the instability evaluation block for each experiment. Symbol shapes indicate instability type, whereas colour indicates the decrease in performance relative to the baseline due to the applied instability. The filled red data point indicates the representative experiment shown in Fig. 4. Points above the dashed unity line indicate experiments in which the stabilizer improved performance, whereas points below the dashed line indicate experiments in which performance was better without the stabilizer. The results in a and b are based on n = 42 independent experiments.

To more deeply understand the stabilizer performance, we performed three analyses. First, we observed that TARs for the stabilizer evaluation were slightly lower than those for the baseline evaluation block (baseline evaluation: 1.70 ± 0.05 targets per second; stabilizer evaluation: 1.31 ± 0.05 targets per second (mean ± s.e.); P < 10⁻⁶, Wilcoxon signed-rank test). We sought to determine which factors may have been responsible for this difference in performance. Specifically, we considered whether BCI control during the stabilizer evaluation trials was correlated with: (1) the number of electrodes dropped out (P = 0.67; correlation between stabilizer recovery and the number of electrodes dropped out; see Supplementary Fig. 3a), which might degrade the overall information content in the recordings; (2) misidentification of stable electrodes (P = 0.38; Supplementary Fig. 3b), which could lead to manifold alignment error; (3) misalignment of the manifold after stabilization (P = 0.07; Supplementary Fig. 3c); or (4) the strength of target direction information in the neural activity (P < 10⁻⁴; Supplementary Fig. 3d). Of these, only the amount of target direction information in neural activity (item 4 above) showed a significant correlation with stabilizer performance at the P ≤ 0.05 level. We speculate that this was either due to a decline in motivation or closed-loop effects resulting from the animals’ responses to the initial application of the instability. Second, we considered whether learning might contribute to the observed performance improvements. We found that the change in TARs between the first and second half of the instability evaluation block (0.02 ± 0.01 targets per second (mean ± s.e.); P = 0.03, two-sided t-test; t(41) = 2.2) was negligible compared with the difference between the stabilizer and instability evaluation blocks (1.0 ± 0.08 targets per second). This indicates that stabilization was necessary for recovery of performance following the introduction of instabilities. Third, we asked whether the stabilizer works in settings with only natural instabilities. Indeed, the stabilizer was able to overcome natural recording instabilities for decoding arm movements, often outperforming supervised recalibration (see Supplementary Fig. 4).

Stabilization enables stable multi-day performance

Next, we tested our stabilized BCI in a multi-day scenario. In these experiments, the stabilizer was used during ongoing BCI control over a 5-d period. During this time, multiple instabilities were applied to the neural activity. This allowed us to assess the performance of the stabilizer when it was run continuously across days rather than turned on following the application of instabilities. On the first day of each multi-day experiment, we calibrated an initial BCI decoder in the same manner as for the single-day experiments. The stabilizer was then turned on and allowed to run continuously using a sliding buffer of recently recorded neural activity. On subsequent days, control began with the final stabilizer update from the previous day. A combination instability was introduced mid-way through each session; the stabilizer was not provided with any information about the time at which these instabilities were introduced. Previous instabilities were removed whenever a new instability was applied, mimicking neural activity changes that drift in a constrained manner^17,31. At the end of the fifth day, we removed all of the applied instabilities and performed a set of trials using the initial non-stabilized decoder.

Consistent with the single-day experiments, introduction of neural instabilities resulted in transient declines in performance, with the stabilizer rapidly restoring control (see Fig. 7 for monkey N and Supplementary Fig. 5 for monkey L). Performance recovery occurred more gradually during the multi-day experiments (average TAR exponential time constant: 5.14 ± 1.20 updates, corresponding to 384.8 ± 89.3 s of control time (mean ± s.e.)) than during the single-day experiments. This was due to using a sliding window of neural activity to update the stabilizer, which contained neural activity with different instabilities for the 128 trials immediately following the introduction of a new instability (see Methods). These results indicate that the stabilizer is capable of compensating for neural recording instabilities occurring across multiple days.

Fig. 7 |. Manifold-based stabilization maintains performance across multiple days.

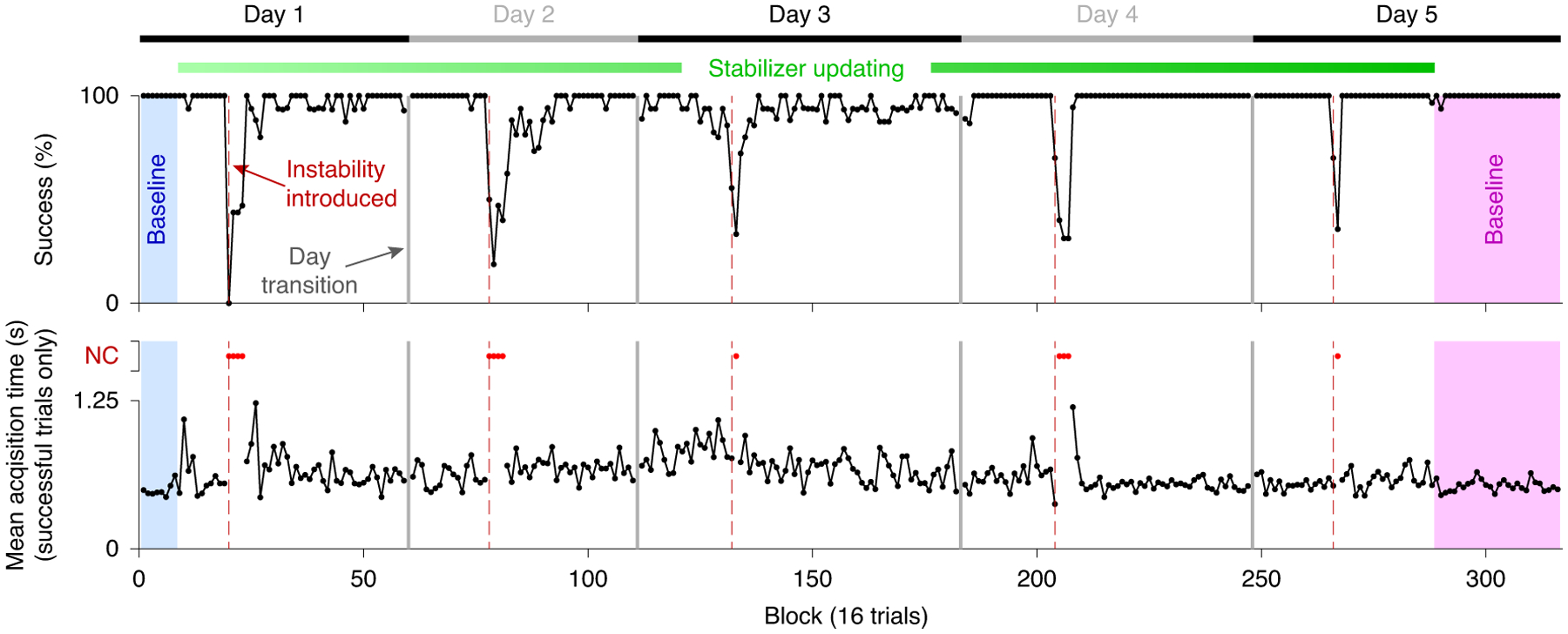
Success rate (top) and target acquisition time (bottom) are shown over the course of a 5-d experiment for monkey N. As in Fig. 4, the shaded blue and magenta regions indicate pre- and post-stabilization baseline blocks, respectively. Vertical grey lines indicate breaks between days, while red dashed lines indicate the application of instabilities. Acquisition times for blocks with success rates of <50% are plotted as red dots.

Stabilization can outperform supervised recalibration

A key feature of our stabilized BCI is that an estimate of the user’s movement intent is not used when updating the stabilizer. This suggests that the stabilizer should be able to counteract neural recording instabilities even when the user is not actively engaged or attempting to use the BCI. We tested this offline by comparing the performance of our stabilized BCI with that of supervised recalibration, which uses knowledge of the BCI target to update the parameters of the decoder. This allowed us to compare our approach with the best possible performance of those self-recalibrating methods that rely on inferring the intent of the user (for example, refs.^13,15,16). We evaluated both the stabilizer and the supervised recalibration methods using the same neural activity, but updated the parameters of the supervised-recalibrated decoder using ground-truth ‘oracle’ knowledge of the instructed movement direction. Thus, supervised recalibration provides an upper bound on the performance of any self-recalibration method that incorporates an estimate of the user’s movement intent.

We compared the performance of supervised recalibration with that of stabilization for those trials immediately following the introduction of the instabilities for the single-day experiments. On these trials, BCI performance was low. Periods of low BCI performance represent a challenging scenario for any recalibration method because subjects can lose motivation. This would result in the neural activity containing less movement-related information, potentially making it more difficult for the recalibration method to restore BCI performance. Performances of supervised recalibration and stabilization were quantified using angular error. The angular error is defined as the angle between each of the estimated movement direction vectors (stabilizer and supervised-recalibrated) and the oracle movement direction (see Methods). Used in this manner, the performance of supervised recalibration reflects the amount of information about intended cursor movement direction present in the neural activity. We found that the stabilizer improved the angular error in 37 out of 41 experiments while supervised recalibration improved angular error in only 28 out of 41 experiments (Fig. 8a). Across the experiments, the stabilizer improved angular error by an average of 20.2° (P < 10⁻⁸, two-sided t-test; t(40) = 7.9), whereas supervised recalibration improved angular error by an average of only 5.7° (P = 0.04, two-sided t-test; t(40) = 2.1; Fig. 8b). The mean of the distribution of paired differences in improvements achieved with stabilization and supervised recalibration on individual experiments (14.5°) was also significantly different from 0 (P < 10⁻³, permutation test; Fig. 8b). This shows that the stabilizer was able to restore control during periods of low BCI performance better than any supervised recalibration approach would have done.

Fig. 8 |. Manifold-based stabilization can outperform supervised recalibration.

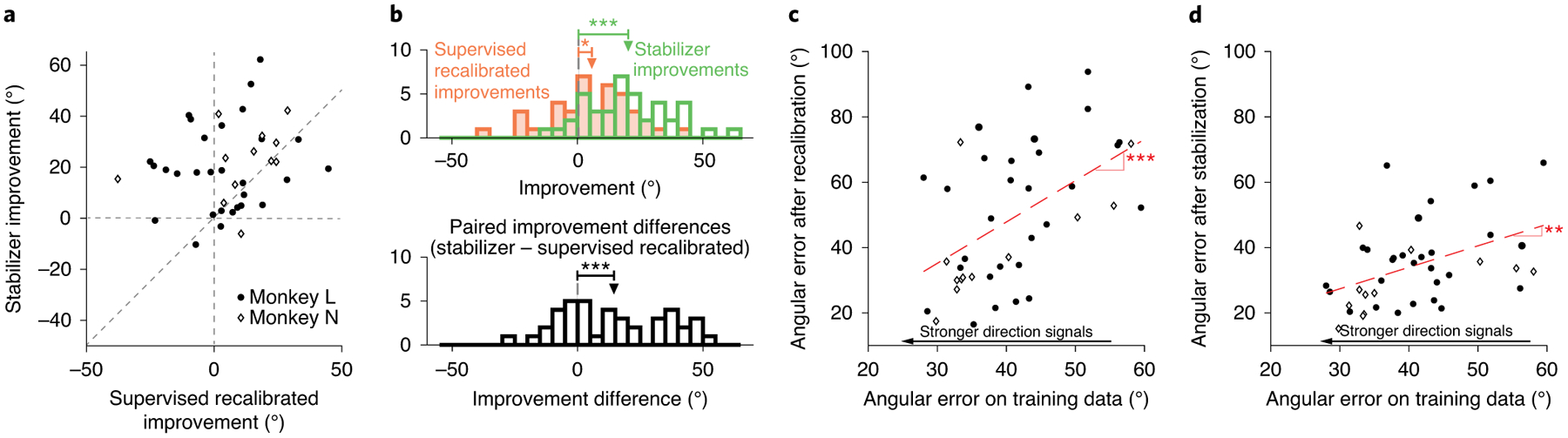
a, Angular error of the decoded velocity of the stabilized versus supervised-recalibrated BCIs, each computed relative to that of the non-stabilized BCI for that experiment. Each dot corresponds to one experiment. b, Histograms of improvements in performance for the supervised-recalibrated and stabilized BCI (top; stabilizer improvements: P < 10⁻⁸; supervised-recalibrated improvements: P = 0.04; paired t-test) and of the paired difference in improvement between the supervised-recalibrated and stabilized BCI for each experiment (bottom; P < 0.001, permutation test). c, Relationship between the angular error of the supervised-recalibrated decoder and the representation of intended cursor direction in the neural activity used for recalibration. Each dot corresponds to one experiment (P < 10⁻³, permutation test). d, As in c but for the manifold-based stabilizer (P = 0.004, permutation test). For all panels: *P < 0.05; **P < 10⁻²; ***P < 10⁻³. The results in a–d are based on n = 41 independent experiments.

The lower performance of supervised recalibration compared with stabilization suggests that, due to the severity of the instability, the animal was no longer fully engaged in the task when BCI performance was low. Under these circumstances, the animal was probably not intending to control the cursor, leading supervised recalibration to perform poorly. In contrast, because stabilization does not rely on an estimate of the intent of the user, it can still function well during periods of low engagement with the task, when the amount of directional information in the neural activity might be low. To test this idea more directly, we assessed the relationship between the performance of each method and the strength of cursor movement direction signals in the neural activity used for stabilization and recalibration (see Methods). For supervised recalibration, we found a strong relationship between performance and the strength of direction signals in the neural activity (slope of linear fit: 1.3; P < 0.001 that the slope was different from 0; permutation test; Fig. 8c). This relationship was weaker for stabilization (slope of linear fit: 0.7; P = 0.004; permutation test; Fig. 8d), indicating that the manifold-based stabilizer was able to restore performance better than supervised recalibration when the animals were less engaged in controlling the BCI.

The ability of the manifold-based stabilizer to maintain BCI control during periods when directional information was low suggests that aspects of the underlying neural manifold might be conserved even when user engagement is low. To examine this further, we quantified the similarity of the manifolds identified by the stabilizer during baseline control and immediately after the introduction of instabilities. The similarity of two manifolds can be quantified by measuring how much one manifold can explain the variance captured by the other. Across all of the single-day experiments included in the above analysis, we found that manifolds identified immediately after the instability was applied captured on average 76 ± 2% (mean ± s.e.) of the shared variance of the baseline manifolds (see Methods). For comparison, randomly generated manifolds captured on average only 17 ± 1% of the shared variance of the baseline manifolds (see Methods). This shows that the manifold is largely conserved across differing levels of movement-related information in the neural activity. The stabilizer leverages this conserved neural manifold to restore control during periods of low BCI performance, when the subject might be less engaged in the task.

Discussion

We developed a stabilized BCI that leverages the low-dimensional structure present in neural activity to enable proficient BCI control in the presence of neural recording instabilities. In a series of single-day closed-loop experiments, the manifold-based stabilizer quickly restored BCI performance following the onset of applied neural instabilities mimicking those encountered in a clinical setting, including those resulting in a near-complete loss of control. During periods when the amount of directional information in the neural activity was low, perhaps because the user was not actively engaged in BCI control, we found that our stabilized BCI outperformed supervised recalibration techniques that rely on estimating the intent of the user. Additionally, in multi-day experiments, we demonstrated the feasibility of our approach during a scenario approximating a clinical use case, in which the stabilizer was used continuously across days to counteract neural recording instabilities as they arose. Used in this manner, our stabilizer would eliminate the burden of recalibration for BCI users, which would provide greater autonomy and possibly lower the cost of care.

Stabilization enables unimpeded BCI performance in the presence of unstable neural recordings by leveraging the low-dimensional structure present in neural population activity. This structure, which captures important features of cortical processing^21–23, probably reflects constraints imposed by the underlying network structure in the brain²⁵. Recent work has provided evidence for the existence of a low-dimensional manifold that is consistent across time^32,33, suggesting that while individual neurons may come and go due to recording instabilities, the representation of movement intent within this manifold is stable. Our stabilized BCI takes advantage of this by using activity in the low-dimensional neural manifold (defined by the set of neurons that are being recorded from at a given point in time) to estimate intended BCI movements. By doing this, we de-emphasize the role of individual neurons in BCI control. Instead, we leverage neural population activity to estimate latent variables that reflect the user’s movement intent. This approach is consistent with findings that the relationship between neural activity and movement intent is stable^34,35, including across long timescales in low-dimensional spaces relevant for BCI control³⁶.

Previous studies have shown that the relationship between neural activity and movement intent can be stable across days to years^34–36. Also, recent work has shown that neural activity tends to reside in a low-dimensional manifold^20–23,25. The key idea of this study is to combine those insights for stable BCI decoding in the face of neural recording instabilities. Even with different but overlapping subsets of recorded neurons, we can identify a stable set of latent states (that is, align estimates of the neural manifold) over time where the latent states represent the movement commands present in the larger circuit from which the neurons are recorded. Given the consistent relationship between the activity of individual neurons and movement intent, one would expect that the latent states would also maintain a stable relationship with movement intent. Indeed, this is what the manifold-based stabilization approach leverages to maintain BCI performance in the presence of neural recording instabilities. These results support the notion that latent states may represent the elemental units of computation and volitional control in the brain^23,25,37.

Our manifold-based stabilization approach can be applied to other BCI systems. Three choices need to be made when setting up a stabilized BCI framework: the method for identifying stable electrodes, the manifold estimation method used by the stabilizer and the decoding algorithm used to drive BCI movements. First, any method to identify stable electrodes can be integrated into our framework; the alignment procedure used by the stabilizer only requires knowledge of a set of electrodes that are stable. We developed a method for identifying electrodes that maintained a stable relationship with the neural manifold (see Methods), but other approaches (for example, refs.^31,38,39) can also be used. Second, different methods for identifying linear manifolds can be used as part of our stabilization approach. This includes factor analysis, principal component analysis and more⁴⁰. We used factor analysis because it focuses on variability that is shared among neurons^20,29. This is in contrast with principal component analysis, which does not distinguish between shared and independent variability. Third, any decoder can be integrated into our stabilized BCI framework. We chose a Kalman filter, which is widely used for BCI decoding^30,41, but other decoders, such as an optimal linear estimator⁴² or linear filter⁴³, can also be used.

This flexibility allows our stabilizer to be extended to work with different types of neural signals, including sorted neural units, local field potentials⁴⁴, electrocorticography (ECoG)^45,46 and electroencephalography (EEG)⁴⁷. EEG and ECoG recordings in particular are prone to instabilities resulting from changes in electrode impedance^48,49. Because EEG and ECoG recordings are highly correlated across electrodes^50,51, these recordings can be described by a low-dimensional manifold. The manifold can be aligned across days using the stabilizer we presented here. The latent state describing the manifold can then be passed to a BCI decoder of the user’s choice, including nonlinear decoders^52–54.

To successfully restore control following recording instabilities, our approach requires a sufficient number of electrodes that are stable across each stabilizer update. This number must be greater than the dimensionality of the latent space to be able to properly align manifolds⁵⁵. We have previously shown that the dimensionality of population activity in primary motor cortex during two-dimensional BCI control is approximately ten²⁵, which is much lower than the number of electrodes (typically 96) on the multi-electrode arrays used for intracortical BCIs. Provided that most electrodes remain stable across successive stabilizer updates, our stabilization approach is likely to continue to work even as the complexity of the task (and potentially the dimensionality of the latent space) increases^22,56 (see Supplementary Fig. 6), such as during higher degree-of-freedom prosthetic limb control⁵⁷.

We found that the manifold-based stabilizer outperformed supervised recalibration during periods when neural activity contained little information about BCI movement direction. The paucity of movement-related information in the neural activity suggests that animals were not actively attempting to control the BCI cursor. This indicates that the stabilizer may be able to restore BCI control even during periods of low user engagement. This would be possible through overlap between the estimates of the neural manifolds made during periods of high and low task engagement. The similarity of the population activity structure, despite differences in the amount of directional information in the neural activity, suggests that much of the manifold reflects constraints imposed by the underlying network, rather than being highly task dependent. This is consistent with observations of similarities between spontaneous and evoked neural activity^24,58–60 and similarities in the structure of neural population activity across tasks⁶¹, as well as with our previous observations that it is difficult to generate patterns of neural activity outside the neural manifold²⁵. The similarity of neural population activity across different task contexts and levels of user engagement may enable our stabilizer to counteract the effect of neural recording instabilities on BCI control after extended periods of inactivity, and possibly even across periods of sleep.

It is interesting to consider how the manifold-based stabilizer might interact with ongoing short- and long-term learning processes. The stabilizer is designed to minimize the need for learning. In our experiments, animals showed no ability to learn to overcome the neural instabilities when the stabilizer was off. When the stabilizer was on, control improved quickly. Our results indicate that learning contributed minimally, if at all, to the improvements we observed following the introduction of instabilities. In further support of this, we did not observe after-effects when returning to the initial stabilizer parameters at the end of each experiment. It is possible that performance of the stabilizer could be negatively affected by changes in the neural manifold. We have found that learning over multiple days can lead to a change in the neural manifold^62,63. In contrast, learning within a single day predominately involves reassociating existing patterns of neural activity with different BCI movements, which would not lead to a change in the manifold⁶⁴. This suggests that stabilization is unlikely to be inhibited by learning over the timescale over which stabilizer updates occur. In fact, the stabilizer could actually enhance BCI performance with practice by engaging long-term learning processes. By compensating for recording instabilities, the stabilizer could give subjects a consistent relationship between the intended and actual movements with which to practice and learn. It is worth considering, in future work, how long-term learning processes might be sculpted to enable even better BCI control^65,66.

Manifold-based stabilization offers distinct advantages over existing approaches for achieving stable BCI performance. Several self-recalibrating BCI algorithms attempt to stabilize BCI performance by re-computing decoder parameters based on estimates of user intent during online control^13,15,16. These approaches have been shown to successfully combat slow degradations in BCI control, but are not designed to restore performance when severe neural recording instabilities result in inaccurate decoder output and/or disengagement of the user. Manifold-based stabilization uses a set of stable electrodes to map neural activity to the same low-dimensional space even in the presence of severe instabilities, allowing control to be restored after sudden degradations in BCI performance. We found that our stabilized BCI was more accurate and more robust than supervised calibration approaches to periods when the amount of movement-related information in the neural activity was low (see Fig. 8). Other self-recalibrating methods exist that track changes in the offsets of the firing rate of individual electrodes^17,18. Our stabilization technique is able to compensate not only for offsets in firing rates but also for general changes in the tuning of neural units.

Another recent approach to achieving stable BCI performance employs a neural network and a large set of initial calibration data collected over multiple days to calibrate a decoder that is able to compensate for a range of instabilities¹⁹. The stabilization approach presented here is also able to maintain performance in the face of a wide range of instabilities, but requires only a small amount of initial calibration data that can be collected within minutes. Decoders can also be calibrated by aligning distributions of neural activity to previously learned distributions of movement kinematics when user-specific kinematic data are not available⁶⁷. This method assumes anisotropic movement distributions that are similar across users, thus requiring engagement of the user to function. Stabilization does not require anisotropic movement distributions, and can be applied even when users are disengaged from BCI control. Additionally, recent work has shown that when performing supervised recalibration, incorporation of previous knowledge of latent dynamics improves BCI performance over time⁶⁸. It is enticing to consider how coupling stabilization with methods that incorporate latent dynamics (for example, ref.³²) could further improve BCI control.

Manifold-based stabilization is complementary to supervised calibration techniques. It aims to stabilize inputs to the BCI decoder, whereas supervised recalibration techniques update the parameters of the decoder directly. While stabilization will reduce the frequency of supervised recalibration needed to maintain a certain BCI performance level, supervised calibration can still be beneficial from time to time.

Our manifold-based framework for stabilizing neural recordings has the potential to be broadly applied across multiple neural recording modalities and device applications beyond BCIs. The field of neural interfaces is rapidly growing; as more devices interface with the brain to treat a diversity of cognitive impairments, including language disorders (for example, ref.⁶⁹) and depression (for example, ref.⁷⁰), it will become increasingly important to be able to identify stable neural representations for cognitive phenomena. Our neural manifold-based stabilization approach provides a means by which to accomplish this, potentially enabling improved therapeutic interventions for a variety of neurological disorders beyond paralysis.

Methods

Electrophysiology and behavioural task.

All animal handling procedures were approved by the University of Pittsburgh Institutional Animal Care and Use Committee and were consistent with the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals. Two male Rhesus macaques (aged 7 and 11 years) were each implanted in the proximal arm region of primary motor cortex with a 96-electrode microelectrode array (Blackrock Microsystems). During the experiments, the animals sat in a primate chair in front of a visual display with both arms loosely restrained and their heads fixed. Neural recordings were thresholded at 3.0 times the root-mean-square voltage independently on each electrode. For each single-day experiment, thresholds were calculated at the beginning of each experimental session while the animal sat calmly in a darkened room. Threshold crossing events were examined at the start of each experiment and any electrodes exhibiting activity determined to be non-neural in origin based on waveform shape were excluded from use in the BCI. On average, 92.9 ± 1.2 (mean ± s.d.) electrodes were used for each experiment. For multi-day experiments, thresholds were set at the beginning of the first day and fixed for the remainder of the experiment.

Animals performed a two-dimensional centre-out cursor task under BCI control. Trials began with the presentation of a cursor and peripheral target. Peripheral targets were selected from one of eight possible locations. The cursor remained fixed at the centre of the workspace for the first 300 ms of each trial (referred to below as the freeze period), after which it was placed under BCI control. The animal was then given 7.5 s to acquire the target with the cursor in order to receive a liquid reward. No target hold time was enforced. Targets were presented in a pseudo-random order during decoder calibration (see ‘Baseline decoder calibration‘ below), such that each of the eight targets was presented once before any target was repeated. Targets were chosen randomly or pseudo-randomly after calibration.

Stabilization and decoder.

The framework we propose for neural stabilization is general and can be used with different methods of identifying stable electrodes and different BCI decoders. Below we describe our method of stabilization, including how stable electrodes were identified and how neural stabilization was implemented for online use, as well as the particular decoder we used in this work.

Neural stabilizer.

We developed a manifold-based stabilizer that maps neural activity to a stable manifold estimated across time. The key idea is that from the neural activity during two separate blocks of trials, we can produce a separate estimate of the manifold. However, only some electrodes are stable between blocks and the coordinate system of a manifold is determined only up to an orthogonal transformation (informally, a rotation). To align the different estimated manifolds, we leveraged electrodes with stable activity between blocks.

We used factor analysis to relate neural activity, $u_t\in {ℝ}^q$ (consisting of counts of threshold crossings on q electrodes at time step t), to a latent state, $z_t\in {ℝ}^{10}$, which describes the location of neural activity within the manifold. According to factor analysis:

$$z_t~\mathcal{N}(0,I)$$

$$u_t\mid z_t~\mathcal{N}\left(\Lambda z_t+\mu ,\Psi \right)$$

where $\Lambda \in {ℝ}^{q\times 10}$ defines the relationship between each electrode and each element of the latent state (known as the loading matrix), $\mu \in {ℝ}^q$ is a vector of mean spike counts for each electrode and $\Psi \in {ℝ}^{q\times q}$ is a diagonal matrix that describes the variability that is independent for each electrode. The columns of Λ form the coordinate system for the manifold. We set the dimensionality of z_t (that is, the number of dimensions of the manifold) to ten for all experimental sessions. Post hoc, we found that the number of latent dimensions needed to capture 95% of the shared variance of the neural activity during calibration trials was between four and eight for our single-day experiments. While this is lower than the value used in our experiments (ten), estimating dimensionality in this manner produces a more consistent estimate of dimensionality at the expense of slightly underestimating the true dimensionality⁷¹. Additionally, when holding all else constant, we have found that stabilizer performance is minimally affected when using an assumed dimensionality greater than the estimated dimensionality of the neural activity but severely impacted when fewer dimensions are used (see Supplementary Fig. 7). In practice, the assumed dimensionality should match the true dimensionality of the neural activity as closely as possible. As the true dimensionality of the manifold increases, a larger number of stable electrodes will be required (so that the number of stable electrodes is greater than the dimensionality of the manifold), and more recording time will be needed to estimate the manifold robustly⁷¹.

In this work, u_t was formed from counts of threshold crossings on 75 electrodes of a multi-electrode array in 45-ms non-overlapping bins. The factor analysis model parameters Λ, μ and Ψ can be estimated given u₁, u₂, … using expectation maximization⁷². Given Λ₁ and Λ₂ estimated from two different blocks of trials, we can ensure the coordinate systems for both estimates of the manifold are aligned by solving the following optimization for $\widehat{O}\in {ℝ}^{10\times 10}$:

$$\widehat{O}={\text{argmin}}_{O:O{O}^T=I}{\Vert {\Lambda }_1(s,:)-{\Lambda }_2(s,:)O^T\Vert }_F^2$$ (1)

where s indexes a subset of the rows of Λ₁ and Λ₂ corresponding to stable electrodes (see ‘Identifying stable electrodes‘ below). In equation (1), O : OO^T = I indicates the set of orthogonal matrices and $\parallel \cdot {\parallel }_F^2$ indicates the square of the Frobenius norm, which is the sum of the squared entries of a matrix. Equation (1) is known as the Procrustes problem and can be solved in closed form⁷³. With the exception of rare loading matrices that contain rank degenerate submatrices, a unique Ô can be recovered as long as the number of electrodes indexed by s (that is, the number of stable electrodes used for manifold alignment) is greater than or equal to the number of dimensions of the manifold (in this case, ten)⁵⁵. After Ô is identified, the coordinate system for Λ₂ is aligned to that for Λ₁ by multiplying Λ₂ by Ô^T.

In this work, we set Λ₁ to be the loading matrix calculated during the initial calibration procedure (see ‘Baseline decoder calibration‘ below). During stabilization, the parameters Λ, μ and Ψ were successively re-estimated from neural activity recorded during BCI use (see ‘Online stabilizer implementation‘ below) and each loading matrix Λ was aligned to Λ₁ using equation (1). After Λ had been aligned, stabilized estimates of latent state ${\widehat{z}}_t$ were obtained from u_t using the following factor analysis projection:

$${\widehat{z}}_t=\beta \left(u_t-\mu \right)$$

where β = Λ^T (ΛΛ^T + Ψ)⁻¹

Identifying stable electrodes.

Manifold alignment can be used in conjunction with any method that can identify stable electrodes across time. The method for identifying stable electrodes need not incorporate any information about the manifold. For example, identification of stable electrodes can be based on waveforms, inter-spike intervals and correlations between recorded neurons^31,38,39. We chose to use a method that identifies electrodes with a stable relationship with the underlying manifold, as parameterized by rows of Λ. We do this by directly comparing estimates of Λ from two different blocks of trials before manifold alignment. Our stable electrode identification method proceeds in two steps. Given Λ₁ and Λ₂ electrodes with corresponding rows of either Λ₁ or Λ₂ with l₂ norms less than a threshold, T, are first identified and removed from consideration. This is done to remove electrodes with rows in Λ that may be hard to estimate and therefore be less reliable for the purposes of manifold alignment. In this work, T was set to 0.01 counts per bin. In practice, thresholding in this manner mainly serves to exclude electrodes that are noisy or have experienced unit drop-out. The value of T used should be lower than the smallest observed norm for valid (that is, low-noise) electrodes.

We then use an iterative procedure to rank and remove electrodes according to how much they have changed their relationship with the underlying manifold (algorithm 1). This is done by searching for electrodes with large changes in the rows of Λ₁ and Λ₂, as these rows parameterize each electrode’s relationship with the underlying manifold. Because the coordinate system of Λ₂ must be aligned to that of Λ₁ for this comparison, we iteratively align loading matrices and remove unstable electrodes with algorithm 1 until a user-specified number, B, of electrodes remains, which are then used as the stable set s. In this work, B was set to 60 for all experiments. We have found that stabilizer performance is consistent across a wide range of numbers of alignment electrodes using neural activity in which natural recording instabilities are present, but decreases when the number of alignment electrodes used is near the dimensionality of the manifold (see Supplementary Fig. 7a). In practice, the value of B used must be larger than the dimensionality of the neural activity, and should be set to the largest value possible while excluding the electrodes with severe instabilities. Used in this manner, the number of alignment electrodes can be viewed as an estimate of the degree of stability expected in the neural activity. When the degree of stability in the neural activity is high, the number of alignment channels used can be large. However, if the degree of stability is low, the number of alignment channels used should be lower.

Algorithm 1.

A greedy algorithm for identifying rows of Λ₁ and Λ₂ that have changed the most. Here, n(s) indicates the number of electrodes indexed by s and \ indicates the set difference. The initial set s includes all electrodes that were not initially removed from consideration due to having small rows in Λ₁ or Λ₂.

Input: Λ1, Λ2, B, s: Indices of rows of Λ1 and Λ2 for potentially stable electrodes.

Output: s

While n(s) > B do

${\Lambda }_1^{\prime }\leftarrow {\Lambda }_1(s,:)$

${\Lambda }_2^{\prime }\leftarrow {\Lambda }_2(s,:)$

$\widehat{O}\leftarrow {\text{argmin}}_{O:O{O}^T=I}{\Vert {\Lambda }_1^{\prime }-{\Lambda }_2^{\prime }{O}^T\Vert }_2$

$\Delta ={\Lambda }_1^{\prime }-{\Lambda }_2^{\prime }{\widehat{O}}^T$

j ← Index of the row of Δ with the largest l2 norm

s = s \ j

end

Our approach for identifying stable electrodes has three benefits for the purposes of stabilization. First, Λ is already estimated in the process of manifold alignment and is available with no added computational cost. Second, electrodes that show a baseline shift but otherwise preserve the way in which they covary with other electrodes can still be used for manifold alignment. This is beneficial because manifold alignment becomes more robust when more electrodes are used. Third, this method for identifying stable electrodes only requires binned spike counts, making it particularly suitable for real-time BCI use, when limitations in data transmission and processing may preclude the availability of features such as waveform shape.

Because our approach for identifying stable electrodes is based on how the activity of each electrode covaries with others, any instabilities that do not result in a change in covariance will be missed. For example, our approach may fail to identify instabilities when a newly appearing neuron has the same tuning curve as the original neuron on that electrode. Such a new neuron is likely to covary with the other neurons in the population in a similar way to the original neuron, since the tuning curve determines much of a neuron’s activity. However, such changes are not likely to be detrimental to BCI decoding. Because the decoder maps patterns of covariability to movement, a newly appearing neuron that covaries with the population in the same manner as the original neuron would maintain the same relationship to the manifold as the original neuron, and thus would produce the same input to the decoder. In other words, the goal of our approach to identifying stable electrodes is not to identify all instabilities that could be identified using waveform shape, interspike interval histograms, peristimulus time histograms and other metrics. Rather, our approach aims to identify only those instabilities that could be detrimental to stabilization and BCI decoding.

Online stabilizer implementation.

The stabilizer was updated nominally every 16 trials using neural data collected during online BCI use. There was slight variability in the number of trials between updates due to the time required to perform the necessary update computations. Neural activity in the first 1 s of each successful or unsuccessful trial (excluding the initial freeze period) was used. For trials <1 s, all neural activity from trial start to target acquisition was used. Updating the stabilizer consisted of calculating new factor analysis parameters, identifying stable electrodes and performing alignment of the coordinate system for the manifold identified by the new factor analysis parameters.

For the single-day experiments, updates to the stabilizer were performed using all accumulated trials performed while stabilization was running (monkey L) or using a 128-trial sliding buffer (monkey N). For the multi-day experiments, a 128-trial sliding buffer was used that was reset at the beginning of each day. Targets were presented randomly while stabilization was running, and both successful and failed trials were used for stabilizer updates. Because targets were presently randomly, the target distribution was approximately uniform for our BCI experiments. We have also assessed how stabilization performs when updating using data with non-uniformities in kinematic sampling (see Supplementary Fig. 8). We found that stabilization was able to improve performance beyond that of a non-stabilized decoder even when targets were sampled non-uniformly up to a ratio of approximately 2:1.

When running stabilization in an online manner, the user must decide both how often the stabilizer should be updated and what data should be used. Stabilization updates can occur as rapidly as the necessary computations can be performed (on the order of several seconds in our experience). The amount of data used determines how responsive the stabilizer is to new instabilities; using small amounts of data will allow the stabilizer to be more responsive to instabilities at the expense of increased variability in the estimates of the manifold. In simulations, we have found that using 128 trials is sufficient to perform stabilization over a wide range of mainfold dimensionalities (see Supplementary Fig. 6). As the dimensionality of the task and/or manifold increases, it may be desirable to use more data for stabilizer updates in order to compensate for any potential decreases in performance that may arise from the need to estimate more parameters from a limited amount of data. Practically, this can be done by increasing the buffer size used for stabilization.

Decoder.

The BCI cursor velocity can be decoded from the stabilized latent state using any standard BCI decoder, including the Kalman filter^30,41, linear filter⁴³ or optimal linear estimator⁴². Here, rather than decoding from the raw recorded activity, we decoded from the stabilized latent state^25,74. In this work, we chose to use a Kalman filter. A Kalman filter is based on a linear dynamical system that describes how cursor velocity changes over time:

$${\mathit{x}}_0~\mathcal{N}\left({\mathit{m}}_0,V_0\right)$$

$$x_t\mid x_{t-1}~\mathcal{N}\left(A{x}_{t-1},Q\right)$$

where ${\mathit{x}}_t\in {ℝ}^2$ comprises the horizontal and vertical cursor velocity at time step t, $m_0\in {ℝ}^2$ and $V_0\in {ℝ}^{2\times 2}$ are the mean and covariance matrix for initial velocity, respectively, and $A\in {ℝ}^{2\times 2}$ and $Q\in {ℝ}^{2\times 2}$ are the state transition and noise covariance matrices. The observation model describes the relationship between the latent state and the cursor velocity:

$${\widehat{z}}_t\mid x_t~\mathcal{N}\left(C{x}_t+d,R\right)$$

where $C\in {ℝ}^{10\times 2}$, $d\in {ℝ}^{10}$ and $R\in {ℝ}^{10\times 10}$ are the parameters of the observation model. The decoded velocity at time step t, ${\widehat{x}}_t$, is obtained using a steady-state Kalman filter

$${\widehat{x}}_t=K\left({\widehat{z}}_t-d\right)+(I-KC)A{\widehat{x}}_{t-1}$$

where K is the steady-state Kalman gain. When estimating ${\widehat{x}}_t$ for the first time bin in a trial, we set ${\widehat{x}}_{t-1}=m_0$. We used an isotropic state noise covariance, which we set by hand. The remaining parameters m₀, V₀, A, C, d and R were fit using maximum likelihood given the estimated latent states and intended cursor velocities during the calibration period (see ‘Baseline decoder calibration‘ below).

After performing all of the experiments, we discovered that the parameters of the Kalman filter for online use were calculated in a manner that differed slightly from the standard equations for the steady-state Kalman filter. By retrospectively decoding all bins from trial start to target acquisition across all trials and experiments with the correct parameters, we found that in 99% of bins the direction of the decoded velocity would have changed by <5.6° and the absolute value of the decoded speed would have changed by <11.4%. Because the same Kalman filter parameters were used whether stabilization was on or off, they could not have produced the benefits of stabilization that we report here.

Baseline decoder calibration.

At the start of each experiment, we fit an initial stabilizer and decoder, which resulted in proficient BCI control. This process consisted of a series of updates to the stabilizer and decoder. First, we obtained an initial set of stabilizer and decoder parameters based on 16 trials of a cursor passive observation task^25,75. During these trials, the BCI cursor was automatically moved in a straight line to the target at a constant velocity. Following this, the animal performed nine 16-trial blocks with the cursor under brain control. Stabilizer and decoder parameters were re-calculated after each block using data accumulated across all BCI blocks. The final baseline stabilizer and decoder were calibrated using 144 trials of BCI data.

Calibration data consisted of spiking activity and cursor velocities over the first 1 s of each successful brain control trial, excluding the initial freeze period. For trials <1 s in duration, all data from the start of cursor control until acquisition of the target were used. Threshold crossings and cursor velocities were binned in non-overlapping 45-ms windows. Velocities for each decoded bin were rotated under the assumption that the animal was attempting to move in a straight line from the decoded cursor position at the end of the bin to the target with the same speed as during online control (that is, cursor velocity magnitudes were preserved)⁴¹. Trials were removed from the calibration set to preserve a uniform number of trials across target conditions.

Generating neural instabilities.

We utilized four types of experimenter-generated neural instabilities to assess the performance of the stabilizer: baseline shifts, unit drop-out, tuning changes and combination instabilities. These instabilities were designed to mimic those frequently observed in clinical BCI recordings, while allowing the severity of the instability to be controlled by the experimenter. Baseline shifts were implemented by adding a randomly generated constant (mean and standard deviation of 0.75 and 0.5 spikes per bin, respectively) to the binned spike count of each electrode. Unit drop-out instabilities were implemented by setting the spike count on 15 electrodes to zero. Tuning change instabilities were implemented by replacing the spike count activity on 15 of the electrodes with that from a held-out electrode set. Finally, combination instabilities were designed to mimic a realistic recording scenario under which multiple types of instabilities can occur, and were generated by simultaneously applying a baseline shift to all electrodes (mean and standard deviation of 0.375 and 0.25 spikes per bin, respectively), a unit drop-out instability to five electrodes and a tuning change instability to ten electrodes.

We selected instabilities to generate large decreases in BCI performance. For baseline shift and unit drop-out instabilities, we selected instabilities that were expected to result in large changes in the progress of the BCI cursor towards the target. Progress was defined as movement of the cursor in the direction of the target from the centre of the workspace⁶⁴. Progress was computed using data from the baseline evaluation block during the first 11 time steps (495 ms) of closed-loop control for each trial (that is, excluding the initial 300-ms freeze period) and then averaged across trials to yield a single value for each baseline evaluation block. Each day, we computed the expected progress of 2,500 randomly generated candidate instabilities. We sought an instability that resulted in a large change in progress by evaluating:

$${\text{argmax}}_{i=1,\dots ,2500}{\left[{\left(p^b-p^i\right)}^2+{\left(s_p^b-s_p^i\right)}^2\right]}^{1/2}$$

where p^b and $s_p^b$ are the mean and standard deviation of progress across trials during the baseline evaluation block and pⁱ and $s_p^i$ are the mean and standard deviation of progress for the ith candidate instability. This allowed us to identify instabilities that resulted in large changes in both the bias (that is, changes in mean progress) and variability (that is, changes in standard deviation of progress) of the decoder output.

For tuning change instabilities, we sought to identify pairs of electrodes with large differences in preferred cursor movement direction. Each day, we calculated the preferred direction of each electrode based on data collected during the baseline evaluation block of the previous experiment. A candidate tuning change electrode pair was then selected at random for which the difference between the preferred direction of each swap pair was at least 60°. We then evaluated the expected progress in the presence of the candidate instability and a candidate instability was selected if it was expected to result in large, non-uniform changes in cursor progress based on visual inspection.

Combination instabilities consisted of applying a baseline shift to all 75 electrodes in the decoder, a drop-out instability to five electrodes and a tuning change instability to ten electrodes. In contrast with pure baseline shift or unit drop-out instabilities, baseline shift and unit drop-out instabilities for combination experiments were each selected from among 1,250 randomly generated candidate instabilities. The electrode pairs used in tuning change instabilities were excluded from the selection of unit drop-out instabilities so that a unit with an applied tuning change was not subsequently dropped out.

Single- and multi-day experiments.

We performed a total of 42 single-day and two multi-day experiments (lasting 5 d each) over the course of the study. Of the single-day experiments, baseline shifts were applied in nine experiments (seven for monkey L and two for monkey N), unit drop-outs were applied in ten experiments (eight for monkey L and two for monkey N), tuning changes were applied in 14 experiments (ten for monkey L and four for monkey N) and combination instabilities were applied in nine experiments (five for monkey L and four for monkey N). One multi-day experiment was performed with each monkey.

Single-day experiments began with the calibration of the initial baseline stabilizer and decoder (see ‘Baseline decoder calibration‘ above). A block of approximately 128 trials was then run to evaluate baseline BCI performance (the baseline evaluation block). The instability was then selected using these data (baseline shift, unit drop-out instabilities only; tuning change instabilities were selected using data from the previous experiment). Following the selection of the instability, an additional block of 32 trials was performed using the baseline stabilizer and decoder to ensure that the monkeys were engaged in the task. After this, the instability was introduced and approximately 320 trials were performed during which stabilizer parameters were updated nominally every 16 trials (the stabilization block). Stabilizer updates were stopped at the end of this block. Two sets of 128 trials were then run with: (1) the final set of stabilizer parameters (the stabilizer evaluation block); and (2) stabilization updates removed (the instability evaluation block). The order of these blocks was randomized across the experiments. The same instability was used for the stabilization, stabilizer evaluation and instability evaluation blocks. The instability was then removed and the animal performed a minimum of 128 additional trials with the initial stabilizer and decoder parameters and without the instability (the post-stabilization baseline block); analysis for this block was restricted to the first 128 trials. In four experiments, the instability evaluation block was presented immediately following the baseline evaluation block.

Multi-day experiments were conducted to evaluate the ability of the stabilizer to handle both naturally occurring neural instabilities and applied instabilities, and to provide a demonstration of a clinical use scenario. On day 1, an initial baseline stabilizer and decoder were calibrated in the same manner as during the single-day experiments, followed by 128 trials of baseline control. Following this, stabilizer updates were turned on, and after approximately 250 trials an instability was applied. All instabilities applied during multi-day experiments were combination instabilities (baseline shift applied to 75 electrodes; tuning change applied to ten electrodes; unit drop-out applied to five electrodes), which were selected in a similar manner as in single-day experiments using data collected with the baseline decoder on day 1. After the application of the instability, the stabilizer was allowed to update for the remainder of the experimental session. On subsequent days, the experiment began using the instability and last stabilizer update from the previous day, with stabilizer updates continuing throughout the day. The data buffer used for updating the stabilizer was reset between days. After approximately 250 trials, the current instability was removed and a new one was applied. At the end of the last day, the instability was removed and a block of trials was performed using the initial stabilizer and decoder parameters calibrated on day 1.

Stabilizer performance evaluation.

Stabilizer performance was quantified using target acquisition time, success rate and TAR. Target acquisition time was defined as the time taken to acquire the target, excluding the 300-ms freeze period at the start of each trial. Success rate was defined as the percentage of targets successfully acquired within the maximum trial time (7.5 s). TAR was the primary metric used to compare performance both within and across experimental sessions, and was defined as the number of targets acquired divided by the time the animal was in control of the BCI cursor. This allowed us to characterize performance using a single metric capturing both success rate and acquisition time.

To assess the significance of changes in BCI performance due to the applied instabilities, we compared TAR before and after instabilities using a Wilcoxon signed-rank test. For single-day experiments, we compared TAR for the last 16 trials of the baseline evaluation block with that of the first 16 trials of the stabilization block immediately following the introduction of the instability and before the first stabilizer update. A permutation test was used to determine the significance of stabilizer performance improvements for individual single-day experiments by randomly permuting the identities of trials in the stabilizer and instability evaluation blocks. The P value for each experiment was calculated as the percentage of times the difference TAR_stabilizer - TAR_instability for the non-permuted data was greater than that of 10,000 random permutations.

To characterize the rate of performance recovery during stabilizer use, we estimated the time constant of an exponential function fit to the post-instability TAR for each stabilizer update. To do this, we calculated mean TARs as a function of stabilizer update. An exponential function was then fit to the mean. The time constant of the fit function characterized how quickly, in terms of stabilizer updates, performance recovered following introduction of the instabilities. We also calculated the stabilizer use time (that is, the amount of BCI control time corresponding to this exponential time constant). To do this, we calculated the average cumulative trial time as a function of stabilizer update, and used interpolation to find the average amount of time elapsed corresponding to the fit time constant. Standard errors in this analysis were calculated using bootstrap resampling over 1,000 iterations.

Comparing stabilization with supervised recalibration.

Most self-recalibrating BCI decoders use retraining procedures that utilize estimates of user intent. The best scenario for retraining in this way is when movement intent is exactly known, in which case such procedures reduce to supervised recalibration. Here, we describe an offline analysis that allows us to compare the performance of the stabilized BCI with the best possible performance of leading self-recalibration approaches that require inferring the intent of the user^13,15,16.

We decoded neural activity during the single-day experiments using decoders that were trained in a supervised manner offline. Supervised recalibration utilized the same two-stage decoder as was used online, and was performed by both updating the parameters of the decoder using oracle knowledge of user intent and updating the stabilizer in the same manner as was done online. The stabilizer was updated along with the decoder because both components would be updated in practice in a standard supervised recalibration session. Oracle intent was formed by rotating the cursor velocities decoded online to point straight at the target^41,76 under the assumption that BCI users seek to move straight to the target from wherever the cursor is. Given bins of neural activity and oracle intent, decoder parameters were updated in a supervised fashion using maximum likelihood estimation, just as they were during initial decoder calibration. We analysed all but one single-day experiment, which was not included in this analysis because a run-time error resulted in data required for supervised retraining not being saved.

To ensure a fair comparison between stabilization and supervised recalibration, three considerations need to be taken into account. First, stabilization updates and supervised recalibration updates should use the same neural activity. We ensured that this was the case by performing supervised recalibration using the same bins of neural activity (augmented with oracle intent) as were used for the stabilizer update. Both stabilization and supervised recalibration used neural activity from the same subset of electrodes used for BCI control. Second, as this was an offline analysis, it was important to remove the benefit of online corrections the animals probably performed when using the stabilized decoders. We accomplished this by evaluating performance for only the last two bins of data before the end of the freeze period (see ‘Electrophysiology and behavioural task‘ above) for each trial. In this period, animals had begun to modulate their neural activity but did not yet have control of the cursor, and were therefore not able perform online corrections. Finally, it is possible that animals adjusted their control strategies with multiple trials of experience controlling the BCI online. To mitigate the effects of this, we limited our analysis to only the first block of trials when stabilization was used in each experiment. This was the second block of trials after the instability was introduced, after the first stabilizer update. Decoding performance after stabilization and supervised recalibration was quantified using angular error, which was defined as the angle between the decoded velocity and a vector pointing straight to the target. We also measured angular error achieved with the baseline decoder without stabilization, allowing us to report the improvements in angular error achieved with both types of updates relative to leaving the baseline decoder in place. The reported angular error for each experiment is the average over all analysed bins in that experiment (two bins of data in the freeze period for each trial after the initial stabilizer update in the online experiment).

To understand the differences in decoding achieved with stabilization and supervised recalibration, we computed the strength of the intended cursor direction signals in the neural activity. As stabilization and supervised recalibration were performed using the same activity, we simply refer to this neural activity as the training data for a given experiment. We performed fivefold cross-validated linear regression to quantify how well oracle direction, as defined above, could be decoded from within the training data on a given day. During cross-validation, the number of bins of data to each target were balanced across folds, and targets with fewer than ten bins in the training data were dropped from the analysis. To prevent overfitting, ten-dimensional latent states were first extracted with factor analysis from the neural activity in all folds before fitting and testing the linear regression models. The strength of direction signals present in the training data on each day was quantified using the average angular error across test folds of cursor velocities predicted with linear regression.

Finally, we measured how closely the manifold identified in the first stabilizer update matched that identified during baseline control. We measured the similarity between manifolds with the percentage variance captured, p_cap, which is a metric of how similar two manifolds, defined by Λ₁ and Λ₂, are. Here, Λ₁ corresponds to the manifold identified during baseline control and Λ₂ corresponds to the manifold identified in the first stabilizer update for each experiment. Values of p_cap vary between 0 and 1. A value of 0 indicates that two manifolds are orthogonal, while a value of 1 indicates that two manifolds define identical subspaces. Intermediate values quantify the percentage of variance of latent state that resides within the manifold defined by Λ₁ which also lies within the manifold defined by Λ₂. For a single-day experiment, p_cap is calculated as:

$$p_{\text{cap}}=\frac{\text{trace }\left(U{U}^T{\Lambda }_1(s,:){\Lambda }_1{(s,:)}^{T}U{U}^T\right)}{\text{trace }\left({\Lambda }_1(s,:){\Lambda }_1{(s,:)}^T\right)}$$

where s are indices corresponding to electrodes with activity that have been unperturbed or only undergone an offset in firing rates and U is a matrix with orthonormal columns spanning the column space of Λ₂(s, :). We compared only the portions of manifolds for the electrodes indexed by s, as these portions should be unchanged by recording instabilities. Each of the 41 single-day experiments included in the analysis comparing supervised recalibration with stabilization were included in this analysis. To calculate p_cap values for random manifolds, for each experiment, we randomly generated a Λ matrix with entries drawn independently and identically distributed from a standard normal distribution, and then calculated p_cap in the same way as for the loading matrices identified by the stabilizer.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.