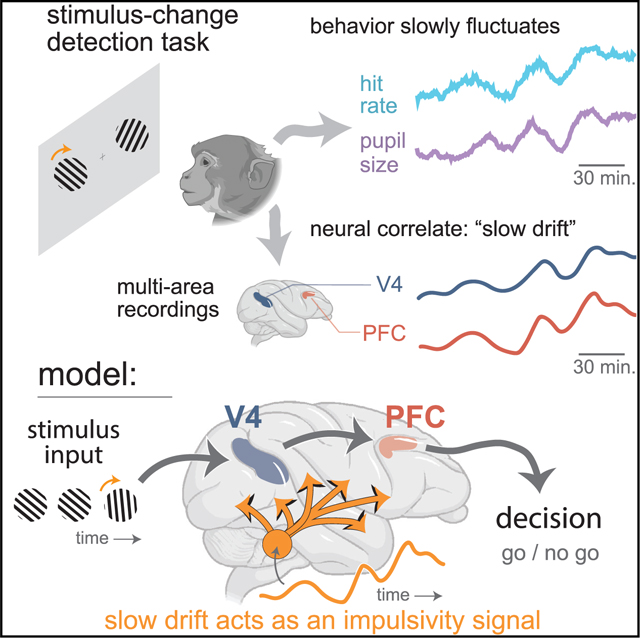
SUMMARY
An animal’s decision depends not only on incoming sensory evidence but also on its fluctuating internal state. This state embodies multiple cognitive factors, such as arousal and fatigue, but it is unclear how these factors influence the neural processes that encode sensory stimuli and form a decision. We discovered that, unprompted by task conditions, animals slowly shifted their likelihood of detecting stimulus changes over the timescale of tens of minutes. Neural population activity from visual area V4, as well as from prefrontal cortex, slowly drifted together with these behavioral fluctuations. We found that this slow drift, rather than altering the encoding of the sensory stimulus, acted as an impulsivity signal, overriding sensory evidence to dictate the final decision. Overall, this work uncovers an internal state embedded in population activity across multiple brain areas and sheds further light on how internal states contribute to the decision-making process.
Graphical Abstract
In Brief
The ability to make a perceptual decision depends both on sensory inputs and on internal cognitive state. Cowley et al. find a slow drift embedded in populations of neurons in visual and prefrontal cortex. Rather than biasing sensory evidence, the slow drift reflects the likelihood of an impulsive decision.
INTRODUCTION
Over the course of a day, we face many perceptual decisions (e.g., a driver waiting for a traffic signal to turn green). These decisions are influenced not only by information at hand (e.g., the color of the traffic signal) but also by a myriad of internal factors that influence our choices at the moment a decision is made (e.g., fatigue from driving). These factors have timescales ranging from many minutes (e.g., arousal) to seconds (e.g., spatial attention) to fractions of a second (e.g., recent visual stimulus history), and, together, they define an “internal state.” When an animal is tasked with making back-to-back perceptual decisions in a laboratory setting, fluctuations in the internal state still influence perceptual outcomes despite the constancy of the statistics of task variables. Indeed, many studies have investigated how and to what extent internal states influence the outcome of a decision (Gold and Shadlen, 2007; Harris and Thiele, 2011; McGinley et al., 2015b), as this provides insight into the cognitive and neural mechanisms underlying decision making (Shadlen and Kiani, 2013).
Perceptual decisions have often been characterized with models that accumulate (noisy) sensory evidence, such as variants of the drift-diffusion model (Krajbich and Rangel, 2011; Brunton et al., 2013; Ratcliff et al., 2016), and there are neural signatures of this accumulation process (Schall, 2003; Gold and Shadlen, 2007; Kiani and Shadlen, 2009; Fetsch et al., 2011; Hanks et al., 2015; Brody and Hanks, 2016; Hanks and Summerfield, 2017; Huk et al., 2017). Decisions can be better characterized by extending these models to include factors such as an urgency signal (Cisek et al., 2009; Hanks et al., 2014; Murphy et al., 2016), duration of fixation (Krajbich et al., 2010), the expected accuracy of a choice (Purcell and Kiani, 2016), the number of alternative choices (Churchland et al., 2008), the reward or choice history of previous trials (Abrahamyan et al., 2016; Urai et al., 2019), or a model term describing errors (i.e., “lapses”) that occur independently of sensory evidence (Weissman et al., 2006; Pisupati et al., 2019). Less is known about the neural signatures of these cognitive factors (O’Connell et al., 2018). Most of these models focus solely on short-term influences on decisions (e.g., within a single trial or between consecutive trials) despite the presence of long-term influences (i.e., over several minutes to hours) on decisions, such as fatigue (Marcora et al., 2009), arousal (Aston-Jones and Cohen, 2005; McGinley et al., 2015b; Urai et al., 2017; Schriver et al., 2018), and satiety (Allen et al., 2019), among others. This motivates the question of how such long-term changes in a subject’s internal state influence the subject’s choices in a perceptual decision-making task.
In this work, we trained macaque monkeys to make hundreds of perceptual decisions over the course of several hours. We found that the animals’ behavior changed slowly during the task, unprompted by task structure. These slowly changing behaviors included their tendency to report a change when none had happened (i.e., the rate of false alarms), reaction time, and pupil diameter. These behavioral measures covaried with each other over the course of tens of minutes, indicating that they have a shared neural origin. During the task, we simultaneously recorded neural population activity from visual area V4 and prefrontal cortex (PFC), two brain areas that have been implicated in forming perceptual decisions. We identified a slow fluctuation (termed the “slow drift”) in V4 activity that covaried with the slow changes in behavior. Surprisingly, we also found that PFC neurons, despite their physical distance from V4, exhibited a slow drift that was highly correlated with that of V4. We uncovered evidence that this slow drift acts as an arousal or impulsivity signal, which influences the final decision through a pathway independent of sensory evidence. In addition, we found evidence that downstream areas remove or account for this slow drift to prevent it from adversely affecting the sensory readout. This may explain how perceptual decisions can be formed reliably when sensory signals (e.g., V4 activity) drift so profoundly. Overall, this work identifies a slowly varying internal signal present in both V4 and PFC (and likely throughout the cortex) and proposes a role for this signal in the decision-making process.
RESULTS
We trained two adult, male rhesus monkeys (Macaca mulatta) to perform an orientation-change detection task (Figure 1A). Results from a portion of data collected from this experiment have been reported previously (Snyder et al., 2018). After an initial flash of two Gabor stimuli, each succeeding flash had the same probability (30% and 40% for monkeys 1 and 2, respectively) that the orientation of one of the stimuli would change (i.e., a flat hazard function). The animal was trained to detect a change in the stimulus and saccade to it. A “hit” trial was one in which the animal correctly made a saccade to the changed stimulus and then received a reward. A “false alarm” trial was one in which the animal incorrectly made a saccade to a stimulus when no change occurred. To measure the animal’s ability to detect a stimulus change, we used signal detection theory to calculate sensitivity of detection d′ (Macmillan and Creelman, 2004; Luo and Maunsell, 2015). As expected, the animal’s sensitivity increased as the change in orientation increased (Figure 1B, “cued stimulus changed”). To probe the effects of spatial attention, we structured trials into alternating blocks such that for each block a changed stimulus was 90% likely to occur at one location (Figure 1A, “cued stimulus”) and 10% likely to occur at the other location (i.e., the “uncued stimulus”). Animals were more sensitive (based on d′) at detecting stimulus changes at the cued location than changes that occurred at the uncued location (Figure 1B, similar results for second monkey in Figure S1), suggesting that the animals deployed spatial attention to the cued location.
Figure 1. Behavior Slowly Fluctuates during an Experimental Session.
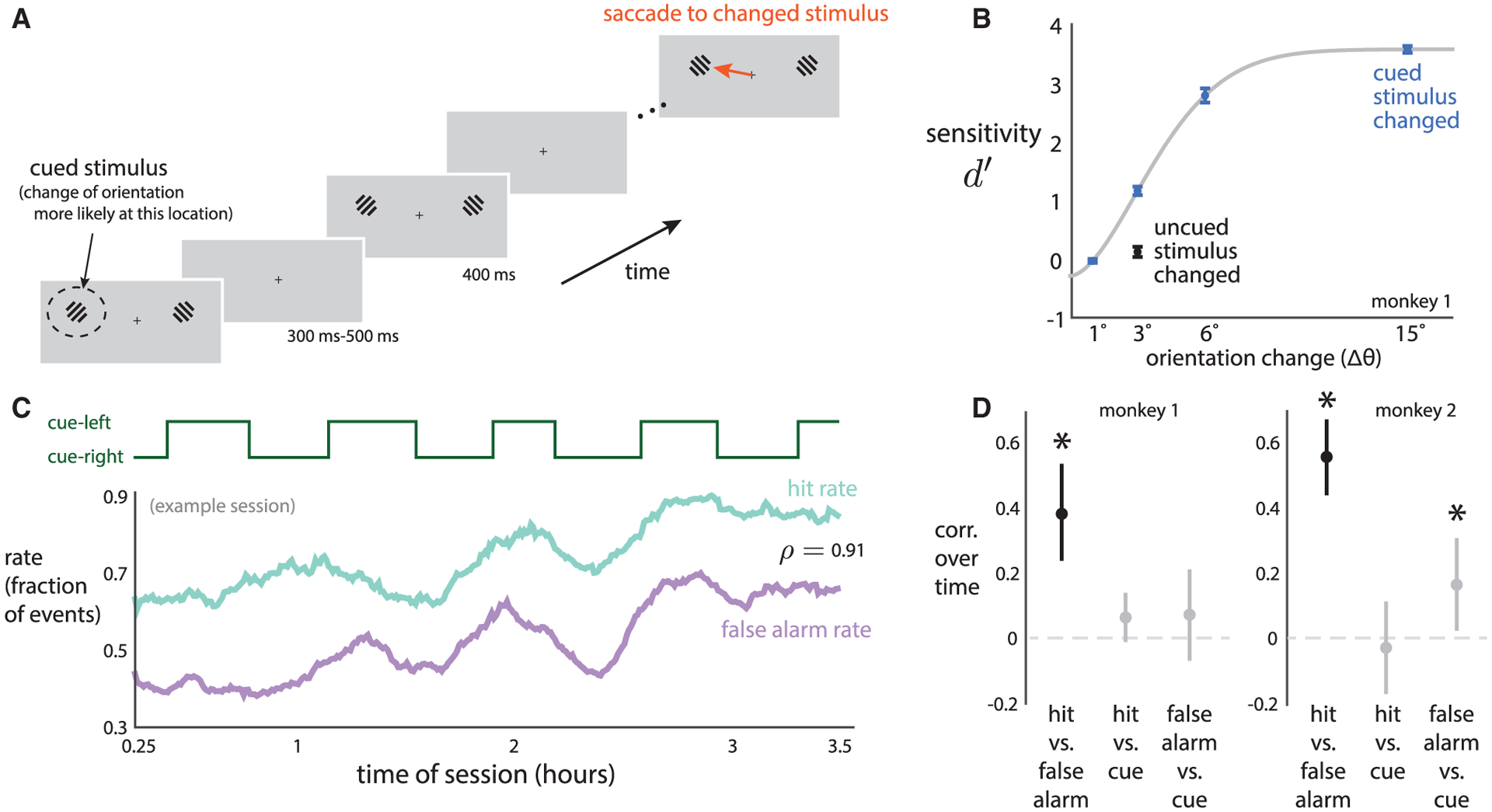
(A) Orientation-change detection task with cued attention. On each stimulus flash, either of two oriented gratings could change orientation. The animal’s task was to saccade to the stimulus location whose orientation changed (orange arrow). The animal was previously cued as to which of the two stimulus locations was more likely to change its orientation (cued stimulus location is indicated by dashed circle, which was not shown to the animal).
(B) The animal’s sensitivity d′ increased with larger orientation changes of the cued stimulus (blue dots: gray line indicates fit with Weibull function). For trials in which the uncued stimulus changed, the animal’s sensitivity was lower (Δθ = 3°, black dot below blue dot, p < 0:002 for both monkeys, paired permutation test). Dots indicate means over sessions, error bars indicate ± 1 SEM.
(C) A representative session in which the hit rate (teal line) and false alarm rate (purple line) slowly covaried over time (Pearson’s ρ = 0:91, p < 0:002, permutation test). For this session, hit rate (ρ = 0:10, p = 0:096) and false alarm rate (ρ = 0:23, p < 0:002) rates had little to no relationship with which stimulus location was cued (top, green line).
(D) Correlations over time between hit rate, false alarm rate, and cued stimulus location (asterisks denote significance over chance levels, p < 0:05, permutation test). Dots indicate medians over sessions, error bars indicate bootstrapped 90% confidence intervals.
See also Figure S1.
Slow Fluctuations in Behavioral Variables Reveal the Presence of a Shifting Internal State
Although task statistics remained constant throughout each recording session (average session duration: 2.3 and 3.0 h for monkeys 1 and 2, respectively), the animal’s internal state was free to vary with the passage of time due to such factors as satiety, fatigue, motivation, etc. Indeed, when we analyzed the animal’s behavior across the entire session, we found fluctuations in its behavior that were hidden from our previous analysis (Figure 1B) for which we collapsed across trials for the purpose of measuring the effect of spatial attention. The time course of two commonly analyzed behavioral variables—hit rate and false alarm rate—slowly fluctuated together over the entire session (Figure 1C, example session, teal and purple lines). The difficulty of the perceptual decisions, the 90% chance of stimulus changes occurring at the cued location within a block, and the uncertainty of when a change would occur yielded high false alarm rates (~50% for this session and on average 30.2% and 40.5% for monkeys 1 and 2, respectively; see STAR Methods). Over the course of the session, a change to a more impulsive behavioral state would result in more correct choices—but also more false alarms—on the difficult trials. Conversely, a more hesitant approach would yield a lower false alarm rate but also reduce the likelihood of correctly detecting difficult stimulus discriminations. For all sessions, we found that hit rate and false alarm rate covaried (Figure 1D, black dots), indicating a fluctuation between a more impulsive and more hesitant state. These two variables drifted together on long timescales (hit rate: 13:4 ± 1:3 min and 15:9 ± 2:2 min for monkeys 1 and 2, respectively; false alarm rate: 14:0 ± 1:3 min and 14:5 ± 1:8 min for monkeys 1 and 2, respectively; mean ± 1 SEM over sessions; see STAR Methods).
One possible explanation for these behavioral fluctuations was that spatial attention was cued to each of the two stimuli in blocks of trials (Figure 1C, green line, each block lasted, on average, 20.4 and 23.7 min for monkeys 1 and 2, respecitvely), and the animal reacted to the switches between blocks. This cueing occurred at the beginning of each block (see STAR Methods) and resulted in robust attentional effects in both behavior and neural activity (Snyder et al., 2018). While the blocks of cued trials could in principle have explained the slow fluctuations in the animal’s behavior that we report here, we found this not to be the case (Figure 1C, example session, teal and purple lines have little to no covariation with green line; Figure 1D, across all sessions, gray dots). We also found that these behavioral shifts did not simply reflect the animal becoming gradually fatigued over the course of the session and “guessing” more at the end, as it was not the case that hit rate and false alarm rate strictly increased during each session (Figure S1). Instead, because task statistics remained constant throughout the session, these behavioral shifts likely reflected a slow change in the animal’s internal state from minute to minute within the session. Such fluctuations could lead the animal to change its behavior—at different times having a higher or lower impetus to make a choice (or conversely, a higher or lower resistance to initiating a movement), leading to correlated fluctuations in hit rate and false alarm rate.
Next, we asked whether these slow fluctuations in behavior were large relative to the prominent behavioral effect of spatial attention that we observed during our task. The behavioral shifts of spatial attention involved large changes in hit rate (0:35 ± 0:09 and 0:41 ± 0:12 for monkeys 1 and 2, respectively; see STAR Methods) but small changes in false alarm rate (0:05 ± 0:04 and 0:03 ± 0:02) between trials in which the changed stimulus occurred in the cued location versus the uncued location. In contrast, the slow fluctuations in behavior had large changes in both hit rate (0:32 ± 0:12; 0:34 ± 0:10 for monkeys 1 and 2) and false alarm rate (0:21 ± 0:09 and 0:32 ± 0:09). These results suggest that the animals’ behavior slowly changed across the session on the order of tens of minutes, at a level that was on par with (but uncorrelated with) the behavioral effects we measured due to spatial attention.
The Activity of V4 Neurons Slowly Drift Together
We next considered whether a neural signature of this fluctuating internal state might be found in the activity of cortical neurons (Figure 2A). We investigated two brain regions, visual area V4 and dorsolateral PFC. We selected these areas because past work has suggested that perceptual decisions might be influenced by noise in sensory neurons (Shadlen et al., 1996) and by top-down control mechanisms (Cumming and Nienborg, 2016). In each animal, we implanted two 100-electrode “Utah” arrays in the same hemisphere to simultaneously record the activity of populations of neurons in V4 and PFC. We began by asking whether V4 activity contained a neural signature of the slow behavioral fluctuations (Figure 1C).
Figure 2. Neural Activity Slowly Drifts throughout a Session.

(A) We simultaneously recorded population activity from visual area V4, thought to transform stimulus input into sensory evidence, and from prefrontal cortex (PFC), thought to be involved in cognitive control signals and decision making. We asked whether these brain areas exhibit a neural signature (orange) of the observed slow fluctuations in behavior (Figure 1C).
(B) Time course of the activity of three neurons from a representative session. Each dot is the 400-ms-binned residual spike count (raw spike count minus mean spike count averaged over stimulus repeats) for one stimulus flash. Dashed lines denote mean residual spike counts for the first 30 min. Insets: spike waveforms corresponding to the three neurons. Each waveform is the mean spike waveform averaged across either the first hour of the session (lighter shade, “first hour”) or the third hour of the session (darker shade, “last hour”). Lines are close to overlapping.
(C) Linear combination of the activity of the 48 simultaneously recorded neurons from the same session as in (B). Each gray dot is a linear combination (identified using PCA; see STAR Methods) of the residual spike counts for one stimulus flash. These projections were then Gaussian smoothed to estimate the slow drift (black line).
(D) Time courses of the slow drifts (computed in the same manner as in C) for all sessions for both monkeys.
See also Figure S4.
First, we considered the activity of individual neurons. We found that some neurons increased their activity (Figure 2B, “neuron 1”), some neurons decreased their activity (Figure 2B, “neuron 3”), and other neurons did not exhibit drift in their activity (Figure 2B, “neuron 2”) during a typical session. We ensured that this was not due to instability in neural recordings (see Figure 2B spike waveform insets, Figure S2, and STAR Methods), or to small movements of the eyes (e.g., microsaccades) that shift the visual image on the retina (Figure S3). In addition, we confirmed that the basic properties of the recorded V4 neurons (i.e., mean firing rates, Fano factors, and noise correlations) were consistent with previous studies (Figure S4, as well as analysis published in Snyder et al., 2018).
To quantify the coordinated drift in activity across the population of simultaneously recorded neurons, we applied principal-component analysis (PCA) to binned spike counts (after subtracting each neuron’s mean response to the stimulus: see STAR Methods) and found a dominant linear combination of the neurons for which their activity drifted strongly. The weights (also known as loadings) of this linear combination represent an axis in the population activity space, which we define as the “slow drift axis.” We then projected the activity onto the slow drift axis (Figure 2C, gray dots) to reveal a substantial fluctuation in neural activity over the course of the 3 h experimental session (Figure 2C, black line). We define this fluctuation as a “slow drift.”
The time course of slow drift varied across sessions (Figure 2D), with a timescale of around 40 min (Figure S4, 32:8 ± 3:1 and 43:5 ± 2:7 min for monkeys 1 and 2, respectively; see STAR Methods). The slow drift was different from the average of activity taken across neurons (Figure S4), which has been proposed as a way to estimate On/Off states and summarize population activity using a single variable (Renart et al., 2010; Harris and Thiele 2011; Okun et al., 2015; Engel et al., 2016; Beaman et al., 2017; but see Snyder et al., 2018). We analyzed the weights of the linear combination (i.e., the slow drift axis) and found that about 50% of neurons had activity that drifted together in the same direction, about 25% drifted in the opposite direction, and the remaining 25% had little to no slow drift (Figure S4). Thus, the slow drift would be difficult to detect using individual neurons recorded sequentially or the average of simultaneously recorded neurons because the slow drift is a coordinated but diverse fluctuation across the population of neurons.
The Slow Drift Covaries with Slow Fluctuations in Behavior
We found that the slow drift is a prominent neural fluctuation with a similar timescale (tens of minutes) as that of fluctuations in behavior, as well as tightly coupled with both hit rate and false alarm rate (Figure 3A). We sought to link our neural and behavioral observations of slow drift more directly. We quantified this relationship in two ways. First, within each session, we found that fluctuations in the slow drift and multiple behavioral variables, including hit rate and false alarm rate, were correlated over time within a session (Figure 3B; see also Figure S5 for individual animals). That the slow drift was correlated with all five behavioral variables tested suggested that the slow drift was correlated with a behavioral pattern in which hit rate, false alarm rate, and pupil diameter increase while trial duration and reaction time decrease (or vice versa). Indeed, we found that the slow drift was correlated with this pattern, which explained 60% of the behavioral variance (Figure S5). This pattern of correlations among behavioral variables was consistent with an underlying shift between an impulsive behavioral state, associated with making more saccades with short reaction times while the pupil is dilated, and a hesitant behavioral state, in which there are less saccades, longer reaction times, and a more constricted pupil.
Figure 3. The Slow Drift of V4 Neural Activity Covaries with Slow Fluctuations in Behavior.
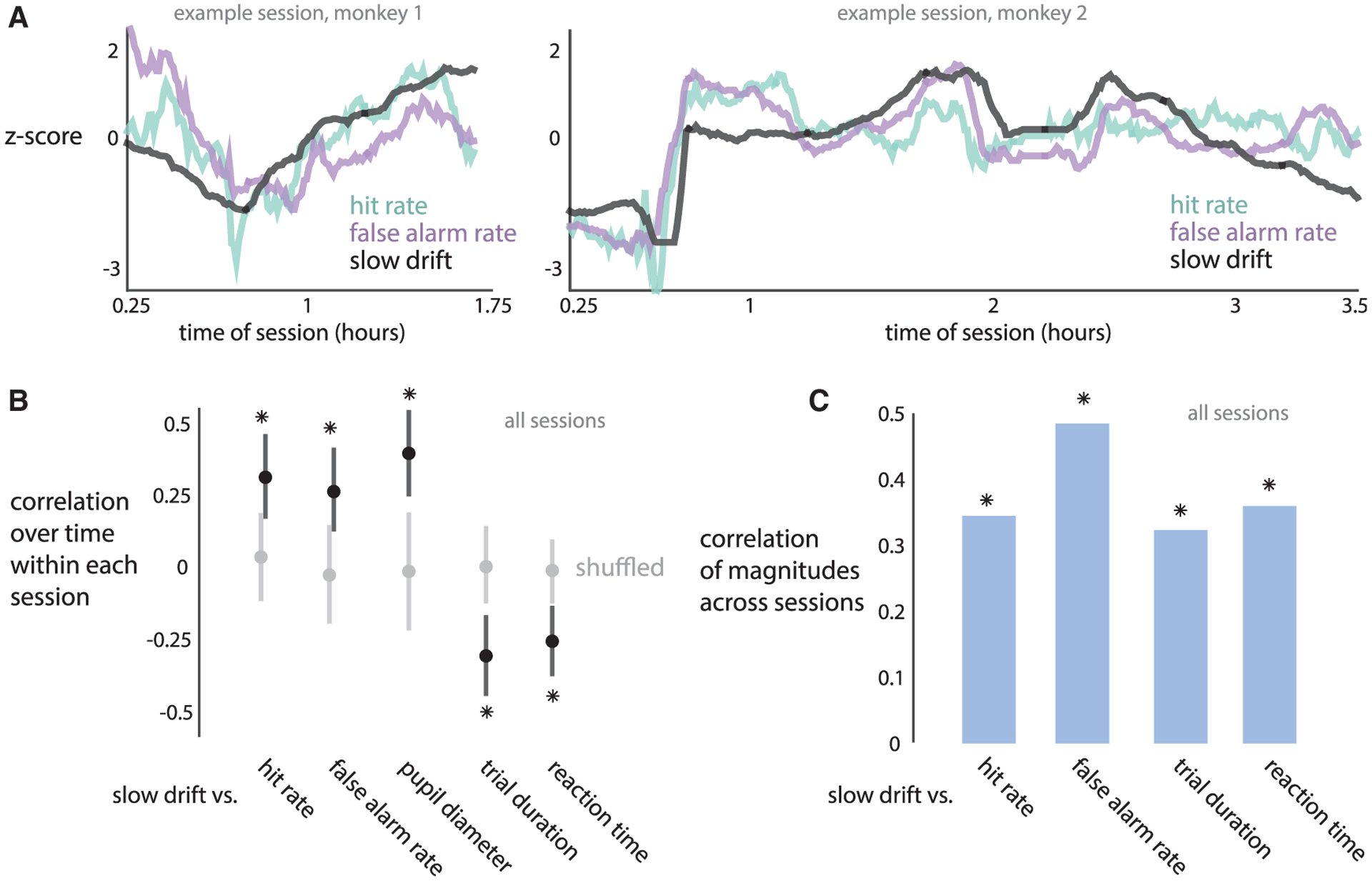
(A) Two example sessions for monkey 1 (left) and monkey 2 (right) in which hit rate, false alarm rate, and the slow drift covaried together (between hit rate and false alarm rate: ρ = 0:63; 0:84 for monkeys 1 and 2; between slow drift and hit rate: ρ = 0:72;0:64; between slow drift and false alarm rate: ρ = 0:27;0:67).
(B) Within each session, the slow drift and behavioral variables were correlated over time (asterisks correspond to a significance of p < 0:002 over shuffling across sessions, permutation test). Dots indicate medians over sessions, error bars indicate bootstrapped 90% confidence intervals.
(C) Across sessions, correlations between the magnitudes of fluctuations of the slow drift and behavioral variables. Slow drift magnitude was the within-session variance over time of the slow drift. Behavioral variable magnitude was the within-session variance over time of that variable. All correlations were significant (asterisks correspond to a significance of p < 0:05 over chance levels, permutation test). The magnitude of pupil diameter was not included because pupil diameter measurements were not comparable across sessions (see STAR Methods).
See also Figure S5.
Second, across sessions, we found that the magnitude of firing rate changes in the slow drift (measured as the variance of the slow drift; see STAR Methods) covaried with the magnitude of behavioral changes (Figure 3C; see Figure S5 for individual animals). Thus, on sessions where the slow drift substantially fluctuated, there were also substantial behavioral changes. Taking both findings together, the slow drift appears to reflect the fluctuations of an underlying internal state.
The Slow Drift Is Unrelated to and Larger than the Neural Effect of Spatial Attention
To evaluate the origin of this neural effect, we asked to what extent the slow drift relates to another well-known modulation of the internal state of the animal, spatial attention (Reynolds and Heeger, 2009; Maunsell, 2015; Moore and Zirnsak, 2017), which we cued to different locations in blocks of trials (Figure 4A). We refer to trials for which the stimulus location was cued either inside or outside the V4 receptive fields as “cue-in” or “cue-out” trials, respectively (Figure 4A, orange and green lines). Similar to how the slow fluctuations in behavior were not correlated with the cued stimulus location (Figures 1C and 1D), we found that the slow drift in neural activity did not covary with the timing of the cued blocks (e.g., Figure 4A, black lines versus orange and green lines; mean |ρ| = 0:18; 0:15 for monkeys 1 and 2, both no greater than expected by chance, p = 0:71 and p = 0:56, one-sided permutation test). Thus, the slow drift was not a neural signature of spatial attention.
Figure 4. The Slow Drift in V4 Activity Is Larger than the Effect of Spatial Attention.
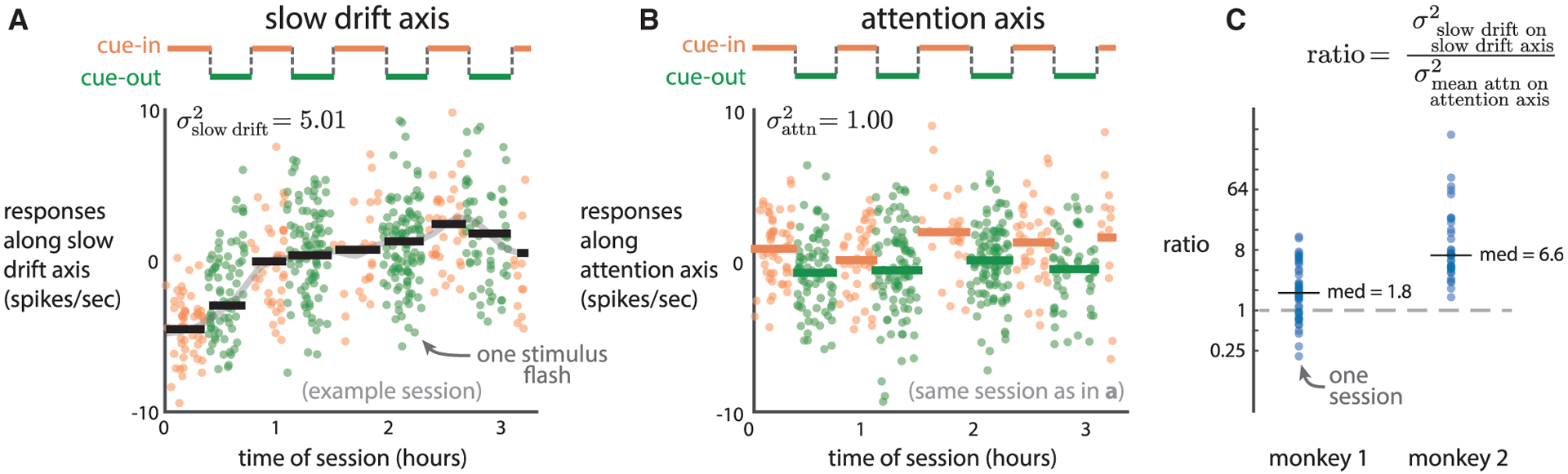
(A) Neural responses (orange and green dots) along the slow drift axis were unrelated to how blocks of trials were cued (black lines versus orange and green lines, |ρ| = 0:06) in an example session. Dot color indicates whether the cued stimulus location was within (“cue-in,” orange) or outside (“cue-out,” green) the receptive fields of the V4 neurons. Black lines indicate the mean activity along the slow drift axis within each cued block. The magnitude of firing rate changes of the slow drift was measured as the variance of the vertical levels of the black lines.
(B) For the same session as in (A), responses along an attention axis capturing the largest difference between mean spike counts during cue-in versus cue-out trials. The effect of attention was measured as the variance of the mean value of responses averaged within each block, where the variance was taken across blocks (i.e., the spread of the orange and green lines).
(C) Ratios across sessions. Medians (“med”) are also shown.
Instead, we used spatial attention to interpret the size of the firing rate modulations corresponding to the slow drift. We measured the magnitude of firing rate changes as the variance of the slow drift over time (Figure 4A, spread of black lines, ) and compared it to the variance of changes in responses across cue-in and cue-out blocks (Figure 4B, spread of orange and green lines, ). Because the slow drift was constrained to be along one axis in firing rate space (i.e., the slow drift axis), we also constrained the response changes due to attention to be along an axis for which the responses most differed between cue-in and cue-out blocks (i.e., the “attention axis”; see STAR Methods). For this example session, the size of the slow drift was 5 times larger than the effect size of attention . The ratio of the size of the slow drift divided by the effect size of attention was greater than 1 for both monkeys (Figure 4C, median ratios: 1.8 and 6.6 for monkeys 1 and 2, respectively, p < 0:002, paired permutation test). These results indicate that the slow drift is a prominent neural fluctuation that leads to larger variation than that of the neural fluctuations due to spatial attention.
Another important neural effect of attention is the decrease in mean noise correlations of pairs of V4 neurons when spatial attention is directed to their receptive field (Cohen and Maunsell, 2009; Mitchell et al., 2009). We confirmed this was the case for the recorded V4 neurons in this experiment (Figure S4). Although we found that the slow drift did not covary with spatial attention, in any task the slow drift could affect measures of population activity, including noise correlation (Cohen and Kohn, 2011) and the outputs of dimensionality reduction (Cunningham and Yu, 2014). This is because the presence of the slow drift may strengthen or weaken the measured effects of cognitive signals that also modulate neural activity, possibly on much smaller timescales. For example, when studying attention modulation in V4 activity, Rabinowitz et al. (2015) found that their model needed a term to account for a “slow drift” in V4 activity, consistent with the slow drift observed in our recorded V4 activity, that otherwise masked the smaller modulations of attention. Thus, accounting for slow drifts in population activity and behavior can be critical when measuring other neural and cognitive effects.
V4 and PFC Neurons Share the Same Slow Drift
The covariation between the slow drift in V4 activity and behavioral variables (Figure 3) suggests that the slow drift could play a role in the decision-making process. However, it is unclear how the slow drift propagates through the neural circuit to ultimately influence the decision outcome. To better understand this, we recorded neural activity in PFC, simultaneous with the V4 recordings (Figure 2A). PFC is a brain area relevant to integrating sensory evidence and forming decisions (Curtis and D’Esposito, 2003; Mante et al., 2013; Raposo et al., 2014), and subregions of PFC receive direct projections from V4 (8 m: Felleman and Van Essen, 1991; Huerta et al., 1987; 9/46d: Markov et al., 2014). One possibility is that PFC has no slow drift, suggesting that the slow drift is a local signal within the neural circuitry for visual processing. Another possibility is that PFC has a slow drift but that this slow drift does not covary with the V4 slow drift, indicating that multiple local signals co-exist within the brain. Finally, it could be that PFC has a slow drift that covaries with the V4 slow drift, suggesting that the slow drift has a global presence in the brain.
To test these possibilities, we applied the same analyses to the PFC activity as we did to the V4 activity (i.e., PCA was applied separately to V4 and PFC activity; see STAR Methods). Visually, we found that PFC activity had a slow drift that was remarkably similar to the V4 slow drift on a session-by-session basis (Figure 5A, black and red lines). We quantified the relationship between the V4 and PFC slow drifts in two ways. First, within each session, we found that the V4 slow drift strongly covaried with the PFC slow drift over time (Figure 5B, orange histogram, median |ρ| = 0:96; 0:93 for monkeys 1 and 2, p < 0:002, permutation test). These correlations were significantly greater than those expected from a control in which PFC had a slow drift unrelated to the V4 slow drift (Figure 5B, gray histogram, median |ρ| = 0:68, significantly less than the median of the real data, p < 0.002, permutation test). We simulated these control slow drifts by generating smooth, random time courses over time from a Gaussian process with a timescale similar to that of the slow drift (45 min; see Figure S4). We confirmed that longer timescales also yielded a median correlation significantly below that of the real data (1 h timescale, median |ρ| = 0:81, p < 0:002, permutation test), indicating that the observed correlations between V4 and PFC slow drifts were not simply due to spurious correlations between smooth, random signals.
Figure 5. V4 and PFC Activity Share a Similar Slow Drift.
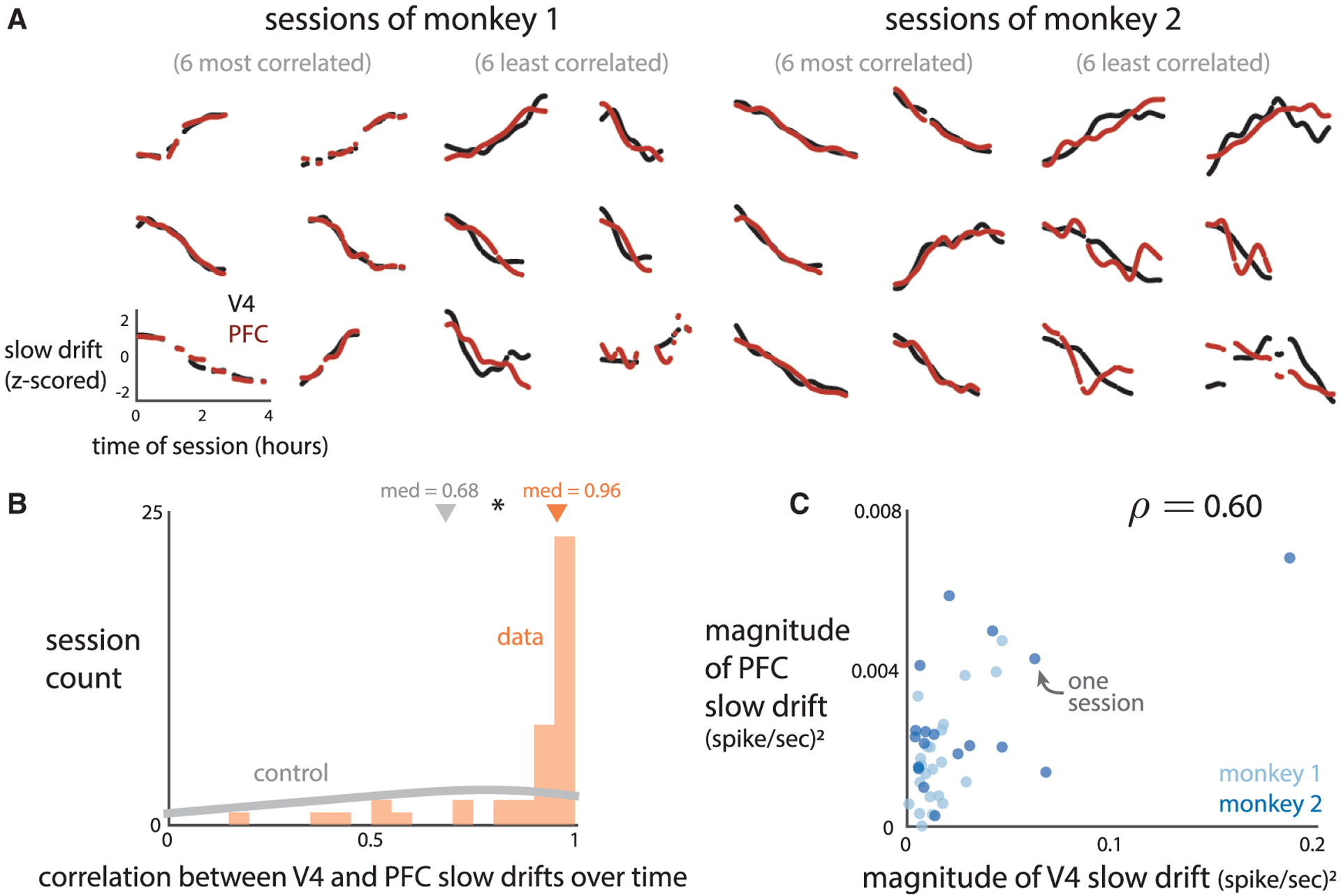
(A) The slow drift of PFC neurons (red) and slow drift of V4 neurons (black) for the 6 most correlated and 6 least correlated sessions for each monkey.
(B) Within each session, the V4 and PFC slow drifts had a larger correlation over time than that for a control in which PFC activity followed a smooth random walk (asterisk denotes p < 0:002, permutation test). Triangles indicate medians (“med”).
(C) Across sessions, the magnitude of fluctuations of the V4 slow drift was correlated with that of the PFC slow drift (ρ = 0:60, p < 0:002, permutation test). Magnitude was measured as the variance of the slow drift over time within a session. Each dot represents one session. The correlation was not solely due to the outlying session (magnitude of V4 slow drift ≈0:2), as its removal still led to a significant correlation (ρ = 0:43, p < 0:005, permutation test).
Second, across sessions, we found that the magnitude of fluctuations of the V4 slow drift correlated with that of the PFC slow drift (Figure 5C, ρ = 0:68; 0:60 for monkeys 1 and 2). Magnitude was measured for each brain area separately as the variance of the slow drift within a session (same metric as in Figure 3C). Thus, when the V4 slow drift had large fluctuations, the PFC slow drift also tended to have large fluctuations for the same session. This finding that PFC had a slow drift that closely matched that in V4 suggests that the slow drift has a global presence in the brain.
The Influence of the Slow Drift on the Decision-Making Process
In previous sections, we identified a slow drift in V4 and PFC activity that was related to slow behavioral fluctuations. These results shed light on the possible roles the slow drift can play in the neural circuit governing decision making. One possibility is that the slow drift reflects a signal that biases sensory evidence to be closer to or farther from a decision threshold. For example, an increase in the slow drift could bias evidence closer to this threshold, leading to an increase in both hit rate and false alarm rate (i.e., a change in criterion). This is consistent with our observations that hit rate, false alarm rate, and the slow drift covaried together (Figure 3B). This possibility can also explain the presence of the slow drift in both V4 and PFC: the slow drift biases sensory evidence (e.g., V4 activity), which is then propagated through the decision circuit (which may include multiple stages of processing) and eventually is read out by a downstream area that helps to form the decision (e.g., PFC) (Figure 6A). The slow drift could arise in sensory areas from bottom-up feedforward sensory noise (Figure 6A, right inset, 1, from the sensory periphery) or from top-down feedback signals (Figure 6A, right inset, 2, from downstream areas), both of which are thought to induce choice probabilities (Cumming and Nienborg, 2016).
Figure 6. Two Models of How the Slow Drift Could Influence the Decision-Making Process.
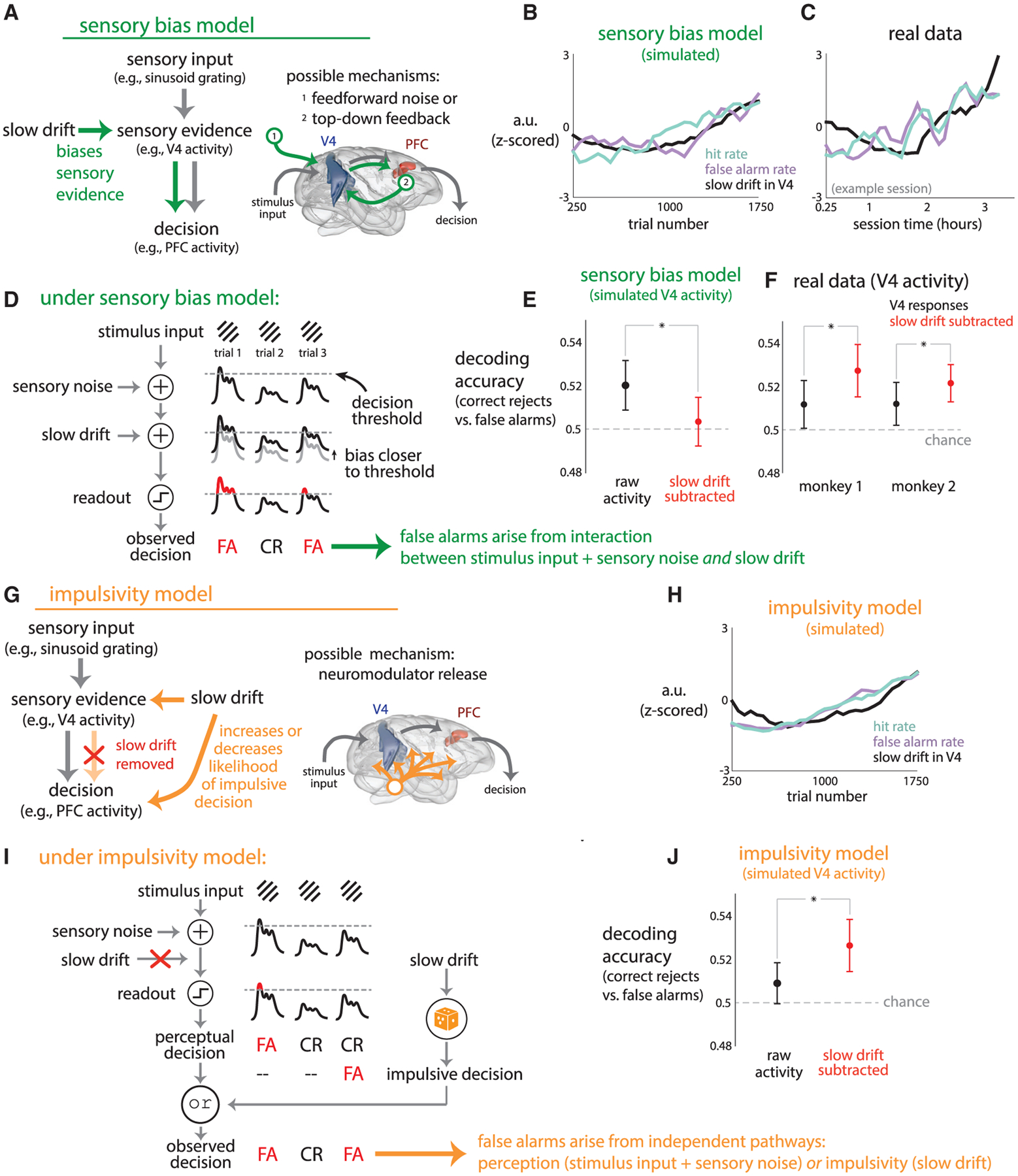
(A) The sensory bias model. The slow drift biases sensory evidence (e.g., V4 activity), and this biased evidence propagates through the decision pathway (possibly through multiple stages of processing) to reach a downstream area (e.g., PFC). The slow drift could arise from feedforward sensory noise (e.g., slow fluctuations in LGN or V1) or from top-down feedback (e.g., a slow modulation originating from PFC) (right inset).
(B) Simulations of the sensory bias model, for which hit rate, false alarm rate, and the slow drift covary over time.
(C) The covariation of the simulated variables in (B) could also be observed in real data (an example session shown). Parameters of the model were not fit to data, and thus, we do not expect an exact match of lines between panels.
(D) Under the sensory bias model, false alarms occur in two ways. First, sensory noise (e.g., feedforward noise from retina or LGN) may corrupt stimulus input (e.g., sinusoidal gratings) and push sensory evidence (e.g., V4 activity, black lines) to pass a decision threshold (dashed line), leading to a perceived change in stimulus and a false alarm (leftmost red FA). Second, the slow drift may bias sensory evidence to pass the decision threshold, also leading to a false alarm (rightmost red FA).
(E) For simulations of the sensory bias model, we measured the extent to which simulated V4 activity (with or without the slow drift) predicted false alarms (see STAR Methods). Decoding accuracy decreased when the slow drift was subtracted from the simulated V4 activity (red dot below black dot, p < 0:002, paired permutation test). Dots indicate means, error bars indicate ± 1 SD over 50 runs.
(F) For the real data, subtracting the slow drift from V4 activity increased decoding performance (red dots above black dots, asterisks correspond to p < 0:05, paired permutation test). Dots indicate means over sessions, error bars indicate ± 1 SEM.
(G) The impulsivity model. The slow drift directly influences downstream areas to increase or decrease the likelihood of an impulsive decision (i.e., a saccade made independently from sensory evidence). The slow drift is present in sensory evidence (e.g., V4 activity), and a downstream area along the decision pathway removes the slow drift from its readout of upstream activity (red X). The slow drift could arise from a brain-wide release of neuromodulators (right inset).
(H) The impulsivity model reproduced the finding in real data that hit rate, false alarm rate, and the slow drift covary over time (cf. C).
(I) Under the impulsivity model, false alarms occur in two ways. First, like in the sensory bias model, sensory noise may lead to a false alarm (leftmost red FA). Second, the slow drift may increase the likelihood of an impulsive decision (orange die), leading to a false alarm (rightmost red FA).
(J) Under the impulsivity model, decoding accuracy of predicting false alarms from V4 activity increased when we subtracted the slow drift from simulated V4 activity (red dot above black dot, p < 0:002, paired permutation test), consistent with the real data (cf. F). Dots indicate means, error bars indicate ± 1 SD over 50 runs.
See also Figure S6.
To test this sensory bias hypothesis, we simulated a simple decision-making model in which V4 activity was thresholded to determine the final decision (Figure S6; see STAR Methods). We biased the simulated V4 activity to be closer to or farther from a decision threshold by adding a slow drift that varied across simulated trials. We confirmed that the outputs of the sensory bias model (Figure 6B) were consistent with our real data (Figure 6C, representative session) in that hit rate, false alarm rate, and slow drift covaried together. Next, we developed an analysis to probe how errors occur on a trial-by-trial basis. Under the sensory bias model, false alarms occur because both sensory noise and the slow drift can push sensory evidence (i.e., V4 activity) past a decision threshold (Figure 6D). Thus, subtracting the slow drift from V4 activity removes an important signal on which the final decision depends. Indeed, in our simulations, we found that subtracting the slow drift from V4 activity led to a decrease in how well V4 activity predicted the occurrence of false alarms within a trial (Figure 6E, red dot below black dot).
To see whether this effect held for real data, we performed the following analysis. We first computed how well V4 activity predicted the occurrence of a false alarm versus a correctly rejected flash within a trial. We considered responses during a 175 ms time window between stimulus onset and saccade onset (see STAR Methods). We found that these responses predicted false alarms above chance (Figure 6F, black dots above dashed line, p < 0:05 for both monkeys, one-sample t test). Next, we subtracted the estimate of the slow drift from V4 activity, re-trained the decoder, and computed the decoding accuracy. We found that subtracting the slow drift significantly increased decoding accuracy (Figure 6F, red dots above black dots). This result did not support the sensory bias model (compare Figure 6E to 6F).
That the slow drift is a neural fluctuation that does not bias sensory evidence is not completely surprising. Previous work has reported neural fluctuations in sensory cortical neurons that are seemingly unrelated to sensory encoding but rather related to factors such as locomotion (Erisken et al., 2014), arousal (McGinley et al., 2015b; Stringer et al., 2019), eye movement (Steinmetz and Moore, 2014), fidgeting (Musall et al., 2019), and thirst (Allen et al., 2019). However, it is unclear how a downstream area could reliably decipher sensory evidence in the presence of constantly drifting neural activity. One intriguing possibility is that the downstream areas that read out activity from sensory areas may somehow account for these fluctuations.
Inspired by this possibility, we hypothesized that the slow drift reflects a separate decision process, independent of sensory evidence, that leads the animal to be more or less likely to make a saccade (i.e., an increase or decrease in both hit rate and false alarm rate). In previous work, similar behavioral processes have been described as urgency in a drift diffusion model (Cisek et al., 2009; Hanks et al., 2014), exploration in a multisensory discrimination task (Pisupati et al., 2019), and impulsivity in a response inhibition framework (Bari and Robbins, 2013). For our purposes, we term this process “impulsivity,” which reflects the animal’s tendency to make a decision without incorporating sensory evidence (Figure 6G). Under this model, the slow drift acts as an impulsivity signal, increasing or decreasing the likelihood of making a saccade independent of sensory evidence. It does this by directly influencing downstream areas that form the decision, overriding the sensory evidence. The slow drift might be attributed to a brain-wide release of neuromodulators (Figure 6G, right inset), consistent with our findings that V4 and PFC slowly drift together (Figure 5). This neuromodulator could arise from brainstem nuclei and influence both sensory processing areas as well as the downstream areas in which the final decision is formed. To prevent the slow drift from interfering with the sensory readout process (i.e., what occurs in the sensory bias model), the impulsivity model removes the slow drift from its perceptual readout (Figure 6G, red X). The brain may perform this removal by having a downstream area access a copy of the slow drift via the same neuromodulator that modulates V4 and subtract this modulation from its sensory readout. For example, if the decision involves a readout of PFC activity, the slow drift (which is present in PFC, Figure 5) can be subtracted out during this readout (e.g., via inhibitory connections).
We simulated the impulsivity model (Figure S6; see STAR Methods) and found that the slow drift produced by the model covaried with hit rate and false alarm rate (Figure 6H), consistent with the real data (Figure 6C). Under this model, some false alarms occur due to sensory noise (Figure 6I, perceptual decision, left FA) while others occur due to impulsivity (Figure 6I, impulsive decision, right FA). We next asked whether subtracting the slow drift from V4 activity increased decoding performance, as observed in the real data (Figure 6F). In this model, the slow drift obscures the sensory evidence in V4 activity (i.e., stimulus input + sensory noise), upon which the decision to saccade or not is based (i.e., whether the sensory evidence crosses a threshold). This is different from the sensory bias model, for which the sensory evidence comprises stimulus input + sensory noise + the slow drift. It then follows that for the impulsivity model, subtracting the slow drift from V4 activity would improve our predictions of false alarms that arise from perceptual decisions because we remove a “nuisance” variable that otherwise obscured the sensory evidence. Indeed, we found this to be the case (Figure 6J, red dot higher than black dot). Thus, the impulsivity model is more consistent with the real data than the sensory bias model (cf. Figures 6J and 6F).
There are two important components of the impulsivity model, and, without both, the model would fail to be consistent with real data. First, without the slow drift acting as an impulsivity signal, the model would fail to have fluctuations in its behavioral output (i.e., teal and purple lines would be flat in Figure 6H). Second, without the removal of the slow drift from readouts of V4 activity, the model would fail to show an increase in decoding accuracy when the slow drift is subtracted from V4 activity (i.e., red dot would not be above black dot in Figure 6J). Thus, both of these components allow the impulsivity model to capture aspects of the real data that the sensory bias model cannot. In the sensory bias model, by contrast, because the slow drift is a component of the sensory evidence that influences the decision-making process, subtraction of the slow drift reduces the ability to predict behavior.
Why Is It Helpful to Remove Slow Drift from Sensory Activity?
Our results are more consistent with the impulsivity model in which a downstream area likely removes the slow drift from its readout of V4 activity. Why would the brain employ such a mechanism? One reason is that if not removed, the slow drift could corrupt sensory information encoded by V4 activity and negatively impact perception and non-impulsive decisions. Consider the following illustrative example. The responses of two V4 neurons to different natural images encode information about these images along a “stimulus-encoding” axis (Figure 7A, left, dashed black line). If the slow drift lies along an axis that is not aligned with the stimulus-encoding axis (Figure 7A, middle, dashed black and purple lines are not aligned), the response encoding remains reliable along the stimulus-encoding axis. However, if the slow drift lies along the stimulus-encoding axis (Figure 7A, right, dashed black and purple lines are aligned), the response encoding would be corrupted because the slow drift perturbs the responses over time independent of which stimulus is shown. Although we considered only one stimulus-encoding axis for this example, a population of neurons likely uses multiple stimulus-encoding axes, each encoding different properties of the natural images.
Figure 7. The Slow Drift Axis Is Aligned to Stimulus-Encoding Axes.
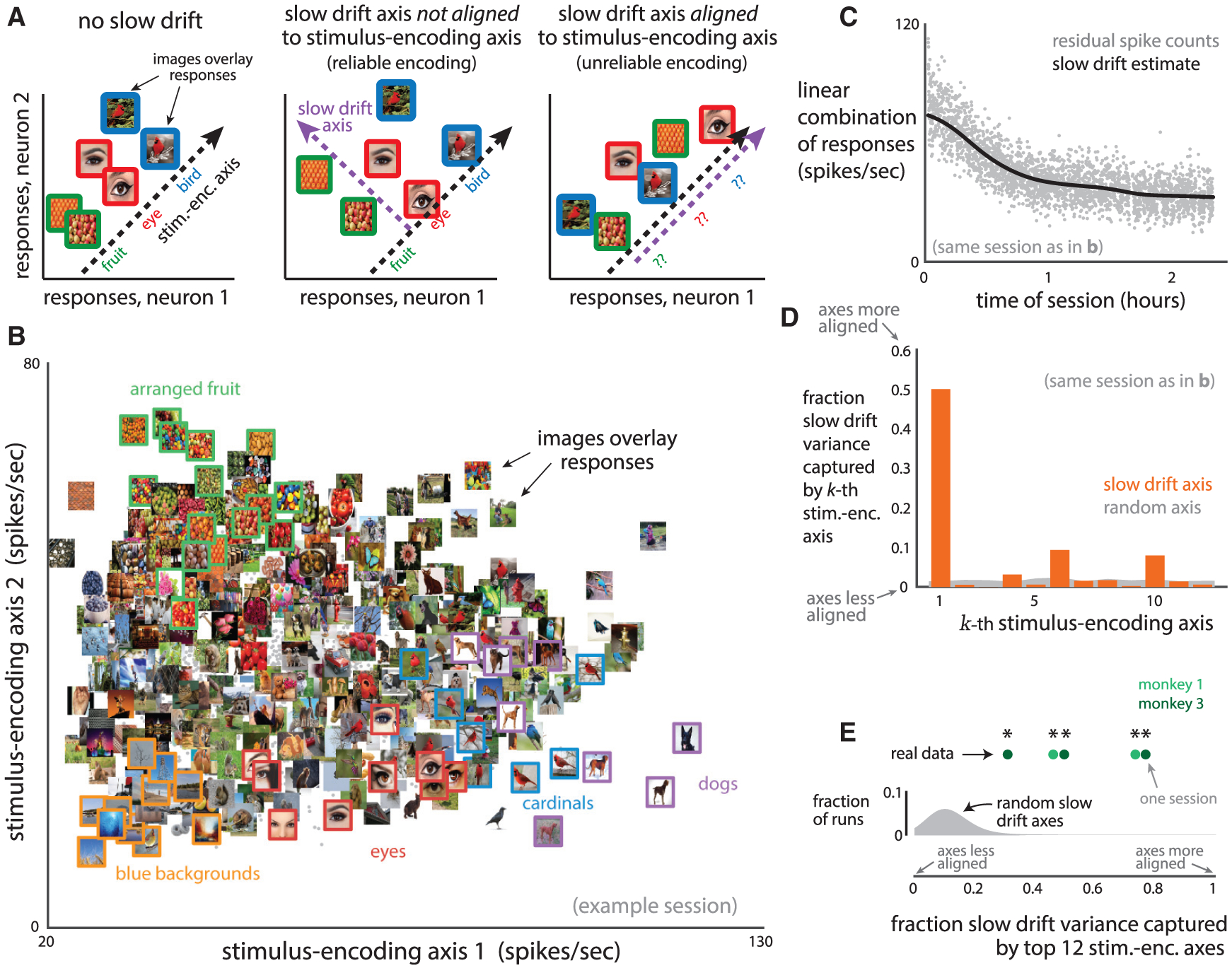
(A) Illustration of how the slow drift may influence the stimulus encoding of two V4 neurons. Without slow drift (left), a downstream area may read out the responses along a stimulus-encoding axis (dashed black line) and faithfully recover stimulus information (e.g., fruit, eye, bird). If the slow drift axis (middle, dashed purple line) is not aligned to the stimulus-encoding axis, the encoding remains reliable. If the slow drift axis is aligned to the stimulus-encoding axis (right), the encoding is corrupted by the slow drift and is unreliable because the slow drift displaces responses over time, independent of which stimulus is shown.
(B) Repeat-averaged V4 responses to 2,000 natural images (gray dots) along the first two stimulus-encoding axes (identified by applying PCA to the responses of 129 neurons for this session). Selected images were overlaid on top of their corresponding responses, and colored outlines denote similar images that resulted in similar responses.
(C) Linear combination of the activity of the 129 simultaneously recorded neurons from the same session as in (B). Same conventions as in Figure 2C. Each gray dot corresponds to the residual spike counts (raw spike counts minus repeat-averaged responses) binned over each trial and projected onto the slow drift axis. These projections are then Gaussian smoothed (black line) to identify the slow drift.
(D) The fraction of slow drift variance captured by each stimulus-encoding axis (orange) for the same session as in (B) and (C). A fraction closer to 1 indicates that the stimulus-encoding and slow drift axis are more aligned. The top two stimulus-encoding axes (k = 1;2) correspond to the two axes in (B). The top 12 stimulus-encoding axes captured 77% of the slow drift variance, significantly higher than if the slow drift lay along a randomly chosen axis (gray, captured on average 9% of the slow drift variance, p < 0:002, proportion of 500 runs whose fraction was greater than that of the slow drift). The small fraction observed for the randomly chosen axes stems from the fact that a random axis is unlikely to align with 12 other axes in a high-dimensional space (where the dimensionality is equal to the number of neurons, 129 in this case).
(E) Summary of results (five sessions from two monkeys, 75 to 129 neurons for each session). The fraction of slow drift variance captured by the top 12 stimulus-encoding axes (green dots) was significantly greater for each session than if the slow drift lay along a random axis (p < 0:002, proportion of 500 runs whose fraction was greater than that of the slow drift, gray distribution corresponds to 500 runs for session with smallest fraction, distributions for other sessions were similar).
See also Figure S7.
Given recent theoretical studies that predict that most neural fluctuations do not corrupt stimulus encoding (Moreno-Bote et al., 2014; Kanitscheider et al., 2015; Kohn et al., 2016) and experimental studies that provide evidence for this prediction (Stringer et al., 2019; Rumyantsev et al., 2020), we predicted that the slow drift would not lie along any of the stimulus-encoding axes. We tested this hypothesis in a separate set of experiments in which monkeys performed a fixation task while viewing many natural images (see STAR Methods). We applied PCA to the trial-averaged responses to identify axes along which they varied the most (Cowley et al., 2016; Stringer et al., 2019) and defined these axes as the “stimulus-encoding axes.” The responses along the top two stimulus-encoding axes appeared to encode complex features of the images, as nearby responses corresponded to similar high-level features (Figure 7B, images of blue backgrounds, eyes, cardinals, dogs, arranged fruits, etc.).
Next, we asked whether V4 activity during this fixation task contained a slow drift as in the change detection task (cf. Figure 2). Using the same approach to identify the slow drift as before, we found a slow drift in the V4 responses (Figure 7C). This suggests that the presence of the slow drift was not dependent on the type of task (change detection versus active fixation) or stimulus set (sinusoidal gratings versus natural images) but rather occurs across multiple contexts.
We then tested whether the slow drift axis was aligned with the top stimulus-encoding axes. We computed the fraction of slow drift variance (i.e., variance of the slow drift across time within a session) captured by each of the top stimulus-encoding axes (Figure 7D, orange) and compared that to a chance level for which the slow drift lies along a random axis (Figure 7D, gray). We found that the total fraction of slow drift variance captured by the top 12 stimulus-encoding axes was significantly greater than the fraction expected if the slow drift lay along a random axis (Figure 7E; see Figure S7 for individual sessions). We also performed this same analysis on neural activity from the orientations presented in the final flash of each trial during the change detection task (i.e., 16 different grating orientations) and found in these data that the slow drift axis was also aligned to the top stimulus-encoding axes (Figure S7).
These results indicate that a slow drift is present in V4 activity across multiple experimental contexts and lies along axes that contain stimulus information likely used by downstream areas. If not removed, the slow drift could corrupt this stimulus information (Figure 7A, right, unreliable encoding). This supports the notion that downstream areas account for the slow drift and remove it from their readouts of V4 activity in order to preserve reliable encoding. Thus, these results are consistent with the impulsivity model, of which an important component is this removal of the slow drift. Indeed, removing some of the neural fluctuations in readouts of visual cortical activity is likely one of the mechanisms by which the brain maintains stable and robust representation of the visual environment.
DISCUSSION
While monkeys perform perceptual decisions, there are slow changes in their behavior over the course of tens of minutes unrelated to task conditions, reflecting a fluctuating internal state. We discovered a neural signature of this internal state in the form of a slow drift in neural activity that covaried over time with the slow fluctuations of behavior. We found that the slow drift is a brain-wide signal present in both V4 and PFC. We further asked what role the slow drift plays in the decision-making process and found that our data were consistent with a model in which the slow drift is removed from readouts of sensory evidence but still influences the ultimate decision as an impulsivity signal. Our work thus reveals that much of the apparent “noise” in the responses of cortical neurons is in fact a neural signature of a fluctuating cognitive factor, evident only when considering the temporal sequence of trials within each session.
Many studies have reported large, ongoing fluctuations in neural activity that are independent of sensory stimulation (Arieli et al., 1996; Harris and Thiele, 2011; McGinley et al., 2015b; Kohn et al., 2016; Engel et al., 2016; Muller et al., 2018). These fluctuations evolve on different timescales, from hundreds of milliseconds (Arieli et al., 1996; Okun et al., 2015; Vinck et al., 2015; Rabinowitz et al., 2015; Beaman et al., 2017; Wasmuht et al., 2019) to seconds (Reimer et al., 2014; Lin et al., 2015; Stringer et al., 2019) to minutes or longer (Aston-Jones and Cohen, 2005; McGinley et al., 2015a; Okun et al., 2019; Milton et al., 2020; Hennig et al., 2020). Studies have found that these fluctuations correlate with experimental and behavioral variables, including pupil diameter (Nassar et al., 2012; Vinck et al., 2015; McGinley et al., 2015a; Joshi et al., 2016; Ebitz and Moore, 2017; Gutnisky et al., 2017a; Mathôt, 2018; Okun et al., 2019; Stringer et al., 2019; Hennig et al., 2020), eye movements (Leopold and Logothetis, 1998; Anderson et al., 2011; Steinmetz and Moore, 2014; Lowet et al., 2018; Saber et al., 2015), locomotion (Erisken et al., 2014; Reimer et al., 2016; Leinweber et al., 2017), wakefulness (Reimer et al., 2014; McGinley et al., 2015b; Milton et al., 2020), attention (Rabinowitz et al., 2015; Snyder et al., 2016; Engel et al., 2016; Moore and Zirnsak, 2017; Huang et al., 2019), task difficulty (Ruff and Cohen, 2014b), and learning (Chaisanguanthum et al., 2014; Ni et al., 2018). In addition, these fluctuations may have a computational purpose, such as changing the structure of noise correlations to improve the fidelity of stimulus encoding (Cohen and Maunsell, 2009; Mitchell et al., 2009; Ruff and Cohen, 2014a; McGinley et al., 2015b; Engel et al., 2016; Beaman et al., 2017; Gutnisky et al., 2017a, 2017b; Ni et al., 2018; Rule et al., 2019), passing information from one brain area to another (Ruff and Cohen, 2016, 2019; Snyder and Smith, 2018; Semedo et al., 2019; Shahidi et al., 2019; Kohn et al., 2020), or integrating sensory evidence with feedback from higher cortical areas (Nienborg and Cumming, 2009; Zhang et al., 2014; Bondy et al., 2018; Stringer et al., 2019). For example, On states of V4 activity, during which the firing rates of many V4 neurons are elevated, have higher behavioral performance than Off states (Engel et al., 2016). It could be the case that the slow drift and the slow fluctuations in behavior reported here arise from long sequences of either On states and Off states, but our analyses suggest that this is not the case (Figure S4). In addition, the slow drift does not appear to be related to changes in synchronized/desynchronized states in V4 activity, as these states were found not to drift over trials or correlate with pupil diameter (Beaman et al., 2017). Instead of improving the fidelity of local neural computations, it appears the slow drift operates on a timescale detrimental for processing stimuli that change rapidly.
It is unclear whether every fluctuation is useful to downstream processing, and it stands to reason that the brain might have developed mechanisms to deal with such internal noise. One possible mechanism for noise removal is the pooling of neurons that encode redundant information by averaging their activity in order to reduce trial-to-trial variability (Zohary et al., 1994; Shadlen and Newsome, 1998). A second related mechanism is that a downstream readout may be configured to ignore much of the trial-to-trial variability of neural activity (Averbeck et al., 2006; Moreno-Bote et al., 2014; Kohn et al., 2016). Such a mechanism might restrict the noise to be along dimensions in population activity space not read out by downstream regions. This mechanism has been proposed to separate neural signals in the visual cortex (Ruff and Cohen, 2019; Semedo et al., 2019; Stringer et al., 2019; Rumyantsev et al., 2020; Zhao et al., 2020), motor system (Kaufman et al., 2014; Elsayed et al., 2016; Stavisky et al., 2017; Hennig et al., 2018; Perich et al., 2018), and oculomotor system (Khanna et al., 2019b), as well as a way to perform economic choice evaluation (Yoo and Hayden, 2018). Our observation that the slow drift aligns well with stimulus-encoding dimensions suggests that this mechanism might not be able to eliminate the “noisy” fluctuations of the slow drift. Our work suggests yet a third type of noise removal, whereby downstream areas remove noisy neural fluctuations from their readouts. This removal could be carried out by a downstream area (e.g., PFC) accessing a separate copy of the slow drift and either subtracting out this copy via inhibition (Wilson et al., 2012) or dividing out this copy via normalization (Carandini and Heeger, 2011). This copy may be accessed through the influence of a neuromodulator or by a downstream area keeping a running estimate of the slow drift in working memory (Cohen et al., 1997). Our work points to potential mechanisms to remove noise as an important area of focus in future studies on the impact of neural variability on perception and behavior.
Our findings raise an interesting conundrum: why does the brain modulate visual cortical activity (i.e., the slow drift) and then remove this signal downstream rather than have no modulation of visual cortical activity at all? One possible explanation for the existence of the slow drift and its internal removal is that through evolution the underlying neural mechanisms governing perception evolved in a coordinated manner with the mechanisms that govern the animal’s internal state in order to achieve high fidelity of stimulus readout while allowing for brain-wide releases of neuromodulators (Rial et al., 2010). The slow drift may also be closely connected to the global fluctuations observed in sleep (Steriade et al., 2001; McGinley et al., 2015b). For example, the slow drift may represent a fluctuating state between high and low levels of alertness, with corresponding differences in neuromodulation.
The observed correlation between hit rate and false alarm rate (Figure 1D) implies that shifts in criterion occurred (i.e., shifts of the decision threshold in signal detection theory). Previous work has shown that activity in PFC (Luo and Maunsell, 2018), but not V4 (Luo and Maunsell, 2015), is associated with shifts in criterion. Here, we found that activity in V4 and PFC was related to criterion (i.e., the slow drift covaried with both hit rate and false alarm rate). Although on the surface these results might appear to be contradictory, they are not. Instead, this difference can be attributed to the fact that Luo and Maunsell specifically measured a spatially selective criterion signal, defined by their task structure, whereas we measured a global criterion shift independent of task structure. In particular, our findings suggest that a shift in criterion is not necessarily due to a bias in sensory evidence (i.e., a change in decision threshold) but instead can be explained by separate decision processes unrelated to sensory evidence, such as impulsivity. That V4 may have multiple signals that co-exist and influence behavior differently is not unexpected. Indeed, in addition to local criterion and impulsivity, neural fluctuations in V4 relate to reward expectation (Baruni et al., 2015), attentional effort (Ghosh and Maunsell, 2019), eye movements (Anderson et al., 2011; Steinmetz and Moore, 2014; Leopold and Logothetis, 1998; Lowet et al., 2018), and task difficulty (Ruff and Cohen, 2014b), suggesting that V4 is part of a flexible, multifaceted circuit.
In this work, the slow drift covaried with hit rate, false alarm rate, pupil diameter, and reaction time. Another important behavioral variable is the rate of small eye movements, or microsaccades (Martinez-Conde et al., 2004; Hafed et al., 2011). Because microsaccades shift the visual stimulus relative to the receptive field of a visual cortical neuron, microsaccades can modulate the firing rates of visual cortical neurons (Leopold and Logothetis, 1998; Bosman et al., 2009; Anderson et al., 2011). Furthermore, the responses of V4 neurons might directly be influenced by the saccade plan through corollary discharge (Crapse and Sommer, 2008; Steinmetz and Moore, 2014; Lowet et al., 2018). We ruled out these possible causes for the observed slow drift in neural activity in control analyses, in which we still observed the presence of the slow drift both in the absence of visual stimuli and when the eyes remained extraordinarily still (Figure S3). This is not to say that the slow drift is independent of microsaccade rate. Indeed, as an impulsivity signal, slow drift may lead to changes in the likelihood of making such small eye movements (e.g., an animal may make more microsaccades during an impulsive state than during a hesitant state).
What is the source of the slow drift? Given that the slow drift is a brain-wide signal that covaries with pupil diameter (Figure 3B), it is conceivable that the slow drift arises from the release of neuromodulators throughout the brain. One candidate neuromodulator is norepinephrine, which is distributed by the locus coeruleus (LC) to many different brain areas on a similar timescale as that of the slow drift (Aston-Jones and Cohen, 2005; McGinley et al., 2015b; Joshi et al., 2016). It has also been proposed that the LC modulates arousal, as the activity of LC neurons has been linked to behavioral variables that reflect arousal, such as pupil diameter (McGinley et al., 2015a; Joshi et al., 2016; Liu et al., 2017) and task performance (Aston-Jones and Cohen, 2005; Eldar et al., 2013). Another candidate neuromodulator is acetylcholine, which is released by the basal forebrain and has been shown to relate to pupil diameter and locomotion (McCormick, 1992; Everitt and Robbins, 1997; McGinley et al., 2015b; Yüzgeç et al., 2018). Further experiments that include electrophysiological recordings from relevant nuclei and experimental manipulation of the levels of different neuromodulators are needed to identify the source of the slow drift.
The decision pathway that transforms the sensory evidence arriving at the retina to a behavioral output of oculomotor neurons likely involves multiple stages of processing across the hierarchy of the visual cortex. If the slow drift arises from the brain-wide release of neuromodulator, then it seems likely the stages of visual cortical processing most involved in discriminating the features of visual stimuli (e.g., V1, V4, IT) are all influenced by this neuromodulator. Given that IT reads out V4 activity (Ungerleider et al., 2008), does IT also inherit the slow drift from its readout of V4? If so, this could potentially double the size of the slow drift at each stage of the hierarchy (i.e., receiving two sources of slow drift: from its input from an upstream area and from the brain-wide release of neuromodulator). This might lead us to expect the size of the slow drift to be larger in downstream areas, consistent with findings that the strength of gain modulations increases along the visual cortical pathway (Goris et al., 2014). Another possibility is that each stage of processing performs a removal of the slow drift from its input (i.e., its readout of upstream activity) via local operations including normalization (Carandini and Heeger, 2011) or subtraction via inhibitory connections (Wilson et al., 2012). If so, the size of the slow drift would remain essentially constant across different stages of the hierarchy. Future work is needed to tease apart these possibilities.
As studies continue to investigate richer, more naturalistic behavior and the underlying cognitive influences, there has been an increasing use of terms such as arousal, motivation, effort, urgency, impulsivity, etc. It is often unclear which label to place on a particular observed change in behavior and/or neural activity (Calhoun et al., 2019). Regardless of the label applied to our data, the slow drift we identified represents a substantial change in neural activity associated with profound fluctuations in behavior during perceptual decisions. This signal was most evident when considering how neurons change their activity together, accounted for a large fraction of the apparent noise in neural activity from trial to trial, and could be found only when we considered the time ordering of trials within a session. Our observation that slow drift is a widespread signal in cortex means that recognizing and accounting for it may be critical in any study that attempts to link cortical activity to behavior.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Matthew A. Smith (mattsmith@cmu.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
Code and data are available by request to the Lead Contact (mattsmith@cmu.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Experimental details have been described previously (Snyder et al., 2018). Three adult male animals (Macaca mulatta) were used for this study. Experimental procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and were performed in accordance with the United States National Research Council’s Guide for the Care and Use of Laboratory Animals.
METHOD DETAILS
Electrophysiology
We recorded extracellular activity from populations of V4 and prefrontal cortex (PFC) in two awake, head-fixed monkeys. After each animal was trained to perform an orientation-change detection task, we chronically implanted two 96-electrode arrays (Blackrock Microsystems; 1 mm in electrode length, 400-μm spacing in a 10×10 grid). For monkey 1 (‘Pe’), we implanted in right V4 and right PFC. For monkey 2 (‘Wa’), we implanted in left V4 and left PFC. V4 arrays were implanted on the prelunate gyrus medial to the inferior occipital sulcus (Snyder et al., 2018), where receptive fields were approximately 7°, 5.25° eccentricity in monkeys 1, 2. PFC arrays were implanted in area 8Ar on the prearcuate gyrus immediately anterior to the arcuate sulcus and medial to the principal sulcus (see Figure 1 in Khanna et al., 2019a). Electrodes of 1 mm in length would reach approximately the middle layers of V4, where the cortical thickness is close to 2 mm, and the superficial layers of PFC, where the cortical thickness is close to 3 mm (Seidlitz et al., 2018). However, the precise layer of our recordings was not verified because it would have required sacrificing the animals for histology.
Voltage signals were spike sorted with semi-supervised sorting algorithms (Shoham et al., 2003) and visually inspected using custom MATLAB software (Kelly et al., 2007), taking into account waveform shapes and inter-spike interval distributions (https://github.com/smithlabvision/spikesort). Our data consisted of both well-isolated single units and multi-units, and we refer to each unit as a “neuron.” After applying rigorous spike waveform controls (see below), each session had 7–54 recorded V4 neurons (24–54 for monkey 1 and 7–35 for monkey 2) with a median of 32 V4 neurons (40, 20 neurons for monkeys 1, 2). For recordings in PFC (for which the same spike waveform controls were applied), each session had 41–93 recorded PFC neurons (41–93 for monkey 1 and 41–85 for monkey 2) with a median of 60 PFC neurons (60, 58 neurons for monkeys 1, 2).
Orientation-change detection task
We trained each animal to perform an orientation-change detection task in which each trial comprised a sequence of flashes, where each flash had two Gabor patch stimuli (one presented in each visual hemifield). After fixating, the animal was rewarded with water or juice for correctly detecting a change in stimulus by making a saccade to the changed stimulus (i.e., a “hit”). Any incorrect decisions, such as breaking fixation, missing a changed stimulus, or making a saccade to an unchanged stimulus, resulted in no reward and a 1 s time out before the next trial began. The display was a gamma-corrected flat-screen cathode ray tube monitor positioned 36 cm from the animal’s eyes with a resolution of 1024×768 pixels, refreshed at a frame rate of 100 Hz. The background of the display was 50% luminance (gray). The gaze of the animal was tracked using an infrared eye tracking system (EyeLink 1000; SR Research, Ottawa, Ontario), and monitored online by experimental control software to ensure fixation within ~1° of the central fixation point throughout each trial. Any trials in which the animal broke this fixation window without regard to the task (e.g., saccades that did not end in one of the two stimulus locations) were removed from our analyses.
Stimulus details
Presented visual stimuli were achromatic, drifting Gabor patches scaled and positioned to roughly cover the aggregate receptive fields (RFs) of the recorded V4 neurons. For monkey 1, Gabor stimuli had a diameter of visual angle 7.02°, and were centered 7.02° below and 7.02° to the left of fixation. For monkey 2, stimuli had a diameter of 4.70° and were centered 2.35° below and 4.70° to the right of fixation. Gabor stimuli were full-contrast with a spatial and temporal frequency that elicited robust responses from the population overall (i.e., not optimized for any particular neuron). For monkey 1, frequencies were 0.85 cycles/° and 8 cycles/s. For monkey 2, frequencies were 0.85 cycles/° and 7 cycles/s. During the task, we presented a Gabor stimulus at the estimated RF location and simultaneously at the mirror-symmetric location in the opposite hemifield.
Trial details
The trial structure of the task was as follows. At the start of the trial, the animal fixated at a centrally-located yellow dot (0.6° in diameter) on a blank, isoluminant screen. Each trial comprised a sequence of flashes, where each flash was a 400 ms presentation of two Gabor stimuli, one in each visual hemifield, followed by a blank screen lasting for 300–500 ms (uniformly distributed). For each trial, the orientation angle of one stimulus was randomly chosen to be 45° or 135°, and the orientation of the stimulus in the opposite hemifield was orthogonal (either 135° or 45°, respectively). Subsequent flashes in the sequence each had a fixed probability (30%, 40% for monkeys 1, 2) of the change in orientation of one of the stimuli (i.e., the “target”). Stimulus sequences continued until either the animal made an eye movement (i.e., a “hit” or a “false alarm”) or the animal remained fixating for 400 ms after a target appeared (i.e., a “miss”). The average sequence length (i.e., the number of flashes per trial, determined either by when a target was presented or when the animal made a false alarm) was 2.9, 2.7 flashes for monkeys 1, 2. The longest sequence length was 20, 14 flashes for monkeys 1, 2. For most of our analyses, we consider the stimulus flashes that occur after the first stimulus flash and before the final stimulus flash in a trial’s sequence (i.e., sequence positions 2, …, M −1 for a sequence with M flashes), which we designate as sample stimuli.
Cueing blocks of trials to probe attention
To probe the effects of spatial attention, trials were blocked in an alternating fashion. Within a “cue-in” block, 90% of the stimulus changes (“valid” trials, randomly chosen) occurred for the stimulus inside the RFs of the recorded V4 neurons, while the remaining 10% of stimulus changes (“invalid” trials) occurred in the opposite visual hemifield. For valid trials, the orientation change was randomly chosen to be 1°, 3°, 6°, or 15° in either the clockwise or anti-clockwise direction. For invalid trials, we restricted the orientation change to be only 3° randomly in either the clockwise or anti-clockwise direction. This restriction was necessary in order to provide enough trials to reasonably estimate the animal’s rate of detecting stimulus changes for these infrequent trials. The other type of block was “cue-out,” which had the same task structure and percentages as cue-in blocks except that for valid trials of cue-out blocks, the stimulus change occurred outside the RFs of the recorded V4 neurons.
Each block lasted until the animal made 80 correct detections in that block, at which point the type of block (cue-in or cue-out) switched. To alert the animal to the direction to attend in each block, each block began with a set of initial trials in which only the valid stimulus was presented (with no stimulus in the opposite hemifield). These initial trials lasted until the animal correctly detected 5 orientation changes, after which pairs of stimuli were presented for the remainder of the block. These initial trials were excluded from all analyses. Block type (left or right cue) alternated within a session, with the first block type counterbalanced across sessions. The average number of trials within each block was 179, 224 trials for monkeys 1, 2. Monkey 1 completed 25 sessions of the experiment; monkey 2 completed 24 sessions. After excluding sessions for equipment failure (for 2 sessions, the photodiode signal used to align eye-tracking and neural data was unexpectedly lost) and sessions with 5 neurons or less (4 sessions), we analyzed 24 sessions completed by monkey 1, and 19 sessions completed by monkey 2.
We reported how the animal’s sensitivity d′ increased for larger changes in grating orientation (Figure 1B; Figure S1). From the hit rate and false alarm rate estimates (see below), we also computed sensitivity as d′ = ϕ(hit rate) − ϕ(false alarm rate), where ϕ(·)is the cumulative distribution function of the Gaussian distribution, following previous studies (Macmillan and Creelman, 2004; Luo and Maunsell, 2015). We note that our task is not a true two-alternative forced choice task, as for each stimulus flash the animal could choose to make a saccade to one of two targets or remain fixating. However, the animal almost always made a saccade to the cued location for false alarm or incorrect trials (greater than 99% of all false alarm and incorrect trials). Thus, we assume that the choice of the animal followed statistics similar to those of a two-alternative forced choice task (a “go/no go” task in our case), and we report sensitivity. Previous work has found that an increase in sensitivity (i.e., the animal performs better at detecting a stimulus change) and also a decrease in criterion (i.e., the animal is more likely to make a saccade and thus increases its hit rate and false alarm rate) can occur concurrently in a spatial attention task (Luo and Maunsell, 2015). The behavior in our task is consistent with the results of this previous work: Sensitivity increased (Figure 1B, 3°) and criterion decreased (mean Δc = −0:46; −0:64 between valid and invalid trials for monkeys 1, 2). This suggests that in our task the spatial cue resulted in both the ability to more finely detect a stimulus change (i.e., an increase in sensitivity) as well as a shift in bias to be more likely to choose the cued location (i.e., a decrease in criterion).
Quantifying the slow fluctuations in behavior
We analyzed two common metrics of the animal’s behavior: hit rate and false alarm rate. Hit rate was defined as the number of correct saccades toward a target divided by the total number of times a target appeared. False alarm rate was defined as the number of saccades toward a sample stimulus (i.e., not a target) divided by the total number of presented sample stimuli (excluding the initial stimulus presentation, which was never a target).
The overall false alarm rates were high for our task (30.2%, 40.5% for monkeys 1, 2) relative to previous studies with similar tasks (e.g., <10% reported in Cohen and Maunsell, 2010; Luo and Maunsell, 2015). Interestingly, our observed rates were close to the likelihood of a change for each flash (30%, 40% for monkeys 1, 2). Thus, one could think of the animal’s behavior as selecting targets with a likelihood very close to the actual change likelihood. However, it is clear the animal was not guessing as it had excellent perceptual performance (Figure 1B). There are multiple differences between our task and previous tasks that could explain the higher false alarm rates for our task. For example, our task was challenging (mean 6.25° orientation changes), leaving the animal often uncertain as to whether a stimulus change had occurred. In addition, because we did not use any catch trials, and 90% of cued trials were valid within a block, the animal could be almost certain of the location when planning to make a saccade. For these reasons, the observed false alarm rates for our task were higher than those reported in some previous studies that employed catch trials or a different distribution of difficulties to explicitly discourage the animal from making false alarms. We view the observed high false alarm rates to be a feature of the task, allowing us to observe large changes in the false alarm rate over the course of the session.
We took running hit rate and false alarm rate estimates in 30 min windows, shifting the window in 6 min increments. The long duration of the time windows (30 min) was necessary to ensure reliable estimates of rate over a relatively small number of trials (~300 trials per 30 min; some periods had many fewer trials due to the animal briefly resting). We computed correlations between hit rate and false alarm rate over time within a session (Figure 1D), and compared them to correlations when we shuffled rates across sessions (within-session time points remained unshuffled). We truncated longer sessions to have the same number of time points as the shorter sessions (discarding any time points that occur after the shorter session ended).
To assess the magnitudes of the slow fluctuations in hit rate and false alarm rate, we compared their absolute changes relative to the shifts in hit rate and false alarm rate due to spatial attention. To measure the behavioral effect size of attention, we computed the hit rate separately for valid and invalid trials across all blocks for each session, and took the difference between the two. To measure the behavioral effect size of the slow fluctuations, we computed the hit rate for each block, and took the maximum difference across all pairs of blocks for that session. We measured differences in false alarm rate in the same manner. For this comparison, we only considered trials for which a stimulus change of ± 3° occurred or would occur if the animal had not false alarmed. This was because invalid trials had stimuli that only changed ± 3°.
Next, we assessed the timescale of these slow fluctuations in behavior. We re-estimated hit rate and false alarm rate as above except shifting windows in 1 min increments (instead of 6 min increments) for greater time resolution. Then, we performed Gaussian smoothing on the running estimates with standard deviations (i.e., timescales) ranging from 1 min to 60 min in 1 min increments. For each candidate timescale, we computed a cross-validated R2 based on leaving out randomly-chosen time points for each fold (10-folds in total) and then predicting the value of each held-out point by taking a Gaussian weighted average of its neighbors. We found the timescale that maximizes this R2. We then increased the timescale until the R2 dropped to 75% of the peak R2. We define this as the timescale of the slow fluctuations in behavior. We provide intuition for this approach in Figure S4. We confirmed that the estimated timescales were similar for different durations of time windows (e.g., 20 min instead of 30 min).
Estimating slow drift in neural activity
To estimate the slow drift in V4 and PFC activity, we first computed residual spike counts by taking the spike counts of each repeat of the same stimulus (binned in a 400 ms epoch starting 50 ms after stimulus onset) and subtracting the mean spike counts averaged across repeats of that stimulus orientation (either 45° or 135°). We then took a running average of the residual spike counts in a 20 min time window, where each window was offset in time from the previous window by 6 min. We chose a 20 min time window (as opposed to the 30 min window chosen for the running estimates of behavioral variables) because here we could reliably estimate the slow drift with a smaller window. Different values of the time window width and window offset yielded similar results. We applied principal component analysis (PCA) to the running average of residual spike count vectors (20 to 40 vectors per session, where the length of each vector equaled the number of neurons), and defined the unit-length vector of weights (i.e., loadings) of the top principal component (PC) as the slow drift axis. We found that on average the slow drift axis explained ~70% of the variance of the running average of residual activity (69%, 77% for monkeys 1, 2). We then projected the residual spike counts (400 ms bins) onto this axis. Next, we performed Gaussian smoothing (with a timescale of 9 min; different values yielded similar results), and defined the Gaussian-smoothed projections as the slow drift. The specified time window width, window offset, and smoothing timescale were chosen in a reasonable range and not optimized. We chose to use PCA instead of factor analysis (FA) (Yu et al., 2009; Williamson et al., 2016), because the length of the time windows (20 min) likely averaged away most Poisson-like response variability that would otherwise be better described by FA. Using FA instead of PCA yielded results similar to those presented here.
Aligning the V4 slow drift across sessions
The sign of the slow drift was arbitrary because PCA identifies the orientation of the slow drift axis in the population activity space up to a 180 rotation. Thus, without an alignment procedure, the sign of the correlation between the V4 slow drift and a behavioral variable was arbitrary. To combine the correlations across sessions (Figure 3B), we needed a way to align the slow drift axis that was consistent across sessions. One possibility was to flip the sign of the slow drift such that the sum of its axis weights was positive. However, this procedure did not account for the possibility that different sessions may have different proportions of recorded neurons with positive or negative weights (and hence making this flipping procedure sensitive to which neurons happened to be recorded in that session). Instead, we adopted a different procedure that established an absolute reference across sessions based on the sample stimuli of the experiment (i.e., grating orientation angles of 45° or 135°). The reasoning behind this alignment procedure was that the slow drift was likely aligned to the stimulus representation of the population of neurons, and because our arrays were implanted in one location and remained there, and the response properties of nearby neurons are similar and likely remain constant over time, this alignment was similar across sessions. We aligned the orientation of the slow drift axis such that the projections of the mean spike counts of the two sample stimuli along the slow drift axis always yielded a higher projection value for the 45° stimulus than that for the 135° stimulus. Importantly, this alignment was independent of any observed behavioral variables, and thus any correlation between the slow drift and a behavioral variable over the session cannot be due to this alignment procedure. This alignment procedure was used in Figure 3B and Figure S5.
There were a small number of sessions in which the population responses to the two orientation angles were not well differentiated. In these cases, the alignment procedure did not produce a meaningful result. To identify and remove those sessions which would have otherwise reduced our ability to observe the relationship between neural effects and behavior, we decoded the stimulus identity (45° or 135°) from the population responses using a linear SVM in a cross-validated manner. When computing the correlations between the slow drift and behavioral variables (Figure 3B), we included only sessions with a decoding accuracy greater than 55% (20/24 sessions for monkey 1, 16/19 sessions for monkey 2). Note that we could have flipped the slow drift such that the higher projection value was for the 135° stimulus instead of the 45° stimulus. This would result in a change of sign with the same magnitudes for all correlations (i.e., in Figure 3B, correlations for hit rate, false alarm rate, and pupil diameter would be negative, and correlations for trial duration and reaction time would be positive).
Controlling for neural recording instabilities
The slow drift could have arisen from non-neural sources, such as neural recording instabilities. Such instabilities may cause the spike waveforms to gradually change shape throughout a session, and thus affect our spike sorting procedure. For example, if the spike waveform changes over time, spike sorting may be more likely to miss spikes at different times of the session, leading to a slow drift. To ensure that the observed slow drift was not due to neural recording instabilities, we used the following two criteria for the inclusion of a V4 or PFC neuron in our analyses.
First, we included only neurons whose spike waveform was stable throughout the session. To do so, we divided the session into 10 non-overlapping time bins of equal size, and computed the mean spike waveform in each bin as well as the mean spike waveform across the entire session. Then, we computed the squared norm of the difference between each bin’s mean waveform and the overall mean waveform. The percent waveform variance was computed as the largest squared norm across bins divided by the variance of the overall mean waveform. Example mean spike waveforms and their corresponding percent waveform variances are shown for V4 and PFC neurons in Figure S2. We removed neurons from our analyses whose percent waveform variance was above 10%. We confirmed that the remaining neurons with the largest percent waveform variances were not more likely to contribute to the slow drift than other neurons (Figure S2).
Second, we excluded any neurons for which there was an abrupt change in activity during the session. For each neuron, we divided the session into 20 non-overlapping time bins of equal size, and computed the mean spike count within each bin. If the change in activity between any two consecutive time bins was greater than 25% of the maximum activity of that neuron (i.e., the largest of the mean spike count values across the 20 bins), the neuron was excluded from all analyses.
Measuring behavioral variables and relating them to the slow drift
To characterize the animal’s behavior, we measured hit rate and false alarm rate (described previously), as well as the following three quantities: 1. Pupil diameter was the mean diameter of the pupil (arbitrary units) during each stimulus flash measured with the EyeLink eye-tracking software (EyeLink 1000; SR Research, Ottawa, Ontario). 2. Trial duration was the total amount of time taken to complete a trial. Because the animal could choose to saccade to an unchanged stimulus flash (thus ending the trial), the animal’s false alarm rate influenced trial duration. We computed trial duration by taking the difference between the stimulus onset of the initial flash and saccade onset (or, when no saccade, the end time of the final flash). 3. Reaction time was computed only for correct trials (i.e., “hits”) as the time between the onset of the changed stimulus in the final flash and saccade onset (the time at which the eyes left the fixation window).
A running mean of each behavioral variable was taken (except pupil diameter, for which a running median was taken) with 30 min overlapping windows in 6 min intervals. The long length of the time window was necessary to have reasonable estimates of hit rate and false alarm rate. For fair comparison between behavioral variables and the slow drift, we also estimated the slow drift as a running mean of residual spike counts along the slow drift axis with the same time window and intervals as those for the behavioral variable estimates (i.e., Gaussian smoothing was not performed here).
We used the running estimates of the behavioral variables and slow drift for two comparisons. First, to assess whether the slow drift and behavioral variables showed similar time courses during a session, we computed the correlation over time between the slow drift and each behavioral variable (hit rate, false alarm rate, pupil diameter, trial duration, and reaction time). To compute the “shuffled” distributions of correlations between the slow drift and behavioral variables, we randomly shuffled slow drifts across sessions and re-computed correlations (200 runs), truncating the longer time series by discarding time points after the shorter times series finished. Second, we assessed if sessions for which the slow drift strongly varied (i.e., had a large magnitude) corresponded to sessions for which the behavioral variables also strongly varied. We measured the magnitude of the slow drift as its variance over time within a session. We normalized the slow drift by the number of neurons for each session to account for differences in the number of neurons across sessions. The variances of pupil diameter across sessions were not comparable because the eye-tracking software output arbitrary units of pupil diameter, and those units changed somewhat from session to session as the tracker position was adjusted. Thus, although values of pupil diameter were comparable within a session, values of pupil diameter were not comparable across sessions. We did not include the variance of pupil diameter in our results (Figure 3C; Figure S5).
Measuring whether neural responses vary more strongly with the slow drift versus attention
To understand how large were the neural activity changes related to the slow drift, we compared it to the size of activity changes related to spatial attention. For spatial attention, we first defined the attention axis as the axis in population activity space that connects the mean response on cue-in trials to that on cue-out trials (Cohen and Maunsell, 2010; Mayo et al., 2015; Snyder et al., 2018). The mean is taken over repeats of the same sample stimulus for a given cue condition. To assess the size of attention’s effect on spike counts for a given session, we computed the mean response along the attention axis for each block of trials (Figure 4B, orange and green lines), and took the variance across blocks . To measure the size of the slow drift, we computed the mean slow drift value for each block (Figure 4A, black lines), and computed the variance of these mean values across the blocks for each session . We compared the relative sizes of the slow drift and attentional effects by taking the ratio . A ratio greater than 1 indicates that the size of the slow drift was larger than the modulation in responses due to attention. Ratios were computed separately for sample stimuli with 45° or 135° orientations, and results were aggregated across orientations and sessions (Figure 4C). To control for the possibility that the attention axis was aligned to the slow drift axis (and hence the slow drift could leak into the estimates of the attentional effect), we subtracted the estimate of the slow drift from responses before projecting them along the attentional axis. For most sessions, we found that the slow drift axis and the attention axis were largely unaligned (i.e., this subtraction procedure often did not change the value of ). Note that included the variance between cue-in and cue-out blocks (i.e., between orange and green lines) as well as the variance within cue-in and cue-out blocks separately (i.e., between orange lines and between green lines). This latter variance is necessary to ensure a fair comparison with the size of the slow drift but implies that is an overestimate. Thus, the true ratios are likely to be even larger than reported in Figure 4C.
Comparing the slow drift between brain areas V4 and PFC
To compare the correlation between the V4 slow drift and PFC slow drift over time (Figure 5B), we computed the correlation between the slow drift identified for each brain area separately. Then, we took the absolute value of the correlation because its sign is arbitrary. We compared the measured correlations to those computed when the PFC slow drifts were simulated as random smooth time courses. Each random time course was drawn from a Gaussian process (GP, Williams and Rasmussen, 2006) using the squared exponential covariance function with a timescale similar to that of the slow drift (45 min, Figure S4). Time points of the random time courses were sampled at the same sampling frequency as the slow drift (with a period of 0.6 min). Correlations between V4 slow drifts and these smooth random time courses were expected to be larger than 0 (Figure 5B, median |ρ| = 0:68) because we took absolute correlations. We also considered larger GP timescales and found that the correlations of the real data (Figure 5B, median |ρ| = 0:96) were still significantly larger than those for simulated slow drifts with a 1 h timescale (median |ρ| = 0:81; p < 0:002, permutation test). We also computed the correlation between the magnitudes of V4 and PFC across sessions (Figure 5C). Magnitude was defined as the variance of the slow drift (either in V4 or PFC) within a session. We normalized the slow drift by the number of neurons to account for differences in the number of neurons recorded in each session.
Models of perceptual decision-making
We propose two models of perceptual decision-making (Figure 6; Figure S6). Both models take as input the stimulus xinput∈ {0, 1} (where xinput = 0 for a sample stimulus and xinput = 1 for a changed stimulus) and feedforward perceptual noise , and output a decision variable d∈ {0, 1} (where d = 0 represents keeping fixation and d = 1 represents making a saccade). Similar to the experiment, each simulated trial comprised a sequence of stimulus flashes where each flash had a 40% chance of changing from xinput = 0 to xinput = 1. In a correct trial, the model outputs decision d = 0 when xinput = 0, and outputs d = 1 when xinput = 1.
Both models also have a slow drift variable s = (1 /2)sin(2π(1 /3500) (t + 2200)), where t = 1, …., 2000 indicates the trial index. We chose this sine function so that s slowly varies over 2,000 trials; other smooth functions are possible. We define v = xinput + εnoise + s which represents V4 activity and provides sensory evidence to decision d. In addition to the εnoise noise, we included another source of noise that directly influenced d, whereby, for each flash, there was a probability ψ that d = 1 or d = 0 (both equally likely), independent of any other variables in the model. This output noise reflects other internal processes in the brain from which we cannot record that may affect an animal’s decision.
Sensory bias model
For the sensory bias model (Figure 6A), the decision is based directly on v, where d = 1 if v > 0:5, else d = 0. An increase in s places v closer to the decision threshold of 0.5, thereby increasing the chance of a false alarm. Conversely, a decrease in s places v further from the decision threshold of 0.5, thereby requiring a higher value of εnoise to cause a false alarm.
Impulsivity model
For the impulsivity model (Figure 6G), the slow drift s directly influences decision d independent of the sensory evidence encoded in V4 activity v. Mathematically, the slow drift determines an impulsivity signal m~Bernoulli(p(s)), where p(s) is the probability of saccade given the slow drift s. We set p(s) = (1 /2)(s + 0.5), which increases linearly as s increases. The decision is d = 1 if m = 1. The decision is also dependent on perceptual readout p = v − s, where the slow drift has been removed. Thus, d = 1 if p > 0:5 or m = 1, else d = 0. Note that the slow drift s does not bias the sensory evidence because s is removed from the V4 activity v. Instead, the slow drift only influences the decision d by overriding the perceptual readout p via the impulsivity signal m.
Model simulations
We ran each model for 2,000 trials, and computed the hit and false alarm rates with running estimates over the 2,000 trials (500-trial window length, where each window was offset by 50 trials). We matched the overall false alarm rate for each model (34%) to the animals’ false alarm rates (~30%, ~40% for monkeys 1, 2) by choosing an appropriate value for the sensory noise parameter (σ = 0:35) as well as for the output noise parameter (ψ = 70%).
Decoding V4 responses to predict the occurrence of false alarms
Because the outputs of both models were consistent with the finding that hit rate, false alarm rate, and the slow drift covary together (Figures 6B, 6C, and 6H), we sought an analysis in which we could test a prediction that differentiated the two models. In particular, we focused on how false alarms (i.e., d = 1 when xinput = 0) occurred for each model. Under the sensory bias model, slow drift s contributes to decision d through the perceptual readout of V4 activity v. Thus, we would expect that for false alarms, d would be more accurately predicted from v than from v − s (i.e., subtracting the slow drift contribution from v). On the other hand, for the impulsivity model, slow drift s contributes to decision d through the impulsivity signal m but not the perceptual readout p (because p = v − s, so the contribution of s does not reach d). The slow drift s acts as perceptual noise in V4 activity v, obscuring the true perceptual signal p (i.e., v = p + s, indicating v comprises the perceptual signal p and the “noisy” slow drift s). In this case, we would expect that for false alarms (i.e., p > 0:5 when xinput = 0), d would be more accurately predicted from v − s than from v, which differs from the sensory bias model. We first performed a decoding analysis to verify that our expectations about these models were correct, and then performed a similar analysis for the real data to test which model’s predictions were most consistent with the real data.
Verifying model predictions
We performed the following decoding analysis for each model (Figures 6E and 6J). First, we decoded whether or not a false alarm occurred from v using a threshold decoder (linear SVM). Next, we decoded from v − s instead of v. Finally, we compared the two decoding accuracies to determine if the decoding accuracy would be higher (as predicted by the sensory bias model) or lower (as predicted by the impulsivity model) when decoding from v than from v − s. Note that we decoded flashes that were either false alarms (i.e., d = 1 when xinput = 0) or correctly-rejected flashes (i.e., d = 0 when xinput = 0) that directly preceded the false alarm flashes. These correctly-rejected flashes were chosen for two reasons. First, they ensured we had an equal number of false alarm and non-false alarm flashes. Second, they forced the decoder to only consider within-trial fluctuations (i.e., εnoise) but not across-trial fluctuations (i.e., slow drift s). If we had instead considered across-trial fluctuations by including any correctly-rejected flash, we would not be able to differentiate between the models, as decoding accuracy for both models would be higher for v than for v − s. This is because s contains information about the overall probability of a false alarm during a session that could be used to predict the occurrence of a false alarm within a session (but not within a trial), and subtracting s would discard this information. We provide further intuition about this point in Figure S6.
Decoding analysis for the real data
We performed a similar decoding analysis for the real data as we did for each model (Figure 6F). The animal’s decision was to saccade (i.e., d = 1) or not to saccade V4 population responses projected onto the slow drift axis (i.e., v is a 1-dimensional signal, see below). For s, we used our estimates of the slow drift of V4 activity (i.e., the population responses projected onto the slow drift axis and then smoothed). We then decoded v and v − s in the same manner as described for the models, using a linear SVM decoder with leave-one-out cross-validation.
For v, we processed V4 activity in the following way. Because decoding accuracy of neural activity predicting false alarms have been reported to be only slightly above chance (e.g., choice probability was found to be ~54%, as reported in Nienborg and Cumming, 2009) and we were considering a small time window of activity (i.e., 175 ms), we leveraged the temporal information of the V4 responses. We computed spike count vectors of the V4 activity in non-overlapping 1 ms time bins (starting at stimulus onset and ending at 175 ms after stimulus onset), and performed Gaussian smoothing with a 10 ms standard deviation for each neuron. Note that compared to estimating the slow drift, the smoothing here is a different order of magnitude (10 ms versus 9 min) and has a different purpose. The reason for smoothing here is to account for small jitters of spike times between flashes that may occur due to the 1 ms bin widths. Trials for which a saccade occurred within 175 ms after stimulus onset were removed (less than 15% of all false alarm trials). The spike count vectors were then projected onto the slow drift axis. Thus, v corresponded to a 175-dimensional vector of projected spike counts (where 175 is the number of 1 ms time bins). For the slow drift s, we used the same procedure as described above, except that we binned activity in 175 ms time bins (instead of 400 ms time bins) and included responses to the final flashes. To obtain v − s, we formed a 175-dimensional vector where each element was the value of s.
We considered the same type of flashes (i.e., false alarms and their preceding correctly-rejected flashes) as those for the models. False alarm trials were limited to cue-in trials only, and each trial was required to have 3 or more stimulus flashes in total. To gain more statistical power, we doubled the number of data points by aggregating false alarm trials across the two orientations of stimuli (45° and 135°) in the following way. For stimulus flashes with a given grating orientation, we subtracted out the mean spike count response (the PSTH on a millisecond timescale) to the preceding correctly-rejected flash from the spike count responses to both the false alarm and correctly-rejected flashes. This ensured that the overall mean response to the correctly-rejected flash was the same for both orientations. We then analyzed all stimulus flashes together regardless of orientation.
The fact that we can weakly predict false alarms from visual cortical activity (Figure 6F, ~52%, significantly greater than the chance level of 50%, p < 0:05 for both monkeys, one sample t test) is consistent with previous work that reported choice probabilities (~55%) for neurons in MT, V1, V2, and V4 (Nienborg and Cumming, 2009; Cumming and Nienborg, 2016; Jasper et al., 2019). However, the observed decoding accuracies are not directly comparable to previously-reported choice probabilities because most previous work computes choice probabilities for a single neuron (here, we use a population of neurons), considers neural activity taken over large time windows (e.g., 1 s compared to 175 ms used here), and uses two-alternative forced choice tasks rather than our sequential task that required long periods of fixation. In an additional analysis, we confirmed that the resulting decoding accuracies were not a by-product of visual response adaptation due to the fact that the final flash always followed the second-to-final flash (Figure S6).
Determining whether the slow drift has the potential to corrupt stimulus encoding
We sought to assess whether the slow drift could corrupt stimulus encoding. To do so, we measured to what extent the slow drift lies within the “stimulus-encoding subspace,” defined as the subspace spanned by the mean responses to many natural images. The rationale is that, if the slow drift lies within the stimulus-encoding subspace, then the corrupted neural response to an image (i.e., corrupted by the slow drift) could be interpreted downstream as a different image.
To identify the stimulus-encoding subspace, we presented a large collection of natural images, which were selected using an adaptive procedure. We opted for an adaptive stimulus selection procedure because we were limited in how many images we could show per session (i.e., ~2,000 images), and a small set of randomly-chosen images cannot fully represent the space of all possible natural images (Hung et al., 2012). In a set of closed-loop experiments separate from those of the orientation-change detection task, we employed an adaptive stimulus selection algorithm, called Adept, to choose a set of 2,000 natural images (out of a candidate set of 20,000) that elicited large and diverse responses (Cowley et al., 2017). We recorded V4 activity in an adult, male rhesus macaque (Macaca mulatta, monkey 3, ‘Wi’) using a Utah electrode array. Surgical and electrophysiology procedures were the same as for the other two monkeys, described above. For another monkey (monkey 1), we did not use adaptive stimulus selection but rather randomly selected 550 images to show.
After choosing the collection of stimuli to show for one recording session, for subsequent sessions we presented the images in random order while the animals performed an active fixation task. The description of this active fixation task is as follows. After the animal fixated for 150 ms on a yellow dot (same display parameters as those for the orientation-change detection task) to initiate a trial, the animal remained fixating while a stimulus clip of images was presented in the RFs of the recorded V4 neurons. After the stimulus clip finished, the animal was required to maintain fixation for 700 ms, after which the fixation dot vanished and a target dot appeared ~10 visual degrees from the location of the fixation dot. The animal received a water reward for correctly making a saccade to the target dot (within a target window of visual angle 5°). For monkey 3, each stimulus clip consisted of 10 natural images randomly selected from the 2,000 Adept-chosen natural images (no image could repeat within the same stimulus clip), and each image was shown for 100 ms. For monkey 1, each stimulus clip comprised three images (of the 550), and each image was presented for 200 ms, interleaved with 200 ms of isoluminant blank screen.
Identifying the stimulus-encoding axes
We identified the stimulus-encoding axes using the following procedure. We computed spike counts in 100 ms bins (for monkey 3) or 200 ms bins (for monkey 1), starting 50 ms after stimulus onset to account for the time it takes sensory information to reach V4. We did not consider responses to an image that had 5 or fewer repeats. We defined the stimulus-encoding axes as the dimensions in population activity space in which the repeat-averaged responses have the greatest variance. We identified these axes using PCA, taking the weight vectors of the top K principal components as the top K stimulus-encoding axes. For our work, we chose K = 12 because this number of stimulus-encoding axes captured a large fraction of stimulus response variance (i.e., variance of repeat-averaged responses taken across images) for each session (62%, 60%, 59% for days 1, 2, 3 of monkey 3, and 70%, 72% for days 1, 2 of monkey 1).
Because repeats were not necessarily equally-spaced throughout a session, we controlled for the possibility that the slow drift “leaked” into the estimation of the stimulus-encoding axes. To do this, we first applied PCA to the repeat-averaged responses and considered all N PCs, where N is the number of neurons. For each PC, we subtracted any “slow drift” from the raw responses along that PC (where the slow drift for each PC was estimated from projected responses using Gaussian smoothing with a 9 min standard deviation). Finally, we re-computed the repeat-averaged responses for which the slow drift was subtracted, and re-applied PCA to these responses. Results were almost identical when we did not perform this removal procedure, suggesting that little to no slow drift had leaked into the repeat-averaged responses (i.e., there were enough repeats to average out the presence of the slow drift).
Comparing the slow drift axis to the stimulus-encoding axes
We first estimated the slow drift of the responses to natural images. We estimated the slow drift axis using the same procedure as that for the orientation-change experiment. Note this slow drift was not necessarily the same as that removed from each stimulus-encoding axis of the repeat-averaged responses in the previous section, as this slow drift could be along an axis orthogonal to the stimulus-encoding axes. Finally, we measured the extent to which the slow drift axis was aligned to the stimulus-encoding axes by computing the fraction of slow drift variance captured by each stimulus-encoding axis. The slow drift variance was the variance of the slow drift over time within a session. A fraction close to 1 indicates that the slow drift axis largely overlaps with the stimulus-encoding axis. A fraction close to 0 indicates that the slow drift axis was close to orthogonal to the stimulus-encoding axis. For reference, we rotated the slow drift axis to a random orientation in population activity space (i.e., “random axis”), and re-computed this fraction.
QUANTIFICATION AND STATISTICAL ANALYSIS
Unless otherwise stated, all statistical hypothesis testing was conducted with permutation tests, which do not assume any parametric form of the underlying probability distributions of the sample. All tests were two-sided and non-paired, unless otherwise noted. We computed p-values with 500 runs, where p < 0:002 indicates the highest significance achievable given the number of runs performed. Permutation tests were performed either for differences in means or differences in medians (the latter used when outliers existed), as noted by context in the text. All correlations were performed with Pearson’s correlation r, unless otherwise stated. We computed the significance of ρactual of the actual data with a ‘shuffle test’ by running 500 shuffles of the samples and re-computing for the jth shuffle. The p-value was measured as the proportion of shuffles with greater than or equal to ρactual for all j, for a one-sided hypothesis test. Error bars in figures represent either ± 1 SEM when estimating means or bootstrapped 90% confidence intervals when estimating medians, as stated. Error bars are for visualization purposes only, and not used for hypothesis testing. No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those of previous related publications (e.g., Cohen and Maunsell, 2009; Mitchell et al., 2009; Luo and Maunsell, 2015).
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| Rhesus macaque (Macaca mulatta) | 2 animals from Covance, 1 from Tulane National Primate Research Center | N/A |
| Software and Algorithms | ||
| MATLAB | MathWorks | RRID: SCR_001622; https://www.mathworks.com/products/matlab/ |
| Custom spike-sorting software | Kelly et al., 2007 | https://github.com/smithlabvision/spikesort |
| Other | ||
| 96-electrode array | Blackrock Microsystems | https:/www./blackrockmicro.com/neuroscience-research-products/neuraldata-acquisition-systems/ |
| Eyelink 1000 eye tracker | SR Research | RRID: SCR_009602; https://www.sr-research.com |
Highlights.
Perceptual behavior naturally shifts over tens of minutes in a discrimination task
A slow drift in visual area V4 is a neural correlate of this behavior
Neurons in multiple brain areas (V4 and prefrontal cortex) share the same slow drift
The slow drift acts as a brain-wide impulsivity signal, overriding sensory evidence
ACKNOWLEDGMENTS
The authors thank Samantha Schmitt for assistance with surgery and data collection. Some elements of the graphical abstract were created with Bio-Render.com, and Figures 2 and 6 in the manuscript contain elements created with the Scalable Brain Atlas (Bakker et al., 2015). B.R.C. was supported by the C.V. Starr Foundation Fellowship. A.C.S. was supported by NIH R00 EY025768 and a NARSAD Young Investigator Award from the Brain and Behavior Research Foundation. K.A. was supported by NSF Graduate Fellowship Grant 1747452. R.C.W. was supported by a Richard King Mellon Foundation Presidential Fellowship in the Life Sciences. B.M.Y. and M.A.S. were supported by NIH R01 MH118929 and R01 EB026953 and NSF NCS 1734916/1954107. B.M.Y. was also supported by NSF NCS BCS1533672, NIH R01 HD071686, NIH CRCNS R01 NS105318, and Simons Foundation 543065. M.A.S. was also supported by NIH R01 EY022928 and P30 EY008098.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2020.07.021.
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPORTING CITATIONS
The following references appear in the Supplemental Information: Kohn, 2007.
REFERENCES
- Abrahamyan A, Silva LL, Dakin SC, Carandini M, and Gardner JL (2016). Adaptable history biases in human perceptual decisions. Proc. Natl. Acad. Sci. USA 113, E3548–E3557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen WE, Chen MZ, Pichamoorthy N, Tien RH, Pachitariu M, Luo L, and Deisseroth K (2019). Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, 253–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson EB, Mitchell JF, and Reynolds JH (2011). Attentional modulation of firing rate varies with burstiness across putative pyramidal neurons in macaque visual area V4. J. Neurosci 31, 10983–10992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arieli A, Sterkin A, Grinvald A, and Aertsen A (1996). Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science 273, 1868–1871. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, and Cohen JD (2005). An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci 28, 403–450. [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, and Pouget A (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci 7, 358–366. [DOI] [PubMed] [Google Scholar]
- Bakker R, Tiesinga P, and Kötter R (2015). The scalable brain atlas: instant web-based access to public brain atlases and related content. Neuroinformatics 13, 353–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bari A, and Robbins TW (2013). Inhibition and impulsivity: behavioral and neural basis of response control. Prog. Neurobiol 108, 44–79. [DOI] [PubMed] [Google Scholar]
- Baruni JK, Lau B, and Salzman CD (2015). Reward expectation differentially modulates attentional behavior and activity in visual area V4. Nat. Neurosci 18, 1656–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaman CB, Eagleman SL, and Dragoi V (2017). Sensory coding accuracy and perceptual performance are improved during the desynchronized cortical state. Nat. Commun 8, 1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bondy AG, Haefner RM, and Cumming BG (2018). Feedback determines the structure of correlated variability in primary visual cortex. Nat. Neurosci 21, 598–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosman CA, Womelsdorf T, Desimone R, and Fries P (2009). A microsaccadic rhythm modulates gamma-band synchronization and behavior. J. Neurosci 29, 9471–9480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody CD, and Hanks TD (2016). Neural underpinnings of the evidence accumulator. Curr. Opin. Neurobiol 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, and Brody CD (2013). Rats and humans can optimally accumulate evidence for decision-making. Science 340, 95–98. [DOI] [PubMed] [Google Scholar]
- Calhoun AJ, Pillow JW, and Murthy M (2019). Unsupervised identification of the internal states that shape natural behavior. Nat. Neurosci 22, 2040–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carandini M, and Heeger DJ (2011). Normalization as a canonical neural computation. Nat. Rev. Neurosci 13, 51–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaisanguanthum KS, Shen HH, and Sabes PN (2014). Motor variability arises from a slow random walk in neural state. J. Neurosci 34, 12071–12080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland AK, Kiani R, and Shadlen MN (2008). Decision-making with multiple alternatives. Nat. Neurosci 11, 693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Puskas GA, and El-Murr S (2009). Decisions in changing conditions: the urgency-gating model. J. Neurosci 29, 11560–11571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Kohn A (2011). Measuring and interpreting neuronal correlations. Nat. Neurosci 14, 811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Maunsell JH (2009). Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci 12, 1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Maunsell JH (2010). A neuronal population measure of attention predicts behavioral performance on individual trials. J. Neurosci 30, 15241–15253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JD, Perlstein WM, Braver TS, Nystrom LE, Noll DC, Jonides J, and Smith EE (1997). Temporal dynamics of brain activation during a working memory task. Nature 386, 604–608. [DOI] [PubMed] [Google Scholar]
- Cowley BR, Smith MA, Kohn A, and Yu BM (2016). Stimulus-driven population activity patterns in macaque primary visual cortex. PLoS Comput. Biol 12, e1005185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley B, Williamson R, Acar K, Smith M, and Yu BM (2017). Adaptive stimulus selection for optimizing neural population responses. Adv. Neural Inf. Process. Sys 30, 1395–1405. [Google Scholar]
- Crapse TB, and Sommer MA (2008). Corollary discharge across the animal kingdom. Nat. Rev. Neurosci 9, 587–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming BG, and Nienborg H (2016). Feedforward and feedback sources of choice probability in neural population responses. Curr. Opin. Neurobiol 37, 126–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham JP, and Yu BM (2014). Dimensionality reduction for large-scale neural recordings. Nat. Neurosci 17, 1500–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtis CE, and D’Esposito M (2003). Persistent activity in the prefrontal cortex during working memory. Trends Cogn. Sci 7, 415–423. [DOI] [PubMed] [Google Scholar]
- Ebitz RB, and Moore T (2017). Selective modulation of the pupil light reflex by microstimulation of prefrontal cortex. J. Neurosci 37, 5008–5018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldar E, Cohen JD, and Niv Y (2013). The effects of neural gain on attention and learning. Nat. Neurosci 16, 1146–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsayed GF, Lara AH, Kaufman MT, Churchland MM, and Cunningham JP (2016). Reorganization between preparatory and movement population responses in motor cortex. Nat. Commun 7, 13239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel TA, Steinmetz NA, Gieselmann MA, Thiele A, Moore T, and Boahen K (2016). Selective modulation of cortical state during spatial attention. Science 354, 1140–1144. [DOI] [PubMed] [Google Scholar]
- Erisken S, Vaiceliunaite A, Jurjut O, Fiorini M, Katzner S, and Busse L (2014). Effects of locomotion extend throughout the mouse early visual system. Curr. Biol 24, 2899–2907. [DOI] [PubMed] [Google Scholar]
- Everitt BJ, and Robbins TW (1997). Central cholinergic systems and cognition. Annu. Rev. Psychol 48, 649–684. [DOI] [PubMed] [Google Scholar]
- Felleman DJ, and Van Essen DC (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Pouget A, DeAngelis GC, and Angelaki DE (2011). Neural correlates of reliability-based cue weighting during multisensory integration. Nat. Neurosci 15, 146–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh S, and Maunsell JH (2019). Visual area v4 encodes history dependent attentional effort and single-trial perceptual detection. bioRxiv. 10.1101/584409. [DOI]
- Gold JI, and Shadlen MN (2007). The neural basis of decision making. Annu. Rev. Neurosci 30, 535–574. [DOI] [PubMed] [Google Scholar]
- Goris RL, Movshon JA, and Simoncelli EP (2014). Partitioning neuronal variability. Nat. Neurosci 17, 858–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutnisky DA, Beaman C, Lew SE, and Dragoi V (2017a). Cortical response states for enhanced sensory discrimination. eLife 6, e29226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutnisky DA, Beaman CB, Lew SE, and Dragoi V (2017b). Spontaneous fluctuations in visual cortical responses influence population coding accuracy. Cereb. Cortex 27, 1409–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafed ZM, Lovejoy LP, and Krauzlis RJ (2011). Modulation of microsaccades in monkey during a covert visual attention task. J. Neurosci 31, 15219–15230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, and Summerfield C (2017). Perceptual decision making in rodents, monkeys, and humans. Neuron 93, 15–31. [DOI] [PubMed] [Google Scholar]
- Hanks T, Kiani R, and Shadlen MN (2014). A neural mechanism of speed-accuracy tradeoff in macaque area LIP. eLife 3, e02260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, and Brody CD (2015). Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520, 220–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, and Thiele A (2011). Cortical state and attention. Nat. Rev. Neurosci 12, 509–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennig JA, Golub MD, Lund PJ, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Yu BM, and Chase SM (2018). Constraints on neural redundancy. eLife 7, e36774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennig JA, Oby ER, Golub MD, Bahureksa LA, Sadtler PT, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Chase SM, et al. (2020). Learning is shaped by abrupt changes in neural engagement. bioRxiv. 10.1101/2020.05.24.112714. [DOI] [PMC free article] [PubMed]
- Huang C, Ruff DA, Pyle R, Rosenbaum R, Cohen MR, and Doiron B (2019). Circuit models of low-dimensional shared variability in cortical networks. Neuron 101, 337–348.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta MF, Krubitzer LA, and Kaas JH (1987). Frontal eye field as defined by intracortical microstimulation in squirrel monkeys, owl monkeys, and macaque monkeys. II. Cortical connections. J. Comp. Neurol 265, 332–361. [DOI] [PubMed] [Google Scholar]
- Huk AC, Katz LN, and Yates JL (2017). The role of the lateral intraparietal area in (the study of) decision making. Annu. Rev. Neurosci 40, 349–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung C-C, Carlson ET, and Connor CE (2012). Medial axis shape coding in macaque inferotemporal cortex. Neuron 74, 1099–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jasper AI, Tanabe S, and Kohn A (2019). Predicting perceptual decisions using visual cortical population responses and choice history. J. Neurosci 39, 6714–6727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S, Li Y, Kalwani RM, and Gold JI (2016). Relationships between pupil diameter and neuronal activity in the locus coeruleus, colliculi, and cingulate cortex. Neuron 89, 221–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanitscheider I, Coen-Cagli R, Kohn A, and Pouget A (2015). Measuring Fisher information accurately in correlated neural populations. PLoS Comput. Biol 11, e1004218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2014). Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci 17, 440–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RC, Smith MA, Samonds JM, Kohn A, Bonds AB, Movshon JA, and Lee TS (2007). Comparison of recordings from microelectrode arrays and single electrodes in the visual cortex. J. Neurosci 27, 261–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanna SB, Scott JA, and Smith MA (2019a). Dynamic shifts of visual and saccadic signals in prefrontal cortical regions 8ar and fef. bioRxiv. 10.1101/817478. [DOI] [PMC free article] [PubMed]
- Khanna SB, Snyder AC, and Smith MA (2019b). Distinct sources of variability affect eye movement preparation. J. Neurosci 39, 4511–4526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, and Shadlen MN (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324, 759–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A (2007). Visual adaptation: physiology, mechanisms, and functional benefits. J. Neurophysiol 97, 3155–3164. [DOI] [PubMed] [Google Scholar]
- Kohn A, Coen-Cagli R, Kanitscheider I, and Pouget A (2016). Correlations and neuronal population information. Annu. Rev. Neurosci 39, 237–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A, Jasper AI, Semedo JD, Gokcen E, Machens CK, and Yu BM (2020). Principles of corticocortical communication: proposed schemes and design considerations. Trends Neurosci. Published online August 5, 2020. 10.1016/j.tins.2020.07.001. [DOI] [PMC free article] [PubMed]
- Krajbich I, and Rangel A (2011). Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proc. Natl. Acad. Sci. USA 108, 13852–13857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krajbich I, Armel C, and Rangel A (2010). Visual fixations and the computation and comparison of value in simple choice. Nat. Neurosci 13, 1292–1298. [DOI] [PubMed] [Google Scholar]
- Leinweber M, Ward DR, Sobczak JM, Attinger A, and Keller GB (2017). A sensorimotor circuit in mouse cortex for visual flow predictions. Neuron 95, 1420–1432.e5. [DOI] [PubMed] [Google Scholar]
- Leopold DA, and Logothetis NK (1998). Microsaccades differentially modulate neural activity in the striate and extrastriate visual cortex. Exp. Brain Res 123, 341–345. [DOI] [PubMed] [Google Scholar]
- Lin I-C, Okun M, Carandini M, and Harris KD (2015). The nature of shared cortical variability. Neuron 87, 644–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Rodenkirch C, Moskowitz N, Schriver B, and Wang Q (2017). Dynamic lateralization of pupil dilation evoked by locus coeruleus activation results from sympathetic, not parasympathetic, contributions. Cell Rep. 20, 3099–3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowet E, Gomes B, Srinivasan K, Zhou H, Schafer RJ, and Desimone R (2018). Enhanced neural processing by covert attention only during microsaccades directed toward the attended stimulus. Neuron 99, 207–214.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo TZ, and Maunsell JH (2015). Neuronal modulations in visual cortex are associated with only one of multiple components of attention. Neuron 86, 1182–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo TZ, and Maunsell JHR (2018). Attentional changes in either criterion or sensitivity are associated with robust modulations in lateral prefrontal cortex. Neuron 97, 1382–1393.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, and Creelman CD (2004). Detection Theory: A User’s Guide (Psychology Press; ). [Google Scholar]
- Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcora SM, Staiano W, and Manning V (2009). Mental fatigue impairs physical performance in humans. J. Appl. Physiol 106, 857–864. [DOI] [PubMed] [Google Scholar]
- Markov NT, Ercsey-Ravasz MM, Ribeiro Gomes AR, Lamy C, Magrou L, Vezoli J, Misery P, Falchier A, Quilodran R, Gariel MA, et al. (2014). A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb. Cortex 24, 17–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Conde S, Macknik SL, and Hubel DH (2004). The role of fixational eye movements in visual perception. Nat. Rev. Neurosci 5, 229–240. [DOI] [PubMed] [Google Scholar]
- Mathôt S (2018). Pupillometry: Psychology, physiology, and function. J. Cogn 1, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maunsell JHR (2015). Neuronal mechanisms of visual attention. Annu. Rev. Vis. Sci 1, 373–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayo JP, Cohen MR, and Maunsell JH (2015). A refined neuronal population measure of visual attention. PLoS ONE 10, e0136570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA (1992). Neurotransmitter actions in the thalamus and cerebral cortex and their role in neuromodulation of thalamocortical activity. Prog. Neurobiol 39, 337–388. [DOI] [PubMed] [Google Scholar]
- McGinley MJ, David SV, and McCormick DA (2015a). Cortical membrane potential signature of optimal states for sensory signal detection. Neuron 87, 179–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley MJ, Vinck M, Reimer J, Batista-Brito R, Zagha E, Cadwell CR, Tolias AS, Cardin JA, and McCormick DA (2015b). Waking state: rapid variations modulate neural and behavioral responses. Neuron 87, 1143–1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milton R, Shahidi N, and Dragoi V (2020). Dynamic states of population activity in prefrontal cortical networks of freely-moving macaque. Nat. Commun 11, 1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, and Reynolds JH (2009). Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron 63, 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore T, and Zirnsak M (2017). Neural mechanisms of selective visual attention. Annu. Rev. Psychol 68, 47–72. [DOI] [PubMed] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, and Pouget A (2014). Information-limiting correlations. Nat. Neurosci 17, 1410–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller L, Chavane F, Reynolds J, and Sejnowski TJ (2018). Cortical travelling waves: mechanisms and computational principles. Nat. Rev. Neurosci 19, 255–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy PR, Boonstra E, and Nieuwenhuis S (2016). Global gain modulation generates time-dependent urgency during perceptual choice in humans. Nat. Commun 7, 13526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Rumsey KM, Wilson RC, Parikh K, Heasly B, and Gold JI (2012). Rational regulation of learning dynamics by pupil-linked arousal systems. Nat. Neurosci 15, 1040–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni AM, Ruff DA, Alberts JJ, Symmonds J, and Cohen MR (2018). Learning and attention reveal a general relationship between population activity and behavior. Science 359, 463–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nienborg H, and Cumming BG (2009). Decision-related activity in sensory neurons reflects more than a neuron’s causal effect. Nature 459, 89–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connell RG, Shadlen MN, Wong-Lin K, and Kelly SP (2018). Bridging neural and computational viewpoints on perceptual decision-making. Trends Neurosci. 41, 838–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M, Steinmetz N, Cossell L, Iacaruso MF, Ko H, Barthó P, Moore T, Hofer SB, Mrsic-Flogel TD, Carandini M, and Harris KD (2015). Diverse coupling of neurons to populations in sensory cortex. Nature 521, 511–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M, Steinmetz NA, Lak A, Dervinis M, and Harris KD (2019). Distinct structure of cortical population activity on fast and infraslow timescales. Cereb. Cortex 29, 2196–2210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perich MG, Gallego JA, and Miller LE (2018). A neural population mechanism for rapid learning. Neuron 100, 964–976.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisupati S, Chartarifsky-Lynn L, Khanal A, and Churchland AK (2019). Lapses in perceptual decisions reflect exploration. bioRxiv. 10.1101/613828. [DOI] [PMC free article] [PubMed]
- Purcell BA, and Kiani R (2016). Hierarchical decision processes that operate over distinct timescales underlie choice and changes in strategy. Proc. Natl. Acad. Sci. USA 113, E4531–E4540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinowitz NC, Goris RL, Cohen M, and Simoncelli EP (2015). Attention stabilizes the shared gain of V4 populations. eLife 4, e08998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raposo D, Kaufman MT, and Churchland AK (2014). A category-free neural population supports evolving demands during decision-making. Nat. Neurosci 17, 1784–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, Brown SD, and McKoon G (2016). Diffusion decision model: Current issues and history. Trends Cogn. Sci 20, 260–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimer J, Froudarakis E, Cadwell CR, Yatsenko D, Denfield GH, and Tolias AS (2014). Pupil fluctuations track fast switching of cortical states during quiet wakefulness. Neuron 84, 355–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimer J, McGinley MJ, Liu Y, Rodenkirch C, Wang Q, McCormick DA, and Tolias AS (2016). Pupil fluctuations track rapid changes in adrenergic and cholinergic activity in cortex. Nat. Commun 7, 13289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, and Harris KD (2010). The asynchronous state in cortical circuits. Science 327, 587–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH, and Heeger DJ (2009). The normalization model of attention. Neuron 61, 168–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rial RV, Akaârir M, Gamundí A, Nicolau C, Garau C, Aparicio S, Tejada S, Gené L, González J, De Vera LM, et al. (2010). Evolution of wakefulness, sleep and hibernation: from reptiles to mammals. Neurosci. Biobehav. Rev 34, 1144–1160. [DOI] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2014a). Attention can either increase or decrease spike count correlations in visual cortex. Nat. Neurosci 17, 1591–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2014b). Global cognitive factors modulate correlated response variability between V4 neurons. J. Neurosci 34, 16408–16416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2016). Attention increases spike count correlations between visual cortical areas. J. Neurosci 36, 7523–7534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2019). Simultaneous multi-area recordings suggest that attention improves performance by reshaping stimulus representations. Nat. Neurosci 22, 1669–1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rule ME, O’Leary T, and Harvey CD (2019). Causes and consequences of representational drift. Curr. Opin. Neurobiol 58, 141–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumyantsev OI, Lecoq JA, Hernandez O, Zhang Y, Savall J, Chrapkiewicz R, Li J, Zeng H, Ganguli S, and Schnitzer MJ (2020). Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105. [DOI] [PubMed] [Google Scholar]
- Saber GT, Pestilli F, and Curtis CE (2015). Saccade planning evokes topographically specific activity in the dorsal and ventral streams. J. Neurosci 35, 245–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schall JD (2003). Neural correlates of decision processes: neural and mental chronometry. Curr. Opin. Neurobiol 13, 182–186. [DOI] [PubMed] [Google Scholar]
- Schriver BJ, Bagdasarov S, and Wang Q (2018). Pupil-linked arousal modulates behavior in rats performing a whisker deflection direction discrimination task. J. Neurophysiol 120, 1655–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidlitz J, Sponheim C, Glen D, Ye FQ, Saleem KS, Leopold DA, Ungerleider L, and Messinger A (2018). A population MRI brain template and analysis tools for the macaque. Neuroimage 170, 121–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semedo JD, Zandvakili A, Machens CK, Yu BM, and Kohn A (2019). Cortical areas interact through a communication subspace. Neuron 102, 249–259.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, and Kiani R (2013). Decision making as a window on cognition. Neuron 80, 791–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, and Newsome WT (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci 18, 3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Britten KH, Newsome WT, and Movshon JA (1996). A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J. Neurosci 16, 1486–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahidi N, Andrei AR, Hu M, and Dragoi V (2019). High-order coordination of cortical spiking activity modulates perceptual accuracy. Nat. Neurosci 22, 1148–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoham S, Fellows MR, and Normann RA (2003). Robust, automatic spike sorting using mixtures of multivariate t-distributions. J. Neurosci. Methods 127, 111–122. [DOI] [PubMed] [Google Scholar]
- Snyder AC, and Smith MA (2018). Early steps toward understanding neuronal communication. Curr. Opin. Neurol 31, 59–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Morais MJ, and Smith MA (2016). Dynamics of excitatory and inhibitory networks are differentially altered by selective attention. J. Neurophysiol 116, 1807–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Yu BM, and Smith MA (2018). Distinct population codes for attention in the absence and presence of visual stimulation. Nat. Commun 9, 4382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stavisky SD, Kao JC, Ryu SI, and Shenoy KV (2017). Motor cortical vi-suomotor feedback activity is initially isolated from downstream targets in output-null neural state space dimensions. Neuron 95, 195–208.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz NA, and Moore T (2014). Eye movement preparation modulates neuronal responses in area V4 when dissociated from attentional demands. Neuron 83, 496–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Timofeev I, and Grenier F (2001). Natural waking and sleep states: a view from inside neocortical neurons. J. Neurophysiol 85, 1969–1985. [DOI] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ungerleider LG, Galkin TW, Desimone R, and Gattass R (2008). Cortical connections of area V4 in the macaque. Cereb. Cortex 18, 477–499. [DOI] [PubMed] [Google Scholar]
- Urai AE, Braun A, and Donner TH (2017). Pupil-linked arousal is driven by decision uncertainty and alters serial choice bias. Nat. Commun 8, 14637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urai AE, de Gee JW, Tsetsos K, and Donner TH (2019). Choice history biases subsequent evidence accumulation. eLife 8, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M, Batista-Brito R, Knoblich U, and Cardin JA (2015). Arousal and locomotion make distinct contributions to cortical activity patterns and visual encoding. Neuron 86, 740–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasmuht DF, Parker AJ, and Krug K (2019). Interneuronal correlations at longer time scales predict decision signals for bistable structure-from-motion perception. Sci. Rep 9, 11449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman DH, Roberts KC, Visscher KM, and Woldorff MG (2006). The neural bases of momentary lapses in attention. Nat. Neurosci 9, 971–978. [DOI] [PubMed] [Google Scholar]
- Williams CK, and Rasmussen CE (2006). Gaussian Processes for Machine Learning (MIT Press; ). [Google Scholar]
- Williamson RC, Cowley BR, Litwin-Kumar A, Doiron B, Kohn A, Smith MA, and Yu BM (2016). Scaling properties of dimensionality reduction for neural populations and network models. PLoS Comput. Biol 12, e1005141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson NR, Runyan CA, Wang FL, and Sur M (2012). Division and subtraction by distinct cortical inhibitory networks in vivo. Nature 488, 343–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo SBM, and Hayden BY (2018). Economic choice as an untangling of options into actions. Neuron 99, 434–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, and Sahani M (2009). Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol 102, 614–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yüzgeç Ö, Prsa M, Zimmermann R, and Huber D (2018). Pupil size coupling to cortical states protects the stability of deep sleep via parasympathetic modulation. Curr. Biol 28, 392–400.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Xu M, Kamigaki T, Hoang Do JP, Chang W-C, Jenvay S, Miyamichi K, Luo L, and Dan Y (2014). Selective attention. Long-range and local circuits for top-down modulation of visual cortex processing. Science 345, 660–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Yates JL, Levi AJ, Huk AC, and Park IM (2020). Stimuluschoice (mis)alignment in primate area MT. PLoS Comput. Biol 16, e1007614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, and Newsome WT (1994). Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370, 140–143. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code and data are available by request to the Lead Contact (mattsmith@cmu.edu).


