Substrate Resistance to Traction Forces Controls Fibroblast Polarization

Abstract

The mechanics of fibronectin-rich extracellular matrix regulate cell physiology in a number of diseases, prompting efforts to elucidate cell mechanosensing mechanisms at the molecular and cellular scale. Here, the use of fibronectin-functionalized silicone elastomers that exhibit considerable frequency dependence in viscoelastic properties unveiled the presence of two cellular processes that respond discreetly to substrate mechanical properties. Weakly cross-linked elastomers supported efficient focal adhesion maturation and fibroblast spreading because of an apparent stiff surface layer. However, they did not enable cytoskeletal and fibroblast polarization; elastomers with high cross-linking and low deformability were required for polarization. Our results suggest as an underlying reason for this behavior the inability of soft elastomer substrates to resist traction forces rather than a lack of sufficient traction force generation. Accordingly, mild inhibition of actomyosin contractility rescued fibroblast polarization even on the softer elastomers. Our findings demonstrate differential dependence of substrate physical properties on distinct mechanosensitive processes and provide a premise to reconcile previously proposed local and global models of cell mechanosensing.

Significance

The mechanisms cells employ to sense and respond to the mechanical properties of their surroundings remain incompletely understood. In this study, we used silicone elastomers for preparing compliant, fibronectin-coated substrates and investigated the adhesion and polarization of human fibroblasts. Our results suggest the existence of at least two discrete mechanosensing processes regulated at different timescales and length (force) scales. Focal adhesion assembly and cell spreading were promoted by a stiff surface layer independent from bulk viscoelasticity, whereas effective cell polarization required elevated elastomer stiffness, sufficient to resist applied cell tractions. The results presented here have implications on the use of elastomer substrates as biomaterials for mechanosensing studies or clinical applications.

Introduction

Cells engage their microenvironment by using specialized receptors that recognize biochemical ligands presented on the extracellular matrix (ECM). The result of ligand-receptor interactions depends on the physical connection of these ligands to their environment; the outcome can differ whether the ligand is soluble compared with being attached to another cell or the ECM and thus the ligand-receptor pair being subject to force (1). The field of mechanosensing has emerged to characterize the processes that enable cells to interpret physical forces that are applied on the cell or that result from the resistance of cell-generated forces on the external environment (2,3). The interplay of biochemical and physical stimuli during mechanosensing is invariably intertwined; how cells sense their surrounding mechanical environment is a function of which ligands are presented and which receptors bind them.

Over the past two decades, numerous demonstrations that alteration of surrounding mechanics is associated with fundamental cell processes (4), fate (5), and pathologies (6,7) have prompted scientists to adopt reductionist, in vitro experimentation to fundamentally understand mechanosensing (8). Engineered hydrogels and silicone elastomers are popular substrate choices as they are easy to fabricate, provide straightforward control over viscoelastic properties, and enable direct, high-resolution observations. However, although the majority of studies have validated the view that substrate elasticity controls cell behavior, important differences were described between materials of similar reported mechanical properties (9, 10, 11, 12).

There are four major reasons for the observed differences on cell behavior when cells are interrogated on substrates of equal nominal stiffness but dissimilar material composition. First, different mechanical characterization techniques probe distinct properties and at different scales. Thus, the resulting stiffness values can vary for the same material (13), and the use of a single nominal stiffness to characterize the substrate can confound conclusions. Second, mechanosensing depends on the biochemical properties of the presented ligands as well as the cell receptors and intracellular composition, rendering mechanosensing sensitive to cell and biochemical factors (14, 15, 16). Third, ligand tethering mechanics can modulate force loading rates and therefore associated mechanotransducing events (17). For example, if the link between ligand and substrate cannot sustain sufficient force, cells are unable to adhere independent of the stiffness of the underlying substrate (18). Besides this extreme binary case, a range of potential force-bearing linkages can exist, which have been shown to affect force loading (19, 20, 21). Moreover, traction force-induced changes in the conformation of large ECM proteins such as fibronectin (FN) can alter receptor-ligand engagement and dynamics (22). Fourth, the often-neglected viscous/plastic component of the substrate can modulate force loading rates, affect ligand density, and influence cell response, as shown through the use of well-characterized, suitable viscoelastic substrates (23, 24, 25, 26, 27, 28, 29).

Given the above considerations, independent control over cell ligand coupling to the underlying substrate and viscoelastic properties of that substrate is desirable to uncouple the relative contribution of both parameters. Hydrogels typically present covalently linked ligands to cells because adsorption of ECM proteins or adhesive peptides onto hydrophilic interfaces is unfavorable. Although there is progress in gaining better control over immobilization chemistries (30,31), there are only a few reports on noncovalent binding of ligands on hydrogels (32, 33, 34). On the other hand, the hydrophobic nature of silicone elastomers allows for efficient adsorption of ECM proteins, and their surface can be modified to additionally enable covalent coupling, albeit with the risk of concurrent modifications in the physicochemical properties of its upper layer (35,36).

In this study, we investigated the interactions of primary fibroblasts with FN-coated substrates, which were produced with the silicone elastomer formulation CY52-276. Even though this formulation has been employed for mechanosensing studies because of a reported Young’s modulus similar to that of tissues at the lower kPa range (37, 38, 39, 40), a comprehensive characterization of its viscoelastic properties is lacking, and variation of the mechanical properties through modulation of cross-linking was not explored. In particular, previous studies have relied on characterization of bulk viscoelastic properties, often reporting a single Young’s modulus value to characterize the substrate. Here, we modulated the ratio between base polymer and curing agent, producing substrates that exhibited frequency-dependent viscoelasticity, spanning a physiologically relevant range of mechanical properties. Furthermore, differences in surface mechanics were explored, revealing the critical role of solid surface tension and its effects on cell adhesion. The possibility of non-covalent FN functionalization of silicone elastomers allowed us to address how potential ECM protein remodeling in conjunction with substrate viscoelasticity affect cell adhesion and polarization. The focus was placed on FN because of the paramount importance of its presence and remodeling in guiding cell behavior during physiological and pathological processes in vivo (41, 42, 43). Our findings shed light on the mechanisms that cells utilize to probe substrate mechanics and indicate that there are two relevant length and timescales that govern focal adhesion (FA) maturation and cell polarization.

Methods

Reagents

A complete list of the commercially available chemicals and antibodies used in this study are presented in Tables S1 and S2, respectively. Fluorescent FN (FFN) was prepared using bovine plasma FN (Life Technologies, Carlsbad, CA) and an Alexa Fluor 488 labeling kit (Cat. A10235; Thermo Fisher Scientific, Waltham, MA), according to the instructions provided.

Elastomer substrates

The silicone-based, two-component elastomer formulation CY52-276 from Dow Corning (Midland, MI) was used to prepare elastomers of varying mechanical properties by changing the weight ratio, ζ (A/B), of its two components. Components A (base) and B (catalyst) were mixed by vigorous magnetic stirring in glass vials for 5 min and degassed in vacuum for 2 min, and the mixture was then applied, or spin-coated, onto different underlying substrates. The elastomer was cured for 3 h at 65–70°C and then stored at room temperature until use. Elastomer substrates were used within 6 months.

FN was coated on elastomers through overnight incubation with freshly prepared phosphate-buffered saline (PBS) solutions at 4°C. To cross-link FN, FN-coated substrates were treated with 4% paraformaldehyde (PFA) in PBS for 15 min at room temperature. Substrates were washed three times with PBS and incubated with 1% bovine serum albumin (BSA) in PBS for 30 min at room temperature. Relative coating efficiencies were calculated through a modified enzyme-linked immunosorbent assay (ELISA). Briefly, FN-coated substrates were incubated with 0.1 μg/mL of antibodies against FN for 1 h at room temperature, followed by washing with PBS and incubation with secondary antibodies coupled to horseradish peroxidase (0.16 μg/mL) for 1 h at room temperature. Wells were washed with PBS, and secondary antibodies were detected using a 3,3′,5,5′-tetramethylbenzidine substrate (Sigma, St. Louis, MO) and absorbance measurements at 630 nm.

Immobilization of fluorescent nanoparticles (200 nm red carboxylate-modified FluoSpheres) on the elastomer surface was adapted from a previous study (44) and was performed as follows: elastomers were treated for 1 h at room temperature with (3-aminopropyl)triethoxysilane in ethanol (10% v/v) and a drop of triethylamine. Elastomers were then washed once with ethanol and twice with water and incubated with an aqueous suspension of 8.2 × 10¹⁰ fluorescent nanoparticles and 1 mg/mL N-(3-Dimethylaminopropyl)-N'-ethylcarbodiimide hydrochloride (EDC) for 1 h at room temperature. Elastomers were then washed with water and PBS before being incubated with FN as detailed above.

To determine the sol fraction of the elastomers, preweighed samples (W_bef) formed on glass coverslips were incubated for 24 h in n-hexane, washed with n-hexane, and dried overnight and then for 1 h under vacuum before measuring their final weight (W_gel). The weight of the sol fraction (W_sol) was calculated as W_sol = W_bef − W_gel and the sol fraction as $\left(W_{sol}/W_{bef}\right)$.

Rheometry

All rheometry measurements were performed on a Malvern Kinexus rheometer (Malvern Panalytical, Malvern, UK) with parallel plate geometry and a temperature-controlled chamber. Temperature was controlled with an accuracy of 0.1°C. Elastomer components were mixed and degassed at room temperature as described above, and ∼250 μL was applied on the bottom plate. The upper plate was then lowered until the sample filled the gap between plates (gap size 500–1000 mm). Initially, a kinetic study was performed after heating the elastomer to 70°C and monitoring the storage modulus $G^{\prime }$ (elastic modulus) and loss modulus $G^{″}$ (viscous modulus) in oscillatory mode for 3 h. The temperature was then equilibrated at 25°C, and a series of measurements in oscillatory mode were performed as follows: 1) a frequency sweep (0.01–10 Hz), 2) a strain sweep (0.2–20%), and 3) creep measurements under different applied shear stress. All experiments were performed for at least three different batches.

Atomic force microscopy

Silicone elastomers were characterized by indentation measurements using a NanoWizard III atomic force microscopy (AFM) (JPK Instruments, Berlin, Germany). Cantilevers with a spherical, borosilicate glass probe (sQube) of 5 μm in diameter were used. Cantilever spring constants were determined using the thermal noise calibration method and ranged between 0.45 and 0.60 N/m. Young’s moduli were derived by fitting force-distance (F-d) curves with a Hertz model or a modified version of that model using a processing script written in Python (source code available upon demand) as described below.

F-d curves were derived correcting the Z-piezo positions with the deflection of the curves. Background force was subtracted fitting a straight line to the end part of the curve. Contact point was first estimated taking the SD (σ) of the end 10% of the curve and estimating where the curve was first lower than −σ.

The Hertz model of a spherical indenter, $F\left(\delta \right)=\frac{4}{3}\frac{E}{1-{\nu }^2}\sqrt{R}{\left(\delta -{\delta }_0\right)}^{3/2}$, where δ > 0 and =0 everywhere else, was fitted to all values below a user-specified maximal force using a nonlinear least-squares method (least-squares method from SciPy, based on the Levenberg-Marquardt algorithm) to optimize $A=\frac{4}{3}\frac{E}{1-{\nu }^2}\sqrt{R}$ and δ₀, where E stands for Young’s modulus, ν for the Poisson’s ratio of the sample, R for the radius of the indenting sphere, δ for the indentation depth, and δ₀ for its zero position. In the case considering the surface tension of the sample, the equation was modified to $F\left(\delta \right)=\frac{4}{3}\frac{E}{1-{\nu }^2}\sqrt{R}{\left(\delta -{\delta }_0\right)}^2+2\pi \text{Γ}\left(\delta -{\delta }_0\right)$. Here, it was possible to fit for B = 2πΓ as well or specify it as an a priori known constant.

For inducing surface deformations of silicone elastomers, a stiff cantilever (nominal value of k = 21–98 N/m; PPP-NCLR from NANOSENSORS, Neuchatel, Switzerland) was used. The elastomer was indented using a conical tip and either the piezo element or by manually lowering the AFM head. Next, while in contact with the surface, the cantilever was laterally moved before being retracted >50 μm above the substrate. Fluorescence images of the elastomer surface were acquired every 1 s.

Cell culture

Primary human dermal fibroblasts (pHDF) were purchased from American Type Culture Collection (ATCC; Manassas, VA) and cultured as subconfluent monolayers at 37°C and 5% CO₂ in Dulbecco’s modified Eagle’s medium (Life Technologies), supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin. pHDF cultures were used until passage 15 and checked monthly for the absence of mycoplasma.

Cell adhesion assays

The efficiency of cell adhesion was evaluated 30 min after seeding on coated substrates inside a 96-well plate. Trypsinized cells were kept in suspension under ice for 10 min before addition to wells (100 μL of 1 × 10⁵ cells/mL corresponding to 3.1 × 10⁴ cells/cm²). After 30 min, wells were washed twice with ice-cold PBS, the solution was aspirated, and plates were placed at −80°C overnight. Relative cell numbers were quantified using the CyQUANT Cell Proliferation Assay kit (Thermo Fisher Scientific). Of note, the sample solution above the substrates was moved to a new 96-well plate for fluorescence measurements to avoid interference from the elastomer substrate.

Microscopy

Immunofluorescence microscopy was performed on cells fixed with 4% PFA in PBS for 15 min at room temperature. Membranes were permeabilized by incubating with Triton X-100 (0.1%) for 5 min, followed by blocking with 1% BSA in PBS. Primary antibodies (diluted 1:100 in 1% BSA) were incubated for 1 h at room temperature or overnight at 4°C. Cells were washed and incubated with secondary Alexa Fluor-labeled antibodies (Life Technologies; diluted 1:150 in 1% BSA) for 1 h at room temperature. 4′,6-Diamidino-2-phenylindole and tetramethylrhodamine phalloidin were used to stain nuclei and filamentous actin (F-actin). Images were acquired on a ZEISS LSM 880 laser scanning confocal microscope using a 63×/1.4 NA oil-immersion objective (ZEISS, Oberkochen, Germany) or a 20×/0.8 NA objective (ZEISS).

Live-cell, time-lapse microscopy on fluorescently labeled FN (FFN)-coated substrates or substrates with immobilized fluorescent beads was performed on a ZEISS LSM 880 confocal microscope or a Leica DMi8 microscope (Leica Microsystems, Wetzlar, Germany). For live-cell imaging, CO₂-independent medium (Cat 18045054; Thermo Fisher Scientific) supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin was used.

Fluorescence recovery after photobleaching analysis was performed using FFN-coated elastomers in PBS solutions on a Leica DMi8 microscope equipped with a 488-nm laser source and a 40×, NA = 0.60 objective. A predefined spot of ∼100 μm² was bleached (within <1 s), and the recovery was monitored over a period of 2 h at 1-min intervals or 10 h at 5-min intervals. Microscopy images were analyzed using ImageJ; the mean fluorescence intensity of the bleached region was measured, corrected for photobleaching due to imaging, and normalized.

Elastomer deformation

To measure cell-induced substrate deformations, elastomers with immobilized fluorescent nanoparticles were employed. Substrates were first equilibrated at 37°C in the environmental stage of a ZEISS LSM 880 laser scanning confocal microscope in the presence of CO₂-independent medium. A small volume of pHDF were subsequently added to obtain a cell density of 5 × 10³ cells/cm², and imaging was immediately set off. Hence, the first image was the reference state of the elastomer. Images were acquired using a water immersion 40× objective (ZEISS, NA = 1.20) at different time points after cell addition. To map substrate deformations, stacks of images before and after cell addition were first aligned using the StackReg plugin of ImageJ (http://bigwww.epfl.ch/thevenaz/stackreg/), followed by particle image velocimetry (PIV) analysis performed using the PIV plugin (https://sites.google.com/site/qingzongtseng/piv). Vector maps were further analyzed as follows: the map data was imported into a Python script (available upon demand) and converted to an image of strain field. This image was converted to a binary using a threshold of 20% of the maximal displacement, and individual patches were identified. This was necessary to handle cases in which more than one cell was present on the image.

The center of each patch was estimated using a weighted mean, and the points were converted to polar coordinates around this center. A radial displacement was calculated by binning the distances to a predefined set of radii (0-R_max pixels with single pixel steps) and calculating their averages and SDs. A linearized exponential fit was performed between the maximum and the first local minimum (if existed) behind it to estimate the decay of the profile.

Image analysis

Cell projected area and aspect ratio, defined as the ratio of the major to the minor axis of a fitted ellipse, were determined through image analysis of single phalloidin-stained cells using the “Cell Outliner” plugin of ImageJ. FA area was determined using a custom-written macro in ImageJ, as previously described (45). An area threshold of 0.4 μm² was set to exclude small focal complexes and noise.

Results

Bulk viscoelastic properties of ultrasoft elastomers

The viscoelastic properties of the silicone elastomer formulation CY52-276 were controlled by the weight ratio (ζ) between the base (component A) and the cross-linker (component B). Lower and higher ratios, compared with the recommended ζ = B/A = 1.0, were prepared to obtain “softer” and “stiffer” substrates, respectively. Reducing ζ below 0.7 resulted in a predominantly viscous, tacky, and difficult to handle material; therefore, the elastomer with ζ = 0.7 was the softest formulation examined. Modulation of mechanical properties and the elastic character of the elastomers were evident by visual inspection after poking with a pipette tip (Video S1). Silicone elastomers formed readily on multiple substrates, including glass or tissue culture polystyrene (TCPS), and their thickness could be controlled from tens to hundreds of micrometers by regulating the rotational speed during spin coating (Fig. S1 A). Elastomers thicker than 100 μm were used for all cell experiments to avoid the influence of the underlying, rigid support (46).

Video S9. Live-Cell, Time-Lapse Fluorescence Confocal Microscopy of pHDF Spreading on Fibronectin-Coated Elastomers (ζ = 1.0) with Immobilized Fluorescent Particles

The first frame (t=0) was acquired a few minutes after cell seeding. Scale bar: 20 μm.

Oscillatory rheology was used to monitor bulk elastomer properties (Fig. 1). The two elastomer components were thoroughly mixed and degassed to remove entrapped air before application between two parallel plates of the rheometer. The temperature was then set at 65°C, and the cross-linking kinetics were monitored over time at a frequency of 1 Hz and 5% strain. The shear storage and loss moduli increased rapidly the first few minutes and reached a plateau within the first 3 h (Fig. S1 B). All subsequent samples were prepared by heating elastomers at 65°C in an oven for 3 h.

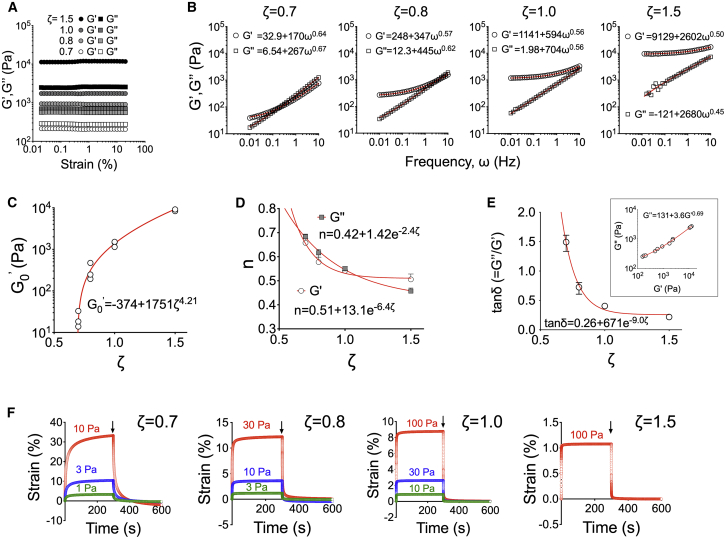
Figure 1.

Control over bulk viscoelasticity of silicone elastomers through the ratio of base polymer to cross-linker. (A) Storage ($G^{\prime }$) and loss $\left(G^{″}\right)$ moduli were measured at a frequency of 1 Hz are independent of strain in the linear viscoelastic regime. (B) $G^{\prime }$and $G^{″}$ as a function of frequency for different ζ ratios. (C) Extrapolated values of storage modulus for zero frequency ($G_0^{\prime }$) as a function of ζ. Data from N = 3 independent experiments are shown. (D) Dependence of exponent n (from $G^{\prime }$,$G^{″}$ = a + bωⁿ) on ratio ζ. Average values and range from N = 3. (E) Dependence of dissipation factor on ratio ζ (average values and range from N = 3); inset shows the relationship between $G^{\prime }$ and$G^{″}$ for data obtained from all elastomers and ζ ratios.$G^{\prime }$ and$G^{″}$ presented were obtained from measurements at 1 Hz frequency and 1% strain. (F) Creep experiments for elastomers with different ζ values and different imposed stresses (indicated on the graphs). For the stiffest elastomers (ζ = 1.5), applied stresses of 10 and 30 Pa did not produce measurable strains; therefore, only the maximal applied stress is presented. After stress removal (arrows), the elastomers relax to their original positions, indicating lack of bulk plastic deformations. To see this figure in color, go online.

Elastomers exhibited a linear viscoelastic regime in the range of 0.1–10% strain (Fig. 1 A). The frequency-dependent storage $\left(G^{\prime }\right)$ and loss $\left(G^{″}\right)$ moduli followed a power law behavior ($G^{\prime }$,$G^{″}\sim {\omega }^n)$, with the storage modulus approaching a plateau at the low frequency limit $\left(G_0^{\prime }\right)$, typical for cross-linked elastomers (Fig. 1 B; (47)). Plotting $G_0^{\prime }$ as a function of ζ revealed the dependence of equilibrium elasticity as a function of ζ, confirming that ζ = 0.7 is the lower limit for producing viscoelastic solids (Fig. 1 C). The obtained value of 3.4 kPa for ζ = 1 is very close to the one previously reported (48). The exponent n for both $G^{\prime }$ and $G^{″}$ decreased with ζ, reflecting the changes in cross-linking density (Fig. 1 D; (47)). Importantly, the loss modulus was comparable to the storage modulus for low ζ, with the dissipation factor tanδ = $G^{″}$/$G^{\prime }$ reaching values >1 at 1% strain and ω = 1 Hz and decreasing to a plateau value of ∼0.25 as ζ increased (Fig. 1 E). The high viscous component of the elastomers raised concerns over potential plastic deformations of the material. However, despite a significant creep behavior for the softer elastomers, there was no evidence of plastic elastomer deformation for strains up to 30% (Fig. 1 F). These data indicate complete connectivity of the polymer network at the macroscale.

Silicone elastomers are solvent-free but may contain an important number of non-cross-linked polymer chains or low molecular weight oligomers, especially as the ratio of cross-linker (ζ) decreases. Indeed, the sol fraction of elastomers increased as ζ decreased with values of 0.37, 0.52, 0.67 and 0.71 for ζ = 1.5, 1.0, 0.8, and 0.7, respectively (mean of two independent experiments; n = 3/experiment).

Overall, control over elastomer mechanical properties was feasible through adjustment of the ratio of cross-linker to base polymer ζ. Despite their important viscous component and high sol fractions, soft elastomers did not exhibit bulk viscoplasticity. Given the large frequency dependence in moduli, we have opted to avoid the use of nominal stiffness values for the rest of the article; instead, we will express our results as a function of ζ, referring to elastomers with low (0.7–0.8) or high (1.0–1.5) ζ as “soft” and “stiff” substrates, respectively.

Solid surface tension contributes to surface mechanical properties

The surface mechanical properties of silicone elastomers were characterized by an additional technique: indentation measurements using micron-sized colloidal probes and AFM. Initial attempts using spherical glass indenters, even when coated with inert BSA, on untreated elastomers were unsuccessful because of the very high adhesion forces observed between tip and elastomer (48,49). Measurements performed in ethanol revealed large adhesion forces and a jump to contact, rendering analysis using standard models problematic (Fig. S2 A). Considering that the targeted application of these materials as cell substrates entails their coating with cell-adhesive ECM proteins, we opted to perform the AFM characterization on BSA-coated elastomers, which effectively eliminated nonspecific adhesion and thus allowed for AFM indentation measurements. Of note, we avoided plasma or ultraviolet treatment to render the elastomer surface hydrophilic through oxidation because such treatments can result in the creation of thin, brittle oxide films exhibiting much higher stiffness compared to the bulk (50,51).

F-d curves from indentation on BSA-coated elastomers were initially fitted using the classical Hertz model. The apparent Young’s modulus (E) of elastomers increased with ζ, for a fixed indentation force of 10 nN and an indentation speed of 1 μm/s, as expected (Fig. 2 A). Consistent with the viscoelastic character of the elastomers (Fig. 1), a decrease in indentation speed resulted in lower Young’s moduli that approached a plateau value (Fig. 2 B). Accordingly, hysteresis was evident, even at an indentation speed of 0.1 μm/s, which was the lowest studied as a compromise between experimental time and simulation of equilibrium conditions (Fig. S2, B and C). Analysis of the F-d curves up to different indentation forces resulted in an apparent Young’s modulus as a function of indentation depth. Interestingly, the calculated modulus increased with decreasing indentation for low values of ζ, whereas the dependence was lost, and in some experiments inversed, at higher ζ values (Fig. 2 C).

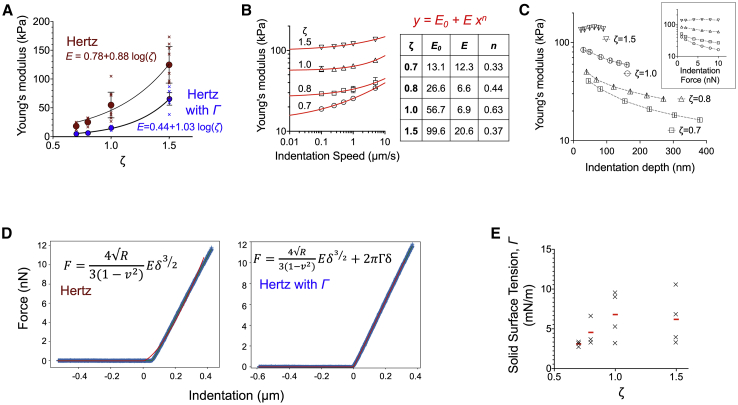
Figure 2.

The surface layer of silicone elastomers exhibits higher apparent stiffness because of solid surface tension. (A) Apparent Young’s moduli were determined by fitting F-d curves from AFM indentation measurements with the standard Hertz model (red data points) or a modified Hertz model that includes a linear term for the solid surface tension (blue data points). An indentation speed of 1 μm/s and a setpoint force of 10 nN were used for the measurements. The x marks indicate independent experiments, and the circles mean values and error bars SEM. (B) Apparent Young’s moduli were determined with the standard Hertz model as a function of indentation speed for elastomers of varying ζ. Data represent the average and error bars the SD from 75 measurements at different locations of the elastomers (one of two independent experiments shown). Data were fitted with a power law equation, with the fitted parameters given in the table. (C) Apparent Young’s moduli were determined with the standard Hertz model as a function of indentation depth for elastomers of varying ζ. The inset shows the data as a function of setpoint force. Data represent the average and error bars the SD from 75 measurements (one of two independent experiments shown). (D) A typical F-d curve derived from indentation of an elastomer with ζ = 0.7 along with best fits for the standard Hertz model and a modified Hertz model that includes a linear surface tension term. (E) Solid surface tension of silicone elastomers were derived from the modified Hertz model. The x symbols indicate independent experiments and the column the average value. To see this figure in color, go online.

E values from the indentation experiments were higher compared with those obtained with rheology assuming a Poisson’s ratio of 0.495 (48), with differences being more pronounced for the softer elastomers (Fig. S2 D). A close look of the Hertz model fits of the F-d curves for elastomers with ζ = 0.7 showed important deviation from the experimental data (Fig. 2 D). We reasoned that this could be because of an important contribution of solid surface tension (Γ) of soft silicone elastomers, as previously reported (48,52). When analyzed using a modified Hertz model that incorporates a linear surface tension term (see details in Methods), the fit quality for the F-d curves was greatly improved, especially for elastomers with the lower ζ values (Fig. 2 D), consistent with the expected larger contribution of surface tension for the softer substrates. The calculated values for Γ range between 3 and 10 mN/m, in agreement with previous reports (Fig. 2 E; (48)). In some cases, the variation in E was large when Γ was left as a fitted parameter; we therefore set as fixed value for Γ the mean calculated value to obtain less scattering (Fig. S2 E). Using the modified Hertz model, the values of E calculated from three different batches were lower and closer to those obtained by rheology (Fig. 2 A). Taken together, our results suggest that surface tension contributes significantly to indentation forces of soft elastomers and raise the question of how the apparent higher surface stiffness affects cell behavior in combination with bulk viscoelasticity.

FN functionalization of elastomers

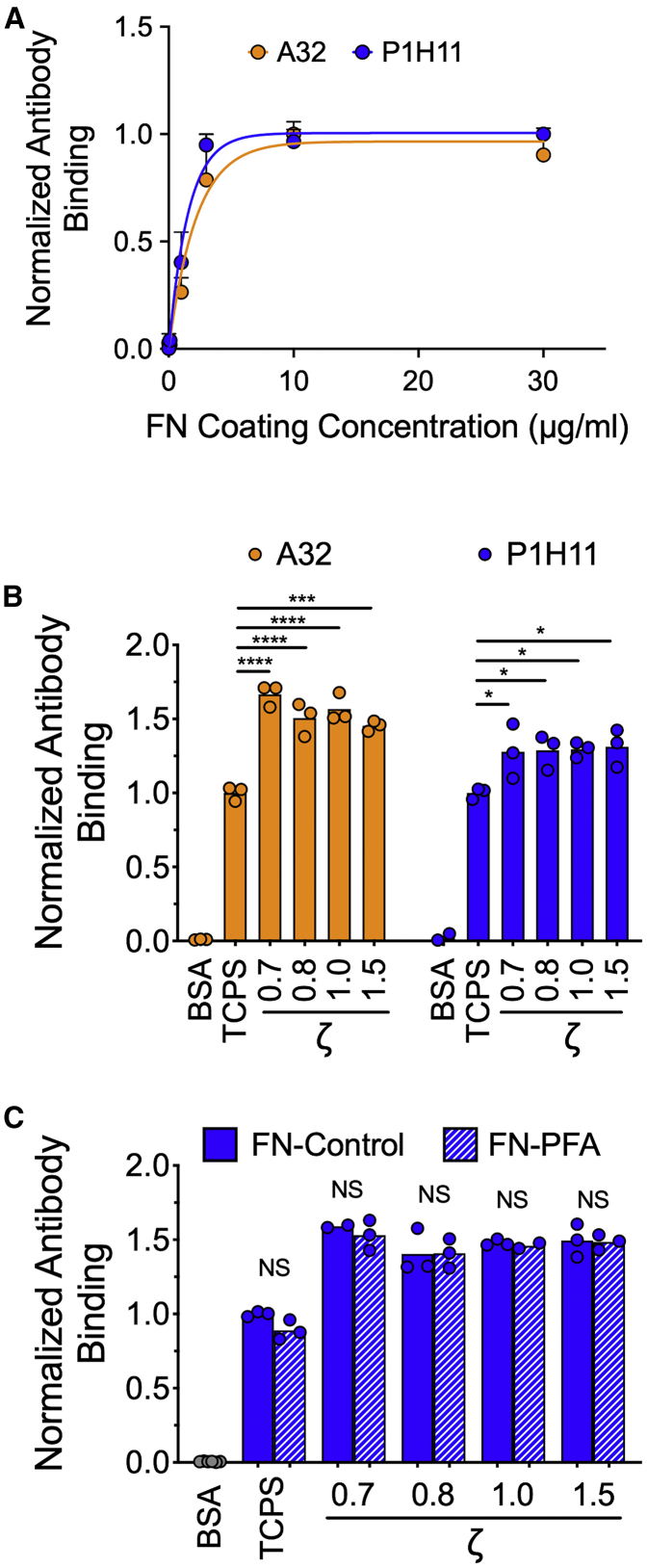
The hydrophobic character of the elastomers allowed coating through simple adsorption of FN from solution. The remaining area between FN was blocked with albumin. The amount of adsorbed FN reached a plateau above coating concentrations of ∼5 μg/mL, as measured using a modified ELISA (Fig. 3 A). The number of adsorbed FN molecules was similar between elastomers of differing ζ ratio (Fig. 3 B), an important prerequisite to attribute changes in cell behavior to substrate mechanical properties. Interestingly, accessibility to the C-terminal heparin II binding and central cell binding domains was higher for FN immobilized on elastomers compared with TCPS, indicating higher binding affinity and/or altered conformation, favoring interactions with cells (Fig. 3 B). At the resolution of optical microscopy, FFN formed a homogeneous coating, with no apparent assembly of fibrils or aggregation (Fig. S3 A). The ability of cells to remodel FN depends on the adhesion strength of FN to its underlying substrate, as well as the physical state of FN (53,54). To alter the latter, FN-coated elastomers were treated with the fixation agent PFA. PFA treatment did not alter the amount of adsorbed FN (Fig. 3 C), as previously shown (54). Taken together, these data show the feasibility of preparing FN-coated elastomers of varying mechanical properties but similar biochemical properties.

Figure 3.

Fibronectin coats elastomers of different mechanical properties with similar efficiency. (A) Coating efficiency of adsorbed FN on untreated silicone elastomers (ζ = 1.0) from FN solutions of different concentrations. FN was detected by a modified ELISA using two different monoclonal anti-FN antibodies; clone P1H11 recognizes the central cell binding domain and clone A32 the heparin II binding domain. Data from two independent experiments are presented; three replicates were measured in each experiment. Lines represent fits of the equation y = A(1 − e^−kx). (B) Coating efficiency from a 10 μg/mL FN solution on untreated silicone elastomers of varying ζ, TCPS, and BSA-coated TCPS. FN adsorption to the substrate was similar on elastomers of different mechanical properties and higher compared to TCPS. Data from one (of two) independent experiment are presented; each data point represents one measurement and the column the mean value. Mean values for elastomers were compared to the control TCPS surface using one-way ANOVA: ^∗p < 0.05, ^∗∗∗p < 0.001, and ^∗∗∗∗p < 0.0001. (C) Coating efficiency from a 10 μg/mL FN solution on FN-coated substrates, untreated (control) or treated with 4% PFA to cross-link FN. Antibody (clone P1H11) binding to immobilized FN was not affected by PFA treatment. Data from one (of two) independent experiment are presented; each data point represents one measurement and the column the mean value. Mean values of PFA-treated samples were compared with controls for each substrate using an unpaired t-test: ^NSp > 0.05. To see this figure in color, go online.

Fibroblast polarization, but not spreading, depend on elastomer stiffness

We next examined how pHDF adhered on FN-coated elastomers as a function of their mechanical properties (ζ ratio) in an effort to comprehend and specify which material properties of the substrate regulate cell response. Previous work has correlated the ability of cells to spread efficiently and assemble mature focal adhesions (FAs) to substrate stiffness. However, this conclusion was drawn primarily from studies on highly elastic hydrogels (30,45,55,56), which do not exhibit the frequency dependence in elastic moduli (Fig. 1) and apparently different surface, compared with bulk, mechanical properties (Fig. 2), like the elastomers described here. Indeed, studies on viscoelastic hydrogels have demonstrated a pronounced effect of the viscous component on the aforementioned processes (23, 24, 25, 26), and work with elastomers has reported mixed results concerning the effect of substrate mechanics on cell adhesion (9,10,12,57), hence the need to clarify how cells respond to the well-characterized elastomers reported here.

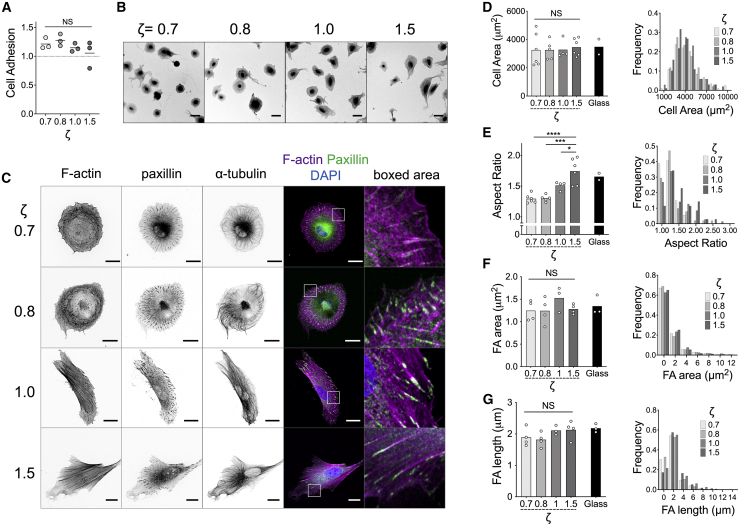
pHDF adhered with high efficiency on FN-coated elastomers, independent of their mechanical properties and similar to traditional FN-coated TCPS (Fig. 4 A). Interestingly, fibroblasts spread to the same extent on soft and stiff elastomers (Fig. 4, B–D), whereas their aspect ratio, which reflects cell polarization, increased with ζ (Fig. 4, B and E). Indeed, high-resolution imaging of the actin cytoskeleton confirmed that on the softer elastomers (ζ = 0.7, 0.8), fibroblasts remained round, with F-actin assembled primarily in contractile transverse arcs and dorsal stress fibers (58), whereas on the stiffer elastomers (ζ = 1.0, 1.5), pronounced, oriented ventral stress fibers were visible (Fig. 4 C). Similarly, the microtubule network was polarized only on the stiffer elastomers (Fig. 4 C). FA morphology was evaluated by immunofluorescence microscopy of paxillin (Fig. 4 C). Fibroblasts assembled large, elongated FAs on all elastomers, independent of ζ, and similar to those assembled on rigid, FN-coated glass (Fig. 4, F and G).

Figure 4.

Elastomer mechanics regulate fibroblast polarization but not spreading area or FA size. (A) Adhesion of pHDF on FN-coated elastomers, normalized to their adhesion on FN-coated TCPS, as a function of ζ. Each data point corresponds to an independent experiment with n = 3. Data were compared using one-way ANOVA: ^NSp > 0.05. (B) Confocal microscopy images of fixed pHDF seeded on FN-coated elastomers for 4 h and stained against F-actin using fluorescent phalloidin to highlight overall cell morphology. Scale bars, 50 μm. (C) High-magnification confocal microscopy images of fixed and immunostained pHDF seeded on FN-coated elastomer for 4 h. Scale bars, 20 μm. (D–G) Column plots (left) showing the average values of cell area (D), aspect ratio (E), FA area (F), and FA length (G) of pHDF seeded on FN-coated elastomers as a function of ζ. Each data point corresponds to the mean value of an independent experiment. Histograms (right) show the relative distribution of values of one such independent experiment. FN-coated glass was used as a control. Mean values for the different elastomers in (D–G) were compared using one-way ANOVA: ^∗p < 0.05; ^∗∗∗p < 0.001; ^∗∗∗∗p < 0.0001, and ^NSp > 0.05. To see this figure in color, go online.

In sum, the viscoelastic properties of elastomers in the studied range did not affect the extent of FA and cell spread area, whereas elevated stiffness was required for fibroblast polarization. These findings suggest that either a different force threshold exists for different cellular processes or that cells employ different mechanisms to mechanosense and respond depending on the length scale and process (FA assembly versus polarization) involved.

Fibroblasts do not remodel adsorbed FN on elastomers

In order for fibroblasts to sense the bulk substrate viscoelasticity, a sufficiently strong mechanical link between the adsorbed FN and the underlying elastomers must exist, so that FN is not simply removed from the surface. Fibroblasts can assemble FN physically adsorbed on glass and other hydrophilic substrates into fibers, in a process that depends on the substrate physicochemical properties (53,59), raising the possibility that cell-generated forces could also result in FN unfolding and/or remodeling on elastomers. pHDF seeded on glass coated with FFN extensively remodeled FN, as expected (Fig. S3 B); FFN was assembled into fibrils, and some of it was internalized by cells (Fig. S3, B and C; Video S2). FFN fibrillogenesis was largely inhibited after treatment of FFN with PFA (Fig. S3 B).

Video S10. Live-Cell, Time-Lapse Fluorescence Confocal Microscopy of pHDF Spreading on Fibronectin-Coated Elastomers (ζ = 0.7) with Immobilized Fluorescent Particles, Along with the Displacement Fields Calculated from the PIV Analysis

The first frame (t=0) was acquired a few minutes after cell seeding. Scale bar: 20 μm.

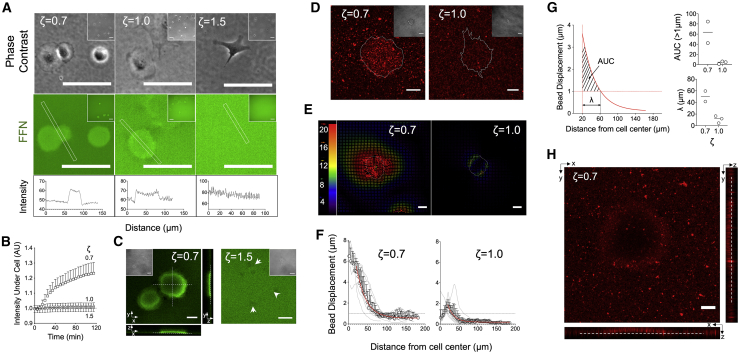
On elastomers, there was surprisingly no visual evidence of FFN fibrillogenesis or uptake as monitored by live-cell, epifluorescence microscopy. On the softer elastomers (ζ = 0.7), a striking accumulation of FFN under spreading cells with darker areas around the cell periphery was observed (Fig. 5 A; Video S3). On the stiffer elastomers, this effect was attenuated (ζ = 1.0) or not observed (ζ = 1.5) (Fig. 5 A; Videos S4 and S5). The change in fluorescence intensity under cells was quantified as a function of time after cell seeding and confirmed the substrate dependence of FFN buildup caused by the cells (Fig. 5 B). Live-cell confocal microscopy of FFN at the surface plane of the softer elastomers (ζ = 0.7) sometimes displayed dark areas under the cell body (Video S6). Confocal z-stacks showed that FFN was at a lower imaging plane, indicating that fibroblasts were markedly deforming elastomers, forming a crater-like structure (Fig. 5 C). On the stiffer elastomers (ζ = 1.5), deformations of the homogeneous FFN coating were hardly visible (Fig. 5 C). Fibroblasts were unable to assemble fibrils using the adsorbed FFN coating (Fig. 5, A and C). However, they were still able to assemble fibrils of endogenously expressed FN, demonstrating their capacity to exert the necessary forces for fibrillogenesis (Fig. S4). The above results demonstrate that cell-generated forces did not lead to fibrillogenesis of adsorbed FN on elastomers and suggest instead that they were transmitted through the adhesive coating to the underlying substrate. These forces induced surface deformations depending on elastomer viscoelasticity, with the softer and more viscous substrates exhibiting FN accumulation under cells over time.

Figure 5.

Fibroblast traction forces lead to substrate deformations but not fibronectin fibril assembly. (A) Epifluorescence and phase contrast images of live pHDF seeded for 3 h on elastomers coated with fluorescently labeled FN (FFN). The intensity of FFN increased under the cell body on the softer (ζ = 0.7) elastomers. (B) Normalized FFN fluorescence intensity under the cell body normalized against background FFN intensity. Mean and SD from two independent experiments are presented (n = 10). (C) Confocal microscopy images of live pHDF seeded on FFN-coated elastomers. On the softer elastomers (ζ = 0.7), surface out-of-plane deformations were observed. Dashed lines and arrows are visual aids. (D) Confocal microscopy images of live pHDF seeded for 2 h on elastomers with immobilized fluorescent beads and coated with FN. (E) Particle image velocimetry (PIV) analysis from bead displacements on elastomers seeded with pHDF for 1 h was used to produce substrate deformation fields. The magnitude of the color-coded vectors is given in pixels, and the white line denotes the cell outline. (F) Bead displacements (deformations) as a function of distance from the cell center was calculated as detailed in the Methods for each cell (gray lines) and averaged (circles with SD). The data (mean ± SD, n = 9 for ζ = 0.7, and n = 14 for ζ = 1.0) were fitted using an exponential decay function (red line) starting from a distance of 20 μm, which corresponds to the typical cell radius. One of two independent experiments is presented. (G) Quantification of two parameters reflecting total substrate deformation and the deformation boundary from the cell edge based on the fitted curves from (F). A threshold value of 1 μm for the deformation vectors was selected to calculate the distance from the cell edge at which deformations drop below the threshold and the area under the fitted curve (AUC) correlating with total substrate deformation. Both the boundary distance and AUC were lower for the stiffer elastomers. Each data point corresponds to an independent experiment and the line the mean. (H) Confocal microscopy image of beads immobilized on a soft elastomer (ζ = 0.7), which is being deformed by a living cell. Orthogonal views are presented to better visualize the crater-like structure formed. Scale bars, 50 μm for (A) and 20 μm for (C, D, E, and H). To see this figure in color, go online.

Video S11. Live-Cell, Time-Lapse Fluorescence Confocal Microscopy of pHDF Spreading on Fibronectin-Coated Elastomers (ζ = 1.0) with Immobilized Fluorescent Particles, Along with the Displacement Fields Calculated from the PIV Analysis

The first frame (t=0) was acquired a few minutes after cell seeding. Scale bar: 20 μm.

Video S12. Time-Lapse Imaging of Fluorescent Particles Immobilized on the Surface of a Soft (ζ = 0.7) Elastomer during AFM-Induced Deformations

A stiff cantilever with a conical tip was manually lowered on the surface of the elastomer and laterally moved to a new position to deform the substrate. After 5 seconds, the cantilever was retracted and the position of beads monitored over time. Scale bar: 20 μm.

Video S1. Poking Silicone Elastomers with a Metal Spatula at 2× Actual Speed

The softer elastomer (ζ=0.7) is sticky and highly deformable, yet elastic, recovering back to its original position after loss of adhesion with the spatula. The stiffer elastomer (ζ=1.5) on the other hand, does not show considerable adhesion.

Video S2. Live-Cell, Time-Lapse, Fluorescence Confocal Microscopy of pHDF Remodeling FFN-Coated Glass Substrates

The first frame (t=0) was acquired 1hour after seeding.

Large-scale deformations of soft elastomers

To confirm that FN accumulation was because of elastomer surface deformation and to examine an alternative way to visualize this process, we immobilized fluorescent beads as fiducial markers on the elastomer surface, which was then coated with FN (44). Beads accumulated rapidly under fibroblasts seeded on the softer elastomers (ζ = 0.7), similar to what was observed for labeled FN (Fig. 5 D; Video S7). Again, there was no evidence for bead removal/internalization from the substrate in any of the data sets analyzed. Time-lapse imaging during cell spreading showed bead displacements over tens of micrometers toward cells on soft elastomers (ζ = 0.7), indicating long-range deformations (Video S8). On the stiffer elastomers (ζ = 1.0), beads were pulled toward cells as a result of traction forces but exhibited much lower magnitude of deformations (Video S9). We applied a PIV algorithm to visualize and quantify substrate deformations (Videos S10 and S11); the displacement fields calculated from images before and 60 min after cell seeding were used to determine the radial deformation profile for cells on elastomers (Fig. 5, E and F). Cell-induced deformations were much larger for the softer elastomers and extended further away from the cell body (Fig. 5, E and F). Interestingly, large deformations were also calculated under the cell body for the softer elastomers, whereas they were maximal at the cell edge for the stiffer elastomers and decayed both toward the cell center and away from the cell. The decrease in substrate deformation was well fitted with an exponential decay from the cell edge, assuming an average cell radius of 20 μm (Fig. 5 F). Defining a deformation field boundary at a threshold of 1 μm displacement, we measured a boundary distance of ∼50 and 15 μm for the soft and stiff elastomers, respectively (Fig. 5 G). As a measure of total strain, we calculated the area under the fitted curve (AUC) from the cell edge till it intercepted the y = 1 line (corresponding to 1-μm displacement), which confirmed the higher deformation on the softer elastomers (Fig. 5 G). In addition, during live-cell microscopy on the softer elastomers (ζ = 0.7), out-of-plane deformations and the creation of a crater-like structure was often noted, similar to what was observed for fluorescent FN-coated elastomers (Fig. 5 H). Fixation of cells for further microscopy analysis resulted in the disappearance, or attenuation of these structures, presumably because of traction force relaxation.

Video S3. Live-Cell, Time-Lapse Epifluorescence Microscopy of pHDF Spreading on FFN-Coated Elastomers with ζ = 0.7

The first frame (t=0) was acquired immediately after cell seeding.

Video S4. Live-Cell, Time-Lapse Epifluorescence Microscopy of pHDF Spreading on FFN-Coated Elastomers with ζ = 1.0

The first frame (t=0) was acquired immediately after cell seeding.

Video S5. Live-Cell, Time-Lapse Epifluorescence Microscopy of pHDF Spreading on FFN-Coated Elastomers with ζ = 1.5

The first frame (t=0) was acquired immediately after cell seeding.

Video S6. Live-Cell, Time-Lapse Fluorescence Confocal Microscopy of pHDF Spreading on FFN-Coated Elastomers with ζ = 0.7

The first frame (t=0) was acquired immediately after cell seeding. Scale bar: 20 μm.

Video S7. Live-Cell, Time-Lapse Epifluorescence Microscopy of pHDF Spreading on Soft, Fibronectin-Coated Elastomers (ζ = 0.7) with Immobilized Fluorescent Particles

The first frame (t=0) was acquired immediately after cell seeding. Fibroblasts rapidly accumulated the particles under their body.

Video S8. Live-Cell, Time-Lapse Fluorescence Confocal Microscopy of pHDF Spreading on Soft, Fibronectin-Coated Elastomers (ζ = 0.7) with Immobilized Fluorescent Particles

The first frame (t=0) was acquired a few minutes after cell seeding. Scale bar: 20 μm.

Overall, the above results demonstrated that cells generate large strains and deformations on the surface of soft elastomers. In combination with the presence of flow-like bead movement, this raised concerns for surface mobility of the coating and the presence of plastic deformations. Fluorescence recovery after photobleaching experiments of FFN on the elastomer substrate showed the absence of fluorescence recovery over hours, indicating that FN is not mobile on the elastomer surface and moves only after application of cell-generated forces (Fig. S5).

We next examined whether cell-induced deformations were reversible upon cell death. Application of a 1% Triton X-100 aqueous solution resulted in rapid cell death; the recovery of FFN to its original homogeneous distribution before cell attachment was practically complete for cells on the stiffer elastomers but only partial on the softer ones as evidenced by the inhomogeneous staining, indicating local plastic deformations of the coating (Fig. S6 A). Accordingly, bead accumulation under cells was still evident after Triton X-100 treatment on soft (ζ = 0.7) elastomers, whereas beads recovered their initial positions on stiffer substrates (ζ = 1.0) (Fig. S6 B). Occasionally, cell death occurred from inadvertent phototoxic effects, with the same result: partial recovery of beads to their original positions on the softer elastomers, thus excluding a specific effect of Triton X-100 (Fig. S6 C). In the above cases, the cell was still present after its death and could potentially act as a cross-linker of the elastomer surface. However, even after cell detachment through treatment with trypsin and gentle pipetting, beads did not recover their original positions (Fig. S6 D).

AFM was used to artificially induce surface deformations and examine potential surface plasticity of bead- and FN-coated elastomers under more controlled conditions. To this end, soft (ζ = 0.7) elastomers were indented with a stiff cantilever, which was then moved laterally to induce surface deformation. After cantilever retraction, the position of beads was monitored over time. Surprisingly, there was no indication of plastic deformations, even when elastomers were largely deformed, and the deformed state was maintained for several minutes (Fig. S7). Observable surface creep was evident upon stress removal (Video S12).

The above results demonstrate that cells induced plastic deformations on the surface of soft elastomers at the micrometer scale, in apparent contradiction with the absence of bulk viscoplasticity (Fig. 1 F) and the lack of plastic deformations after AFM cantilever-generated stresses. Although the reasons for this discrepancy are unclear, we speculate that it can be explained when considering the length and timescales involved; the elastomer consists of connected (cross-linked) polymer chains, which provide the observed macroscopic elasticity, whereas the soluble oligomers present, as evidenced by the high sol fraction of soft elastomers, can flow between the polymer network upon prolonged stress application at the microscale and thus could irreversibly translocate.

Reduction of cell contractility allows cell polarization on soft elastomers

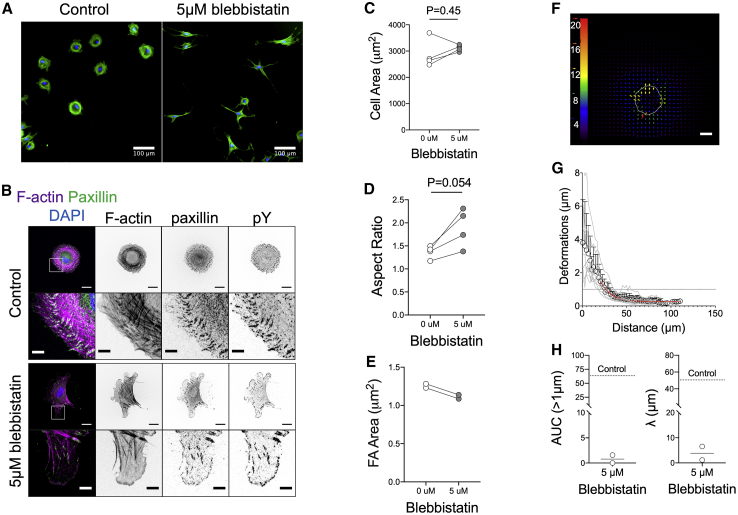
The presence of robust FAs and actin stress fibers, combined with the large induced deformations, led us to hypothesize that fibroblasts were unable to polarize on the softer elastomers because the substrate could not resist the applied traction forces. Indeed, when force generation was reduced through mild, blebbistatin-induced myosin inhibition, fibroblasts polarized on the softer elastomers, as indicated by an increase of their aspect ratio (Fig. 6, A, B, and D) and the alignment of their actin cytoskeleton (Fig. 6, A and B). Blebbistatin was used at concentrations that did not affect cell spread area (Fig. 6 C) and did not impair assembly of mature FAs or stress fibers, which polarized along the main cell axis (Fig. 6 B); nevertheless, blebbistatin-treated cells exhibited slightly smaller FAs (Fig. 6 E). As expected, blebbistatin-treated cells induced smaller elastomer deformations because of contractility inhibition. These counterintuitive findings showed that cells were able to polarize on soft elastomers when the forces transmitted to their substrate were lowered and suggest that substrate resistance to applied traction forces regulates cell polarization.

Figure 6.

Inhibition of myosin II contractility results in reduced substrate deformation and fibroblast polarization on soft elastomers. (A) Epifluorescence microscopy images of phalloidin-stained pHDF seeded for 3 h on soft elastomers (ζ = 0.7), treated with 5 μM blebbistatin or equivalent volume of carrier (DMSO). Nuclei are stained with 4′,6-diamidino-2-phenylindole (blue color). (B) Confocal microscopy images of fixed and immunostained pHDF seeded on soft, FN-coated elastomers (ζ = 0.7), treated with blebbistatin or DMSO. Scale bars, 20 μm/5 μm (details). Quantification of (C) cell area, (D) aspect ratio, and (E) FA area of pHDF cultured for 3 h on soft elastomers (ζ = 0.7), treated with 5 μM blebbistatin or equivalent volume of carrier (DMSO). Each data point represents the mean value of an independent experiment. Data in (C and D) were compared using unpaired t-tests. (F) Typical PIV analysis of bead displacements on an elastomer seeded with blebbistatin-treated pHDF for 1 h. The magnitude of the color-coded vectors is given in pixels and is the same as for Fig. 5E for comparison; the white line denotes the cell outline. Scale bar, 20 μm. (G) Deformation as a function of distance from the cell center for blebbistatin-treated pHDF cells. The data (mean ± SD, n = 8) were fitted using an exponential decay function (red line) starting from a distance of 20 μm, which corresponds to the typical cell radius. One of two independent experiments is presented. (H) Quantification of the boundary distance and AUC for the situation of blebbistatin-treated cells. Comparison with the mean value calculated for control cells (dashed line; data from Fig. 5G) shows how contractility inhibition lowers substrate deformations. To see this figure in color, go online.

Discussion

Much controversy has troubled the field of mechanosensing after conflicting results from studies comparing cell responses on hydrogel versus silicone elastomer substrates of similar bulk stiffness (9,12,57). Our data suggest that one underlying reason for these discrepancies is the lack of thorough characterization of mechanical properties, which here revealed that soft elastomers exhibit a very important viscous component, giving rise to frequency-dependent stiffness, as well as a “stiff” surface layer, which we attribute to surface tension of the functionalized elastomers. Both of these factors are likely to contribute to the observed phenotypes. Because the stiffness sensed by cells can depend on the dynamics (frequency) of stress generation, it is likely that the material will appear soft or stiff depending on how fast cells exert traction forces on it. The presence of solid surface tension giving rise to a stiff surface layer is also expected to regulate cell behavior, as evidenced by the ability of fibroblasts to spread efficiently and assemble FAs even on very compliant elastomers. This result resonates with some old and recently revisited studies, which showed that cells can be cultured even on liquid interfaces when these are stabilized with stiff protein films, despite the lack of an elastic character of the underlying oil (60,61).

Our results argue against the direct comparison between findings obtained from cell mechanosensing studies on dissimilar materials based on single bulk stiffness values alone and call for a thorough, comprehensive characterization of rubber materials, given the large number of developed silicone elastomer formulations (47,62, 63, 64), including preformed, commercial substrates with nominal elasticities (e.g., www.softsubstrates.com). Notably, our findings demonstrated that different elastomer mechanical properties are derived depending on the technique used, supporting conclusions from previous studies (13,62,65) and highlighting the need for multiple dynamic measurements. Ideally, independent control over the elastomer viscous and elastic components would isolate and inform on the effect of viscous dissipation on cell behavior. Recent advances on hydrogel preparation achieved such control and revealed a pronounced effect on cell spreading, but did not report on cell polarization (23,24).

An often used and widely accepted measure of cell mechanosensitivity is the ability of cells to regulate the extent of spreading and assembly of integrin-based FAs. Nevertheless, some findings argue that this measure is inadequate. First, these two processes can be decoupled with cells spreading over large areas with small adhesions (24). Second, large traction forces are not necessary for assembly of mature FAs (15), and adhesion size does not always correlate with exerted tractions (66). In our study, fibroblasts exhibited similar spreading and FA assembly, independent of mechanical properties. Previously, studies have reported both an independence of cell area on substrate elasticity (9,10) and a decrease in cell area on softer elastomers (57). Moreover, a decrease in FA area was noted for “softer” elastomers in one study (10). Important differences in the exact material formulation and corresponding mechanical properties can explain the above discrepancies; for example, in the aforementioned study (10), a different formulation (Sylgard 184) cross-linked at a very low ratio (1:75) of its components, with a nominal value of 5 kPa was considered the soft material, and the FA area was compared to a 2 MPa substrate, which is >1 order of magnitude higher than the range studied here.

In contrast to spread area, important differences in cytoskeletal and cell polarization were observed as a function of elastomer viscoelasticity (Fig. 4). We argue that the inability of cells to break their original symmetry and randomly polarize on the softer elastomers was because these substrates could not resist the overall applied cell tractions exerted on the material through the tightly coupled FN coating. Instead, the material flowed toward the cell and exhibited out-of-plane deformations. The magnitude of traction forces was not directly measured in this study because of the challenges associated with the highly viscous nature of the material and observed surface viscoplasticity. Future developments toward this direction or the use of molecular force probes (67) should provide a quantitative picture of the forces involved. Nevertheless, the presence of stress fibers, large FAs, and endogenous FN fibrillization indicated that sufficient forces for their assembly were generated, in contrast to what was observed on fluid, supported lipid bilayers (68,69). Indeed, mild reduction of myosin II activity enabled cells to polarize even on the softest materials, which in this case resisted the attenuated applied forces. This is in contrast to the reported effects of contractility inhibition on elastic hydrogels, in which less contractile cells gain the ability to assemble focal adhesions and proliferate faster on soft hydrogels (55,70). We thus propose that cell polarization on soft, deformable materials depends on the ability of the substrate to counterbalance applied traction forces and thus provide sufficient friction to align actin stress fibers and form a force dipole at the cell scale along a predominant orientation (71). In other words, it is not the absolute mechanical properties of the substrate that determine polarization but the force balance between the cell and the substrate.

We propose that the overall behavior of fibroblasts on elastomers can be explained by considering two different processes of mechanosensing that differ substantially in length and time scale: 1) the maturation of FAs at the subcellular scale through recruitment of integrins and associated adhesome proteins and 2) the cell polarization through cell-scale traction force generation. We suggest that the first process occurs through local changes brought about by rapid force loading on individual integrins and adaptor proteins, such that the substrate appears stiff, whereas the second process proceeds through probing of substrate mechanics by slower processes that involve larger force application.

Current models of substrate mechanosensing at the FA level assert that concurrent integrin engagement of the substrate and actin filaments through force-sensitive adaptor proteins underlies the fate of force transmission and adhesion cluster maturation (55,72,73). These “molecular clutch” models recently evolved to account also for a viscous element, revealing that viscosity contributes to cell response depending on the timescales involved and especially at lower substrate elasticities (23,69). Integrins engaged simultaneously with the ECM and actin will be subjected to forces arising from actin retrograde flow in the order of 10–100 nm/s (55,73,74). Assuming a soft substrate with a linear spring constant of 1 pN/nm, this flow translates to loading rates on the integrins and adaptor proteins in the order of 10–100 pN/s while the “clutch” is engaged. At these high rates and assuming an average force per integrin-actin linkage of a few pN (75,76), e.g., 5 pN, integrins will probe the elastomer surface in less than a second, which will thus “appear” stiff based on the frequency dependence of measured elasticity (2–20 Hz, Fig. 1). Thus, forces could stabilize integrin-FN bonds and lead to FA maturation; importantly, these forces may be myosin II independent and instead stem from actin polymerization dynamics (56).

Clutch-based models rely on molecular interactions and mechanisms at the scale of FAs and thus cannot alone explain the process of polarization at the cellular scale. Several studies have suggested that mechanosensing emerges instead from larger-scale mechanisms that integrate information from cytoskeletal forces over the dimension of the cell (66,77,78). Cells pull periodically on their ligands using multiple FAs, and thus, related forces arising from multiple cytoskeleton-integrin-ECM linkages are substantially higher in the nN range. Such forces presumably probe a larger length scale and the bulk of the substrate. Moreover, at the cell scale, cells use a lower frequency range (loading rate) to probe their substrate (79, 80, 81) compared with that described for FAs above; at these lower frequencies (0.01–0.1 Hz), the elastomer would appear softer (Fig. 1) and would not resist the forces applied by cells but instead flow as was observed. Obviously, for this cell-scale mechanosensing to occur, initial assembly and maturation of FAs is a prerequisite. Therefore, our proposal is compatible with previously proposed local and global models of cell mechanosensing.

We recognize some potential complications of attributing the phenotype of cells on the ultrasoft elastomers solely on substrate mechanical properties. First, cells deformed the morphology of the substrate at the cell scale, increasing the area of interaction and modifying the microtopography, which is known to effect cell behavior on its own right (82). Second, the ligand density was altered as a result of substrate deformation, another effect that is expected to alter the level of intracellular signaling (83). Future work using micropatterned, adhesive islands with areas of a typical cell, separated by nonadhesive regions, would control available area of interaction and adhesion ligand density to address these limitations.

In summary, the results of our study using well-characterized silicone elastomers suggest that cell mechanosensing is a multiscale process. Hence, efforts should be devoted to bridge different scales in models, account for substrate viscosity and deformability, and provide a thorough dynamic characterization of substrates used in mechanosensing studies.

Author Contributions

D.M. designed the study, performed experiments, analyzed data, supervised the project, and wrote the manuscript. T.H. analyzed experimental data and commented on the drafted manuscript. L.H. performed immunofluorescence microscopy and fibronectin ELISAs. J.P.S. supervised, secured funding for the project, and commented on the drafted manuscript.

Editor: Vivek Shenoy.